| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Две спиновые структуры на М*
Чтобы исследовать глобально поле  на М или хотя бы сказать, что мы понимаем под спинорным полем
на М или хотя бы сказать, что мы понимаем под спинорным полем  на М, необходимо сначала точно определить спиновую структуру пространства М. Это не тривиальная задача, ибо пространство М не односвязно (см. гл. 1, § 5). У пространства М с топологией
на М, необходимо сначала точно определить спиновую структуру пространства М. Это не тривиальная задача, ибо пространство М не односвязно (см. гл. 1, § 5). У пространства М с топологией  [формула (9.2.1)] имеется один-единственный «нестягиваемый» замкнутый контур, а все остальные могут быть непрерывной деформацией переведены в него или в кратный ему. Этот контур можно считать изотропной геодезической, или лучом,
[формула (9.2.1)] имеется один-единственный «нестягиваемый» замкнутый контур, а все остальные могут быть непрерывной деформацией переведены в него или в кратный ему. Этот контур можно считать изотропной геодезической, или лучом,  в М. (То, что ни один ненулевой контур, кратный контуру у, не может быть непрерывно деформирован в точку, должно быть ясно из сказанного в начале § 2.) Значит, в соответствии с изложенным в гл. 1, § 5 в пространстве М должно быть две (и только две) спиновые структуры, и их можно различать, указывая, как следует непрерывно переносить изотропный флаг по у, чтобы получить исходный спин-вектор, а не противоположный ему.
в М. (То, что ни один ненулевой контур, кратный контуру у, не может быть непрерывно деформирован в точку, должно быть ясно из сказанного в начале § 2.) Значит, в соответствии с изложенным в гл. 1, § 5 в пространстве М должно быть две (и только две) спиновые структуры, и их можно различать, указывая, как следует непрерывно переносить изотропный флаг по у, чтобы получить исходный спин-вектор, а не противоположный ему.
Может возникнуть мысль, что здесь существует «очевидный» выбор: считать спин-вектор неизменившимся, если его флаг переносится параллельно самому себе по контуру у. Но это значило бы игнорировать ряд тонкостей, связанных с переходом через гиперповерхность 9. Исходная связность Кристоффеля  определение которой опирается на метрику пространства
определение которой опирается на метрику пространства  , непригодна для определения параллельного переноса через 9. Чтобы все же перейти через 9, можно было бы воспользоваться связностью Кристоффеля
, непригодна для определения параллельного переноса через 9. Чтобы все же перейти через 9, можно было бы воспользоваться связностью Кристоффеля  для какой-нибудь другой метрики. Разумеется, тем самым мы допустили бы некоторый произвол, но суть проблемы не в этом. Рассмотрим изотропный флаг с флагштоком вдоль у: этого вполне достаточно, ибо если есть один ненулевой спин-вектор, определенный вдоль у, то его можно дополнить до спиновой системы отсчета вдоль у и все такие наборы, полученные в результате дополнения исходного спин-вектора до полной спиновой системы отсчета, непрерывно деформируемы друг в друга. Из формулы (7.1.20) следует, что условием параллельного переноса полотнища флага спинора
для какой-нибудь другой метрики. Разумеется, тем самым мы допустили бы некоторый произвол, но суть проблемы не в этом. Рассмотрим изотропный флаг с флагштоком вдоль у: этого вполне достаточно, ибо если есть один ненулевой спин-вектор, определенный вдоль у, то его можно дополнить до спиновой системы отсчета вдоль у и все такие наборы, полученные в результате дополнения исходного спин-вектора до полной спиновой системы отсчета, непрерывно деформируемы друг в друга. Из формулы (7.1.20) следует, что условием параллельного переноса полотнища флага спинора  вдоль направления
вдоль направления  его флагштока является действительность спинового коэффициента
его флагштока является действительность спинового коэффициента  Но, согласно формуле (5.6.29), это свойство сохраняется при конформных
Но, согласно формуле (5.6.29), это свойство сохраняется при конформных
масштабных преобразованиях, а значит, перенос полотнищ флага вдоль направления флагштока не зависит от выбора кристоф-фелевой связности  т. е. не зависит от выбора масштаба для метрики
т. е. не зависит от выбора масштаба для метрики  рассуждение явно носит локальный характер и не требует глобального определения спинора
рассуждение явно носит локальный характер и не требует глобального определения спинора 
Итак, у нас есть естественный конформно-инвариантный способ переноса таких изотропных флагов по контуру у. Упоминавшаяся выше тонкость состоит в следующем: когда мы проносим флаг таким способом по контуру у один раз, направление полотнища флага по возвращении в исходную точку меняется на обратное. Посмотрим, как это происходит.
Возьмем второй луч у, бесконечно мало смещенный относительно у так, что векторы смещения ортогональны направлению у, т. е. лучи у и у изопараметричны (см. гл. 7, § 1). Этому требованию отвечает, например, случай, когда у и у — два соседних луча одной изотропной гиперповерхности. Если полотнище нашего изотропного флага в этом случае направлено от у к у (т. е. является полуплоскостью направлений всех соединяющих у и у векторов смещений), то это полотнище переносится вдоль у параллельно самому себе. Теперь предположим, что, вместо того чтобы быть параллельным лучу у, луч у стал образующей светового конуса с вершиной в произвольной наперед заданной точке Р луча у. В смысле конформности это эквивалентно параллельному случаю, в котором Р лежит на У (см. § 1, 2). Так как параллельный перенос направлений полотнища флага вдоль у конформно-инвариантен, он определяется лучом у во втором случае столь же хорошо, как и в первом. Двигаясь вдоль луча у, можно обнаружить, что в вершине конуса Р векторы смещений, идущие от у к у, меняют свой знак (рис. 9.11). Поскольку изотропный конус имеет только одну вершину, такая ситуация больше нигде на у не повторяется. Все это означает, что параллельный перенос изотропного флага, скажем флага спинора  с флагштоком, расположенным вдоль
с флагштоком, расположенным вдоль  , по всему контуру у в М из точки, являющейся непосредственным будущим точки Р, в точку, являющуюся ее непосредственным прошлым, обращает направление флага. Только от нас зависит, считать ли это обращение эквивалентным отрицательному или положительному повороту на угол
, по всему контуру у в М из точки, являющейся непосредственным будущим точки Р, в точку, являющуюся ее непосредственным прошлым, обращает направление флага. Только от нас зависит, считать ли это обращение эквивалентным отрицательному или положительному повороту на угол  . С таким выбором и связаны упоминавшиеся выше две возможные спиновые структуры пространства М. Будем называть правовинтовой спиновой структурой пространства М структуру, гарантирующую, что следующее замкнутое движение флага спинора
. С таким выбором и связаны упоминавшиеся выше две возможные спиновые структуры пространства М. Будем называть правовинтовой спиновой структурой пространства М структуру, гарантирующую, что следующее замкнутое движение флага спинора  (т. е. «путь флага», см. гл. 1, § 5) должно еще и возвращать сам спинор
(т. е. «путь флага», см. гл. 1, § 5) должно еще и возвращать сам спинор  к его исходному, а не противоположному по знаку, значению: полотнище флага спинора
к его исходному, а не противоположному по знаку, значению: полотнище флага спинора  совершает один
совершает один

Рис. 9.11. Обращение направления полотнища флага при параллельном переносе в случае, когда луч у пересекается с гиперповерхностью  только один раз
только один раз
параллельный перенос из точки Р луча у по у в направлении будущего в точку, являющуюся непосредственным прошлым точки Р, а затем для восстановления связи с исходным положением оно совершает правый поворот на  вокруг направления флагштока, Вторая спиновая структура называется левовинтовой спиновой структурой пространства М. Отметим, что результаты таких двух допустимых движений изотропного флага различаются поворотом на
вокруг направления флагштока, Вторая спиновая структура называется левовинтовой спиновой структурой пространства М. Отметим, что результаты таких двух допустимых движений изотропного флага различаются поворотом на  а значит, они и в самом деле определяют различные спиновые структуры. Поскольку интуитивно смысл понятия «правого» поворота — относительно указывающего в будущее направления вдоль спинора
а значит, они и в самом деле определяют различные спиновые структуры. Поскольку интуитивно смысл понятия «правого» поворота — относительно указывающего в будущее направления вдоль спинора  — вполне ясен, обратившись к повороту вектора, касающегося римановой сферы
— вполне ясен, обратившись к повороту вектора, касающегося римановой сферы  и представляющего направление полотнища флага, можно дать и точное определение: «правый» — значит против часовой стрелки, если смотреть снаружи сферы. К тому же представление о правом вращении позволяет говорить о пространственной проекции изотропного направления будущего вдоль у.
и представляющего направление полотнища флага, можно дать и точное определение: «правый» — значит против часовой стрелки, если смотреть снаружи сферы. К тому же представление о правом вращении позволяет говорить о пространственной проекции изотропного направления будущего вдоль у.
Если нет каких-либо оснований предпочесть правый поворот левому или наоборот, что обе эти спиновые структуы совершенно равноправны. Фактически мы можем сказать следующее:
При пространственном отражении пространства  одна из двух таких спиновых структур заменяется другой.
одна из двух таких спиновых структур заменяется другой.
Напомним, что пространственные отражения переводят нештрихованные спиновые пространства в штрихованные, и наоборот. Связь этого факта с только что обсуждавшимися возможностями выбора спиновой структуры можно усмотреть в следующем. В случае нештрихованного спинора правый поворот на  вокруг флагштока эквивалентен преобразованию
вокруг флагштока эквивалентен преобразованию  а левый поворот на
а левый поворот на  — преобразованию
— преобразованию  общем случае правые и левые повороты на угол а эквивалентны преобразованиям
общем случае правые и левые повороты на угол а эквивалентны преобразованиям  соответственно). В случае же штрихованного спинора
соответственно). В случае же штрихованного спинора  соответствующие преобразования будут иметь вид
соответствующие преобразования будут иметь вид  Таким образом, если принять правовинтовую спиновую структуру пространства М (что мы, как правило, и будем делать), то обнаружится, что параллельный перенос спинора
Таким образом, если принять правовинтовую спиновую структуру пространства М (что мы, как правило, и будем делать), то обнаружится, что параллельный перенос спинора  по контуру V в направлении будущего в исходную точку приводит к первоначальному значению спинора
по контуру V в направлении будущего в исходную точку приводит к первоначальному значению спинора  умноженному на
умноженному на  (поскольку поворот на угол
(поскольку поворот на угол  восстанавливает первоначальное значение этого спинора). Та же процедура, примененная к спинору гадает его первоначальное значение, умноженное на
восстанавливает первоначальное значение этого спинора). Та же процедура, примененная к спинору гадает его первоначальное значение, умноженное на  Если же вместо этого принять левовинтовую спиновую структуру, то множители
Если же вместо этого принять левовинтовую спиновую структуру, то множители  и
и  поменяются местами. (Несколько иной подход можно найти в работе [377].)
поменяются местами. (Несколько иной подход можно найти в работе [377].)
Отметим следующее:
По отношению к отражению во времени пространства обе указанные спиновые структуры инвариантны, хотя такое отражение приводит к замене штрихованных спиноров нештрихованными и наоборот. В этом нетрудно убедиться. Если обратить направление времени, то последствия для движения, определяющего непрерывность спин-вектора, скажем правовинтовой спиновой структуры, будут двоякого рода. Во-первых, поскольку все движения теперь рассматриваются при обращенном времени, положительный поворот на угол  из-за этого обращается и становится отрицательным. Но тут же обращается и пространственное направление, по отношению к которому измеряется поворот, ибо направление будущего вдоль контура у теперь в пространственном отношении противоположно тому, что было. А это ведет ко второму обращению право-лево-вращательности, в результате чего правовинтовая спиновая структура при обращении времени фактически переходит в себя, что справедливо и для левовинтовой структуры.
из-за этого обращается и становится отрицательным. Но тут же обращается и пространственное направление, по отношению к которому измеряется поворот, ибо направление будущего вдоль контура у теперь в пространственном отношении противоположно тому, что было. А это ведет ко второму обращению право-лево-вращательности, в результате чего правовинтовая спиновая структура при обращении времени фактически переходит в себя, что справедливо и для левовинтовой структуры.
Комбинируя последствия пространственного отражения и независимого от него отражения во времени, получаем, что
Пространственно-временное отражение пространства М ведет к взаимной замене двух указанных спинорных структур.
(Отметим, однако, что пространственно-временные отражения не ведут к обмену местами штрихованных и нештрихованных спинорных индексов.)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
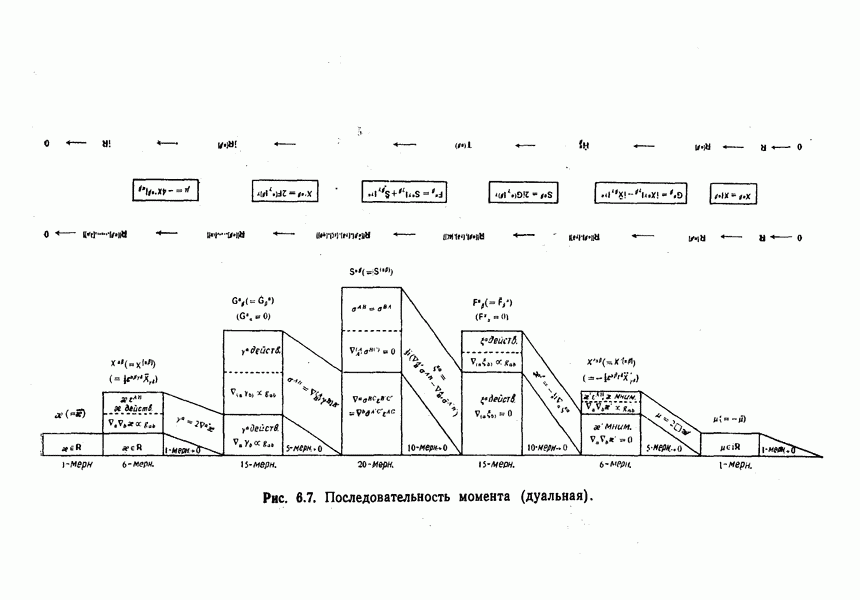
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
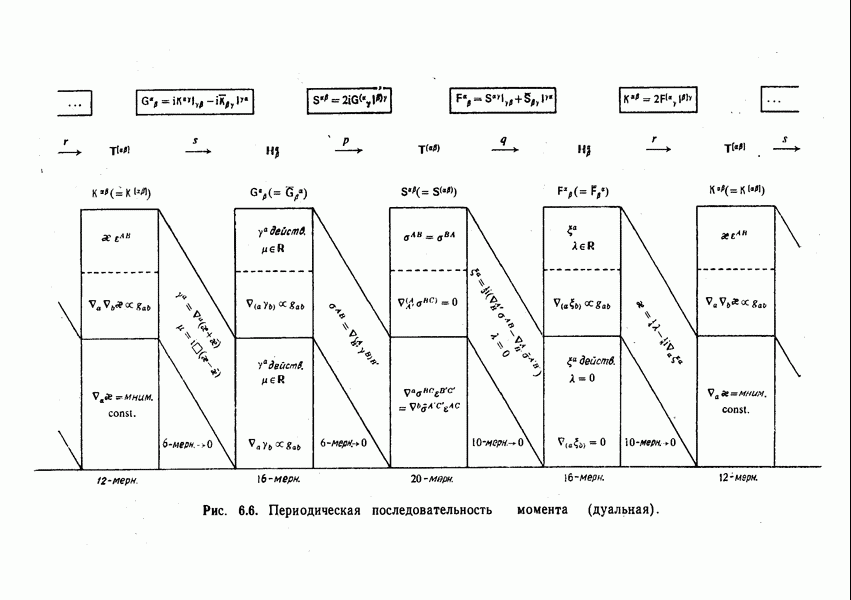
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
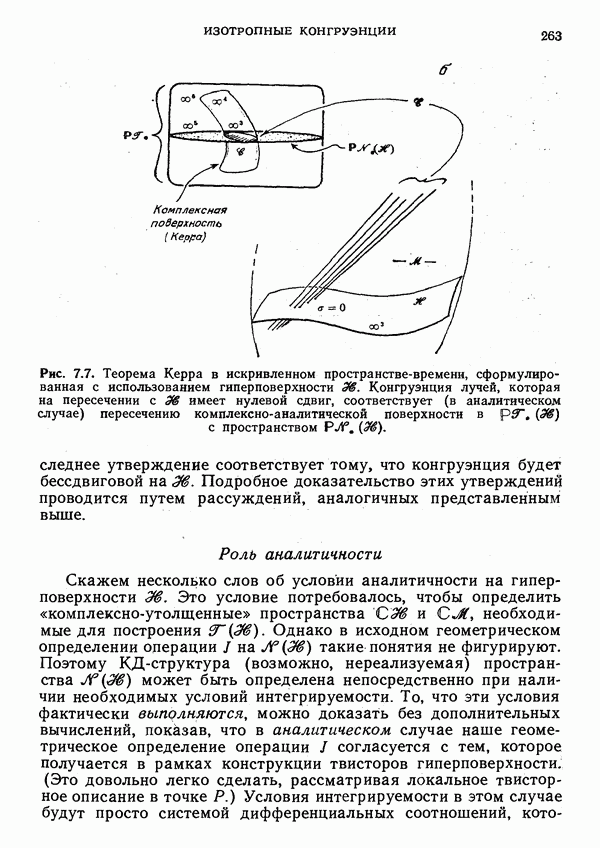
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
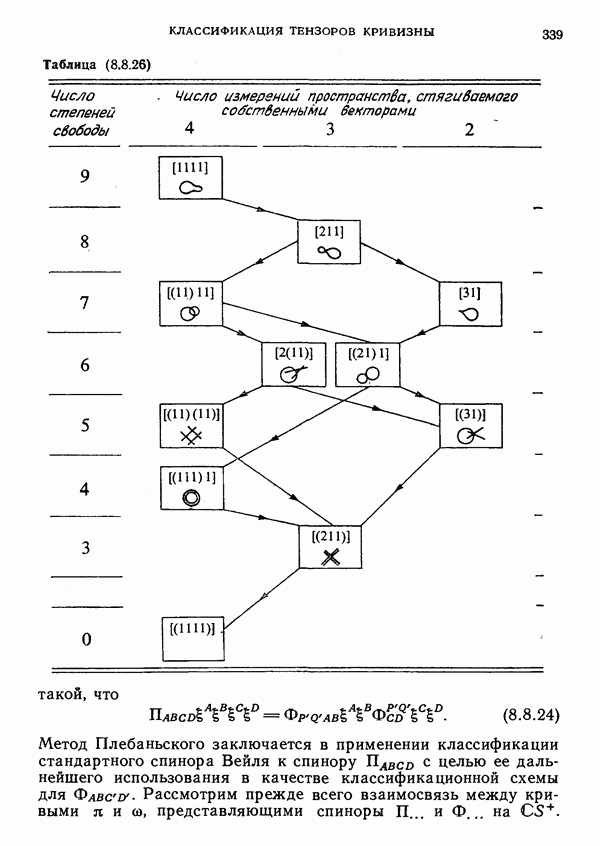
- 8. Классификация тензоров кривизны
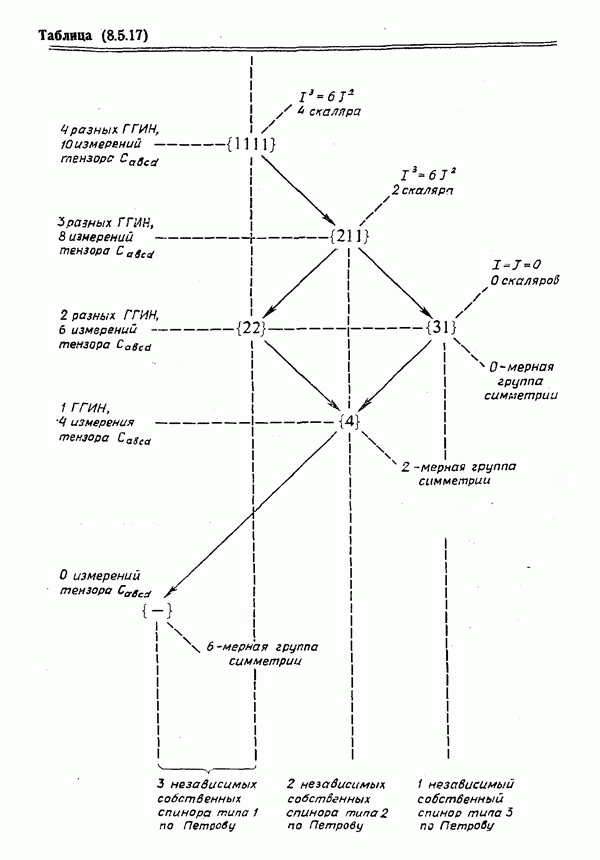
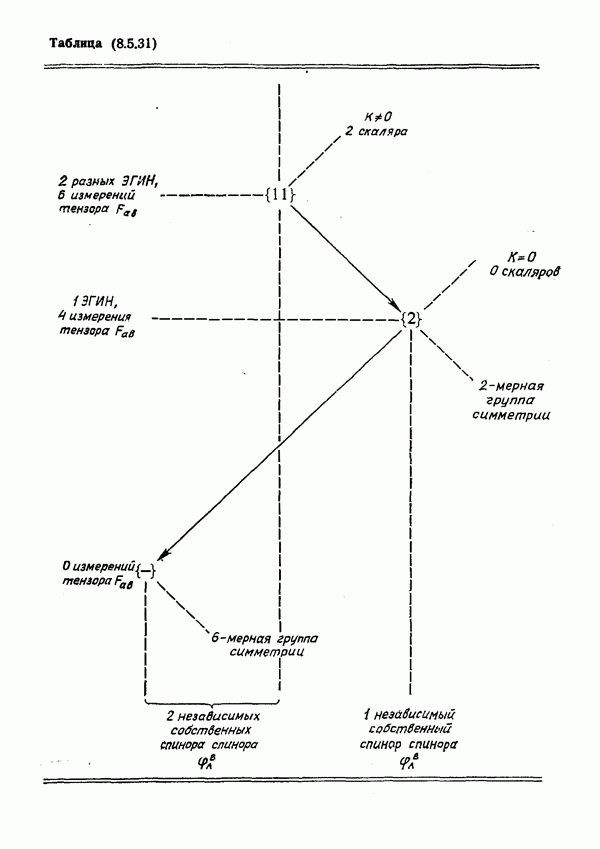
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
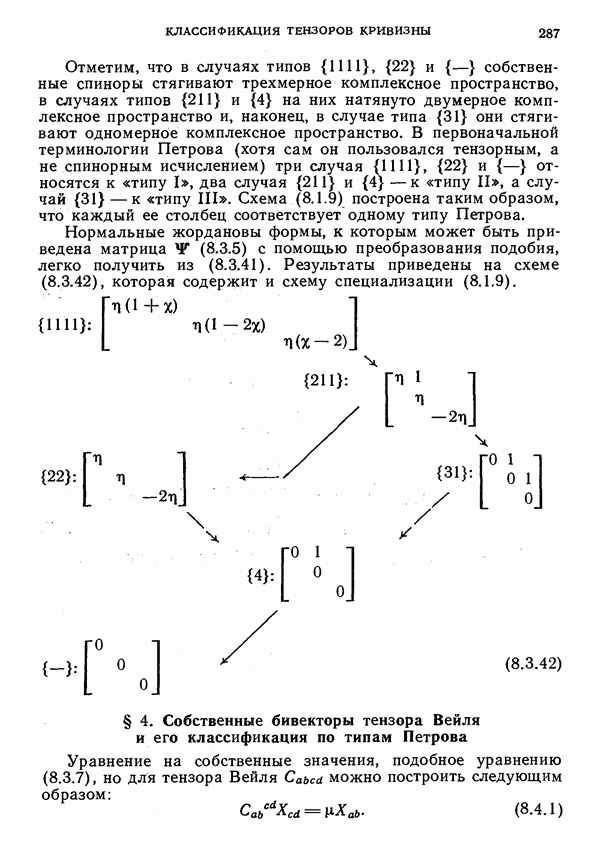
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
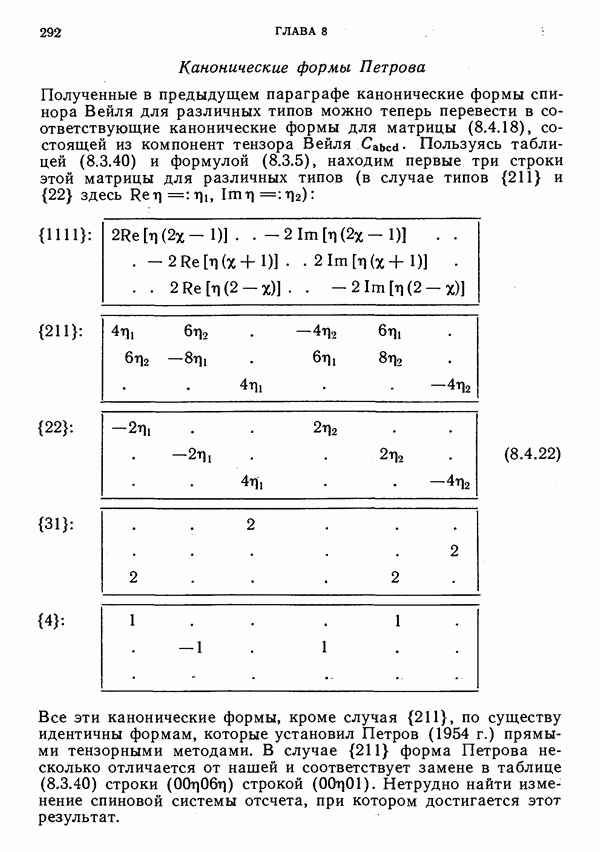
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
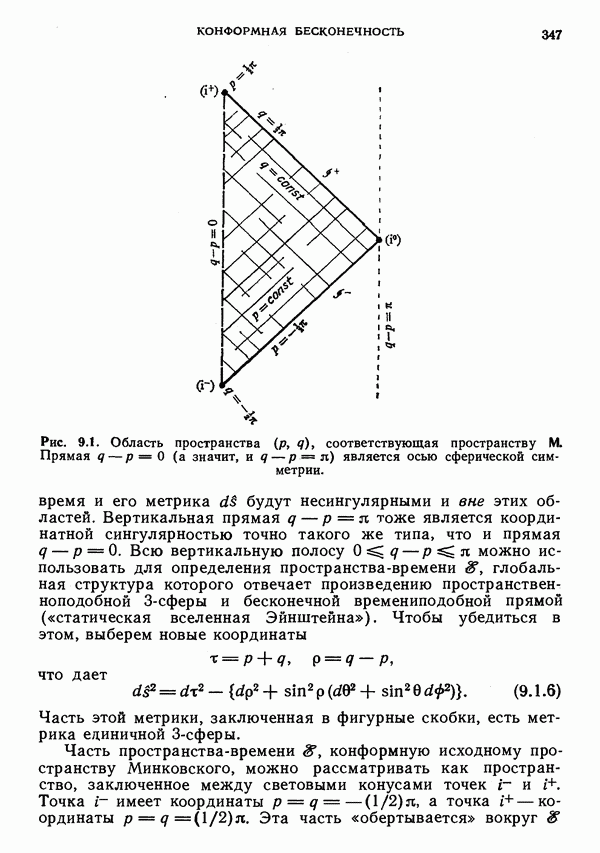
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
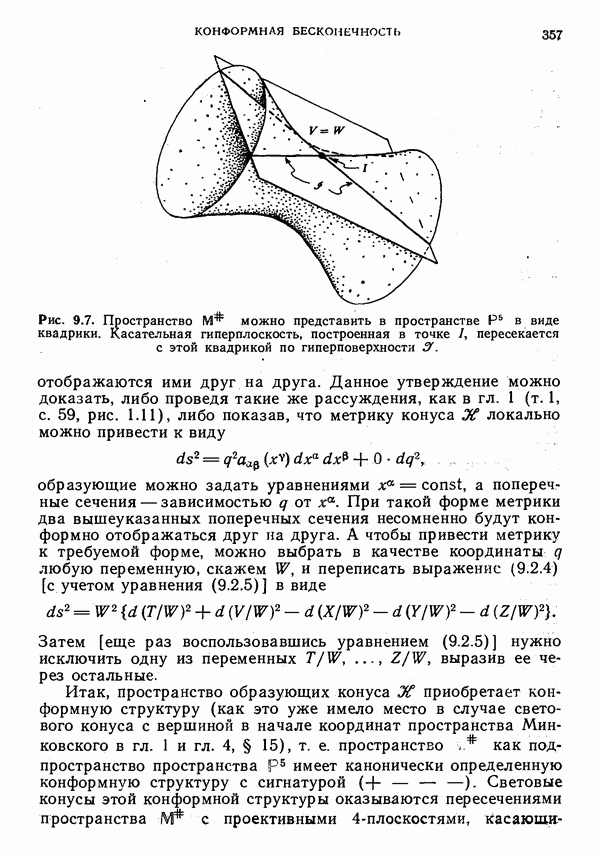
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
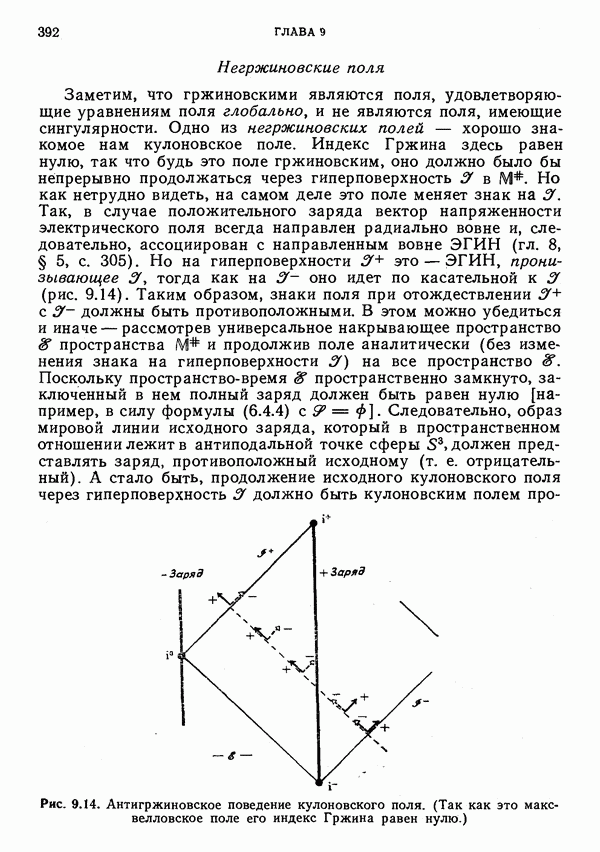
- Негржиновские поля
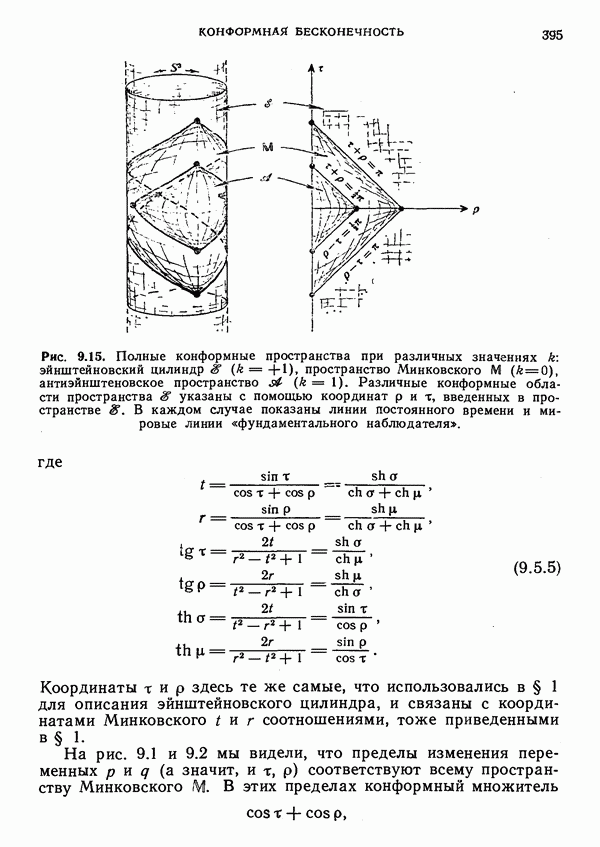
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
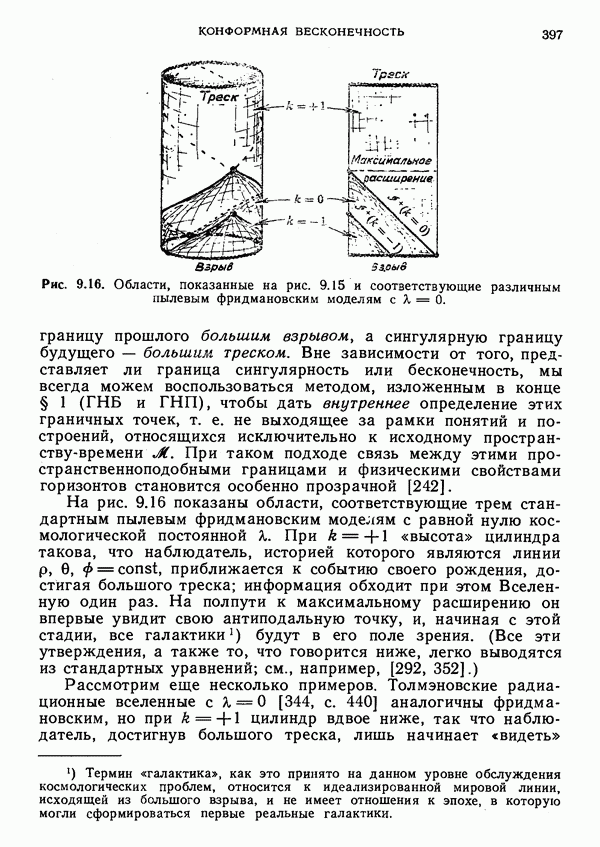
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература