| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение. Спиноры в n измерениях
Спиноры, которые рассматривались в этих двух томах нашей книги, есть частный случай некоего общего понятия. Понятие спинора определено для группы собственных вращений в пространстве произвольного числа измерений лис произвольной сигнатурой.
Спинорный метод оказывается особенно мощным в случае, когда  [и пространство-время имеет сигнатуру
[и пространство-время имеет сигнатуру  но он эффективен и при других значениях
но он эффективен и при других значениях  . И все же, поскольку размерность спинорного пространства растет экспоненциально с ростом
. И все же, поскольку размерность спинорного пространства растет экспоненциально с ростом  спинорный формализм, естественно, наиболее эффективен при сравнительно небольших значениях
спинорный формализм, естественно, наиболее эффективен при сравнительно небольших значениях  Далее, при четных
Далее, при четных  спиноры естественным образом разбиваются на более простые объекты — редуцированные спиноры, которые оказываются наиболее важными элементами теории. При
спиноры естественным образом разбиваются на более простые объекты — редуцированные спиноры, которые оказываются наиболее важными элементами теории. При  это будут знакомые нам пространства нештрихованных и штрихованных спин-векторов, каждое из которых двумерно. При
это будут знакомые нам пространства нештрихованных и штрихованных спин-векторов, каждое из которых двумерно. При  выбрав в качестве соответствующей ортогональной группы группу
выбрав в качестве соответствующей ортогональной группы группу  рассмотренную в гл. 9, § 2, мы увидим, что редуцированные спиноры будут (унивалентными) твисторами и дуальными твисторами — каждое из этих пространств четырехмерно. При
рассмотренную в гл. 9, § 2, мы увидим, что редуцированные спиноры будут (унивалентными) твисторами и дуальными твисторами — каждое из этих пространств четырехмерно. При  в фиксированной точке 2-поверхности в пространстве-времени это будут одномерные пространства скаляров со спиновым весом
в фиксированной точке 2-поверхности в пространстве-времени это будут одномерные пространства скаляров со спиновым весом  или —1/2 (так же как
или —1/2 (так же как  или
или  в гл. 9, § 9). При произвольном четном
в гл. 9, § 9). При произвольном четном  размерность пространства редуцированных спиноров будет равна
размерность пространства редуцированных спиноров будет равна  а размерность соответствующего пространства комбинированных (нередуцированных) спиноров есть
а размерность соответствующего пространства комбинированных (нередуцированных) спиноров есть  При произвольном нечетном
При произвольном нечетном  не существует инвариантной процедуры расщепления на более простые части и размерность спинового
не существует инвариантной процедуры расщепления на более простые части и размерность спинового
пространства равна  . В обоих случаях мы имеем двузначные спинорные объекты (см. т. 1, гл. 1, § 5), которые меняют свой знак при повороте на угол
. В обоих случаях мы имеем двузначные спинорные объекты (см. т. 1, гл. 1, § 5), которые меняют свой знак при повороте на угол  Группа спиновых преобразований
Группа спиновых преобразований  есть двулистное накрытие соответствующей собственной группы вращений
есть двулистное накрытие соответствующей собственной группы вращений  или
или 
В данном приложении мы кратко изложим алгебраические и геометрические основы теории спиноров в  -мерном пространстве. (За подробностями же отсылаем читателя к классическим работам [45, 33]; см. также [346, 347, 55, 284, 2, 178].)
-мерном пространстве. (За подробностями же отсылаем читателя к классическим работам [45, 33]; см. также [346, 347, 55, 284, 2, 178].)
Уравнение Клиффорда; у-матрицы
Обычно исходят из уравнения Клиффорда ( -Дирака)
-Дирака)

где  — (комплексные)
— (комплексные)  -матрицы
-матрицы  принимает значения, указанные выше),
принимает значения, указанные выше),  — компоненты некоторого (действительного или комплексного) л-мерного невырожденного симметричного тензора и I — единичная матрица
— компоненты некоторого (действительного или комплексного) л-мерного невырожденного симметричного тензора и I — единичная матрица  Вводя
Вводя  -мерные абстрактные индексы
-мерные абстрактные индексы  получаем несколько более инвариантную форму записи того же уравнения
получаем несколько более инвариантную форму записи того же уравнения

Объект  можно теперь мыслить как матрицу из элементов с абстрактными индексами, каждый из которых (из элементов) принадлежит
можно теперь мыслить как матрицу из элементов с абстрактными индексами, каждый из которых (из элементов) принадлежит  -мерному векторному пространству
-мерному векторному пространству  (или, быть может, модулю, если мы рассматриваем спинорные поля на
(или, быть может, модулю, если мы рассматриваем спинорные поля на  -многообразии) с невырожденным симметричным метрическим тензором
-многообразии) с невырожденным симметричным метрическим тензором  На данном этапе мы будем считать, что
На данном этапе мы будем считать, что  — комплексное векторное пространство (или модуль), так что вопрос о сигнатуре метрики
— комплексное векторное пространство (или модуль), так что вопрос о сигнатуре метрики  не имеет смысла. В дальнейшем мы кратко рассмотрим условия действительности и проанализируем зависимость структуры спинового пространства от выбора сигнатуры.
не имеет смысла. В дальнейшем мы кратко рассмотрим условия действительности и проанализируем зависимость структуры спинового пространства от выбора сигнатуры.
При полностью инвариантном подходе мы должны мыслить  не как матрицу в явном виде (или набор
не как матрицу в явном виде (или набор  не как матрицы
не как матрицы
в явном виде), а как элемент (элементы) некоторой абстрактной алгебры, порождающий линейные преобразования некоторого абстрактного пространства: спинового пространства. Таким образом, при желании можно ввести (скажем, нижние греческие) абстрактные индексы и написать

где абстрактные индексы  а относятся к спиновому пространству, которое является комплексным векторным пространством
а относятся к спиновому пространству, которое является комплексным векторным пространством  (или модулем
(или модулем  в случае спинорных полей на
в случае спинорных полей на  -многообразии). Мы предположим, что алгебра, генерируемая элементами
-многообразии). Мы предположим, что алгебра, генерируемая элементами  неприводима, и тогда оказывается, что
неприводима, и тогда оказывается, что  имеет размерность
имеет размерность  четное) или
четное) или  нечетное). [Минимальный размер матриц, удовлетворяющих соотношению
нечетное). [Минимальный размер матриц, удовлетворяющих соотношению  будет
будет  Уравнение
Уравнение  можно теперь переписать в виде
можно теперь переписать в виде

Если в пространстве  выбрать некоторый базис
выбрать некоторый базис  то в этом базисе явная реализация матрицы
то в этом базисе явная реализация матрицы  будет иметь вид
будет иметь вид

 — базис, дуальный базису
— базис, дуальный базису  и аналогичные выражения будут справедливы для
и аналогичные выражения будут справедливы для  Однако обозначение
Однако обозначение  или
или  не связано с выбором определенного базиса в пространстве
не связано с выбором определенного базиса в пространстве  и с тем же успехом может использоваться, если рис — абстрактные индексы или частично разлагаются в прямую сумму абстрактных индексов («блочно-абстрактно-индексные» матрицы).
и с тем же успехом может использоваться, если рис — абстрактные индексы или частично разлагаются в прямую сумму абстрактных индексов («блочно-абстрактно-индексные» матрицы).
Независимо от  в пространстве
в пространстве  можно выбрать базис
можно выбрать базис  и дуальный ему базис
и дуальный ему базис  который позволит нам осуществлять переход между величинами
который позволит нам осуществлять переход между величинами

в формуле  и более абстрактными объектами
и более абстрактными объектами  в формуле
в формуле 

Обычно выбирают этот базис так, чтобы метрика  была диагональной со значениями
была диагональной со значениями  (Поскольку пространство
(Поскольку пространство  комплексно, можно даже выбрать все ненулевые значения равными
комплексно, можно даже выбрать все ненулевые значения равными  но так как действительный случай мы будем рассматривать позднее, на этом этапе нам будет удобнее рассматривать оба знака). Тогда уравнение
но так как действительный случай мы будем рассматривать позднее, на этом этапе нам будет удобнее рассматривать оба знака). Тогда уравнение  будет означать, что
будет означать, что
различные матрицы  попарно антикоммутируют и квадраты их равны
попарно антикоммутируют и квадраты их равны  Алгебра Клиффорда
Алгебра Клиффорда  [57] (которая может быть комплексной) есть алгебра над
[57] (которая может быть комплексной) есть алгебра над  генерируемая величинами
генерируемая величинами  удовлетворяющими уравнениям
удовлетворяющими уравнениям  е. это комплексные полиномиальные функции таких величин
е. это комплексные полиномиальные функции таких величин  Элемент
Элемент

алгебры  представляет особый интерес. Отметим, что если
представляет особый интерес. Отметим, что если  — четное число, то он также антикоммутирует с каждой из величин
— четное число, то он также антикоммутирует с каждой из величин  а если
а если  — нечетное, то он коммутирует с каждой из этих величин. Более инвариантная форма записи элемента
— нечетное, то он коммутирует с каждой из этих величин. Более инвариантная форма записи элемента  такова:
такова:

или

где мы ввели альтернирующий тензор

с нормировкой  так что
так что

где  — число отрицательных значений (диагонального) тензора
— число отрицательных значений (диагонального) тензора  Отметим, что
Отметим, что

где  — «сигнатура» тензора
— «сигнатура» тензора 
Рассмотрим случай, когда  — нечетное, так что элемент
— нечетное, так что элемент  коммутирует со всеми элементами алгебры
коммутирует со всеми элементами алгебры  Предположим, что для рассматриваемой алгебры выполняется условие неприводимости; тогда в силу леммы Шура элемент
Предположим, что для рассматриваемой алгебры выполняется условие неприводимости; тогда в силу леммы Шура элемент  должен в этом случае быть пропорционален единичной матрице I:
должен в этом случае быть пропорционален единичной матрице I:

[формула  Коэффициент пропорциональности будет действительным (мнимым), если
Коэффициент пропорциональности будет действительным (мнимым), если  [или
[или  [в формуле
[в формуле  допускаются оба знака].
допускаются оба знака].
В случае же четного  антикоммутативность элемента
антикоммутативность элемента  с каждым из элементов
с каждым из элементов  означает, что эти элементы могут
означает, что эти элементы могут
быть представлены в виде

где  причем множитель
причем множитель  появляется, если
появляется, если  Величины
Величины  и
и  удовлетворяют соотношениям
удовлетворяют соотношениям

в силу равенства  Спиновое пространство
Спиновое пространство  расщепляется в прямую сумму
расщепляется в прямую сумму

где каждое из редуцированных спиновых пространств  имеет размерность
имеет размерность 
В формуле  приняты обозначения, при которых, заменив индексы
приняты обозначения, при которых, заменив индексы  и а у корневого символа индексами
и а у корневого символа индексами  или
или  или
или  и т. д., мы получим символ проекции интересующей нас величины на соответствующее редуцированное спиновое пространство. Явный вид проекционных операторов таков:
и т. д., мы получим символ проекции интересующей нас величины на соответствующее редуцированное спиновое пространство. Явный вид проекционных операторов таков:

так что в индексной форме находим выражения

[фиксировав по принятому соглашению неопределенный знак в формуле  ], которые позволяют получить указанные проекции на редуцированные спиновые пространства. Имеем
], которые позволяют получить указанные проекции на редуцированные спиновые пространства. Имеем

Алгебра Клиффорда и формы
Полная алгебра Клиффорда образована (конечными) суммами вида

Однако в силу формулы  достаточно рассматривать только антисимметризованные произведения
достаточно рассматривать только антисимметризованные произведения

Например:

и аналогичные (но более сложные) выражения для произведений высших порядков. Таким образом, коэффициенты в выражении  можно считать антисимметричными:
можно считать антисимметричными:

и весь ряд  обрывается на
обрывается на  слагаемом. Число формально независимых элементов алгебры Клиффорда равно полному числу независимых компонент тензоров
слагаемом. Число формально независимых элементов алгебры Клиффорда равно полному числу независимых компонент тензоров  [удовлетворяющих условию
[удовлетворяющих условию  т. е.
т. е.

Всякий элемент формальной алгебры можно рассматривать как набор, состоящий из  -формы, 1-формы, 2-формы и т.
-формы, 1-формы, 2-формы и т.  который часто формально записывают в виде (конечной) суммы
который часто формально записывают в виде (конечной) суммы

где

[здесь индексы опускаются, вообще говоря, с помощью метрики  и принято обозначение, введенное в формуле (4.3.10)]. Клиффордово умножение на выражениях
и принято обозначение, введенное в формуле (4.3.10)]. Клиффордово умножение на выражениях  [т. е. индуцированное произведениями выражений вида
[т. е. индуцированное произведениями выражений вида  будет дистрибутивным (и ассоциативным), причем клиффордово произведение
будет дистрибутивным (и ассоциативным), причем клиффордово произведение  -формы на
-формы на  -форму есть линейная комбинация слагаемых, каждое из которых получается вычислением ряда сверток в тензорном произведении форм с последующей антисимметризацией остающихся индексов. [Слагаемое без сверток имеет смысл внешнего произведения (4.3.13) двух
-форму есть линейная комбинация слагаемых, каждое из которых получается вычислением ряда сверток в тензорном произведении форм с последующей антисимметризацией остающихся индексов. [Слагаемое без сверток имеет смысл внешнего произведения (4.3.13) двух 
В том случае, когда  нечетное, из нашего предположения о неприводимости следует, что не все формально различные элементы алгебры Клиффорда линейно-независимы, поскольку величина
нечетное, из нашего предположения о неприводимости следует, что не все формально различные элементы алгебры Клиффорда линейно-независимы, поскольку величина  [формула
[формула  будет пропорциональна единичной матрице 1 [формула
будет пропорциональна единичной матрице 1 [формула  В самом деле, мы находим, что
В самом деле, мы находим, что

где (см. т. 1, с. 322)

причем число индексов  равно
равно  [индексы тензора
[индексы тензора  опускаются с помощью метрики
опускаются с помощью метрики  Если выполняется соотношение
Если выполняется соотношение  то мы находим, что каждая из форм
то мы находим, что каждая из форм  равна своей дуальной форме, умноженной на ±1 или
равна своей дуальной форме, умноженной на ±1 или  С учетом такого отождествления алгебра Клиффорда превращается в полную матричную алгебру (над С) матриц
С учетом такого отождествления алгебра Клиффорда превращается в полную матричную алгебру (над С) матриц  где, как
где, как
установлено выше,  силу формулы
силу формулы  Произвол в выборе знака в формуле
Произвол в выборе знака в формуле  дает два таких неэквивалентных представления, и формальная алгебра Клиффорда в точности представляется как прямая сумма этих двух матричных алгебр, если
дает два таких неэквивалентных представления, и формальная алгебра Клиффорда в точности представляется как прямая сумма этих двух матричных алгебр, если  четное.
четное.
Если  четное, то дополнительных отождествлений нет и полная алгебра Клиффорда может быть представлена полной матричной алгеброй
четное, то дополнительных отождествлений нет и полная алгебра Клиффорда может быть представлена полной матричной алгеброй  -матриц (над
-матриц (над  где
где  (как указано выше). Тем не менее полезно перейти к редуцированным спинорам, величинам вида
(как указано выше). Тем не менее полезно перейти к редуцированным спинорам, величинам вида  возникающим как элементы алгебры
возникающим как элементы алгебры  которые проектируются в нуль при действии как слева, так и справа оператором П [или П] [формула
которые проектируются в нуль при действии как слева, так и справа оператором П [или П] [формула  так что они изображаются слагаемыми с нечетным числом множителей у; а также величинами вида
так что они изображаются слагаемыми с нечетным числом множителей у; а также величинами вида  которые также будут элементами алгебры
которые также будут элементами алгебры  дающими нуль при действии слева [справа] оператором П и справа [слева] оператором П, так что они даются слагаемыми с нечетным числом множителей у.
дающими нуль при действии слева [справа] оператором П и справа [слева] оператором П, так что они даются слагаемыми с нечетным числом множителей у.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
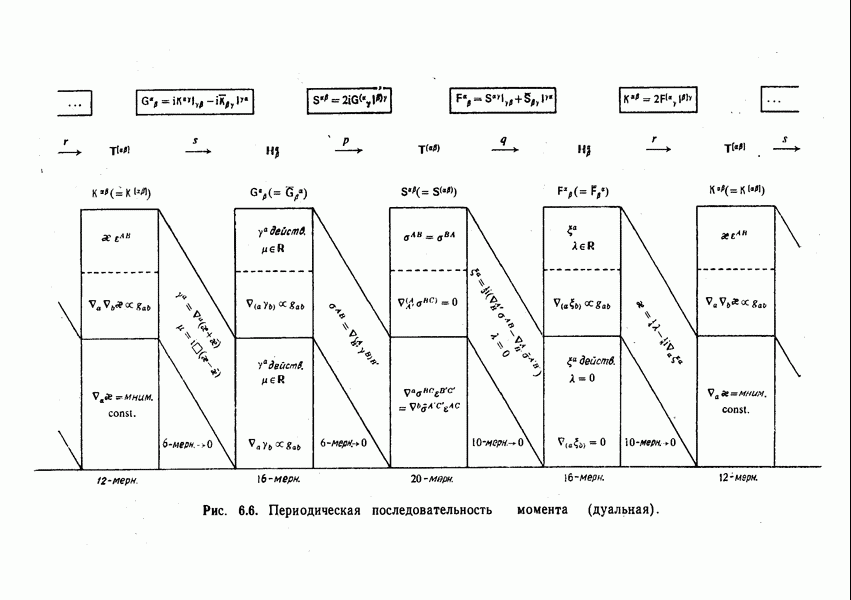
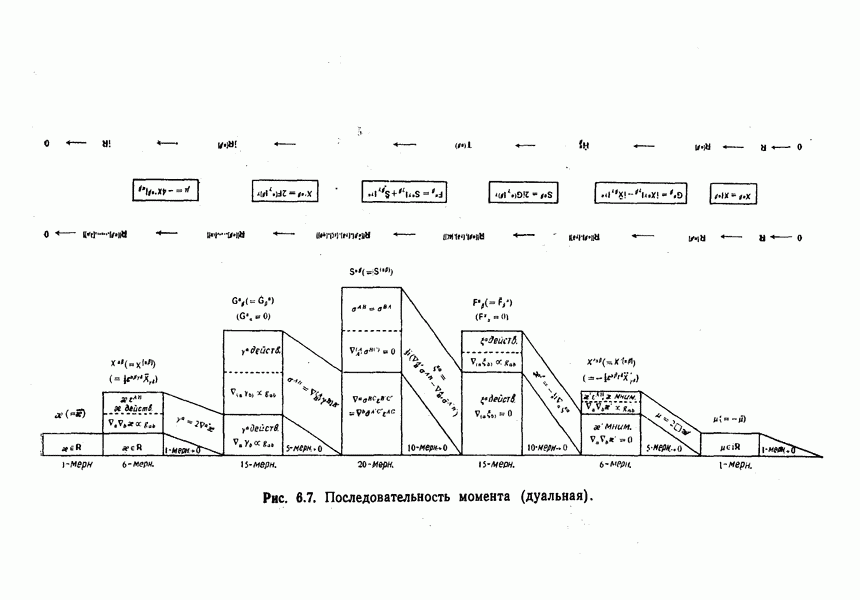
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
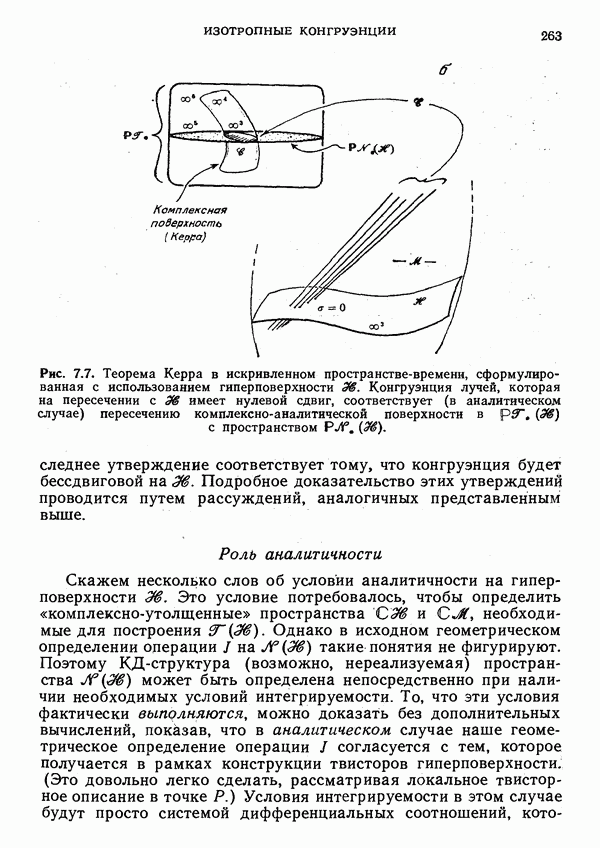
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
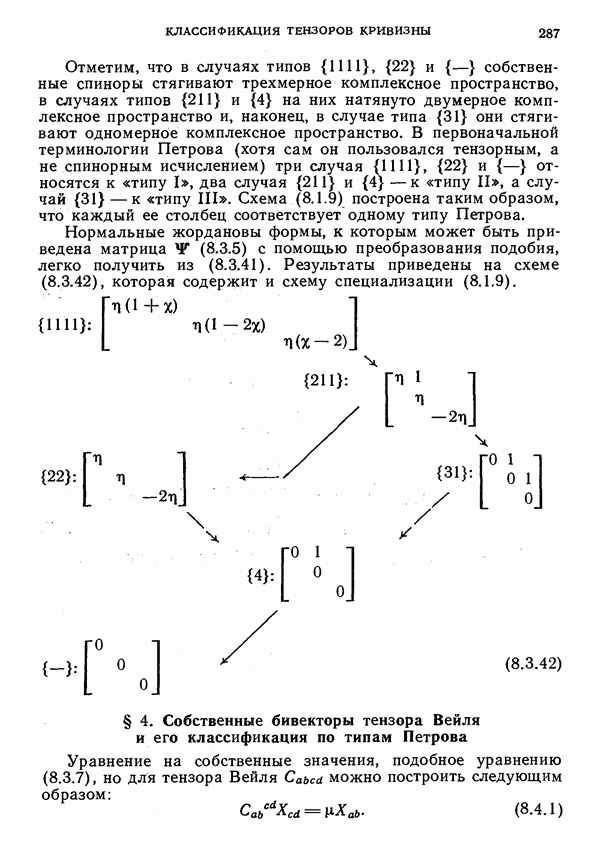
- 8. Классификация тензоров кривизны
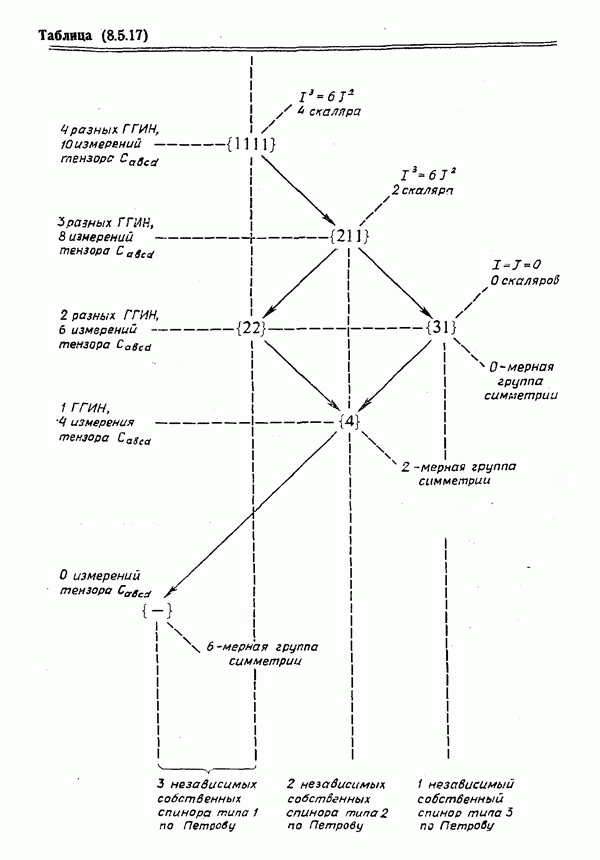
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
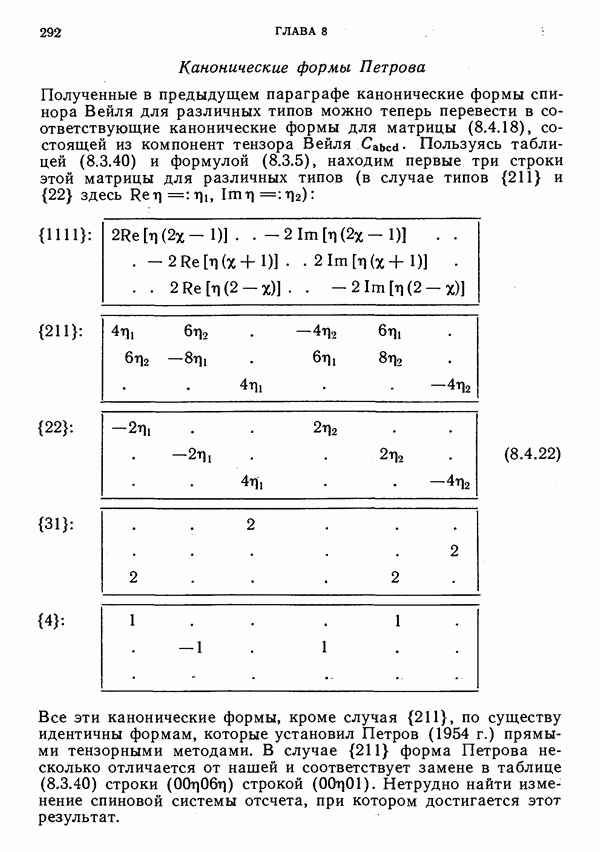
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
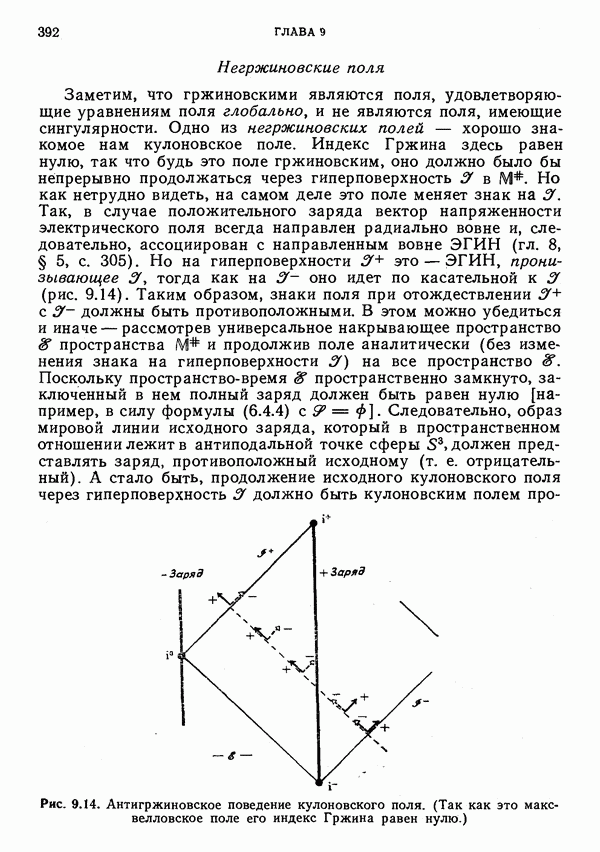
- Негржиновские поля
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература