| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Момент импульса на J+
Теперь проанализируем форму той части выражения (9.9.35), которая описывает момент импульса. Взяв для простоты  воспользовавшись формулами (9.8.83), (9.9.36) (1) и выполнив интегрирование по частям, получим
воспользовавшись формулами (9.8.83), (9.9.36) (1) и выполнив интегрирование по частям, получим 

Коэффициент  при
при  является спин-весовой сферической гармоникой с
является спин-весовой сферической гармоникой с  его линейная оболочка дает все такие гармоники. В этом конкретном отношении выражение (9.8.82) тождественно всем остальным выражениям, предложенным ранее. Но коэффициент
его линейная оболочка дает все такие гармоники. В этом конкретном отношении выражение (9.8.82) тождественно всем остальным выражениям, предложенным ранее. Но коэффициент  во втором члене есть нечто новое, поскольку он имеет более сложную угловую структуру, которая зависит от точного вида решений уравнения (9.9.36) (2). (Более ранние исследования см. в работах [332, 31, 32, 191, 287, 324, 371, 105].)
во втором члене есть нечто новое, поскольку он имеет более сложную угловую структуру, которая зависит от точного вида решений уравнения (9.9.36) (2). (Более ранние исследования см. в работах [332, 31, 32, 191, 287, 324, 371, 105].)
Чтобы лучше понять все это, рассмотрим представление решений уравнений (9.9.36), основанное на «потенциале» величины а. Поскольку величина о имеет спиновый вес, равный 2, из сказанного в т. 1, гл. 4, § 15 [формула (4.15.60)] следует, что уравнение

всегда имеет решение на  а кроме того конформно-инвариант-но на сфере [формула (4.15.32)], где к считается конформной плотностью с весом 1. В выборе величины к (со спин-весом 1), удовлетворяющей уравнению (9.9.83), имеется некоторый произвол: можно добавить слагаемое, содержащее только гармоники с
а кроме того конформно-инвариант-но на сфере [формула (4.15.32)], где к считается конформной плотностью с весом 1. В выборе величины к (со спин-весом 1), удовлетворяющей уравнению (9.9.83), имеется некоторый произвол: можно добавить слагаемое, содержащее только гармоники с  или
или  (четырехмерная свобода). Кроме того, конформную плотность к можно выбрать так, чтобы она была действительной в том и только в том случае, если а является чисто электрической величиной [формулы (9.8.92), (9.8.93)] [219], т. е. если поверхность 9 неконтортна.
(четырехмерная свобода). Кроме того, конформную плотность к можно выбрать так, чтобы она была действительной в том и только в том случае, если а является чисто электрической величиной [формулы (9.8.92), (9.8.93)] [219], т. е. если поверхность 9 неконтортна.
Теперь допустим, что  удовлетворяет соотношению
удовлетворяет соотношению  [формула (9.9.36) (1)]. Как мы уже знаем, следствием этого будет соотношение
[формула (9.9.36) (1)]. Как мы уже знаем, следствием этого будет соотношение  [формула (9.9.38)]. Таким образом, можно решить уравнение
[формула (9.9.38)]. Таким образом, можно решить уравнение  (формула (9.9.36) (2)), положив
(формула (9.9.36) (2)), положив

где

и  имеет спиновый вес, равный 1/2. Следовательно, уравнение (9.9.85) имеет два решения [формула (4.15.60)], что при любом выборе величины
имеет спиновый вес, равный 1/2. Следовательно, уравнение (9.9.85) имеет два решения [формула (4.15.60)], что при любом выборе величины  дает необходимую свободу в величине
дает необходимую свободу в величине  Если подставить выражение (9.9.84) в формулу (9.9.82), то эта свобода по
Если подставить выражение (9.9.84) в формулу (9.9.82), то эта свобода по  приводит в точности к тому типу свободы, который мы и ожидали: при всяком смещении начала, относительно которого берется момент импульса, к моменту импульса добавляются величины, кратные 4-импульсу [формулы (6.3.3), (9.9.51)]. Угловая зависимость коэффициента
приводит в точности к тому типу свободы, который мы и ожидали: при всяком смещении начала, относительно которого берется момент импульса, к моменту импульса добавляются величины, кратные 4-импульсу [формулы (6.3.3), (9.9.51)]. Угловая зависимость коэффициента  в выражении (9.9.82) в этом смысле является зависимостью от угловых интегралов величины а. Это самое главное, в чем наше [259] выражение (9.9.82) отличается от предложенных ранее (см. также [77]).
в выражении (9.9.82) в этом смысле является зависимостью от угловых интегралов величины а. Это самое главное, в чем наше [259] выражение (9.9.82) отличается от предложенных ранее (см. также [77]).
Причиной данного расхождения является принятая в ранних работах иная точка зрения на «начало», относительно которого следует вычислять момент импульса. Раньше полагали, что «начало» дается самим срезом  точно так же, как произвольный хороший срез гиперповерхности
точно так же, как произвольный хороший срез гиперповерхности  пространства М соответствует хорошо определенной точке в М, а именно вершине светового конуса, пересекающего
пространства М соответствует хорошо определенной точке в М, а именно вершине светового конуса, пересекающего  по этому срезу. Однако в случае плохого среза такая интерпретация в М неудовлетворительна. Если любое из этих ранних определений применить к плохому срезу гиперповерхности
по этому срезу. Однако в случае плохого среза такая интерпретация в М неудовлетворительна. Если любое из этих ранних определений применить к плохому срезу гиперповерхности  в пределе (линеаризованного) слабого поля в
в пределе (линеаризованного) слабого поля в  то получатся неверные результаты, тогда как наш подход специально выбран таким образом, чтобы в пределе слабого поля получались правильные результаты. В нашем подходе пространством допустимых (действительных) начал является пространство Минковского
то получатся неверные результаты, тогда как наш подход специально выбран таким образом, чтобы в пределе слабого поля получались правильные результаты. В нашем подходе пространством допустимых (действительных) начал является пространство Минковского  которое интуитивно можно представлять себе как «наилучшую оценку» местоположения плоского пространства начал при взгляде просто из окрестности частного среза гиперповерхности
которое интуитивно можно представлять себе как «наилучшую оценку» местоположения плоского пространства начал при взгляде просто из окрестности частного среза гиперповерхности 
Вектор Киллинга ассоциированный с любым конкретным выбором тензора  по формуле (9.9.6), фактически будет соответствовать вектору Киллинга в
по формуле (9.9.6), фактически будет соответствовать вектору Киллинга в  Сам срез 9 соответствует срезу
Сам срез 9 соответствует срезу  комплексифицированной гиперповерхности комплексифицированного пространства
комплексифицированной гиперповерхности комплексифицированного пространства  имеющей тот же сдвиг а, что и
имеющей тот же сдвиг а, что и  . Срез
. Срез  будет срезом гиперповерхности
будет срезом гиперповерхности  только в том случае, если а — чисто электрическая величина [формула (9.8.93)], так что
только в том случае, если а — чисто электрическая величина [формула (9.8.93)], так что  — неконтортная поверхность. В этом случае вектором определяется частный генератор группы
— неконтортная поверхность. В этом случае вектором определяется частный генератор группы  для
для  а значит [поскольку
а значит [поскольку  можно отождествить друг с другом при
можно отождествить друг с другом при  и частный генератор группы
и частный генератор группы  для
для  Когда величина о не чисто электрическая, мы получаем комплексный БМС-генератор. Однако этот генератор группы
Когда величина о не чисто электрическая, мы получаем комплексный БМС-генератор. Однако этот генератор группы  можно
можно
представить как векторное поле, тангенциальное поверхности  , только тогда, когда
, только тогда, когда  — хороший срез с вектором
— хороший срез с вектором  соответствующим лорендевым вращениям в
соответствующим лорендевым вращениям в  которые сохраняют срез
которые сохраняют срез  . (В этом отношении наш подход существенно отличается от всех предлагавшихся ранее.)
. (В этом отношении наш подход существенно отличается от всех предлагавшихся ранее.)
Однако остается одна серьезная трудность, которая возникает, если рассматривать эволюцию момента импульса системы во времени. Когда присутствует гравитационное излучение, пространство М (9), хотя и остается стандартным пространством Минковского при движении среза 9, тем не менее претерпевает в некотором смысле «сдвиг». Поэтому не совсем ясно, можно ли моменты импульса, отвечающие всем отдельным срезам гиперповерхности  считать «одним и тем же». Эта трудность связана с проблемой, обсуждавшейся в § 8 (см. рис. 9.25), где выяснилось, что процедура выделения (ограниченной) подгруппы Пуанкаре группы
считать «одним и тем же». Эта трудность связана с проблемой, обсуждавшейся в § 8 (см. рис. 9.25), где выяснилось, что процедура выделения (ограниченной) подгруппы Пуанкаре группы  тоже претерпевает некий сдвиг в промежутке между импульсами гравитационного излучения. Но сейчас мы находимся в несколько лучшем положении, поскольку можем точно проследить возникновение «сдвига» по мере того, как срез 9 движется вдоль Правда, строго говоря, интересующая нас подгруппа Пуанкаре «смещается в комплексную область», если а не является чисто электрической величиной,
тоже претерпевает некий сдвиг в промежутке между импульсами гравитационного излучения. Но сейчас мы находимся в несколько лучшем положении, поскольку можем точно проследить возникновение «сдвига» по мере того, как срез 9 движется вдоль Правда, строго говоря, интересующая нас подгруппа Пуанкаре «смещается в комплексную область», если а не является чисто электрической величиной,  это может произойти только тогда, когда пространство-время нестационарно [299, 220]).
это может произойти только тогда, когда пространство-время нестационарно [299, 220]).
Отметим, что этот «сдвиг» полностью обусловлен присутствием излучения и на него не оказывают влияния изменения в выборе среза в период «радиационного молчания» системы. Суть нашего подхода в том, что нам удалось скомпенсировать (полностью, когда поле излучения слабое) «плохой» выбор среза и таким образом в значительной мере «развязать» определение момента импульса от среза.
Проблемы, возникающие при попытках отождествления друг с другом различных пространств М (9), пока что не вполне понятны. Это вопрос адекватного отождествления друг с другом твисторных пространств  т. е. распространения пространства со временем. Свобода, имеющаяся первоначально при такого рода отождествлениях, в некоторой степени дополнительна к той свободе, что имеется при отборе подгруппы Пуанкаре группы
т. е. распространения пространства со временем. Свобода, имеющаяся первоначально при такого рода отождествлениях, в некоторой степени дополнительна к той свободе, что имеется при отборе подгруппы Пуанкаре группы  Если считать спиновые пространства
Если считать спиновые пространства  в точной последовательности (9.9.62) фиксированными — а это, как мы знаем, вполне законное предположение (см. текст, относящийся к формулам (9.9.42), (9.9.43)] — то указанная свобода относится к тому, каким способом в эту последовательность вводится средний член. Это соответствует свободе выполнения комплексной трансляции в пространстве
в точной последовательности (9.9.62) фиксированными — а это, как мы знаем, вполне законное предположение (см. текст, относящийся к формулам (9.9.42), (9.9.43)] — то указанная свобода относится к тому, каким способом в эту последовательность вводится средний член. Это соответствует свободе выполнения комплексной трансляции в пространстве  или действительной трансляции, когда считается, что задана еще и
или действительной трансляции, когда считается, что задана еще и
структура комплексного сопряжения пространства  Для точного распространения момента импульса потребовалось бы исключить эту свободу [312, 313].
Для точного распространения момента импульса потребовалось бы исключить эту свободу [312, 313].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
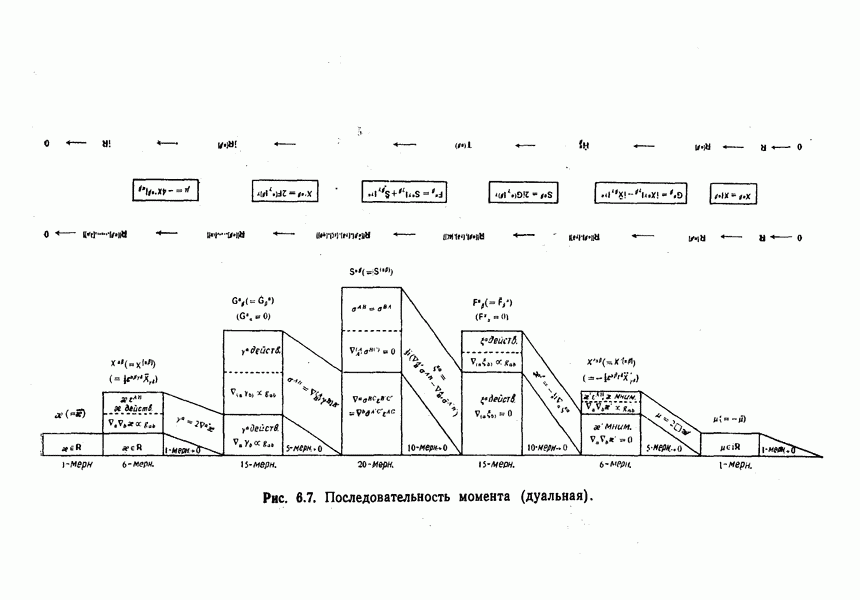
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
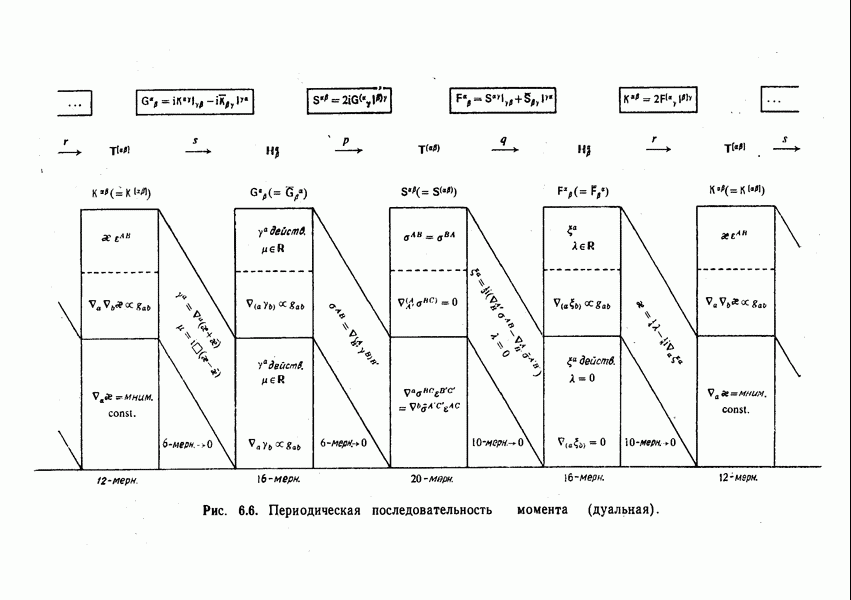
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
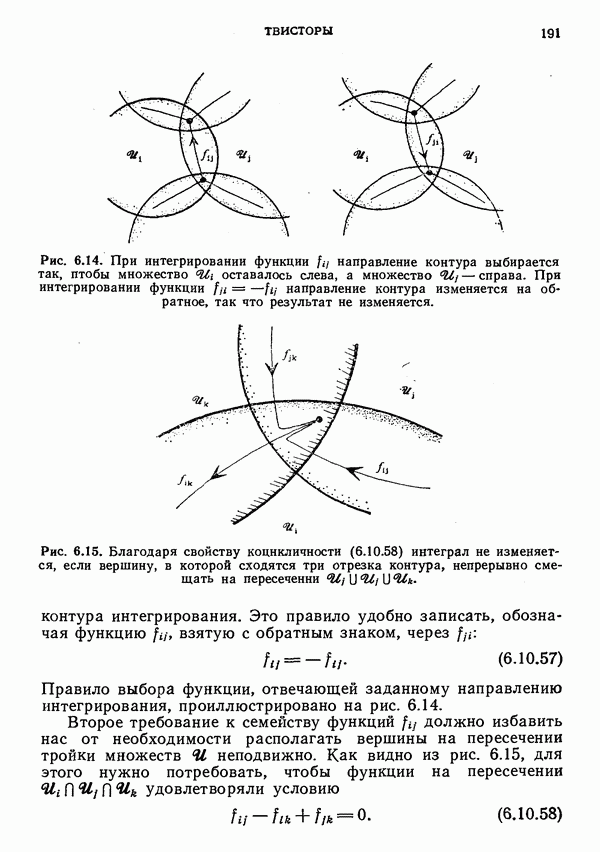
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
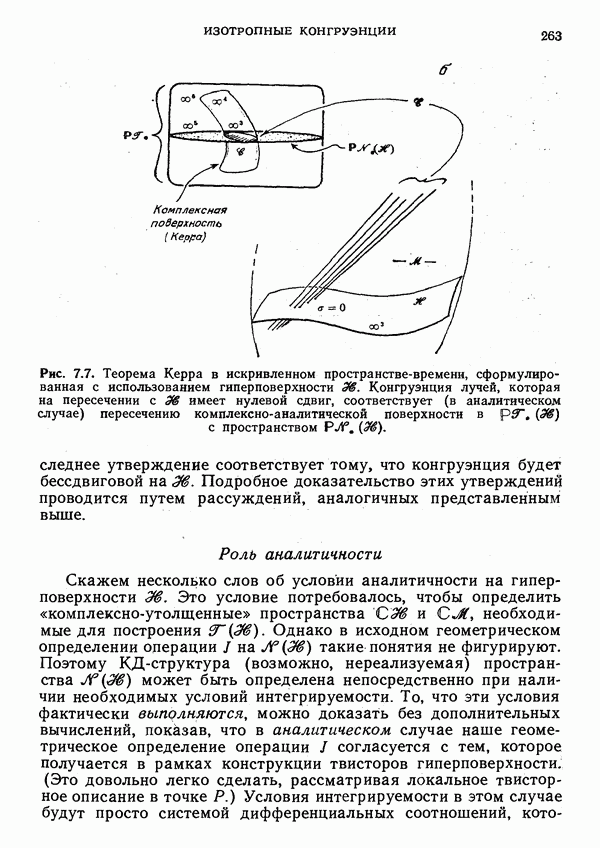
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
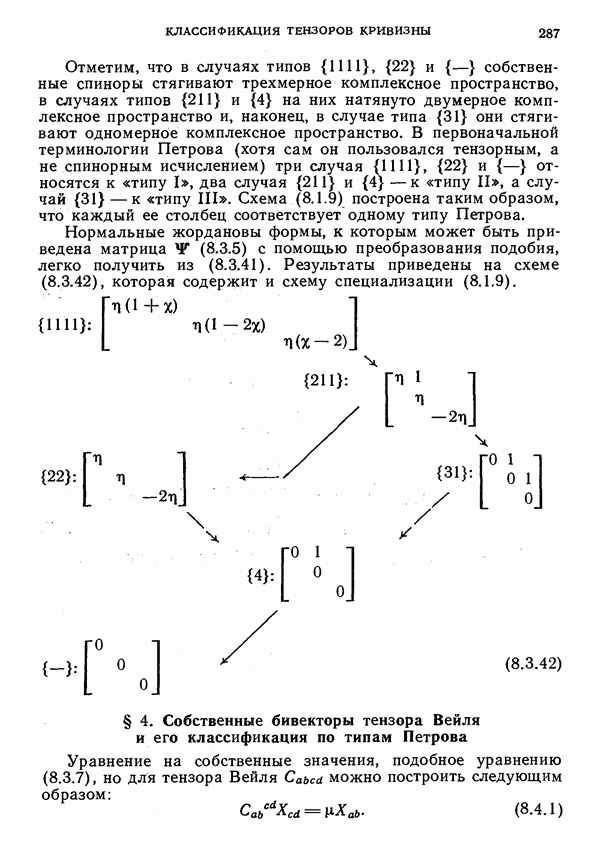
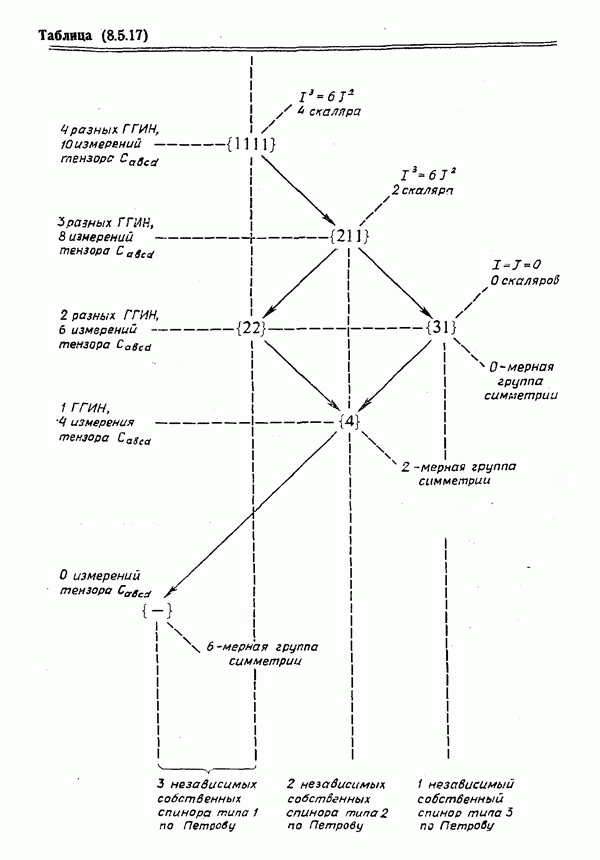
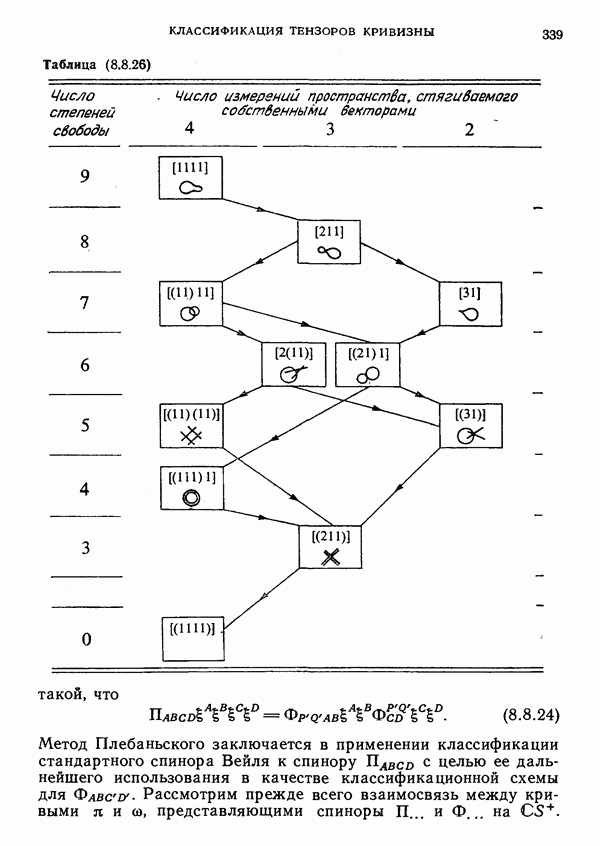
- 8. Классификация тензоров кривизны
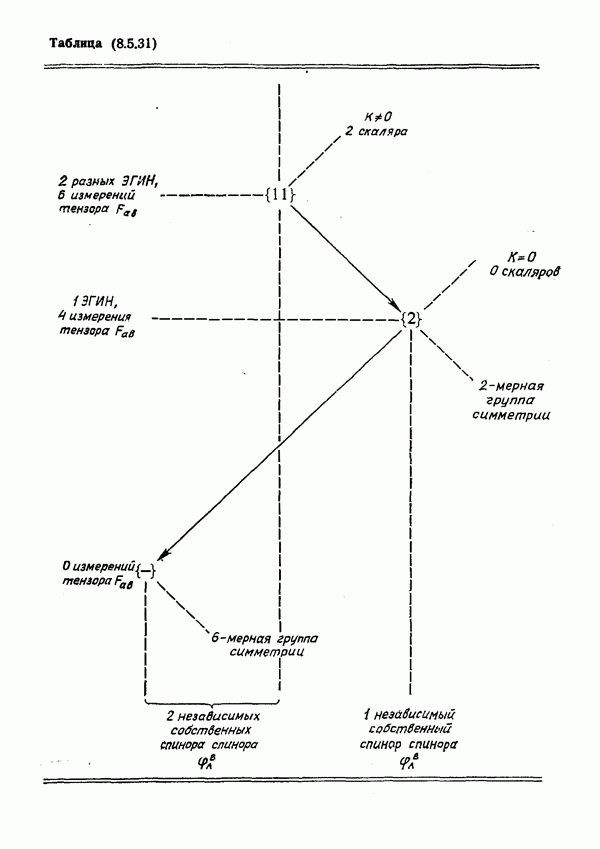
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
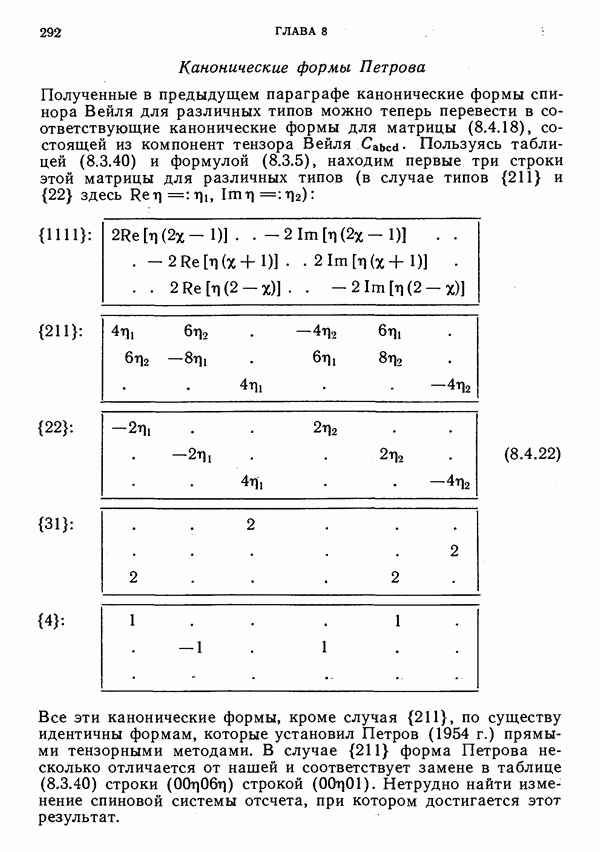
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
- 9. Конформная бесконечность
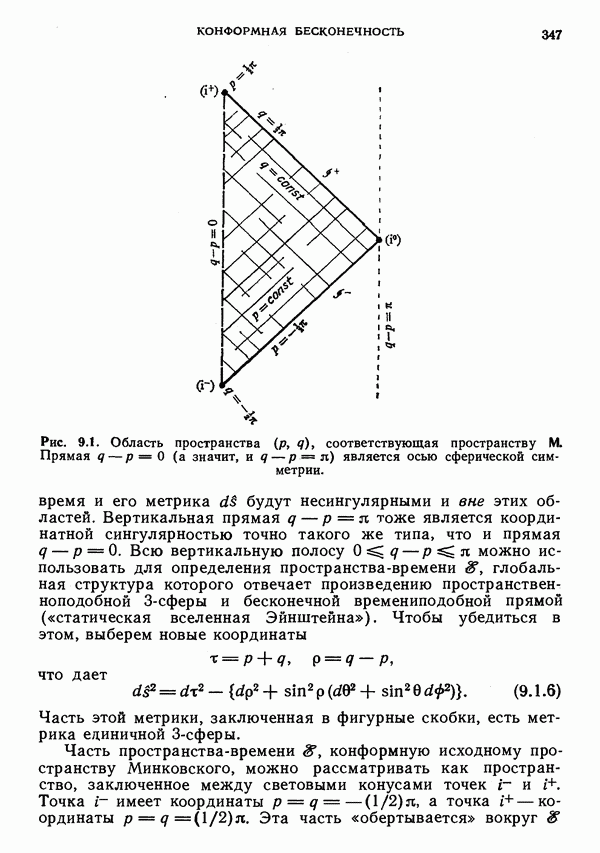
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
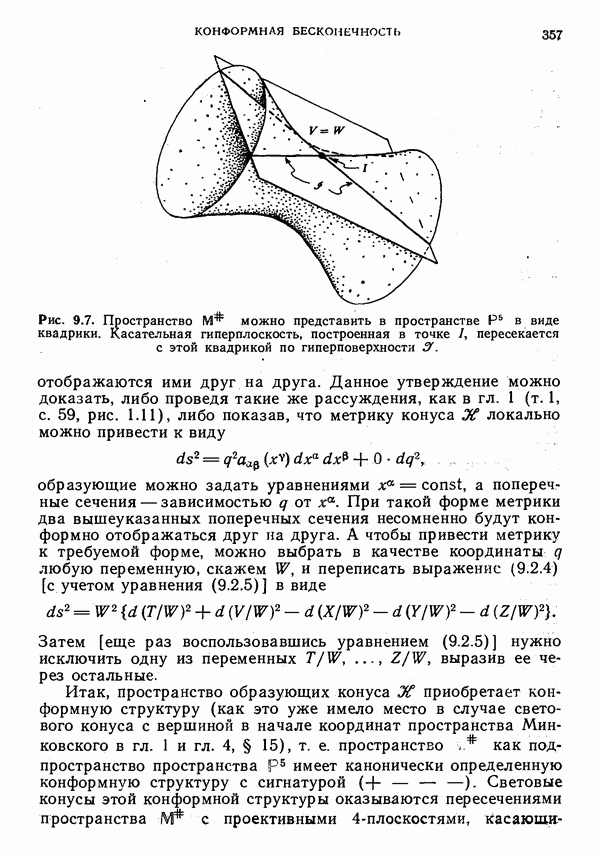
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
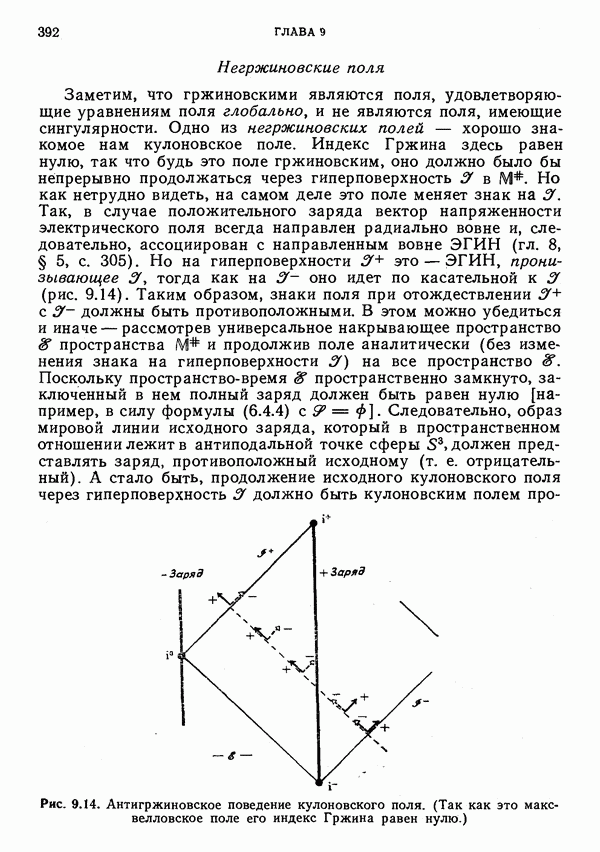
- Негржиновские поля
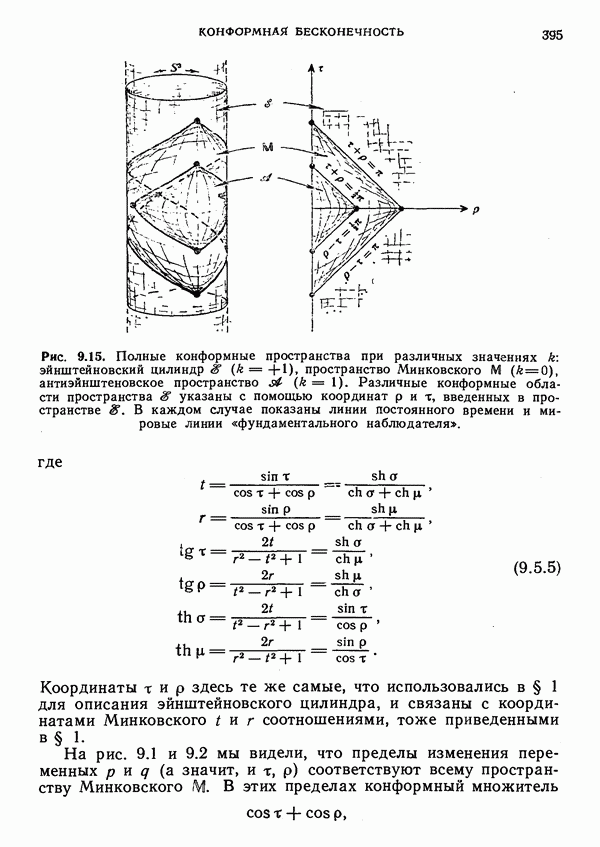
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
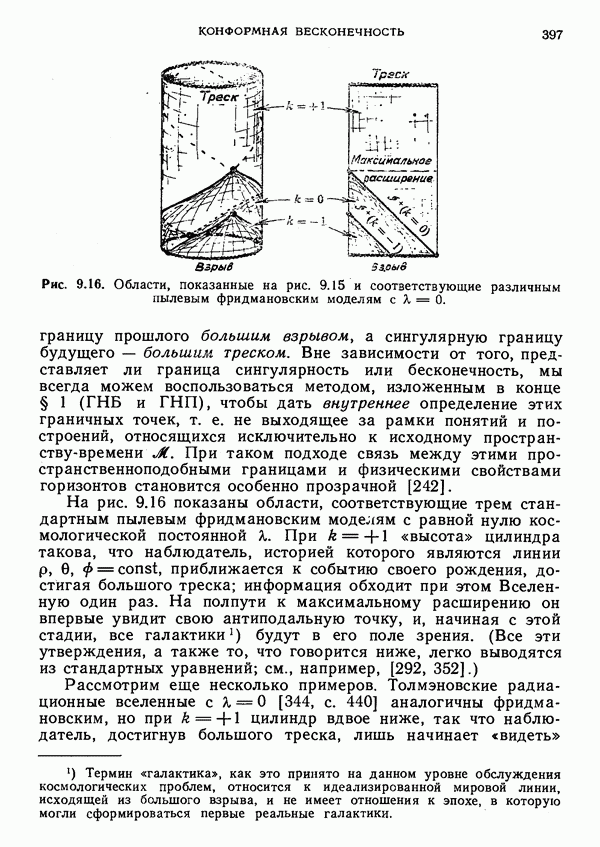
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература