| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Твисторы гиперповерхности
Рассмотрим теперь пространство  и выделим естественную КД-структуру, индуцированную в нем пространственноподобной гиперповерхностью
и выделим естественную КД-структуру, индуцированную в нем пространственноподобной гиперповерхностью  (По предположению гиперповерхность
(По предположению гиперповерхность  согласована с рассматриваемой областью в
согласована с рассматриваемой областью в  так, что каждый луч, отвечающий точкам этой области, пересекает данную гиперповерхность один и только один раз.) Касательное пространство
так, что каждый луч, отвечающий точкам этой области, пересекает данную гиперповерхность один и только один раз.) Касательное пространство  в точке
в точке  образовано лучами, «соседними» с
образовано лучами, «соседними» с  Голоморфное касательное пространство
Голоморфное касательное пространство  в точке
в точке  (рассматриваемое как действительное
(рассматриваемое как действительное

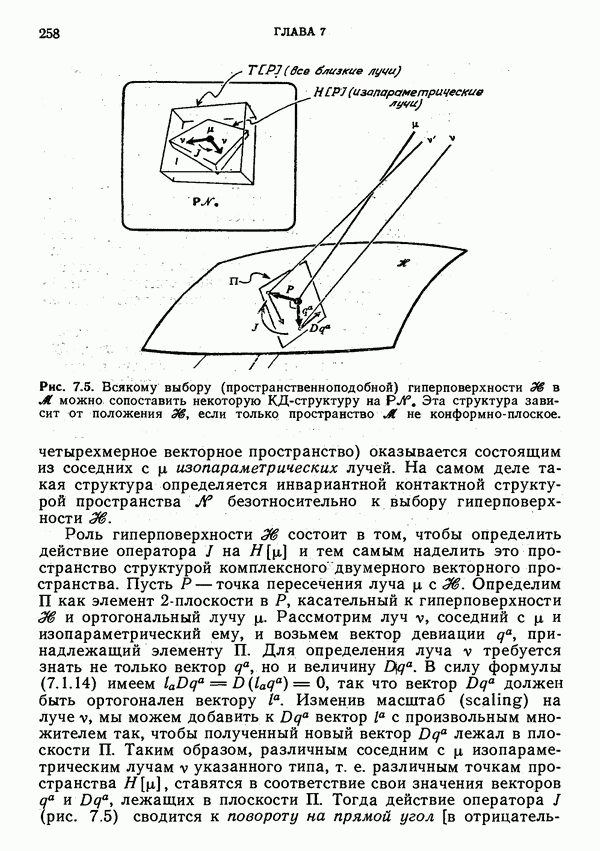
Рис. 7.5. Всякому выбору (пространственноподобной) гиперповерхности в  можно сопоставить некоторую КД-структуру на
можно сопоставить некоторую КД-структуру на  Эта структура зависит от положения
Эта структура зависит от положения  если только пространство
если только пространство  не конформно-плоское.
не конформно-плоское.
четырехмерное векторное пространство) оказывается состоящим из соседних с  изопараметрических лучей. На самом деле такая структура определяется инвариантной контактной структурой пространства
изопараметрических лучей. На самом деле такая структура определяется инвариантной контактной структурой пространства  безотносительно к выбору гиперповерхности
безотносительно к выбору гиперповерхности 
Роль гиперповерхности  состоит в том, чтобы определить действие оператора 1 на
состоит в том, чтобы определить действие оператора 1 на  и тем самым наделить это пространство структурой комплексного двумерного векторного пространства. Пусть Р — точка пересечения луча
и тем самым наделить это пространство структурой комплексного двумерного векторного пространства. Пусть Р — точка пересечения луча  Определим П как элемент 2-плоскости в Р, касательный к гиперповерхности
Определим П как элемент 2-плоскости в Р, касательный к гиперповерхности  и ортогональный лучу
и ортогональный лучу  Рассмотрим луч
Рассмотрим луч  соседний с
соседний с  и изопараметрический ему, и возьмем вектор девиации
и изопараметрический ему, и возьмем вектор девиации  принадлежащий элементу П. Для определения луча
принадлежащий элементу П. Для определения луча  требуется знать не только вектор
требуется знать не только вектор  но и величину
но и величину  . В силу формулы (7.1.14) имеем
. В силу формулы (7.1.14) имеем  так что вектор
так что вектор  должен быть ортогонален вектору
должен быть ортогонален вектору  Изменив масштаб (scaling) на луче
Изменив масштаб (scaling) на луче  мы можем добавить к
мы можем добавить к  вектор
вектор  с произвольным множителем так, чтобы полученный новый вектор
с произвольным множителем так, чтобы полученный новый вектор  лежал в плоскости П. Таким образом, различным соседним с
лежал в плоскости П. Таким образом, различным соседним с  изопараметрическим лучам
изопараметрическим лучам  указанного типа, т. е. различным точкам пространства
указанного типа, т. е. различным точкам пространства  ставятся в соответствие свои значения векторов
ставятся в соответствие свои значения векторов  лежащих в плоскости П. Тогда действие оператора
лежащих в плоскости П. Тогда действие оператора  (рис. 7.5) сводится к повороту на прямой угол
(рис. 7.5) сводится к повороту на прямой угол
[в отрицательном направлении вокруг пространственной проекции вектора  ] векторов
] векторов  в плоскости П [261].
в плоскости П [261].
На рис. 7.2 видно, что пучок соседних с изопараметрических лучей будет бессдвиговым в точке Р в том и только в том случае, если он инвариантен по отношению к действию оператора  определенного выше. Первые две диаграммы на рис. 7.2, изображающие конгруэнцию при наличии сходимости и вращения, инвариантны относительно поворота на прямой угол, тогда как третья, отвечающая наличию сдвига, этим свойством не обладает. Если бы при таком определении операции
определенного выше. Первые две диаграммы на рис. 7.2, изображающие конгруэнцию при наличии сходимости и вращения, инвариантны относительно поворота на прямой угол, тогда как третья, отвечающая наличию сдвига, этим свойством не обладает. Если бы при таком определении операции  она вводила на
она вводила на  реализуемую КД-структуру, то можно было бы доказать теорему о конгруэнциях лучей, бессдвиговых на пересечении с гиперповерхностью
реализуемую КД-структуру, то можно было бы доказать теорему о конгруэнциях лучей, бессдвиговых на пересечении с гиперповерхностью  типа теоремы Керра.
типа теоремы Керра.
Оказывается, что операция  действительно удовлетворяет условиям интегрируемости для КД-структуры (реализуемой, если гиперповерхность
действительно удовлетворяет условиям интегрируемости для КД-структуры (реализуемой, если гиперповерхность  вкладывается аналитически в аналитическое пространство-время
вкладывается аналитически в аналитическое пространство-время  ). Прямое доказательство этого было дано Ле-Брюном [181] и Брайантом 2). Здесь мы наметим схему другого доказательства, которое в аналитическом случае дает требуемое комплексное многообразие
). Прямое доказательство этого было дано Ле-Брюном [181] и Брайантом 2). Здесь мы наметим схему другого доказательства, которое в аналитическом случае дает требуемое комплексное многообразие  явно. Пространство
явно. Пространство  вкладывается в него как действительная гиперповерхность и наследует требуемую КД-структуру.
вкладывается в него как действительная гиперповерхность и наследует требуемую КД-структуру.
Многообразие  будем называть пространством твисторов гиперповерхности
будем называть пространством твисторов гиперповерхности  . В том случае, когда
. В том случае, когда  удовлетворяет в
удовлетворяет в  определенным условиям аналитичности, оно может быть получено следующим образом. (Подробнее см. в работах [250, 261].) Сначала, комплексифицируя гиперповерхность
определенным условиям аналитичности, оно может быть получено следующим образом. (Подробнее см. в работах [250, 261].) Сначала, комплексифицируя гиперповерхность  а также
а также  в окрестности этой гиперповерхности (т. е. выбирая локально-аналитические координаты и полагая, что они принимают комплексные значения с малой мнимой частью, см. гл. 6, § 9, с. 156), получаем несколько «утолщенные» комплексные многообразия
в окрестности этой гиперповерхности (т. е. выбирая локально-аналитические координаты и полагая, что они принимают комплексные значения с малой мнимой частью, см. гл. 6, § 9, с. 156), получаем несколько «утолщенные» комплексные многообразия  Далее рассмотрим комплексные линии в
Далее рассмотрим комплексные линии в  называемые
называемые  -кривыми, касательные векторы к которым (изотропные, комплексные) имеют вид
-кривыми, касательные векторы к которым (изотропные, комплексные) имеют вид

где  нормаль к гиперповерхности
нормаль к гиперповерхности  причем спинор о с переносится вдоль кривой параллельно:
причем спинор о с переносится вдоль кривой параллельно:

Уравнение (7.4.52) сводится к обычному дифференциальному уравнению, определяющему  -кривые.
-кривые.
Значение вектора (7.4.51) в том, что он автоматически является ортогональным нормали  , следовательно, касательным к пространству
, следовательно, касательным к пространству  а также допускает представление вида
а также допускает представление вида  . В плоском или конформно-плоском (комплексном) пространстве-времени
. В плоском или конформно-плоском (комплексном) пространстве-времени  -плоскости [см. текст после формулы (7.4.10), а также гл. 9, § 3] будут вполне изотропными комплексными 2-поверхностями, касательные векторы к которым имеют тот же вид, причем в каждой точке, считая спинор
-плоскости [см. текст после формулы (7.4.10), а также гл. 9, § 3] будут вполне изотропными комплексными 2-поверхностями, касательные векторы к которым имеют тот же вид, причем в каждой точке, считая спинор  фиксированным и варьируя
фиксированным и варьируя  мы получаем все касательное пространство. Если в каждой точке
мы получаем все касательное пространство. Если в каждой точке  -плоскости выбрать спинор
-плоскости выбрать спинор  специальным образом, а именно с помощью процедуры параллельного переноса, то полученным полем будет определяться
специальным образом, а именно с помощью процедуры параллельного переноса, то полученным полем будет определяться  -твистор. Формулы (7.4.51) и (7.4.52) дают проекцию указанных свойств на гиперповерхность
-твистор. Формулы (7.4.51) и (7.4.52) дают проекцию указанных свойств на гиперповерхность  так что, например, в случае конформно-плоского пространства
так что, например, в случае конформно-плоского пространства  решениями уравнения (7.4.52) будут кривые, являющиеся пересечениями гиперповерхности
решениями уравнения (7.4.52) будут кривые, являющиеся пересечениями гиперповерхности  с
с  -плоскостями, которые отвечают
-плоскостями, которые отвечают  -твисторам в
-твисторам в  . В общем случае, ввиду того что мы оперируем только с голоморфными величинами, решения уравнения (7.4.52) образуют комплексное 4-многообразие, совпадающее с искомым пространством
. В общем случае, ввиду того что мы оперируем только с голоморфными величинами, решения уравнения (7.4.52) образуют комплексное 4-многообразие, совпадающее с искомым пространством  Сами
Сами  -кривые есть точки комплексного 3-многообразия
-кривые есть точки комплексного 3-многообразия  Параметр, связанный с параллельно переносимым спинором
Параметр, связанный с параллельно переносимым спинором  дает недостающее комплексное измерение в пространстве
дает недостающее комплексное измерение в пространстве  Элементы этого пространства [или пространства
Элементы этого пространства [или пространства  имеют смысл [проективных] твисторов гиперповерхности.
имеют смысл [проективных] твисторов гиперповерхности.
Соответствующее пространство правильнее было бы обозначать символом  в отличие от пространства
в отличие от пространства  которое строится с помощью векторов
которое строится с помощью векторов

касательных к комплексным  -кривым в пространстве
-кривым в пространстве  причем параллельно переносится штрихованный спинор
причем параллельно переносится штрихованный спинор 

Комплексное сопряжение отображает  -кривые в
-кривые в  -кривые и переводит пространство
-кривые и переводит пространство  в него же.
в него же.
Всякая  -кривая, которая содержит действительную точку (точку гиперповерхности Ж), должна пересекаться с
-кривая, которая содержит действительную точку (точку гиперповерхности Ж), должна пересекаться с

Рис. 7.6. Связь между твисторами гиперповерхости, дуальными твисторами гиперповерхности и изотропными геодезическими. Вообще говоря, не существует простого соответствия между  -кривыми на различных гиперповерхностях. Это связано с тем, что КД-структура, показанная на рис. 7.5, в общем случае зависит от положения гиперповерхности
-кривыми на различных гиперповерхностях. Это связано с тем, что КД-структура, показанная на рис. 7.5, в общем случае зависит от положения гиперповерхности 
комплексно-сопряженной  -кривой в этой точке, поскольку это неподвижная точка операции комплексного сопряжения. (Если пространство
-кривой в этой точке, поскольку это неподвижная точка операции комплексного сопряжения. (Если пространство  достаточно «тонкое» и гиперповерхность
достаточно «тонкое» и гиперповерхность  — пространственноподобная, то
— пространственноподобная, то  -кривая пересекается с сопряженной а-кривой только в таких точках.) Элементы пространства
-кривая пересекается с сопряженной а-кривой только в таких точках.) Элементы пространства  [или
[или  которые отвечают
которые отвечают  -кривым (или
-кривым (или  -кривым, пересекающим Ж), называются изотропными (проективными) твисторами гиперповерхности, и то же относится к элементам пространства
-кривым, пересекающим Ж), называются изотропными (проективными) твисторами гиперповерхности, и то же относится к элементам пространства  [или
[или  ] для
] для  -кривых, пересекающих
-кривых, пересекающих  Пространства изотропных твисторов обозначаются через
Пространства изотропных твисторов обозначаются через  [или
[или  [или
[или  ] соответственно.
] соответственно.
Чтобы связать все с изложенным ранее, заметим, что в точке Р пересечения  -кривой с сопряженной ей
-кривой с сопряженной ей  -кривой (случай изотропного твистора гиперповерхности) мы можем положить
-кривой (случай изотропного твистора гиперповерхности) мы можем положить

(так как при комплексном сопряжении спинор  переходит в
переходит в  Далее, мы определяем
Далее, мы определяем  как луч (с масштабом, задаваемым посредством спинора
как луч (с масштабом, задаваемым посредством спинора  направление которого в точке Р определяется вектором
направление которого в точке Р определяется вектором  (рис. 7.6). Таким образом, пространство
(рис. 7.6). Таким образом, пространство  [или
[или  ] можно локально отождествить с
] можно локально отождествить с  и оно дает требуемую КД-структуру. Отметим, однако, что эта КД-структура зависит от выбора гиперповерхности
и оно дает требуемую КД-структуру. Отметим, однако, что эта КД-структура зависит от выбора гиперповерхности  и (если не считать случая конформно-плоского пространства Ж), вообще говоря, изменяется, если изменяется положение гиперповерхности
и (если не считать случая конформно-плоского пространства Ж), вообще говоря, изменяется, если изменяется положение гиперповерхности  в
в  . При этом согласование с
. При этом согласование с
инвариантной контактной структурой пространства  остается (в том смысле, что голоморфные касательные пространства по-прежнему переходят в пространства изопараметрических лучей, хотя их комплексная структура меняется).
остается (в том смысле, что голоморфные касательные пространства по-прежнему переходят в пространства изопараметрических лучей, хотя их комплексная структура меняется).
Важное свойство этих конструкций — конформная инвариантность:
Предложение
Пространства  и
и  а также формы
а также формы  и
и  описывающие инвариантную контактную структуру, не изменяются при конформном изменении масштаба
описывающие инвариантную контактную структуру, не изменяются при конформном изменении масштаба  метрики многообразия
метрики многообразия  котором выбрано преобразование
котором выбрано преобразование 
Доказательство. Конформная инвариантность пространств  следует из того, что при выбранном масштабном преобразовании мы имеем
следует из того, что при выбранном масштабном преобразовании мы имеем

в силу формул (5.6.2), (5.6.14) и (5.6.15), так что определяющее их уравнение (7.4.52) не изменяется. Инвариантность форм  и 2 при конформном изменении масштаба следует из их инвариантности при переносе вдоль луча
и 2 при конформном изменении масштаба следует из их инвариантности при переносе вдоль луча  поскольку, например, из формулы (7.4.56) видно, что условие параллельного переноса спинора
поскольку, например, из формулы (7.4.56) видно, что условие параллельного переноса спинора  вдоль луча
вдоль луча  не зависит от выбора масштаба на луче
не зависит от выбора масштаба на луче  . В самом деле, изменение масштаба вблизи одной точки луча
. В самом деле, изменение масштаба вблизи одной точки луча  не может, очевидно, привести к изменению значений рассматриваемых форм в удаленных точках. Инвариантность формы
не может, очевидно, привести к изменению значений рассматриваемых форм в удаленных точках. Инвариантность формы  явствует также из выражения (7.4.27), поскольку мы имеем
явствует также из выражения (7.4.27), поскольку мы имеем  а инвариантность формы 2 тогда следует из соотношения (7.4.35).
а инвариантность формы 2 тогда следует из соотношения (7.4.35).
Используя гиперповерхность  можно дать следующую формулировку теоремы Керра:
можно дать следующую формулировку теоремы Керра:
Если все рассматриваемые величины аналитичны, то конгруэнция лучей будет бессдвиговой на пересечении с гиперповерхностью  при том и только при том условии, что она определяется равенством нулю [однородной] голоморфной функции на
при том и только при том условии, что она определяется равенством нулю [однородной] голоморфной функции на  [или
[или  ].
].
Таким образом, конгруэнции, бессдвиговые на гиперповерхности  получаются как пересечение комплексной (голоморфной) гиперповерхности в
получаются как пересечение комплексной (голоморфной) гиперповерхности в  с
с  (рис. 7.7). С точки зрения геометрии КД-структуры на
(рис. 7.7). С точки зрения геометрии КД-структуры на  (см. рис. 7.5) это означает, что такое пересечение (КД-гиперповерхность) должно иметь касательные пространства, пересечения которых с пространством
(см. рис. 7.5) это означает, что такое пересечение (КД-гиперповерхность) должно иметь касательные пространства, пересечения которых с пространством  инвариантны относительно операции I.
инвариантны относительно операции I.

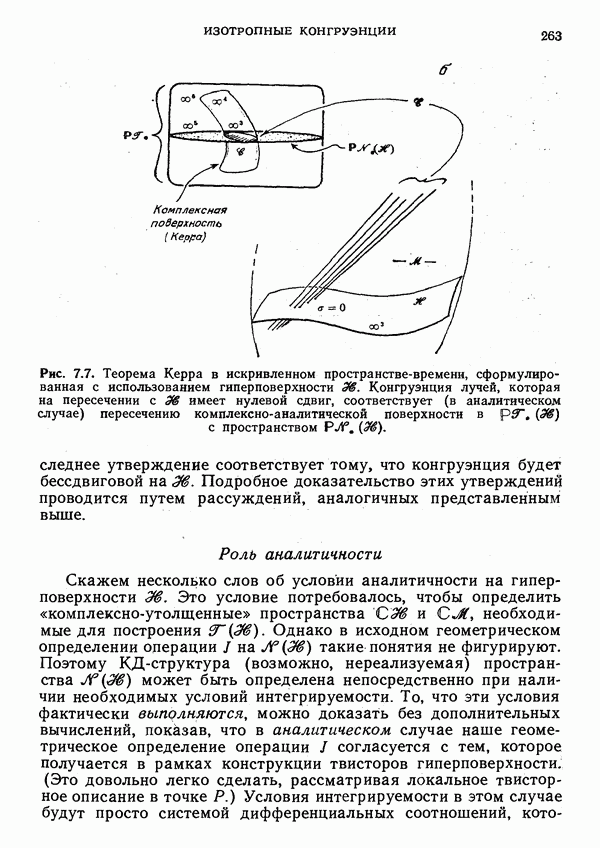
Рис. 7.7. Теорема Керра в искривленном пространстве-времени, сформулированная с использованием гиперповерхности  Конгруэнция лучей, которая на пересечении с
Конгруэнция лучей, которая на пересечении с  имеет нулевой сдвиг, соответствует (в аналитическом случае) пересечению комплексно-аналитической поверхности в
имеет нулевой сдвиг, соответствует (в аналитическом случае) пересечению комплексно-аналитической поверхности в  с пространством
с пространством 
Последнее утверждение соответствует тому, что конгруэнция будет бессдвиговой на  . Подробное доказательство этих утверждений проводится путем рассуждений, аналогичных представленным выше.
. Подробное доказательство этих утверждений проводится путем рассуждений, аналогичных представленным выше.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Краткое содержание тома 1
- § 5 (гл. 1). Спинорные объекты и спиновая структура
- § 2 (гл. 2). Формализм абстрактных индексов в тензорной алгебре
- § 3 (гл. 3). Операции симметрии
- Переход от спинорной к тензорной форме записи, и наоборот; преобразование дуальности
- Некоторые свойства тензоров и спиноров в точке
- Активные лоренцевы и спиновые преобразования
- Ковариантная производная
- Спиновые коэффициенты
- Спинорная форма кривизны
- Тождества для спинора Риччи
- Спинорные тождества Бианки
- Компоненты спинорной кривизны
- Модифицированный формализм спиновых коэффициентов
- Уравнения для модифицированных спиновых коэффициентов
- Геометрия пространственноподобных 2-поверхностей
- На изотропной гиперповерхности
- § 15 (гл. 4). Функции на метрической сфере
- Производные заряженных полей
- Поля Янга — Миллса
- Конформные изменения масштаба
- Безмассовые свободные поля
- Другие полевые уравнения
- Данные на изотропной гиперповерхности
- 6. Твисторы
- § 1. Твисторное уравнение и пространство его решений
- Твисторное уравнение
- Пространство твисторов
- Дуальные твисторы
- Твисторы высшей валентности
- Конформная инвариантность спиральности и скалярного произведения
- § 2. Некоторые геометрические аспекты твисторной алгебры
- Поле флагштоков спинора: конгруэнция Робинсона
- Отношение взаимности твисторов
- Комплексная геометрия
- Представление точек с помощью простых кососимметричных твисторов
- § 3. Твисторы и момент импульса
- Момент импульса произвольной системы
- Представление твистора с помощью одноиндексных твисторов
- § 4. Симметричные твисторы и безмассовые поля
- Общий случай, потенциалы
- Повышение спина
- Другие виды потенциалов; связь с оператором
- § 5. Конформные векторы Киллинга; сохраняющиеся величины и точные последовательности
- Спиноры: Законы сохранения
- Твисторное описание
- Связь с интегралами от источников в линейной гравитации
- Точные последовательности
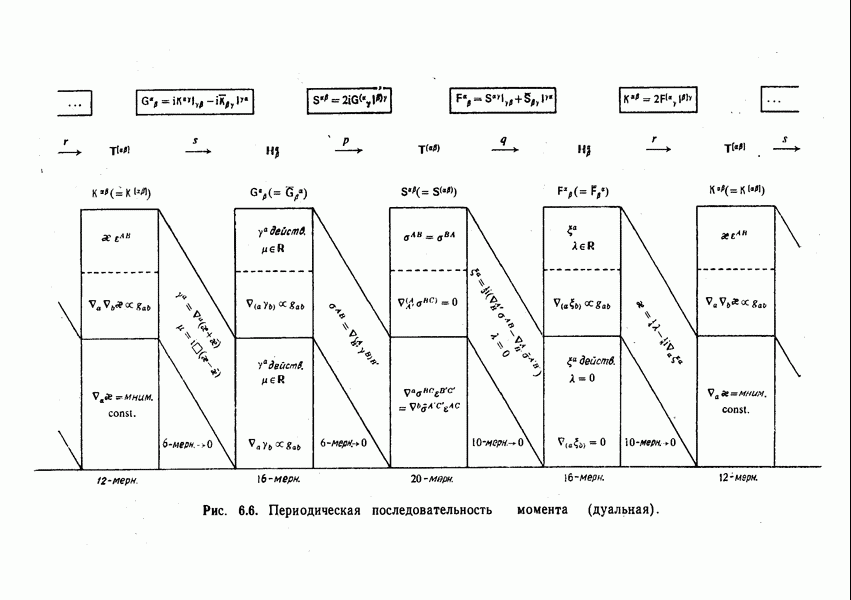
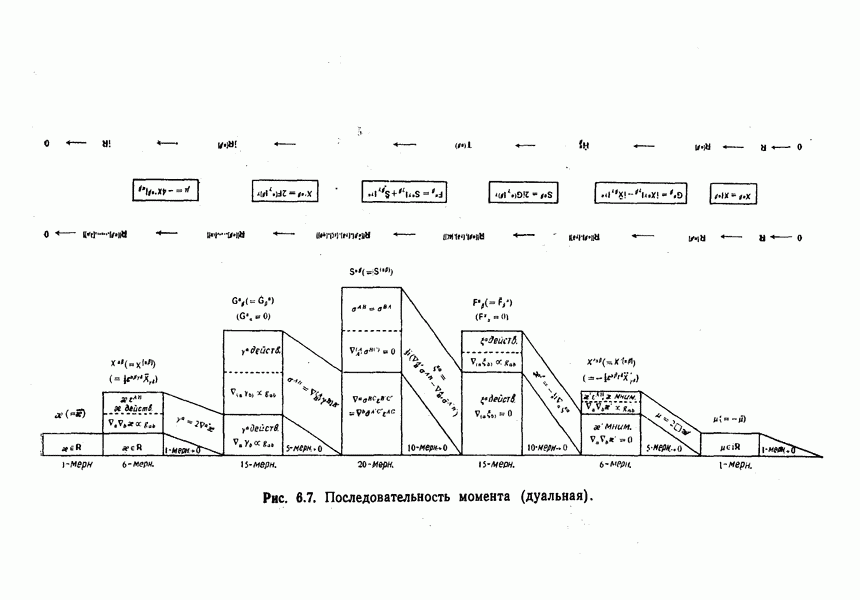
- Последовательности моментов
- Интегралы в линейной теории гравитации
- Спиноры: Десять интегралов, равных нулю
- Роль дуальности в последовательностях момента
- § 6. Производные Ли спиноров
- Связь с теорией твисторов
- § 7. Интегралы движения частиц; конформно-инвариантные операторы
- Спиноры Киллинга для вакуумных решений типа (22)
- Свойства решения Керра
- Конформно-инвариантные первые производные
- Твисторные решения различных уравнений
- Повторные операции; разрешения уравнений
- § 8. Кривизна и конформные преобразования
- Конформные свойства величин
- Конформные отображения плоских пространств
- Конформно-инвариантное волновое уравнение и оператор
- Конформно-инвариантный тензор Баха
- § 9. Локальные твисторы
- Условие совместности для твисторного уравнения
- Определение локального твистора
- Перенос локального твистора
- Кривизна в пространстве локальных твисторов
- Нулевая кривизна Вейля как свойство конформно-плоского пространства
- § 10. Безмассовые поля и когомологии твисторов
- Спиноры: Непроективное представление
- Квантование твисторов
- Спиральность
- Интегралы для спиральности противоположного знака
- Повышение и понижение спиральности
- Массивные твисторные волновые функции
- Геометрия контурных интегралов
- Положительно-частотные поля
- Введение когомологий
- Понятие 1-функции
- r-Функции общего вида
- Нелинейные 1-функции
- Конструкция Уорда
- Пример конструкции Уорда
- 7. Изотропные конгруэнции
- § 1. Изотропные конгруэнции и спиновые коэффициенты
- Интерпретация величин; изопараметричность лучей
- Ортогональность гиперповерхности; изотропные гиперповерхности
- Изопараметричность в теории твисторов
- § 2. Изотропные конгруэнции и кривизна пространства-времени
- Изопараметрические лучи; уравнения Сакса
- Неизопараметрические лучи
- Описание в трехмерном пространстве Минковского
- § 3. Бессдвиговые конгруэнции лучей
- Обобщенная теорема Голдберга — Сакса
- Координаты Керра
- § 4. БСК, твисторы и геометрия лучей
- Твисторная форма теоремы Керра
- Линейные и квадратичные функции твисторов, момент импульса
- Связь с твисторными функциями безмассовых полей
- Пространства и инвариантная контактная структура
- Комплексная структура и КД-структура
- Твисторы гиперповерхности
- Спиноры: Роль аналитичности
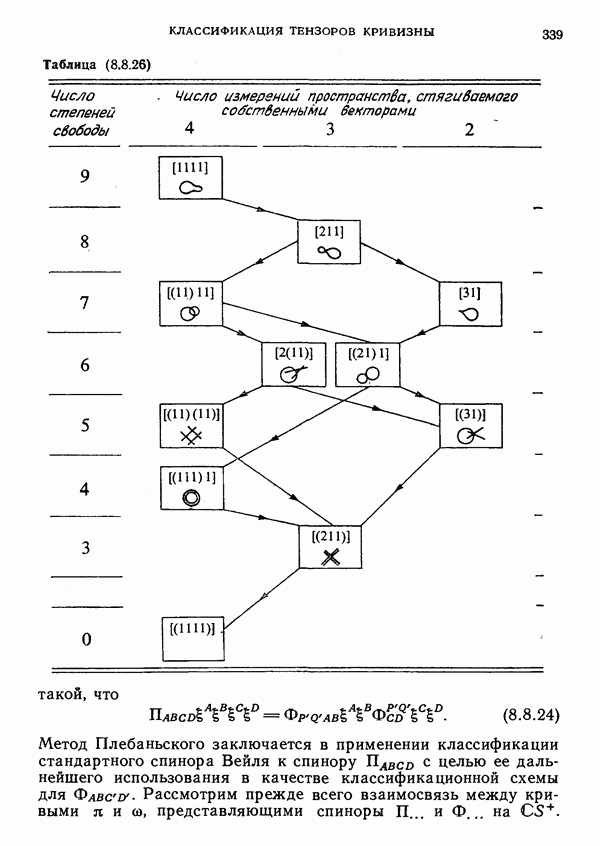
- 8. Классификация тензоров кривизны
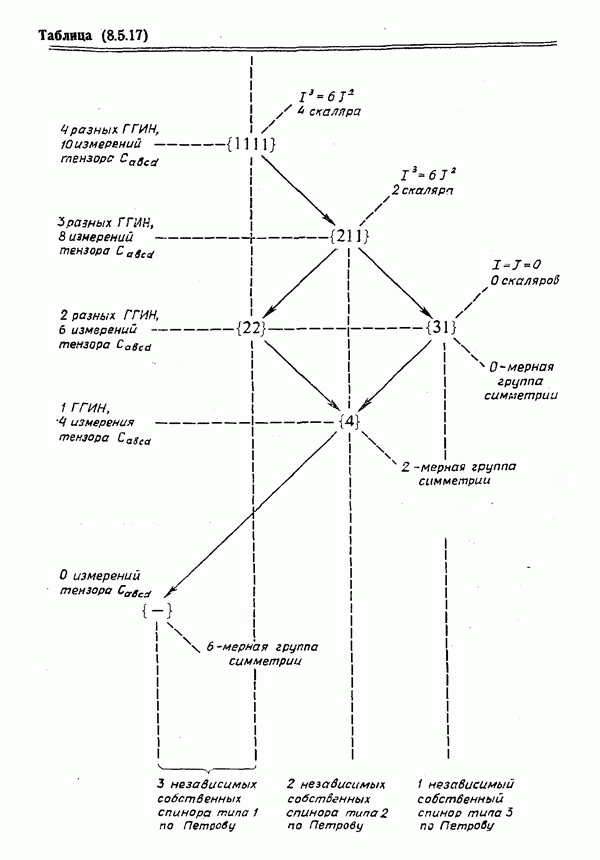
- Спиноры: Схема специализации
- § 2. Представление спинора Вейля на сфере S+
- ГГИН в пространстве-времени высокой симметрии
- «Картина» тензора Вейля на S+
- § 3. Собственные спиноры спинора Вейля
- Соотношение между собственными значениями и двойными отношениями
- Частные случаи
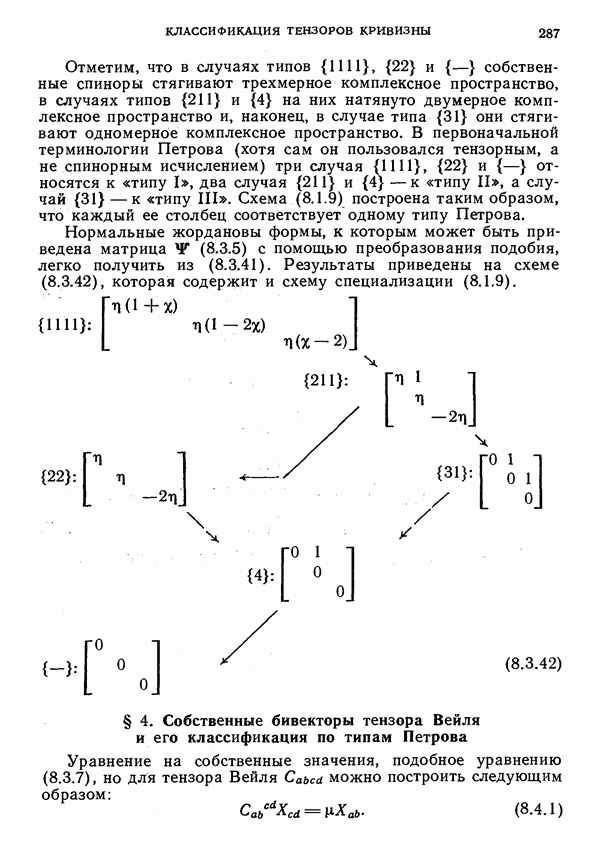
- § 4. Собственные бивекторы тензора Вейля и его классификация по типам Петрова
- Компоненты тензора Вейля в бивекторном базисе
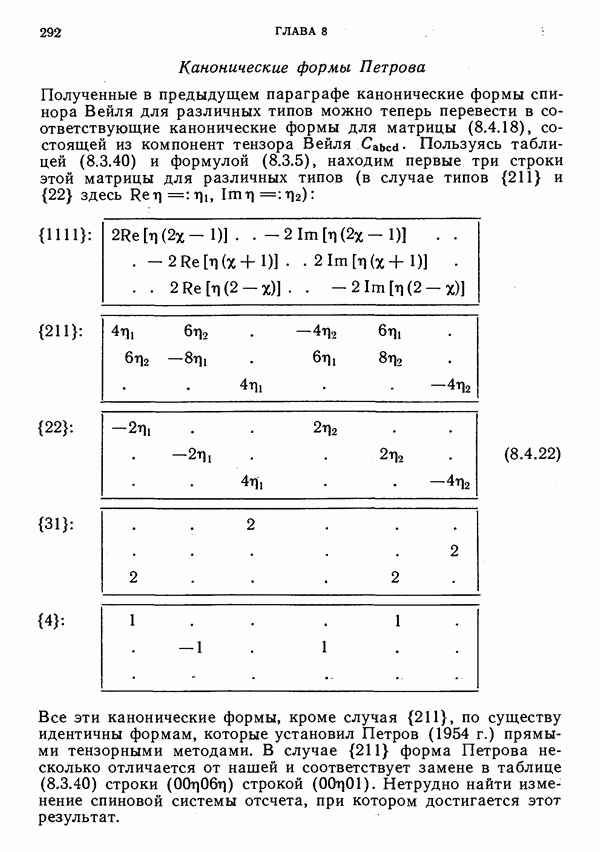
- Канонические формы Петрова
- § 5. Геометрия и симметрия вейлевской кривизны
- Дисфеноид для типа {1111}
- Симметрии в частных случаях типа {1111}
- Тип (211)
- О размерностях групп симметрий
- Классификация тензора Максвелла
- § 6. Коварианты кривизны
- Инварианты полной кривизны
- Система полей Эйнштейна — Максвелла
- § 7. Классификационная схема для спиноров с любым числом индексов
- Приводимость локуса
- Комплексные (р, q) — кривые на CS+
- Процедура классификации спинора
- Структура кривой w (ее кратные точки)
- Кратные точки кривой w
- Локус Rw на S+
- Знак спинора, черный и белый цвета сферы S+
- § 8. Классификация спинора Риччи
- Тип спинора по Плебаньскому
- Физические тензоры энергии-импульса
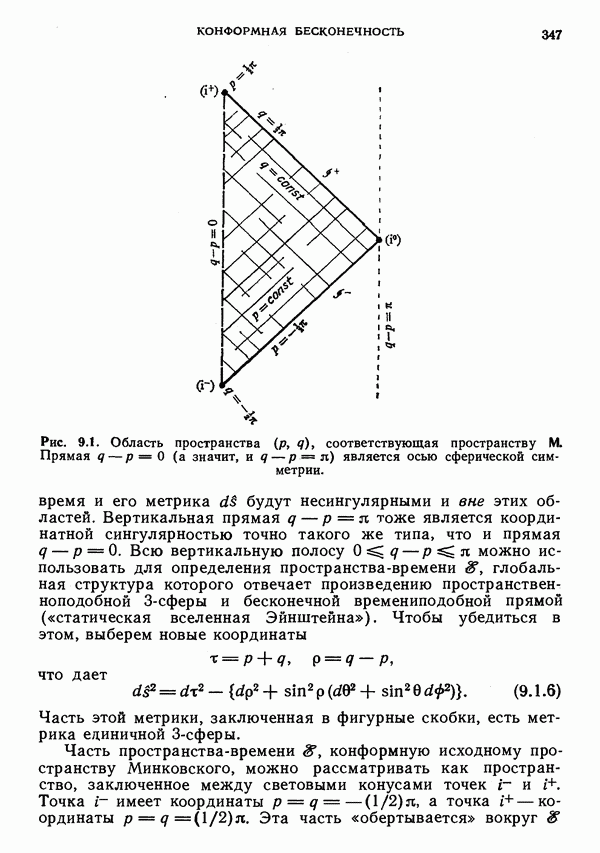
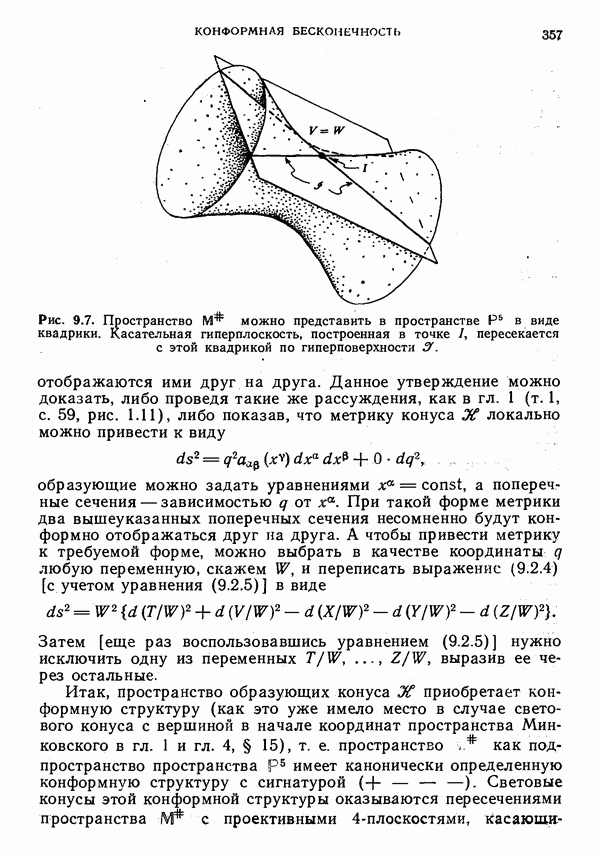
- 9. Конформная бесконечность
- § 1. Бесконечность в случае пространства Минковского
- ГНП и ГНБ
- § 2. Компактифицированное пространство Минковского
- Описание в пространстве Р5
- O(2,4) и конформная группа
- § 3. Комплексифицированное компактифицированное пространство Минковского и твисторная геометрия
- Соответствие Клейна
- Твисторное отношение дуальности
- Действительная структура
- Различные типы комплексных точек в СМ*
- § 4. Четырехзначность твисторов и индекс Гржина
- Две спиновые структуры на М*
- Поведение спинора
- Твисторные спин-расслоения над М*
- Конформные плотности на М*; индекс Гржина
- Теорема Гржина
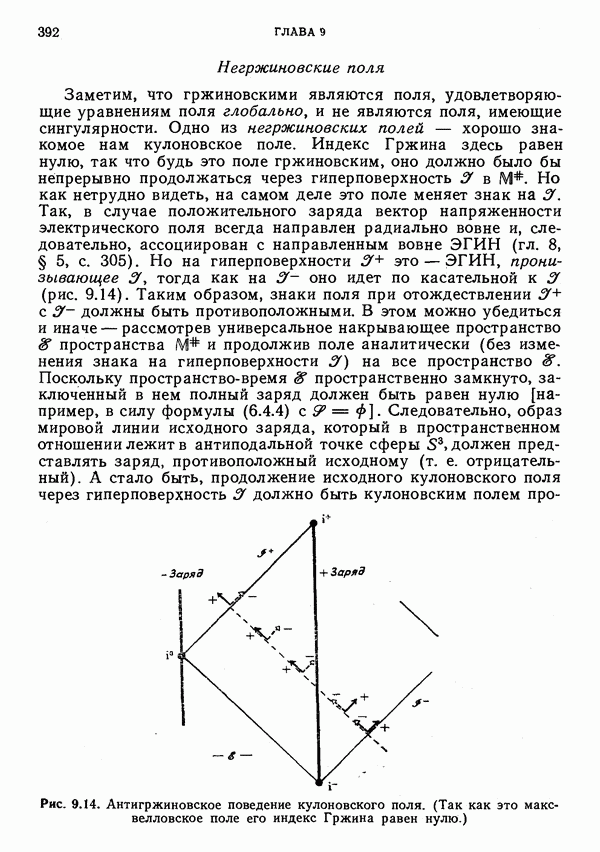
- Негржиновские поля
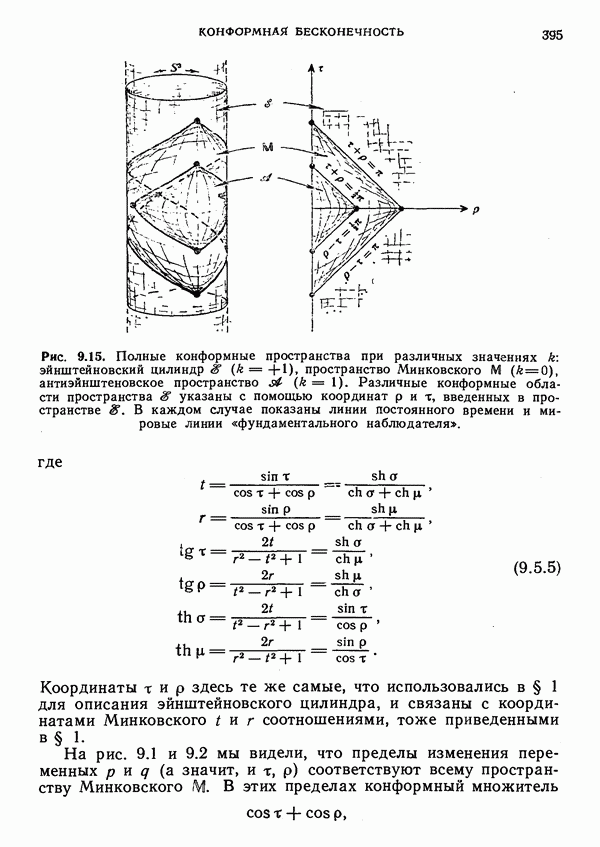
- § 5. Космологические модели и соответствующие твисторы
- Космологические горизонты
- Описание в пространстве Р5
- Деситтеровская и антидеситтеровская модели; твисторы …
- Функции для конформно-плоского пространства-времени
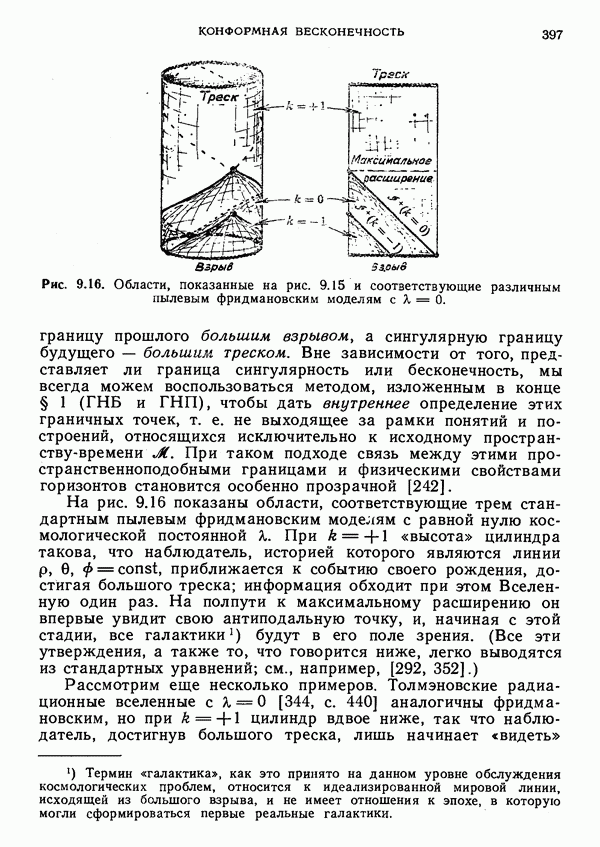
- Модели ФРУ, соответствующие твисторы начальной и конечной сингулярностей
- Явные выражения для функции I
- § 6. Асимптотически простое пространство-время
- Асимптотически-простое пространство-время
- Обращение в нуль тензора Вейля на границе J
- § 7. Последовательное вырождение
- Параллельно переносимые спиновые системы отсчета
- Сравнение аффинных параметров
- Сравнение спиновых систем отсчета
- Доказательство свойства последовательного вырождения
- Поля излучений
- § 8. Группа БМС и структура гиперповерхности J+
- Группа Бонди — Метцнера — Сакса
- Связь между сильной конформной геометрией и твистором
- Интерпретация изотропных углов
- Структура группы БМС
- Сдвиговая структура гиперповерхности J+
- H-пространство и асимптотическое твисторное пространство
- Отношение группы БМС к импульсу и моменту импульса
- Асимптотические разложения в теории Эйнштейна — Максвелла
- § 9. Энергия-импульс и момент импульса
- Усложнения в случае искривленного пространства-времени
- Твисторы двумерной поверхности
- Контортные двумерные поверхности
- Квазилокальный твистор момента импульса
- Определение множителя
- Асимптотическое спиновое пространство
- Свойства нормы на J+
- Эрмитовость твистора на 4-импульс Бонди — Сакса
- Альтернативные выражения для массы Бонди — Сакса
- Пространство Минковского как пространство «начал»
- Момент импульса на J+
- § 10. Потери массы Бонди — Сакса и положительность энергии
- Нелокальность энергии гравитационных волн
- НП-константы
- Подход Виттена в доказательстве положительности массы
- Связь с 4-импульсом Бонди — Сакса
- Спинор в подходе Людвигсена — Виккерса
- 3-форма Спарлинга
- Приложение. Спиноры в n измерениях
- 2-валентные e-спиноры
- Переход от тензоров к спинорам
- Геометрия фундаментальных спиноров
- Условие фундаментальности; структура спинового пространства
- Индуктивное построение спинового пространства
- Некоторые физически интересные случаи; триальность
- Спинорные поля; твисторы в n измерениях
- Послесловие авторов
- Литература