| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Изгиб балки
Будем далее называть балкой достаточно жесткое и тонкое упругое тело. Тонкость и жесткость балки понимаются в том смысле, что как поперечные ее размеры, так и перемещения точек в результате приложения к балке усилий считаются достаточно малыми по сравнению с ее длиной. Мы будем предполагать балку прямолинейной, т. е. считать, что отклонениями ее формы от прямолинейного отрезка можно пренебречь. В отличие от струны (см. § 1 главы 10), балка оказывает сопротивление только изгибающим (т. е. изменяющим кривизну) усилиям. Напротив, мы будем считать, что растягивающим (т. е. изменяющим длину балки как целого) усилиям балка вовсе не поддается. В этом параграфе содержится формальный вывод дифференциальных соотношений, связывающих нагрузку, приложенную к балке, с деформациями балки.
Предположим, что балка расположена вдоль оси  между точками
между точками  Вертикальное перемещение точки балки с абсциссой х будем обозначать через
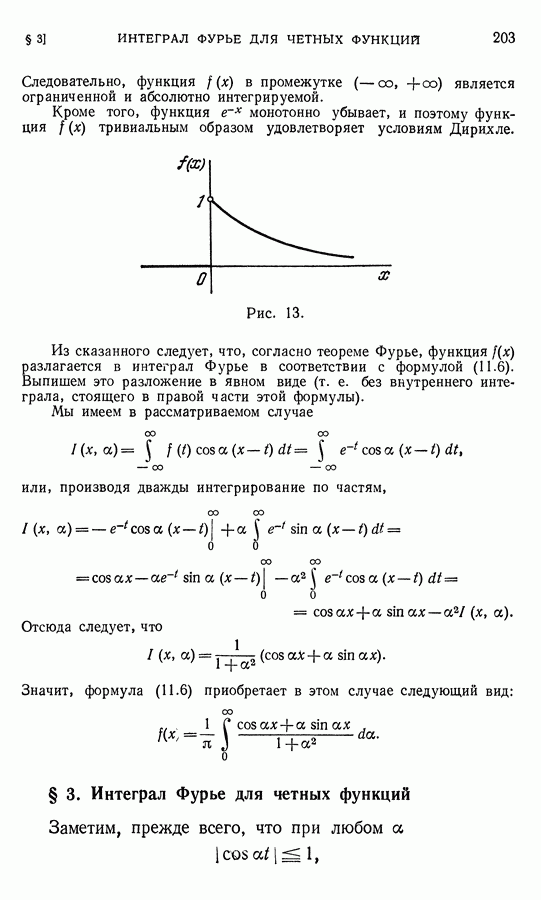
Вертикальное перемещение точки балки с абсциссой х будем обозначать через  Положительным на оси
Положительным на оси  будем считать направление вниз (рис. 26). Мы ограничимся рассмотрением плоского изгиба, т. е. будем предполагать, что все прикладываемые к балке усилия действуют в плоскости
будем считать направление вниз (рис. 26). Мы ограничимся рассмотрением плоского изгиба, т. е. будем предполагать, что все прикладываемые к балке усилия действуют в плоскости 
Для каждой системы нагрузок  приложенных к балке, будем через.
приложенных к балке, будем через.  обозначать вызываемый ею (а также порожденными ею реакциями опор) изгибающий момент в сечении х этой балки.
обозначать вызываемый ею (а также порожденными ею реакциями опор) изгибающий момент в сечении х этой балки.

Рис. 26.
Рассмотрим теперь две прикладываемые к балке системы нагрузок,  и
и 
Мы будем при этом предполагать, что изгибающие усилия, порождаемые нагрузкой  приложенной к предварительно ненагруженной балке, совпадают с дополнительными изгибающими усилиями
приложенной к предварительно ненагруженной балке, совпадают с дополнительными изгибающими усилиями  возникающими в балке, к которой предварительно приложена нагрузка
возникающими в балке, к которой предварительно приложена нагрузка  Иными словами, мы будем считать, что
Иными словами, мы будем считать, что

Разумеется, такое предположение носит чисто физический характер и должно каждый раз проверяться. Ясно вместе с тем, что если нагрузка  «не очень сильно» изменяет прямолинейную форму балки, а нагрузка
«не очень сильно» изменяет прямолинейную форму балки, а нагрузка  — поперечная, то предположение (17.1) не противоречит обстоятельствам дела.
— поперечная, то предположение (17.1) не противоречит обстоятельствам дела.
Из (17.1), предполагая «непрерывность» зависимости значения изгибающего момента  в каждой точке х от нагрузки
в каждой точке х от нагрузки  и обозначая через
и обозначая через  нагрузку
нагрузку  «умноженную» на а (т. е. увеличенную в а раз, если
«умноженную» на а (т. е. увеличенную в а раз, если  , и уменьшенную в
, и уменьшенную в  раз, если
раз, если  ), мы можем получить, что
), мы можем получить, что

Возьмем балку, на которую действует распределенная нагрузка  имеющая некоторую интенсивность
имеющая некоторую интенсивность  в каждой точке х. Пусть характер прикрепления балки
в каждой точке х. Пусть характер прикрепления балки
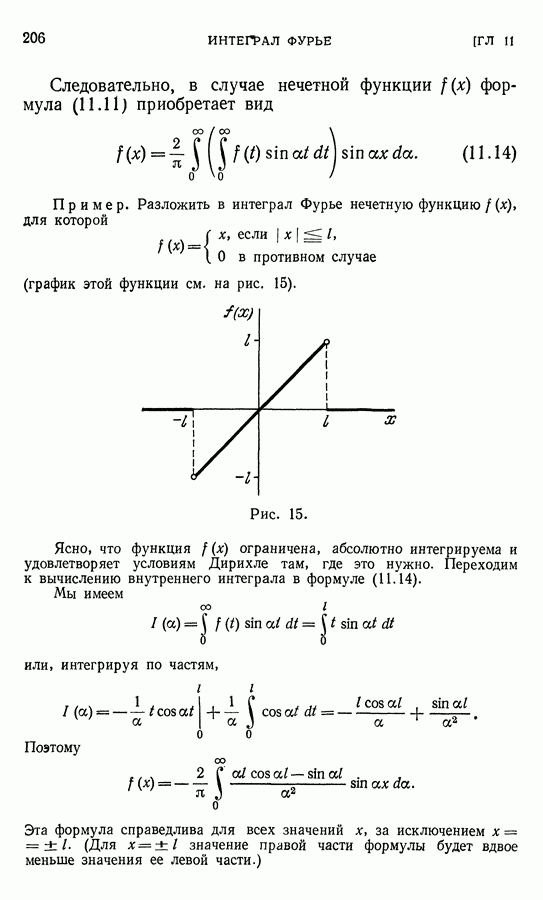
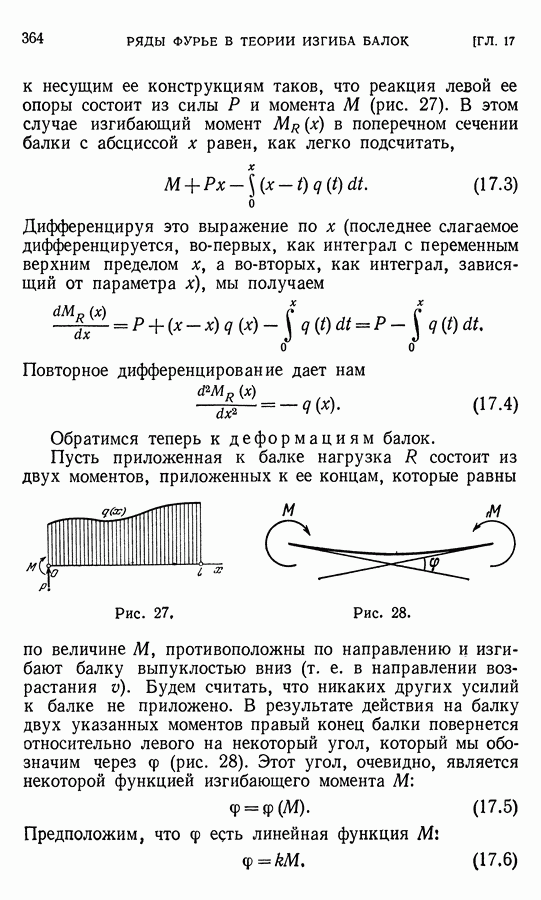
к несущим ее конструкциям таков, что реакция левой ее опоры состоит из силы Р и момента М (рис. 27). В этом случае изгибающий момент  в поперечном сечении балки с абсциссой х равен, как легко подсчитать,
в поперечном сечении балки с абсциссой х равен, как легко подсчитать,

Дифференцируя это выражение по х (последнее слагаемое дифференцируется, во-первых, как интеграл с переменным верхним пределом х, а во-вторых, как интеграл, зависящий от параметра  мы получаем
мы получаем

Повторное дифференцирование дает нам

Обратимся теперь к деформациям балок.
Пусть приложенная к балке нагрузка  состоит из двух моментов, приложенных к ее концам, которые равны по величине М, противоположны по направлению и изгибают балку выпуклостью вниз (т. е. в направлении возрастания
состоит из двух моментов, приложенных к ее концам, которые равны по величине М, противоположны по направлению и изгибают балку выпуклостью вниз (т. е. в направлении возрастания 

Рис. 27,

Рис. 28.
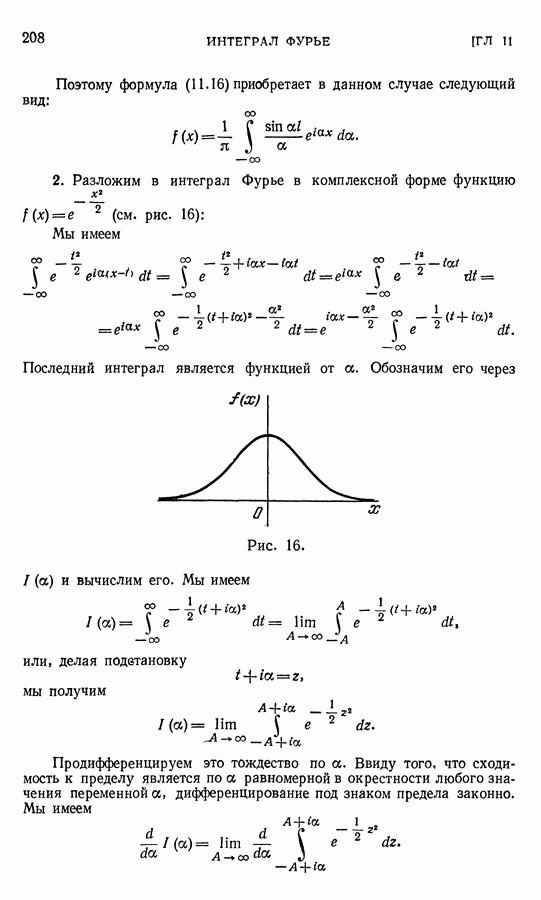
Будем считать, что никаких других усилий к балке не приложено. В результате действия на балку двух указанных моментов правый конец балки повернется относительно левого на некоторый угол, который мы обозначим через  (рис. 28). Этот угол, очевидно, является некоторой функцией изгибающего момента М:
(рис. 28). Этот угол, очевидно, является некоторой функцией изгибающего момента М:

Предположим, что  есть линейная функция
есть линейная функция 

Это предположение соответствует закону Гука о пропорциональности деформаций усилиям. В условиях выбранных нами направлений изгибающих моментов и осей координат (х - направо, a v - вниз) угол  оказывается отрицательным. Поэтому должно быть
оказывается отрицательным. Поэтому должно быть 
Считая впредь рассматриваемую балку однородной по длине, можно показать, как это делается во всех курсах сопротивления материалов, что

где  — длина изгибаемой балки,
— длина изгибаемой балки,  — момент инерции ее поперечного сечения относительно горизонтальной прямой, лежащей в плоскости этого сечения и проходящей через его центр тяжести,
— момент инерции ее поперечного сечения относительно горизонтальной прямой, лежащей в плоскости этого сечения и проходящей через его центр тяжести,  модуль Юнга материала балки.
модуль Юнга материала балки.
В целях полноты изложения напомним этот вывод.

Рис. 29.
В теории изгиба призматических балок обычно принимается «гипотеза плоских сечений» Сен-Венана. Она состоит в предположении, что каждое поперечное сечение ненагруженной балки после приложения к ней изгибающей нагрузки остается плоским и лишь поворачивается около оси изгибающего момента. Формально это равносильно предположению о том, что абсолютное удлинение  в направлении каждой нормали к сечению есть линейная функция координаты
в направлении каждой нормали к сечению есть линейная функция координаты  характеризующей положение этой нормали по высоте балки. Тем самым линейной функцией координаты
характеризующей положение этой нормали по высоте балки. Тем самым линейной функцией координаты  должно быть и нормальное напряжение
должно быть и нормальное напряжение  в каждой точке сечения.
в каждой точке сечения.
Заметим, что при отсутствии продольной нагрузки на балку равнодействующая внутренних продольных усилий в каждом ее сечении должна быть равна нулю. Значит, при одних значениях  нормальные напряжения положительны, а при других — отрицательны. В качестве начала отсчета
нормальные напряжения положительны, а при других — отрицательны. В качестве начала отсчета  выберем тот уровень по высоте балки, на
выберем тот уровень по высоте балки, на
котором нормальные напряжения (а потому — и удлинения) равны нулю.
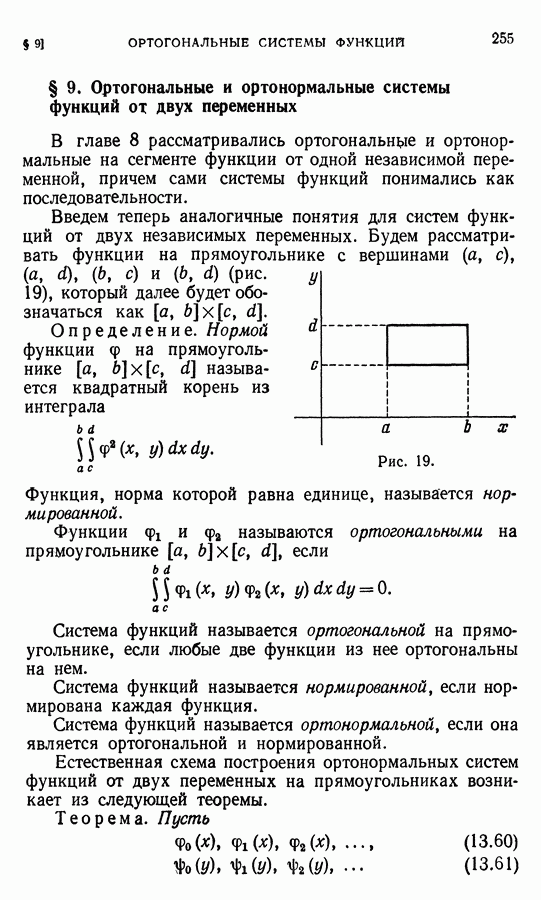
На рис. 29 изображен график удлинения  в зависимости от
в зависимости от  Поскольку балка предполагается жесткой, и углы ее поворота — малыми, угол
Поскольку балка предполагается жесткой, и углы ее поворота — малыми, угол  можно по величине отождествить с его тангенсом и (с учетом выбора направлений осей) написать:
можно по величине отождествить с его тангенсом и (с учетом выбора направлений осей) написать:

А так как напряжение  определяется соотношением
определяется соотношением

должно быть

Обозначим через  ширину балки на уровне
ширину балки на уровне  Тогда усилие, действующее в «элементарном слое»
Тогда усилие, действующее в «элементарном слое»  будет равно
будет равно

а момент всех таких усилий относительно оси  —
—

Последний интеграл есть момент инерции  сечения относительно «нейтрального слоя»
сечения относительно «нейтрального слоя»  Таким образом,
Таким образом,  — что вместе с (17.6) и дает (17.7).
— что вместе с (17.6) и дает (17.7).
В условиях рассматриваемой на рис. 28 нагрузки  в каждом поперечном сечении балки с абсциссой х возникает изгибающий момент
в каждом поперечном сечении балки с абсциссой х возникает изгибающий момент  который, очевидно, постоянен по длине балки и равен М:
который, очевидно, постоянен по длине балки и равен М:

Из (17.6), (17.7) и (17.8) следует, что

Отношение  есть угол поворота балки, отнесенный к единице ее длины, т. е. средняя кривизна балки. Поскольку в наших условиях балка однородна и действующий
есть угол поворота балки, отнесенный к единице ее длины, т. е. средняя кривизна балки. Поскольку в наших условиях балка однородна и действующий
в ней изгибающий момент постоянен по ее длине, кривизна балки во всех ее точках одинакова и равна средней кривизне. Но в условиях предполагаемой жесткости балки ее кривизну можно принять равной второй производной вертикального смещения точки балки по ее длине. Поэтому

Вместе с (17.9) это дает нам

Заметим теперь, что кривизна («искривленность») изогнутой балки в некоторой ее точке х зависит только от изгибающего момента  в этой точке
в этой точке  не зависит от того, какими будут его значения в остальных точках балки. «Физически» (т. е. интуитивно) это представляется совершенно очевидным, а с формальной точки зрения это соответствует принимаемой при изучении напряжений в теле возможности отсекать любую его часть и заменять ее действие на оставшуюся часть тела надлежащей системой сил.
не зависит от того, какими будут его значения в остальных точках балки. «Физически» (т. е. интуитивно) это представляется совершенно очевидным, а с формальной точки зрения это соответствует принимаемой при изучении напряжений в теле возможности отсекать любую его часть и заменять ее действие на оставшуюся часть тела надлежащей системой сил.
Значит, для каждой точки х балки можно написать 

независимо от приложенной к балке нагрузки  Иными словами, функция прогиба
Иными словами, функция прогиба  балки связана с действующим в балке изгибающим моментом
балки связана с действующим в балке изгибающим моментом  дифференциальным уравнением
дифференциальным уравнением

Из (17.12) следует, что, какова бы ни была дважды интегрируемая функция  описывающая изгибающий момент в балке, можно указать соответствующую ей функцию
описывающая изгибающий момент в балке, можно указать соответствующую ей функцию  описывающую прогибы этой балки. Эта функция
описывающую прогибы этой балки. Эта функция  определяется по
определяется по  единственным образом с точностью до линейного слагаемого
единственным образом с точностью до линейного слагаемого  , соответствующего перемещениям балки как твердого тела. Для определения постоянных А и В следует указывать те или иные способы закрепления концов балки. Коль скоро эти
, соответствующего перемещениям балки как твердого тела. Для определения постоянных А и В следует указывать те или иные способы закрепления концов балки. Коль скоро эти
способы закрепления указаны, функция прогиба  определяется по функции изгибающего момента
определяется по функции изгибающего момента  однозначно.
однозначно.
С другой стороны, из того же равенства (17.12) следует, что по любой дважды дифференцируемой функции  для которой выполняются те или иные начальные (или краевые) условия, отвечающие кинематическим условиям закрепления балки, можно указать такую функцию
для которой выполняются те или иные начальные (или краевые) условия, отвечающие кинематическим условиям закрепления балки, можно указать такую функцию  что приложение к балке усилий, приводящих в каждой ее точке х к изгибающему моменту
что приложение к балке усилий, приводящих в каждой ее точке х к изгибающему моменту  породит в каждой точке х вертикальное смещение
породит в каждой точке х вертикальное смещение 
Ввиду линейности дифференциального уравнения (17.12) при любых нагрузках  и
и  для которых выполняется (17.1), должно иметь место и
для которых выполняется (17.1), должно иметь место и

а при любом вещественном а из (17.2) следует:

Отсюда в свою очередь вытекает, что при исключении перемещения балки как твердого тела должно быть

и

Отметим, наконец, что из (17.4) и (17.12) следует:

Это соотношение принято называть дифференциальным уравнением изгиба балки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Часть I
- ГЛАВА 1. ПРОГРЕССИИ
- § 2. Геометрические прогрессии
- § 3. Бесконечные прогрессии; их сходимость и расходимость
- § 4. Элементарные преобразования прогрессий
- § 5. Функциональные прогрессии: область сходимости; равномерная сходимость
- § 6. Почленное интегрирование прогрессий
- § 7. Почленное дифференцирование прогрессий
- § 8. Прогрессии с комплексными членами
- ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ
- § 2. Определение числового ряда и его сходимости
- § 3. Остаток ряда
- § 4. Принцип сходимости Коши
- § 5. Критерий Коши сходимости рядов
- § 6. Необходимый признак сходимости ряда
- § 7. Желательность систематической теории
- § 8. Свойства сходящихся рядов, подобные свойствам сумм
- § 9. Дальнейшие свойства рядов
- ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
- § 1. Признаки сходимости рядов
- § 2. Признаки сравнения
- § 3. Интегральный признак сходимости Маклорена — Коши
- § 4. Применения интегрального признака сходимости
- § 5. Сравнительная оценка различных признаков сходимости
- § 6. Признак сходимости Даламбера
- § 7. Признак сходимости Коши
- § 8. Чувствительность признаков сходимости Даламбера и Коши
- ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- § 2. Абсолютная сходимость и расходимость
- § 3. Возможность переставлять члены в абсолютно сходящихся рядах
- § 4. Условно сходящиеся знакопеременные ряды
- § 5. Умножение абсолютно сходящихся рядов
- § 6. Признак сходимости Лейбница
- § 7. Существенность условий признака сходимости Лейбница
- ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 2. Область сходимости функционального ряда
- § 3. Сходимость последовательности функций. Основные определения
- § 4. Предел последовательности непрерывных функций
- § 5. Переход к пределу под знаком интеграла
- § 6. Переход к пределу под знаком производной
- § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса
- § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами
- § 9. Почленное интегрирование функциональных рядов
- § 10. Почленное дифференцирование функциональных рядов
- ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ
- § 2. Теорема Абеля
- § 3. Круг сходимости ряда
- § 4. Вещественный степенной ряд и его интервал сходимости
- § 5. Равномерная сходимость ряда в круге его сходимости
- § 6. Вещественные ряды
- § 7. Комплексные ряды
- § 8. Разложение функций в степенные ряды
- § 9. Формула Тейлора
- § 10. Ряды Тейлора и Маклорена
- ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ
- § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x
- § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x
- § 4. Показательная функция с комплексным значением показателя
- § 5. Формулы Эйлера
- § 6. Тригонометрические функции от комплексного значения аргумента
- § 7. Гиперболические функции от комплексного значения аргумента
- § 8. Вычисление значений функций при помощи ряда Маклорена
- § 9. Биномиальный ряд
- § 10. Приложения биномиального ряда
- § 11. Разложение в ряд Маклорена логарифмической функции
- § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов
- § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов
- ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 2. Векторы и функции
- § 3. Нормированные и ортогональные функции
- § 4. Нормированные и ортогональные системы функций
- § 5. Нормировка систем функций
- § 6. Разложение по системам функций
- ГЛАВА 9. РЯДЫ ФУРЬЕ
- § 1. Ряды и коэффициенты Фурье
- § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье
- § 3. Разложение периодических функций в ряд Фурье
- § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье
- § 5. Разложение функции f(x) = x
- § 6. Сдвиг сегмента разложения
- § 7. Изменение длины сегмента разложения
- § 8. Четные и нечетные функции
- § 9. Разложение четной функции в ряд Фурье
- § 10. Разложение нечетной функции в ряд Фурье
- § 11. Разложение ряд Фурье функций на сегменте от 0 до пи
- § 12. Комплексная форма записи ряда Фурье
- § 13. Разложение в комплексный ряд Фурье
- § 14. Характер сходимости рядов Фурье
- ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ
- § 2. Начальные и граничные условия
- § 3. Метод разделения переменных
- § 4. Использование граничных условий. Собственные функции и собственные значения
- § 5. Использование начальных условий
- ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ
- § 1. Представление функций интегралом Фурье
- § 2. Простейшие достаточные условия представимости функции интегралом Фурье
- § 3. Интеграл Фурье для четных функций
- § 4. Интеграл Фурье для нечетных функций
- § 5. Комплексная форма интеграла Фурье
- § 6. Понятие о преобразовании Фурье
- § 7. Косинус-преобразование Фурье
- § 8. Синус-преобразование Фурье
- § 9. Спектральная функция
- Часть II
- § 1. Признак сходимости Куммера
- § 2. Признак сходимости Раабе
- § 3. Признак сходимости Бертрана
- § 4. Признак сходимости Гаусса
- § 5. Сходимость знакопеременных рядов
- § 6. Признак сходимости Дирихле
- ГЛАВА 13. ДВОЙНЫЕ РЯДЫ
- § 1. Определение двойного ряда
- § 2. Сходимость двойных рядов
- § 3. Критерии сходимости двойных рядов. Теорема Маркова
- § 4. Свойства двойных рядов и признаки сходимости
- § 5. Абсолютная сходимость двойных рядов
- § 6. Двойные функциональные ряды
- § 7. Двойные степенные ряды
- § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена
- § 9. Ортогональные и ортонормальные системы функций от двух переменных
- § 10. Двойные ряды Фурье
- ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ
- § 2. Линейные преобразования рядов
- § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов
- § 4. Последовательности разностей
- § 5. Преобразование рядов по Эйлеру
- § 6. Преобразование рядов по Куммеру
- ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
- § 1. Расходящиеся геометрические прогрессии
- § 2. Суммирующие функции
- § 3. Суммирование по Пуассону — Абелю
- § 4. Линейность и регулярность суммирования по Пуассону — Абелю
- § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость
- § 6. Теорема Таубера
- § 7. Суммирование по Чезаро
- § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю
- § 9. Суммирование по Эйлеру
- ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ
- § 2. Исследование двух интегралов
- § 3. Исследование одного класса интегралов
- § 4. Доказательство теоремы Дирихле
- § 5. Теорема Фурье
- § 6. Коэффициенты Фурье разрывных функций
- § 7. Скорость сходимости рядов Фурье
- § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей
- § 9. О равномерной сходимости рядов Фурье
- § 10. Неравномерная сходимость последовательностей непрерывных функций
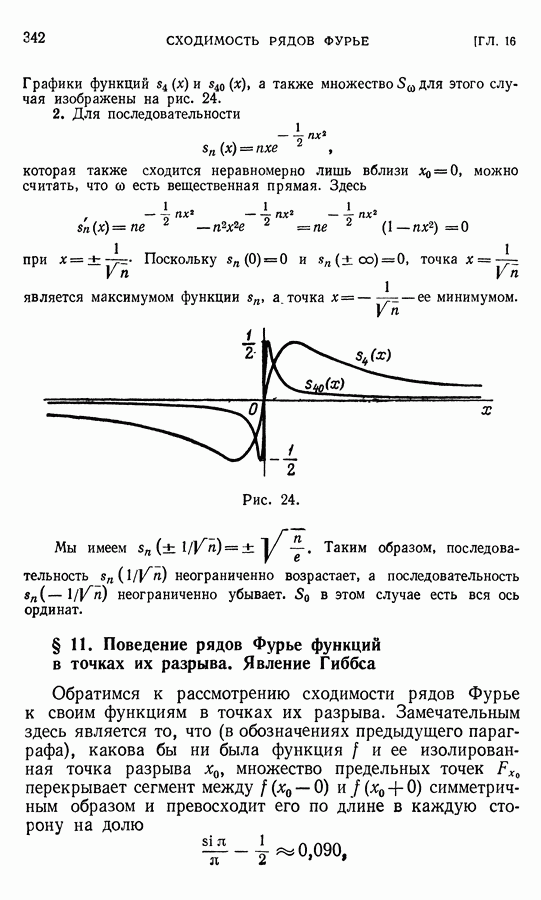
- § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса
- § 12. Экстремальное свойство сумм Фурье
- § 13. Суммирование рядов Фурье по Чезаро. Теорема Фейера
- § 14. Равенство Парсеваля
- § 15. Теорема Вейерштрасса
- ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК
- § 2. Изгиб балки
- § 3. Свободно опертая балка
- § 4. Первая возможность ограничиться двукратным дифференцированием
- § 5. Случай сосредоточенной нагрузки
- § 6. Прогиб балки от распределенной нагрузки
- § 7. Прогиб от сосредоточенного момента
- § 8. Статически неопределимая балка
- § 9. Сложный изгиб балки
- § 10. Балка на упругом основании
- § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки
- § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок
- § 13. Функции прогиба с ортогональными вторыми производными
- § 14. Свободно опертая нагруженная балка
- § 15. Работа продольных сил при сложном изгибе балки
- § 16. Общий случай изгиба балки
- § 17. Общий случай изгиба свободно опертой балки
- § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам
- § 19. Функция прогиба симметрично загруженной балки с жестко заделанными концами