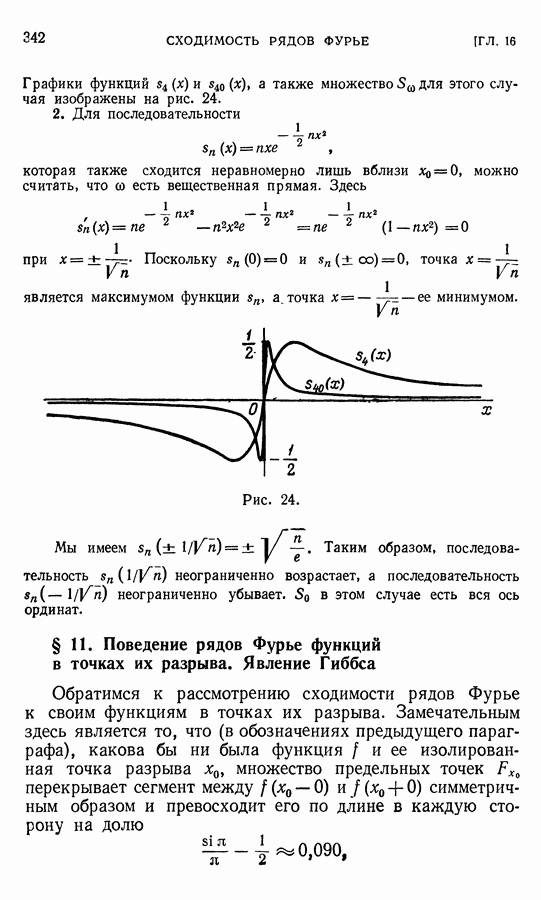
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Свойства сходящихся рядов, подобные свойствам сумм
Теорема 1 (ассоциативный закон для сходящихся рядов). Если в сходящемся ряде

произвольно объединить соседние члены в группы, не нарушая порядка членов:

(разумеется, каждый член при этом должен входить только в одну группу) и найти суммы  членов, входящих в каждую из групп, то составленный из этих сумм ряд
членов, входящих в каждую из групп, то составленный из этих сумм ряд

будет сходиться и иметь ту же сумму, что и первоначальный ряд (2.15).
Доказательство. Составим последовательность частичных сумм ряда (2.15)

Среди них, в частности, окажутся и все суммы вида

т. e. все частичные суммы ряда (2.16). Таким образом, последовательность частичных сумм ряда (2.16)
оказывается подпоследовательностью последовательности частичных сумм ряда (2.15). Но раз последовательность

по условию сходится и имеет предел  ее подпоследовательность
ее подпоследовательность

также должна сходиться и иметь тот же предел. Это и означает, что «сконцентрированный» ряд (2.16) сходится и имеет ту же сумму, что и «редкий» ряд (2.15).
Следствие. Если в результате описанного в условии предыдущей теоремы объединения мы получим ряд (2.16), который расходится, то и первоначально взятый ряд  также расходится.
также расходится.
В самом деле, если бы ряд (2.15) сходился, то сходился бы и ряд (2.16), а мы предположили обратное.
Пример. Выясним сходимость и найдем сумму ряда

Замечая, что при любом 

рассмотрим ряд

Очевидно, для этого ряда

Вообще для  четного:
четного: 

а для  нечетного:
нечетного: 

Совершенно ясно, что

так что ряд (2.20) сходится Но тогда по доказанной теореме сходится и ряд (2.19), получаемый попарным объединением членов ряда (2.20), и сумма этого ряда также равна единице.
Замечание. Подчеркнем, что из сходимости «сконцентрированного» ряда (2.16) сходимость «редкого» ряда (2.15) может и не следовать, как и вообще на основании сходимости одной какой-либо подпоследовательности еще нельзя утверждать о сходимости всей последовательности.
Примеры.
1. Если в ряде

объединить попарно соседние члены:

то мы получим ряд

сходимость которого была установлена в предыдущем примере.
Однако исходный ряд не сходится, потому что для него, как легко проверить, не соблюдается сформулированный в §  необходимый признак сходимости ряда: здесь на нечетных местах стоят единицы, так что
необходимый признак сходимости ряда: здесь на нечетных местах стоят единицы, так что

2. К такому же выводу приводит рассмотрение уже встречавшегося нам ряда

Вместе с тем, если все члены исходного ряда положительны, то обращение теоремы остается в силе: из сходимости ряда (2.16) следует сходимость ряда (2.15). Действительно, для ряда с положительными членами последовательность (2.17) является монотонной и неубывающей. Поэтому она должна сходиться, если сходится какая-либо ее подпоследовательность, например (2.18).
Теорема 2 (дистрибутивный закон для рядов; теорема об умножении ряда на число). Пусть

— некоторый ряд, а с — произвольное число, отличное от нуля. Тогда ряд

сходится тогда и только тогда, когда сходится ряд (2.21). Если ряд (2.21) сходится, и сумма его равна  то сумма ряда (2.22) равна
то сумма ряда (2.22) равна 
Доказательство. Если последовательность частичных сумм ряда (2.21) есть

то последовательностью частичных сумм ряда (2.22), очевидно, будет

Так как

из существования предела слева (которое означает сходимость ряда (2.21) при  следует существование предела справа (т. е. сходимость ряда (2.22)) и равенство (2.23). Наоборот, из существования предела справа следуют существование предела слева и опять-таки равенство (2.23).
следует существование предела справа (т. е. сходимость ряда (2.22)) и равенство (2.23). Наоборот, из существования предела справа следуют существование предела слева и опять-таки равенство (2.23).
Замечание 1. Если в формулировке теоремы допустить случай  то ряд (2.22) будет в этом случае сходиться всегда, и никакой информации из этого факта нам извлечь не удастся.
то ряд (2.22) будет в этом случае сходиться всегда, и никакой информации из этого факта нам извлечь не удастся.
Замечание 2. Мы доказали теоремы о рядах, аналогичные свойствам ассоциативности и дистрибутивности конечных сумм. Теорема о возможности переставлять в ряде члены, аналогичная коммутативности сложения, носит более узкий характер и справедлива уже не для всех рядов.
Пример. Рассмотрим ряд

В этом ряде видны чередующиеся группы равных друг другу положительных и отрицательных членов. Сумма членов в каждой группе по модулю равна единице.
Если суммировать члены ряда (2.24) в том порядке, в каком они написаны, то при завершении каждой группы положительных членов частичная сумма будет равна единице, а при завершении каждой группы отрицательных членов — нулю. Следовательно, этот ряд
расходится, хотя все его частичные суммы ограничены (они лежат между нулем и единицей).
Переставим теперь члены ряда (2.24) следующим образом:

(т. е. после каждого положительного члена будем писать по два отрицательных из следующей группы). Частичные суммы получающегося при этом ряда выглядят достаточно просто:

где  — некоторое целое число, зависящее от
— некоторое целое число, зависящее от  и неограниченно возрастающее вместе с ростом
и неограниченно возрастающее вместе с ростом  Поэтому
Поэтому

так что ряд (2.25) сходится.
Наконец, переставив члены исходного рдца иначе:

(т. е. после  по порядку группы положительных членов ставится
по порядку группы положительных членов ставится  по порядку отрицательный член; так как и групп положительных членов и отрицательных членов бесконечно много, можно считать, что их «одинаково много», и на каждый отрицательный член найдется целая группа положительных членов).
по порядку отрицательный член; так как и групп положительных членов и отрицательных членов бесконечно много, можно считать, что их «одинаково много», и на каждый отрицательный член найдется целая группа положительных членов).
Объединим теперь группы положительных членов вместе со следующим за ним отрицательным членом в один член нового ряда. Каждый член нового ряда будет не меньшим, чем 1/2; поэтому его  частичная сумма
частичная сумма  будет не меньше, чем
будет не меньше, чем 
Следовательно,

т. е. этот ряд расходится, причем последовательность его частичных сумм оказывается неограниченной. Значит, на основании следствия теоремы 1 (об ассоциативном законе) ряд (2.26) также расходится.
Вместе с тем в рядах с положительными членами произвольная перестановка членов не нарушает сходимости рядов и не изменяет суммы сходящихся рядов.
Теорема 3 (Дирихле). Пусть дан ряд

с неотрицательными членами, а ряд

получается из ряда (2.27) произвольной перестановкой его членов. Тогда, если ряд (2.27) сходится, то ряд (2.28) также сходится и имеет ту же сумму, что и ряд (2.27).
Доказательство. Пусть ряд (2.27) сходится и сумма его равна  Рассмотрим частичную сумму ряда (2.28)
Рассмотрим частичную сумму ряда (2.28)

Каждое из слагаемых этой суммы входит в ряд (2.27). Возьмем в раде (2.27) столь большое число  первых членов, чтобы среди них оказались все слагаемые
первых членов, чтобы среди них оказались все слагаемые  и составим
и составим  частичную сумму ряда (2.27):
частичную сумму ряда (2.27):

Так как все слагаемые  входят в
входят в  а остальные слагаемые
а остальные слагаемые  (если такие есть) неотрицательны, должно быть
(если такие есть) неотрицательны, должно быть

Но частичные суммы ряда (2.27), ввиду неотрицательности членов ряда, не превосходят его суммы 

Следовательно,

Так как это неравенство справедливо для любого  все частичные суммы ряда (2.28) ограничены. Поэтому ряд (2.28) сходится и для его суммы
все частичные суммы ряда (2.28) ограничены. Поэтому ряд (2.28) сходится и для его суммы  справедливо
справедливо

Так как теперь в наших рассуждениях ряды (2.27) и (2.28) стали равноправными, должно быть и

откуда следует, что 
Теорема 4 (теорема о сложении рядов). Пусть

— два сходящихся ряда соответственно с суммами  и
и 
Тогда ряд

также сходится и сумма его равна 
Доказательство. Для частичных сумм  ряда (2.29) мы имеем
ряда (2.29) мы имеем

Справа в скобках стоят частичные суммы  рассматриваемых рядов. Устремляя
рассматриваемых рядов. Устремляя  к бесконечности, мы получаем
к бесконечности, мы получаем

а это и требовалось.
Доказанная теорема означает, что сходящиеся ряды можно почленно складывать и при этом складываются их суммы.
Теорема 5. Если

и

— два сходящихся ряда соответственно с суммами  и
и  а
а  — произвольные числа, то ряд
— произвольные числа, то ряд

также сходится и сумма его равна 
Доказательство. Если  то ряд (2.32) превращается в (2.31); если
то ряд (2.32) превращается в (2.31); если  то ряд (2.32) превращается в (2.30), и теорема доказана. Предположим теперь, что
то ряд (2.32) превращается в (2.30), и теорема доказана. Предположим теперь, что  Тогда по теореме 2 сходятся ряды
Тогда по теореме 2 сходятся ряды

а по теореме 4 — ряд (2.32), причем его сумма равна 
Следствие (теорема о вычитании рядов). Если сходятся ряды

и

и имеют суммы  и
и  то сходится ряд
то сходится ряд

и сумма его равна 
В самом деле, полагая в предыдущей теореме  мы получаем требуемое.
мы получаем требуемое.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Часть I
- ГЛАВА 1. ПРОГРЕССИИ
- § 2. Геометрические прогрессии
- § 3. Бесконечные прогрессии; их сходимость и расходимость
- § 4. Элементарные преобразования прогрессий
- § 5. Функциональные прогрессии: область сходимости; равномерная сходимость
- § 6. Почленное интегрирование прогрессий
- § 7. Почленное дифференцирование прогрессий
- § 8. Прогрессии с комплексными членами
- ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ
- § 2. Определение числового ряда и его сходимости
- § 3. Остаток ряда
- § 4. Принцип сходимости Коши
- § 5. Критерий Коши сходимости рядов
- § 6. Необходимый признак сходимости ряда
- § 7. Желательность систематической теории
- § 8. Свойства сходящихся рядов, подобные свойствам сумм
- § 9. Дальнейшие свойства рядов
- ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
- § 1. Признаки сходимости рядов
- § 2. Признаки сравнения
- § 3. Интегральный признак сходимости Маклорена — Коши
- § 4. Применения интегрального признака сходимости
- § 5. Сравнительная оценка различных признаков сходимости
- § 6. Признак сходимости Даламбера
- § 7. Признак сходимости Коши
- § 8. Чувствительность признаков сходимости Даламбера и Коши
- ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- § 2. Абсолютная сходимость и расходимость
- § 3. Возможность переставлять члены в абсолютно сходящихся рядах
- § 4. Условно сходящиеся знакопеременные ряды
- § 5. Умножение абсолютно сходящихся рядов
- § 6. Признак сходимости Лейбница
- § 7. Существенность условий признака сходимости Лейбница
- ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 2. Область сходимости функционального ряда
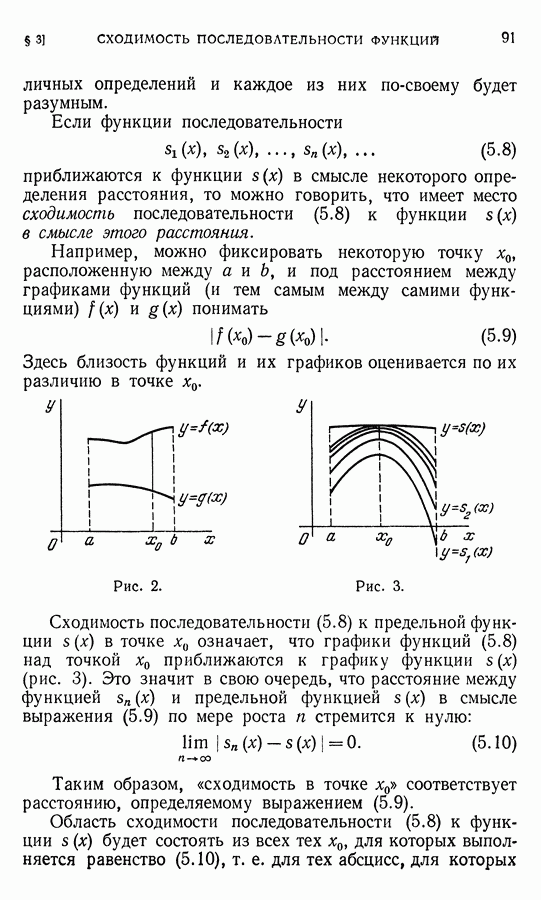
- § 3. Сходимость последовательности функций. Основные определения
- § 4. Предел последовательности непрерывных функций
- § 5. Переход к пределу под знаком интеграла
- § 6. Переход к пределу под знаком производной
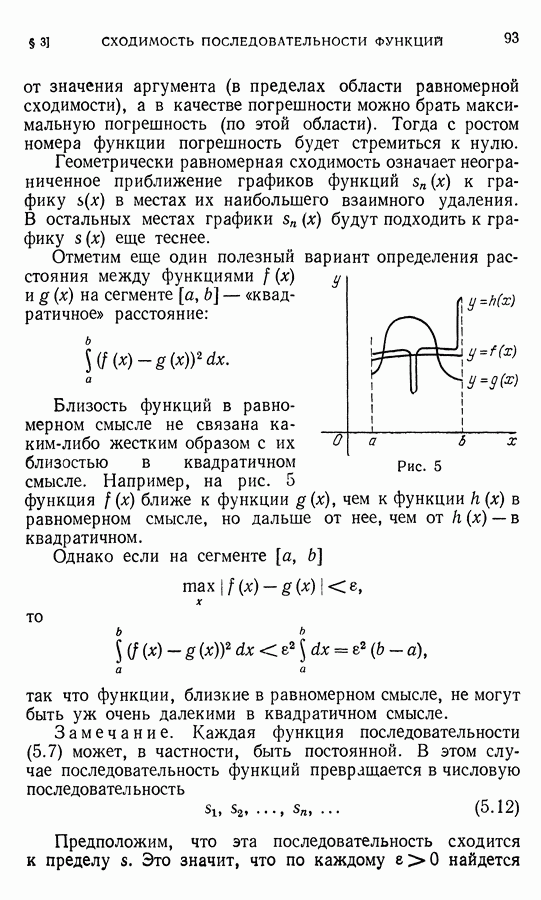
- § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса
- § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами
- § 9. Почленное интегрирование функциональных рядов
- § 10. Почленное дифференцирование функциональных рядов
- ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ
- § 2. Теорема Абеля
- § 3. Круг сходимости ряда
- § 4. Вещественный степенной ряд и его интервал сходимости
- § 5. Равномерная сходимость ряда в круге его сходимости
- § 6. Вещественные ряды
- § 7. Комплексные ряды
- § 8. Разложение функций в степенные ряды
- § 9. Формула Тейлора
- § 10. Ряды Тейлора и Маклорена
- ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ
- § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x
- § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x
- § 4. Показательная функция с комплексным значением показателя
- § 5. Формулы Эйлера
- § 6. Тригонометрические функции от комплексного значения аргумента
- § 7. Гиперболические функции от комплексного значения аргумента
- § 8. Вычисление значений функций при помощи ряда Маклорена
- § 9. Биномиальный ряд
- § 10. Приложения биномиального ряда
- § 11. Разложение в ряд Маклорена логарифмической функции
- § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов
- § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов
- ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 2. Векторы и функции
- § 3. Нормированные и ортогональные функции
- § 4. Нормированные и ортогональные системы функций
- § 5. Нормировка систем функций
- § 6. Разложение по системам функций
- ГЛАВА 9. РЯДЫ ФУРЬЕ
- § 1. Ряды и коэффициенты Фурье
- § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье
- § 3. Разложение периодических функций в ряд Фурье
- § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье
- § 5. Разложение функции f(x) = x
- § 6. Сдвиг сегмента разложения
- § 7. Изменение длины сегмента разложения
- § 8. Четные и нечетные функции
- § 9. Разложение четной функции в ряд Фурье
- § 10. Разложение нечетной функции в ряд Фурье
- § 11. Разложение ряд Фурье функций на сегменте от 0 до пи
- § 12. Комплексная форма записи ряда Фурье
- § 13. Разложение в комплексный ряд Фурье
- § 14. Характер сходимости рядов Фурье
- ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ
- § 2. Начальные и граничные условия
- § 3. Метод разделения переменных
- § 4. Использование граничных условий. Собственные функции и собственные значения
- § 5. Использование начальных условий
- ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ
- § 1. Представление функций интегралом Фурье
- § 2. Простейшие достаточные условия представимости функции интегралом Фурье
- § 3. Интеграл Фурье для четных функций
- § 4. Интеграл Фурье для нечетных функций
- § 5. Комплексная форма интеграла Фурье
- § 6. Понятие о преобразовании Фурье
- § 7. Косинус-преобразование Фурье
- § 8. Синус-преобразование Фурье
- § 9. Спектральная функция
- Часть II
- § 1. Признак сходимости Куммера
- § 2. Признак сходимости Раабе
- § 3. Признак сходимости Бертрана
- § 4. Признак сходимости Гаусса
- § 5. Сходимость знакопеременных рядов
- § 6. Признак сходимости Дирихле
- ГЛАВА 13. ДВОЙНЫЕ РЯДЫ
- § 1. Определение двойного ряда
- § 2. Сходимость двойных рядов
- § 3. Критерии сходимости двойных рядов. Теорема Маркова
- § 4. Свойства двойных рядов и признаки сходимости
- § 5. Абсолютная сходимость двойных рядов
- § 6. Двойные функциональные ряды
- § 7. Двойные степенные ряды
- § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена
- § 9. Ортогональные и ортонормальные системы функций от двух переменных
- § 10. Двойные ряды Фурье
- ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ
- § 2. Линейные преобразования рядов
- § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов
- § 4. Последовательности разностей
- § 5. Преобразование рядов по Эйлеру
- § 6. Преобразование рядов по Куммеру
- ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
- § 1. Расходящиеся геометрические прогрессии
- § 2. Суммирующие функции
- § 3. Суммирование по Пуассону — Абелю
- § 4. Линейность и регулярность суммирования по Пуассону — Абелю
- § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость
- § 6. Теорема Таубера
- § 7. Суммирование по Чезаро
- § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю
- § 9. Суммирование по Эйлеру
- ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ
- § 2. Исследование двух интегралов
- § 3. Исследование одного класса интегралов
- § 4. Доказательство теоремы Дирихле
- § 5. Теорема Фурье
- § 6. Коэффициенты Фурье разрывных функций
- § 7. Скорость сходимости рядов Фурье
- § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей
- § 9. О равномерной сходимости рядов Фурье
- § 10. Неравномерная сходимость последовательностей непрерывных функций
- § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса
- § 12. Экстремальное свойство сумм Фурье
- § 13. Суммирование рядов Фурье по Чезаро. Теорема Фейера
- § 14. Равенство Парсеваля
- § 15. Теорема Вейерштрасса
- ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК
- § 2. Изгиб балки
- § 3. Свободно опертая балка
- § 4. Первая возможность ограничиться двукратным дифференцированием
- § 5. Случай сосредоточенной нагрузки
- § 6. Прогиб балки от распределенной нагрузки
- § 7. Прогиб от сосредоточенного момента
- § 8. Статически неопределимая балка
- § 9. Сложный изгиб балки
- § 10. Балка на упругом основании
- § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки
- § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок
- § 13. Функции прогиба с ортогональными вторыми производными
- § 14. Свободно опертая нагруженная балка
- § 15. Работа продольных сил при сложном изгибе балки
- § 16. Общий случай изгиба балки
- § 17. Общий случай изгиба свободно опертой балки
- § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам
- § 19. Функция прогиба симметрично загруженной балки с жестко заделанными концами