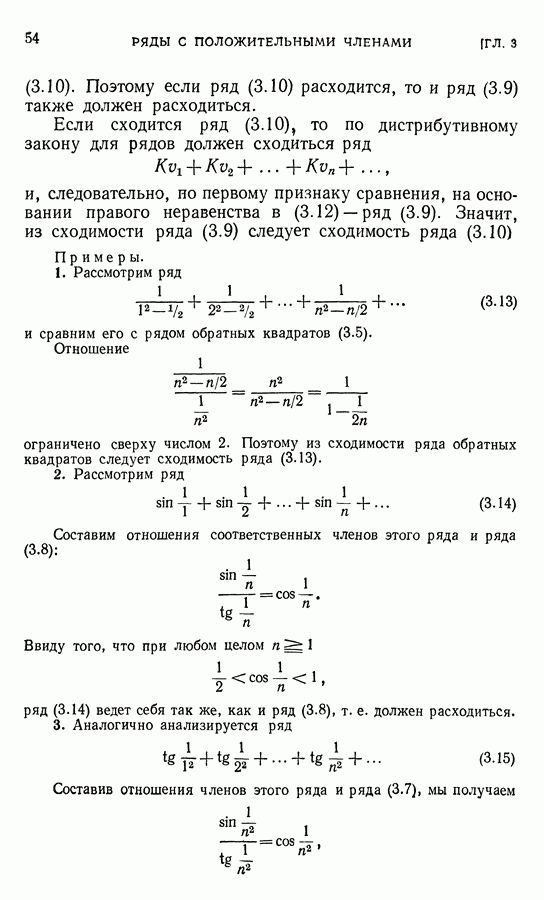
§ 3. Сходимость последовательности функций. Основные определения

Сейчас нам придется вспомнить некоторые факты, касающиеся сходимости последовательности функций. Определение. Последовательность функций

сходится к предельной функции в точке если

т. е. если для каждого найдется такое , что при

Определение. Последовательность функций

сходится к предельной функции в некоторой области (например, в сегменте или в интервале если для каждого из этой области

т. е. если для каждого из нашей области найдется такое «0, что при

Заметим, что в этом определении находится по каждому из нашей области, т. е., вообще говоря, зависит от Несколько иной факт описывается в следующем определении.

Определение. Последовательность функций

сходится к предельной функции равномерно в некоторой данной области, если для каждого существует такое что при и при любом из области

Подчеркнем, что, в отличие от предыдущего определения, здесь утверждается существование в равной мере «обслуживающего» все значения

Различие между описанными видами сходимости последовательностей функций можно наглядно представить себе геометрически.

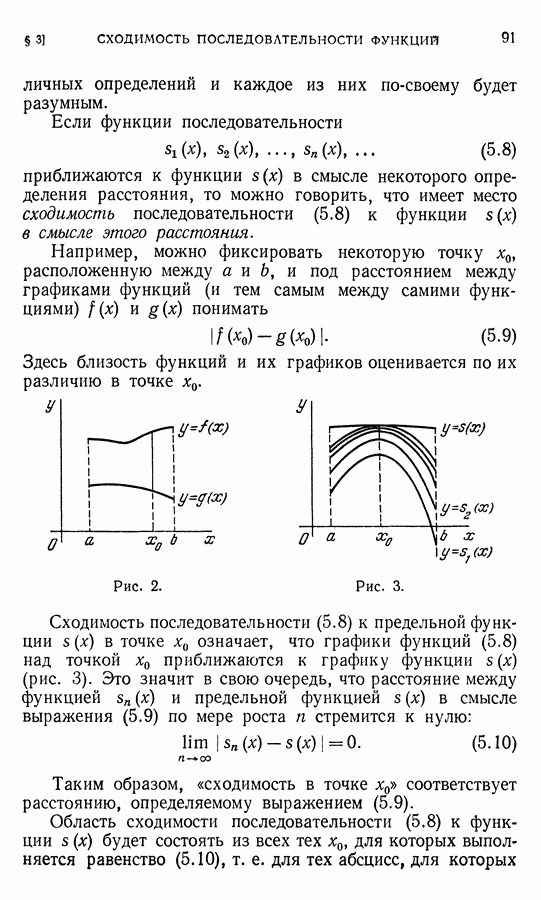
Рассмотрим графики двух функций заданных на некотором промежутке с концами (рис. 2). Ясно, что эти графики могут располагаться «близко» или «далеко» друг от друга. Однако если расстояние между точками на координатной плоскости понимается вполне определенным образом, то расстояние между графиками функций нуждается в специальном определении. Оказывается, что этому расстоянию можно дать несколько

различных определений и каждое из них по-своему будет разумным.

Если функции последовательности

приближаются к функции в смысле некоторого определения расстояния, то можно говорить, что имеет место сходимость последовательности (5.8) к функции в смысле этого расстояния.

Например, можно фиксировать некоторую точку расположенную между и под расстоянием между графиками функций (и тем самым между самими функциями) понимать

Здесь близость функций и их графиков оценивается по их различию в точке

Рис. 2.

Рис. 3.

Сходимость последовательности (5.8) к предельной функции в точке означает, что графики функций (5.8) над точкой приближаются к графику функции (рис. 3). Это значит в свою очередь, что расстояние между функцией и предельной функцией в смысле выражения (5.9) по мере роста стремится к нулю:

Таким образом, «сходимость в точке соответствует расстоянию, определяемому выражением (5.9).

Область сходимости последовательности (5.8) к функции будет состоять из всех тех для которых выполняется равенство (5.10), т. е. для тех абсцисс, для которых

графики функций из последовательности неограниченно приближаются к графику функции

Вместе с тем расстояние между функциями можно описывать не выражением (5.9), а иначе. Например, за расстояние между функциями можно принимать максимальную разность между соответствующими значениями функций

(рис. 4). В тех случаях, когда написанный максимум не достигается, вместо него следует рассматривать точную верхнюю границу значений (Напомним, что точной верхней границей будет в этом случае число, которое не меньше каждого из модулей разностей и к которому значения этих модулей разностей подходят сколь угодно близко.)

Рис. 4.

Приближение в смысле так определенного расстояния функций из последовательности (5.8) к функции означает, что

т. е. каково бы ни было начиная с некоторого будет

Иными словами, каково бы ни было начиная с некоторого при любом х будет

Это и было выше определено как равномерная сходимость последовательности (5.8) к функции на промежутке от а до

При рассмотрении сходимости последовательности функций к предельной функции можно говорить о точности, с которой функции последовательности описывают предельную функцию, или, что то же самое, — о погрешности при таком описании. В условиях равномерной сходимости точность такого описания не зависит

от значения аргумента (в пределах области равномерной сходимости), а в качестве погрешности можно брать максимальную погрешность (по этой области). Тогда с ростом номера функции погрешность будет стремиться к нулю.

Геометрически равномерная сходимость означает неограниченное приближение графиков функций к графику в местах их наибольшего взаимного удаления. В остальных местах графики будут подходить к графику еще теснее.

Рис. 5

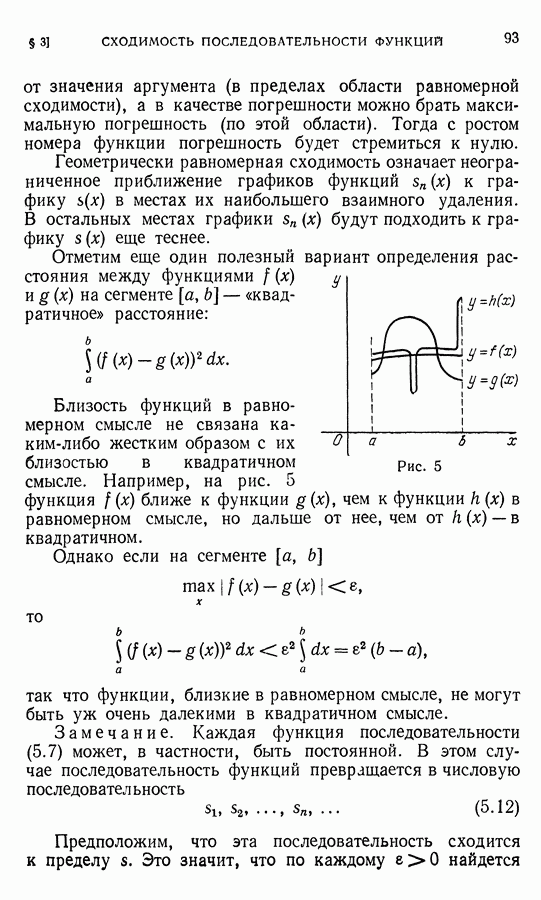
Отметим еще один полезный вариант определения расстояния между функциями на сегменте — «квадратичное» расстояние:

Близость функций в равномерном смысле не связана каким-либо жестким образом с их близостью в квадратичном смысле. Например, на рис. 5 функция ближе к функции чем к функции в равномерном смысле, но дальше от нее, чем от — в квадратичном.

Однако если на сегменте

то

так что функции, близкие в равномерном смысле, не могут быть уж очень далекими в квадратичном смысле.

Замечание. Каждая функция последовательности (5.7) может, в частности, быть постоянной. В этом случае последовательность функций превращается в числовую последовател ьность

Предположим, что эта последовательность сходится к пределу Это значит, что по каждому найдется

такое что при

Находимое так никак не зависит от какого бы то ни было х. Поэтому мы с полным основанием можем формально считать, что последовательность (5.12), т. е. числовой ряд, сходится равномерно для всех значений х.

Пример. Рассмотрим более подробно, чем это было сделано в § 5 главы 1, вопрос о сходимости последовательности функций

Эта последовательность сходится к предельной функции например, в точке Действительно,

Мы можем утверждать также, что рассматриваемая последовательность функций сходится к предельной — функции для всех ибо действительно, для любого из [0, 1) по всякому найдется такое что для

Заметим, однако, что по мере приближения к единице для каждого данного приходится брать все большие и большие значения степени по мере приближения оснований к единице убывают все медленнее и медленнее Достаточно сравнить, например, последовательности

и

Это наводит нас на мысль, что в данном случае по нельзя найти такого что при любом для будет

Такая мысль верна. В самом деле, предположим, что по какому-то (пусть для конкретности будет такое годное для всех нашлось. Это значит, что

для всех из [0, 1). Но этого не может быть, так как в действительности последнее неравенство выполняется не для всех а лишь для тех, для которых

Следовательно, сходимость последовательности функций (5.13) к предельной функции хотя и имеет место для любого х из [0, 1), но не является равномерной сходимостью для

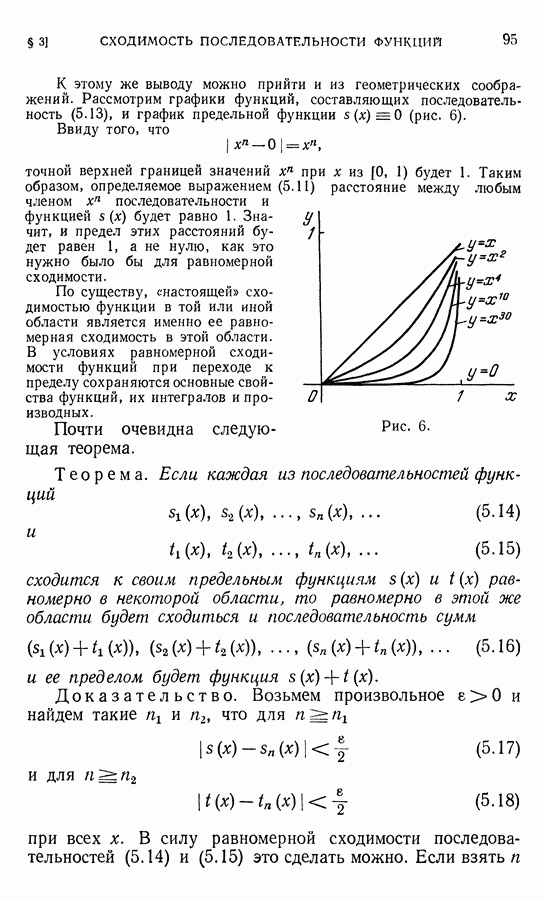
К этому же выводу можно прийти и из геометрических соображений. Рассмотрим графики функций, составляющих последовательность (5.13), и график предельной функции (рис. 6).

Ввиду того, что

точной верхней границей значений при х из [0, 1) будет 1. Таким образом, определяемое выражением (5.11) расстояние между любым членом последовательности и функцией будет равно 1. Значит, и предел этих расстояний будет равен 1, а не нулю, как это нужно было бы для равномерной сходимости.

Рис. 6.

По существу, «настоящей» сходимостью функции в той или иной области является именно ее равномерная сходимость в этой области.

В условиях равномерной сходимости функций при переходе к пределу сохраняются основные свойства функций, их интегралов и производных.

Почти очевидна следующая теорема.

Теорема. Если каждая из последовательностей функций

и

сходится к своим предельным функциям равномерно в некоторой области, то равномерно в этой же области будет сходиться и последовательность сумм

и ее пределом будет функция

Доказательство. Возьмем произвольное и найдем такие что для

и для

при всех х. В силу равномерной сходимости последовательностей (5.14) и (5.15) это сделать можно. Если взять

превосходящим как так и то оба неравенства — (5.17) и (5.18) — будут выполняться.

Сложив эти неравенства, мы получим

по-прежнему при всех . Это означает равномерную сходимость последовательности (5.16).

Утверждение этой теоремы очевидным образом распространяется на суммы произвольного конечного числа слагаемых.