ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ

§ 1. Проекции и разложения векторов

Данный параграф является вспомогательным. В нем излагаются элементарные сведения по векторной алгебре. Читатель, знакомый с ними, может этот параграф при чтении пропустить.

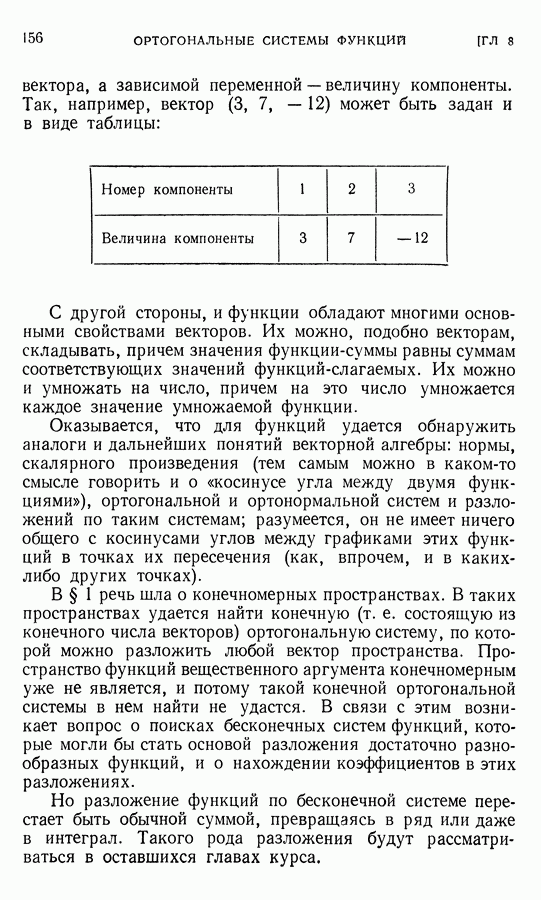
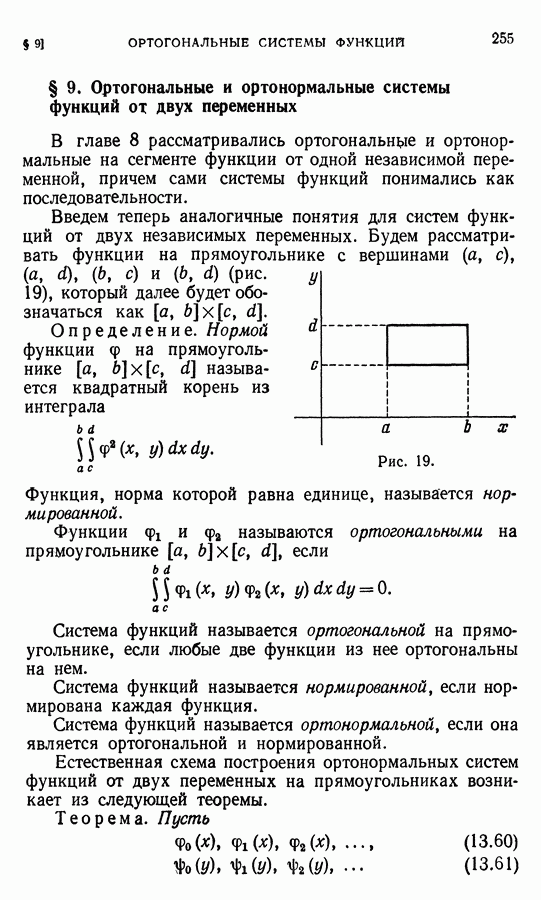
Далее длина любого вектора а будет обозначаться через Иногда длина вектора называется его нормой. Подчеркнем, что длина любого вектора является неотрицательным числом. Пусть вектор а расположен на оси Припишем в этом случае его длине знак если направление а совпадает с направлением и знак если эти направления противоположны. Длину вектора на оси, рассматриваемую вместе с приписанным ей знаком, будем называть алгебраической длиной вектора на оси.

Проекцией вектора а на ось (на направление) называется вектор, расположенный на оси алгебраическая длина которого равна

Далее мы будем рассматривать координатные пространства и векторы, проведенные из начала координат в каждую точку пространства.

Рассмотрим сначала обычное трехмерное векторное пространство с ортами и к, соответствующими направлениям координатных осей X, Y и Любая линейная комбинация этих ортов, т. е. любая сумма вида

где и — вещественные числа, является вектором рассматриваемого пространства. Коэффициенты и называются компонентами вектора (8.2). Сложение векторов осуществляется сложением их соответствующих

компонент, а умножение вектора на число — умножением каждой из компонент на это число.

Наоборот, какой бы мы вектор а в пространстве ни взяли, можно найти такие числа что а приобретает вид (8.2). Таким образом, можно говорить, что каждый вектор а трехмерного пространства может быть разложен «по векторам» и к.

Геометрический смысл компонент в разложении (8.2) данного вектора а достаточно прост, но вместе с тем чрезвычайно важен, и его обобщение послужит нам удобной иллюстрацией при наглядном истолковании разложения функций в ряды.

Эти компоненты суть алгебраические длины проекций вектора а соответственно на координатные оси и

Если есть координатная ось X, то (8.1) приобретает

Перепишем это выражение в координатной форме.

Прежде всего, из теоремы Пифагора следует, что если вектор а имеет вид (8.2), то длина его равна

Кроме того, мы видели, что алгебраическая длина проекции вектора (8.2) на ось X есть х. Учитывая (8.3), это можно записать как

откуда

Но, очевидно,

и (8.4) переписывается как

Аналогично получается, что

Возьмем теперь вектор

Алгебраическая длина проекции на направление вектора а есть сумма алгебраических длин проекций трех векторов на это направление. Но согласно (8,1) эти алгебраические длины будут равны соответственно

(для тех компонент которые неотрицательны, эти выражения просто совпадают с (8.1); для отрицательных же компонент направления соответствующих векторов или противоположны направлениям своих осей, и косинусы изменят знаки, компенсируя отрицательность компонент).

Таким образом, алгебраическая длина проекции на а будет равна

или, учитывая (8.5), (8.6) и (8.7),

Вместе с тем на основании формулы (8.1) эта проекция есть

а

Из (8.8), (8.9) и (8.10) следует, что

Стоящее здесь в числителе выражение

называется скалярным произведением векторов и обычно обозначается через

В частности, при

Непосредственно из определения скалярного произведения видно, что эта операция обладает свойствами коммутативности:

и дистрибутивности относительно действий сложения вектора и умножения вектора на число:

Однако закону ассоциативности скалярное умножение, вообще говоря, не подчиняется: есть вектор с тем же направлением, что и вектор с, а вектор — с тем же направлением, что и а. Поэтому в скалярных произведениях более чем двух векторов порядок выполнения умножений обязательно следует отмечать скобками.

В терминах скалярных произведений и норм формулу (8.11) можно переписать, как

В связи с этим алгебраическая длина проекции на направление вектора а равна

Выраженная в длинах вектора а, она приобретает вид

Важным частным случаем взаимного расположения векторов является тот, когда они взаимно перпендикулярны. Перпендикулярные векторы называются также ортогональными. Очевидно, нулевой вектор, т. е. вектор, все компоненты которого равны нулю, ортогонален любому вектору (в том числе он является единственным вектором, который ортогонален самому себе). Если нам дан некоторый набор векторов, в котором любые два вектора ортогональны друг другу, то этот набор называется ортогональной системой векторов. Говоря о векторах, составляющих ортогональную систему, мы будем считать, что среди этих векторов нет нулевого. Очевидно, всякая

ортогональная система векторов в трехмерном пространстве состоит не более чем из трех векторов

Если векторы ортогональны, то косинус угла между ними обращается в нуль и (8.11) дает нам

Пусть теперь — произвольная ортогональная система векторов, а вектор х является их линейной комбинацией:

Коэффициенты можно выразить через скалярные произведения. Умножим для этого каждую часть (8.13) скалярно на

Но

а ввиду взаимной ортогональности векторов

Следовательно, (8.14) приобретает вид

откуда

Сравнение с формулой (8.12) показывает, что есть алгебраическая длина проекции х на направление выраженная в длинах вектора

Аналогично скалярное умножение (8.13) на дает соответственно

Таким образом, формулу (8.13) можно записать как

Правую часть этой формулы называют разложением вектора х по ортогональной системе

В действительности любой вектор х трехмерного пространства может быть представлен в виде (8.13) и тем

самым в виде (8.17). Мы, однако, намеренно оставляем в стороне этот вопрос, ограничиваясь следующим утверждением: если вектор х имеет вид (8.13), то соответствующие коэффициенты вычисляются по формулам (8.15) и (8.16). Условие: имеет вид...» —не является тривиальным. Проиллюстрируем его содержательность на следующем примере. Пусть нам даны два ортогональных вектора, и вектор х, представленный в виде

Тогда, действуя, как и выше, мы получаем

Очевидно, не всякий вектор трехмерного пространства представим в виде (8.18) (например, если то в виде их линейных комбинаций можно представлять лишь векторы, лежащие в плоскости Однако если это имеет место, то справедлива формула (8.19).

Обратимся к важному частному случаю. Будем называть вектор нормированным, если его длина (норма) равна 1. Система векторов называется нормированной, если каждый входящий в нее вектор нормирован. Очевидно, для превращения вектора в нормированный (или, как говорят, для его нормировки) достаточно разделить вектор на его длину, на его норму.

Ортогональная и нормированная система векторов обычно называется ортонормальной (или ортонормированной) системой.

Вернемся теперь к ортогональной системе векторов и предположим, что она является ортонормальной, т. е. что

В этом случае формула (8.17) приобретает особенно простой вид:

т. е. коэффициенты разложения вектора по ортонормальной системе являются скалярными его произведениями на векторы системы.

Примером ортонормальной системы является тройка векторов , и само задание вектора в виде (8.2) является его разложением по этой системе.

Все сказанное выше можно перенести и на случай конечномерного, -мерного пространства, в котором векторы являются последовательностями из вещественных чисел:

Сложение -мерных векторов и умножение их на вещественные числа, как и в трехмерном случае, производятся покомпонентно.

Компоненты вектора (8.21) можно понимать как алгебраические длины его проекций на координатные оси За длину вектора х естественно принять выражение

Рассматривая плоскость, проходящую через ось вектора х и координатную ось , мы имеем

Если ввести другой вектор

то, подобно тому, как это было в трехмерном пространстве,

где стоящее в числителе выражение называется скалярным произведением векторов х и у. Как и в трехмерном случае, оно обозначается через и является операцией, коммутативной и дистрибутивной относительно сложения векторов и относительно умножения вектора на число.

Называя векторы в -мерном пространстве ортогональными, если их скалярное произведение равно нулю, мы можем говорить об ортогональных системах векторов в -мерном пространстве. Ясно, что в -мерном пространстве ортогональная система векторов может состоять не более чем из векторов.

Пусть произвольная ортогональная система векторов в -мерном пространстве, а вектор х имеет вид

Тогда, умножая это равенство скалярно на получаем, что т. е.

Правая часть этой формулы называется разложением вектора х по ортогональной системе ат.

Если векторы нормированные, т. е. если

то система называется ортонормальной и формула (8.22) приобретает вид

Из наглядных соображений видно (строгого доказательства мы приводить не будем), что при не всякий вектор пространства может быть разложен по системе . Однако из сказанного следует, что если он все-таки разлагается, то это разложение имеет вполне определенный вид, описываемый в (8.22), а для случая ортонормальной системы — в (8.23).

Наконец, если мы умножим почленно равенство (8.23) скалярно на х, то очевидно, получим

Эта формула является многомерным аналогом теоремы Пифагора.

В качестве примера ортонормальной системы в -мерном пространстве векторов (8.21) можно указать систему векторов («координатных ортов»):

По этой системе разлагается любой вектор (8.21) и коэффициентами разложения являются сами компоненты вектора.