| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8. Четные и нечетные функции
Как было установлено, задачу разложения функции  в ряд Фурье на произвольном сегменте
в ряд Фурье на произвольном сегменте  можно свести к задаче разложения несколько видоизмененной функции на сегменте
можно свести к задаче разложения несколько видоизмененной функции на сегменте  . Поэтому мы далее будем ограничиваться только этим свойством.
. Поэтому мы далее будем ограничиваться только этим свойством.
Итак, пусть функция  задана на сегменте
задана на сегменте  и удовлетворяет условиям Дирихле. Займемся исследованием двух частных случаев.
и удовлетворяет условиям Дирихле. Займемся исследованием двух частных случаев.
Напомним, что функция  называется четной, если
называется четной, если

во всей области ее задания; и нечетной, если

(также для всех тех  для которых значение функции определено).
для которых значение функции определено).
Как легко проверить, произведение четной функции на четную, равно как и нечетной на нечетную, четно, а произведение четной и нечетной функции нечетно.
Очевидно, если функция  нечетная, то
нечетная, то

а если функция  четная, то
четная, то

Четность функций изменяется при их дифференцировании и интегрировании.
Теорема 1. Производная четной функции является нечетной функцией, а производная нечетной функции — четной.
Доказательство. Пусть функция  — четная. Тогда при любых
— четная. Тогда при любых  должно быть
должно быть

откуда  или, переходя к пределу,
или, переходя к пределу,

Случай нечетной функции  рассматривается аналогично.
рассматривается аналогично.
Следствие. Вторая производная четной функции четна, а нечетной — нечетна.
Теорема 2. Если функция  нечетна, то ее первообразная
нечетна, то ее первообразная  четна.
четна.
Если функция  четна, а для ее первообразной
четна, а для ее первообразной  имеет место
имеет место  то функция
то функция  нечетна.
нечетна.
Доказательство. Пусть функция  нечетна. Тогда
нечетна. Тогда

Если функция  четна, то при
четна, то при 

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Часть I
- ГЛАВА 1. ПРОГРЕССИИ
- § 2. Геометрические прогрессии
- § 3. Бесконечные прогрессии; их сходимость и расходимость
- § 4. Элементарные преобразования прогрессий
- § 5. Функциональные прогрессии: область сходимости; равномерная сходимость
- § 6. Почленное интегрирование прогрессий
- § 7. Почленное дифференцирование прогрессий
- § 8. Прогрессии с комплексными членами
- ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ
- § 2. Определение числового ряда и его сходимости
- § 3. Остаток ряда
- § 4. Принцип сходимости Коши
- § 5. Критерий Коши сходимости рядов
- § 6. Необходимый признак сходимости ряда
- § 7. Желательность систематической теории
- § 8. Свойства сходящихся рядов, подобные свойствам сумм
- § 9. Дальнейшие свойства рядов
- ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
- § 1. Признаки сходимости рядов
- § 2. Признаки сравнения
- § 3. Интегральный признак сходимости Маклорена — Коши
- § 4. Применения интегрального признака сходимости
- § 5. Сравнительная оценка различных признаков сходимости
- § 6. Признак сходимости Даламбера
- § 7. Признак сходимости Коши
- § 8. Чувствительность признаков сходимости Даламбера и Коши
- ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- § 2. Абсолютная сходимость и расходимость
- § 3. Возможность переставлять члены в абсолютно сходящихся рядах
- § 4. Условно сходящиеся знакопеременные ряды
- § 5. Умножение абсолютно сходящихся рядов
- § 6. Признак сходимости Лейбница
- § 7. Существенность условий признака сходимости Лейбница
- ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 2. Область сходимости функционального ряда
- § 3. Сходимость последовательности функций. Основные определения
- § 4. Предел последовательности непрерывных функций
- § 5. Переход к пределу под знаком интеграла
- § 6. Переход к пределу под знаком производной
- § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса
- § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами
- § 9. Почленное интегрирование функциональных рядов
- § 10. Почленное дифференцирование функциональных рядов
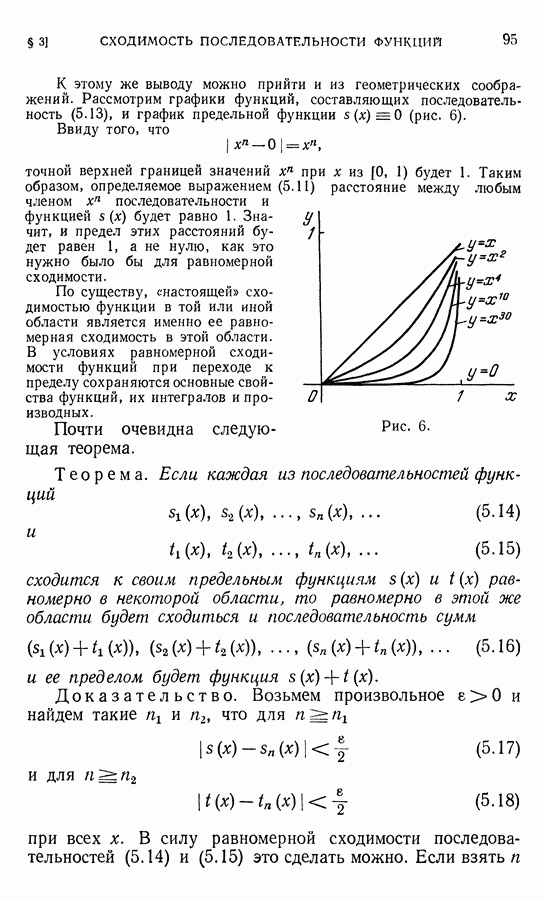
- ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ
- § 2. Теорема Абеля
- § 3. Круг сходимости ряда
- § 4. Вещественный степенной ряд и его интервал сходимости
- § 5. Равномерная сходимость ряда в круге его сходимости
- § 6. Вещественные ряды
- § 7. Комплексные ряды
- § 8. Разложение функций в степенные ряды
- § 9. Формула Тейлора
- § 10. Ряды Тейлора и Маклорена
- ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ
- § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x
- § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x
- § 4. Показательная функция с комплексным значением показателя
- § 5. Формулы Эйлера
- § 6. Тригонометрические функции от комплексного значения аргумента
- § 7. Гиперболические функции от комплексного значения аргумента
- § 8. Вычисление значений функций при помощи ряда Маклорена
- § 9. Биномиальный ряд
- § 10. Приложения биномиального ряда
- § 11. Разложение в ряд Маклорена логарифмической функции
- § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов
- § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов
- ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 2. Векторы и функции
- § 3. Нормированные и ортогональные функции
- § 4. Нормированные и ортогональные системы функций
- § 5. Нормировка систем функций
- § 6. Разложение по системам функций
- ГЛАВА 9. РЯДЫ ФУРЬЕ
- § 1. Ряды и коэффициенты Фурье
- § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье
- § 3. Разложение периодических функций в ряд Фурье
- § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье
- § 5. Разложение функции f(x) = x
- § 6. Сдвиг сегмента разложения
- § 7. Изменение длины сегмента разложения
- § 8. Четные и нечетные функции
- § 9. Разложение четной функции в ряд Фурье
- § 10. Разложение нечетной функции в ряд Фурье
- § 11. Разложение ряд Фурье функций на сегменте от 0 до пи
- § 12. Комплексная форма записи ряда Фурье
- § 13. Разложение в комплексный ряд Фурье
- § 14. Характер сходимости рядов Фурье
- ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ
- § 2. Начальные и граничные условия
- § 3. Метод разделения переменных
- § 4. Использование граничных условий. Собственные функции и собственные значения
- § 5. Использование начальных условий
- ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ
- § 1. Представление функций интегралом Фурье
- § 2. Простейшие достаточные условия представимости функции интегралом Фурье
- § 3. Интеграл Фурье для четных функций
- § 4. Интеграл Фурье для нечетных функций
- § 5. Комплексная форма интеграла Фурье
- § 6. Понятие о преобразовании Фурье
- § 7. Косинус-преобразование Фурье
- § 8. Синус-преобразование Фурье
- § 9. Спектральная функция
- Часть II
- § 1. Признак сходимости Куммера
- § 2. Признак сходимости Раабе
- § 3. Признак сходимости Бертрана
- § 4. Признак сходимости Гаусса
- § 5. Сходимость знакопеременных рядов
- § 6. Признак сходимости Дирихле
- ГЛАВА 13. ДВОЙНЫЕ РЯДЫ
- § 1. Определение двойного ряда
- § 2. Сходимость двойных рядов
- § 3. Критерии сходимости двойных рядов. Теорема Маркова
- § 4. Свойства двойных рядов и признаки сходимости
- § 5. Абсолютная сходимость двойных рядов
- § 6. Двойные функциональные ряды
- § 7. Двойные степенные ряды
- § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена
- § 9. Ортогональные и ортонормальные системы функций от двух переменных
- § 10. Двойные ряды Фурье
- ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ
- § 2. Линейные преобразования рядов
- § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов
- § 4. Последовательности разностей
- § 5. Преобразование рядов по Эйлеру
- § 6. Преобразование рядов по Куммеру
- ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
- § 1. Расходящиеся геометрические прогрессии
- § 2. Суммирующие функции
- § 3. Суммирование по Пуассону — Абелю
- § 4. Линейность и регулярность суммирования по Пуассону — Абелю
- § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость
- § 6. Теорема Таубера
- § 7. Суммирование по Чезаро
- § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю
- § 9. Суммирование по Эйлеру
- ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ
- § 2. Исследование двух интегралов
- § 3. Исследование одного класса интегралов
- § 4. Доказательство теоремы Дирихле
- § 5. Теорема Фурье
- § 6. Коэффициенты Фурье разрывных функций
- § 7. Скорость сходимости рядов Фурье
- § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей
- § 9. О равномерной сходимости рядов Фурье
- § 10. Неравномерная сходимость последовательностей непрерывных функций
- § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса
- § 12. Экстремальное свойство сумм Фурье
- § 13. Суммирование рядов Фурье по Чезаро. Теорема Фейера
- § 14. Равенство Парсеваля
- § 15. Теорема Вейерштрасса
- ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК
- § 2. Изгиб балки
- § 3. Свободно опертая балка
- § 4. Первая возможность ограничиться двукратным дифференцированием
- § 5. Случай сосредоточенной нагрузки
- § 6. Прогиб балки от распределенной нагрузки
- § 7. Прогиб от сосредоточенного момента
- § 8. Статически неопределимая балка
- § 9. Сложный изгиб балки
- § 10. Балка на упругом основании
- § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки
- § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок
- § 13. Функции прогиба с ортогональными вторыми производными
- § 14. Свободно опертая нагруженная балка
- § 15. Работа продольных сил при сложном изгибе балки
- § 16. Общий случай изгиба балки
- § 17. Общий случай изгиба свободно опертой балки
- § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам
- § 19. Функция прогиба симметрично загруженной балки с жестко заделанными концами