| << Предыдущий параграф | Следующий параграф >> |
Пред.
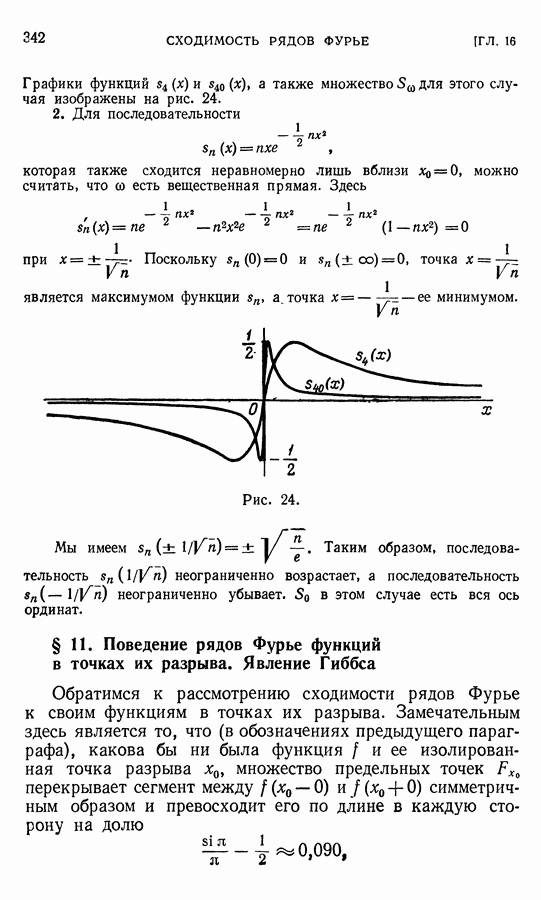
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Показательная функция с комплексным значением показателя
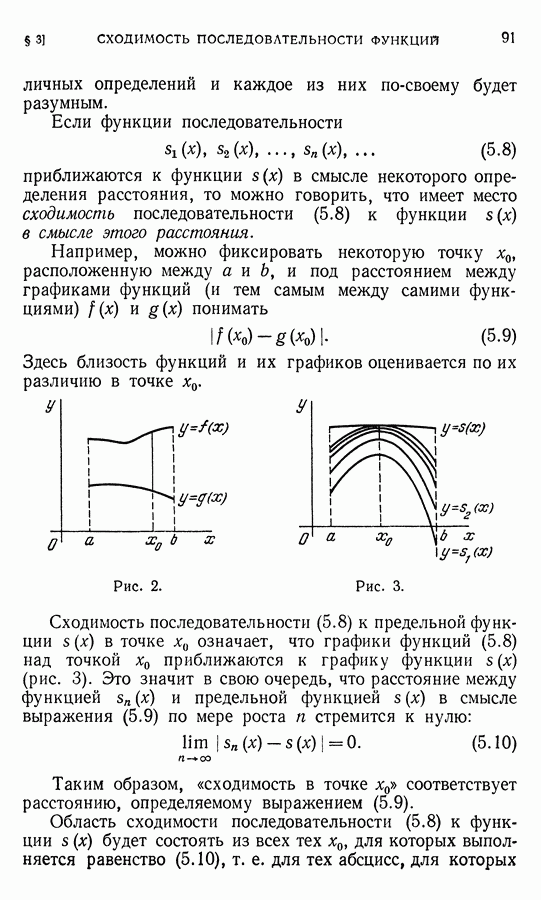
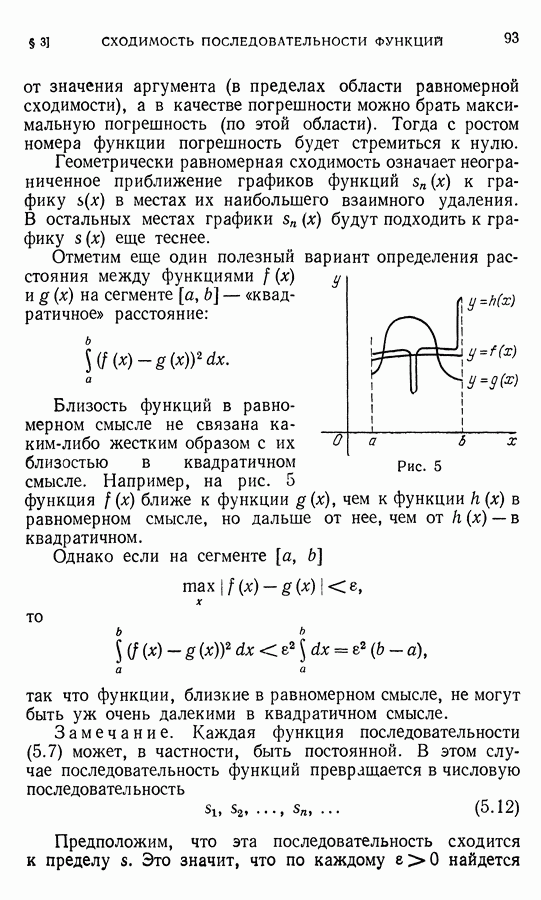
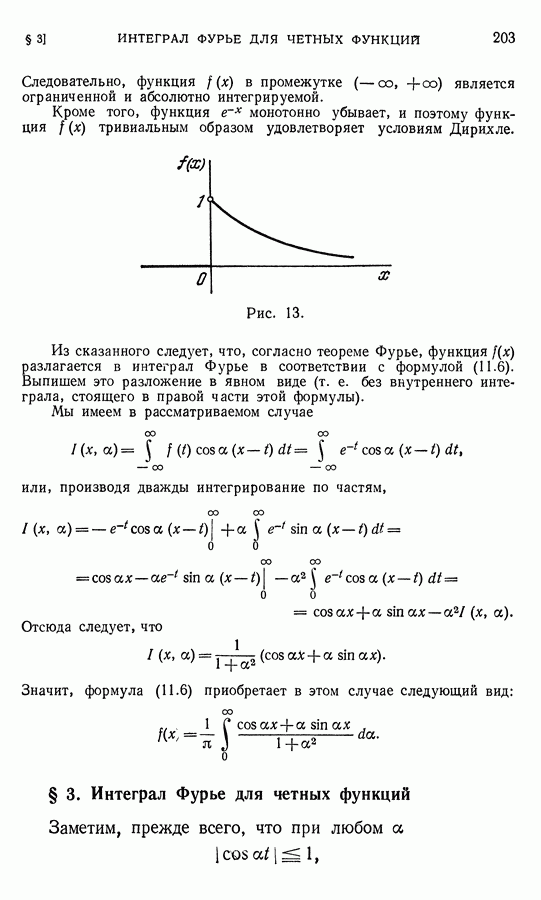
Займемся определением показательной функции  где
где  — вещественное и неотрицательное число, а показатель
— вещественное и неотрицательное число, а показатель  может принимать не только вещественные, но и комплексные значения. Для этого можно взять некоторое характеристическое свойство функций
может принимать не только вещественные, но и комплексные значения. Для этого можно взять некоторое характеристическое свойство функций  для вещественных значений х (т. е. такое свойство, которым обладают только эти функции), которое поддается переносу на случай комплексных значений независимого переменного, и, пользуясь именно этим свойством, распространить определение функции на комплексные значения аргумента.
для вещественных значений х (т. е. такое свойство, которым обладают только эти функции), которое поддается переносу на случай комплексных значений независимого переменного, и, пользуясь именно этим свойством, распространить определение функции на комплексные значения аргумента.
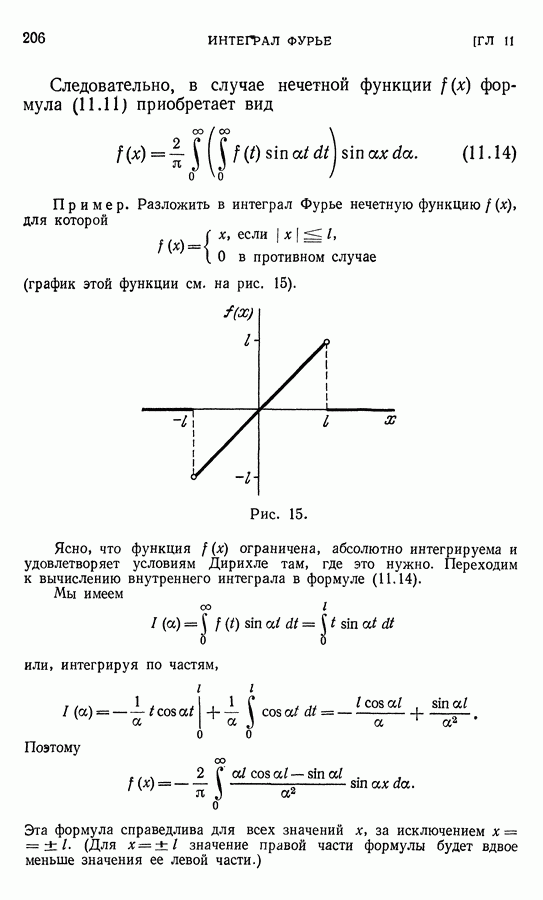
Нам будет удобно, положив  рассматривать функции
рассматривать функции

Лемма. Если непрерывная функция  отлична от тождественного нуля и такова, что для любых х и у
отлична от тождественного нуля и такова, что для любых х и у

то

при некотором а.
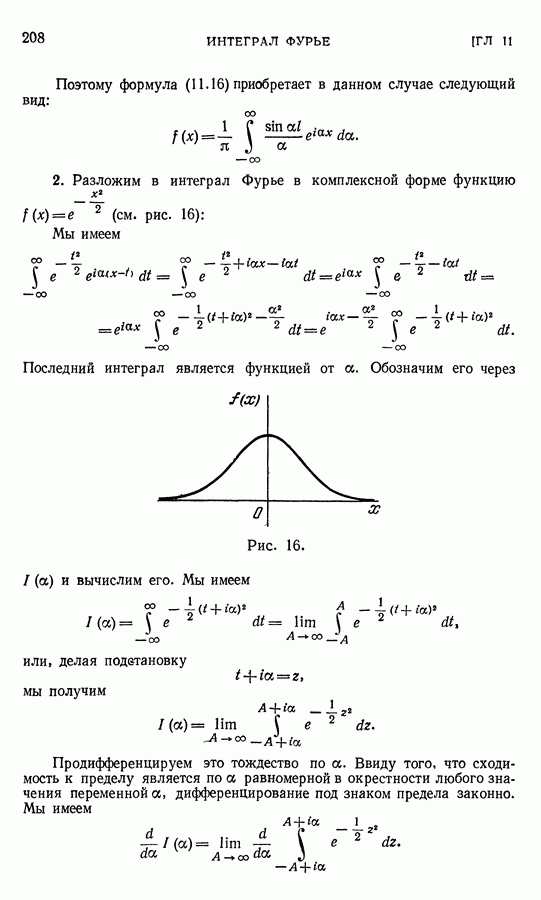
Доказательство. Прежде всего, возьмем такое х, что  . По условию леммы такое х непременно найдется. Для этого значения х должно быть
. По условию леммы такое х непременно найдется. Для этого значения х должно быть

откуда

Кроме того, мы имеем

Если бы было  то, очевидно, при любом целом
то, очевидно, при любом целом 

и в силу обусловленной непрерывности функции 

что противоречит (7.4). Значит, в (7.5) имеет место строгое неравенство.
Следовательно, найдется такое а, что

Далее, для любого значения х вида  (где
(где  — целое положительное число) мы имеем
— целое положительное число) мы имеем

откуда

Пусть теперь  где
где  — целое отрицательное число.
— целое отрицательное число.
Тогда  будет целым положительным числом, и мы на основании условия леммы имеем
будет целым положительным числом, и мы на основании условия леммы имеем

Но по предыдущему

так что (7.6) дает нам

Для рационального значения  должно быть поэтому
должно быть поэтому

Пусть, наконец, х принимает произвольное вещественное значение  Как известно, можно составить
Как известно, можно составить
последовательность рациональных чисел (например, десятичных дробей)  сходящихся к
сходящихся к 

Тогда на основании обусловленной непрерывности функции  и известной непрерывности функции
и известной непрерывности функции  будет
будет

Объединяя все сказанное, мы видим, что

для всех значений х, а это и требовалось.
Следствие. Если функция  удовлетворяет условиям леммы (т. е. при любых х и у выполняется равенство
удовлетворяет условиям леммы (т. е. при любых х и у выполняется равенство  и
и

то

Доказательство. Согласно лемме должно быть

и, в частности,

Вместе с (7.7) это дает нам  откуда и следует требуемое.
откуда и следует требуемое.
Теорема. Пусть значение функции  для любого вещественного или комплексного
для любого вещественного или комплексного  определено как сумма ряда
определено как сумма ряда

Тогда функция  непрерывна, отлична от тождественного нуля и для любых комплексных
непрерывна, отлична от тождественного нуля и для любых комплексных 

Доказательство. Ряд (7.8) сходится при любом вещественном значении  Следовательно, по теореме о непрерывности суммы ряда (§ 5 главы 6) f(z) является непрерывной при любом вещественном значении
Следовательно, по теореме о непрерывности суммы ряда (§ 5 главы 6) f(z) является непрерывной при любом вещественном значении 
функцией. Кроме того,  отлична от тождественного нуля (например,
отлична от тождественного нуля (например,  ).
).
По правилу умножения рядов «по Коши» (см. § 5 главы 4) мы имеем

или, объединяя слагаемые «по диагональным линиям», мы получаем

Из этой теоремы следует, что сумма ряда (7.8), как функция  обладает тем важным характеристическим свойством функции
обладает тем важным характеристическим свойством функции  которое выделяет ее из всех непрерывных функций. Поэтому естественно определить значение суммы ряда (7.8) при произвольном
которое выделяет ее из всех непрерывных функций. Поэтому естественно определить значение суммы ряда (7.8) при произвольном  вещественном или комплексном, как значение фунции
вещественном или комплексном, как значение фунции 

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Часть I
- ГЛАВА 1. ПРОГРЕССИИ
- § 2. Геометрические прогрессии
- § 3. Бесконечные прогрессии; их сходимость и расходимость
- § 4. Элементарные преобразования прогрессий
- § 5. Функциональные прогрессии: область сходимости; равномерная сходимость
- § 6. Почленное интегрирование прогрессий
- § 7. Почленное дифференцирование прогрессий
- § 8. Прогрессии с комплексными членами
- ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ
- § 2. Определение числового ряда и его сходимости
- § 3. Остаток ряда
- § 4. Принцип сходимости Коши
- § 5. Критерий Коши сходимости рядов
- § 6. Необходимый признак сходимости ряда
- § 7. Желательность систематической теории
- § 8. Свойства сходящихся рядов, подобные свойствам сумм
- § 9. Дальнейшие свойства рядов
- ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
- § 1. Признаки сходимости рядов
- § 2. Признаки сравнения
- § 3. Интегральный признак сходимости Маклорена — Коши
- § 4. Применения интегрального признака сходимости
- § 5. Сравнительная оценка различных признаков сходимости
- § 6. Признак сходимости Даламбера
- § 7. Признак сходимости Коши
- § 8. Чувствительность признаков сходимости Даламбера и Коши
- ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
- § 2. Абсолютная сходимость и расходимость
- § 3. Возможность переставлять члены в абсолютно сходящихся рядах
- § 4. Условно сходящиеся знакопеременные ряды
- § 5. Умножение абсолютно сходящихся рядов
- § 6. Признак сходимости Лейбница
- § 7. Существенность условий признака сходимости Лейбница
- ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- § 2. Область сходимости функционального ряда
- § 3. Сходимость последовательности функций. Основные определения
- § 4. Предел последовательности непрерывных функций
- § 5. Переход к пределу под знаком интеграла
- § 6. Переход к пределу под знаком производной
- § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса
- § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами
- § 9. Почленное интегрирование функциональных рядов
- § 10. Почленное дифференцирование функциональных рядов
- ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ
- § 2. Теорема Абеля
- § 3. Круг сходимости ряда
- § 4. Вещественный степенной ряд и его интервал сходимости
- § 5. Равномерная сходимость ряда в круге его сходимости
- § 6. Вещественные ряды
- § 7. Комплексные ряды
- § 8. Разложение функций в степенные ряды
- § 9. Формула Тейлора
- § 10. Ряды Тейлора и Маклорена
- ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ
- § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x
- § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x
- § 4. Показательная функция с комплексным значением показателя
- § 5. Формулы Эйлера
- § 6. Тригонометрические функции от комплексного значения аргумента
- § 7. Гиперболические функции от комплексного значения аргумента
- § 8. Вычисление значений функций при помощи ряда Маклорена
- § 9. Биномиальный ряд
- § 10. Приложения биномиального ряда
- § 11. Разложение в ряд Маклорена логарифмической функции
- § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов
- § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов
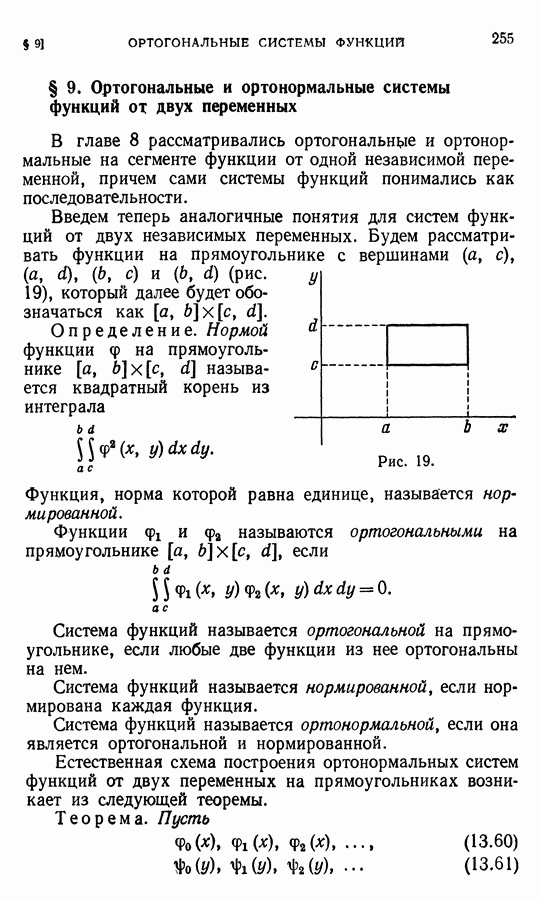
- ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 2. Векторы и функции
- § 3. Нормированные и ортогональные функции
- § 4. Нормированные и ортогональные системы функций
- § 5. Нормировка систем функций
- § 6. Разложение по системам функций
- ГЛАВА 9. РЯДЫ ФУРЬЕ
- § 1. Ряды и коэффициенты Фурье
- § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье
- § 3. Разложение периодических функций в ряд Фурье
- § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье
- § 5. Разложение функции f(x) = x
- § 6. Сдвиг сегмента разложения
- § 7. Изменение длины сегмента разложения
- § 8. Четные и нечетные функции
- § 9. Разложение четной функции в ряд Фурье
- § 10. Разложение нечетной функции в ряд Фурье
- § 11. Разложение ряд Фурье функций на сегменте от 0 до пи
- § 12. Комплексная форма записи ряда Фурье
- § 13. Разложение в комплексный ряд Фурье
- § 14. Характер сходимости рядов Фурье
- ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ
- § 2. Начальные и граничные условия
- § 3. Метод разделения переменных
- § 4. Использование граничных условий. Собственные функции и собственные значения
- § 5. Использование начальных условий
- ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ
- § 1. Представление функций интегралом Фурье
- § 2. Простейшие достаточные условия представимости функции интегралом Фурье
- § 3. Интеграл Фурье для четных функций
- § 4. Интеграл Фурье для нечетных функций
- § 5. Комплексная форма интеграла Фурье
- § 6. Понятие о преобразовании Фурье
- § 7. Косинус-преобразование Фурье
- § 8. Синус-преобразование Фурье
- § 9. Спектральная функция
- Часть II
- § 1. Признак сходимости Куммера
- § 2. Признак сходимости Раабе
- § 3. Признак сходимости Бертрана
- § 4. Признак сходимости Гаусса
- § 5. Сходимость знакопеременных рядов
- § 6. Признак сходимости Дирихле
- ГЛАВА 13. ДВОЙНЫЕ РЯДЫ
- § 1. Определение двойного ряда
- § 2. Сходимость двойных рядов
- § 3. Критерии сходимости двойных рядов. Теорема Маркова
- § 4. Свойства двойных рядов и признаки сходимости
- § 5. Абсолютная сходимость двойных рядов
- § 6. Двойные функциональные ряды
- § 7. Двойные степенные ряды
- § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена
- § 9. Ортогональные и ортонормальные системы функций от двух переменных
- § 10. Двойные ряды Фурье
- ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ
- § 2. Линейные преобразования рядов
- § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов
- § 4. Последовательности разностей
- § 5. Преобразование рядов по Эйлеру
- § 6. Преобразование рядов по Куммеру
- ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
- § 1. Расходящиеся геометрические прогрессии
- § 2. Суммирующие функции
- § 3. Суммирование по Пуассону — Абелю
- § 4. Линейность и регулярность суммирования по Пуассону — Абелю
- § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость
- § 6. Теорема Таубера
- § 7. Суммирование по Чезаро
- § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю
- § 9. Суммирование по Эйлеру
- ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ
- § 2. Исследование двух интегралов
- § 3. Исследование одного класса интегралов
- § 4. Доказательство теоремы Дирихле
- § 5. Теорема Фурье
- § 6. Коэффициенты Фурье разрывных функций
- § 7. Скорость сходимости рядов Фурье
- § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей
- § 9. О равномерной сходимости рядов Фурье
- § 10. Неравномерная сходимость последовательностей непрерывных функций
- § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса
- § 12. Экстремальное свойство сумм Фурье
- § 13. Суммирование рядов Фурье по Чезаро. Теорема Фейера
- § 14. Равенство Парсеваля
- § 15. Теорема Вейерштрасса
- ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК
- § 2. Изгиб балки
- § 3. Свободно опертая балка
- § 4. Первая возможность ограничиться двукратным дифференцированием
- § 5. Случай сосредоточенной нагрузки
- § 6. Прогиб балки от распределенной нагрузки
- § 7. Прогиб от сосредоточенного момента
- § 8. Статически неопределимая балка
- § 9. Сложный изгиб балки
- § 10. Балка на упругом основании
- § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки
- § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок
- § 13. Функции прогиба с ортогональными вторыми производными
- § 14. Свободно опертая нагруженная балка
- § 15. Работа продольных сил при сложном изгибе балки
- § 16. Общий случай изгиба балки
- § 17. Общий случай изгиба свободно опертой балки
- § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам
- § 19. Функция прогиба симметрично загруженной балки с жестко заделанными концами