| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Направляющие косинусы нормали поверхности
1. Поверхность, определенную уравнением

можно рассматривать как поверхность уровпя поля

Градиент этого поля

в любой точке  нашей поверхности (§ 2
нашей поверхности (§ 2
настоящей главы) направлен по нормали. Здесь  значения частных производных левой части уравнения поверхности в рассматриваемой точке
значения частных производных левой части уравнения поверхности в рассматриваемой точке 
Следовательно, направляющие косинусы нормали поверхности имеют вид

2. Замечание.
Направляющие косинусы нормали поверхности

будут определены лишь в тех точках поверхности, в которых функция  дифференцируема и не все частные производные
дифференцируема и не все частные производные

равны нулю. Если все три частные производные равны нулю, т. е.

то направляющие косинусы нормали, а следовательно, и сама нормаль не определяются.
Точки поверхности, в которых не выполняются указанные условия, называются особыми. Примером такой особой точки может служить вершина конической поверхности.
3. Случай, когда уравнение поверхности разрешено относительно третьей координаты z.
Пусть это уравнение имеет вид

Перенеся все члены в левую часть, мы получим

Сопоставив это уравнение с рассмотренным выше уравнением поверхности

мы можем считать, что в данном случае

Поэтому

Обычно пользуются такими обозначениями:

В этих обозначениях

Следовательно, для направляющих косинусов нормали поверхности мы получим формулы

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА
- Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
- 2. Скаляры и векторы.
- 3. Равенство векторов.
- 4. Скользящие и приложенные векторные величины.
- 5. Модуль вектора.
- 6. Орт вектора.
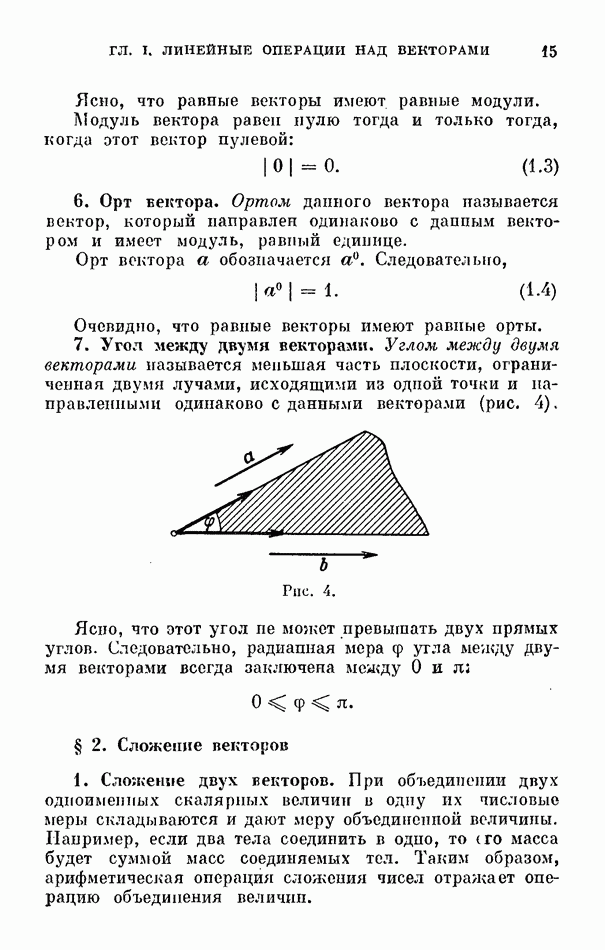
- 7. Угол между двумя векторами.
- § 2. Сложение векторов
- 1. Сложение двух векторов.
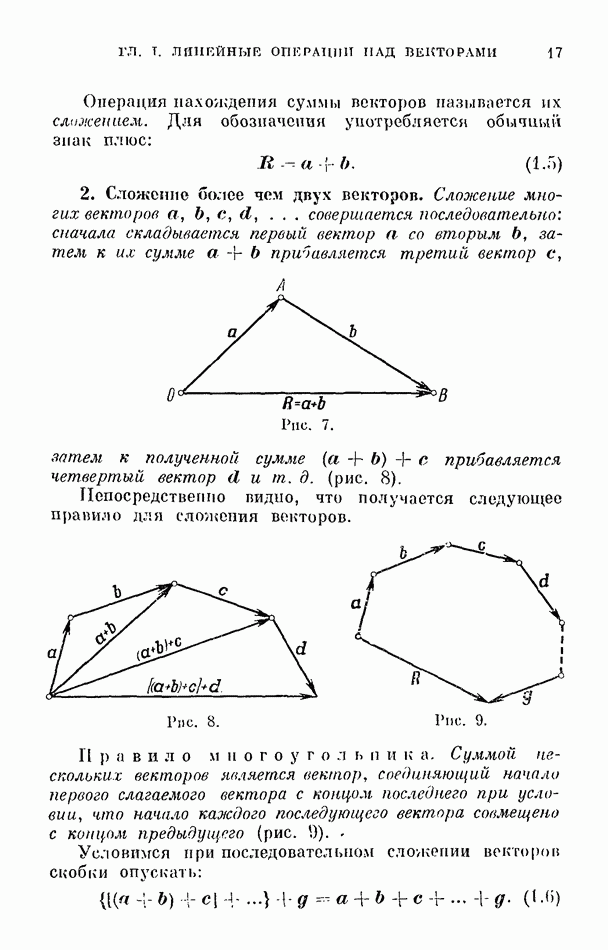
- 2. Сложение более чем двух векторов.
- 3. Модуль суммы.
- 4. Законы сложения.
- § 3. Вычитание векторов
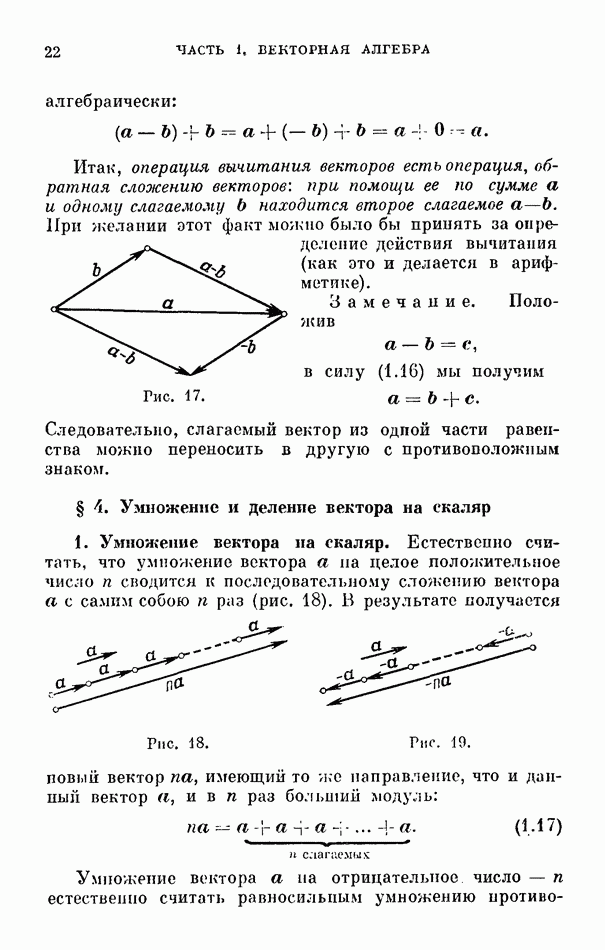
- § 4. Умножение и деление вектора на скаляр
- 2. Законы умножения вектора на скаляр.
- 3. Деление вектора на скаляр.
- 4. Выражение вектора через его модуль и орт.
- § 5. Линейные зависимости между векторами
- 2. Коллинеарные векторы.
- 3. Компланарные векторы.
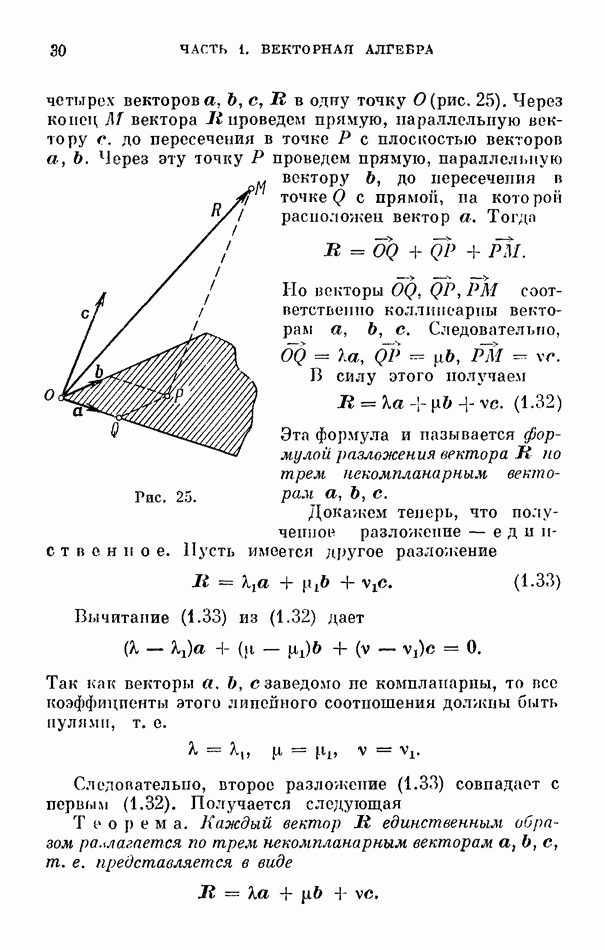
- 4. Разложение вектора по трем некомпланарным векторам.
- 5. Метод координат.
- Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- § 1. Проекции векторов на ось
- § 2. Основные теоремы о скалярных проекциях
- § 3. Прямоугольная система координат в пространстве
- 1. Правая и левая прямоугольные системы координат.
- 2. Разложение вектора по ортам осей
- 3. Линейные операции над векторами в координатной форме.
- 4. Радиус-вектор и координаты точки.
- 5. Определение вектора по его началу и концу.
- 6. Деление отрезка в данном отношении.
- Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ
- § 1. Скалярное произведение двух векторов
- 2. Работа силы.
- 3. Определение.
- 4. Равенство скалярного произведения нулю.
- 5. Законы скалярного умножения.
- 7. Скалярные произведения координатных ортов.
- 8. Скалярное произведение в координатной форме.
- 9. Неопределенность действия, обратного скалярному умножению.
- § 2. Векторное произведение двух векторов
- 3. Условия равенства нулю векторного произведения.
- 4. Законы векторного умножения.
- 5. Векторные произведения координатных ортов.
- 6. Определители.
- 7. Векторное произведение в координатной форме.
- 8. Неопределенность действия, обратного векторному умножению.
- Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ
- § 1. Простейшее произведение трех векторов
- § 2. Векторно-векторное произведение трех векторов
- 3. Правило разложения векторно-векторного произведения.
- § 3. Векторно-скалярное произведение трех векторов
- 2. Законы векторно-скалярного умножения
- 3. Обращение в нуль векторно-скалярного произведения трех векторов.
- 4. Векторно-скалярное произведение в координатной форме.
- § 4. Выражение векторно-скалярного произведения через скалярные произведения
- Глава V. ФУНКЦИИ ВЕКТОРОВ
- § 1. Произведения четырех векторов
- 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения.
- 3. Разложение вектора (а, b, с) R по трем векторам a, b, c.
- 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b
- § 2. Произведения пяти и шести векторов
- 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c.
- 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения.
- § 3. Основные теоремы о функциях векторов
- 1. Рациональные функции векторов.
- 2. Элементарные функции векторов.
- 3. Произвольные скалярные функции от векторов.
- 4. Произвольные векторные функции векторов.
- Глава VI. ОСНОВНЫЕ ЗАДАЧИ
- § 2. Основные задачи, связанные со скалярным умножением векторов
- § 3. Основные задачи, связанные с векторным умножением векторов
- § 4. Основные задачи, связанные с произведениями трех и более векторов
- § 5. Простейшие векторные уравнения
- § 6. Геометрические инварианты фигур
- 2. Треугольник.
- 3. Полные системы инвариантов треугольника.
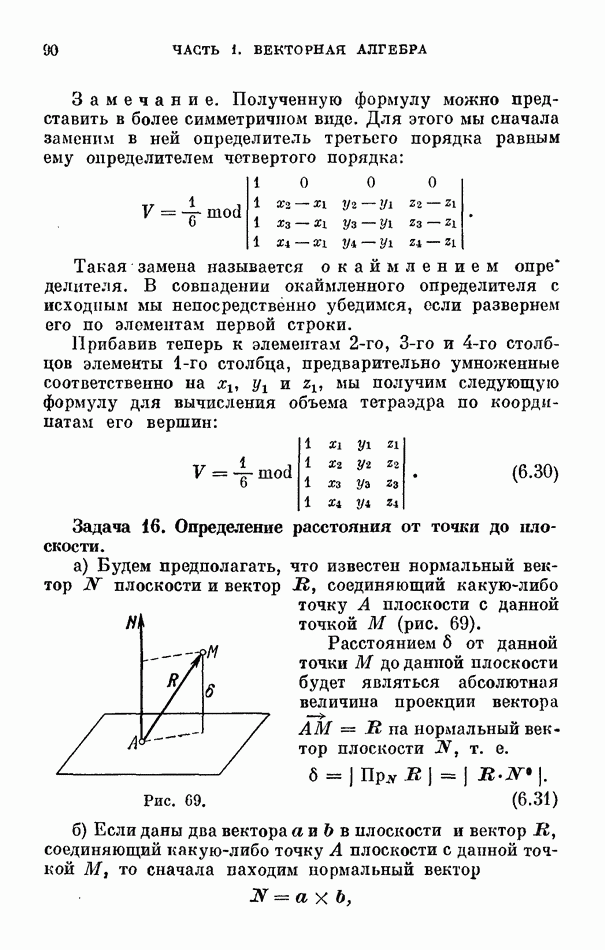
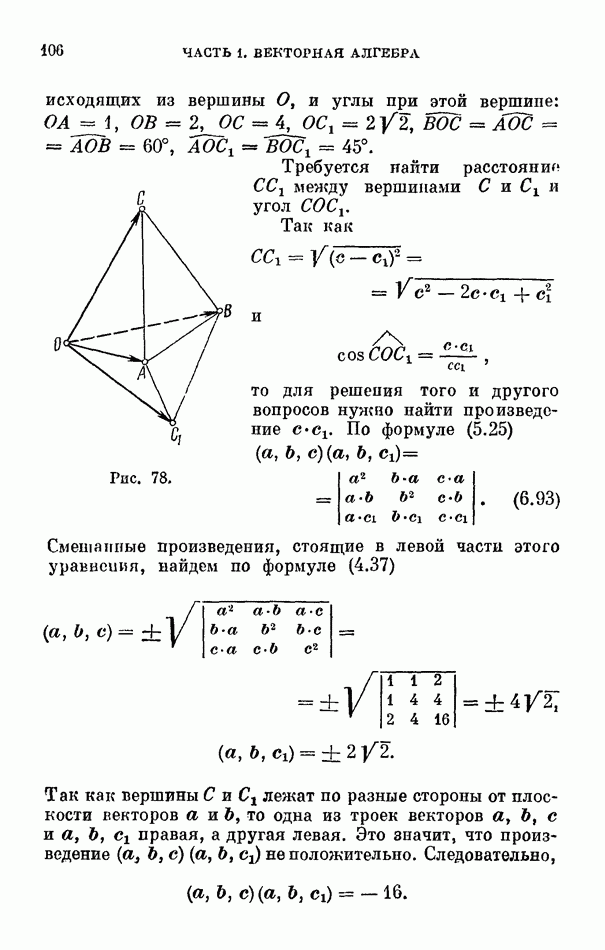
- 4. Тетраэдр.
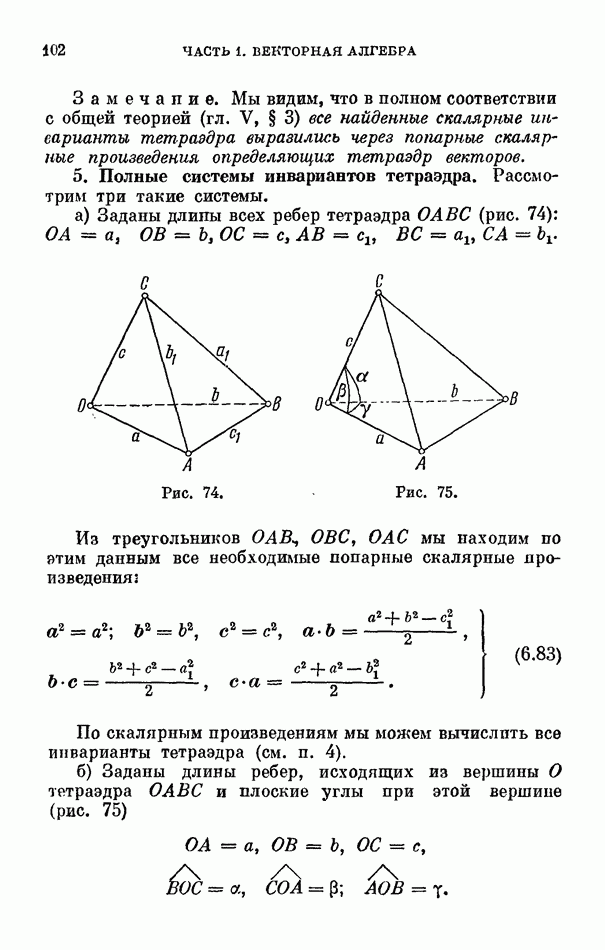
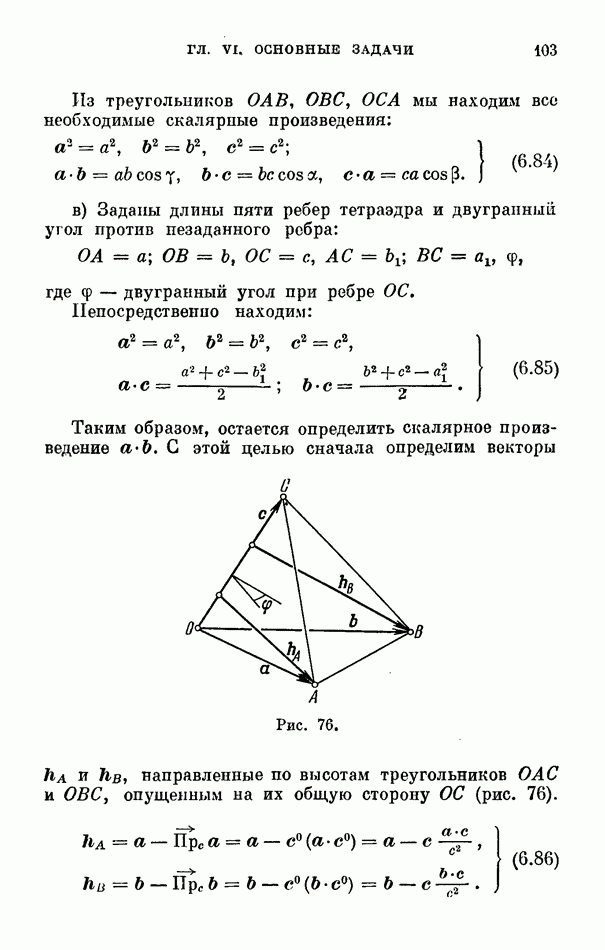
- 5. Полные системы инвариантов тетраэдра.
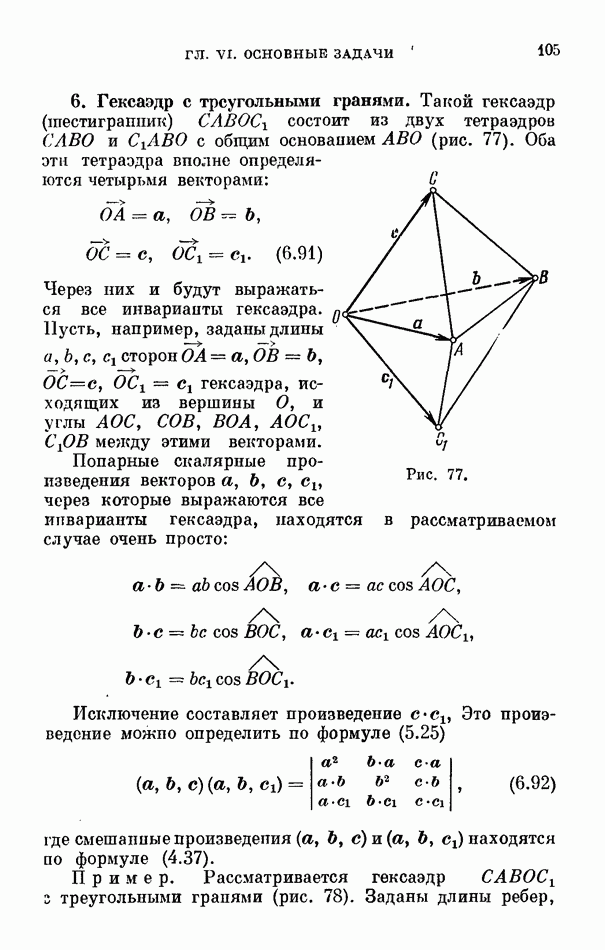
- 6. Гексаэдр с треугольными гранями.
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
- § 1. Векторы, зависящие от скаляра
- 2. Вектор-функция в координатной форме.
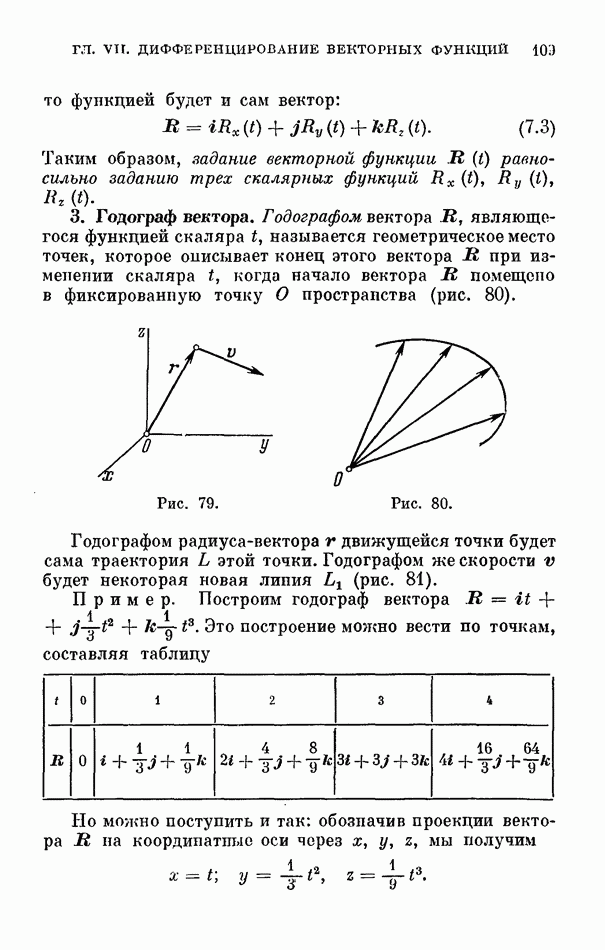
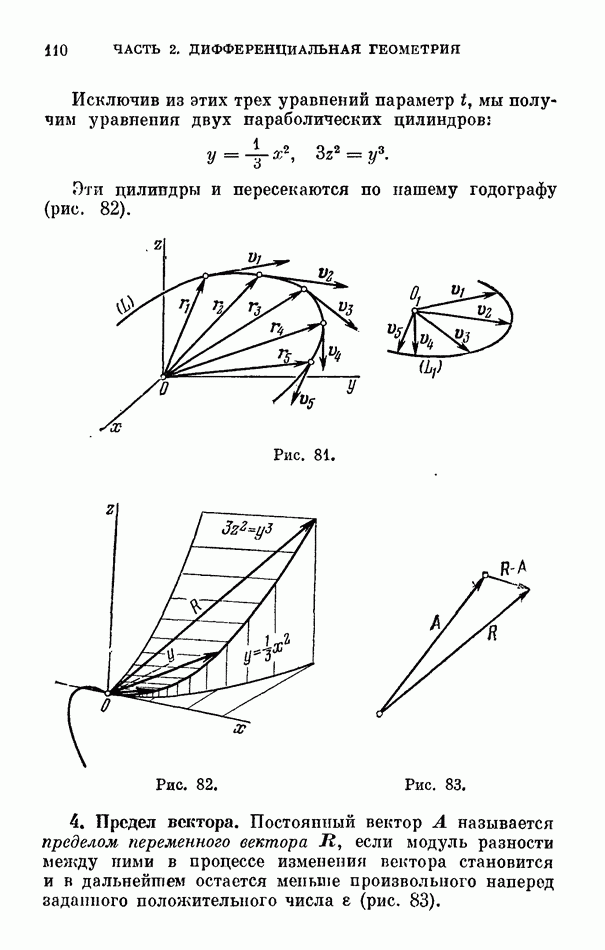
- 3. Годограф вектора.
- 4. Предел вектора.
- § 2. Дифференцирование вектора по скаляру
- 2. Геометрический смысл производной вектора по скаляру.
- 3. Механический смысл производной.
- 5. Дифференциал вектора.
- 6. Инвариантность дифференциала.
- 7. Связь дифференциала вектора с его приращением.
- § 3. Формула Тейлора
- Глава VIII. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ
- § 1. Основные дифференциально-геометрические понятия, связанные с линией
- 2. Касательная.
- 3. Соприкасающаяся плоскость.
- 4. Главная нормаль и бинормаль.
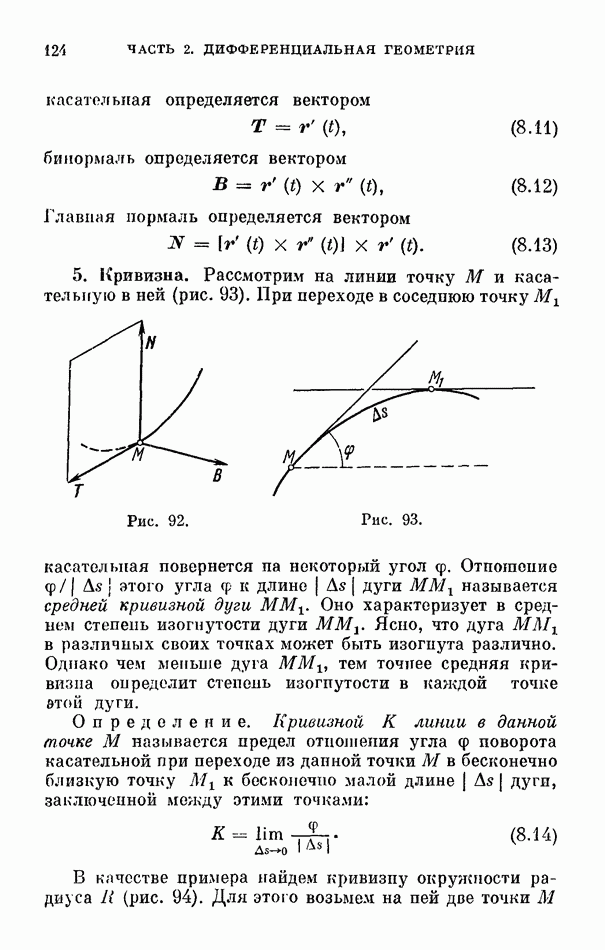
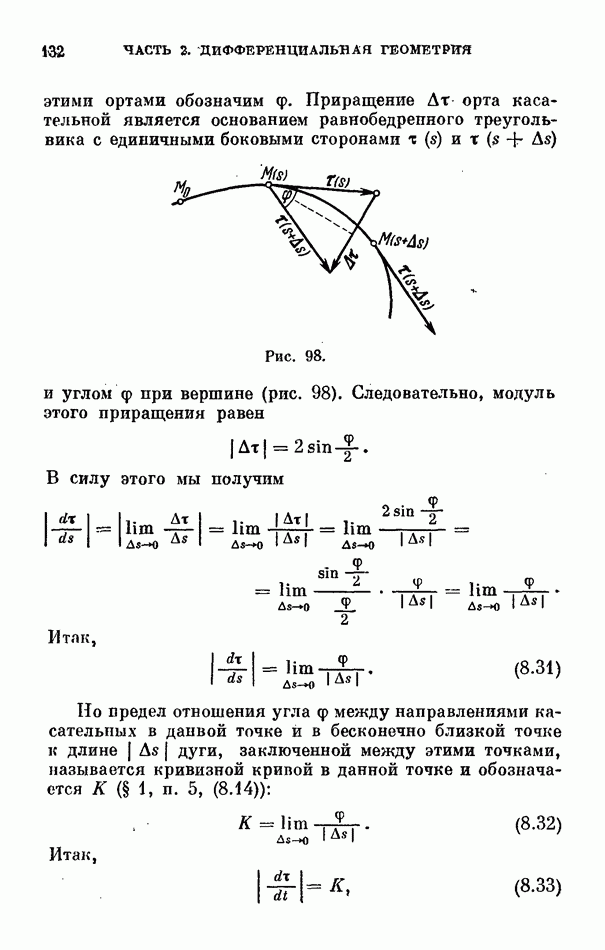
- 5. Кривизна.
- 6. Кручение.
- 7. Длина дуги.
- § 2. Основные формулы дифференциальной геометрии линий в пространстве
- 1. Дуга как параметр. Дифференциал дуги.
- 2. Орт касательной. Первая основная формула.
- 3. Инвариантность геометрических понятий.
- 4. Главная нормаль и кривизна. Вторая основная формула.
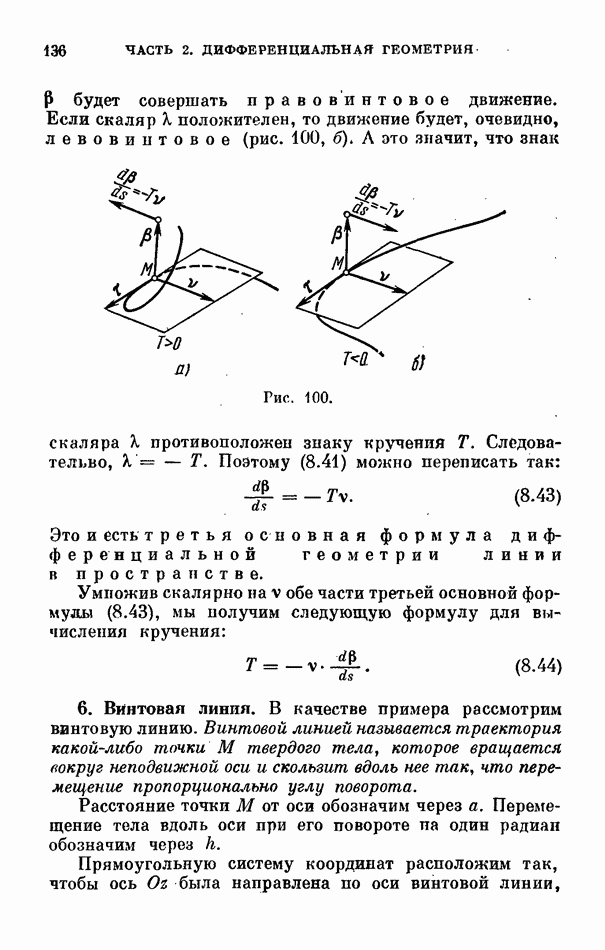
- 5. Бинормаль и кручение. Третья основная формула.
- 6. Винтовая линия.
- § 3. Сопровождающий трехгранник
- 2. Система дифференциальных уравнений движения сопровождающего трехгранника.
- 3. Расположение линии относительно сопровождающего трехгранника.
- 4. Линии без кривизны.
- 5. Линии без кручения.
- § 4. Инвариантные формулы
- Глава IX. ПЛОСКИЕ ЛИНИИ
- § 1. Дифференциальные уравнения плоской линии
- § 2. Кривизна плоской линии
- § 3. Круг кривизны
- § 4. Эволюта
- § 5. Эвольвента
- Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ
- § 1. Скорость и ускорение точки
- § 2. Движение твердого тела вокруг неподвижной точки
- 2. Формула Эйлера.
- 3. Угловая скорость.
- 4. Доказательстве существования угловой скорости твердого тела.
- § 3. Относительная производная вектора
- 2. Абсолютная и относительная производные вектора.
- 3. Общий случай движения твердого тела.
- Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
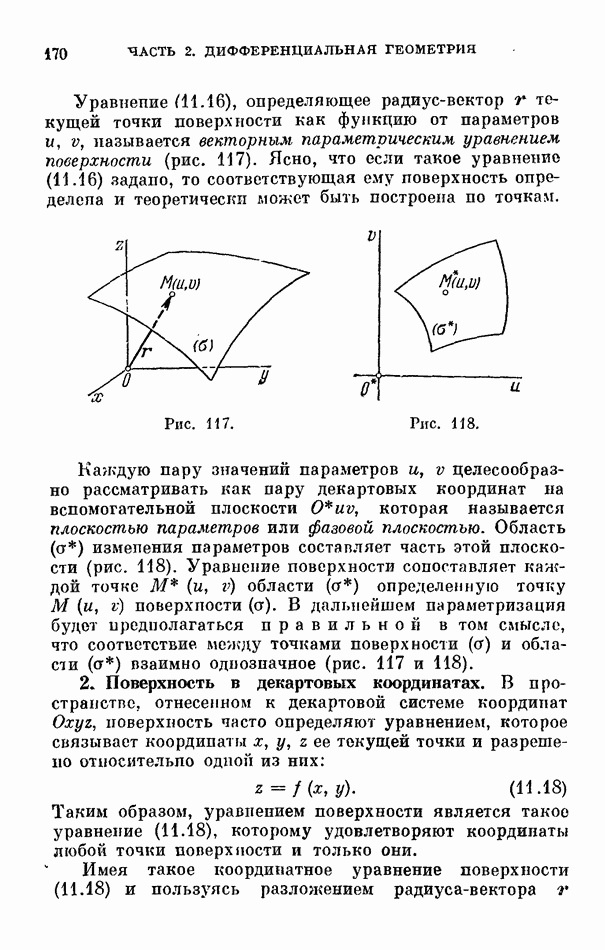
- § 1. Векторные функции нескольких скалярных аргументов
- § 2. Параметризованная поверхность
- 2. Поверхность в декартовых координатах.
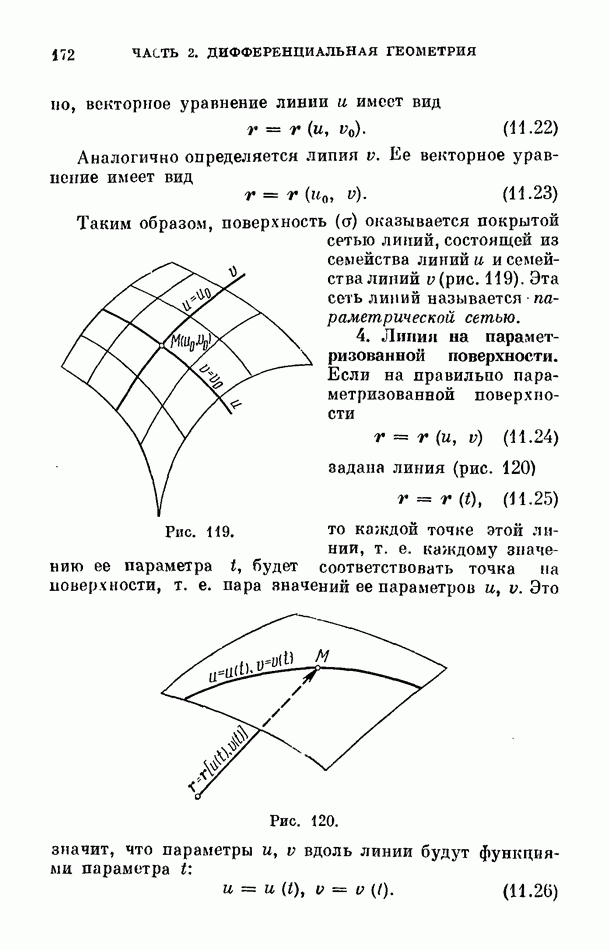
- 3. Параметрическая сеть.
- 4. Линия на параметризованной поверхности.
- § 3. Касательная плоскость и нормаль
- 3. Нормальный вектор.
- 4. Преобразование параметров.
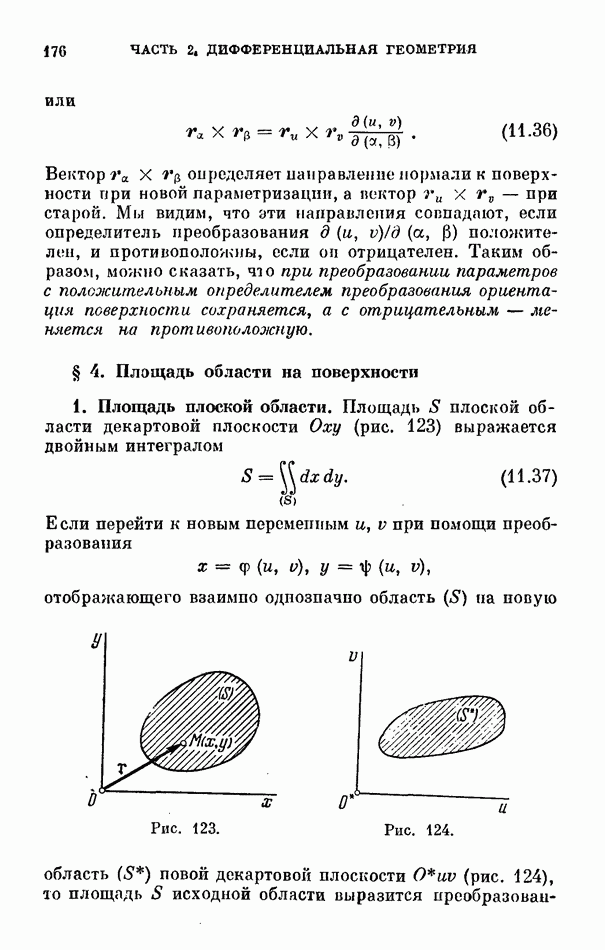
- § 4. Площадь области на поверхности
- 2. Площадь области на поверхности.
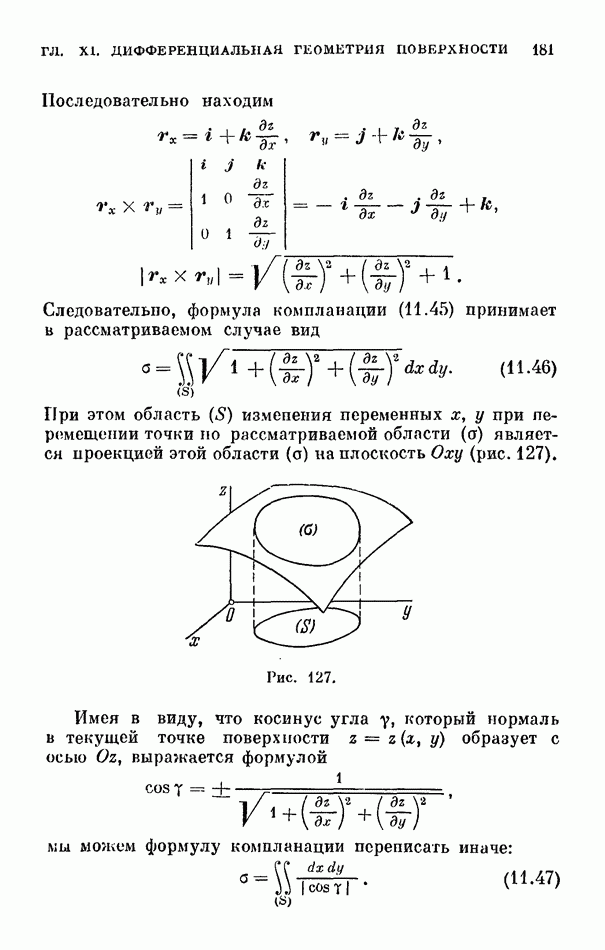
- 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y).
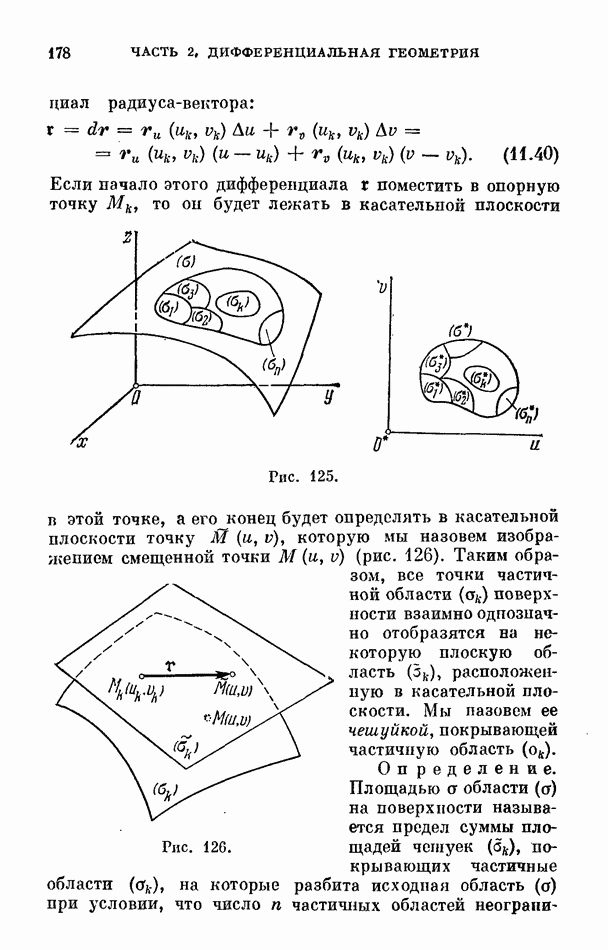
- 4. Элемент площади поверхности.
- 5. Векторный элемент площади поверхности.
- § 5. Первая квадратичная форма поверхности
- 2. Внутренняя геометрия поверхности.
- 3. Длина дуги линии на поверхности.
- 4. Угол между линиями на поверхности.
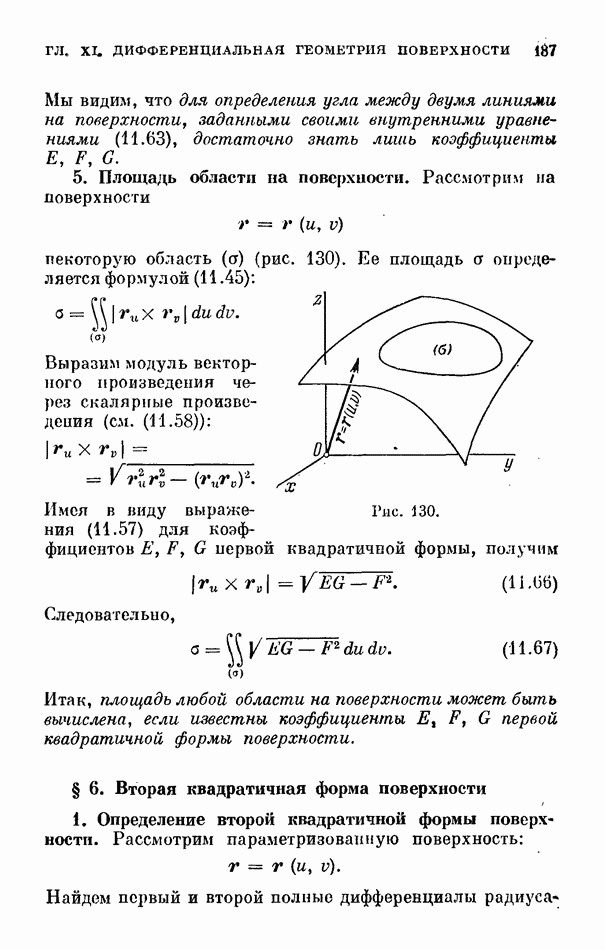
- 5. Площадь области на поверхности.
- § 6. Вторая квадратичная форма поверхности
- 2. Нормальная кривизна линии на поверхности.
- 3. Теорема Менье.
- § 7. Главные направления и главные кривизны поверхности
- 2. Главные направления на поверхности.
- 3. Перпендикулярность главных направлений.
- 4. Формула Эйлера.
- 5. Полная и средняя кривизны поверхности.
- ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ
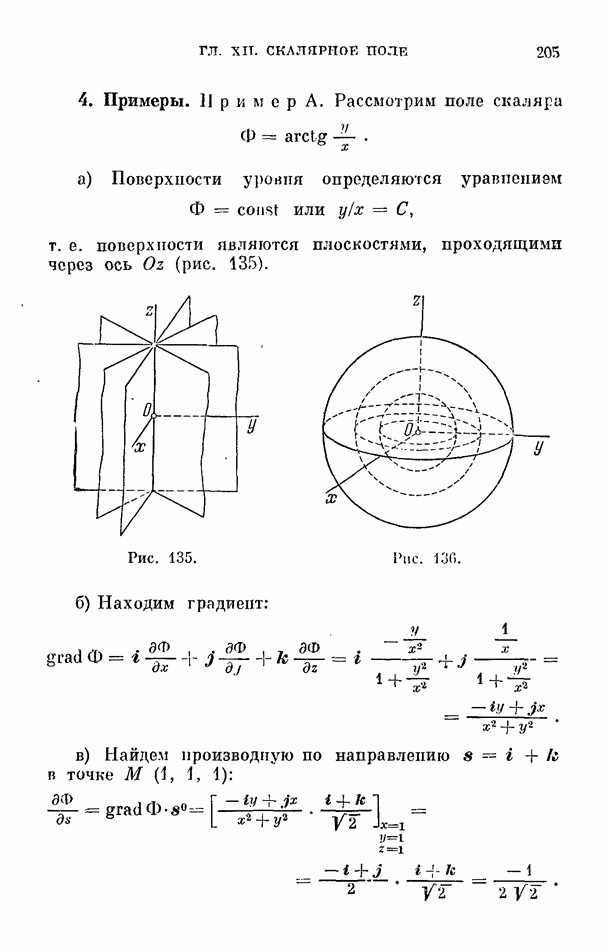
- § 1. Функция поля. Поверхности уровня
- § 2. Градиент поля
- 2. Первая теорема о градиенте.
- § 3. Производная по направлению
- 2. Выражение производной по направлению через градиент.
- 3. Вторая теорема о градиенте.
- § 4. Направляющие косинусы нормали поверхности
- Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ
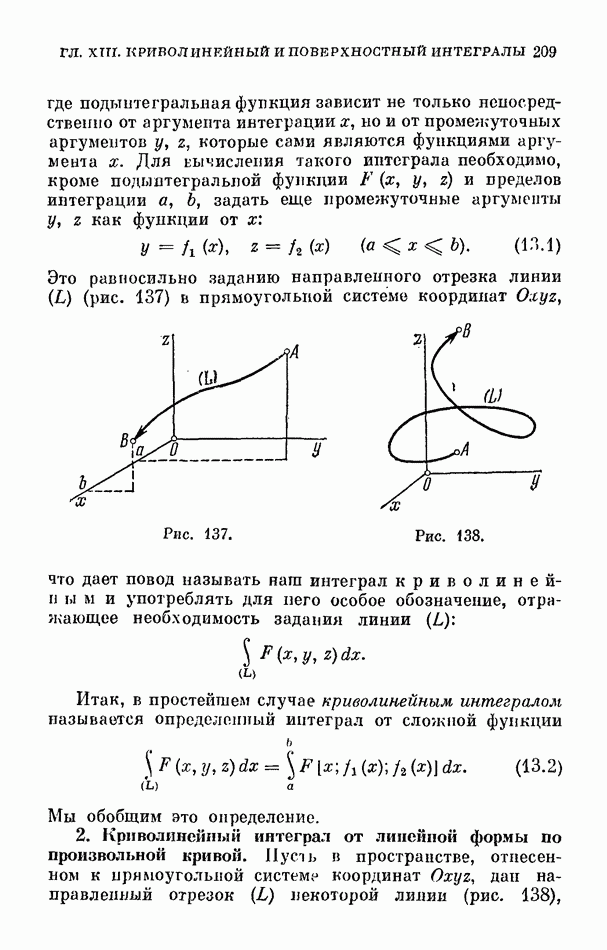
- § 1. Криволинейный интеграл как определенный интеграл от сложной функции
- 2. Криволинейный интеграл от линейной формы по произвольной кривой.
- 3. Основные свойства криволинейного интеграла.
- 4. Обобщенный криволинейный интеграл.
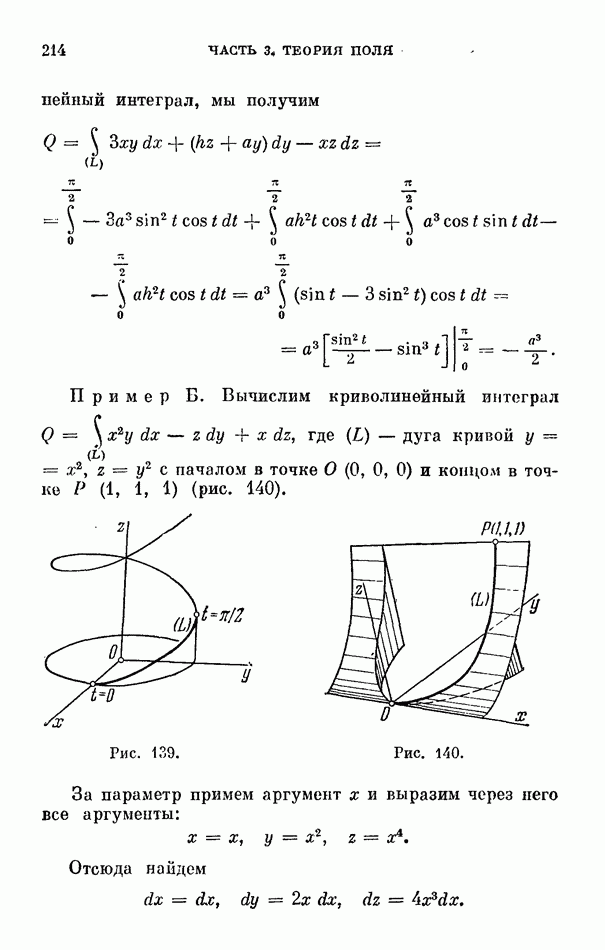
- 5. Примеры.
- § 2. Криволинейный интеграл как предел криволипейной интегральной суммы
- § 3. Поверхностный интеграл как двойной интеграл от сложной функции
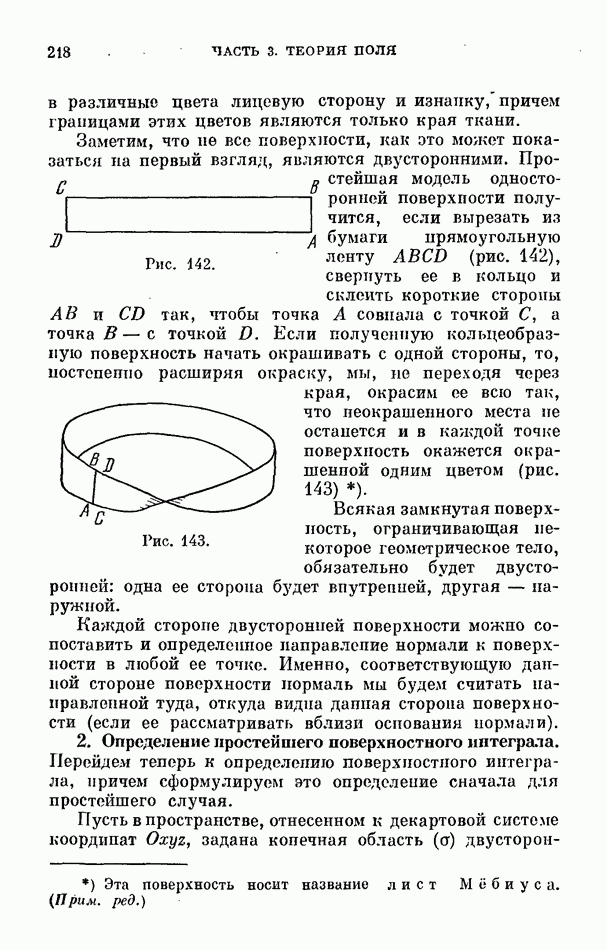
- 2. Определение простейшего поверхностного интеграла.
- 3. Поверхностный интеграл от билинейной формы по произвольной поверхности.
- § 4. Поверхностный интеграл как предел поверхностной интегральной суммы
- § 5. Поверхностный интеграл в параметрической форме
- 2. Параметрический поверхностный интеграл.
- 3. Поверхностный интеграл как предел суммы.
- § 6. Кратный интеграл как предел обобщенной интегральной суммы
- 2. Обобщение основной теоремы о кратном интеграле.
- Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ
- § 1. Векторное поле
- § 2. Векторные линии
- § 3. Циркуляция поля вдоль линии
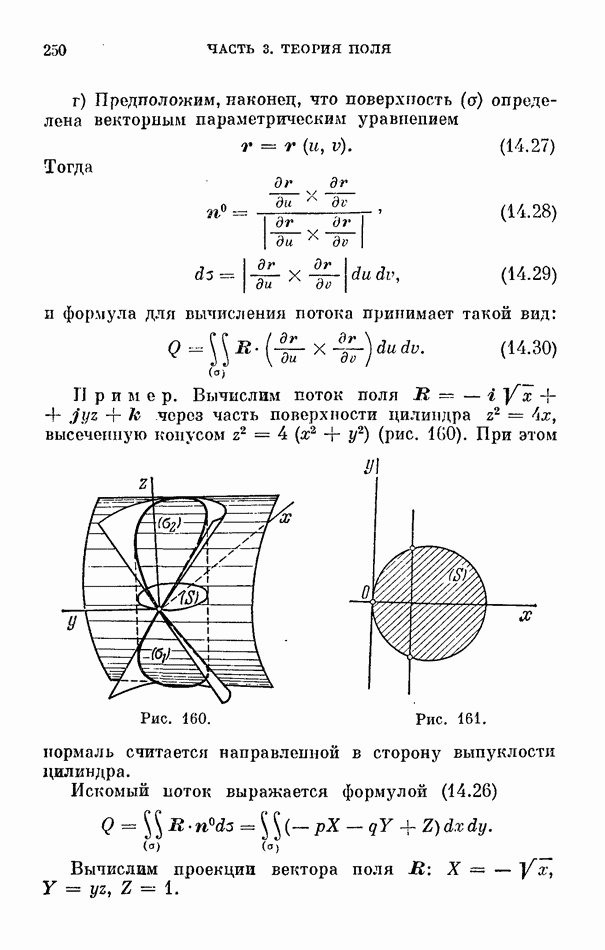
- § 4. Поток поля через поверхность
- Глава XV. ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ
- § 1. Формула Остроградского
- § 2. Дивергенция поля
- 2. Дивергенция как предел отношения.
- 3. Гидромеханический смысл дивергенции.
- 4. Теорема Остроградского.
- Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ
- § 1. Формула Стокса
- § 2. Ротация поля
- § 3. Оператор Гамильтона
- Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ
- § 1. Потенциальное поле
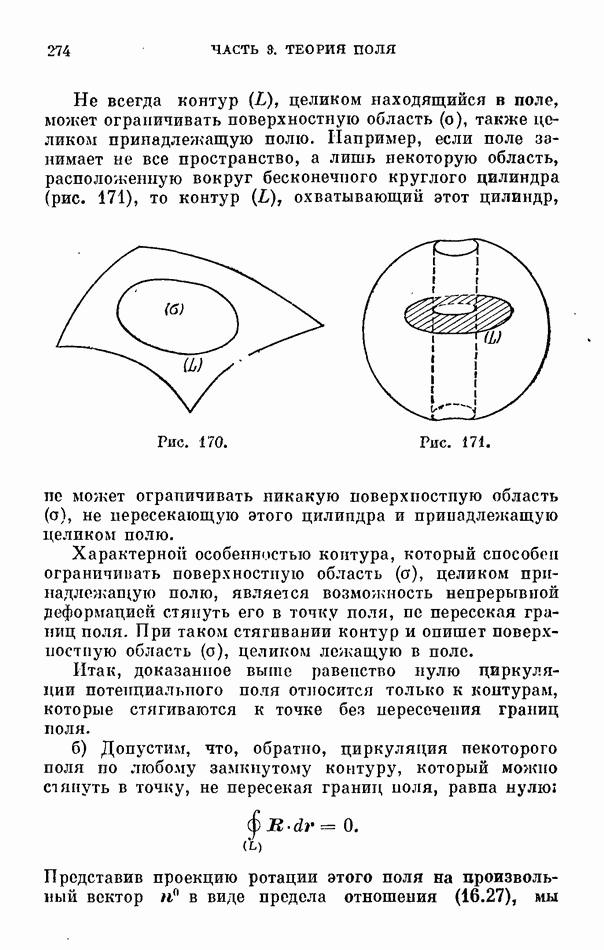
- 3. Циркуляция потенциального поля по замкнутому контуру.
- 4. Циркуляция потенциального поля между двумя точками.
- 5. Потенциал.
- 6. Элемент циркуляции.
- 7. Характеристические признаки потенциального поля.
- 8. Вычисление потенциала.
- 9. Центральное поле.
- 10. Вихревые шнуры.
- § 2. Соленоидальное поле
- 3. Поток соленоидального поля через замкнутую поверхность.
- 4. Трубчатое строение соленоидального поля.
- 5. Векторный потенциал.
- 6. Характеристические признаки соленоидального поля.
- 7. Источники и стоки.
- § 3. Потенциальное несжимаемое поле
- Глава XVIII. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ
- § 1. Электростатическое поле точечного заряда
- 2. Дивергенция поля точечного заряда.
- 3. Поток поля точечного заряда через замкнутую поверхность.
- 4. Ротация поля точечного заряда.
- 5. Потенциал поля точечного заряда.
- § 2. Электростатическое поле системы точечных зарядов
- 2. Дивергенция и ротация поля системы точечных зарядов.
- 3. Поток поля системы точечных зарядов через замкнутую поверхность.
- 4. Потенциал поля системы точечных зарядов.
- 5. Непрерывно распределенный заряд.
- § 3. Магнитное поле тока
- 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу.
- 3. Векторные линии поля H.
- 4. Потенциал поля Н.
- 5. Провод как вихревой шнур.
- Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 1. Криволинейные координаты
- 3. Координатные поверхности и линии.
- 4. Линейный элемент.
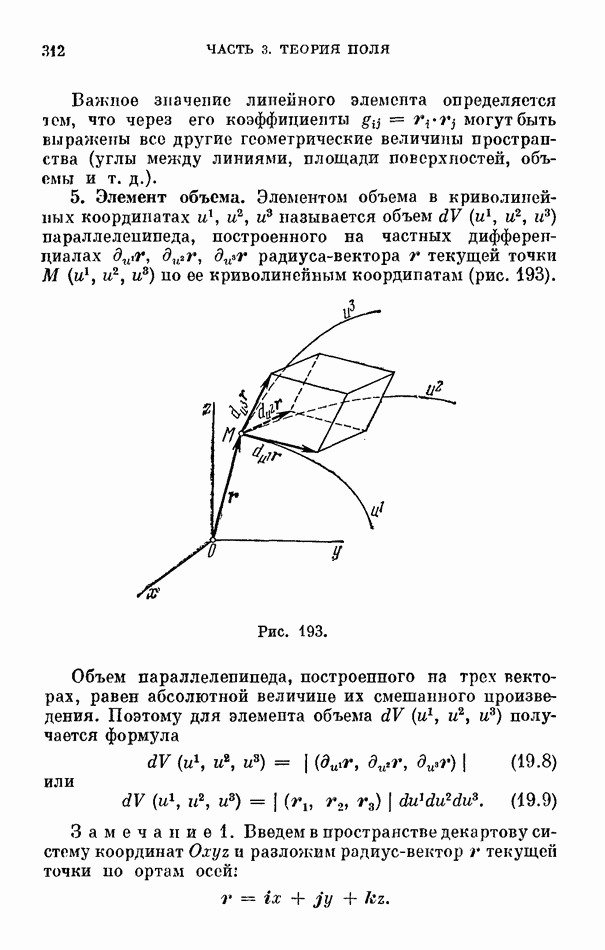
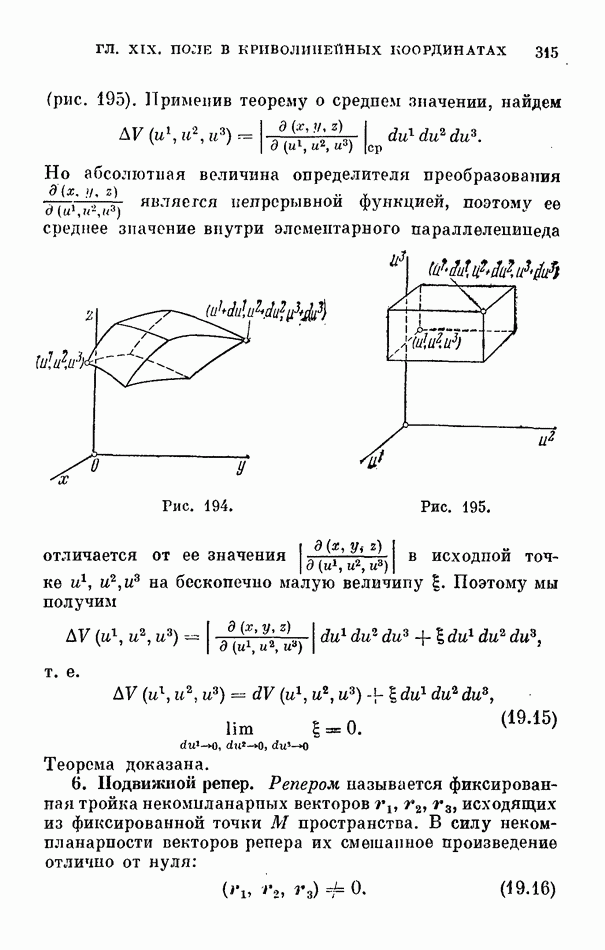
- 5. Элемент объема.
- 6. Подвижной репер.
- 7. Векторное поле в криволиненных координатах.
- § 2. Дифференциальные операции в криволинейных координатах
- 2. Дивергенция в криволинейных координатах.
- 3. Ротация в криволинейных координатах.
- § 3. Ортогональные координаты
- § 4. Цилиндрические координаты
- 2. Линейный элемент и элемент объема в цилиндрических координатах.
- 3. Дифференциальные операции в цилиндрических координатах.
- § 5. Сферические координаты