| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. Ротация в криволинейных координатах.
Будем исходить из формулы Стокса

Предположим, что пространство отнесено к криволинейным координатам 

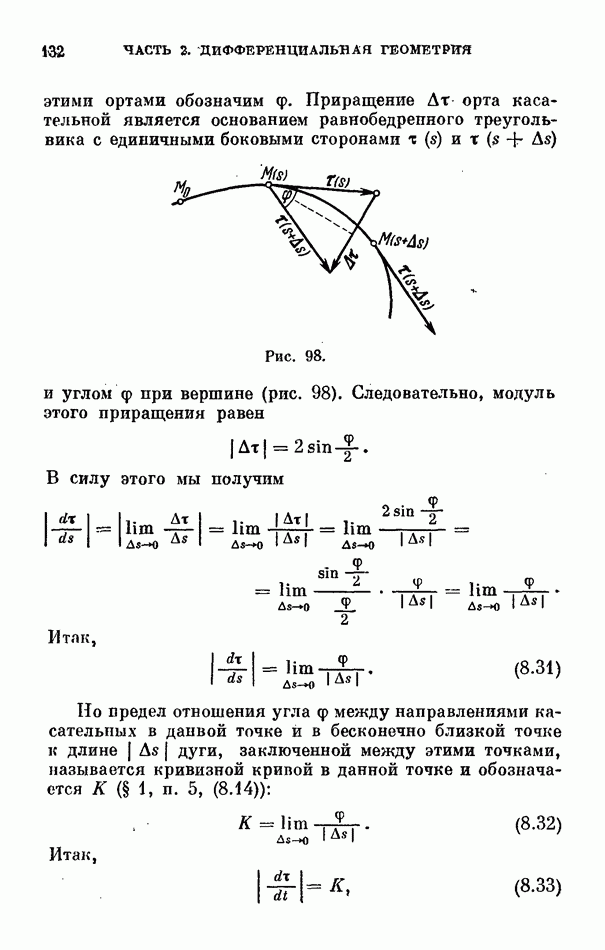
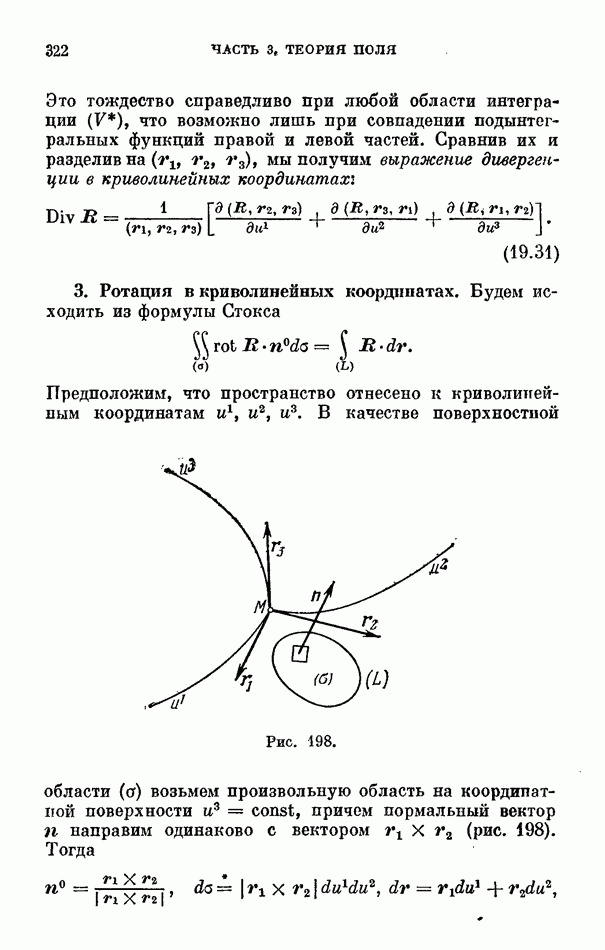
Рис. 198.
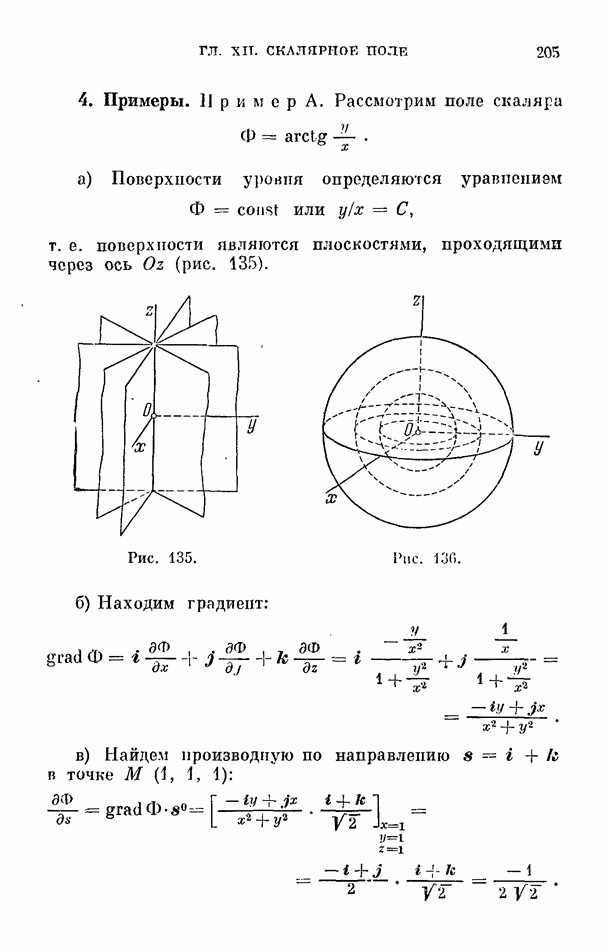
В качестве поверхностной области  возьмем произвольную область на координатной поверхности
возьмем произвольную область на координатной поверхности  причем нормальный вектор
причем нормальный вектор  направим одинаково с вектором
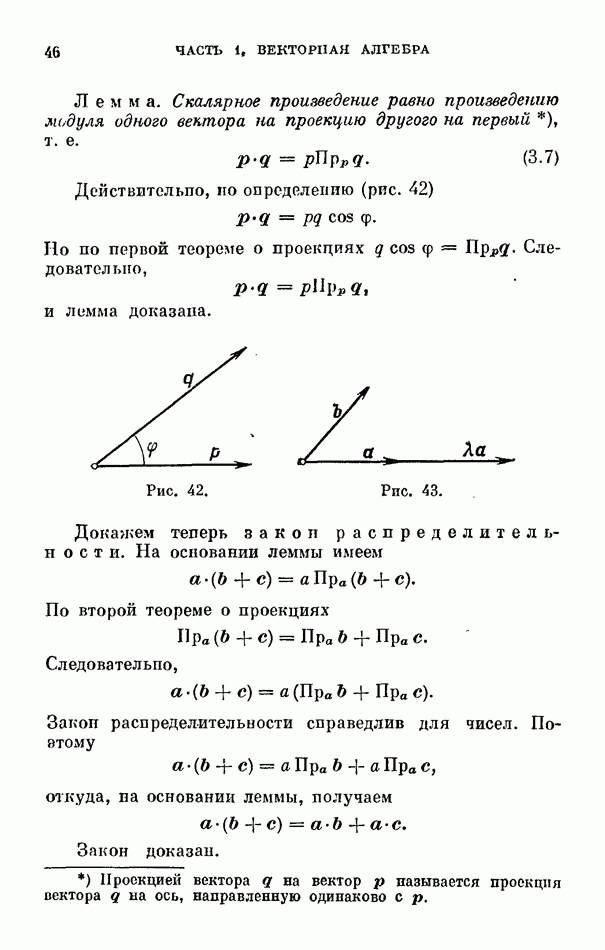
направим одинаково с вектором  (рис. 198). Тогда
(рис. 198). Тогда

и формула Стокса примет вид

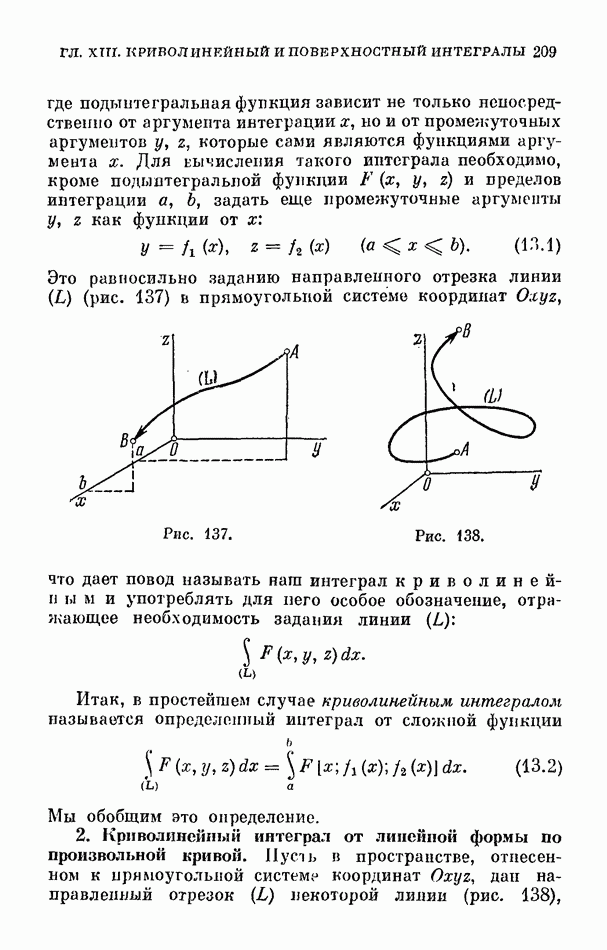
где  — образ поверхностной области
— образ поверхностной области  на вспомогательной декартовой плоскости
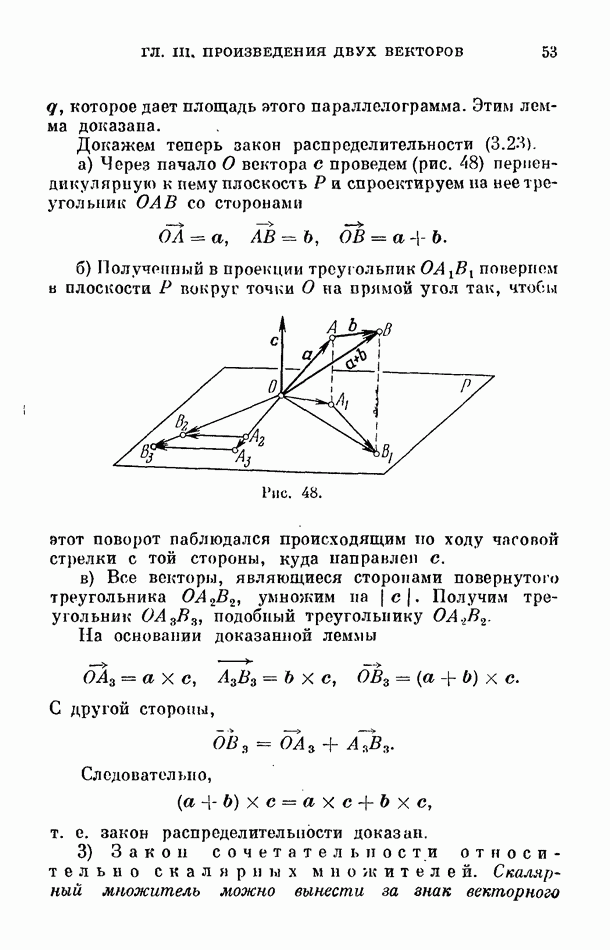
на вспомогательной декартовой плоскости  ограничивающий его контур (рис. 199). Так как область
ограничивающий его контур (рис. 199). Так как область  и контур
и контур  являются плоскими, к криволинейному интегралу в правой части (19.32) можно применить формулу Грипа (16.1), после чего мы получим
являются плоскими, к криволинейному интегралу в правой части (19.32) можно применить формулу Грипа (16.1), после чего мы получим


Рис. 199.
Тождество (19.33) справедливо при любой области интеграции  а это может быть лишь в случае совпадения подынтегральных функций. Следовательно,
а это может быть лишь в случае совпадения подынтегральных функций. Следовательно,

Аналогично найдем

Разложение вектора ротации но векторам  гл подвижного репера имеет вид (см. (19.22)):
гл подвижного репера имеет вид (см. (19.22)):

Подставив сюда найденные выражения для скалярных
произведений ротации на векторные произведения, получим

Непосредственно видно, что полученное выражение для ротации можно записать в виде следующего символического определителя;

Это и есть формула, выражающая ротацию в криволинейной системе координат. Она дает разложение ротации по векторам подвижного репера 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА
- Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
- 2. Скаляры и векторы.
- 3. Равенство векторов.
- 4. Скользящие и приложенные векторные величины.
- 5. Модуль вектора.
- 6. Орт вектора.
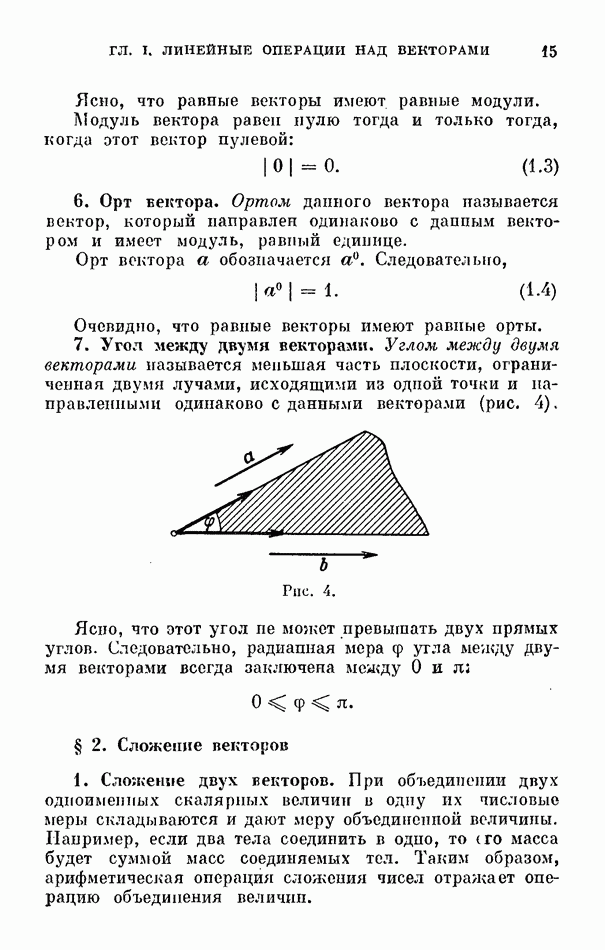
- 7. Угол между двумя векторами.
- § 2. Сложение векторов
- 1. Сложение двух векторов.
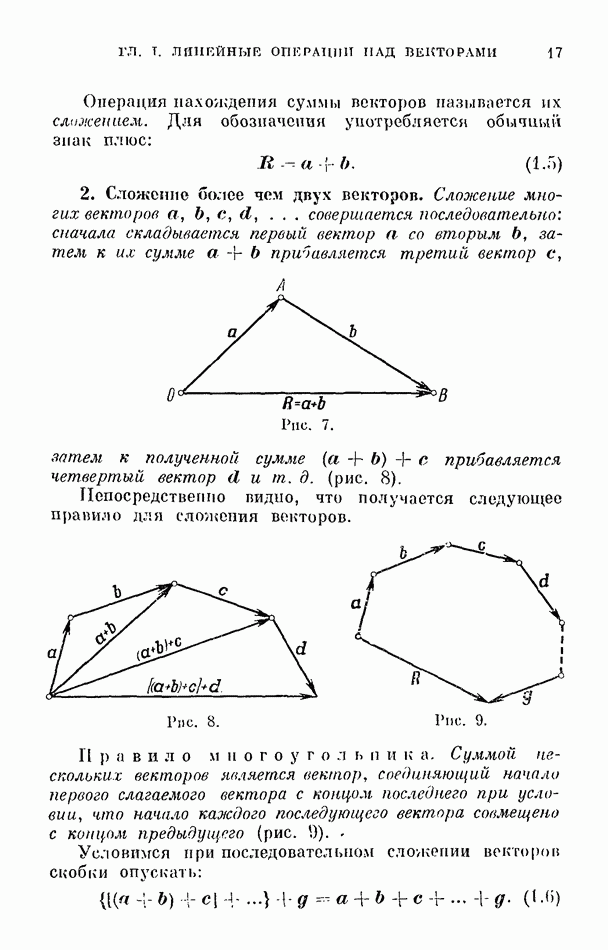
- 2. Сложение более чем двух векторов.
- 3. Модуль суммы.
- 4. Законы сложения.
- § 3. Вычитание векторов
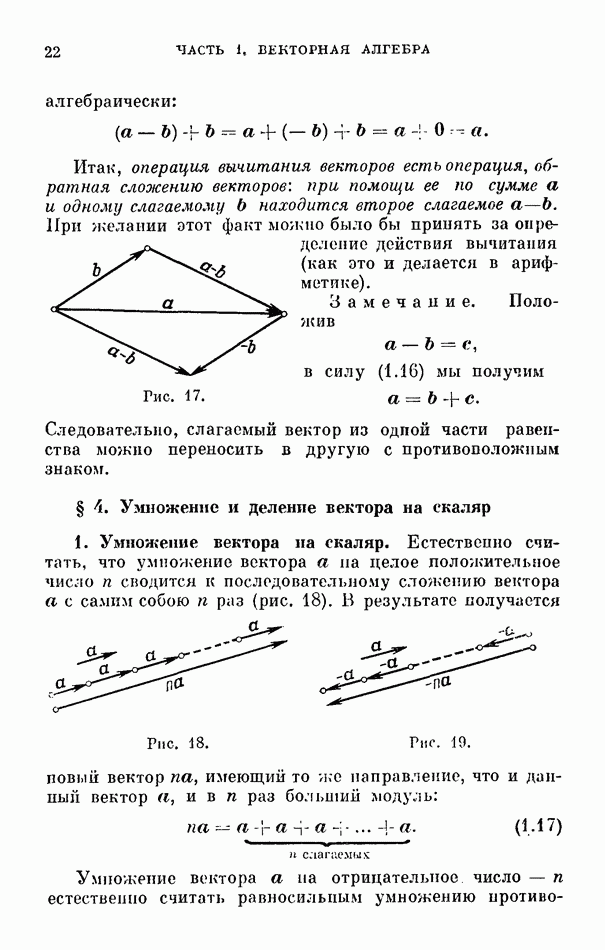
- § 4. Умножение и деление вектора на скаляр
- 2. Законы умножения вектора на скаляр.
- 3. Деление вектора на скаляр.
- 4. Выражение вектора через его модуль и орт.
- § 5. Линейные зависимости между векторами
- 2. Коллинеарные векторы.
- 3. Компланарные векторы.
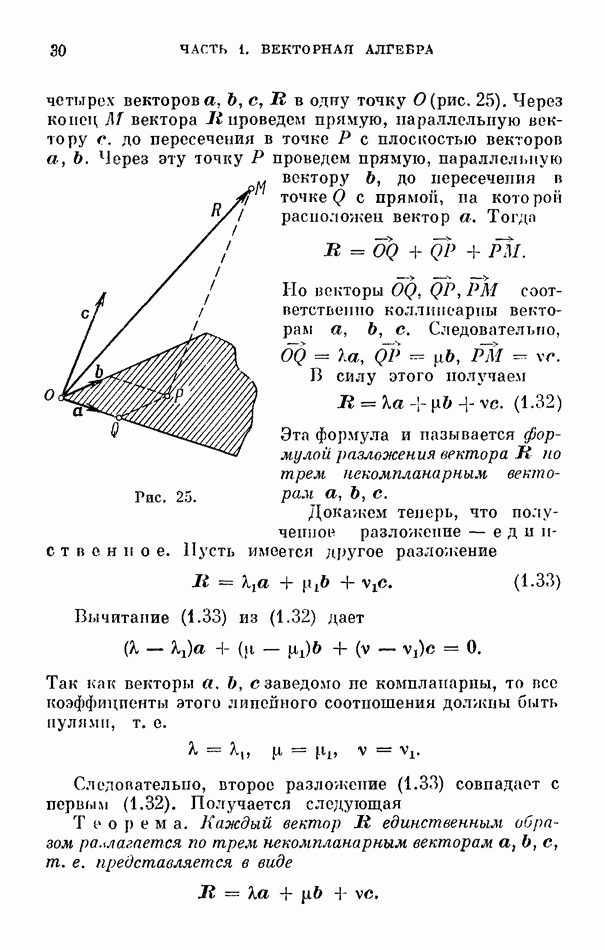
- 4. Разложение вектора по трем некомпланарным векторам.
- 5. Метод координат.
- Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
- § 1. Проекции векторов на ось
- § 2. Основные теоремы о скалярных проекциях
- § 3. Прямоугольная система координат в пространстве
- 1. Правая и левая прямоугольные системы координат.
- 2. Разложение вектора по ортам осей
- 3. Линейные операции над векторами в координатной форме.
- 4. Радиус-вектор и координаты точки.
- 5. Определение вектора по его началу и концу.
- 6. Деление отрезка в данном отношении.
- Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ
- § 1. Скалярное произведение двух векторов
- 2. Работа силы.
- 3. Определение.
- 4. Равенство скалярного произведения нулю.
- 5. Законы скалярного умножения.
- 7. Скалярные произведения координатных ортов.
- 8. Скалярное произведение в координатной форме.
- 9. Неопределенность действия, обратного скалярному умножению.
- § 2. Векторное произведение двух векторов
- 3. Условия равенства нулю векторного произведения.
- 4. Законы векторного умножения.
- 5. Векторные произведения координатных ортов.
- 6. Определители.
- 7. Векторное произведение в координатной форме.
- 8. Неопределенность действия, обратного векторному умножению.
- Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ
- § 1. Простейшее произведение трех векторов
- § 2. Векторно-векторное произведение трех векторов
- 3. Правило разложения векторно-векторного произведения.
- § 3. Векторно-скалярное произведение трех векторов
- 2. Законы векторно-скалярного умножения
- 3. Обращение в нуль векторно-скалярного произведения трех векторов.
- 4. Векторно-скалярное произведение в координатной форме.
- § 4. Выражение векторно-скалярного произведения через скалярные произведения
- Глава V. ФУНКЦИИ ВЕКТОРОВ
- § 1. Произведения четырех векторов
- 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения.
- 3. Разложение вектора (а, b, с) R по трем векторам a, b, c.
- 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b
- § 2. Произведения пяти и шести векторов
- 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c.
- 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения.
- § 3. Основные теоремы о функциях векторов
- 1. Рациональные функции векторов.
- 2. Элементарные функции векторов.
- 3. Произвольные скалярные функции от векторов.
- 4. Произвольные векторные функции векторов.
- Глава VI. ОСНОВНЫЕ ЗАДАЧИ
- § 2. Основные задачи, связанные со скалярным умножением векторов
- § 3. Основные задачи, связанные с векторным умножением векторов
- § 4. Основные задачи, связанные с произведениями трех и более векторов
- § 5. Простейшие векторные уравнения
- § 6. Геометрические инварианты фигур
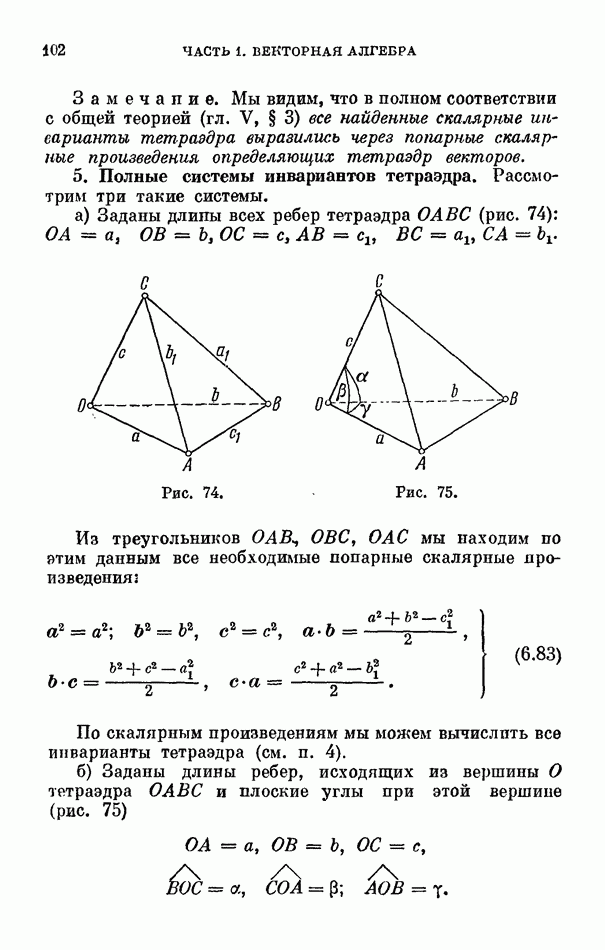
- 2. Треугольник.
- 3. Полные системы инвариантов треугольника.
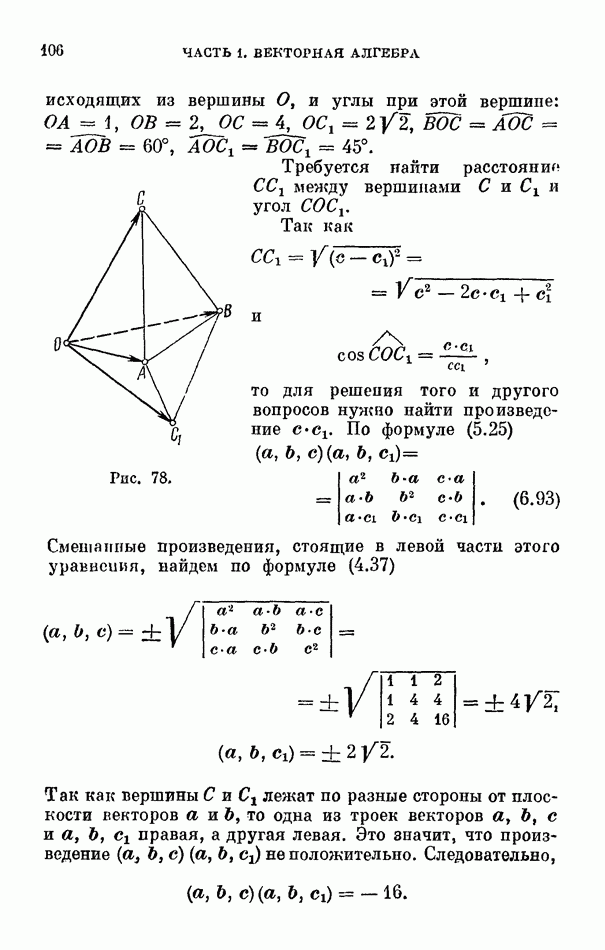
- 4. Тетраэдр.
- 5. Полные системы инвариантов тетраэдра.
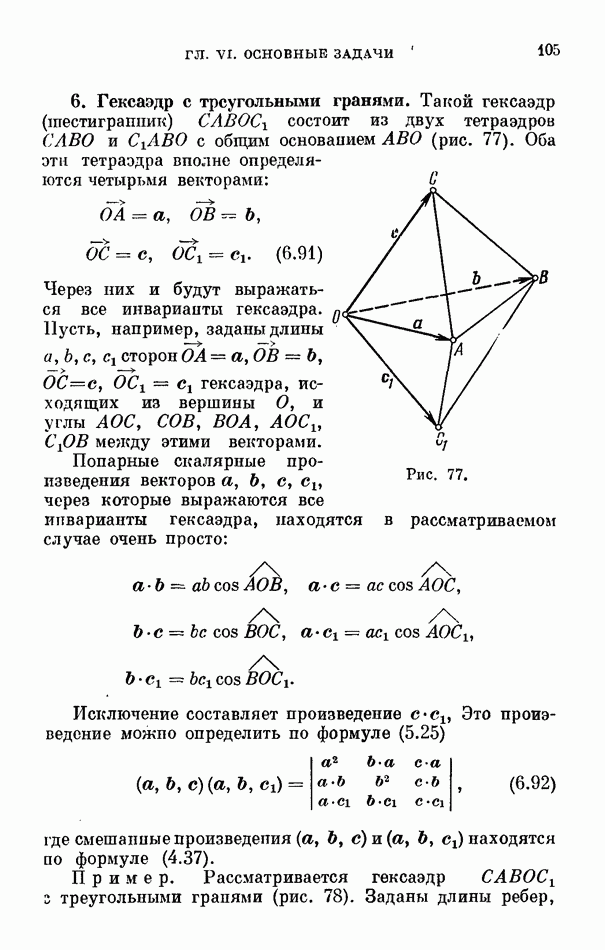
- 6. Гексаэдр с треугольными гранями.
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
- § 1. Векторы, зависящие от скаляра
- 2. Вектор-функция в координатной форме.
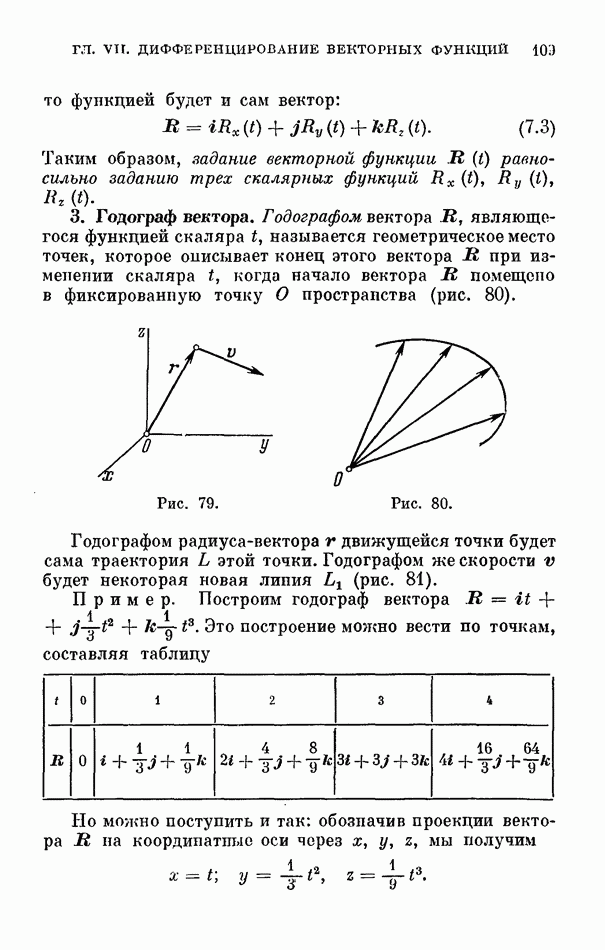
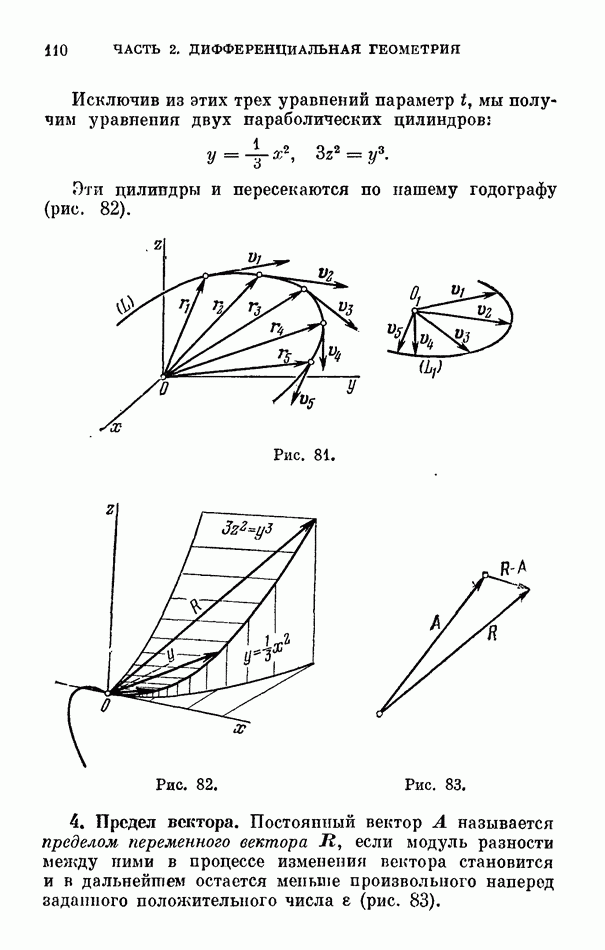
- 3. Годограф вектора.
- 4. Предел вектора.
- § 2. Дифференцирование вектора по скаляру
- 2. Геометрический смысл производной вектора по скаляру.
- 3. Механический смысл производной.
- 5. Дифференциал вектора.
- 6. Инвариантность дифференциала.
- 7. Связь дифференциала вектора с его приращением.
- § 3. Формула Тейлора
- Глава VIII. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ
- § 1. Основные дифференциально-геометрические понятия, связанные с линией
- 2. Касательная.
- 3. Соприкасающаяся плоскость.
- 4. Главная нормаль и бинормаль.
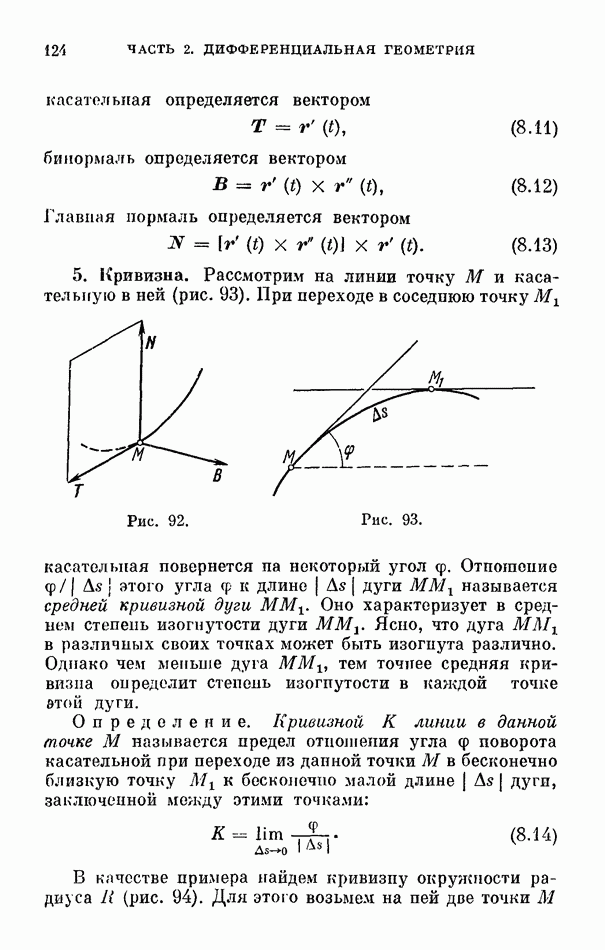
- 5. Кривизна.
- 6. Кручение.
- 7. Длина дуги.
- § 2. Основные формулы дифференциальной геометрии линий в пространстве
- 1. Дуга как параметр. Дифференциал дуги.
- 2. Орт касательной. Первая основная формула.
- 3. Инвариантность геометрических понятий.
- 4. Главная нормаль и кривизна. Вторая основная формула.
- 5. Бинормаль и кручение. Третья основная формула.
- 6. Винтовая линия.
- § 3. Сопровождающий трехгранник
- 2. Система дифференциальных уравнений движения сопровождающего трехгранника.
- 3. Расположение линии относительно сопровождающего трехгранника.
- 4. Линии без кривизны.
- 5. Линии без кручения.
- § 4. Инвариантные формулы
- Глава IX. ПЛОСКИЕ ЛИНИИ
- § 1. Дифференциальные уравнения плоской линии
- § 2. Кривизна плоской линии
- § 3. Круг кривизны
- § 4. Эволюта
- § 5. Эвольвента
- Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ
- § 1. Скорость и ускорение точки
- § 2. Движение твердого тела вокруг неподвижной точки
- 2. Формула Эйлера.
- 3. Угловая скорость.
- 4. Доказательстве существования угловой скорости твердого тела.
- § 3. Относительная производная вектора
- 2. Абсолютная и относительная производные вектора.
- 3. Общий случай движения твердого тела.
- Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
- § 1. Векторные функции нескольких скалярных аргументов
- § 2. Параметризованная поверхность
- 2. Поверхность в декартовых координатах.
- 3. Параметрическая сеть.
- 4. Линия на параметризованной поверхности.
- § 3. Касательная плоскость и нормаль
- 3. Нормальный вектор.
- 4. Преобразование параметров.
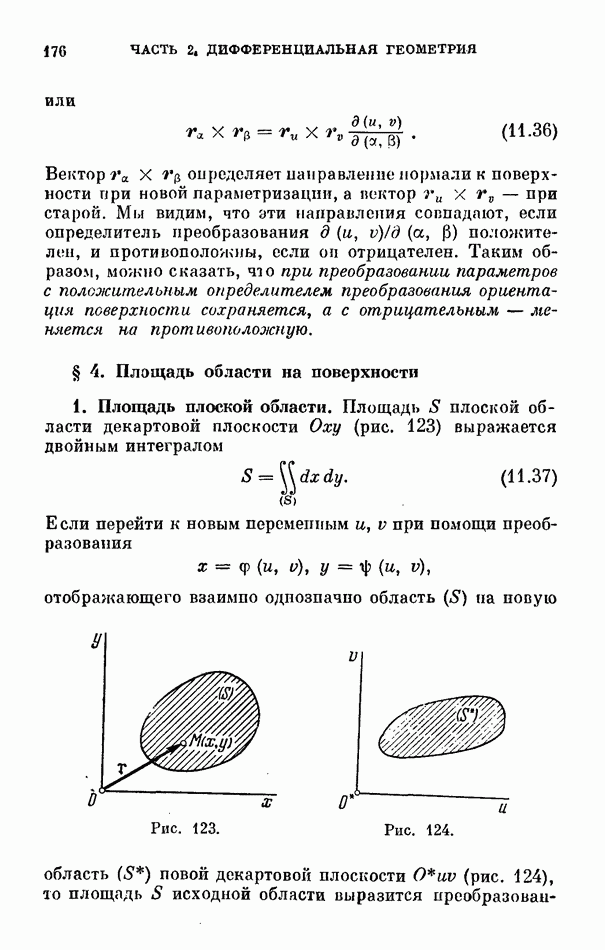
- § 4. Площадь области на поверхности
- 2. Площадь области на поверхности.
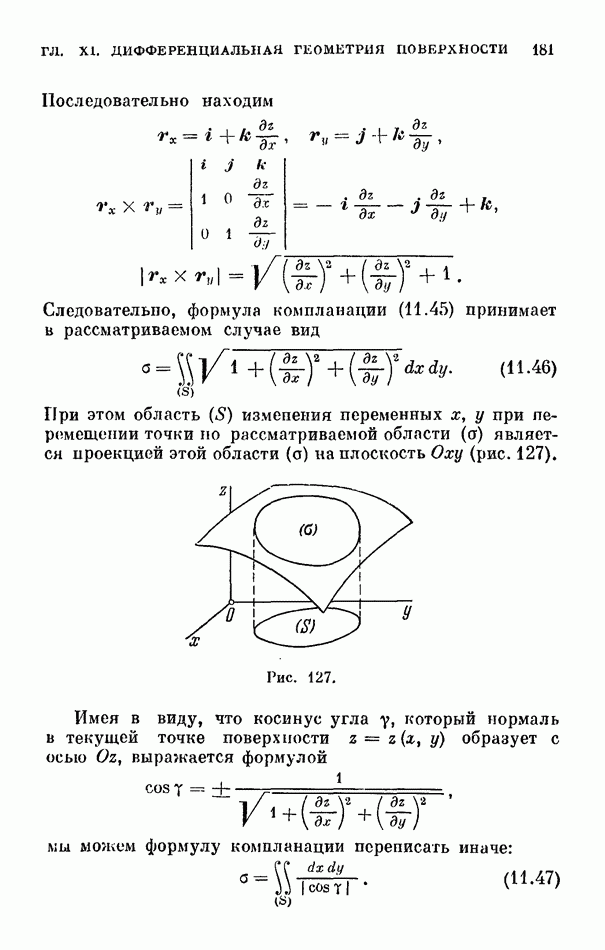
- 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y).
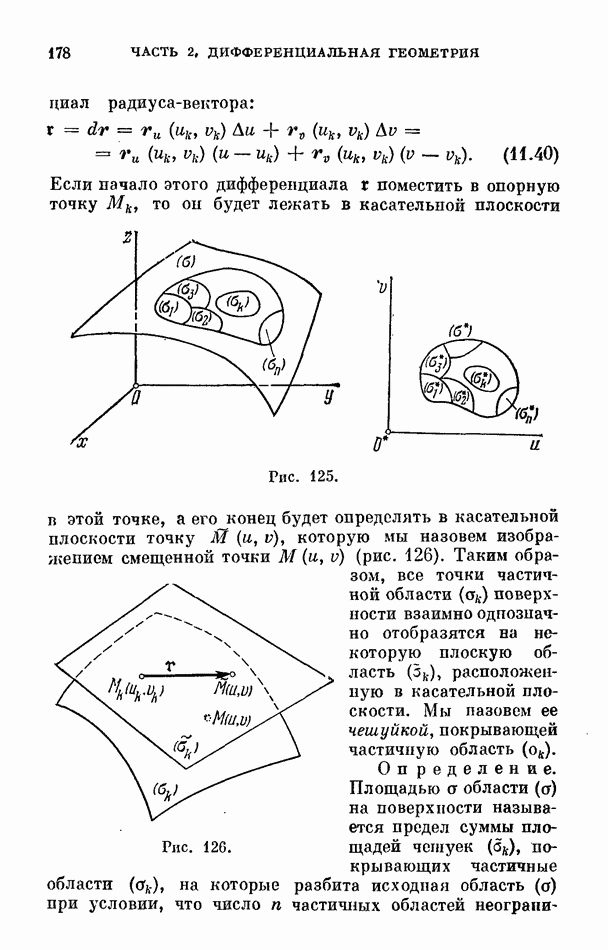
- 4. Элемент площади поверхности.
- 5. Векторный элемент площади поверхности.
- § 5. Первая квадратичная форма поверхности
- 2. Внутренняя геометрия поверхности.
- 3. Длина дуги линии на поверхности.
- 4. Угол между линиями на поверхности.
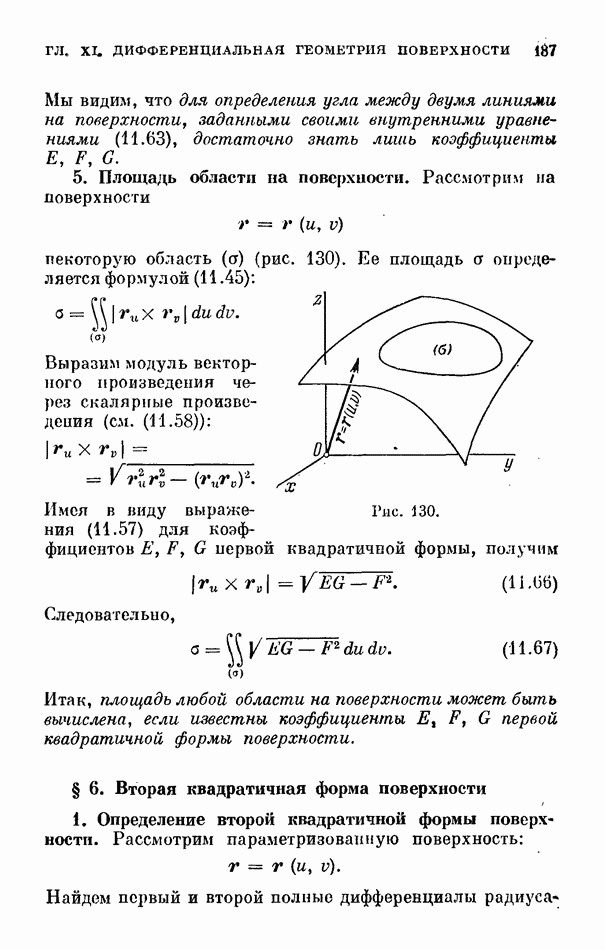
- 5. Площадь области на поверхности.
- § 6. Вторая квадратичная форма поверхности
- 2. Нормальная кривизна линии на поверхности.
- 3. Теорема Менье.
- § 7. Главные направления и главные кривизны поверхности
- 2. Главные направления на поверхности.
- 3. Перпендикулярность главных направлений.
- 4. Формула Эйлера.
- 5. Полная и средняя кривизны поверхности.
- ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ
- § 1. Функция поля. Поверхности уровня
- § 2. Градиент поля
- 2. Первая теорема о градиенте.
- § 3. Производная по направлению
- 2. Выражение производной по направлению через градиент.
- 3. Вторая теорема о градиенте.
- § 4. Направляющие косинусы нормали поверхности
- Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ
- § 1. Криволинейный интеграл как определенный интеграл от сложной функции
- 2. Криволинейный интеграл от линейной формы по произвольной кривой.
- 3. Основные свойства криволинейного интеграла.
- 4. Обобщенный криволинейный интеграл.
- 5. Примеры.
- § 2. Криволинейный интеграл как предел криволипейной интегральной суммы
- § 3. Поверхностный интеграл как двойной интеграл от сложной функции
- 2. Определение простейшего поверхностного интеграла.
- 3. Поверхностный интеграл от билинейной формы по произвольной поверхности.
- § 4. Поверхностный интеграл как предел поверхностной интегральной суммы
- § 5. Поверхностный интеграл в параметрической форме
- 2. Параметрический поверхностный интеграл.
- 3. Поверхностный интеграл как предел суммы.
- § 6. Кратный интеграл как предел обобщенной интегральной суммы
- 2. Обобщение основной теоремы о кратном интеграле.
- Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ
- § 1. Векторное поле
- § 2. Векторные линии
- § 3. Циркуляция поля вдоль линии
- § 4. Поток поля через поверхность
- Глава XV. ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ
- § 1. Формула Остроградского
- § 2. Дивергенция поля
- 2. Дивергенция как предел отношения.
- 3. Гидромеханический смысл дивергенции.
- 4. Теорема Остроградского.
- Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ
- § 1. Формула Стокса
- § 2. Ротация поля
- § 3. Оператор Гамильтона
- Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ
- § 1. Потенциальное поле
- 3. Циркуляция потенциального поля по замкнутому контуру.
- 4. Циркуляция потенциального поля между двумя точками.
- 5. Потенциал.
- 6. Элемент циркуляции.
- 7. Характеристические признаки потенциального поля.
- 8. Вычисление потенциала.
- 9. Центральное поле.
- 10. Вихревые шнуры.
- § 2. Соленоидальное поле
- 3. Поток соленоидального поля через замкнутую поверхность.
- 4. Трубчатое строение соленоидального поля.
- 5. Векторный потенциал.
- 6. Характеристические признаки соленоидального поля.
- 7. Источники и стоки.
- § 3. Потенциальное несжимаемое поле
- Глава XVIII. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ
- § 1. Электростатическое поле точечного заряда
- 2. Дивергенция поля точечного заряда.
- 3. Поток поля точечного заряда через замкнутую поверхность.
- 4. Ротация поля точечного заряда.
- 5. Потенциал поля точечного заряда.
- § 2. Электростатическое поле системы точечных зарядов
- 2. Дивергенция и ротация поля системы точечных зарядов.
- 3. Поток поля системы точечных зарядов через замкнутую поверхность.
- 4. Потенциал поля системы точечных зарядов.
- 5. Непрерывно распределенный заряд.
- § 3. Магнитное поле тока
- 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу.
- 3. Векторные линии поля H.
- 4. Потенциал поля Н.
- 5. Провод как вихревой шнур.
- Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 1. Криволинейные координаты
- 3. Координатные поверхности и линии.
- 4. Линейный элемент.
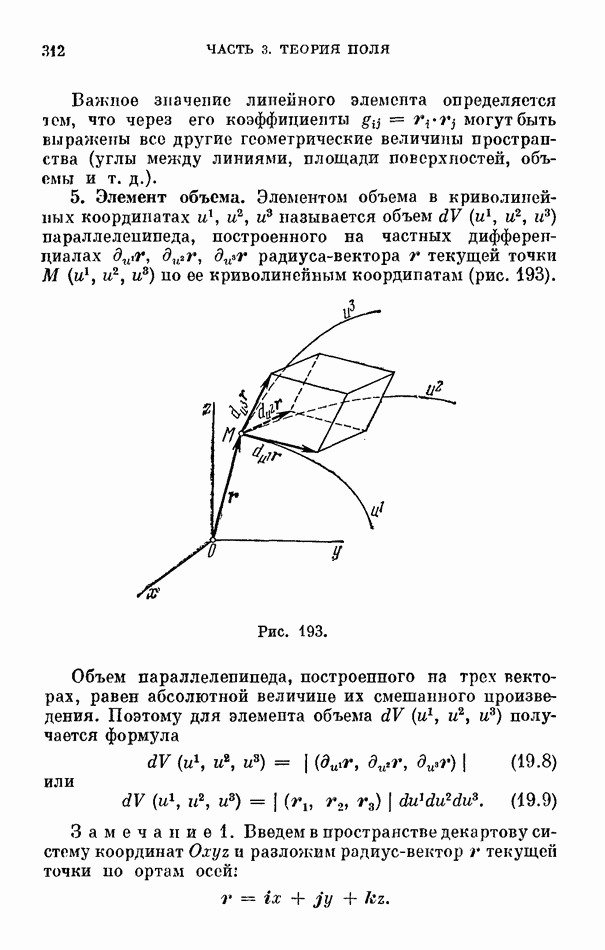
- 5. Элемент объема.
- 6. Подвижной репер.
- 7. Векторное поле в криволиненных координатах.
- § 2. Дифференциальные операции в криволинейных координатах
- 2. Дивергенция в криволинейных координатах.
- 3. Ротация в криволинейных координатах.
- § 3. Ортогональные координаты
- § 4. Цилиндрические координаты
- 2. Линейный элемент и элемент объема в цилиндрических координатах.
- 3. Дифференциальные операции в цилиндрических координатах.
- § 5. Сферические координаты