| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
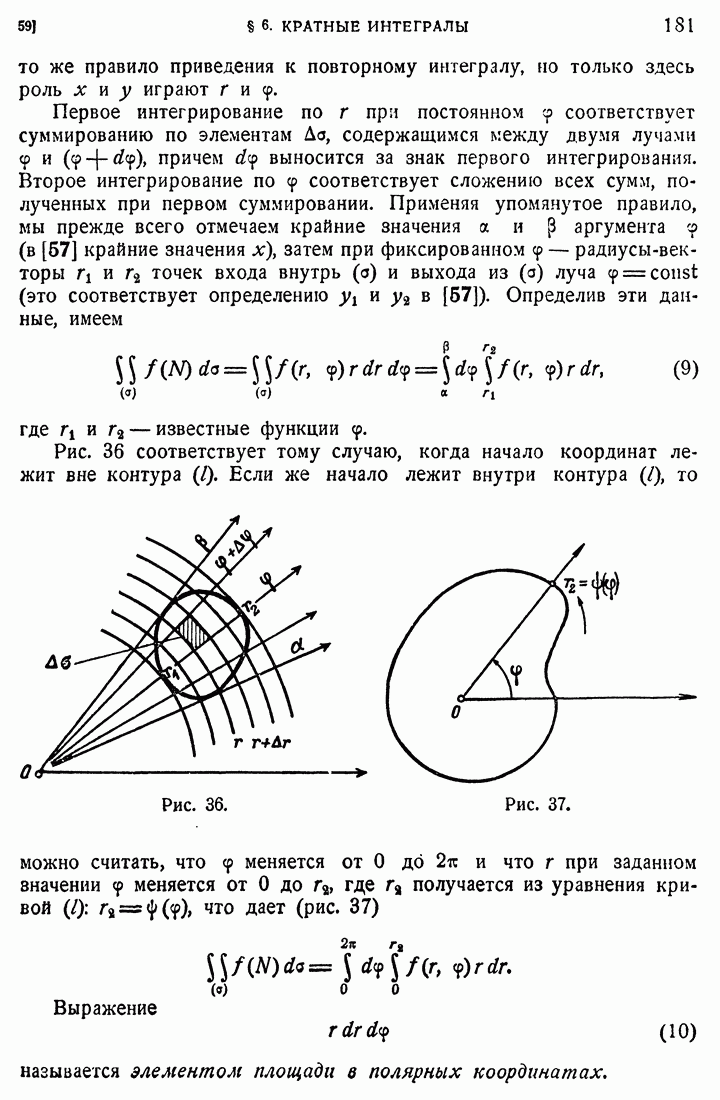
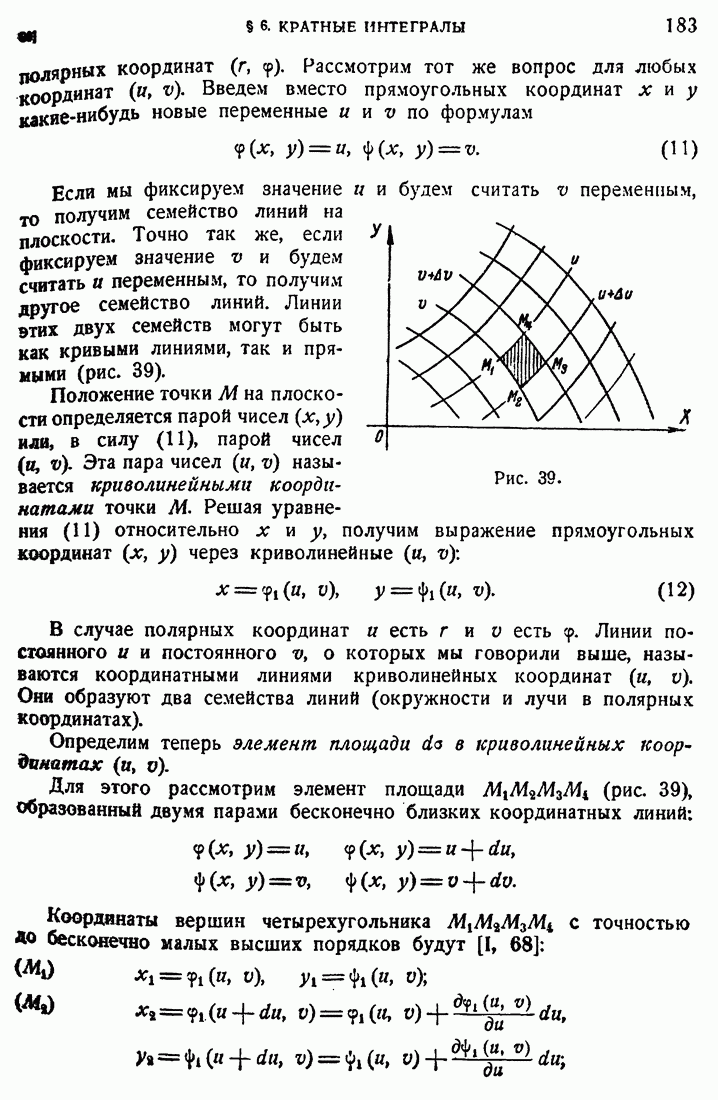
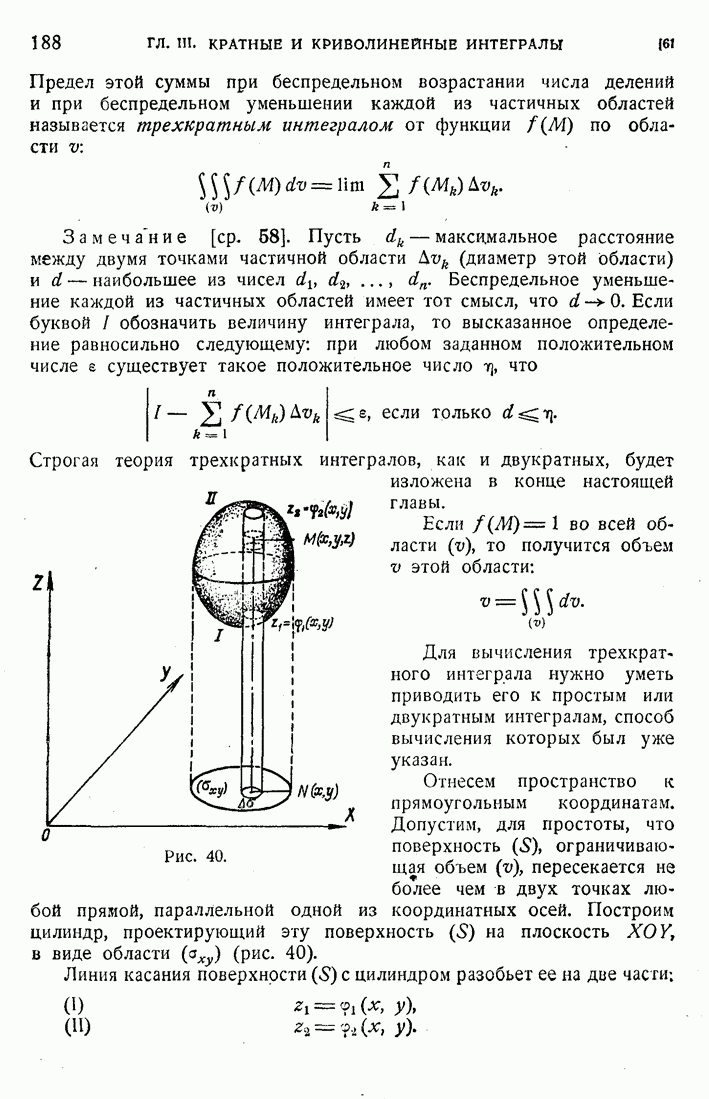
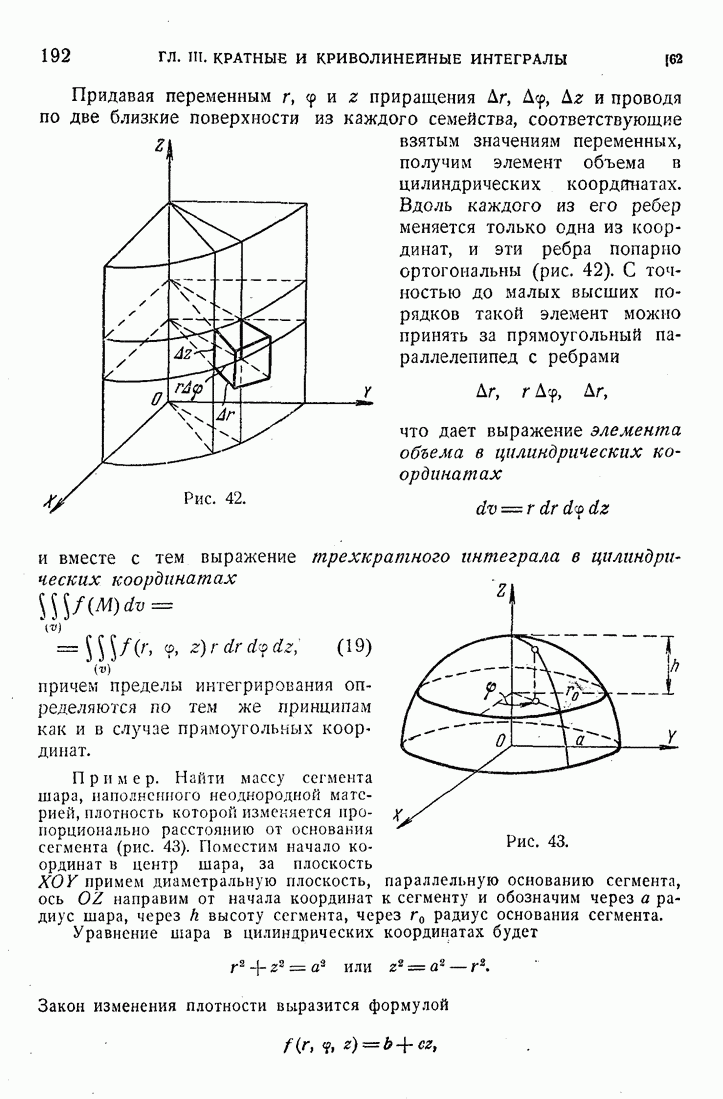
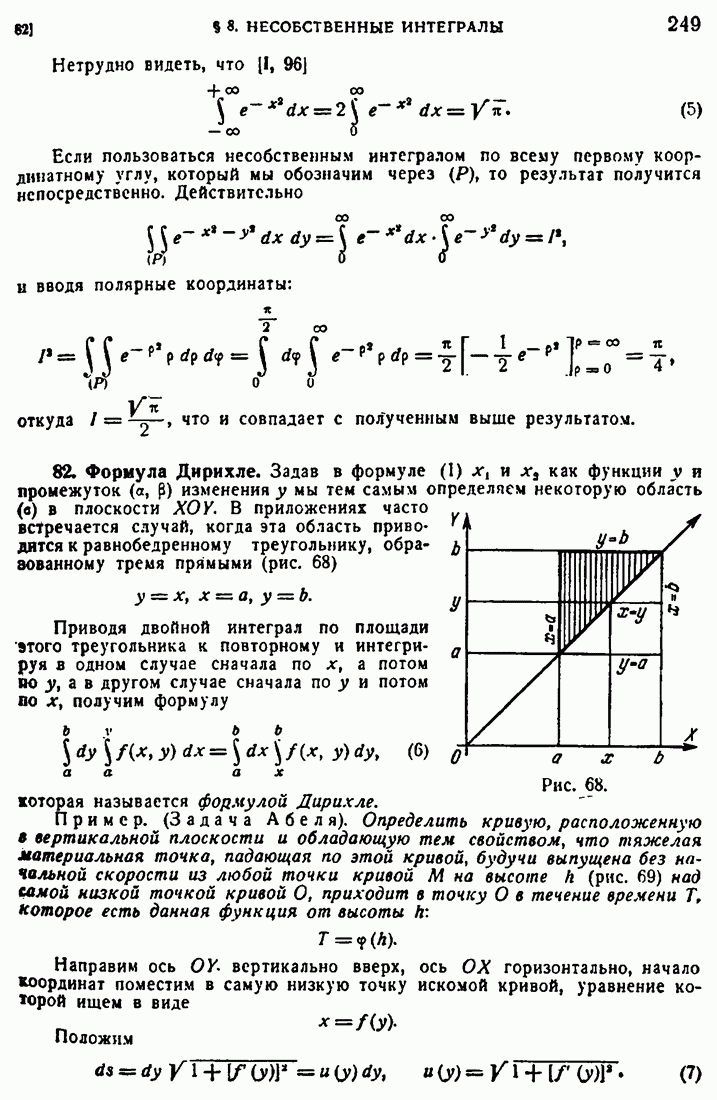
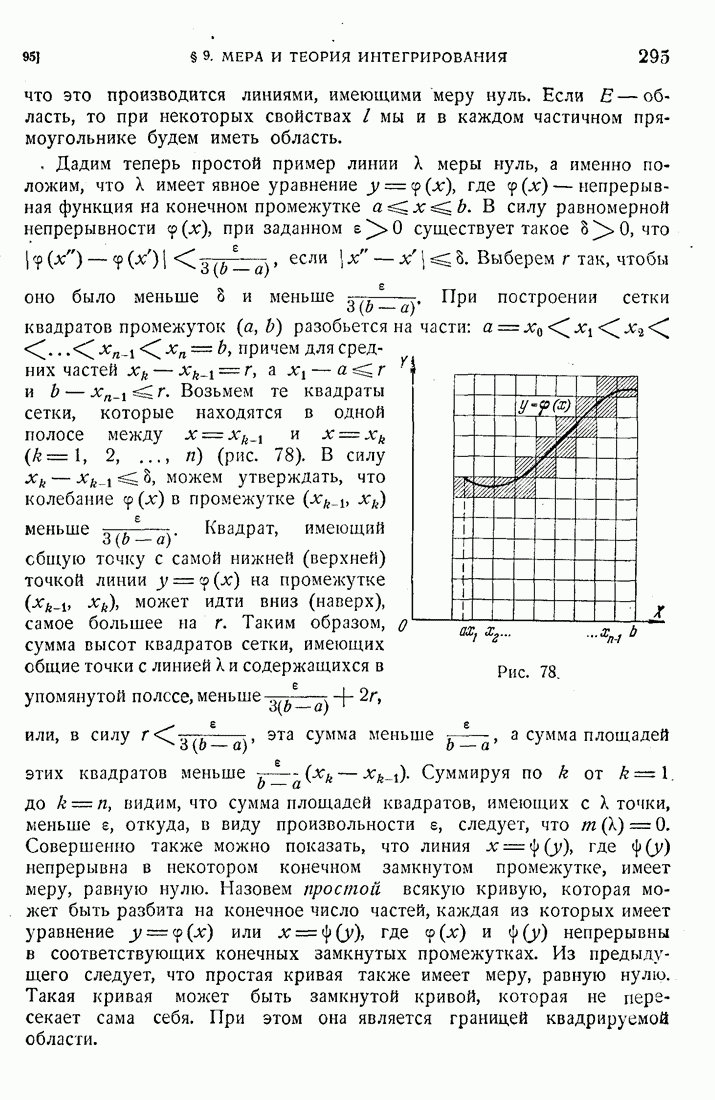
210. Потенциал объемных масс.
Рассмотрим неоднородное уравнение Лапласа

в конечной области (D) с поверхностью (S). Общее решение этого уравнения есть сумма какого-либо частного его решения и гармонической в D функции. Пусть имеется решение уравнения (54), к которому применима формула (9). Поскольку производная от 1 по любому фиксированному направлению удовлетворяет уравнению Лапласа, то подынтегральная функция в поверхностном интеграле формулы (9) и сам этот интеграл суть гармонические функции в D. Таким образом тройной интеграл должен удовлетворять уравнению (54). Но в силу (54) в этом интеграле  можно заменить на
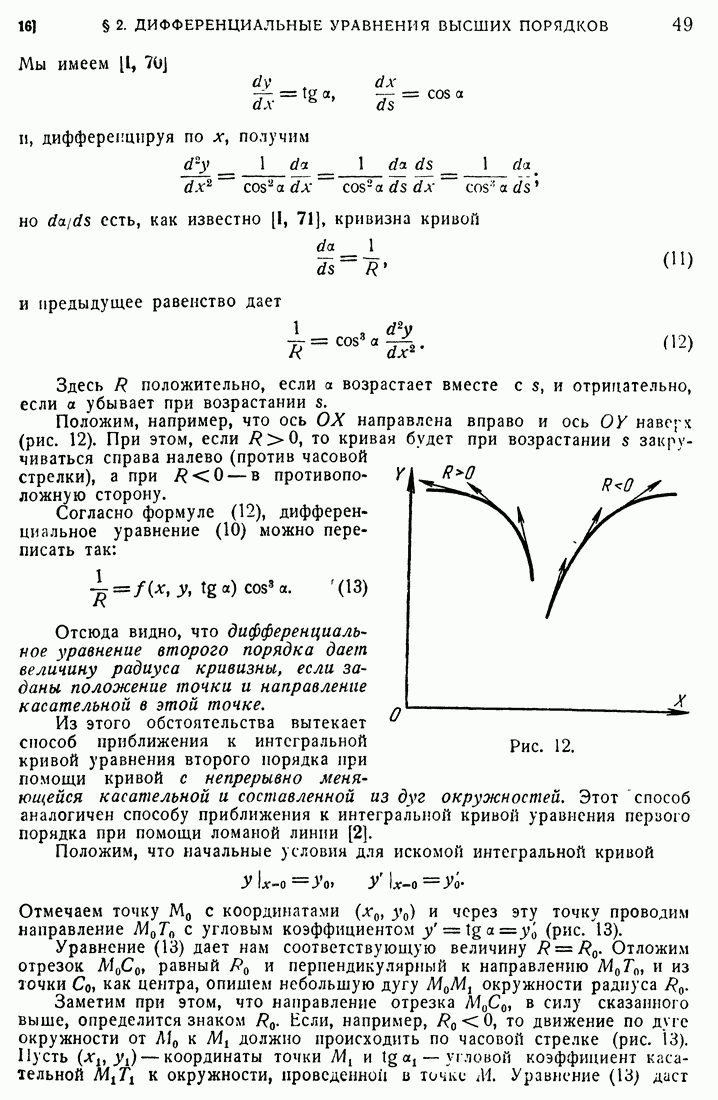
можно заменить на  , и таким образом мы получаем частное решение
, и таким образом мы получаем частное решение
уравнения (54) вида

Мы получили этот результат, предполагая, что уравнение (54) имеет решение, к которому применима формула (9). Для полного решения задачи нам надо более подробно исследовать объемный потенциал (55) при определенных предположениях относительно функции  . Мы положим
. Мы положим  и будем исследовать следующий потенциал объемных масс
и будем исследовать следующий потенциал объемных масс

или

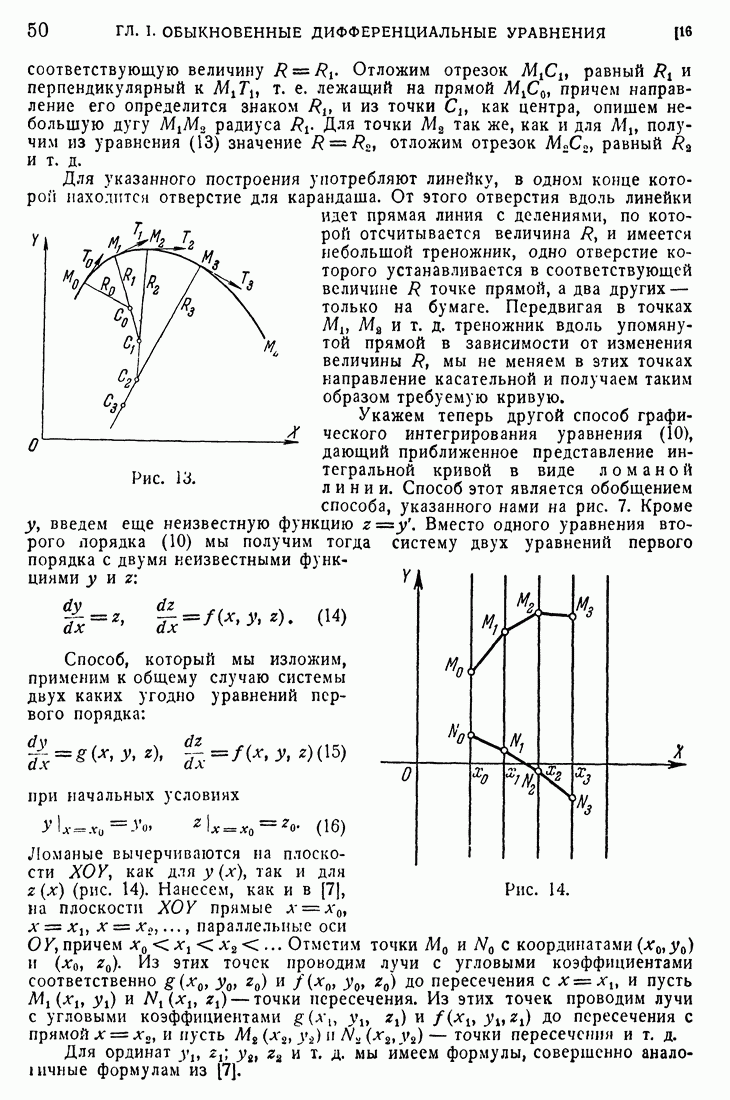
Положим, что  непрерывна в (D) вплоть до (S). Как мы уже упоминали, интеграл (56) является собственным интегралом, если М лежит вне (D). В этом случае функция
непрерывна в (D) вплоть до (S). Как мы уже упоминали, интеграл (56) является собственным интегралом, если М лежит вне (D). В этом случае функция  имеет частные производные всех порядков. Эти производные могут быть получены дифференцированием под знаком интеграла, и
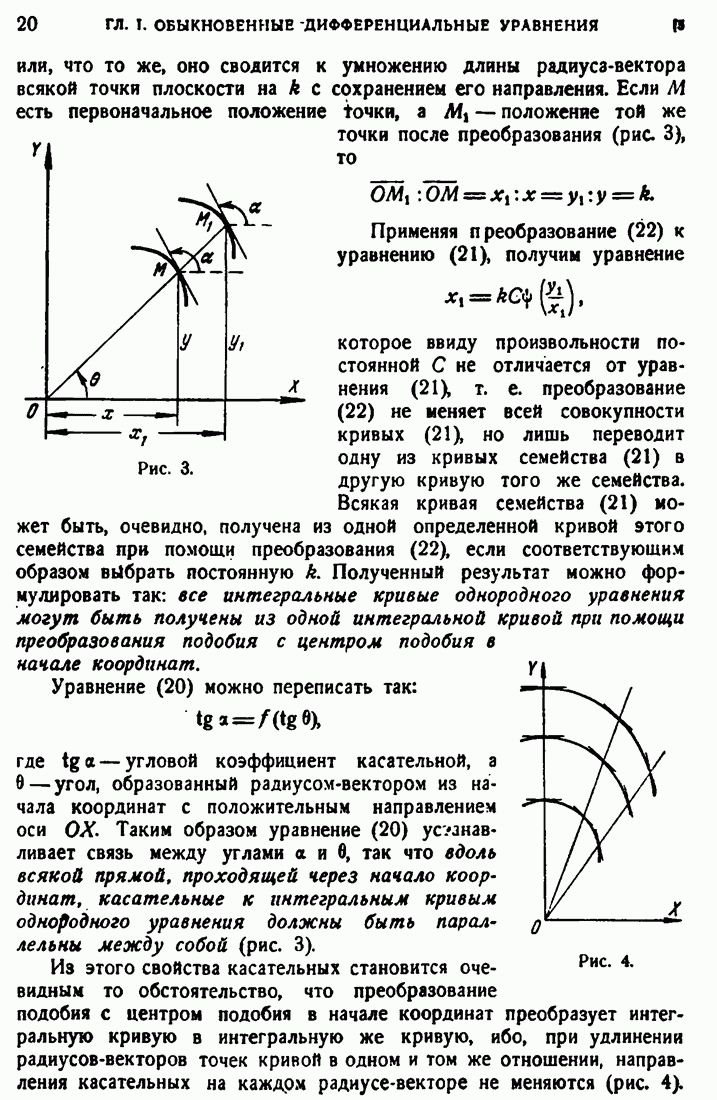
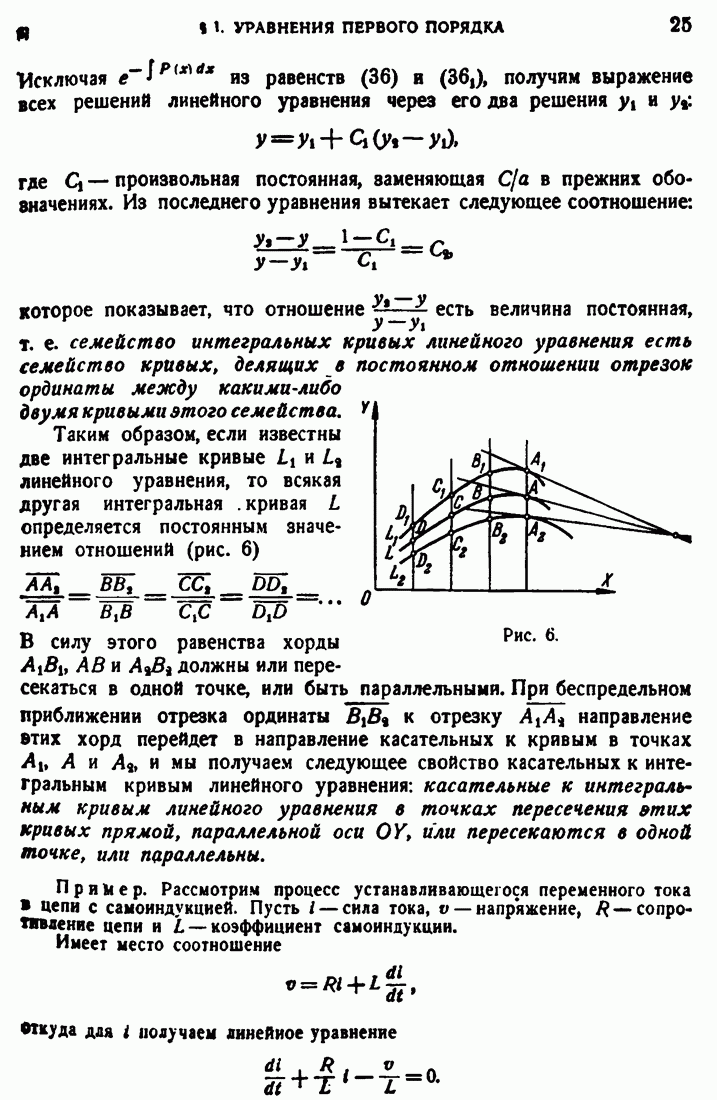
имеет частные производные всех порядков. Эти производные могут быть получены дифференцированием под знаком интеграла, и  удовлетворяет уравнению Лапласа
удовлетворяет уравнению Лапласа  . Если М принадлежит (D), то существует несобственный интеграл (56) и существует также интеграл, полученный путем дифференцирования подынтегральной функции, например, по
. Если М принадлежит (D), то существует несобственный интеграл (56) и существует также интеграл, полученный путем дифференцирования подынтегральной функции, например, по  . Но не было доказано, что он дает частную производную от V по
. Но не было доказано, что он дает частную производную от V по  Докажем по поводу интеграла (56) две теоремы:
Докажем по поводу интеграла (56) две теоремы:
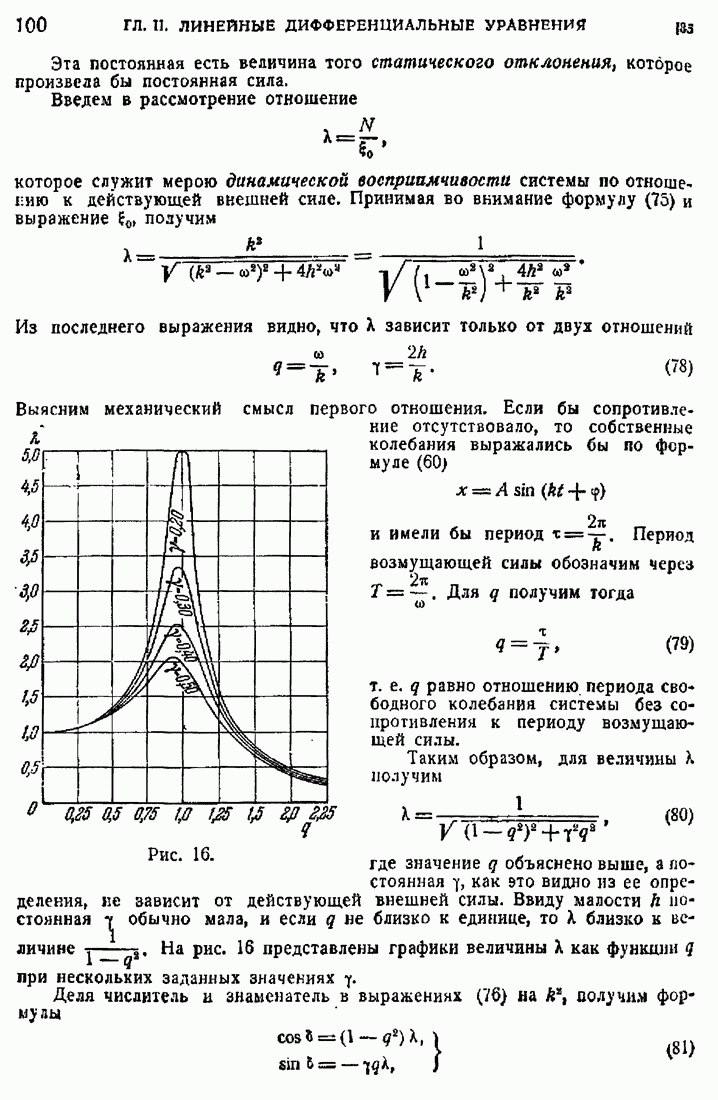
Теорема 1. Если  непрерывна в области (D) вплоть до (S), то
непрерывна в области (D) вплоть до (S), то  и ее частные производные первого порядка непрерывны во всем пространстве, и упомянутые частные производные могут быть получены дифференцированием под знаком интеграла.
и ее частные производные первого порядка непрерывны во всем пространстве, и упомянутые частные производные могут быть получены дифференцированием под знаком интеграла.
Доказательство будем проводить при любом положении М относительно сбласти (D). Вместо у введем новую функцию, которая отличается от у лишь при  , где
, где  — заданное положительное число, но которая сама непрерывна и имеет непрерывные производные по координатам вплоть до
— заданное положительное число, но которая сама непрерывна и имеет непрерывные производные по координатам вплоть до  . Для этого заменим — при
. Для этого заменим — при  полиномом: а
полиномом: а  выбрав
выбрав  так, чтобы при
так, чтобы при  иметь
иметь

что дает непрерывность производных на стыке функции  и
и  , т. е. при
, т. е. при  . Написанные формулы дают
. Написанные формулы дают  и мы приходим к функции
и мы приходим к функции  определенной равенствами
определенной равенствами

Подставляя эту функцию вместо  в интеграл (66), получим вместо
в интеграл (66), получим вместо  новую функцию
новую функцию

непрерывную во всем пространстве и с непрерывными частными производными, которые могут быть получены дифференцированием под знаком интеграла, поскольку подынтегральная функция интеграла формулы (58) сама непрерывна и имеет непрерывные производные при  Мы можем, например, написать
Мы можем, например, написать

Составим разность

Поскольку  совпадают при
совпадают при  разность, стоящая справа, равна нулю для всех точек
разность, стоящая справа, равна нулю для всех точек  лежащих вне сферы
лежащих вне сферы  с центром М и радиусом е. Если, например, М лежит вне (D) и
с центром М и радиусом е. Если, например, М лежит вне (D) и  меньше расстояния от М до (D), то интеграл, стоящий в правой части (60), равен нулю.
меньше расстояния от М до (D), то интеграл, стоящий в правой части (60), равен нулю.
В других случаях сфера  может частично или целиком попадать в (D). Обозначая через
может частично или целиком попадать в (D). Обозначая через  наибольшее абсолютное значение
наибольшее абсолютное значение  в (D) и принимая во внимание, что
в (D) и принимая во внимание, что  положительная функция, мы получим для подынтегральной функции правой части оценку
положительная функция, мы получим для подынтегральной функции правой части оценку

и вне сферы  подынтегральная функция, как указано выше, обращается в нуль. Если мы проинтегрируем положительную функцию, стоящую в правой части (61), по всей сфере
подынтегральная функция, как указано выше, обращается в нуль. Если мы проинтегрируем положительную функцию, стоящую в правой части (61), по всей сфере  то получим.
то получим.
очевидно, следующую оценку:

Подставляя вместо  вторую из формул (57) и выполняя квадратуры, получим
вторую из формул (57) и выполняя квадратуры, получим

Отсюда видно, что при  непрерывные функции
непрерывные функции  равномерно по отношению к положению точки М стремятся к
равномерно по отношению к положению точки М стремятся к  , а потому
, а потому  есть также непрерывная функция [I, 144]. Для исследования частных производных функции
есть также непрерывная функция [I, 144]. Для исследования частных производных функции  составим интеграл, который получается дифференцированием интеграла формулы (56) по
составим интеграл, который получается дифференцированием интеграла формулы (56) по  под знаком интеграла, и обозначим полученную функцию через
под знаком интеграла, и обозначим полученную функцию через  :
:

Составим, как и выше, разность

Принимая во внимание, что для любой функции  мы имеем
мы имеем

и что  , можем для подынтегральной функции последнего интеграла написать неравенство
, можем для подынтегральной функции последнего интеграла написать неравенство

и, совершенно так же, как и выше

Принимая во внимание, что, в силу (57),

и выполняя квадратуры, получим

откуда следует, что при в  производная - равномерно относительно М стремится к W (М). Выше было доказано, что
производная - равномерно относительно М стремится к W (М). Выше было доказано, что 
равномерно стремится к  . Принимая во внимание теорему из [I, 144], мы видим, что W (М) есть частная производная от
. Принимая во внимание теорему из [I, 144], мы видим, что W (М) есть частная производная от  по х, т. е., в силу (62),
по х, т. е., в силу (62),

Непрерывность W (М) вытекает из непрерывности частных производных (59) и равномерного стремления их к пределу  и теорема доказана полностью. Производные по у и z исследуются точно так же. Отметим, что при доказательстве теоремы мы использовали лишь ограниченность
и теорема доказана полностью. Производные по у и z исследуются точно так же. Отметим, что при доказательстве теоремы мы использовали лишь ограниченность  и ее интегрируемость.
и ее интегрируемость.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
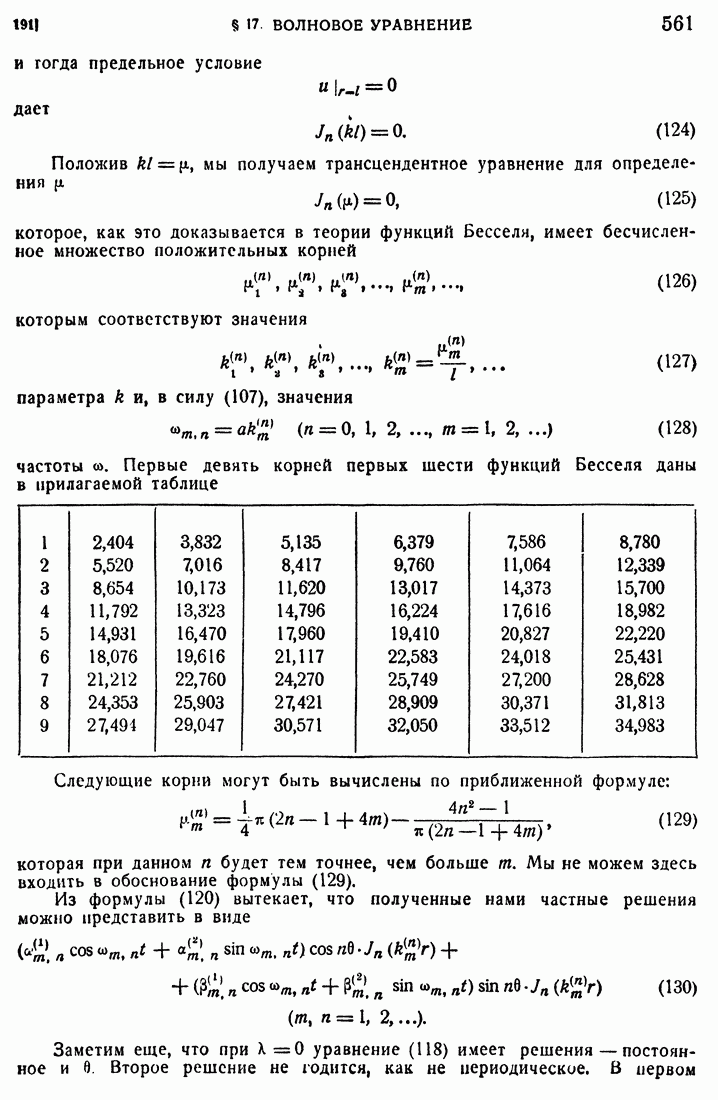
- 33. Линейные уравнения и колебательные явления.
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
- 53. Сходимость метода Эйлера — Коши.
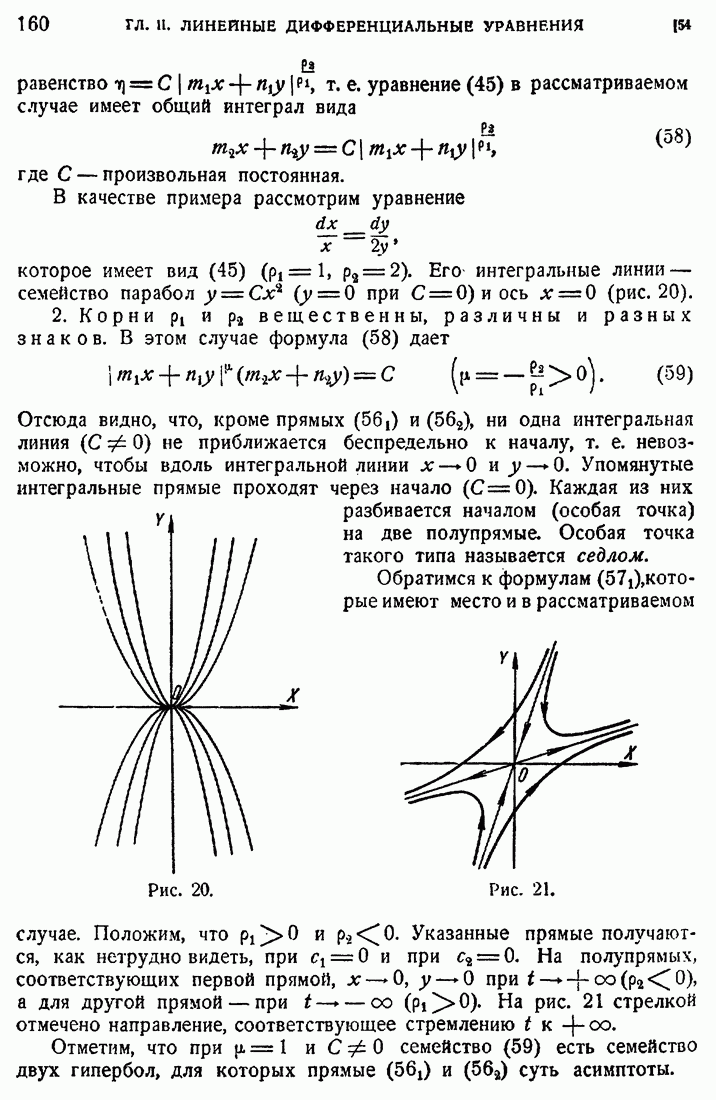
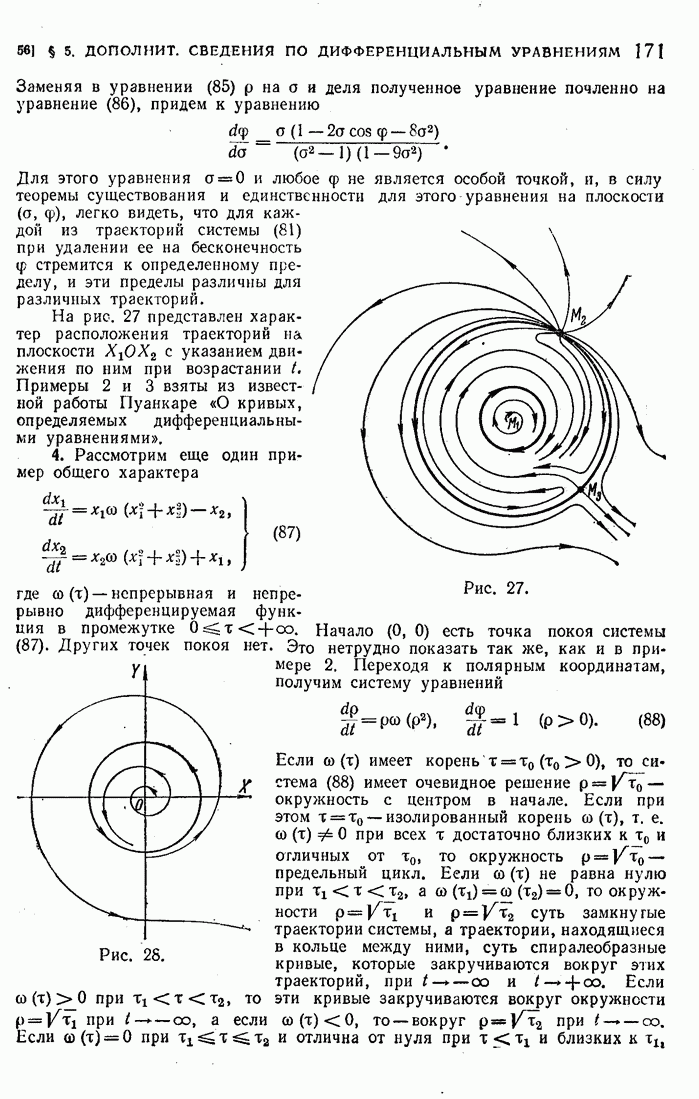
- 54. Особые точки дифференциальных уравнений первого порядка.
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
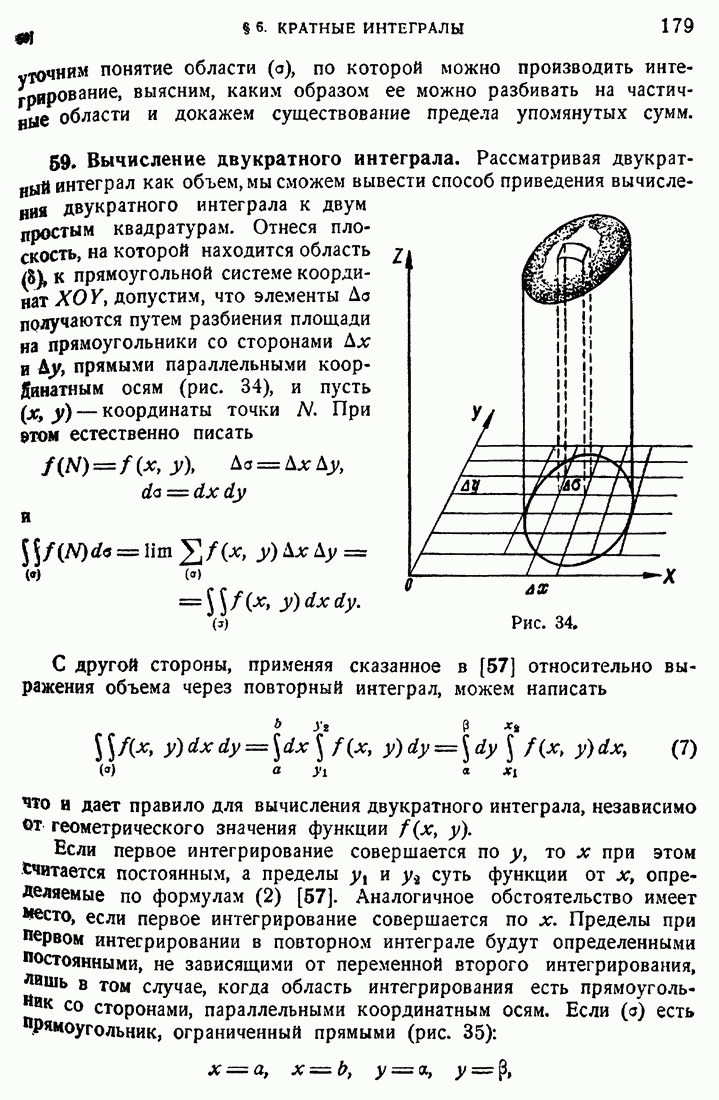
- 58. Двукратный интеграл.
- 59. Вычисление двукратного интеграла.
- 60. Криволинейные координаты.
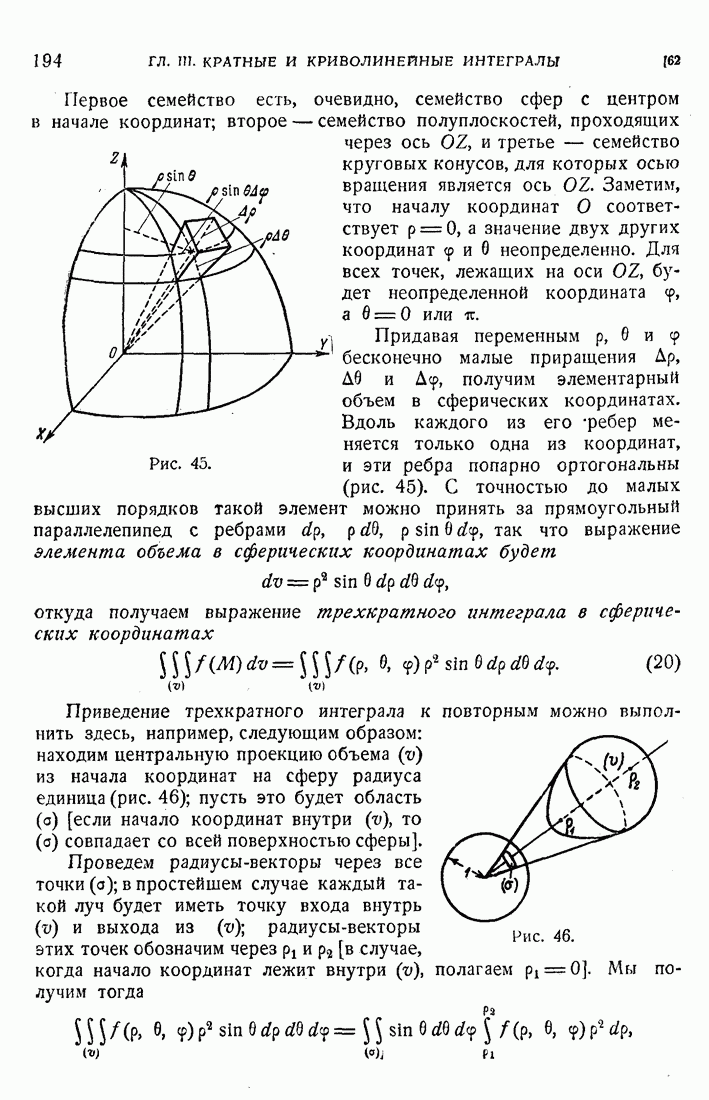
- 61. Трехкратный интеграл
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
- 67. Интегралы по определенной стороне поверхности.
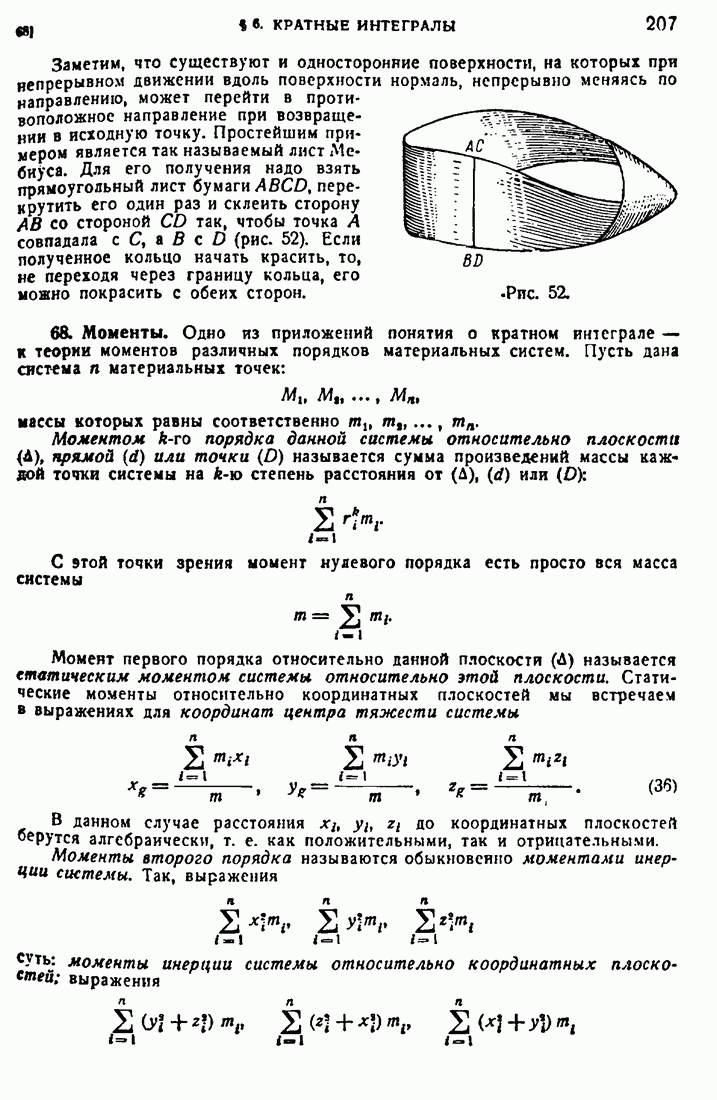
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
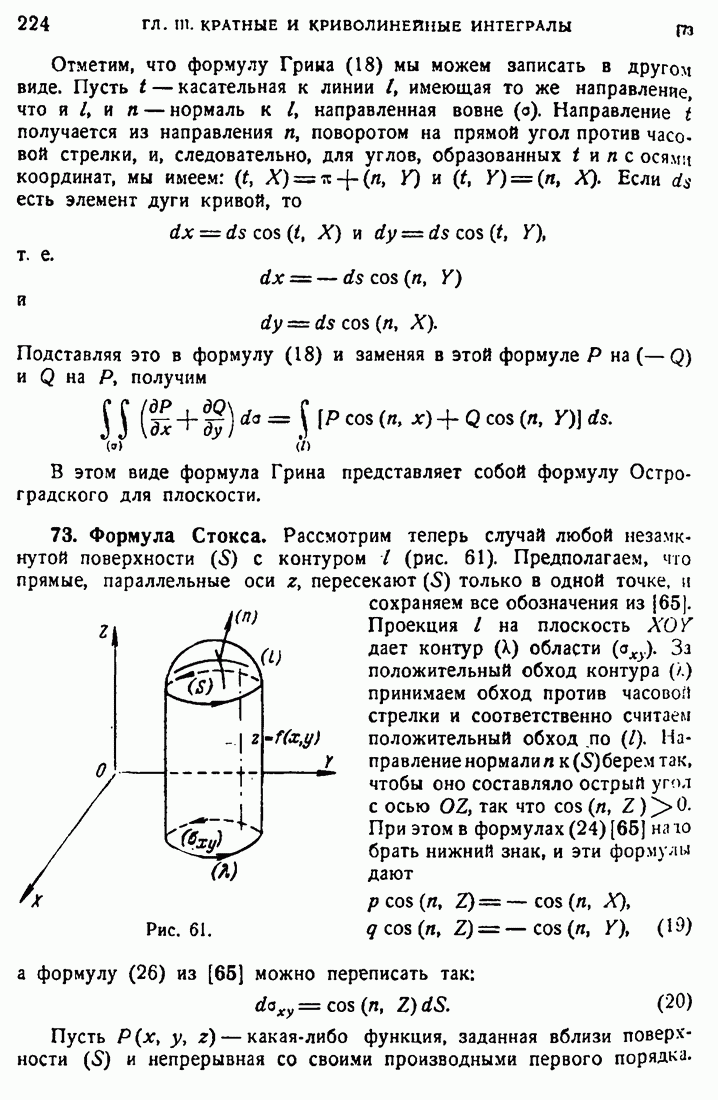
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
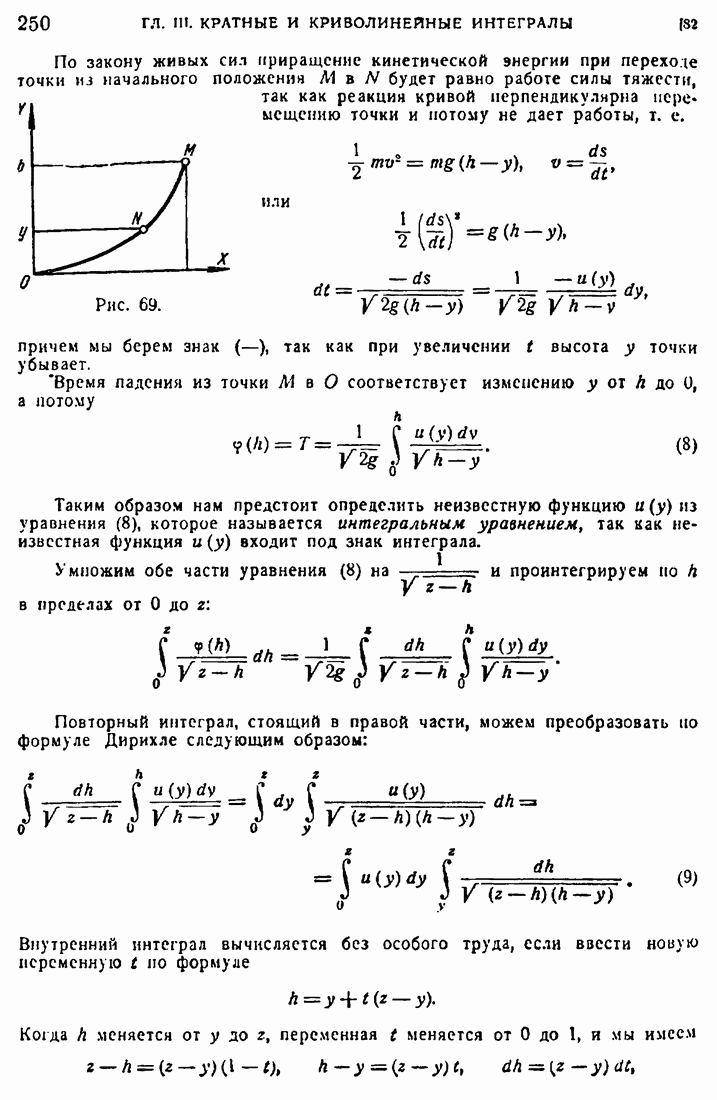
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
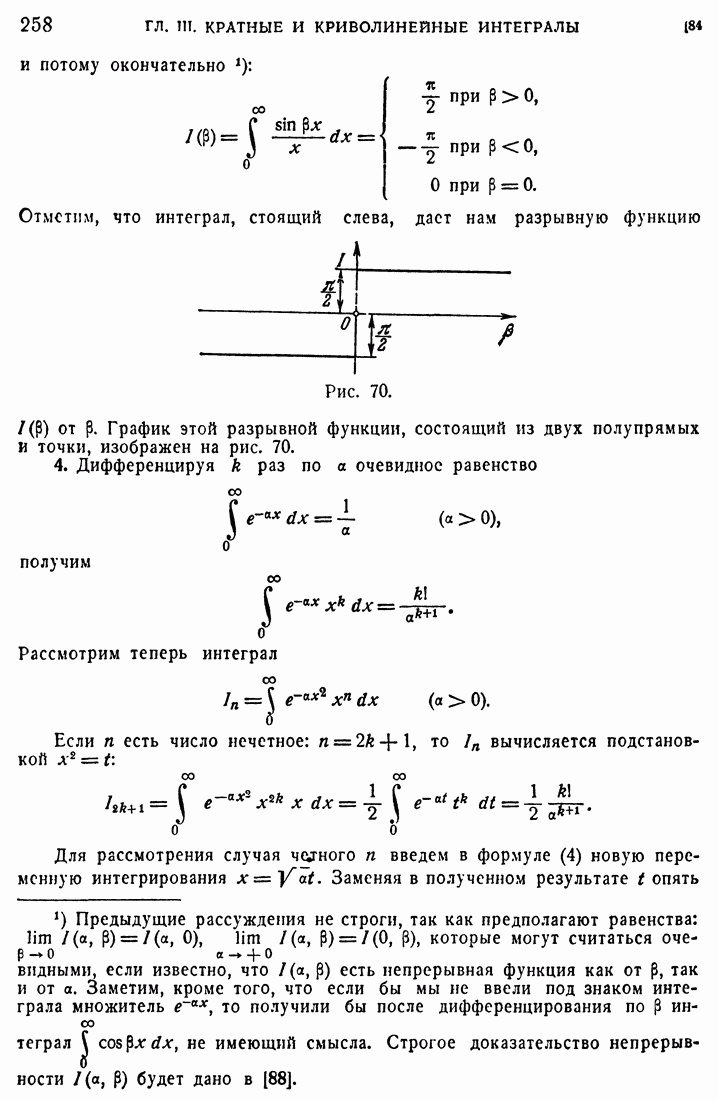
- 84. Примеры.
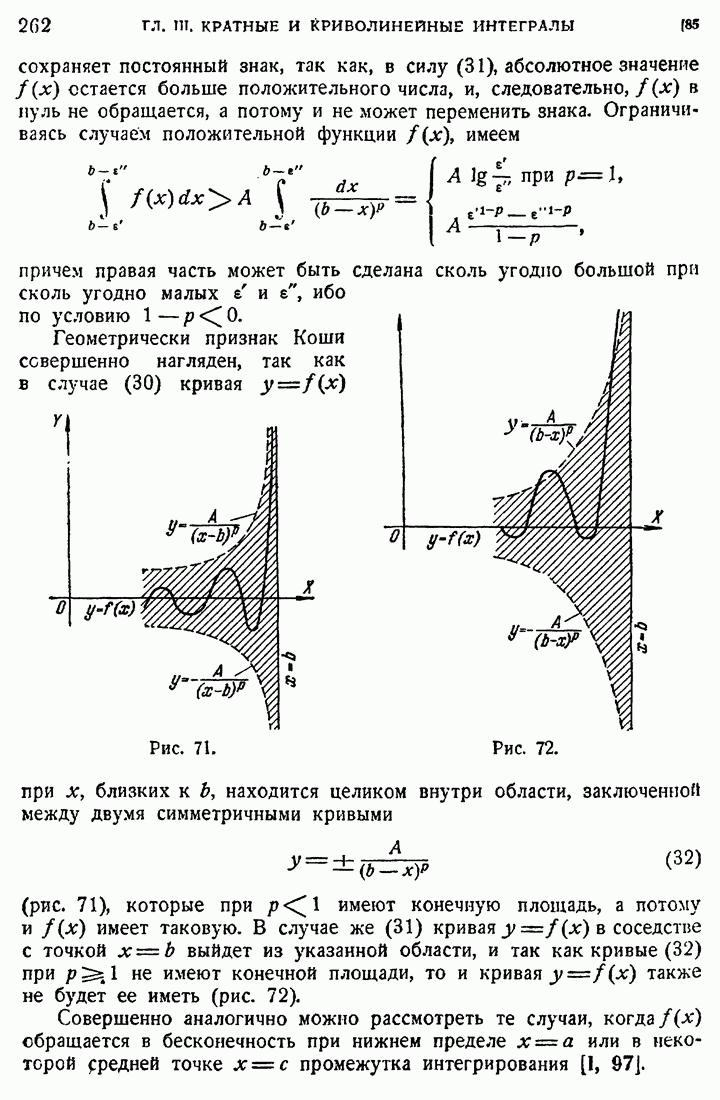
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
- 156. Примеры.
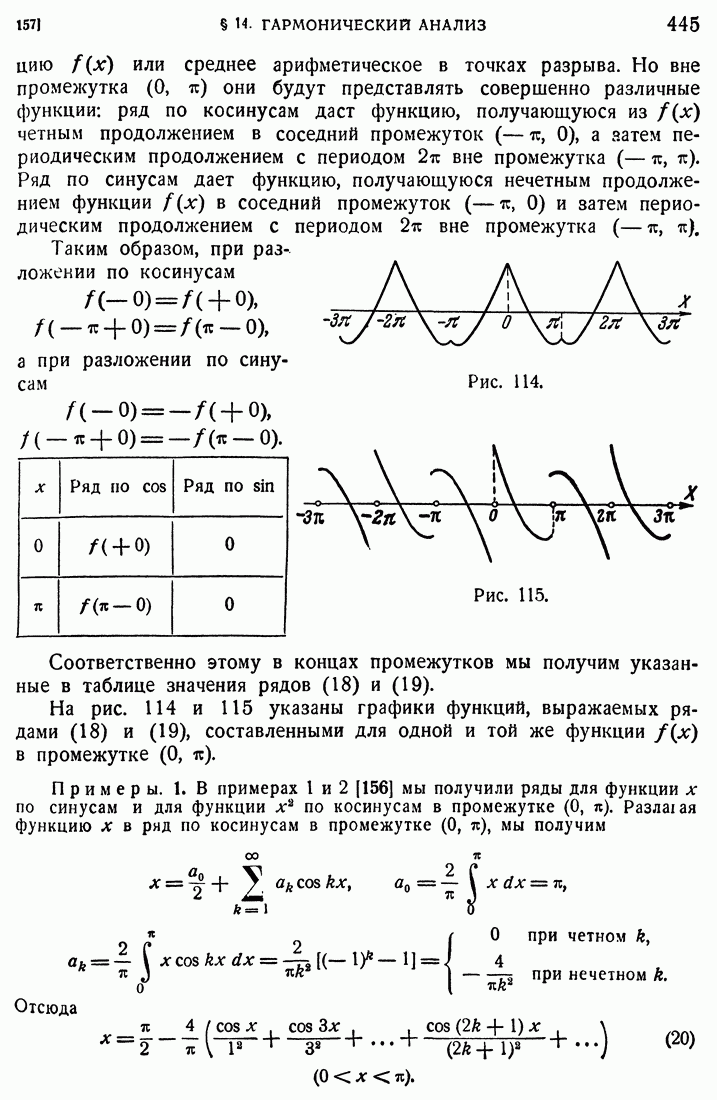
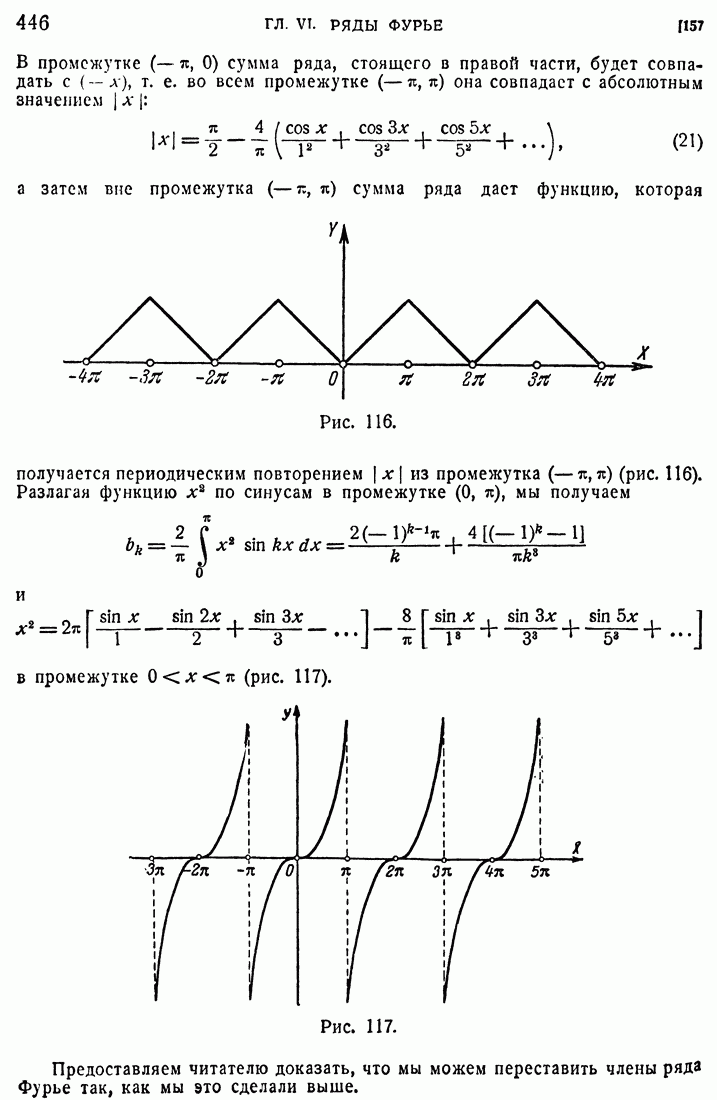
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
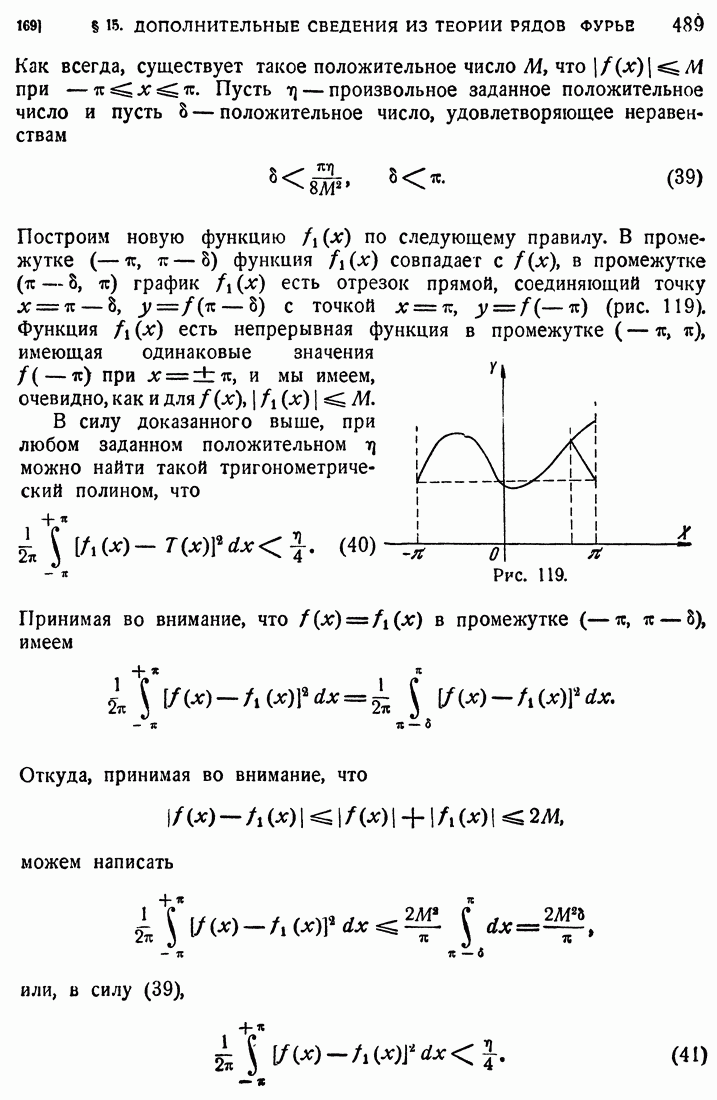
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
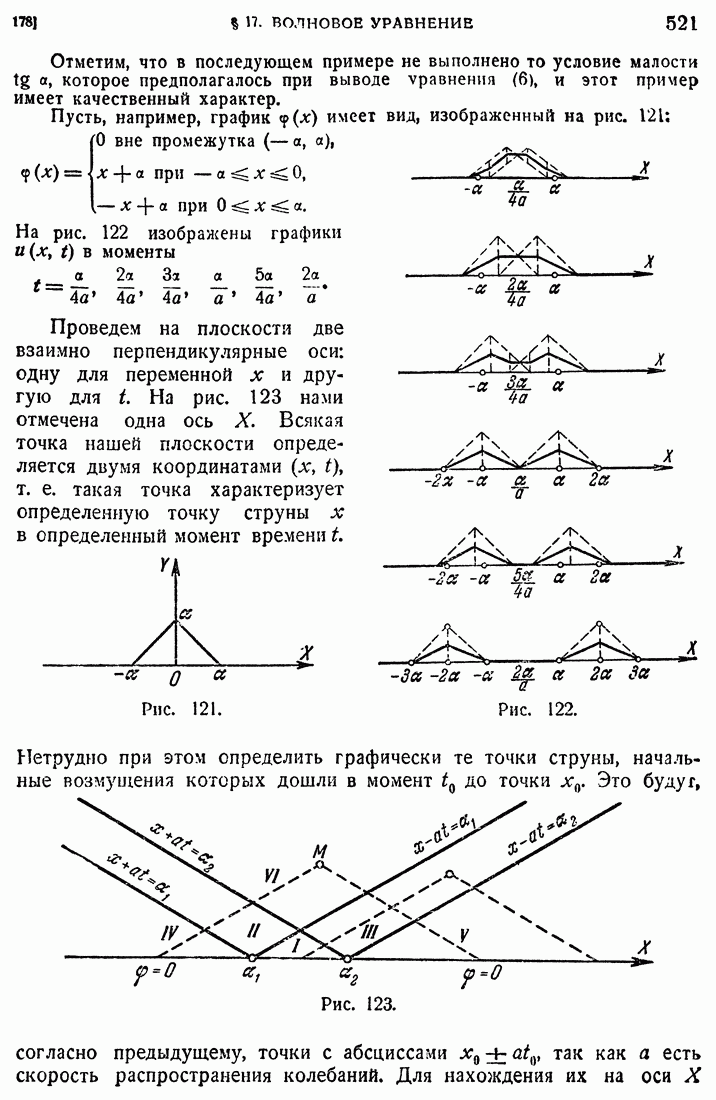
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
- 219. Теорема единственности.