| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
50. Метод последовательных приближений для линейных уравнений.
Мы уже несколько раз упоминали о теореме существования и единственности для дифференциальных уравнений. Приведем доказательство этой теоремы сначала для случая линейных дифференциальных уравнений. Для доказательств мы применим так называемый метод последовательных приближений, которым мы уже пользовались для приближенного вычисления корней уравнений [I, 193].
Для определенности рассмотрим систему двух линейных однородных уравнений

и начальные условия

Будем считать, что коэффициенты уравнении (I) суть непрерывные функции  в некотором конечном замкнутом промежутке
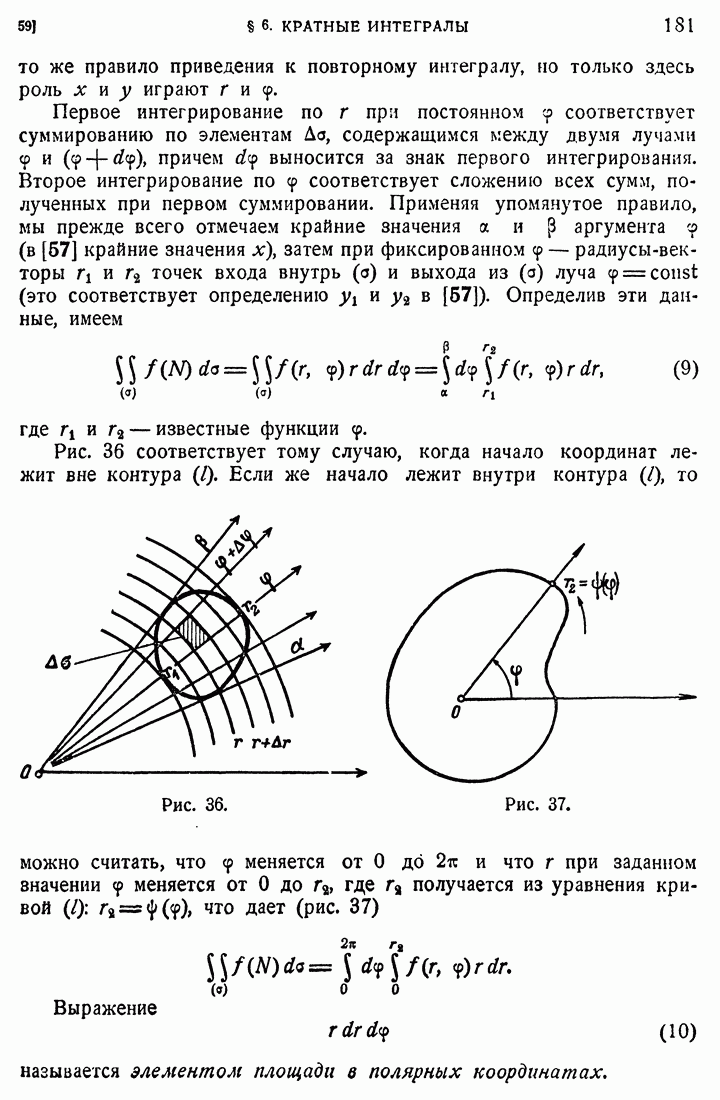
в некотором конечном замкнутом промежутке  содержащем начальное значение
содержащем начальное значение  и в дальнейшем изложении мы считаем, что
и в дальнейшем изложении мы считаем, что  принадлежит
принадлежит 
Решения у и z системы (1) должны быть, конечно, непрерывным: функциями, имеющими производную, и из самих уравнении видно, что и производные и будут непрерывными функциями [1]. Интегрируя уравнения (1) почленно от  до
до  и принимая во внимание (2), получим
и принимая во внимание (2), получим

Здесь мы для отчетливости выписали аргументы у функции  , а переменную интегрирования обозначили через t, чтобы не путать ее с верхним пределом интегрирования
, а переменную интегрирования обозначили через t, чтобы не путать ее с верхним пределом интегрирования  Итак, уравнения (I) с начальными условиями (2) приводят нас к уравнениям (3).
Итак, уравнения (I) с начальными условиями (2) приводят нас к уравнениям (3).
Покажем теперь, наоборот, что если непрерывные функции  удовлетворяют уравнениям (3), то они удовлетворяют уравнениям (1) и начальным условиям (2). Действительно, полагая в уравнениях
удовлетворяют уравнениям (3), то они удовлетворяют уравнениям (1) и начальным условиям (2). Действительно, полагая в уравнениях  и принимая во внимание, что интеграл с одинаковыми пределами равен нулю, получим начальные условия (2), а дифференцируя уравнения (3) по
и принимая во внимание, что интеграл с одинаковыми пределами равен нулю, получим начальные условия (2), а дифференцируя уравнения (3) по  получим уравнения
получим уравнения  и сказанного следует, что уравнения (3) в указанном смысле равносильны уравнениям (1) с начальными условиями (2), и в дальнейшем мы будем рассматривать лишь уравнения (3). Отметим, что в этих уравнениях искомые функции
и сказанного следует, что уравнения (3) в указанном смысле равносильны уравнениям (1) с начальными условиями (2), и в дальнейшем мы будем рассматривать лишь уравнения (3). Отметим, что в этих уравнениях искомые функции  входят как в левую часть, так и под знак интеграла в правую часть.
входят как в левую часть, так и под знак интеграла в правую часть.
Выясним идею метода последовательных приближений. Считая начальные значения  и z первыми приближениями к искомым функциям у и
и z первыми приближениями к искомым функциям у и  заменяем в правых частях уравнении (3) у и z на
заменяем в правых частях уравнении (3) у и z на  Таким образом, получим функции
Таким образом, получим функции 

являющиеся вторым приближением к у и  . Эти функции
. Эти функции  очевидно, непрерывны в вышеупомянутом промежутке
очевидно, непрерывны в вышеупомянутом промежутке  . Заменяя теперь в правых частях уравнений (3)
. Заменяя теперь в правых частях уравнений (3)  на
на  на
на  , получим третье приближение и
, получим третье приближение и 

причем и  опять непрерывны в промежутке I и т. д. Общая формула, дающая
опять непрерывны в промежутке I и т. д. Общая формула, дающая  приближение, будет
приближение, будет

В промежутке I коэффициенты уравнений (I) суть, по услопию, непрерывные функции, а потому в этом промежутке они будут по абсолютной величине не больше некоторого определенного положительного числа  :
:

Обозначим, кроме того, буквой  наибольшее из двух положительных чисел
наибольшее из двух положительных чисел  , т. е.
, т. е.

В дальнейшем мы будем рассматривать лишь часть промежутка  , лежащую справа от
, лежащую справа от  , т. е. будем считать
, т. е. будем считать  . Рассмотрение левой части может быть сделано так же.
. Рассмотрение левой части может быть сделано так же.
Оценим разности между соседними последовательными приближениями. Первая из формул (4) дает

Заменяя под интегралом все величины абсолютными значениями и большими величинами, в силу (6) и (7) получим [I, 95]

то есть

и совершенно так же

Первое из уравнений  будет
будет

вычитая из него почленно первое из уравнений (4), получим

или

Заменяя опять под интегралами все величины абсолютными значениями  пользуясь (6), (8) и
пользуясь (6), (8) и  , получим
, получим

откуда окончательно

Совершенно так же

Далее, берем первые из уравнений (5) при  . Почленно вычитая, получим
. Почленно вычитая, получим

Пользуясь (6), (9) и  , как и выше, будем иметь
, как и выше, будем иметь

откуда

Продолжая так и дальше, можем написать общие оценки разности двух соседних приближений

Пользуясь этими оценками, нетрудно показать, что функции  равномерно стремятся к некоторым предельным функциям
равномерно стремятся к некоторым предельным функциям  при беспредельном увеличении значка
при беспредельном увеличении значка  . Докажем это для последовательности функций
. Докажем это для последовательности функций  Эту последовательность мы можем заменить бесконечным рядом
Эту последовательность мы можем заменить бесконечным рядом

у которого сумма первых  членов равна
членов равна  и мы должны, таким образом, доказать равномерную сходимость ряда (11) [1, 144]. Если I есть длина промежутка I, в котором меняется
и мы должны, таким образом, доказать равномерную сходимость ряда (11) [1, 144]. Если I есть длина промежутка I, в котором меняется  , то первая из формул (10) показывает, что члены ряда (11) по абсолютной величине не превосходят положительных чисел
, то первая из формул (10) показывает, что члены ряда (11) по абсолютной величине не превосходят положительных чисел

а ряд, составленный из этих чисел, сходится по признаку Даламбера, так как отношение последующего члена к предыдущему, равное  стремится к нулю при беспредельном возрастании
стремится к нулю при беспредельном возрастании  . То же следует и из разложения е [I, 129]. Таким образом, согласно признаку Вейерштрасса [I 147], ряд (11) равномерно сходится в промежутке
. То же следует и из разложения е [I, 129]. Таким образом, согласно признаку Вейерштрасса [I 147], ряд (11) равномерно сходится в промежутке  , т. е. в этом промежутке
, т. е. в этом промежутке  равномерно стремятся к некоторой функции
равномерно стремятся к некоторой функции  Совершенно так же можно доказать, что и последовательность
Совершенно так же можно доказать, что и последовательность  равномерно стремится в
равномерно стремится в  к некоторой предельной функции
к некоторой предельной функции  имеет место равномерное по отношению
имеет место равномерное по отношению  стремление к пределу:
стремление к пределу:

Функции  непрерывны в I и, следовательно, то же можно утверждать и относительно предельных функций
непрерывны в I и, следовательно, то же можно утверждать и относительно предельных функций  Отметим, что для части промежутка
Отметим, что для части промежутка  лежащей слева от
лежащей слева от  мы должны в правых частях неравенств (8) и
мы должны в правых частях неравенств (8) и  заменить
заменить
 на
на  . В дальнейших оценках надо будет
. В дальнейших оценках надо будет  ваменить
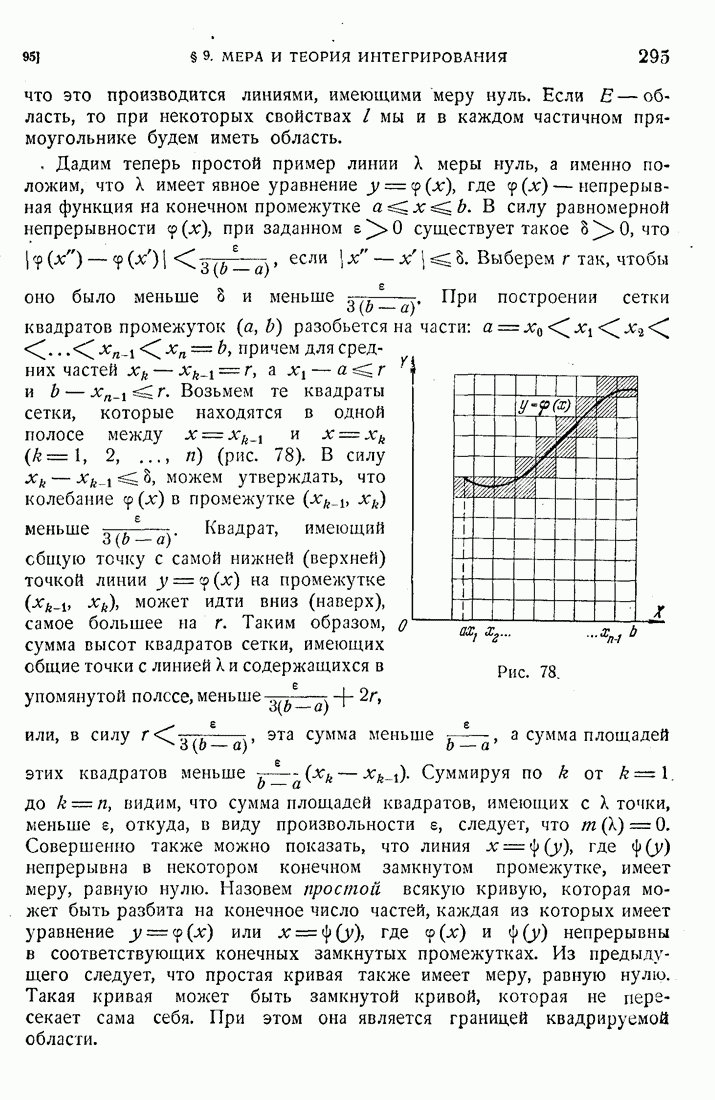
ваменить  и т. д. Неравенства (10) останутся справедливыми для всего промежутка I при условии замены
и т. д. Неравенства (10) останутся справедливыми для всего промежутка I при условии замены  абсолютным вначениещ этой разности.
абсолютным вначениещ этой разности.
Докажем теперь, что предельные функции удовлетворяют уравнениям (3), т. е. уравнениям (1) и предельным условиям (2). Это непосредственно вытекает из формул (5), если в обеих частях этих уравнений перейти к пределу при  . Тогда
. Тогда  будут стремиться к
будут стремиться к  , и в пределе для
, и в пределе для  получим уравнения (3). Проведем строго этот предельный переход. Из (12) следует
получим уравнения (3). Проведем строго этот предельный переход. Из (12) следует

Докажем, что эти предельные переходы имеют место равномерно по отношению к t в промежутке  Ограничимся первой формулой. Оценим разности между пределом и переменной:
Ограничимся первой формулой. Оценим разности между пределом и переменной:

В силу равномерного стремления  при любом заданном
при любом заданном  существует число N, одно и то же для всех t из I такое, что
существует число N, одно и то же для всех t из I такое, что

Отсюда, в силу (6), следует, что при любых t из  имеет место при
имеет место при  неравенство
неравенство

что и доказывает равномерное стремление к пределу в формулах  во всем промежутке
во всем промежутке  любой его части
любой его части  . Обращаемся к формулам (5) и пользуемся возможностью перехода к пределу под знаком интеграла для равномерно сходящихся последовательностей [I, 146]. Переходя к пределу, получаем из этих формул уравнения (3) для
. Обращаемся к формулам (5) и пользуемся возможностью перехода к пределу под знаком интеграла для равномерно сходящихся последовательностей [I, 146]. Переходя к пределу, получаем из этих формул уравнения (3) для  .
.
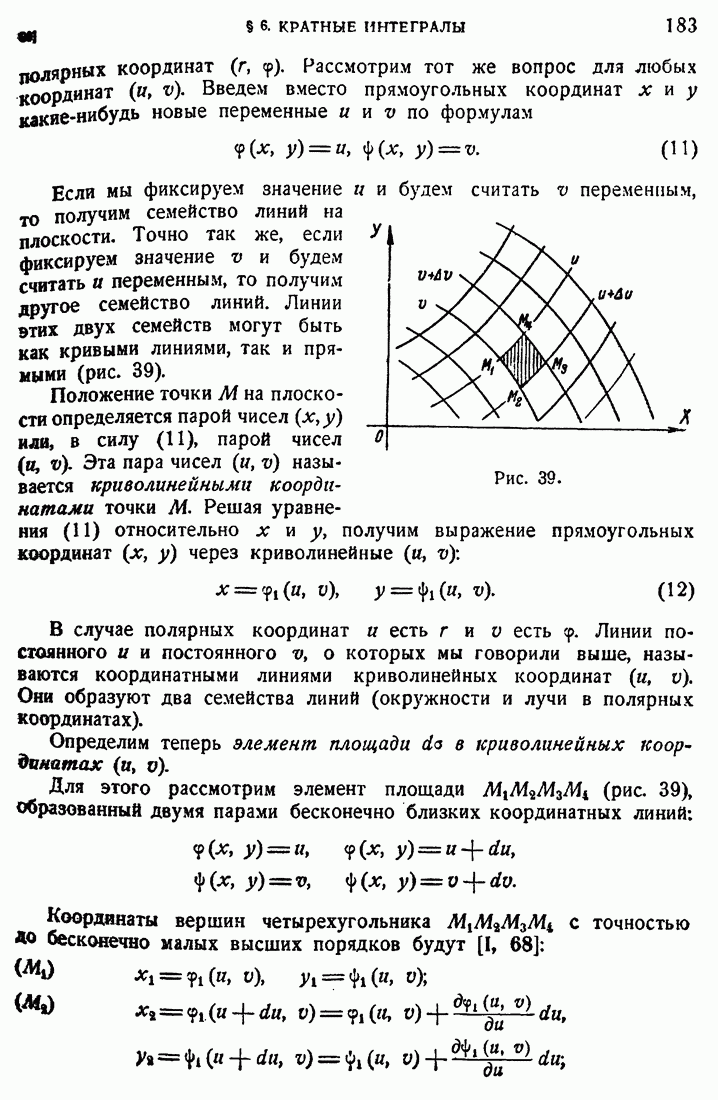
Резюмируя, можем сказать, что метод последовательных приближений дал нам решение системы (1) при начальных условиях (2), т. е. мы доказали существование решения. Покажем теперь, что искомое решение единственно. Пусть уравнения (3) имеют два решения:  . Подставляя в уравнение (3) сначала одно, а потом
. Подставляя в уравнение (3) сначала одно, а потом
другое решение и вычитая почленно, будем иметь

Возьмем справа от  промежуток
промежуток  такой длины
такой длины  чтобы произведение
чтобы произведение  было меньше единицы. Докажем, что в этом промежутке упомянутые два решения совпадают. Если бы это было не
было меньше единицы. Докажем, что в этом промежутке упомянутые два решения совпадают. Если бы это было не  , то абсолютные значения разностей
, то абсолютные значения разностей

имели бы в  положительный максимум, который мы обозначим числом 3. Пусть он достигается, например, первой разностью в точке
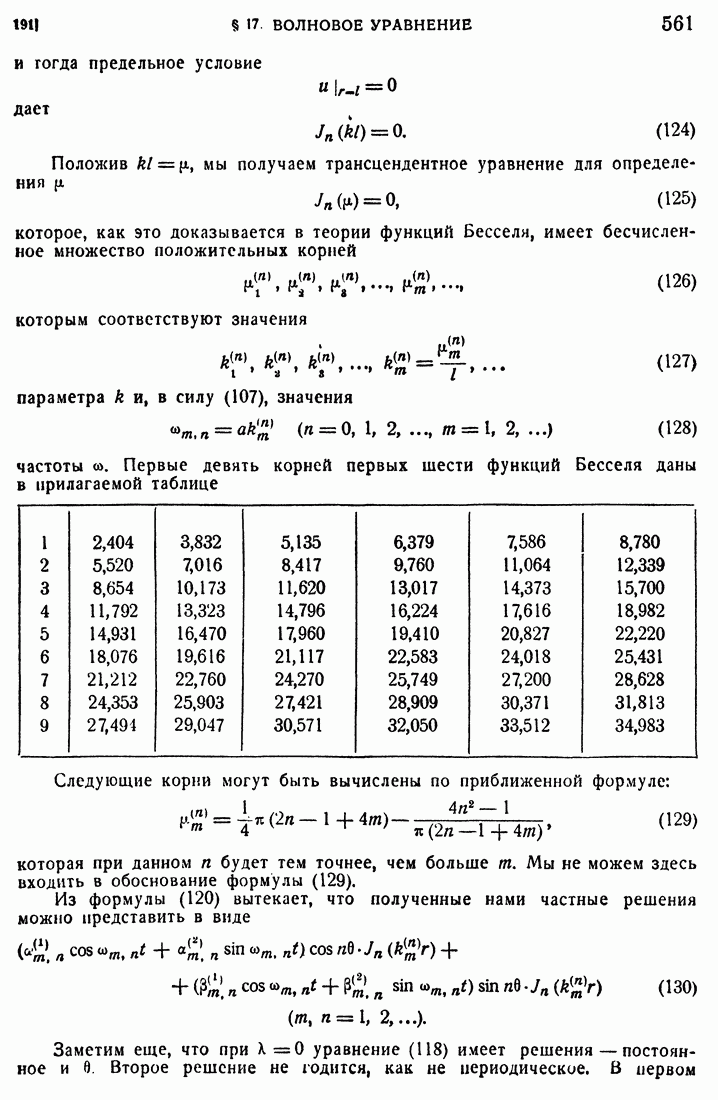
положительный максимум, который мы обозначим числом 3. Пусть он достигается, например, первой разностью в точке

и

Рассмотрим первое из уравнений (13) при  . Оценивая интеграл, как это мы делали выше, получим, в силу (14,),
. Оценивая интеграл, как это мы делали выше, получим, в силу (14,),

откуда, пользуясь (14), а также тем, что S, принадлежит промежутку 

а последнее неравенство нелепо, ибо, по условию,
Итак, нами доказано, что решения у, z и К, Z должны совпадать на промежутке  , где
, где  Выбирая значения
Выбирая значения  при
при  и качестве начальных условии, повторяем доказательство единственности для промежутка
и качестве начальных условии, повторяем доказательство единственности для промежутка  , где
, где  . Покрывая, таким образом, часть промежутка
. Покрывая, таким образом, часть промежутка  лежащего справа от
лежащего справа от  несколькими промежутками длины
несколькими промежутками длины  или меньшей (последний из покрывающих промежутков), можем утверждать совпадение решений на всей части
или меньшей (последний из покрывающих промежутков), можем утверждать совпадение решений на всей части  , лежащей справа от
, лежащей справа от  Аналогично поступаем и для части, лежащей слева от
Аналогично поступаем и для части, лежащей слева от  Формулируем теперь окончательный результат: система (1) при начальных условиях (2) имеет одно определенное решение, которое существует в промежутке I, в котором коэффициенты системы (I) непрерывные функции, и это решение может быть получено по методу последовательных приближений.
Формулируем теперь окончательный результат: система (1) при начальных условиях (2) имеет одно определенное решение, которое существует в промежутке I, в котором коэффициенты системы (I) непрерывные функции, и это решение может быть получено по методу последовательных приближений.
Отметим, что при вычислении первого приближения  можем в формулах (4) заменить под знаком интеграла
можем в формулах (4) заменить под знаком интеграла 
любыми функциями  непрерывными на промежутке
непрерывными на промежутке  Все последующее доказательство сохраняется. Не останавливаясь на доказательстве, приведем две оценки для абсолютного значения разностей
Все последующее доказательство сохраняется. Не останавливаясь на доказательстве, приведем две оценки для абсолютного значения разностей  при
при  :
:

Для использования второй оценки надо знать оценку квадратной скобки, стоящей под знаком интеграла.
Указанный выше результат, касающийся существования и единственности решения, а также сходимости метода последовательных приближений, справедлив и в том случае, когда  есть открытый промежуток
есть открытый промежуток  ибо, в силу указанного выше, мы будем иметь существование и единственность решения во всяком конечном замкнутом промежутке
ибо, в силу указанного выше, мы будем иметь существование и единственность решения во всяком конечном замкнутом промежутке  содержащем значение
содержащем значение  и принадлежащем промежутку
и принадлежащем промежутку  .
.
Мы могли бы рассматривать и неоднородную систему, т. е. прибавить к правым частям уравнений (1) функции  непрерывные в промежутке
непрерывные в промежутке  или общую линейную систему
или общую линейную систему  уравнений с
уравнений с  искомыми функциями
искомыми функциями

Предыдущее доказательство при этом остается в силе.
Линейное уравнение второго порядка

может быть написано в виде системы, если ввести, кроме у, искомую Функцию z = y:

и таким образом высказанный выше результат справедлив и для уравнения (15) при начальных условиях

в промежутке l непрерывности коэффициентов р(х) и q(x)
Пользуясь условиями (16), можем переписать уравнение (15) в виде

причем двукратный интеграл можно заменить простым по формуле (22) из [17]. Равенство (17) дает возможность применять метод последовательных приближений к уравнению (15) и не приводя этого уравнения к системе.
Пример. Применим метод последовательных приближений к примеру, рассмотренному нами в [46]:

Нозьмем начальные условия  . Уравнение (17) в данном случае будет
. Уравнение (17) в данном случае будет

Подставлял справа  , получим второе приближение
, получим второе приближение

Третье приближение будет

Переходя к пределу, получим степенной ряд

который мы имели в (46]. Коэффициент  есть непрерывная функция на бесконечном промежутке
есть непрерывная функция на бесконечном промежутке  , и написанный ряд сходится в этом промежутке. Это легко проверить, пользуясь признаком Даламбера [I, 121].
, и написанный ряд сходится в этом промежутке. Это легко проверить, пользуясь признаком Даламбера [I, 121].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
- 33. Линейные уравнения и колебательные явления.
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
- 53. Сходимость метода Эйлера — Коши.
- 54. Особые точки дифференциальных уравнений первого порядка.
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
- 58. Двукратный интеграл.
- 59. Вычисление двукратного интеграла.
- 60. Криволинейные координаты.
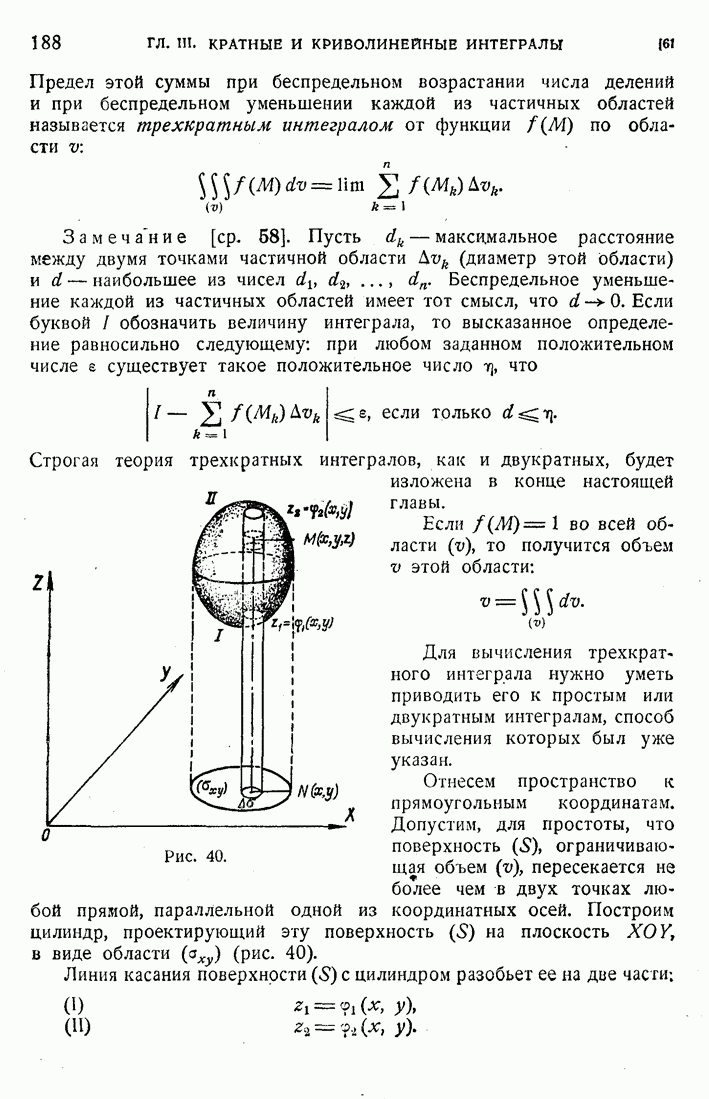
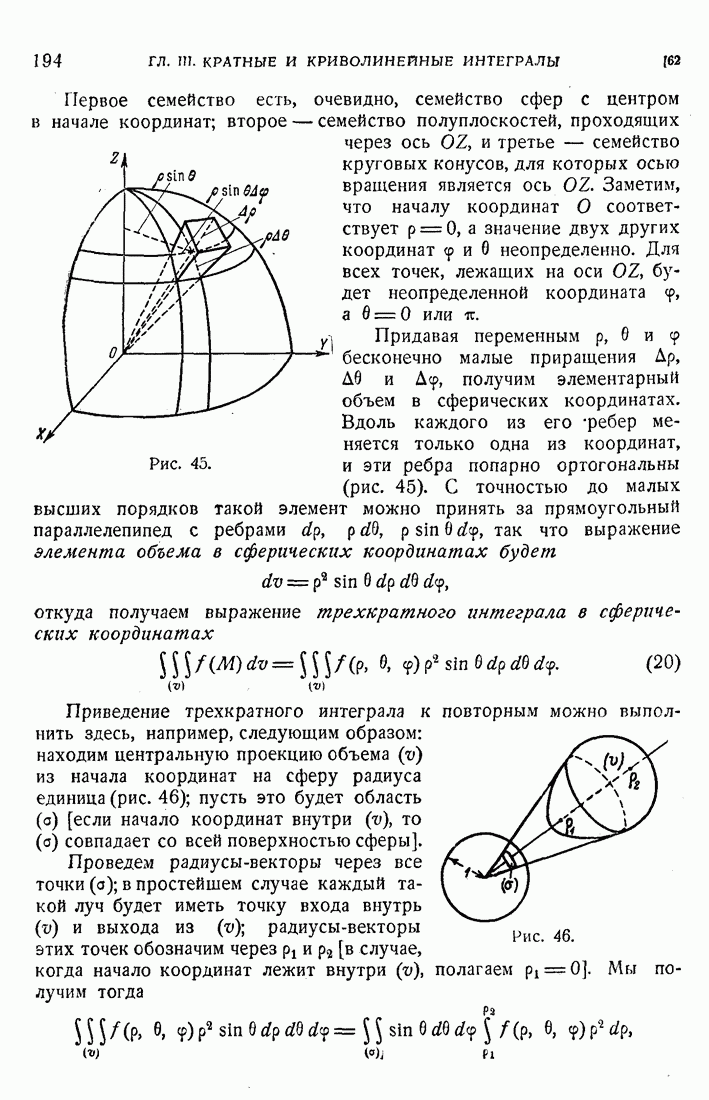
- 61. Трехкратный интеграл
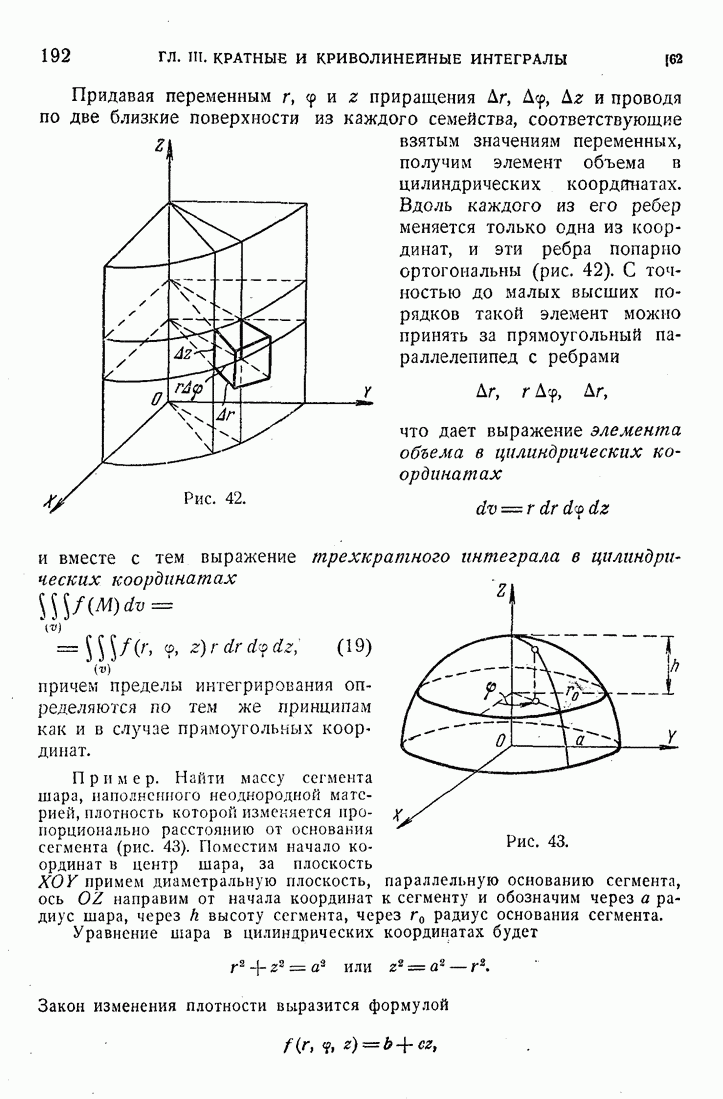
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
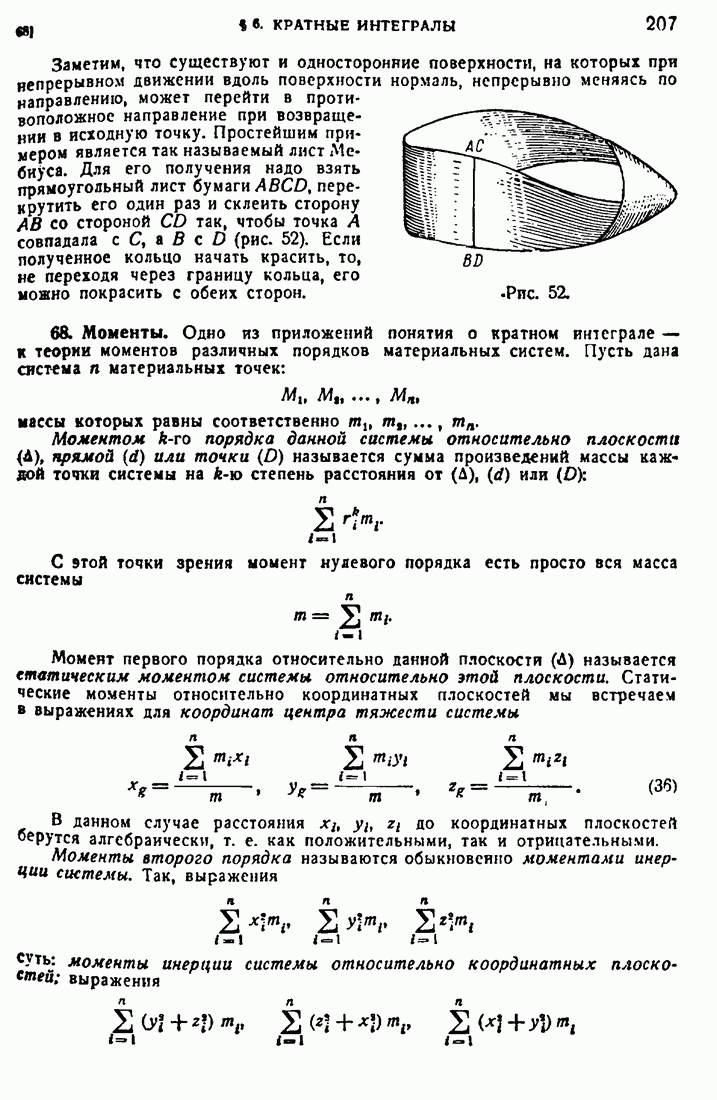
- 67. Интегралы по определенной стороне поверхности.
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
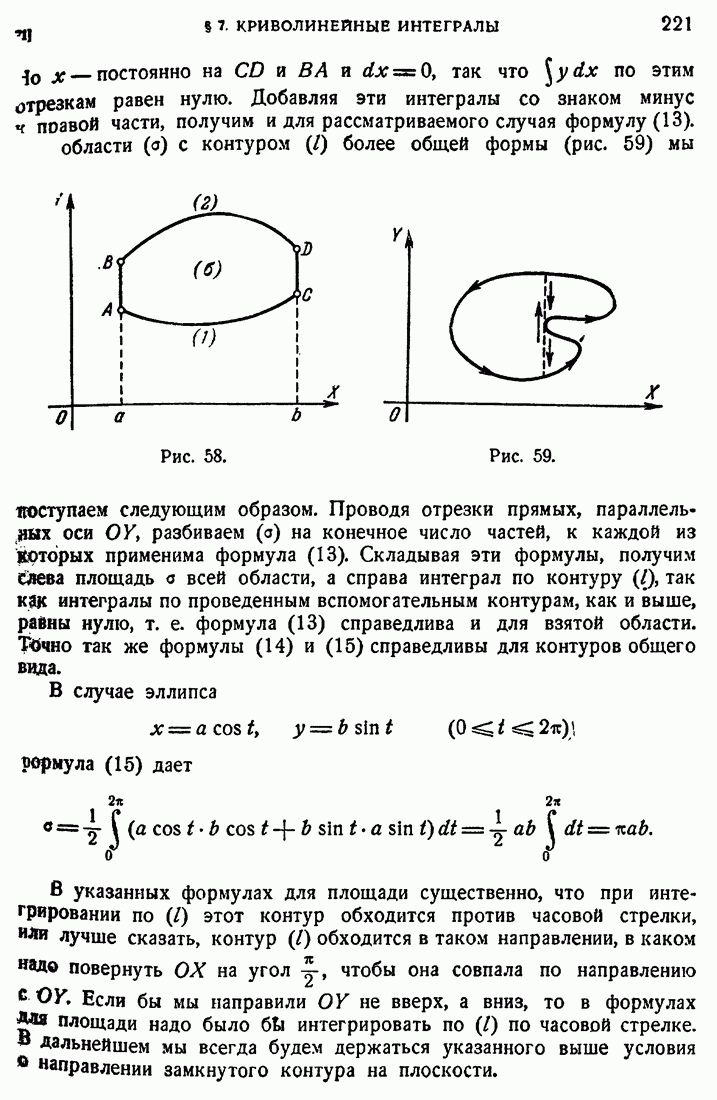
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
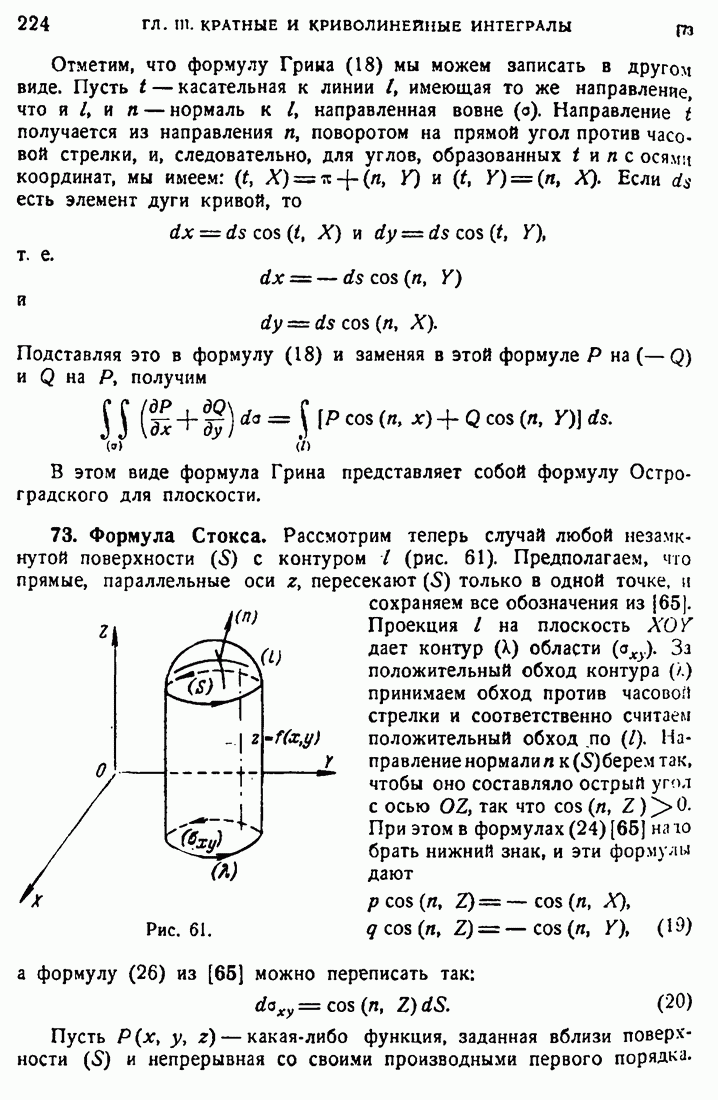
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
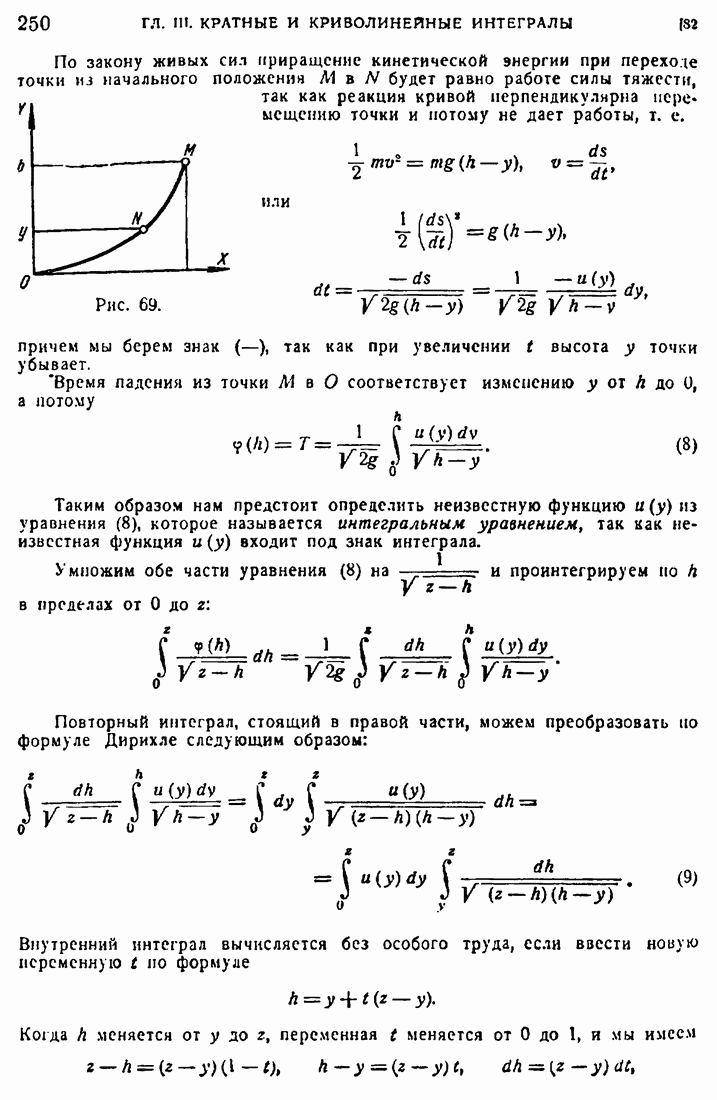
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
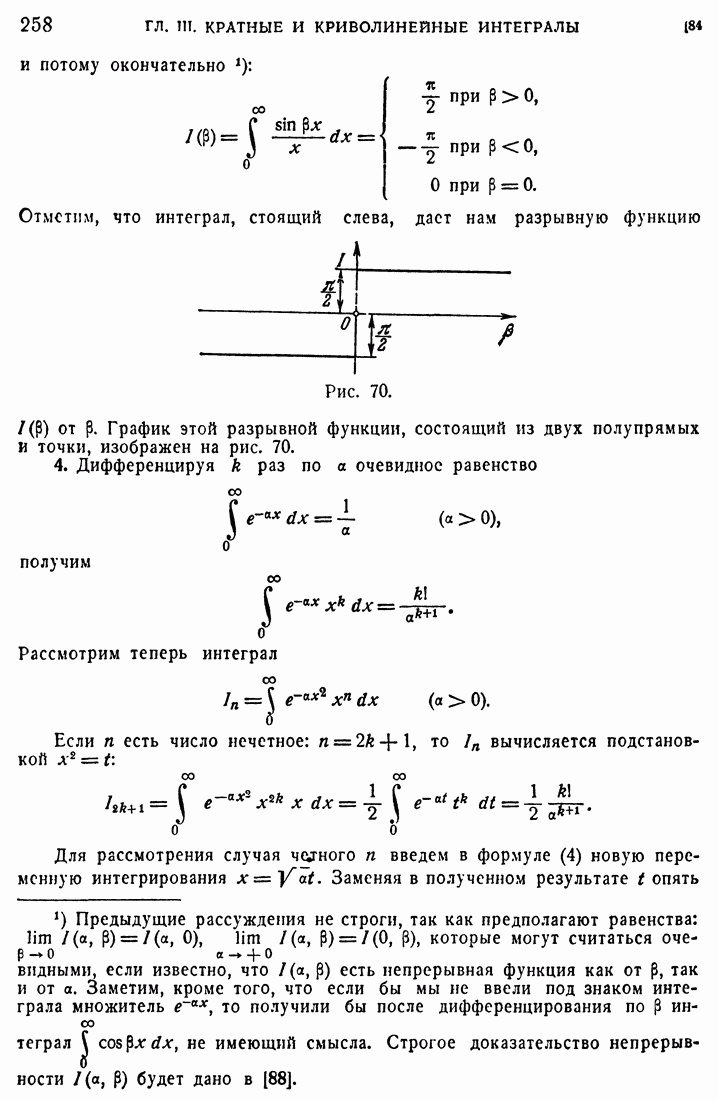
- 84. Примеры.
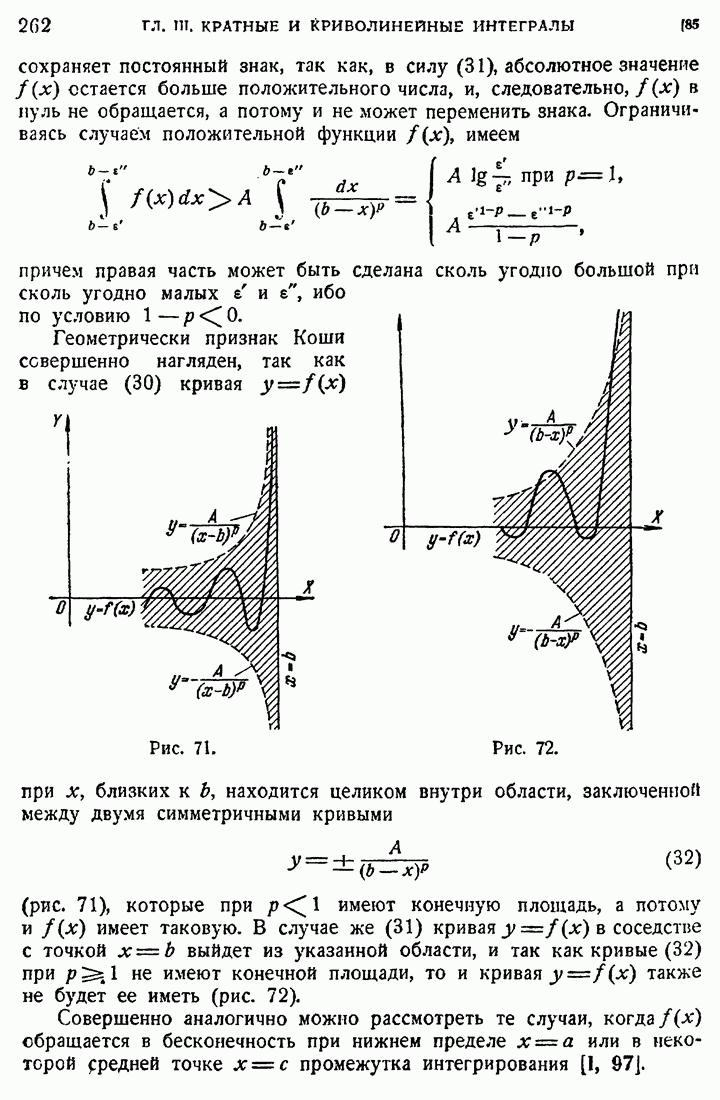
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
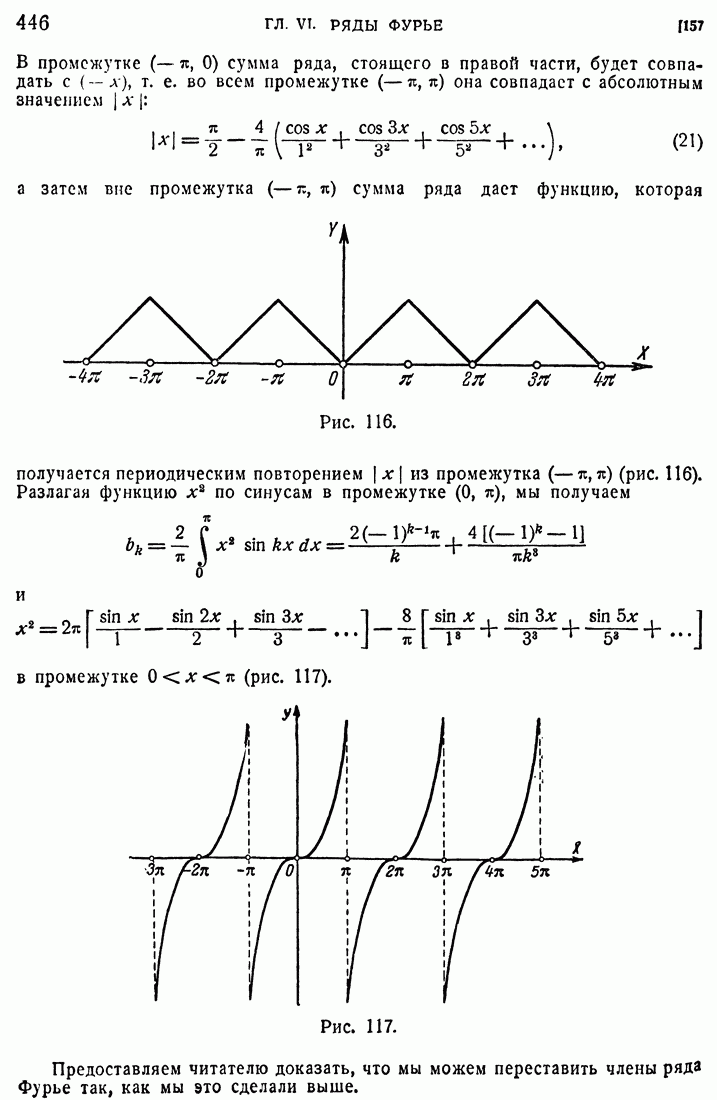
- 156. Примеры.
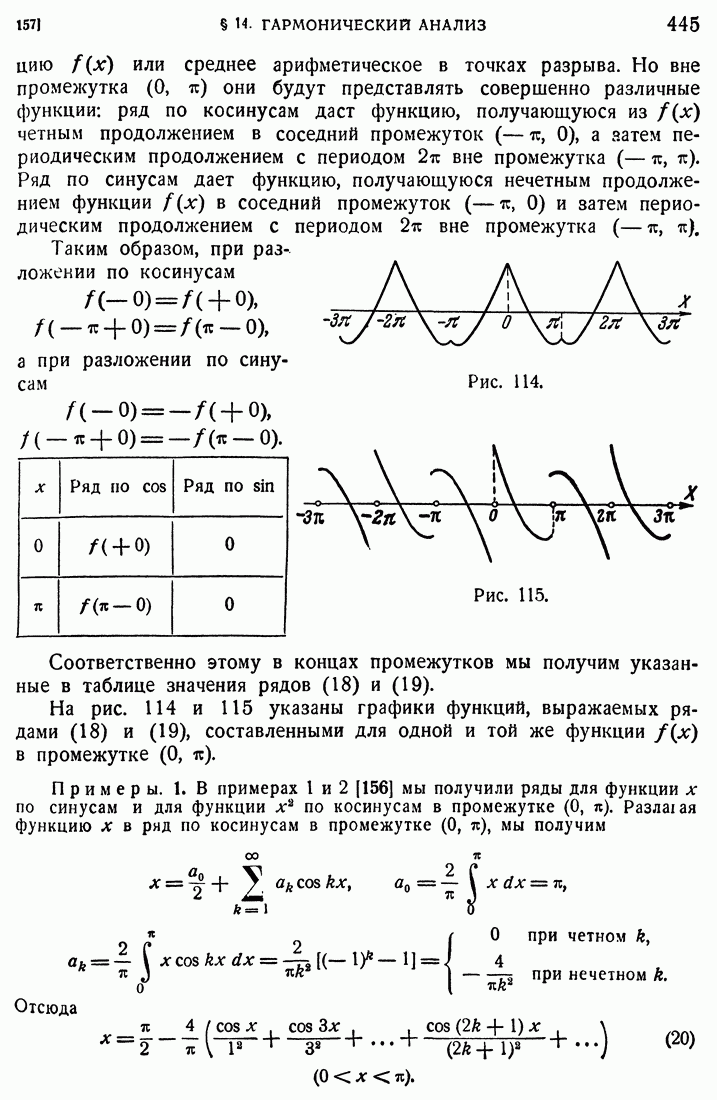
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
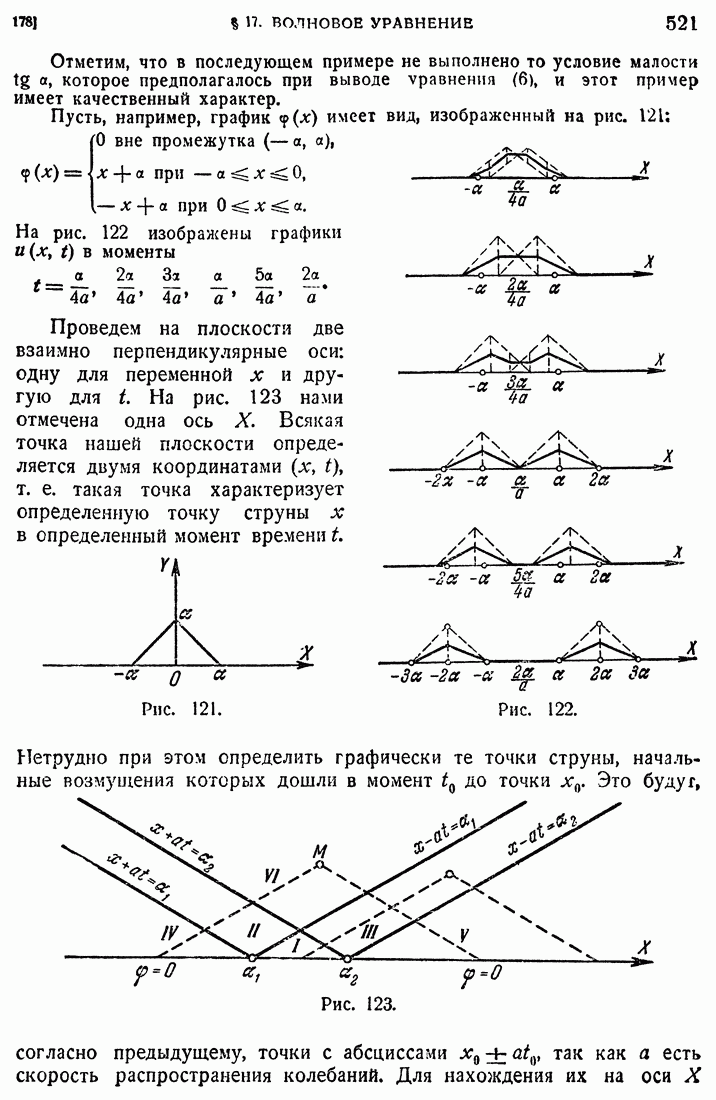
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
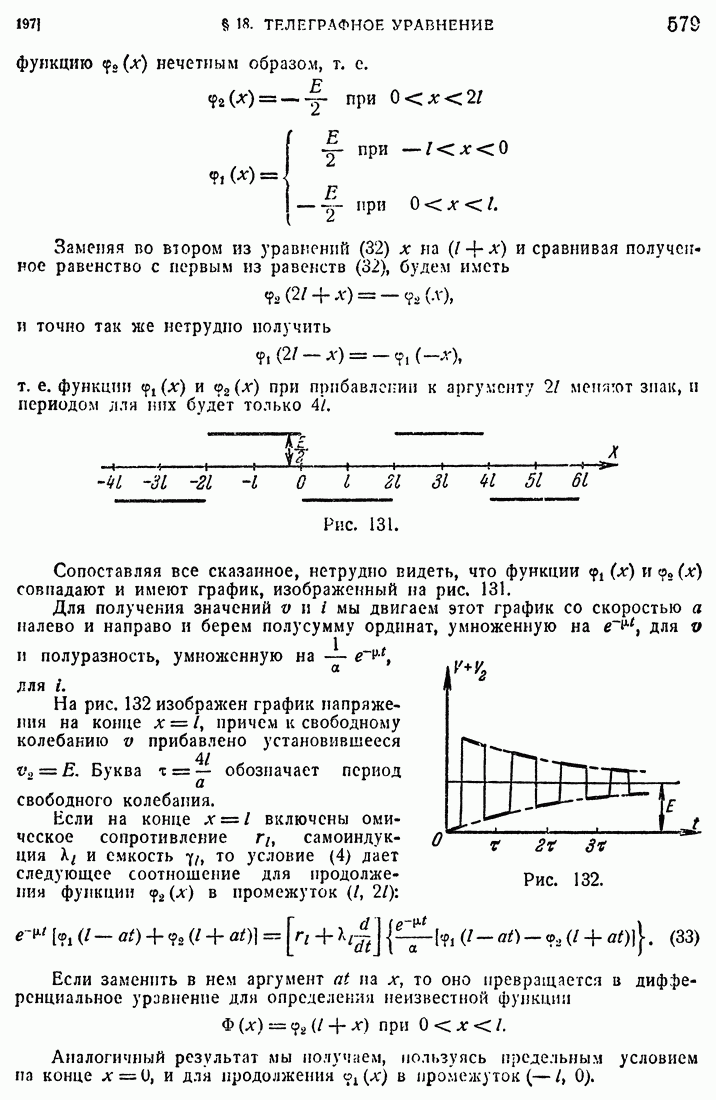
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
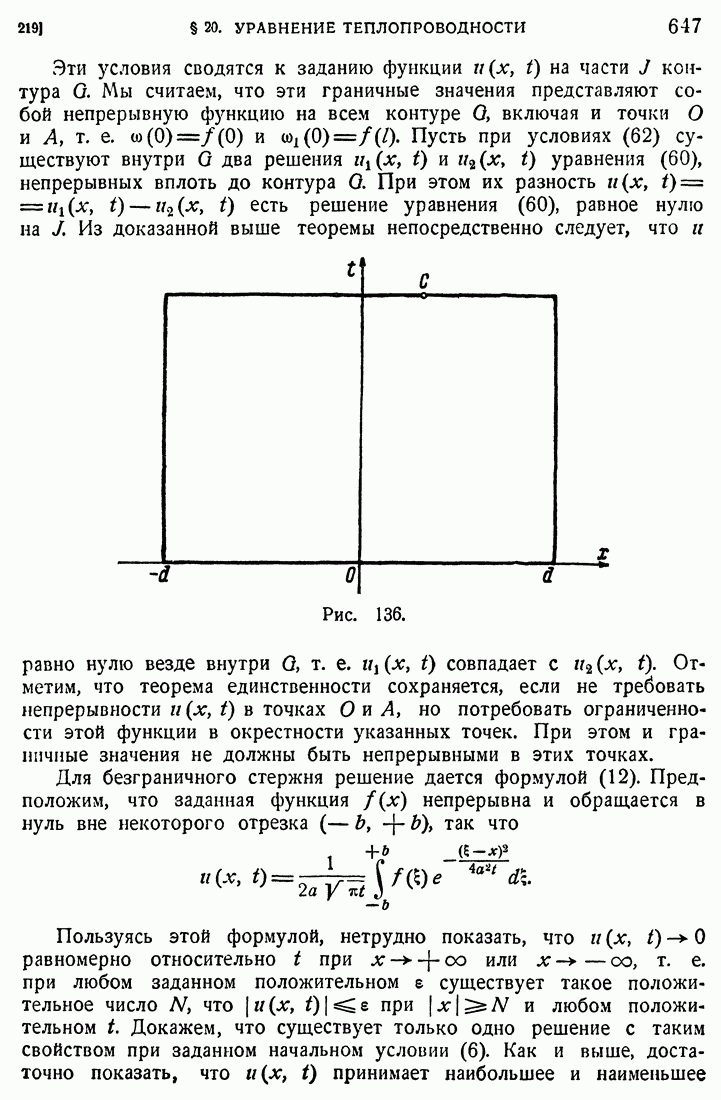
- 219. Теорема единственности.