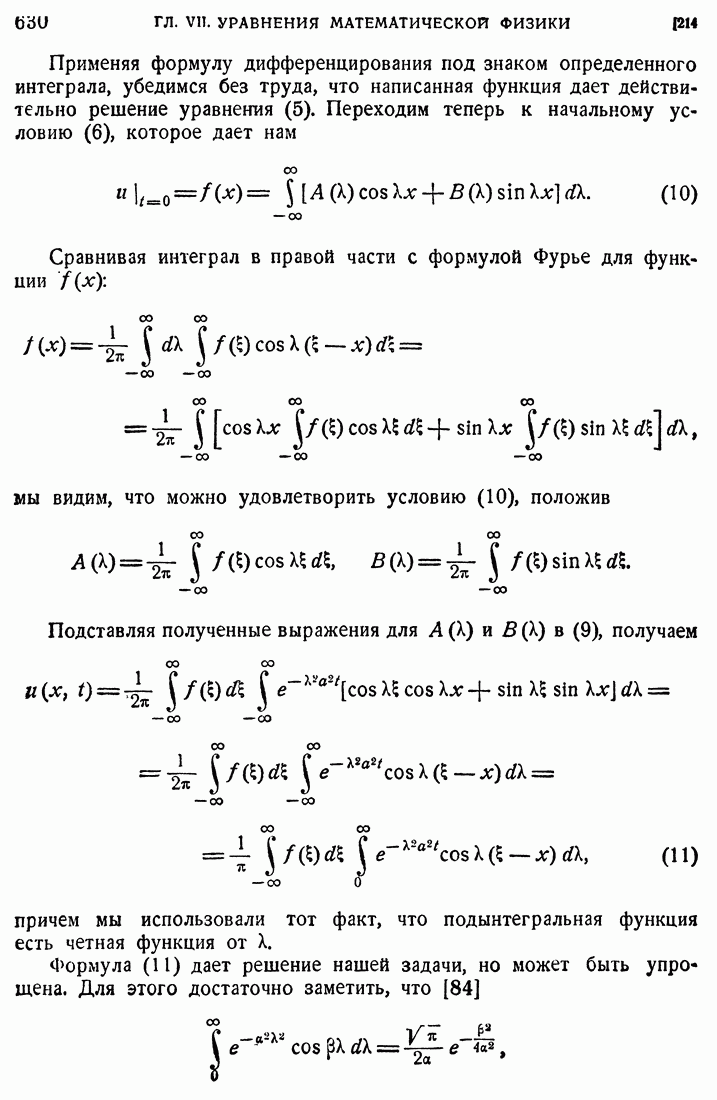| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
54. Особые точки дифференциальных уравнений первого порядка.
Если правая часть уравнения

в точке  и ее окрестности есть непрерывная функция, имеющая непрерывную производную по у, то через эту точку по теореме А [2] проходит одна и только одна интегральная кривая. Если эти условия не выполняются, то такое утверждение может и не иметь места. Напишем дифференциальное уравнение в форме, содержащей дифференциалы
и ее окрестности есть непрерывная функция, имеющая непрерывную производную по у, то через эту точку по теореме А [2] проходит одна и только одна интегральная кривая. Если эти условия не выполняются, то такое утверждение может и не иметь места. Напишем дифференциальное уравнение в форме, содержащей дифференциалы

и положим, что  - функции однозначные, непрерывные и имеющие непрерывные производные
- функции однозначные, непрерывные и имеющие непрерывные производные  и у на всей плоскости
и у на всей плоскости  Если
Если  , то уравнение (41) запишем в виде
, то уравнение (41) запишем в виде

и при соблюдении указанных условий точка  будет находиться внутри некоторой области В теоремы А для уравнения
будет находиться внутри некоторой области В теоремы А для уравнения  Если
Если
 то уравнение (41) запишем в виде
то уравнение (41) запишем в виде

и относительно точки  можем утверждать то же, что и выше для уравнения
можем утверждать то же, что и выше для уравнения  . Особыми точками уравнения (41) назовем те точки, координаты которых суть вещественные решения системы уравнений
. Особыми точками уравнения (41) назовем те точки, координаты которых суть вещественные решения системы уравнений

В таких точках уравнение (41) теряет смысл.
Таким образом, мы толкуем уравнение (41) как или уравнение  или уравнение (422) [см. 2].
или уравнение (422) [см. 2].
В следующем параграфе мы заменим (41) системой

и приведем в общих чертах исследование этой системы. Мы будем пользоваться этим приемом, как удобным практическим приемом, и в примере, к разбору которого мы переходим. Положим, что  многочлены первой степени, и особая точка находится в начале координат, т. е. уравнение (41) имеет вид
многочлены первой степени, и особая точка находится в начале координат, т. е. уравнение (41) имеет вид

где

При этом прямые  пересекаются в точке (0, 0), и все точки, кроме (0, 0), принадлежат области теоремы существования и единственности уравнения (42,) или (422).
пересекаются в точке (0, 0), и все точки, кроме (0, 0), принадлежат области теоремы существования и единственности уравнения (42,) или (422).
Уравнение (45), как нетрудно видеть, есть однородное уравнение и может быть проинтегрировано способом, указанным в [5]. Но мы применим другой способ, а именно, вводя новые переменные I и  мы приведем сперва уравнение (45) к виду, более удобному для непосредственного исследования. Положим
мы приведем сперва уравнение (45) к виду, более удобному для непосредственного исследования. Положим

где  постоянные. Имеем:
постоянные. Имеем:

Из уравнения (45), составляя производную пропорцию, получим

Определим теперь коэффициенты в формулах (47) так, чтобы знаменатели написанных дробей были соответственно пропорциональны  Для первого знаменателя будем иметь
Для первого знаменателя будем иметь

откуда, сравнивая коэффициенты при х и у, получим систему уравнений для определения  линейную однородную по отношению
линейную однородную по отношению 

Точно так же, обращаясь ко второму знаменателю и приравнивая его  получим систему
получим систему

причем  может иметь и другое значение. Нулевые решения систем
может иметь и другое значение. Нулевые решения систем  и (492) не годятся, так как при этом преобразование переменных (47) теряет смысл. Нужно, чтобы эти системы имели решения, отличные от нулевого. Для этого необходимо и достаточно, чтобы коэффициенты указанных систем удовлетворяли условию
и (492) не годятся, так как при этом преобразование переменных (47) теряет смысл. Нужно, чтобы эти системы имели решения, отличные от нулевого. Для этого необходимо и достаточно, чтобы коэффициенты указанных систем удовлетворяли условию

то есть

При выполнении этого условия как система  так и система (493) приведутся к одному уравнению, и можно получить для неизвестных
так и система (493) приведутся к одному уравнению, и можно получить для неизвестных  решения, отличные от нулевого. Отметим, что, в силу предположения (46), уравнение (50) не может иметь корня
решения, отличные от нулевого. Отметим, что, в силу предположения (46), уравнение (50) не может иметь корня 
Рассмотрим сначала тот случай, когда уравнение (50) имеет различные вещественные корни  Подставляя в
Подставляя в  сможем найти отличные от нулевого решения
сможем найти отличные от нулевого решения  этих систем. Покажем, что
этих систем. Покажем, что

т. е. что из уравнений (47) мы можем выразить  через Е, Положим, например, что
через Е, Положим, например, что  Фиксируя
Фиксируя  , получаем
, получаем  откуда
откуда  т. е. приходим к
т. е. приходим к 
Поскольку  можно полагать равными любому числу, отличному от нуля, можем считать, что
можно полагать равными любому числу, отличному от нуля, можем считать, что  и из (47) получаем
и из (47) получаем

В переменных  уравнение (45) имеет вид
уравнение (45) имеет вид

Мы толкуем это уравнение, как и уравнение (41), в виде двух уравнений

Обозначая через  общую величину отношении (53), придем к двум дифференциальным уравнениям
общую величину отношении (53), придем к двум дифференциальным уравнениям

откуда

где  — произвольные постоянные. Лишняя произвольная постоянная получилась за счет возможности замены t на
— произвольные постоянные. Лишняя произвольная постоянная получилась за счет возможности замены t на  где — произвольная постоянная. Отметим, что уравнение (53.2) имеет очевидное решение
где — произвольная постоянная. Отметим, что уравнение (53.2) имеет очевидное решение  , а уравнение (53,) решение
, а уравнение (53,) решение  т. е. уравнение (45) имеет интегральными линиями прямые
т. е. уравнение (45) имеет интегральными линиями прямые

Точнее говоря, мы должны говорить о четырех полупрямых, исключая начало, в котором уравнение (45) теряет смысл. Эти полупрямые стремятся к началу. Рассмотрим теперь отдельно следующие случаи: 1. Корни  вещественны, различны и одинаковых знаков. Подставляя в формулы (52) вместо
вещественны, различны и одинаковых знаков. Подставляя в формулы (52) вместо  их выражения (55) и решая относительно
их выражения (55) и решая относительно  и у, получаем параметрическое уравнение интегральных линий
и у, получаем параметрическое уравнение интегральных линий

Если исключить прямые  и значения
и значения  которым соответствует
которым соответствует  то
то  переменные
переменные  и
и  не обращаются в нуль ни при каком t и формулы
не обращаются в нуль ни при каком t и формулы  не дают точки
не дают точки  . Если
. Если  положительны, то, не нарушая общности, можем считать
положительны, то, не нарушая общности, можем считать  а если
а если  отрицательны, то будем считать
отрицательны, то будем считать  . В первом случае из формул
. В первом случае из формул  и
и  следует, что
следует, что  при
при  . Если же
. Если же  то мы получим тот же результат при
то мы получим тот же результат при  , т. е.
, т. е.  все интегральные линии
все интегральные линии  стремятся к точке (0, 0), и если мы добавим к ним эту точку, то получим линии, имеющие в этой точке общую касательную
стремятся к точке (0, 0), и если мы добавим к ним эту точку, то получим линии, имеющие в этой точке общую касательную  Исключение в отношении последнего утверждения относительно касательной составляет интегральная прямая
Исключение в отношении последнего утверждения относительно касательной составляет интегральная прямая  Особая точка описанного типа называется узлом. В дальнейшем мы дадим полное определение узла. Отметим, что из
Особая точка описанного типа называется узлом. В дальнейшем мы дадим полное определение узла. Отметим, что из  и
и  следует
следует
равенство  т. е. уравнение (45) в рассматриваемом случае имеет общий интеграл вида
т. е. уравнение (45) в рассматриваемом случае имеет общий интеграл вида

где С — произвольная постоянная.
В качестве примера рассмотрим уравнение

которое имеет вид  . Его интегральные линии — семейство парабол
. Его интегральные линии — семейство парабол  при
при 
Корни  вещественны, различны и разных знаков. В этом случае формула (58) дает
вещественны, различны и разных знаков. В этом случае формула (58) дает

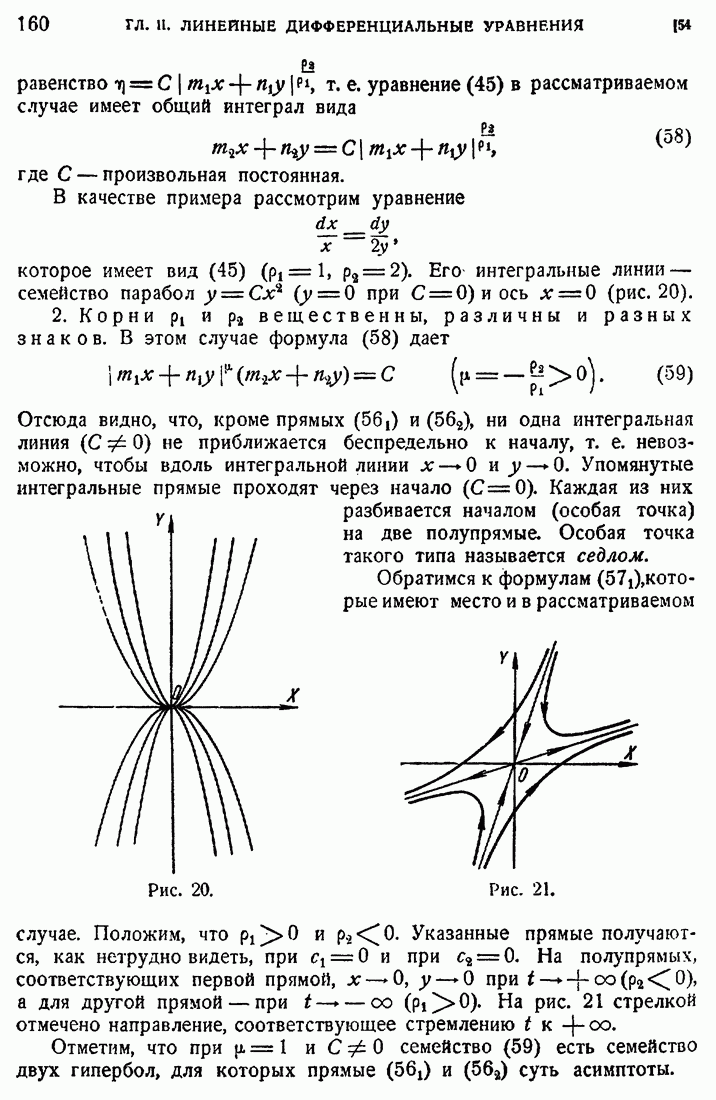
Отсюда видно, что, кроме прямых  и (562), ни одна интегральная линия (С Ф 0) не приближается беспредельно к началу, т. е. невозможно, чтобы вдоль интегральной линии
и (562), ни одна интегральная линия (С Ф 0) не приближается беспредельно к началу, т. е. невозможно, чтобы вдоль интегральной линии  . Упомянутые интегральные прямые проходят через начало
. Упомянутые интегральные прямые проходят через начало  . Каждая из них разбивается началом (особая точка) на две полупрямые. Особая точка такого типа называется седлом.
. Каждая из них разбивается началом (особая точка) на две полупрямые. Особая точка такого типа называется седлом.
Обратимся к формулам  имеют место и в рассматриваемом случае.
имеют место и в рассматриваемом случае.

Рис. 20.

Рис. 21.
Положим, что  . Указанные прямые получаются, как нетрудно видеть, при
. Указанные прямые получаются, как нетрудно видеть, при  и при
и при  . На полупрямых, соответствующих первой прямой,
. На полупрямых, соответствующих первой прямой,  при
при  а для другой прямой
а для другой прямой  при
при  На рис. 21 стрелкой отмечено направление, соответствующее стремлению t к
На рис. 21 стрелкой отмечено направление, соответствующее стремлению t к 
Отметим, что при  семейство (59) есть семейство двух гипербол, для которых прямые
семейство (59) есть семейство двух гипербол, для которых прямые  и (562) суть асимптоты.
и (562) суть асимптоты.
3. Корни  - мнимые сопряженные:
- мнимые сопряженные:  причем
причем  отличны от нуля. Подставляя в коэффициенты системы
отличны от нуля. Подставляя в коэффициенты системы  получим для
получим для  отличное от нуля решение, состоящее из комплексных чисел. Подставляя в коэффициенты системы
отличное от нуля решение, состоящее из комплексных чисел. Подставляя в коэффициенты системы  можем утверждать в виду вещественности
можем утверждать в виду вещественности  что отличное от нулевого решение системы будет
что отличное от нулевого решение системы будет  причем через а мы обозначаем комплексное число, сопряженное с а.
причем через а мы обозначаем комплексное число, сопряженное с а.
Из формул (47) мы видим, что, в силу вещественности  и у, величины
и у, величины  и суть комплексные сопряженные. Таким образом, левая и правая части равенства (53) должны быть комплексными сопряженными (или вещественными), и из самого факта их равенства следует, что эти величины должны быть вещественными. Обозначая их общую величину через
и суть комплексные сопряженные. Таким образом, левая и правая части равенства (53) должны быть комплексными сопряженными (или вещественными), и из самого факта их равенства следует, что эти величины должны быть вещественными. Обозначая их общую величину через  приходим к уравнениям (54 и (542), интегрирование которых с учетом того, что
приходим к уравнениям (54 и (542), интегрирование которых с учетом того, что  — комплексные сопряженные, дает
— комплексные сопряженные, дает

где  комплексная постоянная. При
комплексная постоянная. При  получаем
получаем  , т. е. особую точку
, т. е. особую точку  . При
. При  имеем
имеем  и эта величина
и эта величина  при
при  если а
если а  и при
и при  при
при 

Рис. 22.
Принимая во внимание линейную зависимость между переменными  можем утверждать, что все интегральные кривые уравнения (45) стремятся одним своим концом к особой точке (0, 0). Пользуясь формулами (60) и указанной зависимостью между переменными, нетрудно показать, что при приближении к точке (0, 0) все интегральные кривые спиралеобразно закручиваются вокруг этой точки в одном и том же направлении (рис. 22). Особая точка такого типа называется фокусом. Если мы положим
можем утверждать, что все интегральные кривые уравнения (45) стремятся одним своим концом к особой точке (0, 0). Пользуясь формулами (60) и указанной зависимостью между переменными, нетрудно показать, что при приближении к точке (0, 0) все интегральные кривые спиралеобразно закручиваются вокруг этой точки в одном и том же направлении (рис. 22). Особая точка такого типа называется фокусом. Если мы положим  где и и v вещественны, то эти переменные выражаются через х и У по формулам вида
где и и v вещественны, то эти переменные выражаются через х и У по формулам вида

где  вещественны и
вещественны и 
Эти формулы дают возможность выразить  через u, v и убедиться на основании (60) в указанном выше поведении интегральных кривых на плоскости XOY вблизи точки (0, 0).
через u, v и убедиться на основании (60) в указанном выше поведении интегральных кривых на плоскости XOY вблизи точки (0, 0).
Для рассмотренных выше трех случаев мы имеем следующий характерный факт: при произвольном, но достаточно малом изменении
коэффициентов  мы остаемся при прежнем предположении о корнях
мы остаемся при прежнем предположении о корнях  , а следовательно, не меняется и характер расположения интегральных кривых в скрестнссти особой точки. Иное мы будем иметь в следующем случае.
, а следовательно, не меняется и характер расположения интегральных кривых в скрестнссти особой точки. Иное мы будем иметь в следующем случае.
4. Корни  — чисто мнимые:
— чисто мнимые:  . Мы имеем формулы (60) при
. Мы имеем формулы (60) при  из которых следует, что
из которых следует, что  откуда, принимая во внимание (61), получаем семейство интегральных кривых уравнения (45)
откуда, принимая во внимание (61), получаем семейство интегральных кривых уравнения (45)

т. е. интегральные кривые — подобные эллипсы или окружности. Ни одна интегральная кривая не проходит через особую точку, и эта последняя окружена замкнутыми интегральными линиями (рис. 23). Такая особая точка называется центром. В этом случае при сколь угодно малом изменении коэффициентов  чисто мнимых корней
чисто мнимых корней  может появиться вещественная часть и центр превратится в фокус.
может появиться вещественная часть и центр превратится в фокус.

Рис. 23.
5. Уравнение (50) имеет кратный корень  отличный от нуля. При подстановке в коэффициенты системы
отличный от нуля. При подстановке в коэффициенты системы  или
или  могут встретиться два случая: или все коэффициенты при этом обратятся в нуль, или среди коэффициентов будет по крайней мере один, отличный от нуля. Рассмотрим сначала первый случай
могут встретиться два случая: или все коэффициенты при этом обратятся в нуль, или среди коэффициентов будет по крайней мере один, отличный от нуля. Рассмотрим сначала первый случай

при этом система (45) будет иметь вид

и ее общий интеграл  будет семейством прямых, проходящих через начало, т. е. начало координат будет узлом.
будет семейством прямых, проходящих через начало, т. е. начало координат будет узлом.
Среди коэффициентов  есть по крайней мере один, отличный от нуля. Нетрудно видеть, что при этом и
есть по крайней мере один, отличный от нуля. Нетрудно видеть, что при этом и  не могут оба быть равны нулю. Действительно, если
не могут оба быть равны нулю. Действительно, если  то, принимая во внимание кратность корня
то, принимая во внимание кратность корня  уравнения (50), получим
уравнения (50), получим  при сделанном предположении уравнение (50) превращается в уравнение
при сделанном предположении уравнение (50) превращается в уравнение  и условие кратности корня этого уравнения дает
и условие кратности корня этого уравнения дает  и общая величина
и общая величина  и есть кратный корень уравнения. Итак, если предположить
и есть кратный корень уравнения. Итак, если предположить  , то выполнены условия (63), что противоречит сделанному
, то выполнены условия (63), что противоречит сделанному
нами предположению. Поэтому хотя бы один из коэффициентов или  отличен от нуля. Положим, например, что
отличен от нуля. Положим, например, что  Кратный корень уравнения (50) будет, очевидно,
Кратный корень уравнения (50) будет, очевидно,

и система  при подстановке
при подстановке  должна привестись, как мы выше упоминали, к одному уравнению
должна привестись, как мы выше упоминали, к одному уравнению

Выберем  т. е.
т. е.

оставляя вторую переменную у прежней. Дифференциальное уравнение можно будет написать в виде

или, подставляя вместо  его выражение, определяемое из формулы (64),
его выражение, определяемое из формулы (64),

т. е.

Интегрируя это линейное уравнение, получаем

При  имеем
имеем  и
и  Освобождаясь от знаменателя а уравнении (65), видим, что имеется еще решение
Освобождаясь от знаменателя а уравнении (65), видим, что имеется еще решение  т. е.
т. е.

Все интегральные линии стремятся одним своим концом к точке (0, 0) а касаются в этой точке прямой (66), т. е. мы имеем узел, но только С одной касательной в особой точке (рис. 24). Случай, когда уравнение (50) имеет корень  не представляет интереса. Считая естественно, что ни один из знаменателей в Уравнении (45) не равен тождественно нулю, мы видим, что эти знаменатели в рассматриваемом. случае отличаются лишь постоянным множителем, отличным от нуля, так что уравнение приводится к виду
не представляет интереса. Считая естественно, что ни один из знаменателей в Уравнении (45) не равен тождественно нулю, мы видим, что эти знаменатели в рассматриваемом. случае отличаются лишь постоянным множителем, отличным от нуля, так что уравнение приводится к виду
 где k — некоторая постоянная, отличная от нуля. Семейство интегральных линий есть семейство параллельных прямых.
где k — некоторая постоянная, отличная от нуля. Семейство интегральных линий есть семейство параллельных прямых.
Если мы в знаменателях уравнения (45) заменим х и у на  то получим, очевидно, те же картины расположения интегральных кривых, что и выше, но вместо (0, 0) особой будет точка
то получим, очевидно, те же картины расположения интегральных кривых, что и выше, но вместо (0, 0) особой будет точка 
Положим, что в уравнении  многочлены, равные нулю в точке (0,0), и выделим из них члены с первыми степенями
многочлены, равные нулю в точке (0,0), и выделим из них члены с первыми степенями

где  равны нулю в точке (0, 0) и их частные производные по х и у также равны нулю в этой точке. При этом в случаях: 1), 2) и 3) картина интегральных линий в окрестности точки (0, 0) будет того же характера, что и для уравнения (45), т. е. в случае 1) точка (0, 0) будет узлом; в случае 2) — седлом и в случае 3) — фокусом.
равны нулю в точке (0, 0) и их частные производные по х и у также равны нулю в этой точке. При этом в случаях: 1), 2) и 3) картина интегральных линий в окрестности точки (0, 0) будет того же характера, что и для уравнения (45), т. е. в случае 1) точка (0, 0) будет узлом; в случае 2) — седлом и в случае 3) — фокусом.

Рис. 24.
Сформулируем результат более точно. В случае 1) все интегральные кривые, начинающиеся достаточно близко к точке (0, 0), стремятся одним своим концом к этой точке и при добавлении этой точки имеют в ней определенную касательную, причем две интегральные кривые имеют в точке (0, 0) общую касательную, т. е. составляют при добавлении этой точки одну кривую с непрерывно меняющейся касательной, а все остальные интегральные кривые имеют в точке (0, 0) другую общую касательную.
В случае 2) в окрестности (0, 0) существуют две пары интегральных кривых, стремящихся к точке (0, 0), причем кривые каждой пары вместе с точкой (0, 0) образуют одну кривую с непрерывно меняющейся касательной. Остальные интегральные кривые в окрестности (0, 0) не стремятся к этой точке и расположены примерно так, как и для уравнения (45).
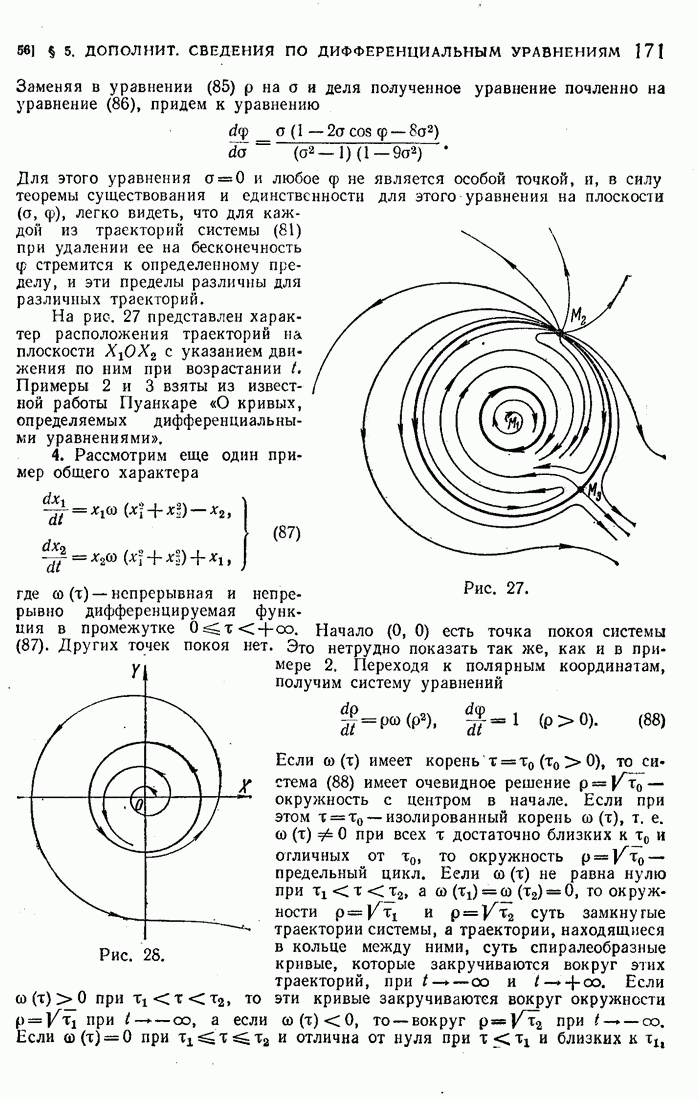
В случае 3) все интегральные кривые в окрестности (0, 0), как и для уравнения (45), беспредельно приближаются к этой точке, спиралеобразно закручиваясь в одном и том же направлении.
В случае 4) особая точка может быть или фокусом или центром. В последнем случае все интегральные кривые, начинающиеся достаточно близко к особой точке, суть замкнутые кривые, содержащие особую точку внутри.
Указанные выше результаты сохраняются и для того, более общего случая, когда  определены только в окрестности (0, 0),
определены только в окрестности (0, 0),
имеют в этой окрестности (включая точку (0, 0)) непрерывные частные производные до третьего порядка и частные производные первого порядка равны нулю в точке (0, 0).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
- 33. Линейные уравнения и колебательные явления.
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
- 53. Сходимость метода Эйлера — Коши.
- 54. Особые точки дифференциальных уравнений первого порядка.
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
- 58. Двукратный интеграл.
- 59. Вычисление двукратного интеграла.
- 60. Криволинейные координаты.
- 61. Трехкратный интеграл
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
- 67. Интегралы по определенной стороне поверхности.
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
- 84. Примеры.
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
- 156. Примеры.
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
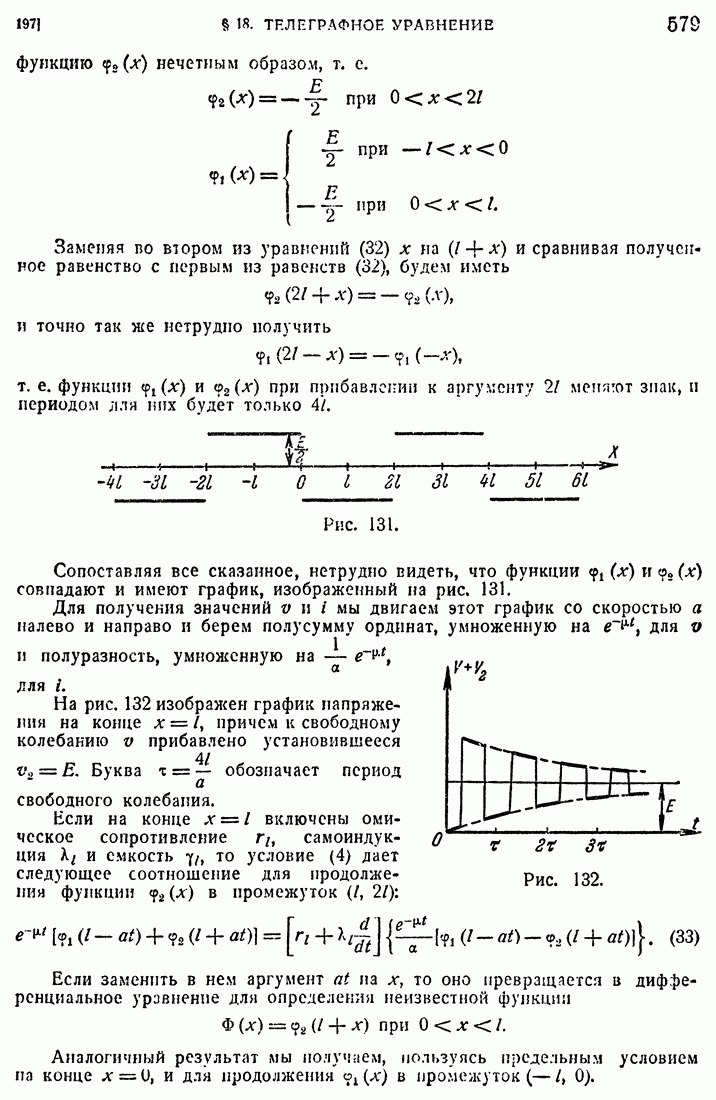
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
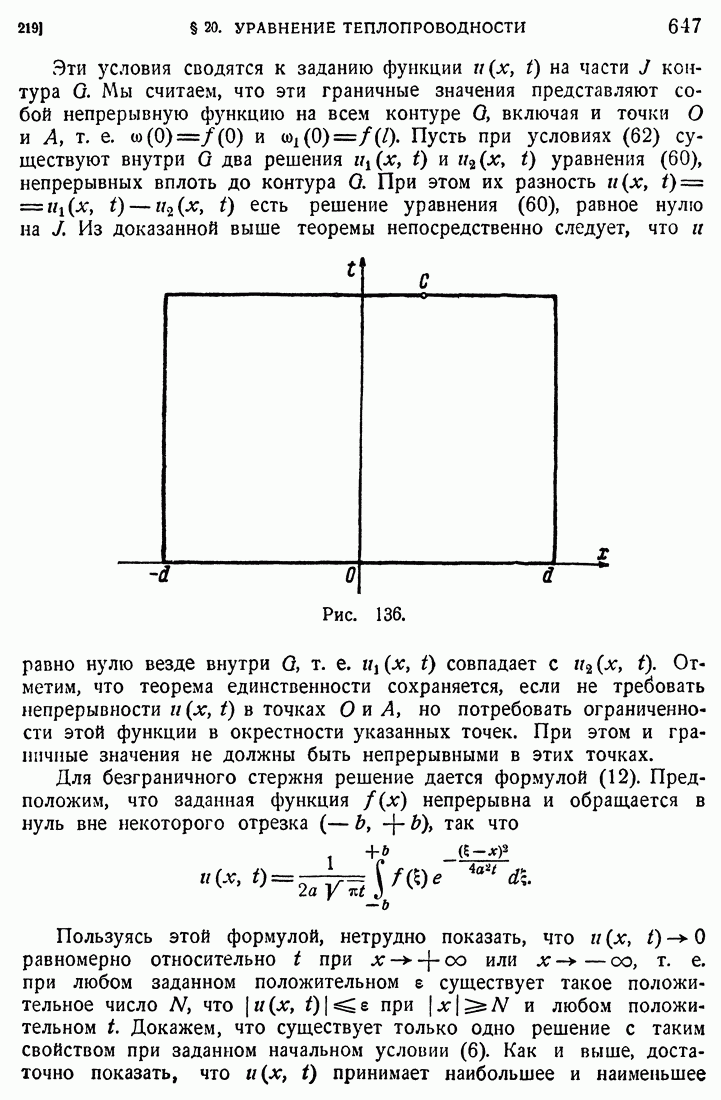
- 219. Теорема единственности.