| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
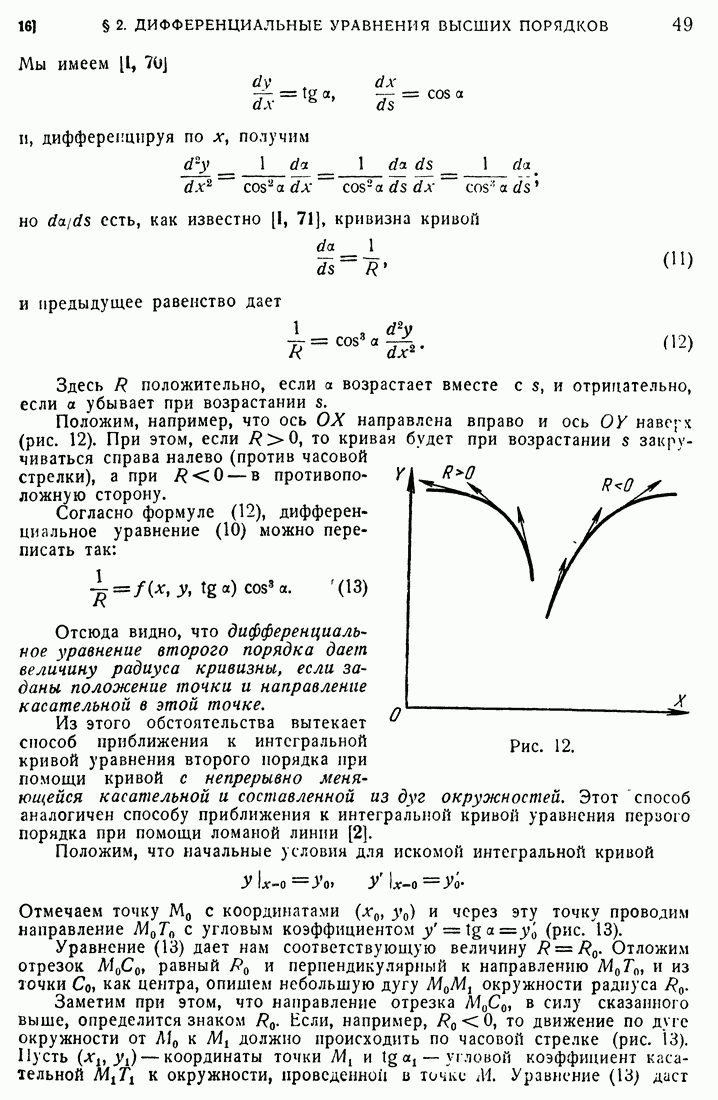
15
16
17
18
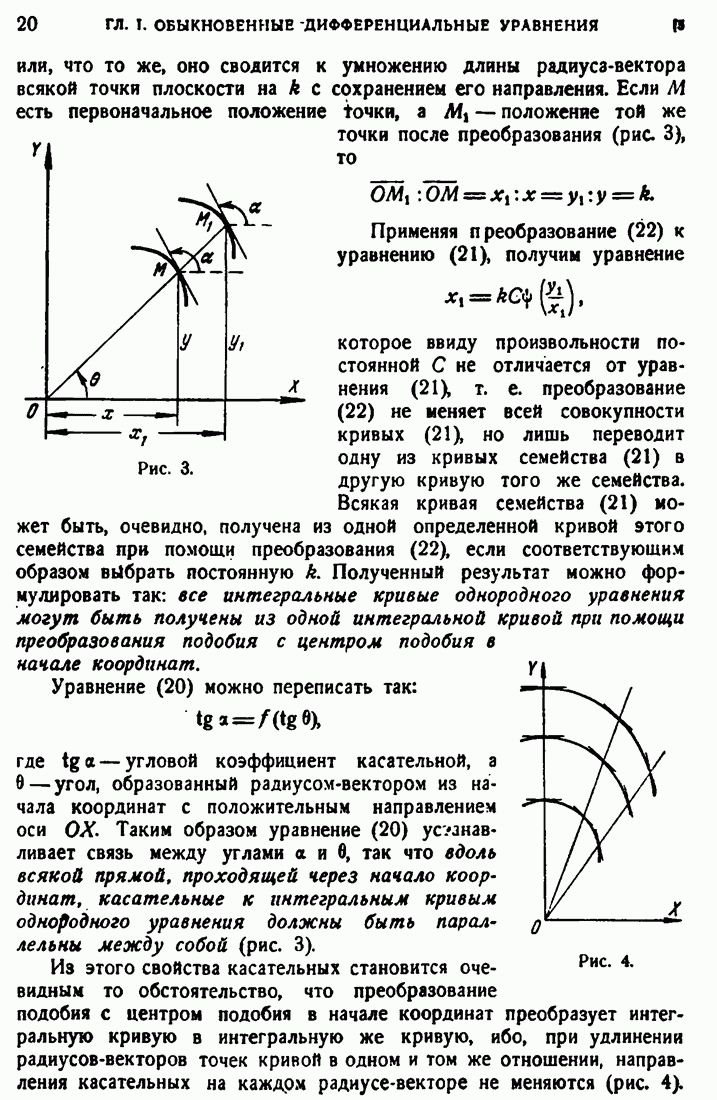
19
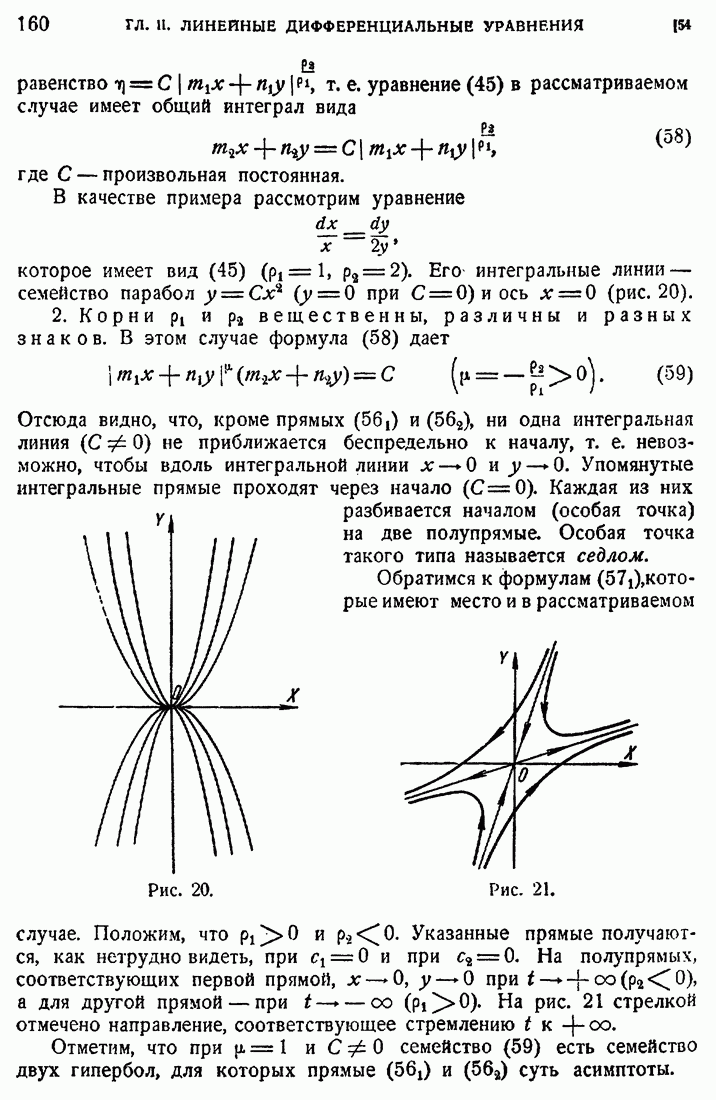
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
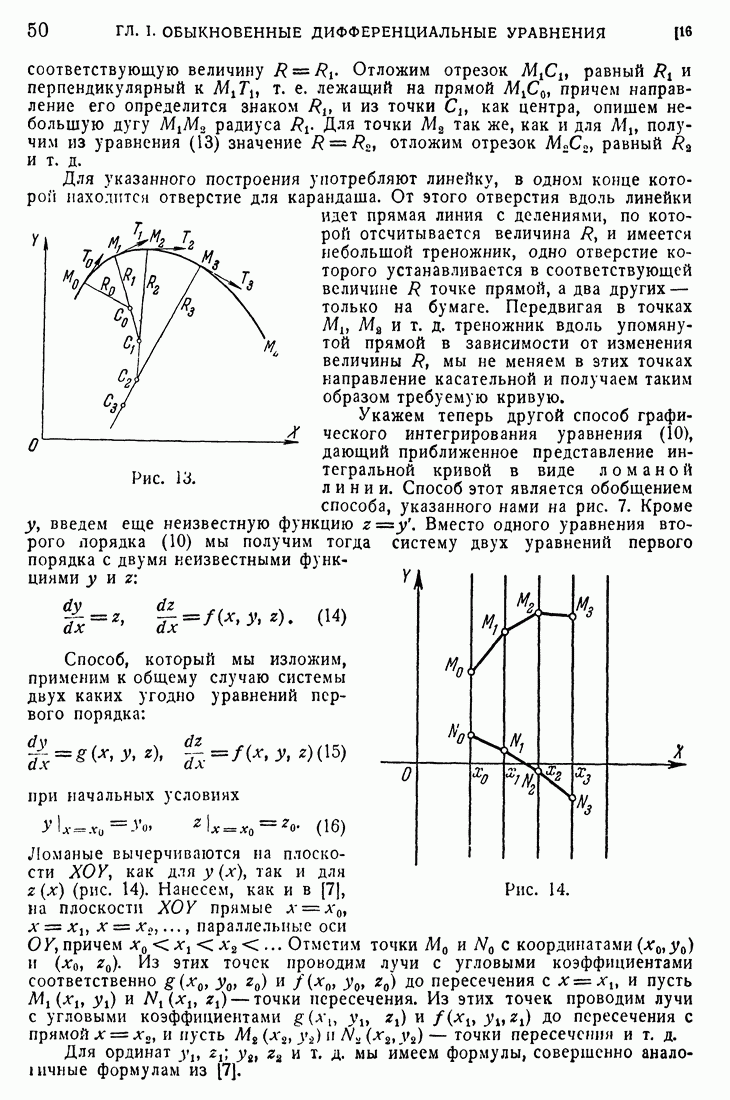
49
50
51
52
53
54
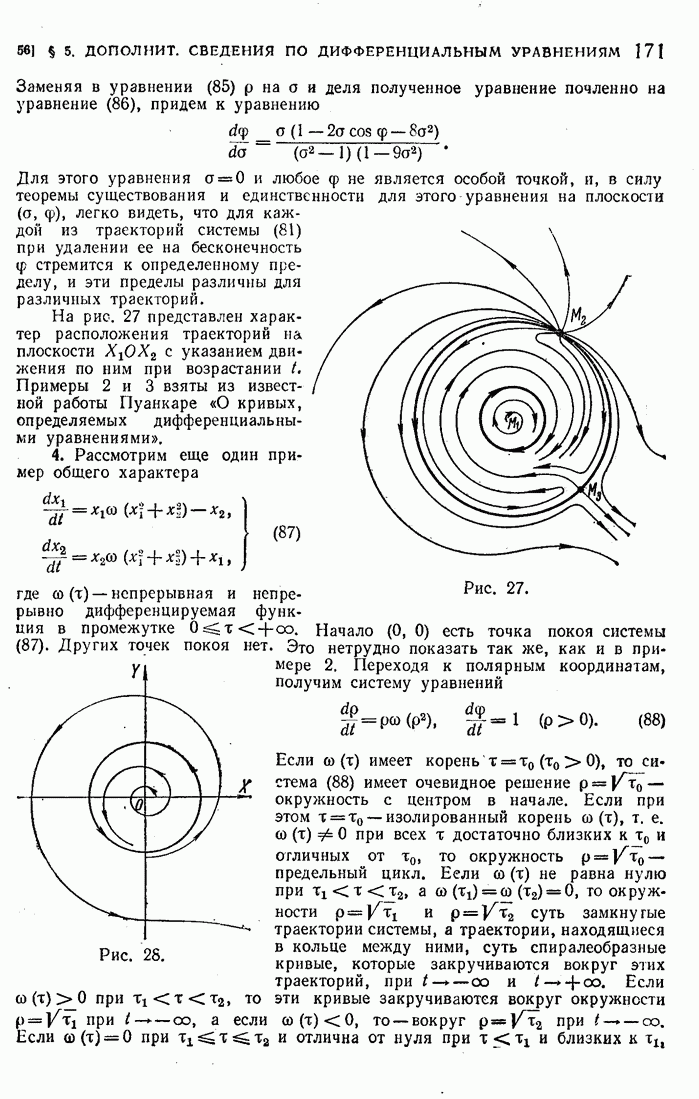
55
56
57
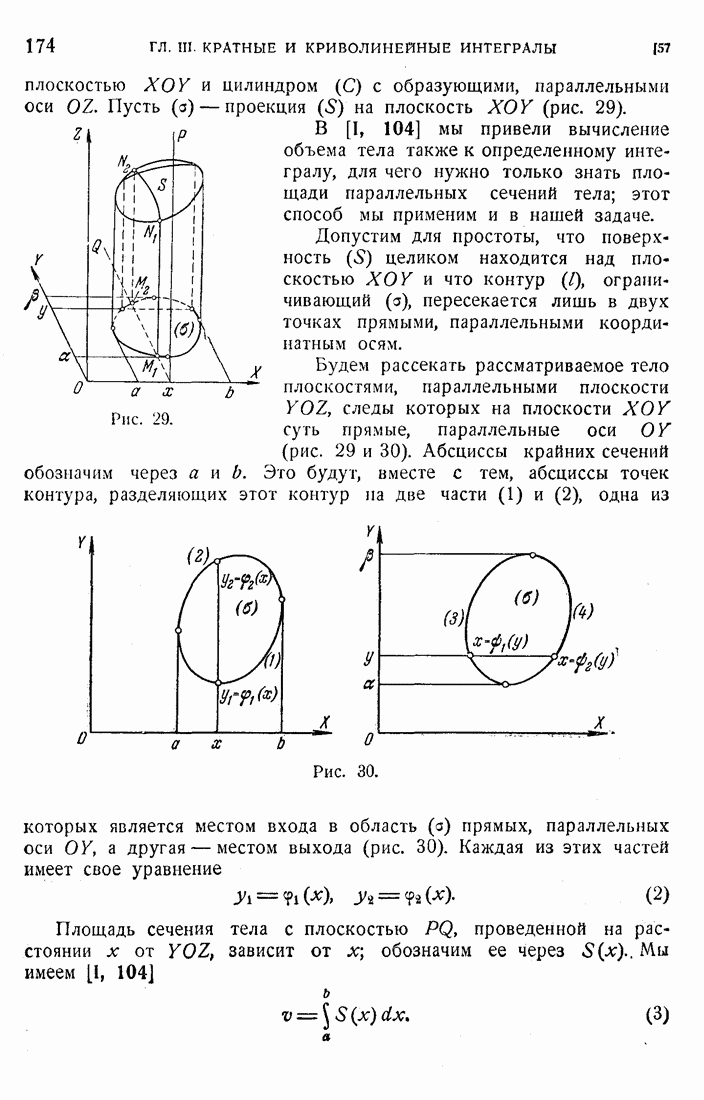
58
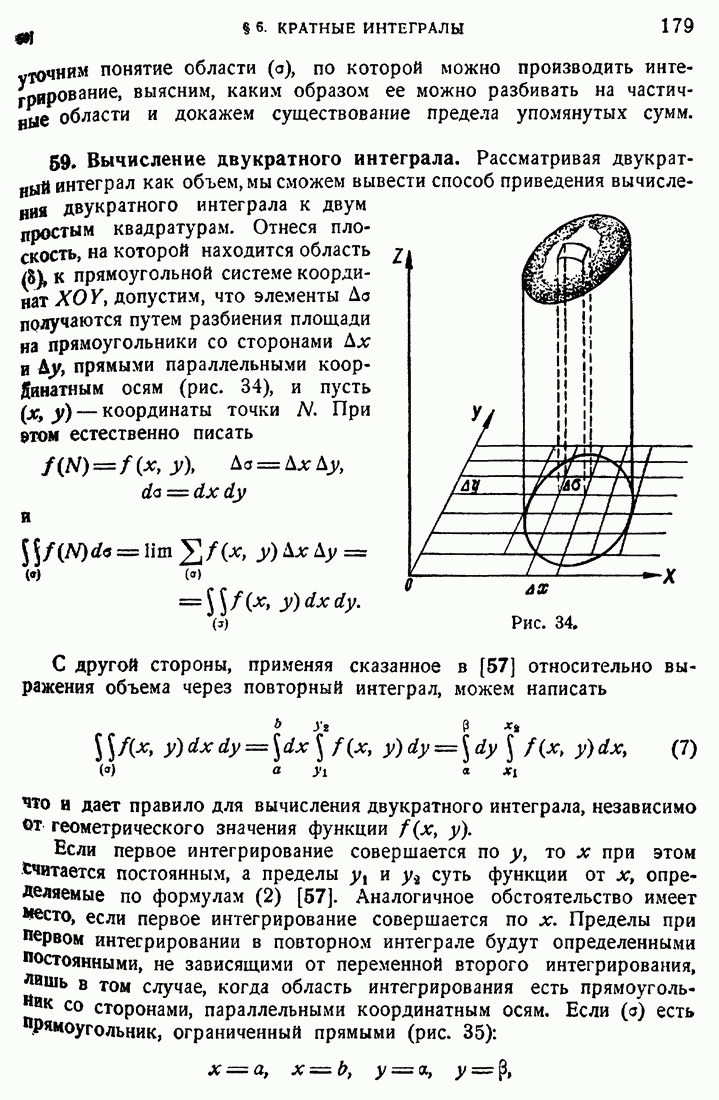
59
60
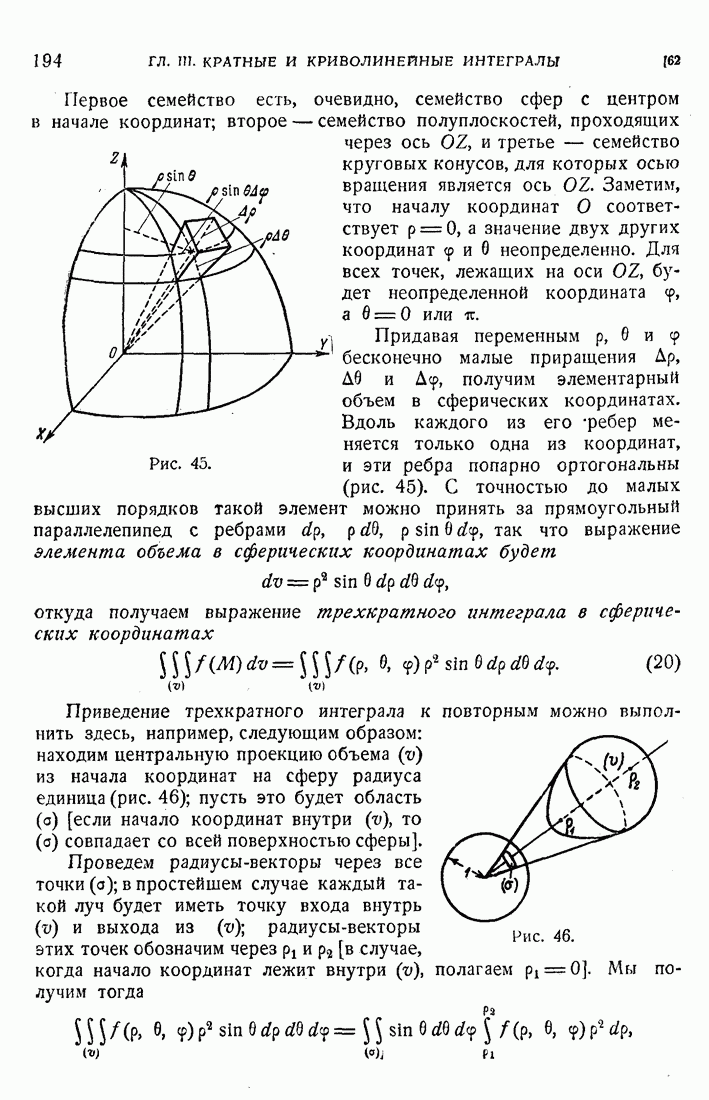
61
62
63
64
65
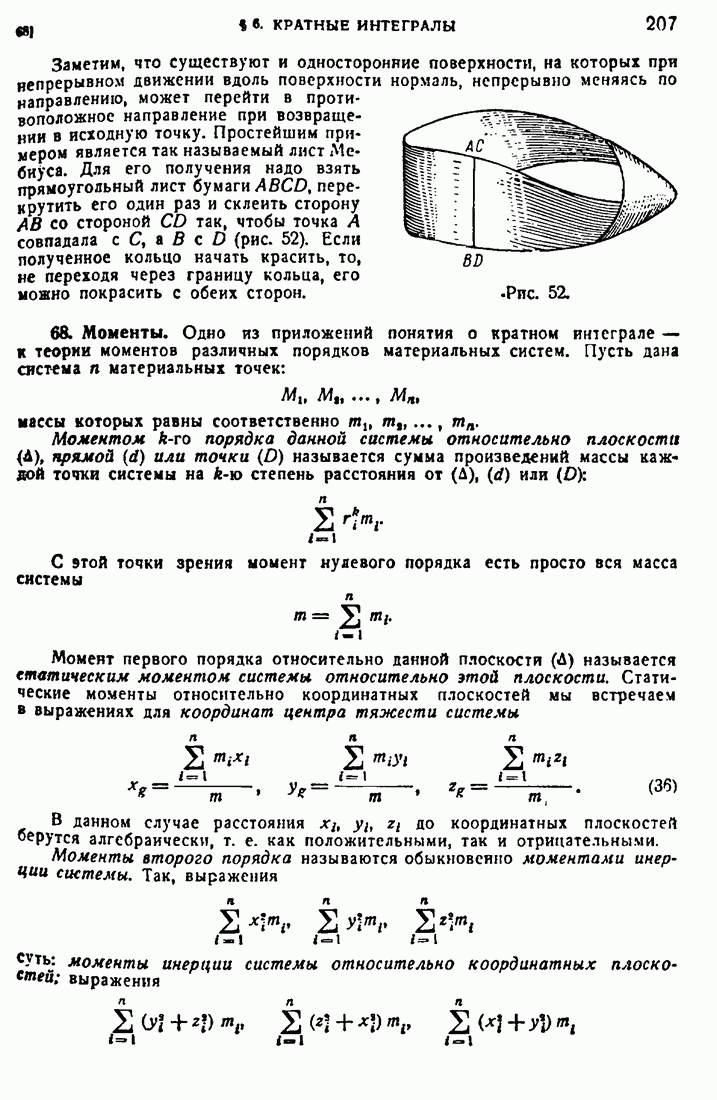
66
67
68
69
70
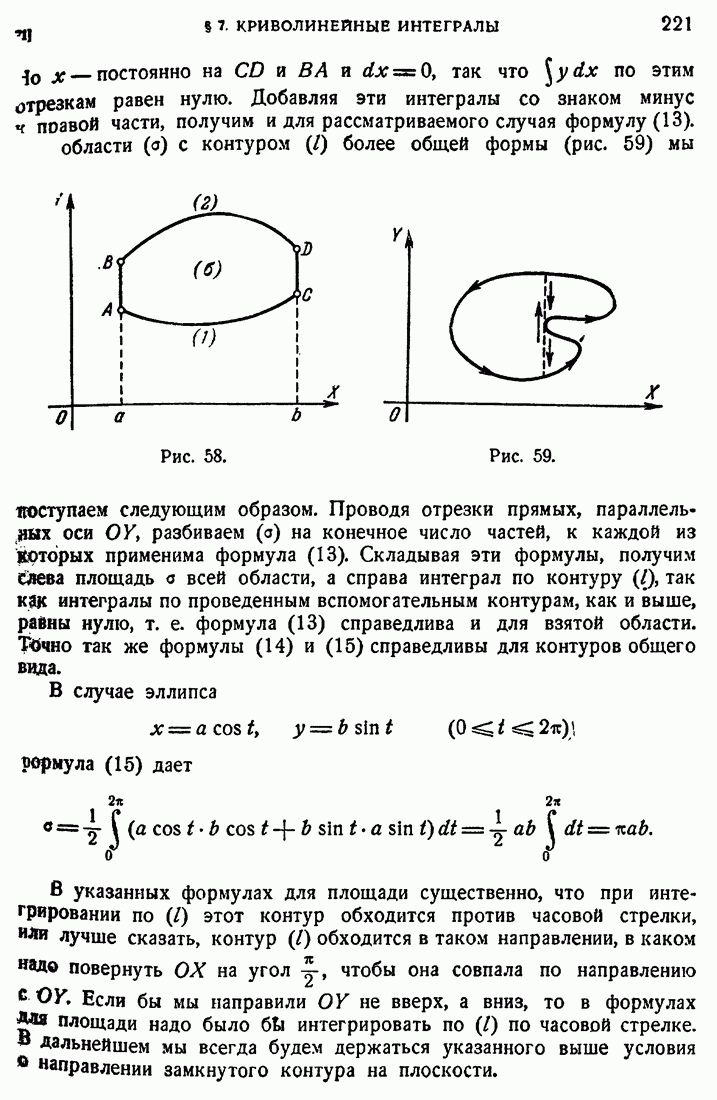
71
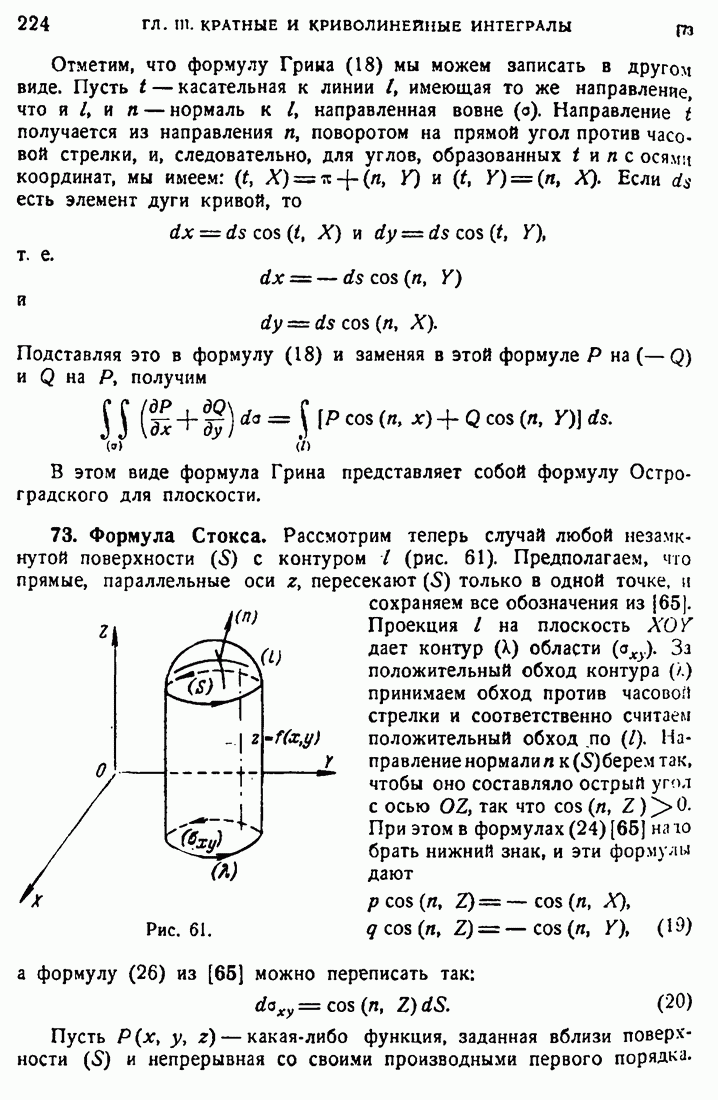
72
73
74
75
76
77
78
79
80
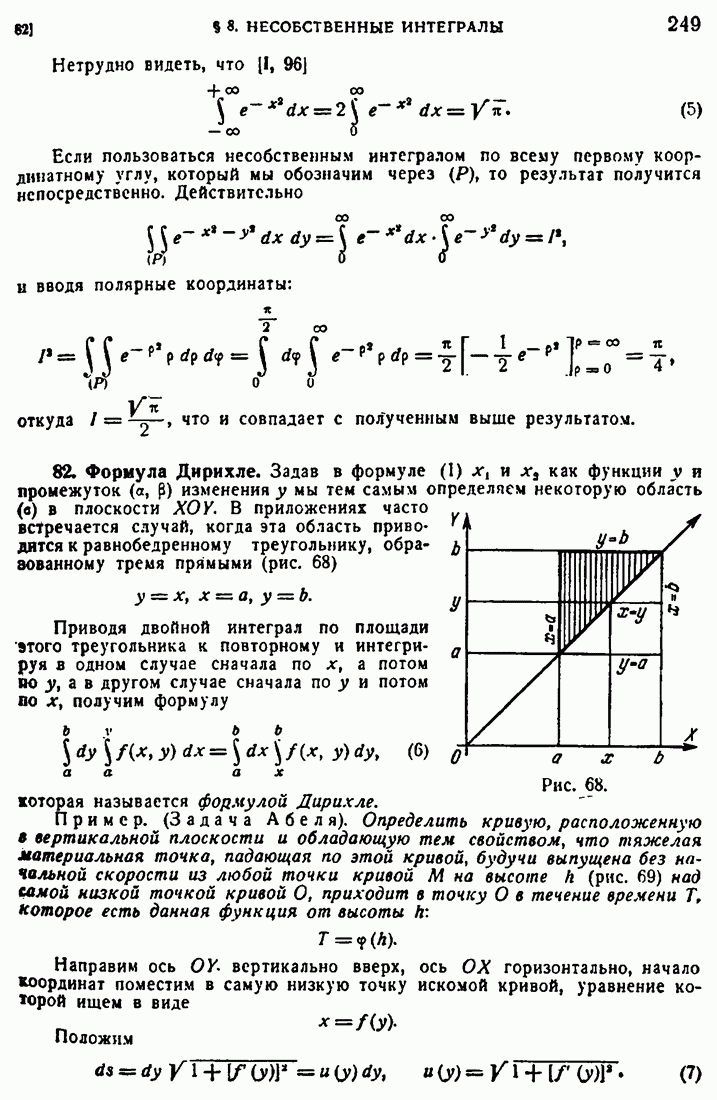
81
82
83
84
85
86
87
88
89
90
91
92
93
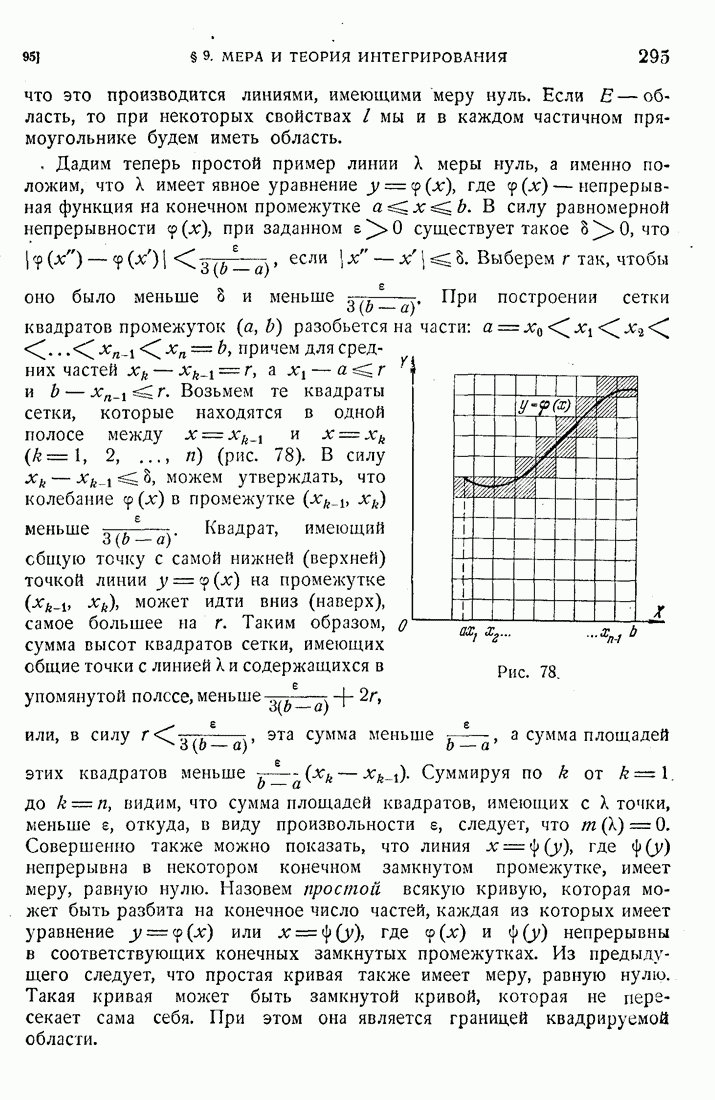
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
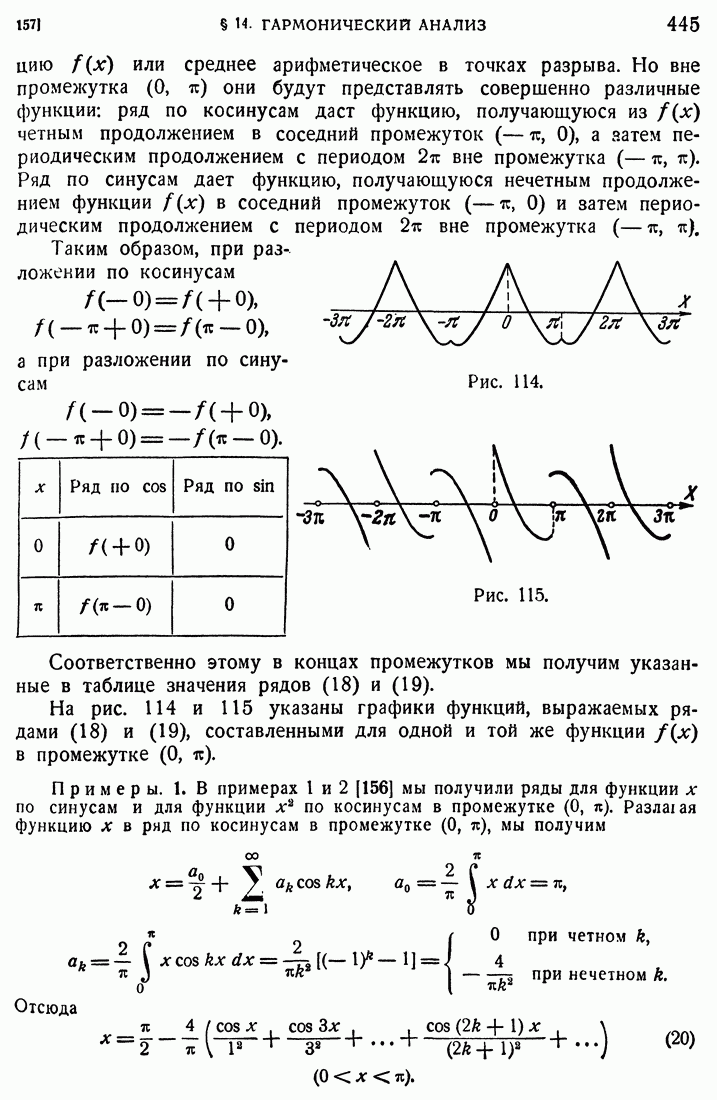
114
115
116
117
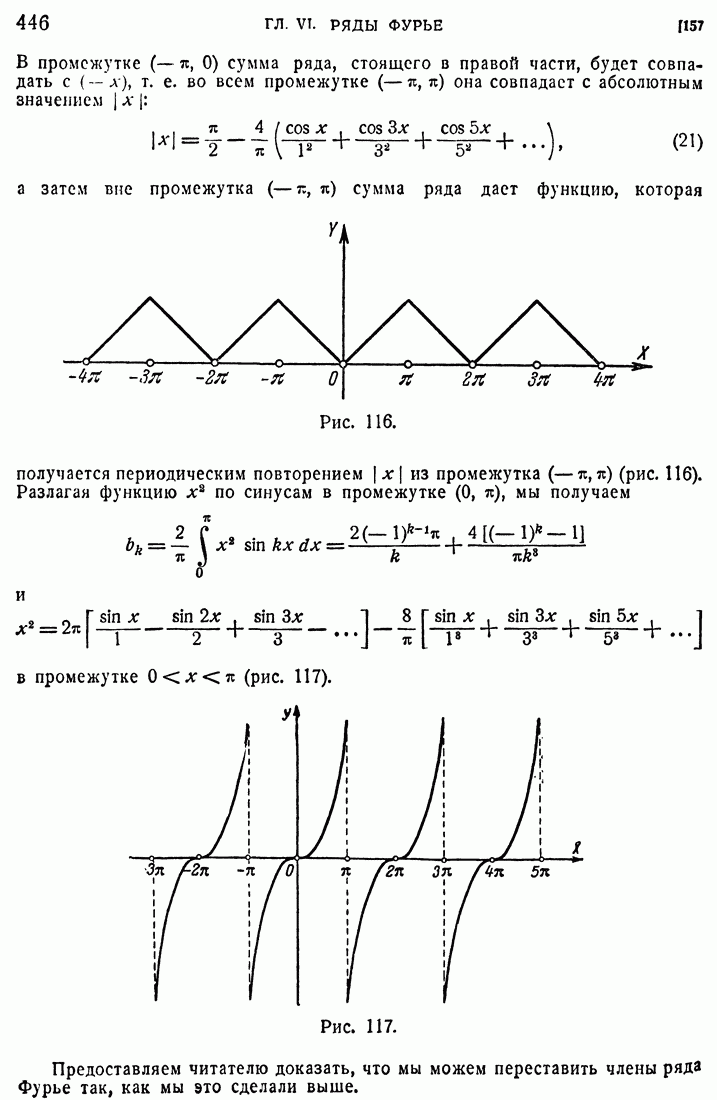
118
119
120
121
122
123
124
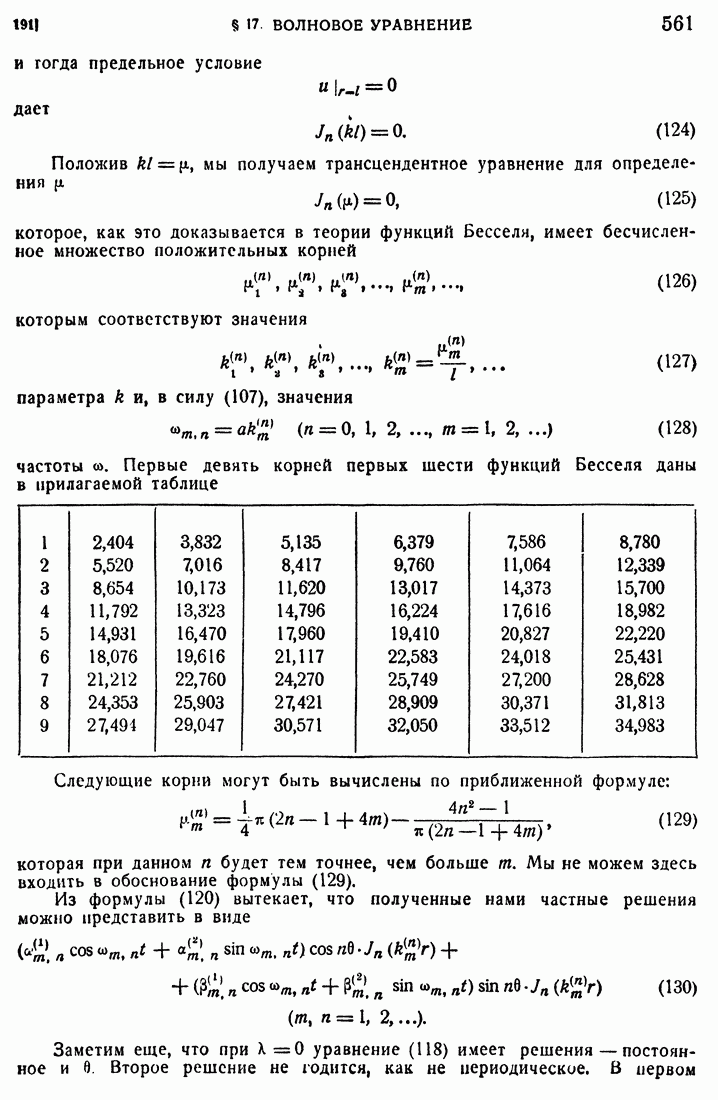
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
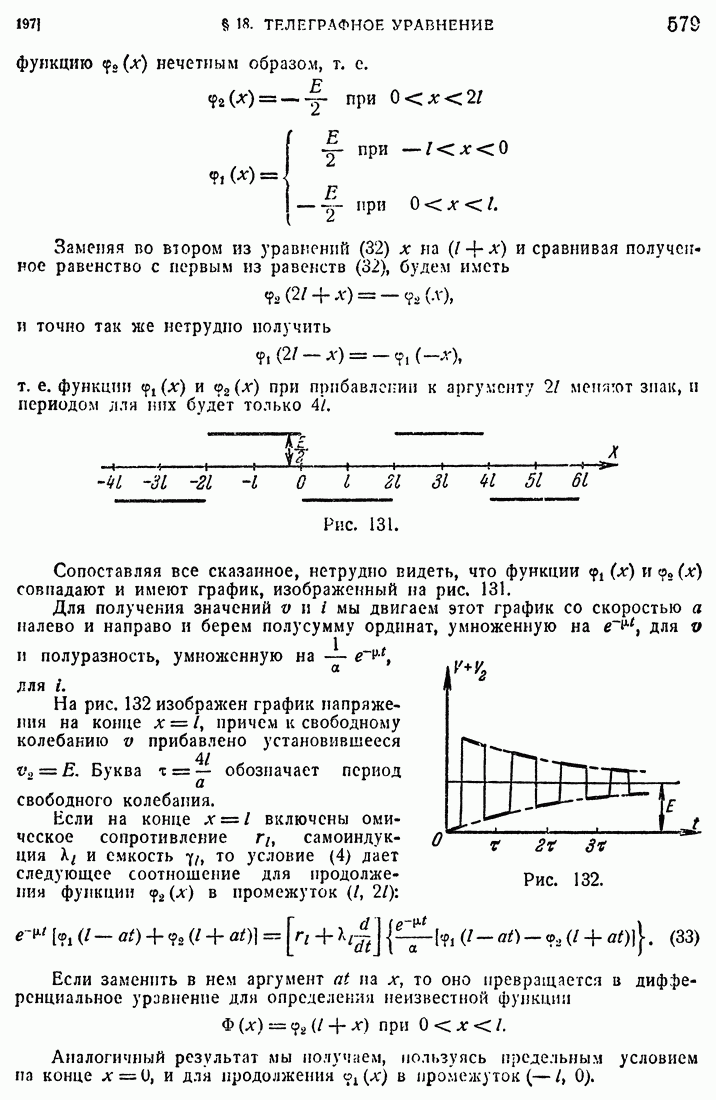
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
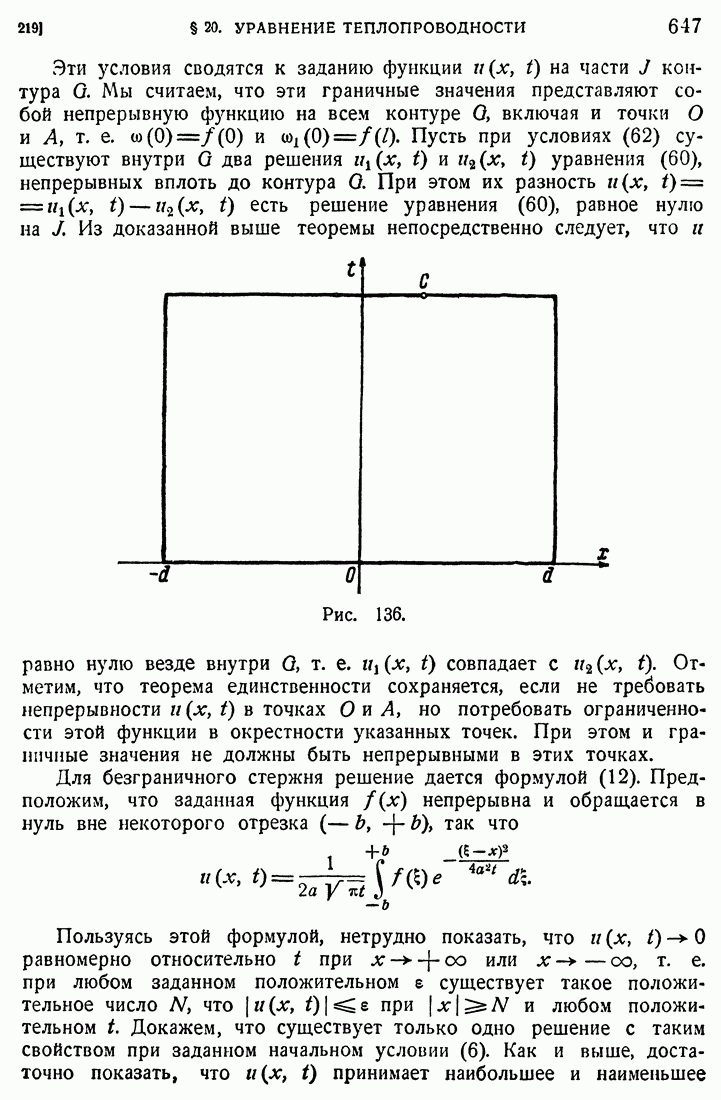
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
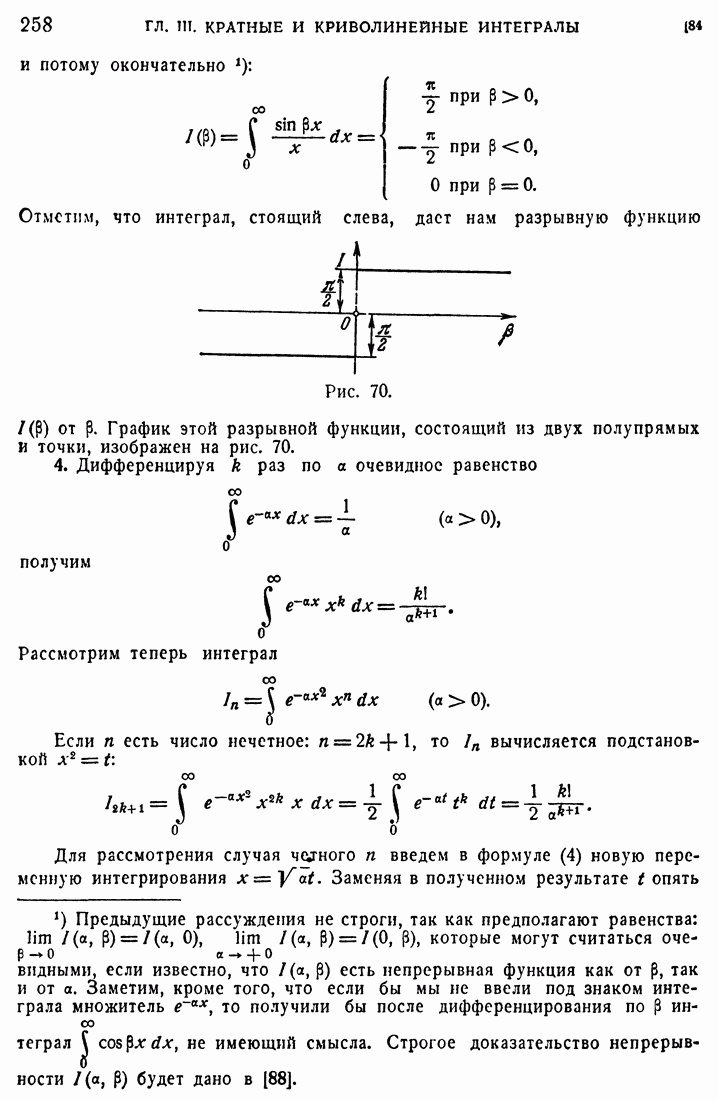
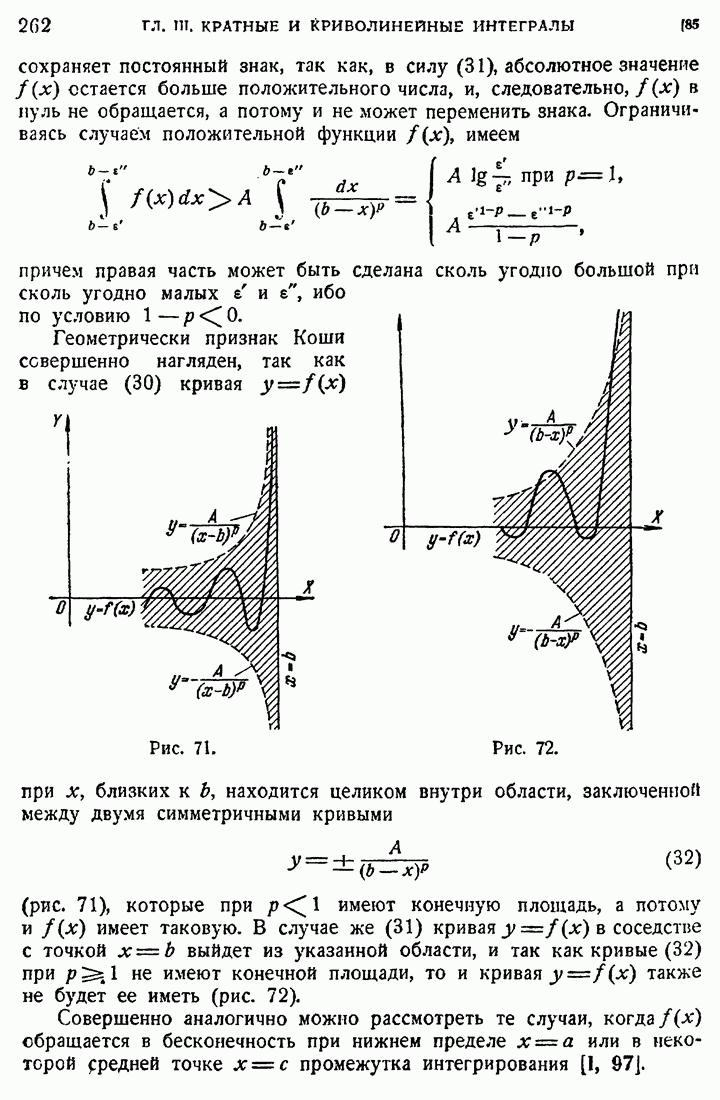
88. Примеры.
1. Рассмотрим более подробно пример 3 из [84]:

Считаем пока, что a — фиксированное положительное число, и рассматриваем интеграл (56) как интеграл, зависящий от параметра  . Заметим, что
. Заметим, что
отношение сохраняет непрерывность и при  и обращается при
и обращается при  в
в  , так что интеграл (56) является несобственным только вследствие бесконечного предела. При положительных
, так что интеграл (56) является несобственным только вследствие бесконечного предела. При положительных  мы имеем
мы имеем  следовательно,
следовательно,  а интеграл
а интеграл

сходятся, и, следовательно, по доказанному признаку, интеграл  сходится равномерно относительно р. Дифференцируя его по
сходится равномерно относительно р. Дифференцируя его по  под знаком интеграла, получим интеграл
под знаком интеграла, получим интеграл

который, в силу  также сходится равномерно. Отсюда вытекает, что интеграл (56) есть непрерывная функция от
также сходится равномерно. Отсюда вытекает, что интеграл (56) есть непрерывная функция от  и что его можно дифференцировать под знаком интеграла. Для оправдания всех вычислений упомянутого примера остается еще доказать, что
и что его можно дифференцировать под знаком интеграла. Для оправдания всех вычислений упомянутого примера остается еще доказать, что  , т. е. что интеграл (56) при фиксированном Р есть непрерывная функция от а справа от нуля. Мы докажем, что он есть непрерывная функция от а при
, т. е. что интеграл (56) при фиксированном Р есть непрерывная функция от а справа от нуля. Мы докажем, что он есть непрерывная функция от а при  . Выше мы уже показали, что он сходится и при
. Выше мы уже показали, что он сходится и при 
Не ограничивая общности, можем считать  так как случай
так как случай  приводится к случаю
приводится к случаю  простой переменой знака интеграла, в случае же
простой переменой знака интеграла, в случае же  утверждение очевидно.
утверждение очевидно.
Будем поступать аналогично тому, как это мы делали в [86] с интегралом Френеля. Разобьем весь промежуток  ) на части
) на части

такие, что в первой части подынтегральная функция

имеет знак  во второй - знак (-) и т. д. Положим
во второй - знак (-) и т. д. Положим

Вводя вместо  новую переменную
новую переменную  получим
получим

отауда видно, что  положительные и убывают при возрастании
положительные и убывают при возрастании 
Кроме того, из неравенства

следует, что  при
при  .
.
Итак, мы можем представить при  наш интеграл в виде суммы знакопеременного ряда
наш интеграл в виде суммы знакопеременного ряда 

Остаточный член этого ряда, в силу (57) и теоремы [I, 123], имеет оценку

не зависящую от а, причем  при
при  . Отсюда вытекает равномерная сходимость ряда при
. Отсюда вытекает равномерная сходимость ряда при  следовательно (I, 146], непрерывность его суммы, поскольку члены ряда
следовательно (I, 146], непрерывность его суммы, поскольку члены ряда  в силу
в силу  суть, непрерывные функции.
суть, непрерывные функции.
Заметим, что из одной равномерной сходимости ряда (58) при  бел дополнительных рассуждений еще не следует равномерной сходимости интеграла. В данном случае можно доказать, что и интеграл равномерно сходится при а 0.
бел дополнительных рассуждений еще не следует равномерной сходимости интеграла. В данном случае можно доказать, что и интеграл равномерно сходится при а 0.
Заметим, что интеграл

равный у при  при
при  и нулю при
и нулю при  дает функцию от
дает функцию от  имеющую разрыв непрерывности при
имеющую разрыв непрерывности при  Отсюда вытекает, что написанный интеграл не может сходиться равномерно относительно
Отсюда вытекает, что написанный интеграл не может сходиться равномерно относительно  в промежутка изменения
в промежутка изменения  , содержащем
, содержащем  Если мы возьмем этот промежуток правее нуля, то величина интеграла у имеет производную по
Если мы возьмем этот промежуток правее нуля, то величина интеграла у имеет производную по  , равную нулю, по интеграл нельзя дифференцировать по
, равную нулю, по интеграл нельзя дифференцировать по  под знаком интеграла, так как после такого дифференцирования получается интеграл по промежутку
под знаком интеграла, так как после такого дифференцирования получается интеграл по промежутку  не имеющий смысла.
не имеющий смысла.
2. В примере 4 из  мы дифференцировали k раз по а интеграл:
мы дифференцировали k раз по а интеграл:

под знаком интеграла. Для доказательства законности этой операции досаточно показать, что при целом положительном k интегралы

сходятся равномерно во всяком промежутке где  . Так как в промежутке интегрирования
. Так как в промежутке интегрирования  то очевидно
то очевидно  и в силу доказанного в
и в силу доказанного в  признака равномерной сходимости нам достаточно доказать сходимость интеграла
признака равномерной сходимости нам достаточно доказать сходимость интеграла

Но если обозначить  , то, применяя обычным образом правило Лопиталя 11,65), убедимся, что
, то, применяя обычным образом правило Лопиталя 11,65), убедимся, что  при
при  и по признаку, указанному в [85], видим, что написанный интеграл действительно сходится.
и по признаку, указанному в [85], видим, что написанный интеграл действительно сходится.
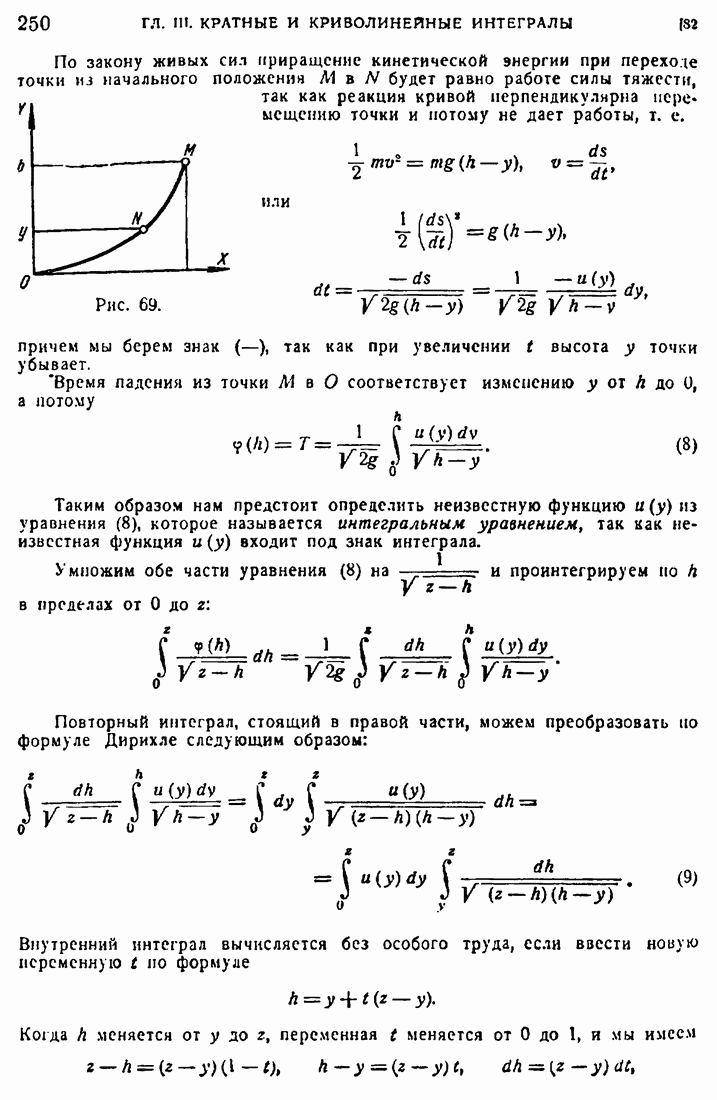
3. В [82] мы получили решение задачи Абеля в виде

Покажем, как можно вычислить производную в правой части этого равенства. Обозначим

Дифференцируя по  под знаком интеграла, мы получили бы под знаком интеграла
под знаком интеграла, мы получили бы под знаком интеграла  что дало бы расходящийся интеграл [85], а потому надо поступать иначе. Преобразуем интеграл
что дало бы расходящийся интеграл [85], а потому надо поступать иначе. Преобразуем интеграл  интегрированием по частям, предполагая существование непрерывной и ограниченной в окрестности
интегрированием по частям, предполагая существование непрерывной и ограниченной в окрестности  производной
производной  при
при 

Напомним, что  . Это будет постоянная, которая будет, вообще говоря, отличной от нуля, тогда как но самому своему определению
. Это будет постоянная, которая будет, вообще говоря, отличной от нуля, тогда как но самому своему определению  Дифференцируя написанную выше формулу, мы найдем, в силу (21), из [83]:
Дифференцируя написанную выше формулу, мы найдем, в силу (21), из [83]:

Если  есть постоянная, то
есть постоянная, то  , и мы имеем полученную уже ранее формулу. Если
, и мы имеем полученную уже ранее формулу. Если  то оказывается
то оказывается

Мы не привели доказательства того, что для несобственного интеграла  применима формула (21) из [83]. Заметим, что если вместо
применима формула (21) из [83]. Заметим, что если вместо  ввести новую переменную интегрирования и по формуле:
ввести новую переменную интегрирования и по формуле:  то для
то для  получим интеграл с постоянными пределами
получим интеграл с постоянными пределами

Предполагая, как и выше, существование непрерывной и ограниченной производной  при
при  , можем, как нетрудно проверить, дифференцировать под знаком интеграла:
, можем, как нетрудно проверить, дифференцировать под знаком интеграла:

Производя в первом слагаемом интегрирование по частям и возвращаясь к прежней переменной  получим опять формулу (59).
получим опять формулу (59).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮ
- ГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Определение решения по начальному условию. Теорема существования и единственности.
- 3. Уравнения с отделяющимися переменными.
- 4. Примеры.
- 5. Однородное уравнение.
- 6. Линейные уравнения и уравнение Бернулли.
- 7. Способ Эйлера—Коши.
- 8. Применение степенных рядов.
- 9. Общий интеграл и особое решение.
- 10. Уравнения, не решенные относительно у’.
- 11. Уравнение Клеро.
- 12. Уравнение Лагранжа.
- 13. Огибающие семейства кривых и особые решения.
- 14. Изогональные траектории.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И СИСТЕМЫ УРАВНЕНИЙ
- 16. Графические способы интегрирования дифференциального уравнения второго порядка.
- 17. Уравнение у^(n)=f(x).
- 18. Понижение порядка дифференциального уравнения.
- 19. Системы обыкновенных дифференциальных уравнений.
- 20. Примеры.
- 21. Системы уравнений и уравнения высших порядков.
- 22. Линейные уравнения с частными производными.
- 23. Геометрическая интерпретация.
- 24. Примеры.
- ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 25. Линейные однородные уравнения второго порядка.
- 26. Линейные неоднородные уравнения второго порядка.
- 27. Линейные уравнения высших порядков.
- 28. Однородные уравнения второго порядка с постоянными коэффициентами.
- 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- 30. Частные случаи.
- 31. Корни решений и колеблющиеся решения
- 32. Линейные уравнения высших порядков с постоянными коэффициентами.
- 33. Линейные уравнения и колебательные явления.
- 34. Собственные и вынужденные колебания.
- 35. Синусоидальная внешняя сила и резонанс.
- 36. Предельные задачи.
- 37. Примеры.
- 38. Символический метод.
- 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами.
- 40. Линейные неоднородные уравнения с постоянными коэффициентами.
- 41. Пример.
- 42 Уравнение Эйлера.
- 43. Системы линейных уравнений с постоянными коэффициентами.
- 44. Примеры
- § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
- 45. Интегрирование линейного уравнения с помощью степенного ряда
- 46. Примеры.
- 47. Разложение решения в обобщенный степенной ряд.
- 48. Уравнение Бесселя
- 49. Уравнения, приводящиеся к уравнению Бесселя
- § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 50. Метод последовательных приближений для линейных уравнений.
- 51. Случай нелинейного уравнения.
- 52. Дополнения к теореме существования и единственности.
- 53. Сходимость метода Эйлера — Коши.
- 54. Особые точки дифференциальных уравнений первого порядка.
- 55. Автономные системы.
- 56. Примеры.
- ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 6. КРАТНЫЕ ИНТЕГРАЛЫ
- 58. Двукратный интеграл.
- 59. Вычисление двукратного интеграла.
- 60. Криволинейные координаты.
- 61. Трехкратный интеграл
- 62. Цилиндрические и сферические координаты.
- 63. Криволинейные координаты в пространстве.
- 64. Основные свойства кратных интегралов.
- 65. Площадь поверхности.
- 66. Интегралы по поверхности и формула Остроградского.
- 67. Интегралы по определенной стороне поверхности.
- 68. Моменты.
- § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- 69. Определение криволинейного интеграла.
- 70. Работа силового поля. Примеры.
- 71. Площадь и криволинейный интеграл.
- 72. Формула Грина
- 73. Формула Стокса.
- 74. Независимость криволинейного интеграла от пути на плоскости.
- 75. Случай многосвязной области.
- 76. Независимость криволинейного интеграла от пути в пространстве.
- 77. Установившееся течение жидкости.
- 78. Интегрирующий множитель.
- 79. Уравнение в полных дифференциалах для случая трех переменных.
- 80. Замена переменных в двойном интеграле.
- § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 81. Интегрирование под знаком интеграла.
- 82. Формула Дирихле.
- 83. Дифференцирование под знаком интеграла
- 84. Примеры.
- 85. Несобственные интегралы.
- 86. Неабсолютно сходящиеся интегралы.
- 87. Равномерно сходящиеся интегралы.
- 88. Примеры.
- 89. Несобственные кратные интегралы.
- 90. Примеры.
- § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ
- 92. Основные теоремы.
- 93. Счетные множества. Действия над точечными множествами.
- 94. Мера Жордана.
- 95. Квадрируемые множества.
- 96. Независимость от выбора осей.
- 97. Случай любого числа измерений.
- 98. Интегрируемые функции.
- 99. Вычисление двойного интеграла.
- 100. n-кратные интегралы.
- 101. Примеры.
- 102. Внешняя мера Лебега.
- 103. Измеримые множества.
- 104. Измеримые функции.
- 105. Дополнительные сведения.
- 106. Интеграл Лебега.
- 107. Свойства интеграла Лебега.
- 108. Интегралы от неограниченных функций.
- 109. Предельный переход под знаком интеграла.
- 110. Теорема Фубини.
- 111. Интегралы по множеству бесконечной меры.
- ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ
- 112. Сложение и вычитание векторов.
- 113. Умножение вектора на скаляр. Компланарность векторов.
- 114. Разложение вектора по трем некомпланарным векторам.
- 115. Скалярное произведение.
- 116. Векторное произведение.
- 117. Соотношения между скалярным к векторным произведениями.
- 118. Скорости точек вращающегося твердого тела; момент вектора.
- § 11 ТЕОРИЯ ПОЛЯ
- 119. Дифференцирование вектора
- 120. Скалярное поле и его градиент.
- 121. Векторное поле; расходимость и вихрь.
- 122. Потенциальное и соленоидальное поля.
- 123. Направленный элемент поверхности.
- 124. Некоторые формулы векторного анализа.
- 125. Движение твердого тела и малая деформация.
- 126. Уравнение непрерывности.
- 127. Уравнения гидродинамики идеальной жидкости.
- 128. Уравнения распространения звука.
- 129. Уравнение теплопроводности.
- 130. Уравнения Максвелла.
- 131. Выражение оператора Лапласа в ортогональных координатах.
- 132. Операция дифференцирования для случая переменного поля.
- ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 133. Плоская кривая, ее кривизна и эволюта.
- 134. Эвольвента.
- 135. Естественное уравнение кривой.
- 136. Основные элементы кривой в пространстве.
- 137. Формулы Френе.
- 138. Соприкасающаяся плоскость.
- 139. Винтовые линии.
- 140. Поле единичных векторов.
- § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 141. Параметрические уравнения поверхности.
- 142. Первая дифференциальная форма Гаусса.
- 143. Вторая дифференциальная форма Гаусса.
- 144. О кривизне линий, начерченных на поверхности.
- 145. Индикатриса Дюпена и формула Эйлера.
- 146. Определение главных радиусов кривизны и главных направлений.
- 147. Линии кривизны.
- 148. Теорема Дюпена.
- 149. Примеры.
- 150. Гауссова кривизна.
- 151. Вариация элемента площади и средняя кривизна.
- 152. Огибающая семейства поверхностей и кривых.
- 153. Развертывающиеся поверхности.
- ГЛАВА VI. РЯДЫ ФУРЬЕ
- 154. Ортогональность тригонометрических функций.
- 155. Теорема Дирихле.
- 156. Примеры.
- 157. Разложение в промежутке (0, п).
- 158. Периодические функции периода 2l.
- 159. Средняя квадратичная погрешность.
- 160. Общие ортогональные системы функций.
- 161. Класс L2
- 162. Сходимость в среднем.
- 163. Ортонормированные системы в L2.
- § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ
- 164. Разложение в ряд Фурье.
- 165. Вторая теорема о среднем.
- 166. Интеграл Дирихле.
- 167. Теорема Дирихле.
- 168. Приближение к непрерывной функции полиномами.
- 169. Формула замкнутости.
- 170. Характер сходимости рядов Фурье.
- 171. Улучшение сходимости рядов Фурье.
- 172. Пример.
- § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ
- 173. Формула Фурье.
- 174. Ряды Фурье в комплексной форме.
- 176. Кратные ряды Фурье.
- ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 176. Уравнение колебаний струны.
- 177. Решение Даламбера.
- 178. Частные случаи.
- 179. Ограниченная струна.
- 180. Способ Фурье.
- 181. Гармоники и стоячие волны.
- 182. Вынужденные колебания.
- 183. Сосредоточенная сила.
- 184. Формула Пуассона.
- 185. Цилиндрические волны.
- 186. Случай n-мерного пространства.
- 187. Неоднородное волновое уравнение.
- 188. Точечный источник.
- 189. Поперечные колебания мембран.
- 190. Прямоугольная мембрана.
- 191. Круглая мембрана.
- 192. Теорема единственности.
- 193. Применение интеграла Фурье.
- § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ
- 195. Установившиеся процессы.
- 196. Устанавливающиеся процессы.
- 197. Примеры.
- 198. Обобщенное уравнение колебаний струны.
- 199. Неограниченная цепь в общем случае.
- 200. Способ Фурье для ограниченной цепи.
- 201. Обобщенное волновое уравнение.
- § 19. УРАВНЕНИЕ ЛАПЛАСА
- 202. Гармонические функции.
- 203. Формула Грина.
- 204. Основные свойства гармонических функций.
- 205. Решение задачи Дирихле для круга.
- 206. Интеграл Пуассона.
- 207. Задача Дирихле для сферы.
- 208. Функция Грина.
- 209. Случай полупространства.
- 210. Потенциал объемных масс.
- 211. Уравнение Пуассона.
- 212. Формула Кирхгофа.
- § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
- 214. Неограниченный стержень.
- 215. Стержень, ограниченный с одного конца.
- 216. Стержень, ограниченный с обоих концов.
- 217. Дополнительные замечания.
- 218. Случай сферы.
- 219. Теорема единственности.