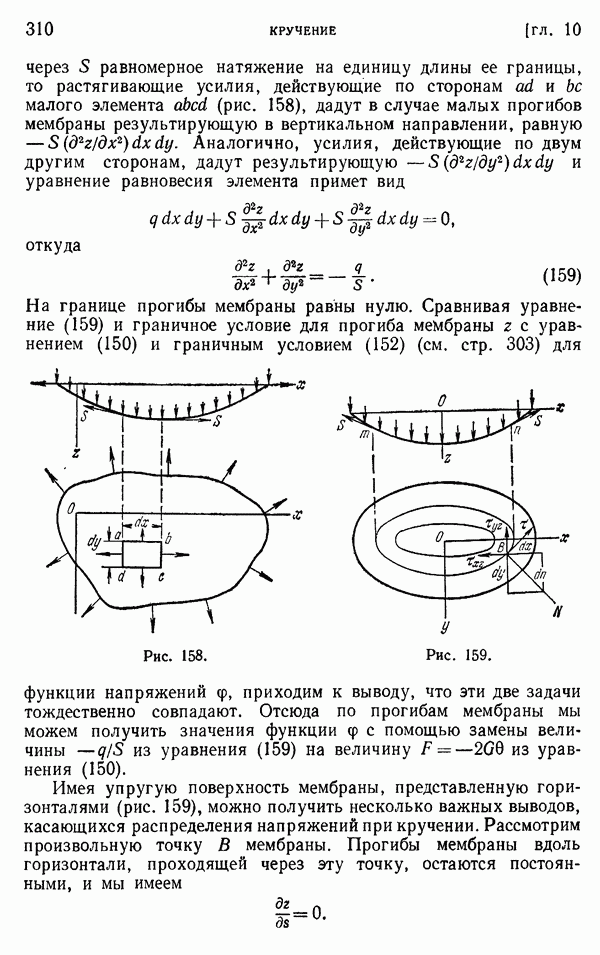
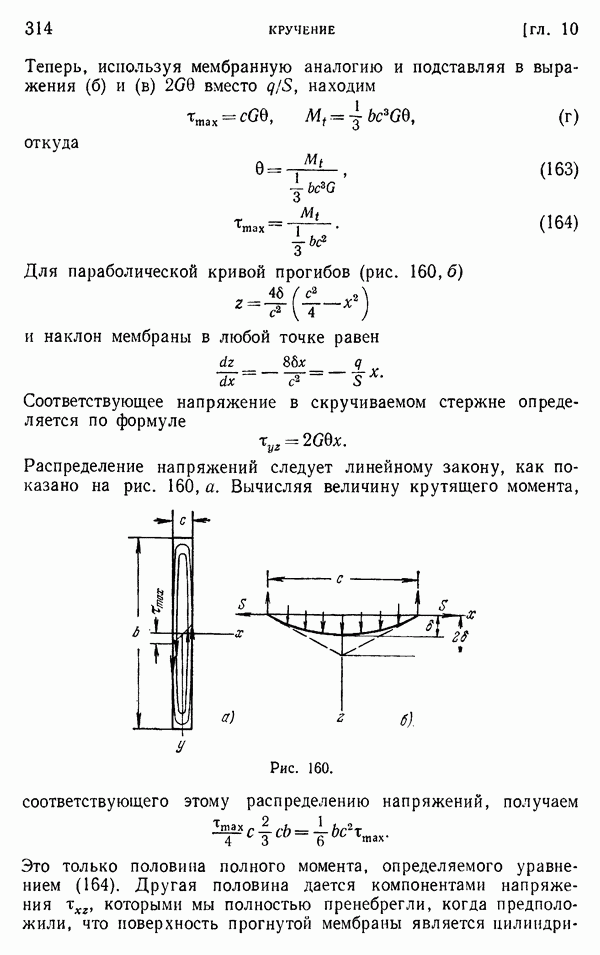
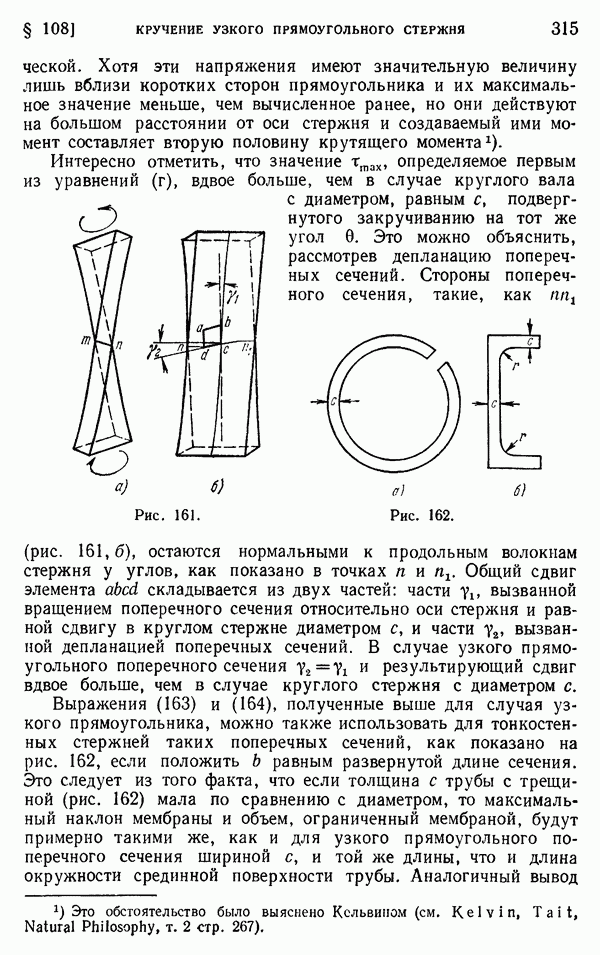
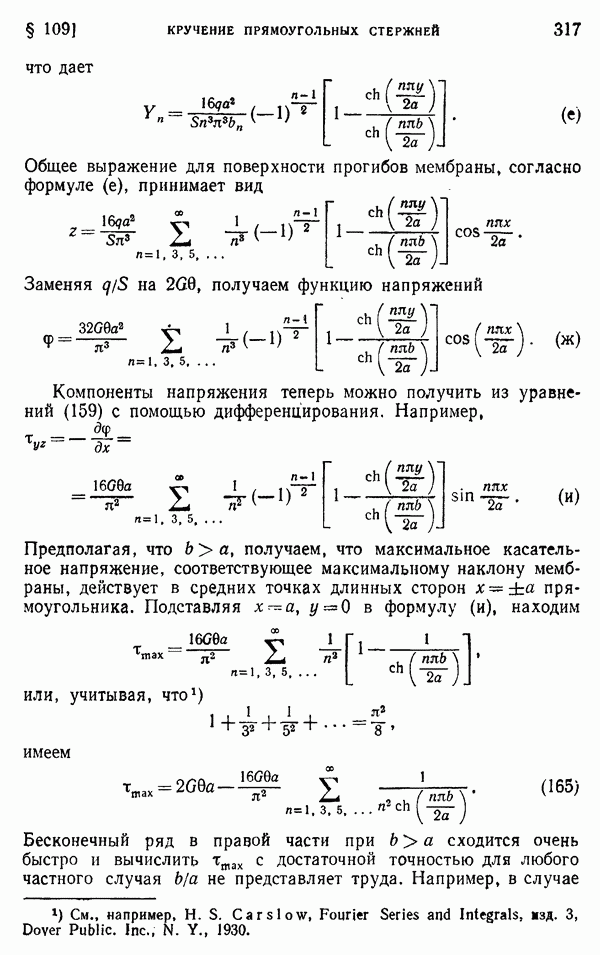
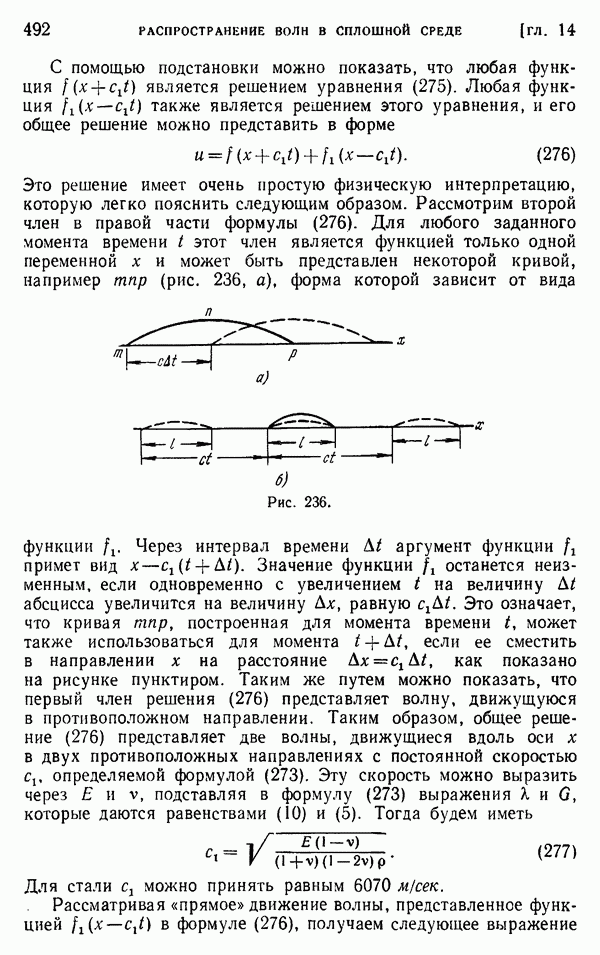
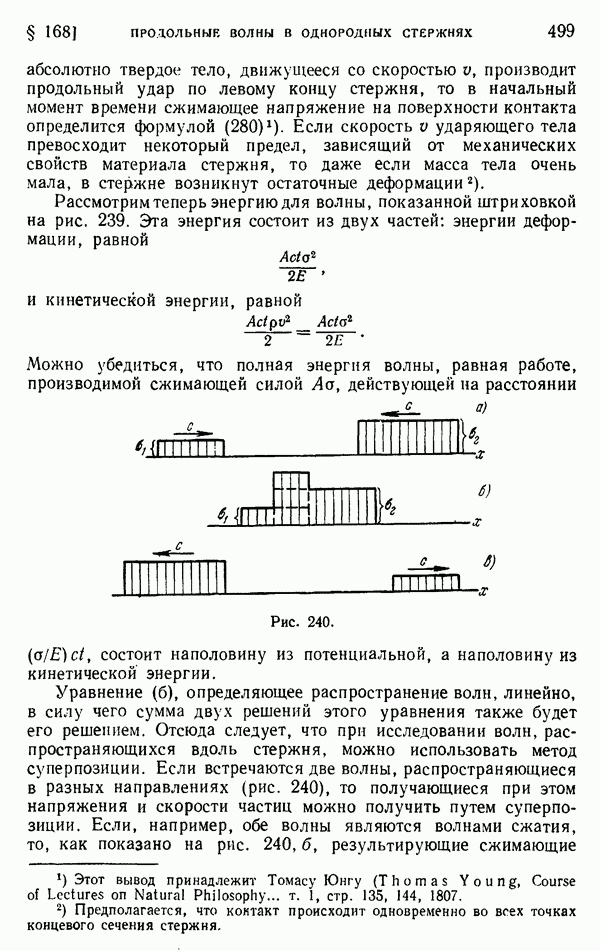
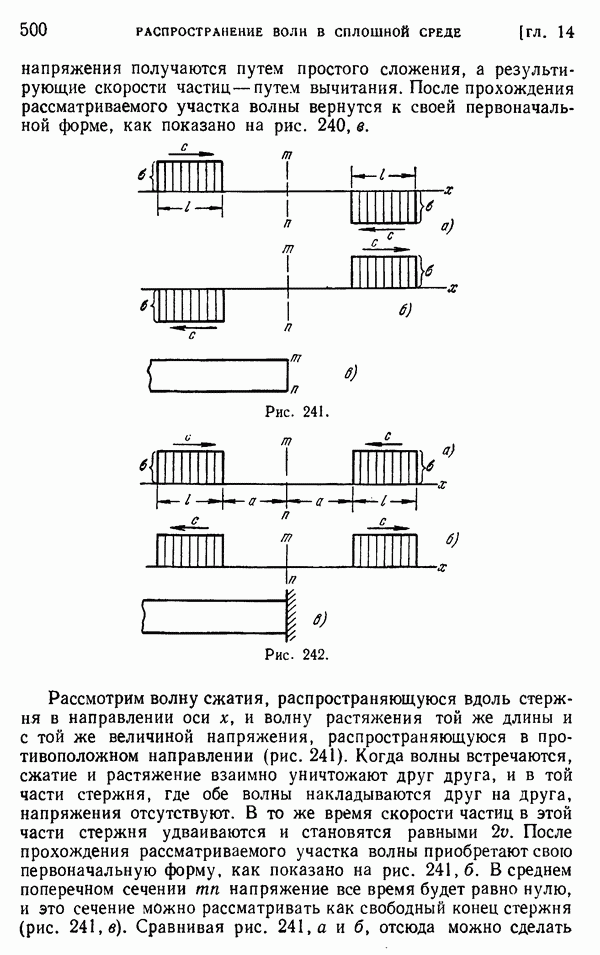
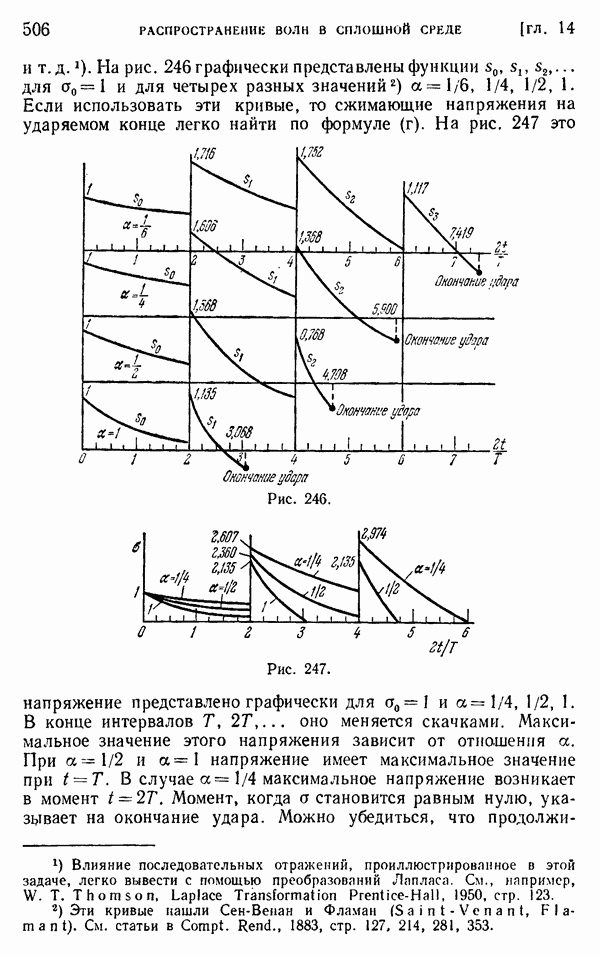
| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ОТ РЕДАКТОРА ПЕРЕВОДА
Превосходные руководства, написанные недавно скончавшимся выдающимся ученым, педагогом и инженером С. П. Тимошенко (1878—1972), охватывают почти все разделы механики твердого тела: техническую механику, сопротивление материалов, статику сооружений, теорию колебаний, теорию упругости, теорию пластинок и оболочек, теорию упругой устойчивости и историю развития механики деформируемых тел. Большинство этих книг на протяжении более полувека служат во всем мире основными пособиями по механике в высших технических учебных заведениях и настольными руководствами для инженеров и исследователей. Как правило, они многократно переиздавались и (в некоторых случаях при участии учеников С. П. Тимошенко) подвергались модернизации.
Успех этих книг, конечно, не случаен. Он тесно связан с многообразием интересов, широкой эрудицией и глубиной, которые характеризуют собственные научные изыскания С. П. Тимошенко.
Среди книг, написанных этим замечательным механиком, особое место по праву занимает «Курс теории упругости» в двух частях, основанный на лекциях, читавшихся им в Киевском политехническом институте (1907-1910 гг.) и в Петербургском
институте инженеров путей сообщения (1912 - 1914 гг.). Первая его часть (изданная в 1914 г.) была посвящена телам, все размеры которых имеют одинаковый порядок, а вторая (изданная в 1916 г.) - статике, устойчивости и колебаниям стержней и пластинок. В то время теория упругости излагалась преимущественно в университетских курсах и нередко трактовалась как раздел математической физики, вне связи с техническими приложениями. Блестящий курс С. П. Тимошенко был одним из первых руководств, предназначенных для нужд инженеров. Отказавшись от изложения ряда разделов, имеющих чисто теоретическое значение (теоремы существования и единственности, общие методы интегрирования, теория строения упругих тел и др.), автор сосредоточил внимание на прикладных вопросах: оценке пределов применимости элементарных решений сопротивления материалов, задачах, для которых неприменимы элементарные подходы (в частности, о концентрации напряжений в зонах резких изменений формы тела или распределения нагрузки), экспериментальных и приближенных аналитических способах исследования. В курсе нашли отражение и собственные интересные результаты автора. Книга эта и ныне не потеряла своего значения. Она была переиздана без изменений в 1972 г. и вновь получила высокую оценку.
Стремительное развитие техники ставит перед теорией упругости все новые задачи, и лицо ее непрерывно меняется. Естественно, что на протяжении последующих неполных шести десятилетий С. П. Тимошенко нашел необходимым неоднократно существенно перерабатывать и дополнять свой курс.
Впервые это было сделано в 1934 г., когда в США на английском языке была опубликована под заглавием «Теория упругости» сильно переработанная первая часть «Курса». Порядок изложения материала был изменен. Чтобы облегчить читателю усвоение материала, вначале подробно излагалась теория плоской задачи и лишь затем — трехмерная теория. Нашли отражение многие важные успехи в теории, достигнутые за прошедшее двадцатилетие. Заключительная глава была посвящена распространению волн в упругой среде. На основе второй части «Курса» С. П. Тимошенко написал три монографии: по теории
колебаний, по теории пластинок, и оболочек и по теории упругой устойчивости.
В дальнейшем «Теория упругости» перерабатывалась автором дважды. Ее второе издание было опубликовано в США в 1951, а третье — в 1970 г., причем в обоих случаях к этой работе был привлечен его ученик Дж. Н. Гудьер (1905-1969) - один из крупнейших в США специалистов по теории упругости, известный у нас как один из авторов книги «Упругость и пластичность» (изд-во «Иностранная литература», 1960), написанной им совместно с Ф. Г. Ходжем.
Подробные сведения об изменениях, внесенных в эти два переиздания книги, содержатся в предисловии авторов.
Предлагаемый перевод осуществлен с последнего американского издания 1970 г. Написанное еще в 1951 г. приложение к книге «Применение конечно-разностных уравнений в теории упругости» представляется теперь несколько неполным. Помимо него, в переводное издание включено приложение, посвященное методу конечных элементов. Оно написано переводчиком книги М. И. Рейтманом.
Перевод первого издания книги давно стал у нас библиографической редкостью. Появление предлагаемого современного руководства по теории упругости, предназначенного для инженеров, студентов технических учебных заведений и исследователей, заполнит имеющийся пробел в нашей литературе и будет, без сомнения, содействовать прогрессу технических приложений этой дисциплины.
Г. С. Шапиро
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
При подготовке этой книги для третьего издания сохранены первоначальные цель и план первого издания—дать инженерам существенные основы знаний по теории упругости в столь простой форме, какую позволяет этот предмет, вместе с набором решений частных задач, важных для инженерной практики и проектирования. Многочисленные ссылки в подстрочных примечаниях показывают читателю, как можно продолжить изучение некоторых вопросов. Поскольку теперь эти ссылки легко пополнить с помощью реферативного журнала Applied Mechanics Reviews, новые ссылки вводились очень экономно. Мелкий шрифт, как и прежде, используется для разделов, которые могут быть пропущены при первом чтении.
Весь текст был вновь просмотрен, и в него внесены незначительные изменения, как за счет исключения и перекомпоновки, так и путем добавления некоторых разделов.
Основные дополнения отразили развитие отдельных разделов, интерес к которым повысился со времени появления в 1951 г. второго издания. В главах 3 и 4 введен анализ влияния концов и теория собственных решений, связанных с принципом Сен-Ве-нана. Ввиду быстрого роста приложений дислокационных упругих решений в науке о поведении материалов, эти разрывные в смещениях решения излагаются более подробно (теория краевых и винтовых дислокаций в главах 4, 8, 9 и 12). К главе 5 добавлены вводные сведения о методе «муара» с иллюстрацией его применения на практике. Изложение понятия об энергии деформации и вариационных принципов проведено в трехмерном случае и включено в главу 9, что дало основу для новых разделов по термоупругости в главе 13. Обсуждение использования комплексных потенциалов для двумерных задач пополнено группой новых параграфов, основанных на хорошо известных теперь методах Н. И. Мусхелишвили. Этот подход несколько отличается
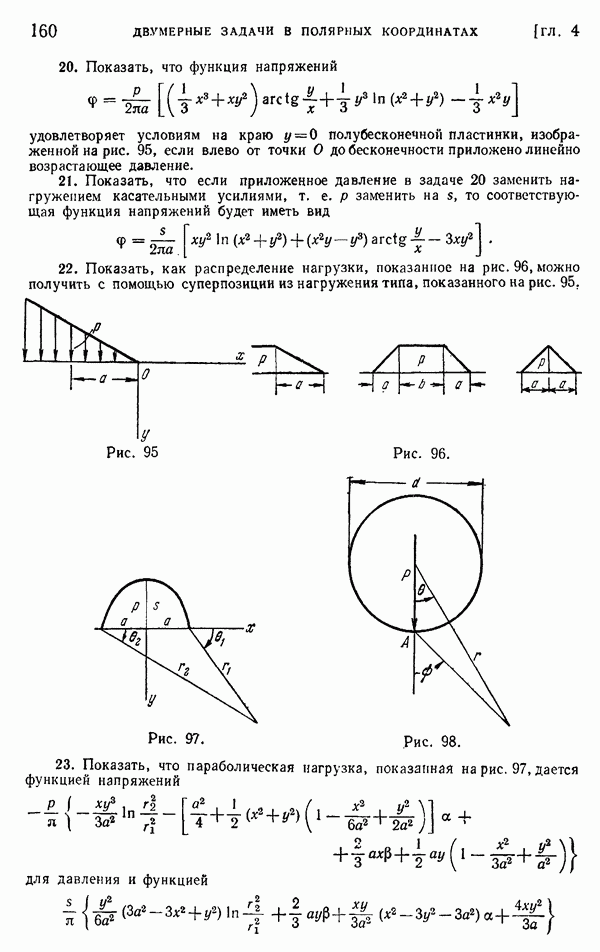
от прежнего, так как в нем используются преимущества решений, развитых ранее только для аналитических функций. Дано подробное изложение новых решений для эллиптического отверстия, которые важны в современной механике разрушения (теории трещин). Исследование осесимметричных напряжений в главе 12 упрощено, и добавлены новые разделы, в которых более приближенный анализ случая разрезанного кольца как одного витка спиральной пружины заменен более точной теорией. В силу значительного роста приложений, например в ядерной энергетике, глава 13 «Температурные напряжения» расширена за счет включения термоупругой теоремы взаимности и полученных из нее нескольких полезных результатов. Кроме того, исследование двумерных задач дополнено двумя заключительными параграфами, последний из которых устанавливает взаимосвязь двумерных задач термоупругости с комплексными потенциалами и методами Н. И. Мусхелишвили из главы 6. В главе 14, посвященной распространению волн, перестройка изложения придала больше значения основам трехмерной теории. Добавлено также решение для действия взрывного давления в сферической полости. Приложение, посвященное численному методу конечных разностей, включает пример использования ЭВМ для решения задачи с большим числом неизвестных.
Некоторые из упомянутых изменений, позволяющих упростить анализ, возникли в процессе преподавания курса в Стэнфордском университете за последние двадцать лет. Много полезных предложений, поправок и даже целиком сформулированных задач с решениями исходят от многочисленных студентов и читателей. Всем им приносится самая искренняя признательность за их неоценимую помощь.
Почти все задачи заимствованы из экзаменационных билетов, предлагаемых на экзаменах в Стэнфордском университете. Отсюда читатель может примерно оценить, какая часть книги соответствует учебному курсу, занимающему несколько меньше трех часов в неделю в течение академического года.
Дж. Н. Гудьер
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Многочисленные уточнения и успехи, которые достигнуты в теории упругости и ее приложениях со времени выхода первого издания, отражены во многих добавлениях и изменениях, помещенных в настоящем издании. В то же время построение книги большей частью остается прежним.
Разделы, касающиеся метода фотоупругости, двумерных задач в криволинейных координатах и температурных напряжений, расширены и выделены в отдельные новые главы, содержащие многие методы и решения, которых не было в прежнем издании. Добавлено приложение, относящееся к методу конечных разностей, в том числе к методу релаксации. Новые параграфы, включенные в другие главы, относятся к теории розетки датчиков деформаций, гравитационным напряжениям, принципу Сен-Венана, компонентам вращения, теореме взаимности, общим решениям, приближенному характеру решений при плоском напряженном состоянии, центру кручения и центру изгиба, концентрации напряжений при кручении вблизи закруглений, приближенному исследованию тонкостенных сечений (например, авиационных) при кручении и изгибе, а также к круговому цилиндру при действии пояскового давления.
Добавлены также задачи для студентов, охватывающие материал книги вплоть до конца главы о кручении.
Нам доставляет удовольствие выразить большую признательность читателям книги, которые внесли много полезных предложений.
С. П. Тимошенко, Дж. Н. Гудьер
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
В течение последних лет теория упругости нашла широкое применение при решении инженерных задач. Существует много случаев, когда элементарные методы сопротивления материалов оказываются непригодными для того, чтобы дать удовлетворительную информацию о распределении напряжений в инженерных конструкциях; тогда приходится прибегать к более совершенным методам теории упругости. Элементарная теория недостаточна, чтобы составить представление о местных напряжениях вблизи зон приложения нагрузок и вблизи опор балок. Равным образом она не может дать удовлетворительное объяснение в тех случаях, когда исследуется распределение напряжений в телах, все размеры которых представляют собой величины одного и того же порядка. Напряжения в роликах и шариках подшипников можно найти, только используя методы теории упругости. Элементарная теория не дает также способа исследования напряжений в местах резкого изменения поперечного сечения балок или валов. Известно, что во входящих углах наблюдается высокая концентрация напряжений. В результате этого именно там прежде всего начинают возникать трещины, особенно если конструкция подвергается действию знакопеременных напряжений. Большинство эксплуатационных поломок деталей машин можно отнести за счет этих трещин.
За последние годы в решении таких практически важных задач были достигнуты значительные успехи. В тех случаях, когда получить точное решеиие затруднительно, были развиты приближенные методы. В некоторых случаях решения были получены с помощью экспериментальных методов. В качестве примера можно назвать метод фотоупругости для решения двумерных задач теории упругости. Приборы для применения методов фото-, упругости можно теперь найти как в университетах, так и во многих промышленных испытательных лабораториях. Результаты
исследований методами фотоупругости оказались особенно полезными при изучении различных случаев концентрации напряжений в местах резкого изменения поперечных сечений и у закруглений малого радиуса на входящих углах. Без сомнения эти результаты оказали значительное влияние на современное конструирование деталей машин и способствовали во многих случаях улучшению конструкции путем устранения слабых мест, от которых могли бы начинаться трещины.
Другим примером успешного приложения экспериментов при решении задач теории упругости является метод мыльной пленки для определения напряжений при кручении и изгибе призматических стержней. Трудная проблема решения дифференциальных уравнений в частных производных при заданных граничных условиях заменяется в этом случае измерениями наклонов и прогибов соответствующим образом натянутой и нагруженной мыльной пленки. Эксперименты показывают, что таким путем можно получить не только визуальную картину распределения напряжений, но и приобрести необходимую информацию относительно величины напряжений с точностью, достаточной для практи- ческих целей.
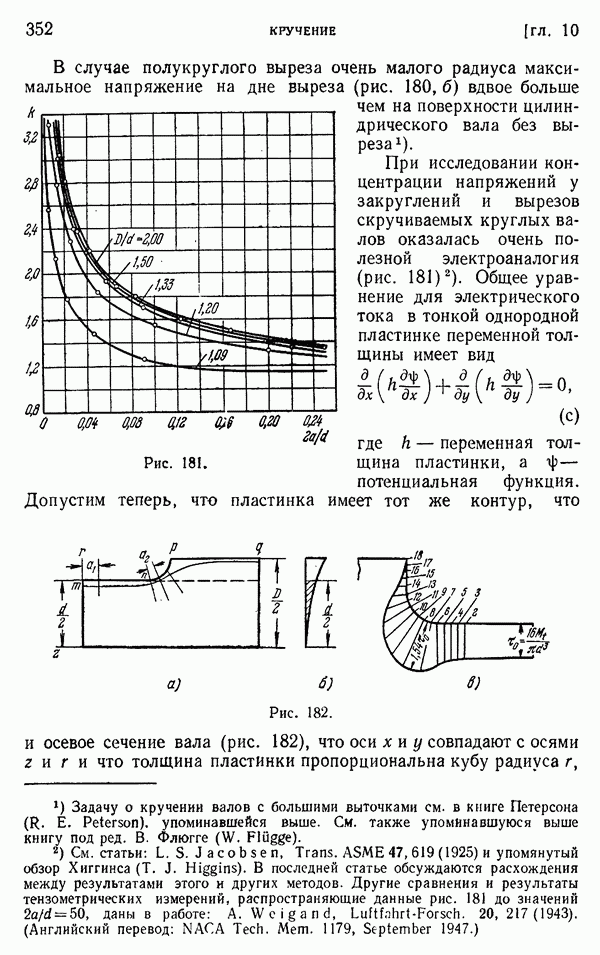
Далее представляет интерес электроаналогия, которая дает способ исследования напряжений при кручении в валах переменного диаметра у закруглений и вырезов. Аналогия между задачей изгиба пластинок и плоской задачей теории упругости также может с успехом использоваться при решении важных технических задач.
При подготовке этой книги ставилась цель дать инженерам в доступной форме необходимые основные сведения по теории упругости. Кроме того, имелось в виду дать сводку решений частных задач, представляющих практический интерес, и описать приближенные и экспериментальные методы решения задач теории упругости.
Имея в виду практические приложения теории упругости, автор не останавливается на вопросах, которые представляют преимущественно теоретический интерес и не находят в настоящее время применения в технике, чтобы уделить большее внимание рассмотрению конкретных задач. Только на основе подробного изучения таких задач и сравнения результатов точных
исследований с приближенными решениями, которые обычно излагаются в элементарных курсах сопротивления материалов, проектировщик может добиться полного понимания распределения напряжений в инженерных конструкциях и научится успешно использовать более точные методы анализа напряжений.
При рассмотрении частных задач в большинстве случаев применяется метод прямого определения напряжений с использованием уравнений совместности деформаций в напряжениях. Этот метод более привычен для инженеров, которые обычно интересуются величиной напряжений. При введении соответствующим образом подобранной функции напряжений этот метод, кроме того, является часто более простым, чем использование уравнений равновесия в перемещениях.
Во многих случаях в книге применяется также энергетический метод решения задач теории упругости. При этом интегрирование дифференциальных уравнений заменяется исследованием условия минимума некоторых интегралов. При помощи метода Ритца эта задача вариационного исчисления сводится к простой задаче отыскания минимума функции. Таким способом удается получить приближенные решения во многих практически важных случаях.
Чтобы упростить изложение, книга начинается с рассмотрения двумерных задач, и лишь после того как читатель освоится с различными методами, используемыми при решении задач теории упругости, рассматриваются трехмерные задачи. Те части книги, которые, хотя и имеют практическое применение, но при первом чтении могут быть пропущены, набраны мелким шрифтом. Читатель может вернуться к изучению таких задач, овладев более существенными разделами книги.
Математические выводы приведены в элементарной форме и обычно не требуют больших математических знаний, чем даются в высших технических учебных заведениях. В случаях изложения более сложных задач приводятся все необходимые объяснения и промежуточные выкладки, чтобы читатель мог без затруднений следить за ходом вывода. Лишь в нескольких случаях приведены окончательные результаты без полных выводов. Но при этом всегда даются необходимые ссылки на литературу, в которой эти выводы можно найти.
В многочисленных примечаниях даются ссылки на статьи и книги по теории упругости, которые могут иметь практическое значение. Эти ссылки могут представить практический интерес для тех инженеров, которые пожелают более детально изучить некоторые частные вопросы. Они дают также картину современного развития теории упругости и могут быть полезны студентам старших курсов, которые собираются работать в этой области науки.
При подготовке данной книги автор широко пользовался книгой «Курс теории упругости», часть 1, издание Института инженеров путей сообщения, С.-Петербург, 1914, по тому же предмету, которая представляет собой курс лекций по теории упругости, читавшийся в нескольких русских высших технических учебных заведениях.
Автору в его работе помогли д-р Л. Доннел и д-р Дж. Н. Гудьер, которые прочли всю рукопись; автор признателен им за многочисленные исправления и предложения. Автор пользуется возможностью выразить также благодарность проф. Дж. Г. Маккелафу, д-ру Э. Э. Вейбелю, проф. М. Садовскому и Д. Г. Юнгу, которые помогли при окончательной подготовке книги, прочитав некоторые части рукописи. Автор благодарен также Л. С. Венстра за изготовление чертежей и Э. Д. Вебстер за печатание рукописи.
С. П. Тимошенко
| Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
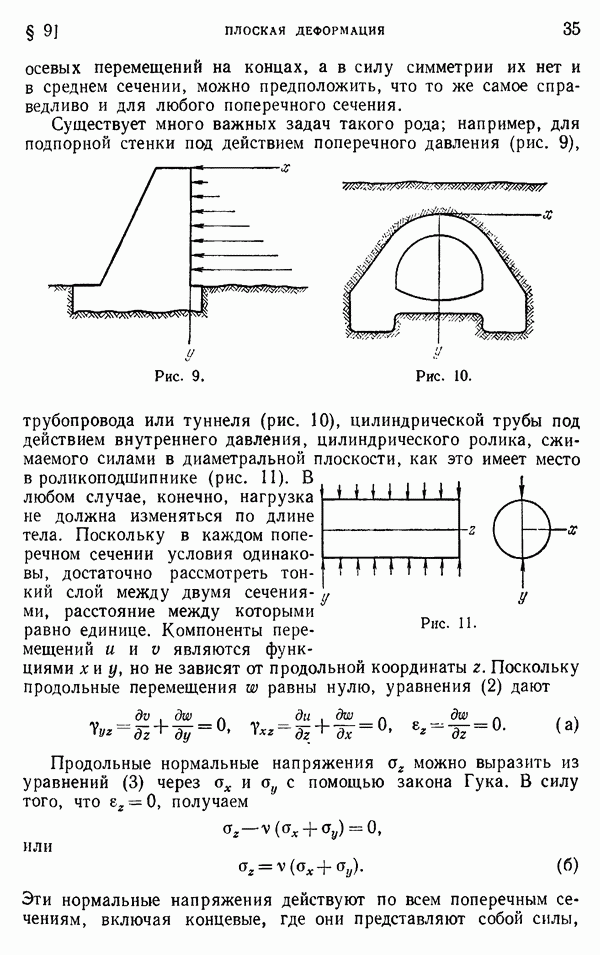
- § 9. Плоская деформация
- § 10. Напряжения в точке
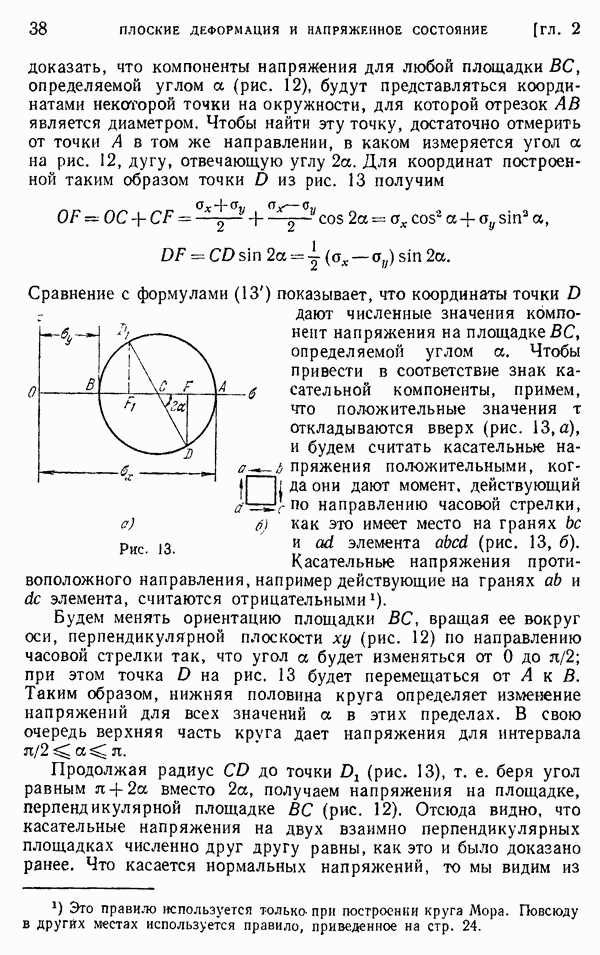
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
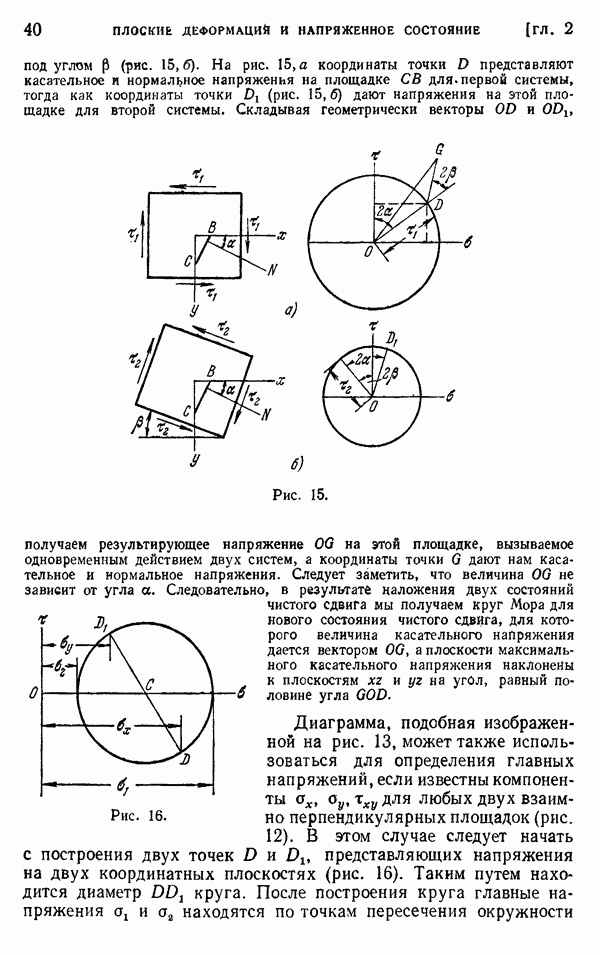
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
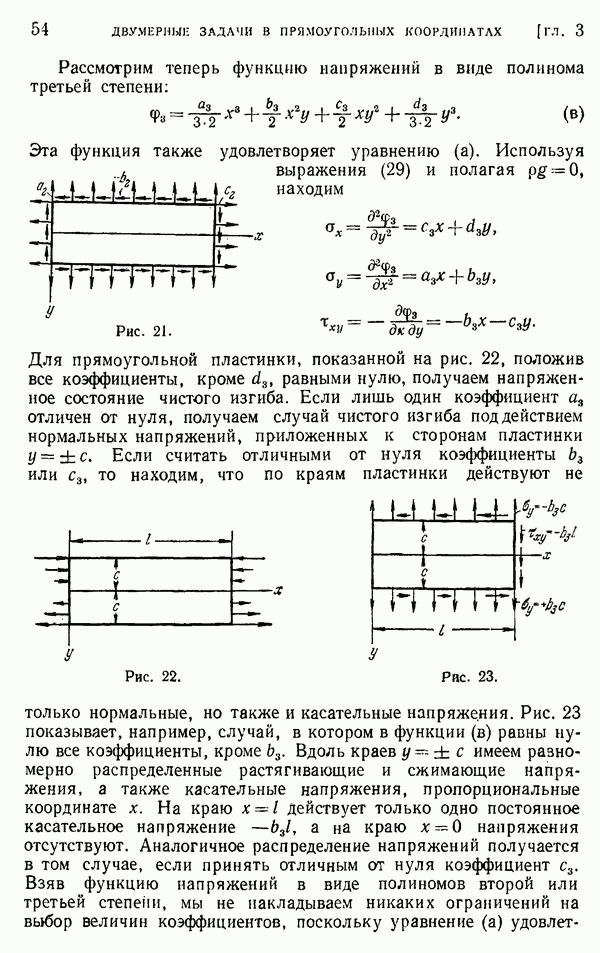
- § 22. Изгиб балки равномерной нагрузкой
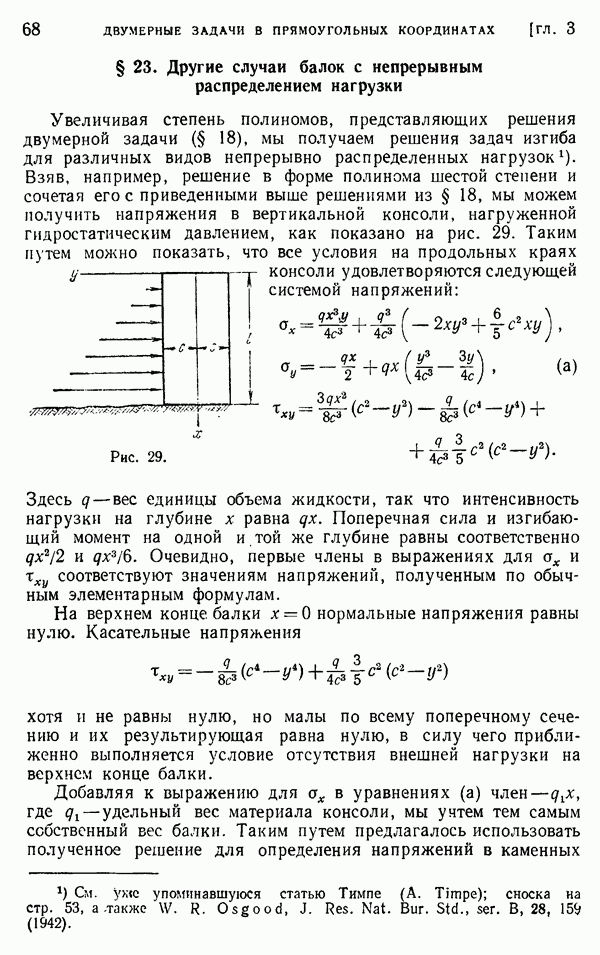
- § 23. Другие случаи балок с непрерывным распределением нагрузки
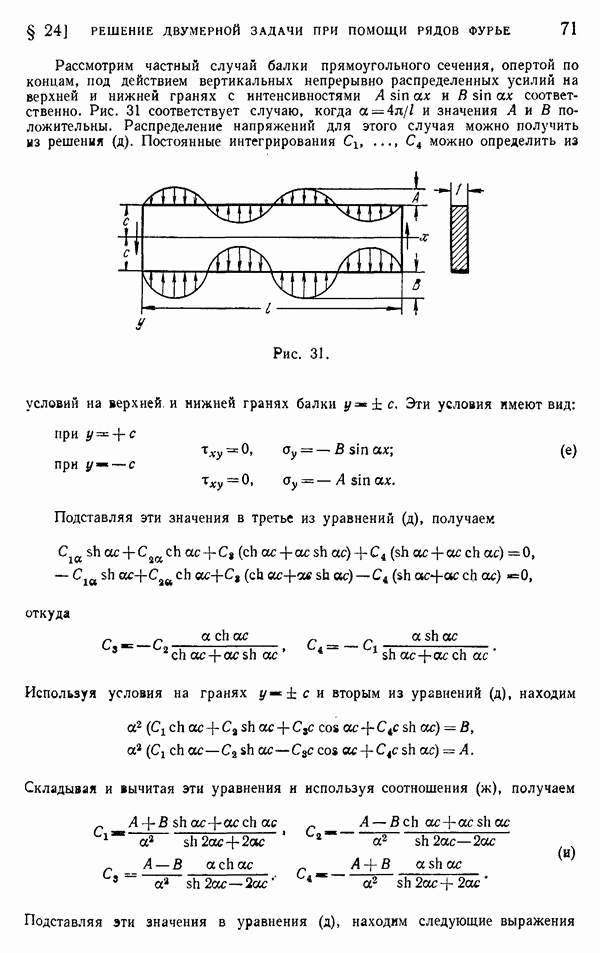
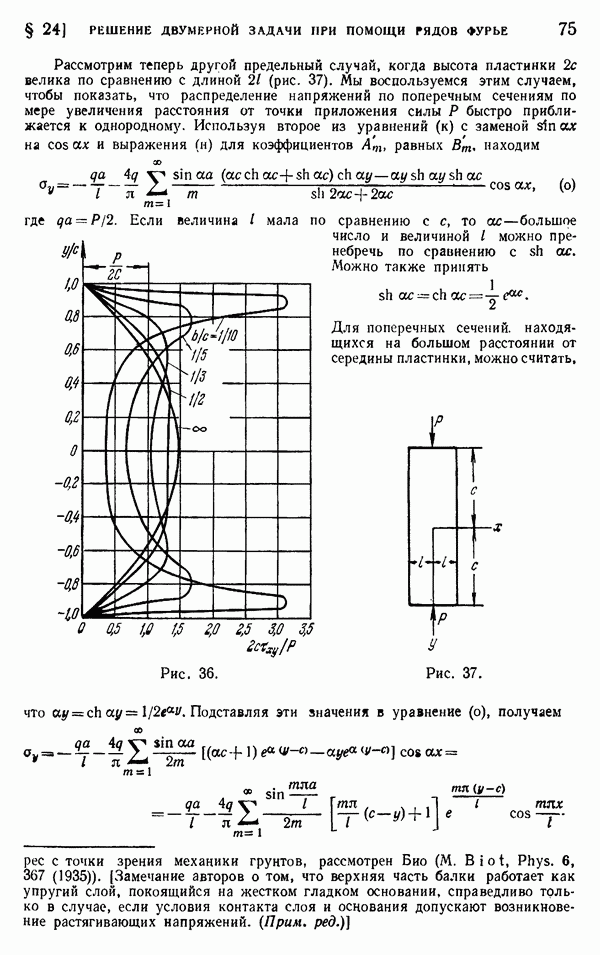
- § 24. Решение двумерной задачи при помощи рядов Фурье
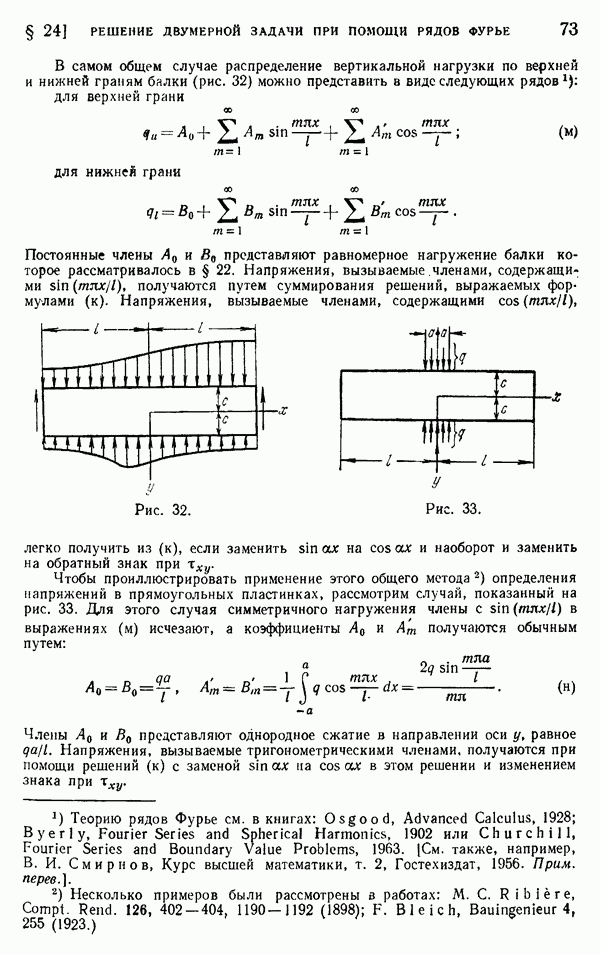
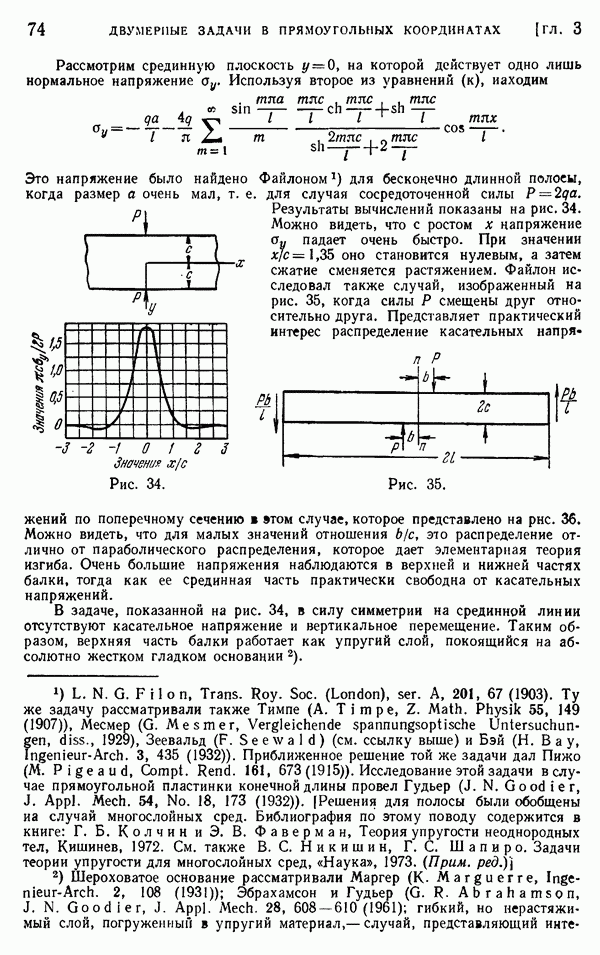
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
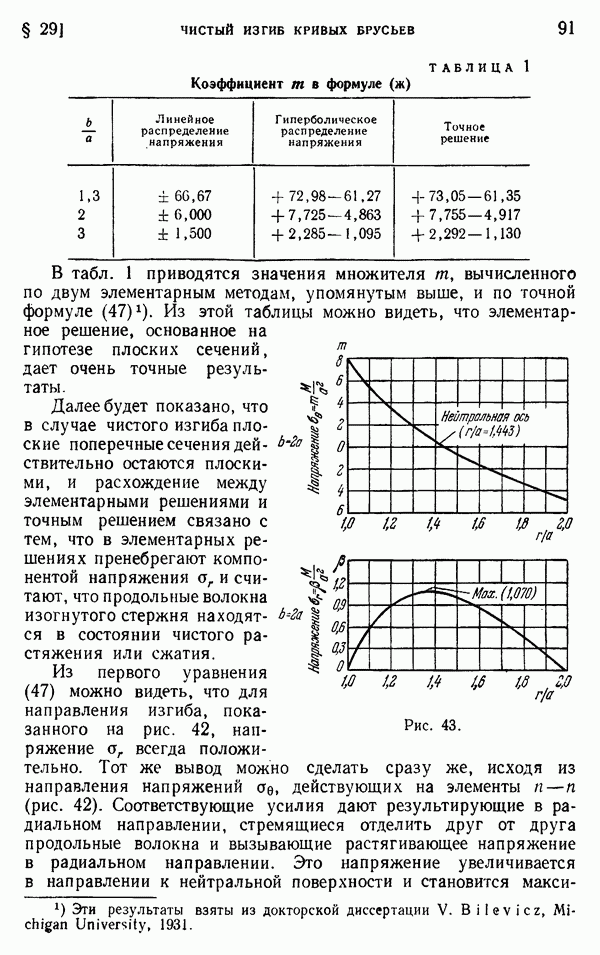
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
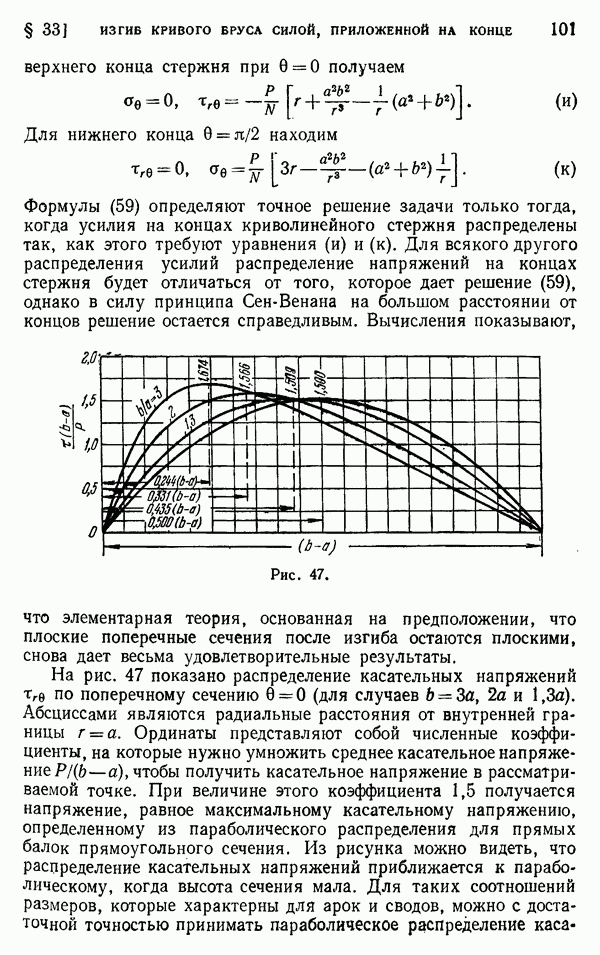
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
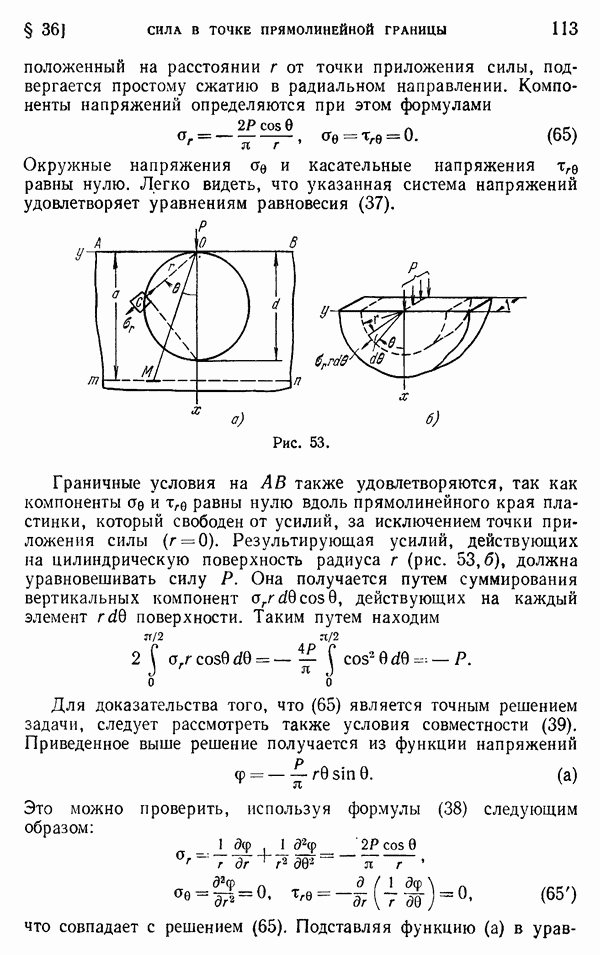
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
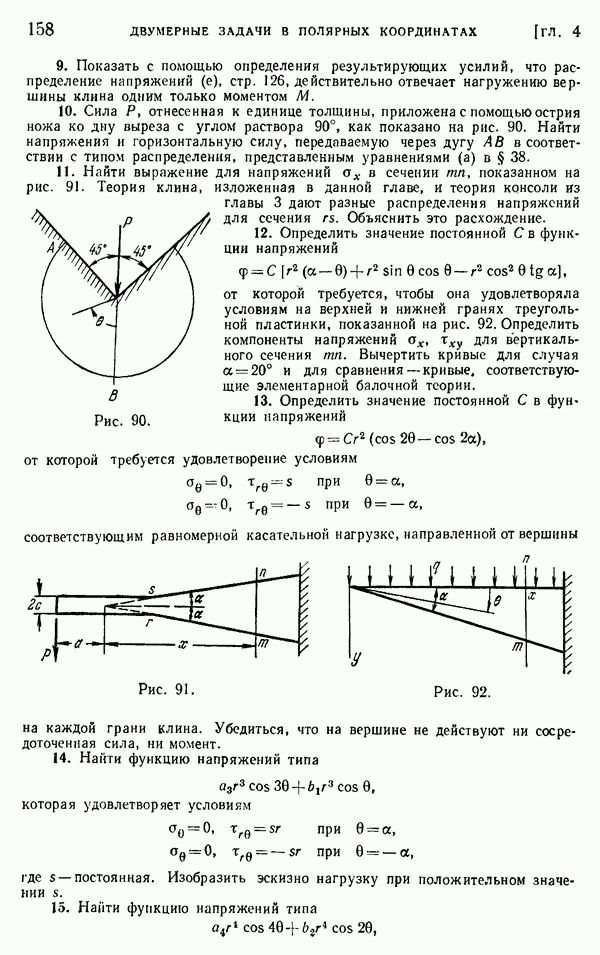
- § 39. Изгибающий момент, действующий на острие клина
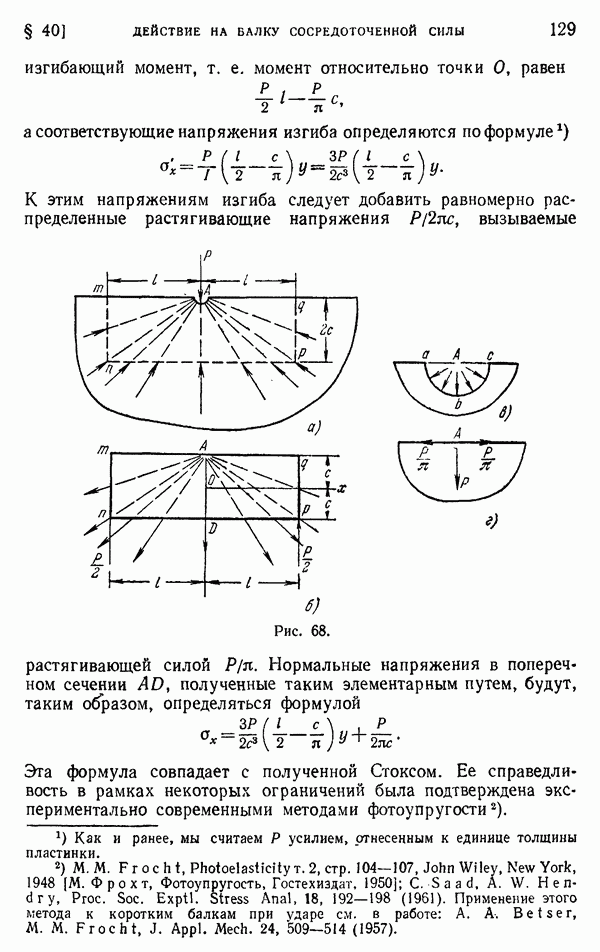
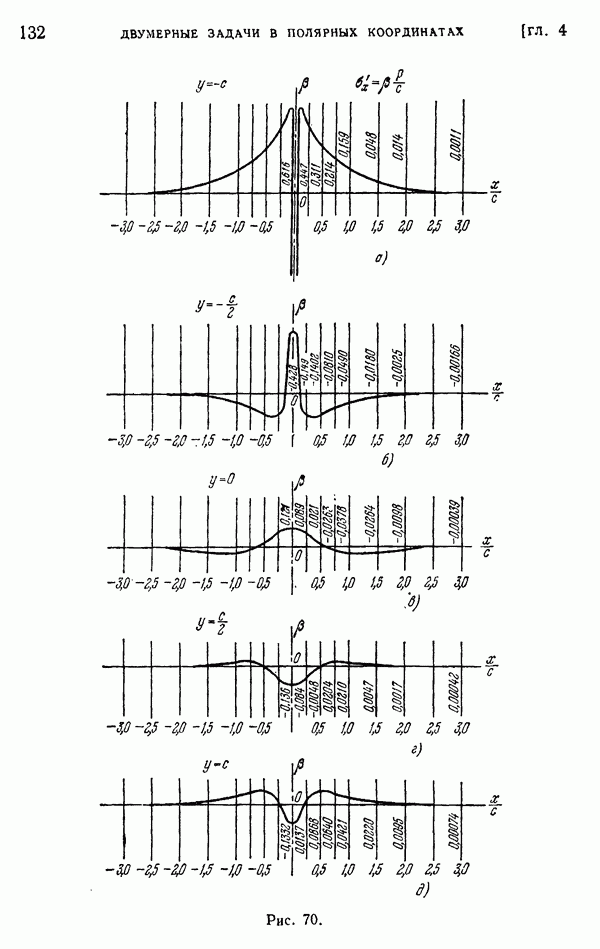
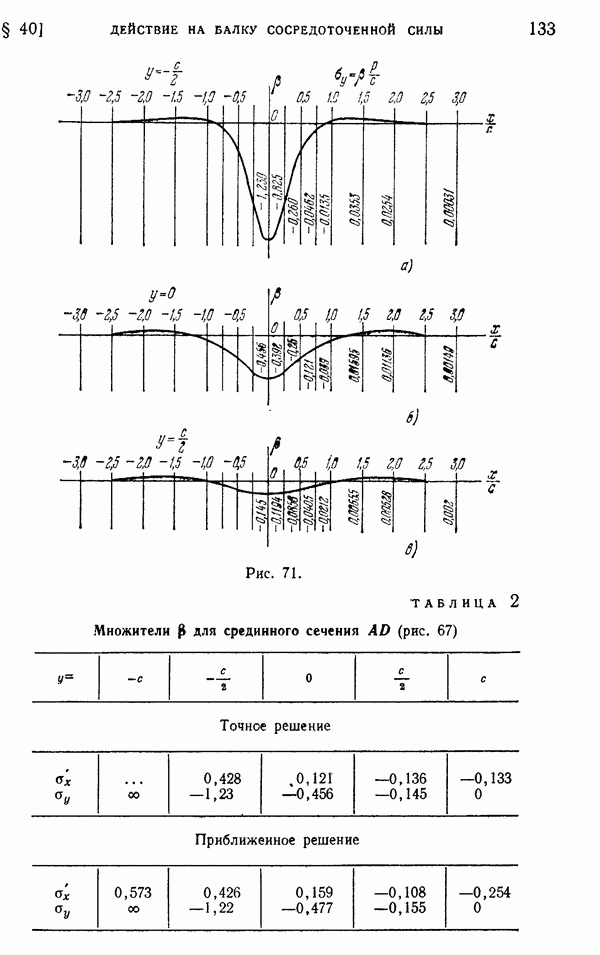
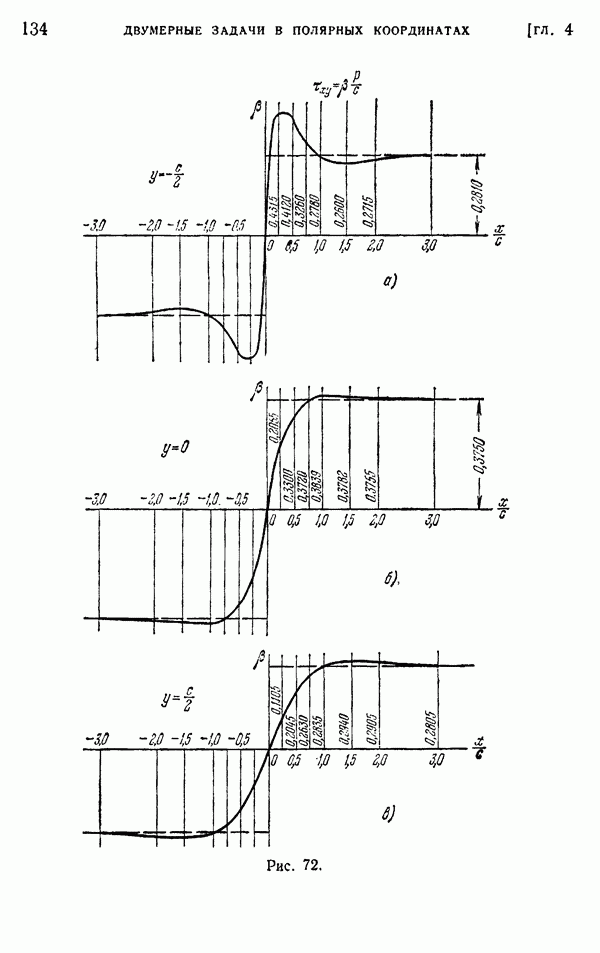
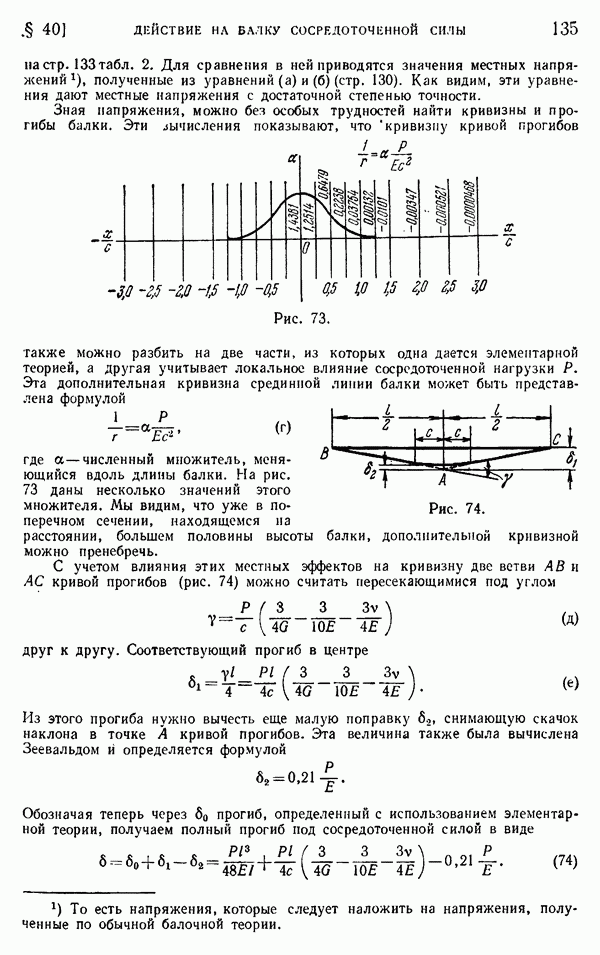
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
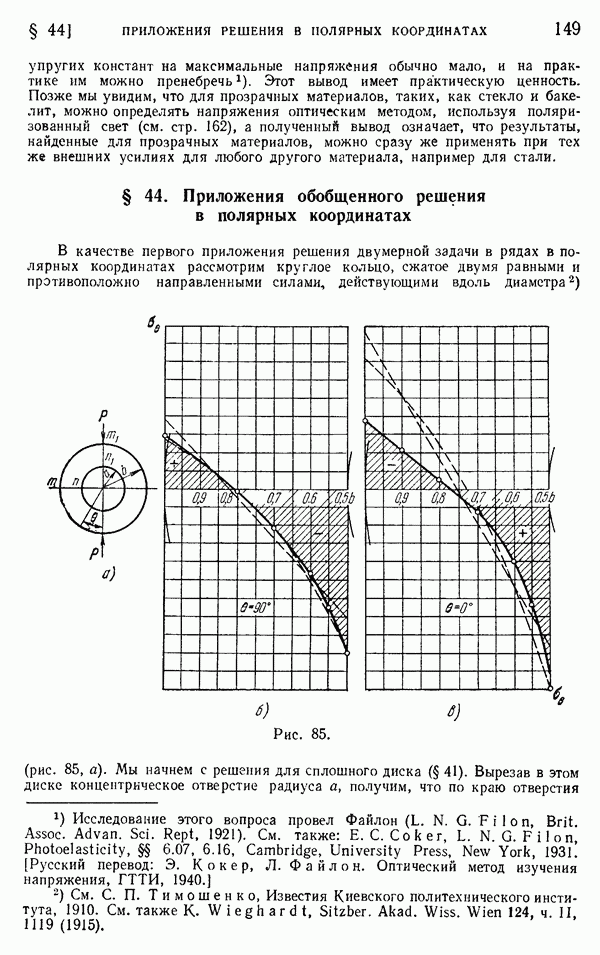
- § 44. Приложения обобщенного решения в полярных координатах
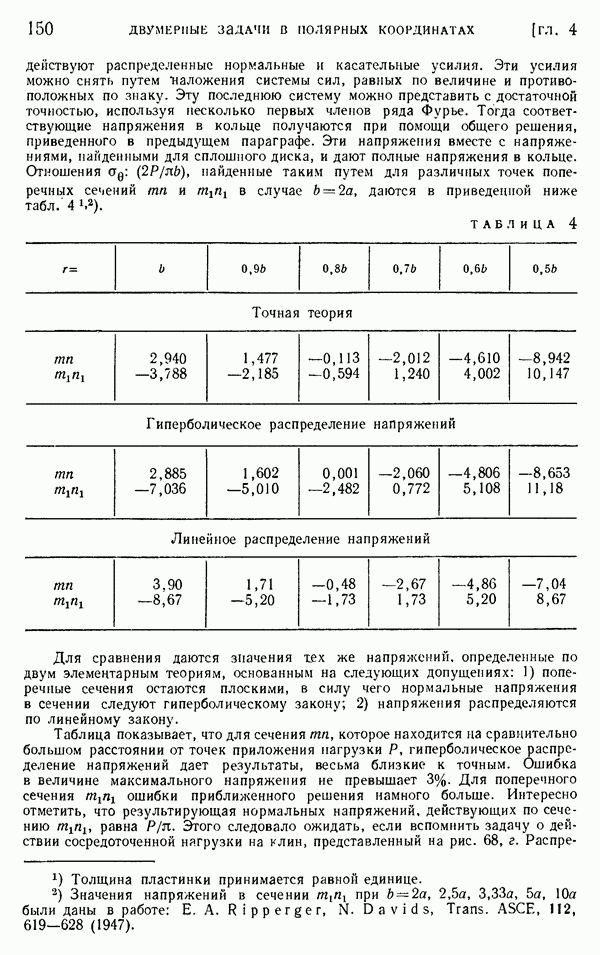
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
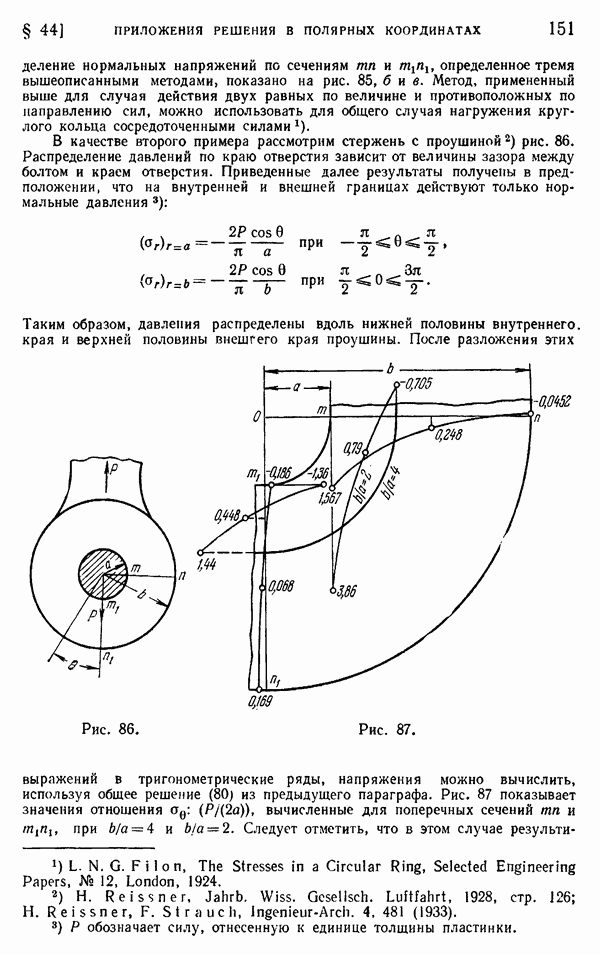
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
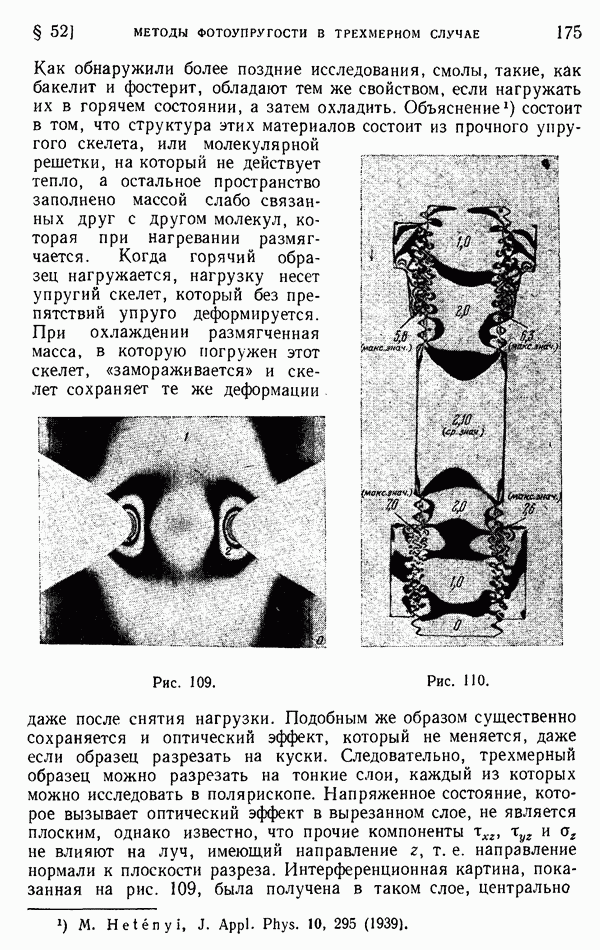
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
- § 52. Методы фотоупругости в трехмерном случае
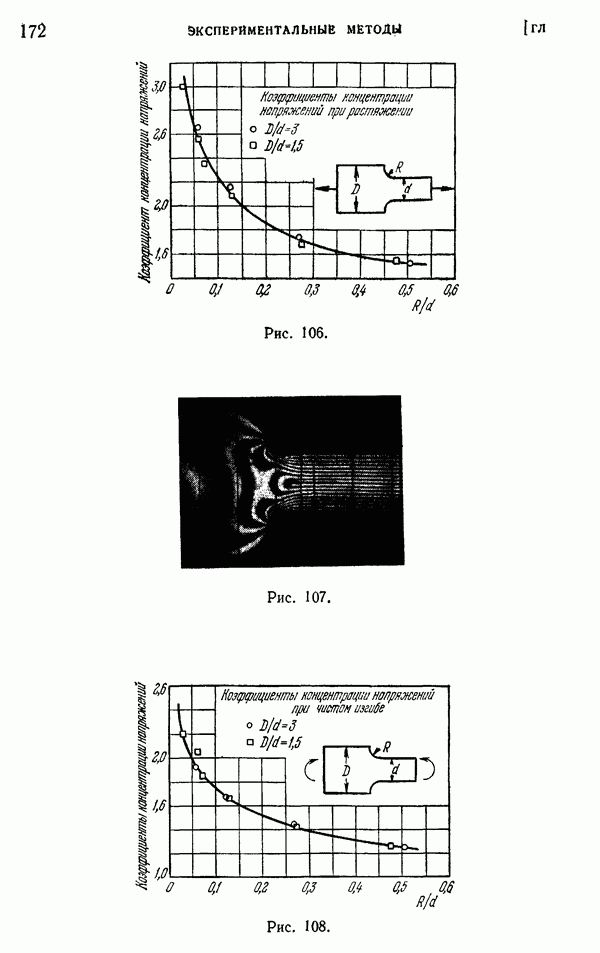
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
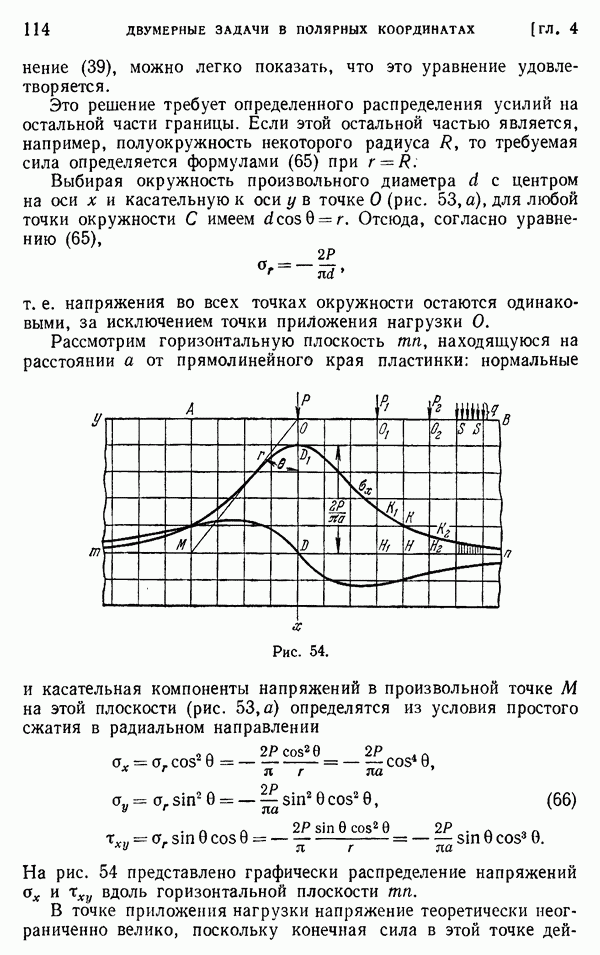
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
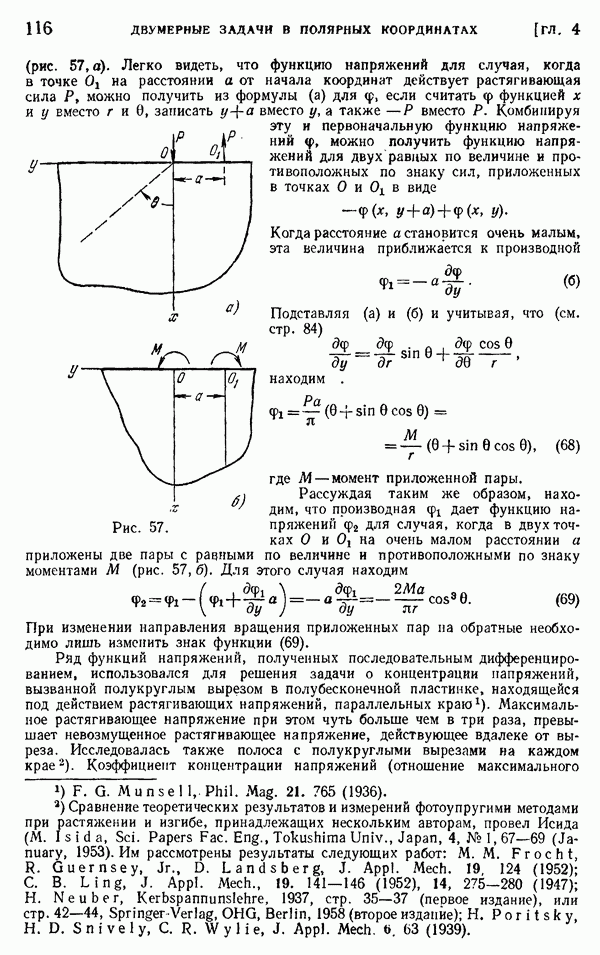
- § 64. Гиперболические границы. Вырезы
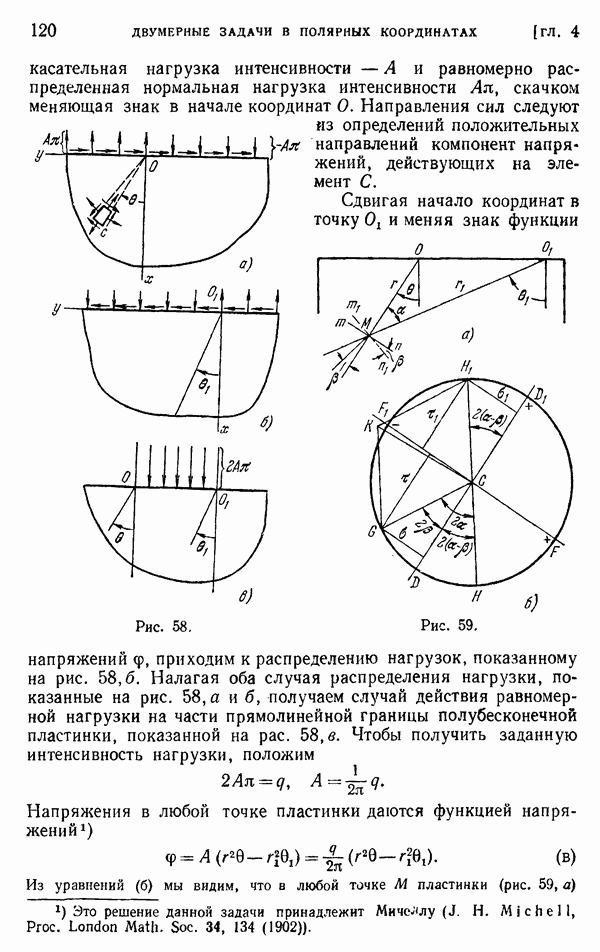
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
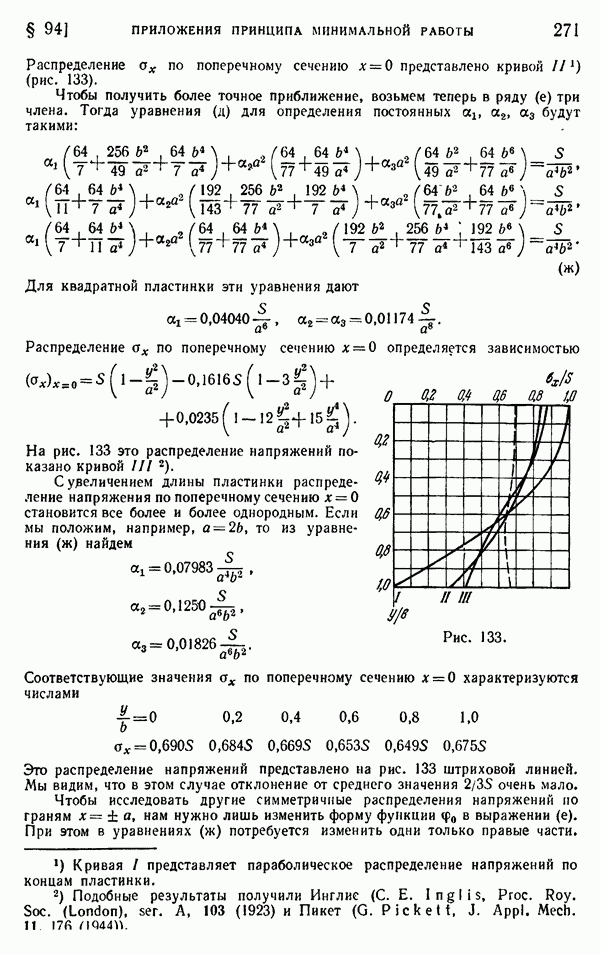
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
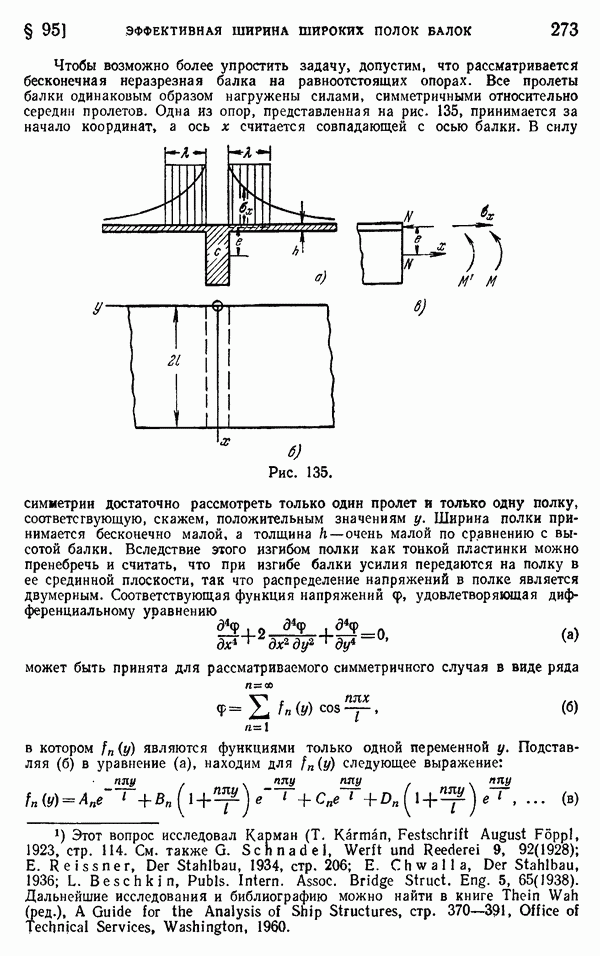
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
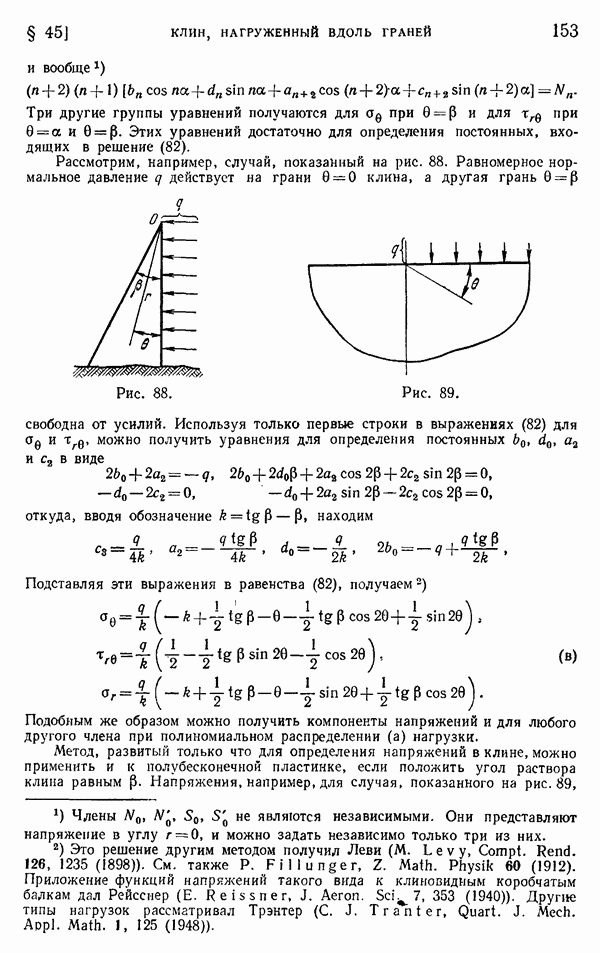
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
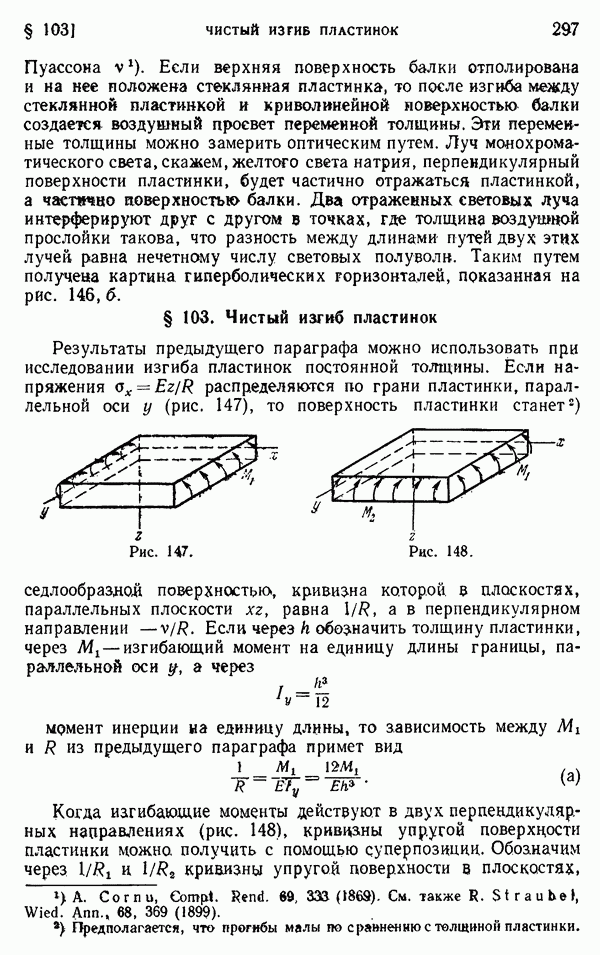
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
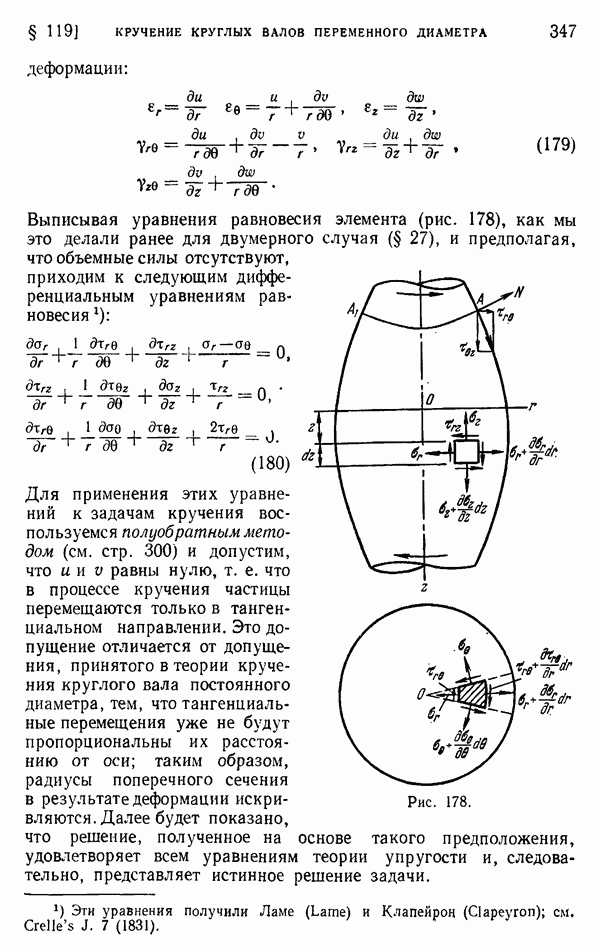
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
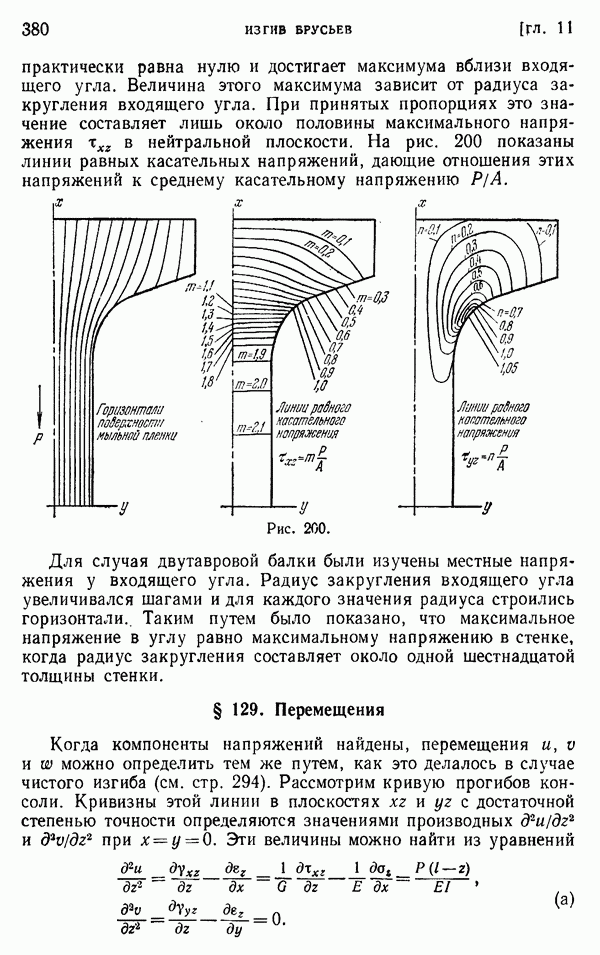
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
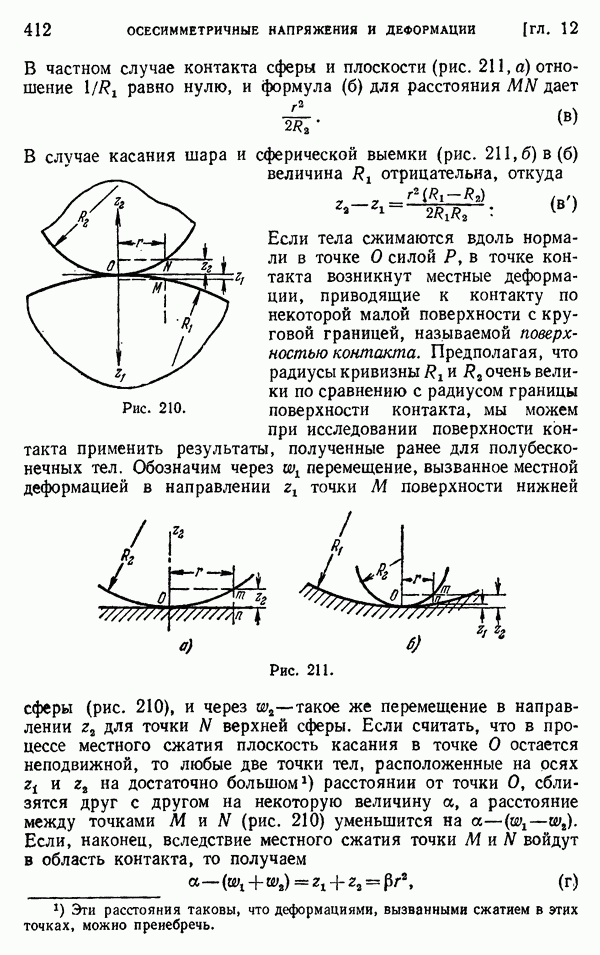
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
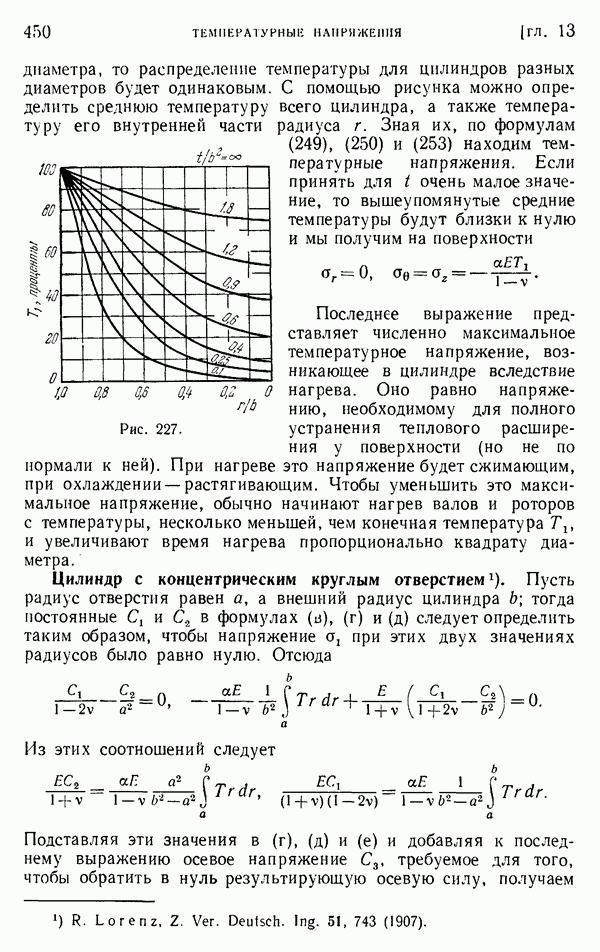
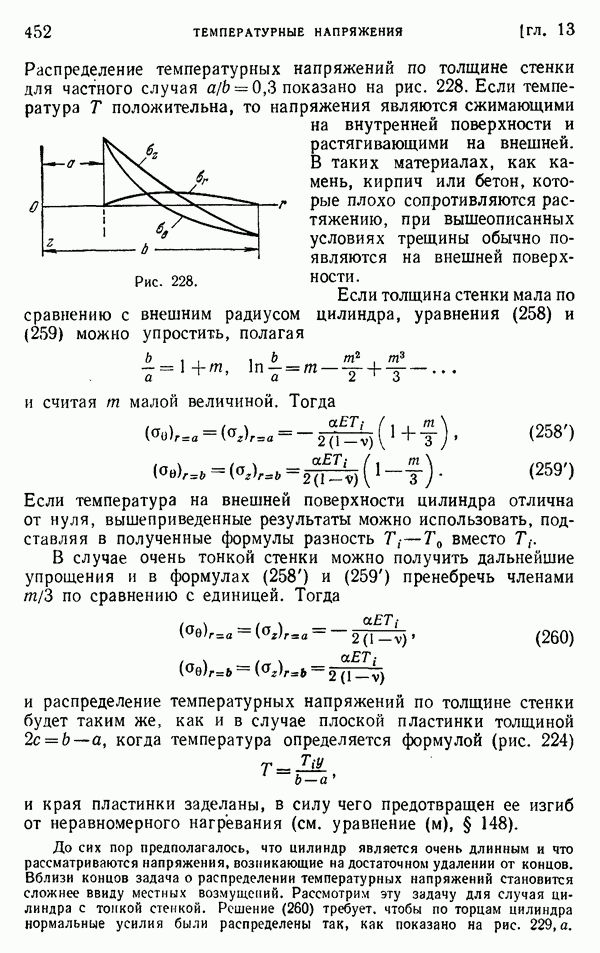
- § 144. Круглый цилиндр под действием опоясывающего давления
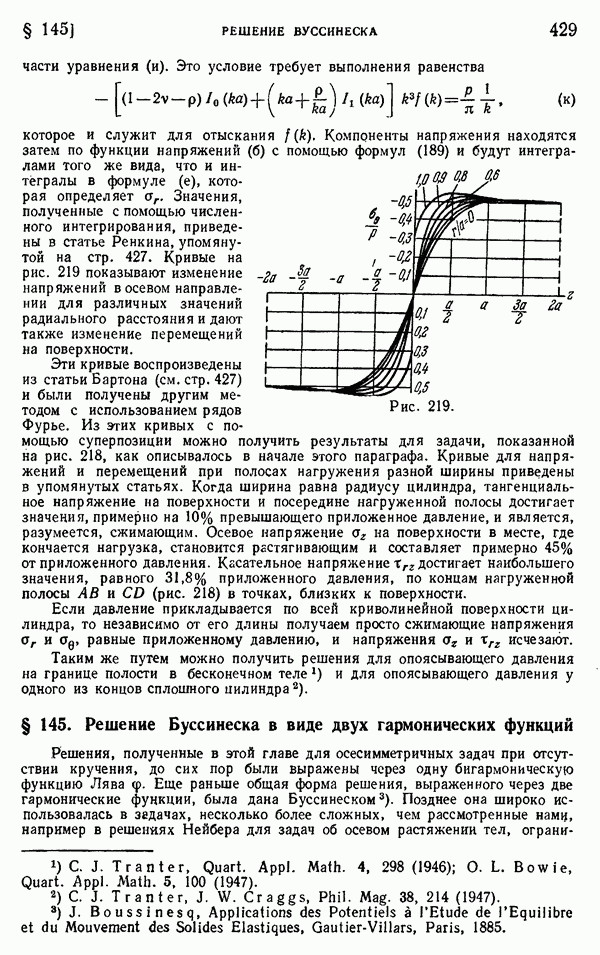
- § 145. Решение Буссинеска в виде двух гармонических функций
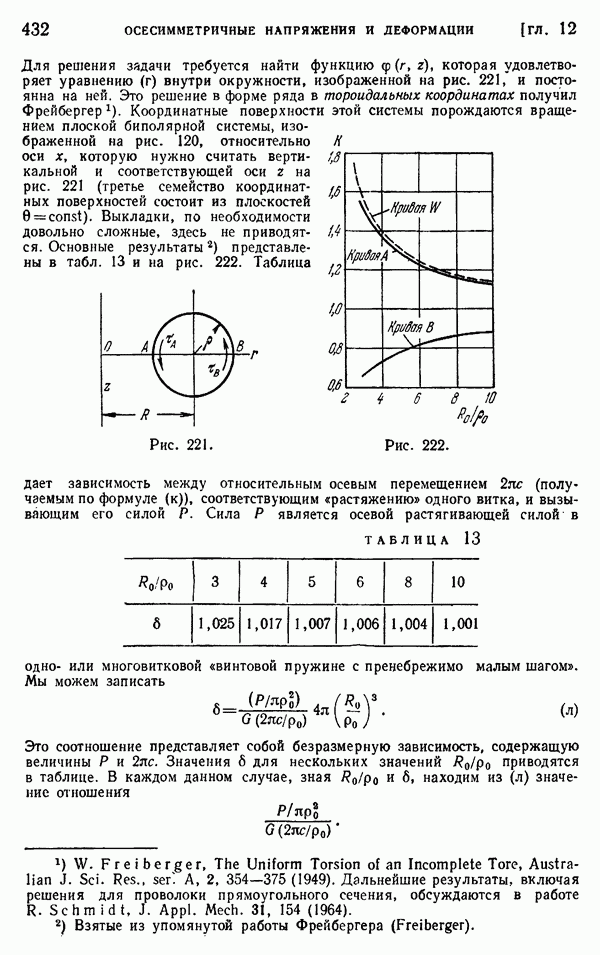
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
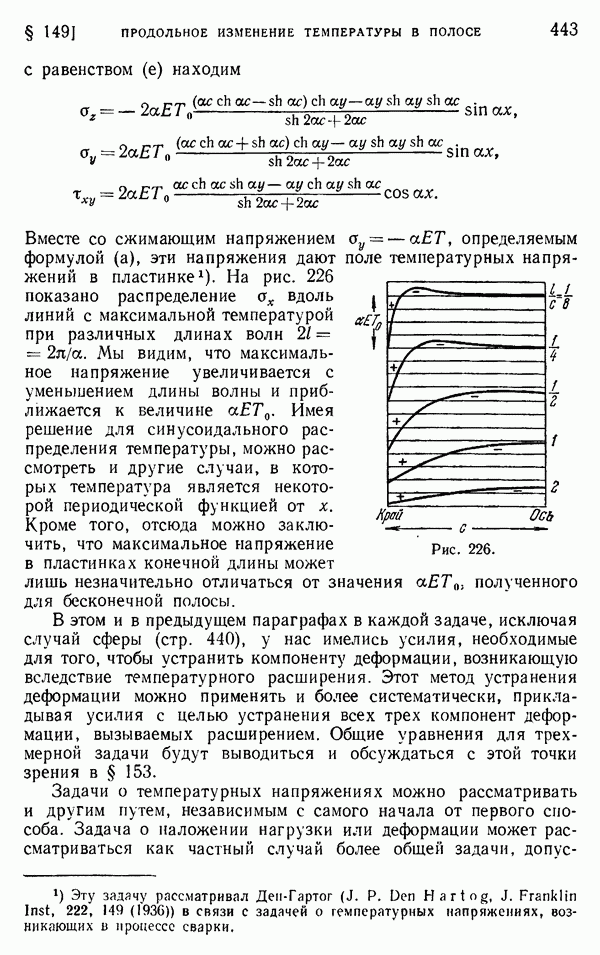
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
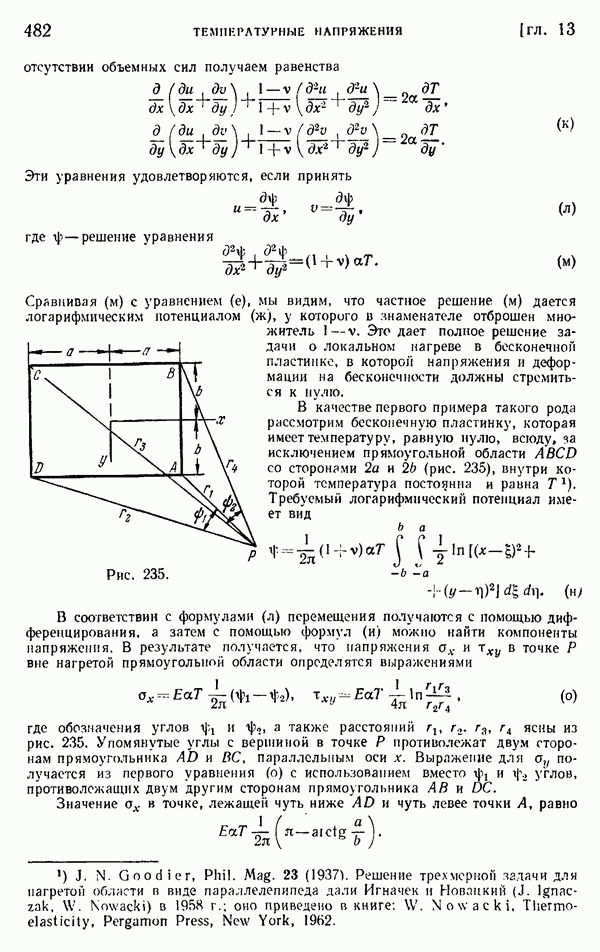
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
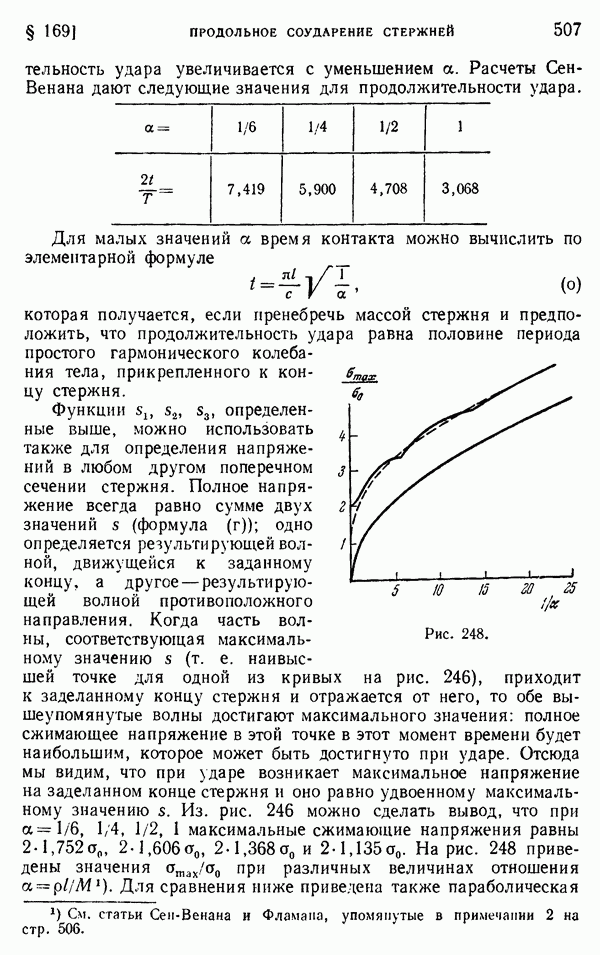
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
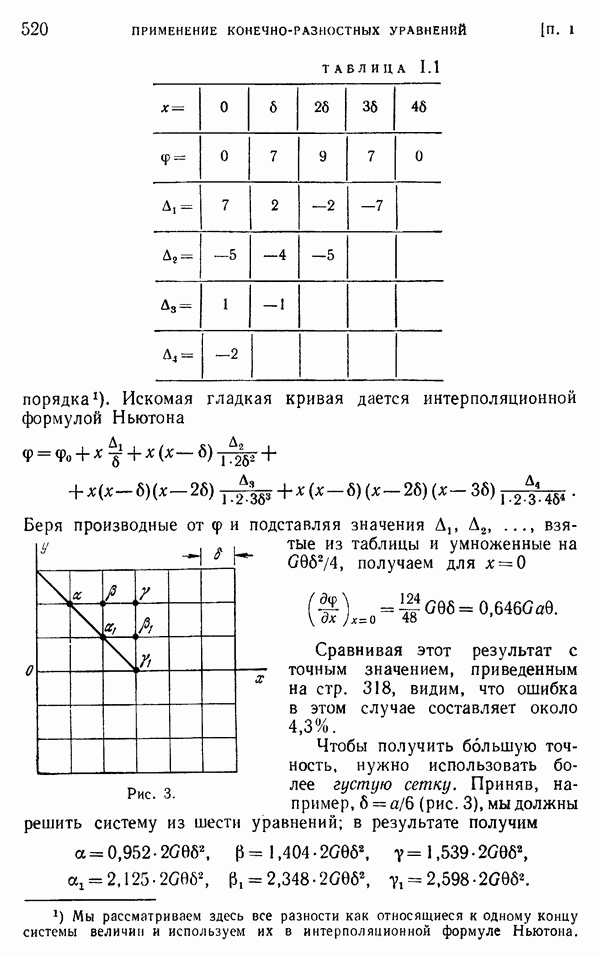
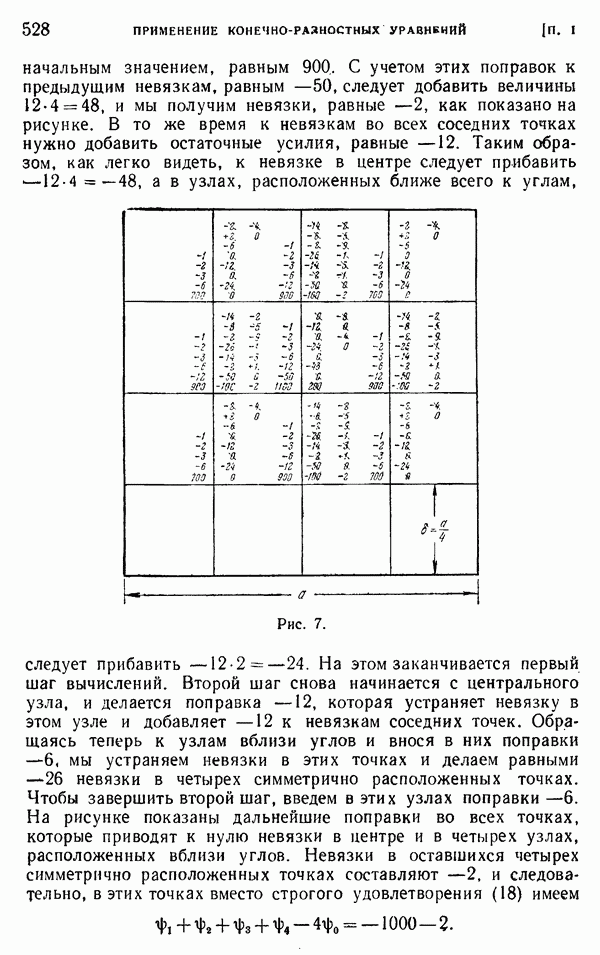
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
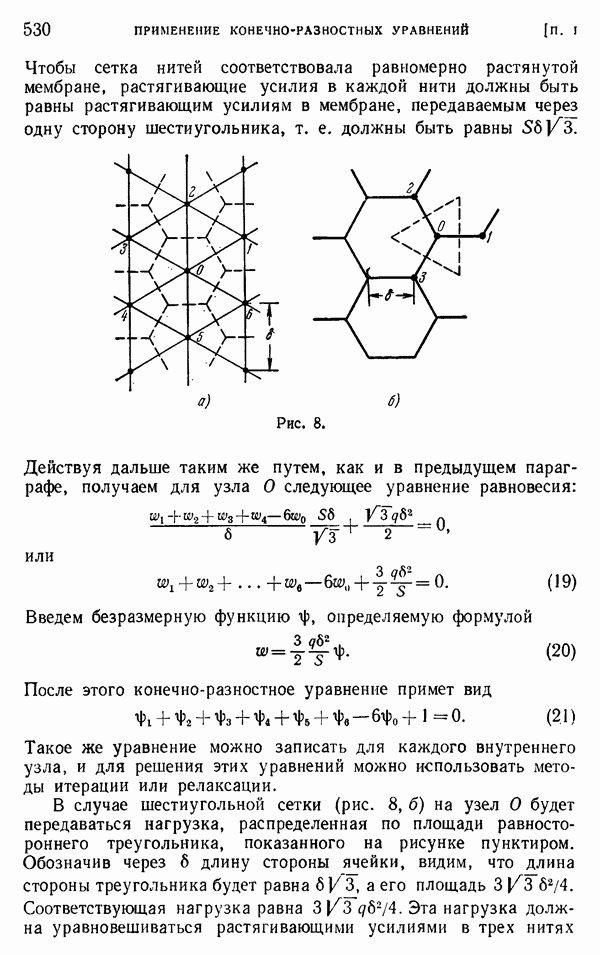
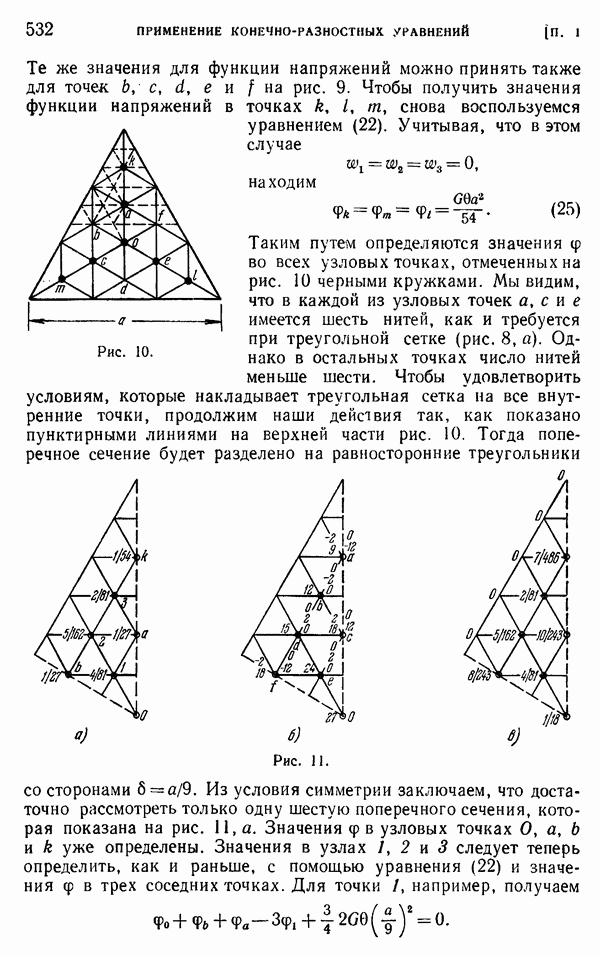
- § 4. Треугольные и шестиугольные сетки
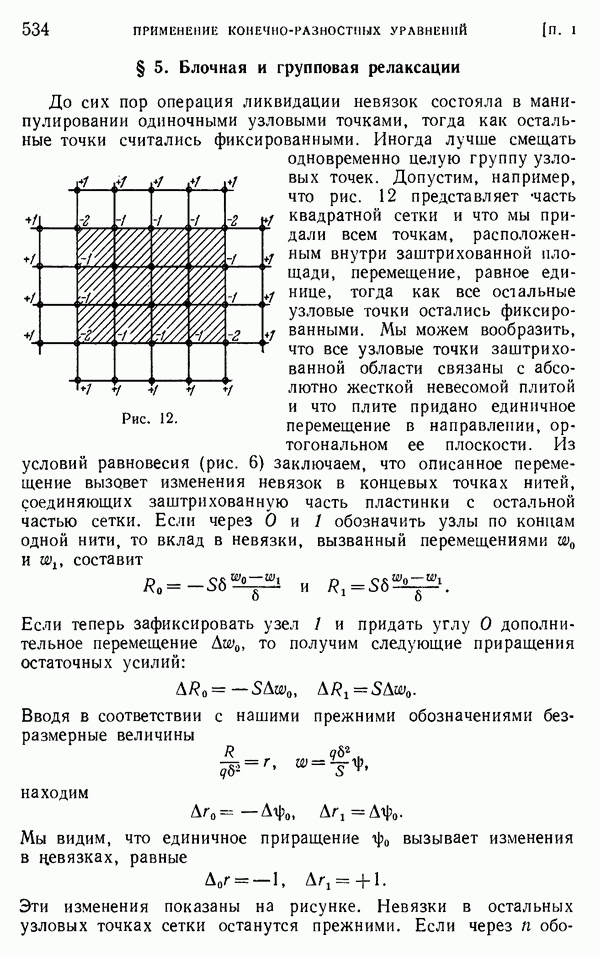
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
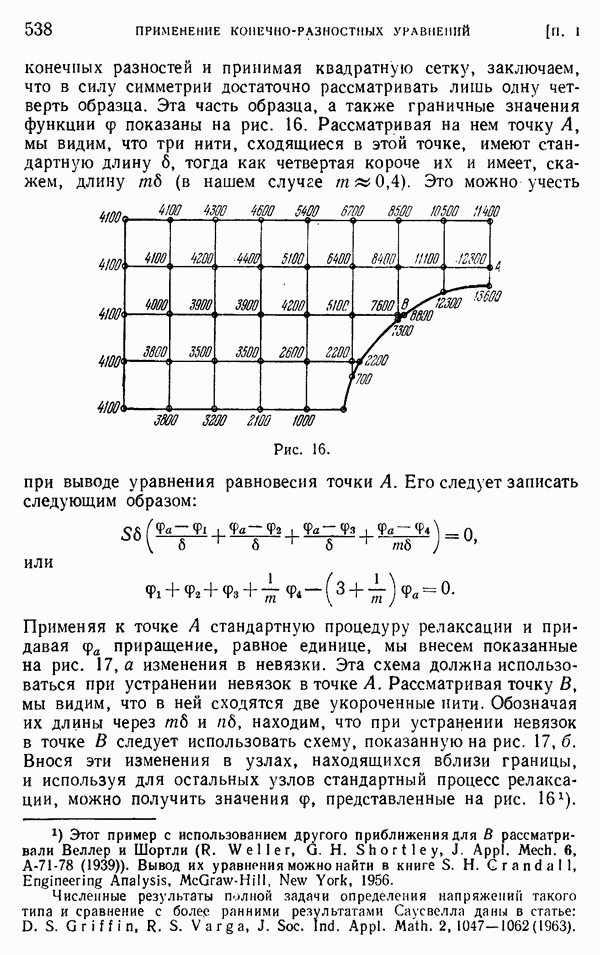
- § 7. Точки, расположенные вблизи границы
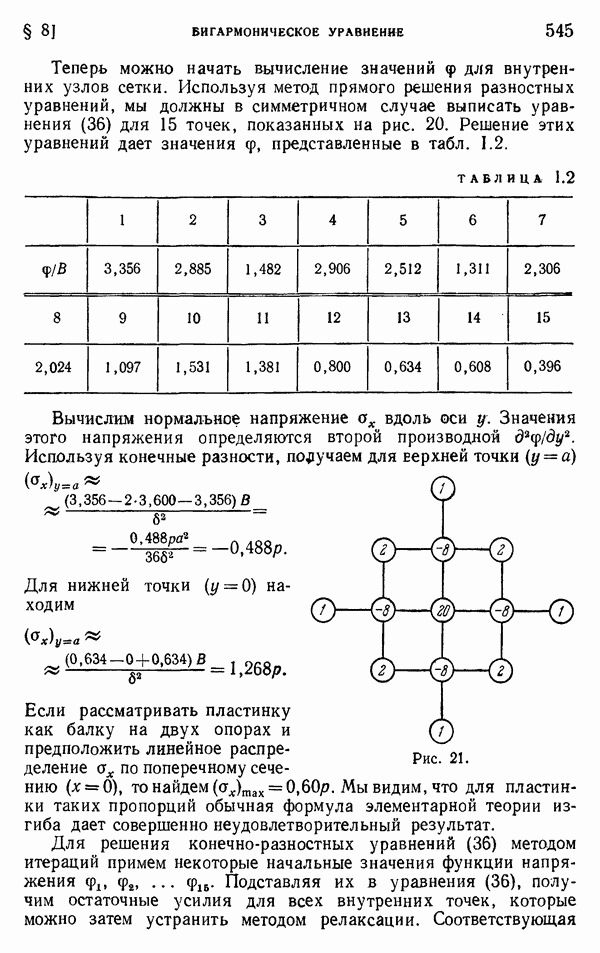
- § 8. Бигармоническое уравнение
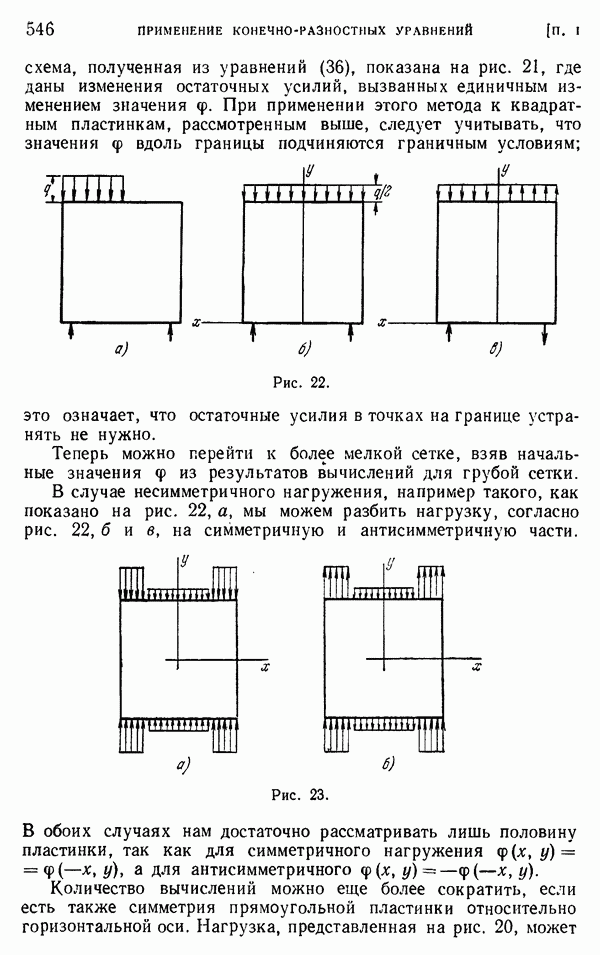
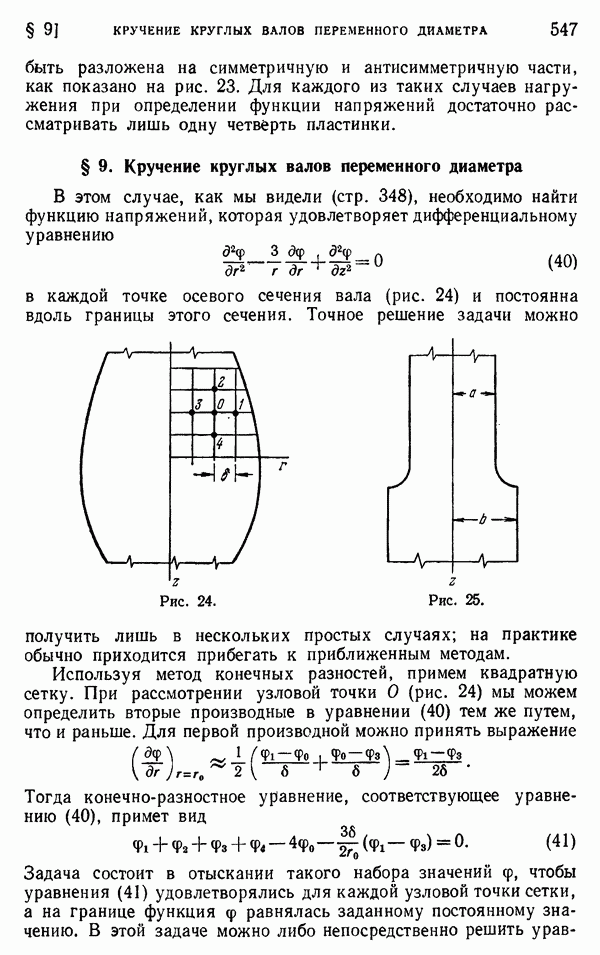
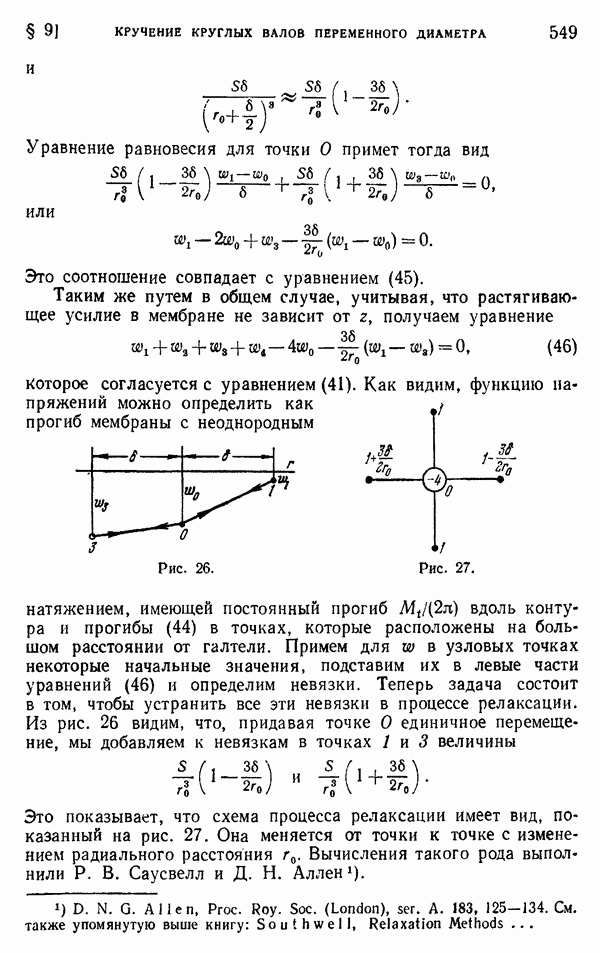
- § 9. Кручение круглых валов переменного диаметра
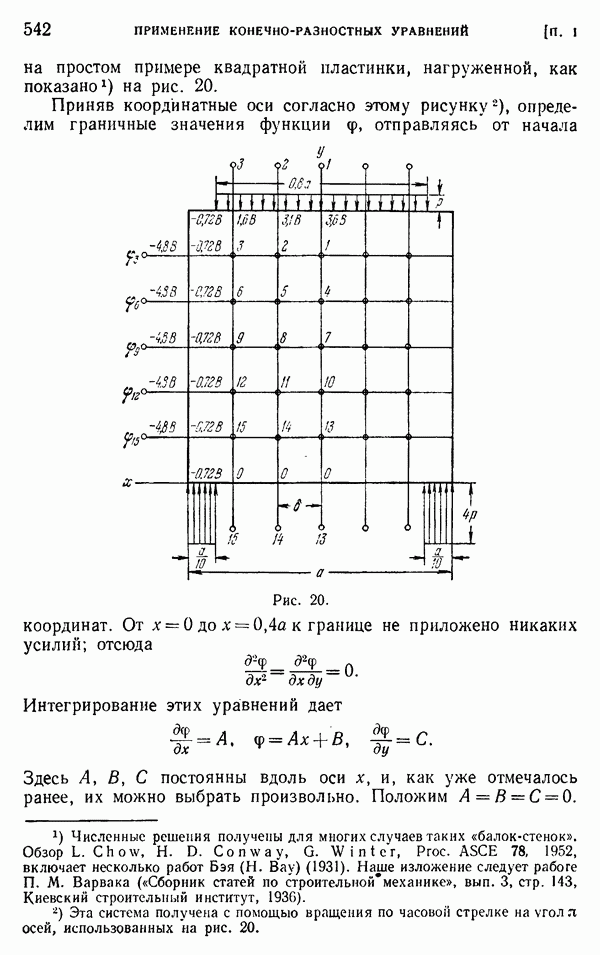
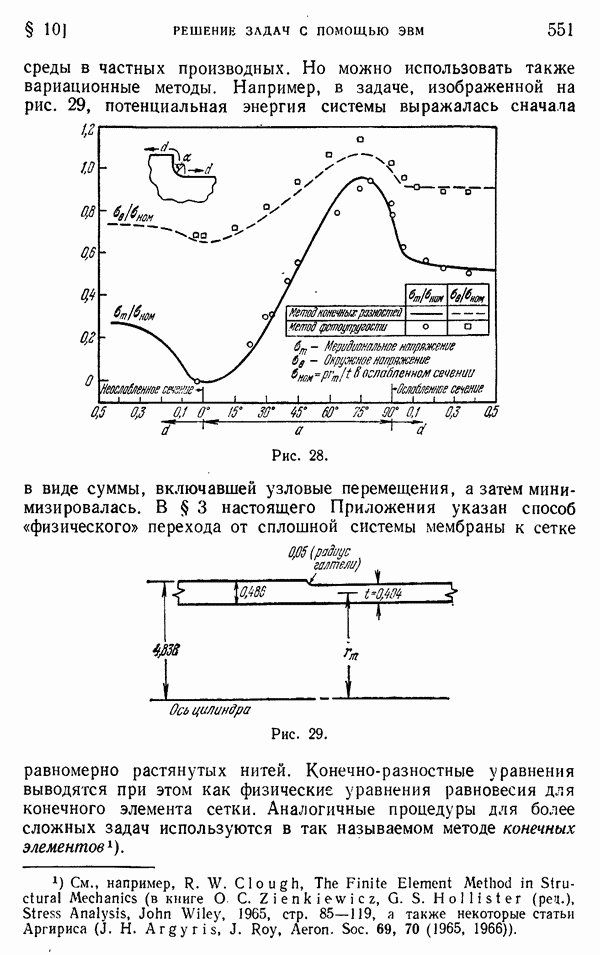
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
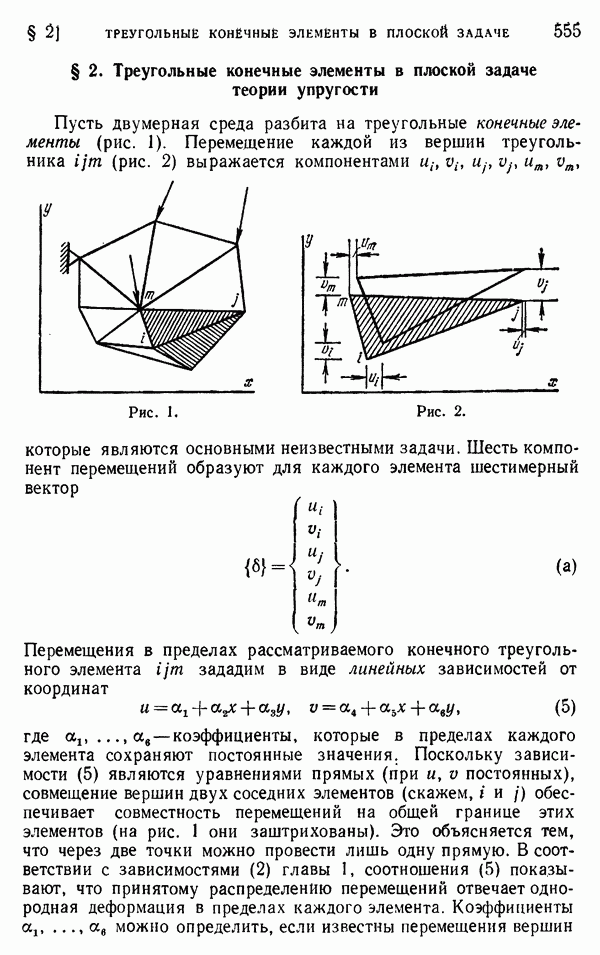
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
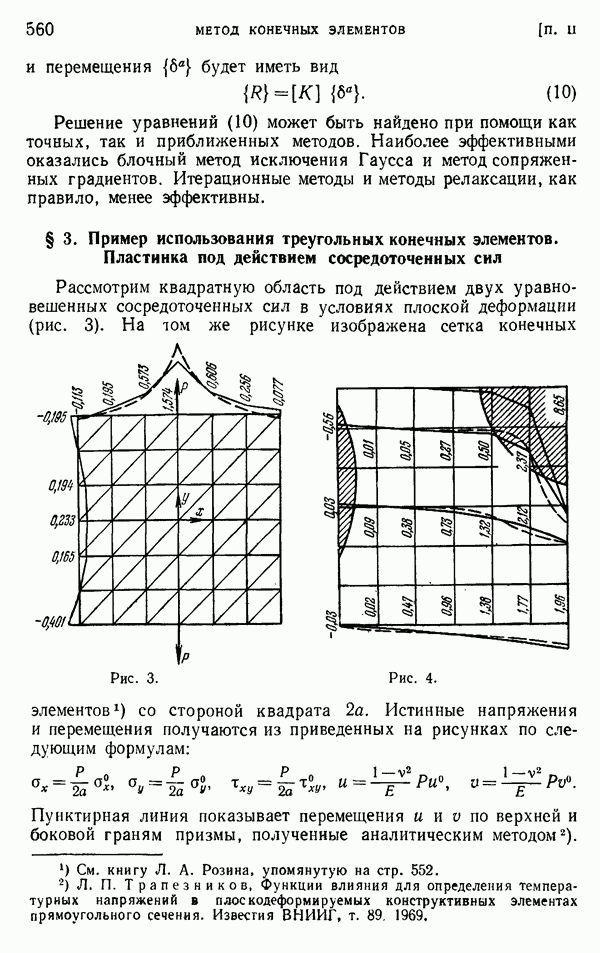
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
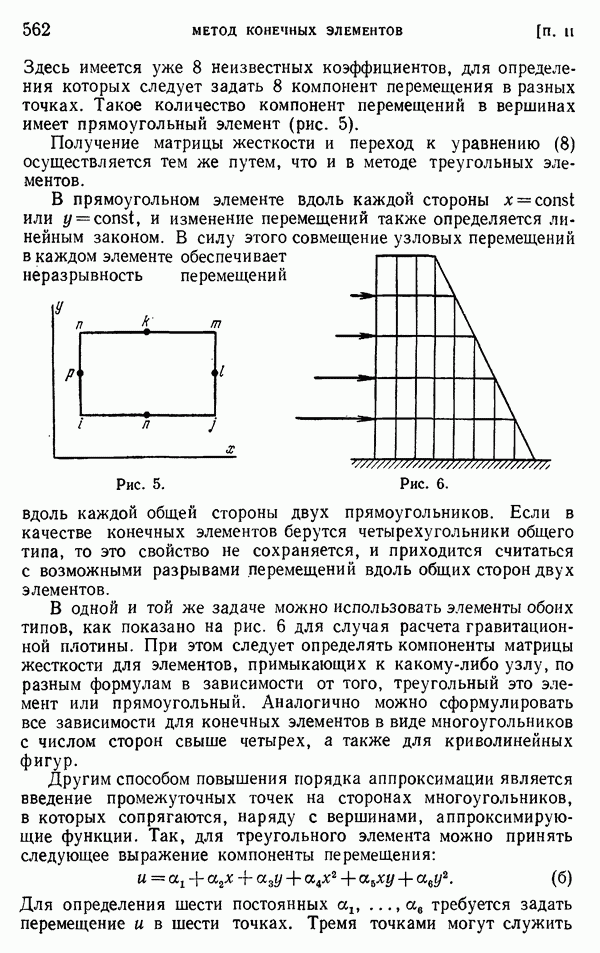
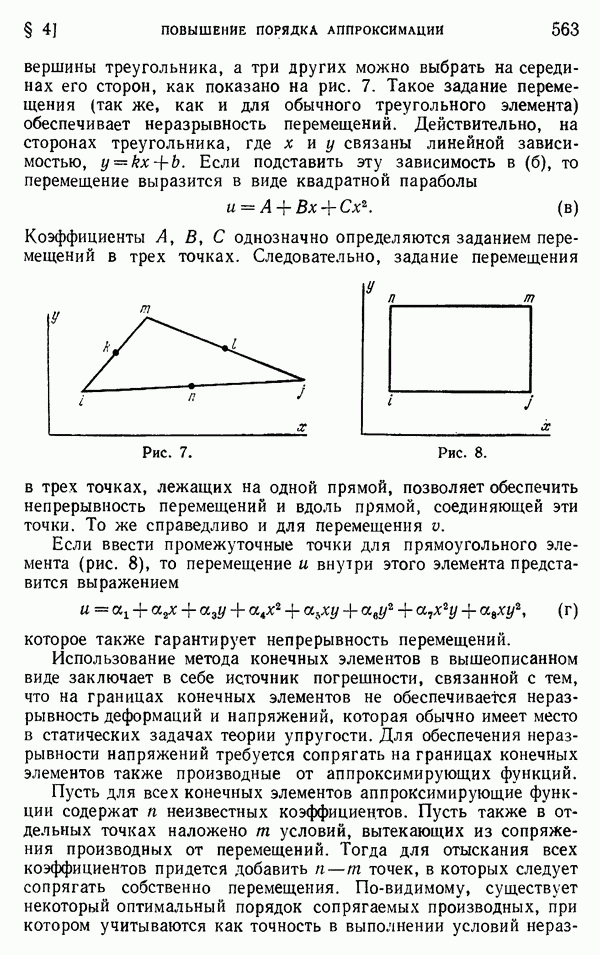
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи