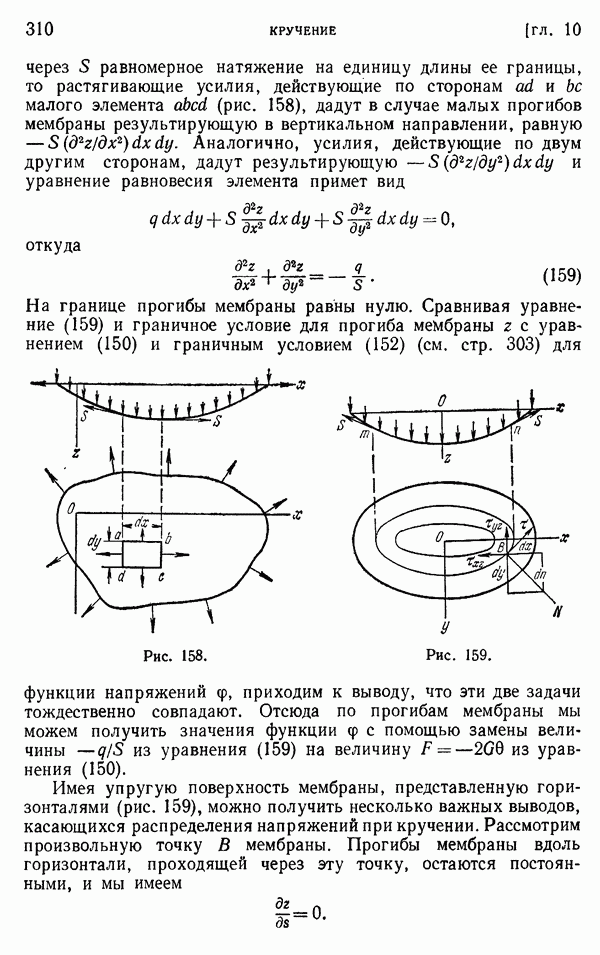
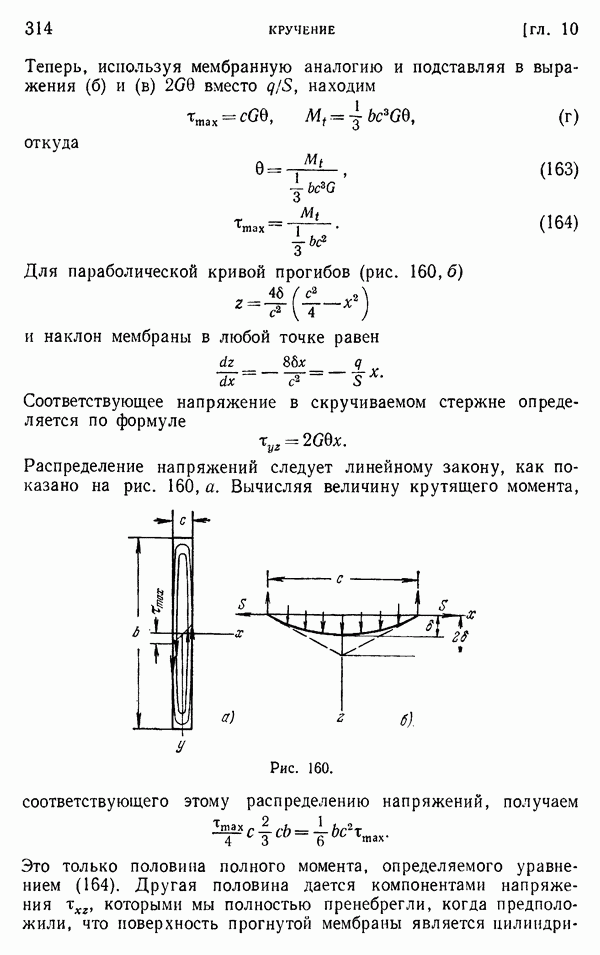
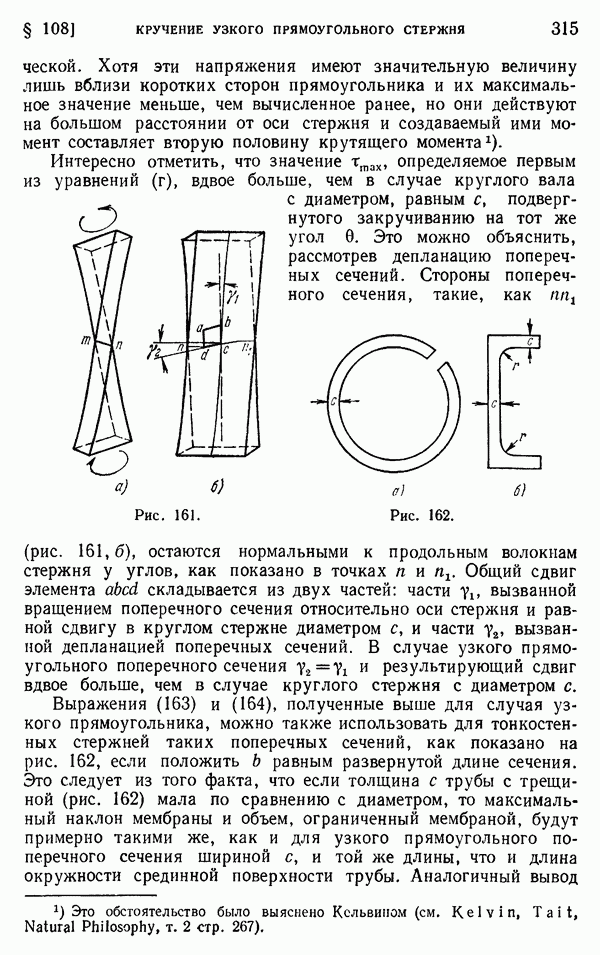
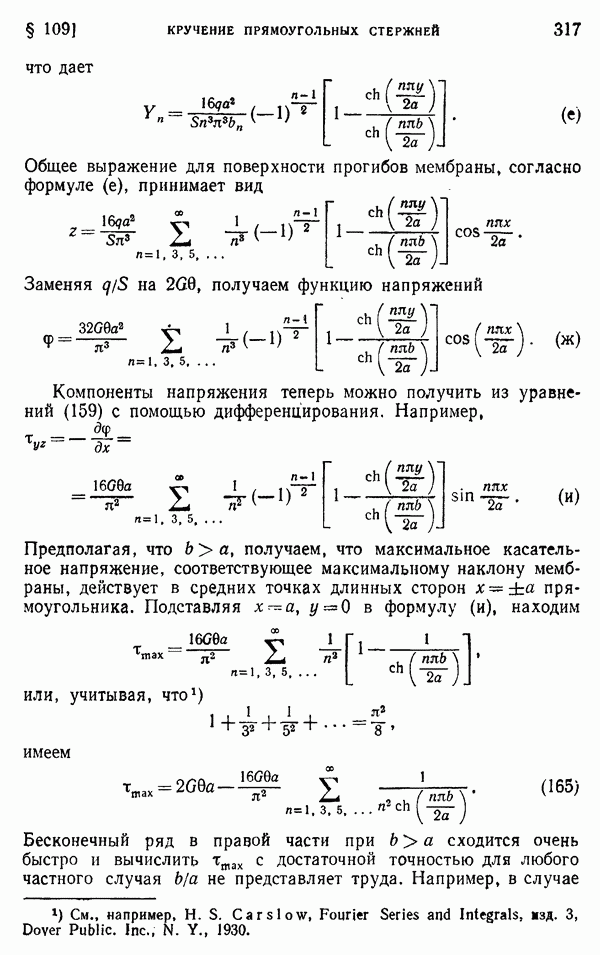
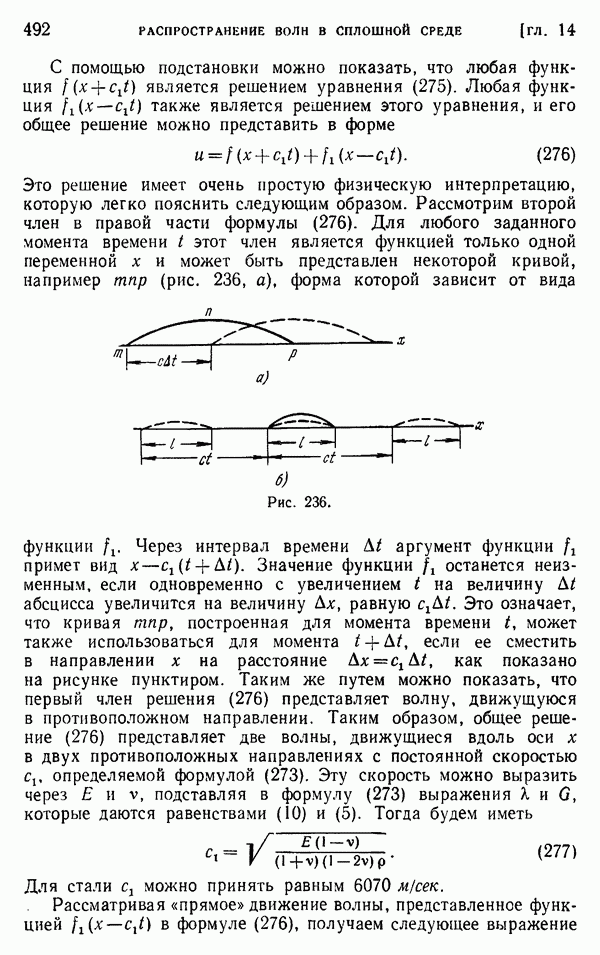
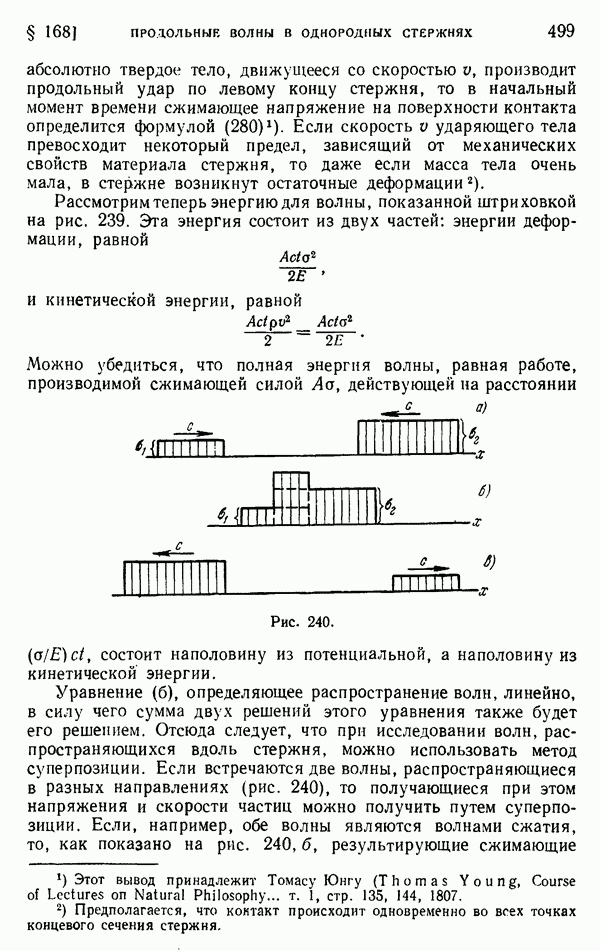
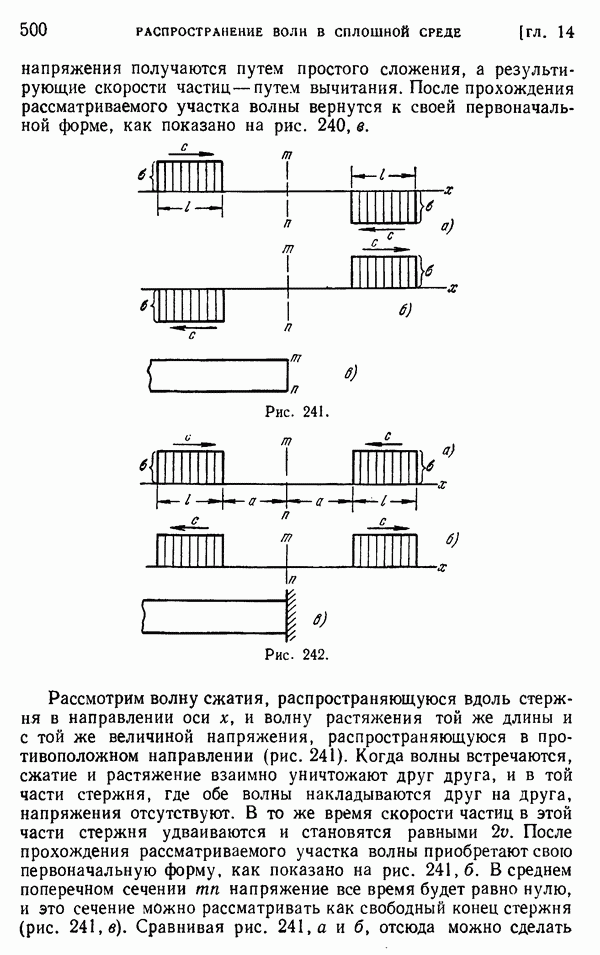
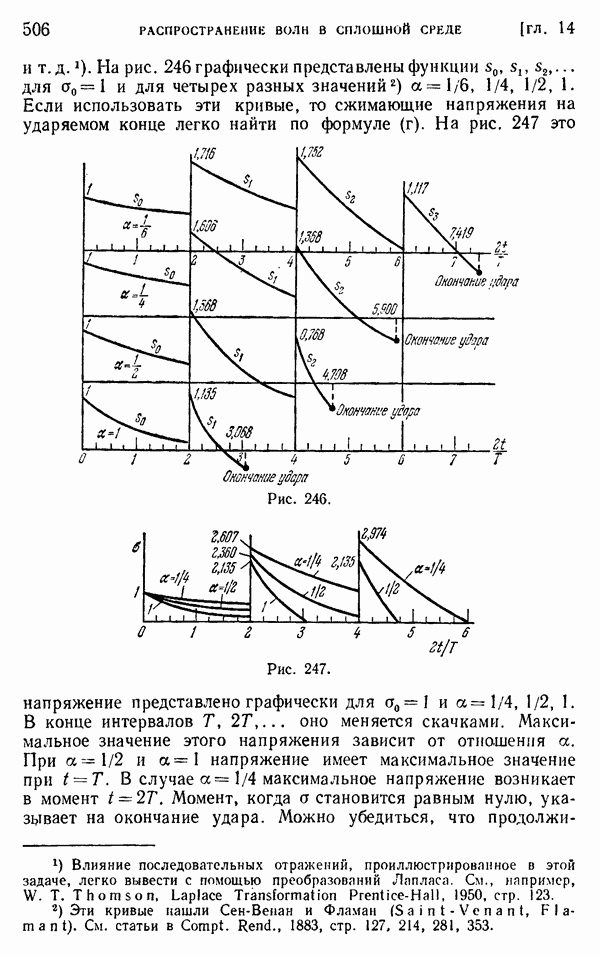
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 93. Теорема Кастильяно
В предыдущем параграфе равновесная форма упругого тела, подвергнутого действию заданных массовых сил и при заданных граничных условиях, сопоставлялась со смежными формами, получающимися в результате виртуальных перемещений  из положения равновесия. Было установлено, что истинные перемещения, отвечающие положению устойчивого равновесия, доставляют минимум потенциальной энергии системы.
из положения равновесия. Было установлено, что истинные перемещения, отвечающие положению устойчивого равновесия, доставляют минимум потенциальной энергии системы.
Рассмотрим теперь вместо перемещений напряжения, отвечающие положению равновесия. Мы знаем, что дифференциальные уравнения равновесия (123) вместе с граничными условиями (124) недостаточны для определения компонент напряжения. Мы можем найти множество различных распределений напряжений, удовлетворяющих уравнениям равновесия и граничным условиям; в связи с этим возникает вопрос: как отличить истинное напряженное состояние от всех других статически возможных распределений напряжений?
Обозначим через  компоненты истинного напряжения, отвечающие положению равновесия, а через
компоненты истинного напряжения, отвечающие положению равновесия, а через  малые вариации этих компонент, такие, что новые компоненты напряжения
малые вариации этих компонент, такие, что новые компоненты напряжения  удовлетворяют тем же уравнениям равновесия (123). Затем, вычитая уравнения для одной системы из уравнений для другой системы, находим, что вариации компонент напряжения удовлетворяют трем уравнениям вида
удовлетворяют тем же уравнениям равновесия (123). Затем, вычитая уравнения для одной системы из уравнений для другой системы, находим, что вариации компонент напряжения удовлетворяют трем уравнениям вида

Этой вариации компонент напряжения будут соответствовать вариации поверхностных усилий. Обозначим через  эти малые изменения поверхностных усилий; тогда, на основании граничных условий (124), находим три уравнения вида
эти малые изменения поверхностных усилий; тогда, на основании граничных условий (124), находим три уравнения вида

Рассмотрим теперь изменение энергии деформации тела, вызванное вышеописанными изменениями компонент напряжения. Взяв энергию деформации в единице объема в виде функции компонент напряжения (131), получим для изменения этой энергии выражение

имеющее в правой части шесть членов, причем

и т. д., а также

и т. д., откуда

Следовательно, полное изменение потенциальной энергии, вызванное изменениями компонент напряжения, составит

Исследуем это изменение энергии. Чтобы учесть граничные условия (б), нам потребуется теорема, известная под названием теоремы о дивергенции, или теоремы Гаусса, или леммы Грина. Пусть в некоторой области, ограниченной поверхностью  которая имеет направляющие косинусы внешней нормали
которая имеет направляющие косинусы внешней нормали  существуют три функции пространственных координат
существуют три функции пространственных координат  Теорема формулируется в виде равенства
Теорема формулируется в виде равенства

где объемный интеграл в левой части берется по всему объему, ограниченному поверхностью  а поверхностный интеграл в правой части — по всей ограничивающей поверхности
а поверхностный интеграл в правой части — по всей ограничивающей поверхности  Поверхность
Поверхность 
может представлять внешнюю поверхность тела, а вместе с ней и поверхности одной или нескольких внутренних областей (полостей). Для наших целей удобно сперва принять

Тогда теорема (138) дает

Выполняя дифференцирование внутри квадратных скобок в левой части, получаем

Согласно зависимости (а) выражение в скобках обращается в нуль. Теперь соотношение (е) принимает вид

Таким же путем, приняв вначале вместо (д) выражения

получаемые с помощью циклической перестановки в (д), приходим к результату, который выписан ниже с помощью циклической перестановки в (и):

Далее с помощью еще одной циклической перестановки имеем

Складывая соотношения (и), и используя зависимость между перемещениями и деформациями (2), находим

Левая часть этого равенства, как и в равенстве (г), равна  . Таким образом, при сохранении равновесия вариация энергии деформации в форме (131), отвечающая вариациям компонент напряжения дается формулой
. Таким образом, при сохранении равновесия вариация энергии деформации в форме (131), отвечающая вариациям компонент напряжения дается формулой

Истинными напряжениями являются те, которые удовлетворяют
этому уравнению. Такие вариации являются математическими, а не физическими. Физические вариации напряжений, вызываемые вариациями граничных нагрузок, подвержены более жестким ограничениям, нежели уравнения равновесия в форме (а). Однако с математической точки зрения интеграл в формуле (139), если  есть функция шести переменных, а именно, согласно (131), шести компонент напряжения, обладает вариацией независимо от способа изменения этих шести переменных.
есть функция шести переменных, а именно, согласно (131), шести компонент напряжения, обладает вариацией независимо от способа изменения этих шести переменных.
В строительной механике энергия деформации линейно-упругой конструкции под действием системы сосредоточенных сил  может быть выражена в виде квадратичной функции от этих сил. Тогда
может быть выражена в виде квадратичной функции от этих сил. Тогда

и мы получаем теорему Кастильяно для соответствующих компонент перемещения 

из того факта, что

Аналогия между (140) и (139) очевидна. Теорему (140) часто называют теоремой Кастильяно.
Возвращаясь к формуле (139), отметим, что вариации напряжения могут быть и такими, что краевые усилия X, Y, Z остаются неизменными. Тогда  в трех условиях вида (б) равны нулю, а формула (139) принимает простой вид
в трех условиях вида (б) равны нулю, а формула (139) принимает простой вид

Следовательно, для таких вариаций функция V стационарна. Мы исследовали, начиная с (в), только приращения и вариации первого порядка. Из рассмотрения вариаций второго порядка можно показать, что V в действительности достигает минимума. Теорему (141) иногда называют принципом минимальной работы, как и ее аналог для сосредоточенных сил в строительной механике.
Для плоской деформации или плоского напряженного состояния имеем  или
или  и (139) немедленно приводится к виду
и (139) немедленно приводится к виду

где V берется в соответствующей форме, например в форме (133) для плоского напряженного состояния, а интеграл при единичной
толщине слоя представляет собой контурный интеграл вдоль граничной кривой с элементом дуги 
Сформулированы и более общие вариационные принципы, в которых одновременно варьируются как напряжения, так и перемещения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
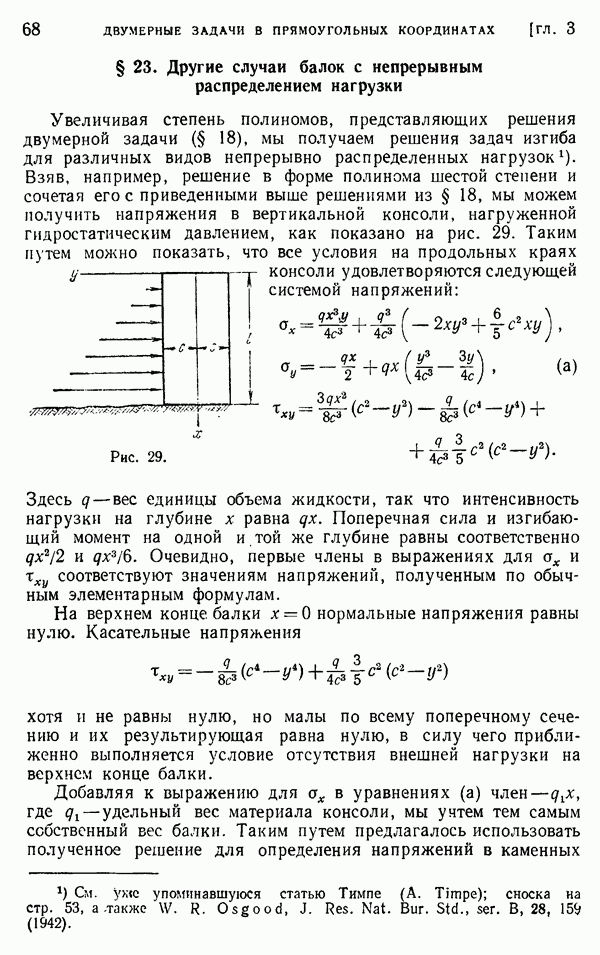
- § 23. Другие случаи балок с непрерывным распределением нагрузки
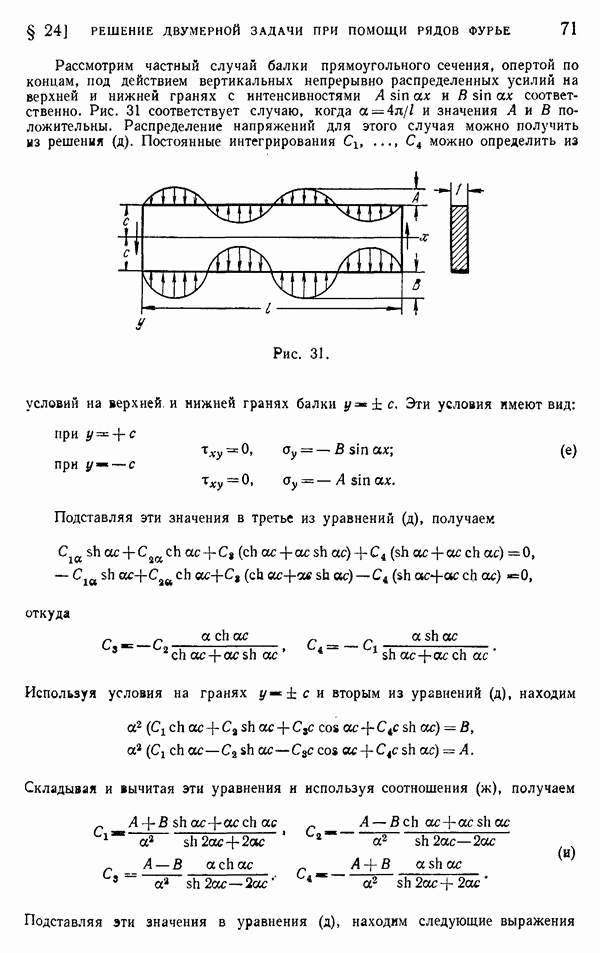
- § 24. Решение двумерной задачи при помощи рядов Фурье
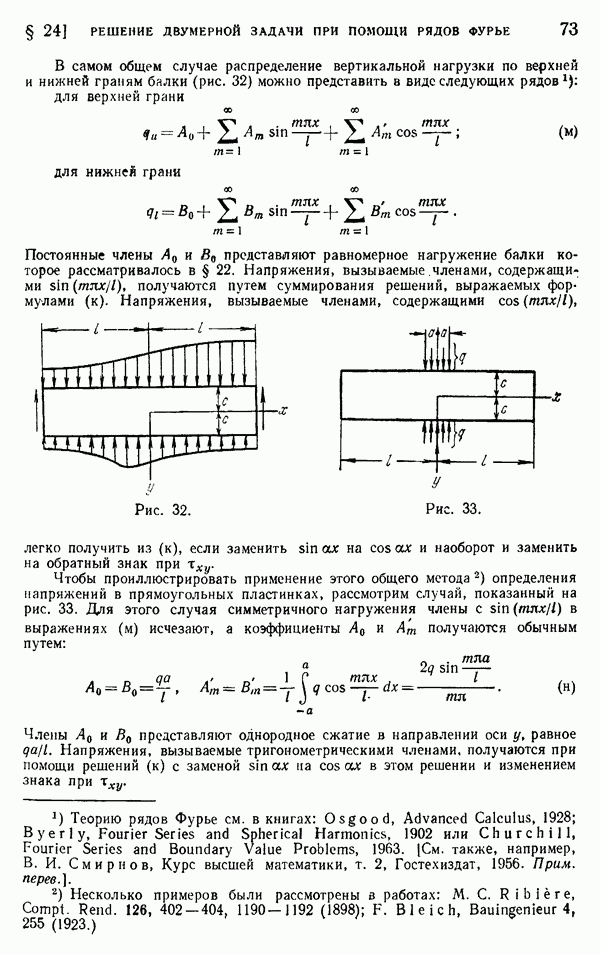
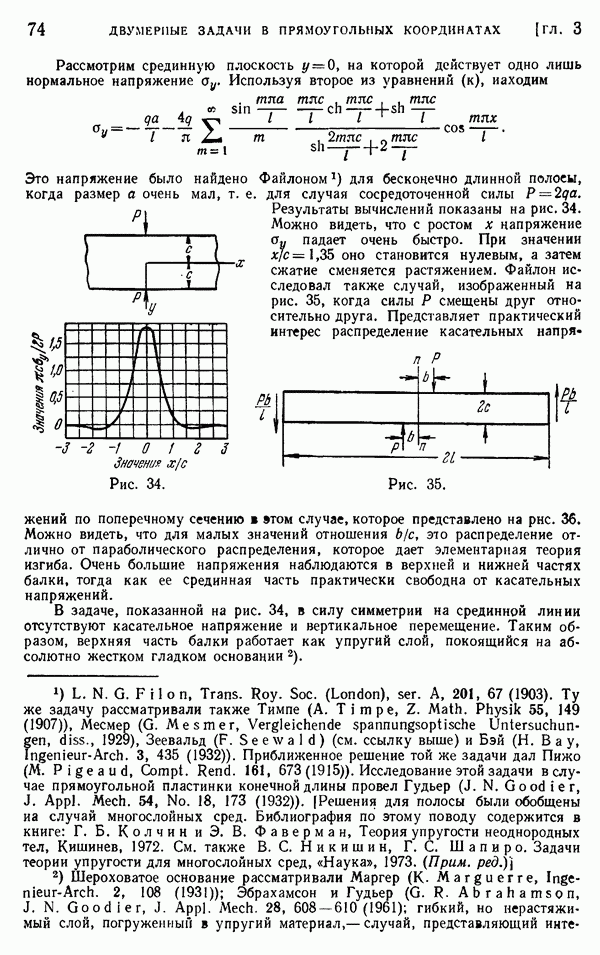
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
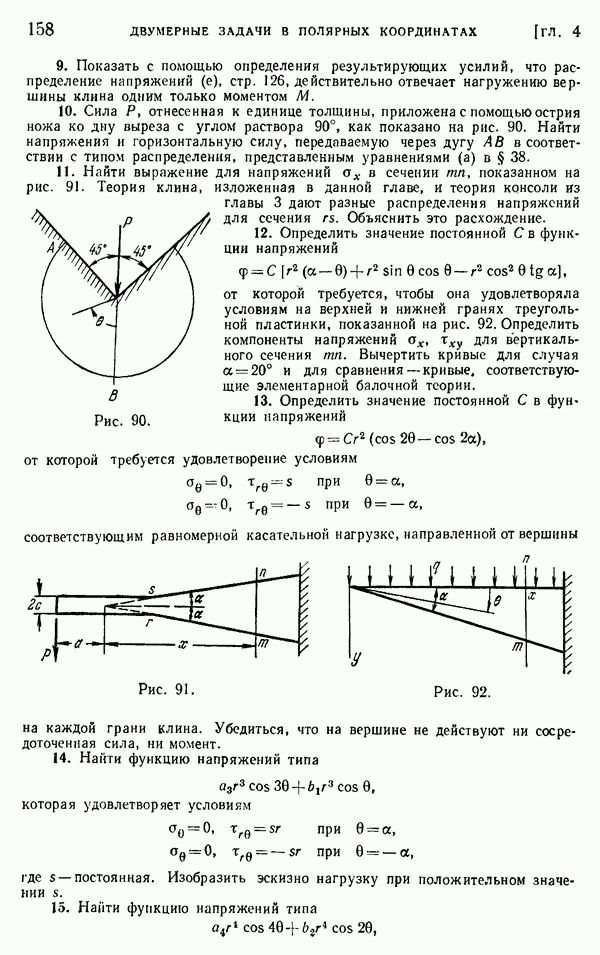
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
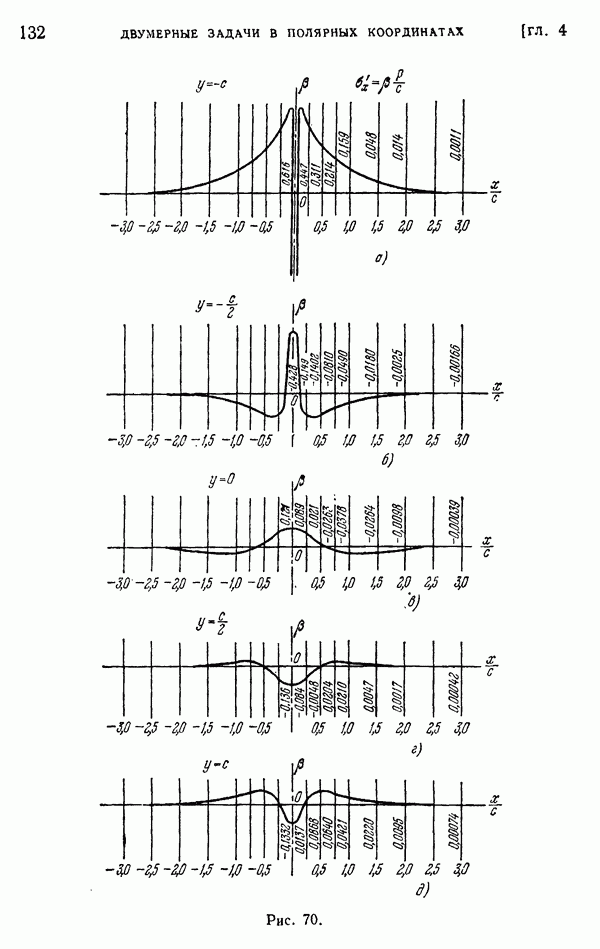
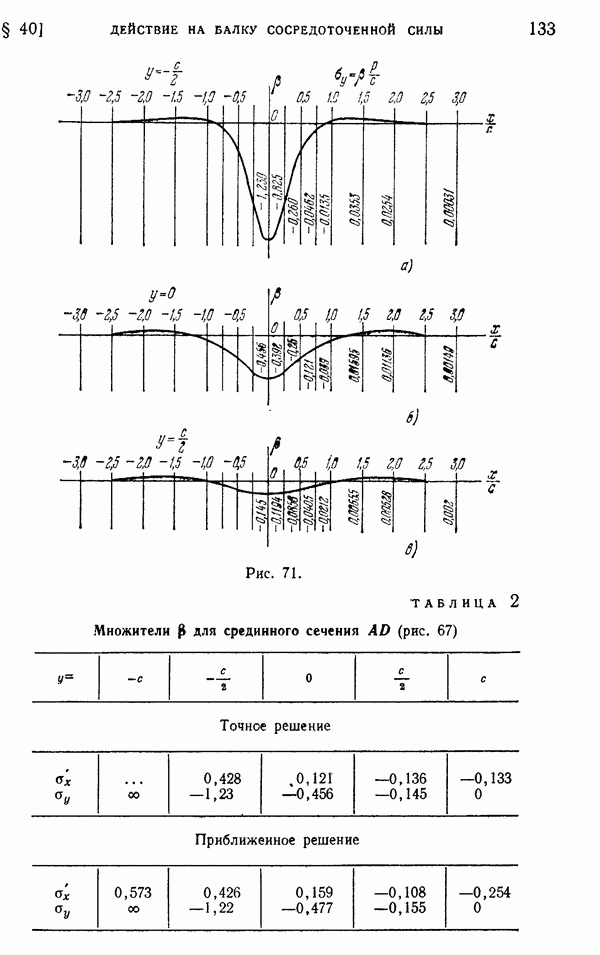
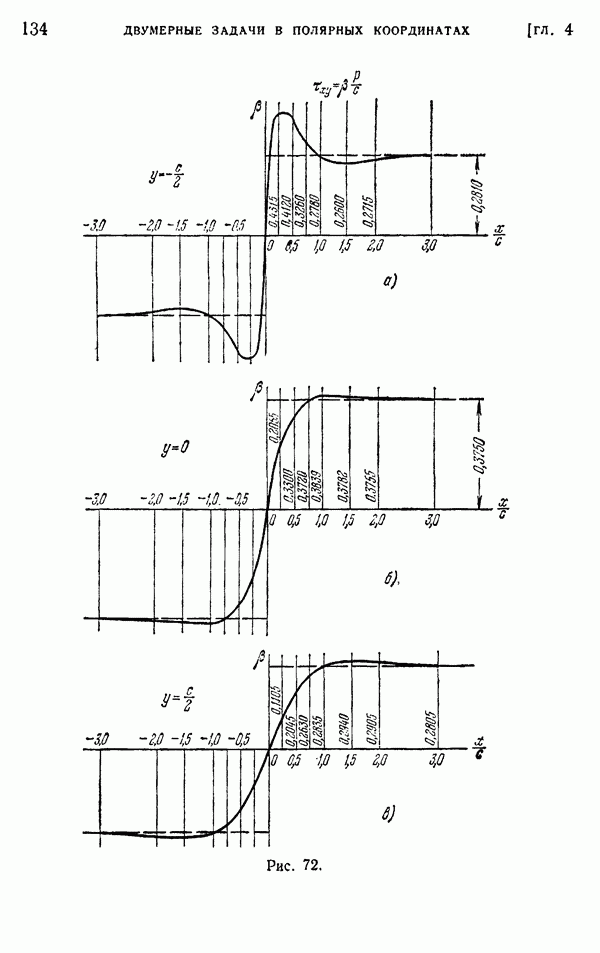
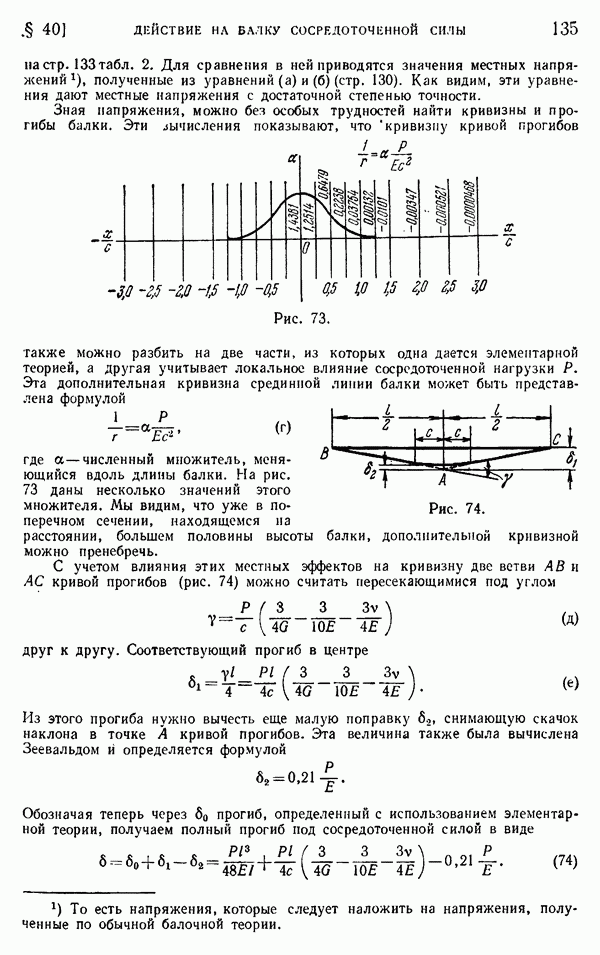
- § 40. Действие на балку сосредоточенной силы
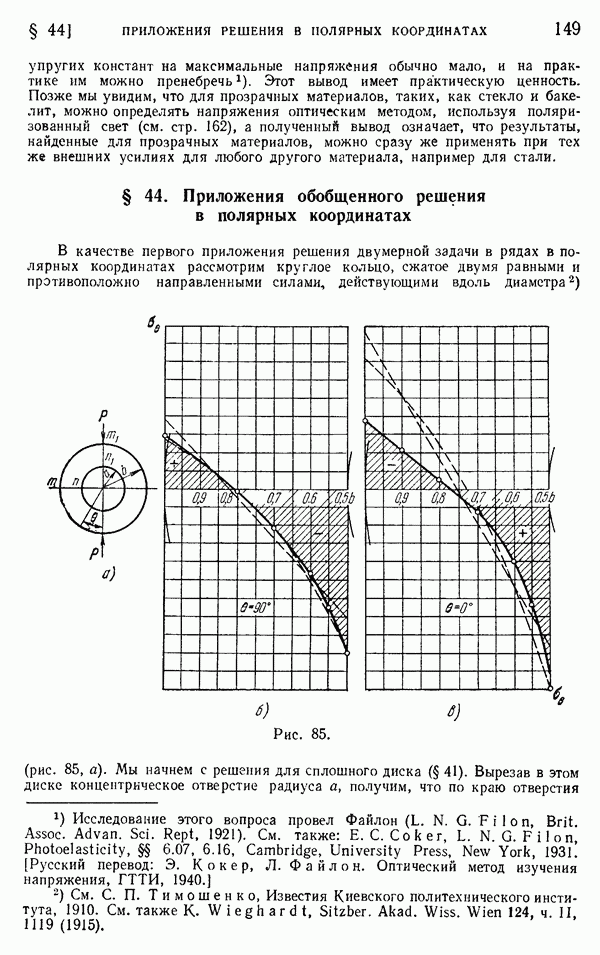
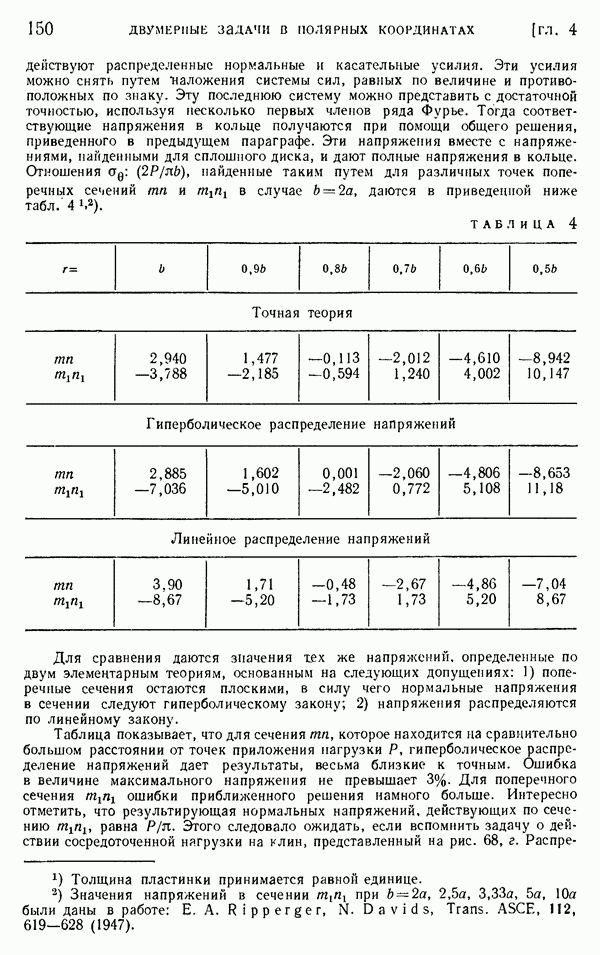
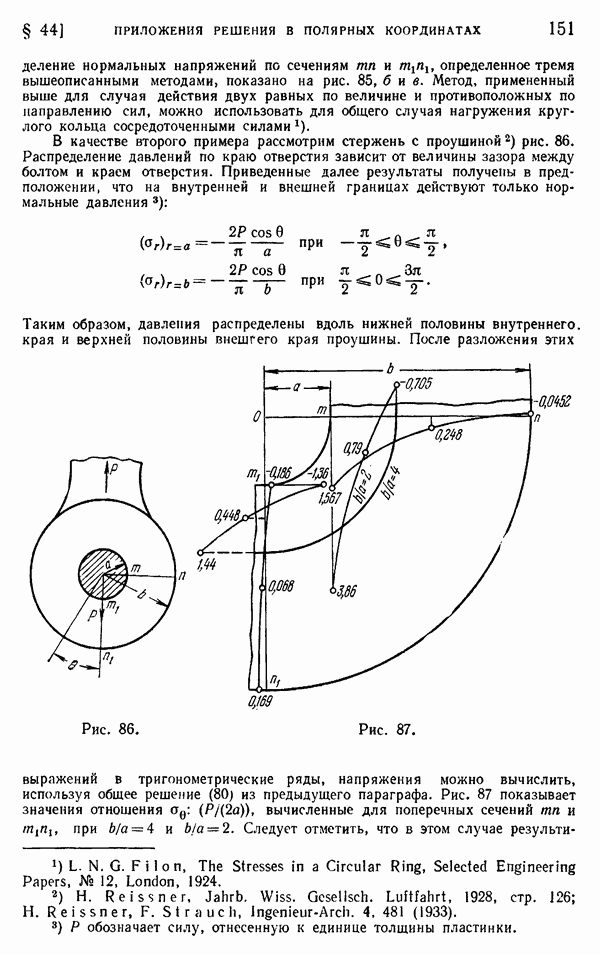
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
- § 44. Приложения обобщенного решения в полярных координатах
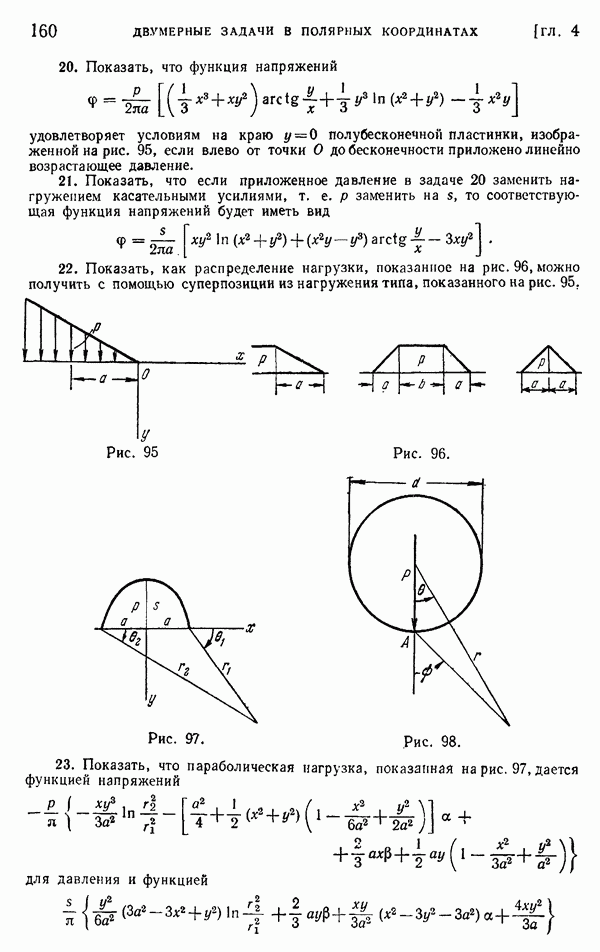
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
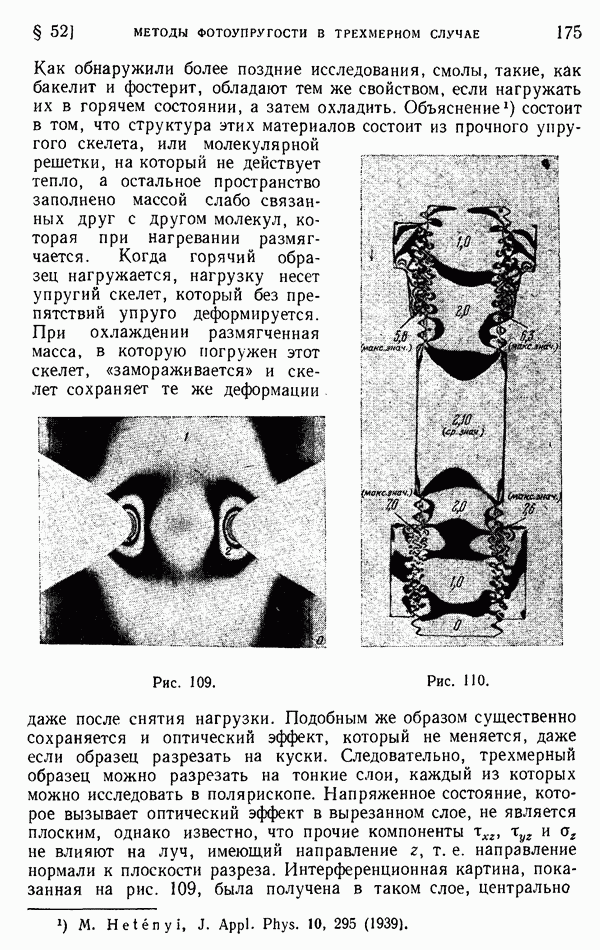
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
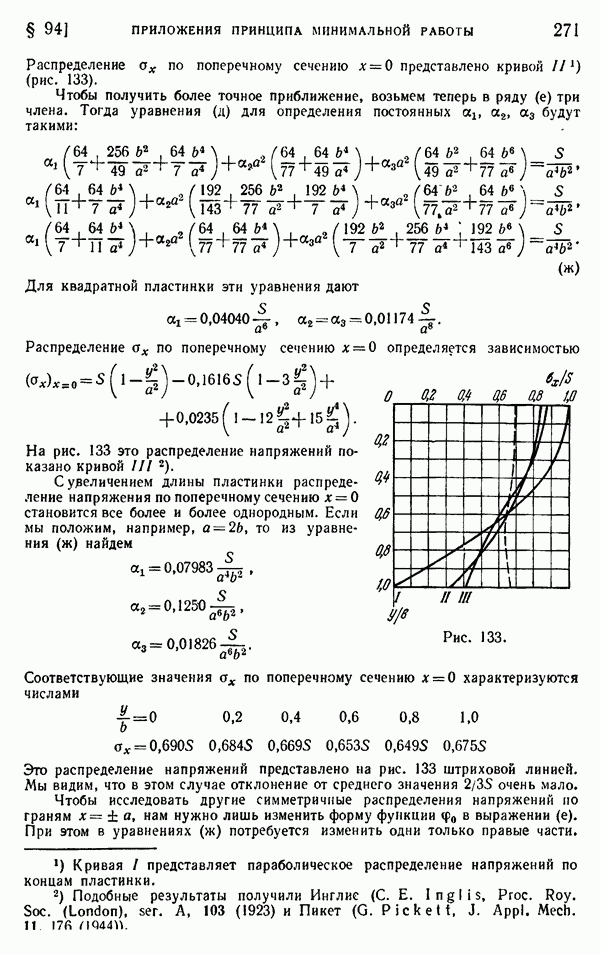
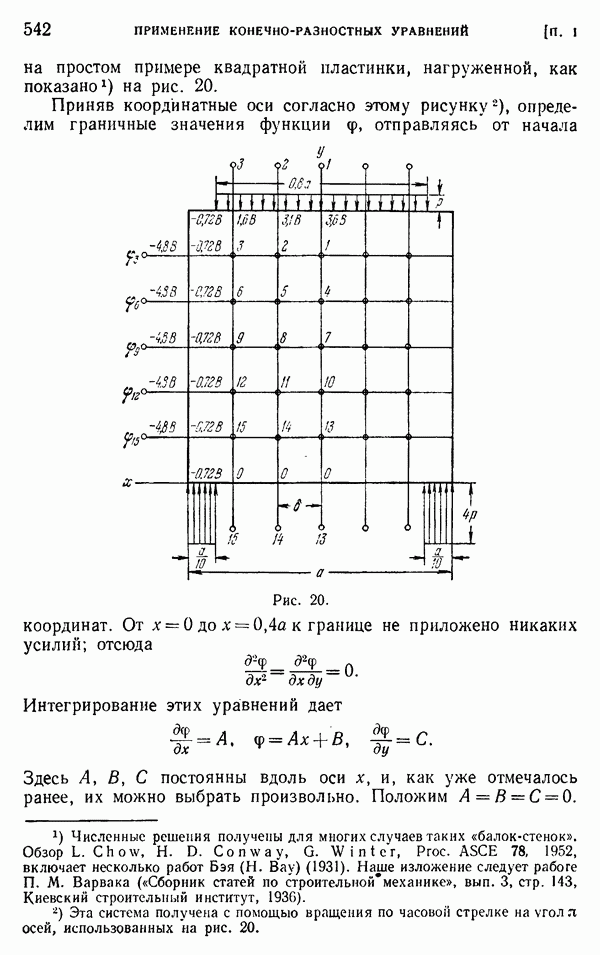
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
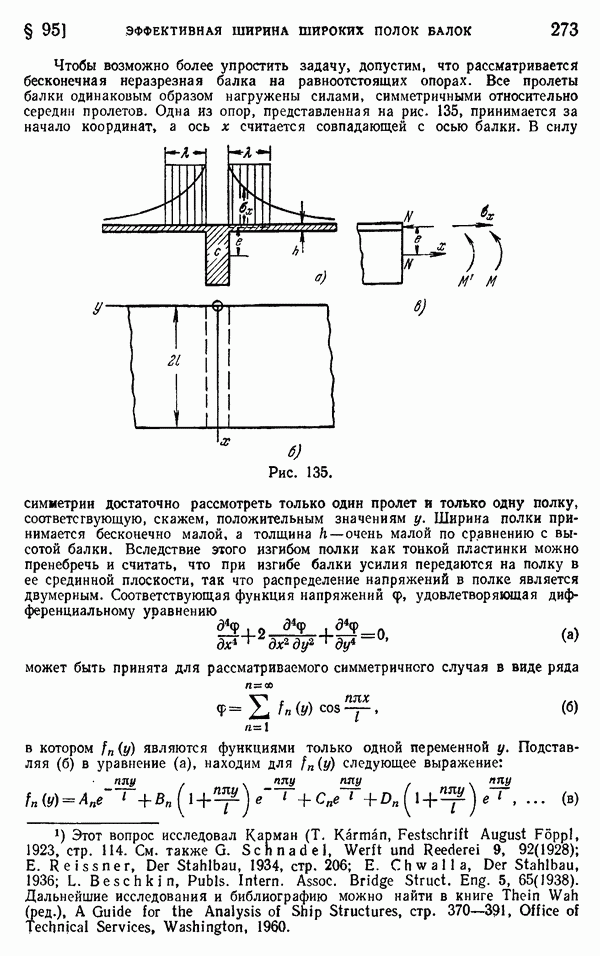
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
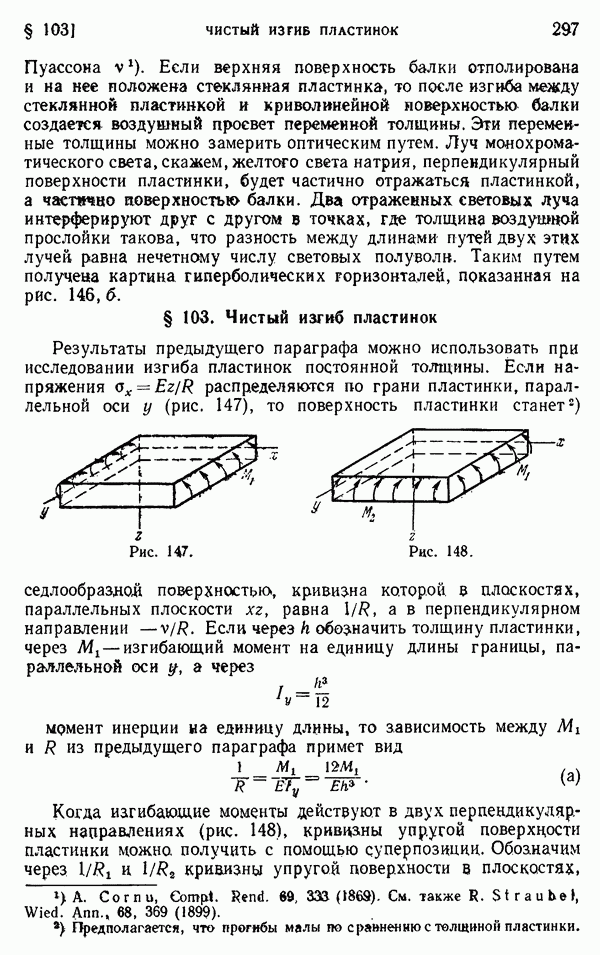
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
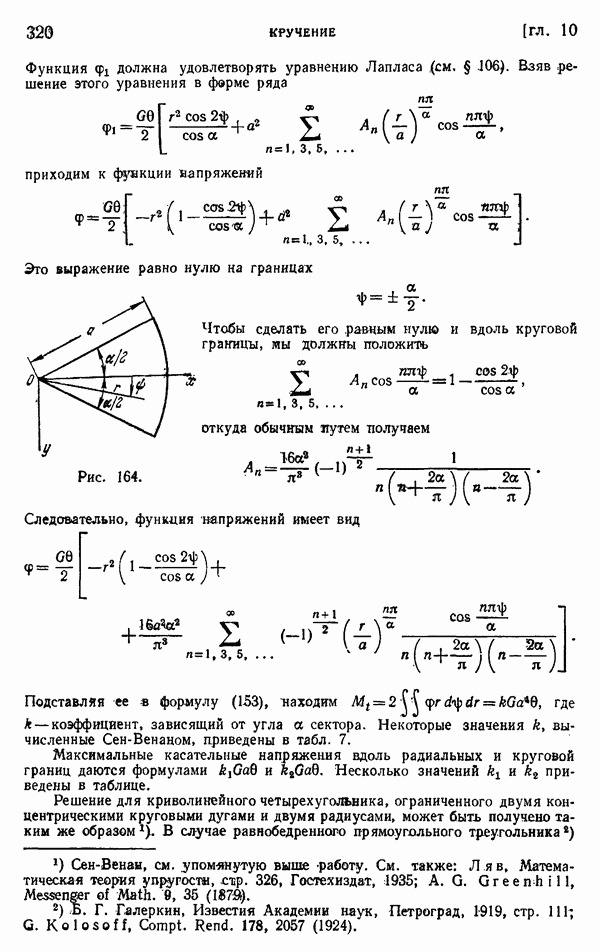
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
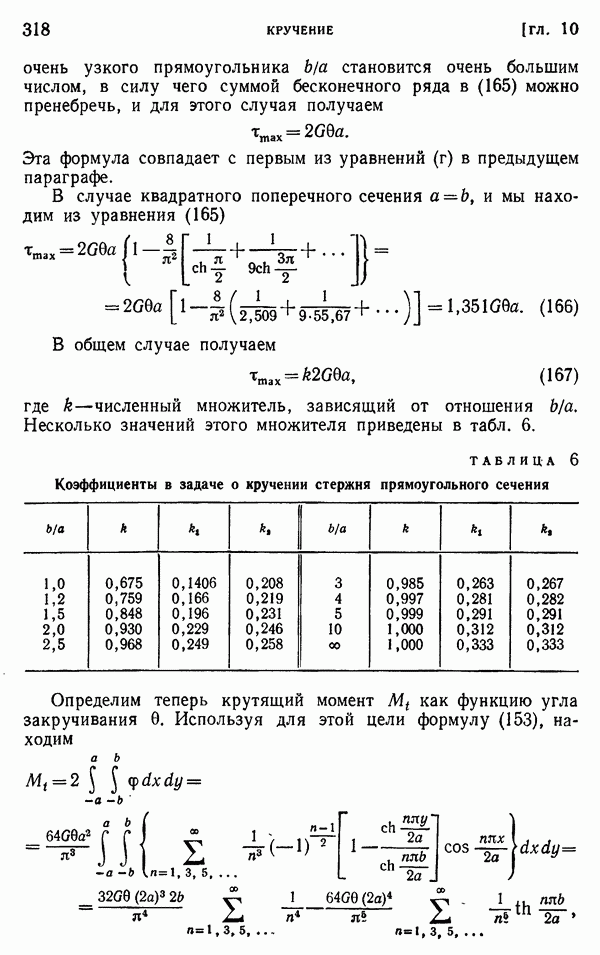
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
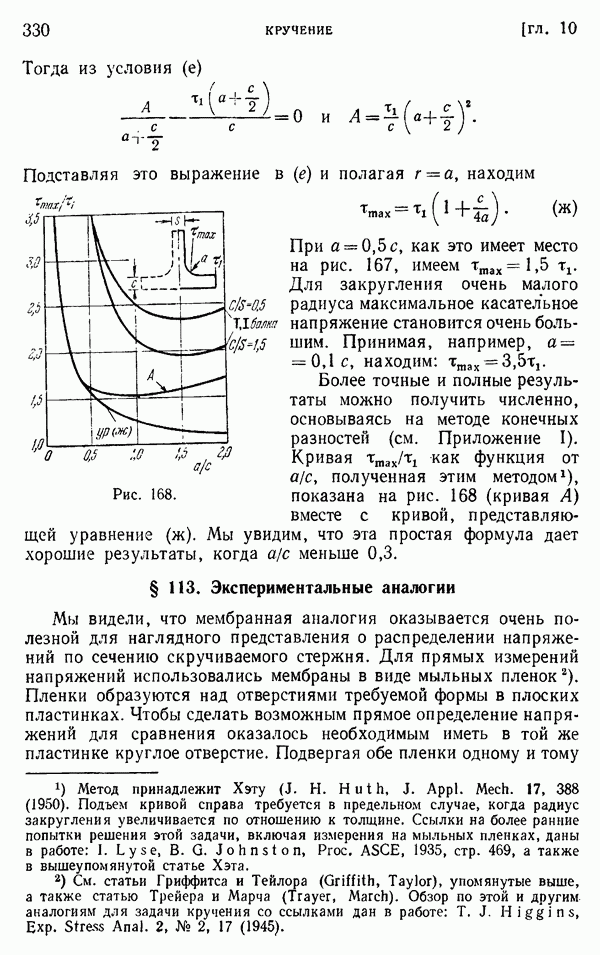
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
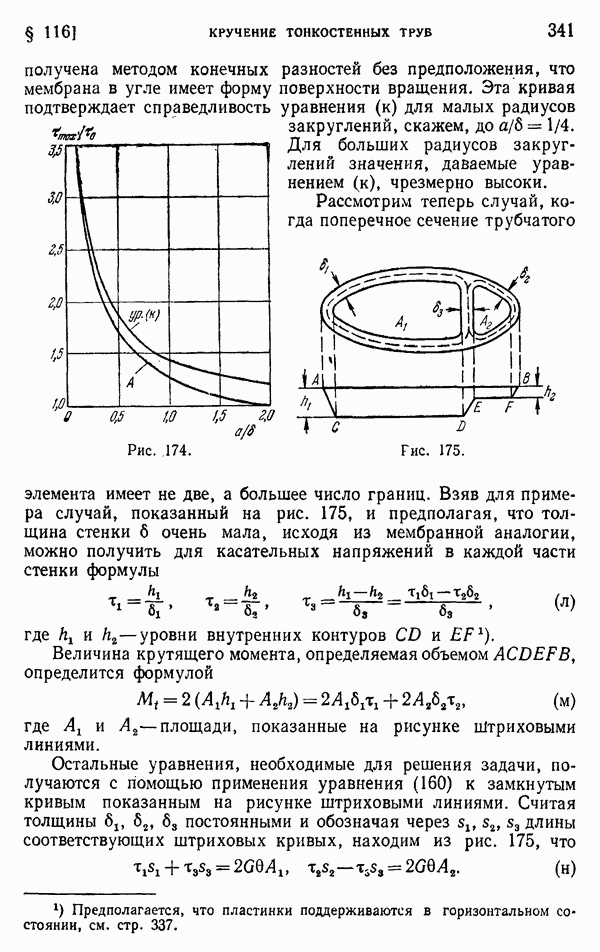
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
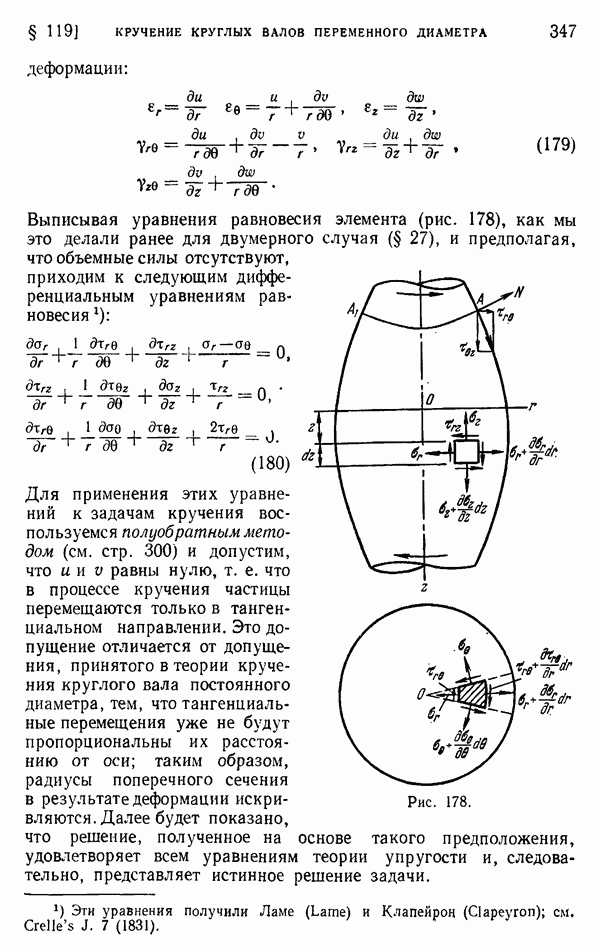
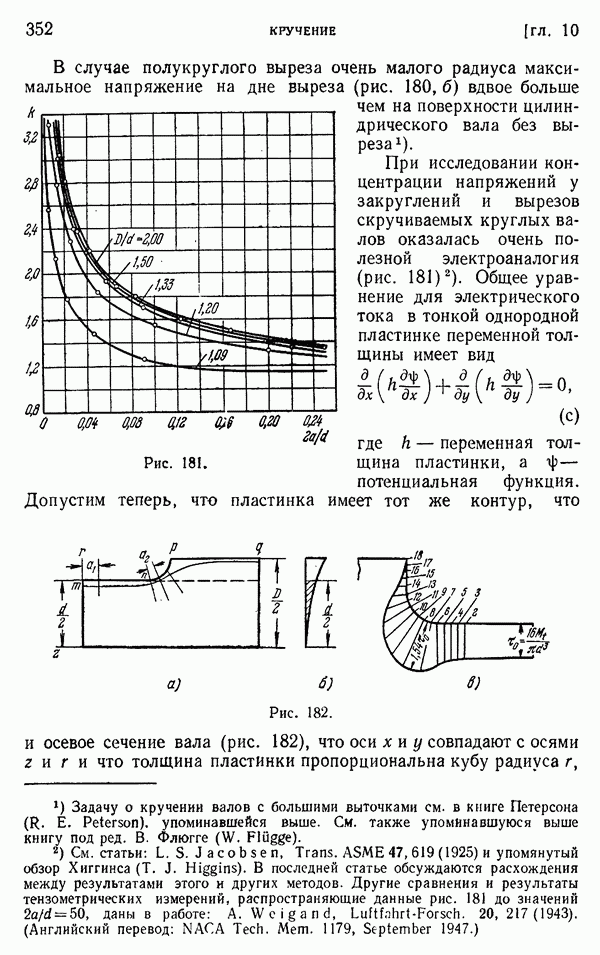
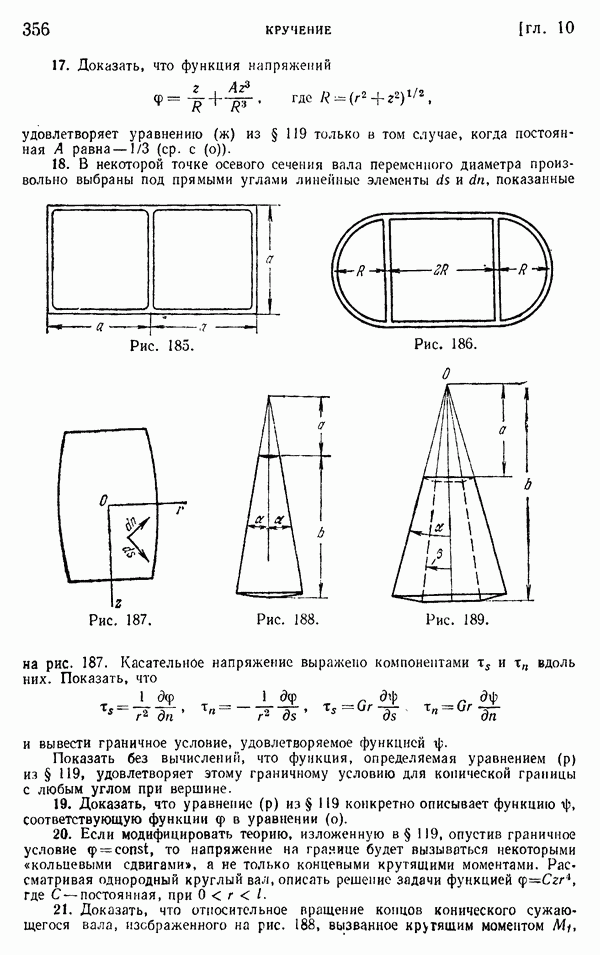
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
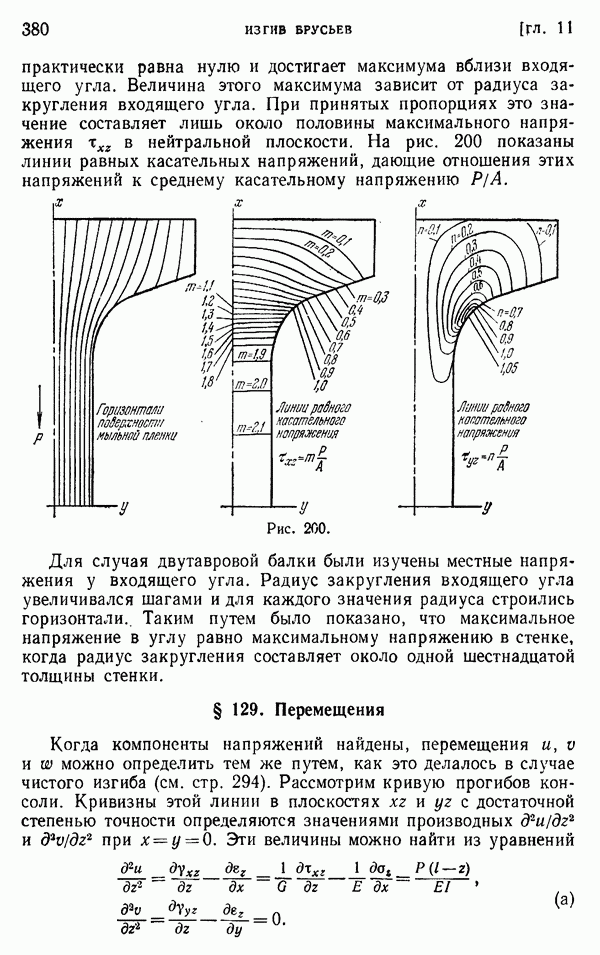
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
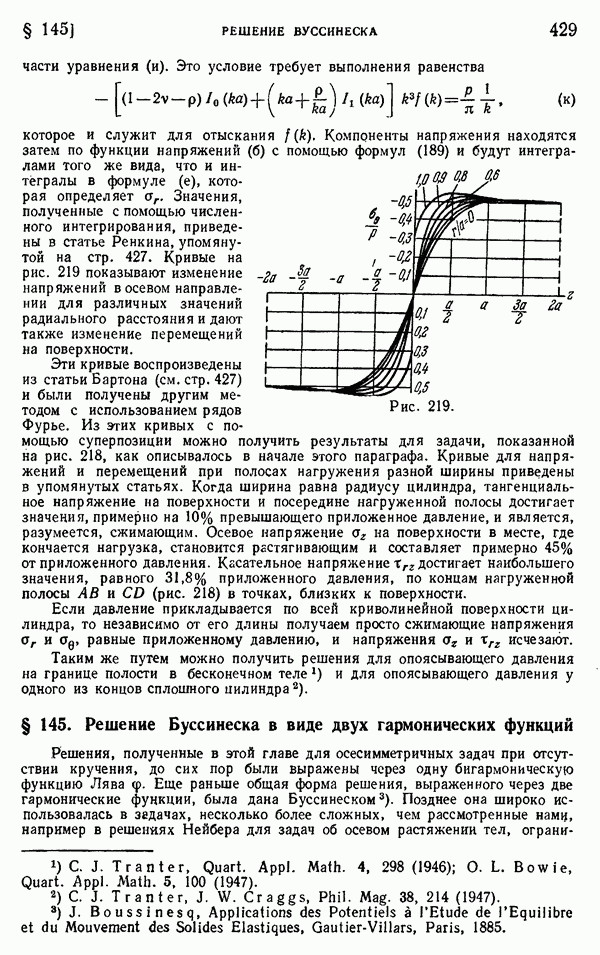
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
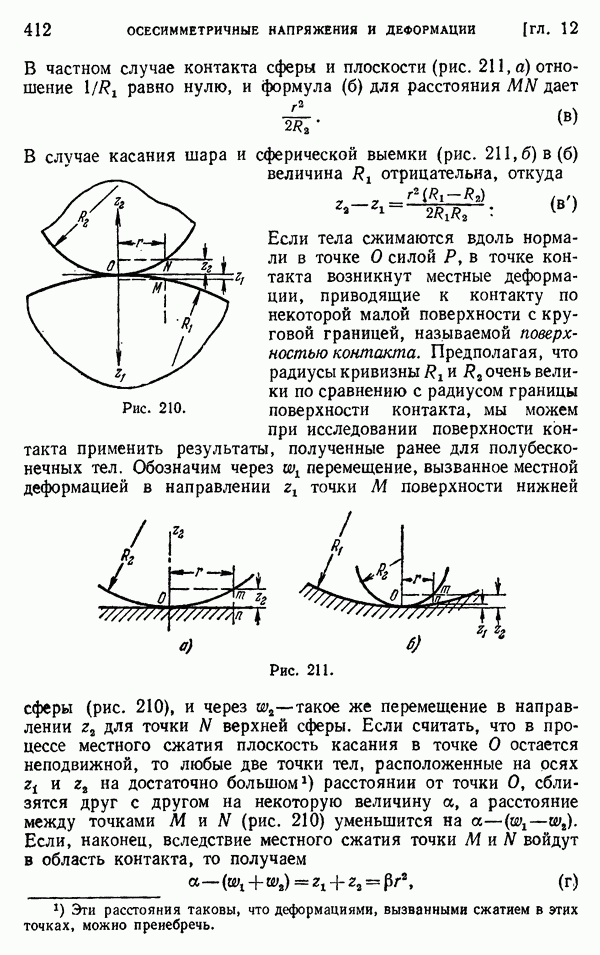
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
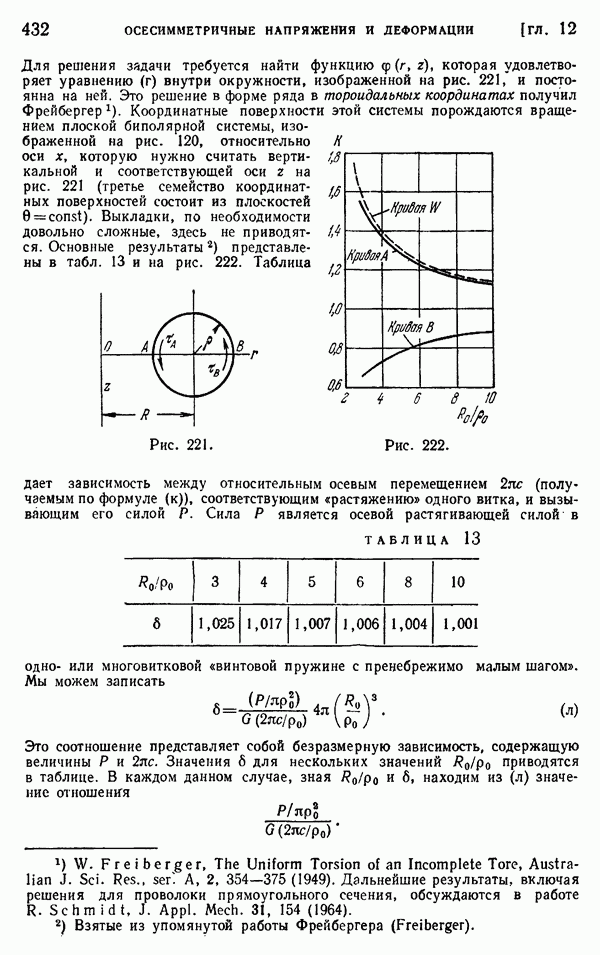
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
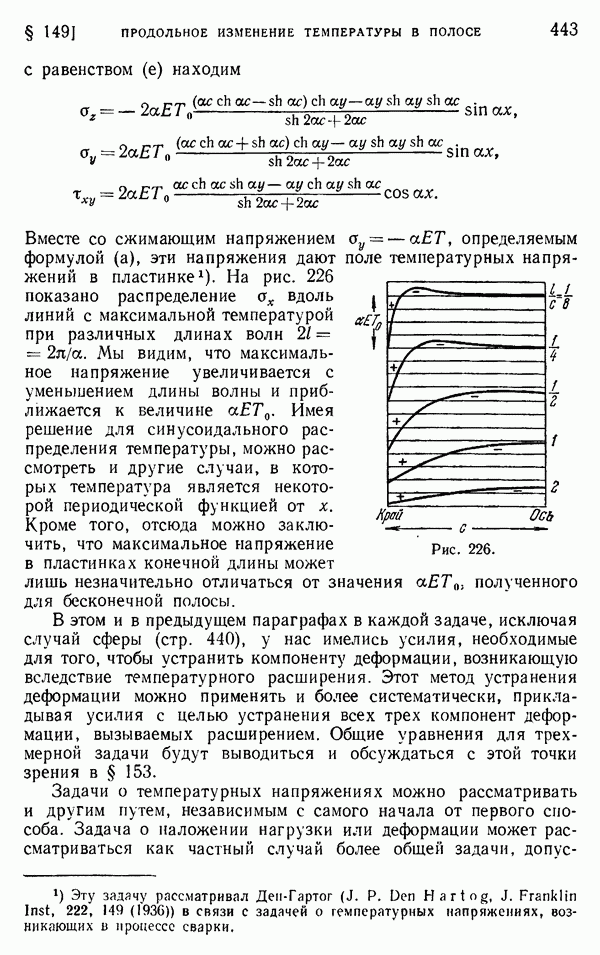
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
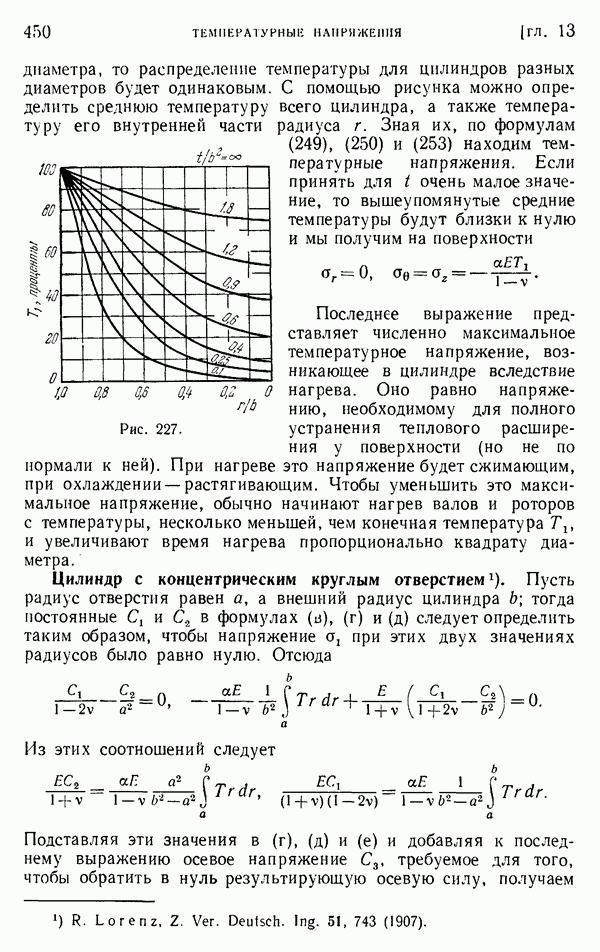
- § 151. Длинный круглый цилиндр
- § 152. Сфера
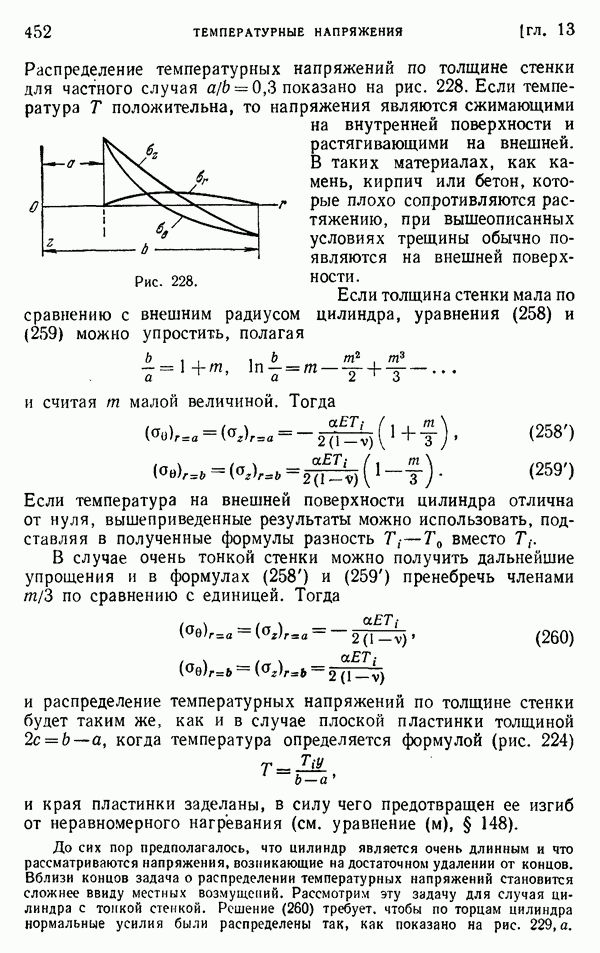
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
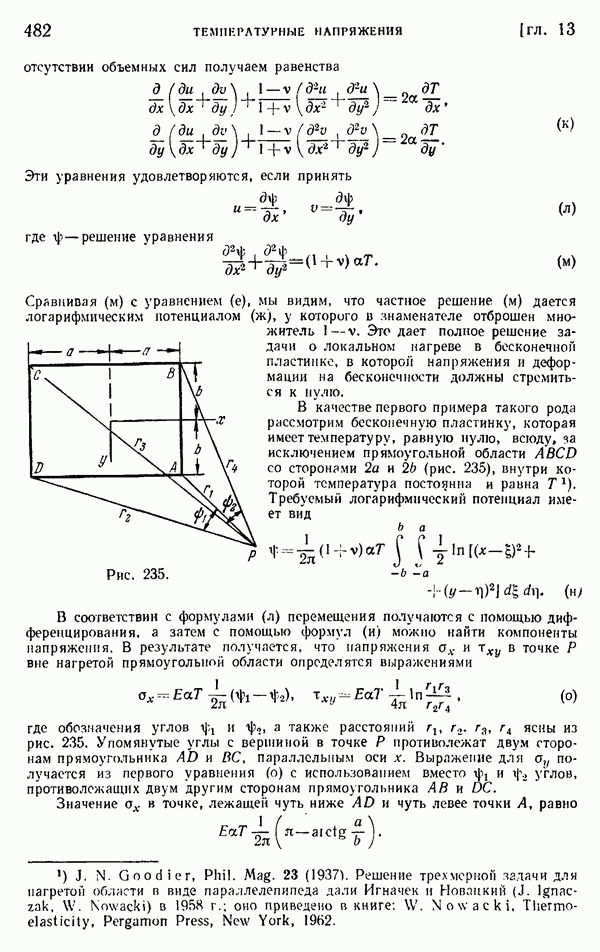
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
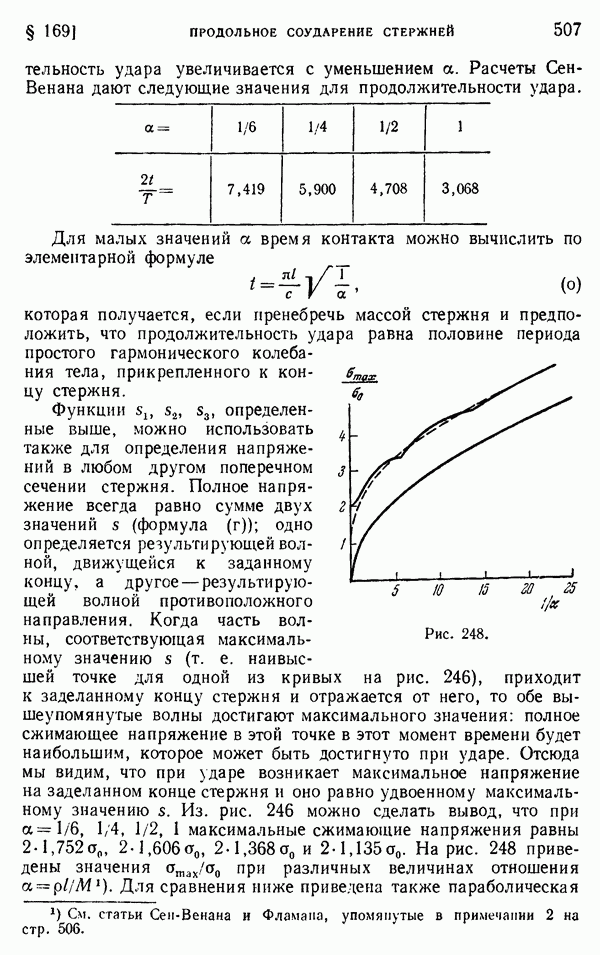
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
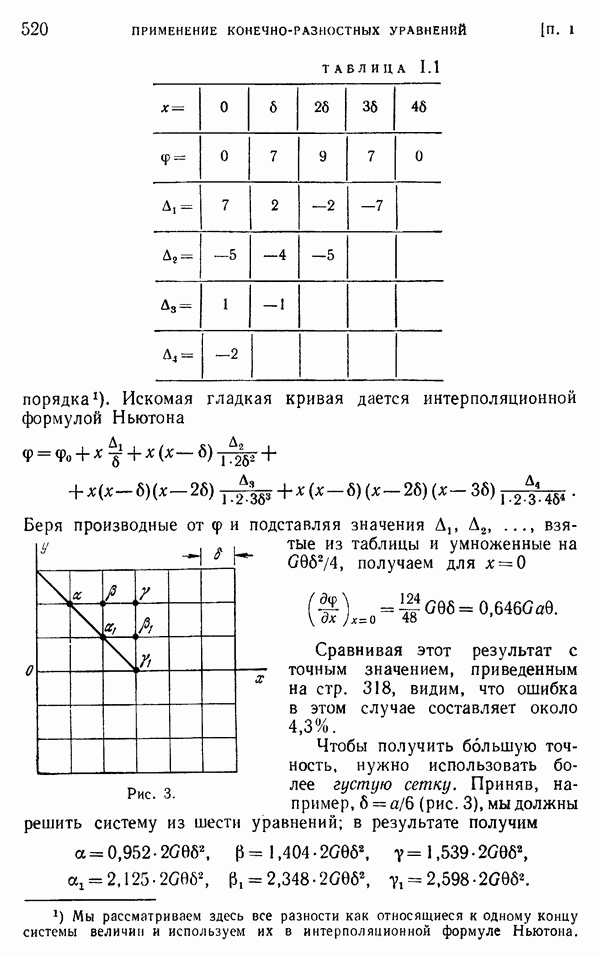
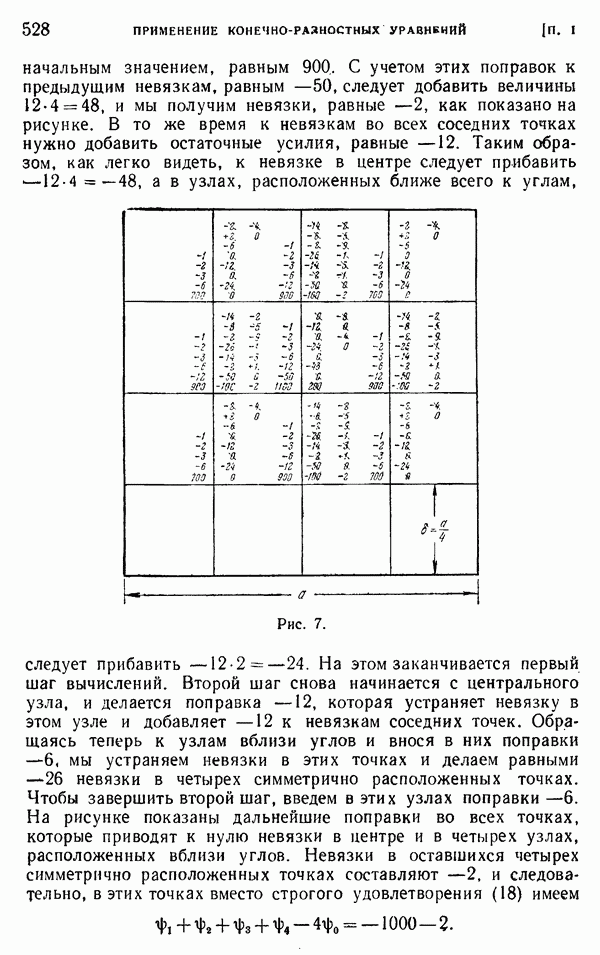
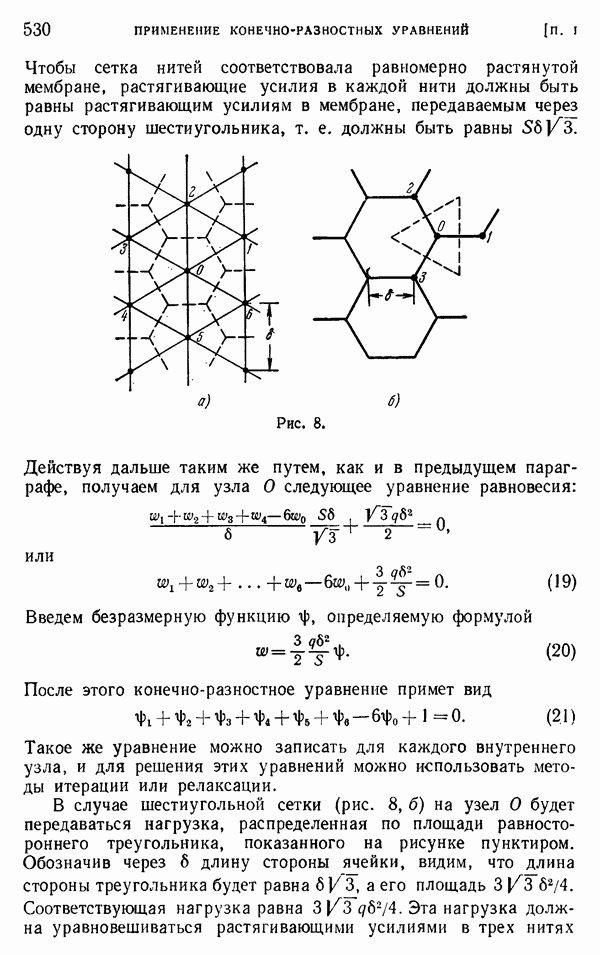
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
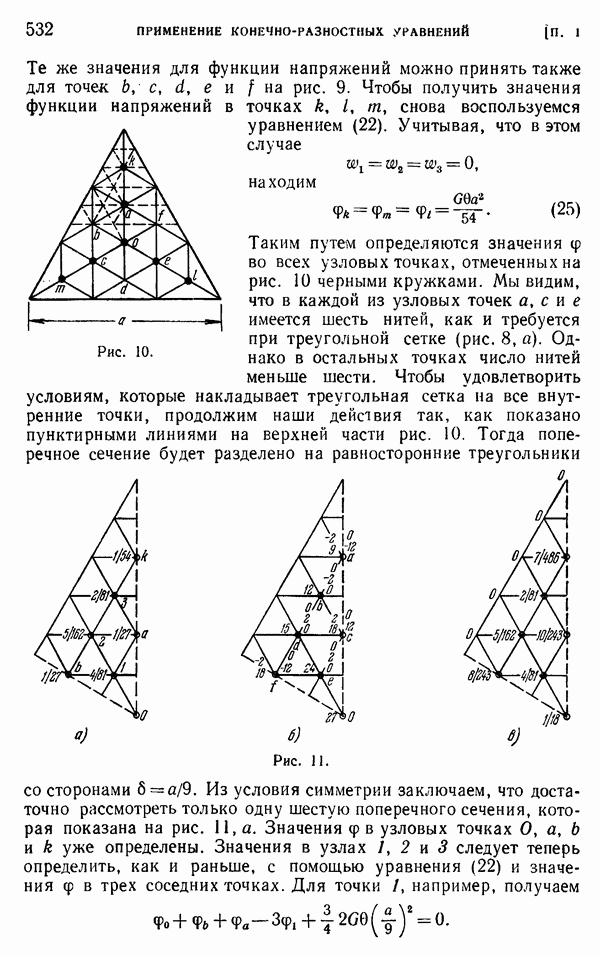
- § 4. Треугольные и шестиугольные сетки
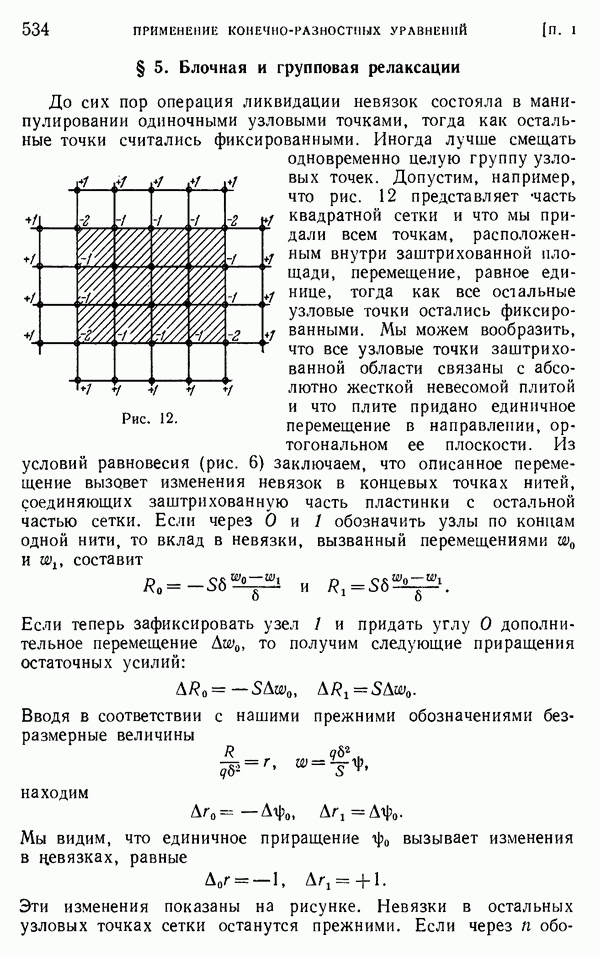
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
- § 7. Точки, расположенные вблизи границы
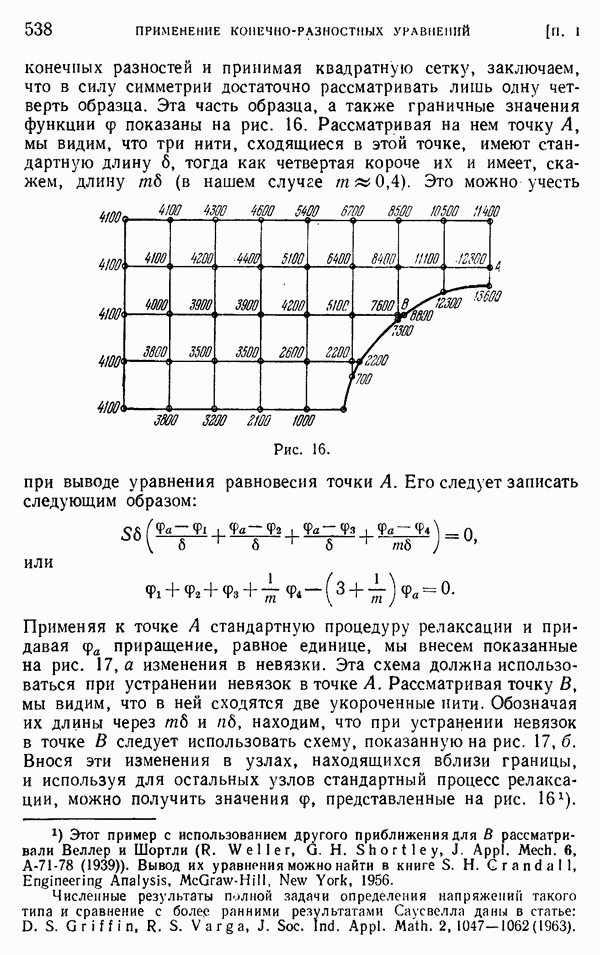
- § 8. Бигармоническое уравнение
- § 9. Кручение круглых валов переменного диаметра
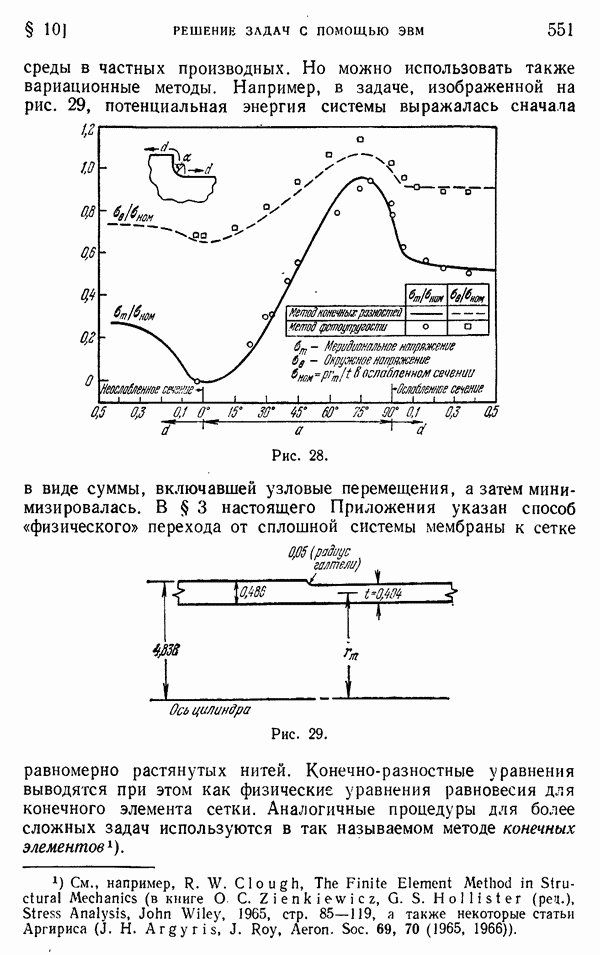
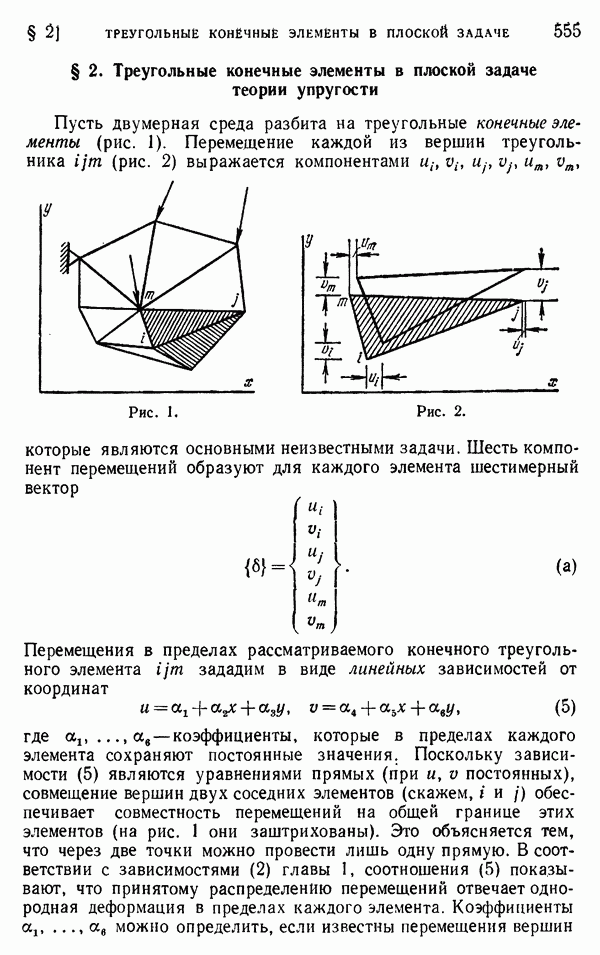
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
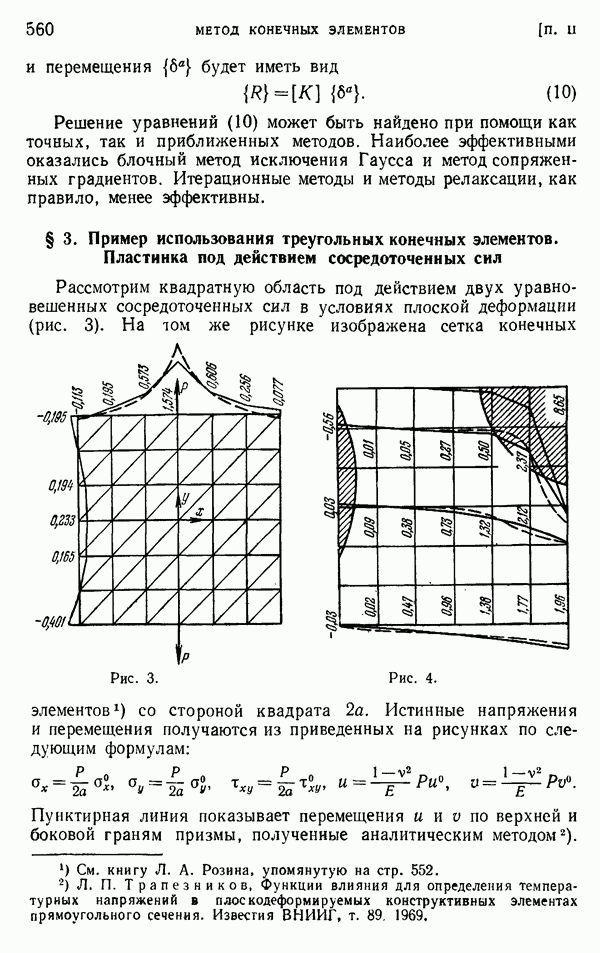
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
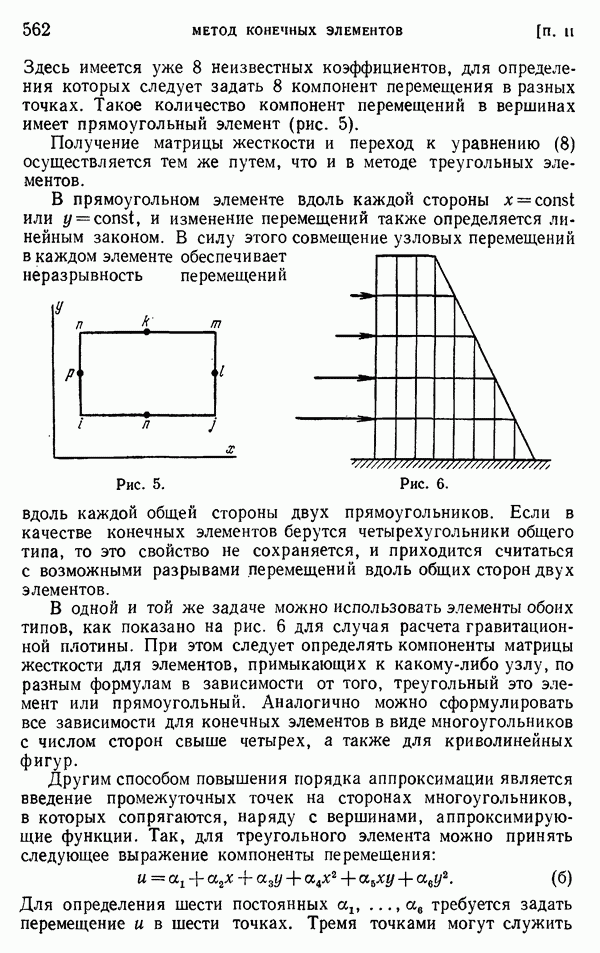
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
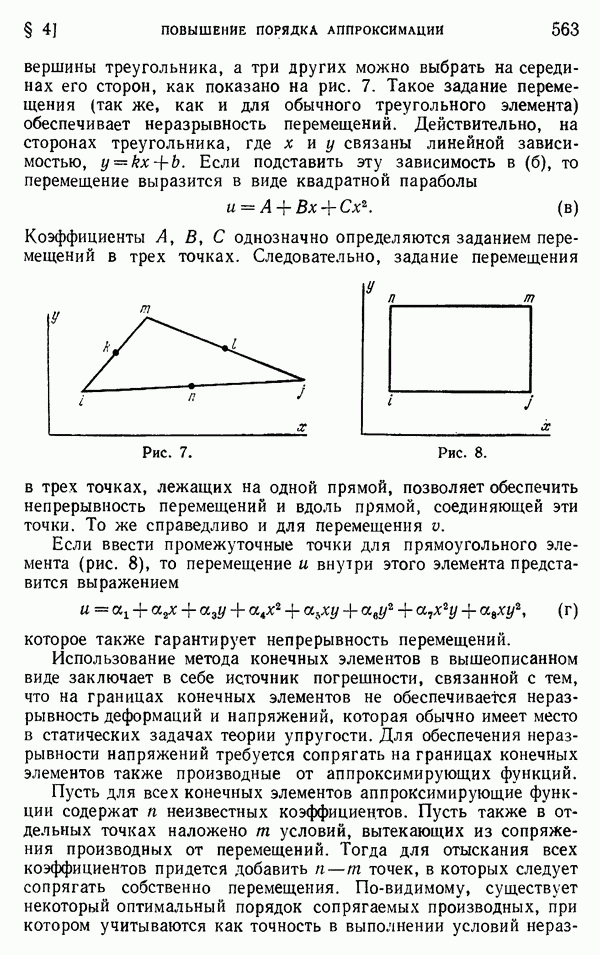
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи