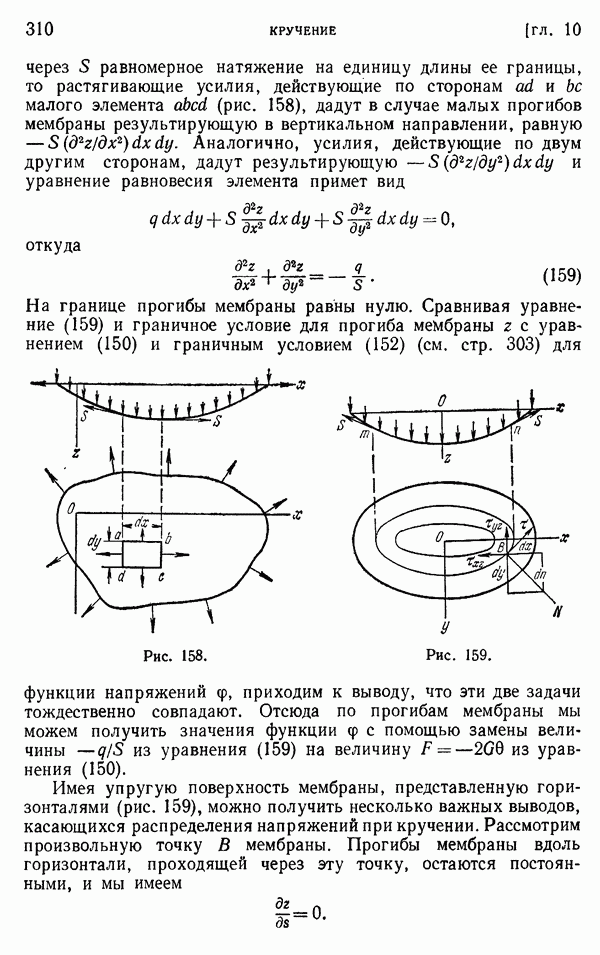
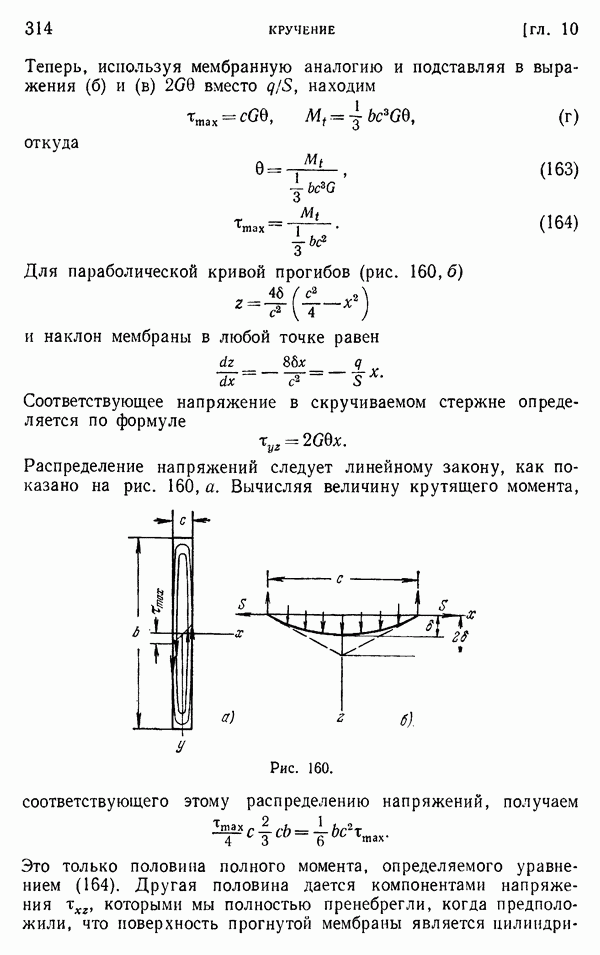
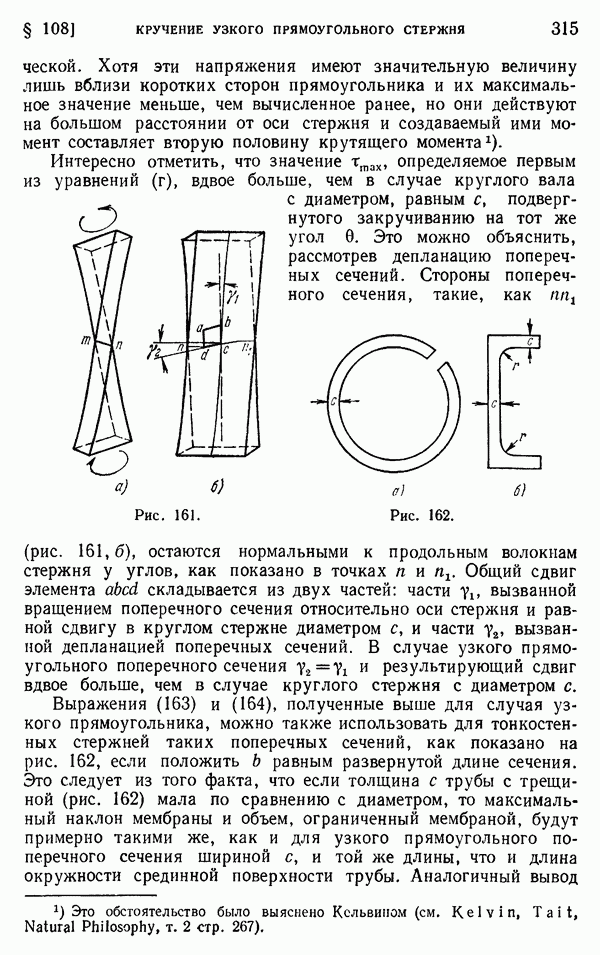
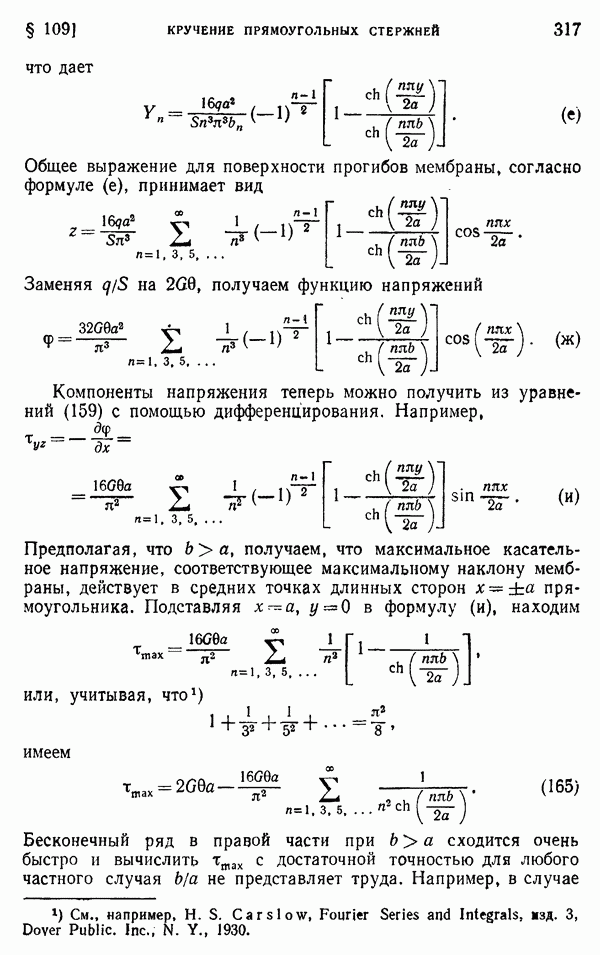
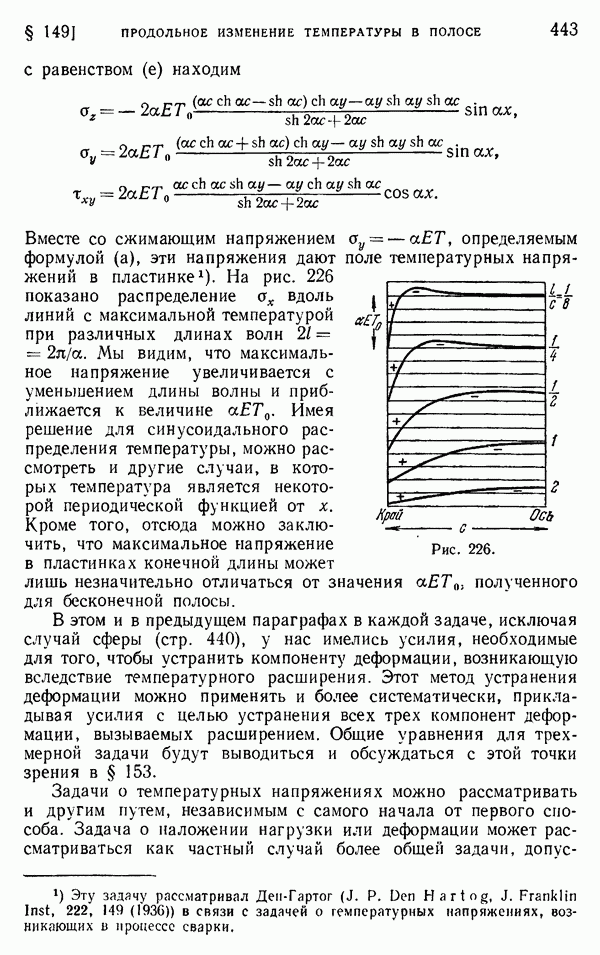
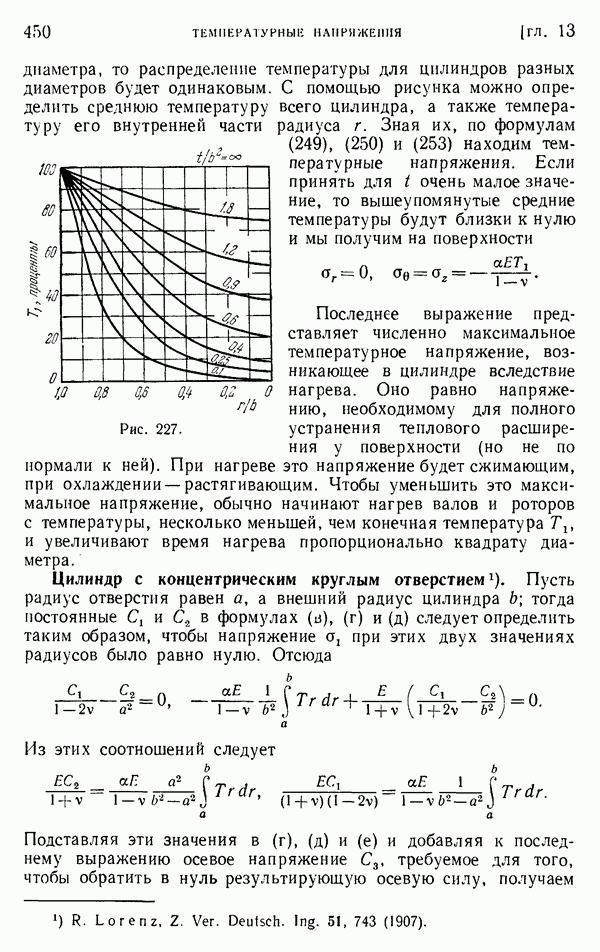
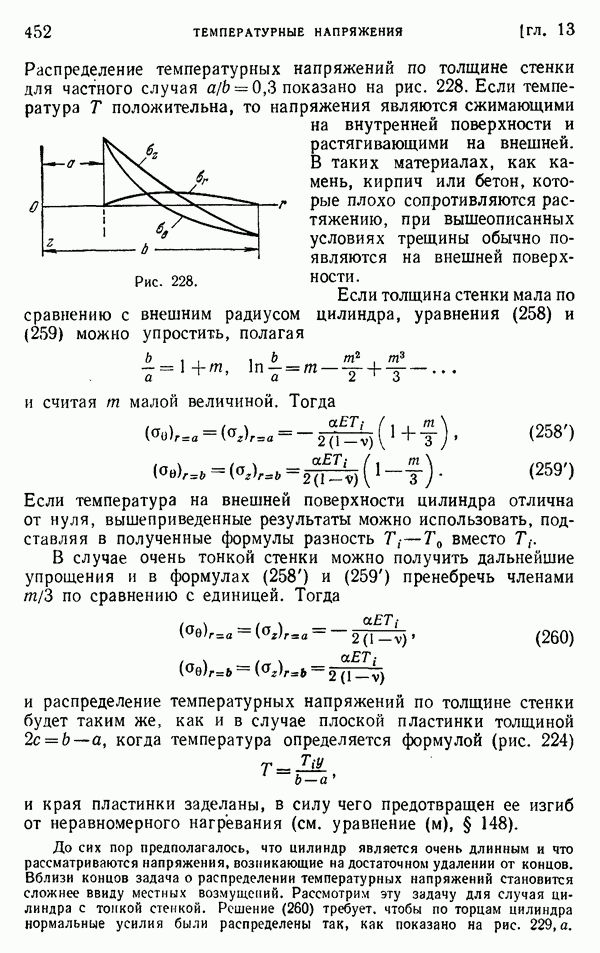
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 162. Решения общих уравнений. Термоупругий потенциал перемещения
Любое частное решение уравнений (264) сводит задачу об определении температурных напряжений к обычной задаче о действии на тело поверхностных сил. Решение для  с помощью равенств (а) и (б) § 153 и с использованием уравнений (2) приводит к значениям компонент напряжений. Требуемые поверхностные усилия, которые должны действовать вместе с неоднородным распределением температуры, чтобы вызвать эти напряжения, находятся затем из уравнений (124). Устранение этих усилий с целью освобождения границ от нагрузки, для того чтобы напряжения вызывались исключительно неоднородным распределением температуры, представляет собой обычную задачу о действии нагрузок на поверхности упругого тела.
с помощью равенств (а) и (б) § 153 и с использованием уравнений (2) приводит к значениям компонент напряжений. Требуемые поверхностные усилия, которые должны действовать вместе с неоднородным распределением температуры, чтобы вызвать эти напряжения, находятся затем из уравнений (124). Устранение этих усилий с целью освобождения границ от нагрузки, для того чтобы напряжения вызывались исключительно неоднородным распределением температуры, представляет собой обычную задачу о действии нагрузок на поверхности упругого тела.
Один из способов получения частных решений уравнений (264) состоит в том, что принимается

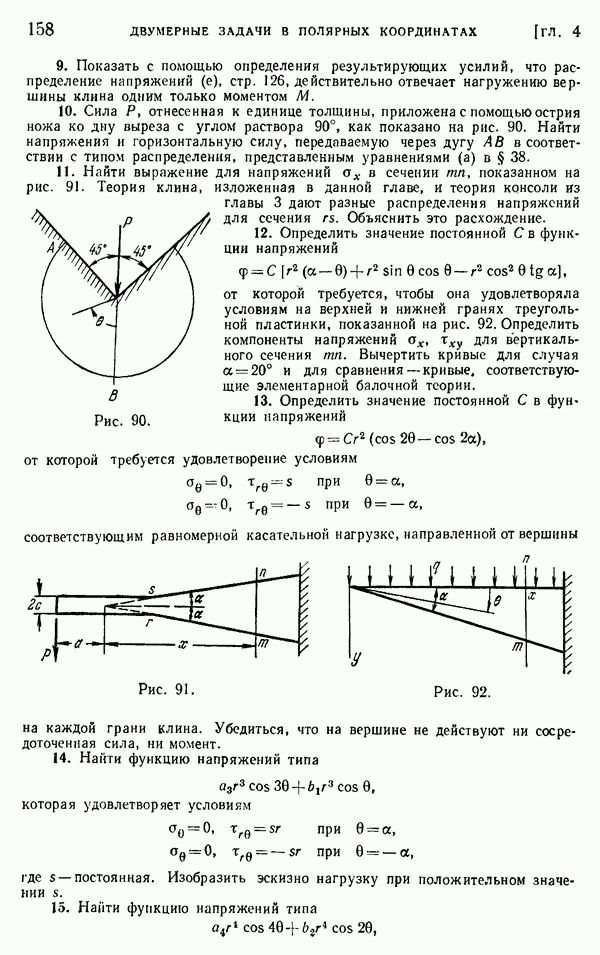
где  — функция переменных
— функция переменных  а также времени
а также времени  если температура меняется со временем. Такая функция называется термоупругим потенциалом, перемещений.
если температура меняется со временем. Такая функция называется термоупругим потенциалом, перемещений.
Используя формулы (5) и (10), мы можем записать уравнения (264) в форме

Поскольку  уравнения (а) приводят к формуле
уравнения (а) приводят к формуле  а соотношения (б) принимают вид
а соотношения (б) принимают вид

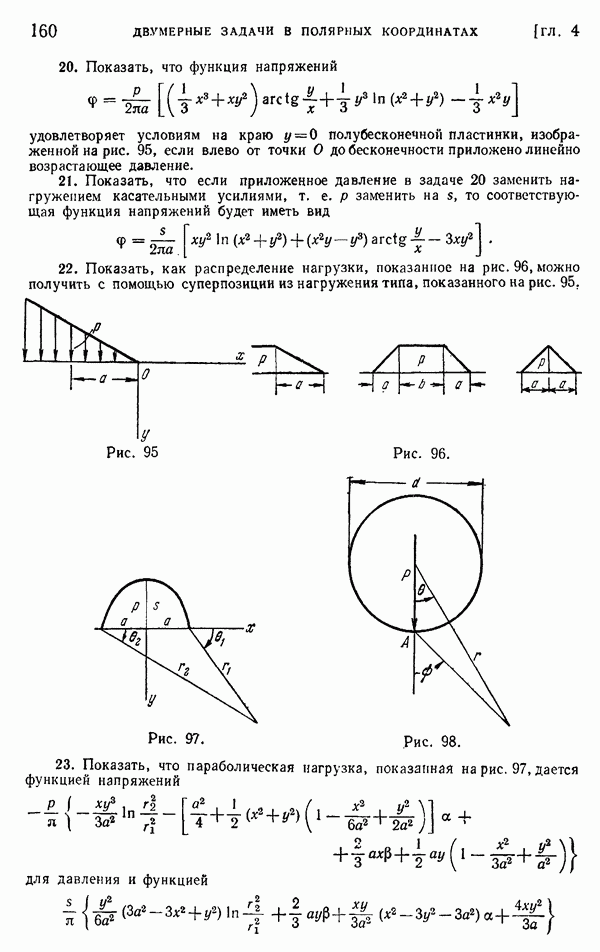
(второе и третье уравнения получены из первого заменой  на
на  Все эти три уравнения, очевидно, будут удовлетворяться, если принять функцию
Все эти три уравнения, очевидно, будут удовлетворяться, если принять функцию  в форме решения уравнения
в форме решения уравнения

Решения уравнений этого типа рассматриваются в теории потенциала. Решение можно выписать в виде потенциала тяготения для распределения
вещества с плотностью  который выражаегся формулой
который выражаегся формулой

где  температура точки с координатами
температура точки с координатами  , определяющими положение элемента объема
, определяющими положение элемента объема  — расстояние между этой точкой и точкой с координатами
— расстояние между этой точкой и точкой с координатами  Уравнение (д) дает полное решение задачи о температурных напряжениях в бесконечном теле, в котором температура равна нулю всюду, кроме некоторой нагретой или охлажденной области. Исследованы случаи, когда такая область имеет форму эллипсоида вращения и равномерно нагретого полубесконечного круглого цилиндра. Для случая области в виде эллипсоида максимальное напряжение, которое может возникнуть, равно
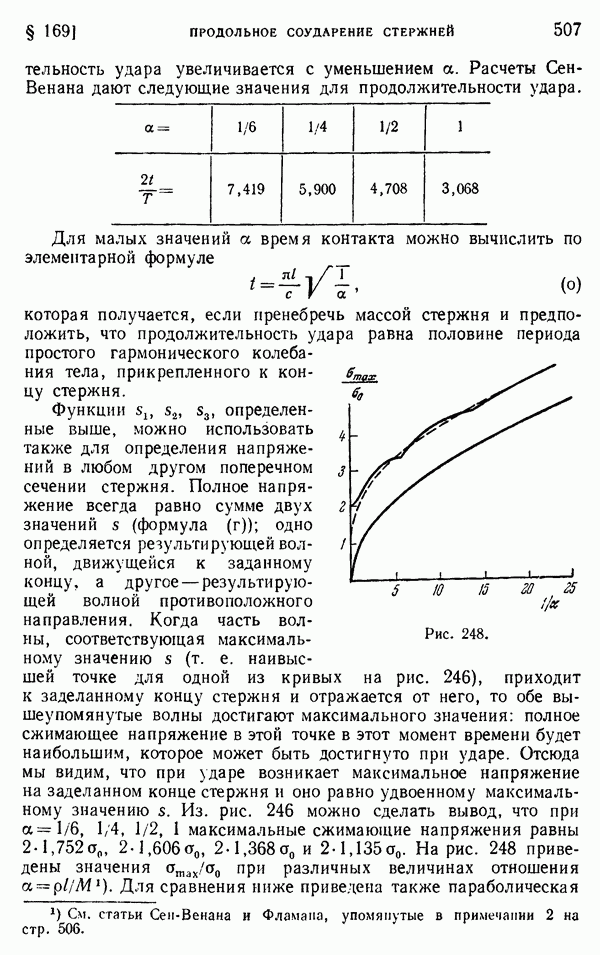
Уравнение (д) дает полное решение задачи о температурных напряжениях в бесконечном теле, в котором температура равна нулю всюду, кроме некоторой нагретой или охлажденной области. Исследованы случаи, когда такая область имеет форму эллипсоида вращения и равномерно нагретого полубесконечного круглого цилиндра. Для случая области в виде эллипсоида максимальное напряжение, которое может возникнуть, равно  и направлено по нормали к поверхности эллипсоида в точках наибольшей кривизны образующего эллипса. Такая величина напряжения встречается лишь для двух предельных случаев сильно сплюснутого или сильно вытянутого эллипсоидов вращения. В промежуточных случаях максимальные напряжения уменьшаются, а для сферической области соответствующее значение составляет две трети от вышеприведенного.
и направлено по нормали к поверхности эллипсоида в точках наибольшей кривизны образующего эллипса. Такая величина напряжения встречается лишь для двух предельных случаев сильно сплюснутого или сильно вытянутого эллипсоидов вращения. В промежуточных случаях максимальные напряжения уменьшаются, а для сферической области соответствующее значение составляет две трети от вышеприведенного.
Когда Т не зависит от  получаем случай плоской деформации, в котором
получаем случай плоской деформации, в котором  , u и v не зависят от
, u и v не зависят от  . Уравнение (г) принимает вид
. Уравнение (г) принимает вид

Его частное решение дает логарифмический потенциал

где

Для тонкой пластинки при постоянной по толщине температуре Т мы можем считать напряженное состояние плоским, т. е. считать, что  и функции
и функции  не зависят от
не зависят от  . Тогда зависимости между напряжениями и
. Тогда зависимости между напряжениями и  не зависят от
не зависят от  Уравнение
Уравнение  принимает вид
принимает вид

Подставляя эти значения напряжений в уравнения равновесия (18), при
отсутствии объемных сил получаем равенства

Эти уравнения удовлетворяются, если принять

где  — решение уравнения
— решение уравнения

Сравнивая (м) с уравнением (е), мы видим, что частное решение (м) дается логарифмическим потенциалом  которого в знаменателе отброшен множитель
которого в знаменателе отброшен множитель  . Это дает полное решение задачи о локальном нагреве в бесконечной пластинке, в которой напряжения и деформации на бесконечности должны стремиться к нулю.
. Это дает полное решение задачи о локальном нагреве в бесконечной пластинке, в которой напряжения и деформации на бесконечности должны стремиться к нулю.
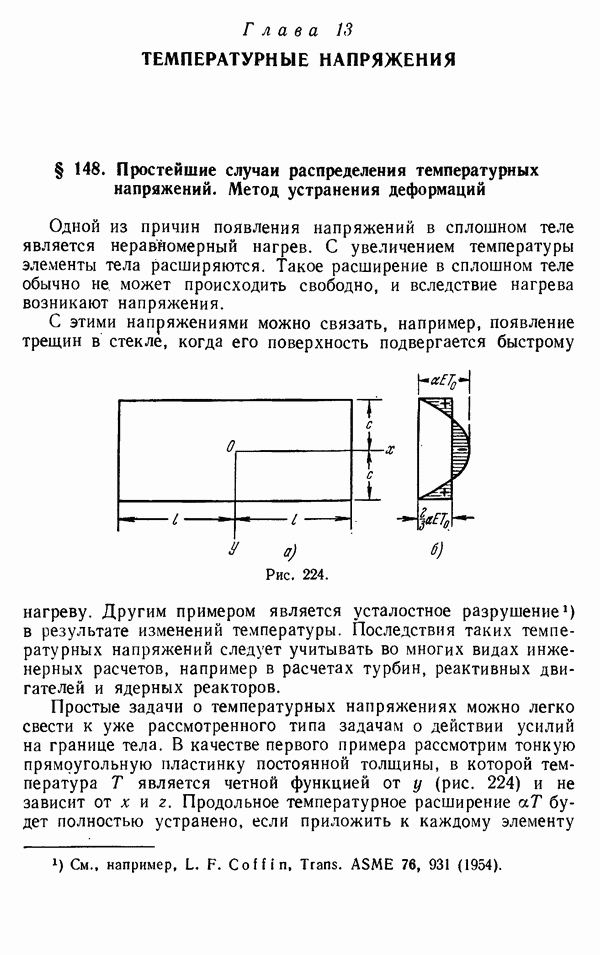
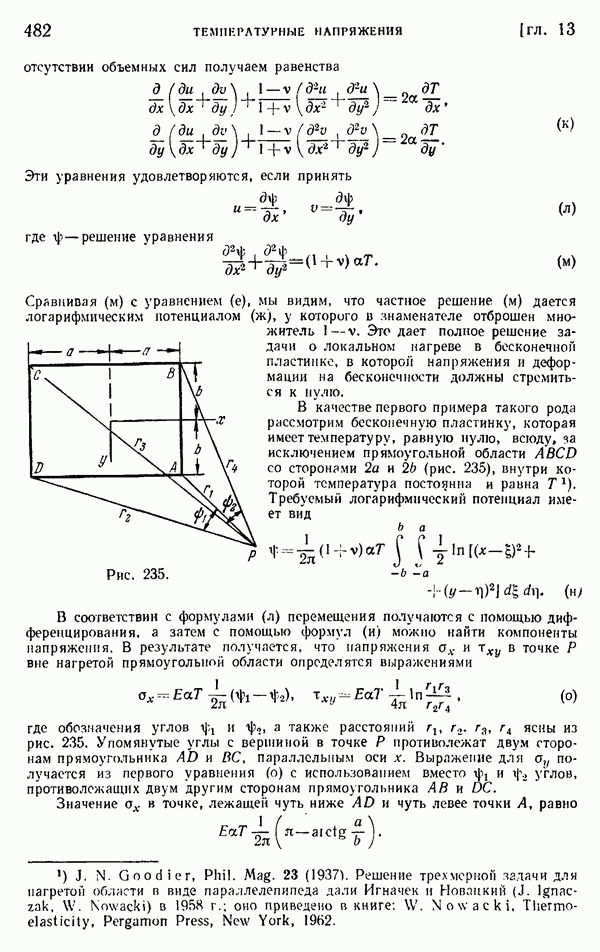
В качестве первого примера такого рода рассмотрим бесконечную пластинку, которая имеет температуру, равную нулю, всюду, за исключением прямоугольной области  со сторонами
со сторонами  (рис. 235), внутри которой температура постоянна и равна. Требуемый логарифмический потенциал имеет вид
(рис. 235), внутри которой температура постоянна и равна. Требуемый логарифмический потенциал имеет вид


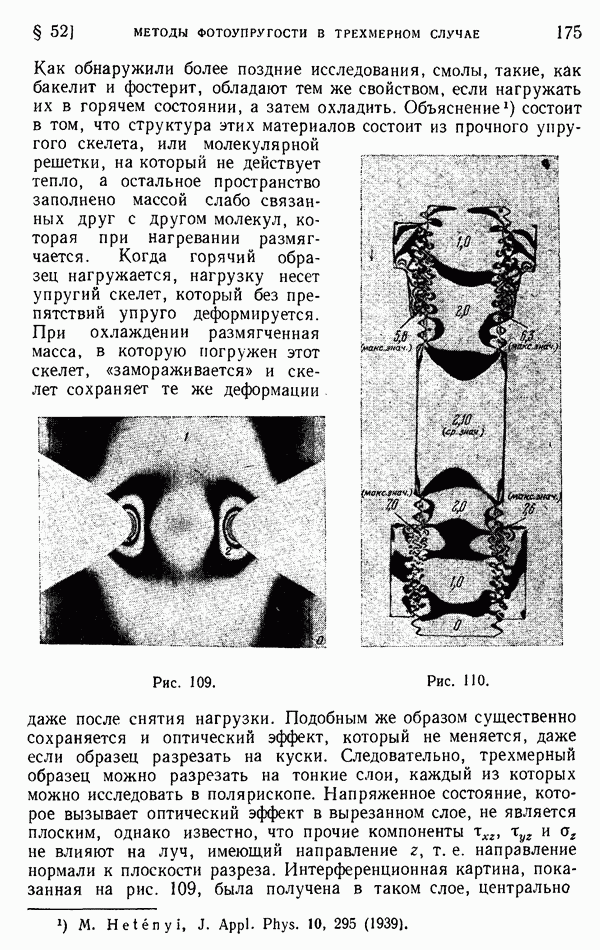
Рис. 235.
В соответствии с формулами  перемещения получаются с помощью дифференцирования, а затем с помощью формул (и) можно найти компоненты напряжения. В результате получается, что напряжения
перемещения получаются с помощью дифференцирования, а затем с помощью формул (и) можно найти компоненты напряжения. В результате получается, что напряжения  в точке Р вне нагретой прямоугольной области определятся выражениями
в точке Р вне нагретой прямоугольной области определятся выражениями

где обозначения углов  и а также расстояний
и а также расстояний  ясны из рис. 235. Упомянутые углы с вершиной в точке Р противолежат двум сторонам прямоугольника
ясны из рис. 235. Упомянутые углы с вершиной в точке Р противолежат двум сторонам прямоугольника  и
и  параллельным оси х. Выражение для
параллельным оси х. Выражение для  получается из первого уравнения (о) с использованием вместо и
получается из первого уравнения (о) с использованием вместо и  углов, противолежащих двум другим сторонам прямоугольника
углов, противолежащих двум другим сторонам прямоугольника  и
и 
Значение  в точке, лежащей чуть ниже
в точке, лежащей чуть ниже  и чуть левее точки А, равно
и чуть левее точки А, равно

Для прямоугольника, бесконечно длинного в направлении оси  оно является наибольшим и составляет
оно является наибольшим и составляет  При обходе вокруг угла прямоугольника обе нормальные компоненты напряжений резко меняются. Касательное напряжение
При обходе вокруг угла прямоугольника обе нормальные компоненты напряжений резко меняются. Касательное напряжение  при приближении к углу стремится к бесконечности. Эти особенности являются, разумеется, следствием идеальной заостренности углов нагретого прямоугольника.
при приближении к углу стремится к бесконечности. Эти особенности являются, разумеется, следствием идеальной заостренности углов нагретого прямоугольника.
Если нагретая область имеет не прямоугольную, а эллиптическую форму 1), с границей, заданной уравнением эллипса

то значение напряжения  вблизи эллиптической границы, но вне ее, у конца большой оси составляет
вблизи эллиптической границы, но вне ее, у конца большой оси составляет

что для очень узкого эллипса приближается к  Если нагретая область является кругом, то напряжение
Если нагретая область является кругом, то напряжение  в этой точке равно
в этой точке равно  Значение
Значение  конца малой оси составляет
конца малой оси составляет

и для очень узкого эллипса приближается к нулю.
Метод, изложенный в этом параграфе, становится особенно простым, когда температура, меняясь со временем, удовлетворяет дифференциальному уравнению теплопроводности 2)

где х — коэффициент теплопроводности, деленный на теплоемкость и плотность. Дифференцируя уравнение (г) по  и затем подставляя выражение для
и затем подставляя выражение для  из формулы
из формулы  находим, что функция
находим, что функция  должна удовлетворять уравнению
должна удовлетворять уравнению

Следовательно, можно принять

Интеграл от этого выражения, пригодный для случая, когда температура со временем стремится к нулю, имеет вид

в чем можно убедиться путем подстановки  в уравнение (г) и использования уравнения
в уравнение (г) и использования уравнения 
В качестве примера рассмотрим длинный круговой цилиндр (случай плоской деформации), который охлаждается или нагревается до стационарного состояния. Распределение температуры не симметрично относительно оси, но не зависит от осевой координаты  Температура в этом случае представляется
Температура в этом случае представляется
в форме ряда, члены которого имеют вид

где действительные и мнимые части  равны
равны  Согласно уравнению (а) функция
Согласно уравнению (а) функция  соответствующая этому температурному члену, будет иметь следующее выражение:
соответствующая этому температурному члену, будет иметь следующее выражение:

Ряд таких членов, отвечающий ряду для температуры Т, будет представлять частное решение общих уравнений (б). Перемещения можно вычислить с помощью уравнений (а) или их аналогов в полярных координатах:

где и и V — радиальная и окружная компоненты перемещения. Осевая компонента  в случае плоской деформации равна нулю.
в случае плоской деформации равна нулю.
Компоненты деформации получаются с использованием результатов § 30. Компоненты напряжений после этого можно найти по формулам (а) и (б) для плоской деформации из § 153, а для компоненты  воспользоваться последним из уравнений (51).
воспользоваться последним из уравнений (51).
Когда такое решение получено, то в общем случае оказывается, что оно дает ненулевые усилия  на криволинейной поверхности цилиндра. Влияние устранения этих усилий находится с помощью решения обычной задачи для плоской деформации с использованием общей функции напряжений в полярных координатах, приведенной в § 431).
на криволинейной поверхности цилиндра. Влияние устранения этих усилий находится с помощью решения обычной задачи для плоской деформации с использованием общей функции напряжений в полярных координатах, приведенной в § 431).
В более общем случае можно включать в условия задачи внутреннее выделение тепла в единице объема со скоростью  Тогда к правой части уравнения (п) нужно добавить член
Тогда к правой части уравнения (п) нужно добавить член  где с — теплоемкость,
где с — теплоемкость,  плотность. Выражение
плотность. Выражение

удовлетворяет уравнению (г), если

Здесь  в общем случае является функцией как переменной
в общем случае является функцией как переменной  так и переменных
так и переменных  а через
а через  обозначена температура Т в момент
обозначена температура Т в момент 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
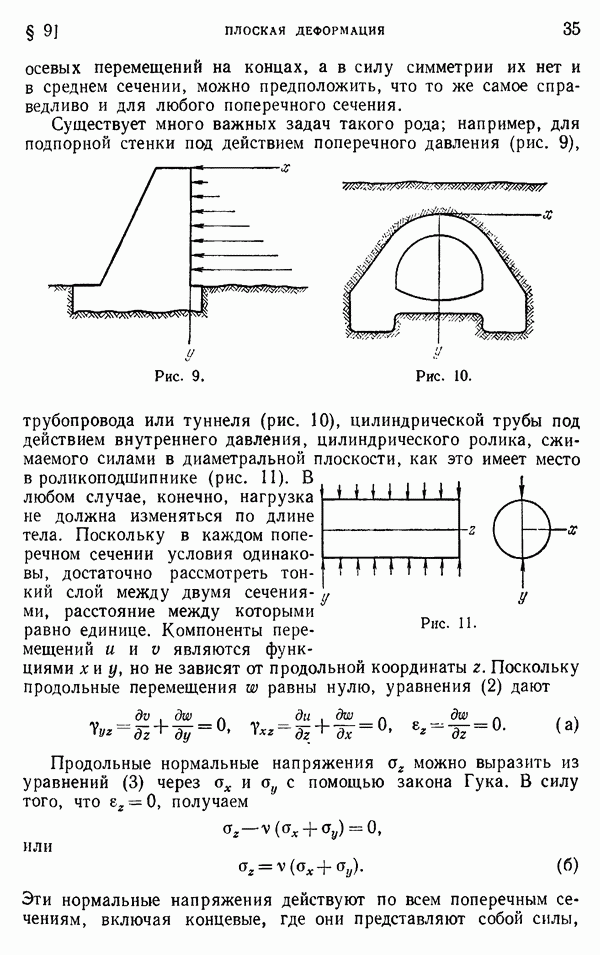
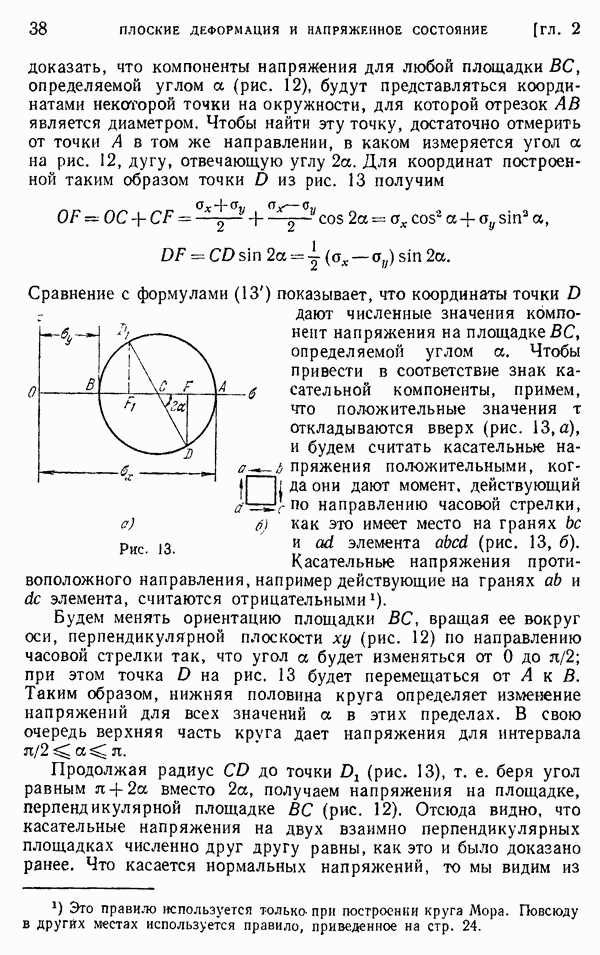
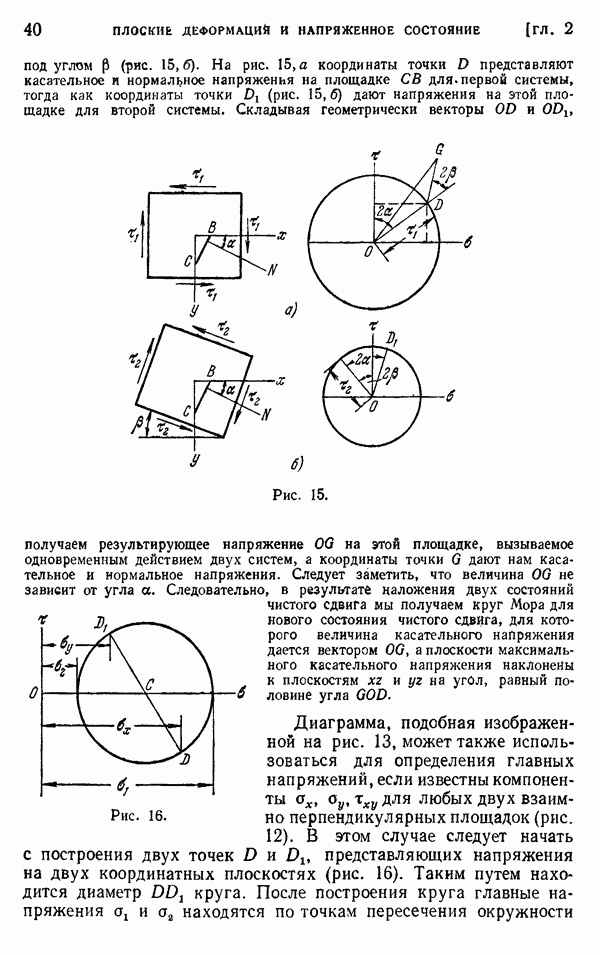
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
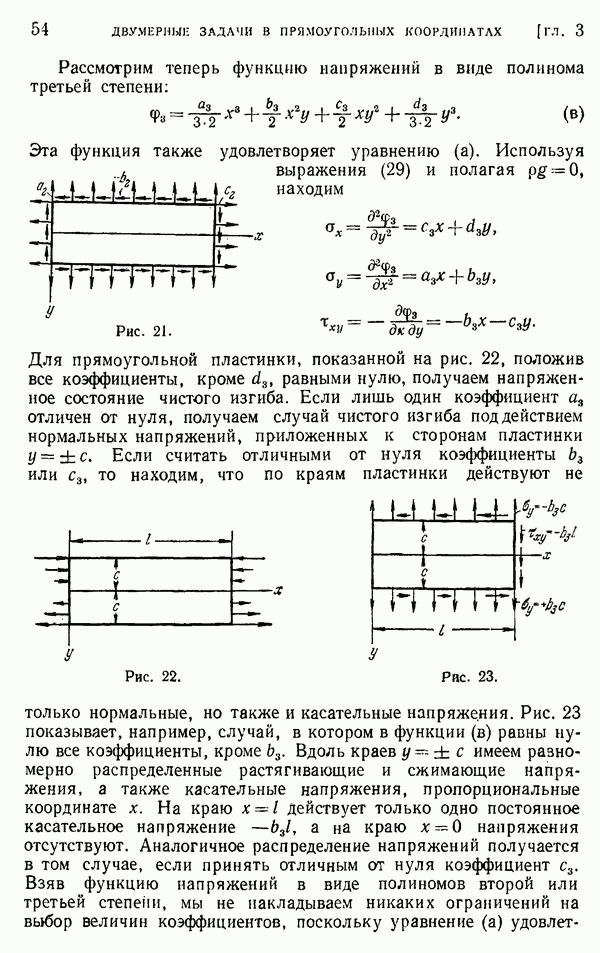
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
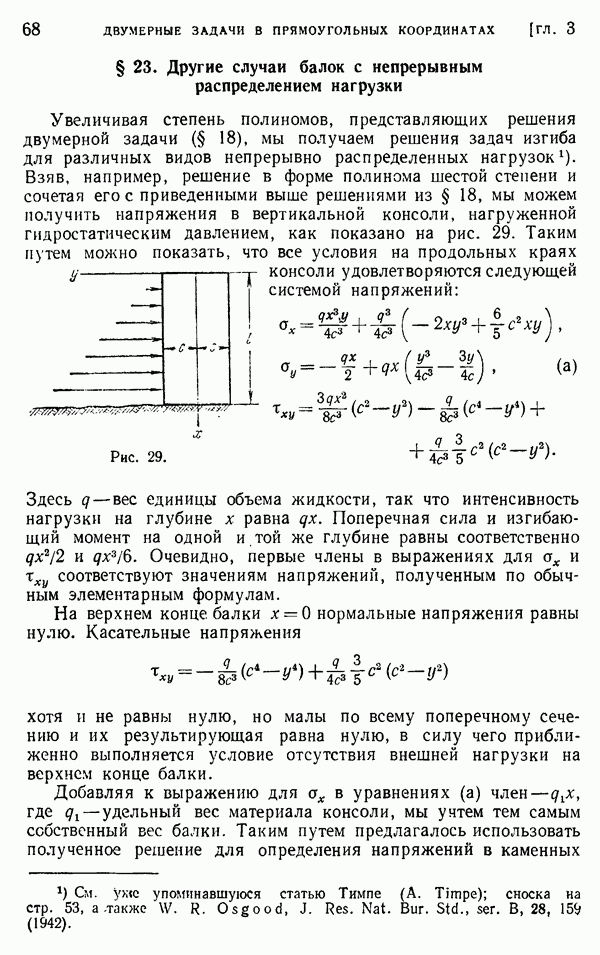
- § 23. Другие случаи балок с непрерывным распределением нагрузки
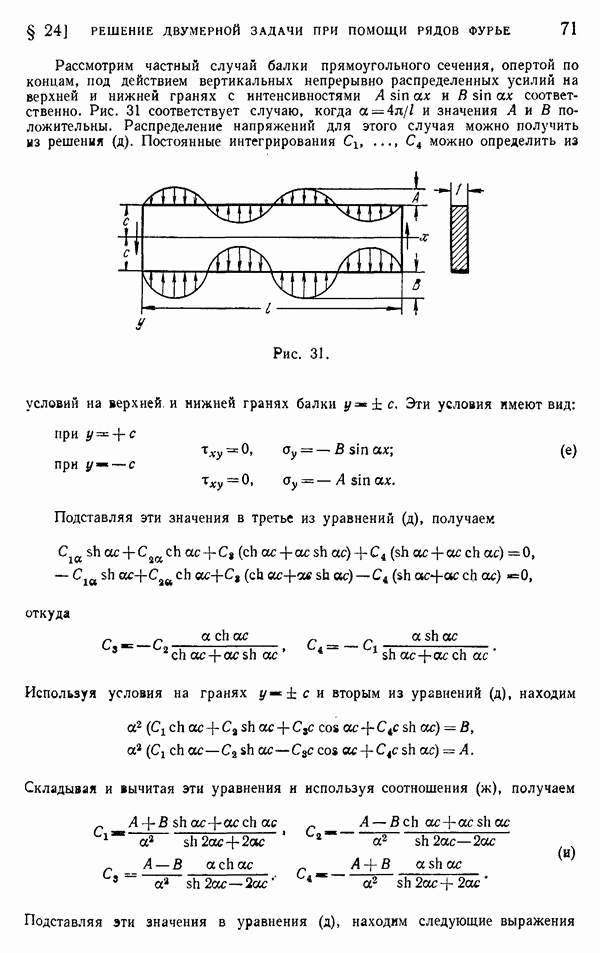
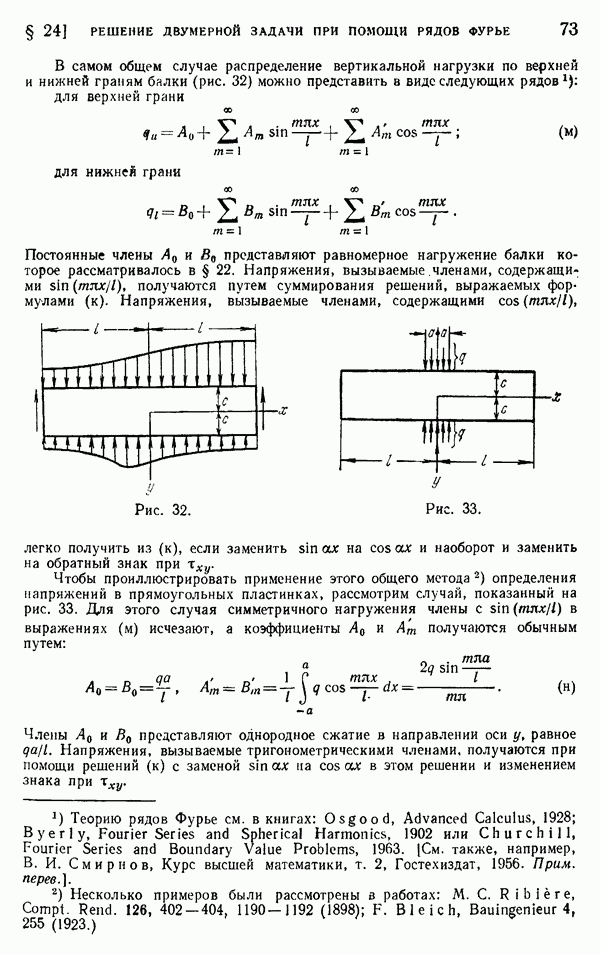
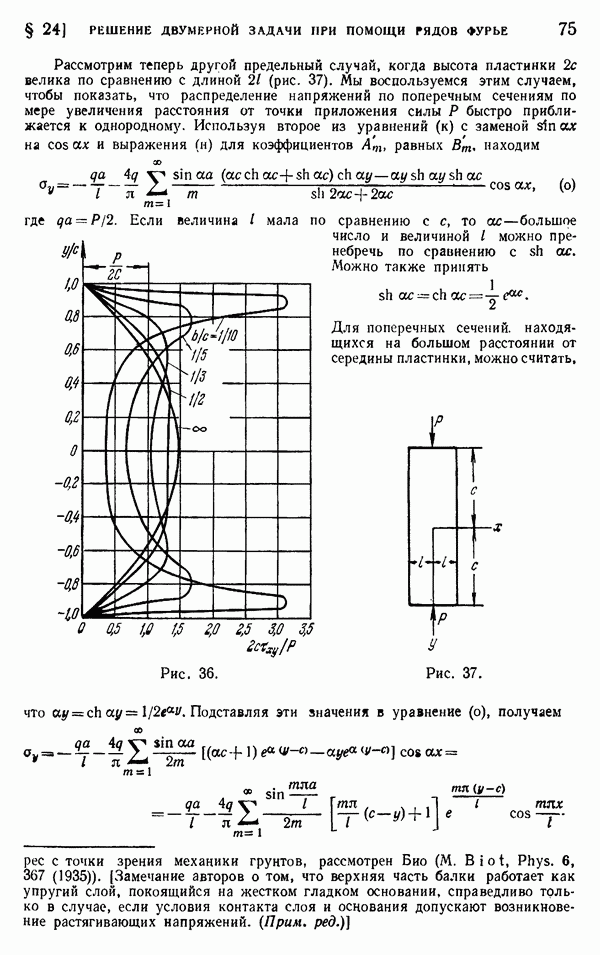
- § 24. Решение двумерной задачи при помощи рядов Фурье
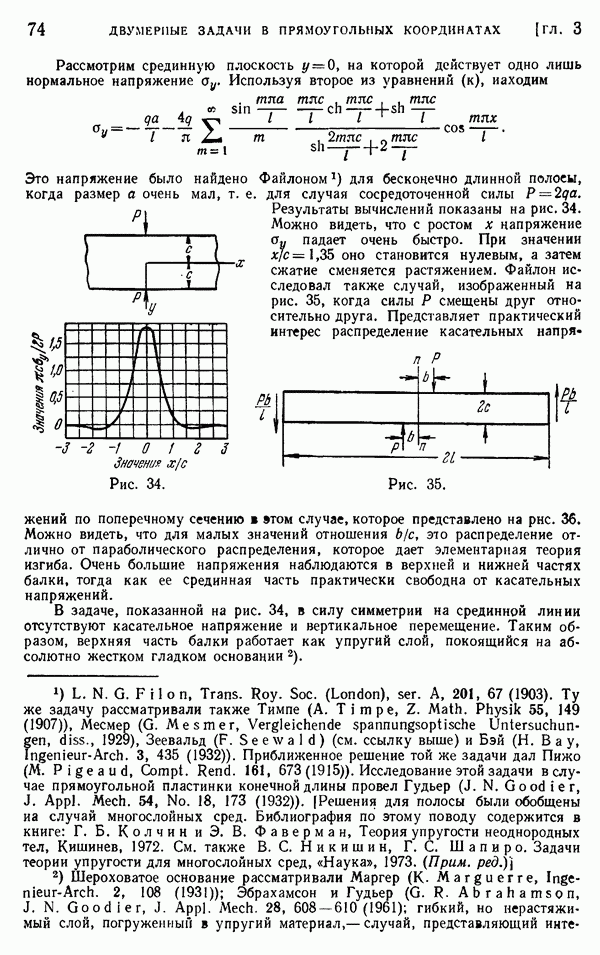
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
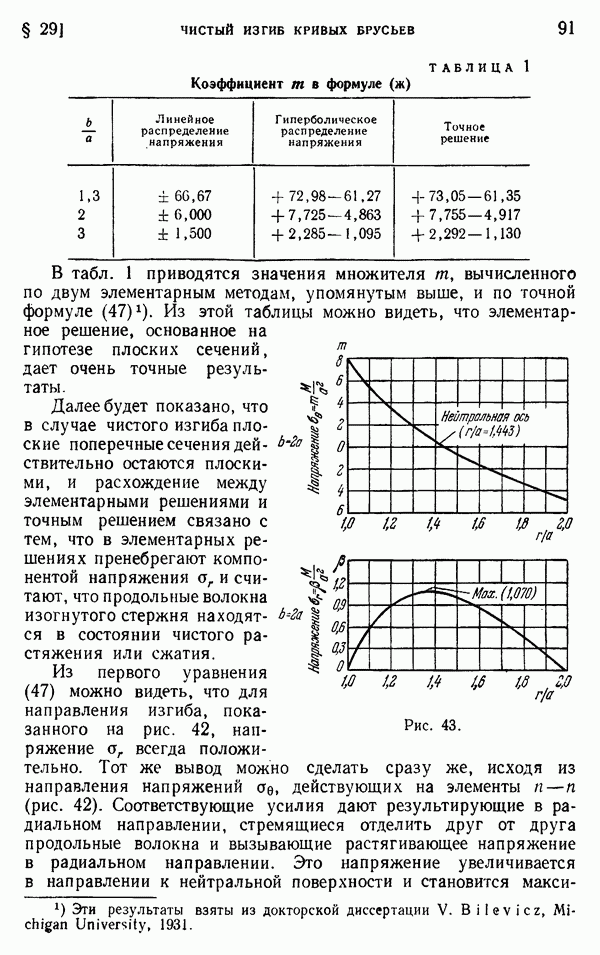
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
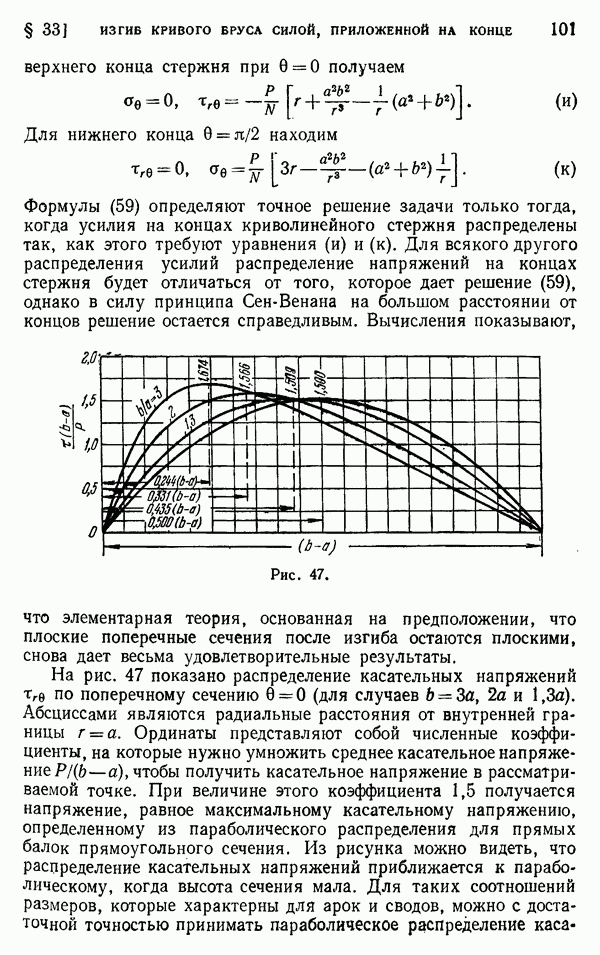
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
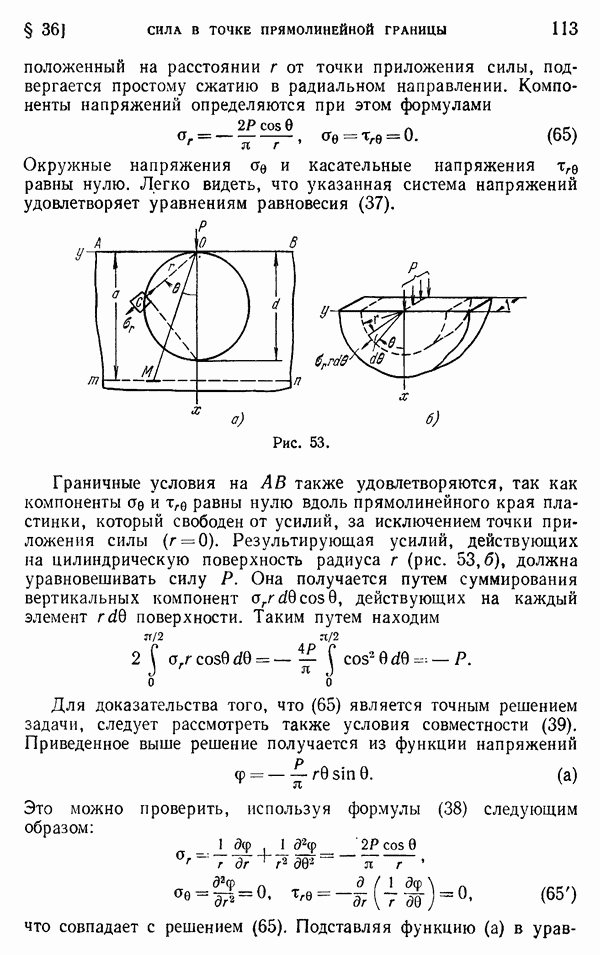
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
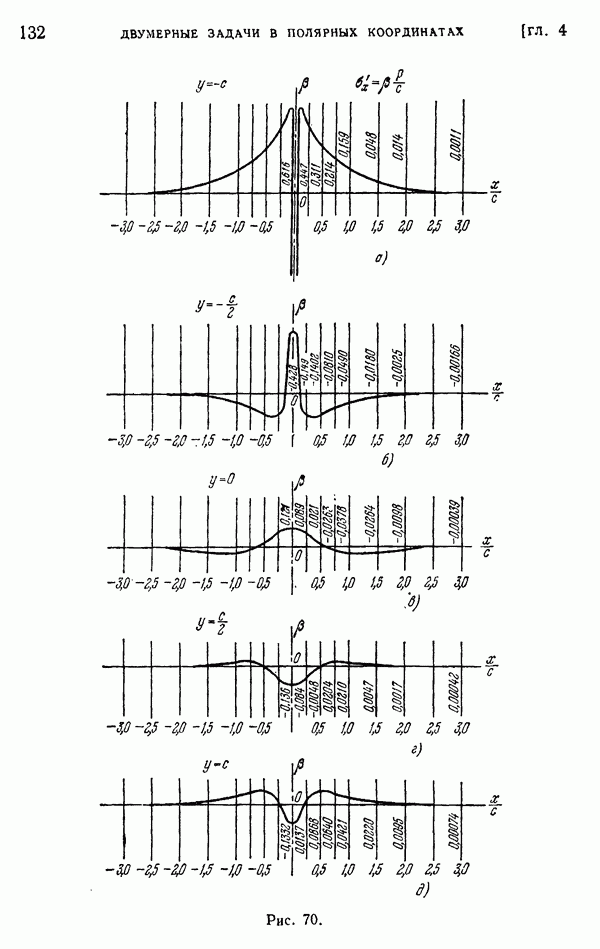
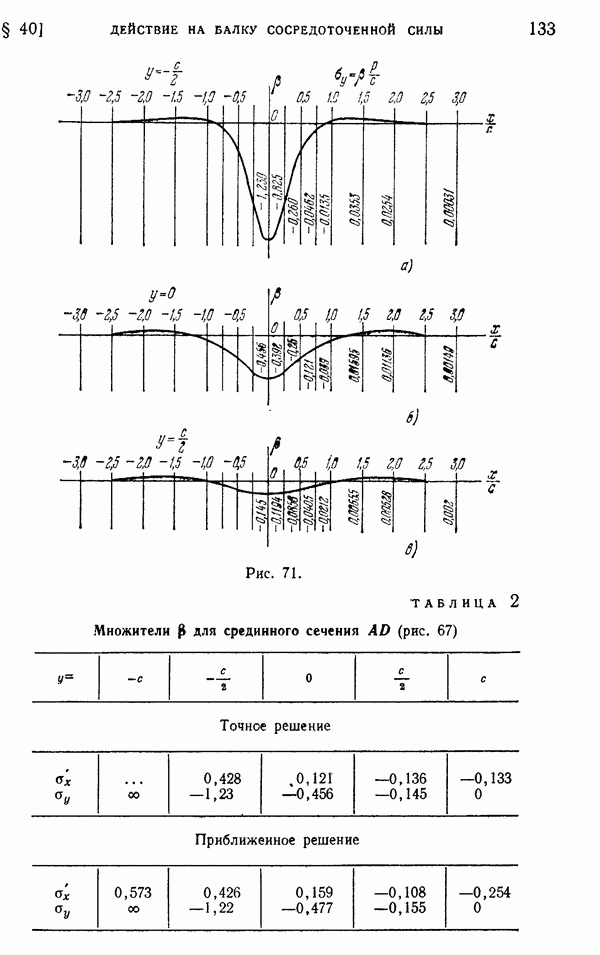
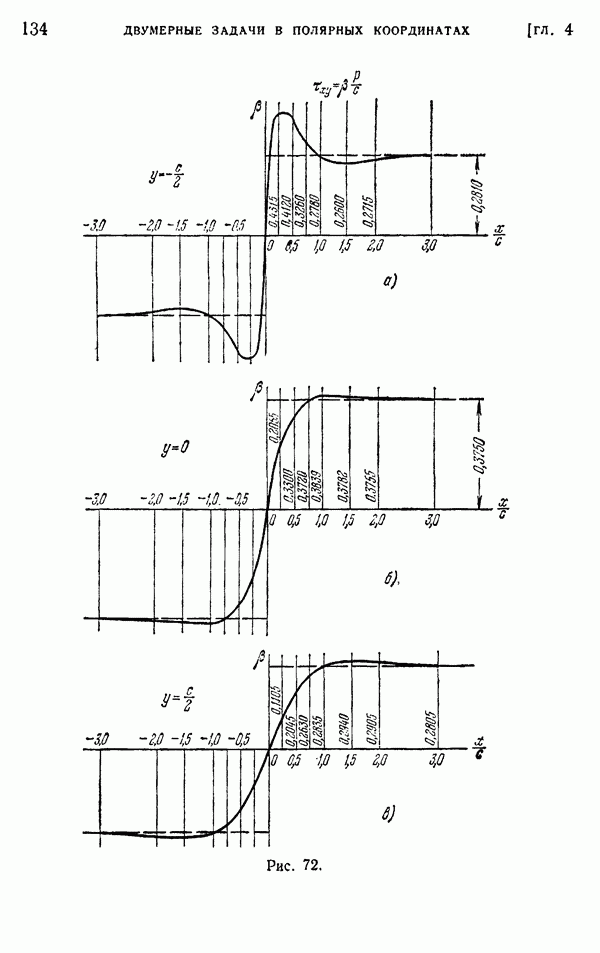
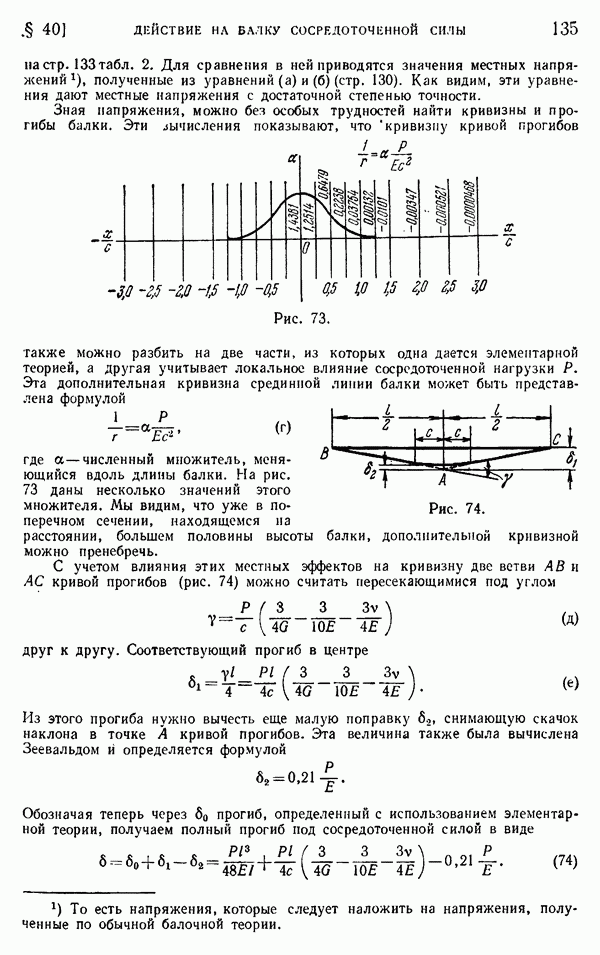
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
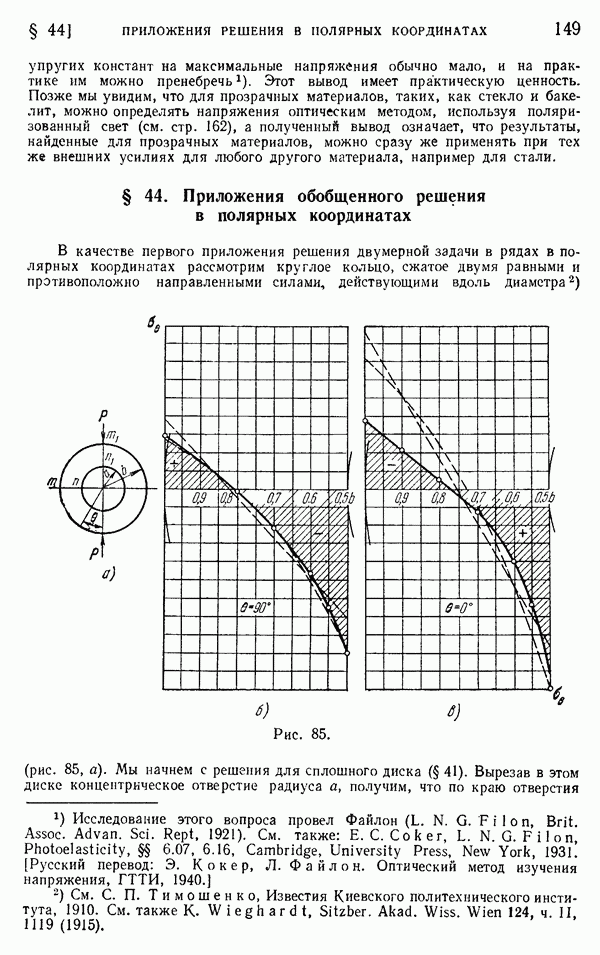
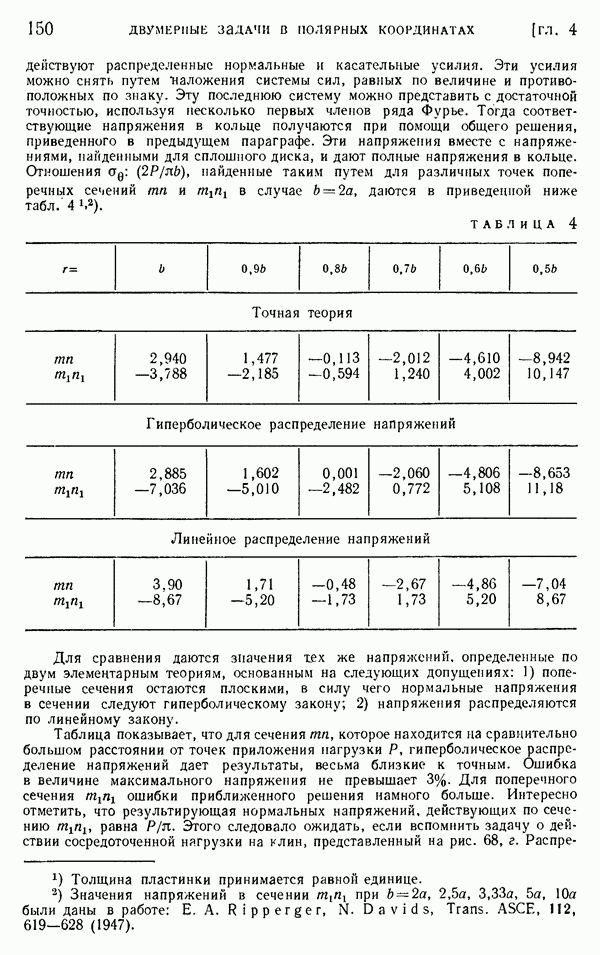
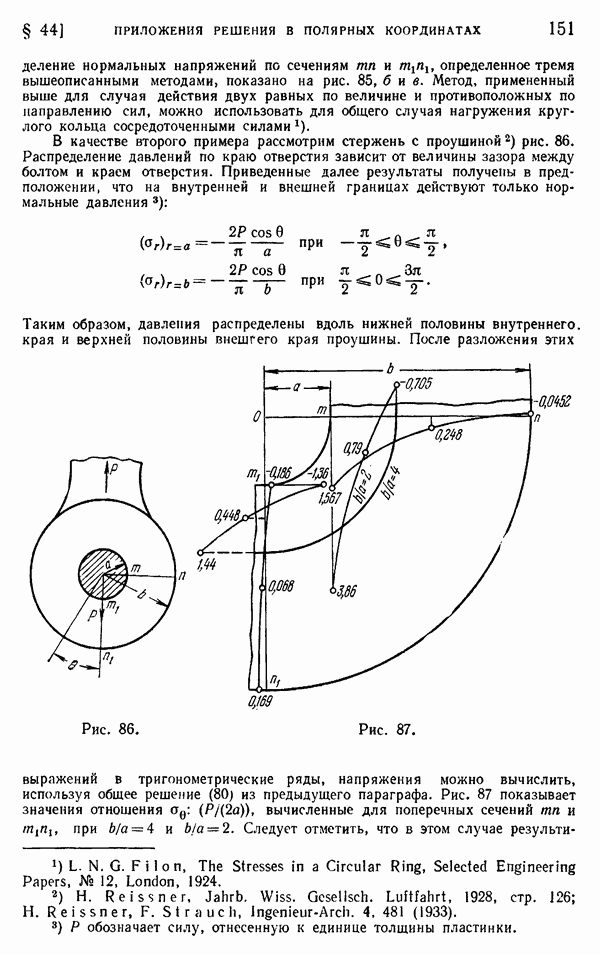
- § 43. Обобщенное решение двумерной задачи в полярных координатах
- § 44. Приложения обобщенного решения в полярных координатах
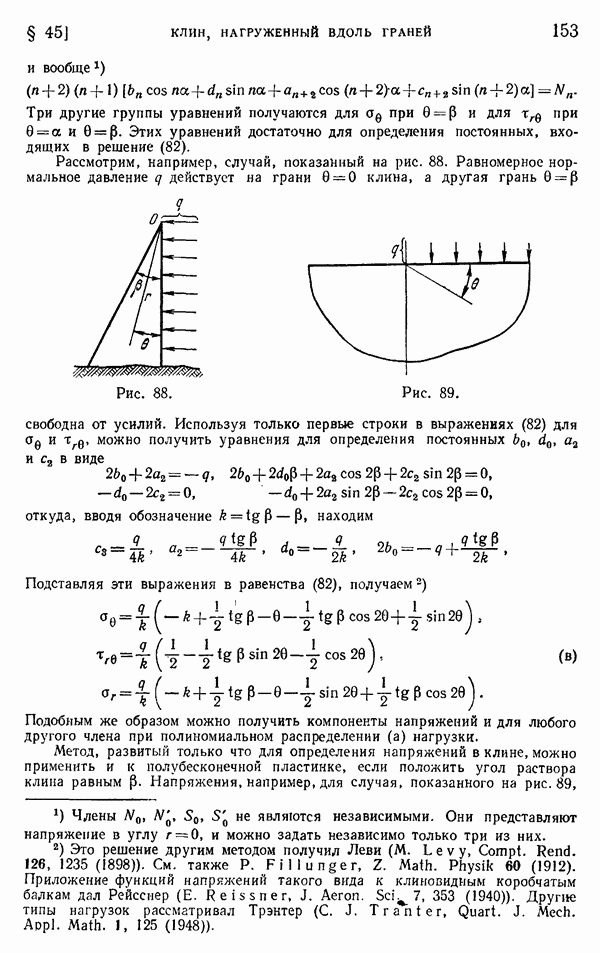
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
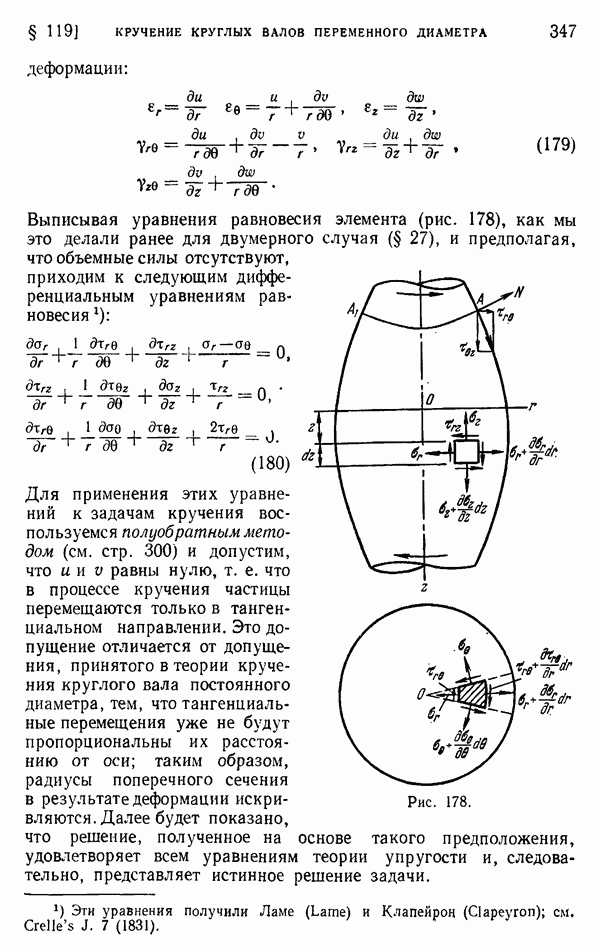
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
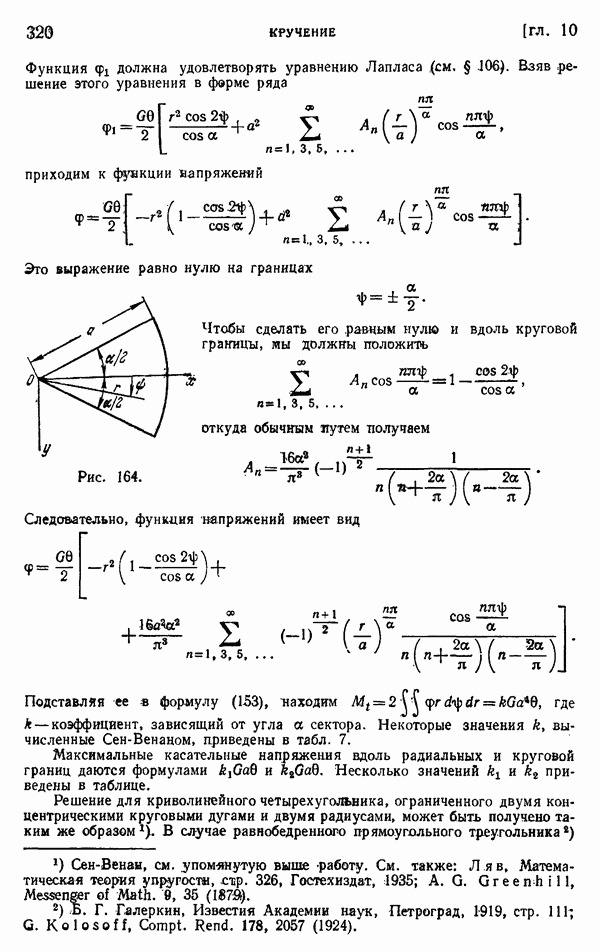
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
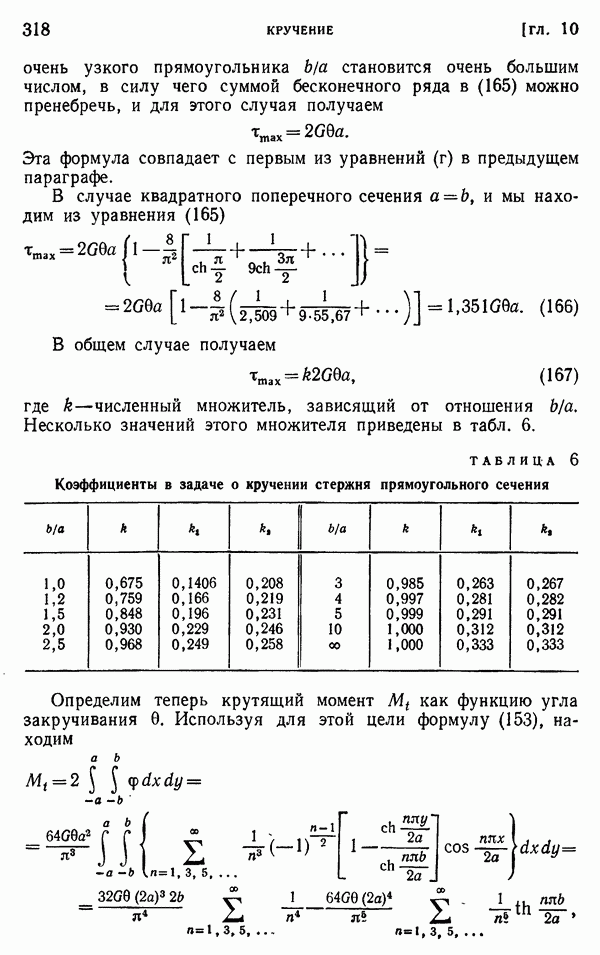
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
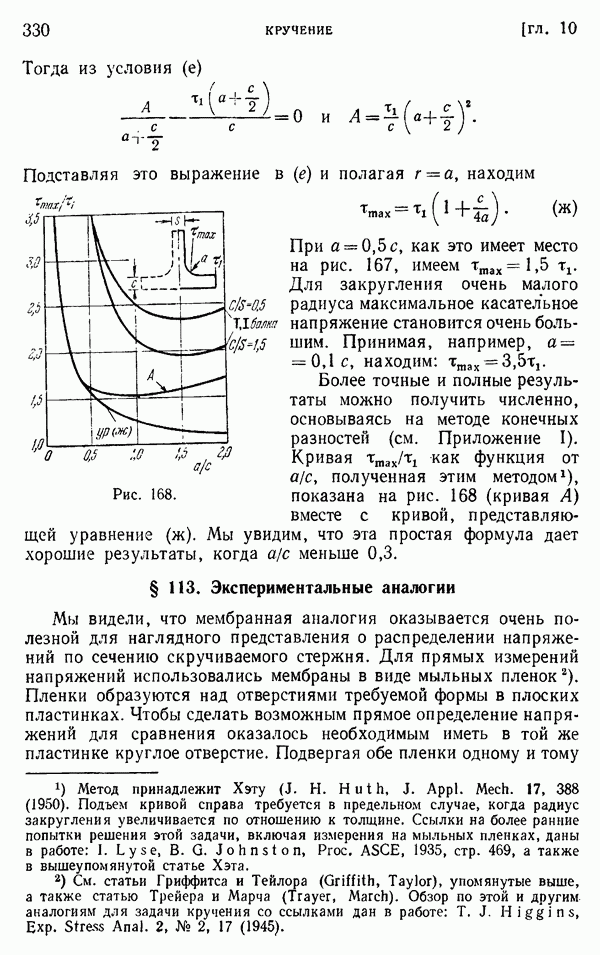
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
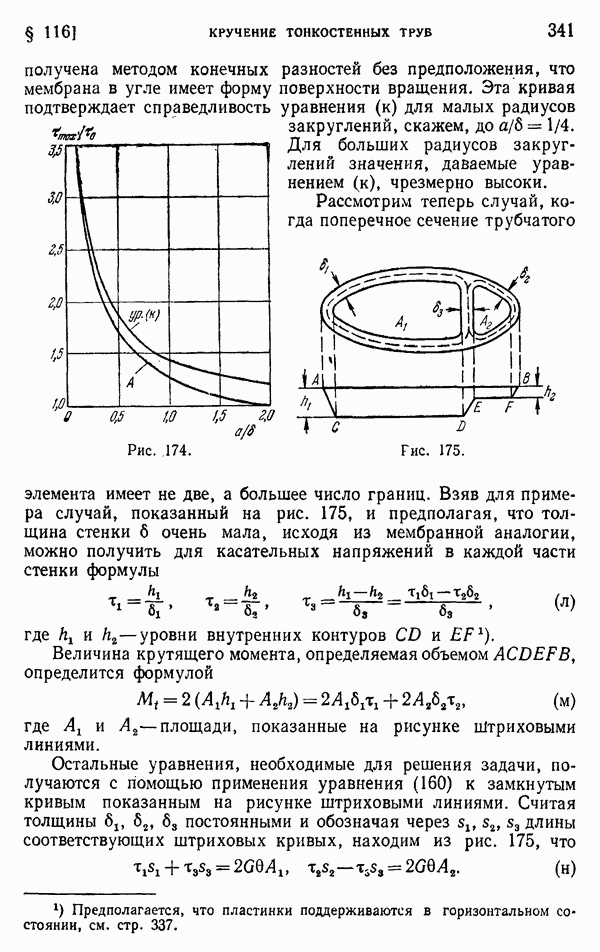
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
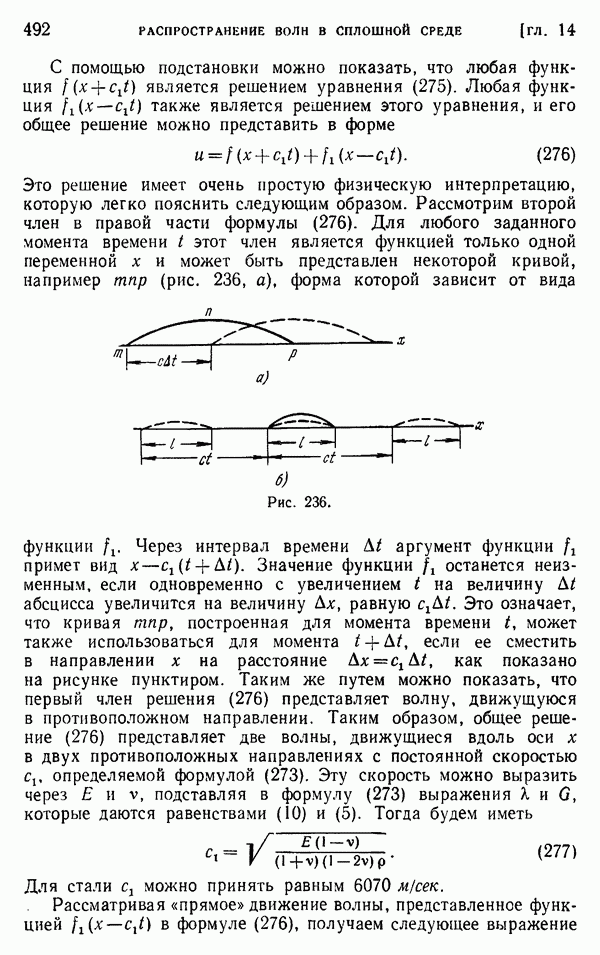
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
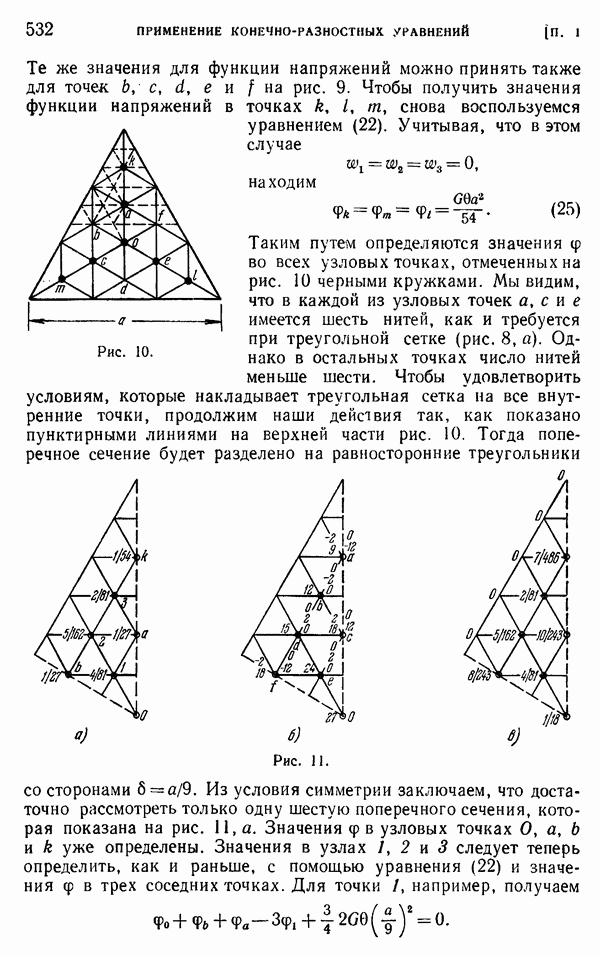
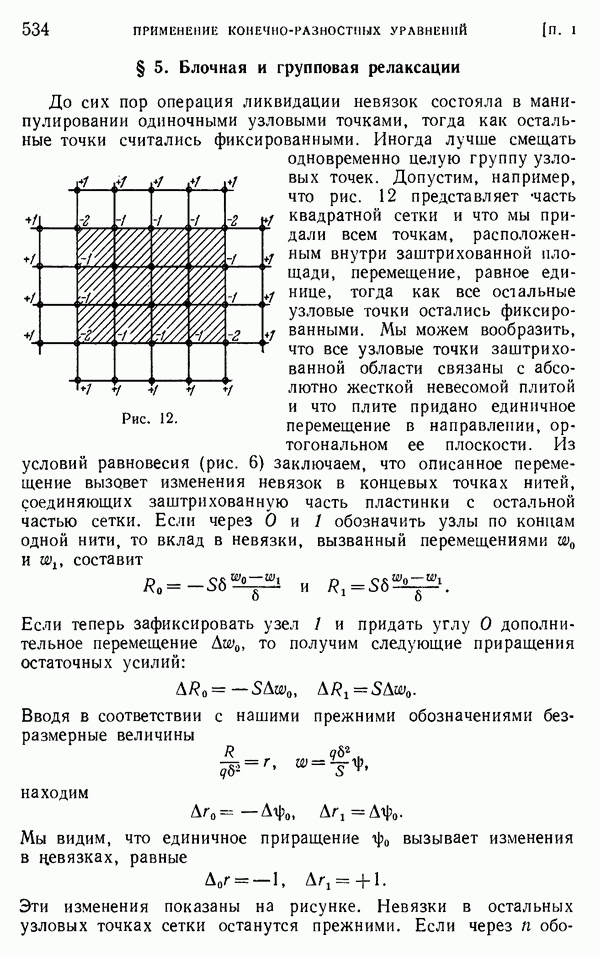
- § 4. Треугольные и шестиугольные сетки
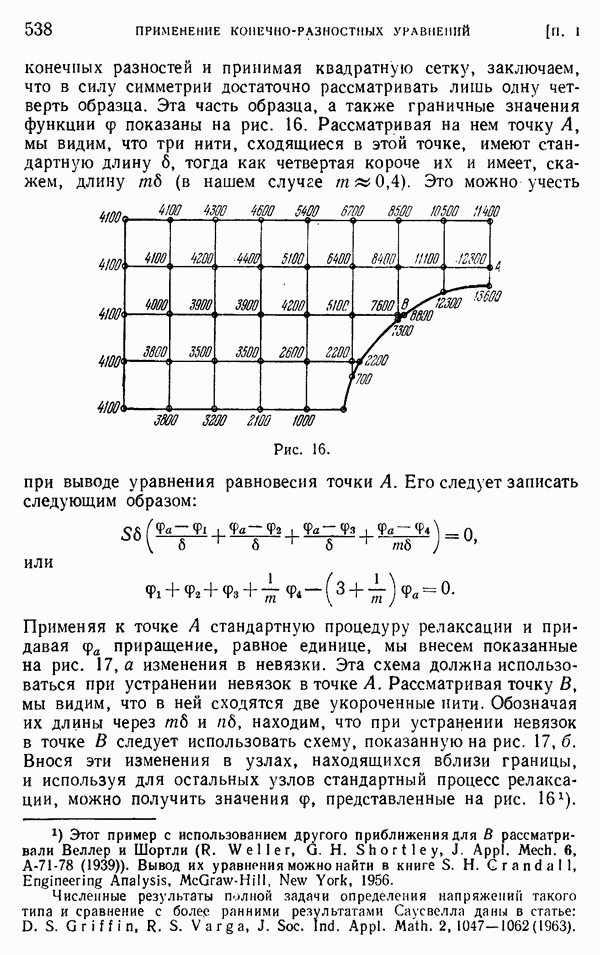
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
- § 7. Точки, расположенные вблизи границы
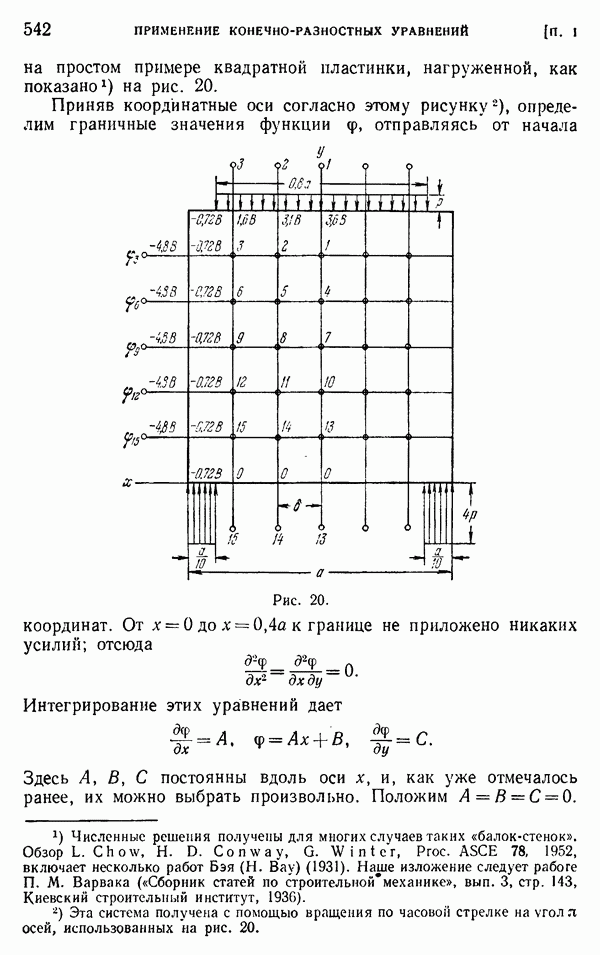
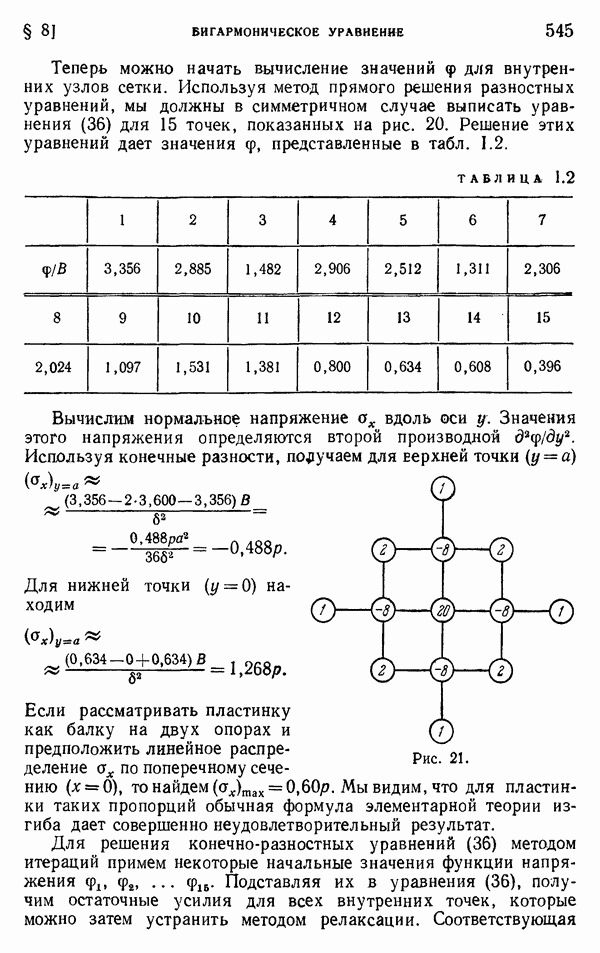
- § 8. Бигармоническое уравнение
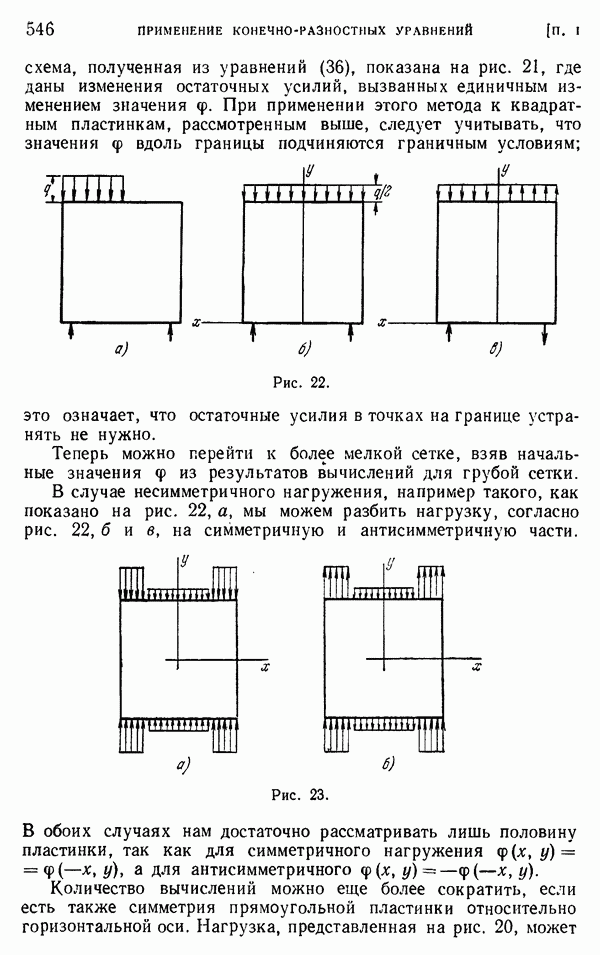
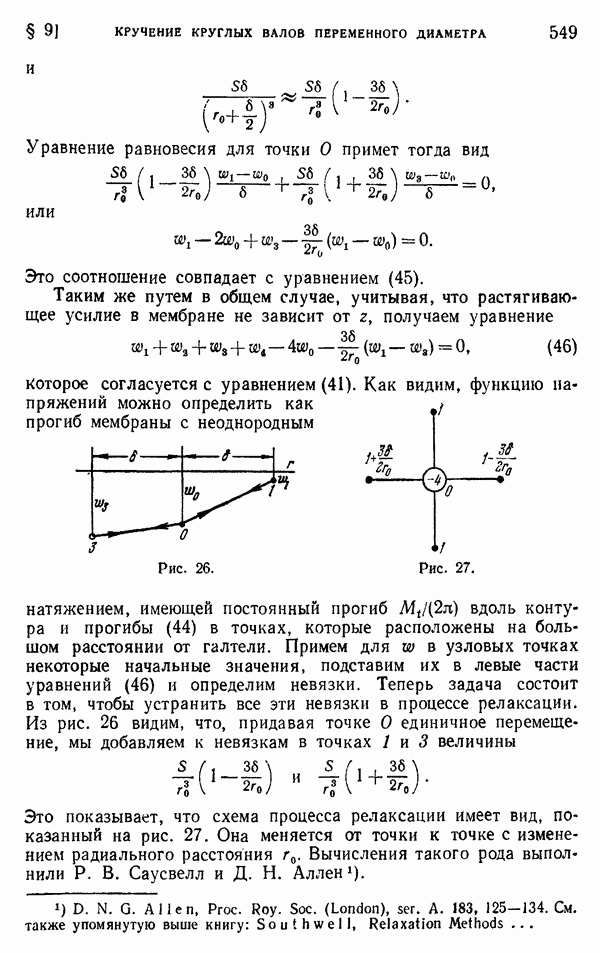
- § 9. Кручение круглых валов переменного диаметра
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи