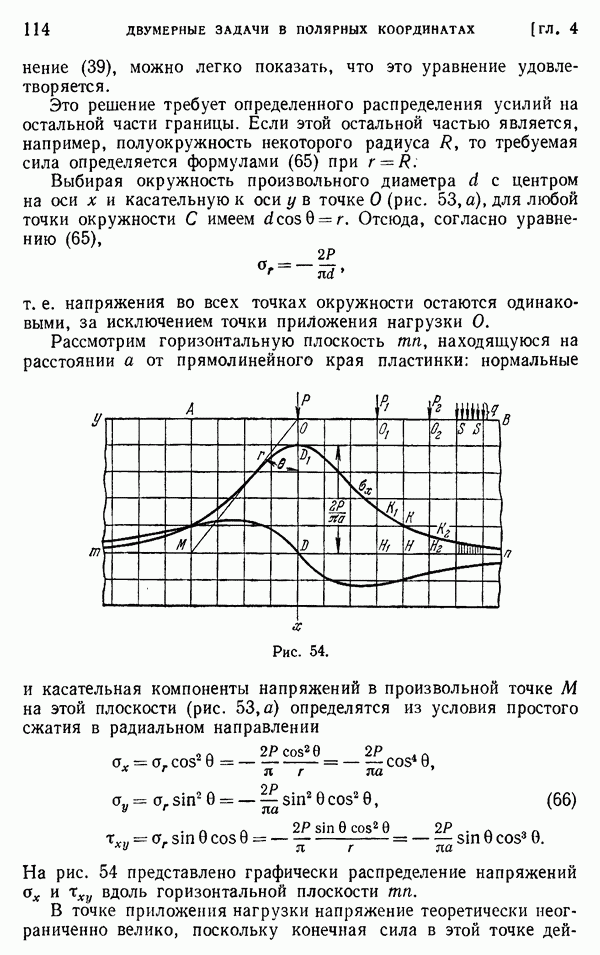
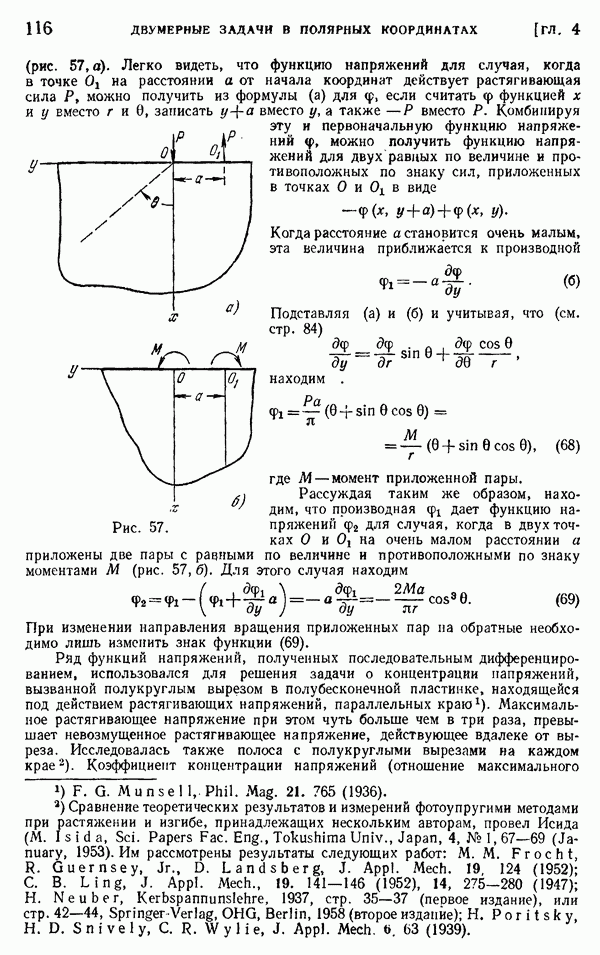
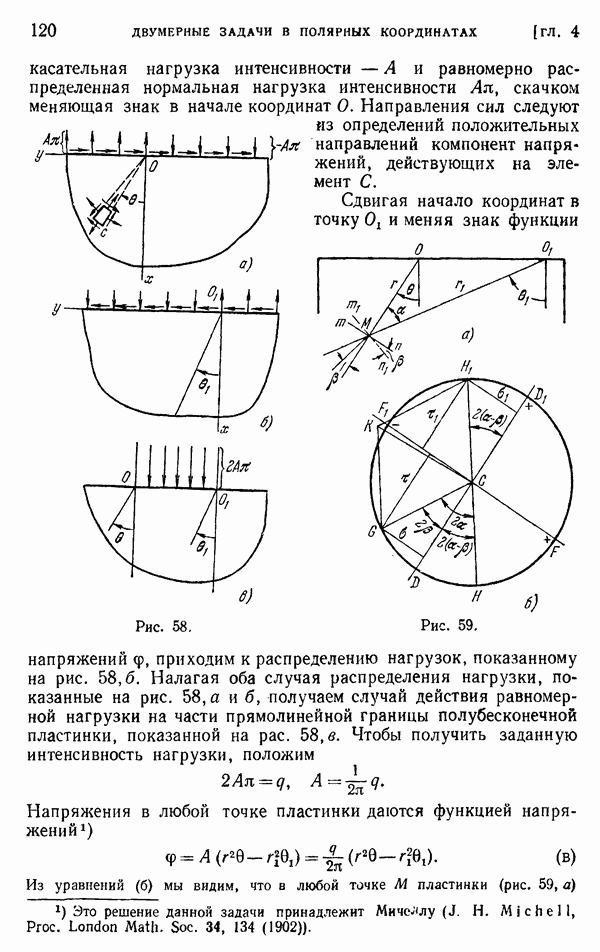
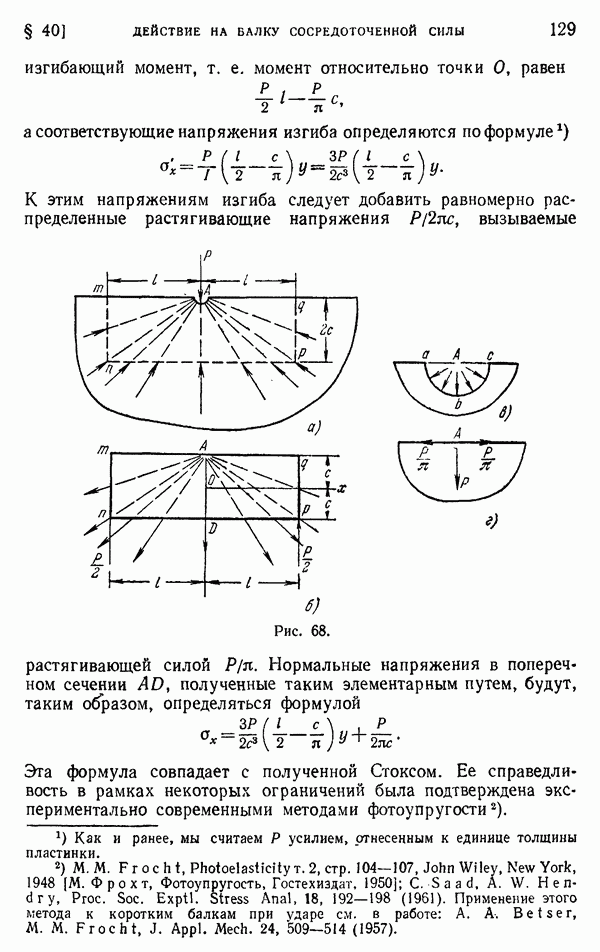
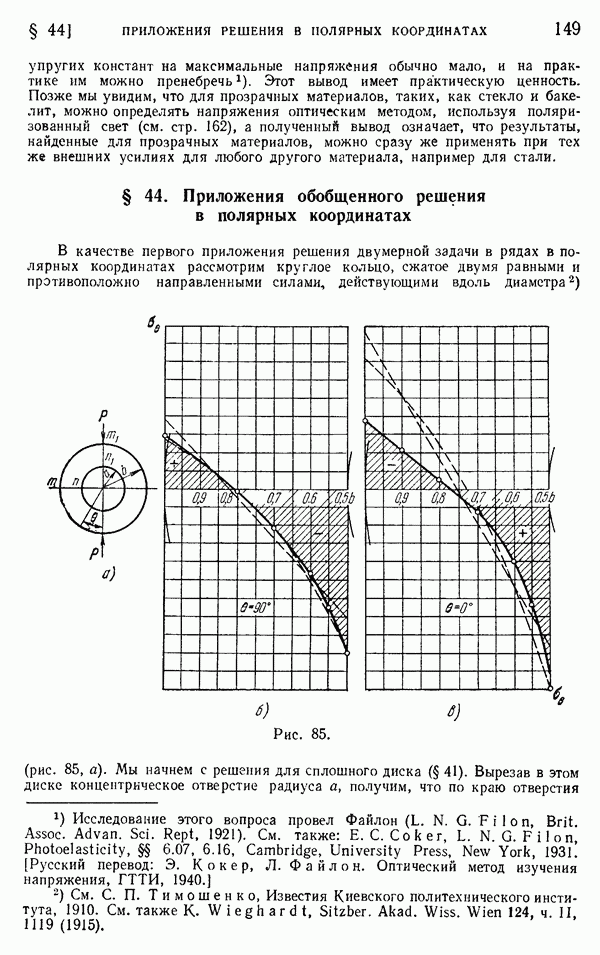
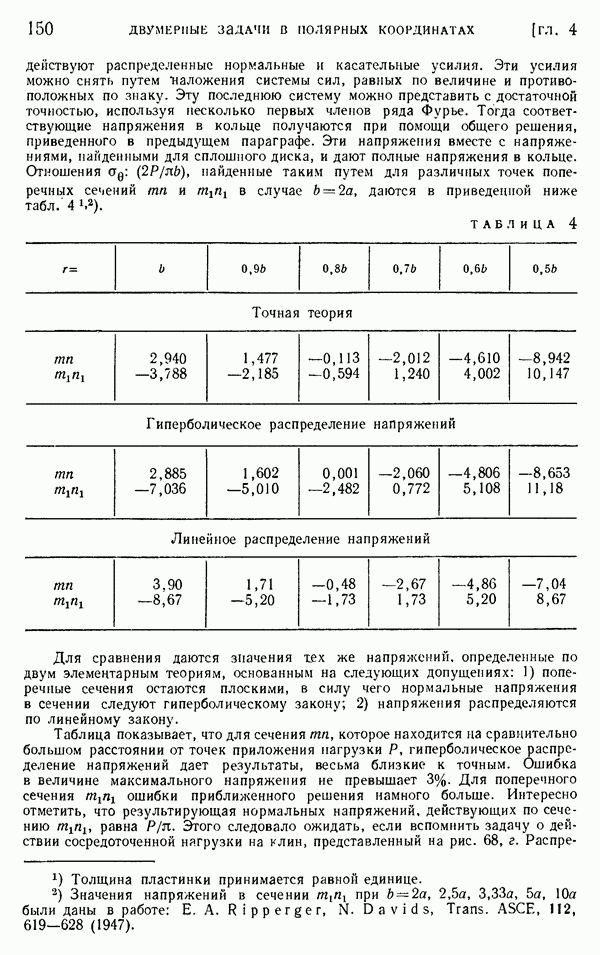
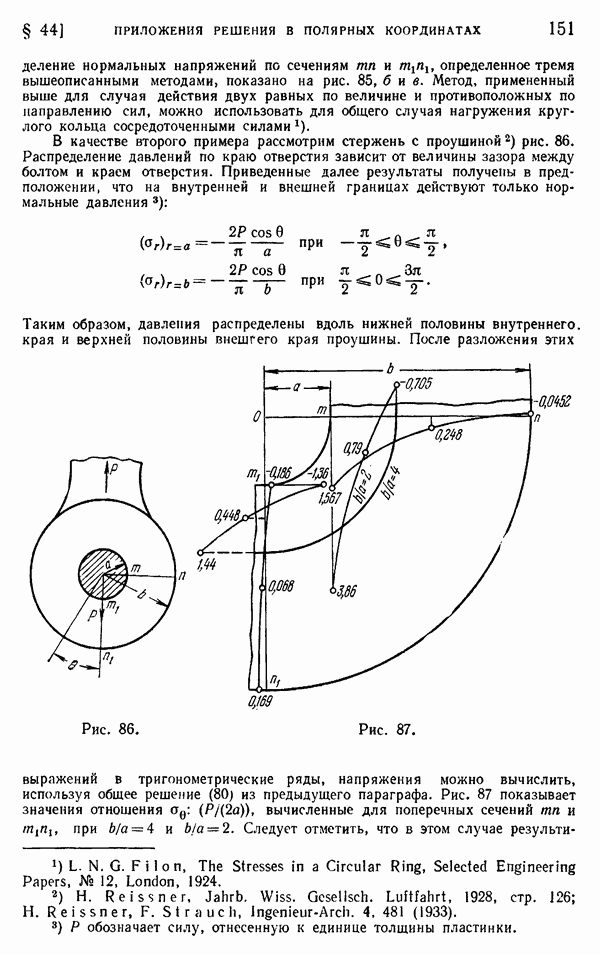
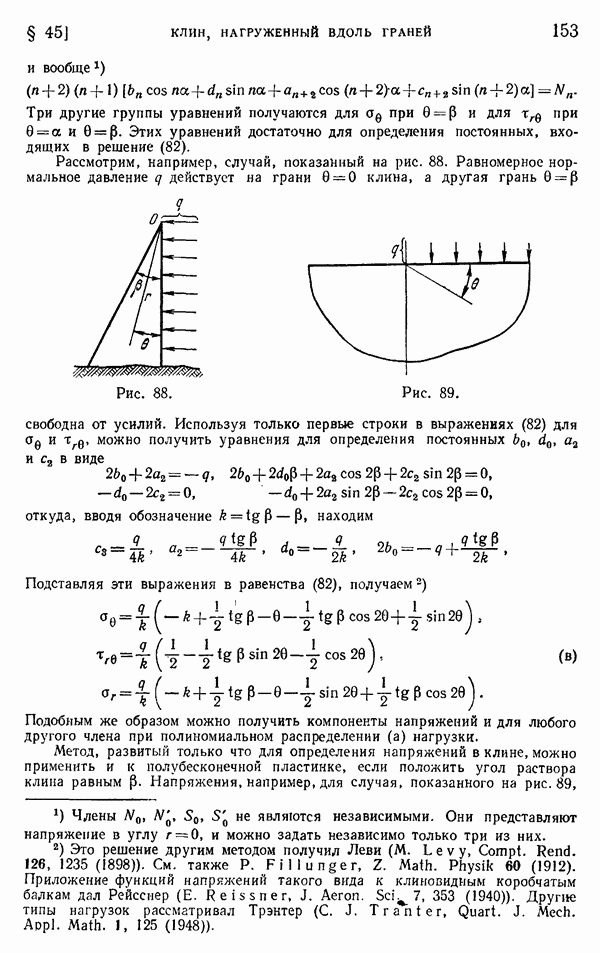
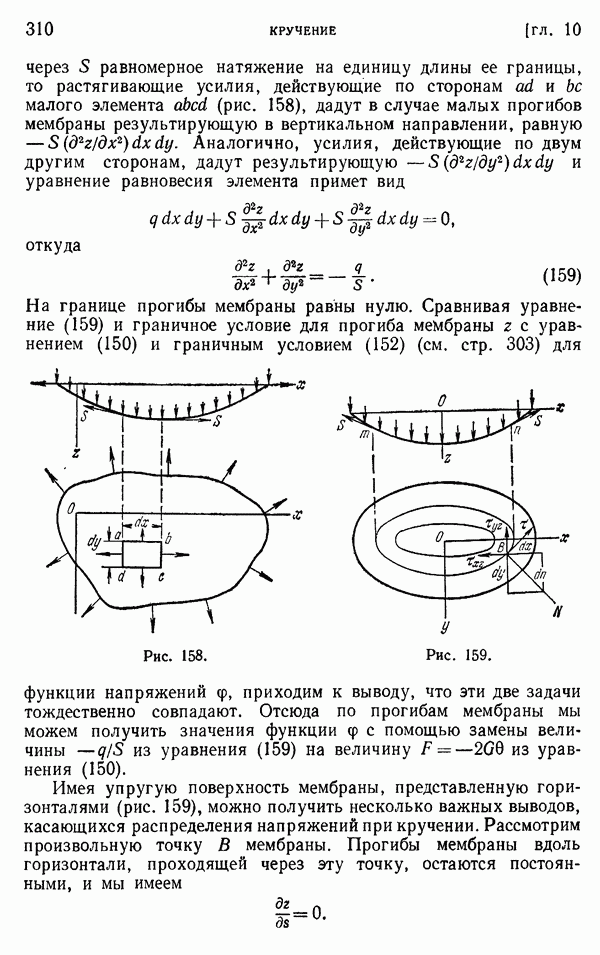
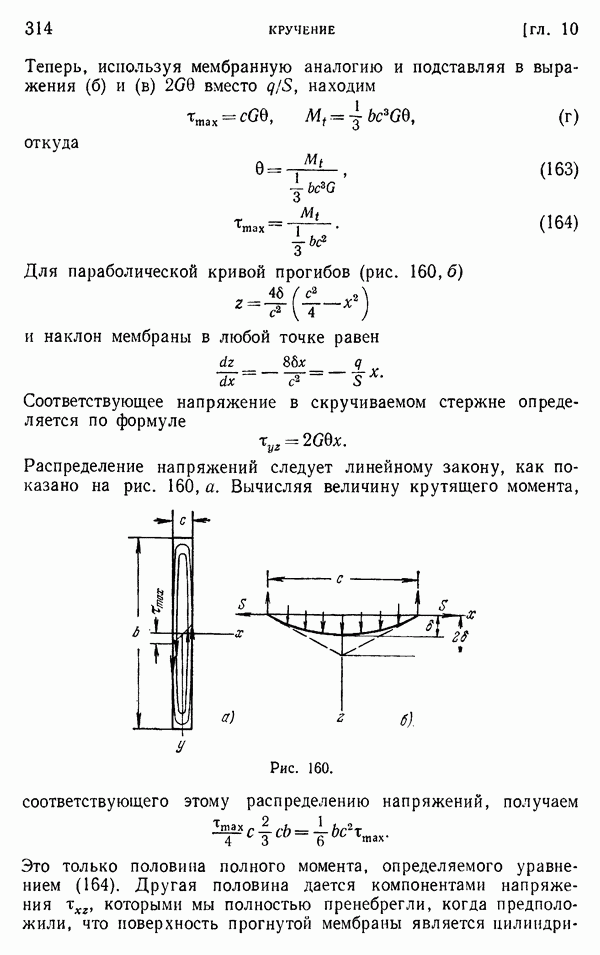
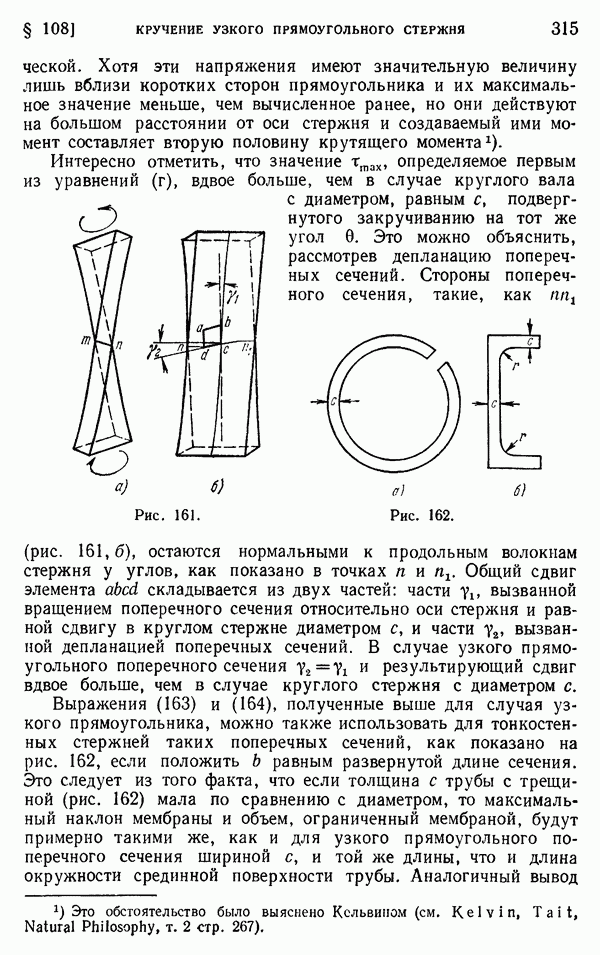
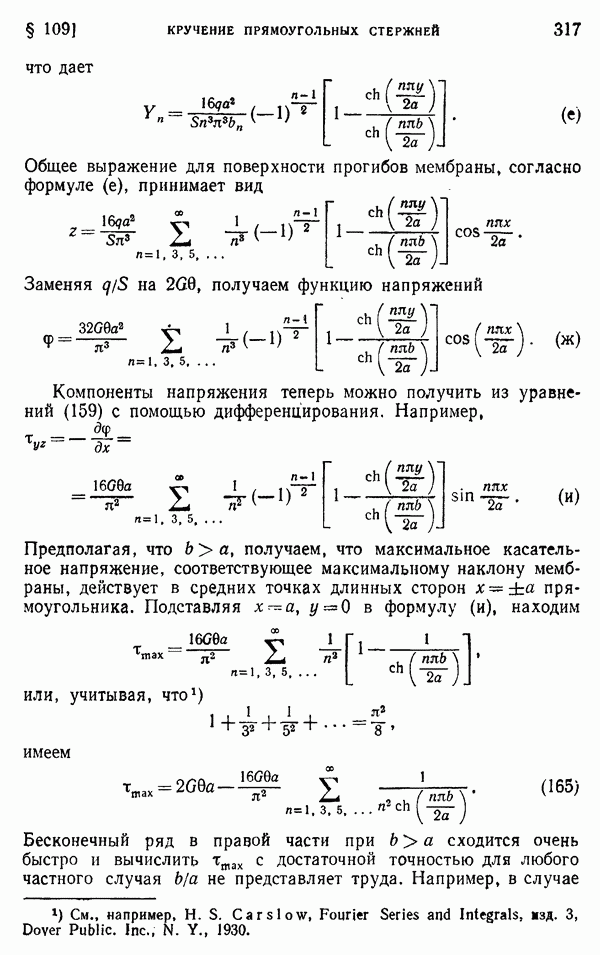
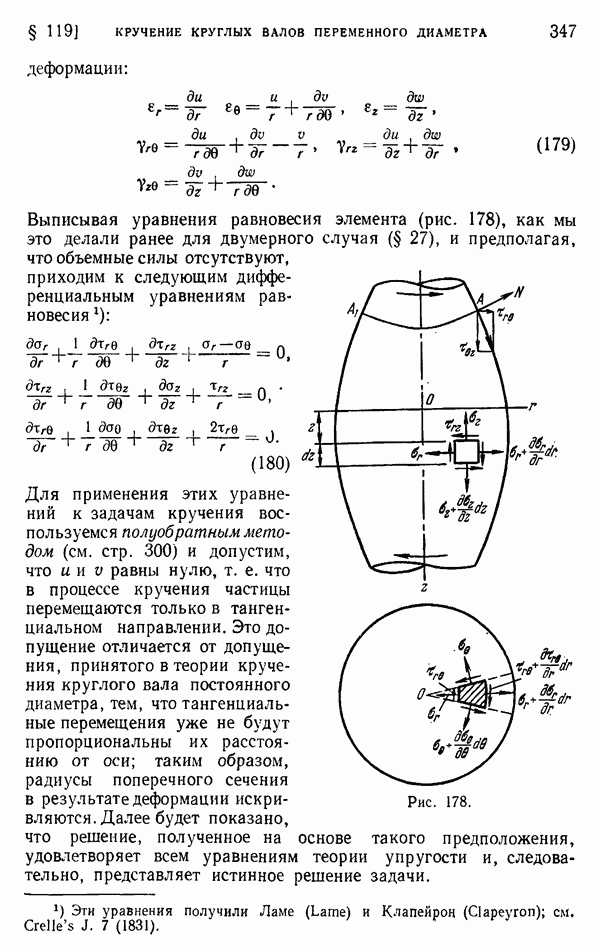
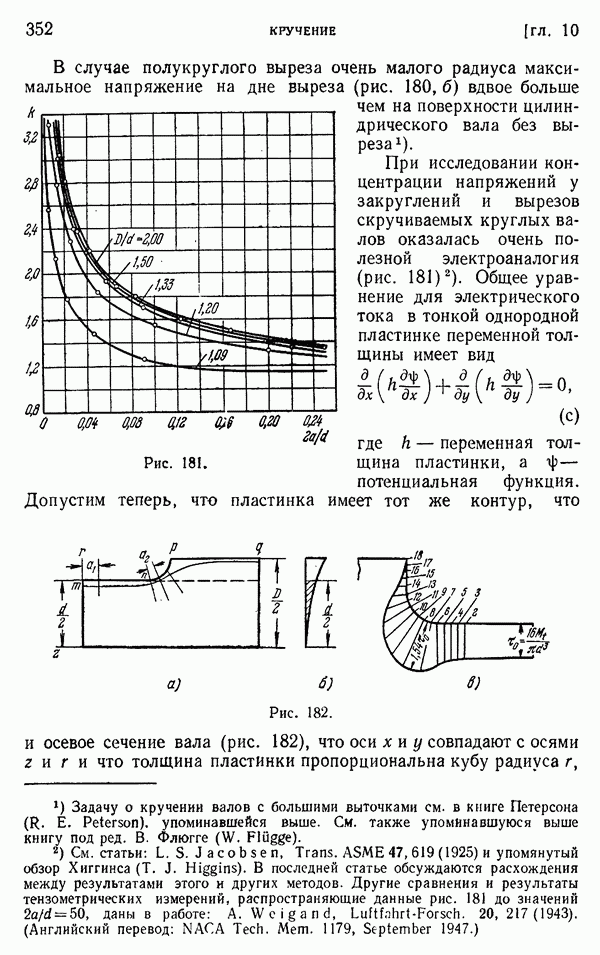
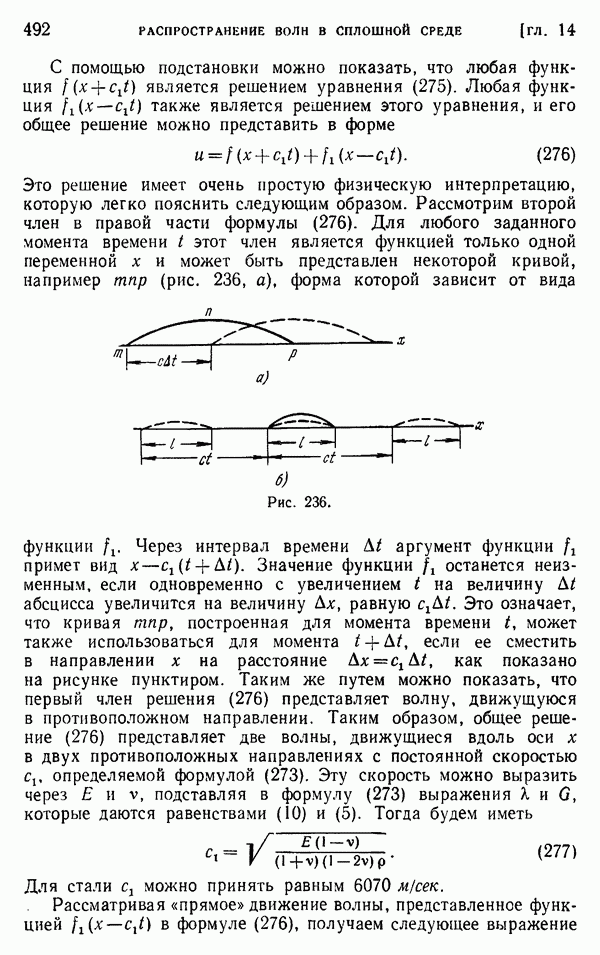
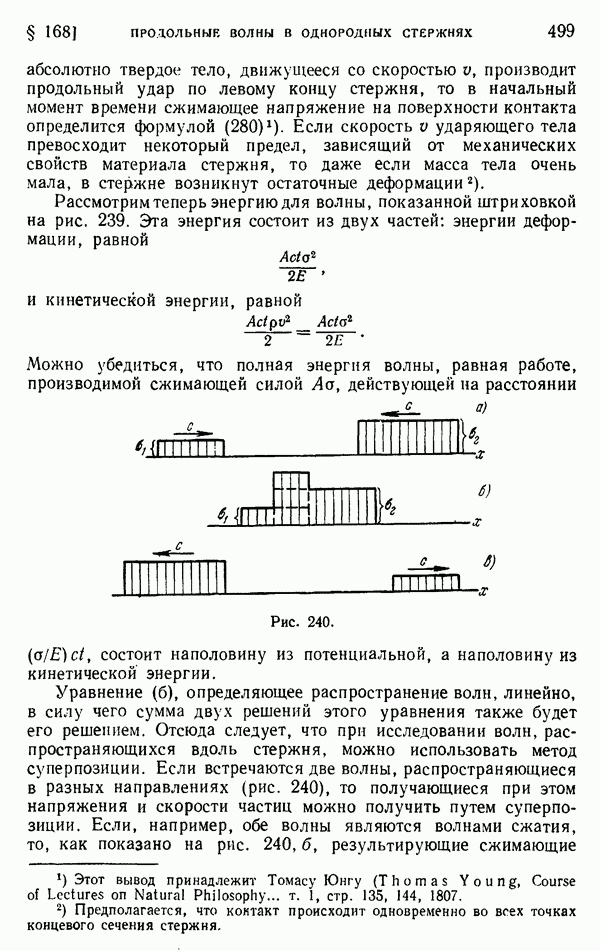
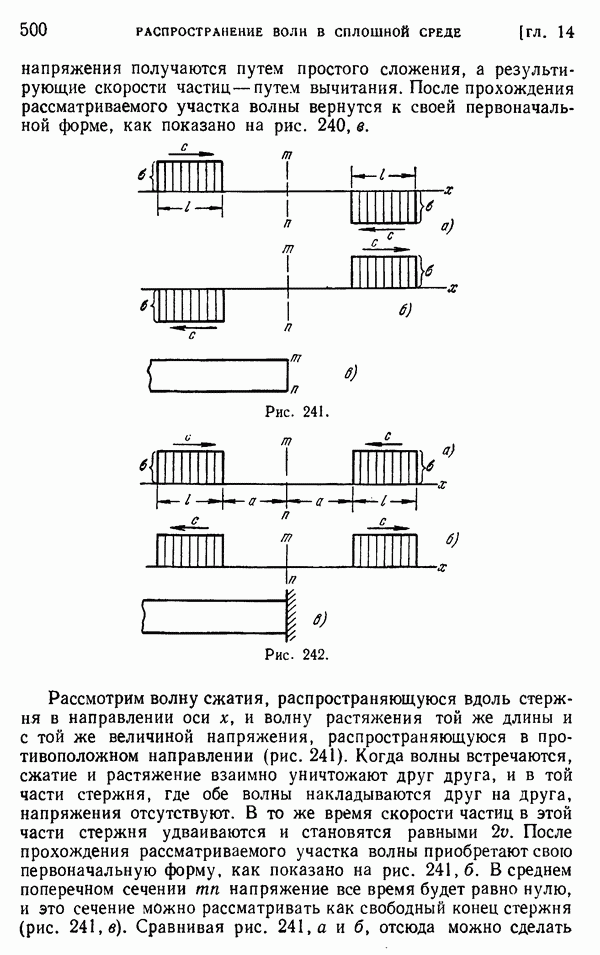
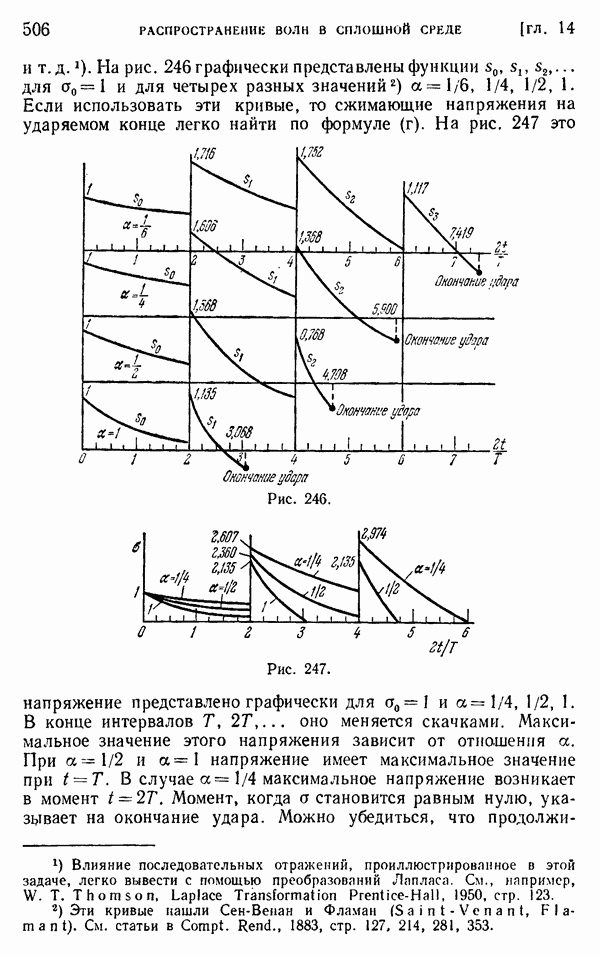
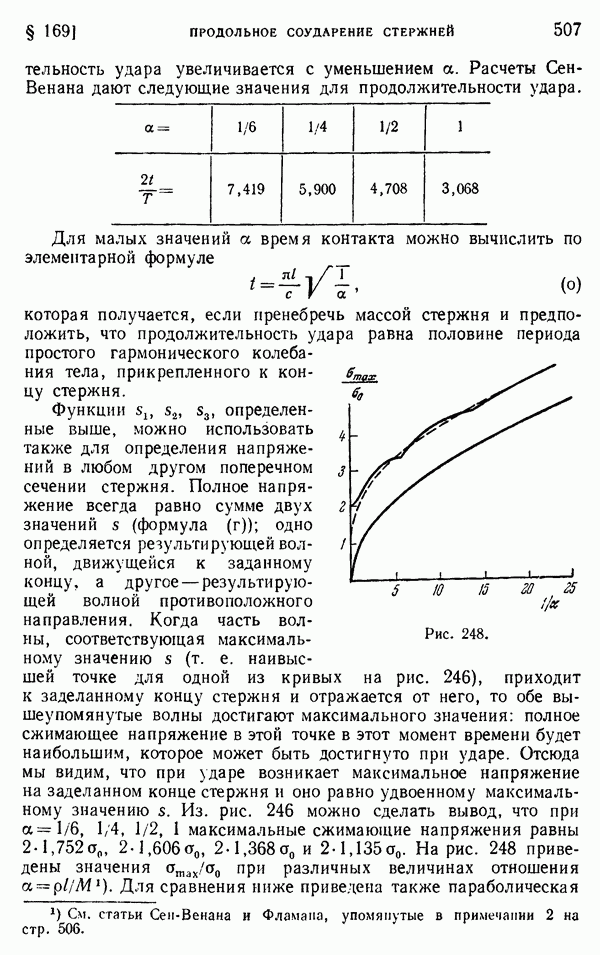
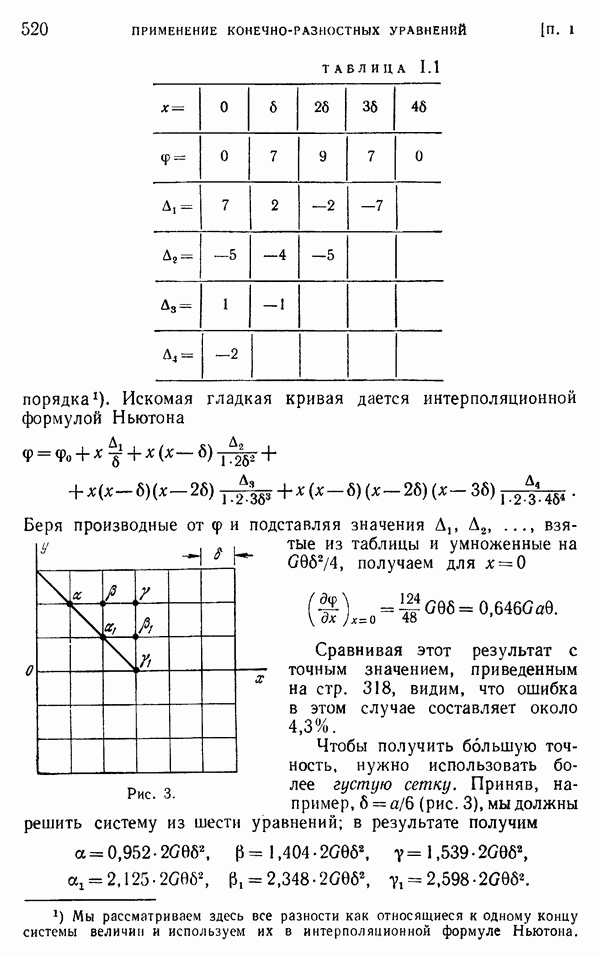
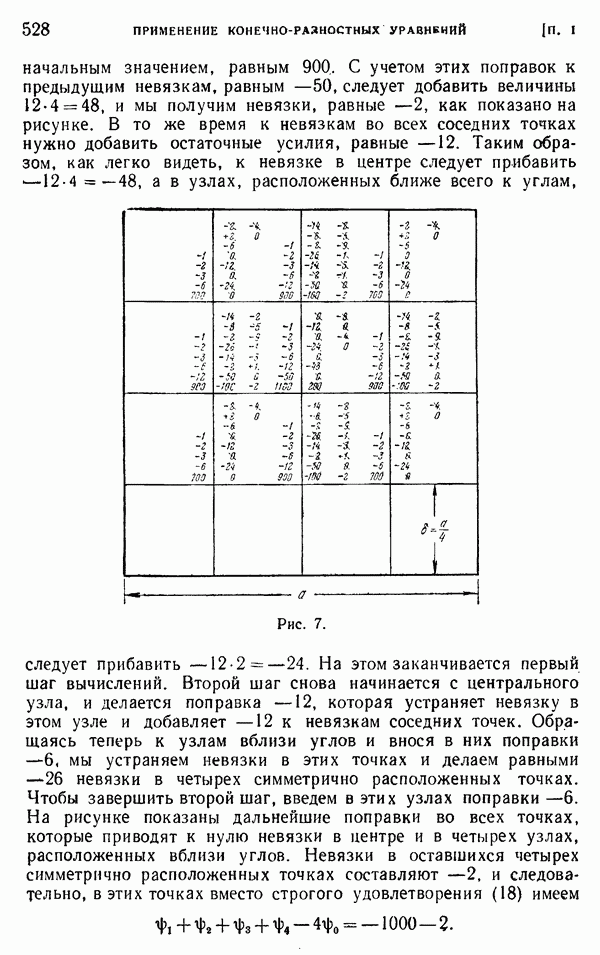
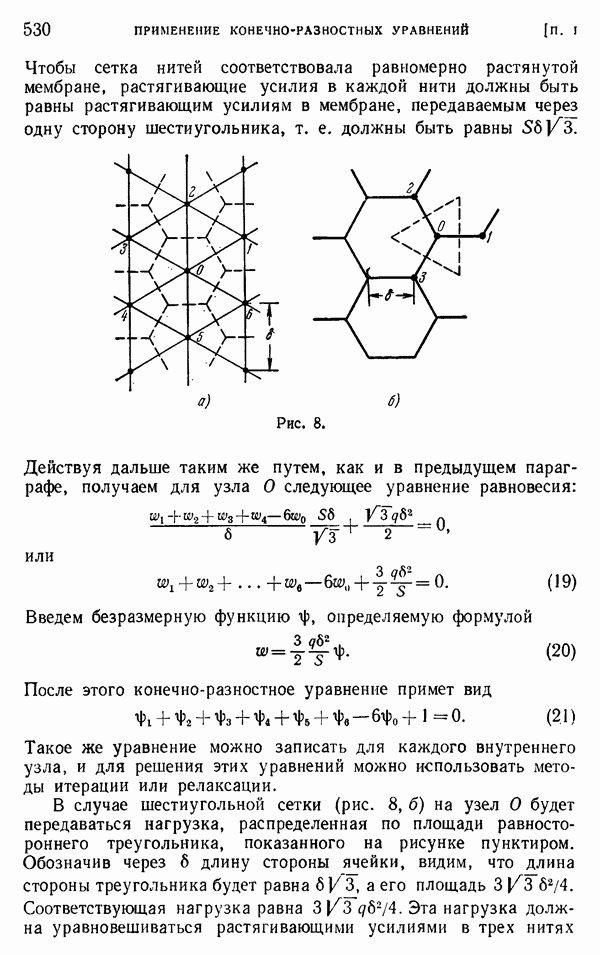
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 160. Двумерные задачи со стационарным потоком тепла
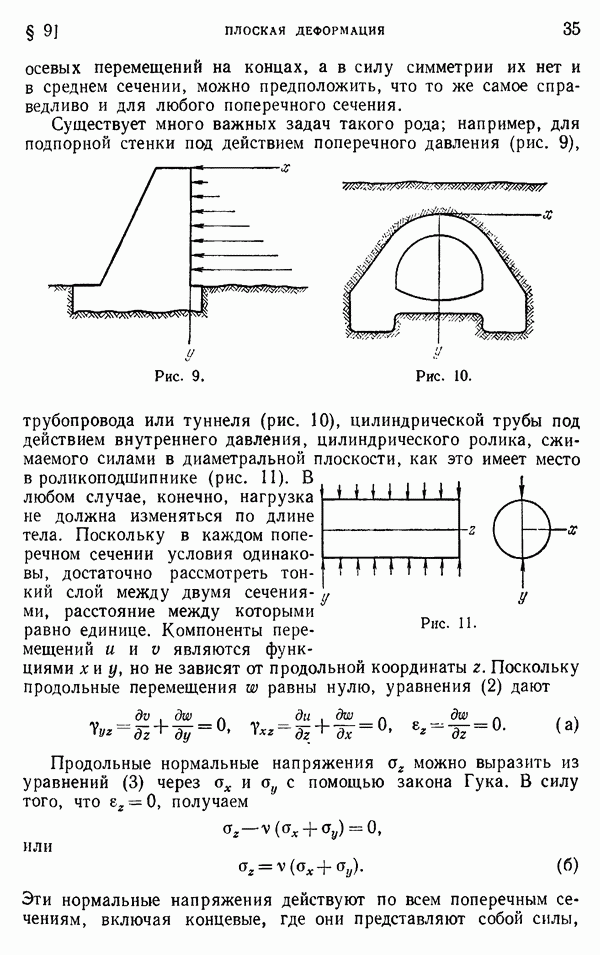
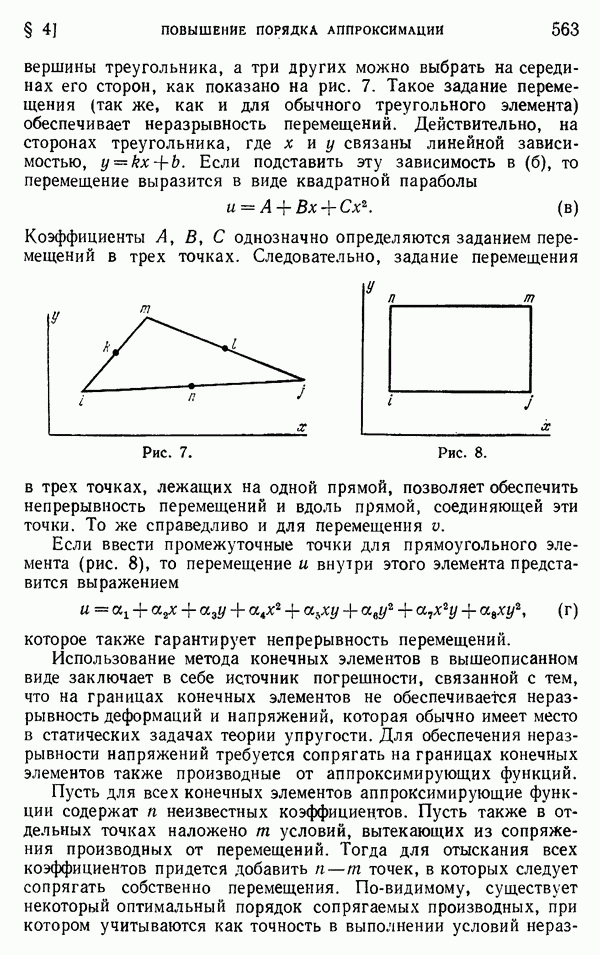
При наличии стационарного потока тепла, параллельного плоскости  как это имеет место в тонкой пластинке или в длинном цилиндре при отсутствии изменения температуры в осевом (г) направлении, температура Т должна удовлетворять уравнению
как это имеет место в тонкой пластинке или в длинном цилиндре при отсутствии изменения температуры в осевом (г) направлении, температура Т должна удовлетворять уравнению

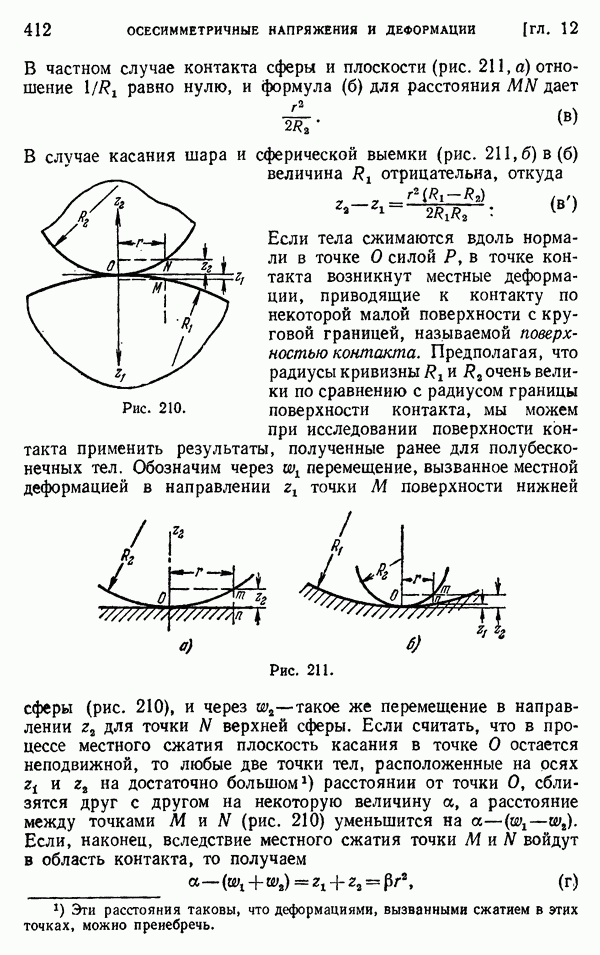
Рассмотрим цилиндр (не обязательно круглый), находящийся в состоянии плоской деформации (при  ). Соотношения между напряжениями и деформациями в декартовых координатах аналогичны уравнениям (а) и (б) в § 151 для случая плоской деформации. По аналогии с уравнениями (б) получаем
). Соотношения между напряжениями и деформациями в декартовых координатах аналогичны уравнениям (а) и (б) в § 151 для случая плоской деформации. По аналогии с уравнениями (б) получаем

Зададимся теперь вопросом: могут ли  быть равными нулю? Полагая в уравнениях (б)
быть равными нулю? Полагая в уравнениях (б)  , находим
, находим

и, разумеется, 
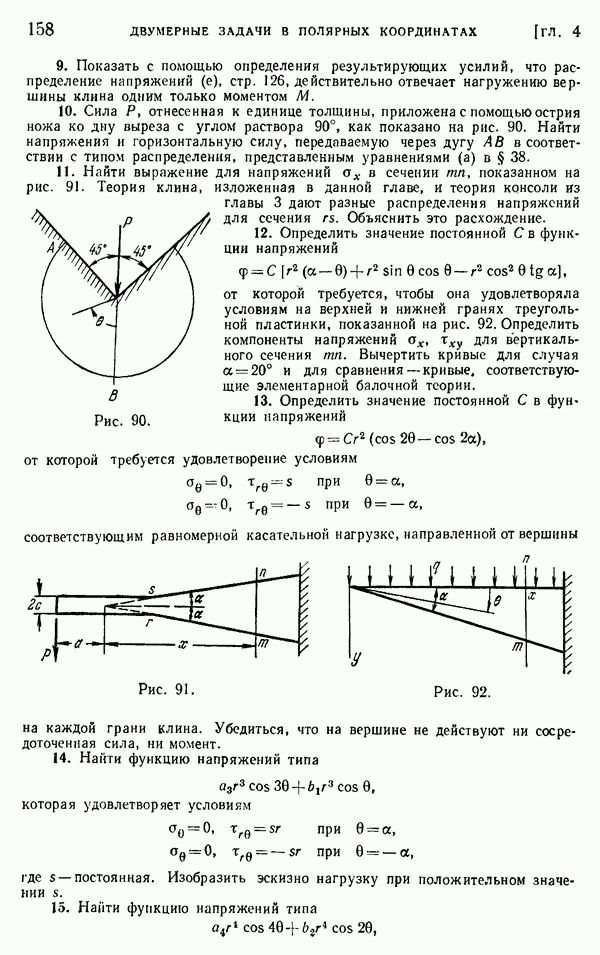
Эти компоненты деформации физически возможны лишь в том случае, если они удовлетворяют условиям совместности (125). Поскольку  а остальные компоненты деформации не зависят от z, все условия (125), за исключением первого, удовлетворяются. Первое условие приводится к уравнению
а остальные компоненты деформации не зависят от z, все условия (125), за исключением первого, удовлетворяются. Первое условие приводится к уравнению

Но с учетом соотношений (в) и (а) это уравнение также удовлетворяется. Отсюда мы находим, что при стационарном потоке
тепла уравнения равновесия, граничное условие, выражающее отсутствие нагрузки на криволинейной поверхности, и условия совместности удовлетворяются, если принять

Для сплошного цилиндра вышеприведенные условия являются полными, и мы можем сделать вывод, что при стационарном состоянии двумерной теплопередачи не будет температурных напряжений, за исключением осевого напряжения  определяемого по формуле (г), которое служит для выполнения условия
определяемого по формуле (г), которое служит для выполнения условия  плоской деформации. В случае длинного цилиндра без связей, наложенных на концах, мы получаем приближенное решение, справедливое всюду, кроме окрестности концов, если наложить одноосное растяжение—сжатие и чистый изгиб таким образом, чтобы свести к нулю результирующие усилия и моменты по концам, связанные с напряжениями
плоской деформации. В случае длинного цилиндра без связей, наложенных на концах, мы получаем приближенное решение, справедливое всюду, кроме окрестности концов, если наложить одноосное растяжение—сжатие и чистый изгиб таким образом, чтобы свести к нулю результирующие усилия и моменты по концам, связанные с напряжениями 

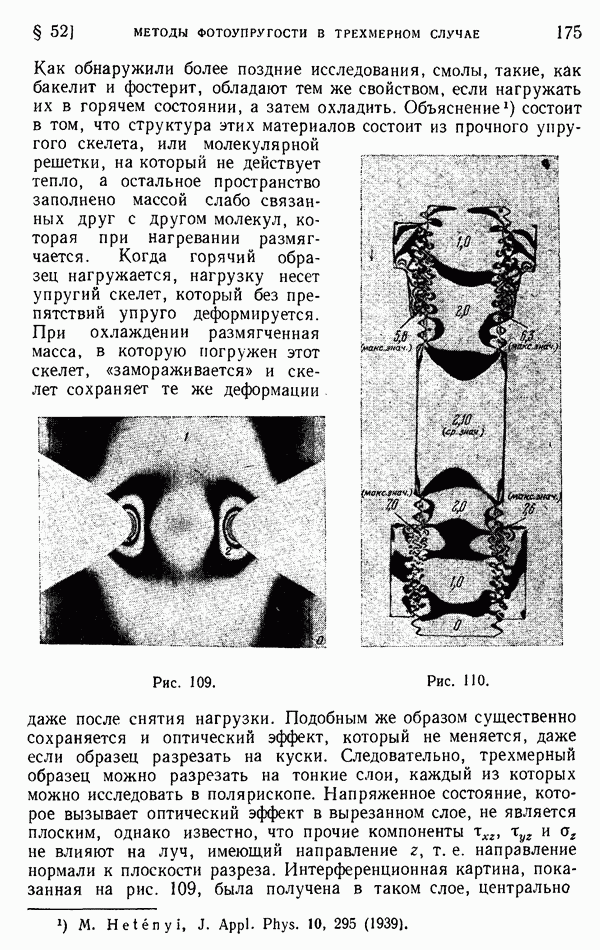
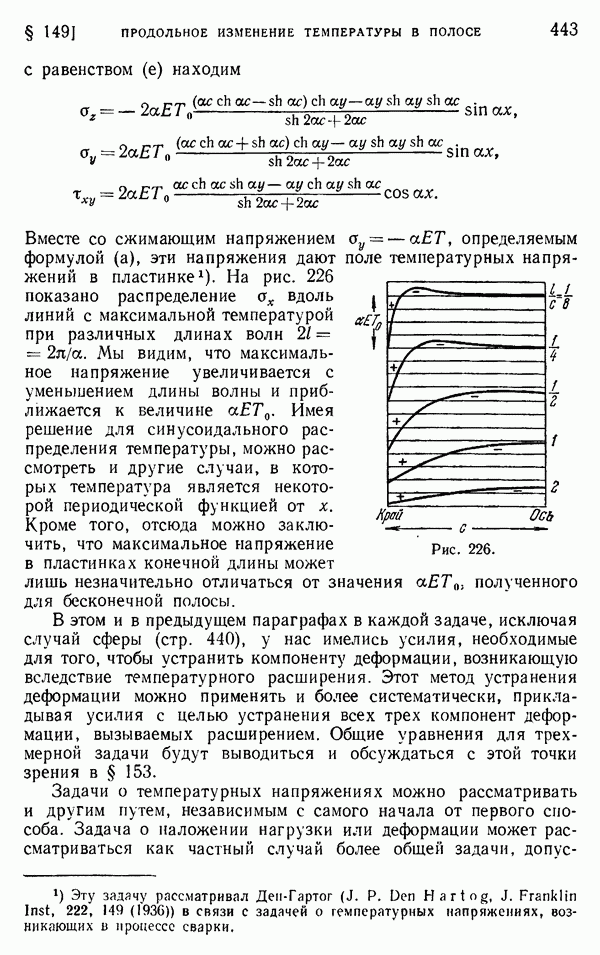
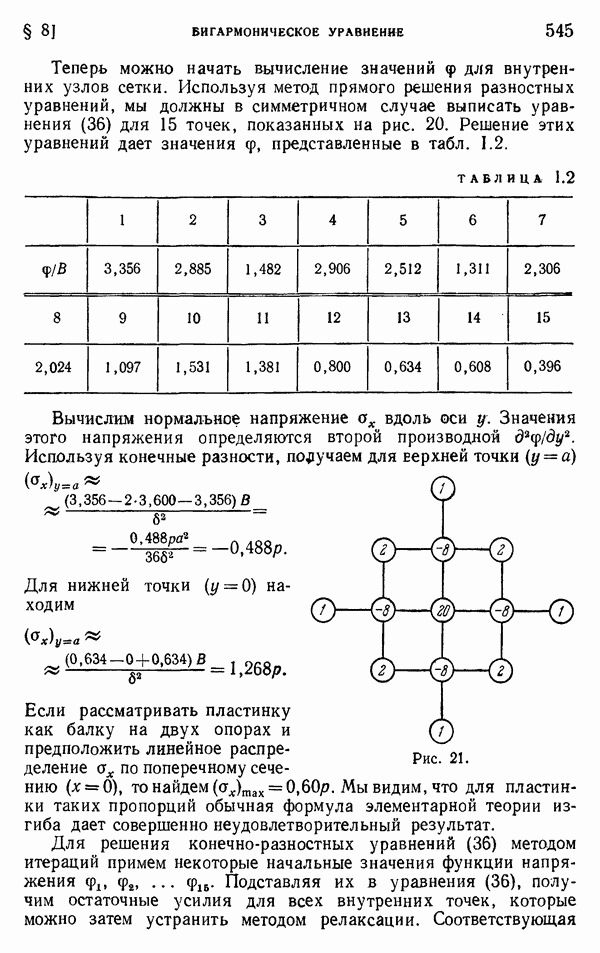
Рис. 234.
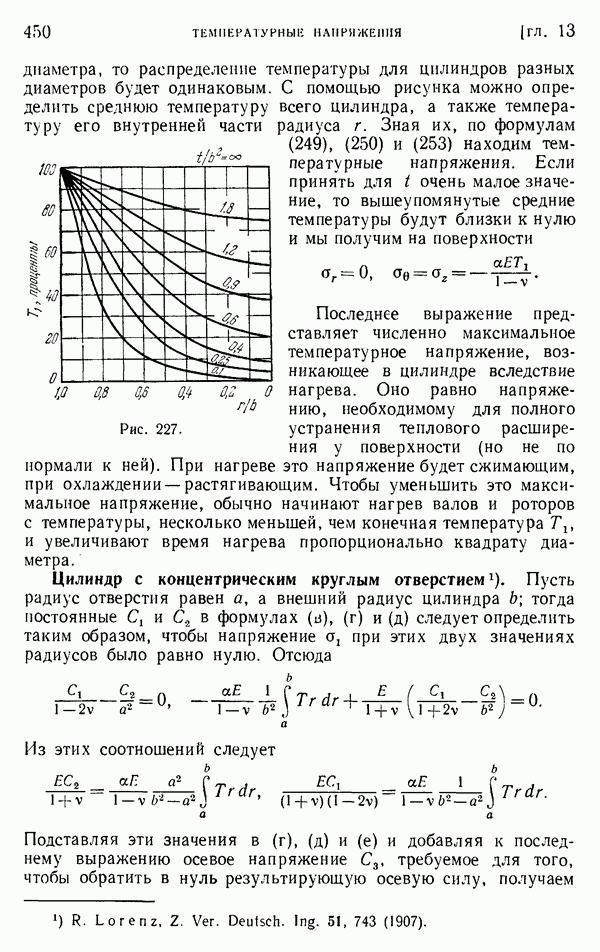
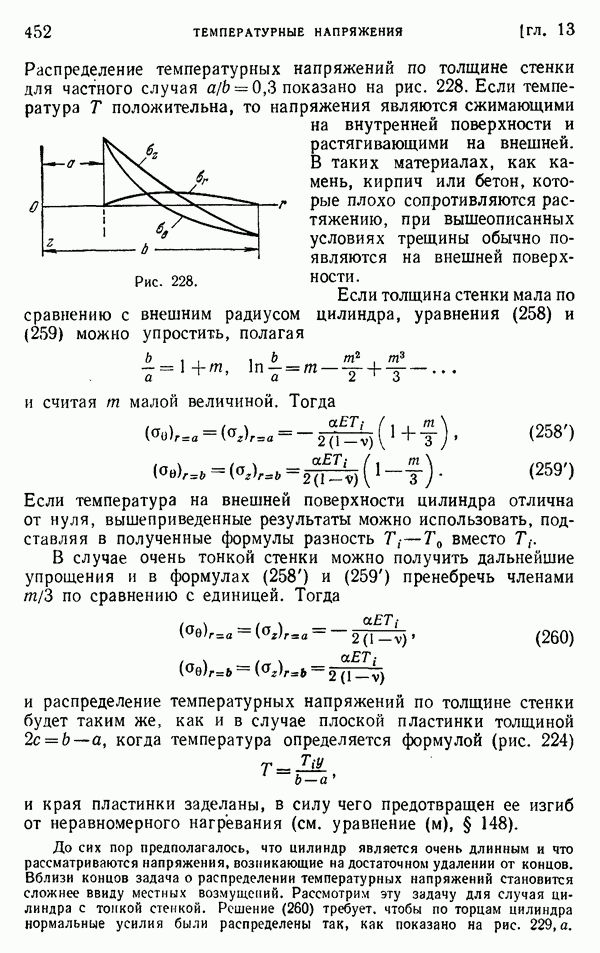
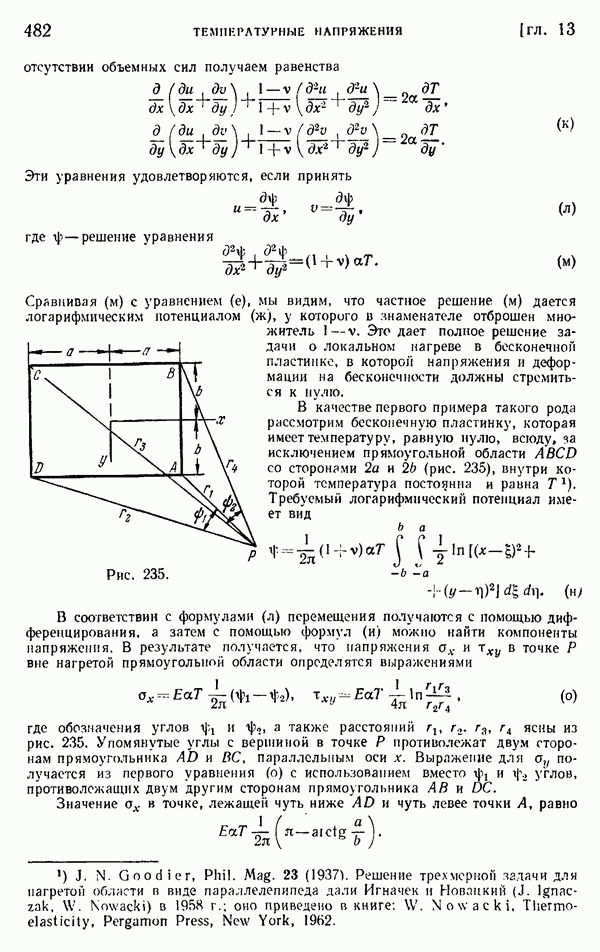
Для полого цилиндра мы не можем, однако, сделать вывод, что формулы (г) служат решением задачи о плоской деформации. Необходимо исследовать соответствующие перемещения. Весьма возможно, что они окажутся разрывными, подобно тому, как это описано на стр. 95 и 104—105.
Допустим, например, что цилиндр представляет собой трубу и что в нем сделан продольный разрез, как показано на рис. 234, б. Если внутренняя часть стенки трубы теплее наружной, то труба будет стремиться развернуться, а щель будет раскрываться. Между двумя стенками щели будет иметь место разрыв перемещения. Следовательно, перемещение должно быть представлено разрывными функциями от 0. Поперечное сечение в этом случае является сплошным, т. е. односвязным, и напряжения для задачи плоской деформации даются в точности формулами (г). Однако если труба не имеет щели (рис. 234, а), разрывы перемещения физически невозможны. Это показывает, что принятое распределение температуры вызовет фактически компоненты напряжения  которые представляют напряженное состояние, вызванное стягиванием друг к другу разделенных граней щели вплоть до их соединения. Такая операция повлияет также на компоненту
которые представляют напряженное состояние, вызванное стягиванием друг к другу разделенных граней щели вплоть до их соединения. Такая операция повлияет также на компоненту 
Для дальнейшего исследования этого вопроса перепишем уравнения (в) в виде

где  . Поскольку
. Поскольку  мы можем запнсагь
мы можем запнсагь

а также

где  — компонента вращения (см. стр. 243). Уравнения (е) и (ж) дают в этом случае
— компонента вращения (см. стр. 243). Уравнения (е) и (ж) дают в этом случае

что в сочетании с соотношениями (д) приводит к условиям

Уравнения (к) представляют собой уравнения Коши—Римана, обсуждавшиеся в § 55. Они показывают, что функция  является аналитической функцией комплексной переменной
является аналитической функцией комплексной переменной  Обозначая эту функцию через
Обозначая эту функцию через  получаем
получаем

Если  - значения компонент
- значения компонент  в точках 1 и 2 поперечного сечения цилиндра, то разности
в точках 1 и 2 поперечного сечения цилиндра, то разности  можно выразить формулами
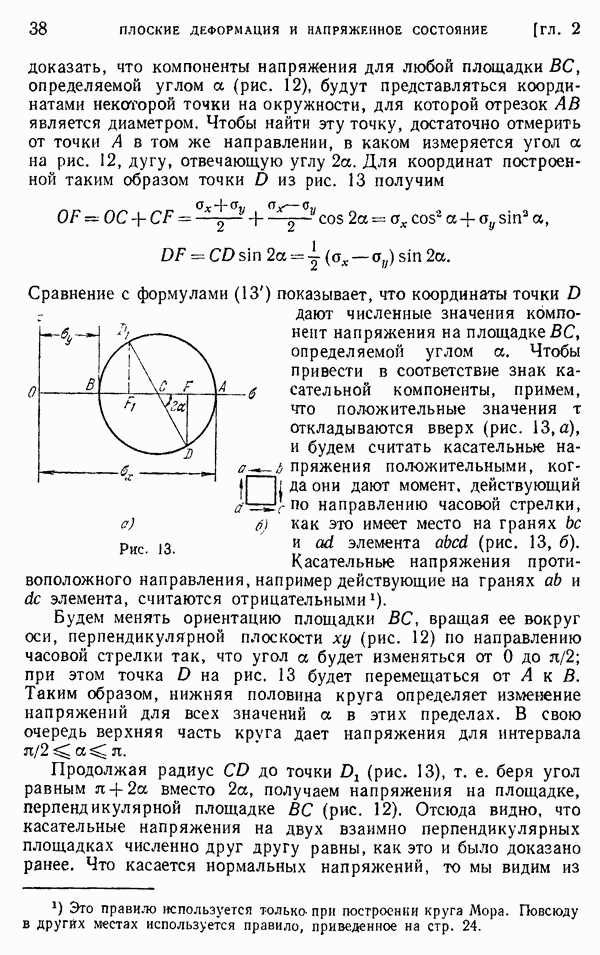
можно выразить формулами

где интегралы берутся вдоль любой кривой, соединяющей эти две точки и лежащей целиком внутри сечения. Умножая второе соотношение на  и складывая с первым, находим
и складывая с первым, находим

С помощью уравнений (д) и (и) легко убедиться, что интеграл в правой части равен  или
или  Таким образом, уравнение (м) принимает вид
Таким образом, уравнение (м) принимает вид

Перемещения будут однозначными, если этот интеграл обращается в нуль для любого замкнутого контура (например, для окружности, изображенной пунктиром на рис. 234), находящегося целиком в пределах поперечного сечения. Ниже мы воспользуемся этим результатом при решении задачи о температурных напряжениях в полом круглом цилиндре.
Для вращения  (см. § 83) имеем зависимость
(см. § 83) имеем зависимость

которая с использованием (к) приводится к виду

Поскольку деформация  пропорциональна Т, этот интеграл пропорционален количеству тепла, проходящего за единицу времени через дугу единичной длины, вырезанную из кривой, соединяющей точки 1 и 2. Если эта кривая замкнутая, разность
пропорциональна Т, этот интеграл пропорционален количеству тепла, проходящего за единицу времени через дугу единичной длины, вырезанную из кривой, соединяющей точки 1 и 2. Если эта кривая замкнутая, разность  должна обращаться в нуль, и следовательно, должен быть равен нулю и общий поток тепла, пересекающий эту кривую
должна обращаться в нуль, и следовательно, должен быть равен нулю и общий поток тепла, пересекающий эту кривую  Если поток тепла направлен от внутренней поверхности трубы к внешней или наоборот, это условие не выполняется, и формулы (г) для напряжения будут некорректны.
Если поток тепла направлен от внутренней поверхности трубы к внешней или наоборот, это условие не выполняется, и формулы (г) для напряжения будут некорректны.
Однако если труба имеет разрез (щель), как показано на рис. 234, б, то перемещение или вращение в точке 2 могут отличаться от соответствующих величин в точке  например, в том случае, когда нагрев вызывает раскрытие щели. Тогда простое напряженное состояние, определяемое формулами (г), будет корректным решением задачи. Чтобы прийти к напряженному состоянию в трубе при отсутствии щели, нам следует наложить напряженное состояние, вызываемое смыканием стенок, щели. Определение таких дислокационных напряжений включает решение задач типа, представленного на рис. 45 и 48.
например, в том случае, когда нагрев вызывает раскрытие щели. Тогда простое напряженное состояние, определяемое формулами (г), будет корректным решением задачи. Чтобы прийти к напряженному состоянию в трубе при отсутствии щели, нам следует наложить напряженное состояние, вызываемое смыканием стенок, щели. Определение таких дислокационных напряжений включает решение задач типа, представленного на рис. 45 и 48.
Рассмотрим, например, полый круговой цилиндр с внешним радиусом  центральным отверстием радиуса а. Если температура Т на внутренней поверхности распределена равномерно, а температура на внешней поверхности равна нулю, то температура Т в точке, определяемой любым радиусом
центральным отверстием радиуса а. Если температура Т на внутренней поверхности распределена равномерно, а температура на внешней поверхности равна нулю, то температура Т в точке, определяемой любым радиусом  дается формулой (п) из § 151. Мы можем записать эту формулу в виде
дается формулой (п) из § 151. Мы можем записать эту формулу в виде

где

Постоянный член  в формуле (о) можно отбросить, так как однородное изменение температуры не вызывает температурных напряжений. Далее, поскольку
в формуле (о) можно отбросить, так как однородное изменение температуры не вызывает температурных напряжений. Далее, поскольку  имеем
имеем

Обозначая  через В, из уравнения (н) имеем
через В, из уравнения (н) имеем

Это уравнение применимо к любой кривой, соединяющей точки 1 и 2 и целиком лежащей внутри сечения. Оно дает относительное перемещение этих двух точек для случая, когда температура определяется формулой (о), а напряжения — формулами (г).
Применяя это уравнение к круговому пути радиуса  начинающемуся в точке 1 (рис. 234), огибающему отверстие, и заканчивающемуся в точке 2, поскольку
начинающемуся в точке 1 (рис. 234), огибающему отверстие, и заканчивающемуся в точке 2, поскольку  имеем
имеем

Подставляя эту зависимость в  находим
находим

Относительное перемещение не равно нулю, и следовательно, нужно считать, что цилиндр имеет щель, ввиду наличия которой точка 2 может смещаться относительно точки 1 по вертикали на величину  (рис. 234, б). Движение верхней стенки щели относительно нижней равносильно вращению на угол
(рис. 234, б). Движение верхней стенки щели относительно нижней равносильно вращению на угол  в направлении часовой стрелки относительно центра сечения цилиндра. При этом В отрицательно, если величина Т положительна. В этом случае щель раскрывается на величину центрального
в направлении часовой стрелки относительно центра сечения цилиндра. При этом В отрицательно, если величина Т положительна. В этом случае щель раскрывается на величину центрального  Задача о смыкании стенок такой щели уже решалась на стр. 95 для случая плоского напряженного состояния. Это решение можно преобразовать для случая плоской деформации с помощью подстановок, приведенных на стр. 446. Компоненты напряжения, получающиеся в результате, в сочетании с осевым напряжением
Задача о смыкании стенок такой щели уже решалась на стр. 95 для случая плоского напряженного состояния. Это решение можно преобразовать для случая плоской деформации с помощью подстановок, приведенных на стр. 446. Компоненты напряжения, получающиеся в результате, в сочетании с осевым напряжением  получаемым по формулам (г), становятся тождественно равными компонентам, определяемым уравнениями (257) при отсутствии осевой силы.
получаемым по формулам (г), становятся тождественно равными компонентам, определяемым уравнениями (257) при отсутствии осевой силы.
Температуры на внутренней и внешней поверхностях цилиндра, изменяющиеся вдоль круговых границ, можно представить в виде рядов Фурье

Температурные напряжения, вызванные несколькими членами этих рядов, можно рассматривать раздельно, температурные напряжения, связанные постоянными членами  рассматривались в предыдущем случае при
рассматривались в предыдущем случае при  Членам
Членам  в функции Z соответствуют члены, пропорциональные
в функции Z соответствуют члены, пропорциональные

Теперь интеграл  взятый вдоль полной окружности радиуса
взятый вдоль полной окружности радиуса  обратится в нуль (если только
обратится в нуль (если только  так как
так как

Это выражение, очевидно, равно нулю, если только  Если же
Если же  то получаем
то получаем

Таким образом, единственным членом в  который дает ненулевое значение интеграла в правой части уравнения
который дает ненулевое значение интеграла в правой части уравнения  является член
является член  Отсюда следует, что члены, содержащие
Отсюда следует, что члены, содержащие  и высшие гармоники в рядах
и высшие гармоники в рядах 
представляющих температуры, не вызывают относительного перемещения двух граней щели в трубе с разрезом. Результирующий тепловой поток от внутренней поверхности трубы к ее внешней поверхности, отвечающий таким членам, равен нулю, и они вызывают только напряжения, определяемые формулами (г).
Членами в рядах  которые приводят к членам, содержащим
которые приводят к членам, содержащим  в функции
в функции  являются члены с
являются члены с  При этом достаточно рассмотреть лишь члены с
При этом достаточно рассмотреть лишь члены с  так как влияние членов с
так как влияние членов с  можно получить из формул, соответствующих
можно получить из формул, соответствующих  изменив начало отсчета
изменив начало отсчета  . В связи с этим рассмотрим лишь
. В связи с этим рассмотрим лишь

Задача об отыскании стационарного распределения температуры, отвечающего этим ее значениям на границах, решается, если считать температуру Т действительной частью функции

и найти такие значения  при которых удовлетворяются условия
при которых удовлетворяются условия  Эти значения таковы:
Эти значения таковы:

Член  отвечает значению функции
отвечает значению функции

Внося это значение в уравнение  находим, что разрыв в перемещении определяется формулой
находим, что разрыв в перемещении определяется формулой

откуда

Это означает, что верхняя граница разреза на рис. 234 перемещается вниз на величину  в пространство, занимаемое нижней гранью и находящимся под ней матерййлом. Физически это, разумеется, невозможно, и этому препятствуют действующие между гранями усилия, достаточные для создания противодействующего перемещения. Напряженное состояние, вызываемое этими противодействующими перемещениями, определяется так, как это описано в конце § 43, но теперь уже, конечно, для случая плоской деформации.
в пространство, занимаемое нижней гранью и находящимся под ней матерййлом. Физически это, разумеется, невозможно, и этому препятствуют действующие между гранями усилия, достаточные для создания противодействующего перемещения. Напряженное состояние, вызываемое этими противодействующими перемещениями, определяется так, как это описано в конце § 43, но теперь уже, конечно, для случая плоской деформации.
Для этого случая  получаем
получаем

и аналогично тому, как получена формула (а) § 151, находим

здесь

Если концы свободны, то следует также рассмотреть осевые напряжения, связанные со снятием усилий и моментов на каждом конце.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
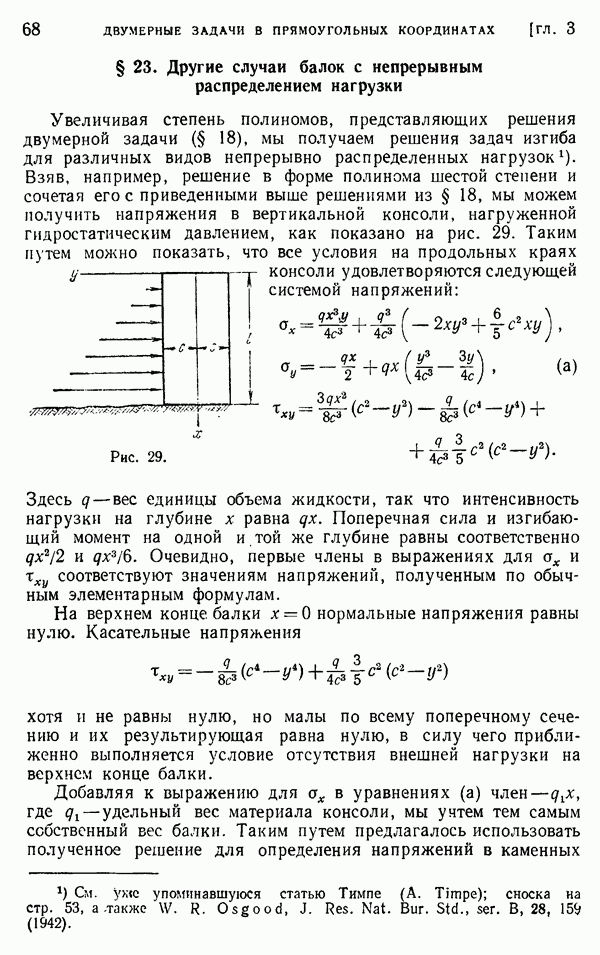
- § 23. Другие случаи балок с непрерывным распределением нагрузки
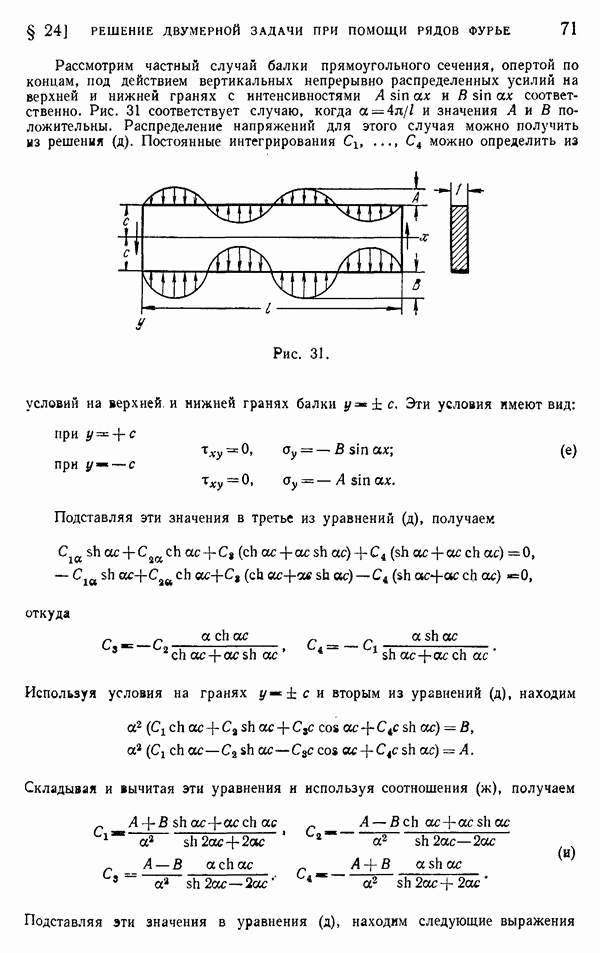
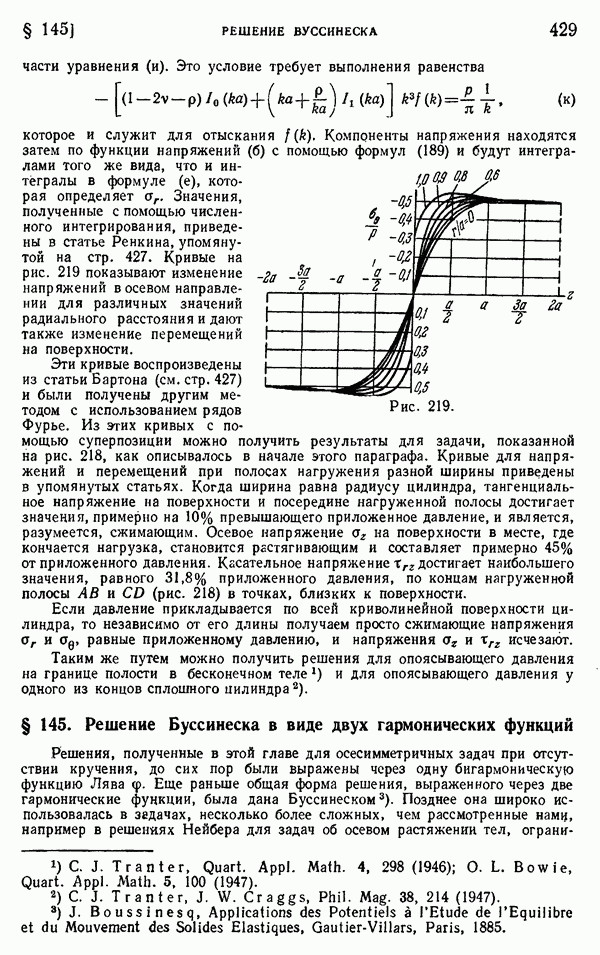
- § 24. Решение двумерной задачи при помощи рядов Фурье
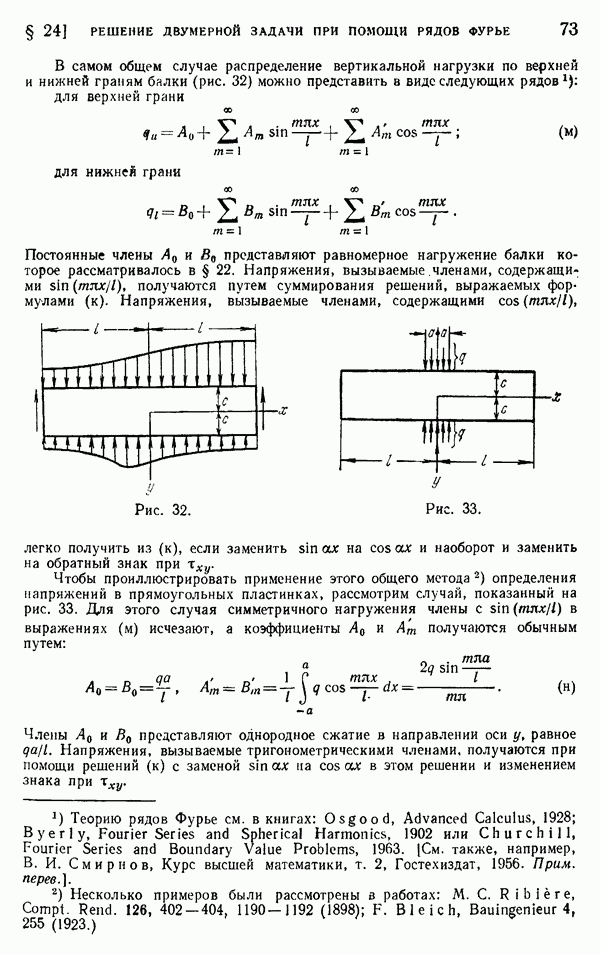
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
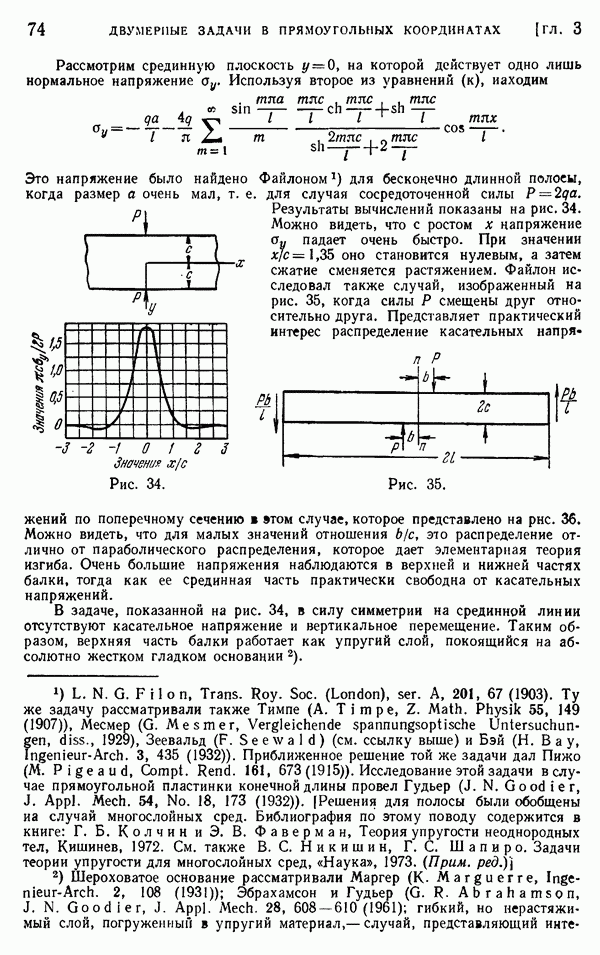
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
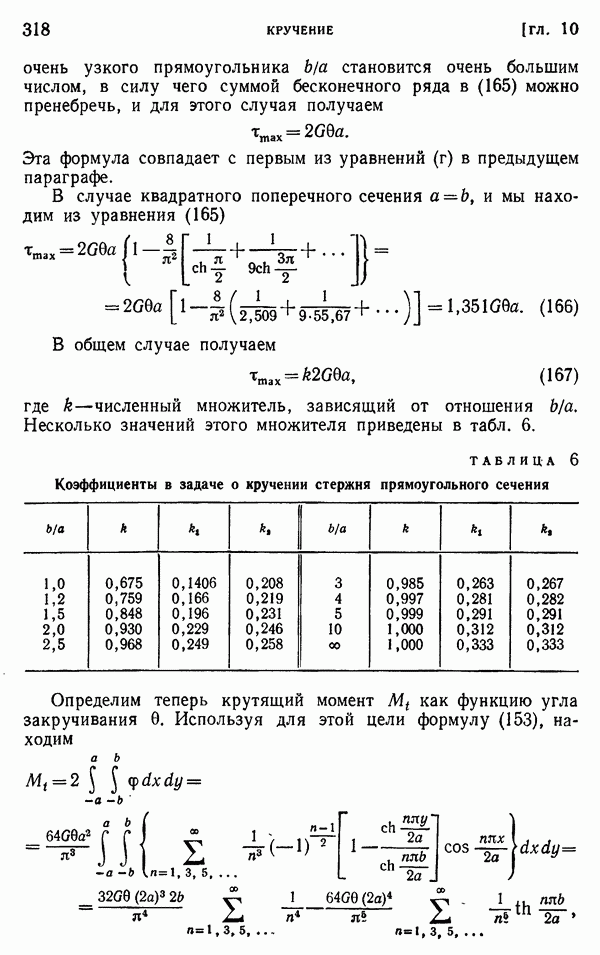
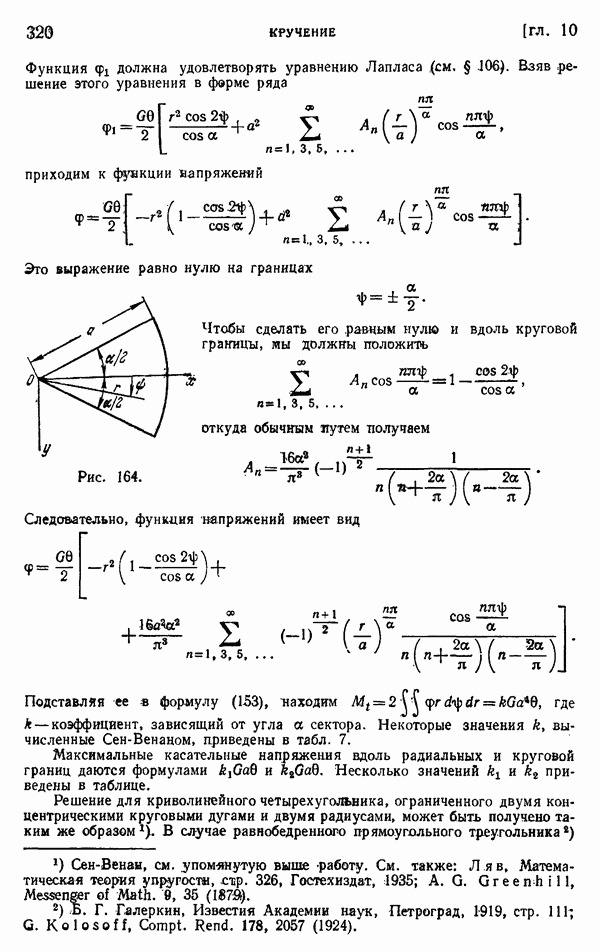
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
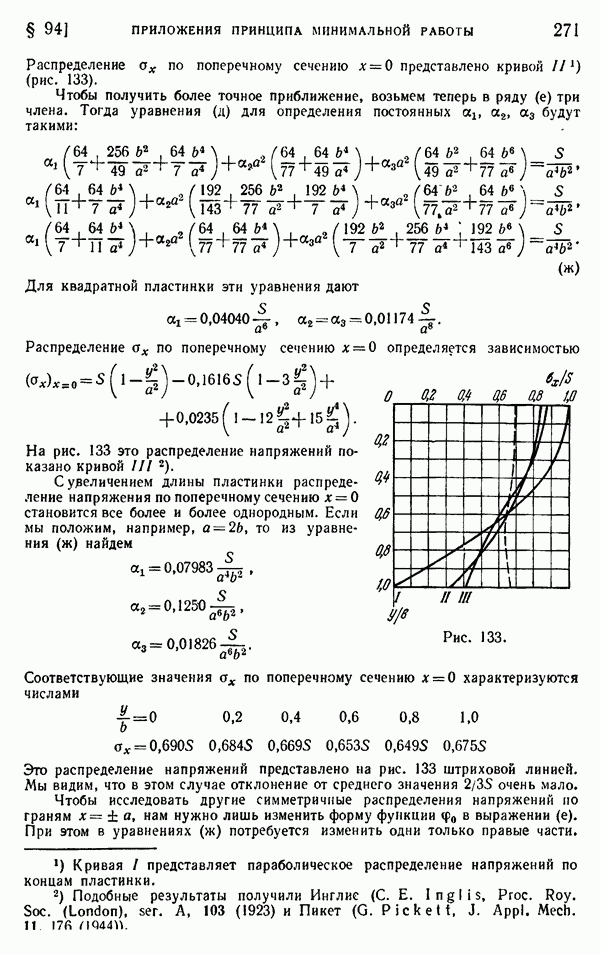
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
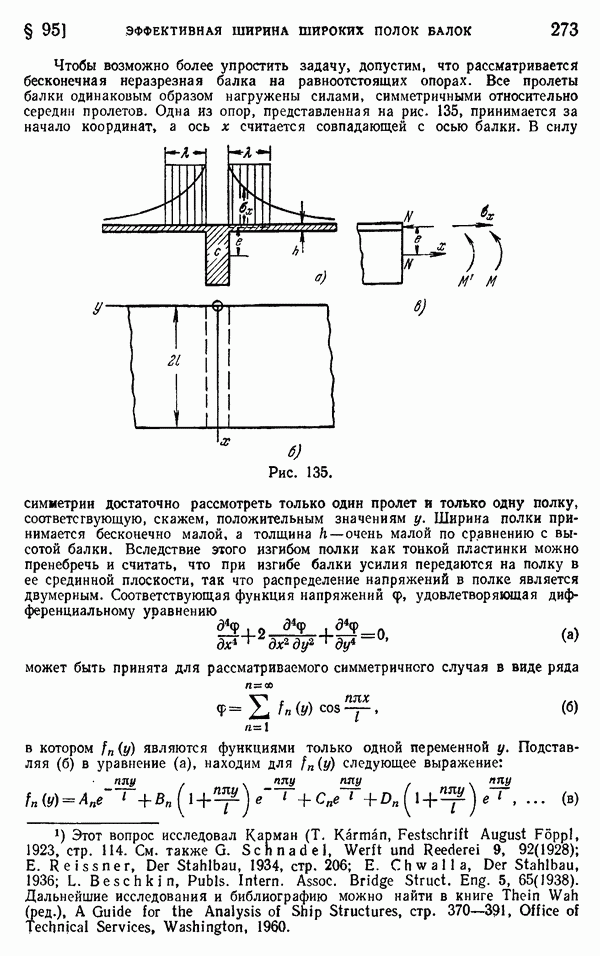
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
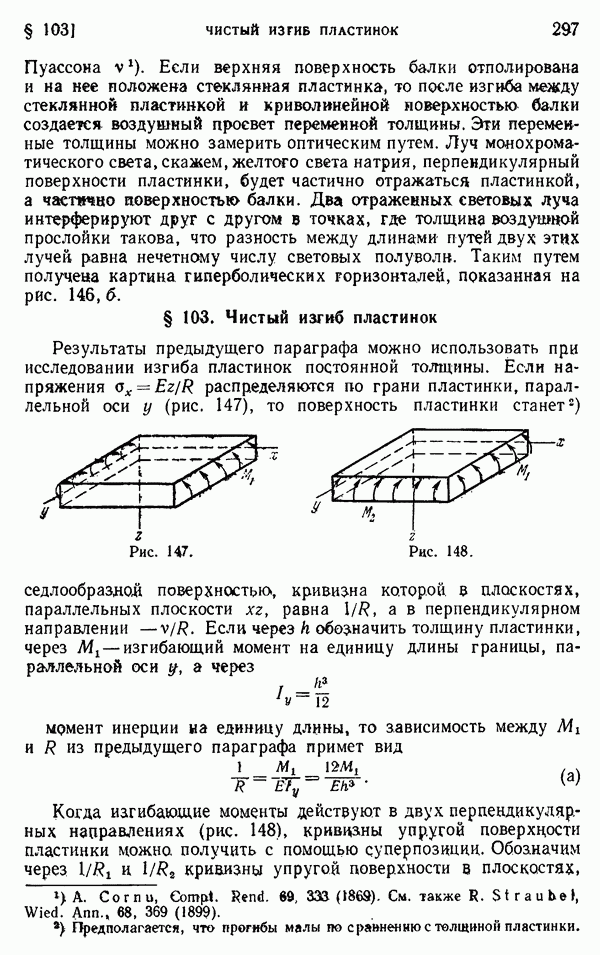
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
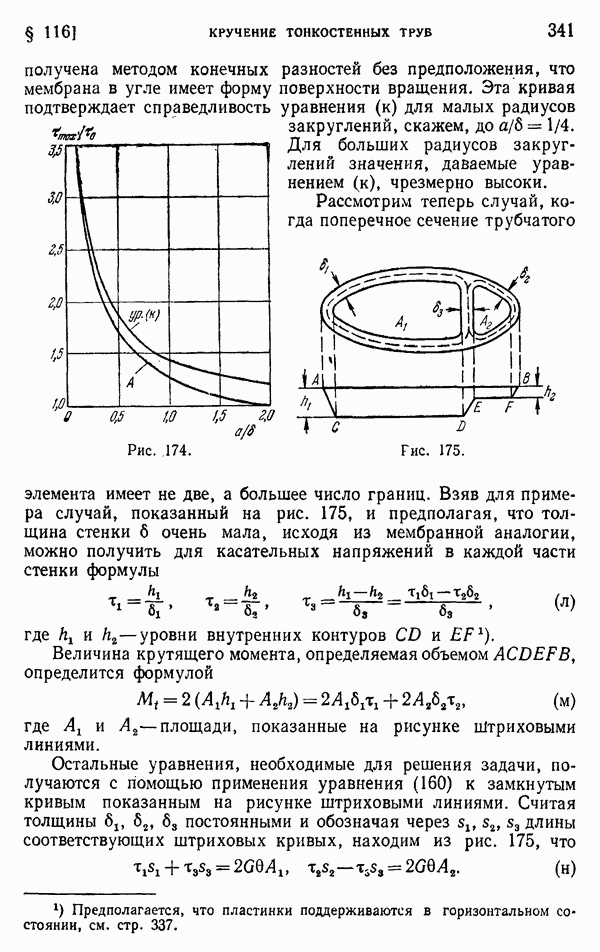
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
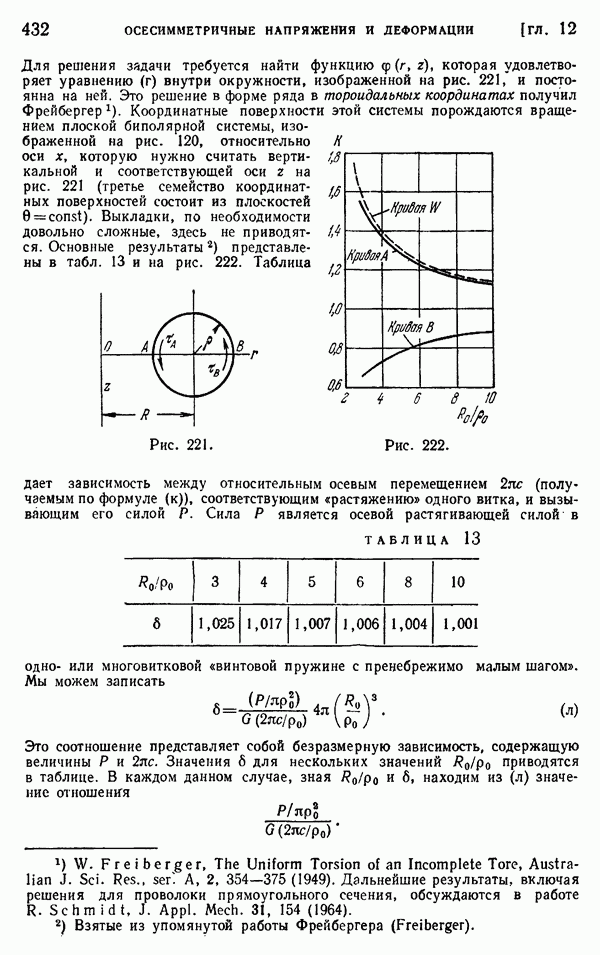
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
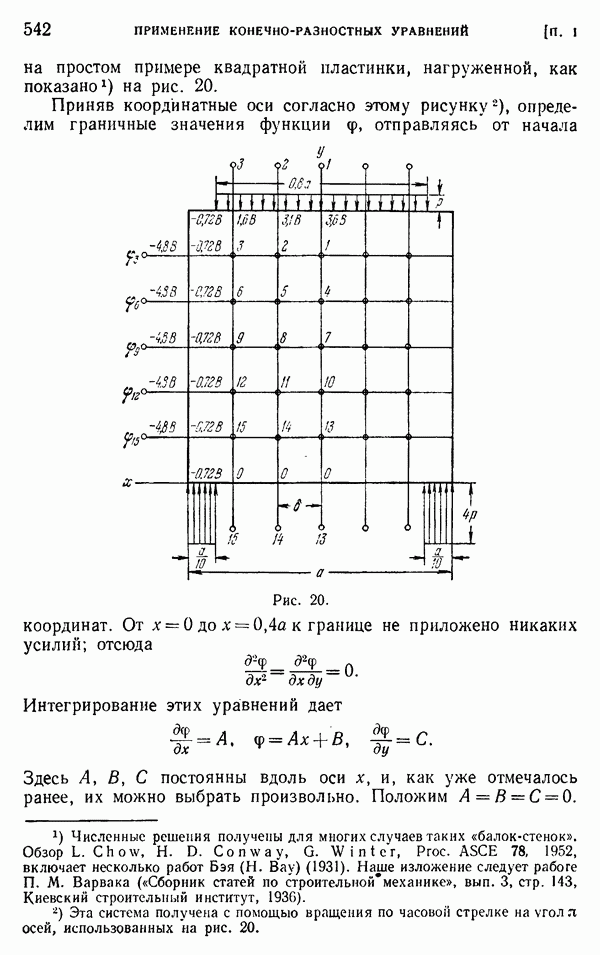
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
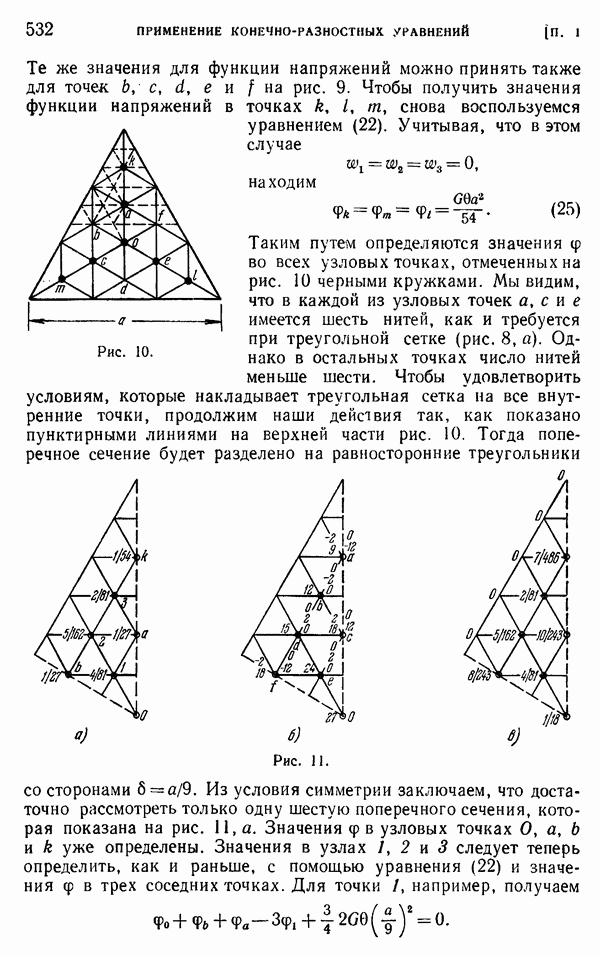
- § 4. Треугольные и шестиугольные сетки
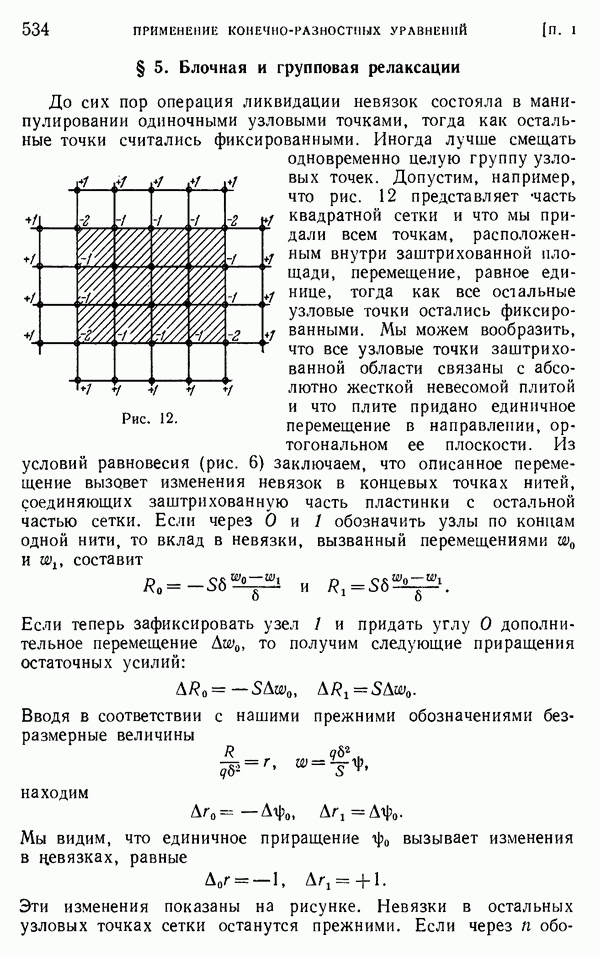
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
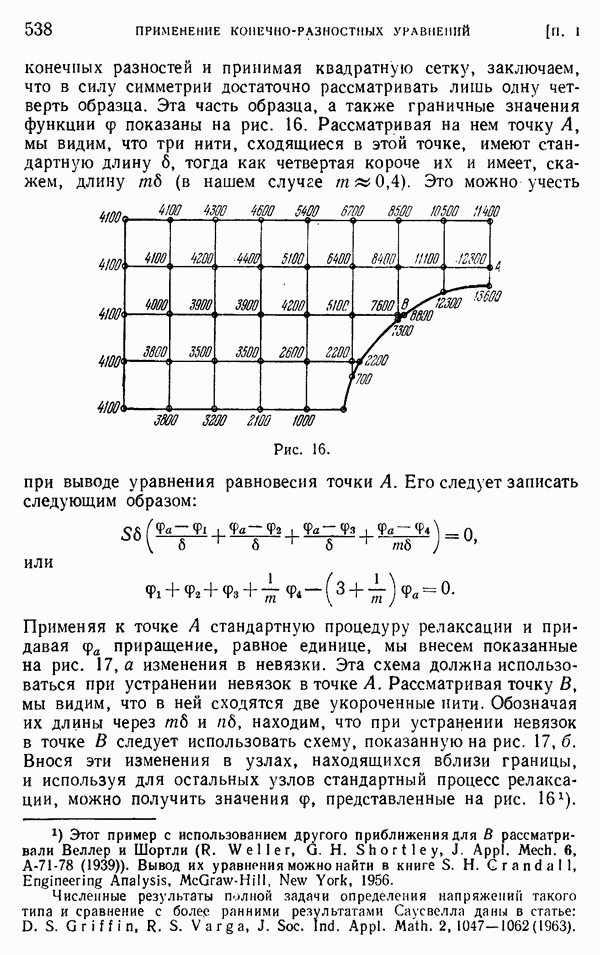
- § 7. Точки, расположенные вблизи границы
- § 8. Бигармоническое уравнение
- § 9. Кручение круглых валов переменного диаметра
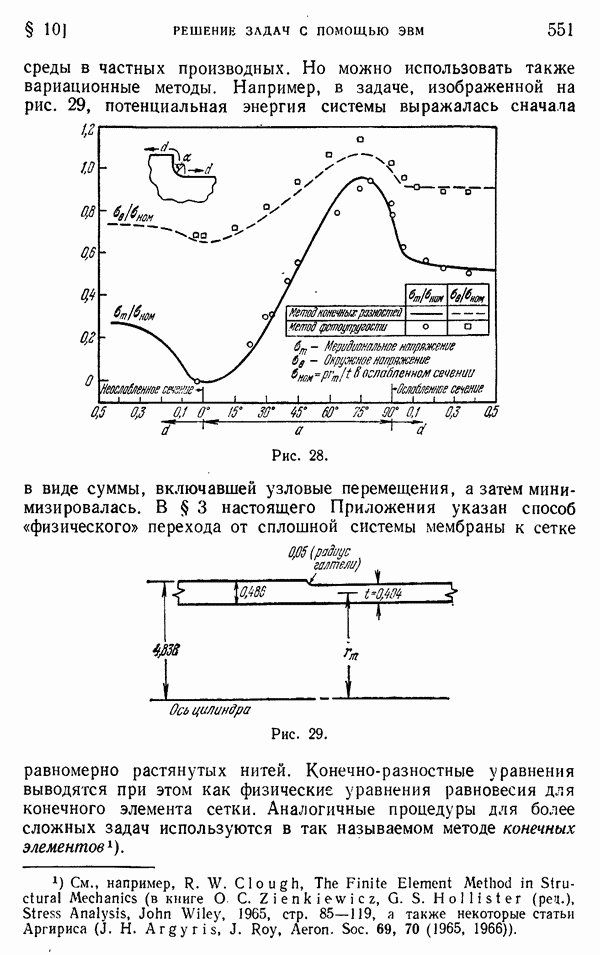
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
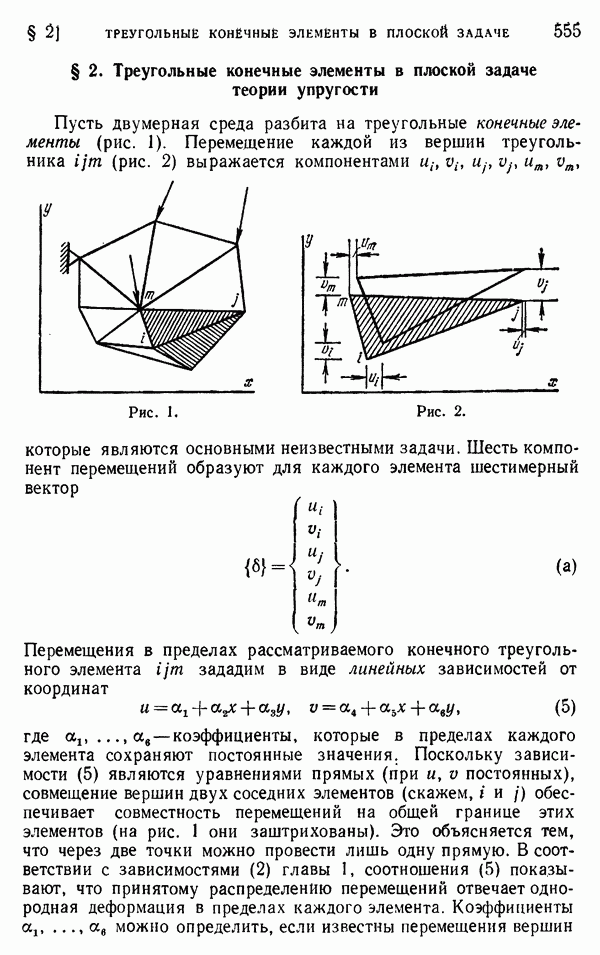
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
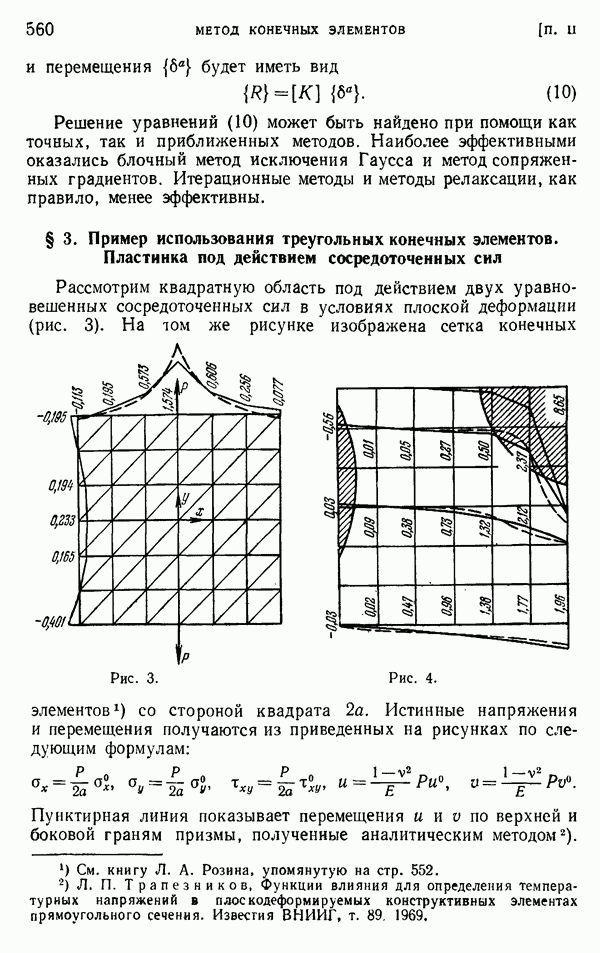
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
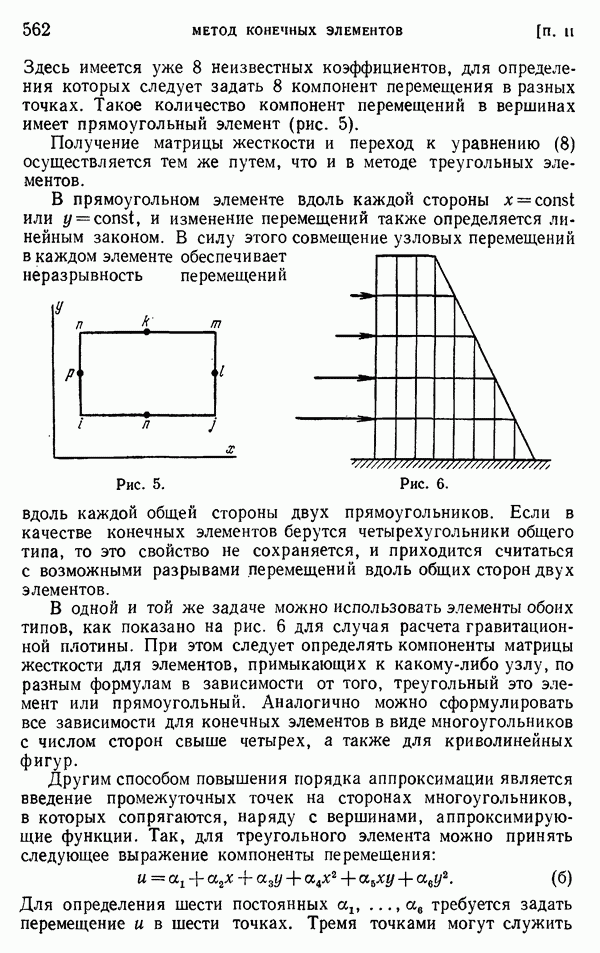
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи