| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 90. Энергия деформации
Если однородный стержень подвергается простому растяжению, то при удлинении стержня силы, приложенные к его концам, совершат некоторую работу.
Таким образом, если на элемент стержня, показанный на рис. 130, действует лишь одно нормальное напряжение  то соответствующая сила
то соответствующая сила  совершает работу на перемещении
совершает работу на перемещении 
Зависимость между этими двумя величинами в процессе нагружения изображается прямой линией ОА на рис.  а работа, совершенная в процессе деформации, определяется площадью
а работа, совершенная в процессе деформации, определяется площадью  треугольника
треугольника  . Обозначая эту работу через
. Обозначая эту работу через  имеем
имеем


Рис. 130.
Очевидно, что такая же работа совершается во всех подобных элементах, если они имеют тот же объем. А теперь зададимся вопросом: что стало с этой работой, в какой вид или виды энергии она перешла?
Адиабатическое сжатие газа вызывает повышение его температуры. Когда адиабатически сжимается обычный стальной стержень, происходит аналогичное, очень малое повышение температуры. Начальная температура может быть восстановлена затем путем отнятия тепла. Такое изменение температуры изменяет и деформацию, однако это изменение касается очень малой доли адиабатической деформации. Если бы это было не так, то между адиабатическим и изотермическим модулями упругости наблюдалось бы значительное различие. В действительности это различие для обычных металлов очень мало. Например, адиабатический модуль Юнга для железа превышает изотермический модуль всего на 0,26%. Такого рода различиями мы будем здесь пренебрегать. Работа, затраченная на деформацию элемента, переходит в накапливаемую в нем энергию, называемую энергией деформации. При этом предполагается, что элемент остается упругим и не образуется кинетическая энергия.
Те же соображения используются и в том случае, когда на элемент действуют все шесть компонент напряжения  (рис. 3). Сохранение энергии требует, чтобы работа зависела только от конечных значений, но не от порядка, в котором прикладываются силы. В противном случае, производя нагружение в одном порядке, а разгрузку — в другом, мы могли бы получить большее количество работы. Следовательно, при полном цикле деформирования из элемента можно было бы извлечь некоторую величину работы.
(рис. 3). Сохранение энергии требует, чтобы работа зависела только от конечных значений, но не от порядка, в котором прикладываются силы. В противном случае, производя нагружение в одном порядке, а разгрузку — в другом, мы могли бы получить большее количество работы. Следовательно, при полном цикле деформирования из элемента можно было бы извлечь некоторую величину работы.
Определение совершенной работы проще всего произвести, если силы или напряжения возрастают одновременно в одном и том же отношении. Тогда зависимость между каждой силой и соответствующим ей перемещением остается линейной, как показано на рис. 130, б, и работа, совершенная этими силами, равна

где

Таким образом,  представляет собой суммарную работу, приходящуюся на единицу объема, или энергию деформации в единице объема.
представляет собой суммарную работу, приходящуюся на единицу объема, или энергию деформации в единице объема.
В предыдущих рассуждениях напряжения на противоположных гранях элемента считались равными и предполагалось, что объемных сил нет. Рассмотрим теперь работу, совершенную над элементом, когда напряжения по
объему тела изменяются и имеются объемные силы. Рассмотрим сначала усилие  на грани 1 элемента (рис. 130, а); оно совершает работу на перемещении и этой грани, и величина этой работы равна
на грани 1 элемента (рис. 130, а); оно совершает работу на перемещении и этой грани, и величина этой работы равна  где индекс 1 показывает, что функции
где индекс 1 показывает, что функции  и и должны определяться в точке
и и должны определяться в точке  . Сила
. Сила  на грани 2 совершает работу
на грани 2 совершает работу  . Полная работа на обеих гранях
. Полная работа на обеих гранях

в пределе будет равна

Вычисляя работу, совершенную касательными напряжениями  на гранях 1 и 2 и складывая ее с работой, определяемой выражением (г), находим работу, совершенную на обеих гранях всеми тремя компонентами напряжения:
на гранях 1 и 2 и складывая ее с работой, определяемой выражением (г), находим работу, совершенную на обеих гранях всеми тремя компонентами напряжения:

где  — компоненты перемещения в направлениях
— компоненты перемещения в направлениях  Подобным же образом может быть определена работа, совершенная на двух других парах граней. Для полной работы, совершенной напряжениями на всех этих гранях, получаем выражение
Подобным же образом может быть определена работа, совершенная на двух других парах граней. Для полной работы, совершенной напряжениями на всех этих гранях, получаем выражение

При нагружении тела объемные силы  и прочие совершают работу
и прочие совершают работу

Полная работа, совершенная над элементом, представляется суммой работ  Выполняя в (д) дифференцирование, находим для этой полной работы выражение
Выполняя в (д) дифференцирование, находим для этой полной работы выражение

Согласно уравнениям равновесия (123), выведенным в § 84, множители в скобках при  равны нулю. Величины, умножаемые на компоненты напряжения, согласно формулам (2), равны
равны нулю. Величины, умножаемые на компоненты напряжения, согласно формулам (2), равны  соответственно. Следовательно, полная работа, совершенная над элементом, сводится к значению, определяемому выражениями (б) и (в). Таким образом, эти формулы будут определять работу, совершенную над элементом упругого тела, или энергию, накопленную им, и в том случае, когда напряжения распределены по телу неоднородно и имеются объемные силы.
соответственно. Следовательно, полная работа, совершенная над элементом, сводится к значению, определяемому выражениями (б) и (в). Таким образом, эти формулы будут определять работу, совершенную над элементом упругого тела, или энергию, накопленную им, и в том случае, когда напряжения распределены по телу неоднородно и имеются объемные силы.
С помощью закона Гука (см. равенства (3) и (6)) мы можем выразить функцию  определяемую равенством (в), как функцию одних только компонент напряжения:
определяемую равенством (в), как функцию одних только компонент напряжения:

Легко проверить, что

где  -инварианты напряжения, введенные в § 79.
-инварианты напряжения, введенные в § 79.
Поступая несколько иначе, мы можем использовать соотношения (11) и выразить  как функцию одних только компонент деформации. Тогда
как функцию одних только компонент деформации. Тогда

где

Формула (132) непосредственно показывает, что величина  всегда положительна.
всегда положительна.
Легко показать, что производная от функции  , определяемой формулой (132), по любой компоненте деформации дает соответствующую компоненту напряжения. Так, например, взяв производную по
, определяемой формулой (132), по любой компоненте деформации дает соответствующую компоненту напряжения. Так, например, взяв производную по  и используя первое из соотношений (11), находим, что
и используя первое из соотношений (11), находим, что

Для случая плоского напряженного состояния, в котором  выражение (131) принимает вид
выражение (131) принимает вид

или через компоненты деформации

Полная энергия диформации V деформируемого упругого тела получается из энергии деформации в единице объема  путем интегрирования. Обозначая элемент объема через
путем интегрирования. Обозначая элемент объема через  получаем
получаем

Эта формула определяет полную работу по преодолению сопротивления внутренних сил, совершенную при нагружении. Если мы представим себе тело как совокупность очень большого числа частиц, соединенных пружинами, то эта формула будет представлять работу, совершаемую при растяжении и сжатии пружин. Для получения работы, которую совершили над частицами тела внутренние силы, нужно поменять знак на обратный.
Величина энергии деформации, накопленной в единице объема материала, иногда используется как критерий для определения предельного напряжения,
при котором происходит разрушение  Чтобы согласовать теорию с тем фактом, что изотропные материалы могут выдерживать очень большие гидростатические давления без возникновения течения, было предложено разделить энергию деформации на две части, одна из которых связана с изменениями объема, а другая — со сдвигами, и считать, что прочность определяется лишь второй частью энергии 2).
Чтобы согласовать теорию с тем фактом, что изотропные материалы могут выдерживать очень большие гидростатические давления без возникновения течения, было предложено разделить энергию деформации на две части, одна из которых связана с изменениями объема, а другая — со сдвигами, и считать, что прочность определяется лишь второй частью энергии 2).
Мы знаем, что изменение объема пропорционально сумме трех нормальных компонент напряжения (см. формулу (8)), так что если эта сумма равна нулю, то деформация связана только с изменением формы. Каждую компоненту напряжения можно разложить на две части

где

Поскольку отсюда

напряженное состояние  вызывает только формоизменение, а изменение объема зависит лишь от величины равномерного растяжения
вызывает только формоизменение, а изменение объема зависит лишь от величины равномерного растяжения  Часть полной энергии, связанная с этим изменением объема, согласно формуле (8), равна
Часть полной энергии, связанная с этим изменением объема, согласно формуле (8), равна

Вычитая это выражение из (131) и используя тождество

мы можем представить ту часть полной энергии, которая связана с формоизменением, в виде

В случае простого растяжения в направлении х отлична от нуля только величина  и энергия формоизменения (136) равна
и энергия формоизменения (136) равна  . В случае чистого сдвига, скажем, между плоскостями
. В случае чистого сдвига, скажем, между плоскостями  от нуля отлична только - компонента
от нуля отлична только - компонента  и энергия формоизменения равна
и энергия формоизменения равна  Если верно, что при любой системе напряжений разрушение происходит тогда, когда энергия формоизменения достигает определенного предела (характерного для материала),
Если верно, что при любой системе напряжений разрушение происходит тогда, когда энергия формоизменения достигает определенного предела (характерного для материала),
то отношение между критическим значением самого по себе растягивающего напряжения и самого по себе касательного напряжения находятся из уравнения

откуда

Эксперименты со сталью показывают, что отношение между пределом текучести на растяжение и пределом текучести на сдвиг находится в очень хорошем согласии с уравнением  Вводя в рассмотрение энергию деформации, можно связать принцип Сен-Венана (см. стр. 57) с накоплением энергии. Этот принцип эквивалентен утверждению, что самоуравновешенное распределение усилий на малой части упругого тела вызывает лишь местные напряжения.
Вводя в рассмотрение энергию деформации, можно связать принцип Сен-Венана (см. стр. 57) с накоплением энергии. Этот принцип эквивалентен утверждению, что самоуравновешенное распределение усилий на малой части упругого тела вызывает лишь местные напряжения.
При таком распределении приложенные усилия совершают работу лишь за счет деформации нагруженной области. Зафиксируем положение и ориентацию некоторого поверхностного элемента этой области. Если обозначить через  порядок величины (например, среднее значение) силы, действующей на единицу площади, а через а — характерный линейный размер (например, диаметр) нагруженной части, то компоненты деформации будут иметь порядок
порядок величины (например, среднее значение) силы, действующей на единицу площади, а через а — характерный линейный размер (например, диаметр) нагруженной части, то компоненты деформации будут иметь порядок  а относительные перемещения в пределах нагруженной части будут порядка
а относительные перемещения в пределах нагруженной части будут порядка  Совершенная работа будет иметь порядок
Совершенная работа будет иметь порядок  или
или 
С другой стороны, компоненты напряжения порядка  вызывают энергию в единице объема порядка
вызывают энергию в единице объема порядка  Следовательно, в соответствии с формулировкой принципа совершенная работа достаточна лишь для объема порядка
Следовательно, в соответствии с формулировкой принципа совершенная работа достаточна лишь для объема порядка 
Здесь предполагалось, что тело имеет строго заданную форму и следует закону Гука. Последнее ограничение можно снять, если считать, что Е в вышеприведенных рассуждениях определяет просто порядок величины наклона кривых напряжения — деформация для рассматриваемого материала. Если тело не является существенно трехмерным, как это имеет место, например, в случае балки с очень тонкой стенкой или тонкой цилиндрической оболочки, то самоуравновешенное распределение усилий на одном конце может передаваться на расстояния, во много раз превышающие высоту балки или диаметр оболочки 3).
Приведенные выше рассуждения можно без изменения повторить для нагрузки с ненулевой результирующей, если в пределах нагруженной части или вблизи нее имеется закрепленный элемент поверхности. Таким образом, если деформируемый материал скреплен с абсолютно твердым, то давление, приложенное к малой части первого материала вблизи закрепления вызовет лишь местные напряжения.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
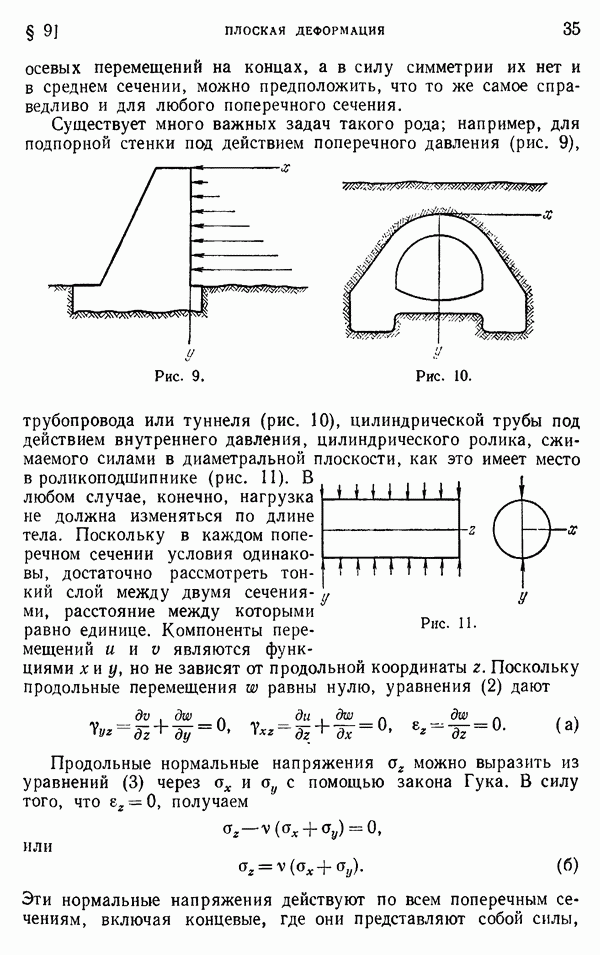
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
- § 23. Другие случаи балок с непрерывным распределением нагрузки
- § 24. Решение двумерной задачи при помощи рядов Фурье
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
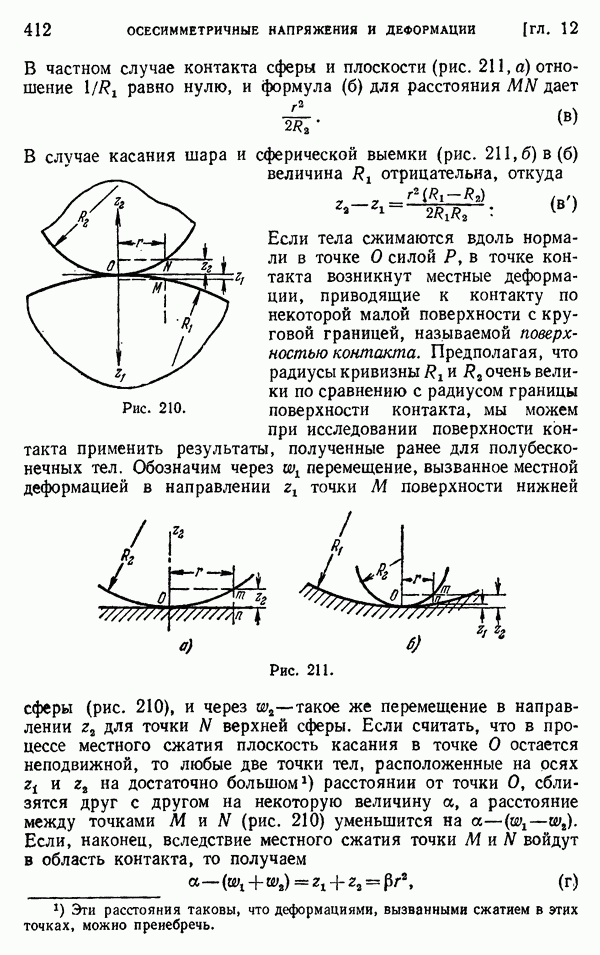
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
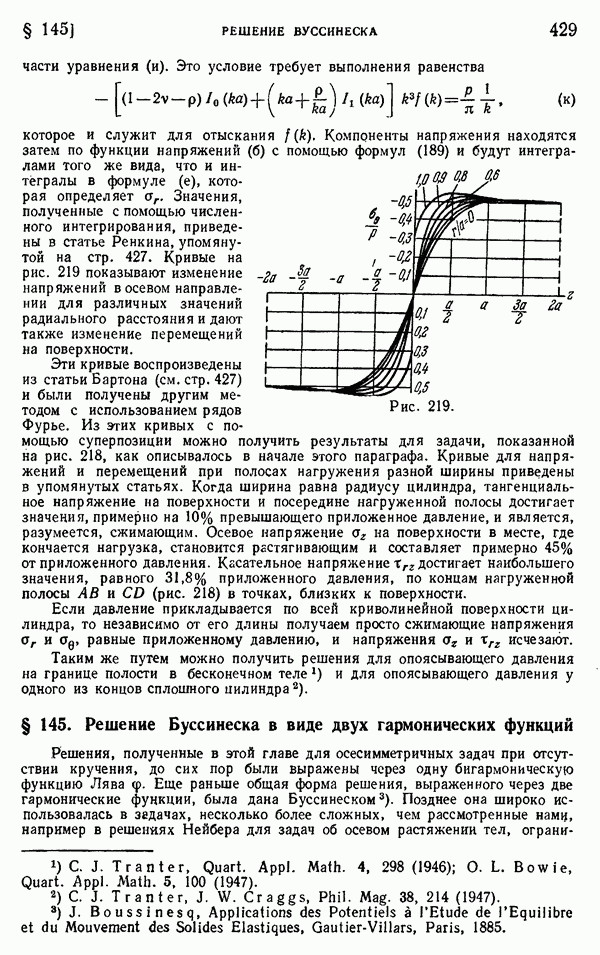
- § 144. Круглый цилиндр под действием опоясывающего давления
- § 145. Решение Буссинеска в виде двух гармонических функций
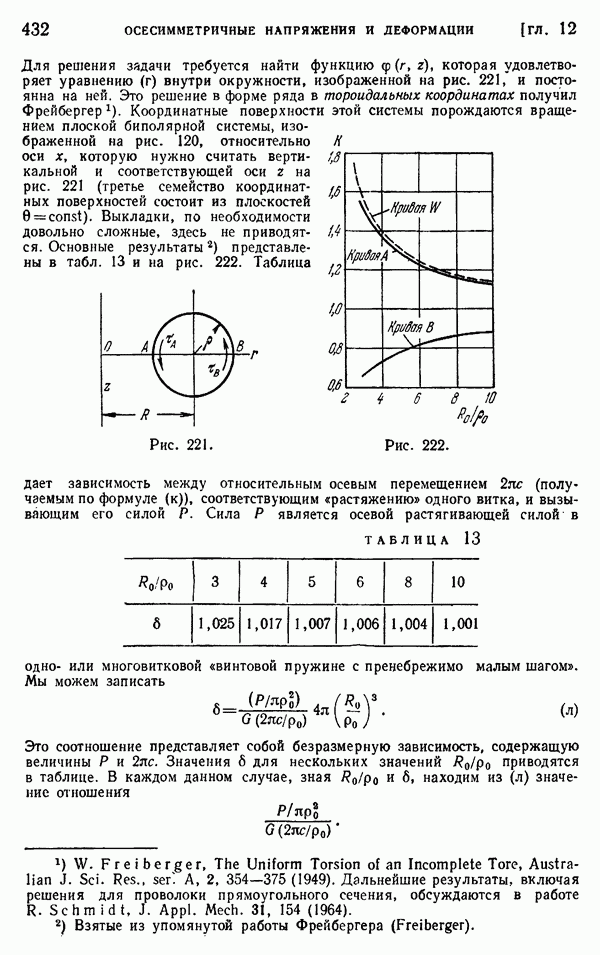
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
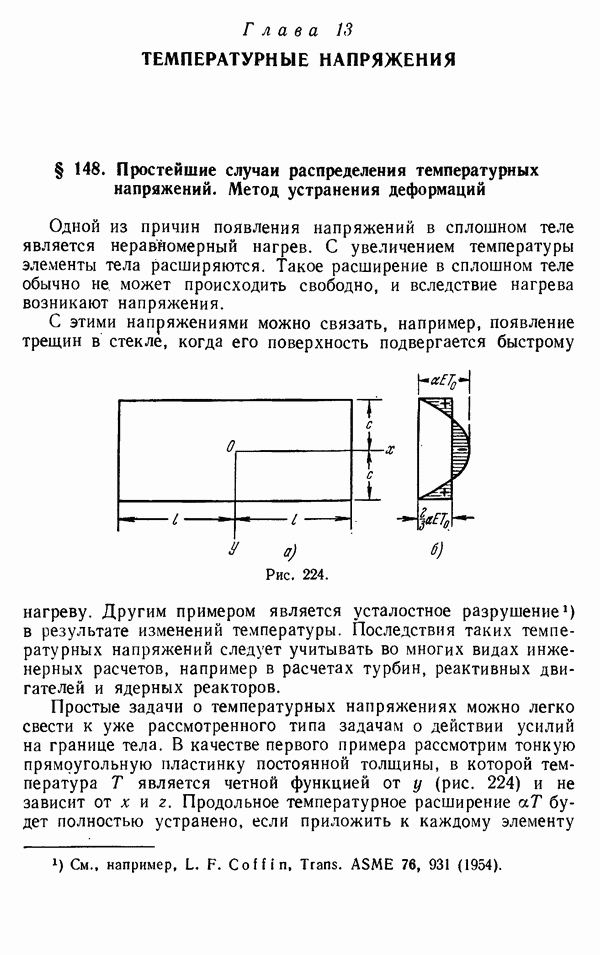
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
- § 4. Треугольные и шестиугольные сетки
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
- § 7. Точки, расположенные вблизи границы
- § 8. Бигармоническое уравнение
- § 9. Кручение круглых валов переменного диаметра
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи