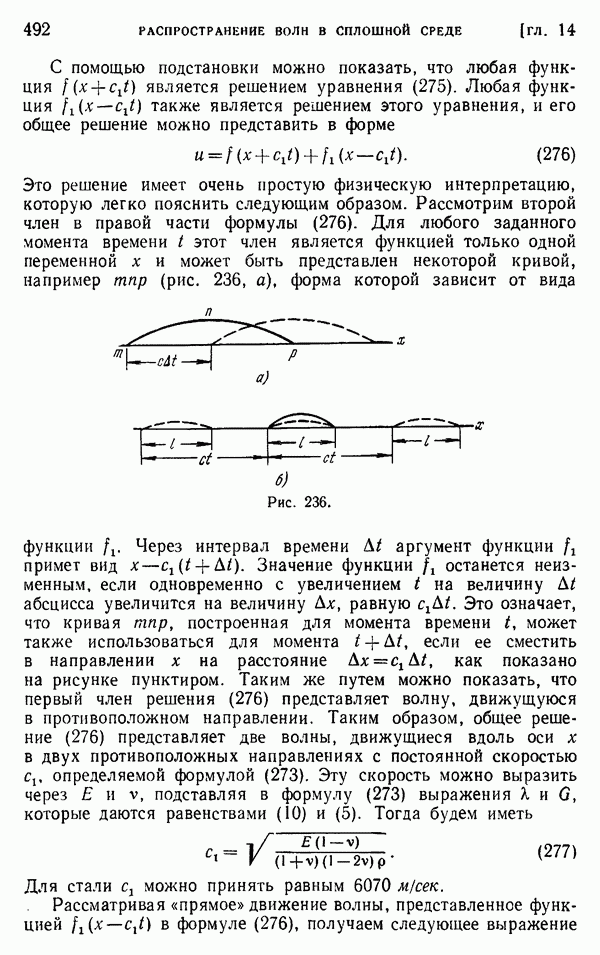
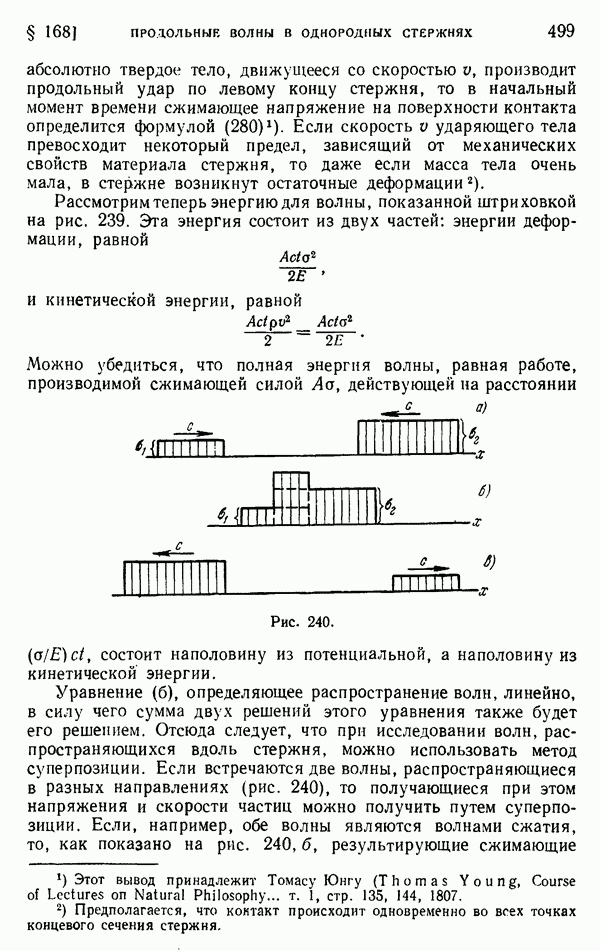
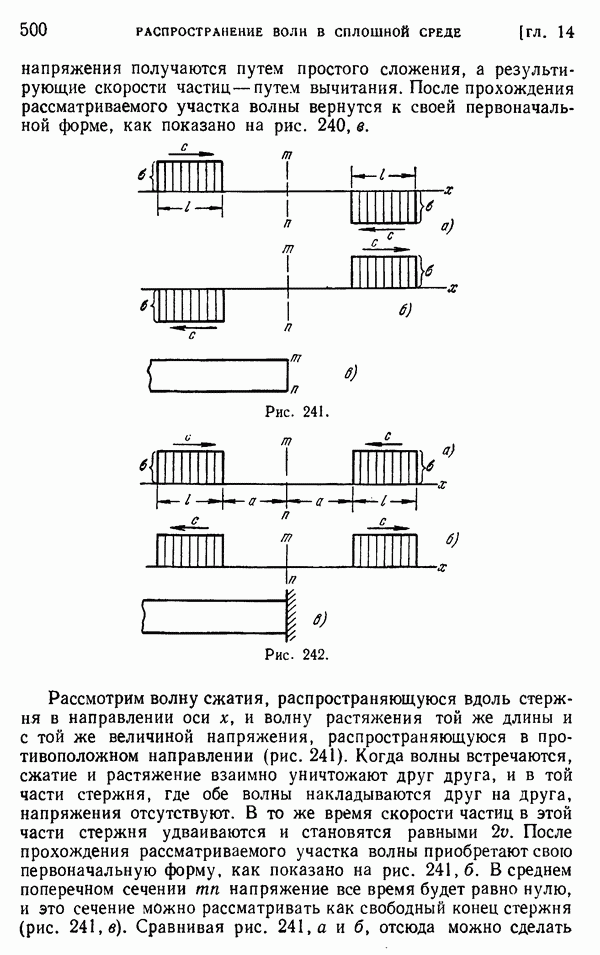
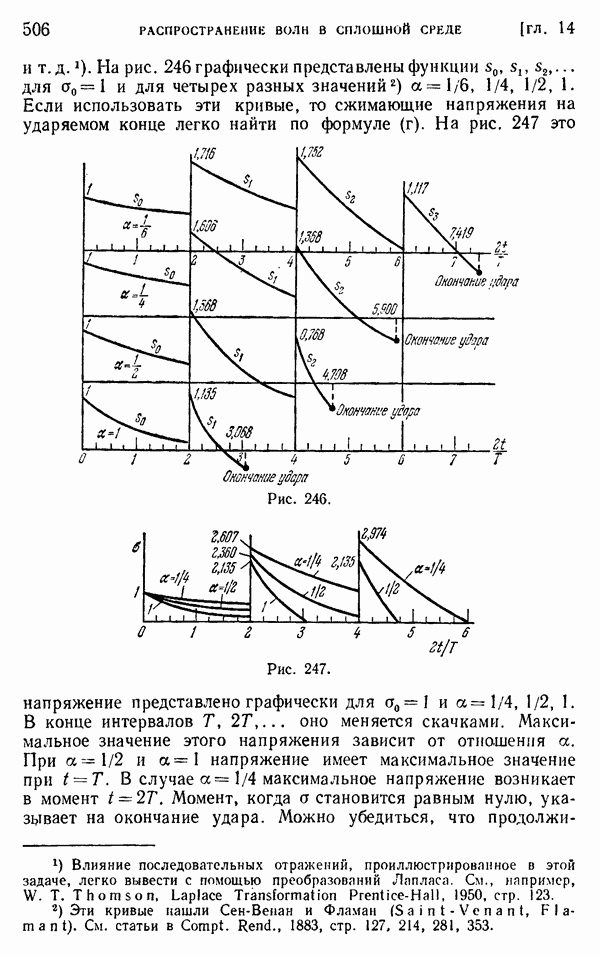
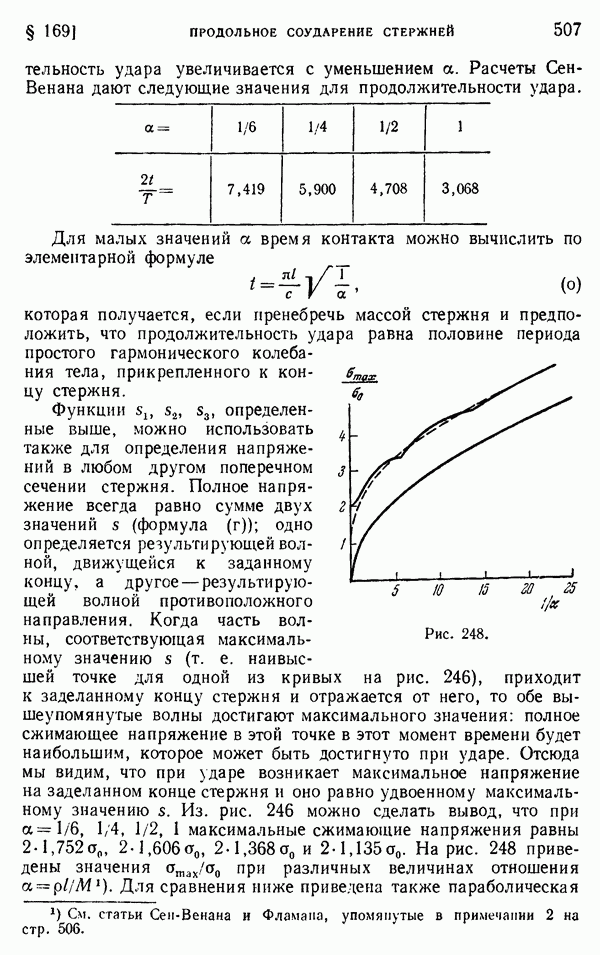
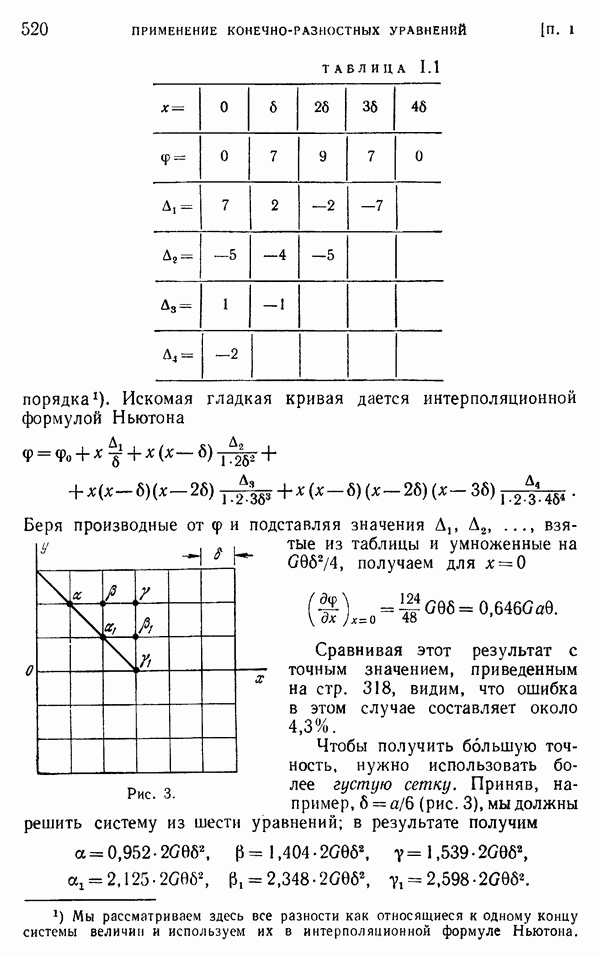
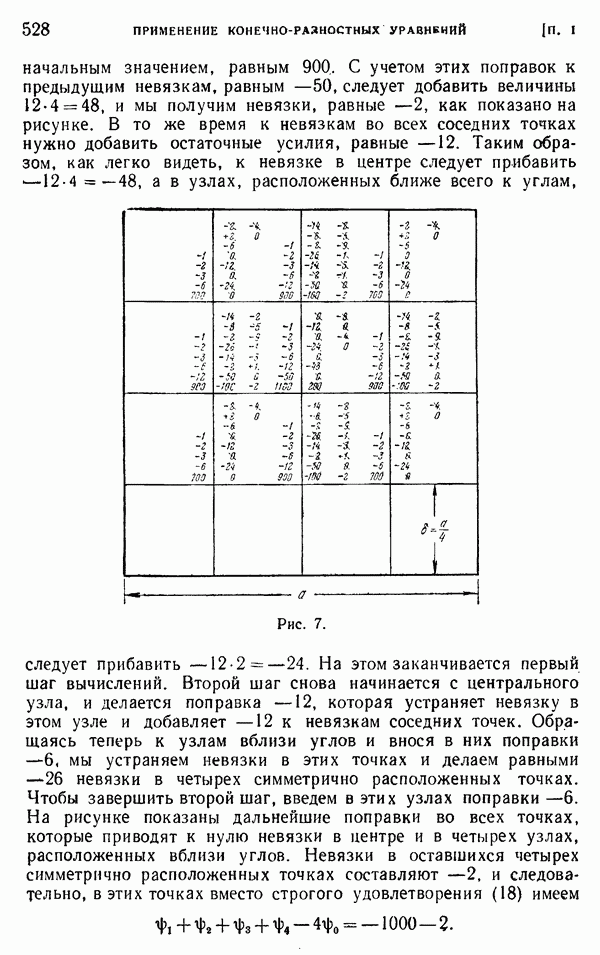
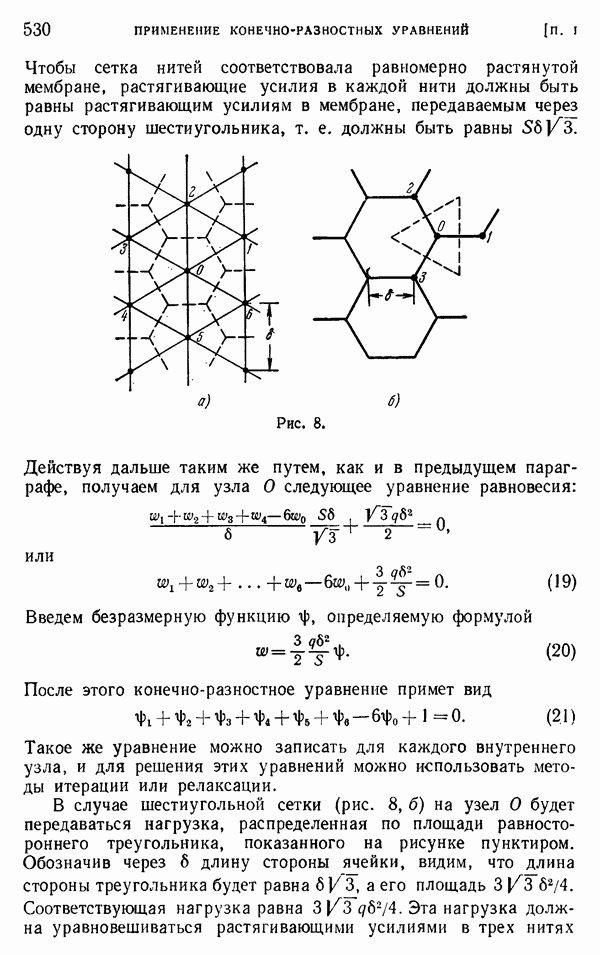
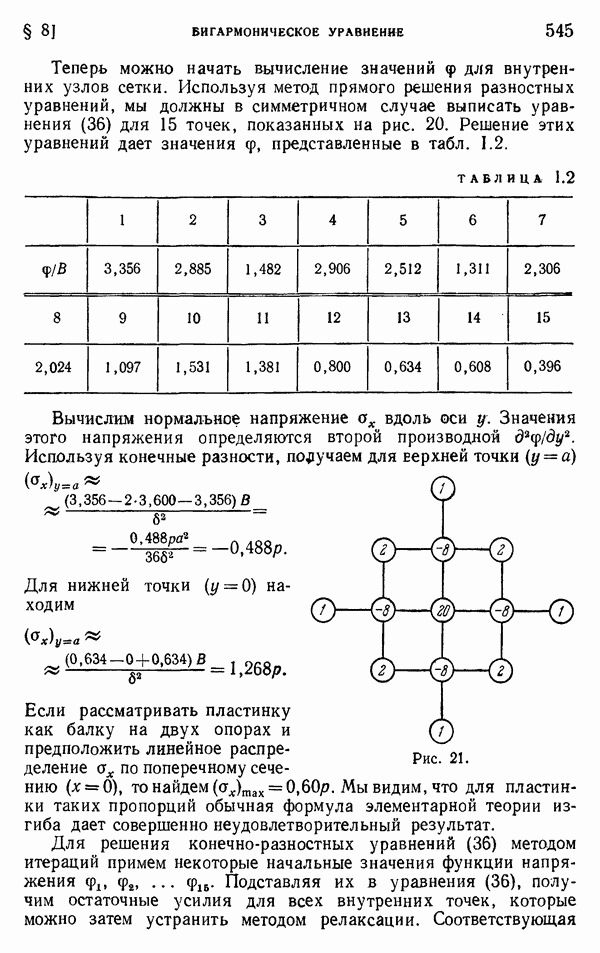
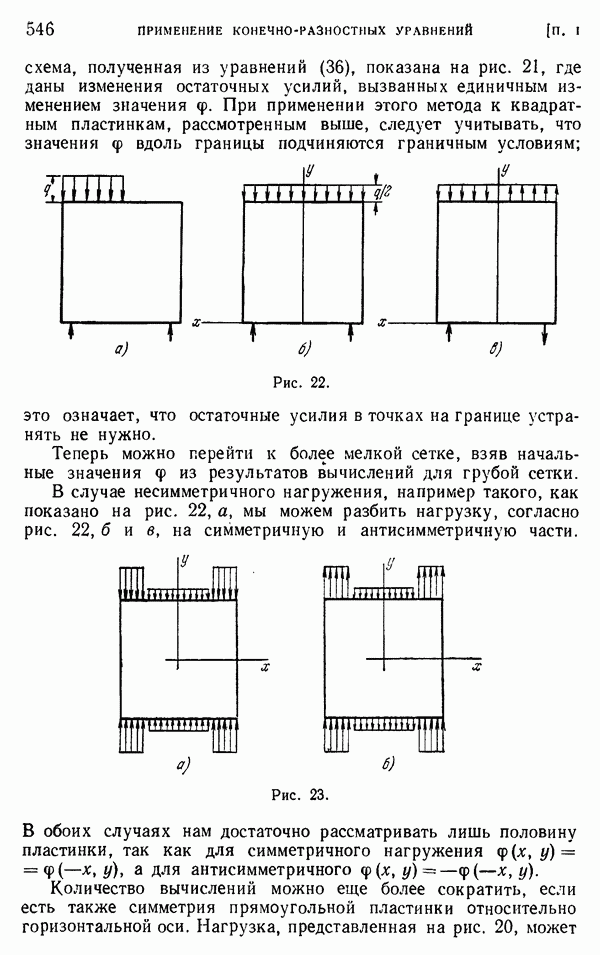
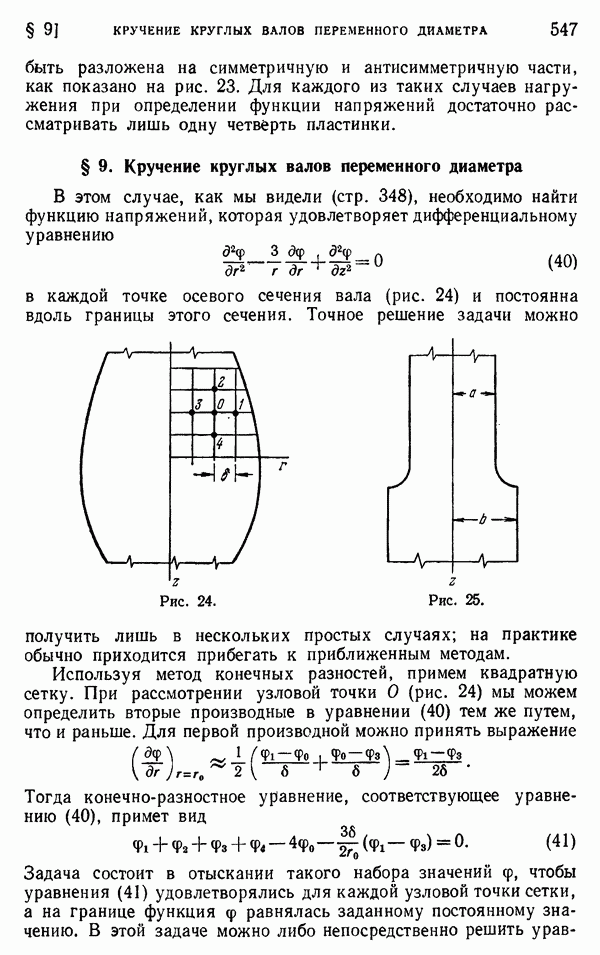
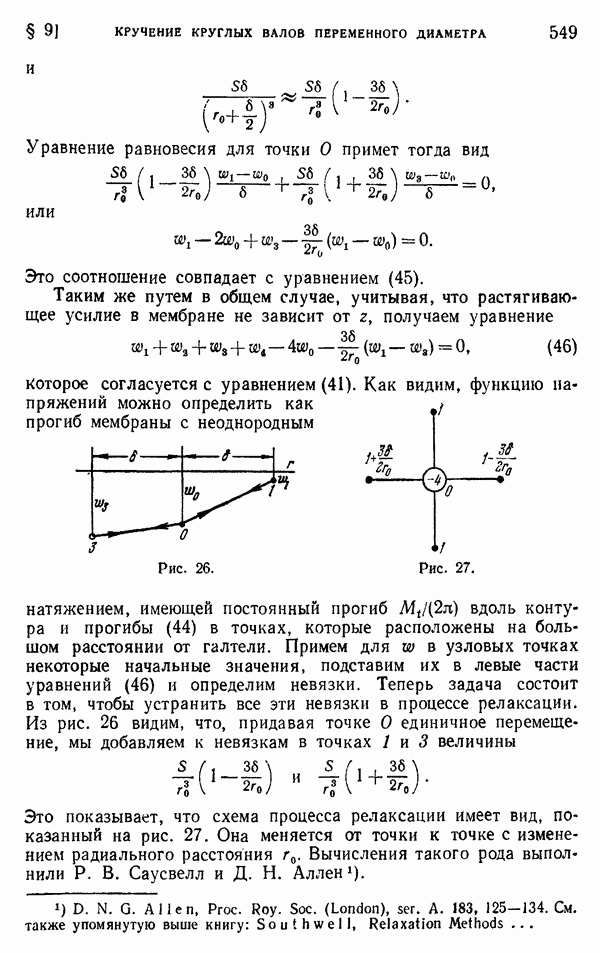
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 56. Функции напряжений, выраженные через гармонические и комплексные функции
Если  — некоторая функция от х и у, то при помощи операции дифференцирования находим, что
— некоторая функция от х и у, то при помощи операции дифференцирования находим, что

Если  - гармоническая функция, то скобка в правой части обращается в нуль. При этом функция
- гармоническая функция, то скобка в правой части обращается в нуль. При этом функция  также является гармонической, поскольку
также является гармонической, поскольку

Таким образом, повторное применение оператора Лапласа к выражению (а) дает

что можно переписать также в виде

Сравнение с уравнением (а) (стр. 53) показывает, что функция  может использоваться в качестве функции напряжений, если
может использоваться в качестве функции напряжений, если  — гармоническая функция. То же самое справедливо и в отношении функции
— гармоническая функция. То же самое справедливо и в отношении функции  а также, разумеется, в отношении самой функции
а также, разумеется, в отношении самой функции 
Путем непосредственного дифференцирования можно легко показать, что  также удовлетворяет тому же самому дифференциальному уравнению и может приниматься в качестве функции напряжений, если — гармоническая функция. Например, выбирая две гармонические функции
также удовлетворяет тому же самому дифференциальному уравнению и может приниматься в качестве функции напряжений, если — гармоническая функция. Например, выбирая две гармонические функции

из функций (и) (стр. 182) и умножая их на у, получаем с помощью суперпозиции функцию напряжений (г) (стр. 70). Взяв гармонические функции (к) и (л) (стр. 182) в их первоначальном виде или умножив их на  или
или  можно построить все члены функции напряжений в полярных координатах, определяемой уравнением (80).
можно построить все члены функции напряжений в полярных координатах, определяемой уравнением (80).
Вопрос о том, может ли быть получена таким образом любая функция напряжений, остается для нас открытым. Но ответ на
него будет получен сразу же в процессе выражения общей функции напряжений через две произвольные функции.
Обозначая оператор Лапласа

через  , можно записать уравнение (а) на стр. 53 в виде
, можно записать уравнение (а) на стр. 53 в виде  или
или  Обозначая через Р оператор
Обозначая через Р оператор  равный а
равный а  замечаем, что Р — гармоническая функция и, следовательно, должна иметь сопряженную гармоническую функцию
замечаем, что Р — гармоническая функция и, следовательно, должна иметь сопряженную гармоническую функцию  Следовательно,
Следовательно,  - аналитическая функция от
- аналитическая функция от  , и можно записать
, и можно записать

Интеграл от этой функции по z представляет собой другую аналитическую функцию, скажем  Тогда, обозначая действительную и мнимую части
Тогда, обозначая действительную и мнимую части  через
через  и
и  получаем
получаем

откуда  Кроме того, получаем
Кроме того, получаем

Приравнивая действительные части в первом и последнем членах, находим

Поскольку  - сопряженные функции, они удовлетворяют уравнениям (д) § 55, откуда
- сопряженные функции, они удовлетворяют уравнениям (д) § 55, откуда

Так как  то из уравнений (д) и (е) следует, что
то из уравнений (д) и (е) следует, что  гармоническая функция; действительно,
гармоническая функция; действительно,

Таким образом, для любой функции напряжений  имеем
имеем

где  — некоторая гармоническая функция. Следовательно,
— некоторая гармоническая функция. Следовательно,

Это соотношение показывает, что любая функция напряжений может быть образована из выбранных соответствующим образом сопряженных функций  и гармонической функции
и гармонической функции 
Выражение (83) весьма полезно. Заметим, однако, что использование обеих функций  не обязательно. Вместо уравнения (ж)
не обязательно. Вместо уравнения (ж)
мы можем записать

а это показывает, что функция  является гармонической, скажем, равной
является гармонической, скажем, равной  . В силу этого любую функцию напряжений можно представить в форме
. В силу этого любую функцию напряжений можно представить в форме

где  - соответствующим образом подобранные гармонические функции.
- соответствующим образом подобранные гармонические функции.
Возвращаясь к уравнению (83), введем функцию  которая является гармонической и сопряженной к
которая является гармонической и сопряженной к  и запишем
и запишем

Тогда легко проверить, что действительная часть функции

тождественно равна правой части уравнения (83). Следовательно, функцию напряжений можно представить в виде

где символ  обозначает «действительную часть»,
обозначает «действительную часть»,  обозначает
обозначает  — соответствующим образом подобранные аналитические функции. И наоборот, при любом выборе
— соответствующим образом подобранные аналитические функции. И наоборот, при любом выборе  уравнение (84) дает функцию напряжений, т. е. решение уравнения (а), стр. 53. Позже это уравнение будет применено к решению некоторых задач, представляющих практический интерес.
уравнение (84) дает функцию напряжений, т. е. решение уравнения (а), стр. 53. Позже это уравнение будет применено к решению некоторых задач, представляющих практический интерес.
Записывая «комплексную функцию напряжений», содержащуюся в скобках в выражении (84), как

и учитывая, что  — по-прежнему является функцией от
— по-прежнему является функцией от  находим, что любая функция напряжений может быть представлена в виде
находим, что любая функция напряжений может быть представлена в виде

где  гармонические функции.
гармонические функции.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
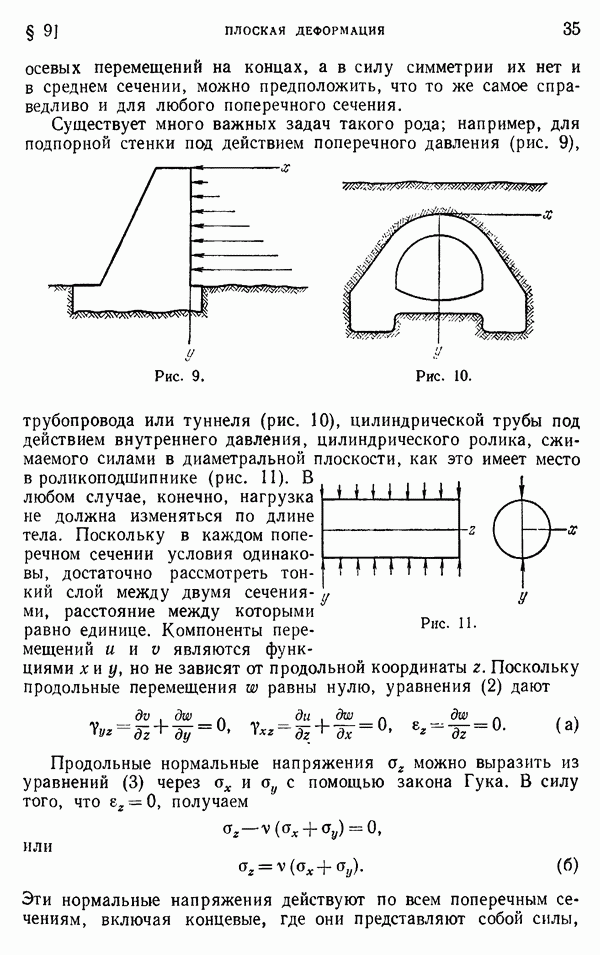
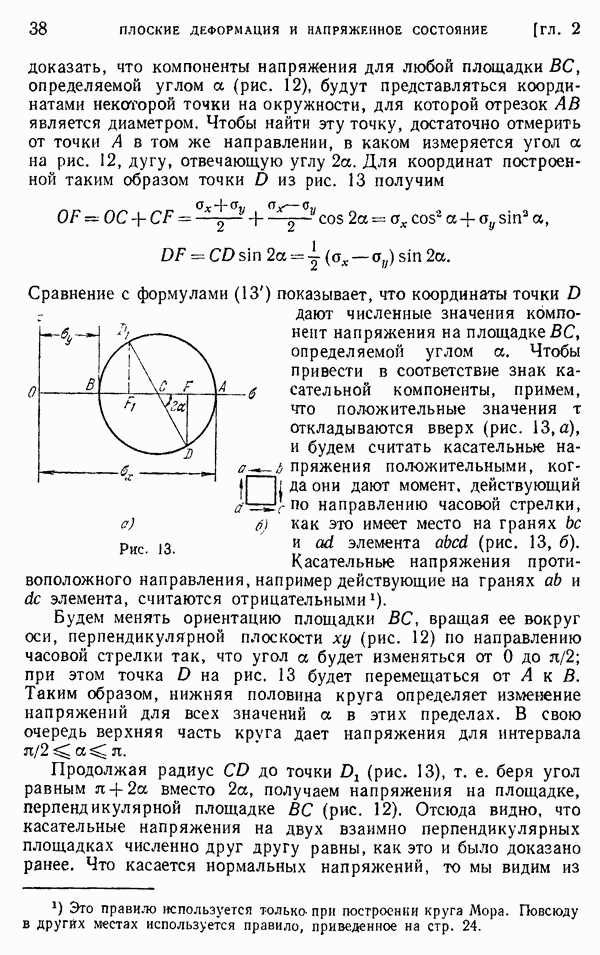
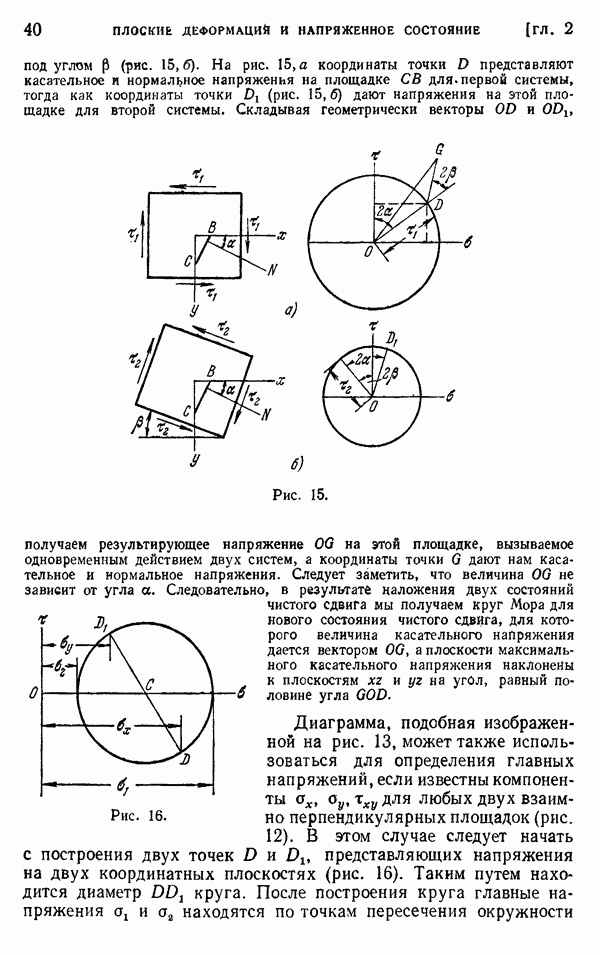
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
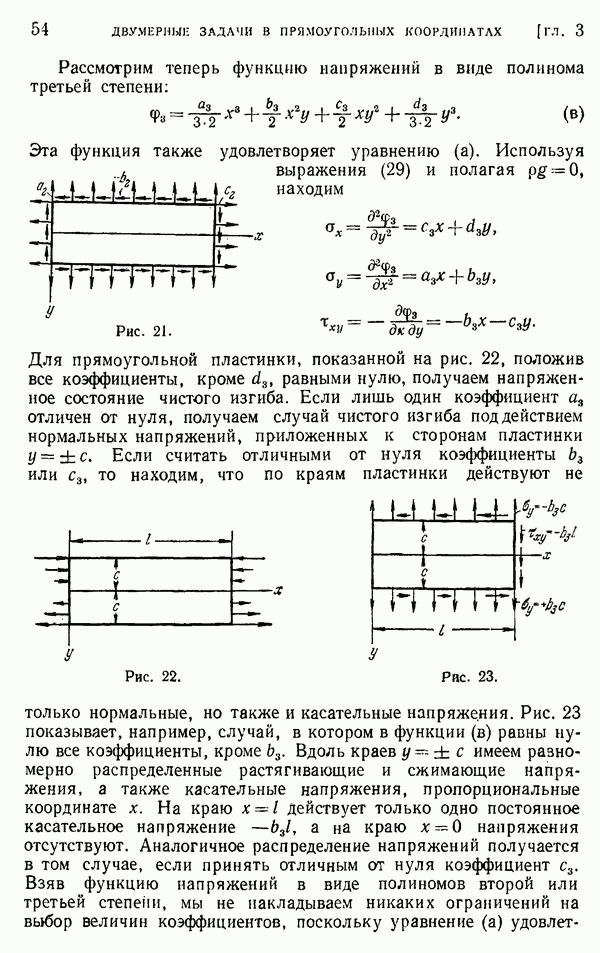
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
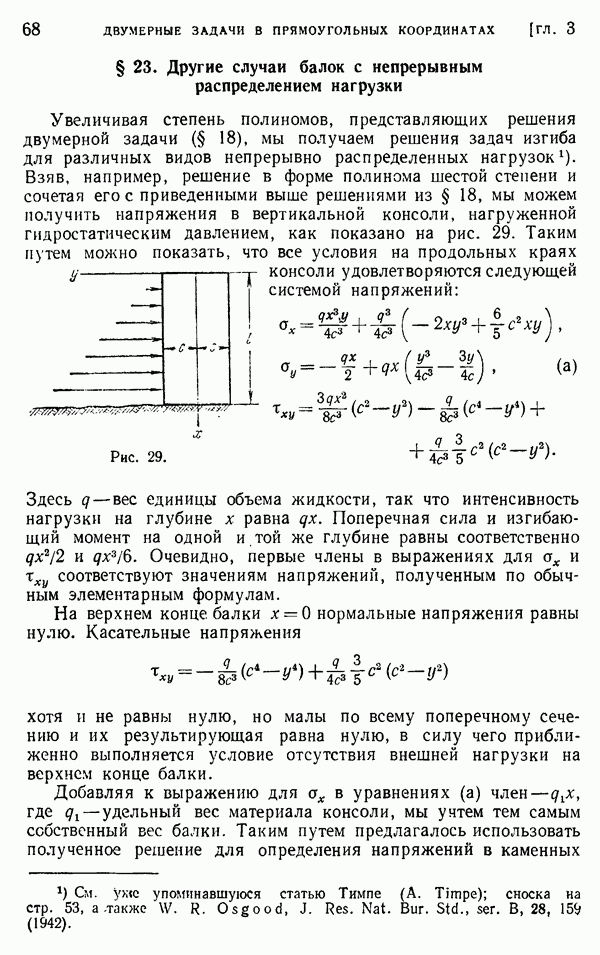
- § 23. Другие случаи балок с непрерывным распределением нагрузки
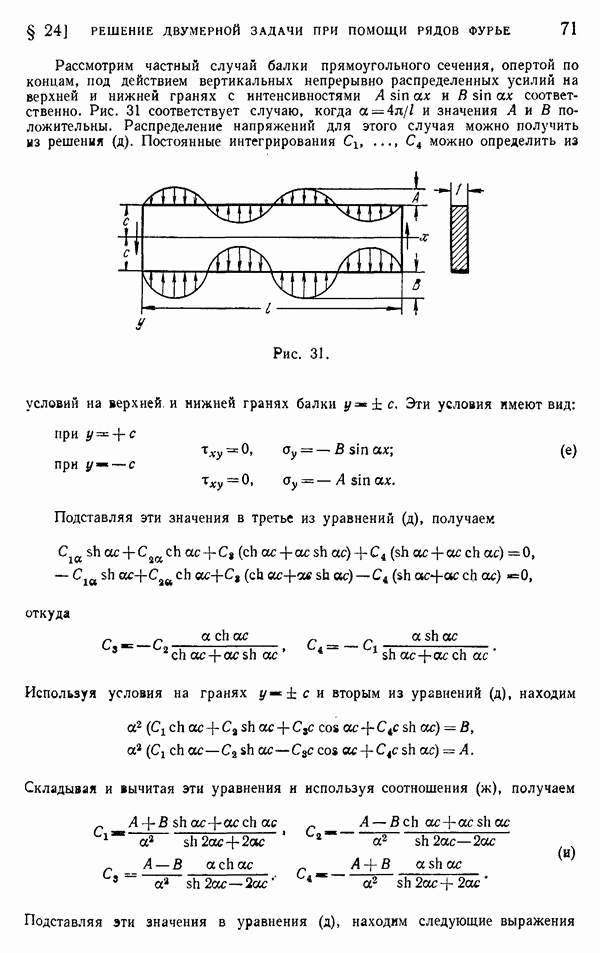
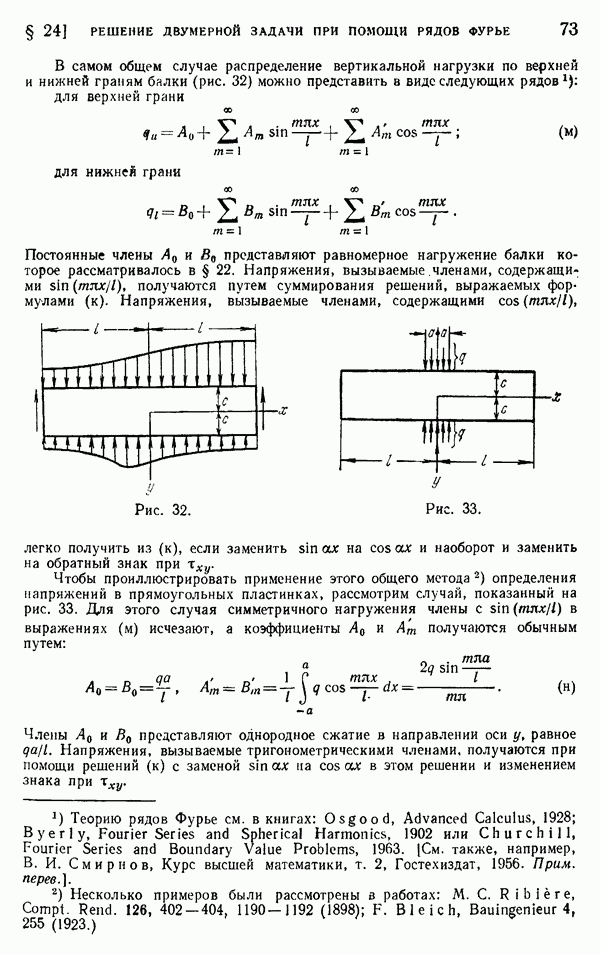
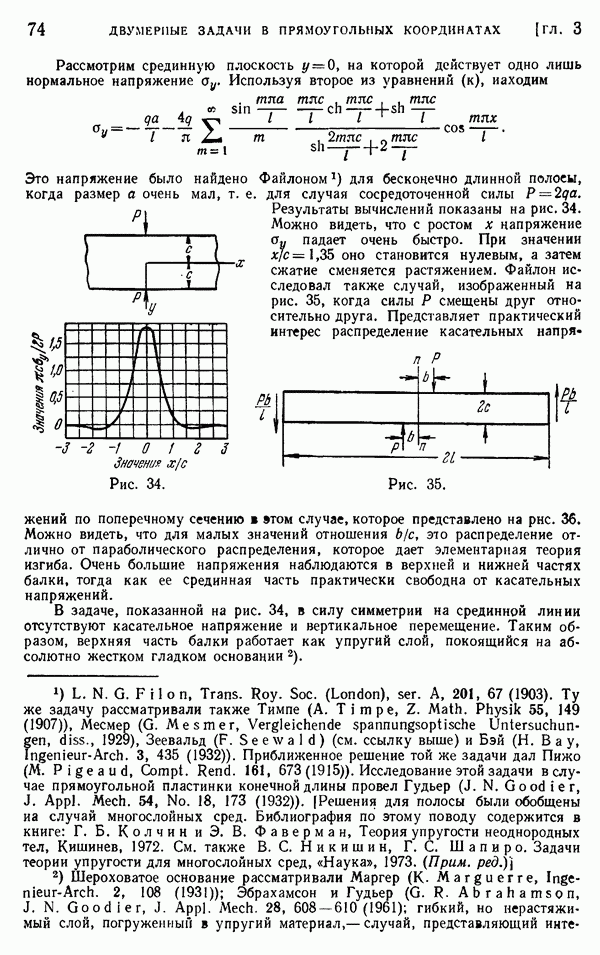
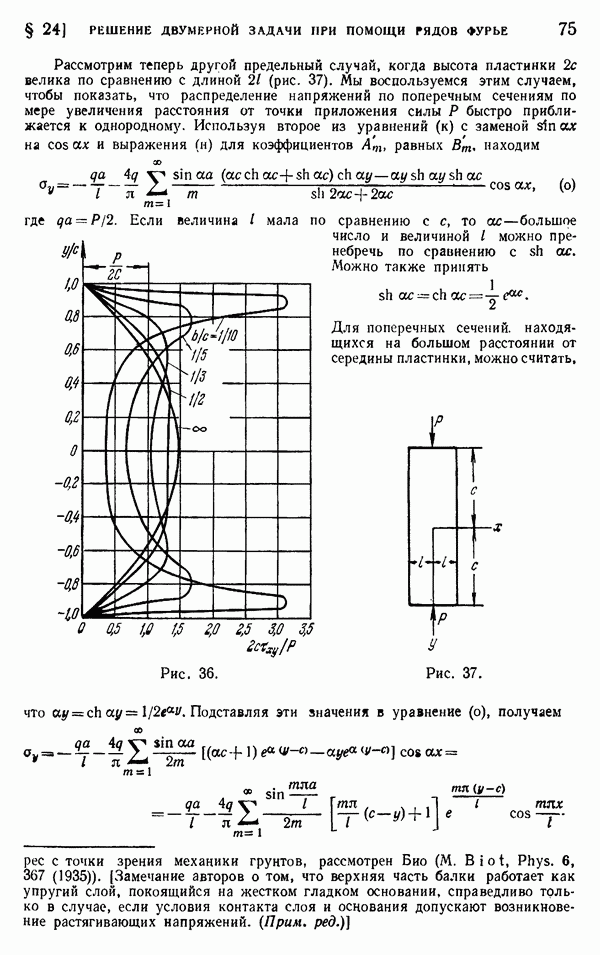
- § 24. Решение двумерной задачи при помощи рядов Фурье
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
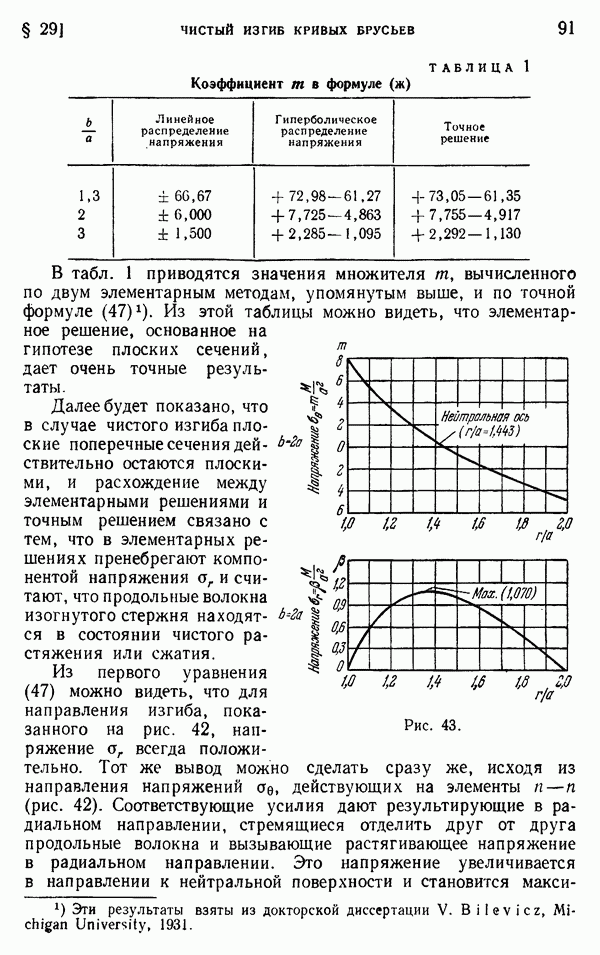
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
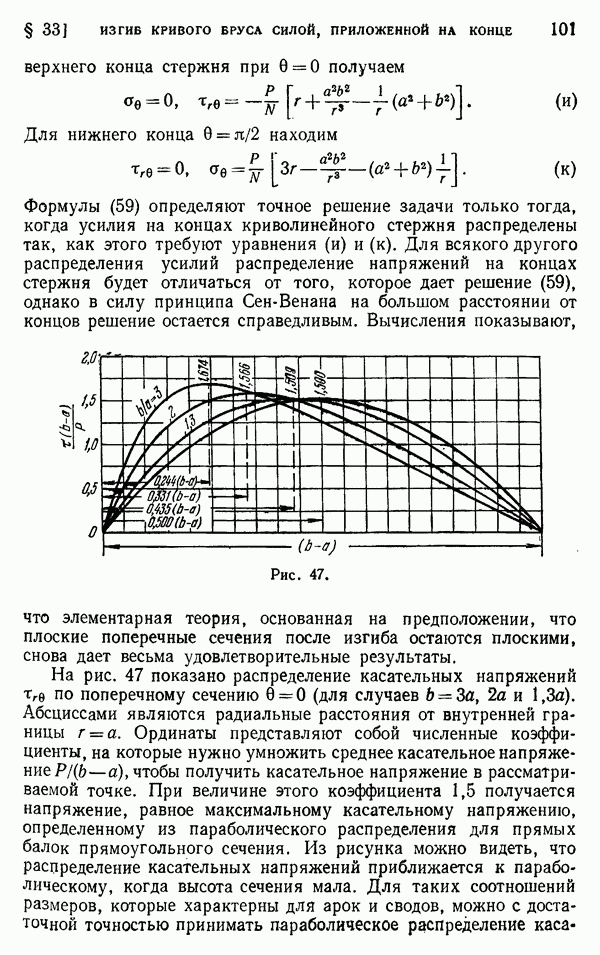
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
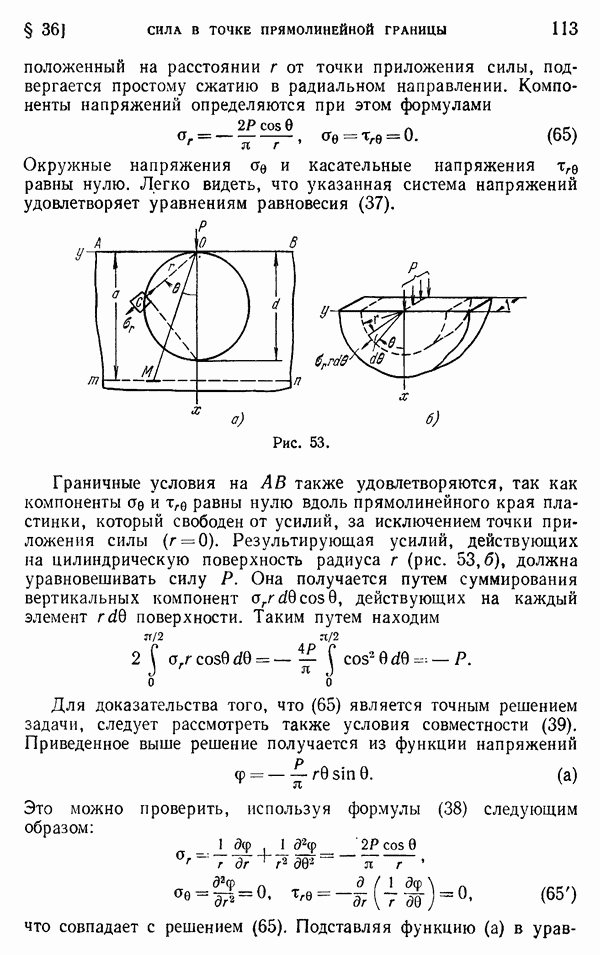
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
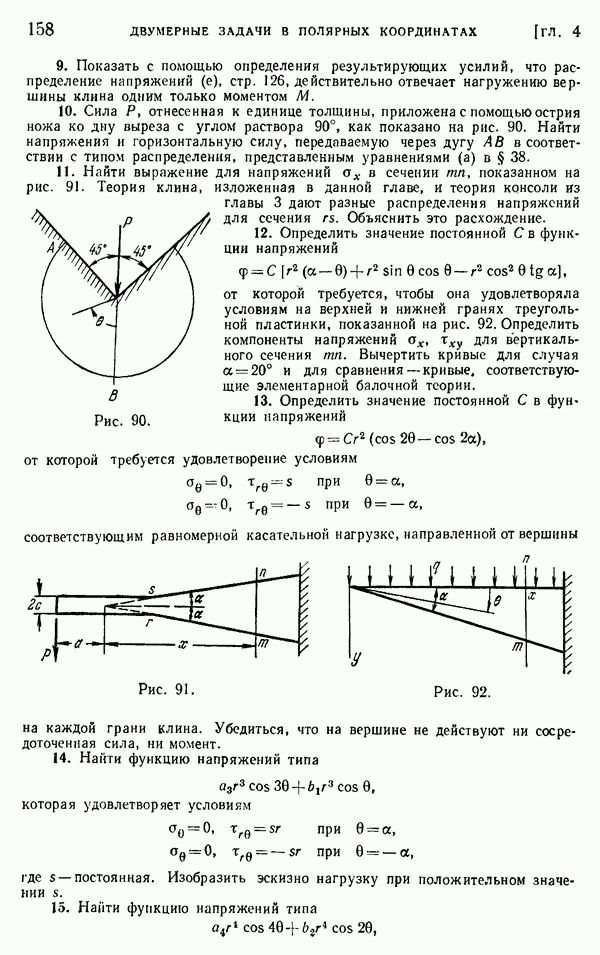
- § 39. Изгибающий момент, действующий на острие клина
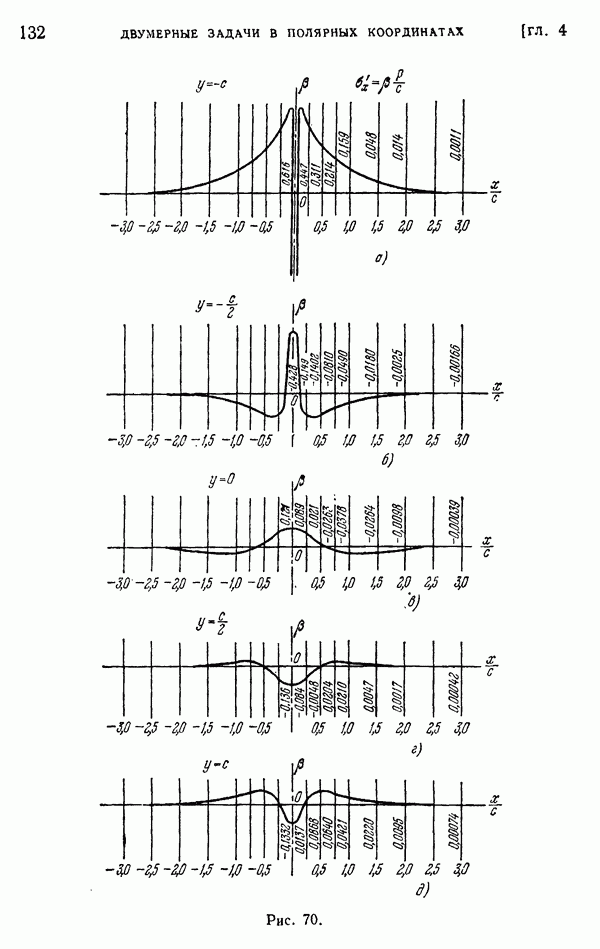
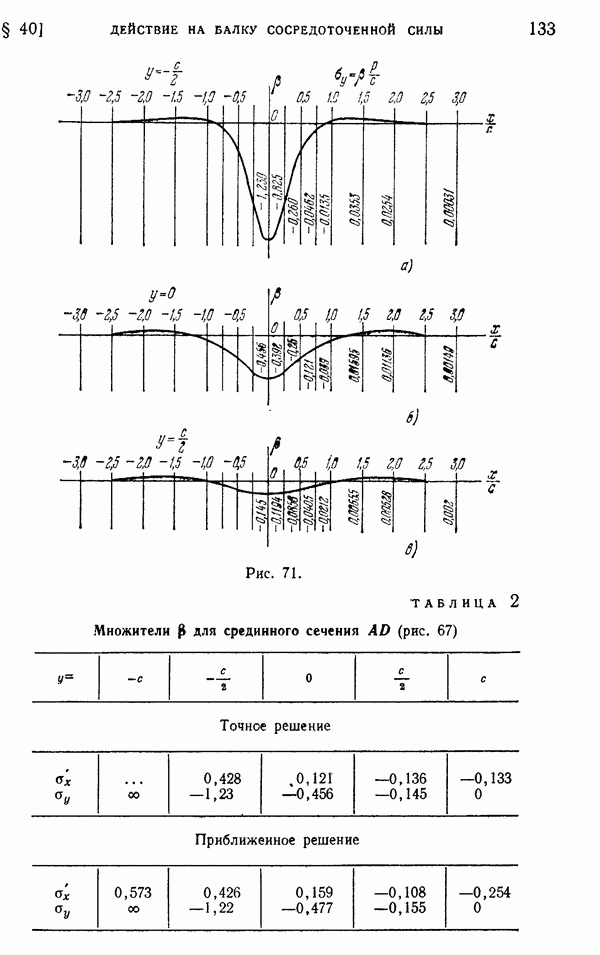
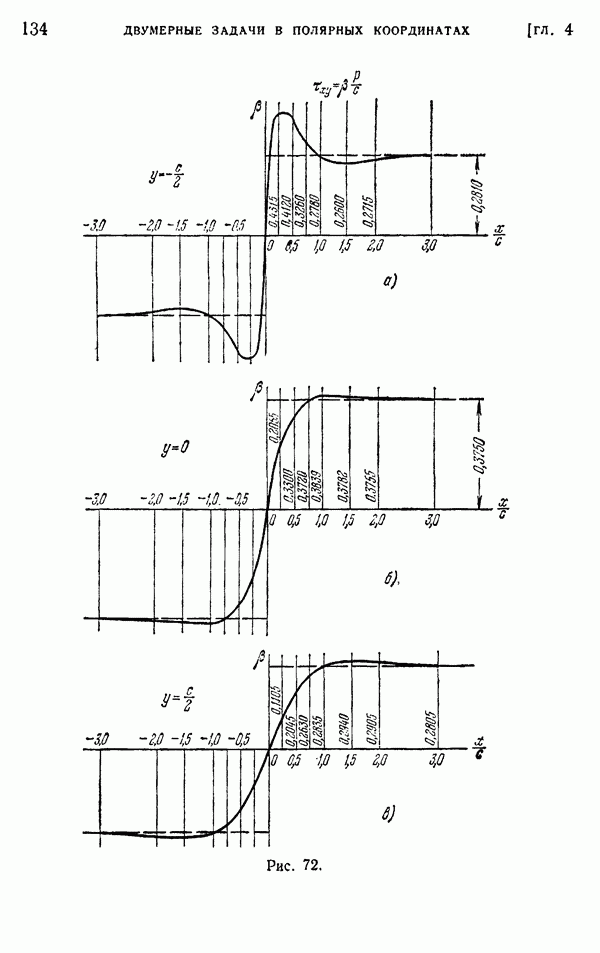
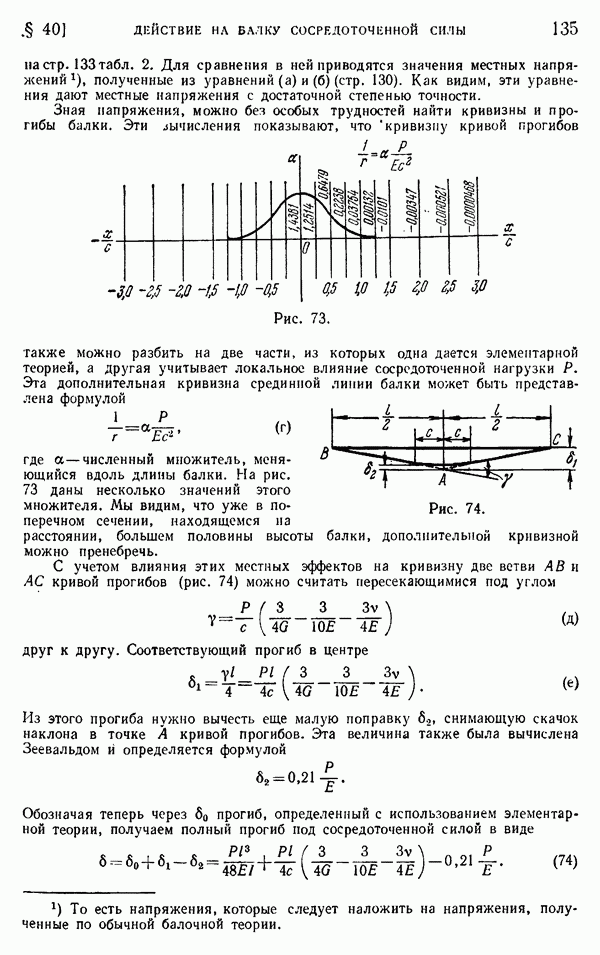
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
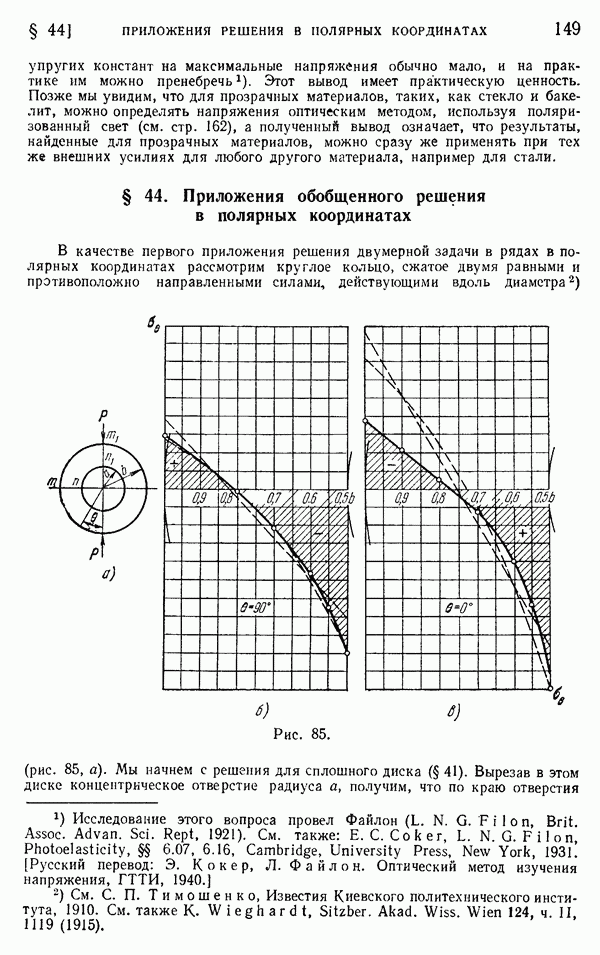
- § 43. Обобщенное решение двумерной задачи в полярных координатах
- § 44. Приложения обобщенного решения в полярных координатах
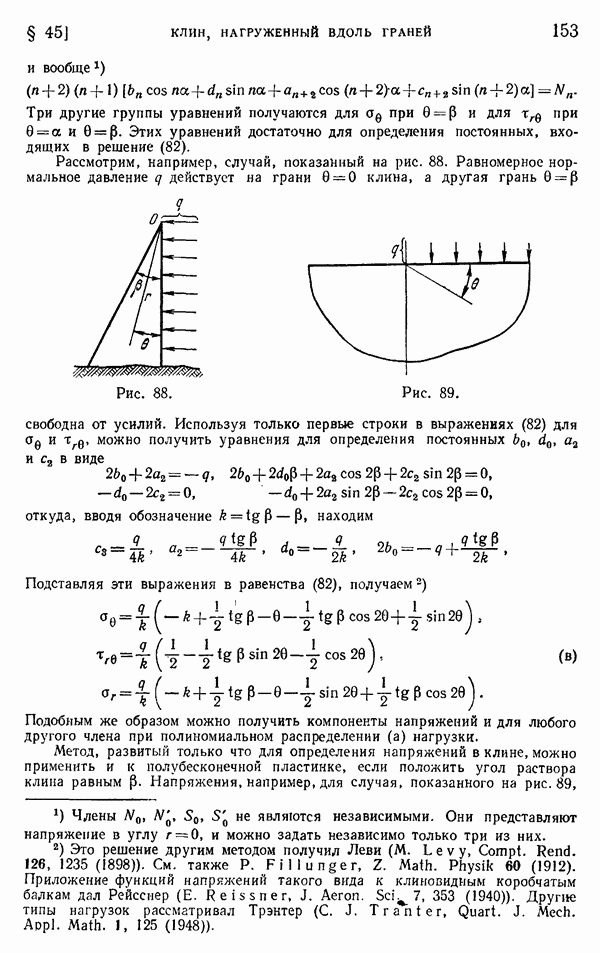
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
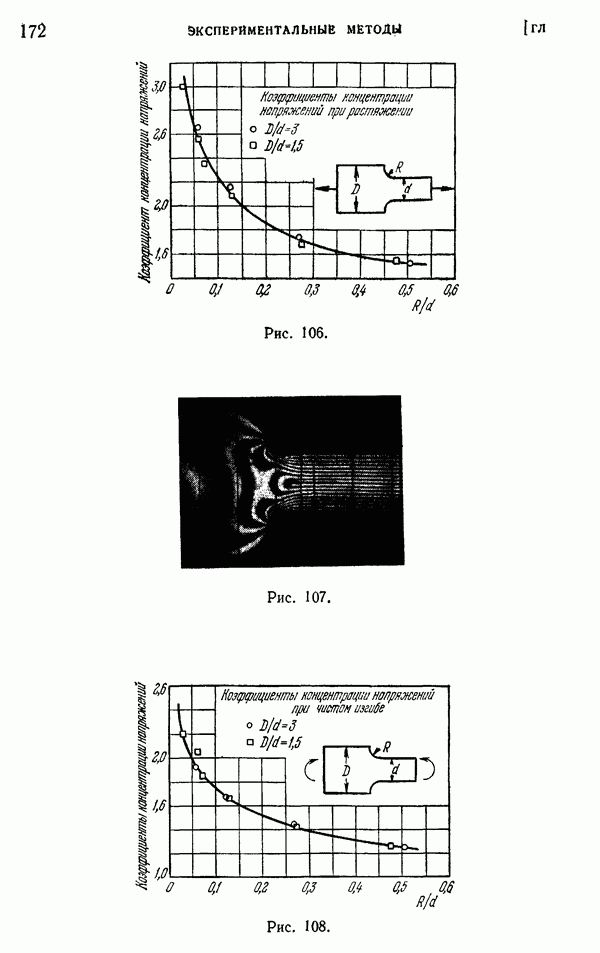
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
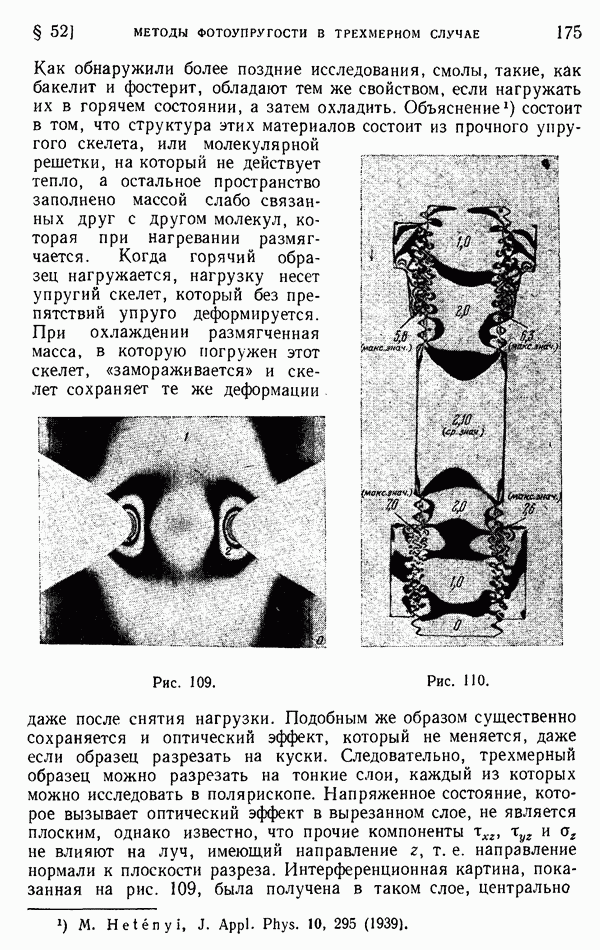
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
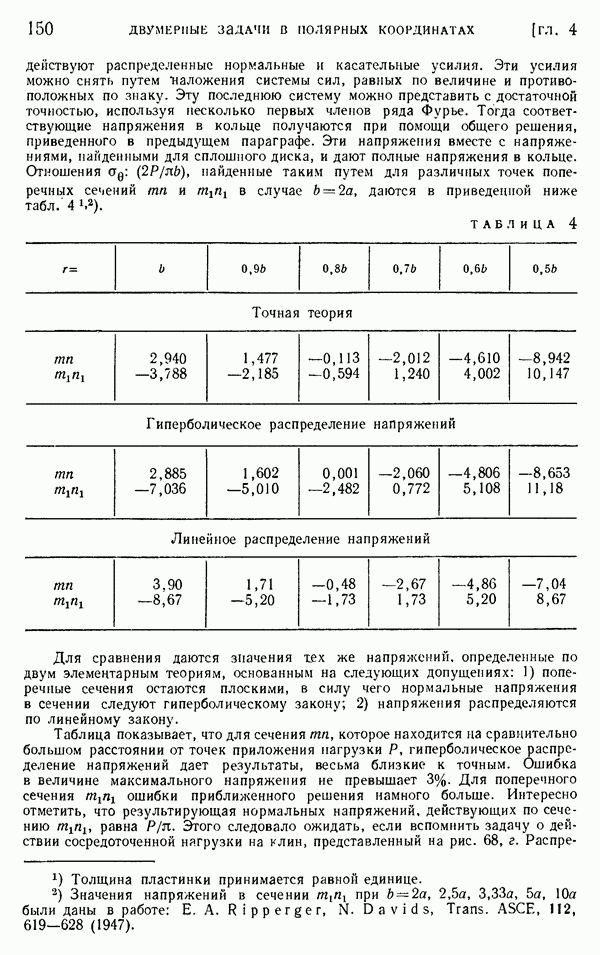
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
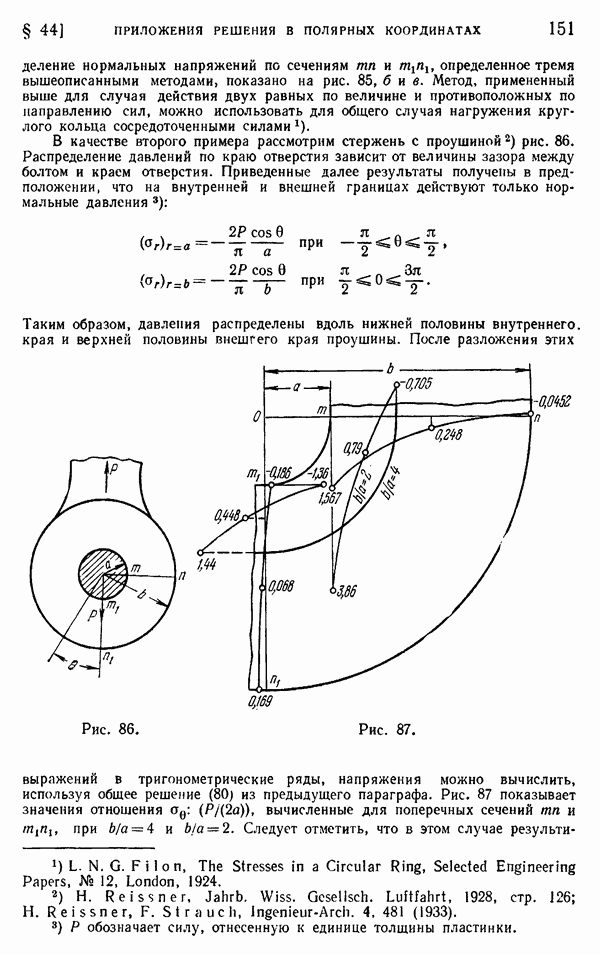
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
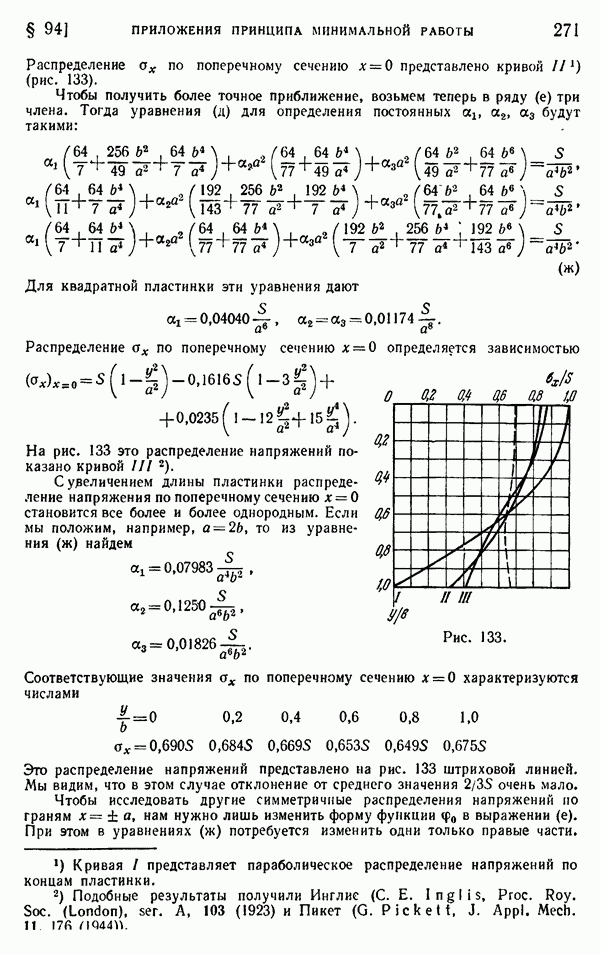
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
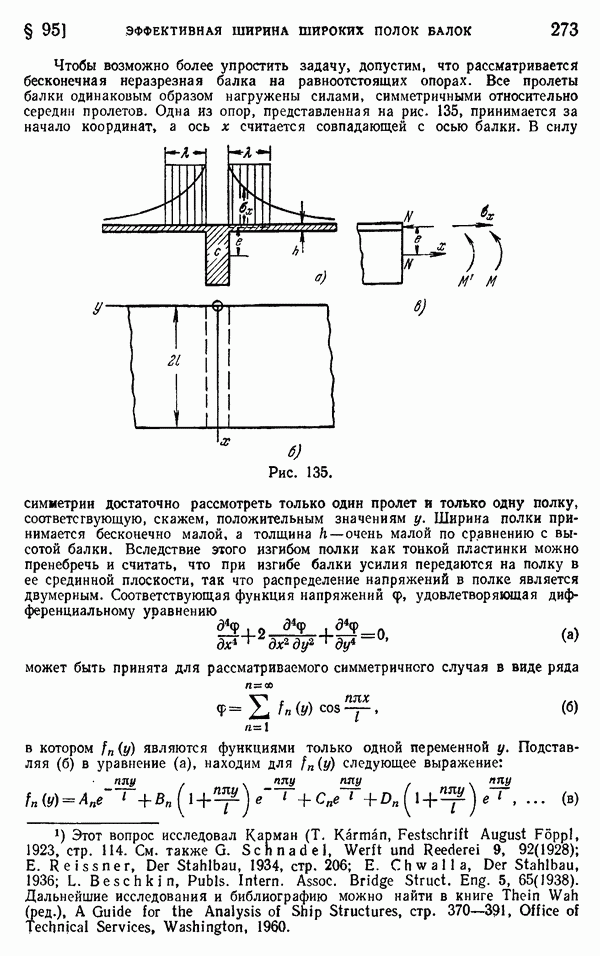
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
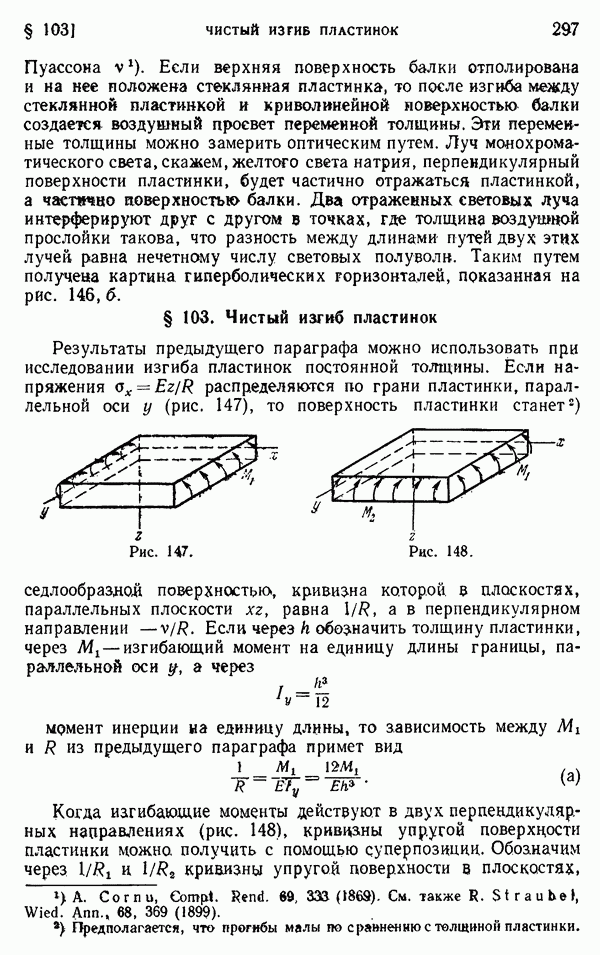
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
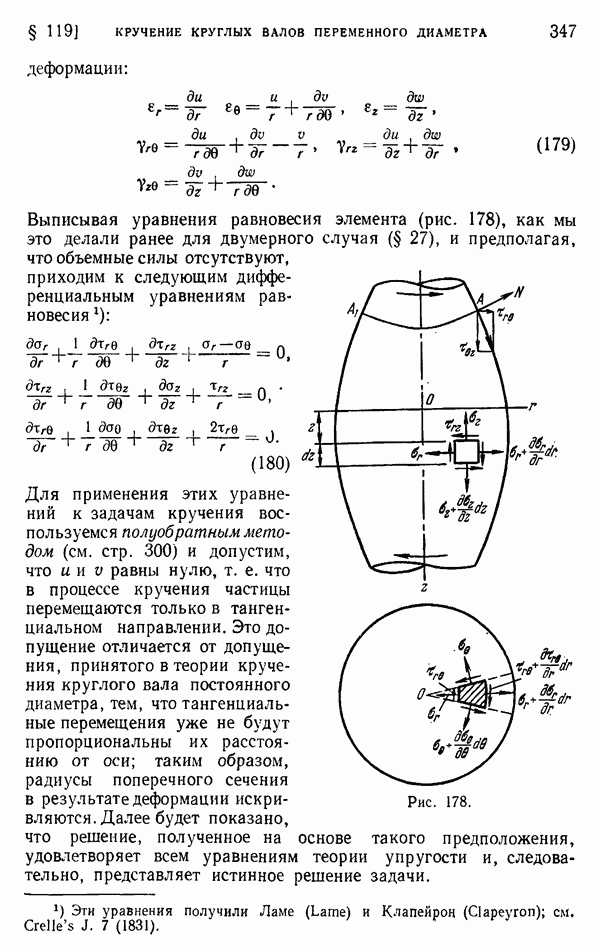
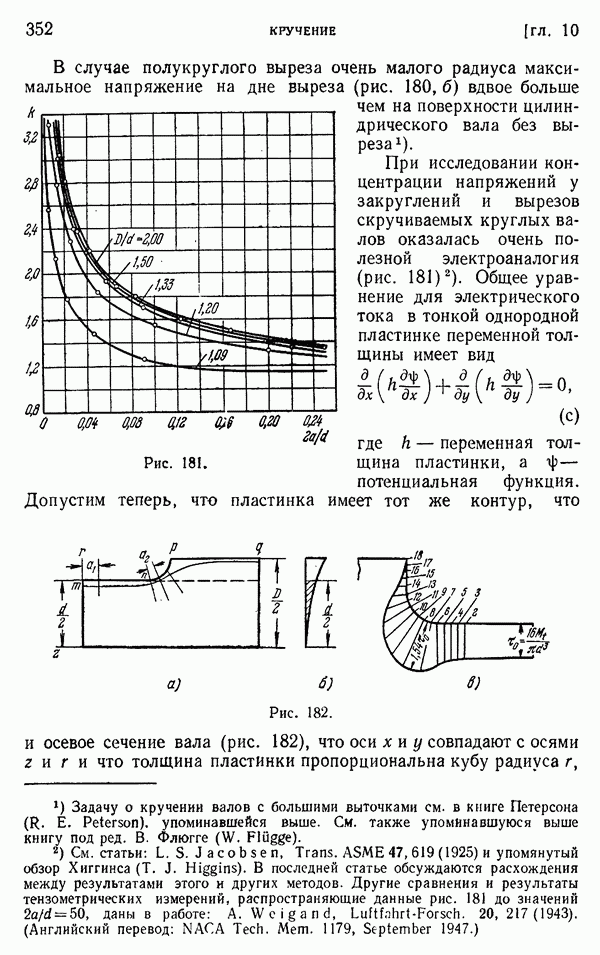
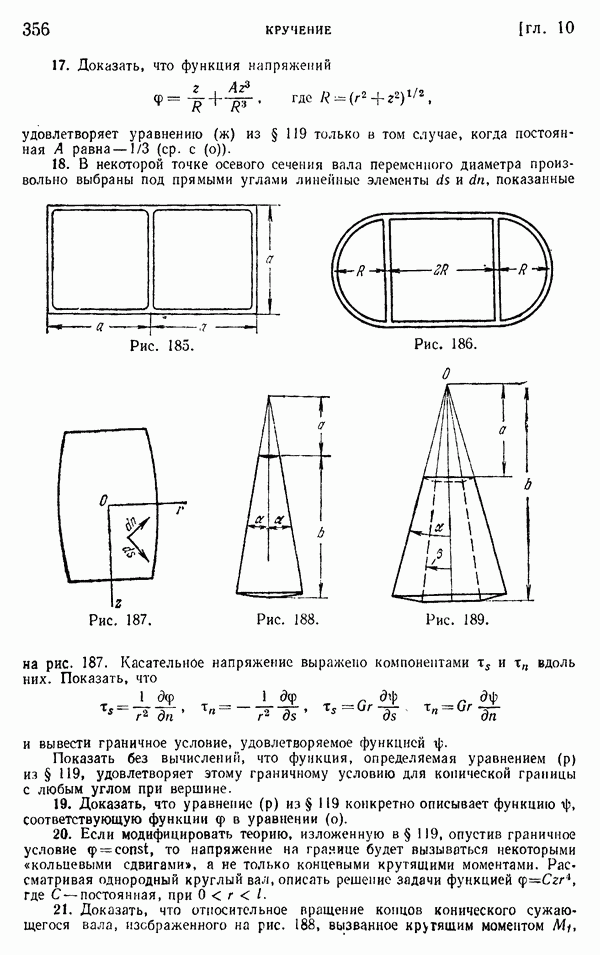
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
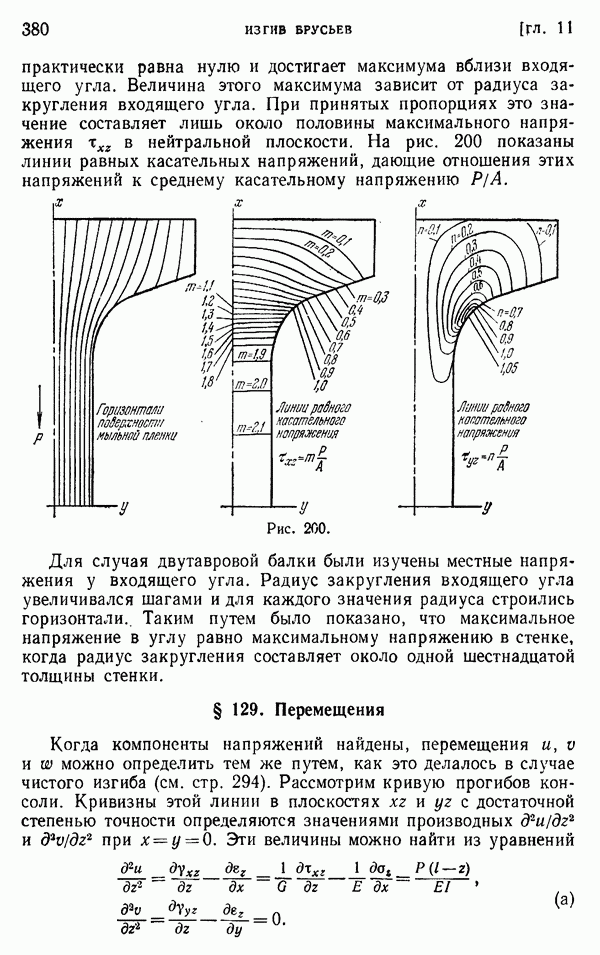
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
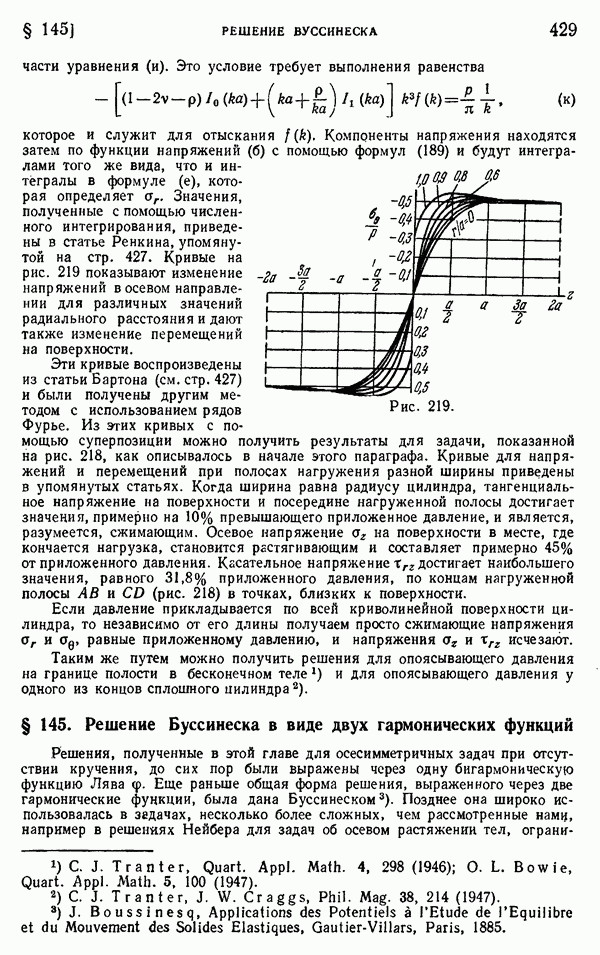
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
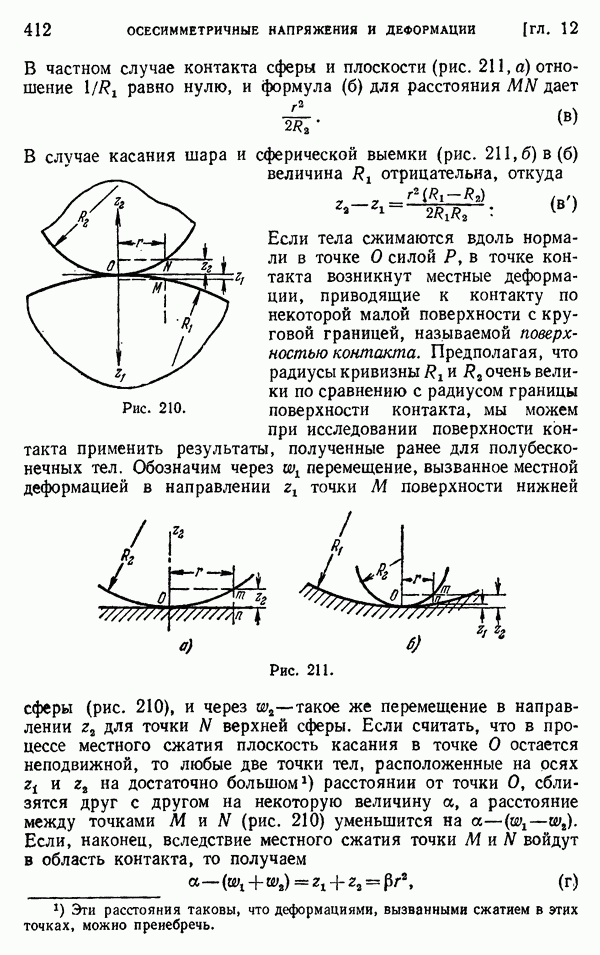
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
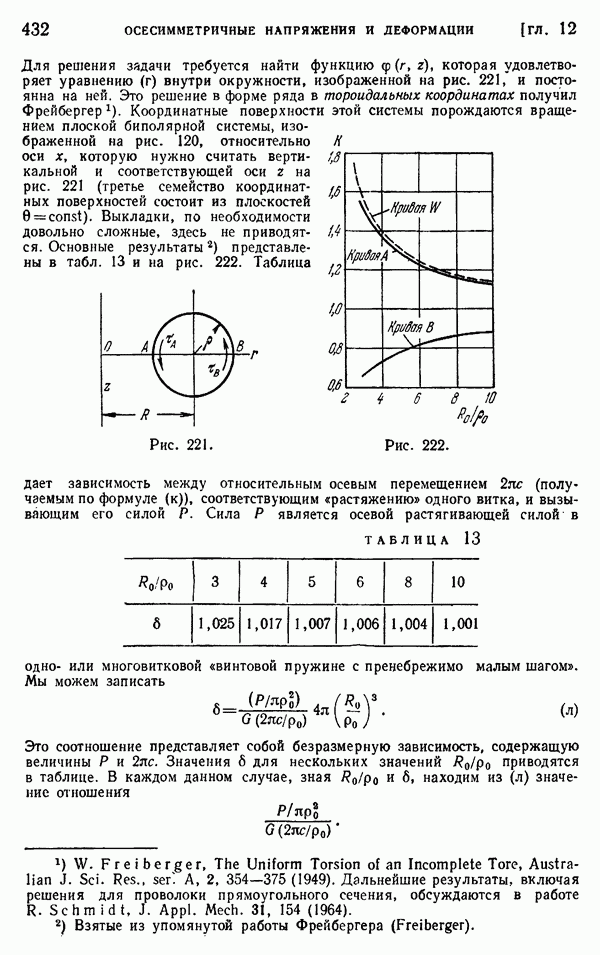
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
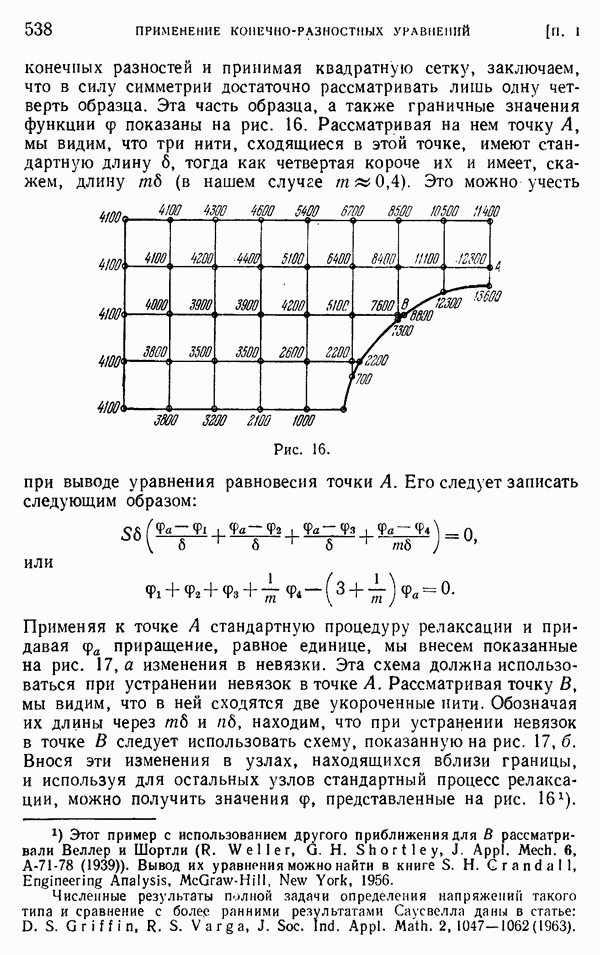
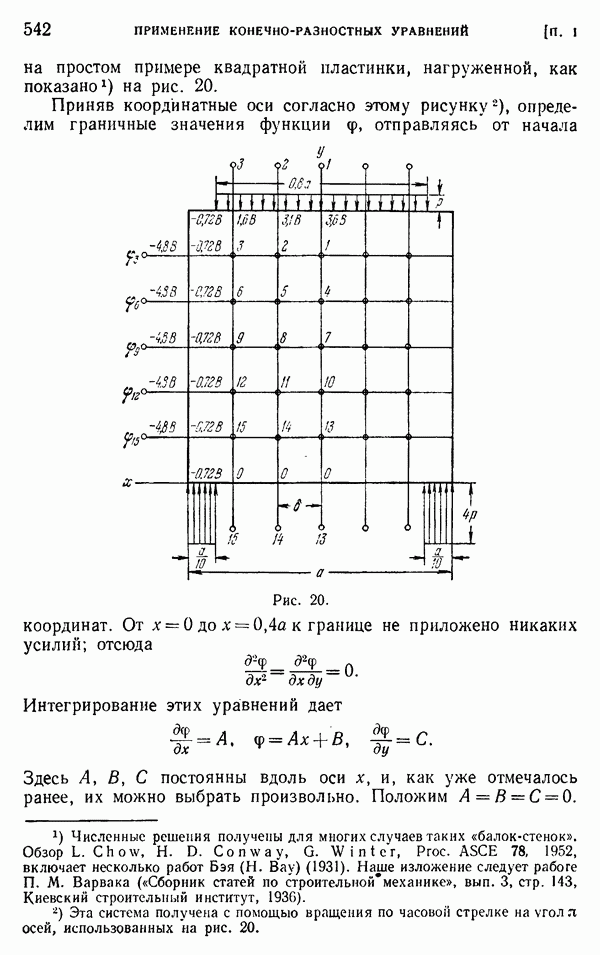
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
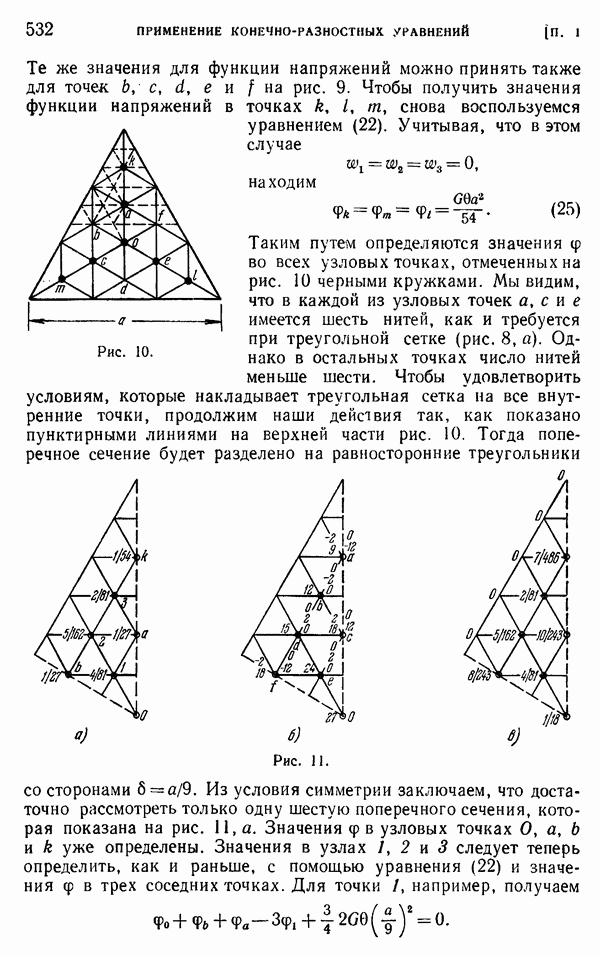
- § 4. Треугольные и шестиугольные сетки
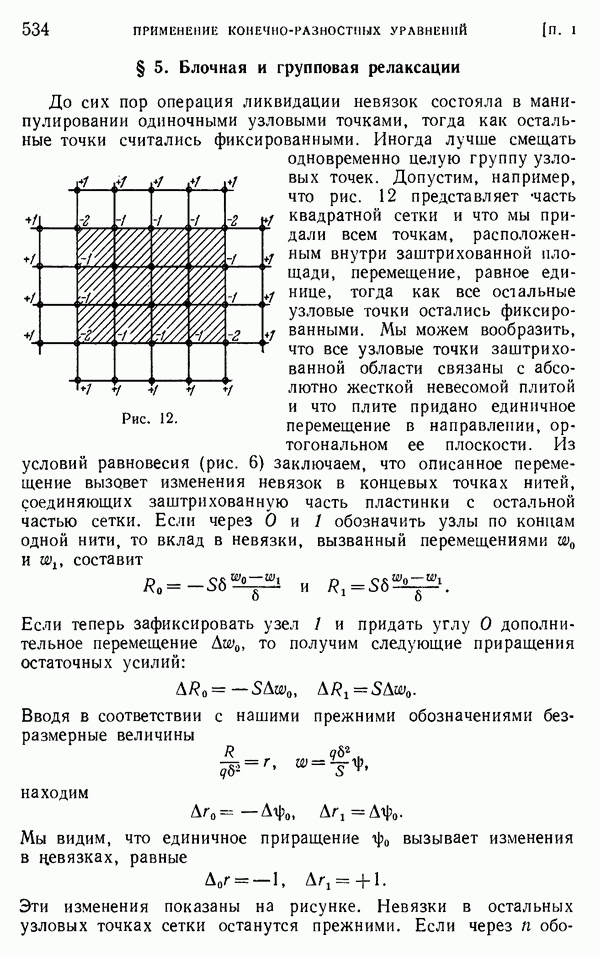
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
- § 7. Точки, расположенные вблизи границы
- § 8. Бигармоническое уравнение
- § 9. Кручение круглых валов переменного диаметра
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи