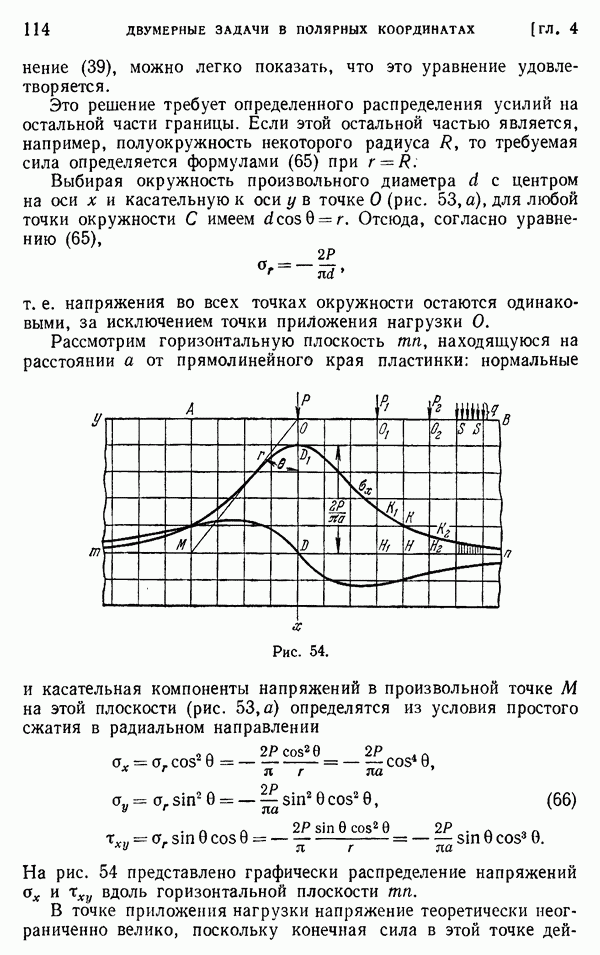
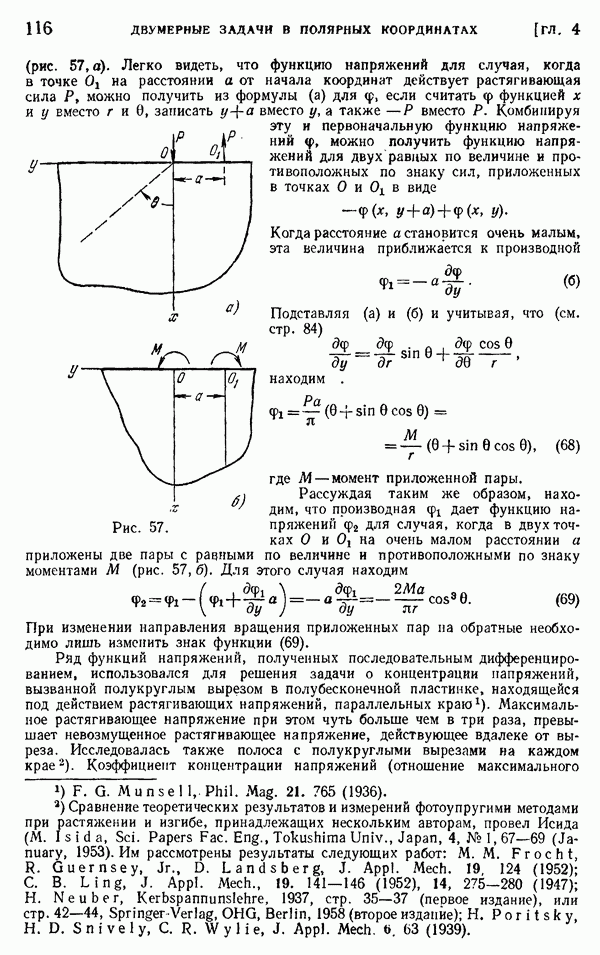
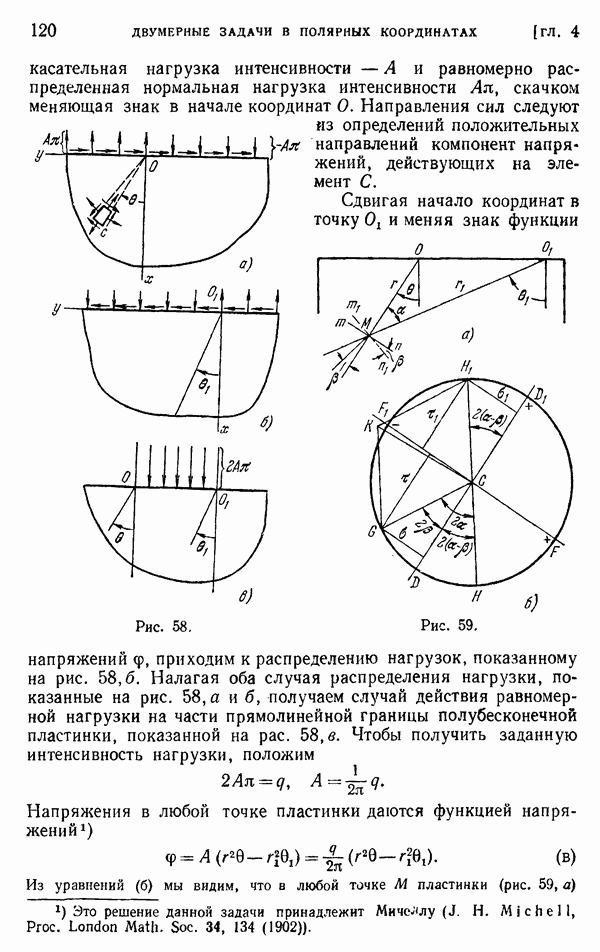
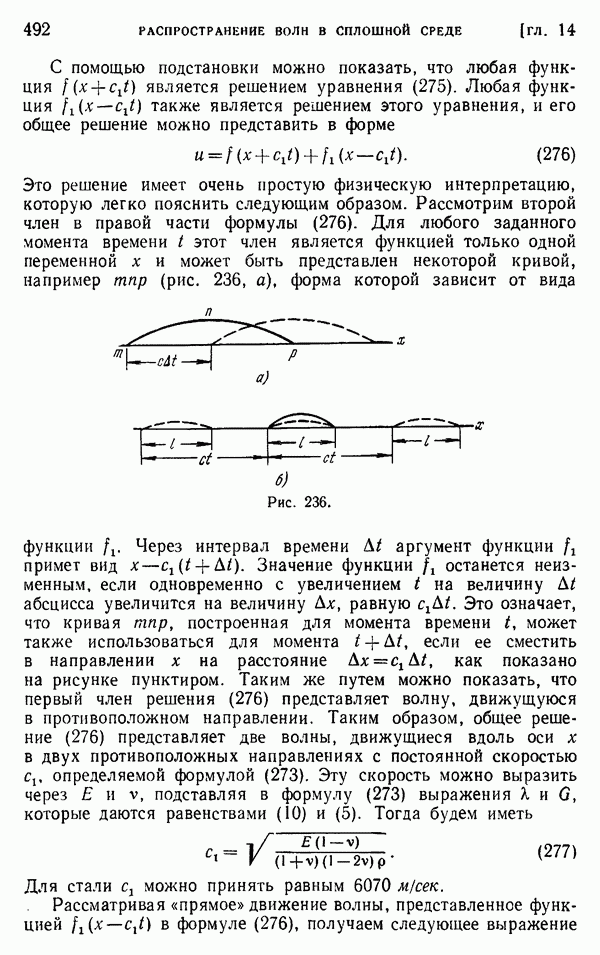
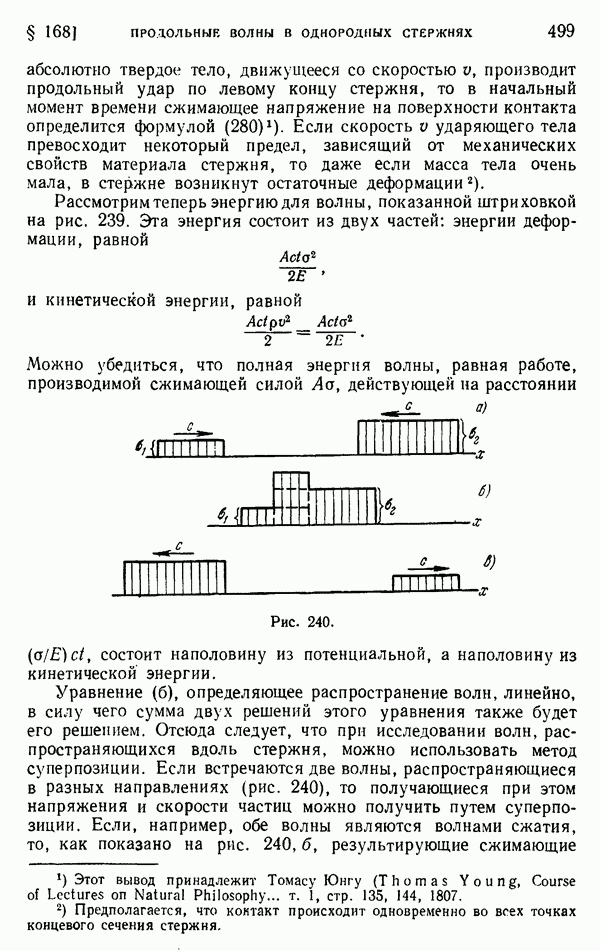
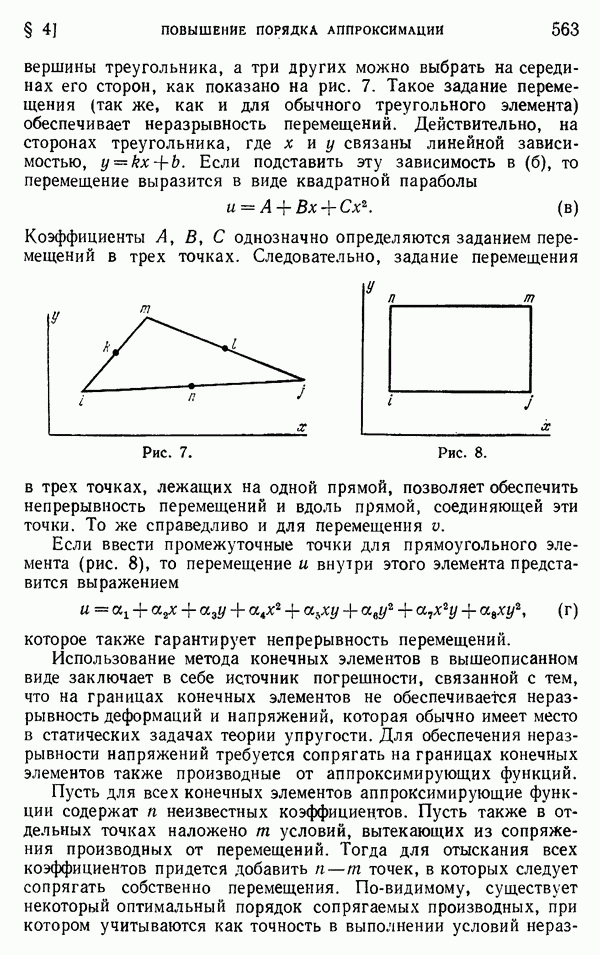
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Метод релаксации
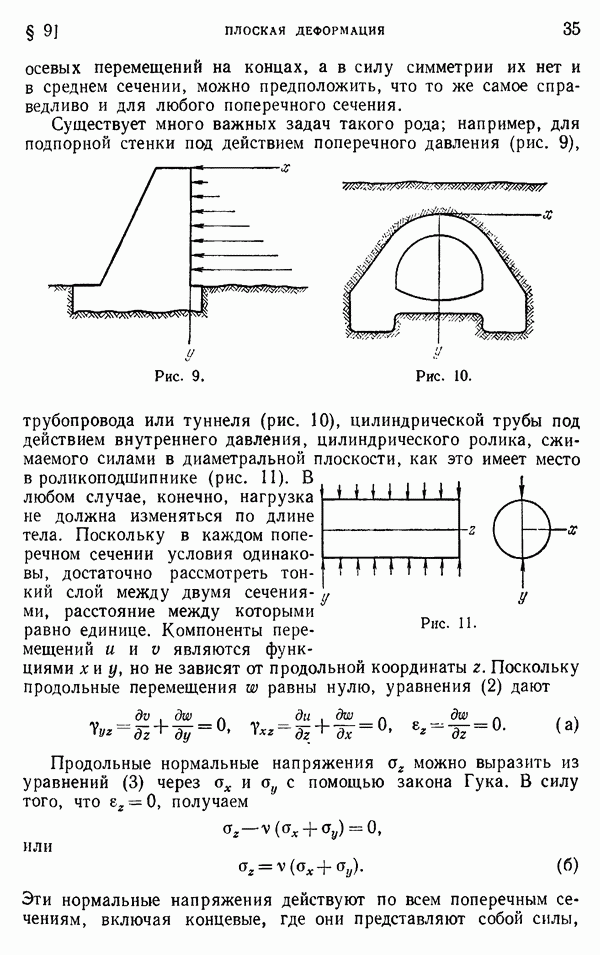
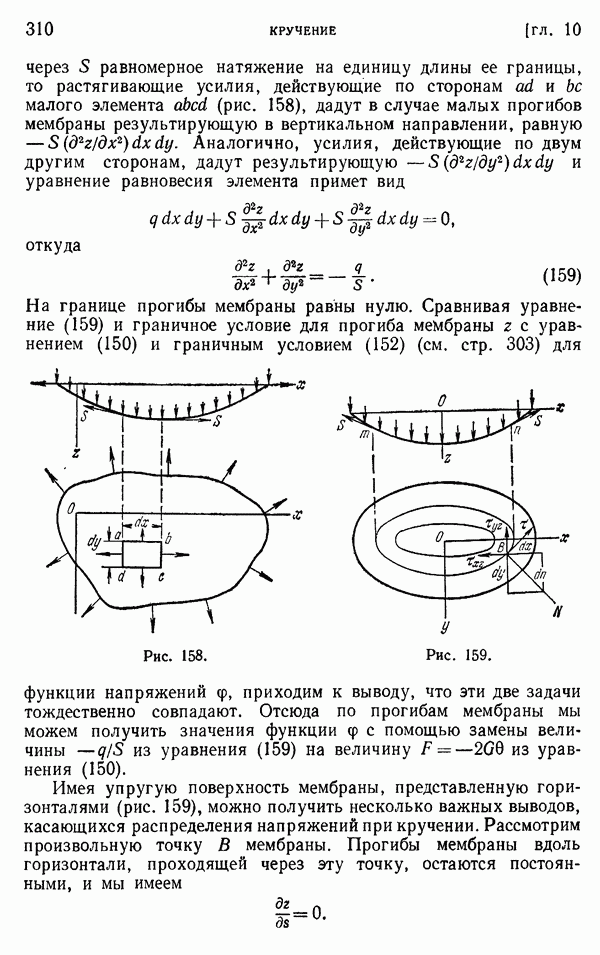
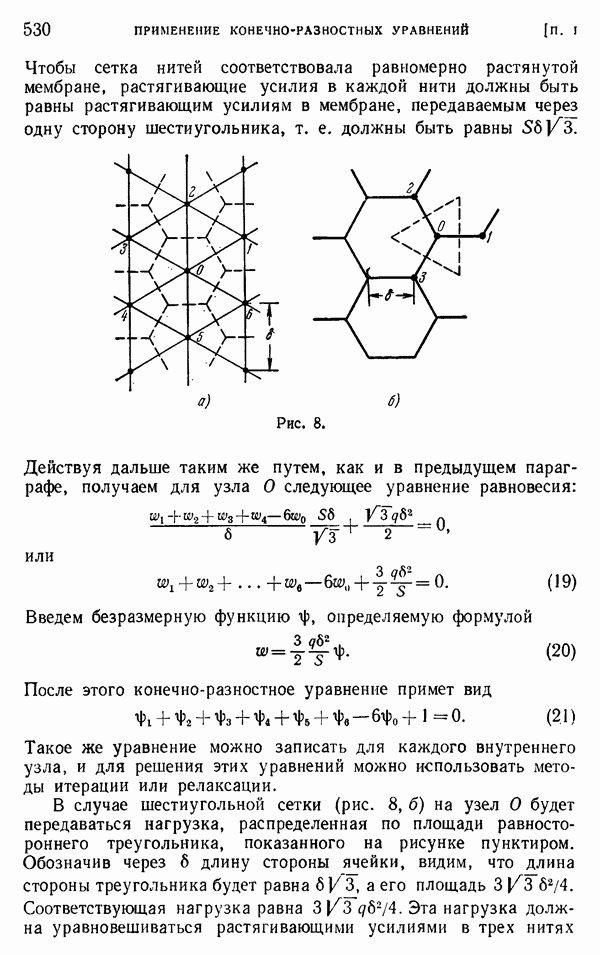
Один из методов решения разностных уравнений типа уравнений (8) из предыдущего параграфа развил Р. В. Саусвелл, который назвал его методом релаксации. Саусвелл исходил из мембранной аналогии Л. Прандтля, которая основывается на том факте, что дифференциальное уравнение (4) для задач кручения имеет тот же вид, что и уравнение

определяющее прогиб равномерно растянутой и нагруженной в поперечном направлении мембраны. В этом уравнении через  обозначен прогиб, отсчитываемый от горизонтальной плоской в начальном положении поверхности мембраны,
обозначен прогиб, отсчитываемый от горизонтальной плоской в начальном положении поверхности мембраны,  — интенсивность распределенной нагрузки,
— интенсивность распределенной нагрузки,  постоянное растягивающее усилие на единицу длины контура мембраны. Задача сводится к отысканию прогибов
постоянное растягивающее усилие на единицу длины контура мембраны. Задача сводится к отысканию прогибов  как функции переменных х и у, которая удовлетворяет уравнению (9) в каждой точке мембраны и обращается в нуль на ее границе.
как функции переменных х и у, которая удовлетворяет уравнению (9) в каждой точке мембраны и обращается в нуль на ее границе.
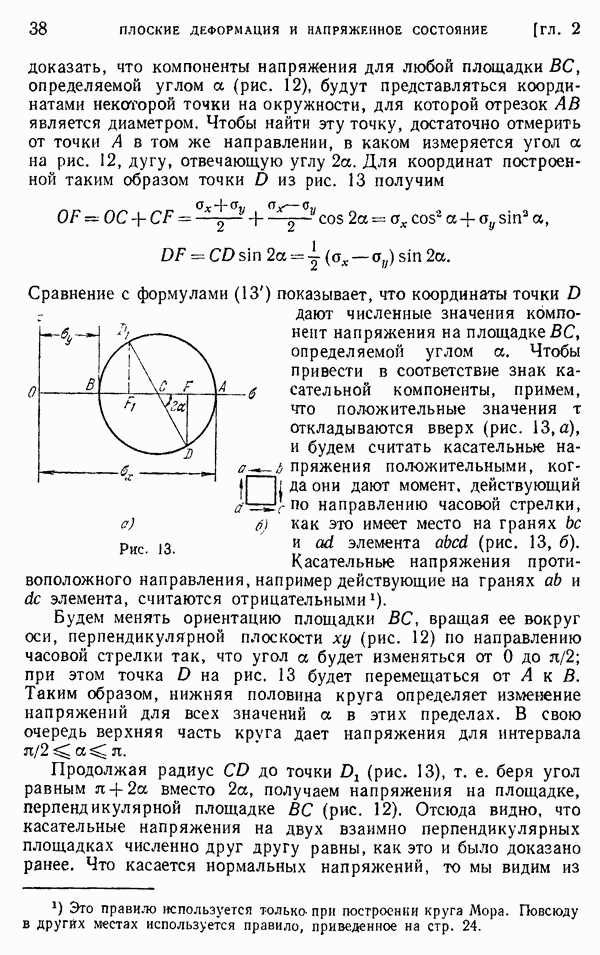
Выведем теперь соответствующее уравнение в конечных разностях. Для этой цели заменим мембрану квадратной сеткой из
равномерно растянутых нитей (рис. 1). Рассматривая точку О и обозначая через  растягивающее усилие в нити, видим, что действие нитей
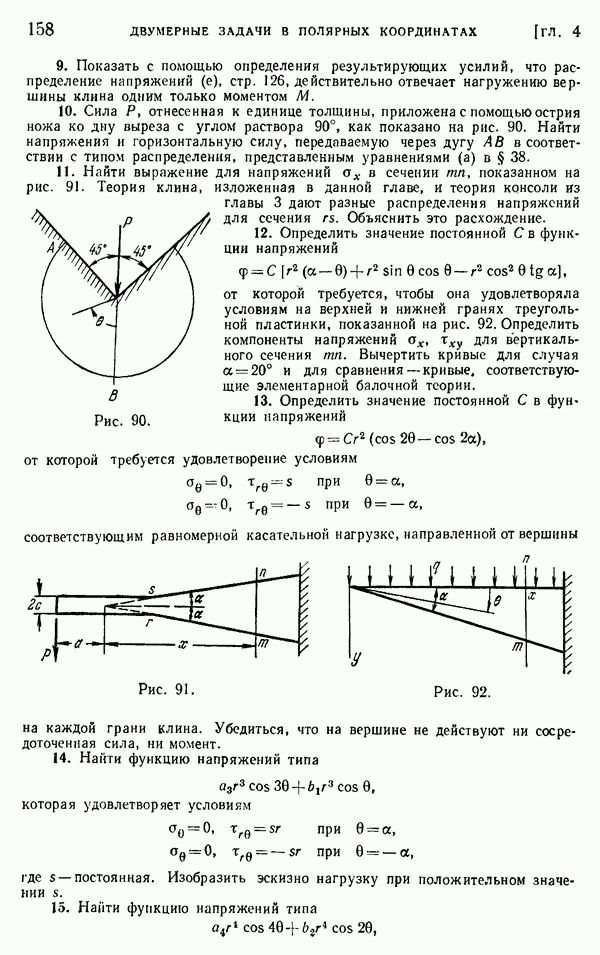
растягивающее усилие в нити, видим, что действие нитей  на узел О (рис. 6) приводится к направленному вверх усилию, равному
на узел О (рис. 6) приводится к направленному вверх усилию, равному

Подобное выражение можно записать и для усилия, к которому сводится действие на узел двух других нитей  Заменяя непрерывную нагрузку, действующую на мембрану, сосредоточенными силами
Заменяя непрерывную нагрузку, действующую на мембрану, сосредоточенными силами  приложенными в узлах, мы можем теперь записать уравнение равновесия узла в виде
приложенными в узлах, мы можем теперь записать уравнение равновесия узла в виде


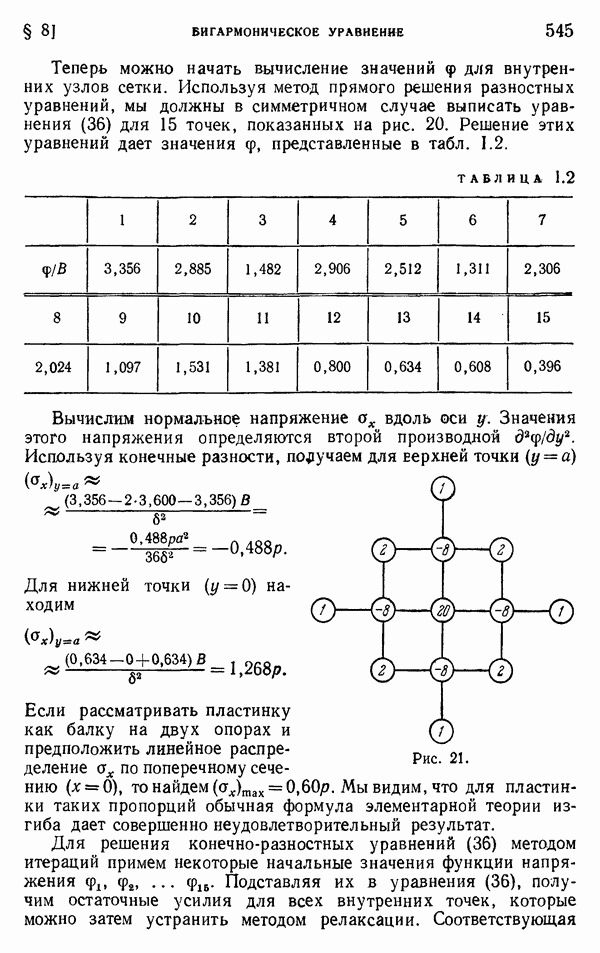
Рис. 6.
Это и есть конечно-разностное уравнение, соответствующее дифференциальному уравнению (9). Чтобы решить задачу, нам нужно найти такую систему значений прогибов до, при которой уравнение (11) будет удовлетворяться в каждом узле сетки.
Мы будем исходить из некоторых начальных значений прогибов  Подставляя их в уравнение (II), как правило, получаем, что условия равновесия не удовлетворяются, и, чтобы сохранить принятые прогибы мембраны, нужно ввести в узловых точках опоры. Тогда величины
Подставляя их в уравнение (II), как правило, получаем, что условия равновесия не удовлетворяются, и, чтобы сохранить принятые прогибы мембраны, нужно ввести в узловых точках опоры. Тогда величины

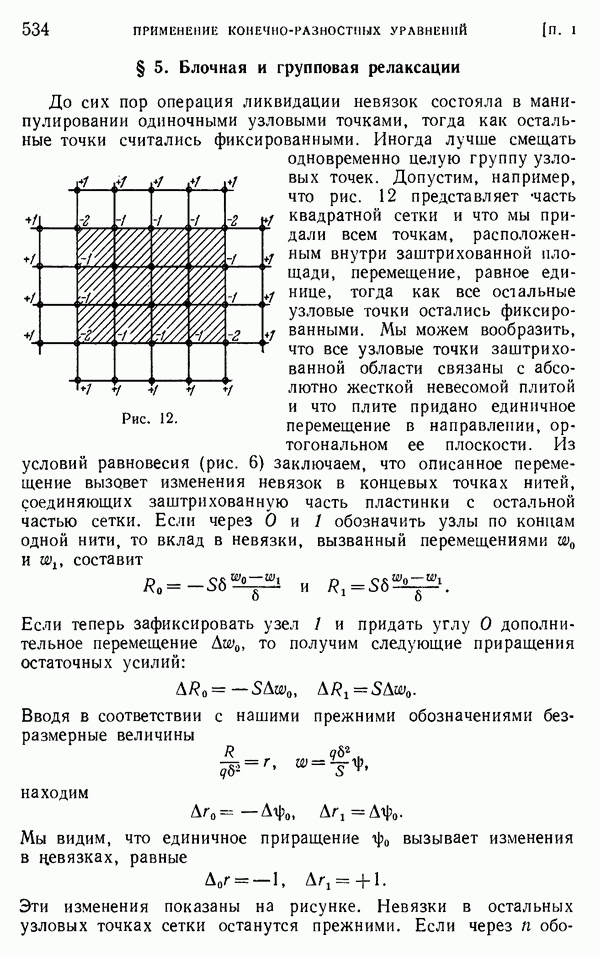
будут представлять части нагрузки, передаваемой на эти опоры. Назовем эти величины остаточными усилиями или невязками. Представим себе теперь, что опоры принадлежат к типу винтовых домкратов, так что в любой узловой точке можно вызвать любое требуемое перемещение. Тогда с помощью соответствующего выбора перемещений опор мы можем обратить в нуль все невязки (12). Такие перемещения будут представлять поправки, которые нужно добавить к принятым вначале прогибам  чтобы получить истинные значения
чтобы получить истинные значения 
Процедура, которой следует Саусвелл, манипулируя с перемещениями опор, подобна той, которую развил К. А. Чалышев для рам с высокой степенью статической неопределимости.
Сначала смещаем одну из опор, скажем, опору О (рис. 6), считая все другие опоры закрепленными. Из уравнений типа (11) можно видеть, что смещению опоры вниз на величину  будет соответствовать вертикальная сила —
будет соответствовать вертикальная сила —  действующая в узловой точке О. Знак минус показывает, что сила направлена вверх. Выбирая величину перемещения так, чтобы выполнялось требование
действующая в узловой точке О. Знак минус показывает, что сила направлена вверх. Выбирая величину перемещения так, чтобы выполнялось требование

мы обращаем остаточное усилие (12) в нуль; на опору О больше не будет передаваться никакого давления, но в то же время давление  передается на соседние опоры, и их остаточные усилия увеличатся на ту же величину. Поступая таким же образом со всеми прочими опорами и повторяя эту процедуру несколько раз, мы приведем все невязочные усилия к малым величинам, которыми можно пренебречь. Полные перемещения опор, накопленные при выполнении такой процедуры, должны быть сложены с соответствующими знаками с начальными значениями
передается на соседние опоры, и их остаточные усилия увеличатся на ту же величину. Поступая таким же образом со всеми прочими опорами и повторяя эту процедуру несколько раз, мы приведем все невязочные усилия к малым величинам, которыми можно пренебречь. Полные перемещения опор, накопленные при выполнении такой процедуры, должны быть сложены с соответствующими знаками с начальными значениями  дает в сумме истинные перемещения растянутой квадратной сетки.
дает в сумме истинные перемещения растянутой квадратной сетки.
Чтобы упростить вычисления, требуемые при этой процедуре, приведем уравнение (11) к безразмерной форме с помощью подстановки

Таким образом, получаем

где  - безразмерные величины.
- безразмерные величины.
Задача сводится теперь к отысканию такого набора значений  чтобы уравнение (15) удовлетворялось во всех внутренних точках сетки. При этом на границе функция должна быть равна нулю. Для нахождения решения используем описанный выше способ и примем некоторые начальные значения
чтобы уравнение (15) удовлетворялось во всех внутренних точках сетки. При этом на границе функция должна быть равна нулю. Для нахождения решения используем описанный выше способ и примем некоторые начальные значения  Они не будут удовлетворять уравнениям равновесия (15), и у нас появятся невязки
Они не будут удовлетворять уравнениям равновесия (15), и у нас появятся невязки

которые в этом случае будут безразмерными числами.
Наша задача состоит в том, чтобы добавить к принятым значениям  такие поправки, которые ликвидировали бы невязки. Добавляя к
такие поправки, которые ликвидировали бы невязки. Добавляя к  поправку
поправку  мы добавляем к невязке
мы добавляем к невязке  величину
величину  а к невязкам соседних точек — величины
а к невязкам соседних точек — величины  Приняв
Приняв  мы устраняем невязку в узловой точке О и как-то изменим невязки в соседних точках. Действуя таким же путем во всех узлах сетки и повторяя эту процедуру
мы устраняем невязку в узловой точке О и как-то изменим невязки в соседних точках. Действуя таким же путем во всех узлах сетки и повторяя эту процедуру
много раз, мы уменьшим остаточные усилия до пренебрежимо малых значений и, следовательно, получим с достаточной точностью значения  Соответствующие значения
Соответствующие значения  могут быть после этого получения по формуле (14).
могут быть после этого получения по формуле (14).
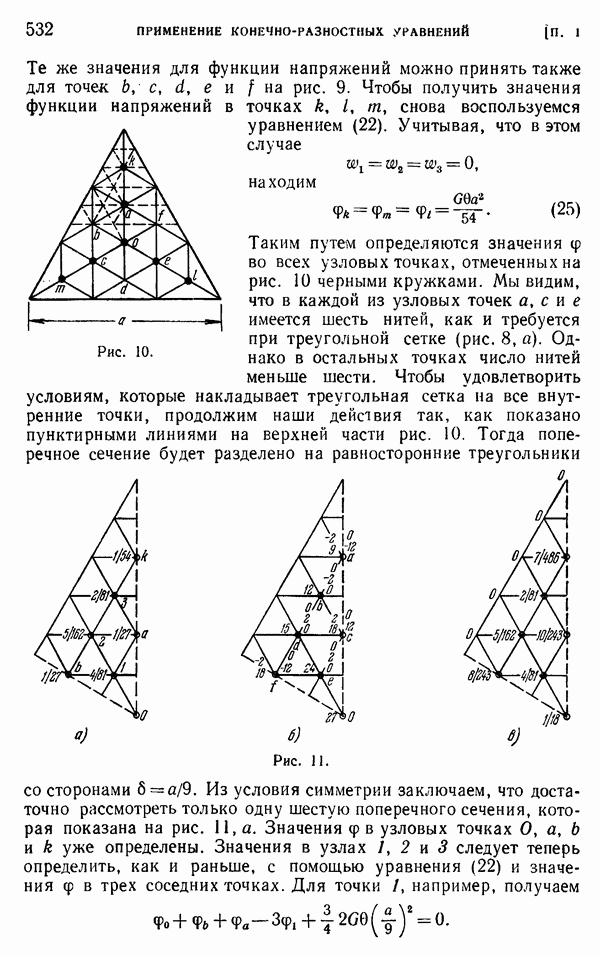
Чтобы проиллюстрировать эту процедуру, рассмотрим задачу о кручении стержня квадратного сечения, уже рассмотренную ранее в § 1. В этом случае имеем дифференциальное уравнение (4). Чтобы привести его к безразмерной форме, положим

Тогда конечно-разностное уравнение (5) примет вид

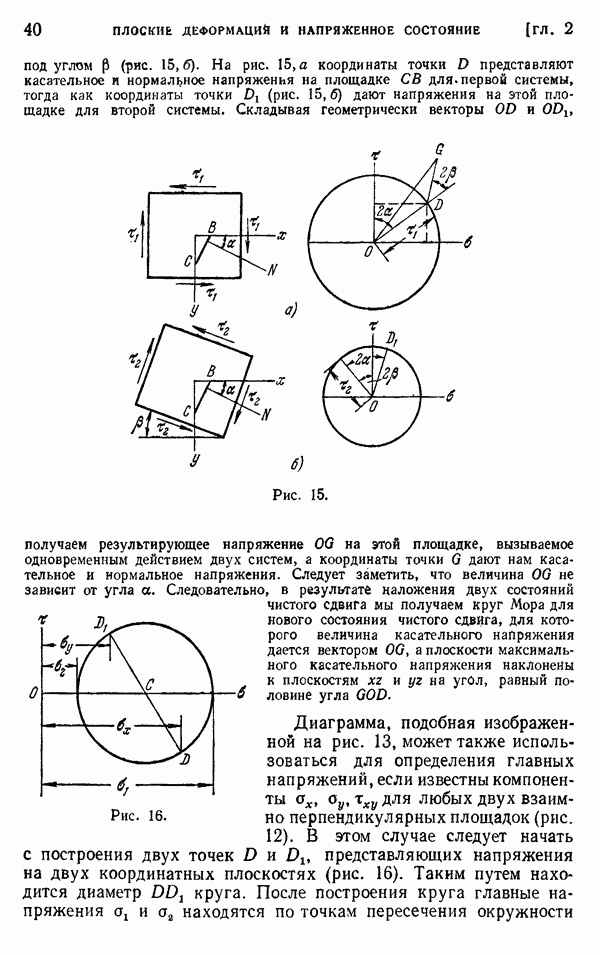
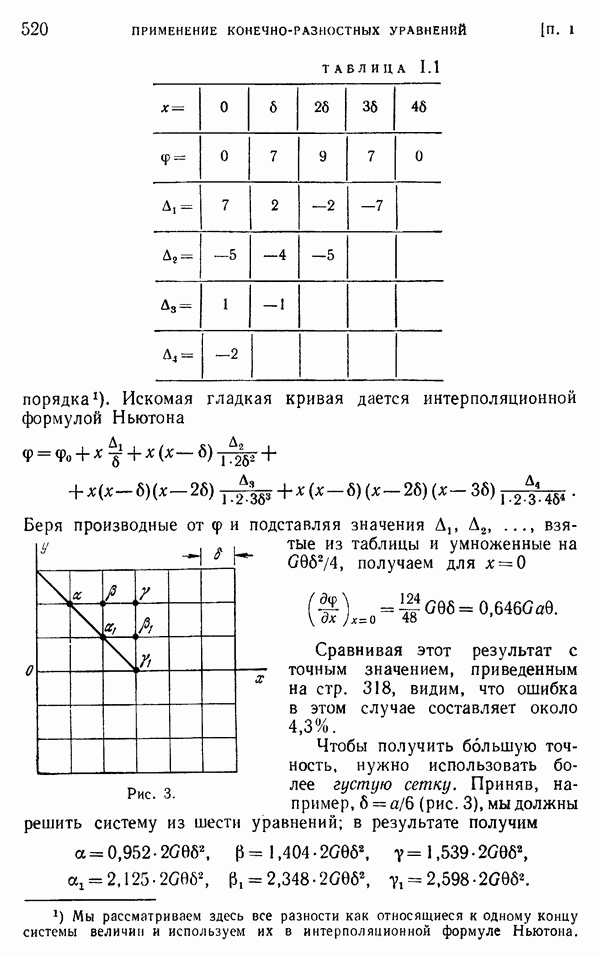
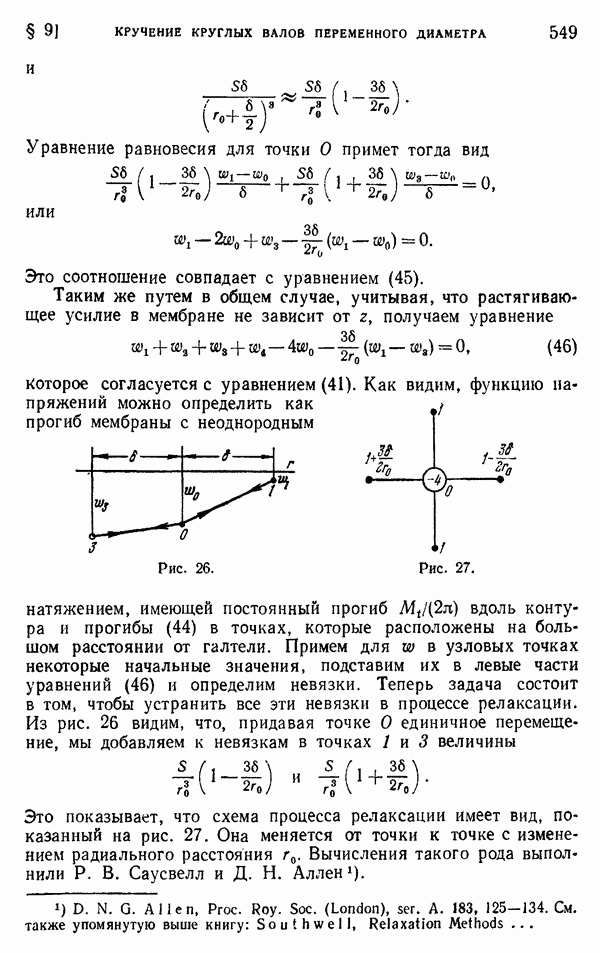
Знаменатель 1000 введен в уравнение (17) с той целью, чтобы сделать  достаточно большими числами, для которых в последней цифре позволительно пренебречь половиной по сравнению с единицей. Таким образом, нам придется оперировать только целыми числами. Чтобы сделать наш пример возможно более простым, начнем с грубой сетки, представленной на рис. 2. Тогда нам придется искать значения
достаточно большими числами, для которых в последней цифре позволительно пренебречь половиной по сравнению с единицей. Таким образом, нам придется оперировать только целыми числами. Чтобы сделать наш пример возможно более простым, начнем с грубой сетки, представленной на рис. 2. Тогда нам придется искать значения  лишь для трех точек, для которых мы уже знаем точные значения (см. стр. 520). Вычертим квадратную сетку в достаточно крупном масштабе, чтобы на ней можно было записывать результаты промежуточных вычислений (рис. 7). Расчет начинается с принятых начальных значений
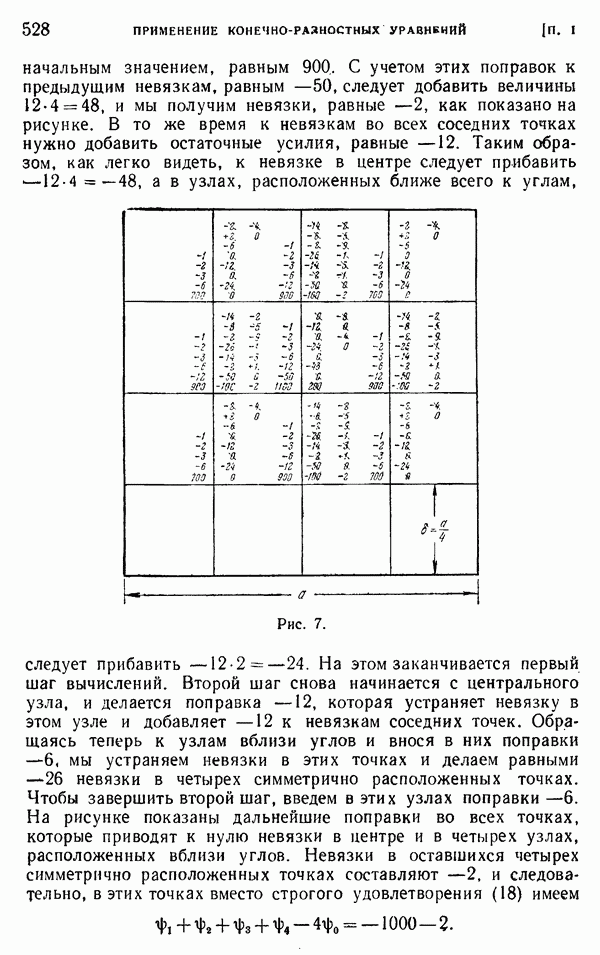
лишь для трех точек, для которых мы уже знаем точные значения (см. стр. 520). Вычертим квадратную сетку в достаточно крупном масштабе, чтобы на ней можно было записывать результаты промежуточных вычислений (рис. 7). Расчет начинается с принятых начальных значений  которые мы запишем левей и выше каждой узловой точки. Значения 700, 900 и 1100 намеренно взяты несколько отличными от полученных ранее точных значений. Подставляя эти значения вместе с нулевыми значениями на границе в левую часть уравнения (18), находим остаточные усилия для всех узлов. Эти усилия записаны правее и выше каждого узла. Наибольшее остаточное усилие, равное 200, получается в центре сетки, и мы начнем процесс релаксации с этого узла. Добавляя к принятому значению 1100 поправку 50, которая записана на рисунке над числом 1100, полностью устраним невязку в центре. Поэтому вычеркиваем число 200 и ставим вместо него нуль. Теперь нам нужно изменить невязки в соседних узлах. Прибавим 50 к каждой из невязок и выпишем новое значение —50 над первоначальными значениями, как показано на рисунке. На этом заканчивается работа с центральным узлом сетки. Теперь мы имеем четыре симметрично расположенные точки с невязками, равными —50, и поправки удобно внести во все эти значения одновременно. Примем для всех этих точек одну и ту же поправку, равную —121). Эти поправки напишем над
которые мы запишем левей и выше каждой узловой точки. Значения 700, 900 и 1100 намеренно взяты несколько отличными от полученных ранее точных значений. Подставляя эти значения вместе с нулевыми значениями на границе в левую часть уравнения (18), находим остаточные усилия для всех узлов. Эти усилия записаны правее и выше каждого узла. Наибольшее остаточное усилие, равное 200, получается в центре сетки, и мы начнем процесс релаксации с этого узла. Добавляя к принятому значению 1100 поправку 50, которая записана на рисунке над числом 1100, полностью устраним невязку в центре. Поэтому вычеркиваем число 200 и ставим вместо него нуль. Теперь нам нужно изменить невязки в соседних узлах. Прибавим 50 к каждой из невязок и выпишем новое значение —50 над первоначальными значениями, как показано на рисунке. На этом заканчивается работа с центральным узлом сетки. Теперь мы имеем четыре симметрично расположенные точки с невязками, равными —50, и поправки удобно внести во все эти значения одновременно. Примем для всех этих точек одну и ту же поправку, равную —121). Эти поправки напишем над
начальным значением, равным 900,. С учетом этих поправок к предыдущим невязкам, равным —50, следует добавить величины  и мы получим невязки, равные —2, как показано на рисунке. В то же время к невязкам во всех соседних точках нужно добавить остаточные усилия, равные —12. Таким образом, как легко видеть, к невязке в центре следует прибавить
и мы получим невязки, равные —2, как показано на рисунке. В то же время к невязкам во всех соседних точках нужно добавить остаточные усилия, равные —12. Таким образом, как легко видеть, к невязке в центре следует прибавить  , а в узлах, расположенных ближе всего к углам, следует прибавить
, а в узлах, расположенных ближе всего к углам, следует прибавить  .
.
Рис. 7. (см. скан)
На этом заканчивается первый шаг вычислений. Второй шаг снова начинается с центрального узла, и делается поправка —12, которая устраняет невязку в этом узле и добавляет —12 к невязкам соседних точек. Обращаясь теперь к узлам вблизи углов и внося в них поправки —6, мы устраняем невязки в этих точках и делаем равными —26 невязки в четырех симметрично расположенных точках. Чтобы завершить второй шаг, введем в этих узлах поправки —6. На рисунке показаны дальнейшие поправки во всех точках, которые приводят к нулю невязки в центре и в четырех узлах, расположенных вблизи углов. Невязки в оставшихся четырех симметрично расположенных точках составляют —2, и следовательно, в этих точках вместо строгого удовлетворения (18) имеем

Невязку справа, равную —2, нужно сравнить  Очевидно, эта невязка соответствует очень малому остаточному усилию. Чтобы найти значения
Очевидно, эта невязка соответствует очень малому остаточному усилию. Чтобы найти значения  прибавим к начальным значениям все введенные поправки. Получим
прибавим к начальным значениям все введенные поправки. Получим

После этого формула (17) дает для  следующие значения:
следующие значения:

которые находятся в очень хорошем согласии с результатами, полученными ранее (см. стр. 520).
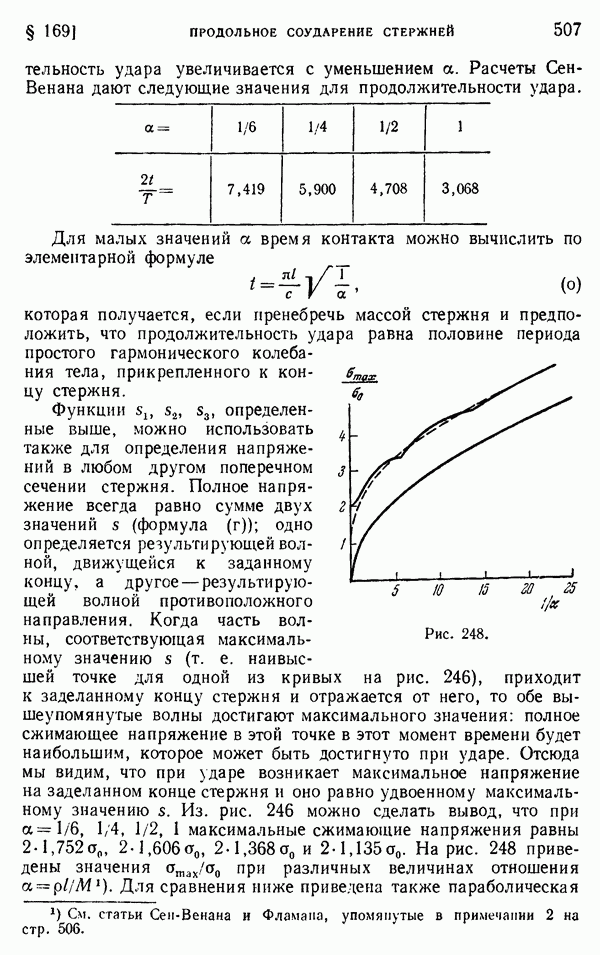
Как видим, метод Саусвелла дает нам физическую картину итерационного процесса решения уравнений (15), что может оказаться полезным при выборе порядка, в котором следует рассматривать узлы сетки.
Чтобы получить лучшее приближение, нам нужно перейти к более густой сетке. Используя метод, проиллюстрированный на рис. 5, мы получаем начальные значения  для квадратной сетки с размером ячейки
для квадратной сетки с размером ячейки  . Применяя к этим значениям стандартную процедуру релаксации, можно получить значения
. Применяя к этим значениям стандартную процедуру релаксации, можно получить значения  для более густой сетки и вычислить более точное значение максимального напряжения. Имея два значения максимального напряжения, найденные при
для более густой сетки и вычислить более точное значение максимального напряжения. Имея два значения максимального напряжения, найденные при  и при
и при  , можно с помощью экстраполяции получить лучшее приближение, как это поясняется в § 1.
, можно с помощью экстраполяции получить лучшее приближение, как это поясняется в § 1.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
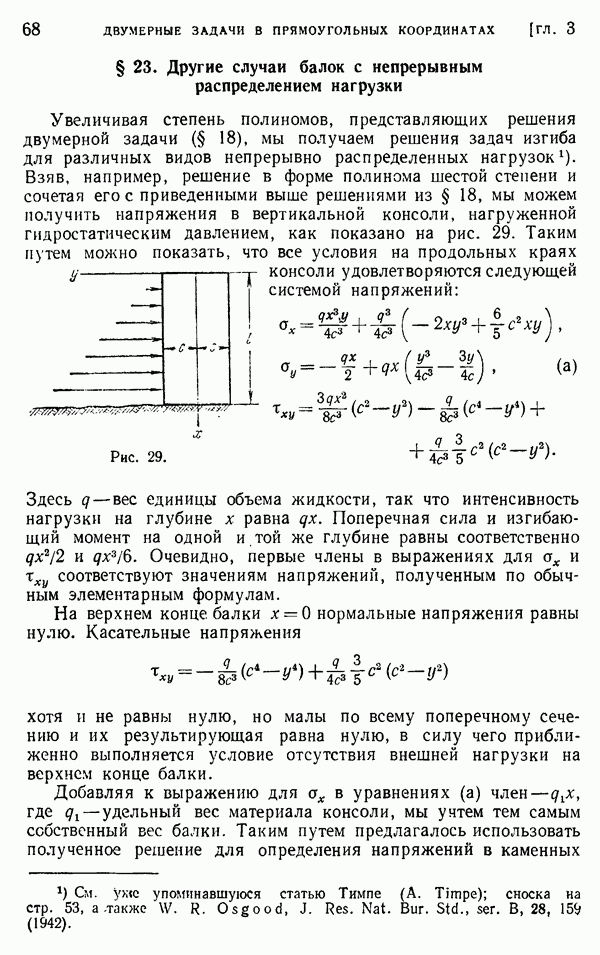
- § 23. Другие случаи балок с непрерывным распределением нагрузки
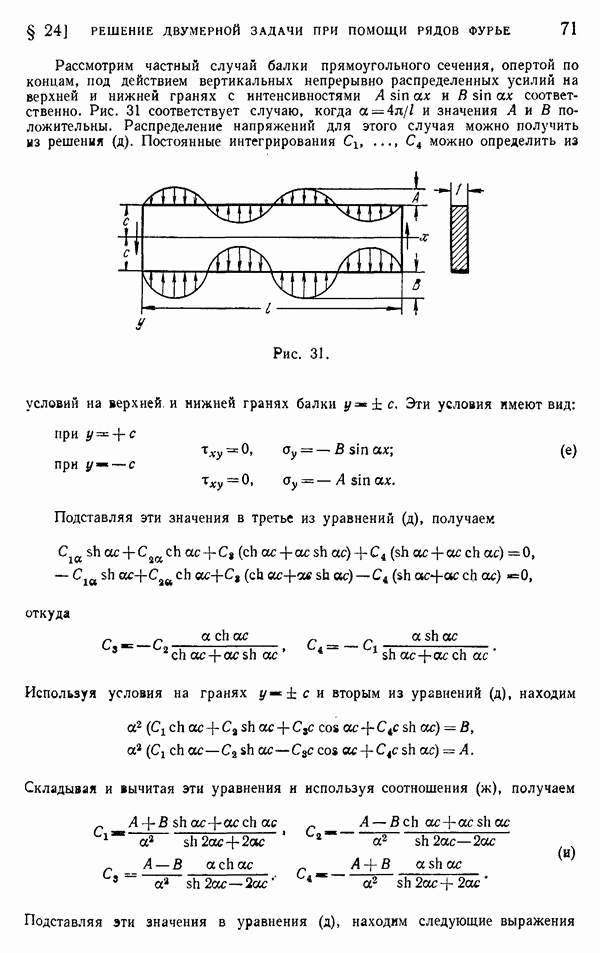
- § 24. Решение двумерной задачи при помощи рядов Фурье
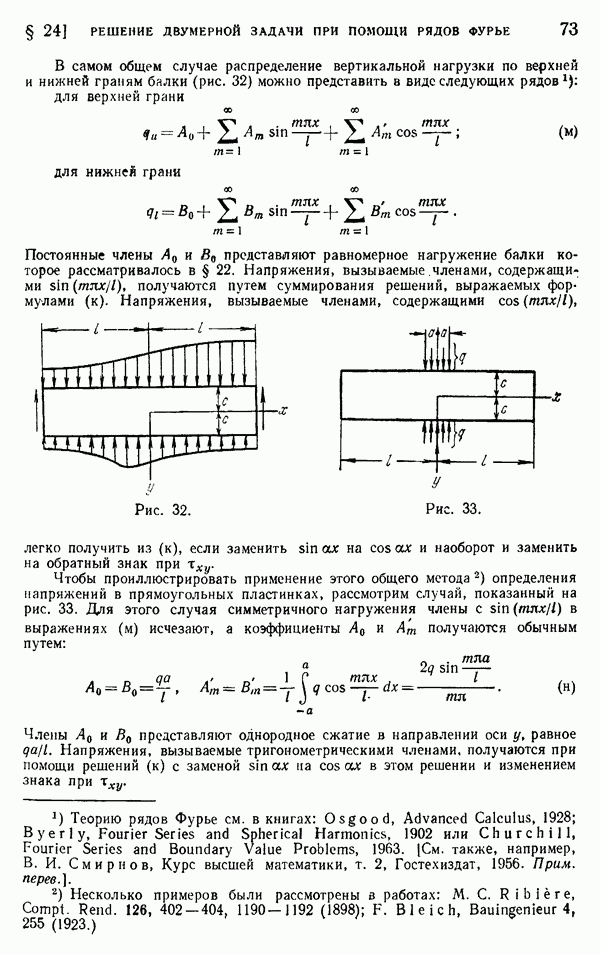
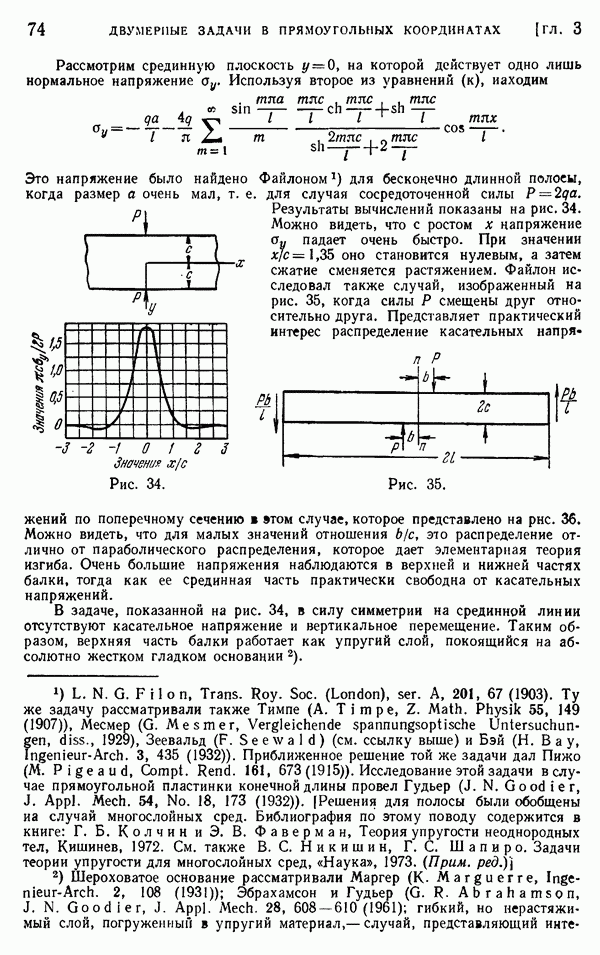
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
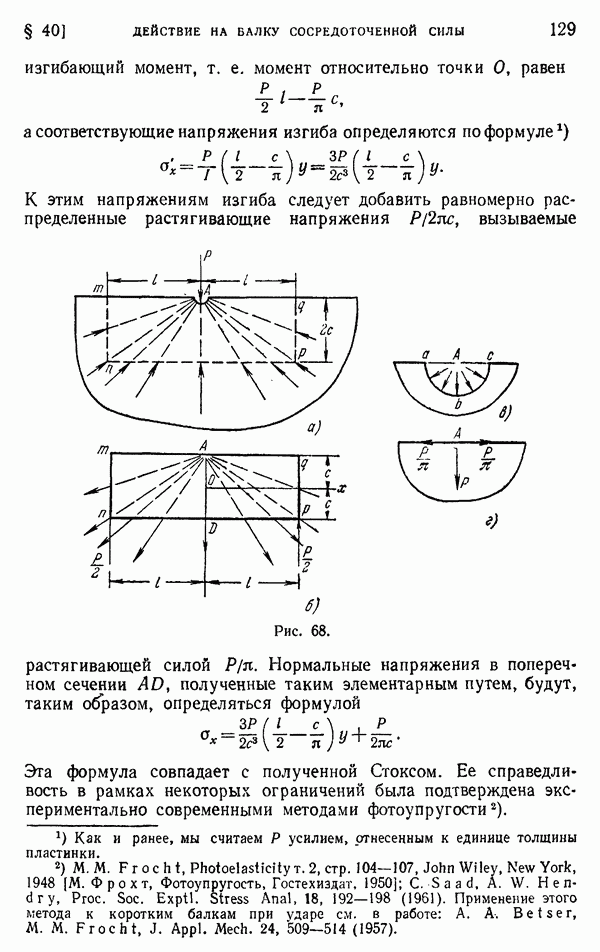
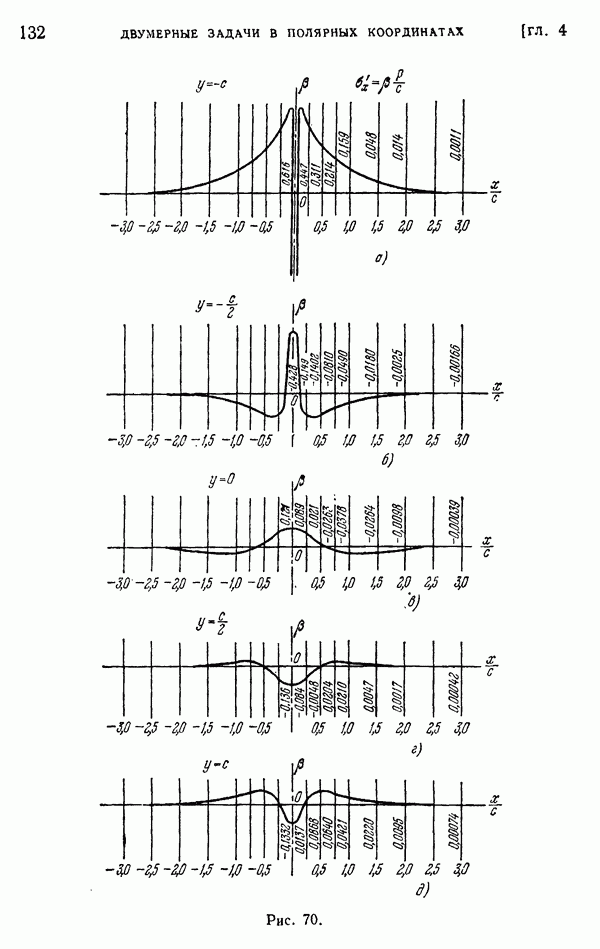
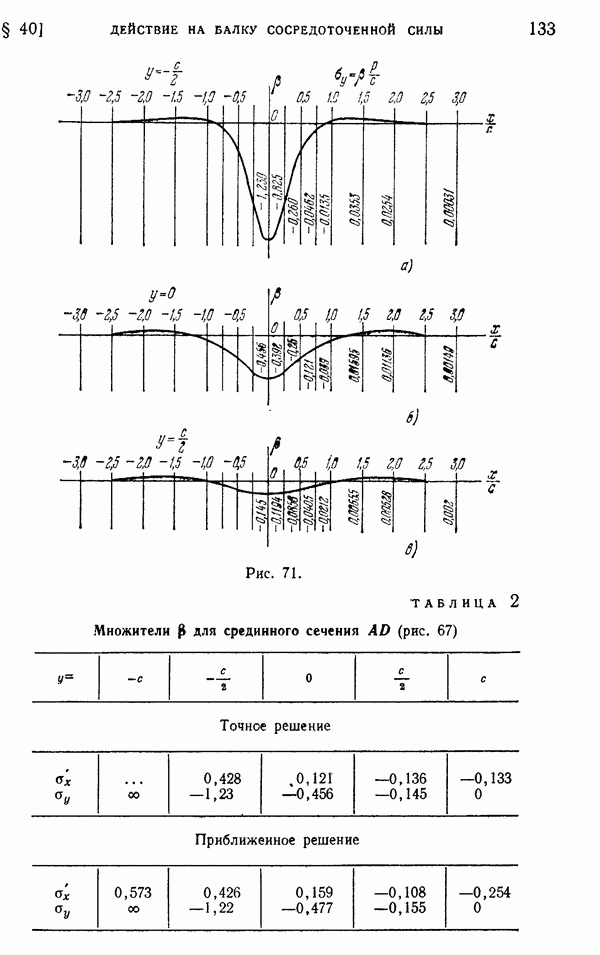
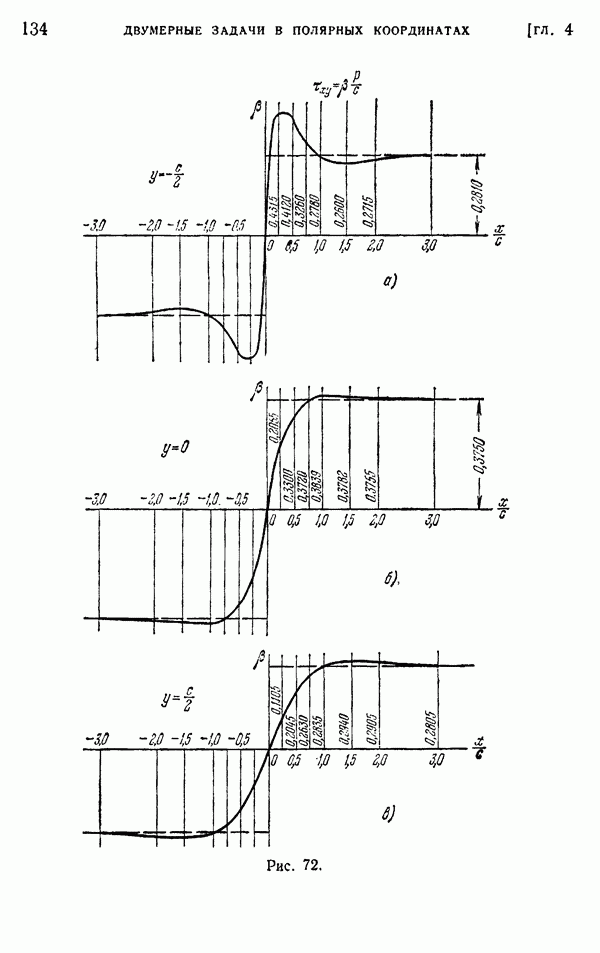
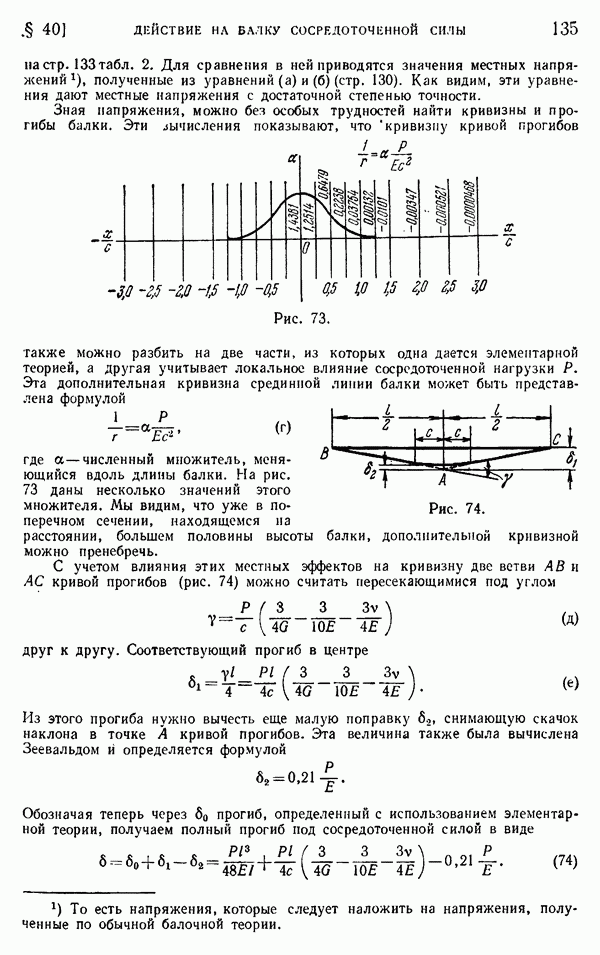
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
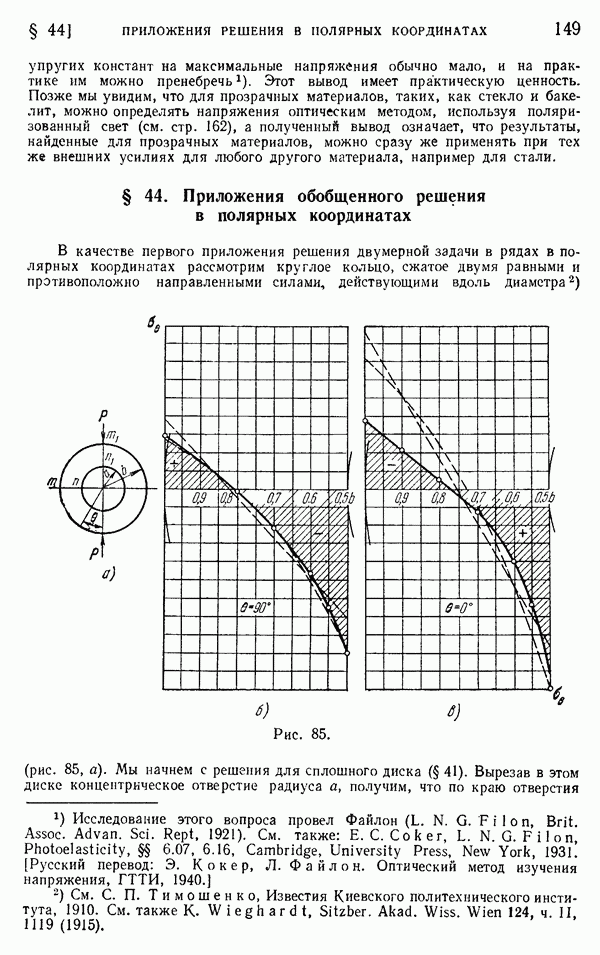
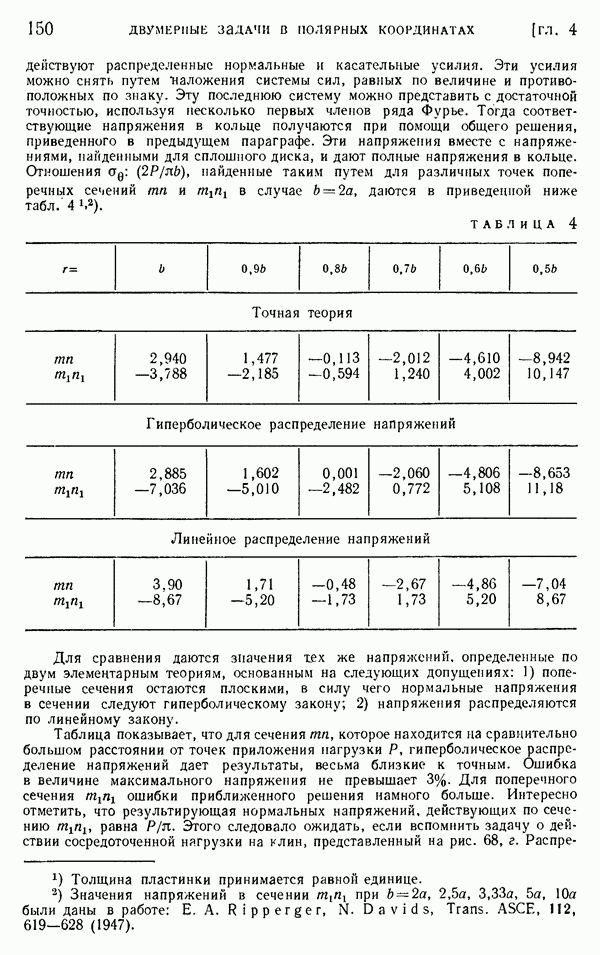
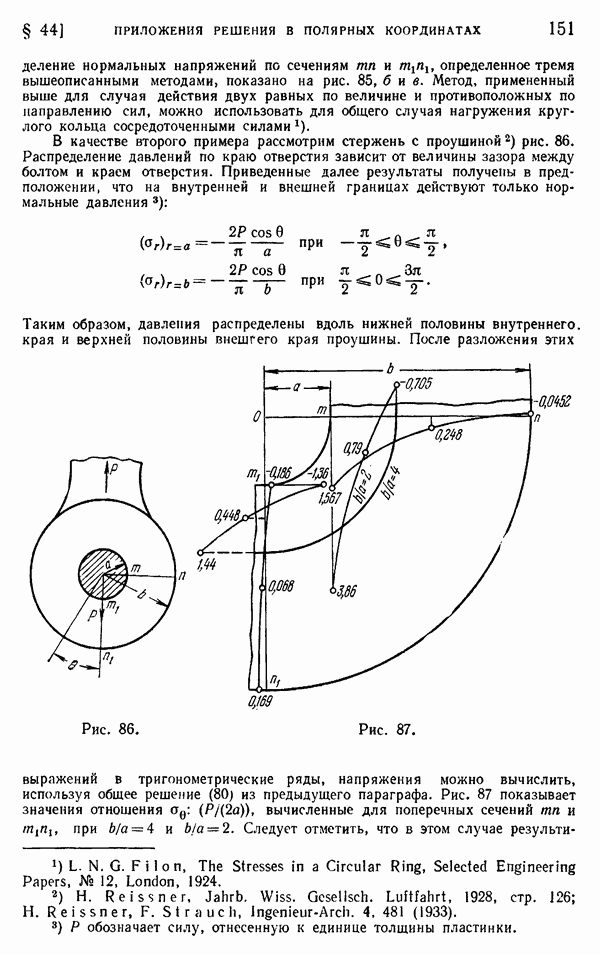
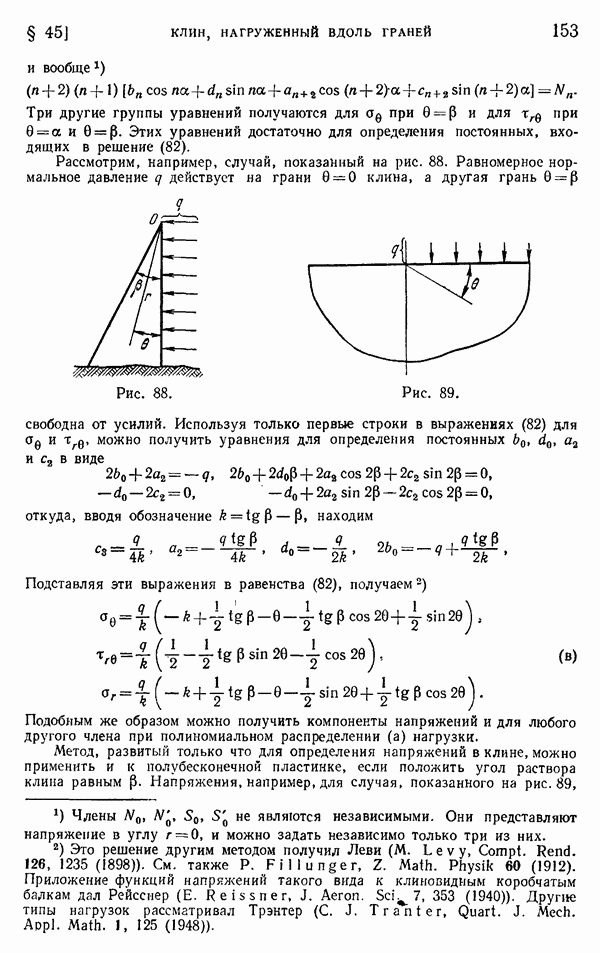
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
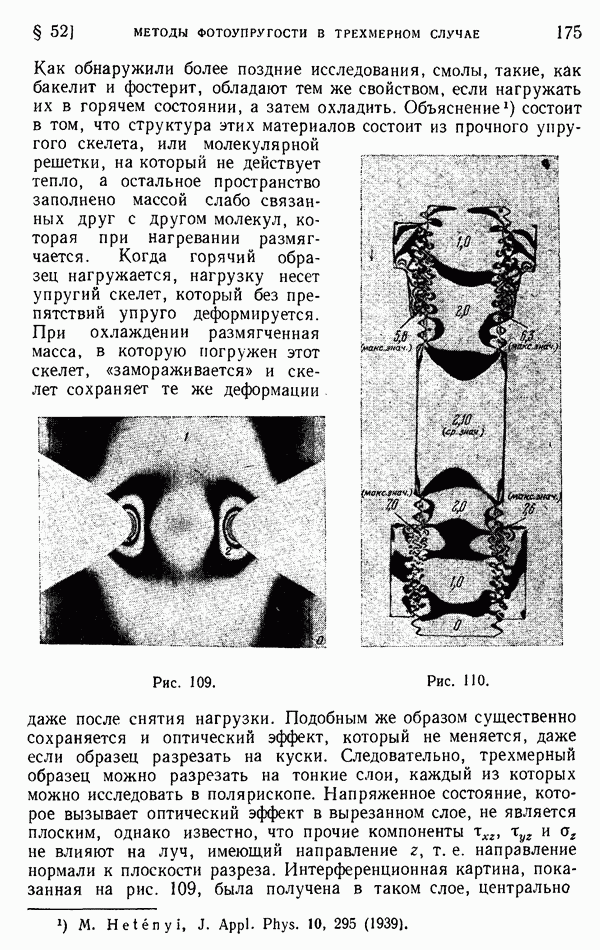
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
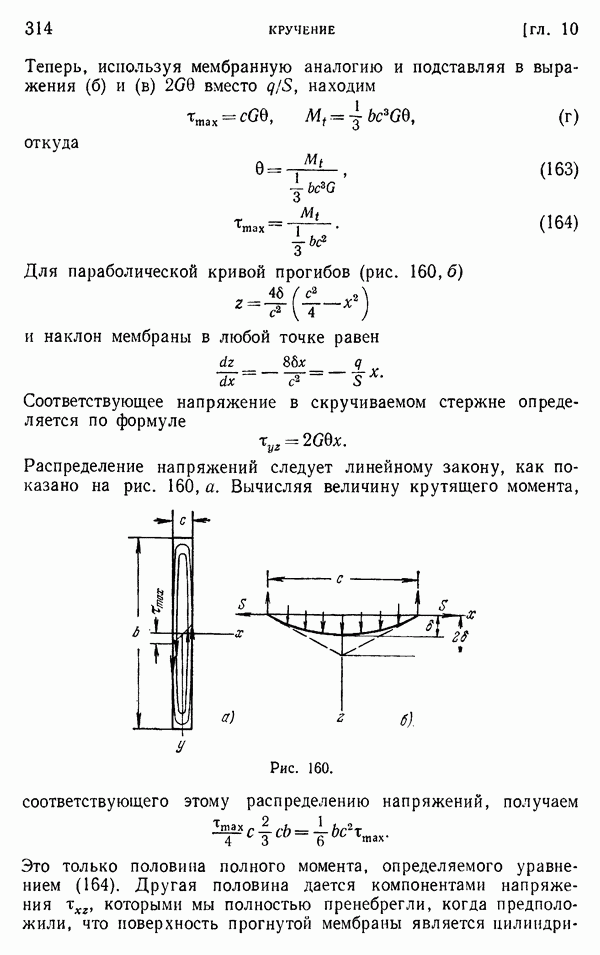
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
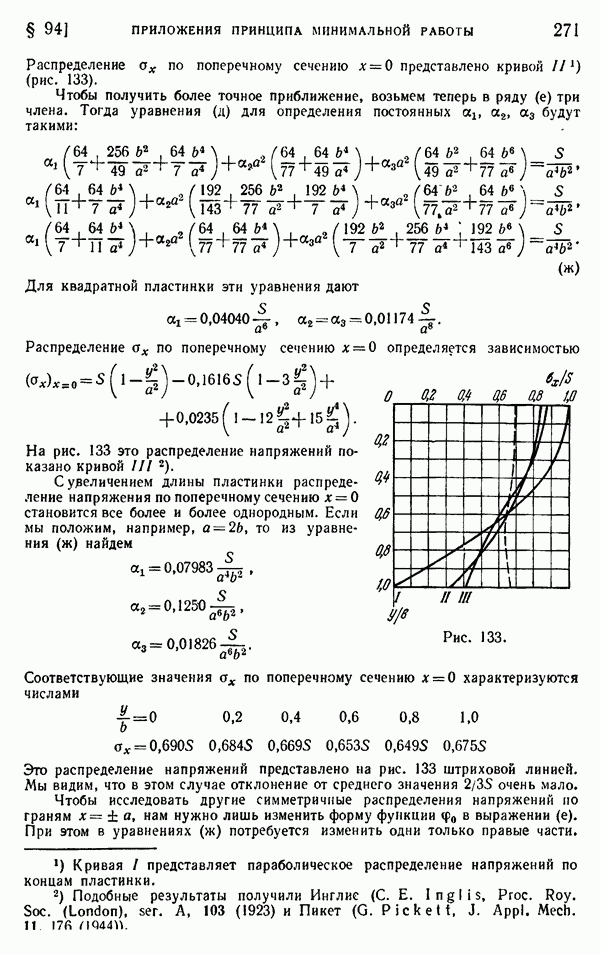
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
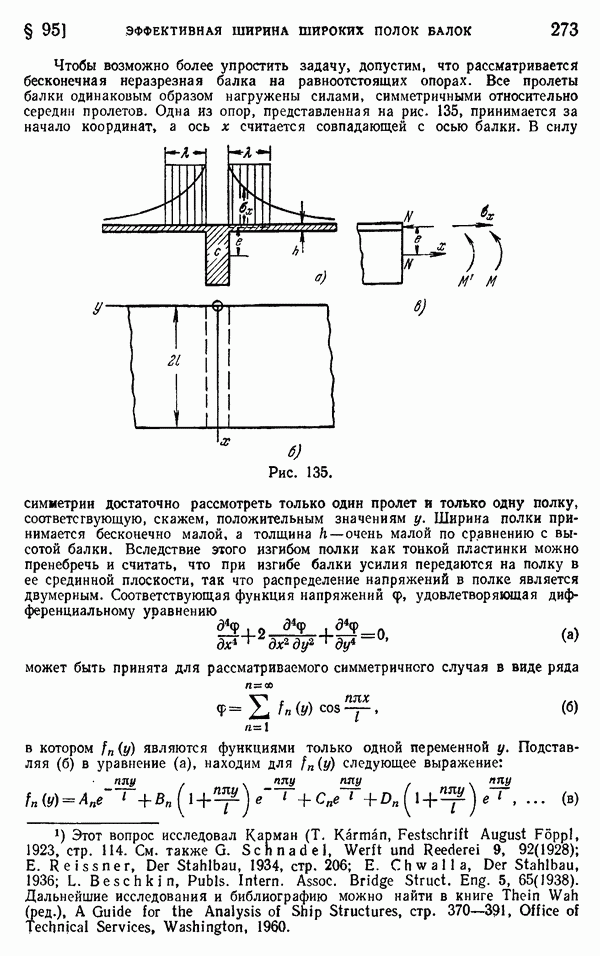
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
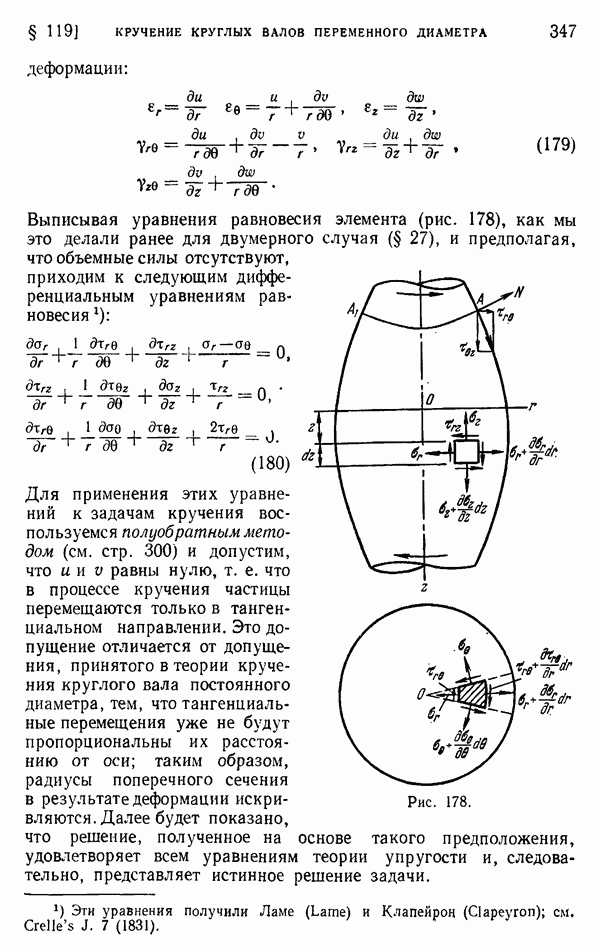
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
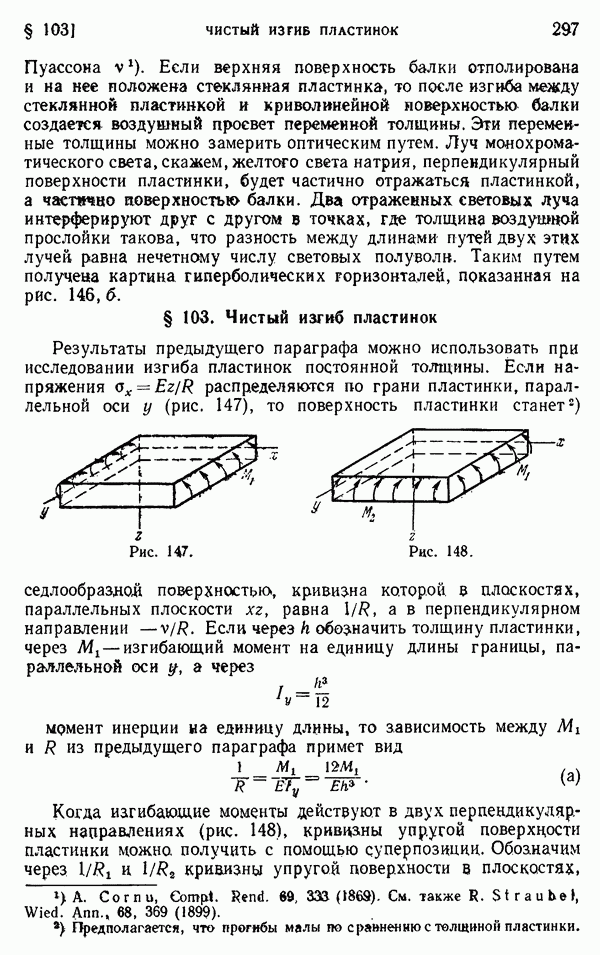
- § 103. Чистый изгиб пластинок
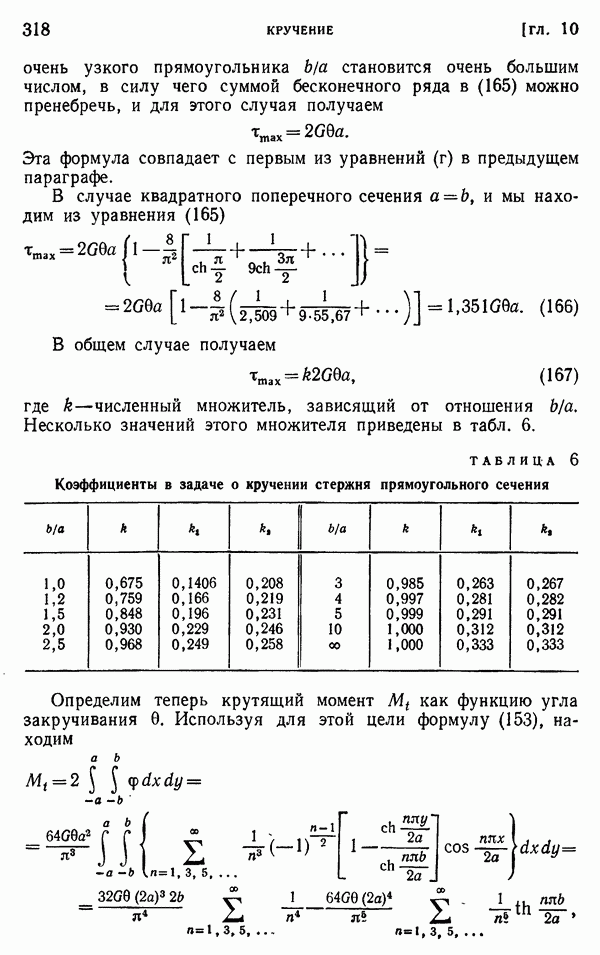
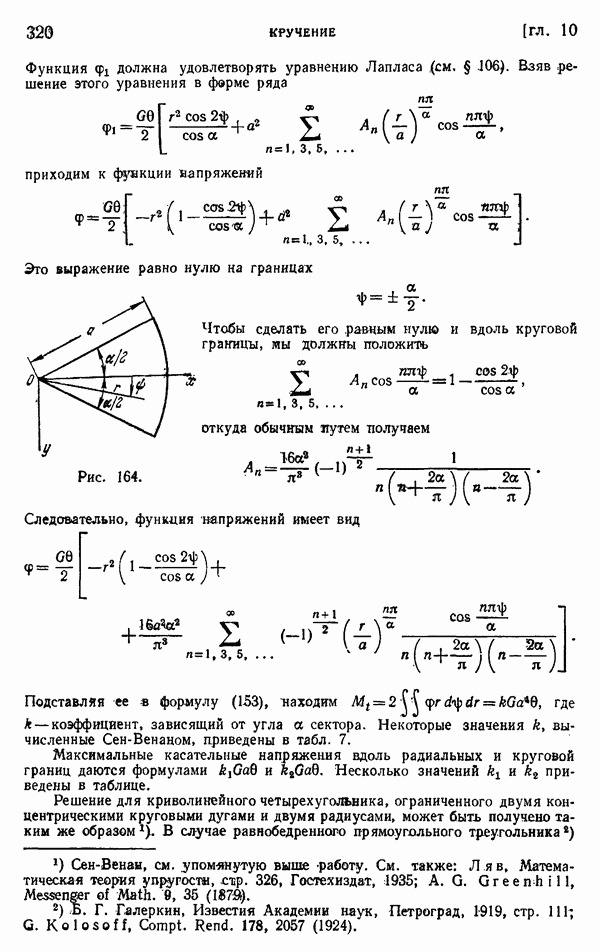
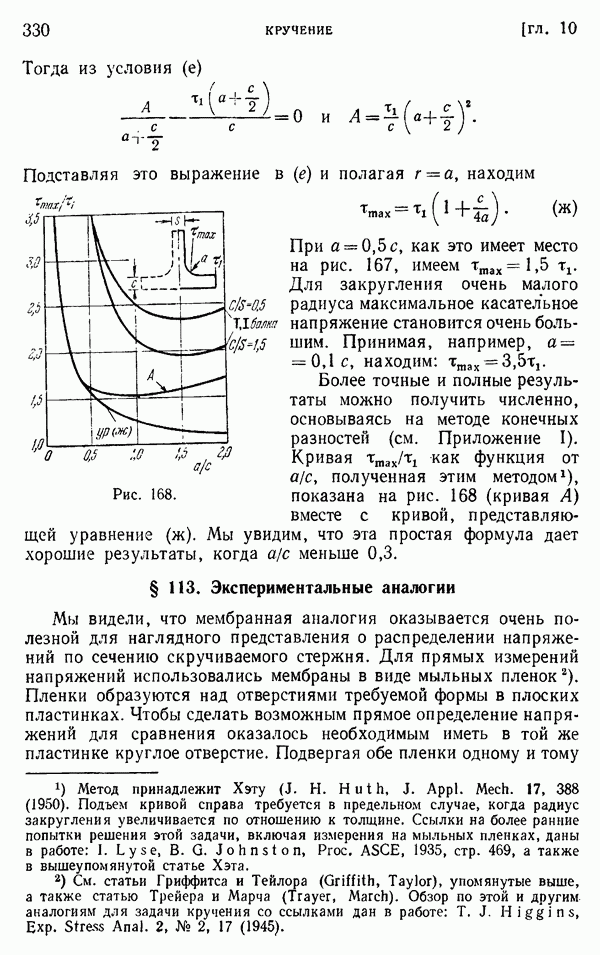
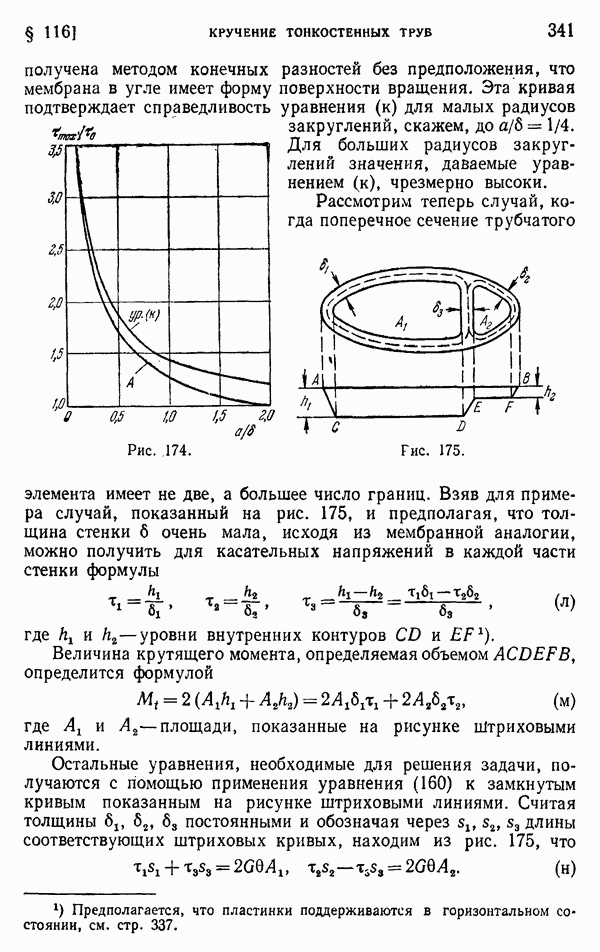
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
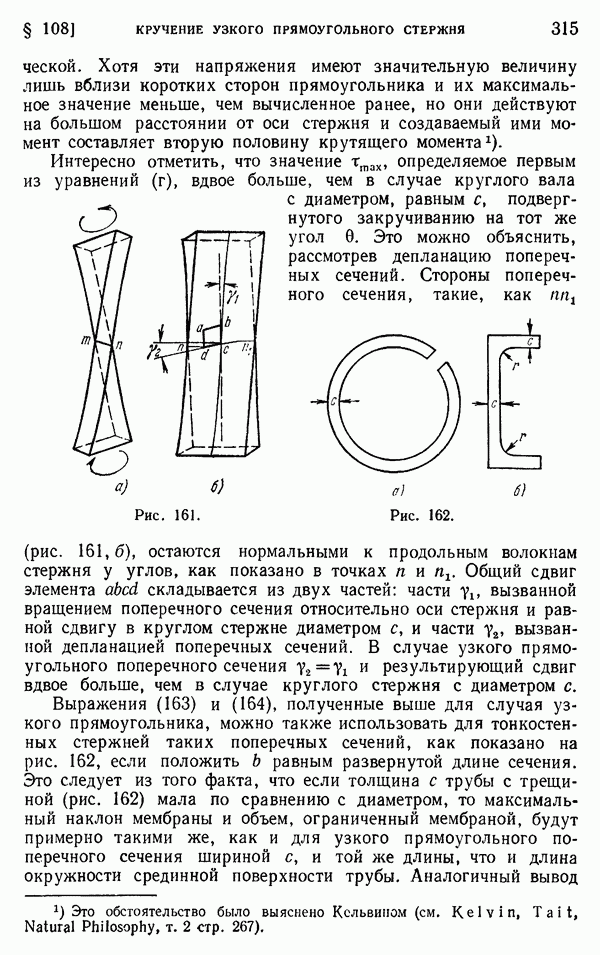
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
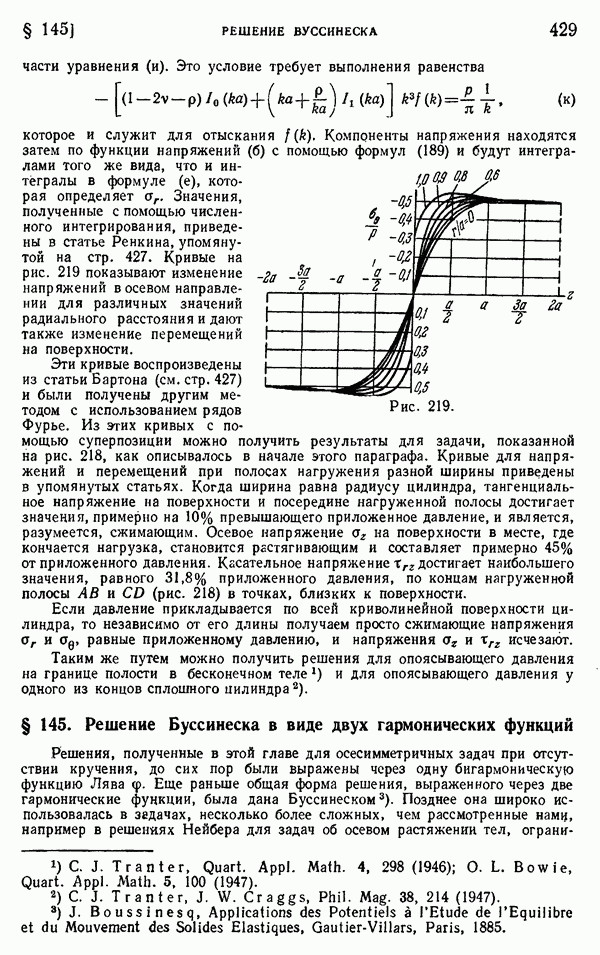
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
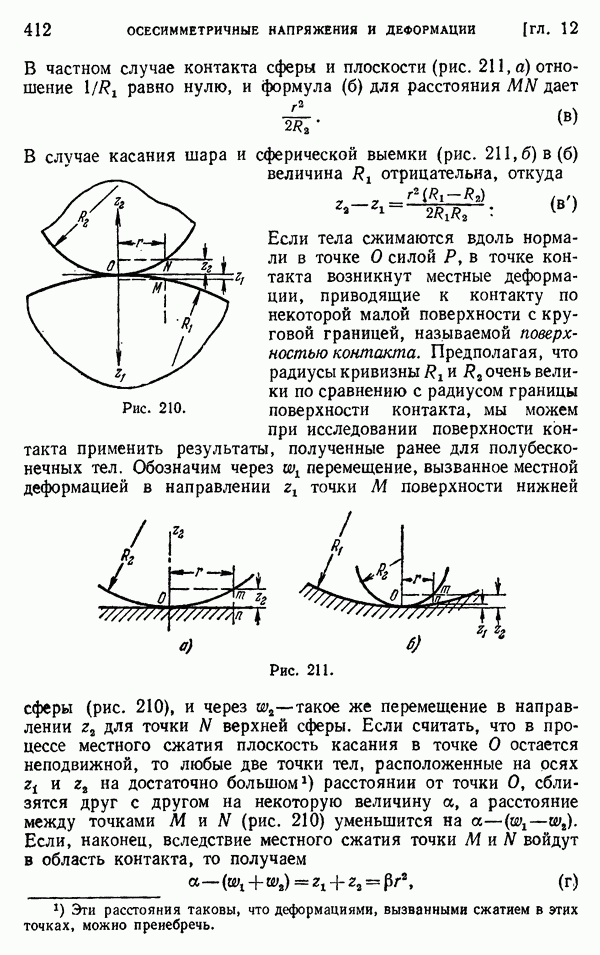
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
- § 145. Решение Буссинеска в виде двух гармонических функций
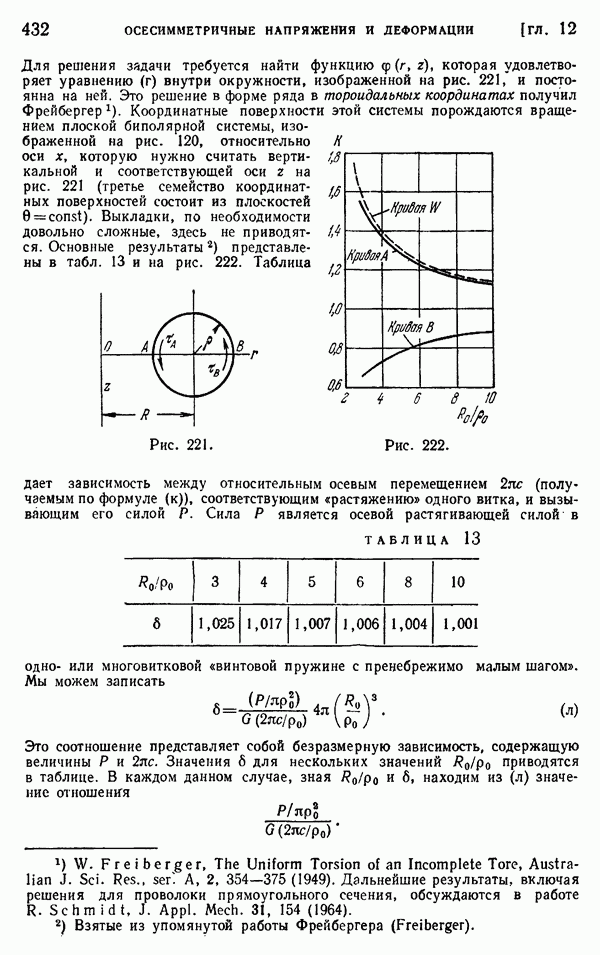
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
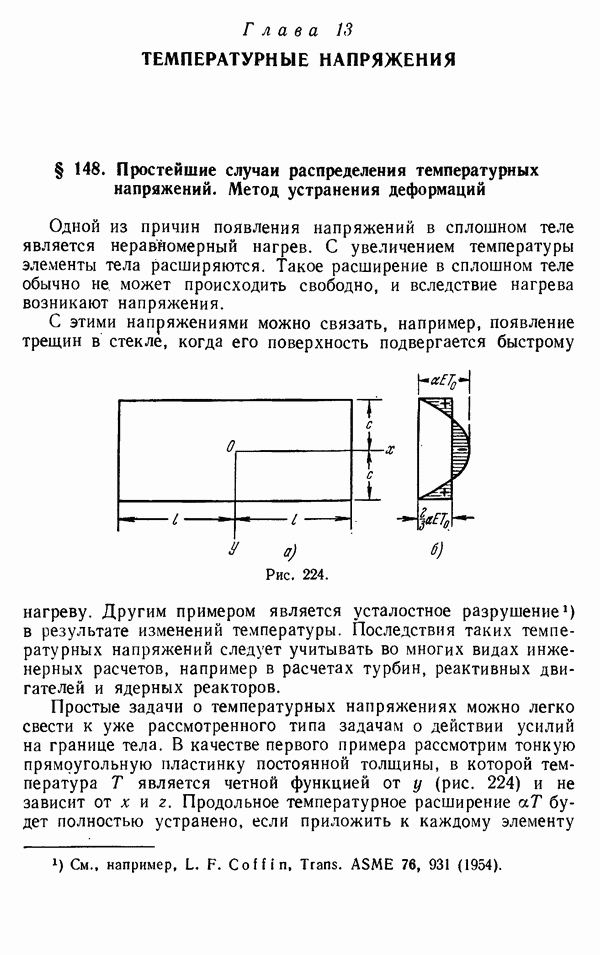
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
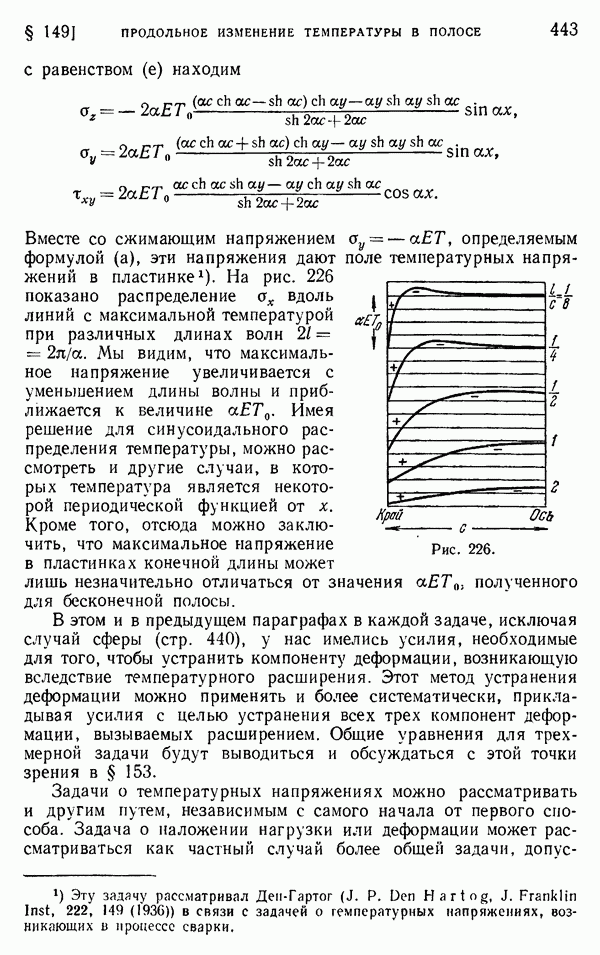
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
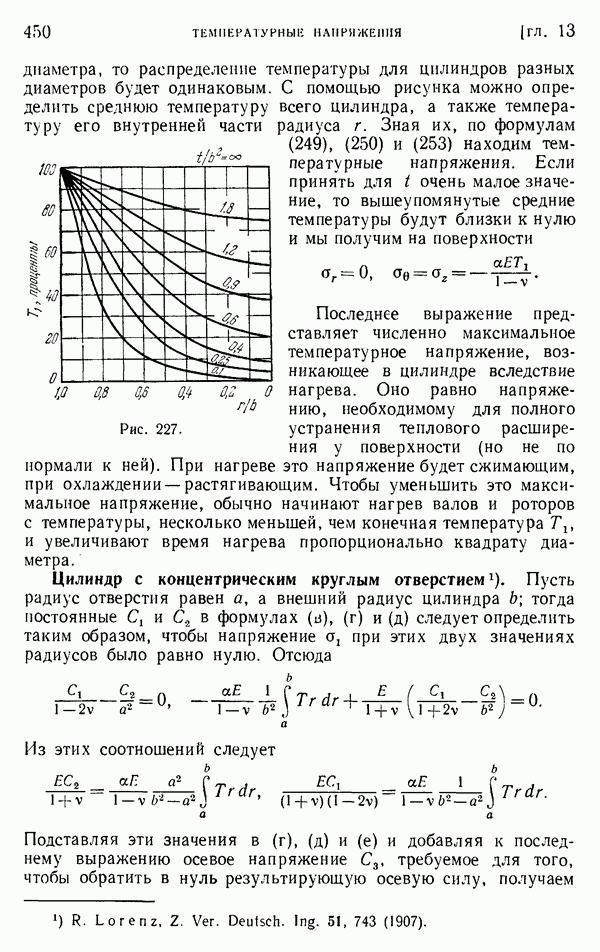
- § 151. Длинный круглый цилиндр
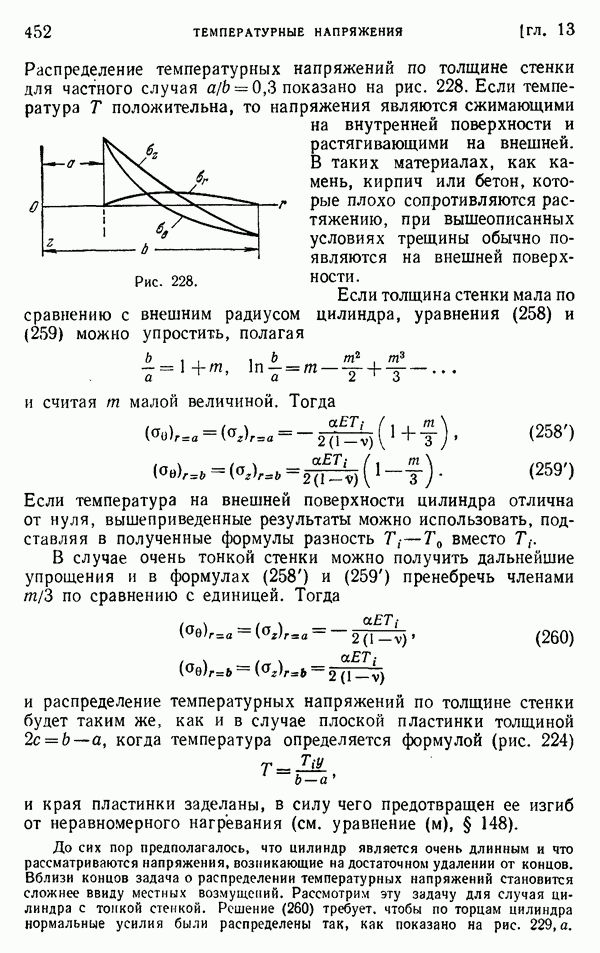
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
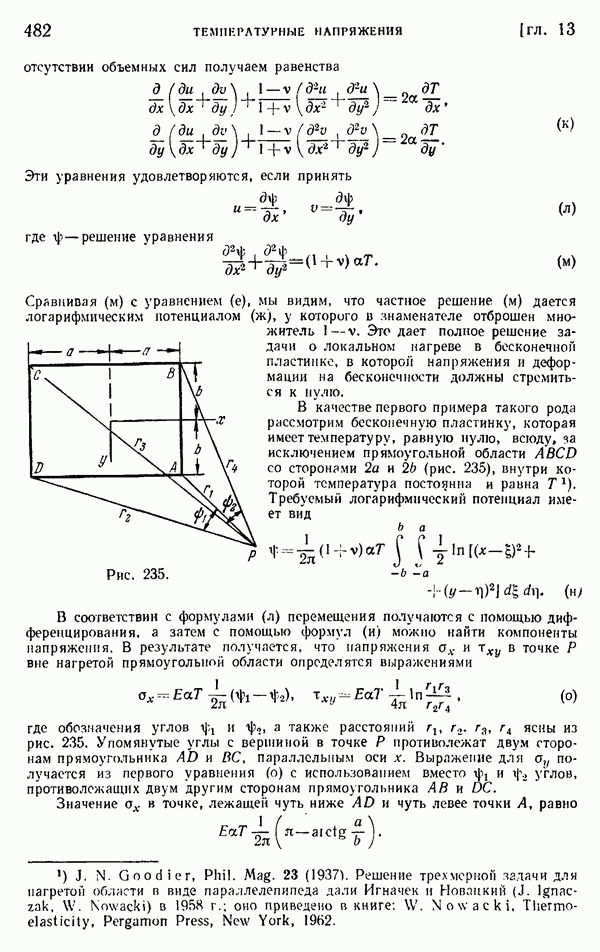
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
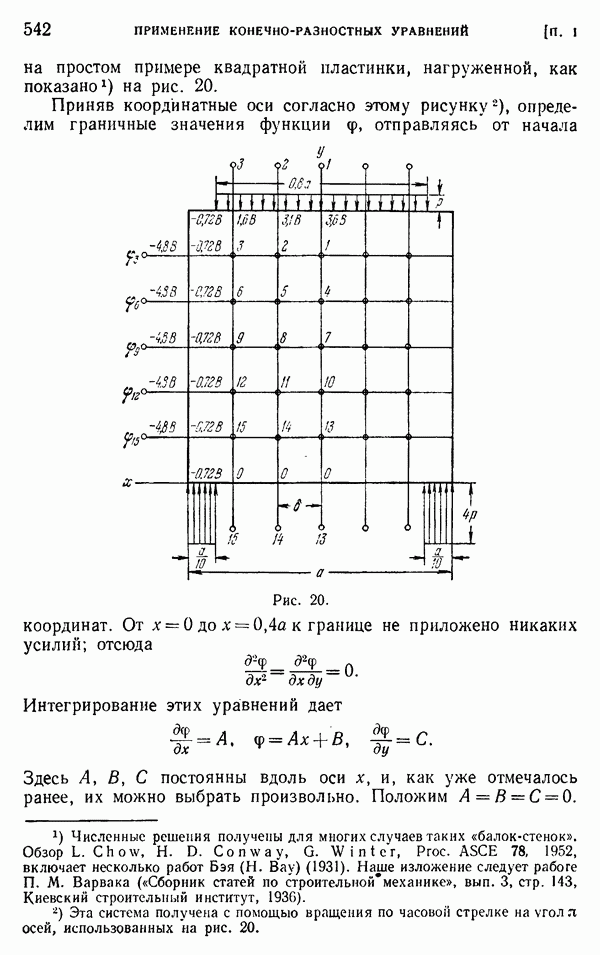
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
- § 4. Треугольные и шестиугольные сетки
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
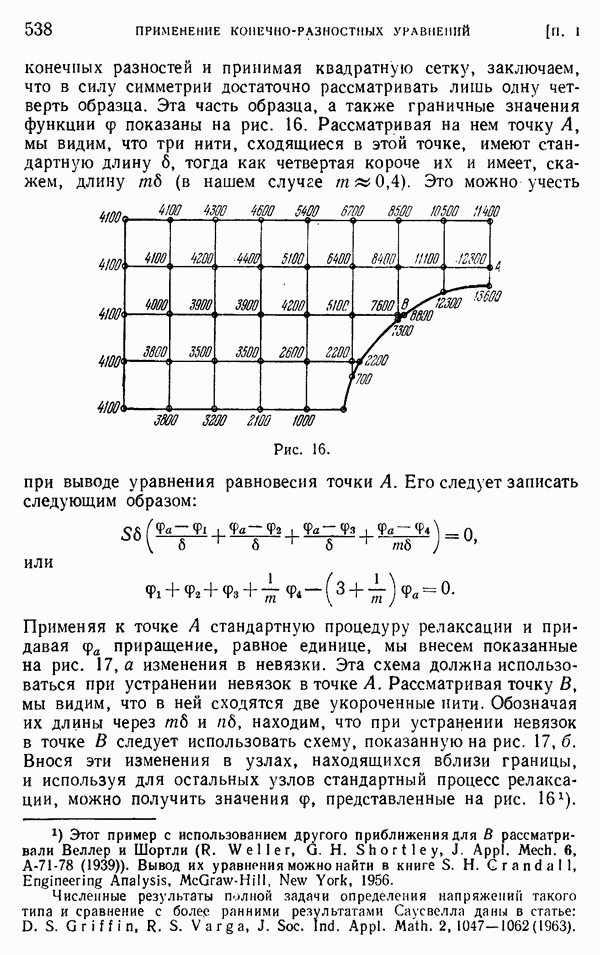
- § 7. Точки, расположенные вблизи границы
- § 8. Бигармоническое уравнение
- § 9. Кручение круглых валов переменного диаметра
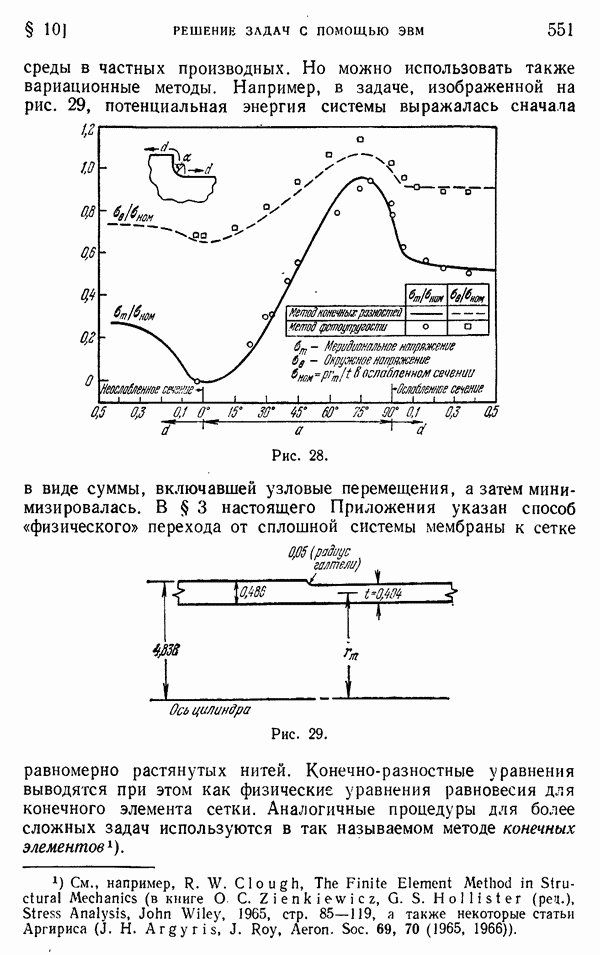
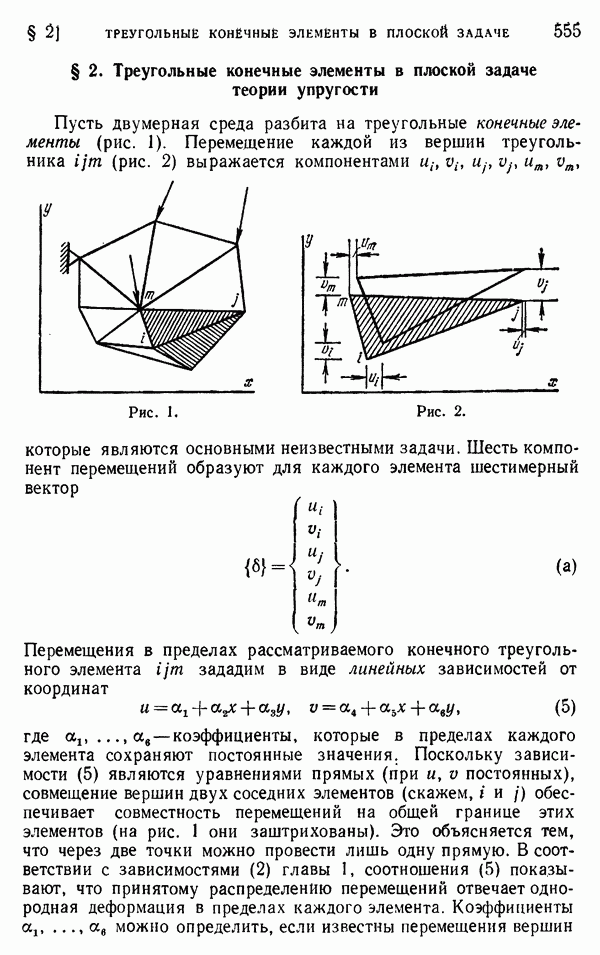
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
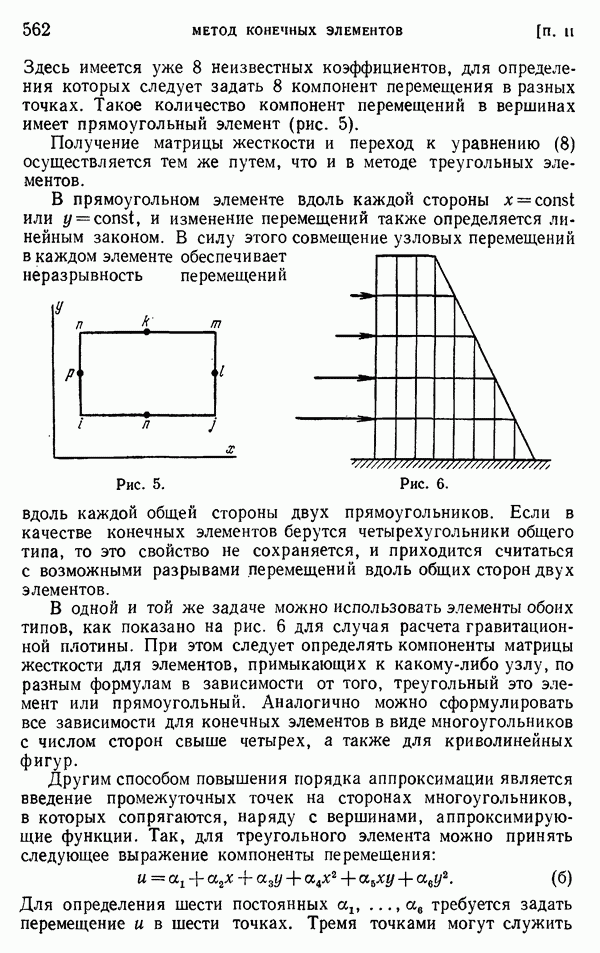
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи