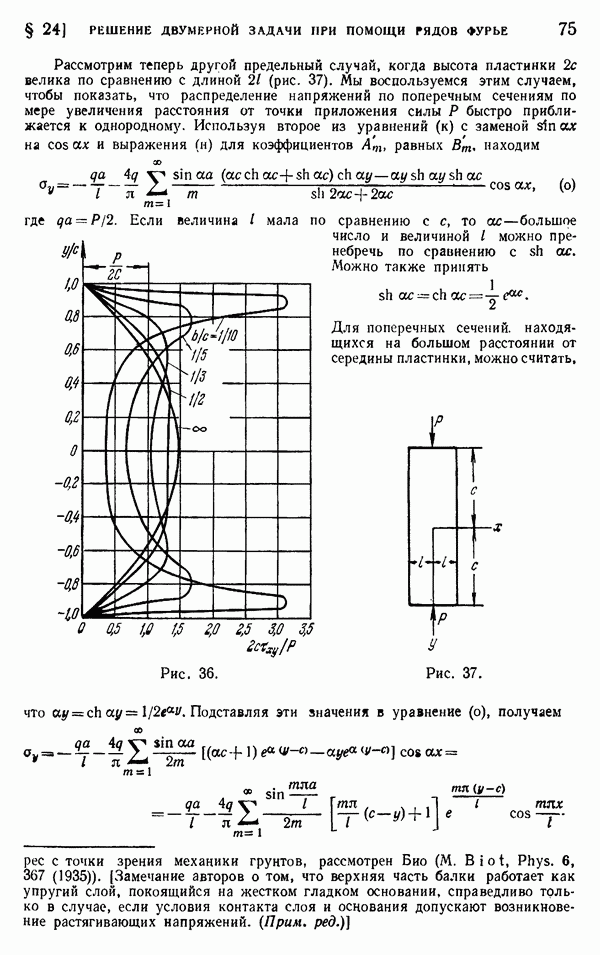
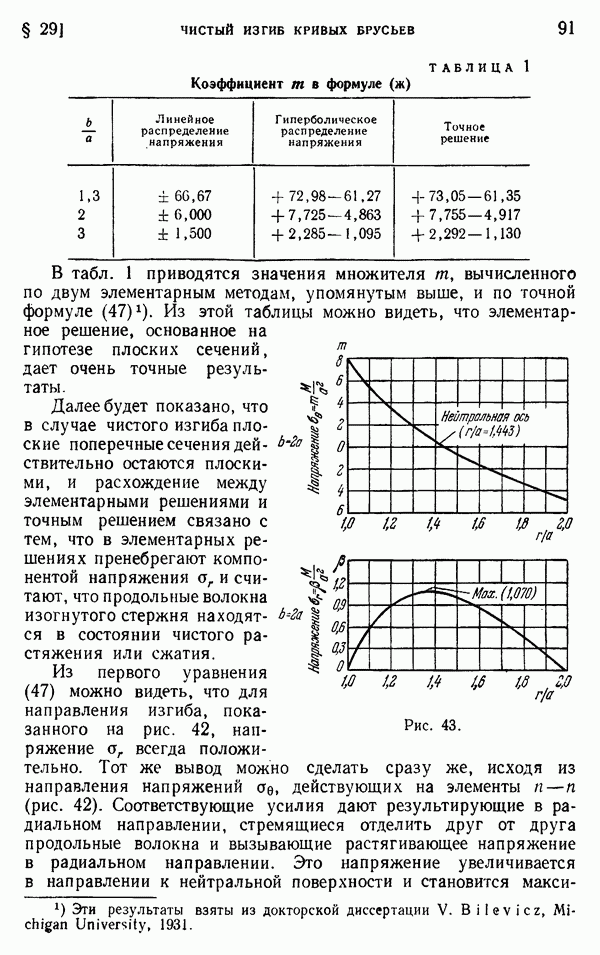
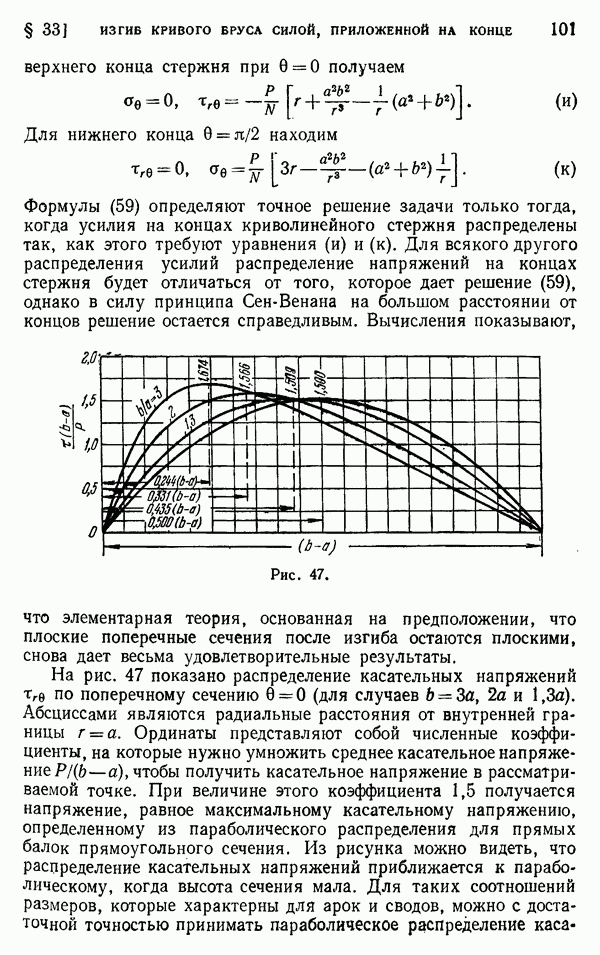
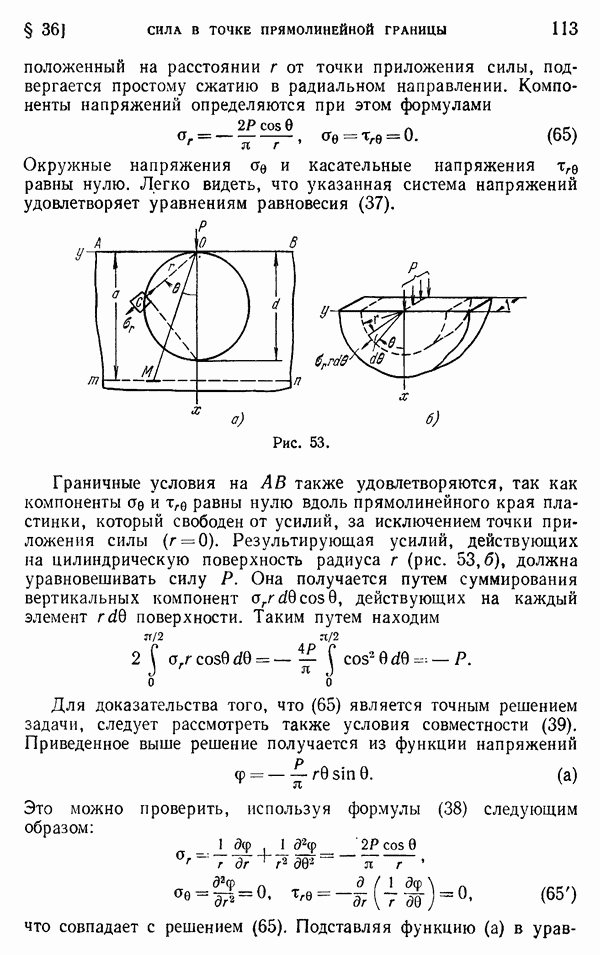
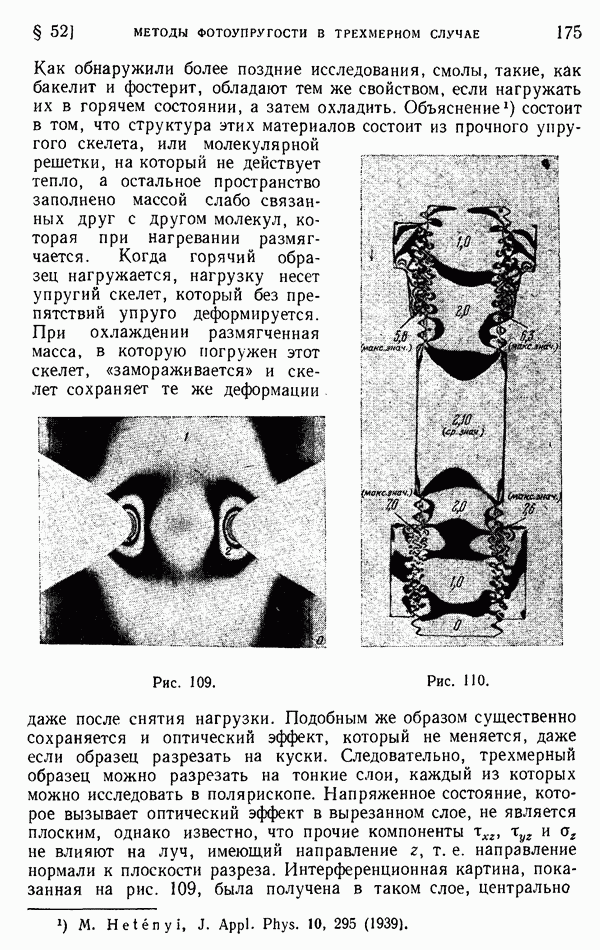
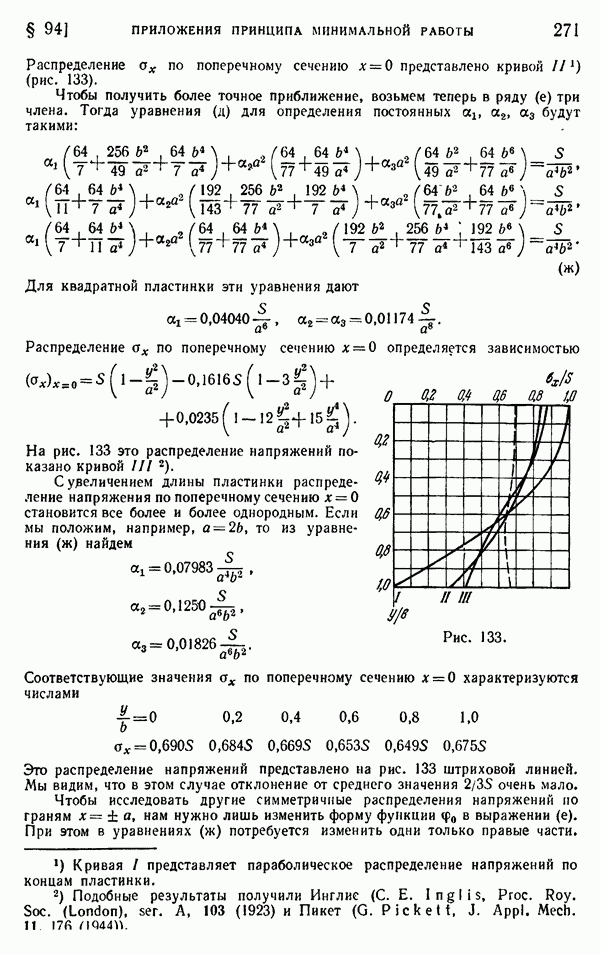
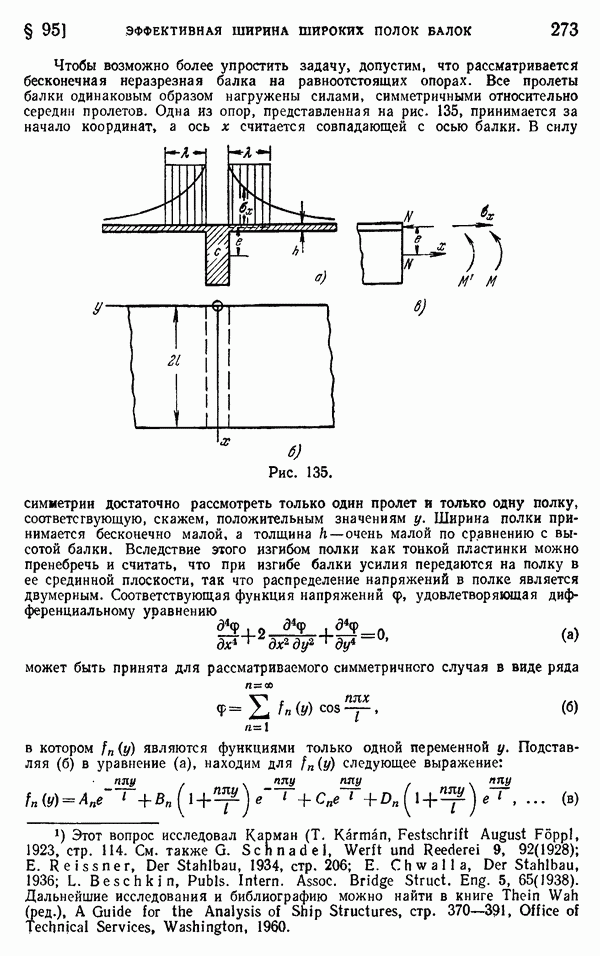
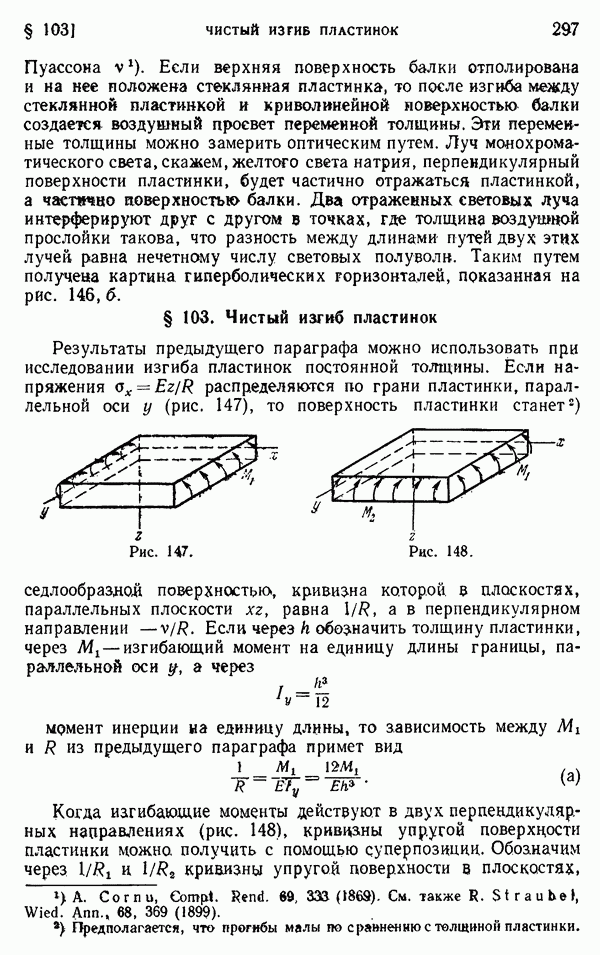
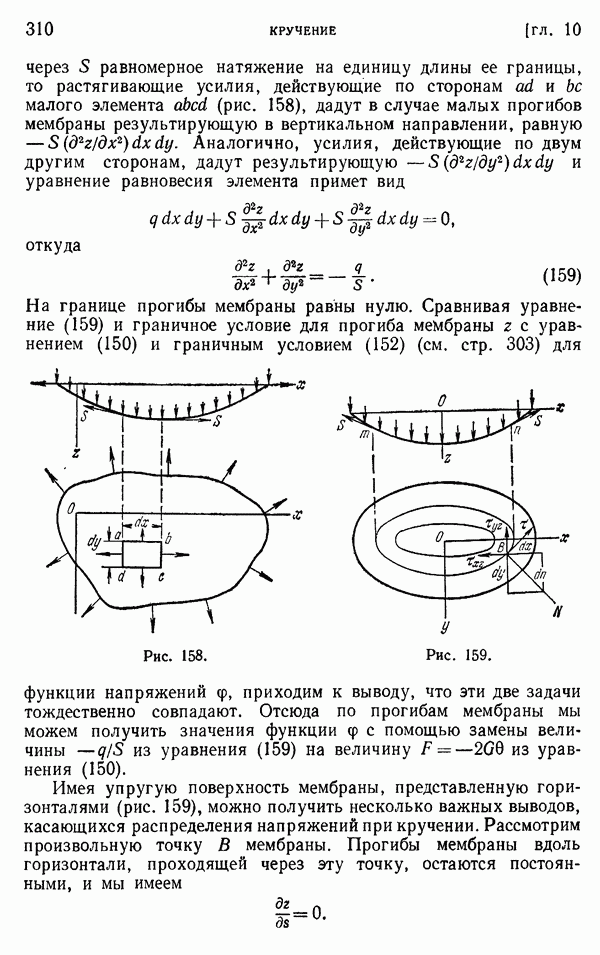
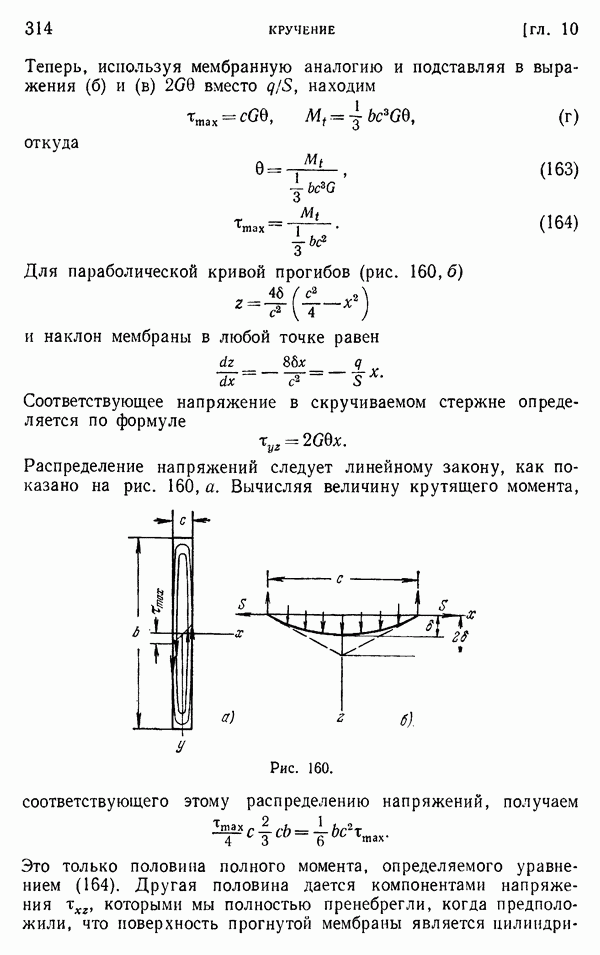
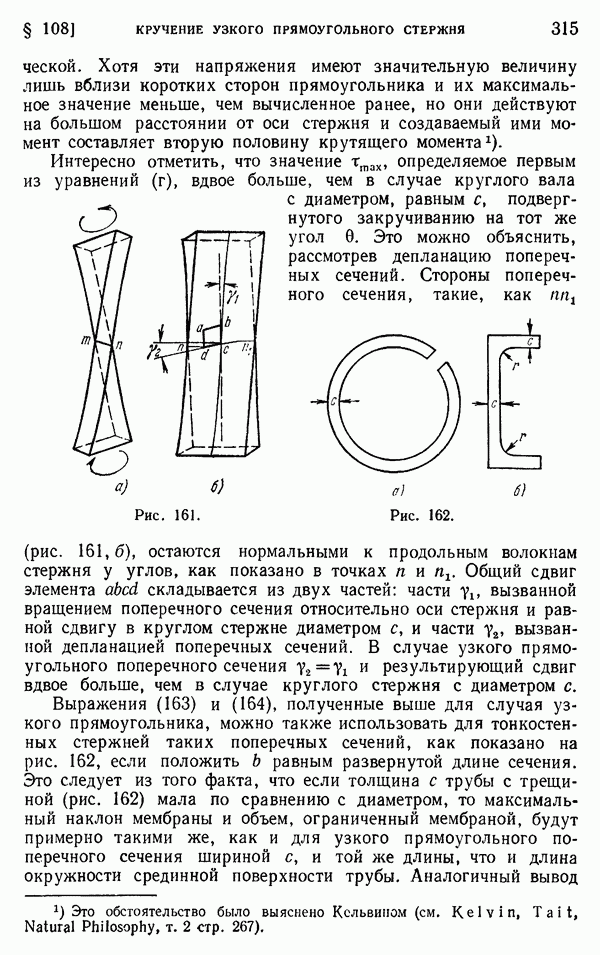
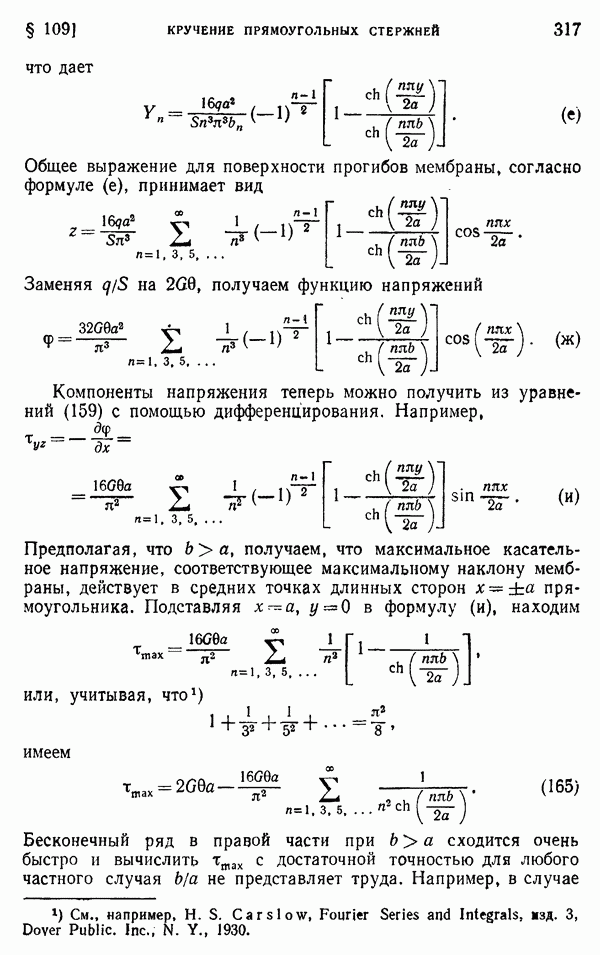
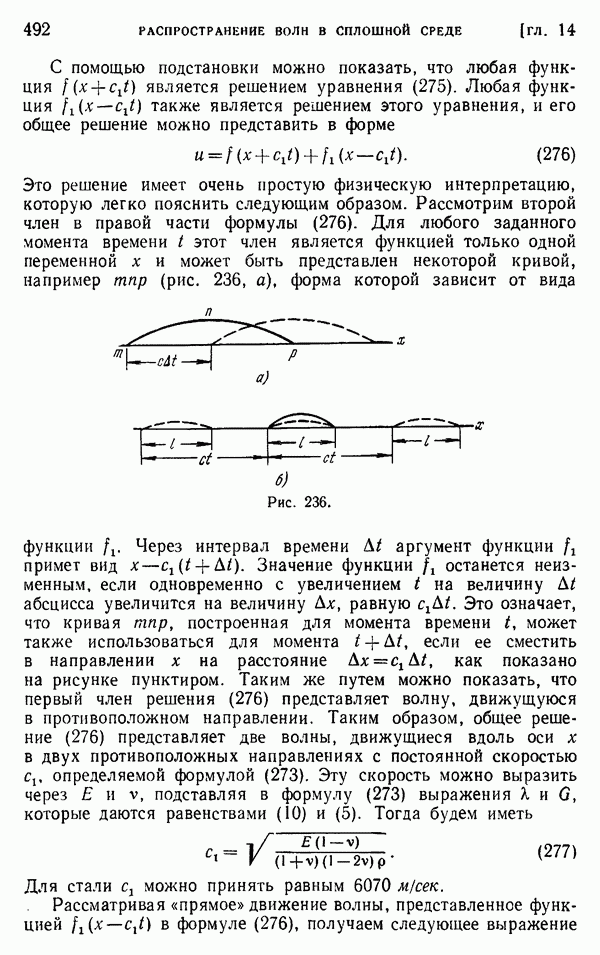
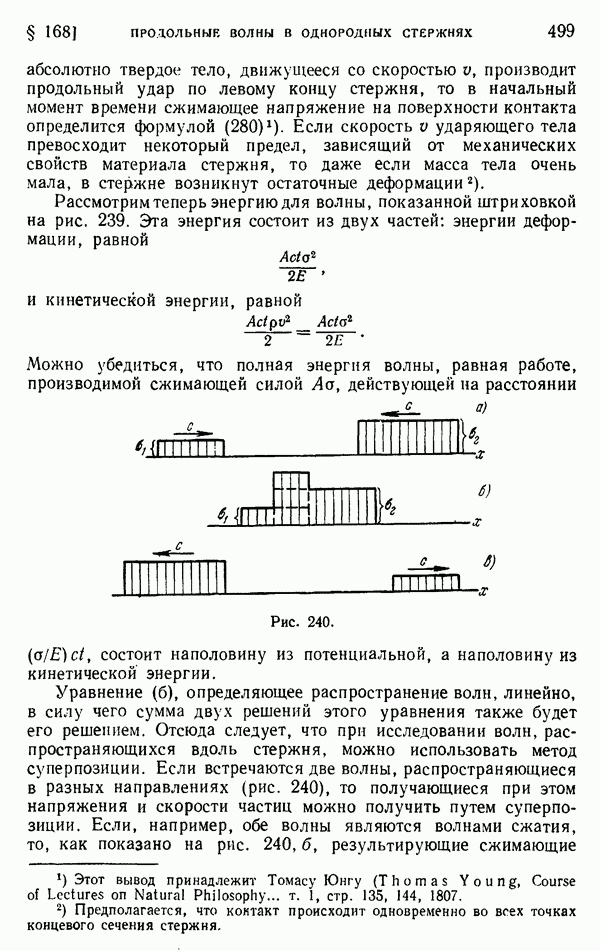
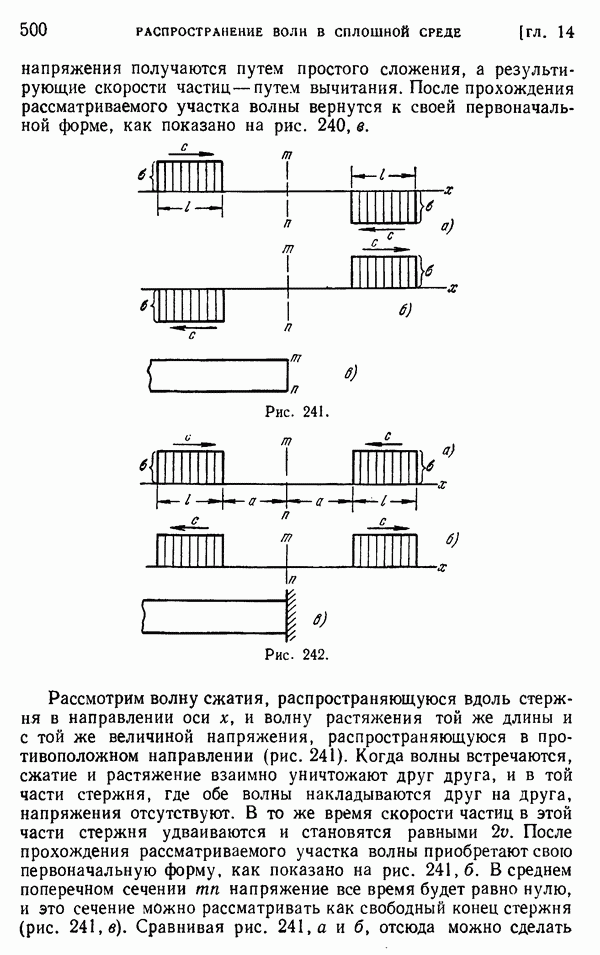
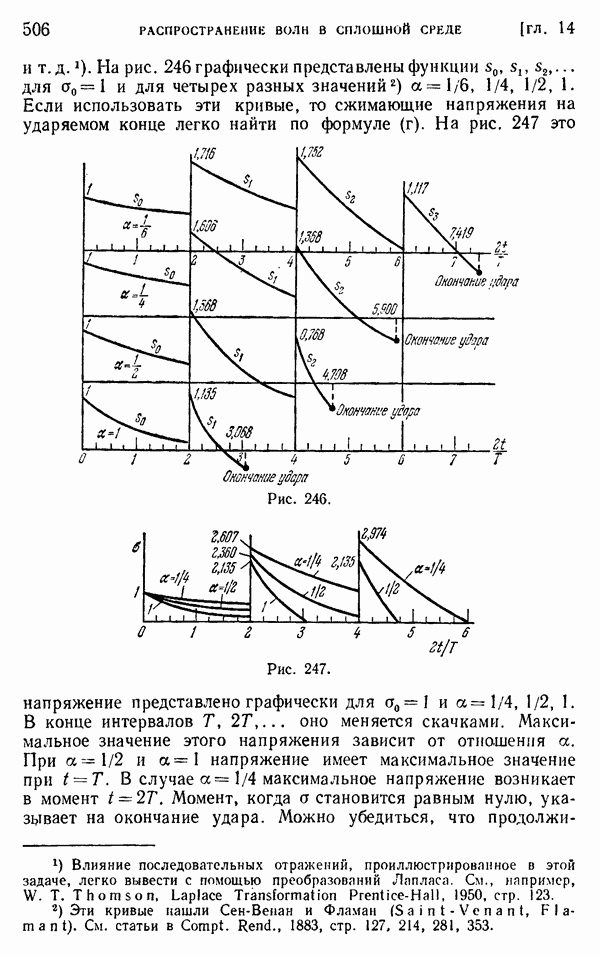
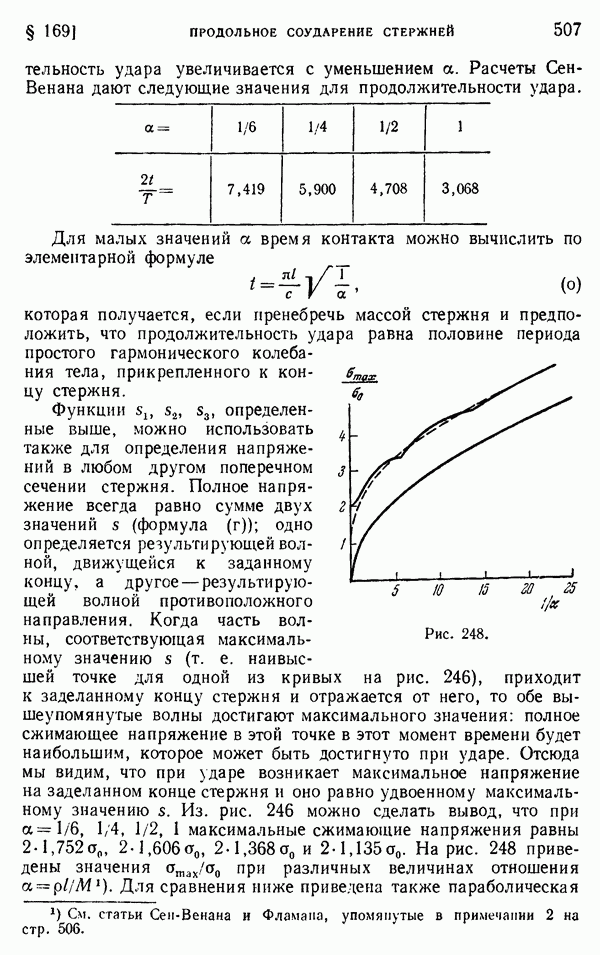
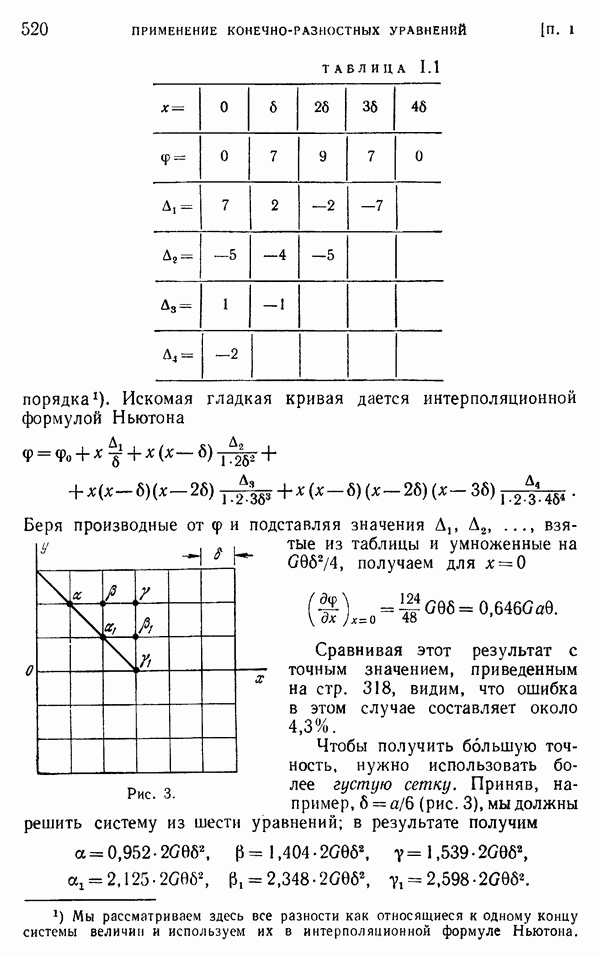
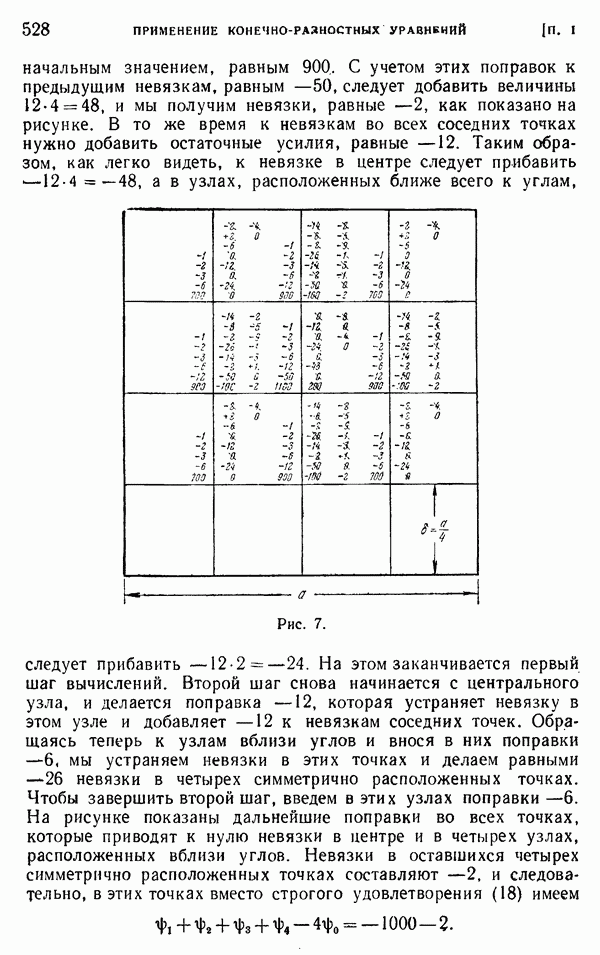
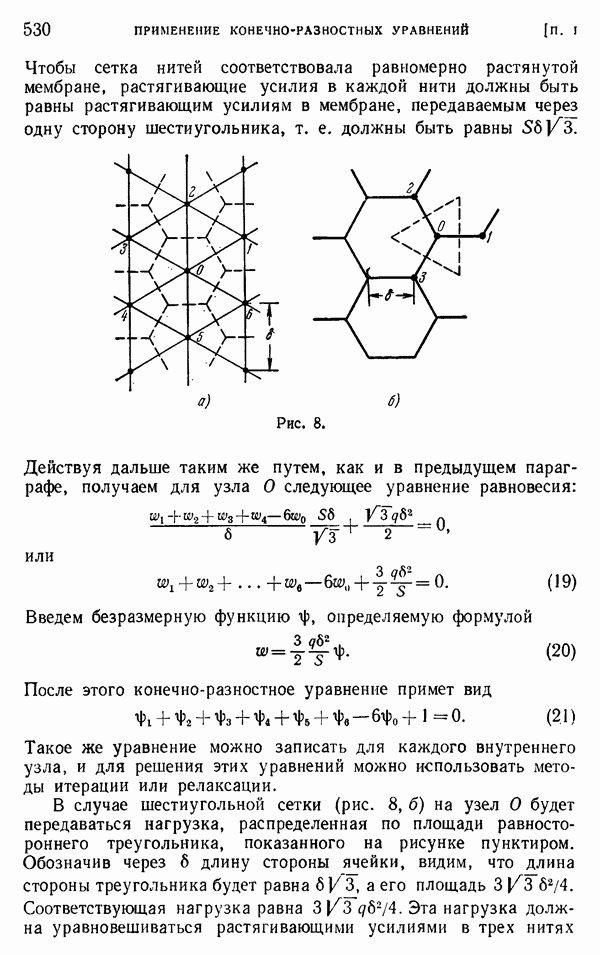
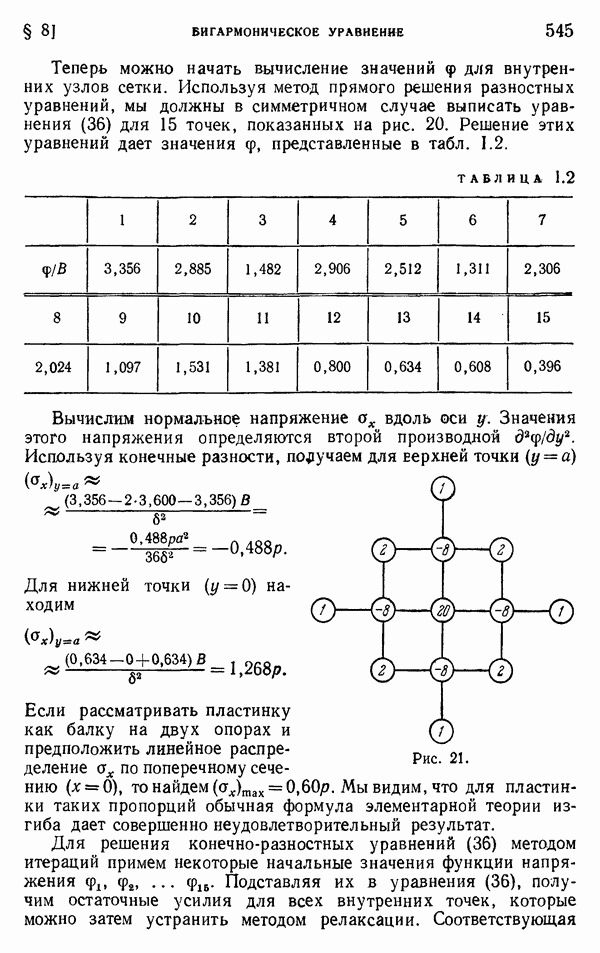
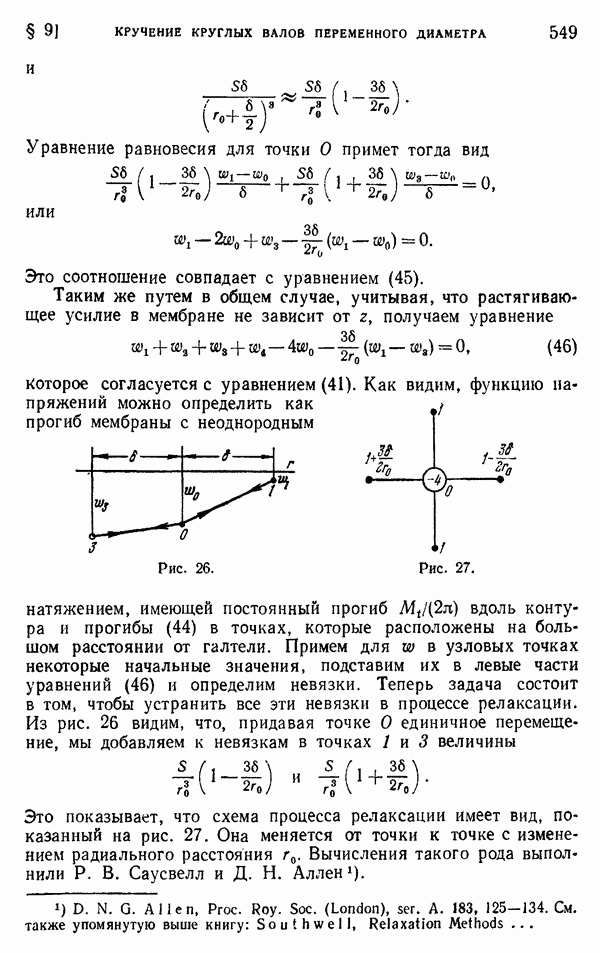
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 115. Кручение полых валов
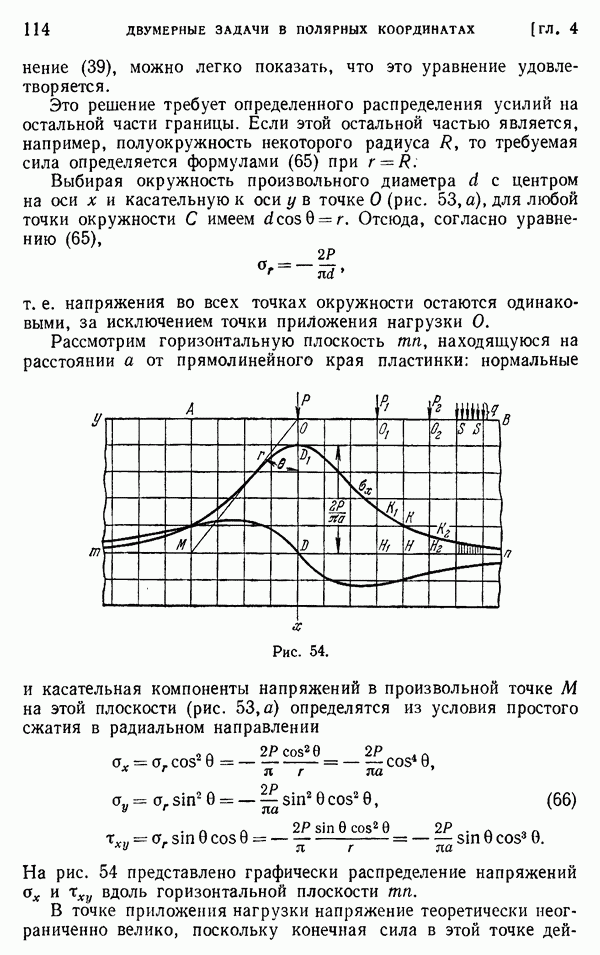
До сих пор наши рассуждения относились к валам, поперечные сечения которых ограничивались одной кривой. Рассмотрим теперь полые валы, границы поперечных сечений которых состоят из двух (и более) контуров. Простейшая задача такого рода касается круглого вала, внутренняя граница которого совпадает с одной из траекторий напряжений (см. стр. 310) сплошного вала, имеющего ту же внешнюю границу, что и полый вал.
Рассмотрим, например, эллиптическое поперечное сечение (рис. 153). Функция наряжений для сплошного вала имеет вид

Кривая

является эллипсом, который геометрически подобен внешней границе поперечного сечения. Вдоль этого эллипса функция напряжений  остается постоянной; следовательно, при
остается постоянной; следовательно, при  меньших единицы, этот эллипс является траекторией напряжений для сплошного эллиптического вала. Представим теперь эллиптическую поверхность, порождаемую этой траекторией напряжений, с. осью, параллельной оси вала. Тогда из сделанного выше вывода относительно направления касательных напряжений следует, что в направлении, нормальном к этой цилиндрической поверхности, напряжения действовать не будут. Мы можем поэтому считать, что часть материала, ограниченная этой цилиндрической поверхностью, удалена без изменения распределения напряжений во внешней части вала. Следовательно, функция напряжений в форме (а) применима и к полому валу.
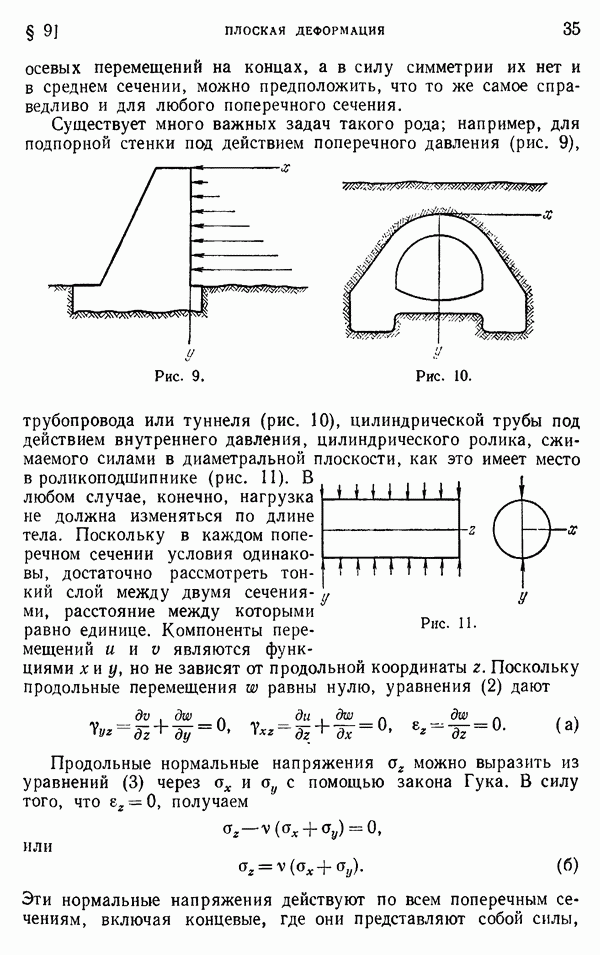
меньших единицы, этот эллипс является траекторией напряжений для сплошного эллиптического вала. Представим теперь эллиптическую поверхность, порождаемую этой траекторией напряжений, с. осью, параллельной оси вала. Тогда из сделанного выше вывода относительно направления касательных напряжений следует, что в направлении, нормальном к этой цилиндрической поверхности, напряжения действовать не будут. Мы можем поэтому считать, что часть материала, ограниченная этой цилиндрической поверхностью, удалена без изменения распределения напряжений во внешней части вала. Следовательно, функция напряжений в форме (а) применима и к полому валу.
Для заданного угла закручивания 0 напряжения в полом валу будут такими же, как и в сплошном валу. Однако крутящий момент будет меньше на величину, которая в случае сплошного вала приходится на часть поперечного сечения, которую заняло отверстие. Из уравнения (156) мы видим, что эта часть
находится в отношении  к полному крутящему моменту. Следовательно, для полого вала вместо выражения (156) будем иметь
к полному крутящему моменту. Следовательно, для полого вала вместо выражения (156) будем иметь

и для функции напряжений (а) получаем

Формула для максимального касательного напряжения принимает вид

Согласно мембранной аналогии средняя часть мембраны, соответствующая отверстию в валу (рис. 171), должна быть заменена горизонтальной пластинкой 
Отметим, что равномерное давление, расп ределенное по части  мембраны, статически эквивалентно давлению той же величины, равномерно распределенному по пластинке
мембраны, статически эквивалентно давлению той же величины, равномерно распределенному по пластинке  а растягивающие усилия в мембране, действующие вдоль границы этой пластинки, находятся в равновесии с равномерной нагрузкой на пластинке. Следовательно, в рассматриваемом случае может использоваться тот же экспериментальный метод с мыльной пленкой, что и раньше, так как замена части мембраны
а растягивающие усилия в мембране, действующие вдоль границы этой пластинки, находятся в равновесии с равномерной нагрузкой на пластинке. Следовательно, в рассматриваемом случае может использоваться тот же экспериментальный метод с мыльной пленкой, что и раньше, так как замена части мембраны  пластинкой
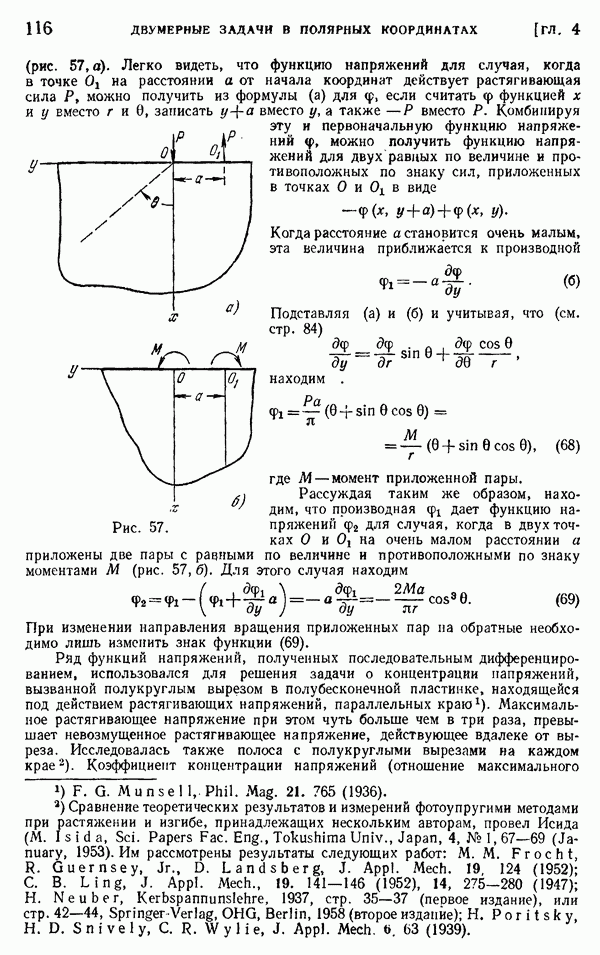
пластинкой  не вызывает изменений в конфигурации и в условиях равновесия остальной части мембраны. Рассмотрим теперь более сложный случай, когда границы отверстия уже не являются траекториями напряжений для сплошного вала. Из общей теории кручения мы знаем (см. § 104), что вдоль каждой границы функция напряжений должна быть постоянной, однако эти постоянные не могут выбираться произвольно. При рассмотрении многосвязных границ в двумерных задачах было показано, что в подобных случаях необходимо обращаться к выражениям для перемещений, и постоянные интегрирования следует подбирать таким образом, чтобы эти выражения становились однозначными. Аналогичная процедура необходима и по отношению к задачам о кручении полых валов. Постоянные значения функции напряжений вдоль границ следует определять таким образом, чтобы перемещения были однозначными. Тогда будет получено достаточное число уравнений для определения
не вызывает изменений в конфигурации и в условиях равновесия остальной части мембраны. Рассмотрим теперь более сложный случай, когда границы отверстия уже не являются траекториями напряжений для сплошного вала. Из общей теории кручения мы знаем (см. § 104), что вдоль каждой границы функция напряжений должна быть постоянной, однако эти постоянные не могут выбираться произвольно. При рассмотрении многосвязных границ в двумерных задачах было показано, что в подобных случаях необходимо обращаться к выражениям для перемещений, и постоянные интегрирования следует подбирать таким образом, чтобы эти выражения становились однозначными. Аналогичная процедура необходима и по отношению к задачам о кручении полых валов. Постоянные значения функции напряжений вдоль границ следует определять таким образом, чтобы перемещения были однозначными. Тогда будет получено достаточное число уравнений для определения

Рис. 171.
этих постоянных. Из соотношений (б) и (г) § 104 имеем

Теперь вычислим интеграл

вдоль каждой границы. Используя формулы (в) и разлагая полное напряжение на компоненты, находим

Первый интеграл должен обращаться в нуль из условия, что интегрирование производится по замкнутой кривой и что  является однозначной функцией. Отсюда
является однозначной функцией. Отсюда

Интеграл в правой части равен удвоенной площади А области, заключенной внутри контура. Следовательно,

Таким образом, мы должны определить постоянные значения функции напряжений вдоль границ отверстий так, чтобы для каждой границы удовлетворялось уравнение (175).
Для любой замкнутой кривой, проведенной внутри поперечного сечения и целиком лежащей внутри материала, первый и второй интегралы (174) представляют собой линейный интеграл от тангенциальной компоненты касательного напряжения  взятого вдоль кривой, и по аналогии с циркуляцией в гидродинамике, его можно назвать циркуляцией касательных напряжений. Тогда соотношение (175) сохраняет силу и его можно назвать теоремой о циркуляции касательных напряжений.
взятого вдоль кривой, и по аналогии с циркуляцией в гидродинамике, его можно назвать циркуляцией касательных напряжений. Тогда соотношение (175) сохраняет силу и его можно назвать теоремой о циркуляции касательных напряжений.
Значение формулы (175) для мембранной аналогии рассматривалось на стр. 312. Оно показывает, что в мембране уровень каждой пластинки, такой, как пластинка  (рис. 171), должен выбираться так, чтобы вертикальная нагрузка на пластинку была равна по величине и противоположна по знаку вертикальной компоненте результирующей растягивающих усилий, с которыми мембрана действует на пластинку. Если границы отверстия совпадают с траекториями напряжений для соответствующего сплошного вала, вышеприведенного условия достаточно, чтобы обеспечить равновесие пластинок. В общем случае этого условия недостаточно, и для удержания пластинки в равновесии в
(рис. 171), должен выбираться так, чтобы вертикальная нагрузка на пластинку была равна по величине и противоположна по знаку вертикальной компоненте результирующей растягивающих усилий, с которыми мембрана действует на пластинку. Если границы отверстия совпадают с траекториями напряжений для соответствующего сплошного вала, вышеприведенного условия достаточно, чтобы обеспечить равновесие пластинок. В общем случае этого условия недостаточно, и для удержания пластинки в равновесии в
горизонтальном положении приходится прибегать к специальным направляющим приспособлениям. Это усложняет эксперименты с мыльными пленками для круглых валов.
Чтобы устранить это затруднение, можно воспользоваться следующим приемом. В пластинке проделывается отверстие, соответствующее внешней границе сечения. Каждый из внутренних контуров, отвечающих полостям вала, устанавливается на вертикальной скользящей каретке, так что высоту ее можно легко менять. Принимая эти высоты произвольно и натягивая на границах пленку, получаем поверхность, которая удовлетворяет уравнению (150) и граничным условиям (152), но уравнение (175) в общем случае не будет удовлетворено, и пленка не будет представлять распределения напряжений в полом валу. Повторяя этот эксперимент столько раз, сколько имеется контуров, и каждый раз проводя измерения на пленке, мы получаем доста точно информации, чтобы определить истинные значения уровней внутренних границ и, наконец, натягиваем пленку нужным нам образом. Это доказывается следующим образом: если  — число контуров, и
— число контуров, и  поверхности пленки, полученные при
поверхности пленки, полученные при  различных положениях кареток, то функция
различных положениях кареток, то функция

где  — численные коэффициенты, также является решением уравнения (150), когда
— численные коэффициенты, также является решением уравнения (150), когда

Теперь, учитывая, что касательное напряжение равно наклону мембраны, и подставляя выражение (д) в уравнения (175), получаем  уравнений вида
уравнений вида

из которых можно получить коэффициенты  как функции от
как функции от  .
.
Затем из (д) находится истинная функция напряжений 2). Этот метод был применен Гриффитсом и Тейлором для определения напряжений в полом круглом валу, имеющем вырез. Таким путем было показано, что максимальное напряжение можно значительно уменьшить, тем самым повысив прочность вала, если расположить полость эксцентрично.
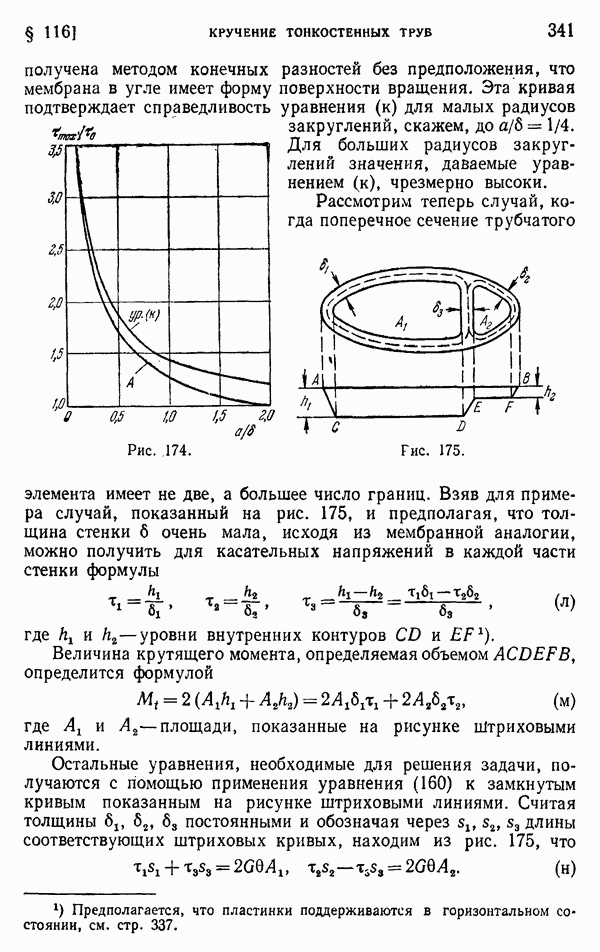
Крутящий момент для вала с одним или несколькими отверстиями можно получить, определяя удвоенный объем, заключенный между мембраной и пластинкой. Чтобы убедиться в этом, вычислим крутящий момент, вызываемый касательными напряжениями, распределенными по элементарному кольцу между двумя соседними траекториями напряжений, как показано на рис. 171, который теперь представляет произвольное полое сечение. Обозначая через  переменную ширину кольца и рассматривая заштрихованный на рисунке элемент, получаем, что касательное усилие,
переменную ширину кольца и рассматривая заштрихованный на рисунке элемент, получаем, что касательное усилие,
действующее на элемент, равно  а его момент относительно точки О есть
а его момент относительно точки О есть  Тогда момент для элементарного кольца относительно той же точки равен
Тогда момент для элементарного кольца относительно той же точки равен

где интегрирование производится по всей длине кольца. Обозначив через А площадь, ограниченную кольцом, и учитывая, что  — наклон мембраны, в силу чего
— наклон мембраны, в силу чего  представляет собой разность уровней
представляет собой разность уровней  для двух смежных контурных линий, из (е) находим
для двух смежных контурных линий, из (е) находим

т. е. крутящий момент, соответствующий элементарному кольцу, определяется заштрихованным на рисунке удвоенным объемом его. Полный момент определяется суммой этих объемов, т. е. объемом между  мембраной
мембраной  и
и  и плоской пластинкой
и плоской пластинкой  . Подобный вывод можно сделать и для случая нескольких отверстий.
. Подобный вывод можно сделать и для случая нескольких отверстий.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
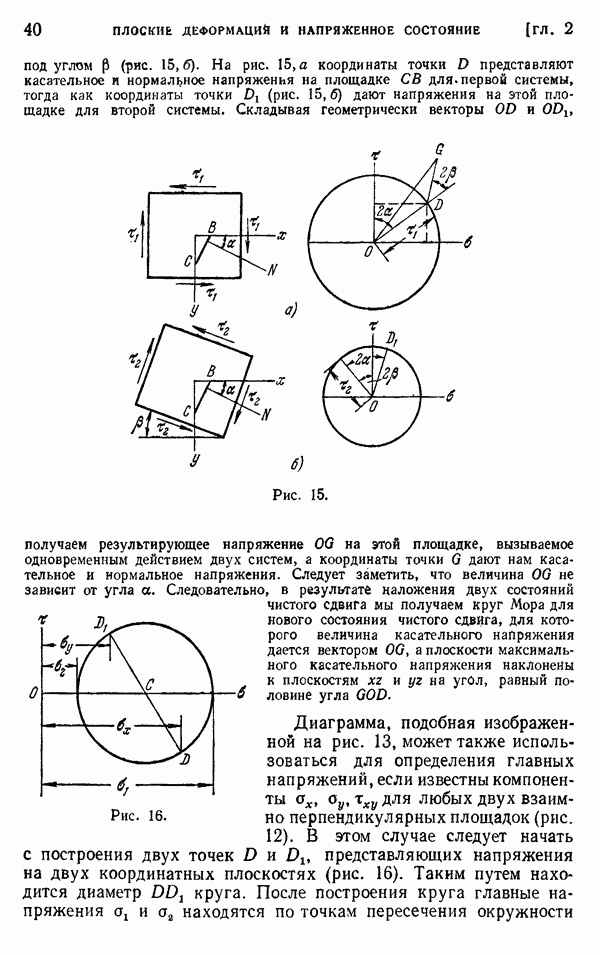
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
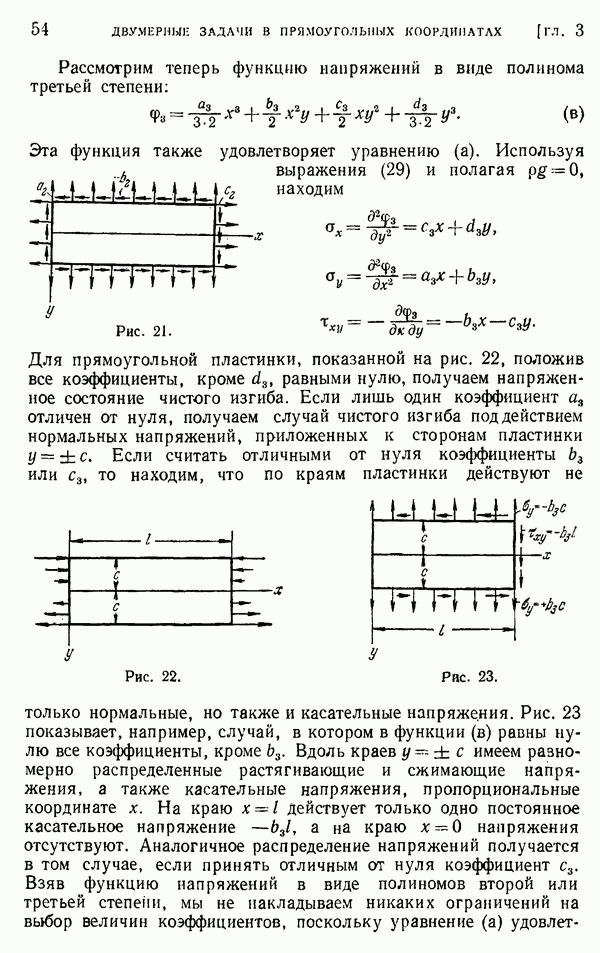
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
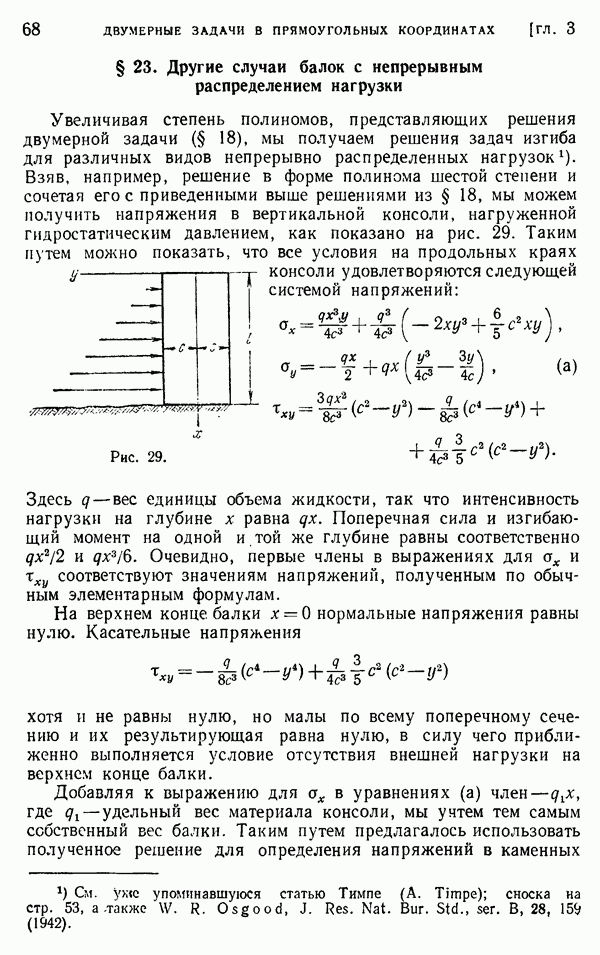
- § 23. Другие случаи балок с непрерывным распределением нагрузки
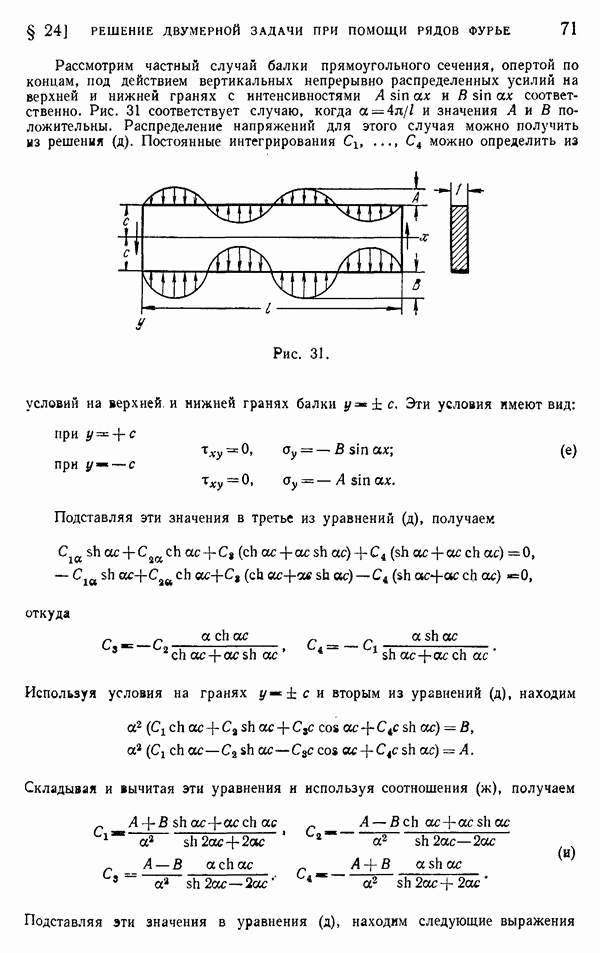
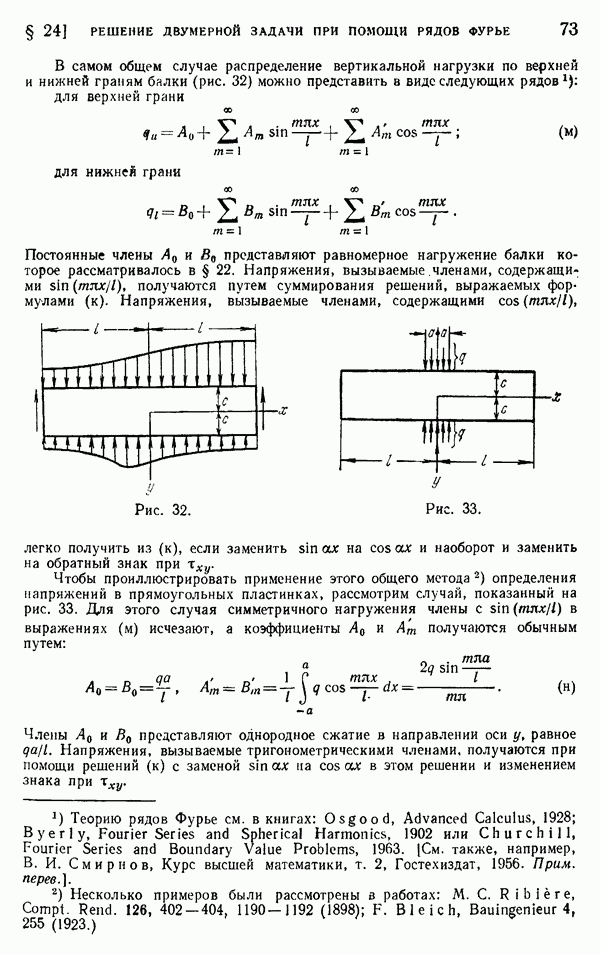
- § 24. Решение двумерной задачи при помощи рядов Фурье
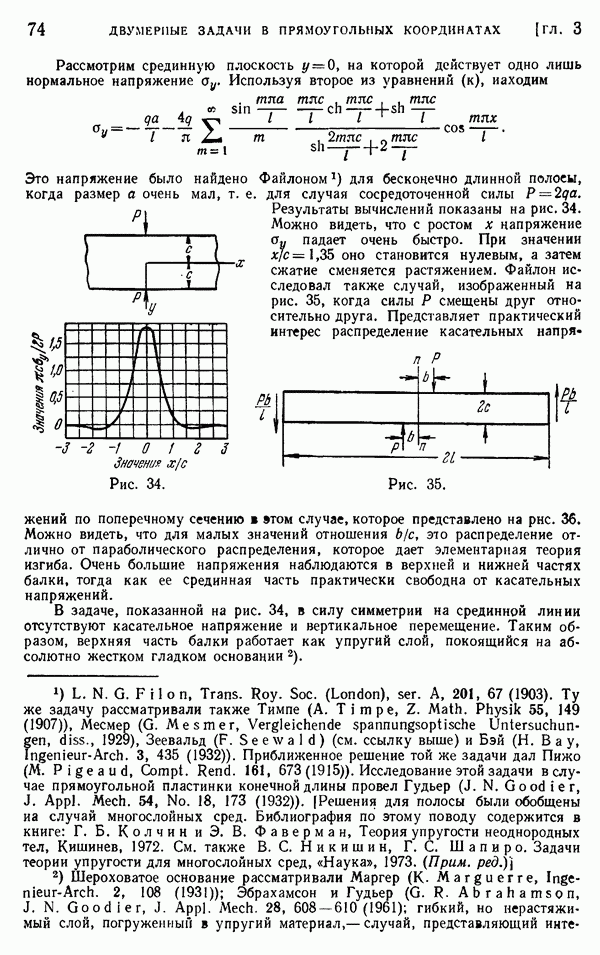
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
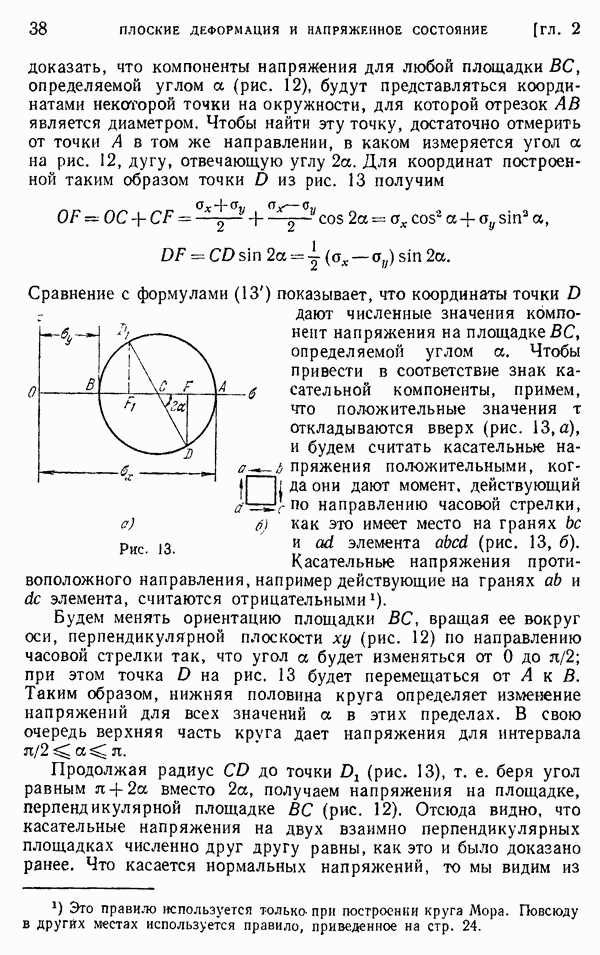
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
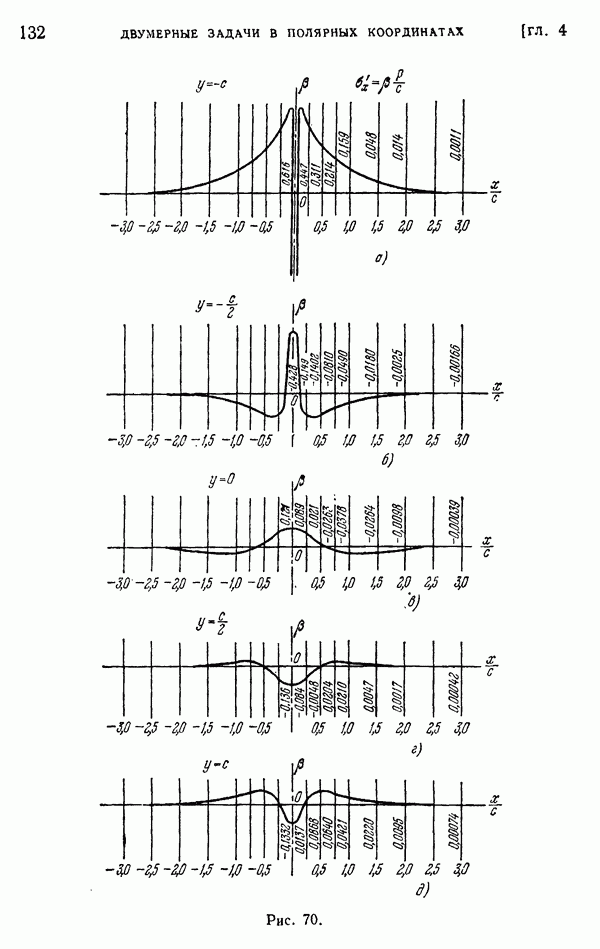
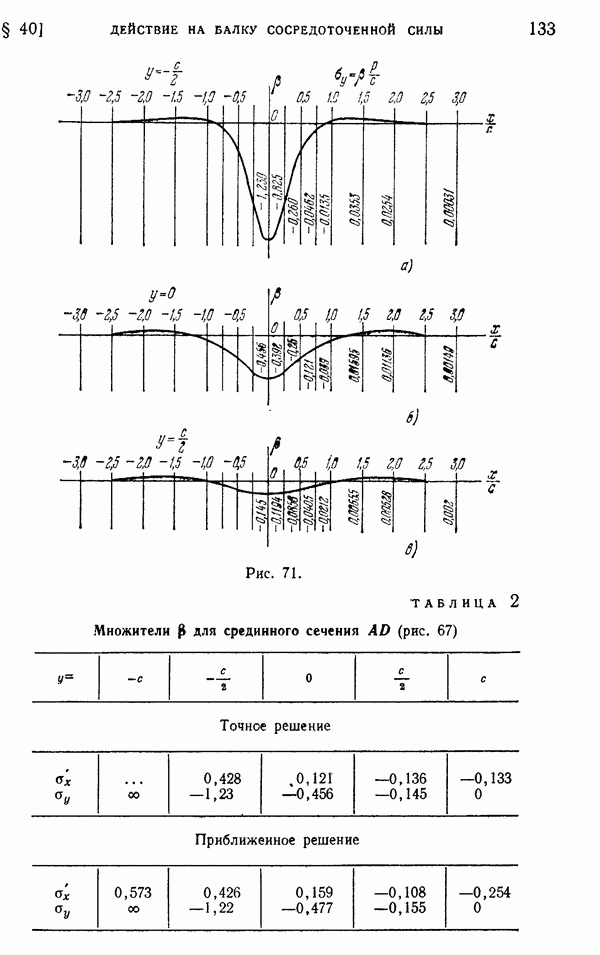
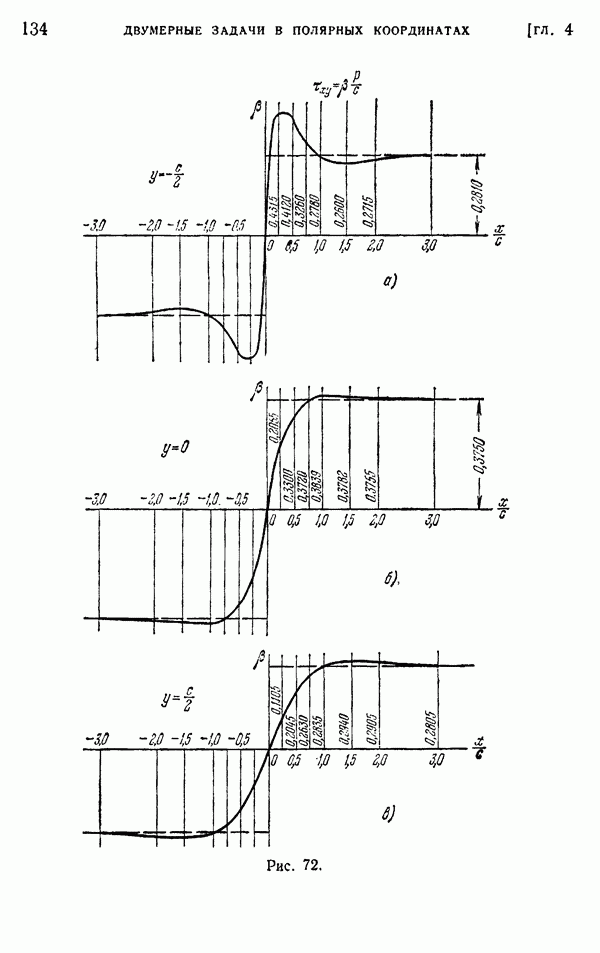
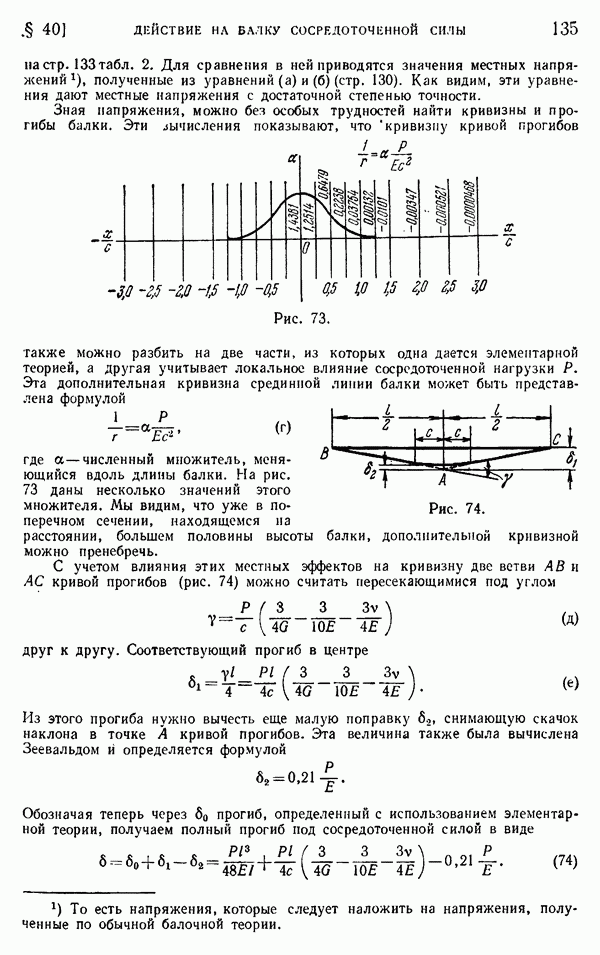
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
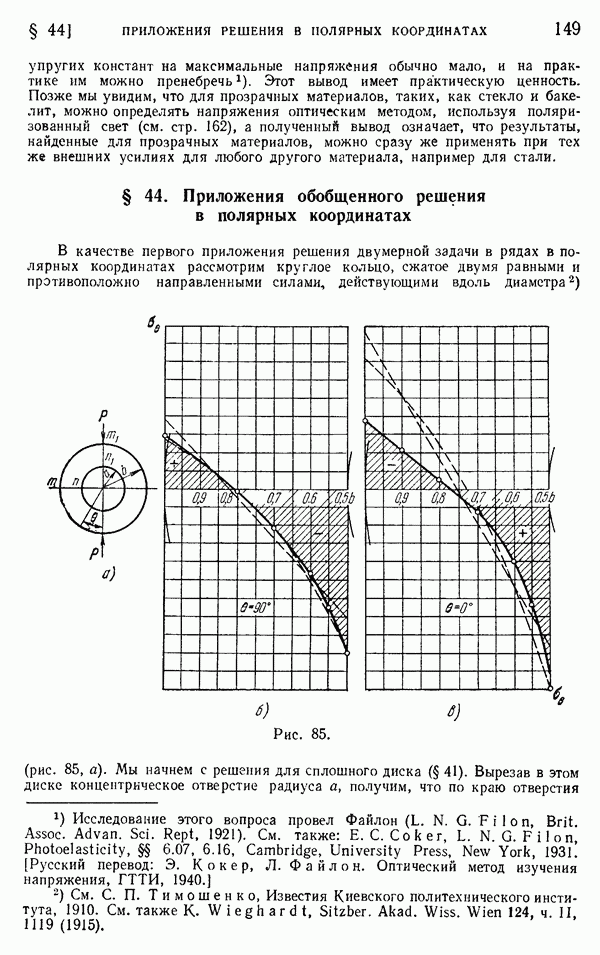
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
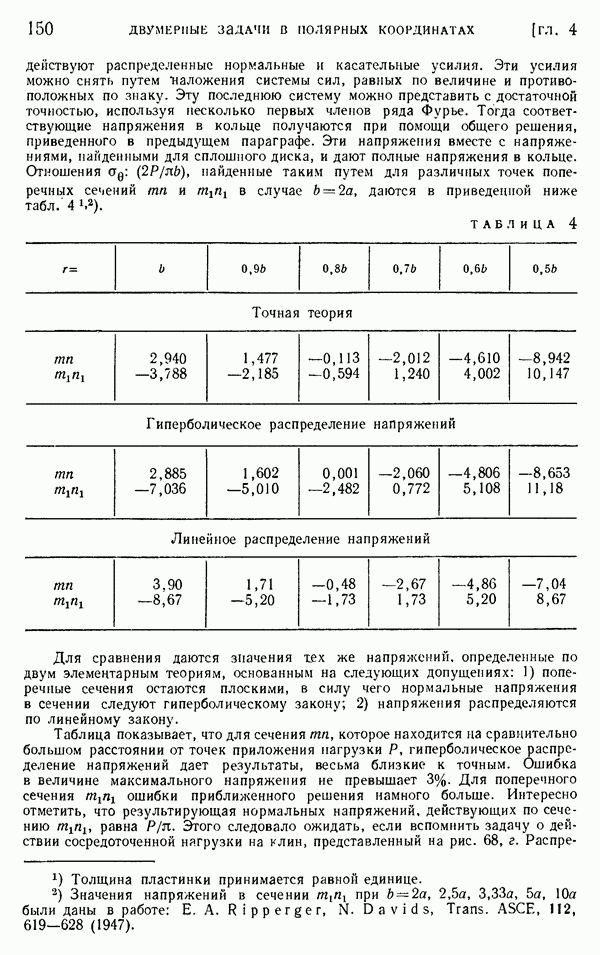
- § 83. Вращение
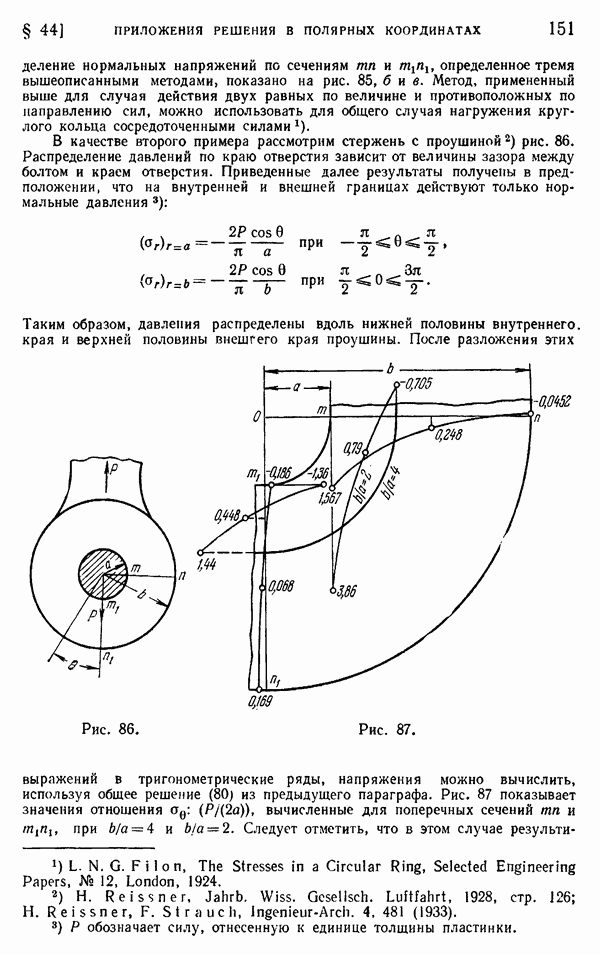
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
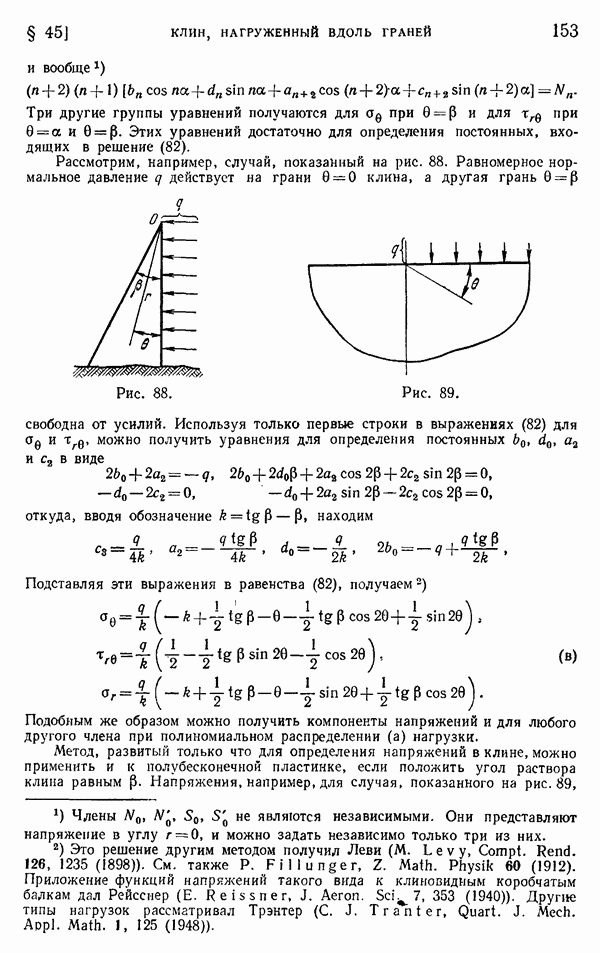
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
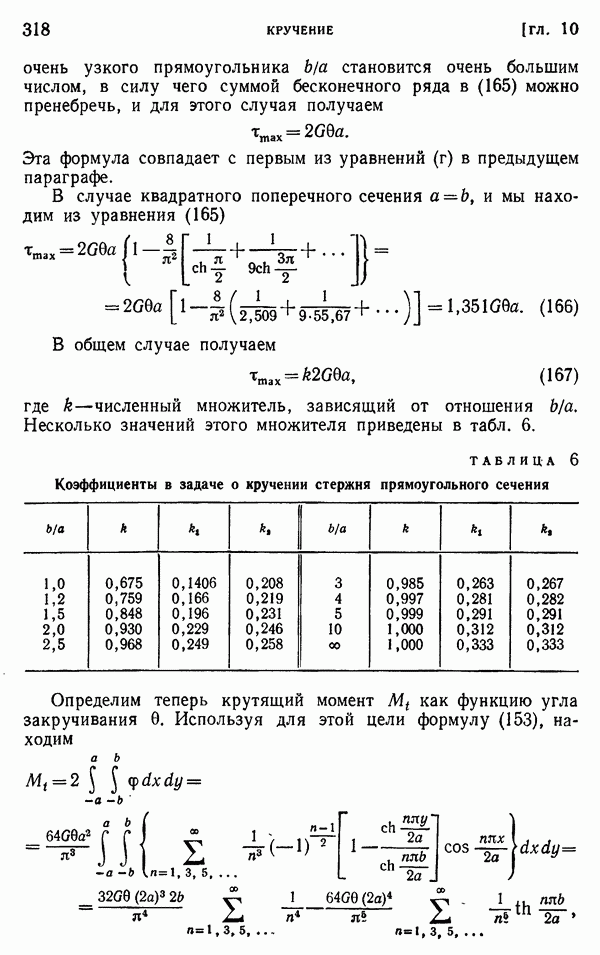
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
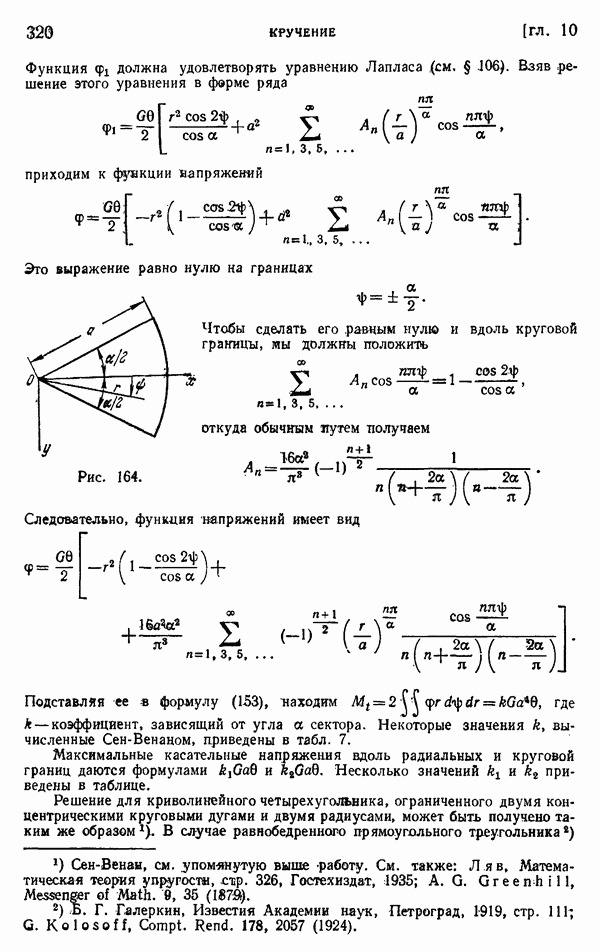
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
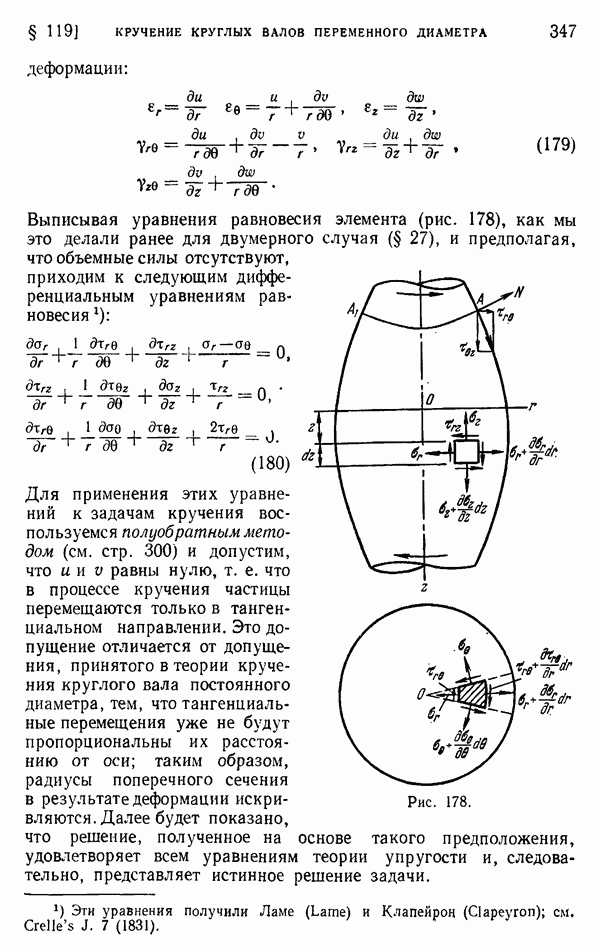
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
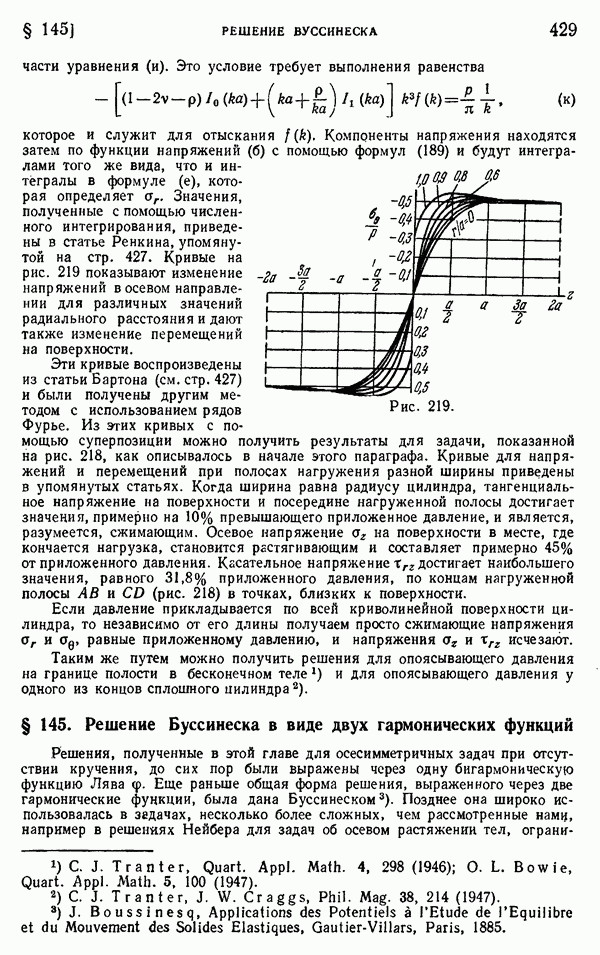
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
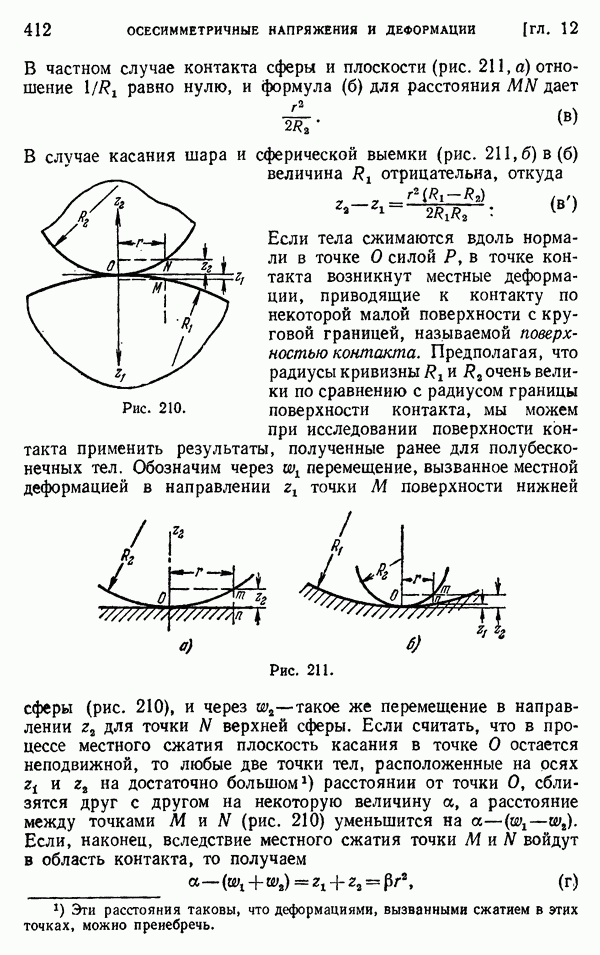
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
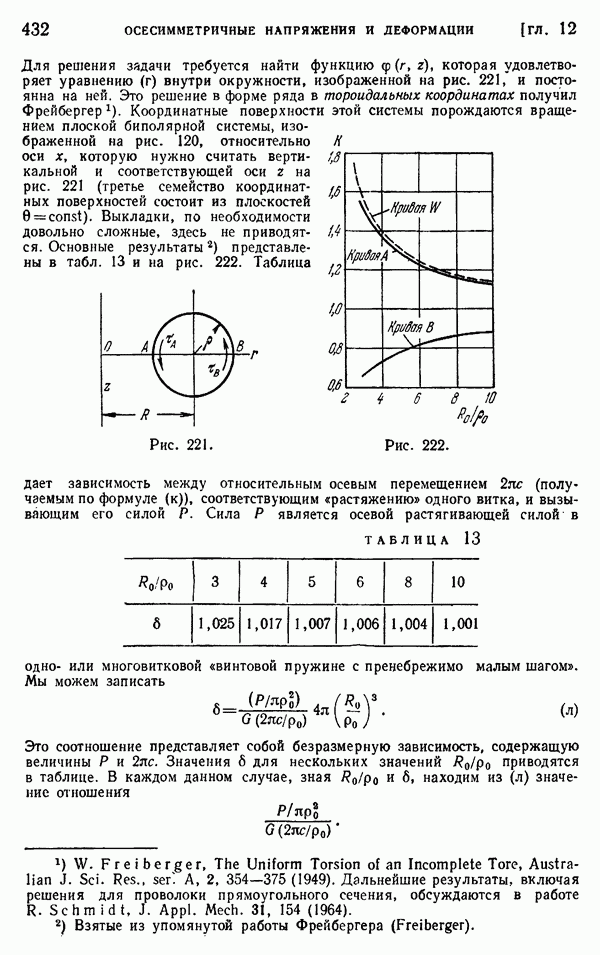
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
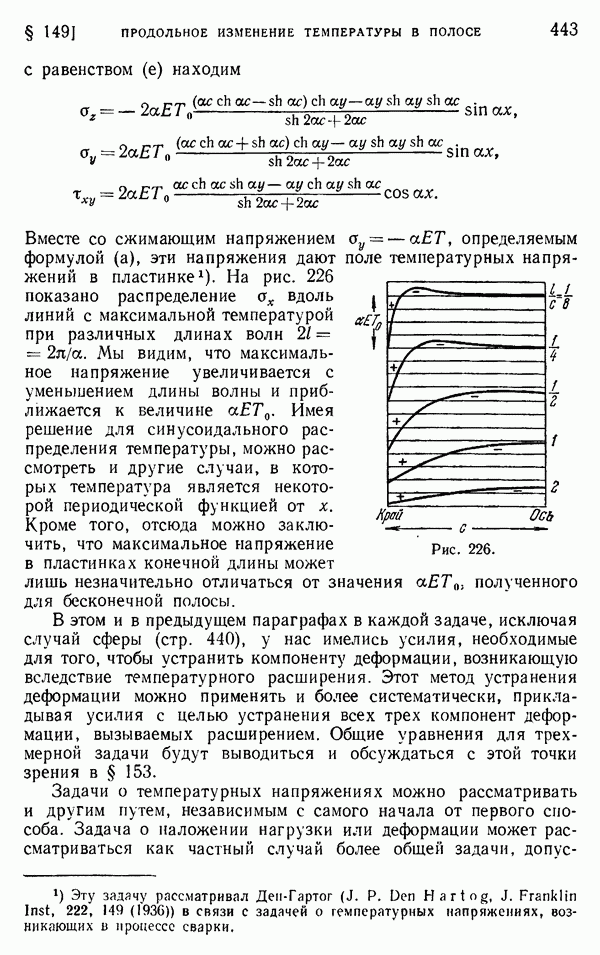
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
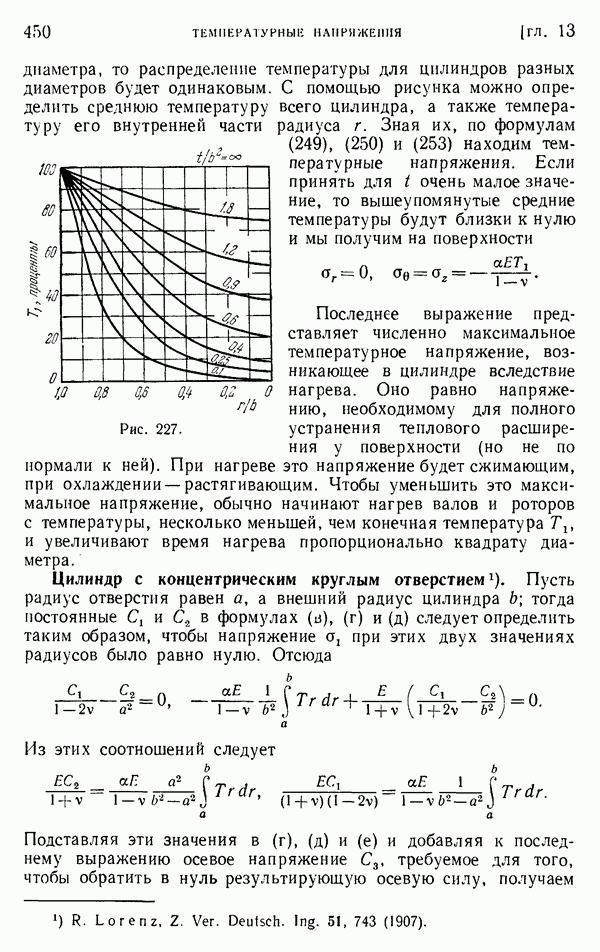
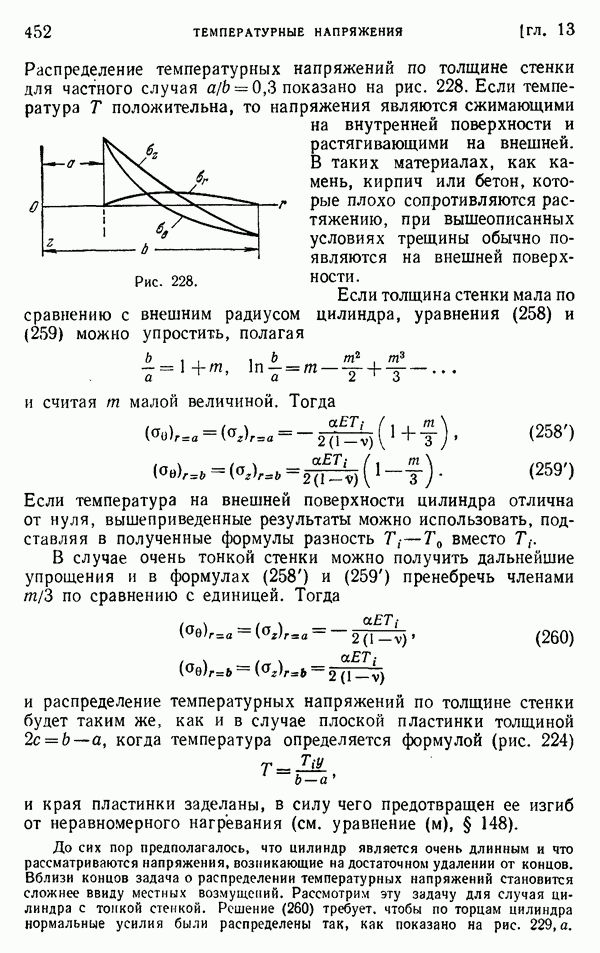
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
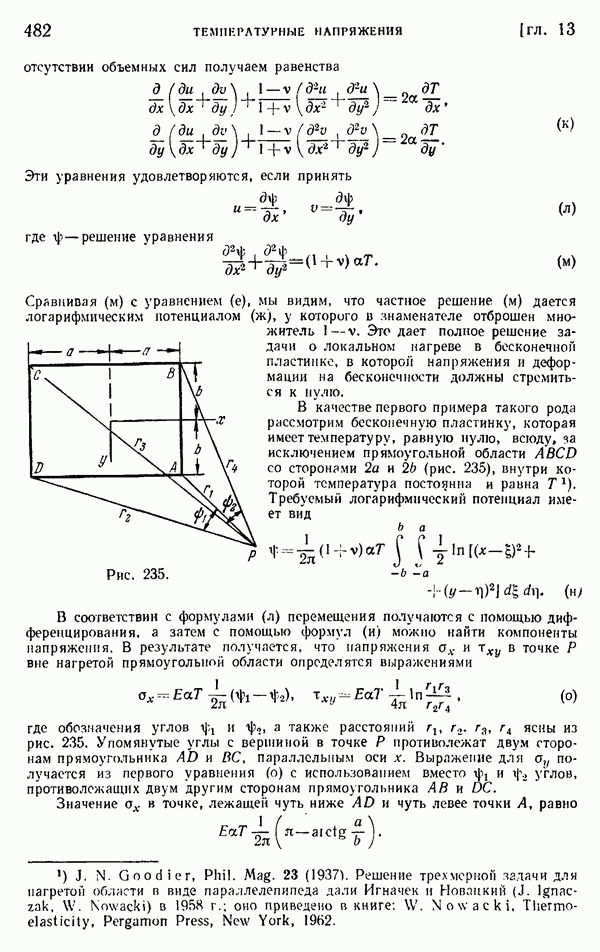
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
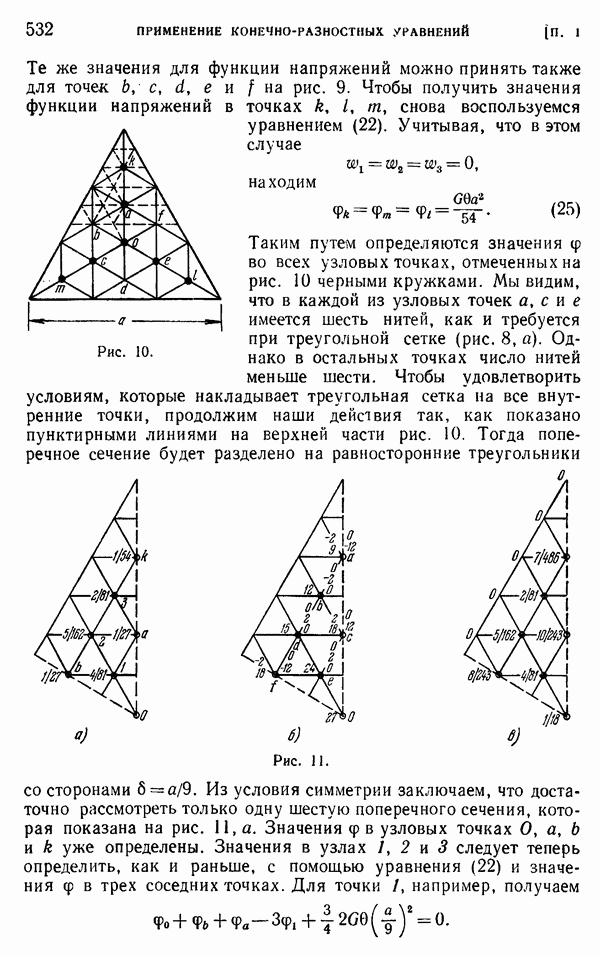
- § 4. Треугольные и шестиугольные сетки
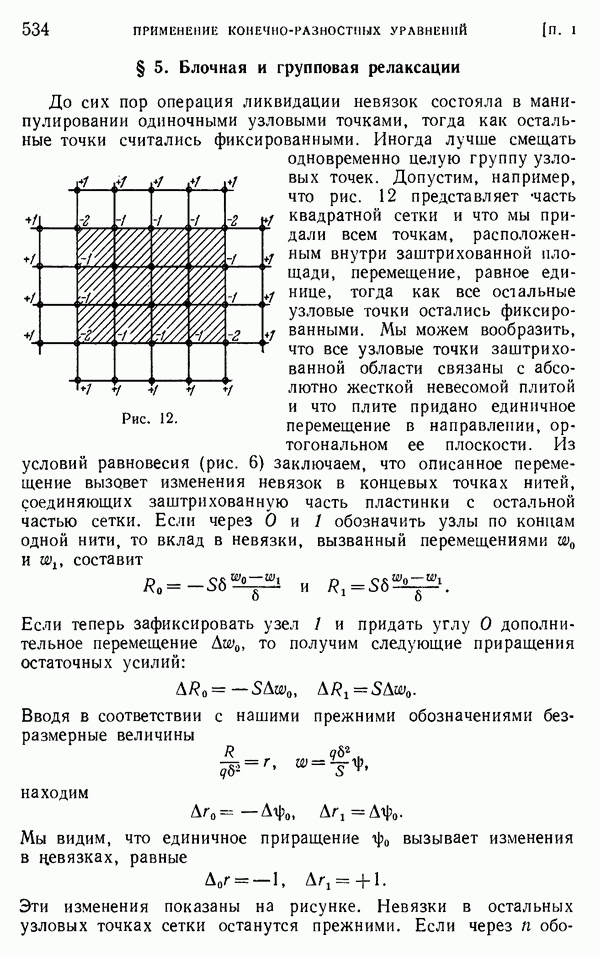
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
- § 7. Точки, расположенные вблизи границы
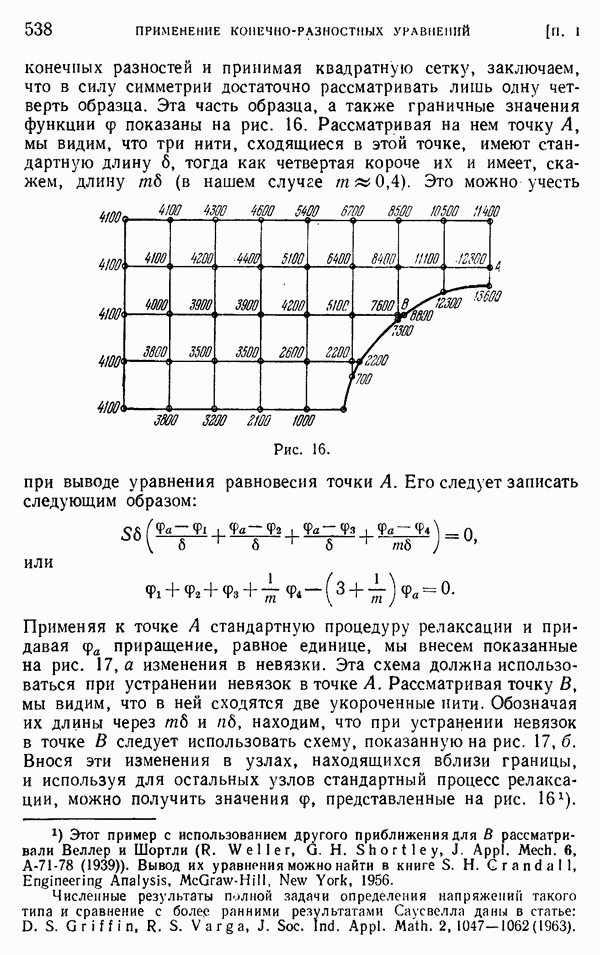
- § 8. Бигармоническое уравнение
- § 9. Кручение круглых валов переменного диаметра
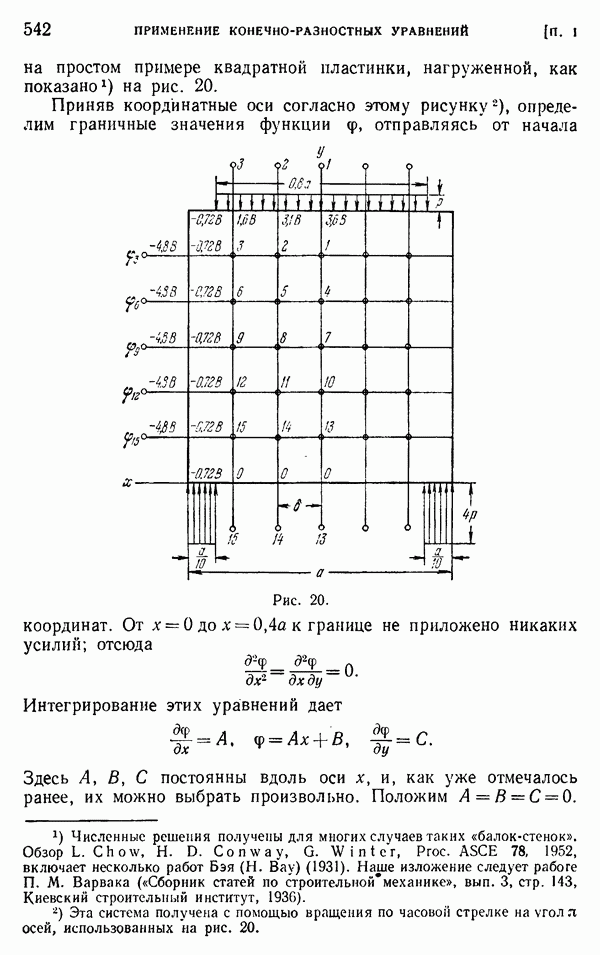
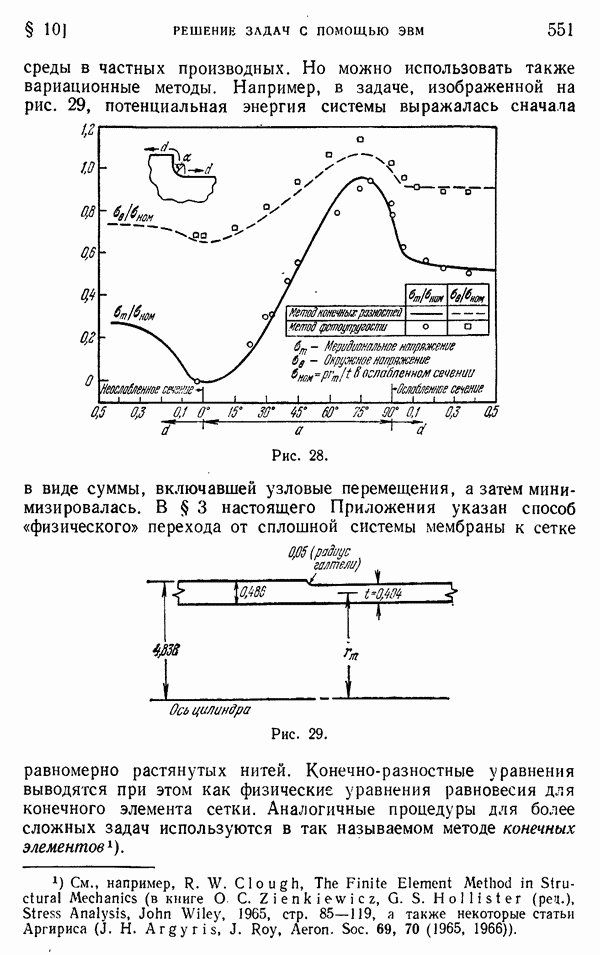
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
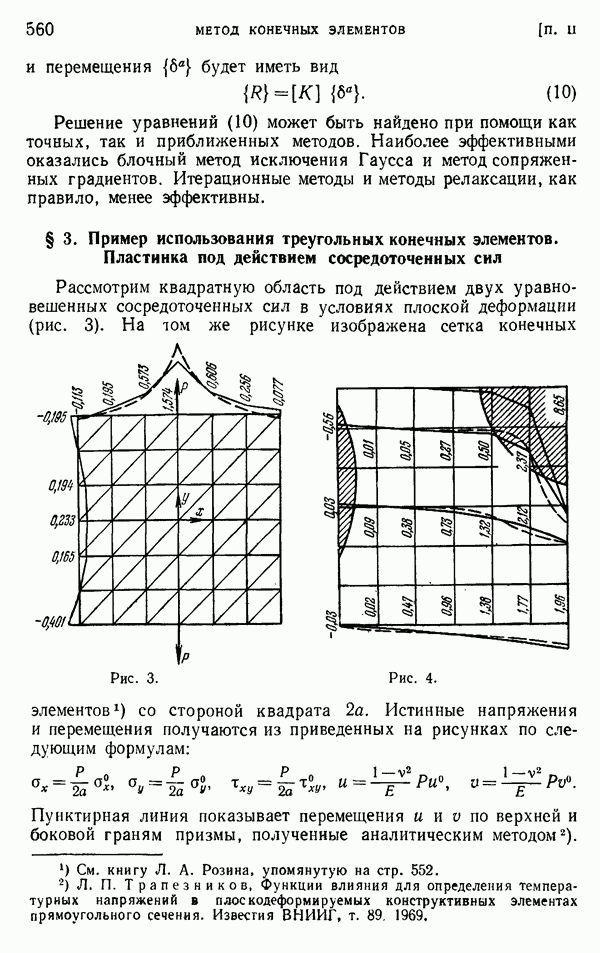
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
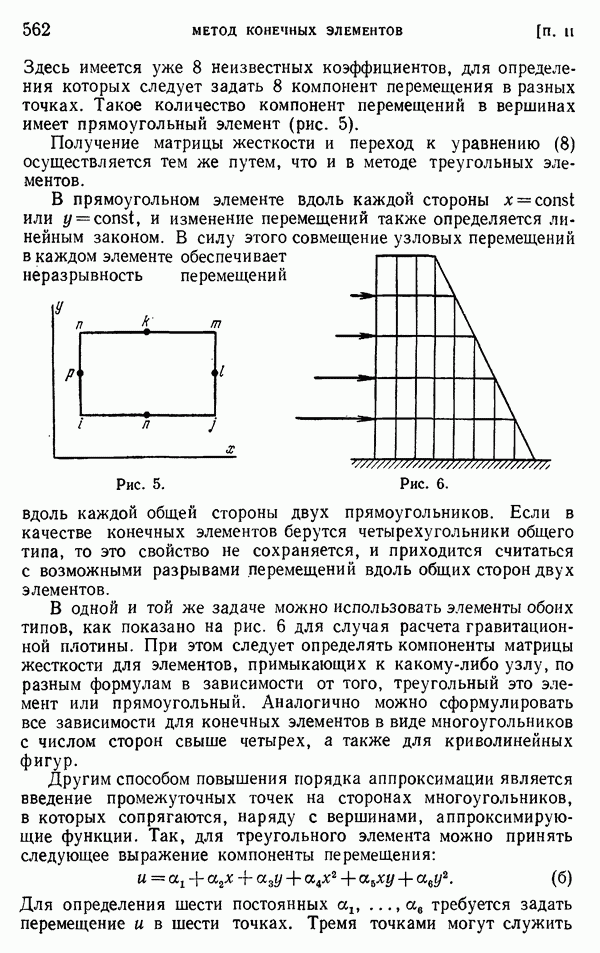
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
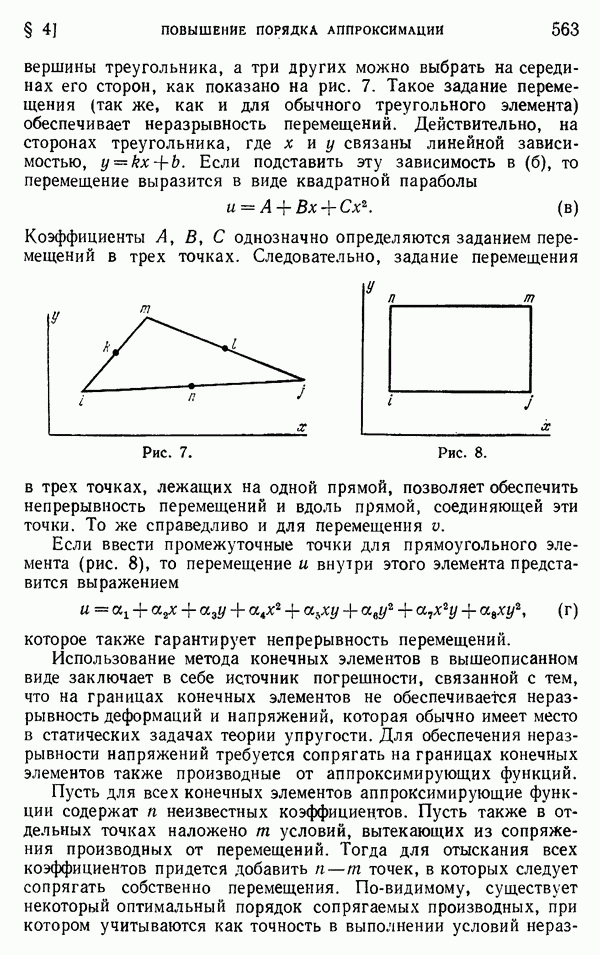
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи