| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
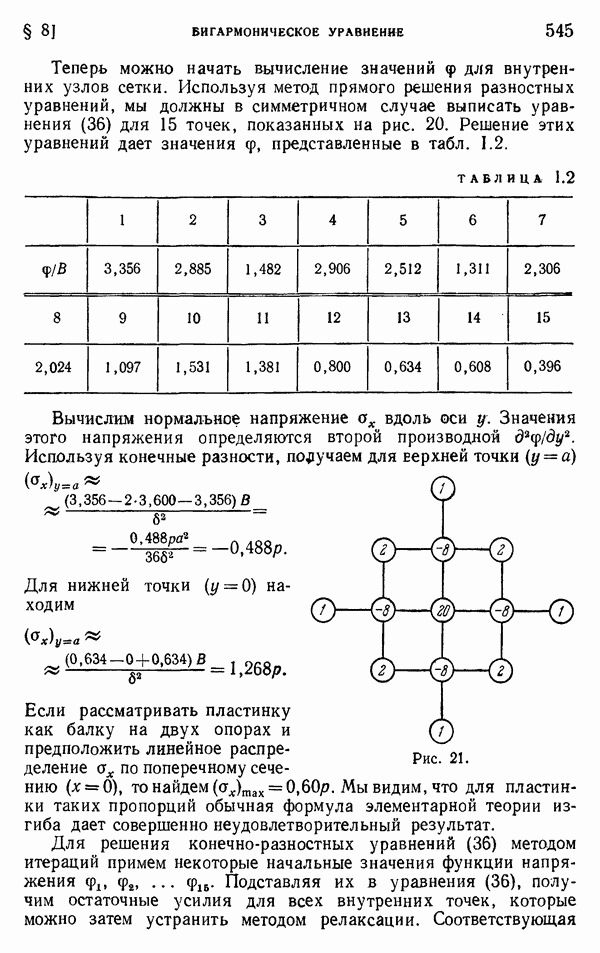
§ 169. Продольное соударение стержней
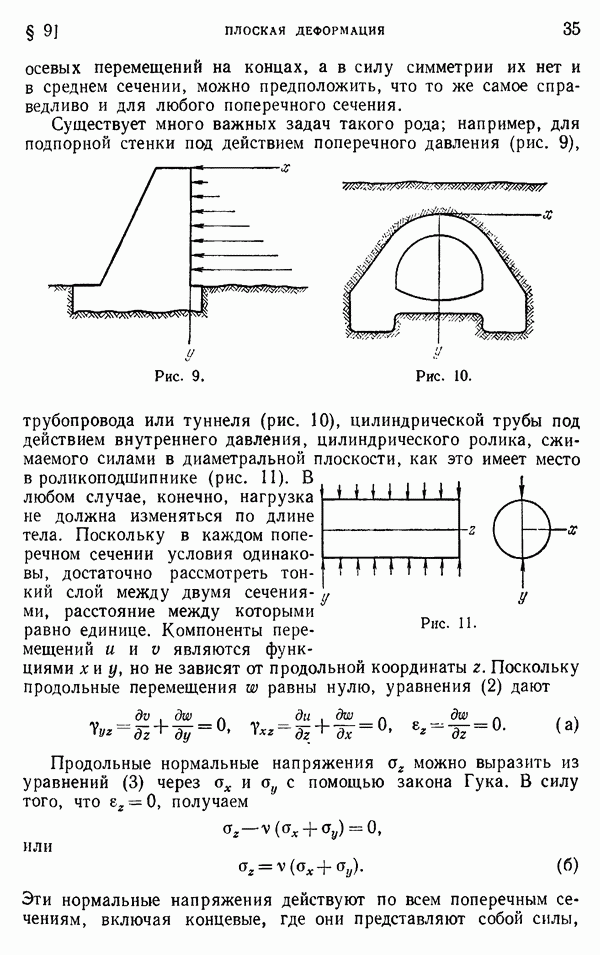
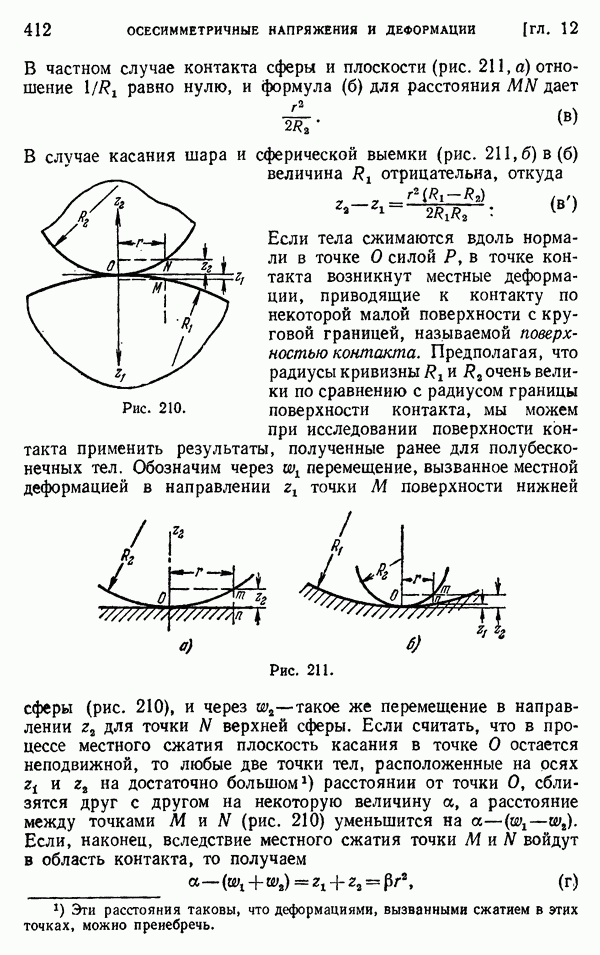
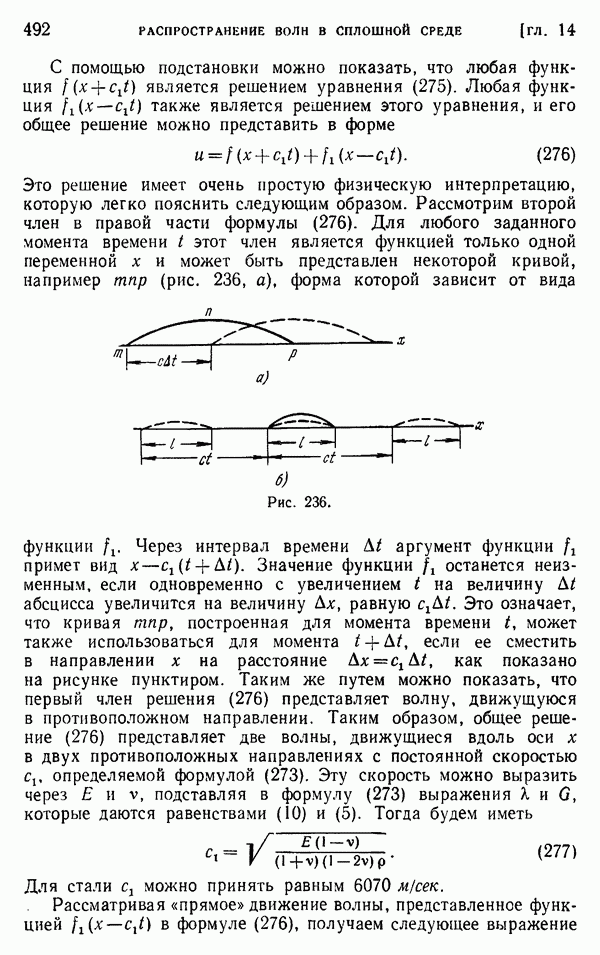
Если происходит продольное соударение двух одинаковых стержней из одного и того же материала, движущихся со скоростью  (рис. 243, а), то в процессе удара плоскость контакта
(рис. 243, а), то в процессе удара плоскость контакта  будет неподвижна, а вдоль обоих стержней со скоростью с начнут распространяться две одинаковые волны сжатия. Скорости частиц в волнах, наложенные на начальные скорости стержней, приведут зоны волн в состояние покоя, и в момент, когда эти волны достигнут свободных концов стержней
будет неподвижна, а вдоль обоих стержней со скоростью с начнут распространяться две одинаковые волны сжатия. Скорости частиц в волнах, наложенные на начальные скорости стержней, приведут зоны волн в состояние покоя, и в момент, когда эти волны достигнут свободных концов стержней  оба стержня будут подвергнуты равномерному сжатию и находиться в состоянии покоя. Затем волны сжатия отразятся от свободных концов в виде волн растяжения, которые начнут распространяться в направлении поперечного сечения контакта
оба стержня будут подвергнуты равномерному сжатию и находиться в состоянии покоя. Затем волны сжатия отразятся от свободных концов в виде волн растяжения, которые начнут распространяться в направлении поперечного сечения контакта  В этих волнах скорости частиц, равные
В этих волнах скорости частиц, равные  будут теперь направлены от сечения
будут теперь направлены от сечения  и когда волны достигнут плоскости контакта, стержни разделятся со скоростью, равной их начальной скорости
и когда волны достигнут плоскости контакта, стержни разделятся со скоростью, равной их начальной скорости  Продолжительность соударения в этом случае будет, очевидно, равна
Продолжительность соударения в этом случае будет, очевидно, равна  а сжимающее напряжение, согласно формуле (279), станет равным
а сжимающее напряжение, согласно формуле (279), станет равным 

Рис. 243.
Рассмотрим теперь более общий случай, когда стержни 1 и 2 (рис. 243, б) движутся со скоростями  причем
причем  . В момент удара в обоих стержнях начнут распространяться две одинаковые волны сжатия. Соответствующие скорости частиц
. В момент удара в обоих стержнях начнут распространяться две одинаковые волны сжатия. Соответствующие скорости частиц
относительно напряженных частей движущихся стержней будут равны и в каждом стержне направлены от поверхности контакта. Чтобы абсолютные скорости частиц обоих стержней на поверхности контакта были одинаковы, величина этих скоростей должна быть равна  Через промежуток времени, равный
Через промежуток времени, равный  волны сжатия достигнут свободных концов стержней. Оба стержня в этот момент будут находиться в состоянии однородного сжатия, абсолютные значения скоростей всех частиц стержней будут равны
волны сжатия достигнут свободных концов стержней. Оба стержня в этот момент будут находиться в состоянии однородного сжатия, абсолютные значения скоростей всех частиц стержней будут равны

Затем волны сжатия отразятся от свободных концов в виде волн растяжения и в момент  когда эти волны достигнут поверхности контакта двух стержней, скорости стержней 1 и 2 станут равными
когда эти волны достигнут поверхности контакта двух стержней, скорости стержней 1 и 2 станут равными


Рис. 244.
Таким образом, стержни в процессе удара обмениваются скоростями.
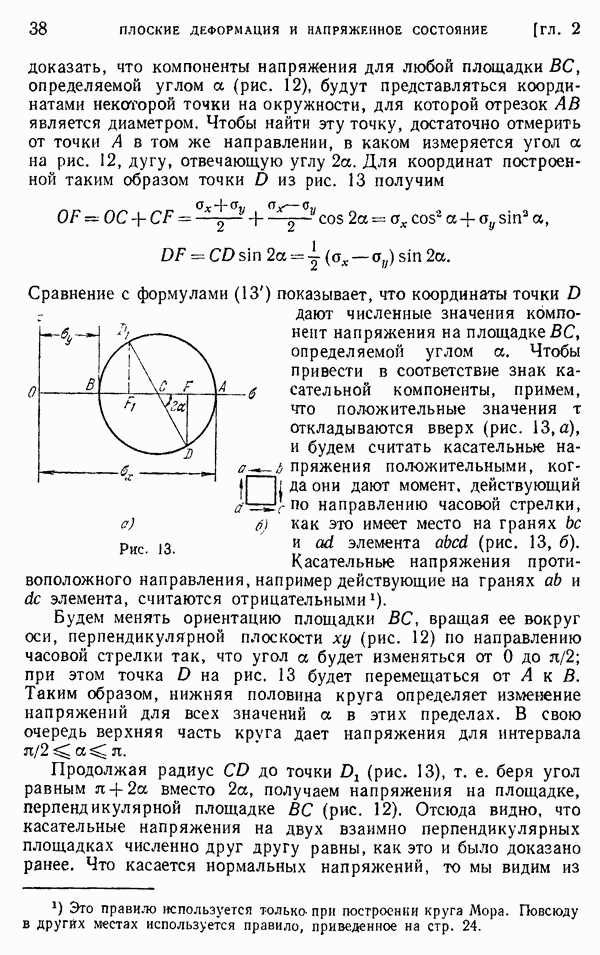
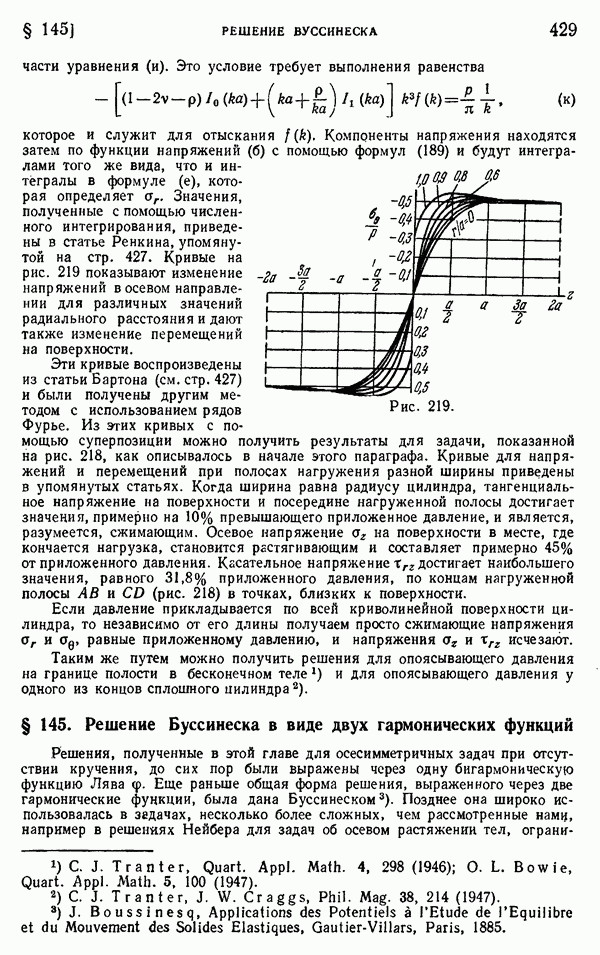
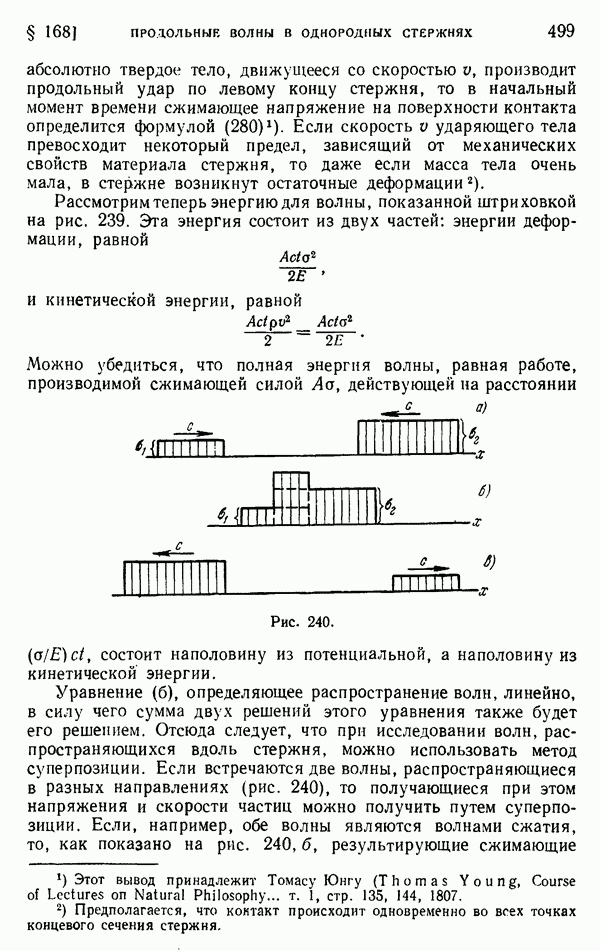
Если рассмотренные стержни имеют разные длины  (рис. 244, а), условия соударения вначале будут такими же, как и в предыдущем случае. Однако после промежутка времени
(рис. 244, а), условия соударения вначале будут такими же, как и в предыдущем случае. Однако после промежутка времени  когда отраженная волна в более коротком стержне достигнет поверхности контакта
когда отраженная волна в более коротком стержне достигнет поверхности контакта  она начнет распространяться вдоль более длинного стержня и возникнет состояние, изображенное на рис. 244, б. Волна растяжения от стержня
она начнет распространяться вдоль более длинного стержня и возникнет состояние, изображенное на рис. 244, б. Волна растяжения от стержня  уничтожит сжатие на поверхности контакта стержней, но контакт будет продолжаться, пока волна сжатия в более длинном стержне (заштрихованная на рисунке) не вернется после отражения к поверхности контакта в момент
уничтожит сжатие на поверхности контакта стержней, но контакт будет продолжаться, пока волна сжатия в более длинном стержне (заштрихованная на рисунке) не вернется после отражения к поверхности контакта в момент 
В случае двух стержней одинаковой длины каждый из них после отскока будет иметь во всех точках одну и ту же скорость и будет двигаться как абсолютно твердое тело. Их полная энергия будет энергией поступательного движения. В случае стержней разной длины более длинный стержень после отскока будет содержать движущуюся в нем волну, и при определении полной энергии стержня следует учитывать и энергию этой волны.
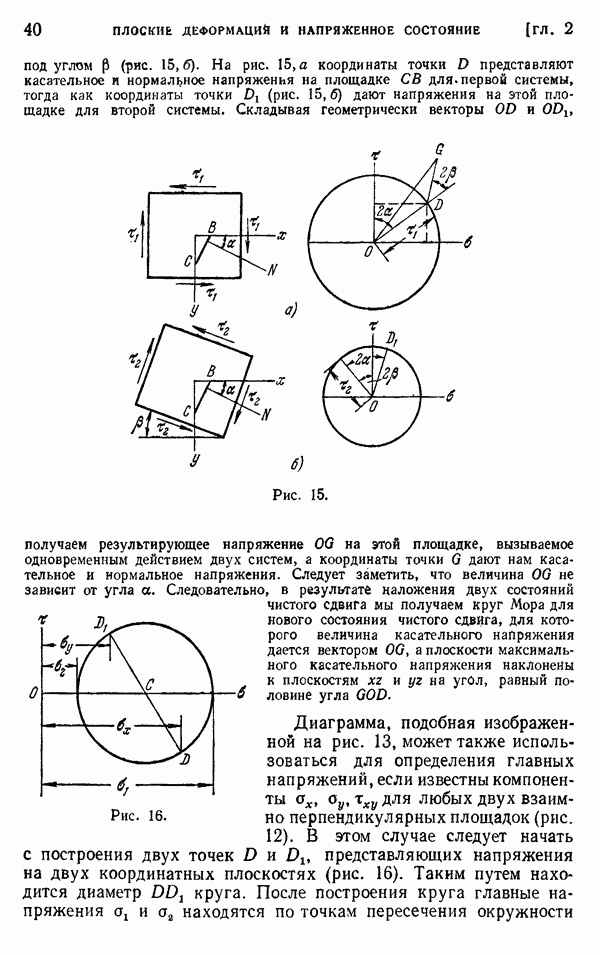
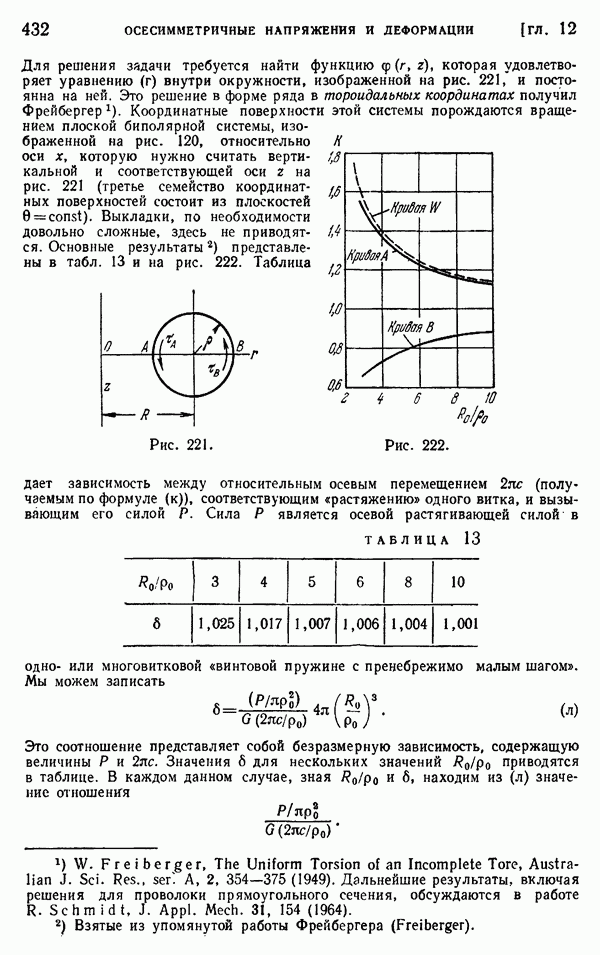
Рассмотрим теперь более сложную задачу о стержне с заделанным концом, другой конец которого испытывает удар движущейся массой (рис. 245). Обозначим через М массу движущегося тела, отнесенную к единице площади поперечного сечения стержня, а через  начальную скорость тела. Если считать тело абсолютно твердым, то скорость частиц на конце стержня в момент соударения
начальную скорость тела. Если считать тело абсолютно твердым, то скорость частиц на конце стержня в момент соударения  будет равна
будет равна  а начальное напряжение сжатия, согласно формуле (279),
а начальное напряжение сжатия, согласно формуле (279),


Рис. 245.
Вследствие сопротивления стержня скорость движущегося тела, а следовательно, и давление на стержень будут постепенно уменьшаться, и мы получаем распространяющуюся вдоль стержня волну сжатия с уменьшающимся сжимающим напряжением (рис. 245, б). Изменение сжимающего усилия во времени легко найти из уравнения движения тела. Обозначая через а переменное сжимающее напряжение на конце стержня и через у — переменную скорость тела, получаем

Подставляя вместо скорости  ее выражение согласно формуле (279), находим
ее выражение согласно формуле (279), находим

откуда

Это уравнение можно использовать, пока  При
При  волна сжатия с давлением
волна сжатия с давлением  на фронте возвратится к концу стержня, который находится в контакте с ударяющим телом. Скорость тела не может измениться скачком, поэтому эта волна отразится от места контакта как от заделанного конца.
на фронте возвратится к концу стержня, который находится в контакте с ударяющим телом. Скорость тела не может измениться скачком, поэтому эта волна отразится от места контакта как от заделанного конца.
Сжимающее напряжение на поверхности контакта увеличится скачком на величину  как показано на рис. 245, в. Такое внезапное повышение давления будет происходить в процессе удара в конце каждого интервала времени
как показано на рис. 245, в. Такое внезапное повышение давления будет происходить в процессе удара в конце каждого интервала времени  и для каждого такого интервала мы должны получить различные выражения для а. Для первого интервала
и для каждого такого интервала мы должны получить различные выражения для а. Для первого интервала  используем уравнение (в). Для второго интервала
используем уравнение (в). Для второго интервала  имеем условия, представленные на рис.
имеем условия, представленные на рис.  сжимающее напряжение а будет вызвано двумя волнами, движущимися от ударяемого конца, и одной волной, движущейся к этому концу. Обозначим через
сжимающее напряжение а будет вызвано двумя волнами, движущимися от ударяемого конца, и одной волной, движущейся к этому концу. Обозначим через  полные сжимающие напряжения, возникающие на ударяемом конце от всех волн, движущихся от этого конца, после прошествия интервалов времени
полные сжимающие напряжения, возникающие на ударяемом конце от всех волн, движущихся от этого конца, после прошествия интервалов времени  Волны, приходящие назад к ударяемому концу, — это волны, посланные в предыдущем интервале времени и отставшие на время Т за счет того, что они прошли вдоль стержня путь туда и обратно. Таким образом, сжатие, вызываемое этими волнами на ударяемом конце, получается путем подстановки
Волны, приходящие назад к ударяемому концу, — это волны, посланные в предыдущем интервале времени и отставшие на время Т за счет того, что они прошли вдоль стержня путь туда и обратно. Таким образом, сжатие, вызываемое этими волнами на ударяемом конце, получается путем подстановки  вместо Т в выражение для сжатия от волн, посланных ударяемым концом в предыдущем интервале времени. Общее выражение для полного сжимающего напряжения в промежутке
вместо Т в выражение для сжатия от волн, посланных ударяемым концом в предыдущем интервале времени. Общее выражение для полного сжимающего напряжения в промежутке  находится отсюда по формуле
находится отсюда по формуле

Скорость частиц на ударяемом конце получается как разность между скоростью давления  волн, уходящих от ударяемого конца, и давления
волн, уходящих от ударяемого конца, и давления  волн, движущихся к ударяемому концу. Таким образом, согласно формуле (279), получаем
волн, движущихся к ударяемому концу. Таким образом, согласно формуле (279), получаем

Зависимость между  и можно теперь получить, используя уравнение движения (б) ударяющего тела. Обозначив через а отношение массы стержня к массе ударяющего тела, получаем
и можно теперь получить, используя уравнение движения (б) ударяющего тела. Обозначив через а отношение массы стержня к массе ударяющего тела, получаем 

Используя эту зависимость вместе с соотношениями  приводим уравнение (б) к виду
приводим уравнение (б) к виду

Умножая это уравнение на  получаем ешчт
получаем ешчт 

или

откуда

где С — постоянная интегрирования. Воспользуемся теперь этой зависимостью для вывода выражений последовательных значений  . В течение первого интервала времени
. В течение первого интервала времени  сжимающие напряжения даются формулой (в), и мы можем положить
сжимающие напряжения даются формулой (в), и мы можем положить

Подставляя это значение вместо в формулу (ж), имеем

Постоянная интегрирования С находится из условия, что в момент  сжимающие напряжения на ударяемом конце внезапно увеличиваются на величину
сжимающие напряжения на ударяемом конце внезапно увеличиваются на величину  (рис. 245, в). Отсюда, используя формулу (г), получаем
(рис. 245, в). Отсюда, используя формулу (г), получаем

откуда

Подставляя это значение постоянной в формулу (к), имеем

Поступая далее таким же образом и подставляя в формулу  вместо
вместо  находим
находим

Далее тем же путем получаем

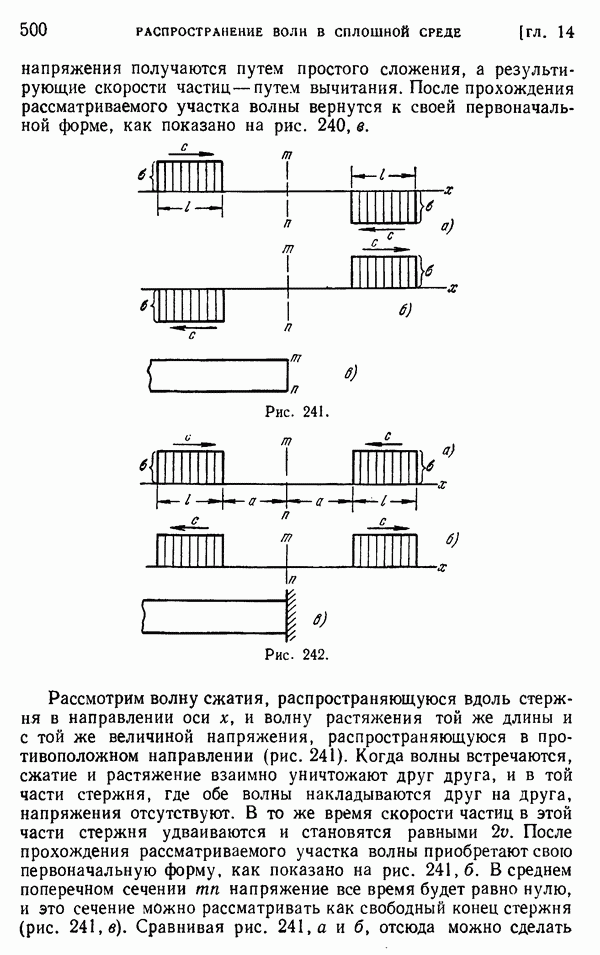
и т.д. На рис. 246 графически представлены функции  для
для  и для четырех разных значений
и для четырех разных значений  Если использовать эти кривые, то сжимающие напряжения на ударяемом конце легко найти по формуле (г).
Если использовать эти кривые, то сжимающие напряжения на ударяемом конце легко найти по формуле (г).

Рис. 246.

Рис. 247.
На рис. 247 это напряжение представлено графически для  . В конце интервалов
. В конце интервалов  оно меняется скачками. Максимальное значение этого напряжения зависит от отношения а. При
оно меняется скачками. Максимальное значение этого напряжения зависит от отношения а. При  напряжение имеет максимальное значение при
напряжение имеет максимальное значение при  . В случае
. В случае  максимальное напряжение возникает в момент
максимальное напряжение возникает в момент  Момент, когда а становится равным нулю, указывает на окончание удара. Можно убедиться, что
Момент, когда а становится равным нулю, указывает на окончание удара. Можно убедиться, что
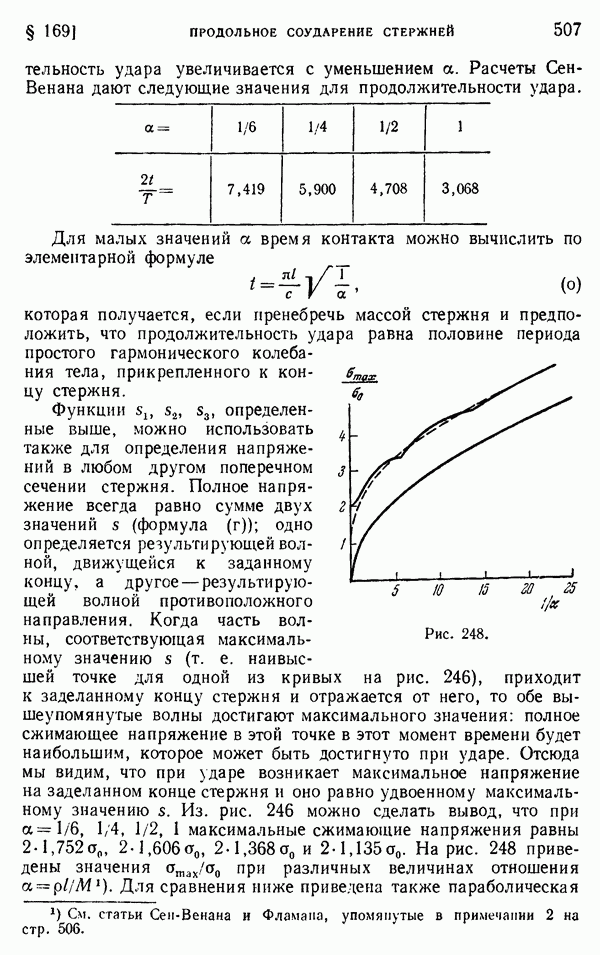
продолжительность удара увеличивается с уменьшением а. Расчеты Сен-Венана дают следующие значения для продолжительности удара.

Для малых значений а время контакта можно вычислить по элементарной формуле

которая получается, если пренебречь массой стержня и предположить, что продолжительность удара равна половине периода простого гармонического колебания тела, прикрепленного к концу стержня.

Рис. 248.
Функции  определенные выше, можно использовать также для определения напряжений в любом другом поперечном сечении стержня. Полное напряжение всегда равно сумме двух значений
определенные выше, можно использовать также для определения напряжений в любом другом поперечном сечении стержня. Полное напряжение всегда равно сумме двух значений  (формула (г)); одно определяется результирующей волной, движущейся к заданному концу, а другое — результирующей волной противоположного направления. Когда часть волны, соответствующая максимальному значению
(формула (г)); одно определяется результирующей волной, движущейся к заданному концу, а другое — результирующей волной противоположного направления. Когда часть волны, соответствующая максимальному значению  (т. е. наивысшей точке для одной из кривых на рис. 246), приходит к заделанному концу стержня и отражается от него, то обе вышеупомянутые волны достигают максимального значения: полное сжимающее напряжение в этой точке в этот момент времени будет наибольшим, которое может быть достигнуто при ударе. Отсюда мы видим, что при ударе возникает максимальное напряжение на заделанном конце стержня и оно равно удвоенному максимальному значению
(т. е. наивысшей точке для одной из кривых на рис. 246), приходит к заделанному концу стержня и отражается от него, то обе вышеупомянутые волны достигают максимального значения: полное сжимающее напряжение в этой точке в этот момент времени будет наибольшим, которое может быть достигнуто при ударе. Отсюда мы видим, что при ударе возникает максимальное напряжение на заделанном конце стержня и оно равно удвоенному максимальному значению  Из. рис. 246 можно сделать вывод, что при
Из. рис. 246 можно сделать вывод, что при  максимальные сжимающие напряжения равны
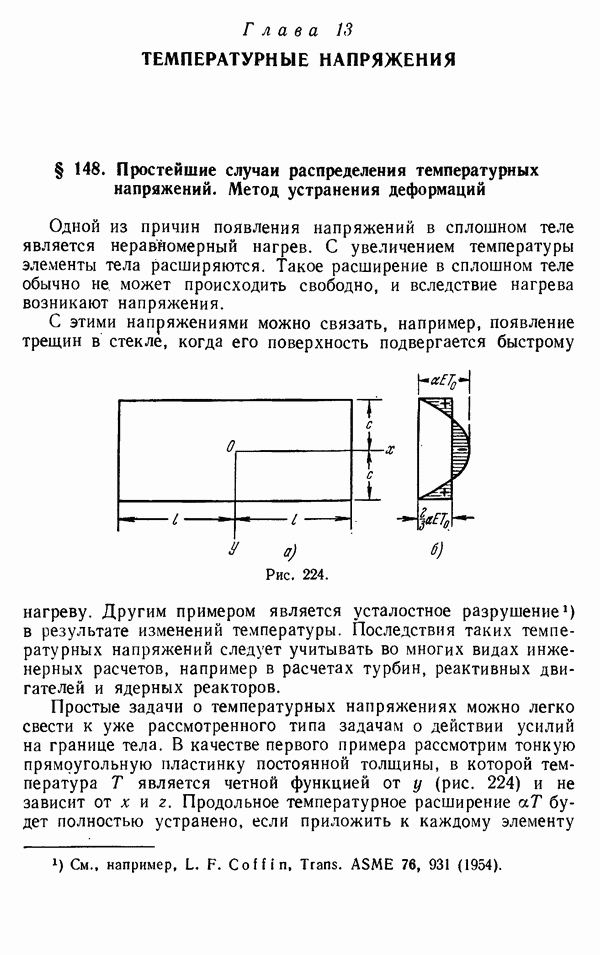
максимальные сжимающие напряжения равны  На рис. 248 приведены значения
На рис. 248 приведены значения  при различных величинах отношения
при различных величинах отношения  Для сравнения ниже приведена также параболическая
Для сравнения ниже приведена также параболическая
кривая, полученная по формуле

которую можно легко получить элементарным способом, пренебрегая массой стержня и приравнивая энергию деформации стержня кинетической энергии ударяющего тела. Пунктирная кривая показывает эту параболическую кривую, определяемую формулой

Легко видеть, что при больших значениях  эта формула всегда дает хорошее приближение.
эта формула всегда дает хорошее приближение.
Изложенная выше теория удара основана на допущении, что контакт происходит мгновенно по всей поверхности конца стержня.

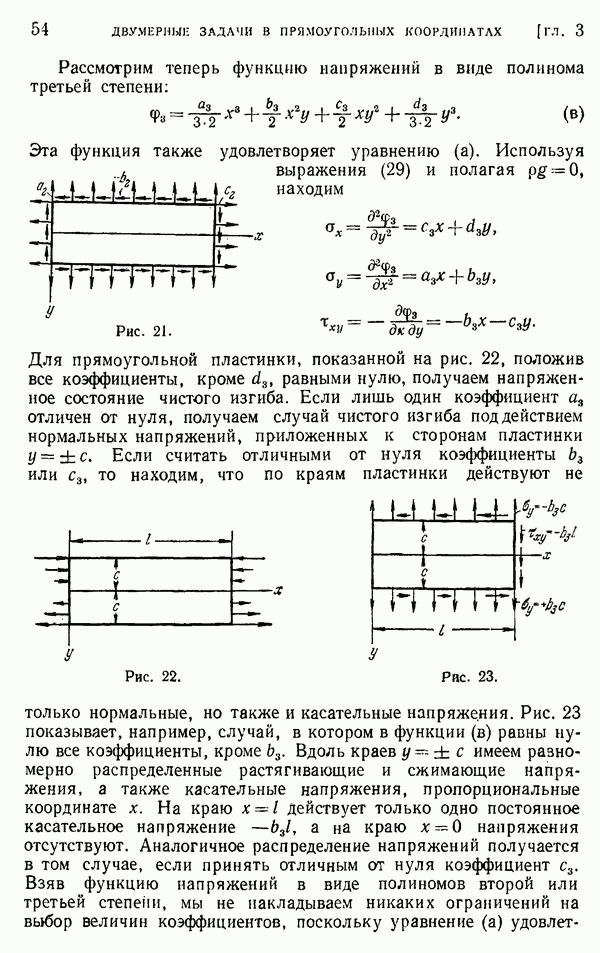
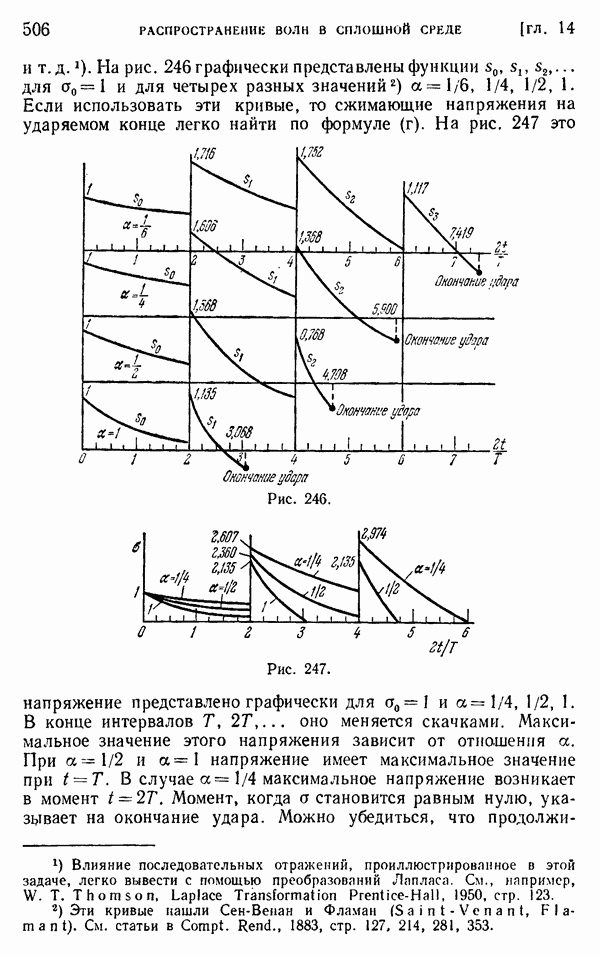
Рис. 249.
Осциллограммы сигналов от датчиков информации, показывающие зависимость формы волны от скорости удара. Диаметр стержня 12 мм, датчики деформации расположены на расстоянии 75 см от места удара; скорости ударяющего тела: с) 15 см/сек, б) 10 см/сек, в) 7,5 см/сек.
Это условие трудно реализовать на практике. Чтобы обеспечить в точности плоские поверхности торцов стержней, точно вьтерить их движение и свести к минимуму влияние воздушной пленки, уловленной между ударяющимися концами стержней, необходимы тщательные меры предосторожности. Только тогда опытные данные о распространении волн можно согласовать с изложенной элементарной теорией. Рис. 249, взятый из статьи Беккера и Конвея, показывает осциллографические записи формы волн, которые передаются вдоль круглых стержней и отражаются от плоских концов, причем в случае рис. 249, в с пренебрежимым искажением. В более ранних экспериментальных работах
ударяющимся концам стержней придавали криволинейную сферическую форму и местные деформации в области контакта учитывались на основе теории Герца.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
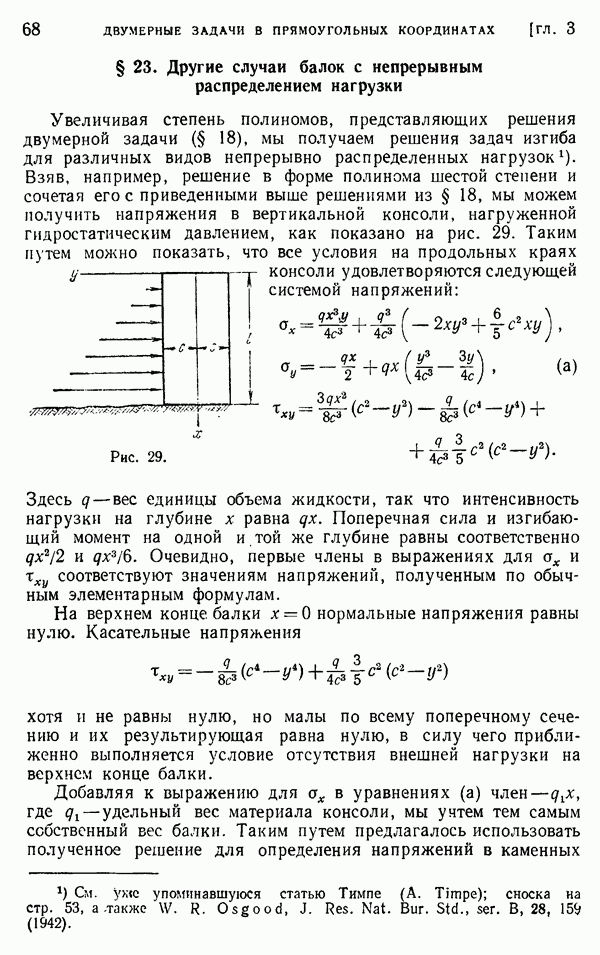
- § 22. Изгиб балки равномерной нагрузкой
- § 23. Другие случаи балок с непрерывным распределением нагрузки
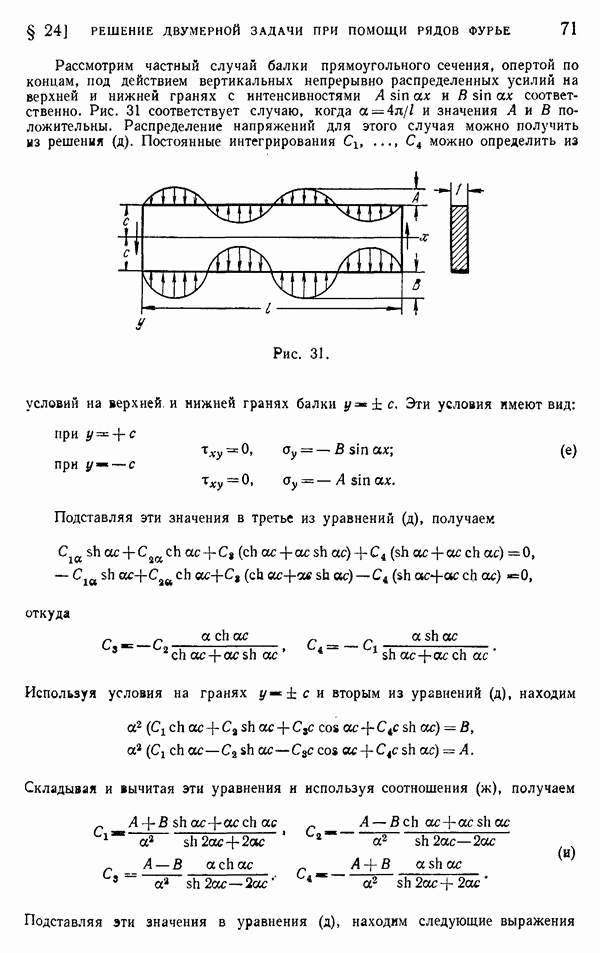
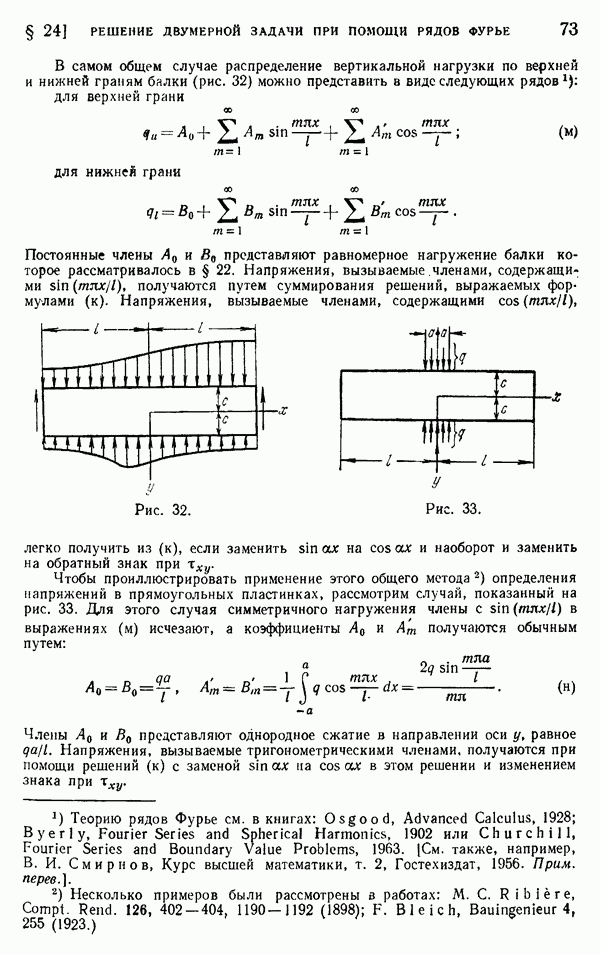
- § 24. Решение двумерной задачи при помощи рядов Фурье
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
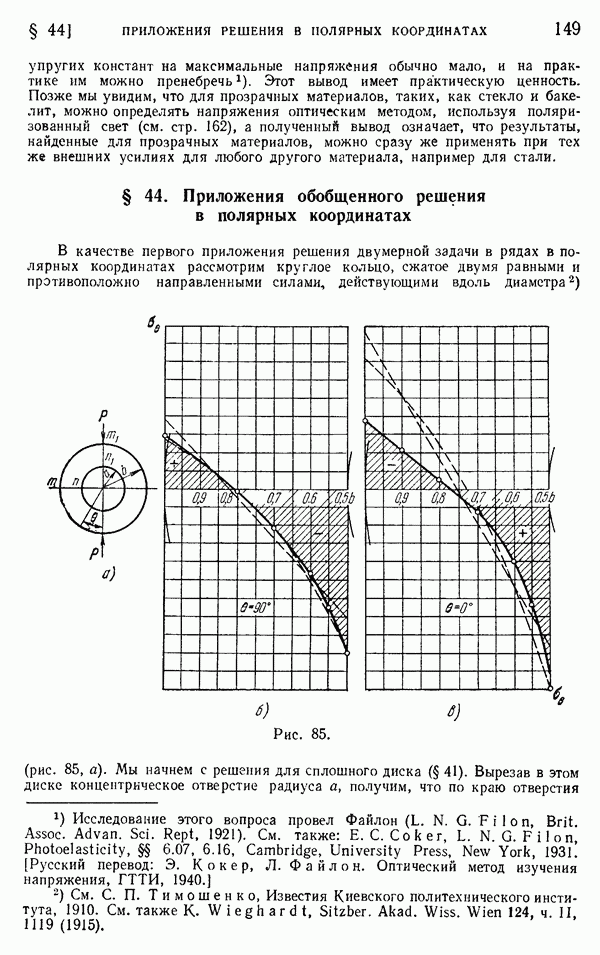
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
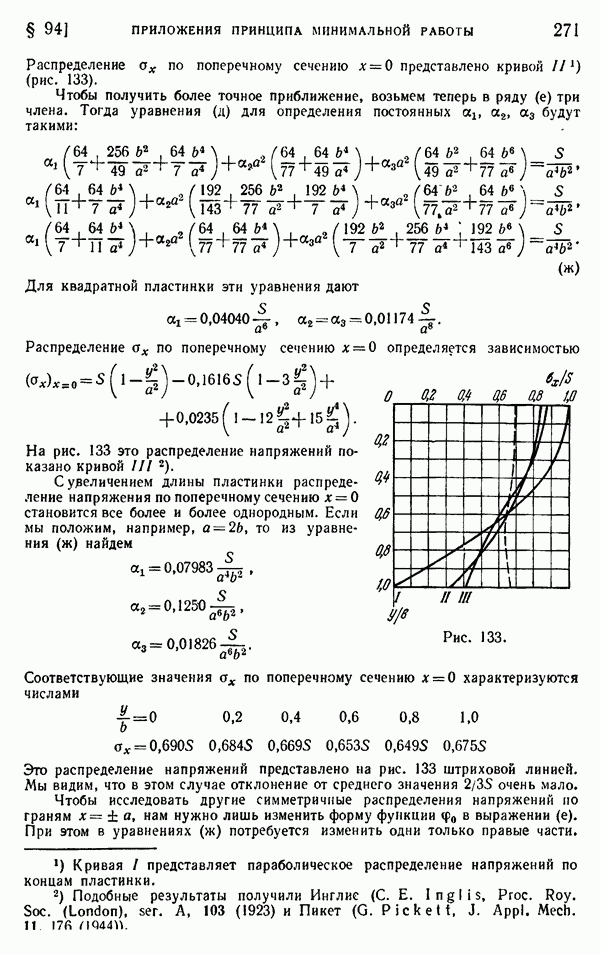
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
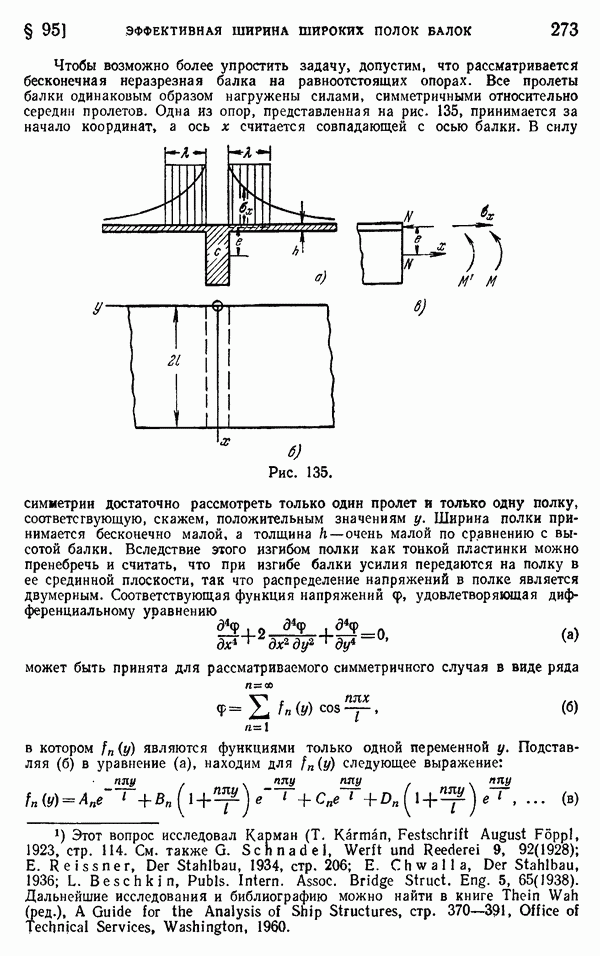
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
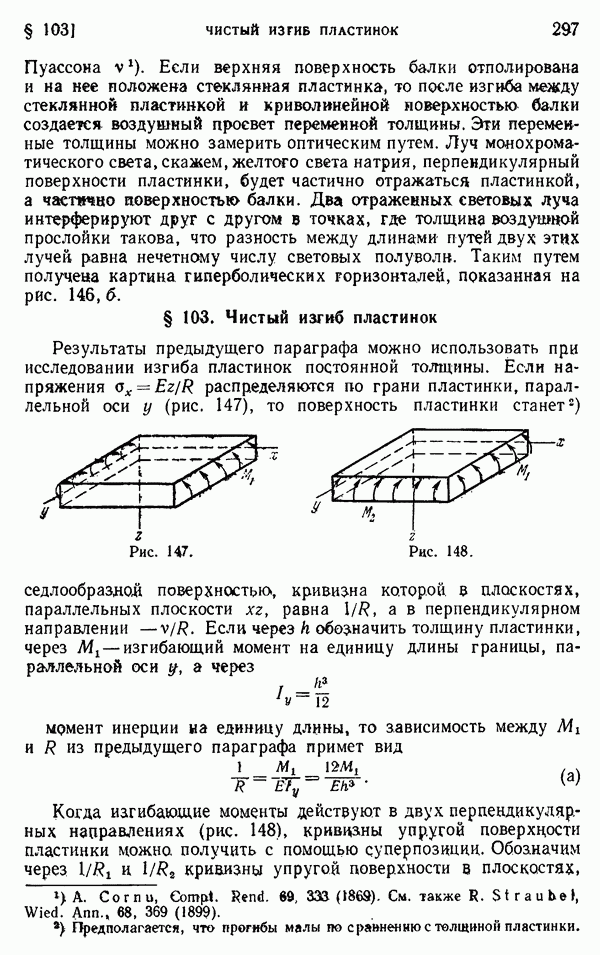
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
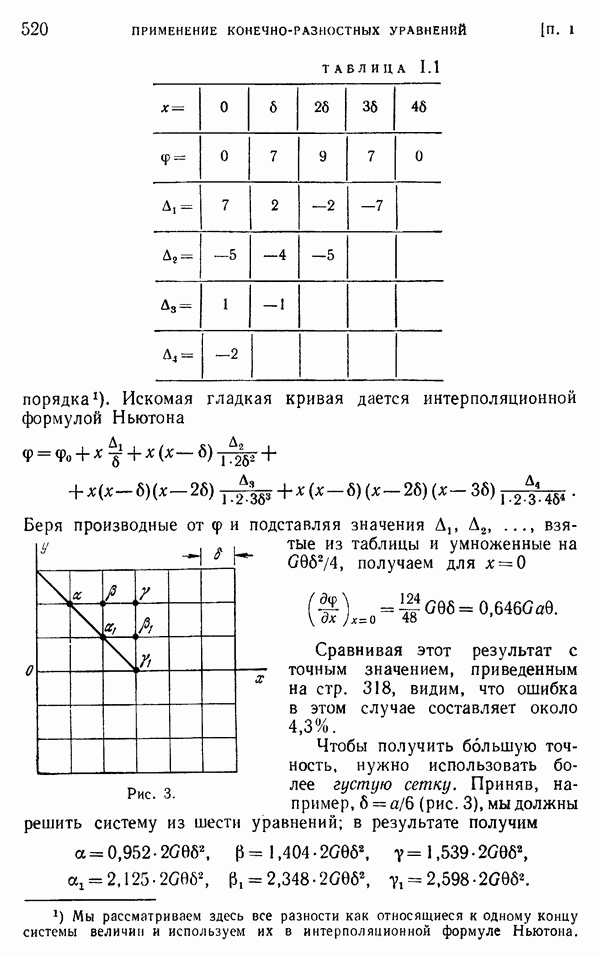
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
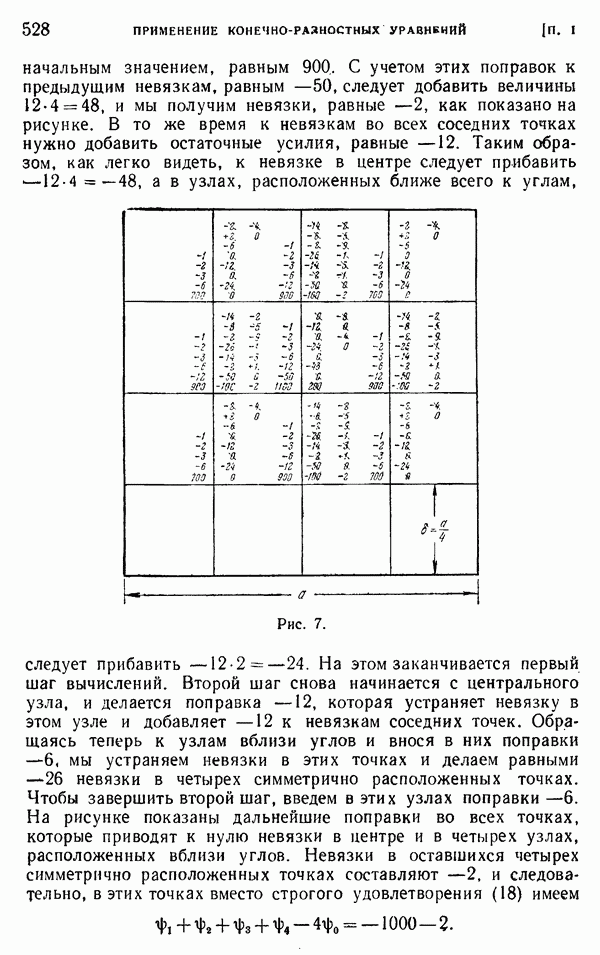
- § 3. Метод релаксации
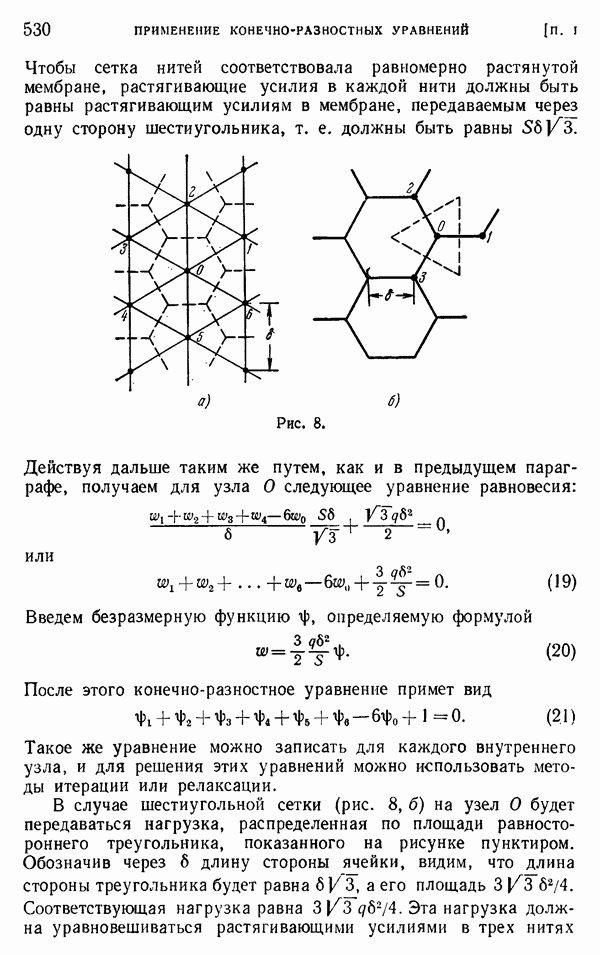
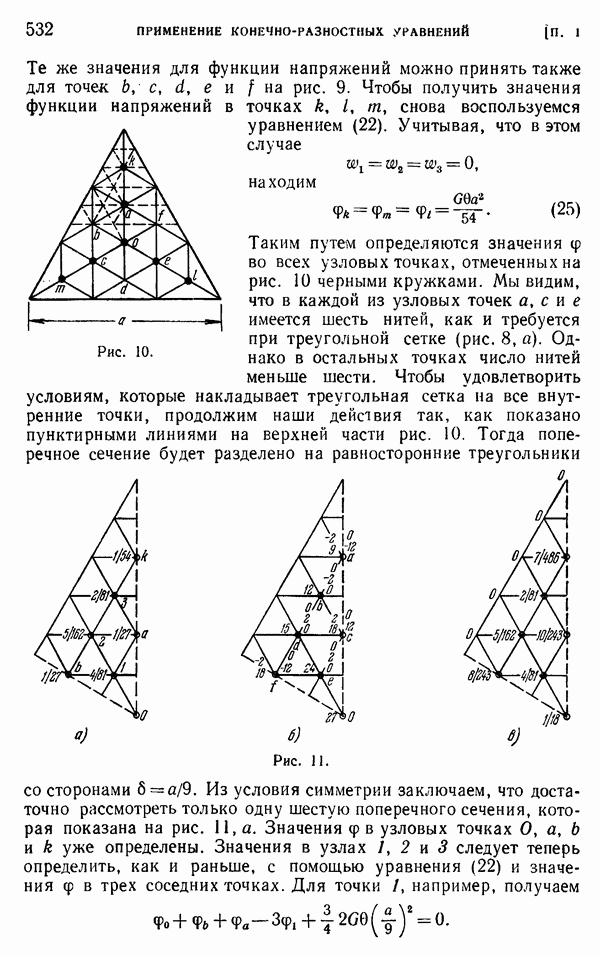
- § 4. Треугольные и шестиугольные сетки
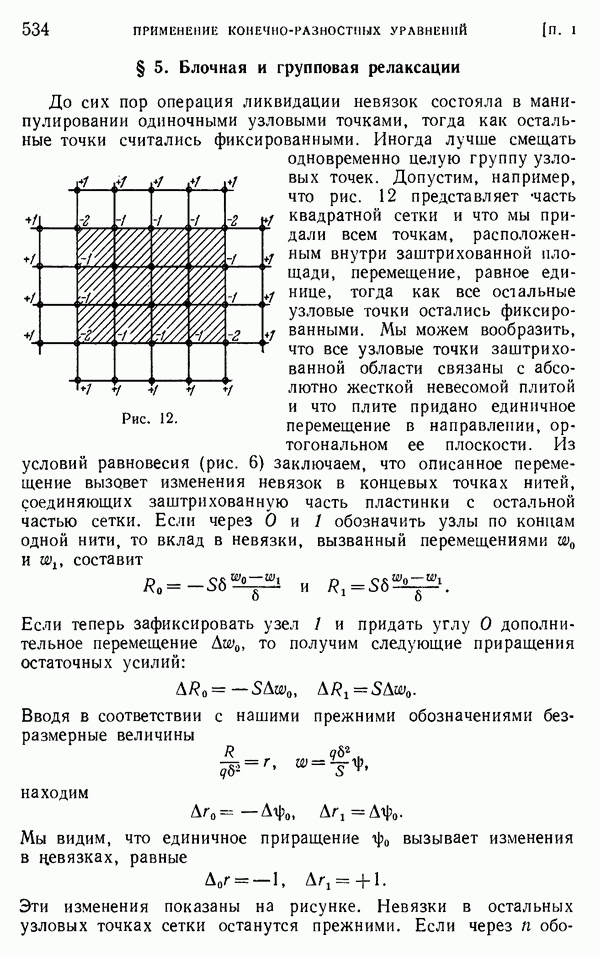
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
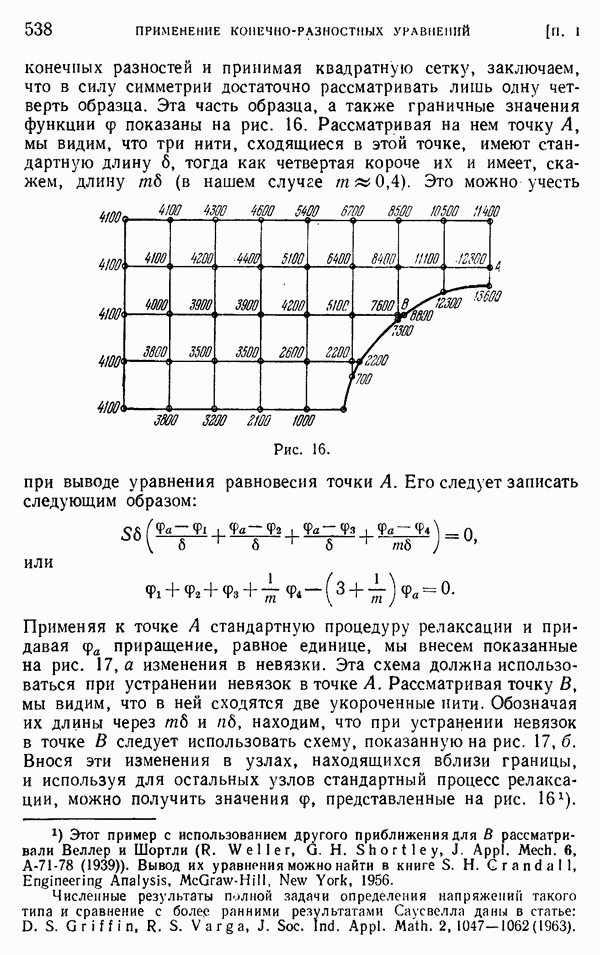
- § 7. Точки, расположенные вблизи границы
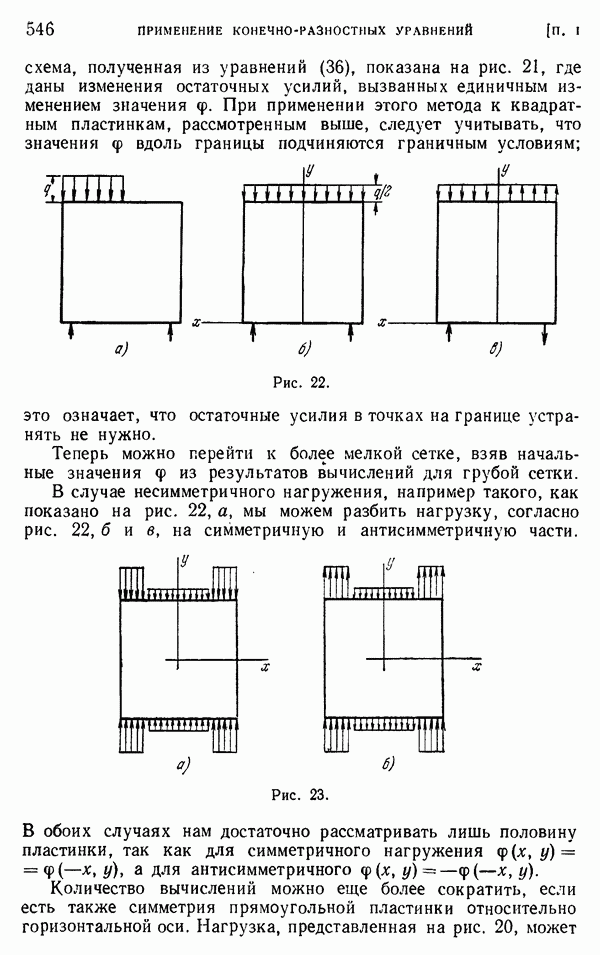
- § 8. Бигармоническое уравнение
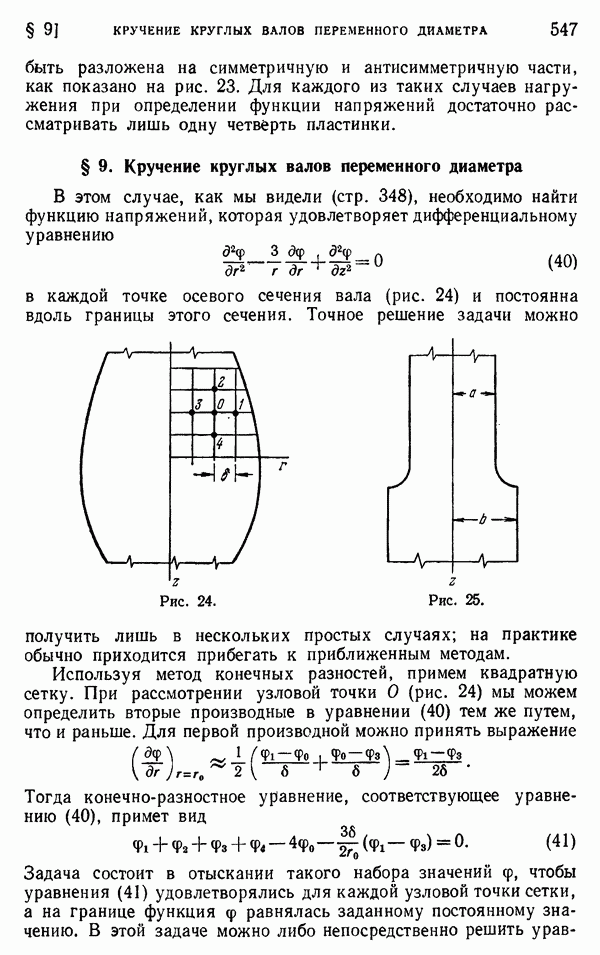
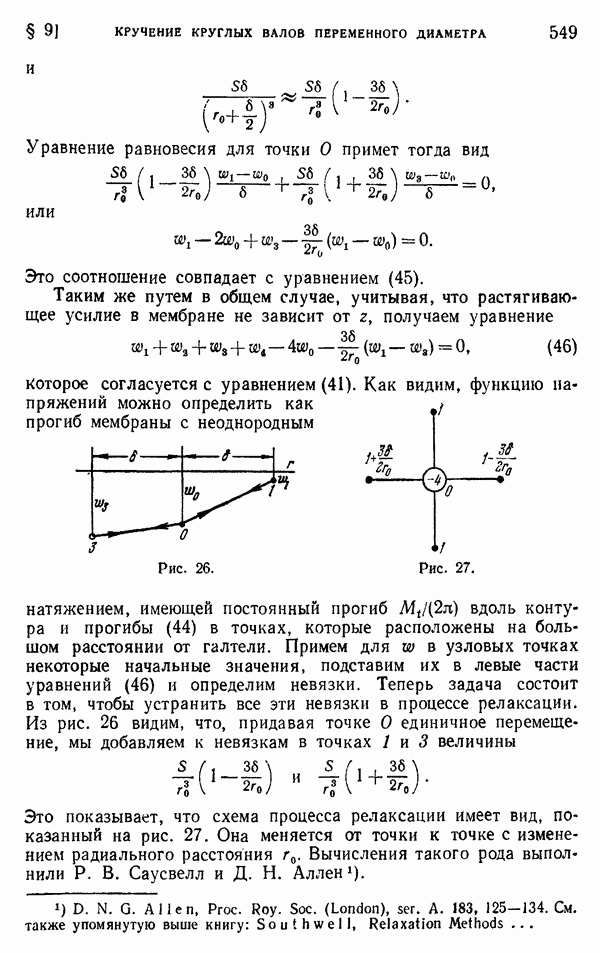
- § 9. Кручение круглых валов переменного диаметра
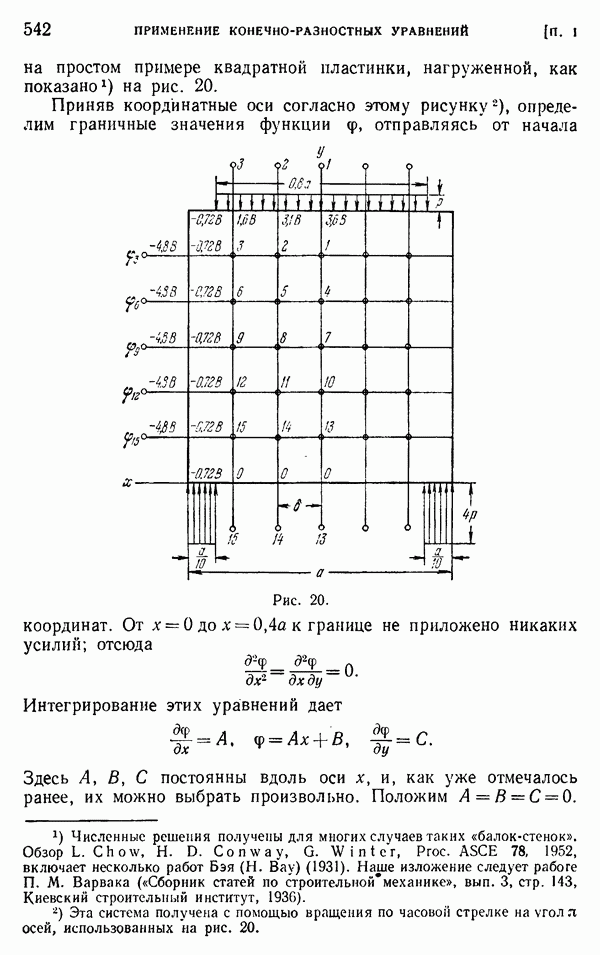
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи