| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
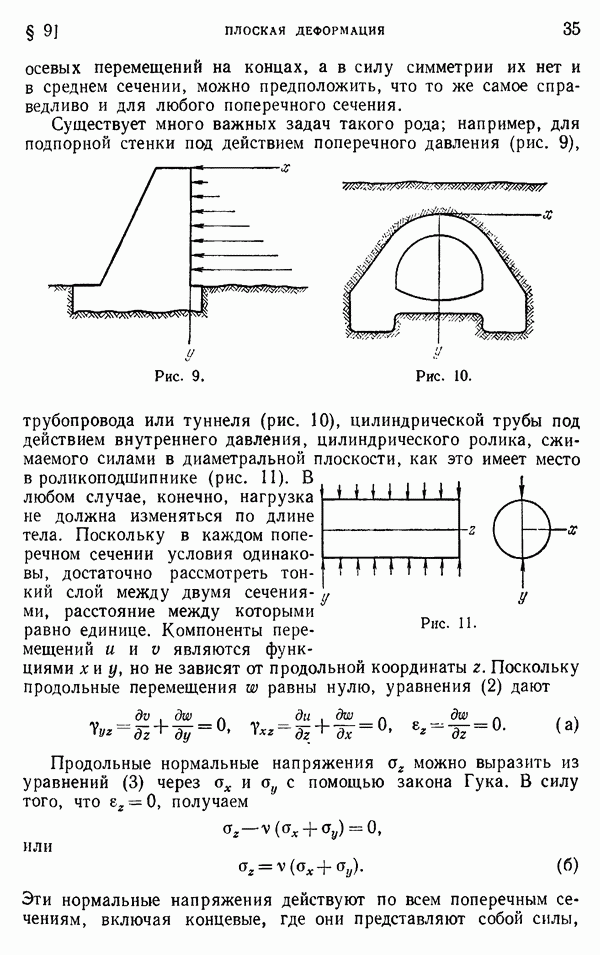
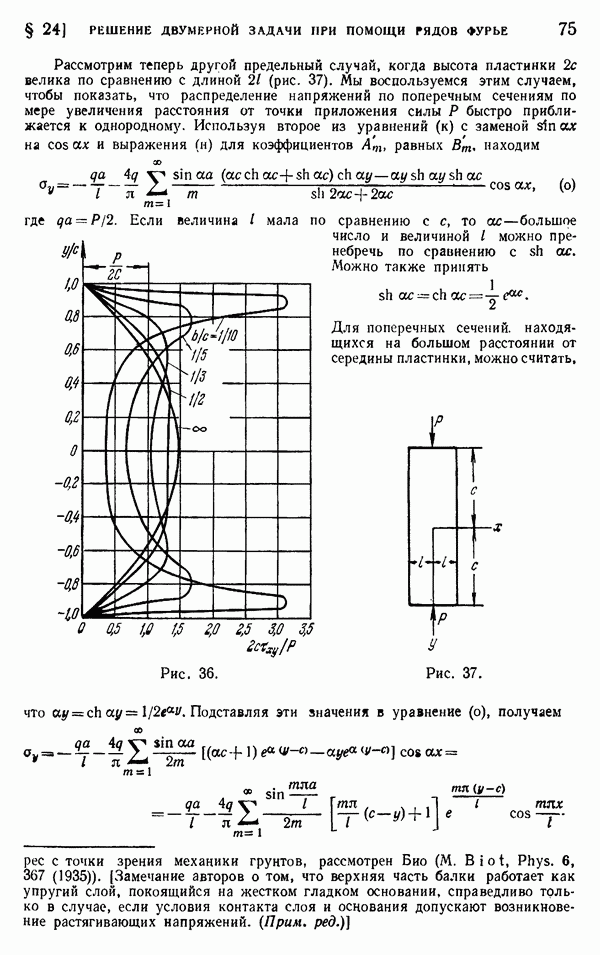
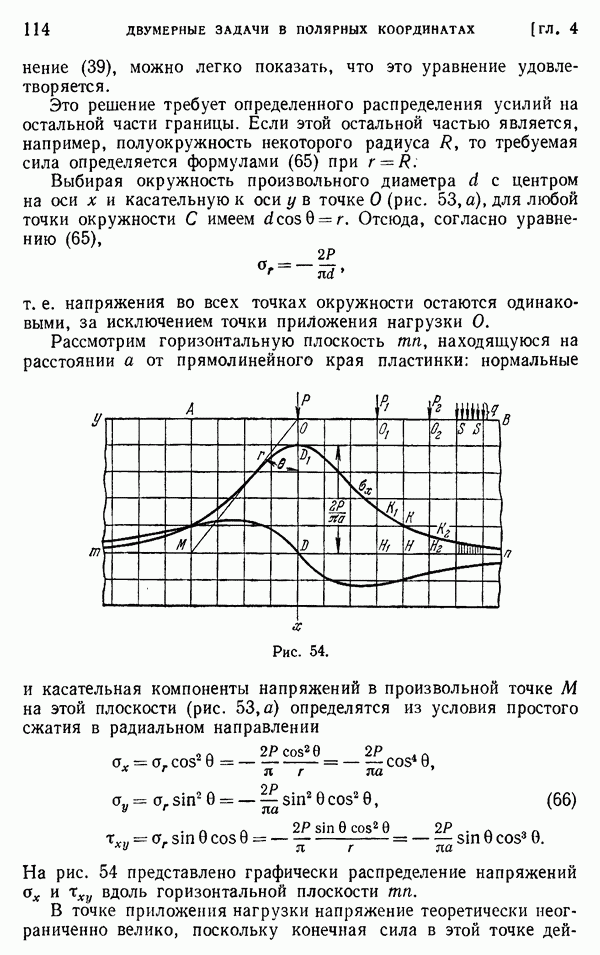
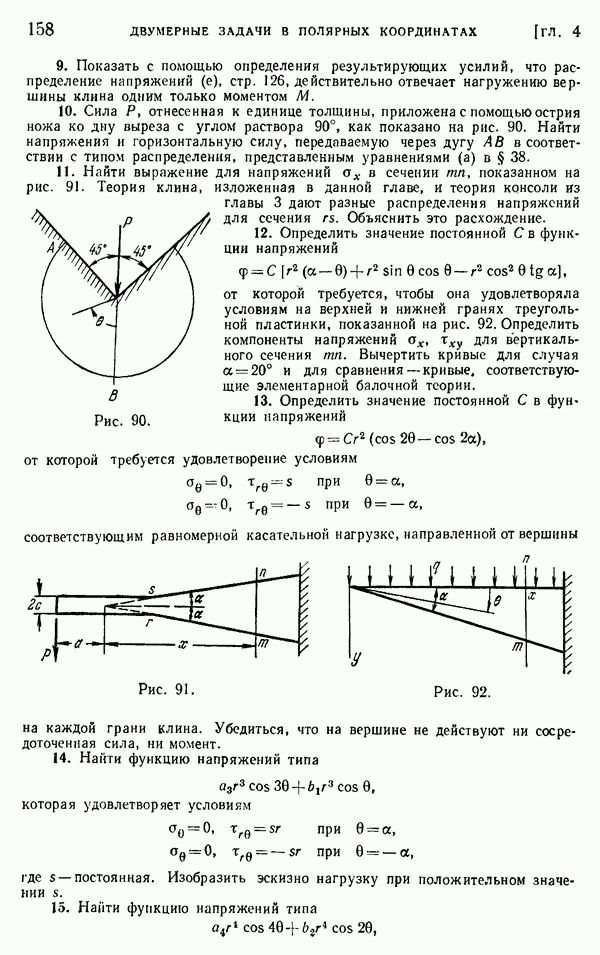
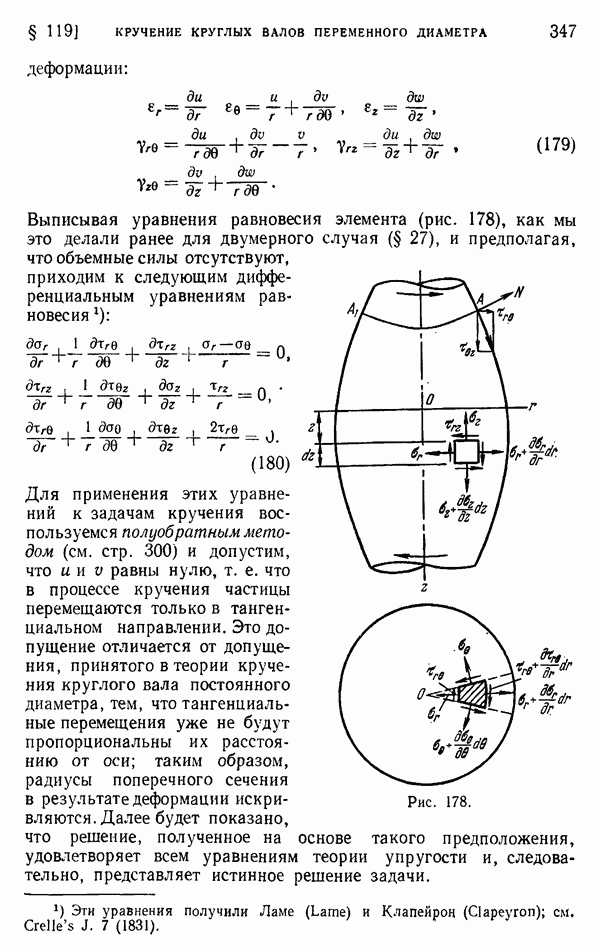
§ 34. Краевые дислокации
В § 33 компоненты перемещений  были получены, исходя из компонент напряжения (59). Постоянные
были получены, исходя из компонент напряжения (59). Постоянные  для задачи, представленной на рис. 46, определялись формулами (ж).
для задачи, представленной на рис. 46, определялись формулами (ж).
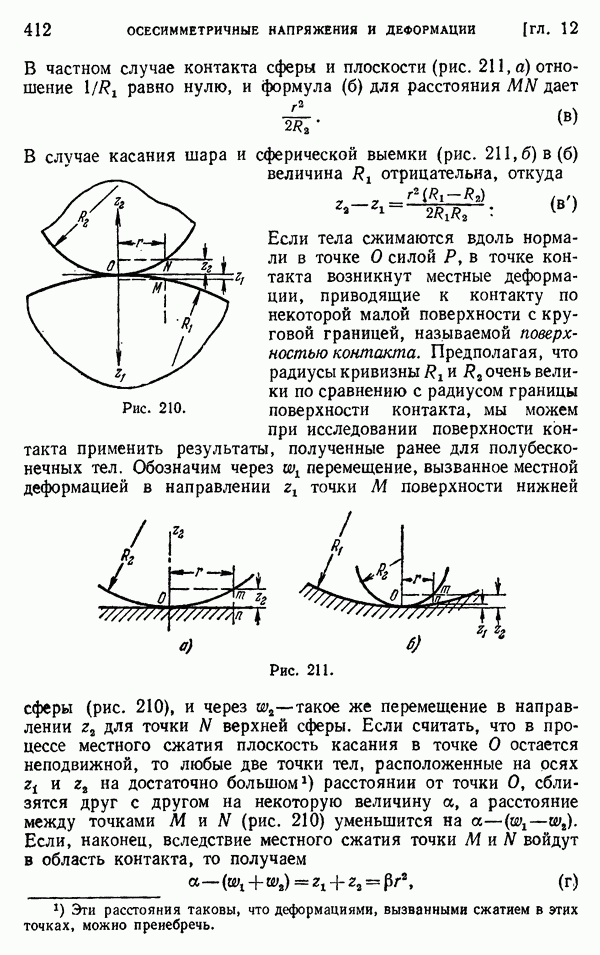
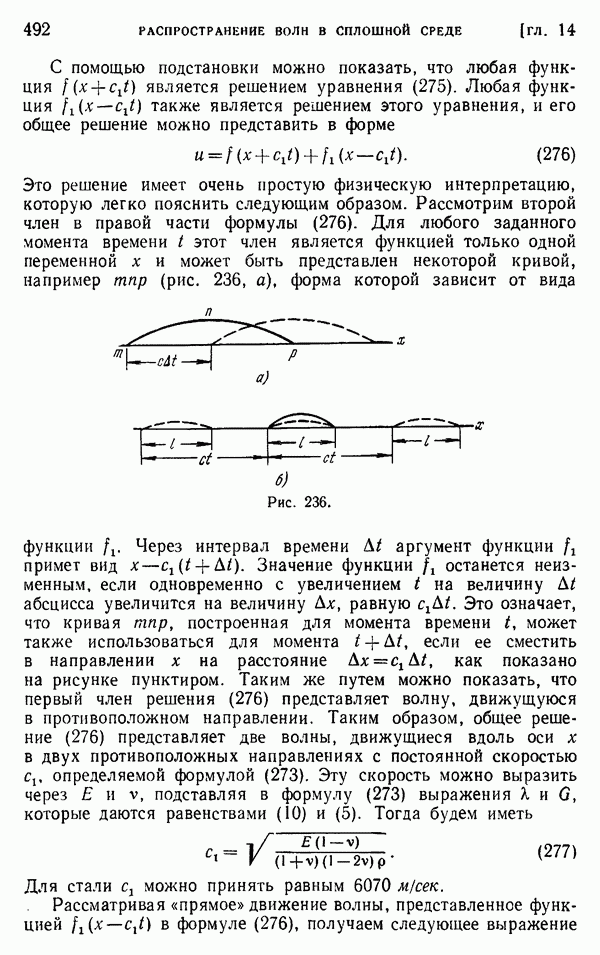
Приложение этого решения к задаче о четверти кольца не связано с существом дела. С равным успехом то же решение можно применить и к почти полному кольцу (рис. 48, а, б). Его можно также интерпретировать для случая, когда заданы не силы, а перемещения.

Рис. 48.
Рассмотрим перемещения  из § 33. Обратим внимание на то, что первый член в выражении для и может привести к разрыву перемещений. Рассмотрим рис. 48, б. На этом рисунке изображено первоначально полное кольцо с радиальным разрезом при
из § 33. Обратим внимание на то, что первый член в выражении для и может привести к разрыву перемещений. Рассмотрим рис. 48, б. На этом рисунке изображено первоначально полное кольцо с радиальным разрезом при  . На нижней поверхности разреза
. На нижней поверхности разреза  , а на верхней
, а на верхней  где
где  — бесконечно малая величина. Если вычислить и по формуле
— бесконечно малая величина. Если вычислить и по формуле  для двух этих значений
для двух этих значений  , то результаты будут различаться на величину
, то результаты будут различаться на величину  Таким образом,
Таким образом,

Из формулы  тогда получаем
тогда получаем

Это относительное смещение двух поверхностей разреза показано на рис. 48, б символом 6. Усилие Р, необходимое для того, чтобы произвести это смещение, находится из последнего уравнения (ж) § 33, куда нужно подставить  определяемое по формуле (б). Если две поверхности приварены друг к другу после того, как наложено перемещение
определяемое по формуле (б). Если две поверхности приварены друг к другу после того, как наложено перемещение  каждая из них в виде действия и противодействия передает на другую указанное усилие Р. Кольцо при этом находится в состоянии самонапряжения, называемом «краевой дислокацией». Соответствующее плоское деформированное состояние является основой для объяснения пластической деформации в кристаллах металлов.
каждая из них в виде действия и противодействия передает на другую указанное усилие Р. Кольцо при этом находится в состоянии самонапряжения, называемом «краевой дислокацией». Соответствующее плоское деформированное состояние является основой для объяснения пластической деформации в кристаллах металлов.
Рис. 48, а показывает кольцо с зазором шириной  с параллельными берегами. Если сначала сделать тонкий разрез, а затем
с параллельными берегами. Если сначала сделать тонкий разрез, а затем
наложить относительные перемещения, для того чтобы раскрыть разрез, то разрыв перемещений возникнет уже не для и, а для  Его можно получить из решения § 33, если принять, что правая поверхность разреза занимает положение
Его можно получить из решения § 33, если принять, что правая поверхность разреза занимает положение  а левая
а левая  Тогда, поскольку положительное направление
Тогда, поскольку положительное направление  совпадает с направлением возрастания 0, получаем
совпадает с направлением возрастания 0, получаем

Используя вторую из формул  § 33, находим
§ 33, находим

Тот факт, что значения  различаются только знаком, означает, что и напряжения в этих двух случаях должны различаться только по знаку. Величина Р находится из третьего соотношения (ж) в § 33, после чего из двух первых находятся А и В. Это соответствие можно было предвидеть на основании того факта, что если сделать оба разреза, показанные на рис. 48, а и б, то четверть кольца будет вырезана полностью. Относительное перемещение
различаются только знаком, означает, что и напряжения в этих двух случаях должны различаться только по знаку. Величина Р находится из третьего соотношения (ж) в § 33, после чего из двух первых находятся А и В. Это соответствие можно было предвидеть на основании того факта, что если сделать оба разреза, показанные на рис. 48, а и б, то четверть кольца будет вырезана полностью. Относительное перемещение  на рис. 48, а и относительное перемещение
на рис. 48, а и относительное перемещение  на рис. 48, б можно вызвать одновременно, если сдвинуть четверть кольца вправо на величину
на рис. 48, б можно вызвать одновременно, если сдвинуть четверть кольца вправо на величину  Это не вызовет никаких напряжений, и следовательно, оба вида дислокации должны иметь равные и противоположные по знаку напряжения, если каждая из них существует отдельно. Это обстоятельство служит примером общей «теоремы об эквивалентных разрезах».
Это не вызовет никаких напряжений, и следовательно, оба вида дислокации должны иметь равные и противоположные по знаку напряжения, если каждая из них существует отдельно. Это обстоятельство служит примером общей «теоремы об эквивалентных разрезах».
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
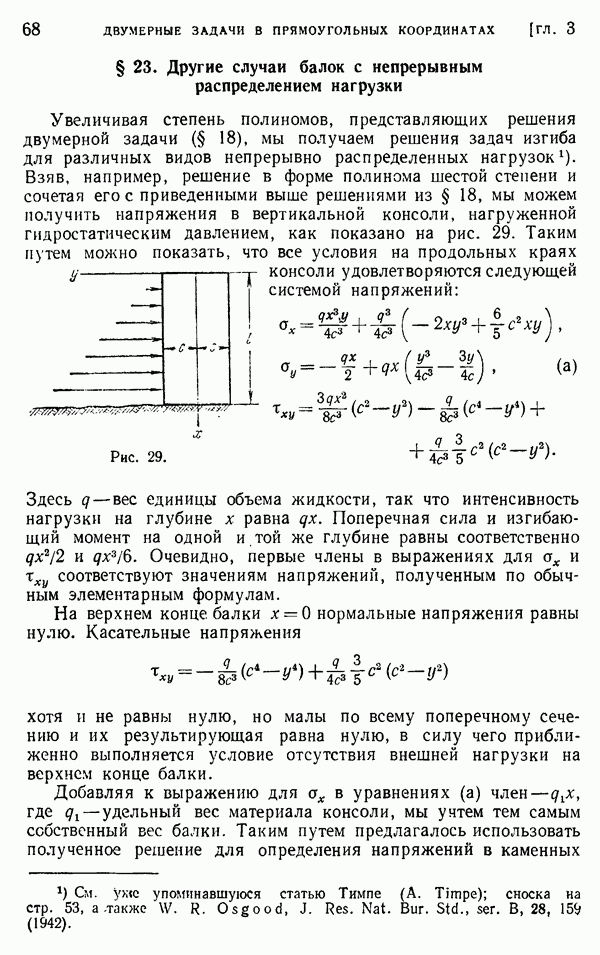
- § 23. Другие случаи балок с непрерывным распределением нагрузки
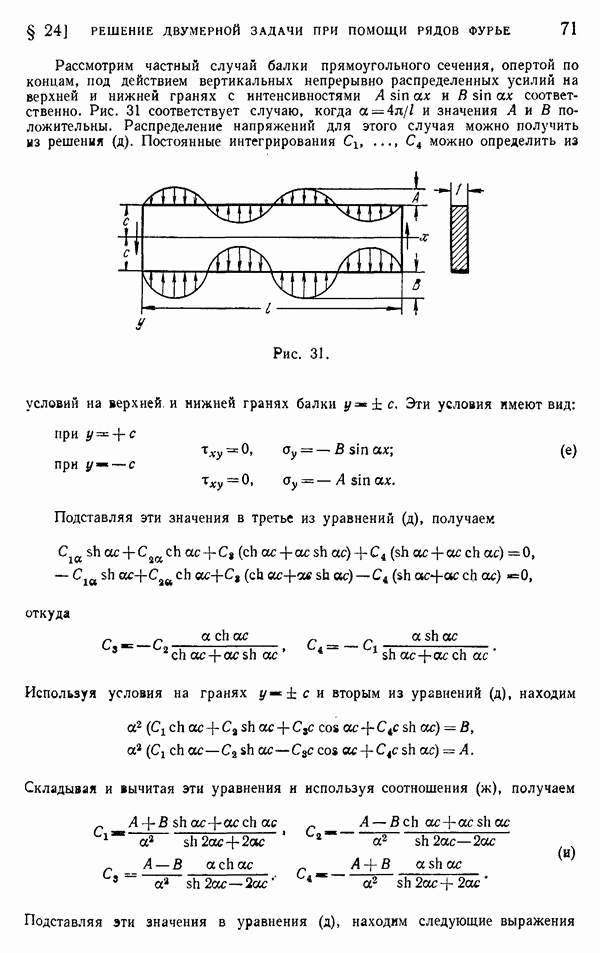
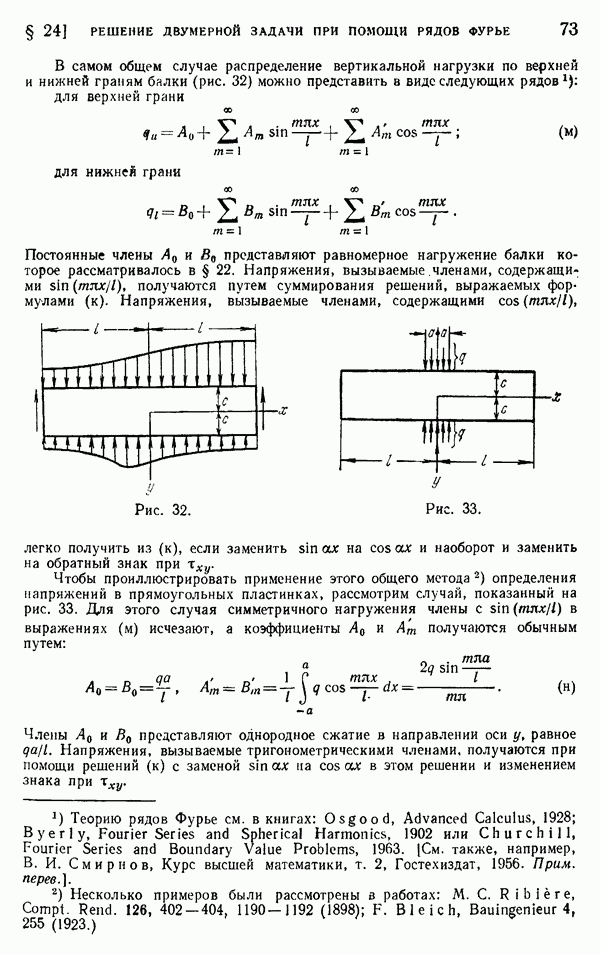
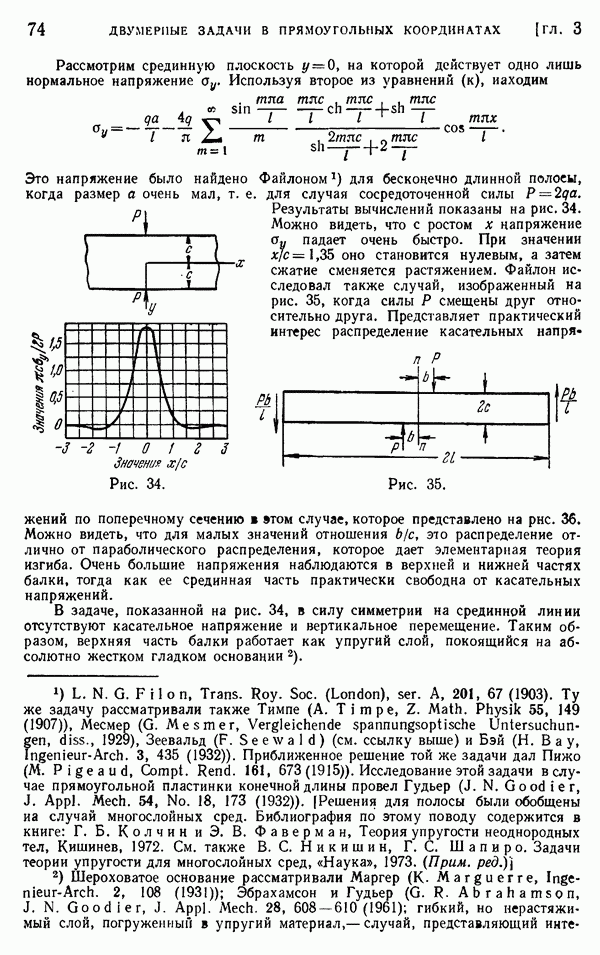
- § 24. Решение двумерной задачи при помощи рядов Фурье
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
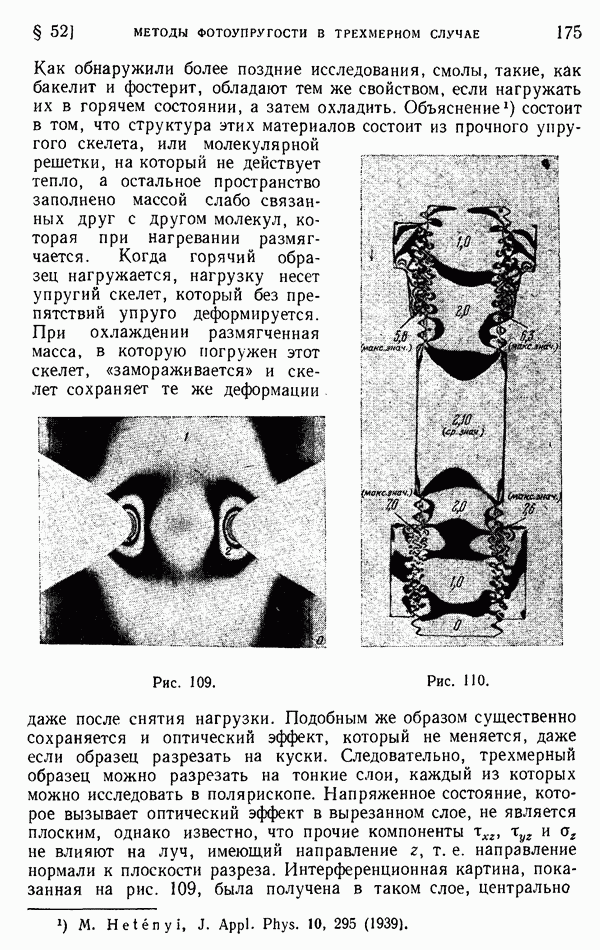
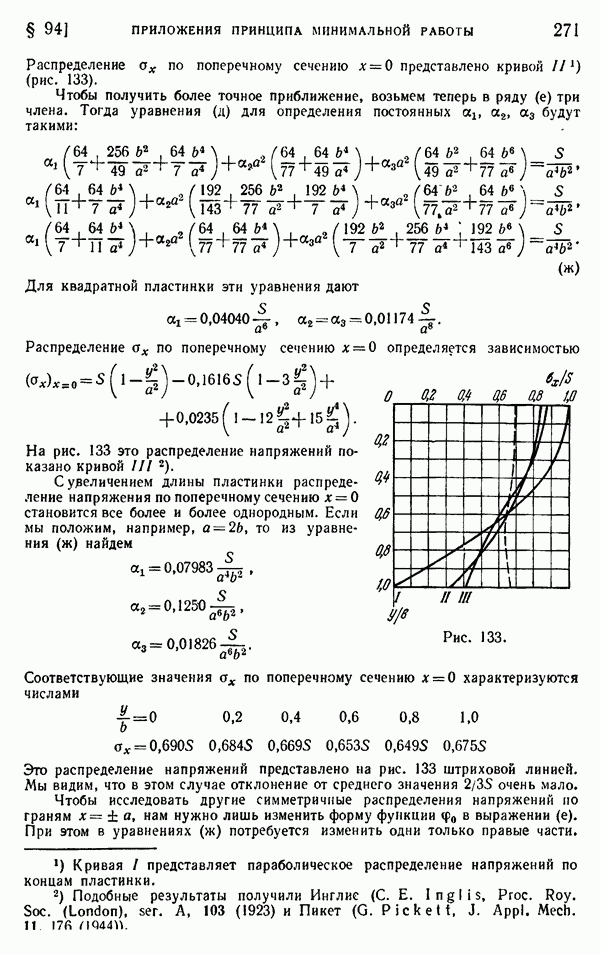
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
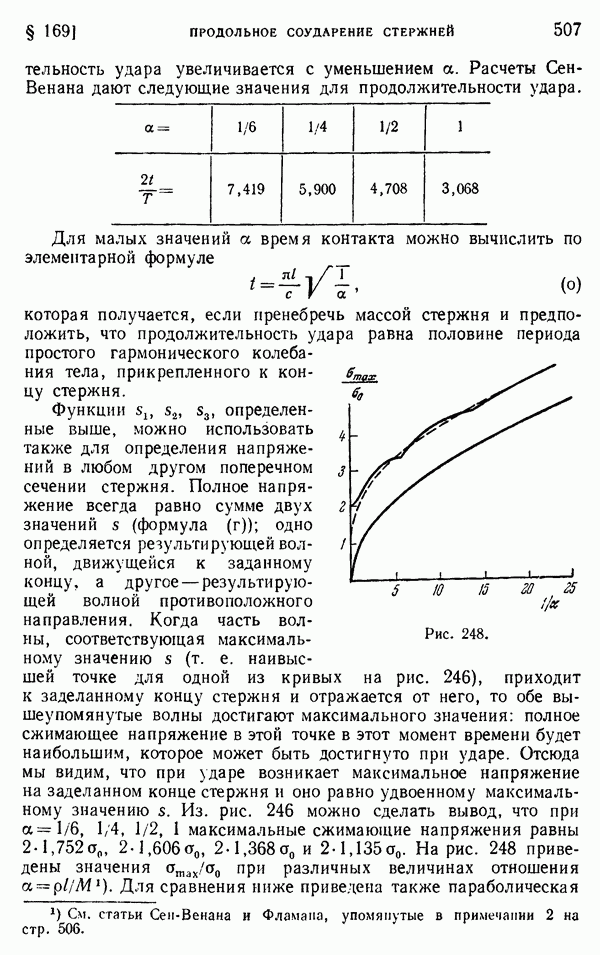
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
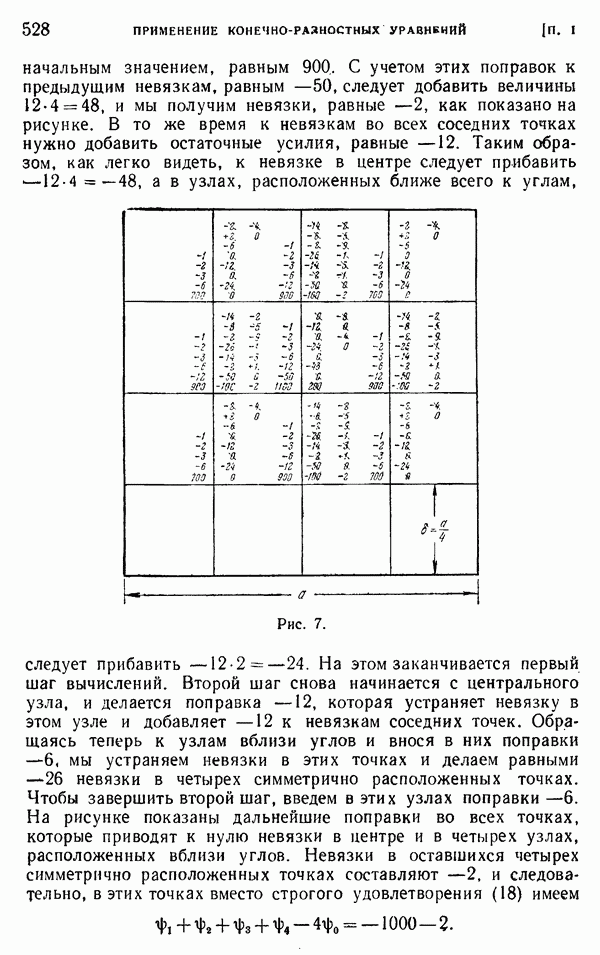
- § 3. Метод релаксации
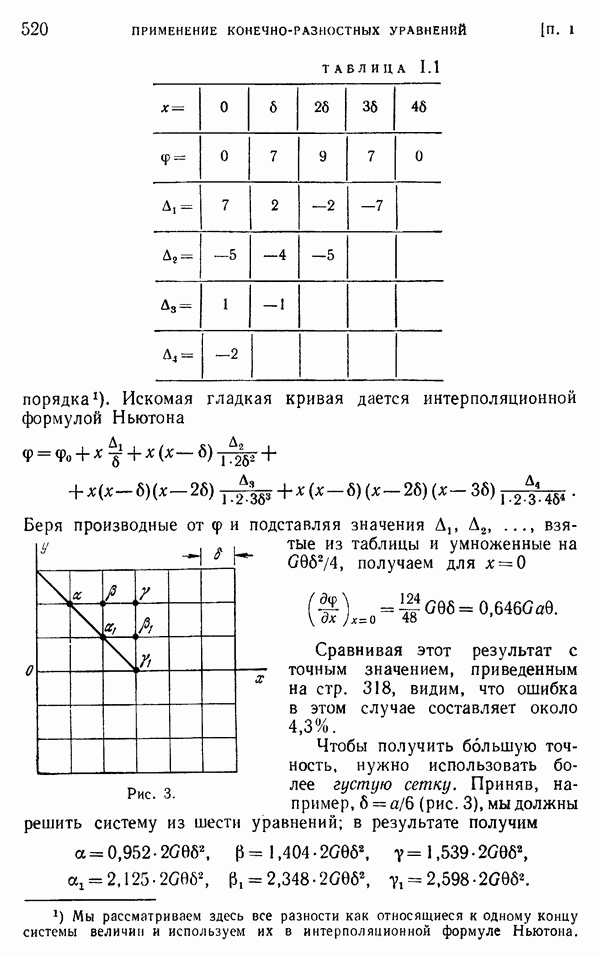
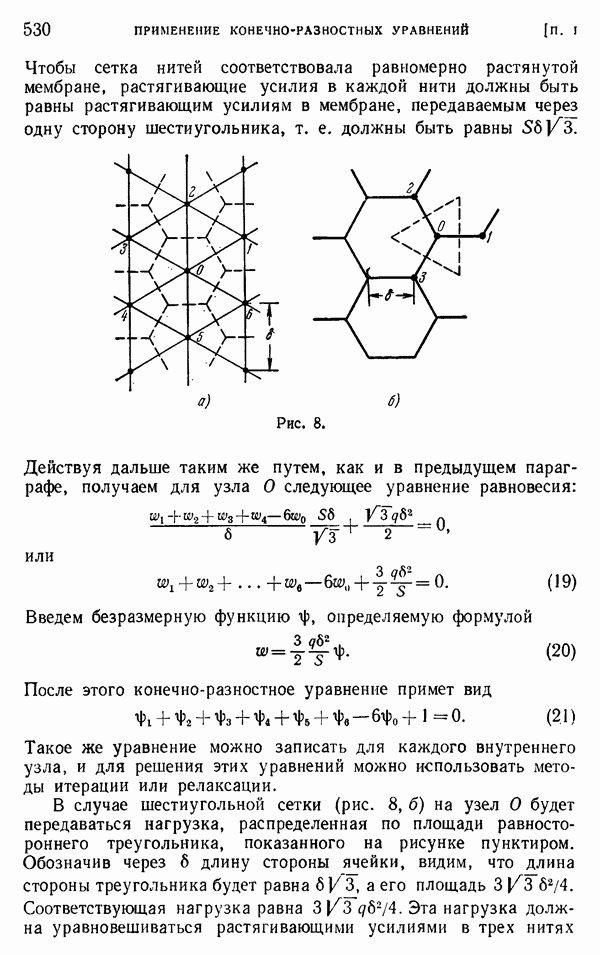
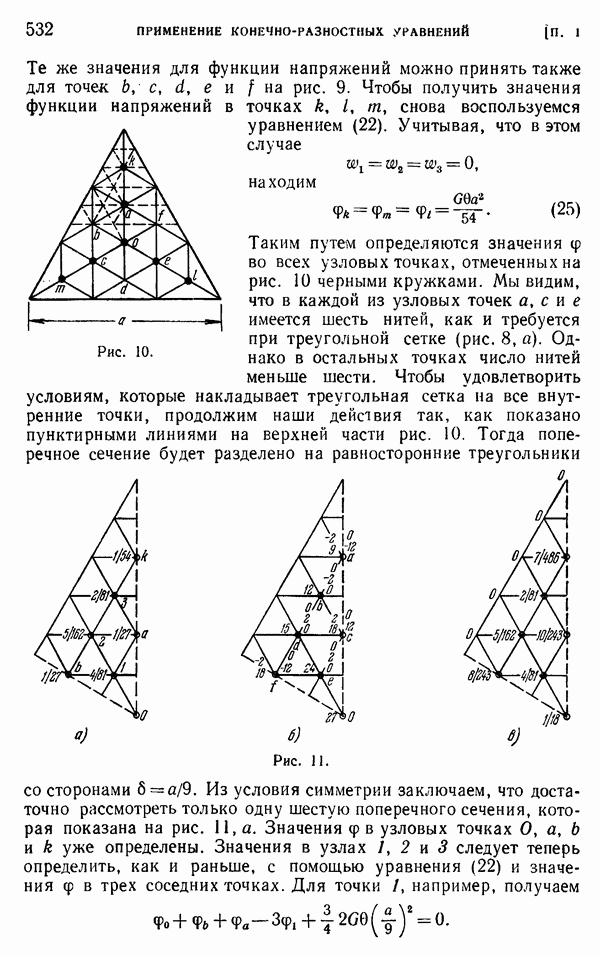
- § 4. Треугольные и шестиугольные сетки
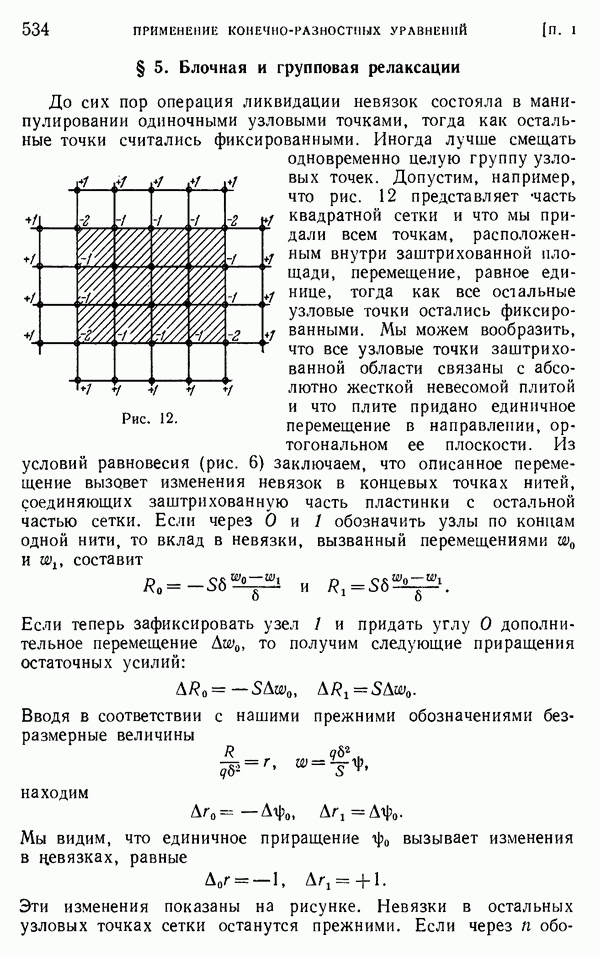
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
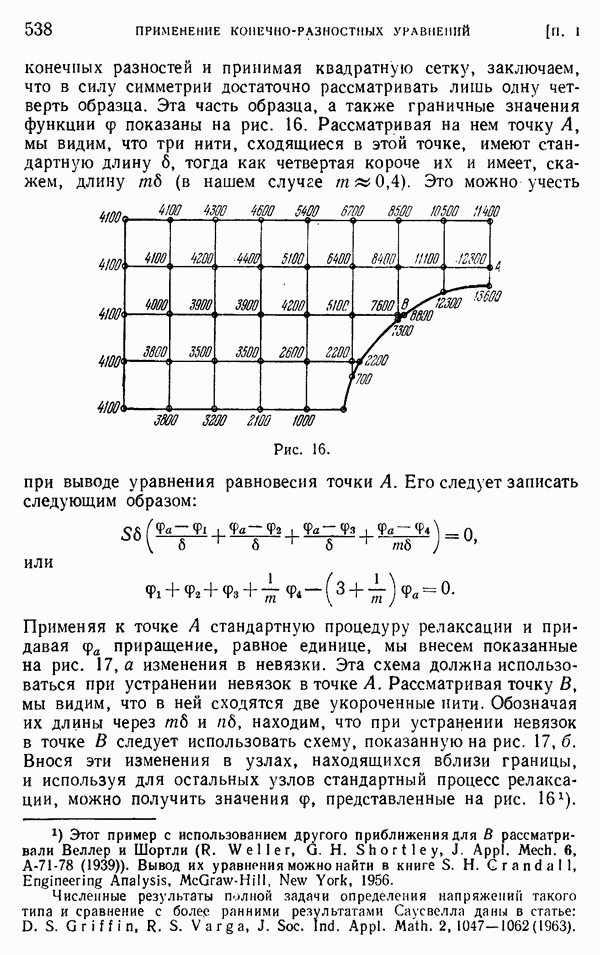
- § 7. Точки, расположенные вблизи границы
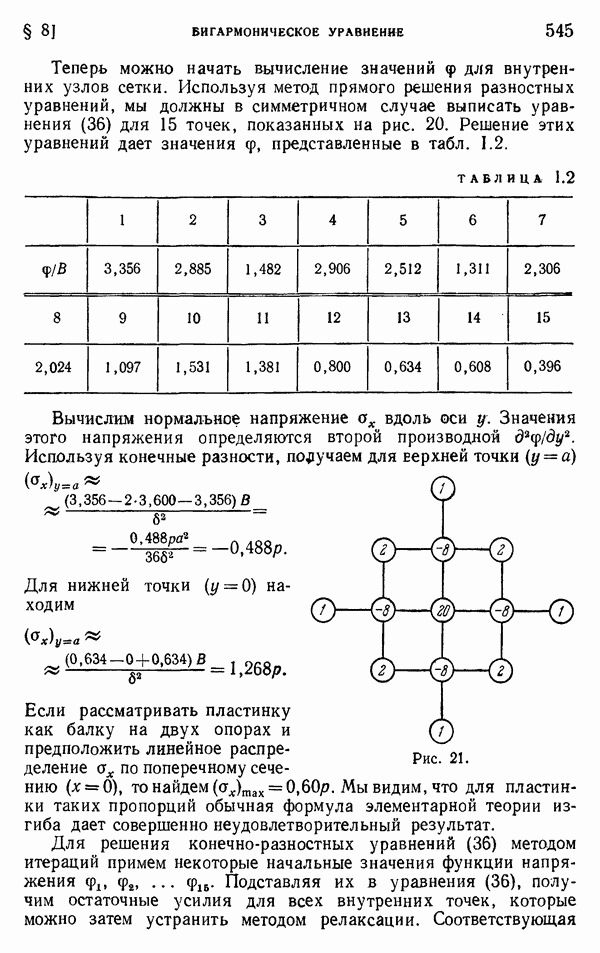
- § 8. Бигармоническое уравнение
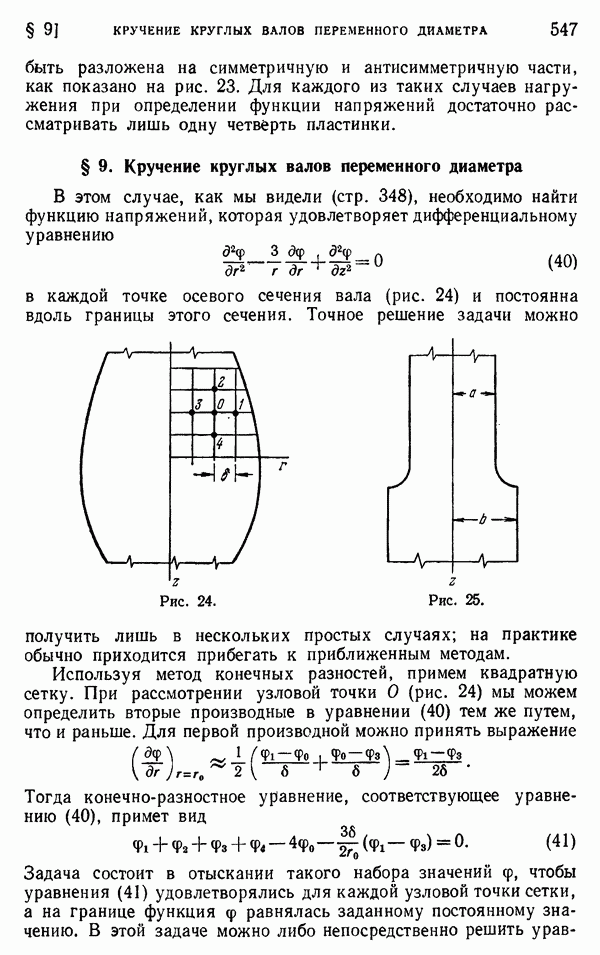
- § 9. Кручение круглых валов переменного диаметра
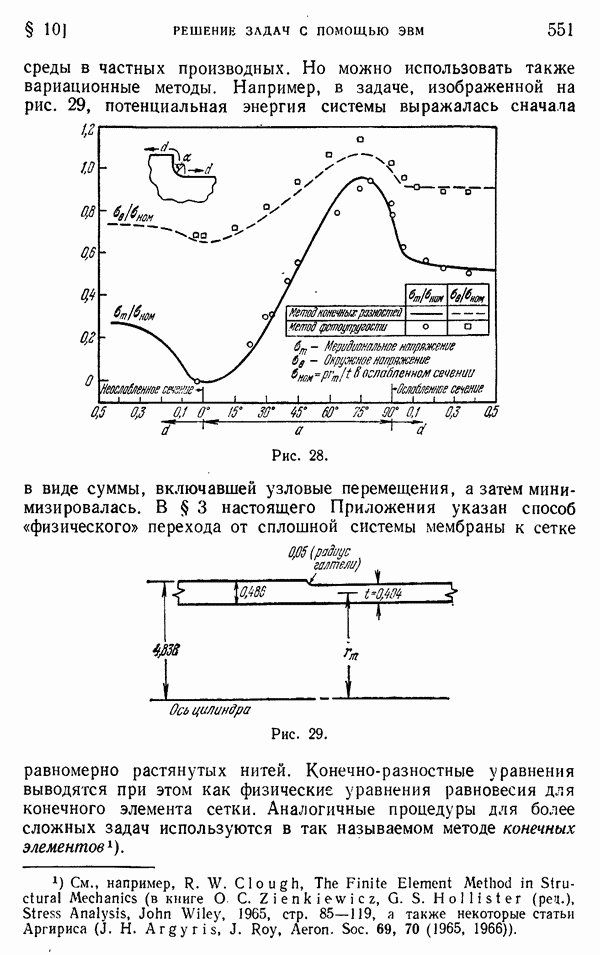
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
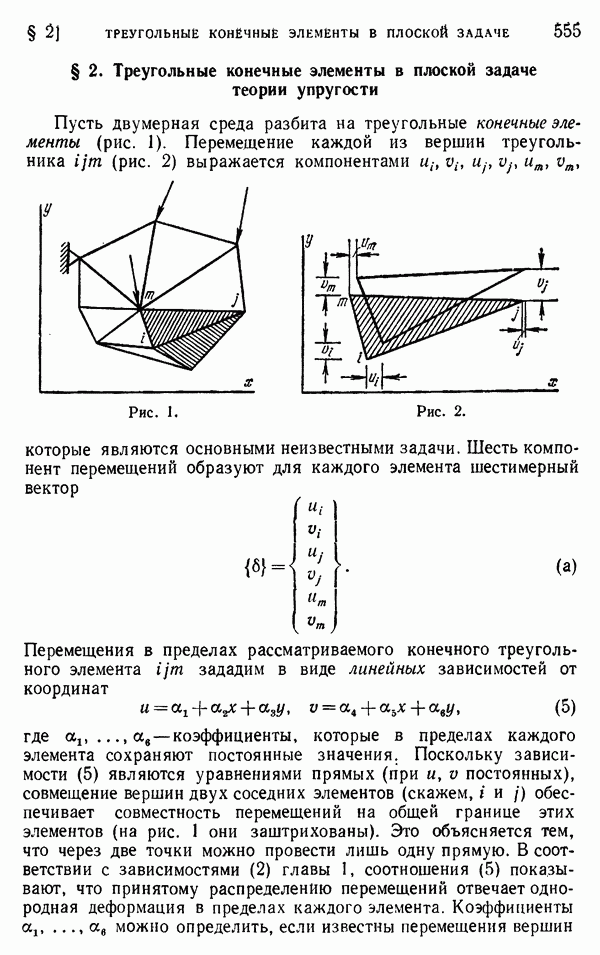
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
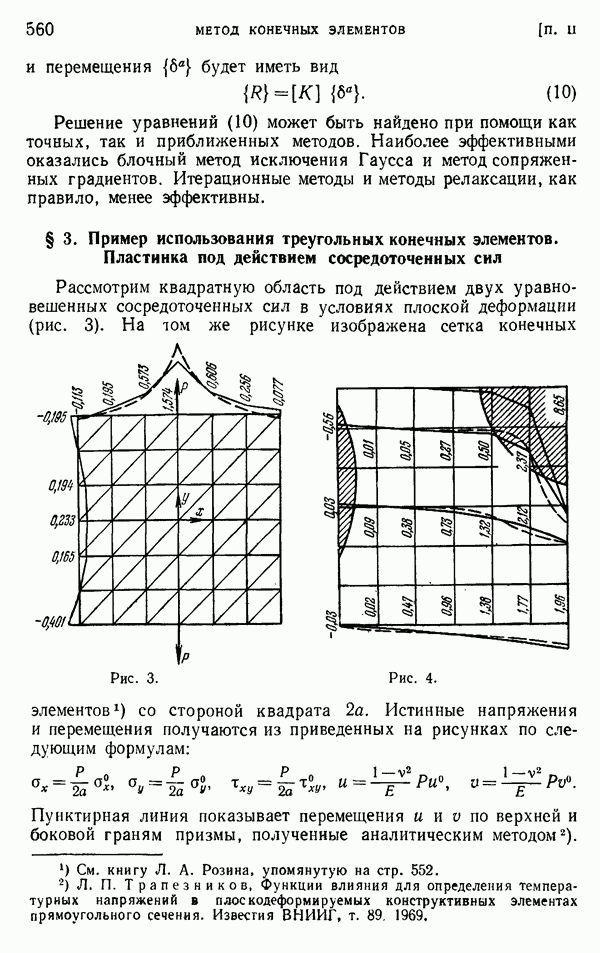
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
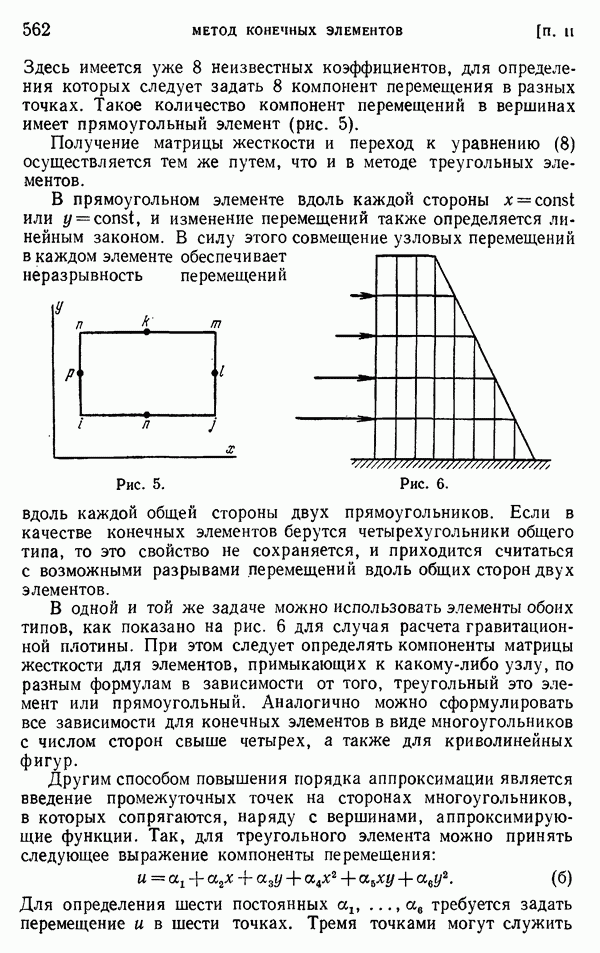
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи