| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
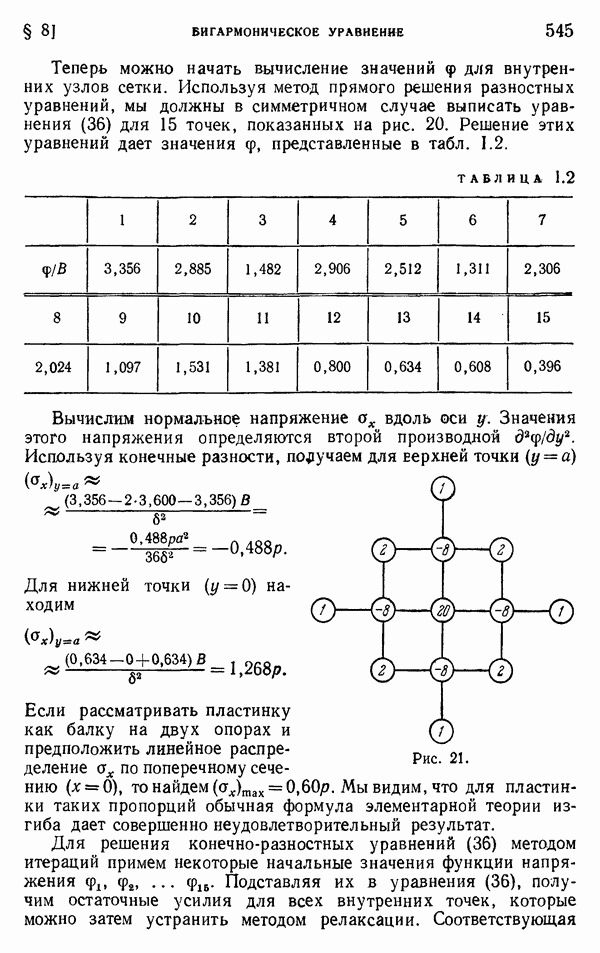
§ 40. Действие на балку сосредоточенной силы
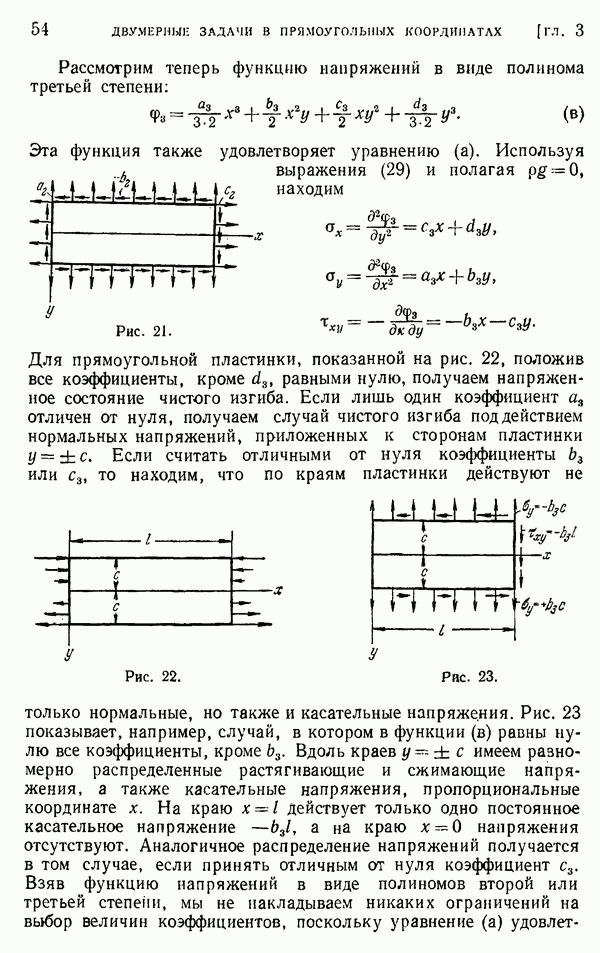
Задача о распределении напряжений в балке при действии сосредоточенной силы представляет большой практический интерес. Ранее было показано (§ 23), что в балке узкого прямоугольного поперечного сечения с непрерывной нагрузкой применение элементарной теории изгиба дает возможность получить
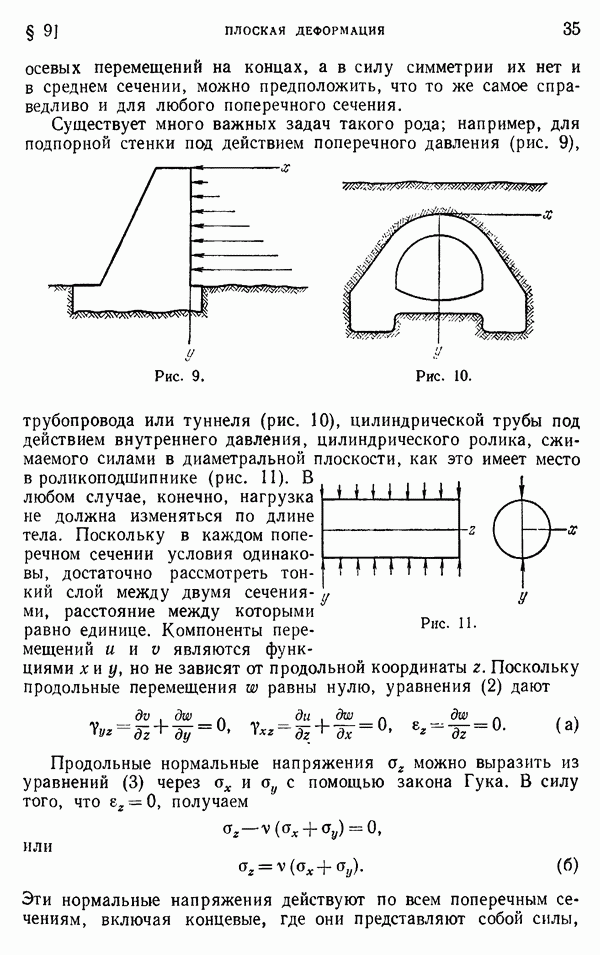
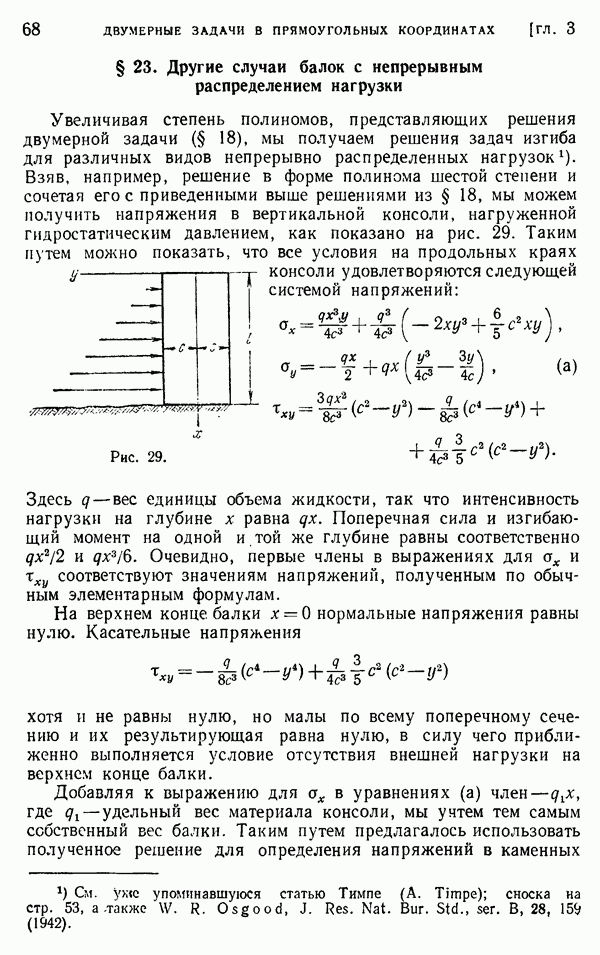
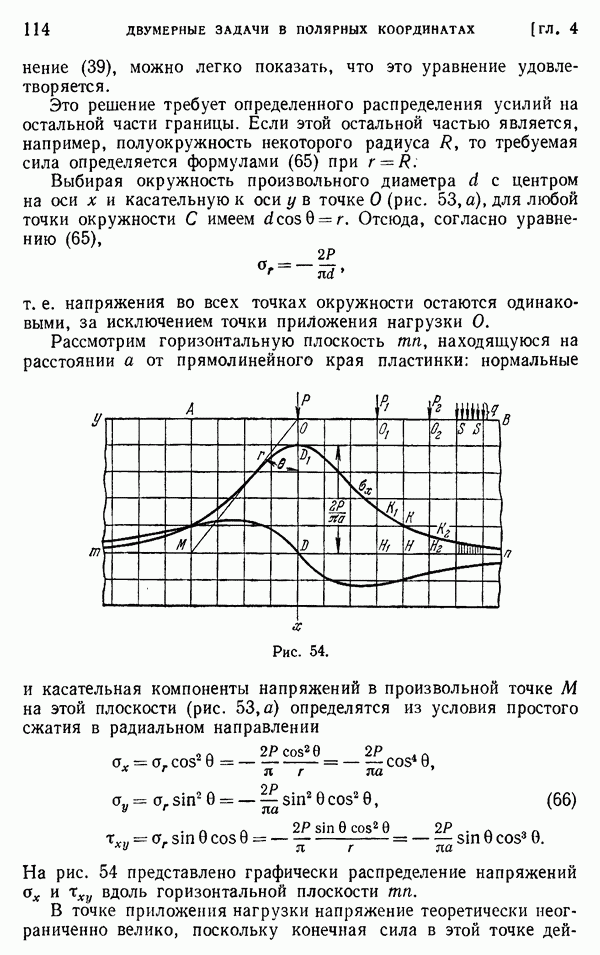
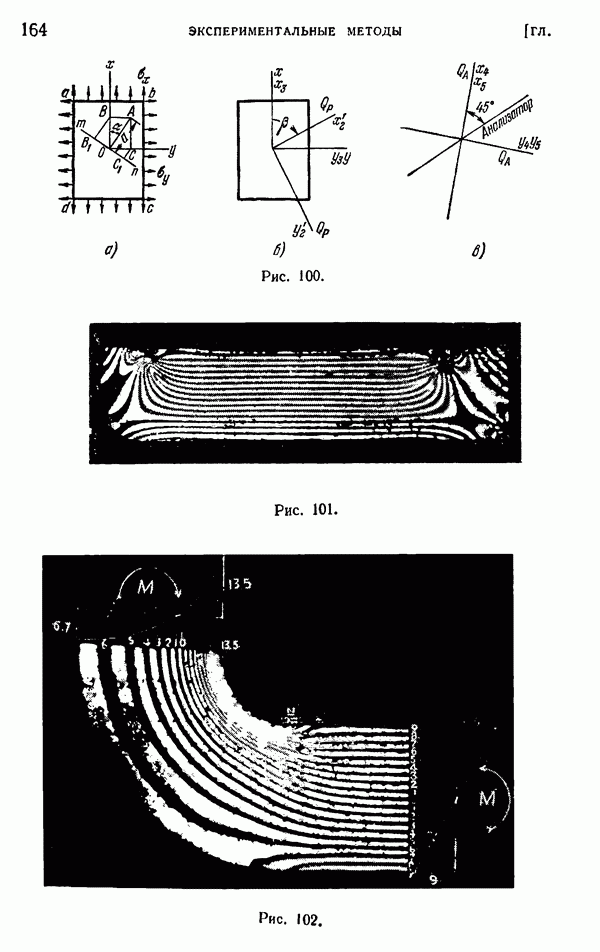
распределение напряжений с удовлетворительной точностью. Однако вблизи точки приложения сосредоточенной силы следует ожидать серьезного местного возмущения в характере распределения напряжений, в связи с чем возникает необходимость дальнейшего исследования этой задачи. Впервые изучение местных напряжений провел экспериментально Карус Вильсон. Проводя опыты с прямоугольной балкой из стекла на двух опорах (рис. 57), нагруженной в центре, и используя поляризованный свет (см. стр. 163), он показал, что в точке А, где приложена нагрузка, распределение напряжений близко к тому, которое наблюдается в полубесконечной пластинке под действием нормальной сосредоточенной силы. Вдоль поперечного сечения  нормальное напряжение
нормальное напряжение  не следует линейному закону, а в точке
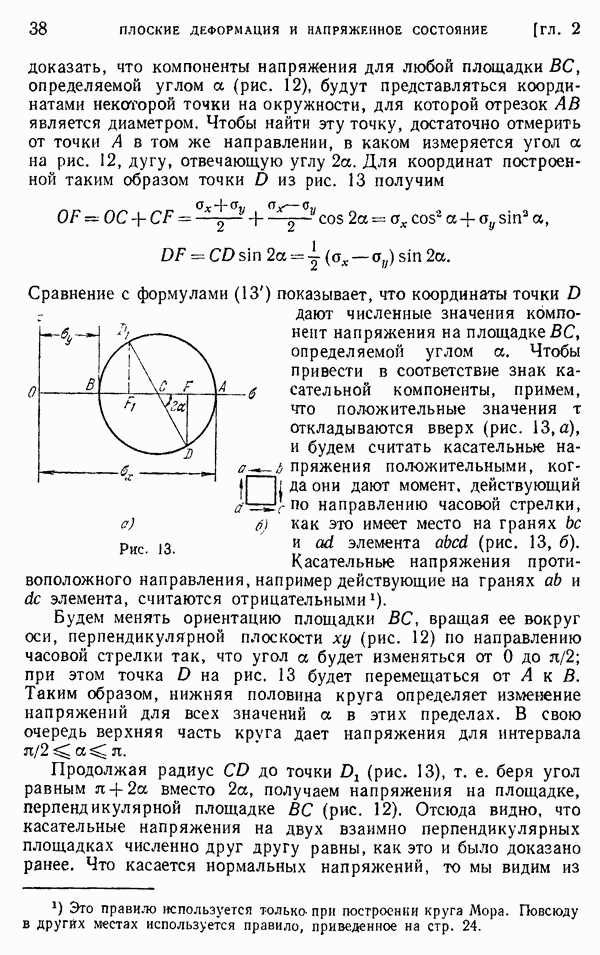
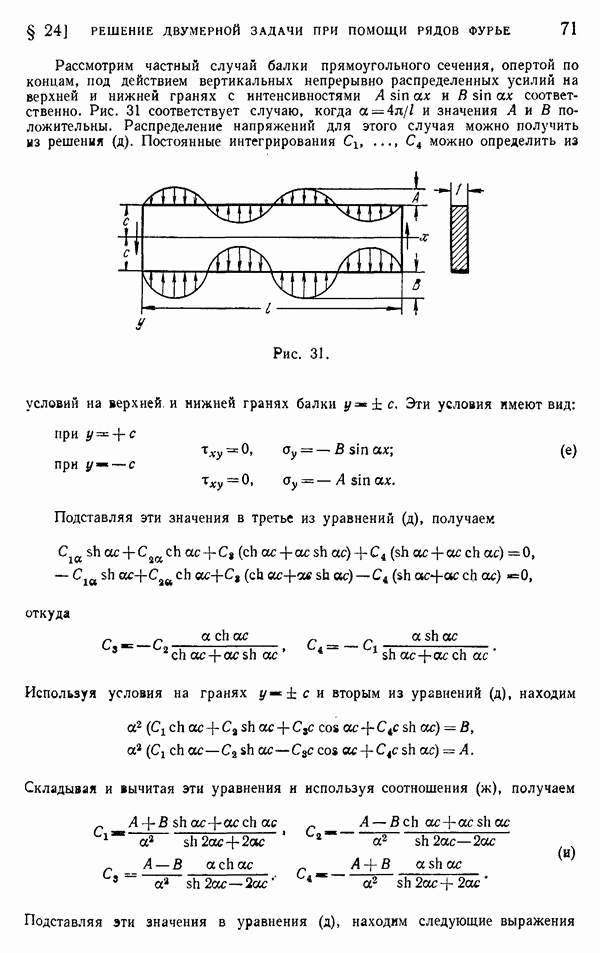
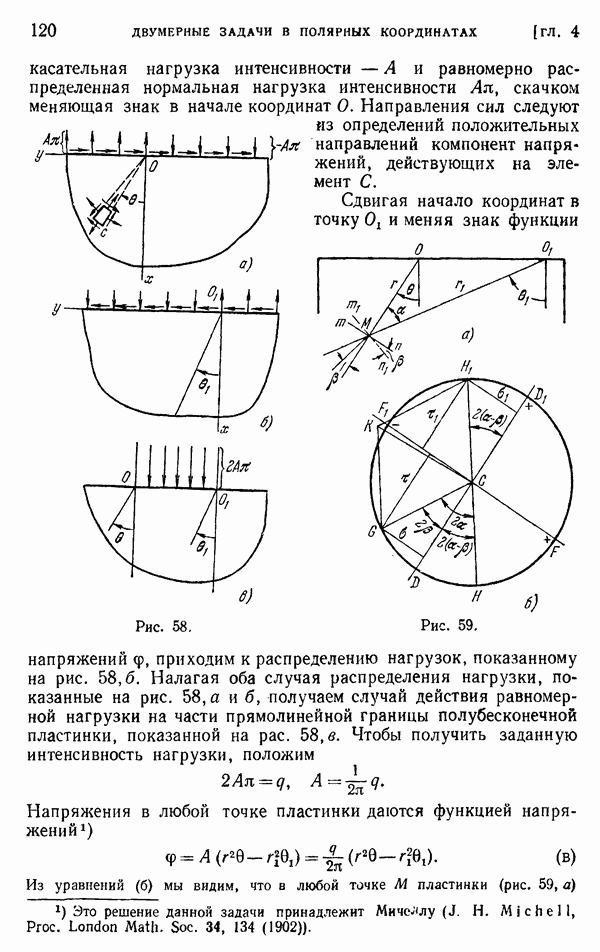
не следует линейному закону, а в точке  расположенной напротив точки А, растягивающее напряжение меньше, чем следовало бы ожидать, исходя из элементарной теории балки. Эти результаты на основании некоторых эмпирических предпосылок объяснил Стокс. Система, представленная на рис. 67, может быть получена путем наложения двух систем, показанных на рис. 68. Радиальные сжимающие напряжения, действующие в сечениях
расположенной напротив точки А, растягивающее напряжение меньше, чем следовало бы ожидать, исходя из элементарной теории балки. Эти результаты на основании некоторых эмпирических предпосылок объяснил Стокс. Система, представленная на рис. 67, может быть получена путем наложения двух систем, показанных на рис. 68. Радиальные сжимающие напряжения, действующие в сечениях  и
и  полубесконечной пластинки (рис. 68, а), снимаются равными им радиальными растягивающими напряжениями, действующими на гранях прямоугольной балки, опертой в точках пир (рис. 68, б). Чтобы получить случай, рассмотренный Стоксом, нужно наложить напряжения в такой балке на напряжения в полубесконечной пластинке.
полубесконечной пластинки (рис. 68, а), снимаются равными им радиальными растягивающими напряжениями, действующими на гранях прямоугольной балки, опертой в точках пир (рис. 68, б). Чтобы получить случай, рассмотренный Стоксом, нужно наложить напряжения в такой балке на напряжения в полубесконечной пластинке.

Рис. 67.
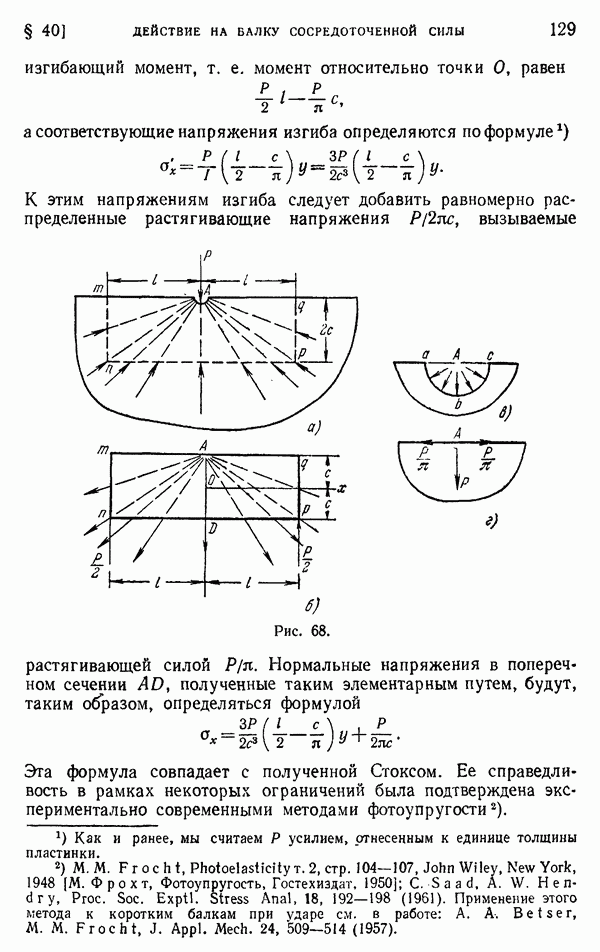
При определении напряжений в балке можно использовать элементарную балочную теорию. Изгибающий момент в среднем сечении  балки получается, если от момента силы реакции
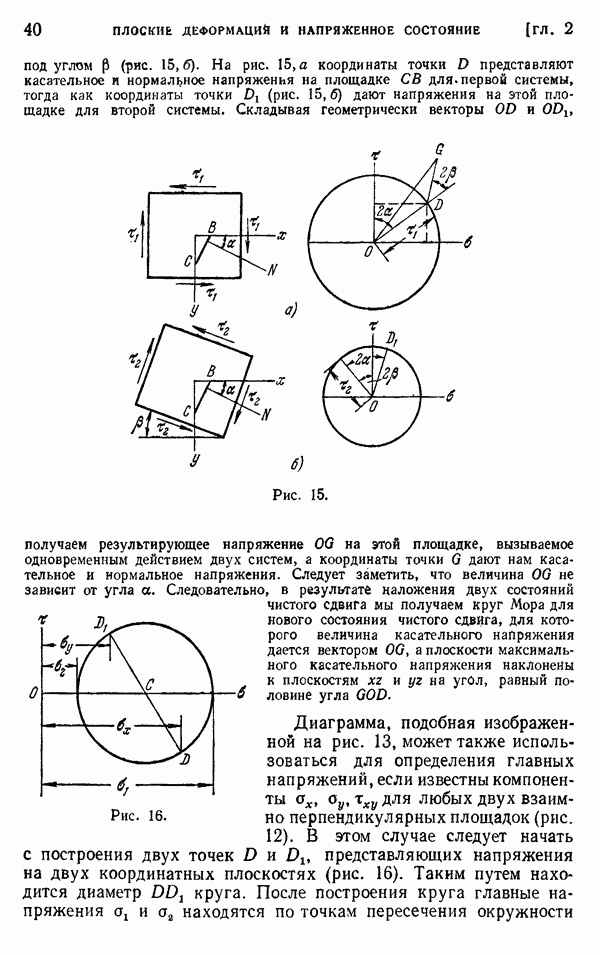
балки получается, если от момента силы реакции  отнять момент всех радиально направленных растягивающих усилий, приложенных к половине балки. Этот момент легко вычислить, если учесть, что радиально распределенные растягивающие усилия статически эквивалентны давлению, распределенному по квадранту
отнять момент всех радиально направленных растягивающих усилий, приложенных к половине балки. Этот момент легко вычислить, если учесть, что радиально распределенные растягивающие усилия статически эквивалентны давлению, распределенному по квадранту  цилиндрической поверхности
цилиндрической поверхности  расположенной у точки А (рис. 68, в). Или же, согласно уравнению (65), эти усилия эквивалентны горизонтальной силе
расположенной у точки А (рис. 68, в). Или же, согласно уравнению (65), эти усилия эквивалентны горизонтальной силе  и вертикальной силе Р, приложенным в точке А (рис. 68, г). Тогда
и вертикальной силе Р, приложенным в точке А (рис. 68, г). Тогда
изгибающий момент, т. е. момент относительно точки О, равен

а соответствующие напряжения изгиба определяются по формуле

К этим напряжениям изгиба следует добавить равномерно распределенные растягивающие напряжения  вызываемые растягивающей силой
вызываемые растягивающей силой 

Рис. 68.
Нормальные напряжения в поперечном сечении  полученные таким элементарным путем, будут, таким образом, определяться формулой
полученные таким элементарным путем, будут, таким образом, определяться формулой

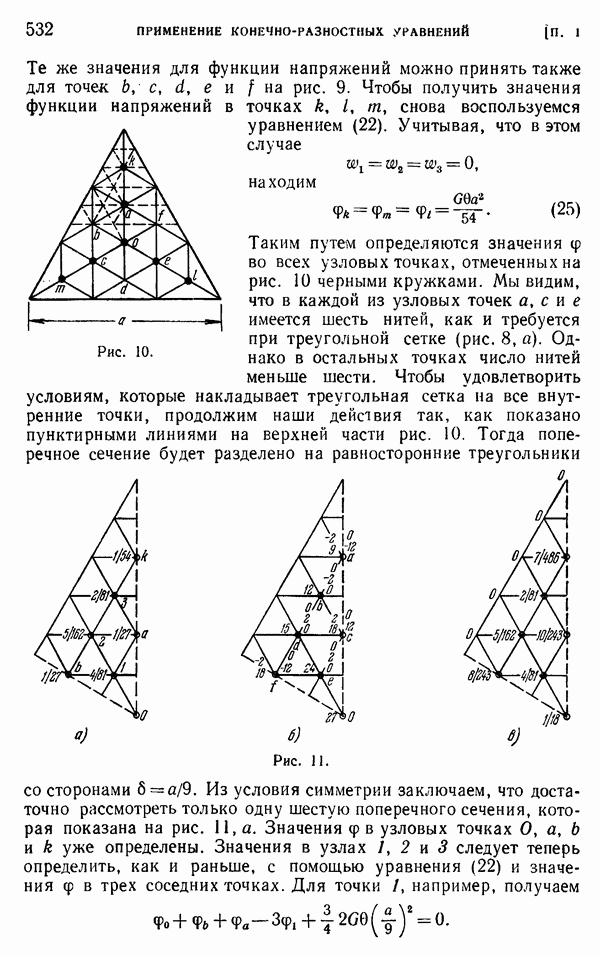
Эта формула совпадает с полученной Стоксом. Ее справедливость в рамках некоторых ограничений была подтверждена экспериментально современными методами фотоупругости.
Несколько лучшее приближение можно получить, если учесть, что к нижней грани балки прикладывается распределенная нагрузка (рис. 68, б) и использовать уравнения (36). Интенсивность такой нагрузки в точке D из уравнения (65) равна  Подставляя данное значение в (36) и комбинируя результат со значением
Подставляя данное значение в (36) и комбинируя результат со значением  полученным выше, получаем во втором приближении
полученным выше, получаем во втором приближении

Эти напряжения нужно наложить на напряжения

действующие в полубесконечной пластинке, в результате получатся напряжения в сечении 
Сравнение с более точным решением, приведенным ниже (см. таблицу 2, стр. 133), показывает, что уравнения (а) и (б) дают с очень высокой точностью напряжения во всех точках, за исключением точки D на нижней грани балки, где поправка к простой балочной формуле дается выражением

тогда как более точное решение дает всего 
Решение той же задачи с помощью тригонометрических рядов получил Файлом.  применил это решение к случаю действия сосредоточенных сил и для нескольких частных случаев провел вычисления (см. § 24), которые находятся в хорошем согласии с более поздними исследованиями.
применил это решение к случаю действия сосредоточенных сил и для нескольких частных случаев провел вычисления (см. § 24), которые находятся в хорошем согласии с более поздними исследованиями.
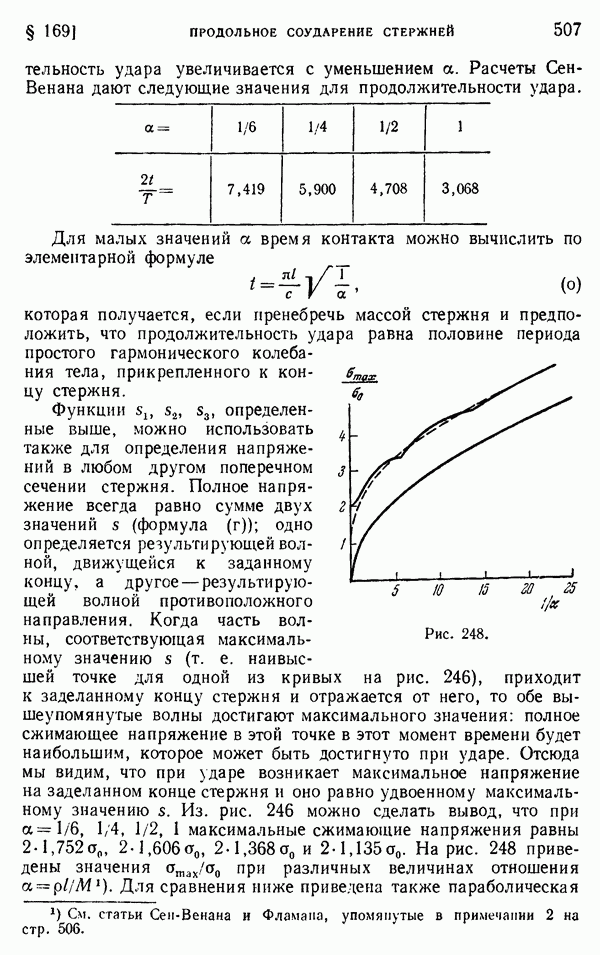
Дальнейшего прогресса в этой области достиг Лэмб, который рассмотрел бесконечную балку, нагруженную через равные промежутки равными сосредоточенными силами, действующими попеременно вверх и вниз, и получил для нескольких случаев выражения кривой прогибов. Полученные результаты показывают, что элементарная теория изгиба Бернулли—Эйлера является весьма точной, если высота балки мала по сравнению с длиной. Было также показано, что уточнения для поперечной силы, даваемые элементарной теорией Ренкина и Грасхофа (см. стр. 67), являются несколько завышенными и должны быть уменьшены примерно на 25%.
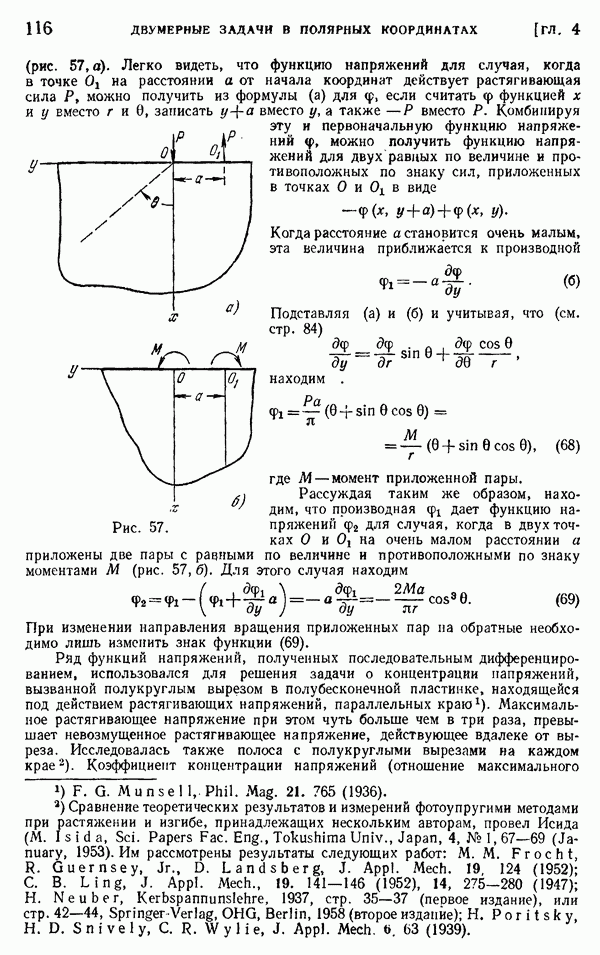
Более детальное исследование распределения напряжений и кривизны вблизи точки приложения сосредоточенной силы провели Карман и Зеевальд. Карман рассмотрел бесконечно длинную балку и использовал решение для бесконечной пластинки с двумя равными и противоположными моментами, действующими в двух соседних точках прямолинейной границы (рис. 57, б). Напряжения вдоль нижней грани балки, которые вводятся благодаря такой процедуре, можно снять, если использовать решение в виде тригонометрических рядов (§ 24), которое для бесконечно длинной балки представляется интегралом Фурье. Таким путем Карман пришел к функции напряжений

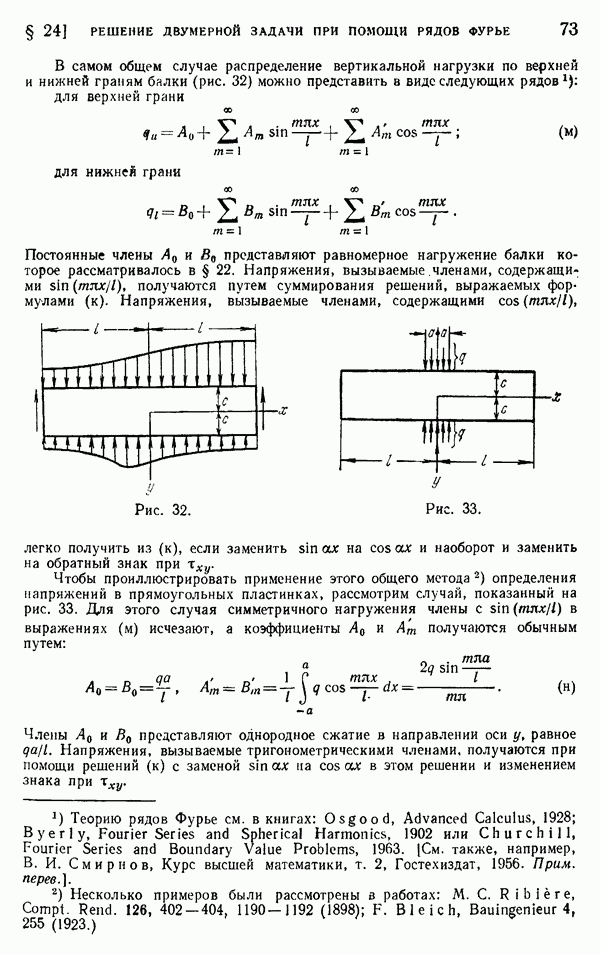
Эта функция дает распределение напряжений в балке, когда эпюра изгибающих моментов состоит из очень узкого прямоугольника, как показано на рис. 69. В самом общем случае нагружения балки вертикальными силами, приложенными на верхней грани балки, соответствующая эпюра изгибающих моментов может быть разделена на элементарные прямоугольники, подобные показанному на рис. 69, а соответствующую функцию напряжений можно получить путем интегрирования выражения (в) вдоль длины балки.

Рис. 69.
Этот метод решения Зеевальд применил к случаю балки, нагруженной сосредоточенной силой Р (рис. 67). Он показал, что напряжение  можно разбить на две части: одну из них можно вычислить по элементарной балочной формуле, другая характеризует локальный эффект вблизи точки приложения силы. Эту последнюю часть напряжения, обозначаемую через
можно разбить на две части: одну из них можно вычислить по элементарной балочной формуле, другая характеризует локальный эффект вблизи точки приложения силы. Эту последнюю часть напряжения, обозначаемую через  можно представить в форме
можно представить в форме  где
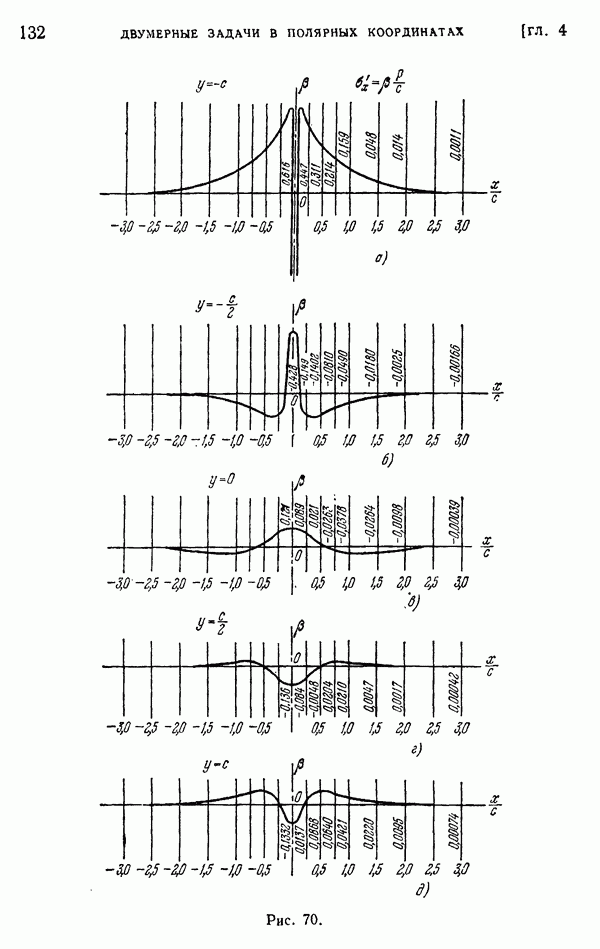
где  — численный множитель, зависящий от положения точки, в которой определяется местное напряжение. Значения этого множителя даны на рис. 70. Две другие компоненты напряжения
— численный множитель, зависящий от положения точки, в которой определяется местное напряжение. Значения этого множителя даны на рис. 70. Две другие компоненты напряжения  также можно представить в форме
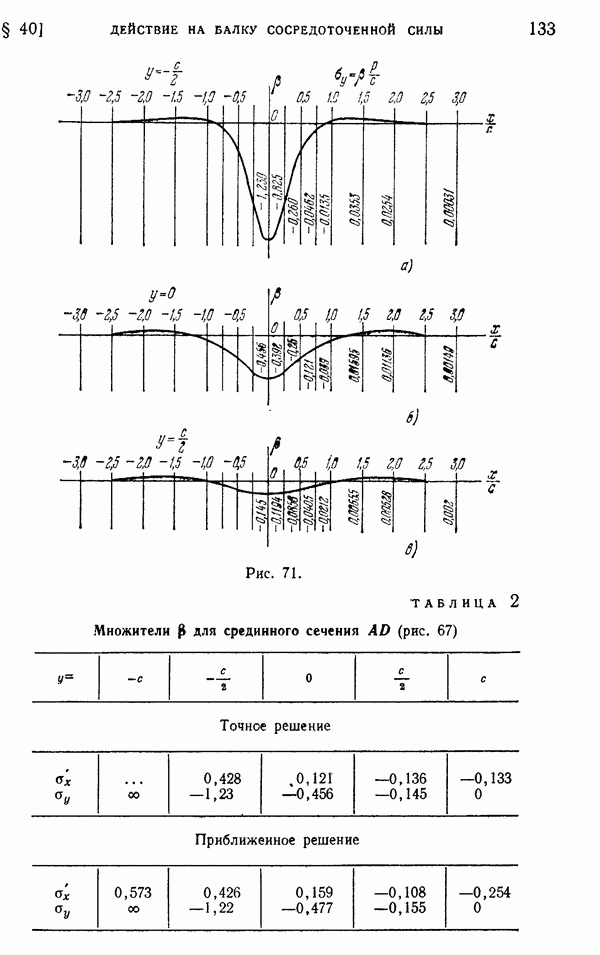
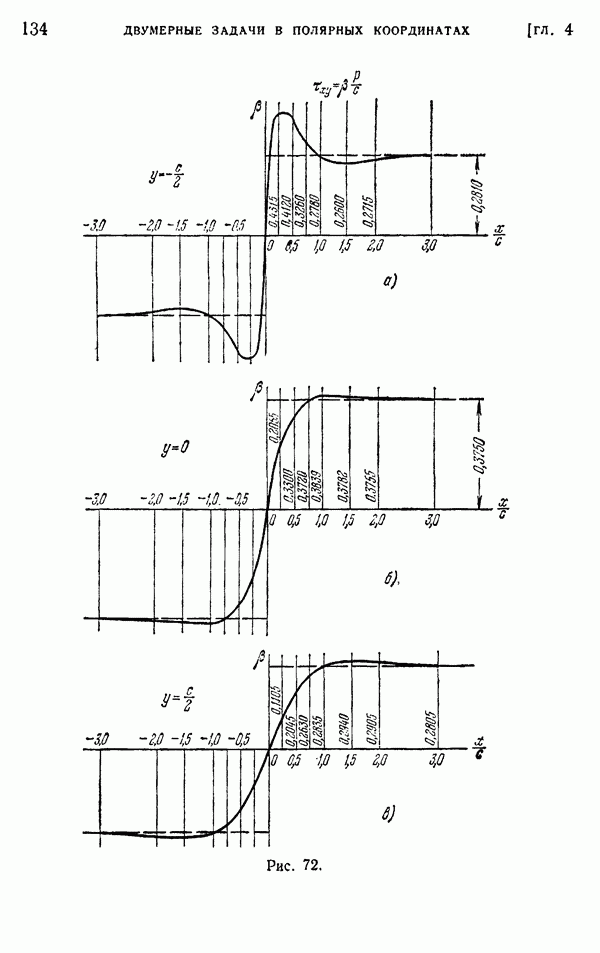
также можно представить в форме  Соответствующие значения Сдаются на рис. 71 и 72. Из них можно видеть, что местные напряжения весьма быстро падают с увеличением расстояния от точки приложения нагрузки, и на расстоянии, равном высоте балки, ими обычно можно пренебречь. Используя значения множителя
Соответствующие значения Сдаются на рис. 71 и 72. Из них можно видеть, что местные напряжения весьма быстро падают с увеличением расстояния от точки приложения нагрузки, и на расстоянии, равном высоте балки, ими обычно можно пренебречь. Используя значения множителя  при
при  можно найти местные напряжения в пяти точках поперечного сечения
можно найти местные напряжения в пяти точках поперечного сечения  при данной нагрузке (рис. 67) по приводимой
при данной нагрузке (рис. 67) по приводимой

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
на стр. 133 табл. 2. Для сравнения в ней приводятся значения местных напряжений, полученные из уравнений (а) и (б) (стр. 130). Как видим, эти уравнения дают местные напряжения с достаточной степенью точности.
Зная напряжения, можно без особых трудностей найти кривизны и прогибы балки.

Рис. 73.

Рис. 74.
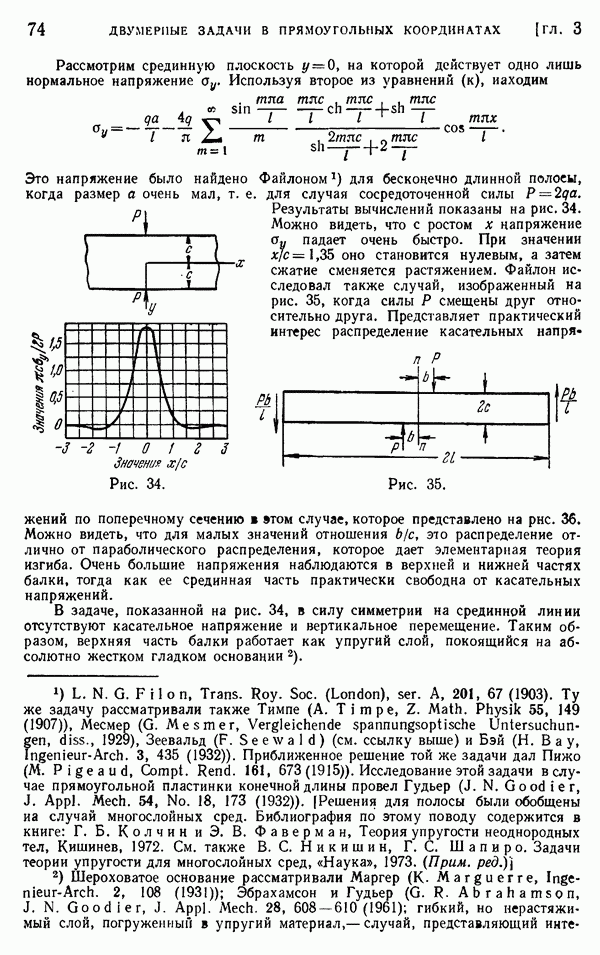
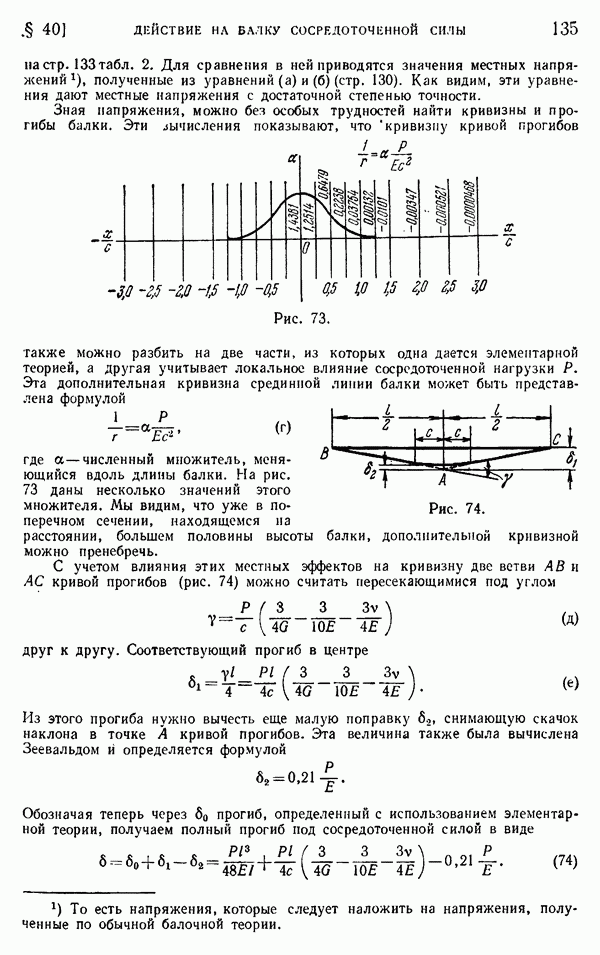
Эти вычисления показывают, что кривизну кривой прогибов также можно разбить на две части, из которых одна дается элементарной теорией, а другая учитывает локальное влияние сосредоточенной нагрузки Р. Эта дополнительная кривизна срединной линии балки может быть представлена формулой

где а — численный множитель, меняющийся вдоль длины балки. На рис. 73 даны несколько значений этого множителя. Мы видим, что уже в поперечном сечении, находящемся на расстоянии, большем половины высоты балки, дополнительной кривизной можно пренебречь.
С учетом влияния этих местных эффектов на кривизну две ветви  кривой прогибов (рис. 74) можно считать пересекающимися под углом
кривой прогибов (рис. 74) можно считать пересекающимися под углом

друг к другу. Соответствующий прогиб в центре

Из этого прогиба нужно вычесть еще малую поправку  снимающую скачок наклона в точке А кривой прогибов. Эта величина также была вычислена Зеевальдом и определяется формулой
снимающую скачок наклона в точке А кривой прогибов. Эта величина также была вычислена Зеевальдом и определяется формулой

Обозначая теперь через  прогиб, определенный с использованием элементарной теории, получаем полный прогиб под сосредоточенной силой в виде
прогиб, определенный с использованием элементарной теории, получаем полный прогиб под сосредоточенной силой в виде

При  эта формула дает
эта формула дает

Элементарная теория Ренкииа—Грасхофа (см. стр. 67) для этого случая приводит к выражению

Очевидно, что равенство  дает завышенное значение поправки, связанной со сдвигом. В этих формулах не учтен прогиб, вызванный местными деформациями на опорах.
дает завышенное значение поправки, связанной со сдвигом. В этих формулах не учтен прогиб, вызванный местными деформациями на опорах.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
- § 23. Другие случаи балок с непрерывным распределением нагрузки
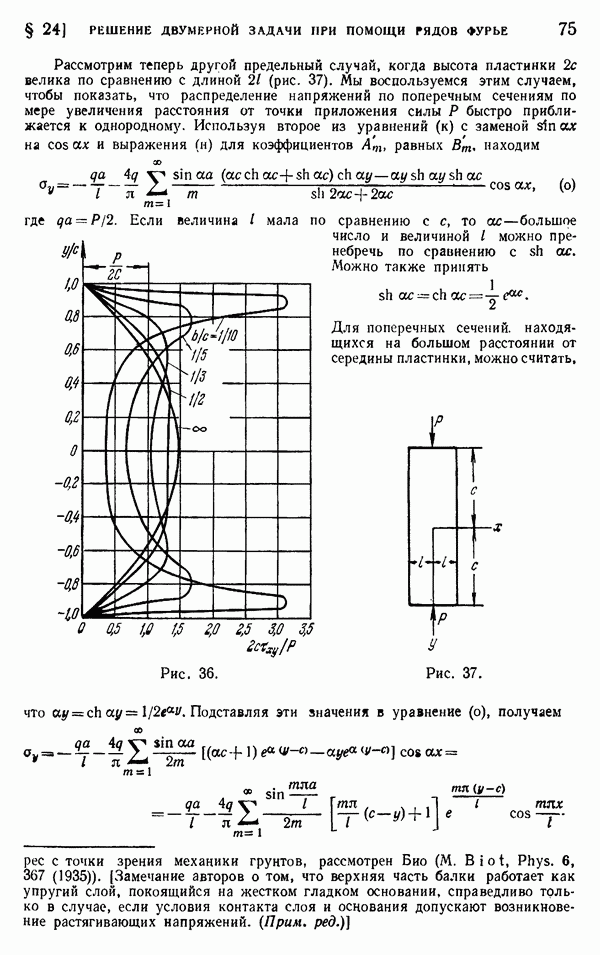
- § 24. Решение двумерной задачи при помощи рядов Фурье
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
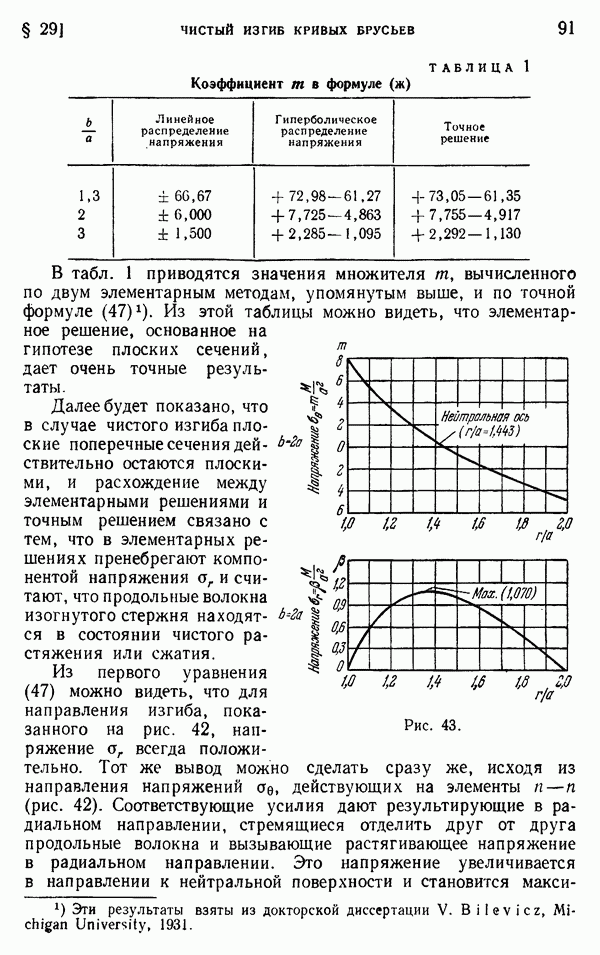
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
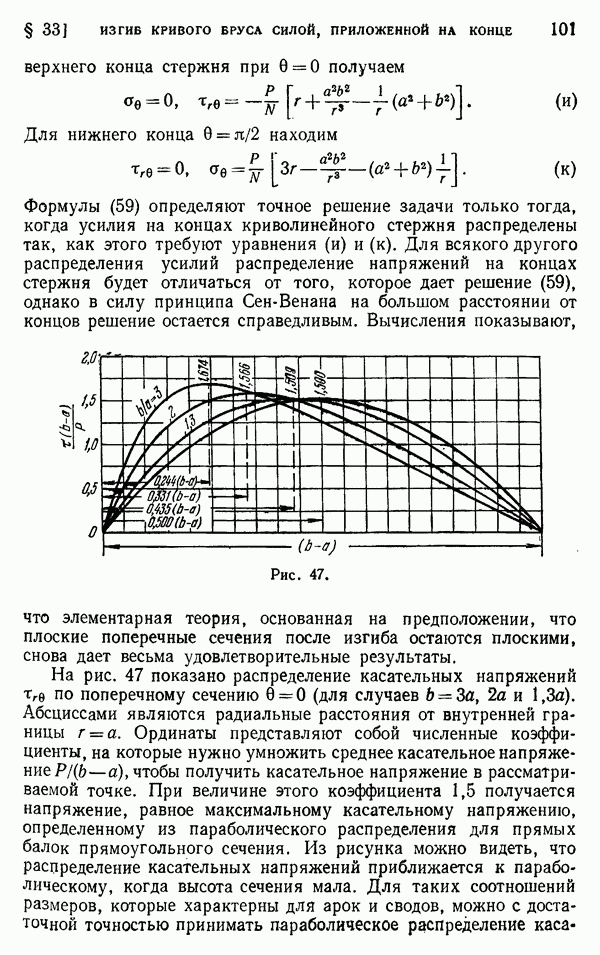
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
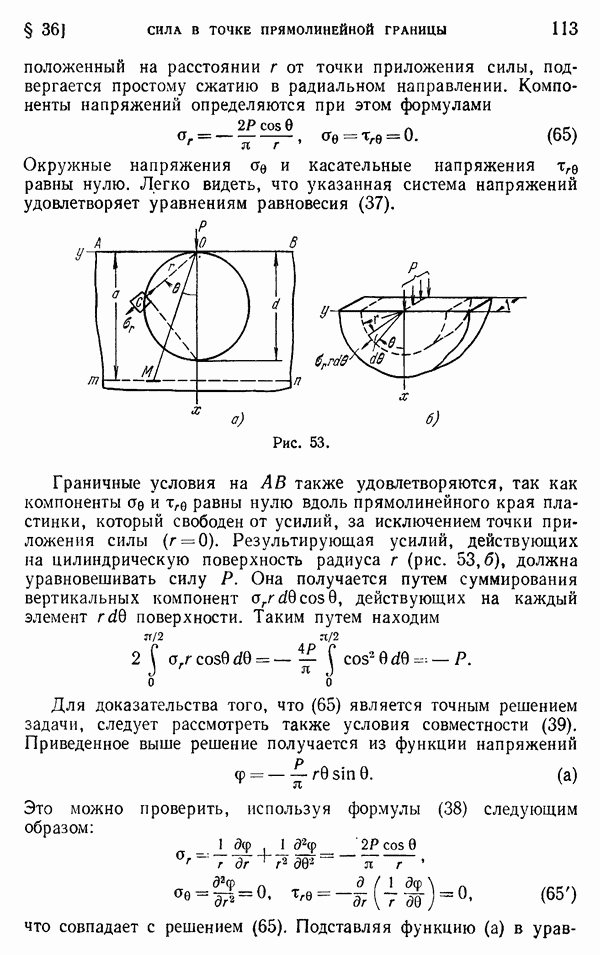
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
- § 39. Изгибающий момент, действующий на острие клина
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
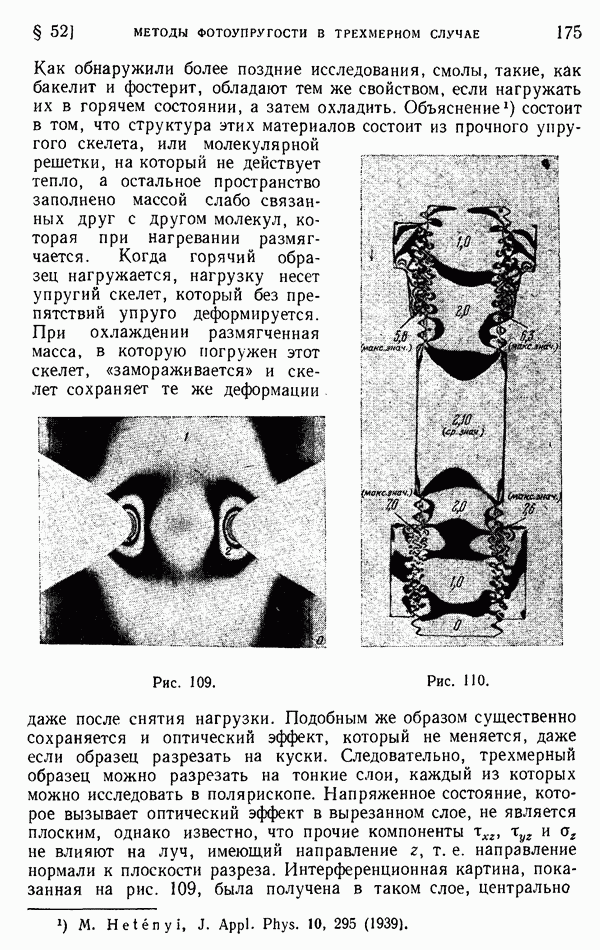
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
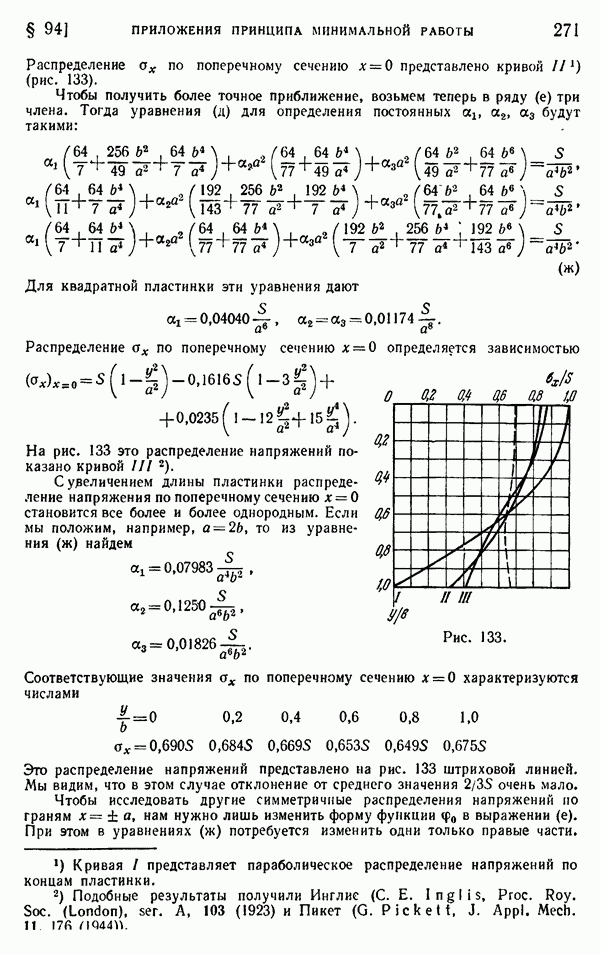
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
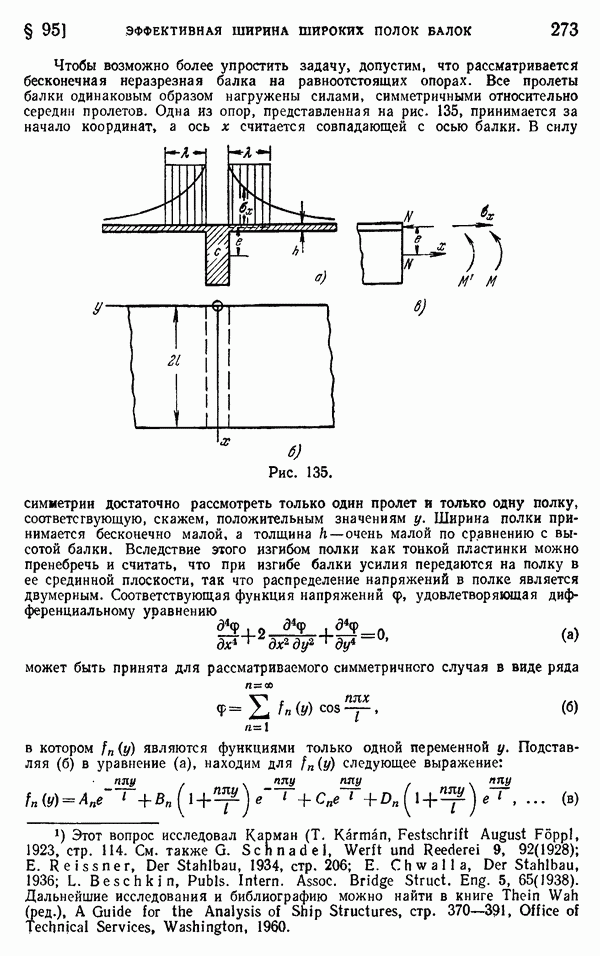
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
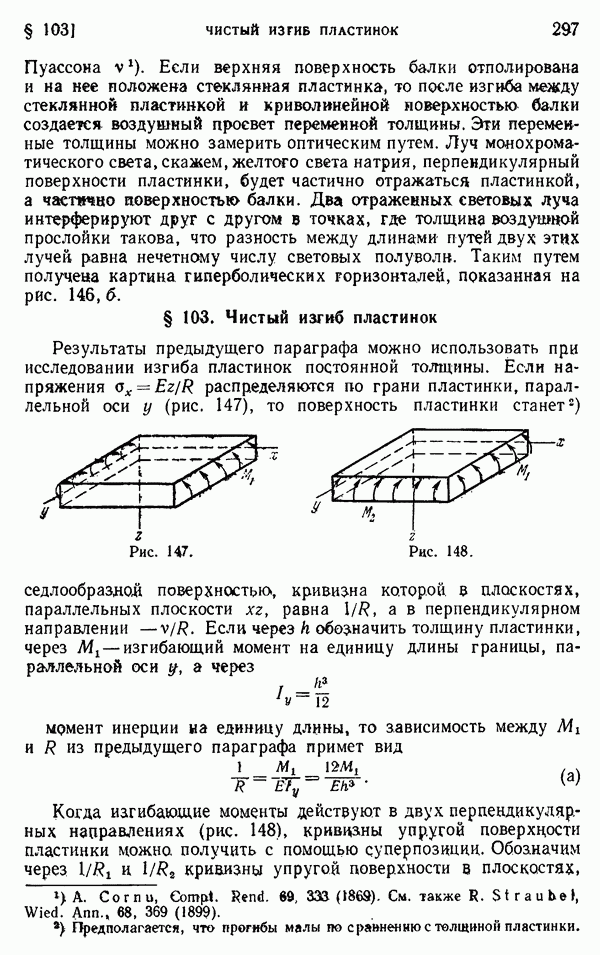
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
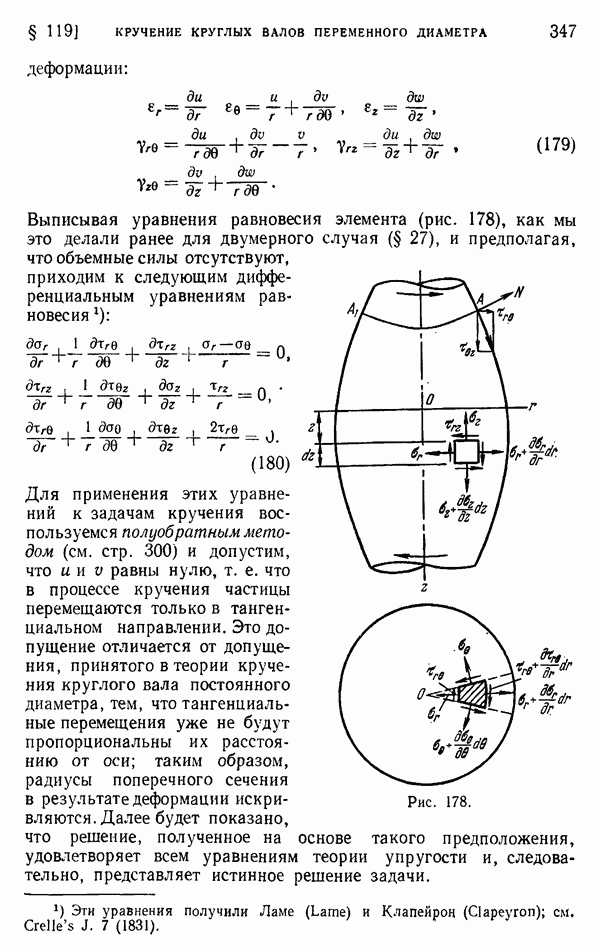
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
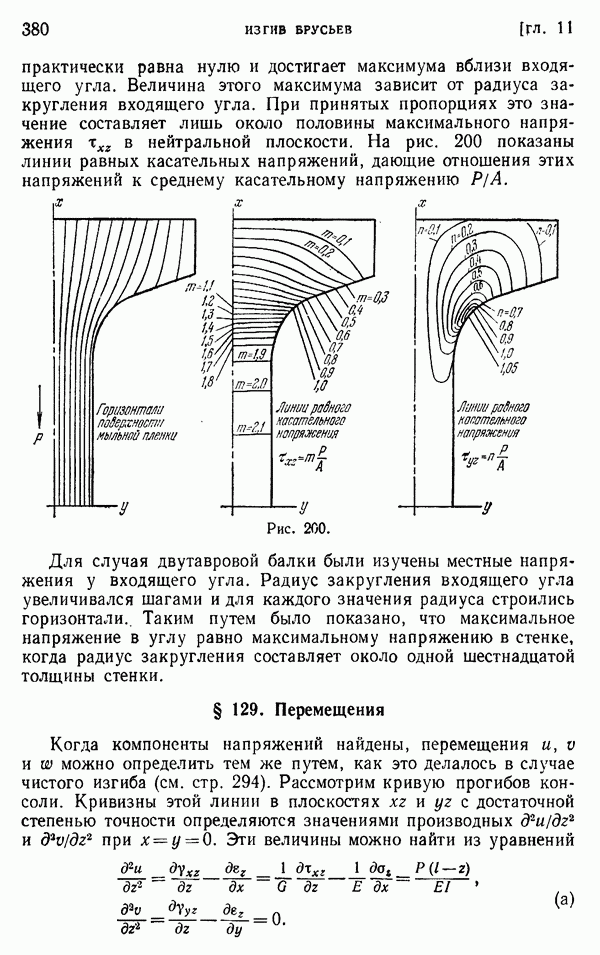
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
- § 151. Длинный круглый цилиндр
- § 152. Сфера
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
- § 4. Треугольные и шестиугольные сетки
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
- § 7. Точки, расположенные вблизи границы
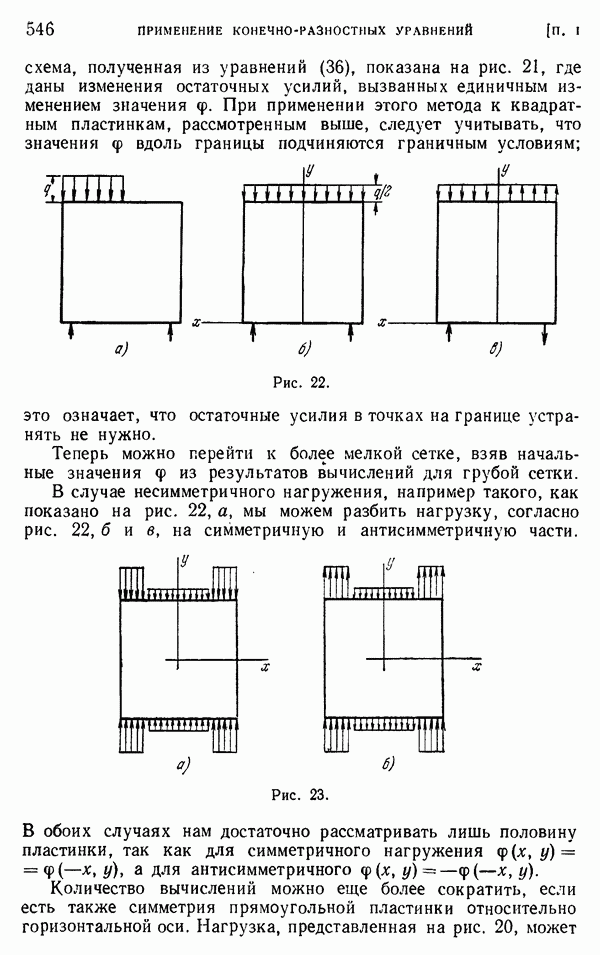
- § 8. Бигармоническое уравнение
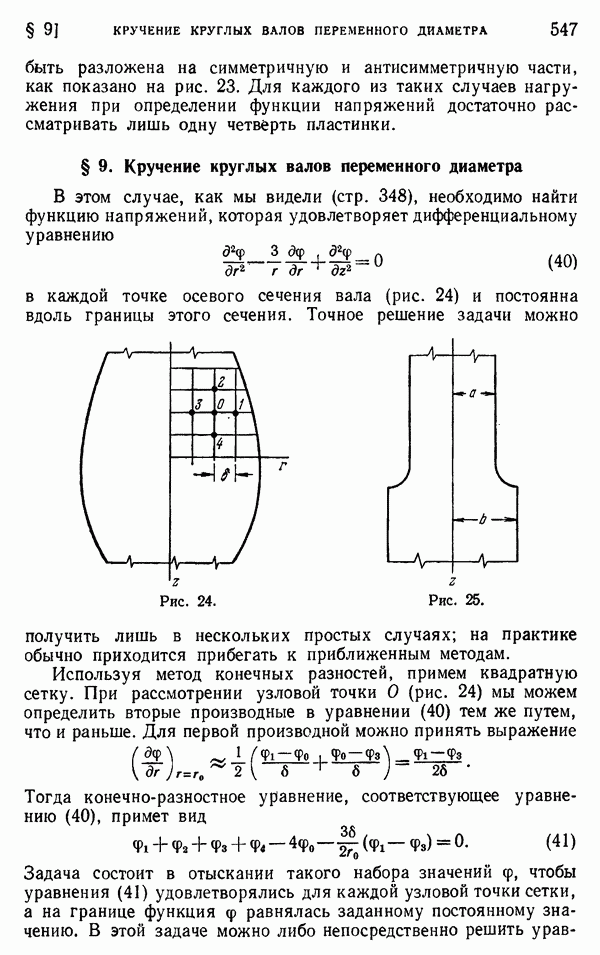
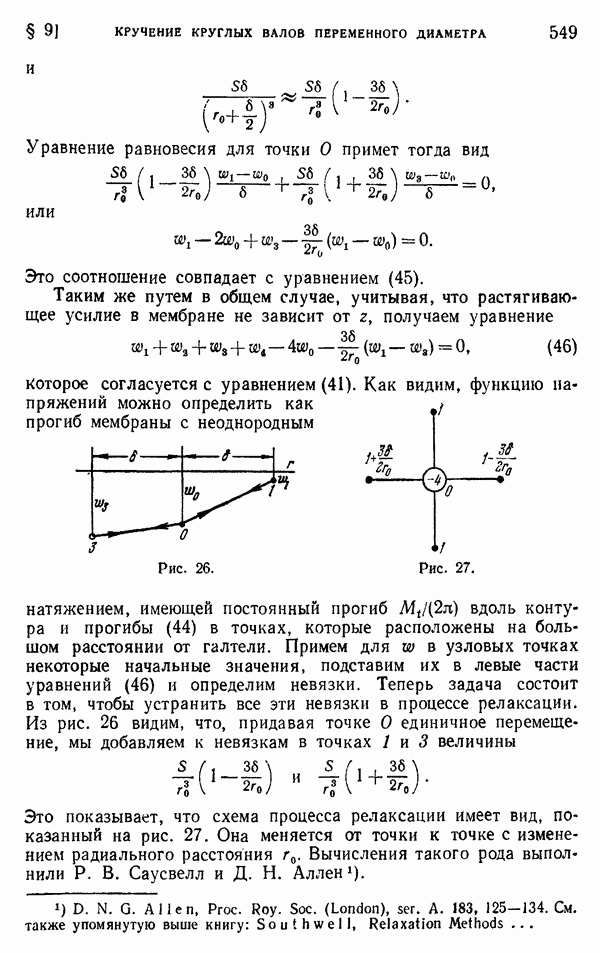
- § 9. Кручение круглых валов переменного диаметра
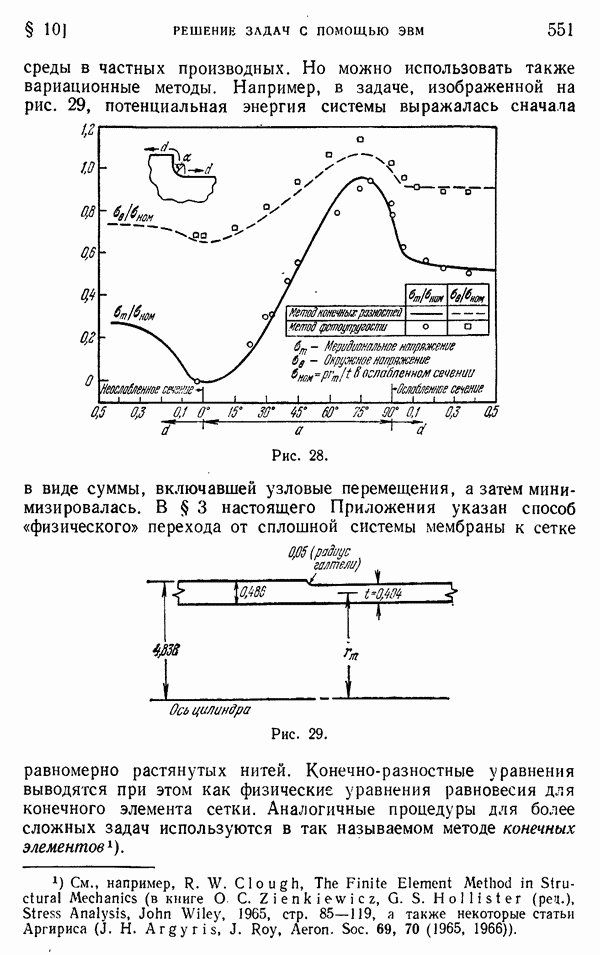
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
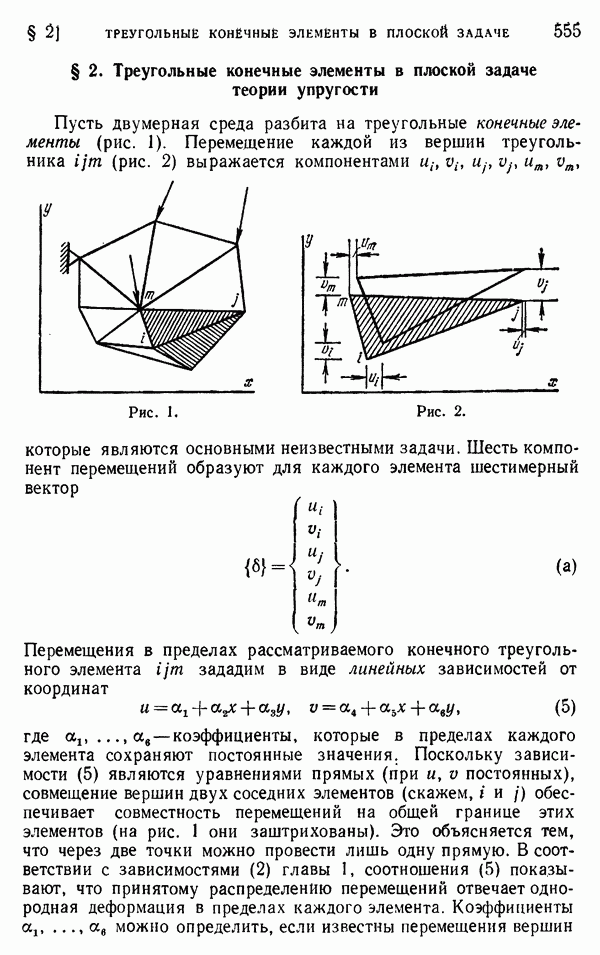
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
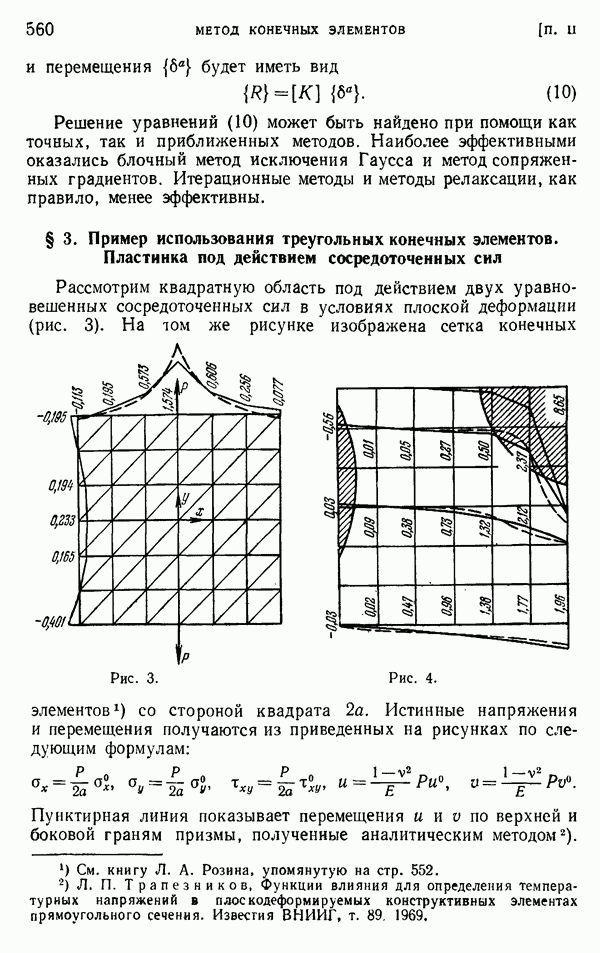
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
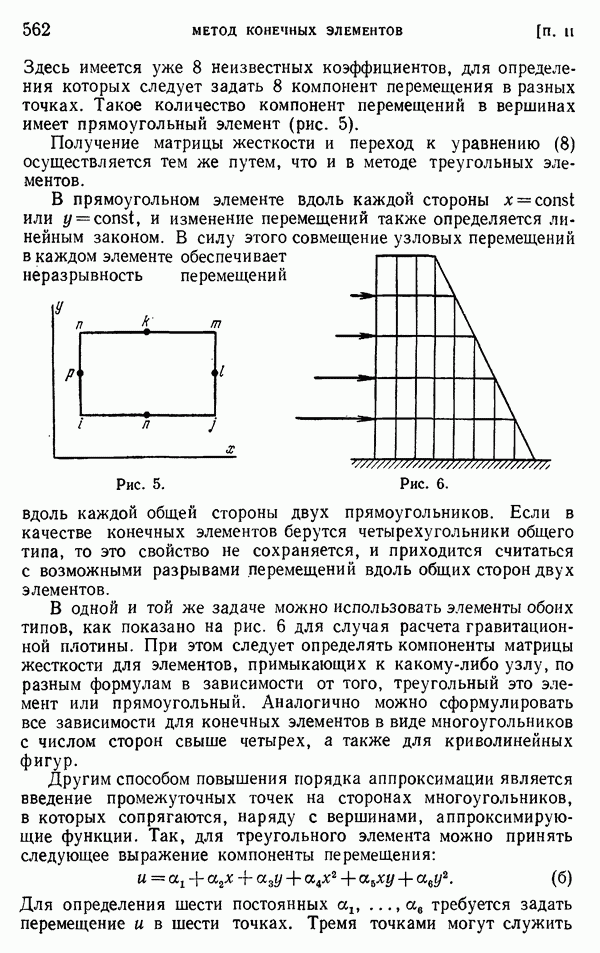
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи