| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
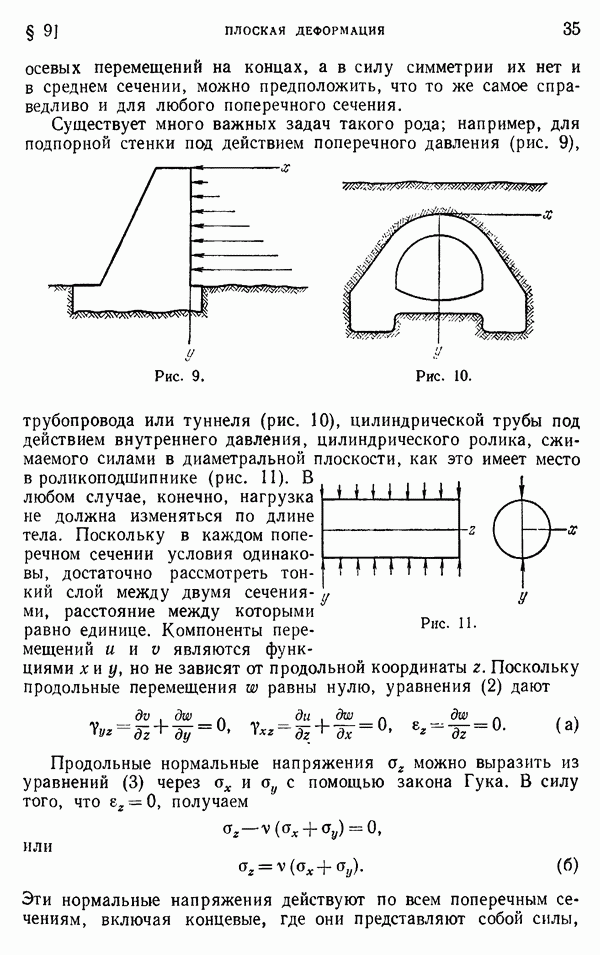
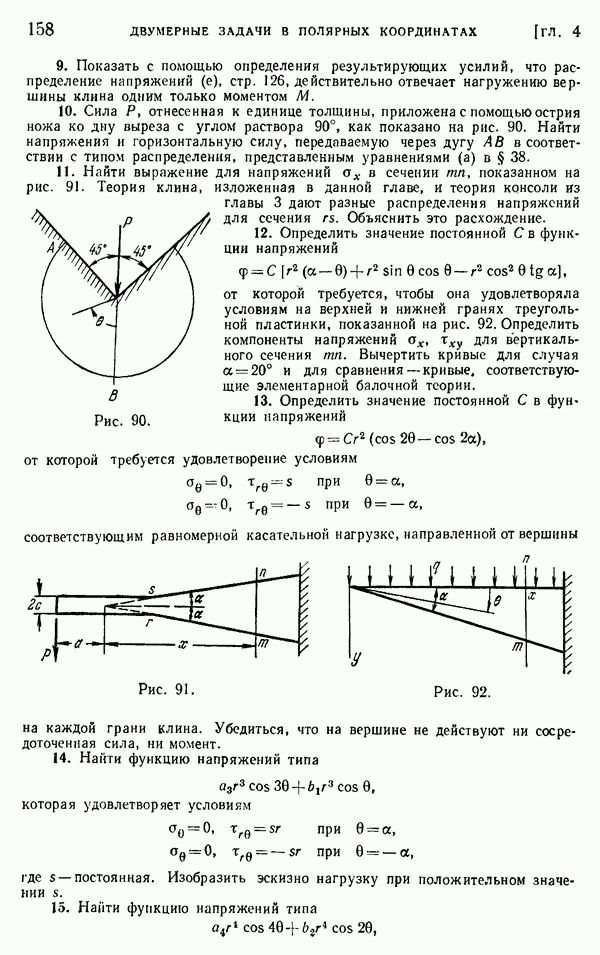
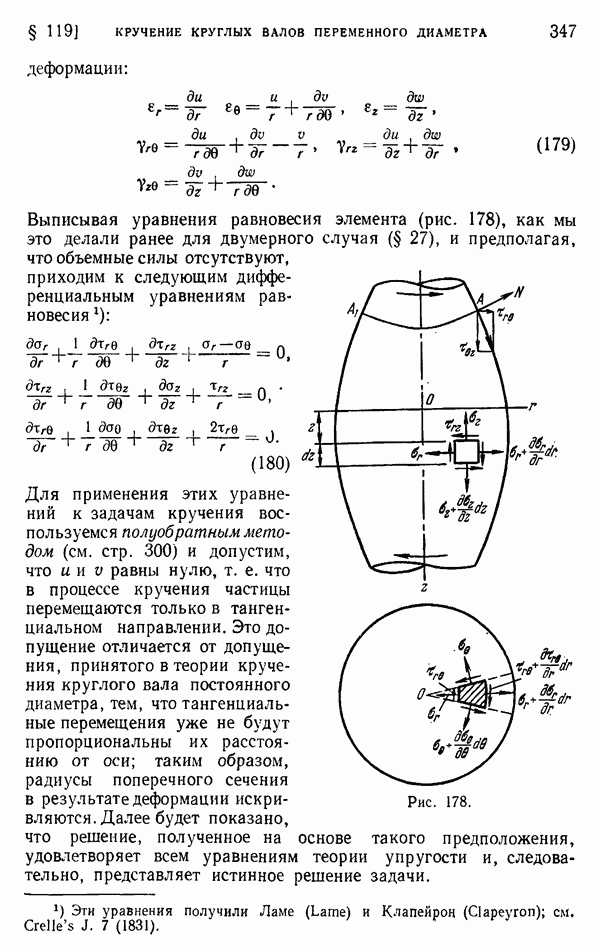
§ 116. Кручение тонкостенных труб
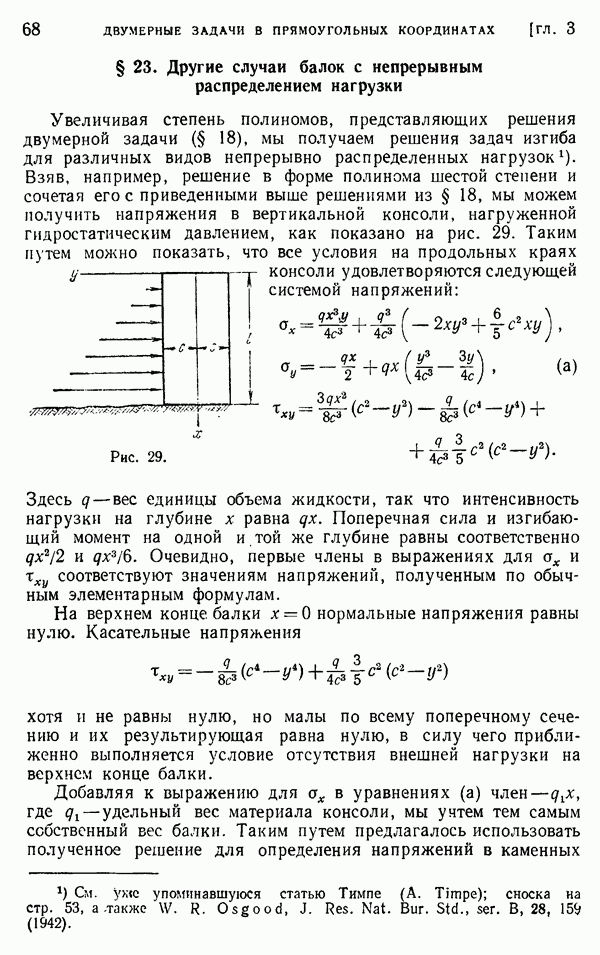
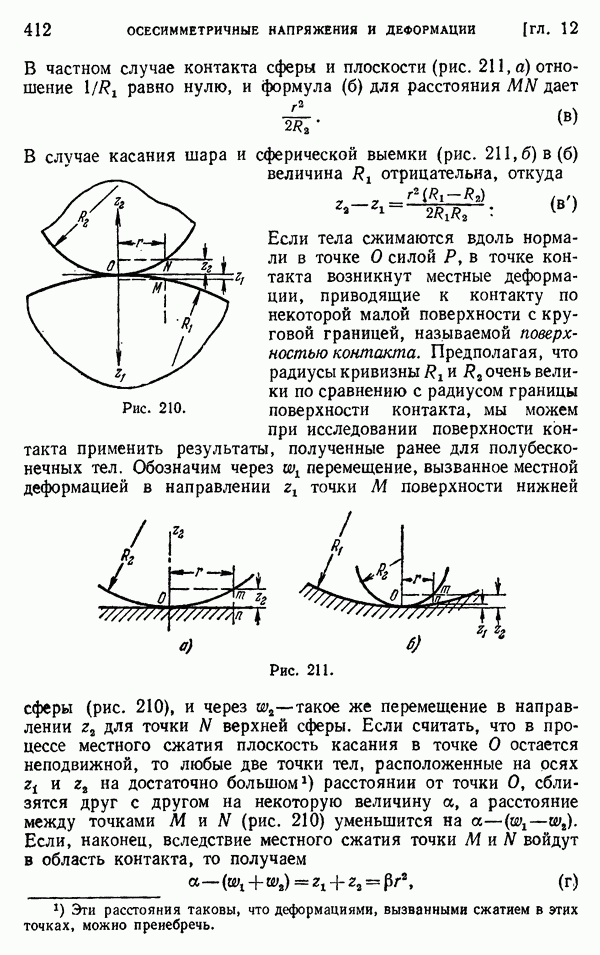
Используя мембранную аналогию, легко получить решение задачи о кручении для тонкостенных труб. Обозначим через  и
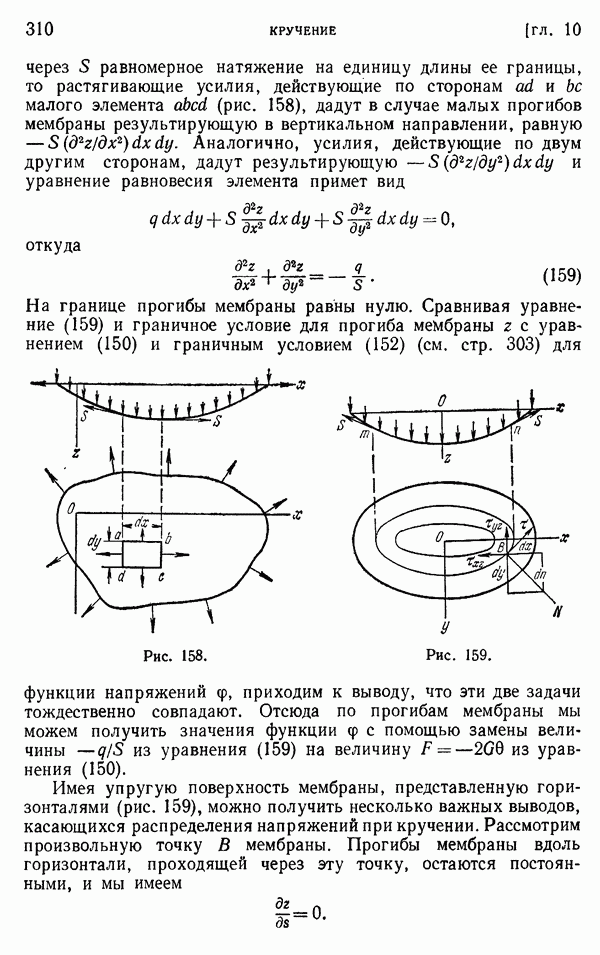
и  (рис. 172) уровни внешней и внутренней границ, а через АС и DB — поперечное сечение мембраны, натянутой на эти границы. В случае тонкой стенки мы можем пренебречь изменениями наклона мембраны по ее толщине и предположить что АС и BD — прямые линии. Это эквивалентно предположению, что касательные напряжения по толщине трубы распределены равномерно. Тогда, обозначая через
(рис. 172) уровни внешней и внутренней границ, а через АС и DB — поперечное сечение мембраны, натянутой на эти границы. В случае тонкой стенки мы можем пренебречь изменениями наклона мембраны по ее толщине и предположить что АС и BD — прямые линии. Это эквивалентно предположению, что касательные напряжения по толщине трубы распределены равномерно. Тогда, обозначая через  разность в уровне этих двух границ, а через
разность в уровне этих двух границ, а через  — переменную толщину стенки, получаем, что напряжение в любой точке, определяемое наклоном мембраны, равно
— переменную толщину стенки, получаем, что напряжение в любой точке, определяемое наклоном мембраны, равно


Рис. 172.
Таким образом, напряжение  обратно пропорционально толщине стенки и в силу этого достигает максимума там, где толщина стенки минимальна.
обратно пропорционально толщине стенки и в силу этого достигает максимума там, где толщина стенки минимальна.
Чтобы установить зависимость между напряжением и крутящим моментом М, снова используем мембранную аналогию и определим крутящий момент, исходя из объема  Отсюда
Отсюда

здесь А — усредненное значение площади, заключенной между внешним и внутренним контурами поперечного сечения трубы. Из зависимости (б) получаем простую формулу для определения касательного напряжения

Для определения угла закручивания 0 применим формулу (160). Тогда

откуда

В случае трубы постоянной толщины значение  постоянно и формула (177) дает
постоянно и формула (177) дает

где  — длина срединной линии кольцевого сечения трубы.
— длина срединной линии кольцевого сечения трубы.

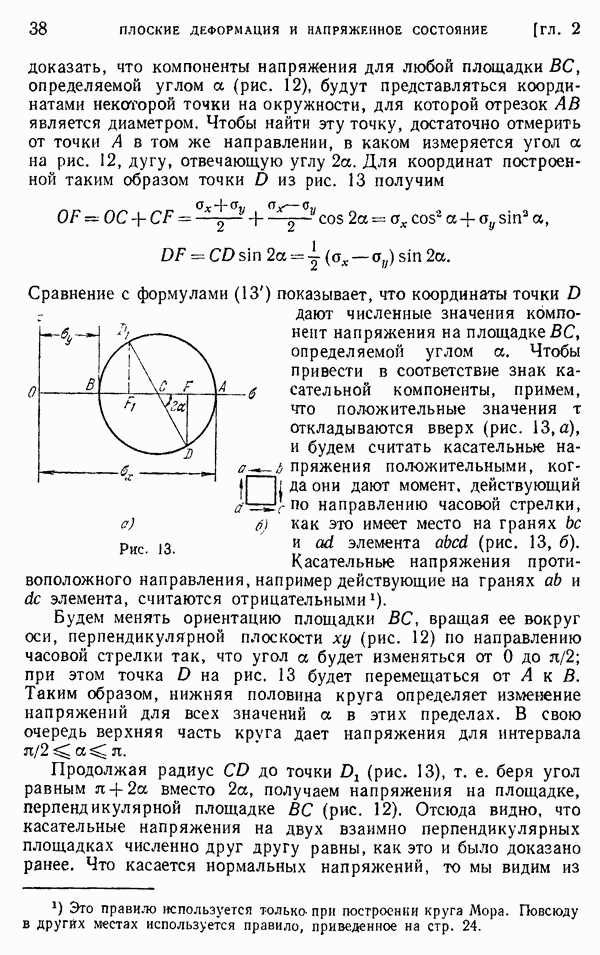
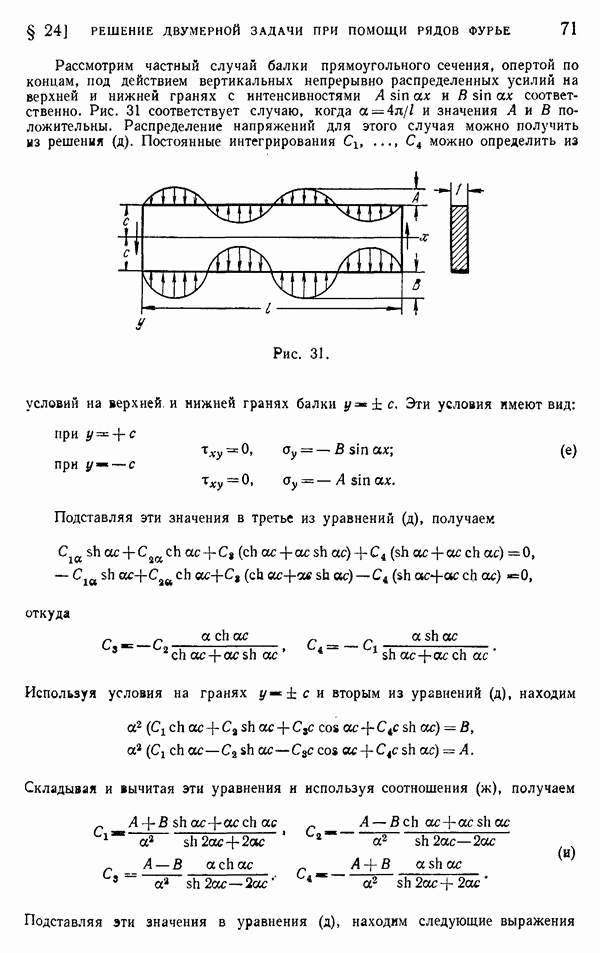
Рис. 173.
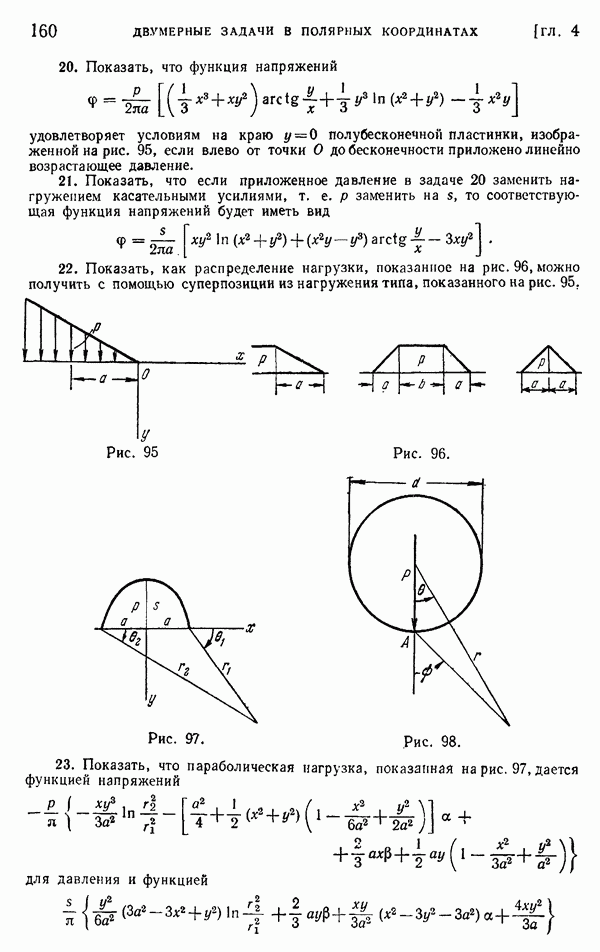
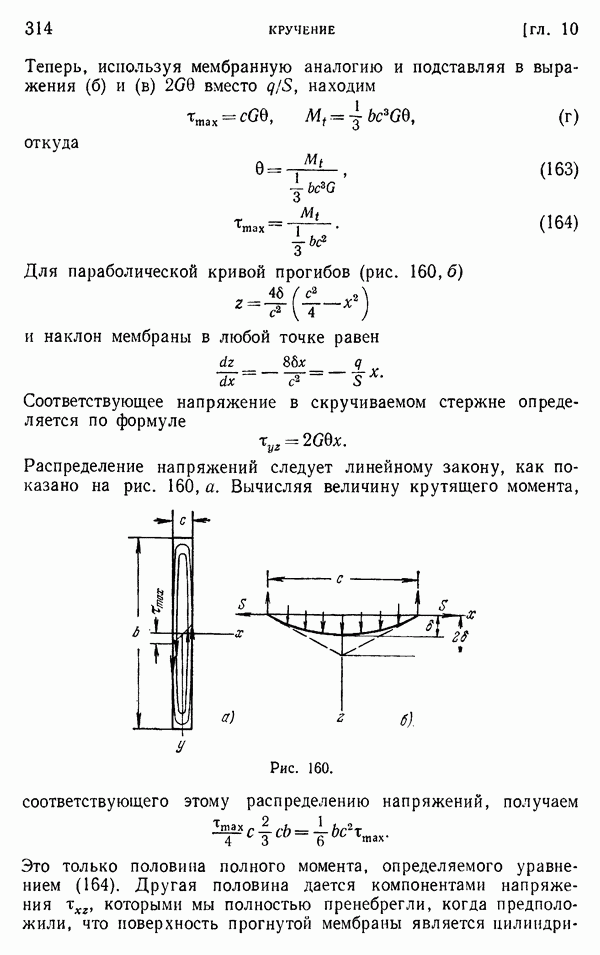
Если труба имеет входящие углы, как в случае, представленном на рис. 173, в этих углах может возникнуть значительная концентрация напряжений. Максимальное напряжение оказывается выше напряжения, полученного из уравнения (176), и зависит от радиуса а закругления входящего угла (рис. 173, б). Для определения этого максимального напряжения мы воспользуемся мембранной аналогией, как это уже делалось для входящих углов прокатных сечений (§ 112). Уравнение мембраны у входящего угла можно принять в форме

Заменяя  на
на  и учитывая, что
и учитывая, что  (см. рис. 172), находим
(см. рис. 172), находим

Если предположить, что труба имеет постоянную толщину  и обозначить через
и обозначить через  полученное по формуле (176) напряжение на
полученное по формуле (176) напряжение на
значительном расстоянии от угла, то из (в) найдем

Подставляя этот результат в формулу (г), имеем

Общее решение этого уравнения имеет вид

Предполагая, что выступающие углы поперечного сечения имеют закругления радиуса а, как показано на рисунке, можно определить постоянную интегрирования С из равенства

которое следует из гидродинамической аналогии (§ 114); действительно, если идеальная жидкость циркулирует по каналу, имеющему форму кольцевого поперечного сечения трубчатого элемента, то количество жидкости, проходящее через каждое поперечное сечение канала, должно оставаться постоянным. Подставляя выражение (е). для  в уравнение (ж) и производя интегрирование, находим
в уравнение (ж) и производя интегрирование, находим

далее из уравнения (е) следует

Для тонкостенной трубы отношения  будут малыми, в силу чего формула (и) приводится к виду
будут малыми, в силу чего формула (и) приводится к виду

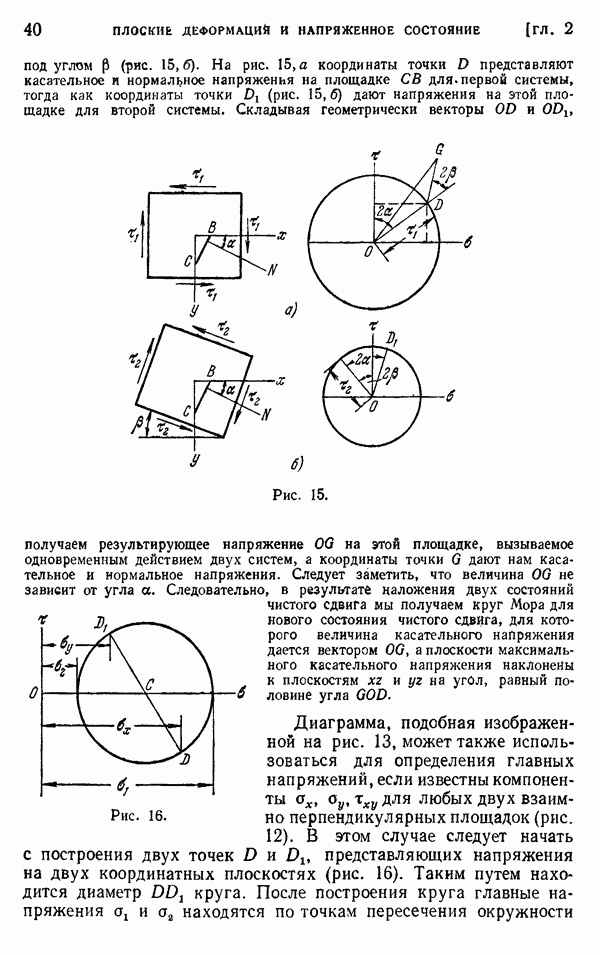
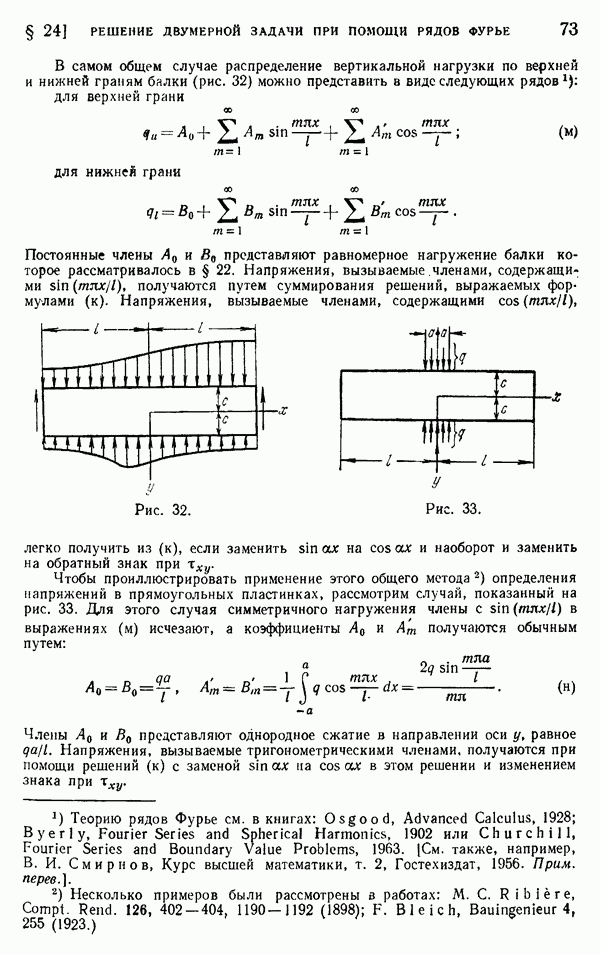
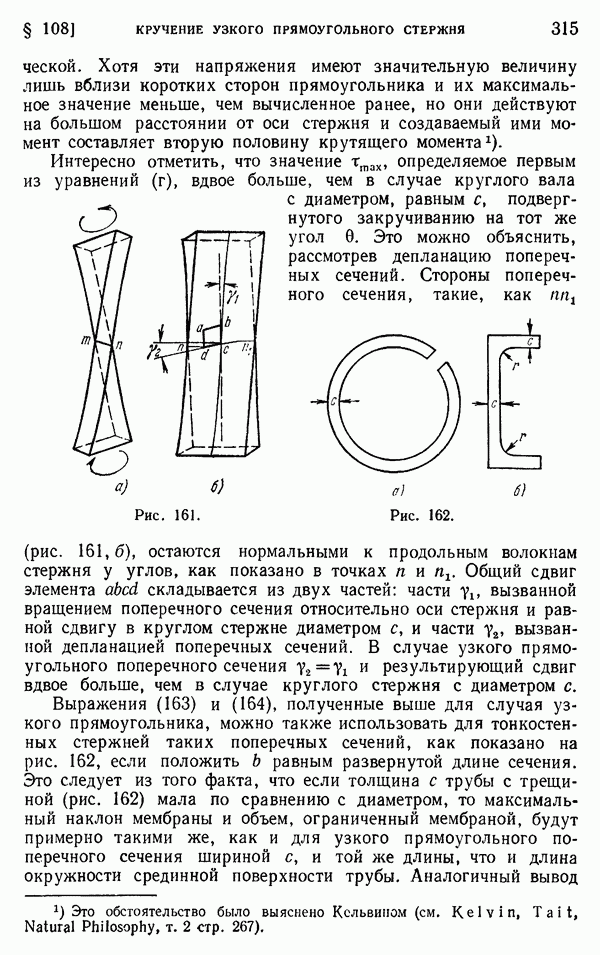
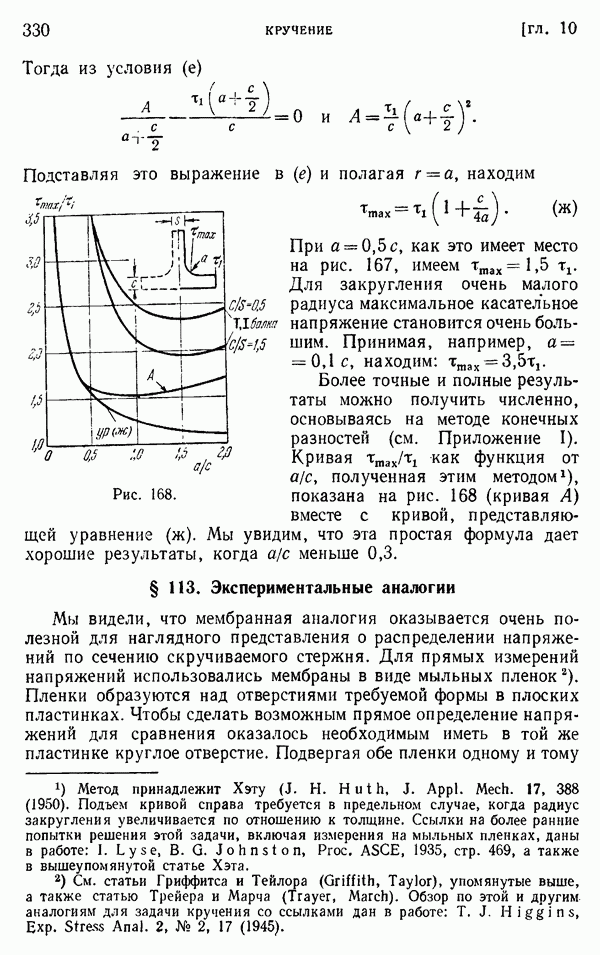
Полагая  получаем напряжение вблизи входящего угла. Оно показано на рис. 174. Другая кривая (А на рис. 174) была
получаем напряжение вблизи входящего угла. Оно показано на рис. 174. Другая кривая (А на рис. 174) была
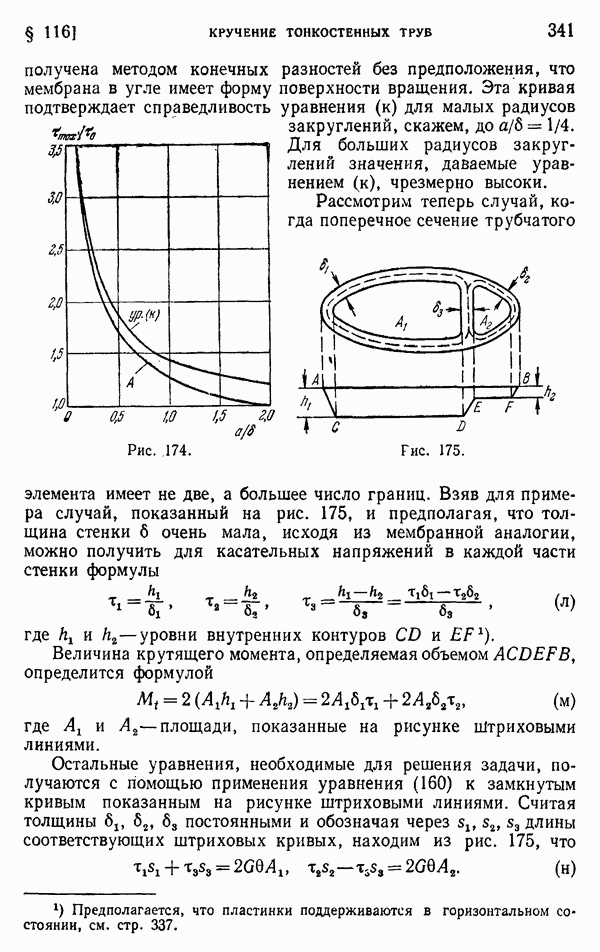
получена методом конечных разностей без предположения, что мембрана в угле имеет форму поверхности вращения. Эта кривая подтверждает справедливость уравнения (к) для малых радиусов закруглений, скажем, до  . Для больших радиусов закруглений значения, даваемые уравнением (к), чрезмерно высоки.
. Для больших радиусов закруглений значения, даваемые уравнением (к), чрезмерно высоки.
Рассмотрим теперь случай, когда поперечное сечение трубчатого элемента имеет не две, а большее число границ.

Рис. 174.

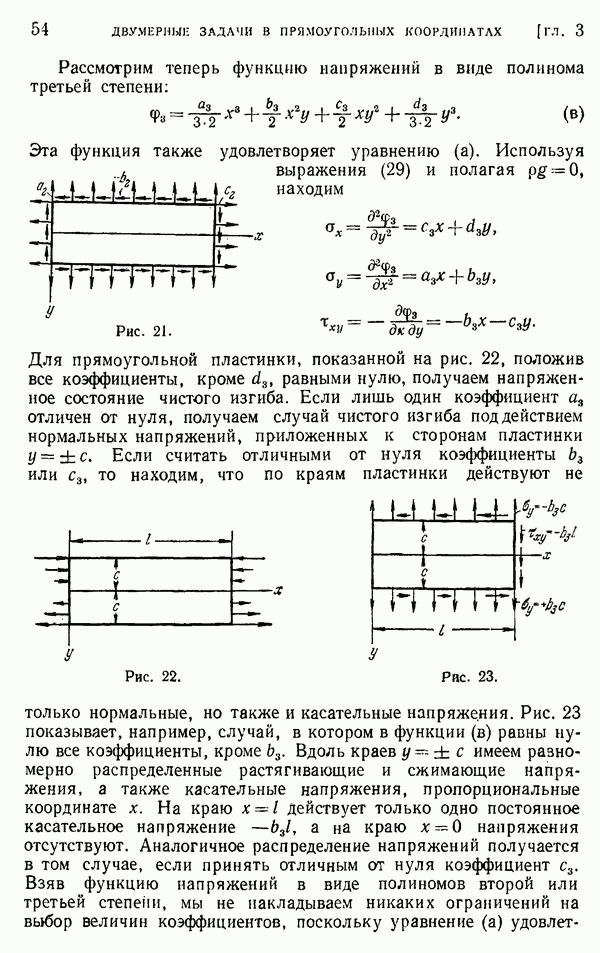
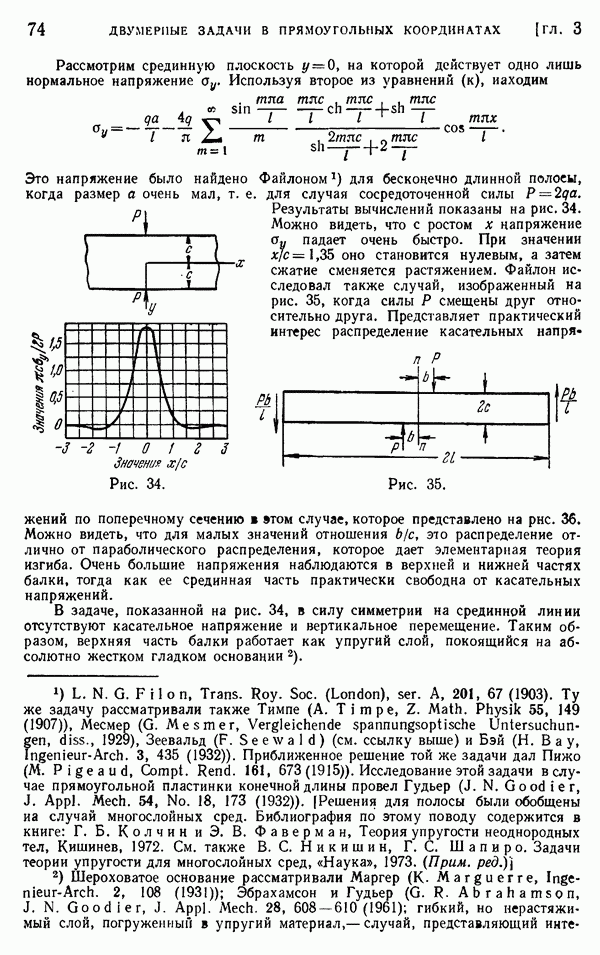
Рис. 175.
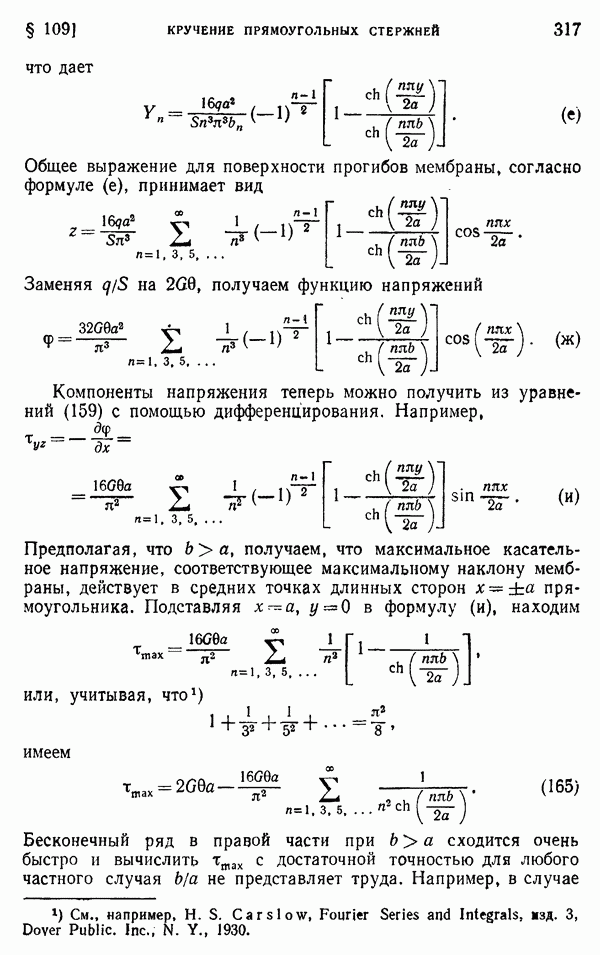
Взяв для примера случай, показанный на рис. 175, и предполагая, что толщина стенки  очень мала, исходя из мембранной аналогии, можно получить для касательных напряжений в каждой части стенки формулы
очень мала, исходя из мембранной аналогии, можно получить для касательных напряжений в каждой части стенки формулы

где  — уровни внутренних контуров
— уровни внутренних контуров 
Величина крутящего момента, определяемая объемом  определится формулой
определится формулой

где  — площади, показанные на рисунке Штриховыми линиями.
— площади, показанные на рисунке Штриховыми линиями.
Остальные уравнения, необходимые для решения задачи, получаются с помощью применения уравнения (160) к замкнутым кривым показанным на рисунке штриховыми линиями. Считая толщины  постоянными и обозначая через
постоянными и обозначая через  длины соответствующих штриховых кривых, находим из рис. 175, что
длины соответствующих штриховых кривых, находим из рис. 175, что

Используя последнюю из формул (л) и соотношения (м) и (н), находим напряжения  как функции крутящего момента
как функции крутящего момента

В случае симметричного поперечного сечения  . В этом случае крутящий момент воспринимается внешней стенкой трубы и промежуточная стенка остается ненапряженной.
. В этом случае крутящий момент воспринимается внешней стенкой трубы и промежуточная стенка остается ненапряженной.
Чтобы получить угол закручивания для любого сечения, подобного показанному на рис. 175, нужно подставить значения напряжений в одно из уравнений  Таким образом, угол
Таким образом, угол  можно получить как функцию крутящего момента
можно получить как функцию крутящего момента 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ОБОЗНАЧЕНИЯ
- Глава 1. ВВЕДЕНИЕ
- § 1. Упругость
- § 2. Напряжения
- § 3. Обозначения для сил и напряжений
- § 4. Компоненты напряжений
- § 5. Компоненты деформаций
- § 6. Закон Гука
- § 7. Индексные обозначения
- Глава 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПЛОСКАЯ ДЕФОРМАЦИЯ
- § 8. Плоское напряженное состояние
- § 9. Плоская деформация
- § 10. Напряжения в точке
- § 11. Деформации в точке
- § 12. Измерение поверхностных деформаций
- § 13. Построение круга деформаций Мора для розетки
- § 14. Дифференциальные уравнения равновесия
- § 15. Граничные условия
- § 16. Уравнения совместности
- § 17. Функция напряжений
- Глава 3. ДВУМЕРНЫЕ ЗАДАЧИ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
- § 19. Концевые эффекты. Принцип Сен-Венана
- § 20. Определение перемещений
- § 21. Изгиб консоли, нагруженной на конце
- § 22. Изгиб балки равномерной нагрузкой
- § 23. Другие случаи балок с непрерывным распределением нагрузки
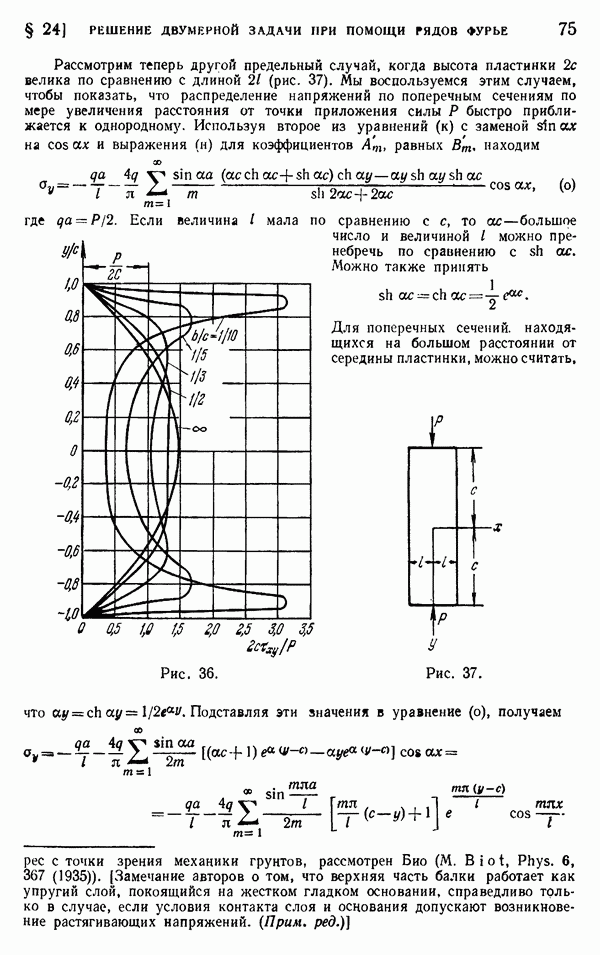
- § 24. Решение двумерной задачи при помощи рядов Фурье
- § 25. Другие приложения рядов Фурье. Нагрузка от собственного веса
- § 26. Влияние концов. Собственные функции
- Глава 4. ДВУМЕРНЫЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
- § 27. Общие уравнения в полярных координатах
- § 28. Полярно-симметричное распределение напряжений
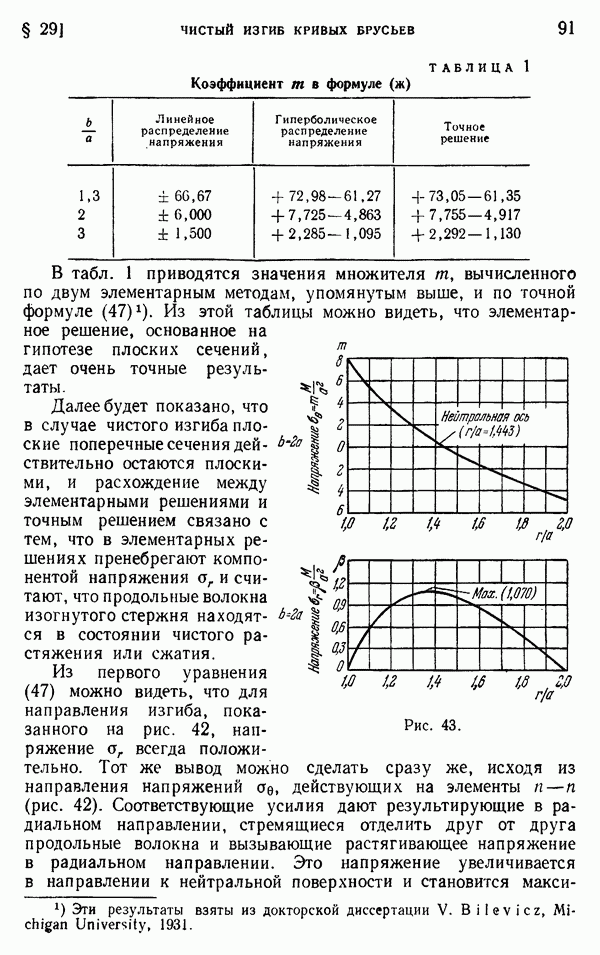
- § 29. Чистый изгиб кривых брусьев
- § 30. Компоненты деформаций в полярных координатах
- § 31. Перемещения при симметричных полях напряжений
- § 32. Вращающиеся диски
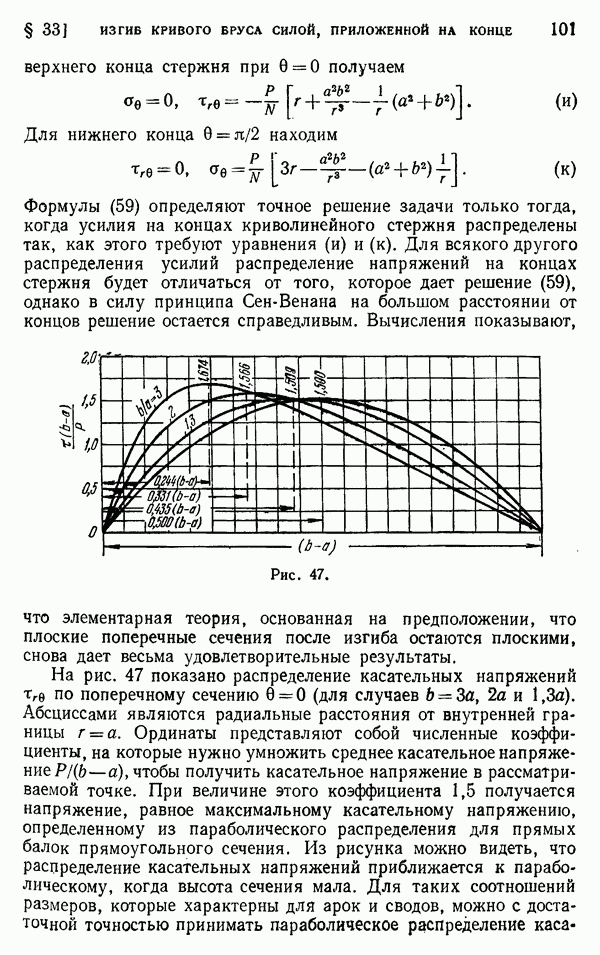
- § 33. Изгиб кривого бруса силой, приложенной на конце
- § 34. Краевые дислокации
- § 35. Влияние круглого отверстия на распределение напряжений в пластинке
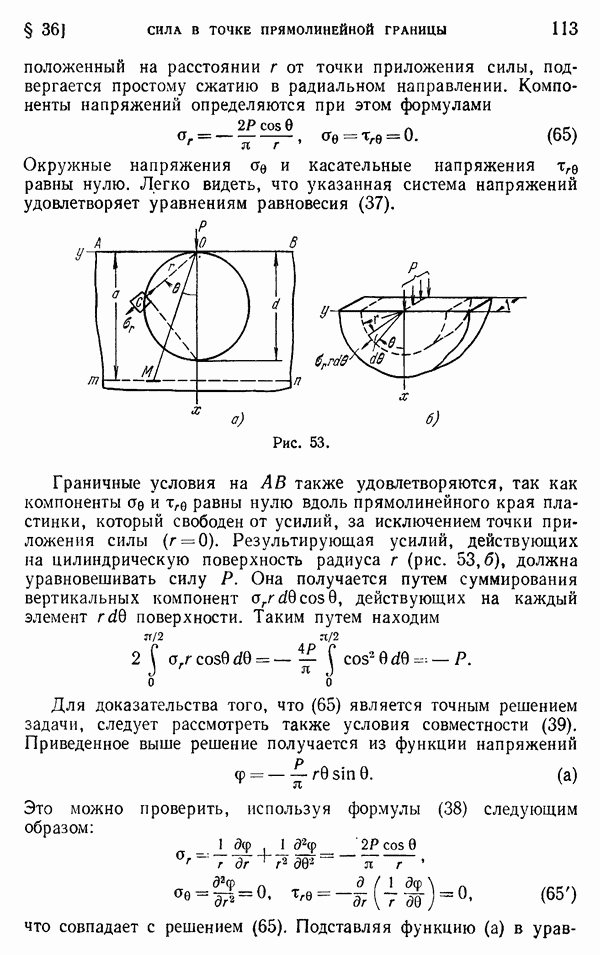
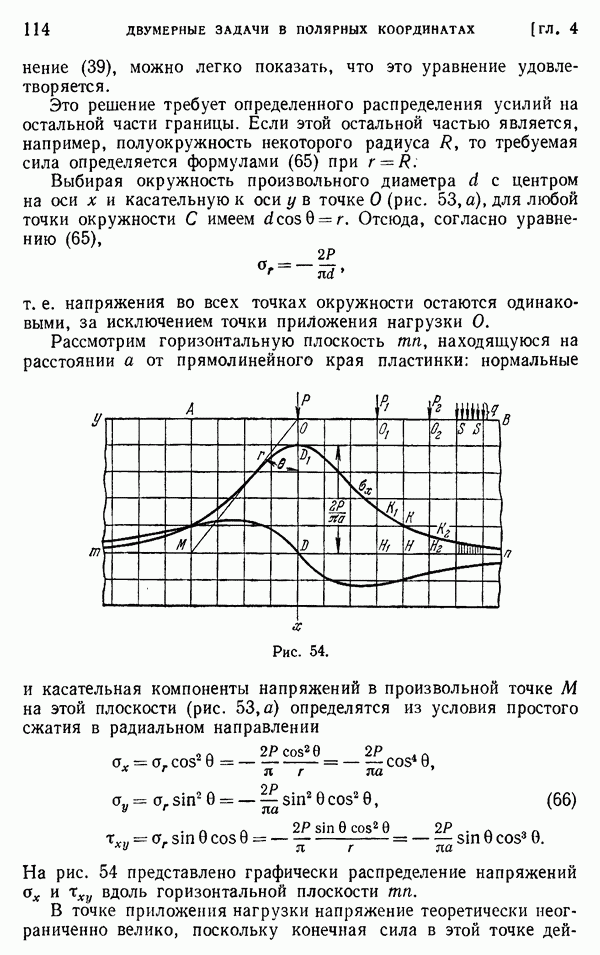
- § 36. Сосредоточенная сила, приложенная в некоторой точке прямолинейной границы
- § 37. Произвольная вертикальная нагрузка на прямолинейной границе
- § 38. Сила, действующая на острие клина
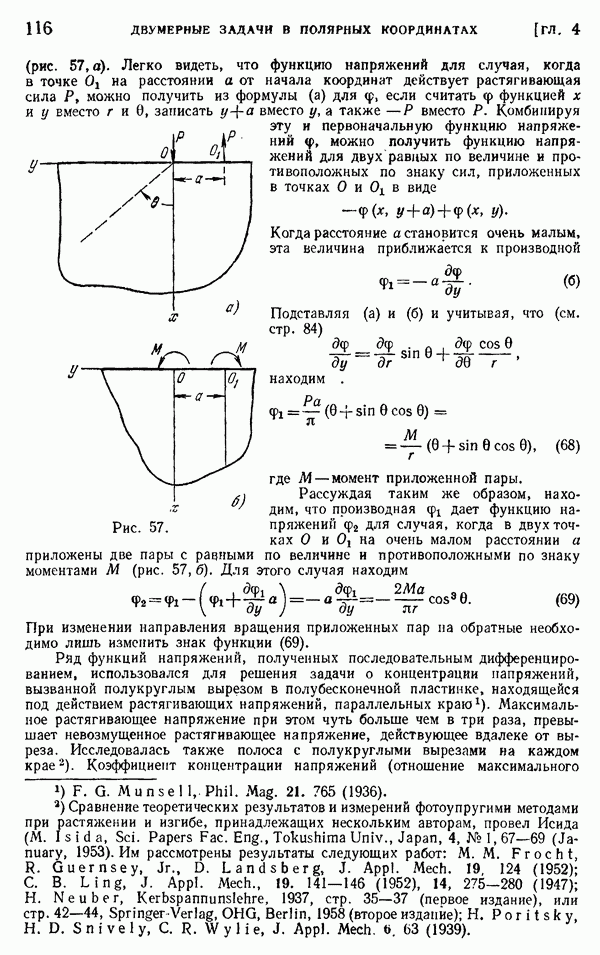
- § 39. Изгибающий момент, действующий на острие клина
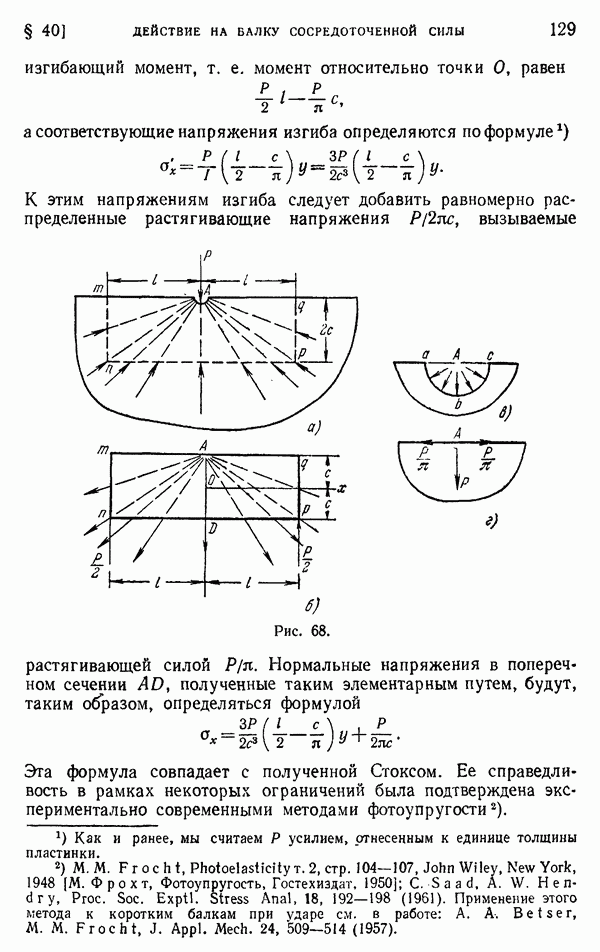
- § 40. Действие на балку сосредоточенной силы
- § 41. Напряжения в круглом диске
- § 42. Сила, действующая в точке бесконечной пластинки
- § 43. Обобщенное решение двумерной задачи в полярных координатах
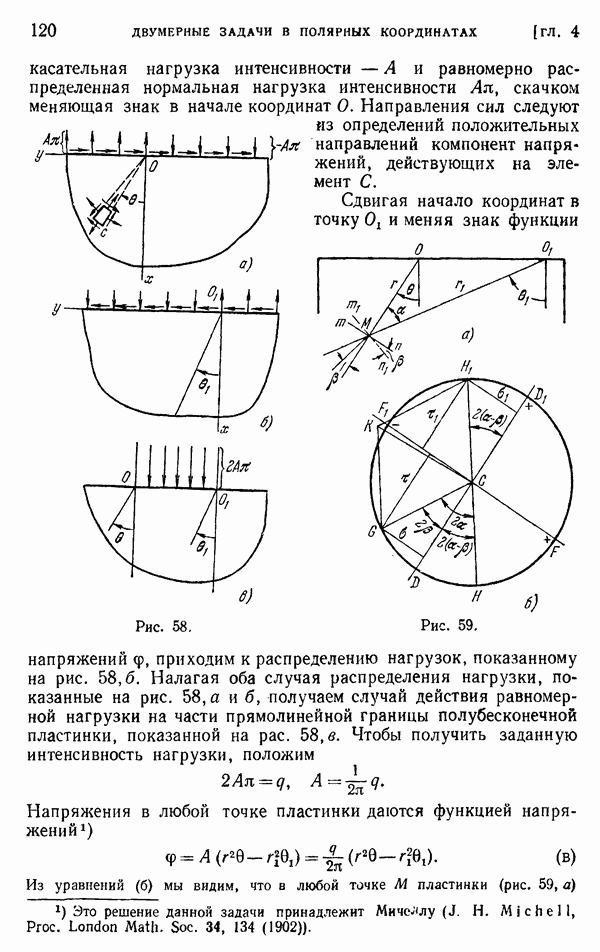
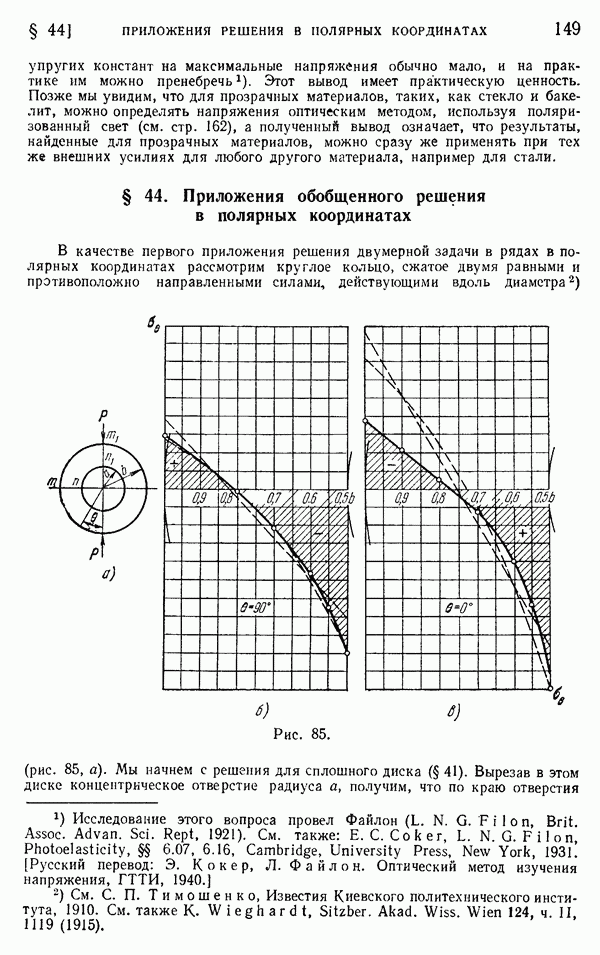
- § 44. Приложения обобщенного решения в полярных координатах
- § 45. Клин, нагруженный вдоль граней
- § 46. Собственные решения для клиньев и вырезов
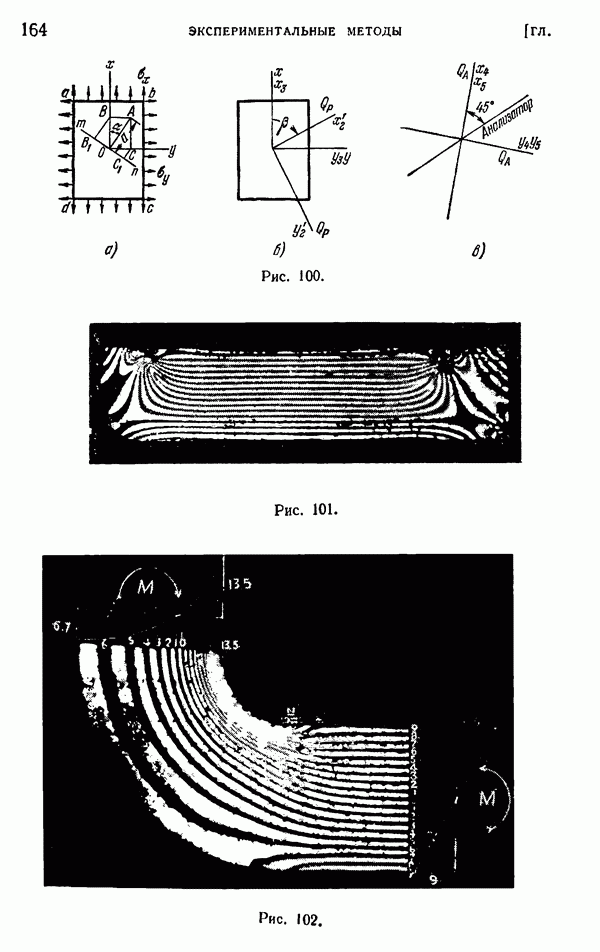
- Глава 5. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ. МЕТОД ФОТОУПРУГОСТИ И МЕТОД «МУАРА»
- § 47. Экспериментальные методы и проверка теоретических решений
- § 48. Измерение напряжений фотоупругим методом
- § 49. Круговой полярископ
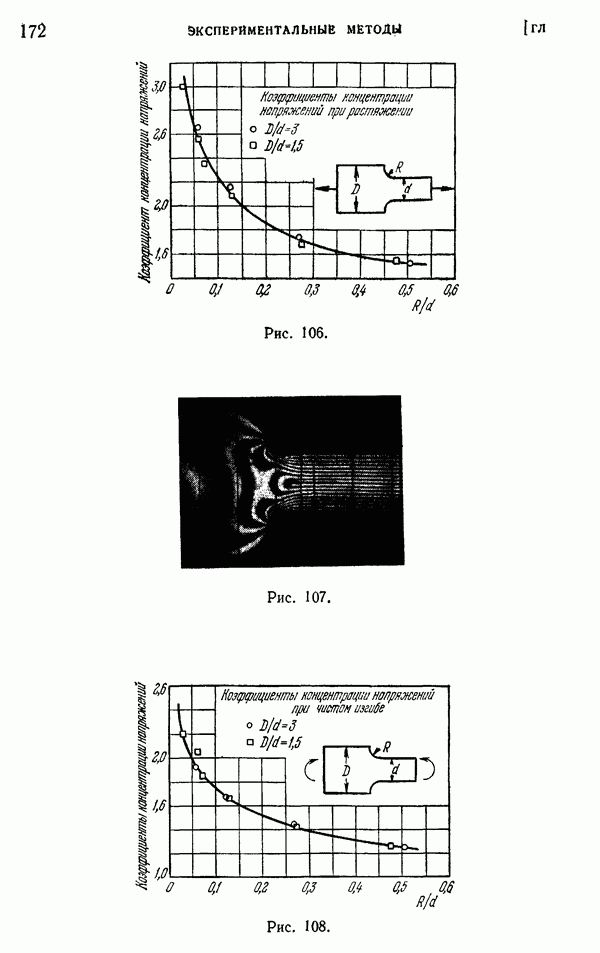
- § 50. Примеры определения напряжений фотоупругим методом
- § 51. Определение главных напряжений
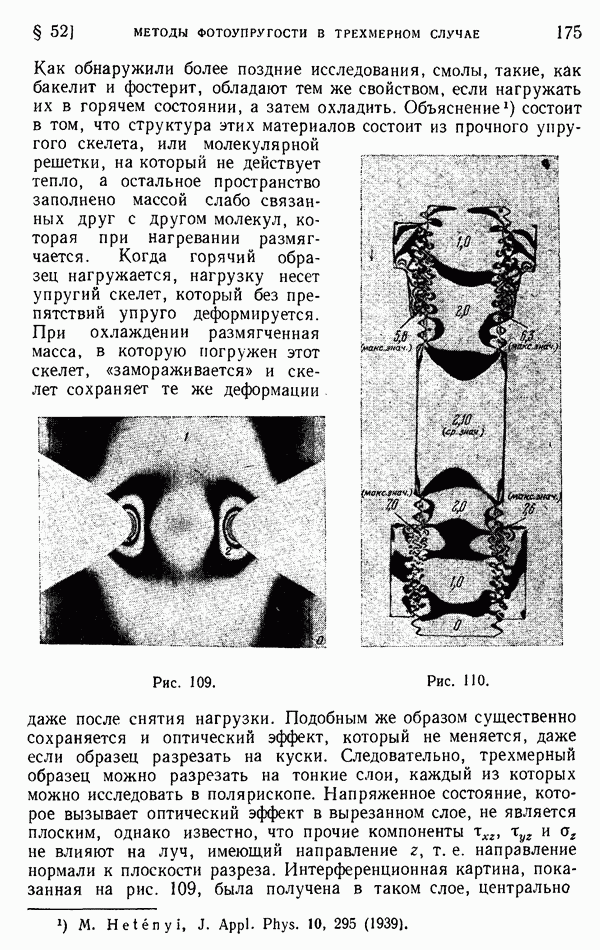
- § 52. Методы фотоупругости в трехмерном случае
- § 53. Метод муара
- Глава 6. ДВУМЕРНЫЕ ЗАДАЧИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- § 54. Функции комплексного переменного
- § 55. Аналитические функции и уравнение Лапласа
- § 56. Функции напряжений, выраженные через гармонические и комплексные функции
- § 57. Перемещения, отвечающие заданной функции напряжений
- § 58. Выражение напряжений и перемещений через комплексные потенциалы
- § 59. Результирующая напряжений, действующих по некоторой кривой. Граничные условия
- § 60. Криволинейные координаты
- § 61. Компоненты напряжений в криволинейных координатах
- § 62. Решения в эллиптических координатах. Эллиптическое отверстие в пластинке с однородным напряженным состоянием
- § 63. Эллиптическое отверстие в пластинке, подвергнутой одноосному растяжению
- § 64. Гиперболические границы. Вырезы
- § 65. Биполярные координаты
- § 66. Решения в биполярных координатах
- § 67. Определение комплексных потенциалов по заданным граничным условиям. Методы Н. И. Мусхелишвили
- § 68. Формулы для комплексных потенциалов
- § 69. Свойства напряжений и деформаций, отвечающих комплексным потенциалам, аналитическим в области материала, расположенной вокруг отверстия
- § 70. Теоремы для граничных интегралов
- § 71. Отображающая функция для эллиптического отверстия. Второй граничный интеграл
- § 72. Эллиптическое отверстие. Формула для …
- § 73. Эллиптическое отверстие. Частные задачи
- Глава 7. АНАЛИЗ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ПРОСТРАНСТВЕННОМ СЛУЧАЕ
- § 75. Главные напряжения
- § 76. Эллипсоид напряжений и направляющая поверхность напряжений
- § 77. Определение главных напряжений
- § 78. Инварианты напряжений
- § 79. Определение максимального касательного напряжения
- § 80. Однородная деформация
- § 81. Деформации в точке тела
- § 82. Главные оси деформаций
- § 83. Вращение
- Глава 8. ОБЩИЕ ТЕОРЕМЫ
- § 84. Дифференциальные уравнения равновесия
- § 85. Условия совместности
- § 86. Определение перемещений
- § 87. Уравнения равновесия в перемещениях
- § 88. Общее решение для перемещений
- § 89. Принцип суперпозиции
- § 90. Энергия деформации
- § 91. Энергия деформации для краевой дислокации
- § 92. Принцип виртуальной работы
- § 93. Теорема Кастильяно
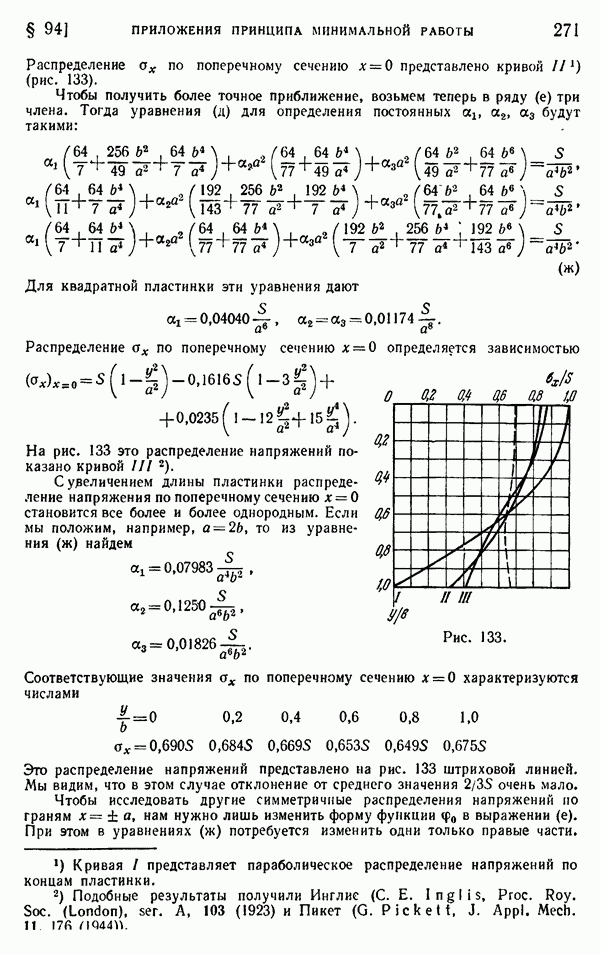
- § 94. Приложения принципа минимальной работы. Прямоугольные пластинки
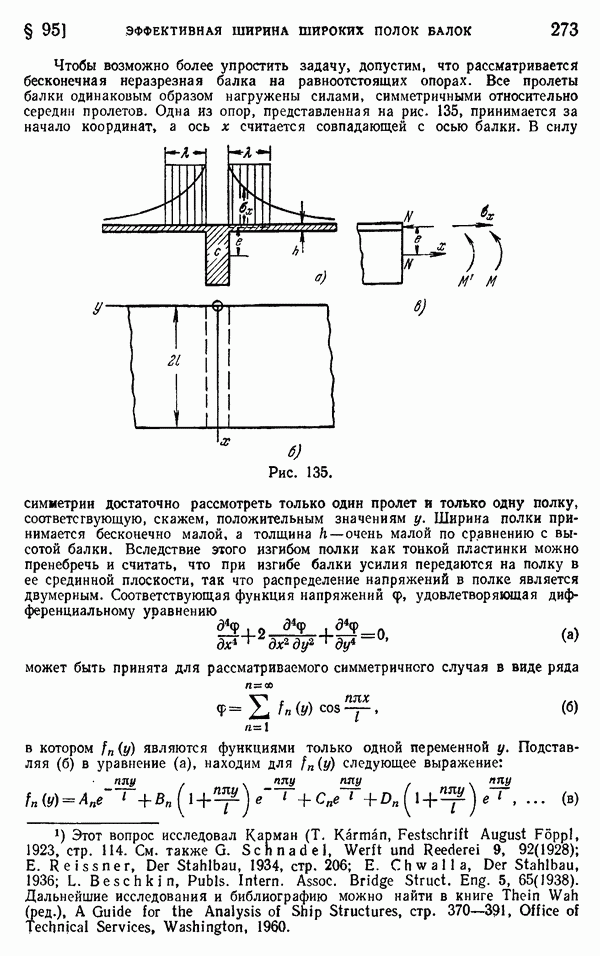
- § 95. Эффективная ширина широких полок балок
- § 96. Единственность решения
- § 97. Теорема взаимности
- § 98. Приближенный характер решений для плоского напряженного состояния
- Глава 9. ЭЛЕМЕНТАРНЫЕ ТРЕХМЕРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 99. Однородное напряженное состояние
- § 100. Растяжение призматического стержня под действием собственного веса
- § 101. Кручение круглых валов постоянного поперечного сечения
- § 102. Чистый изгиб призматических стержней
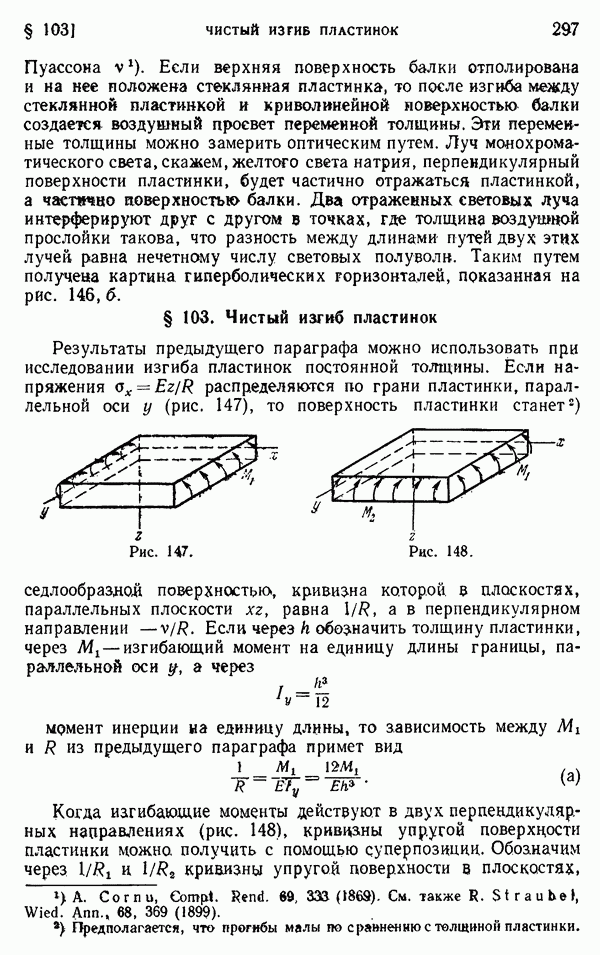
- § 103. Чистый изгиб пластинок
- Глава 10. КРУЧЕНИЕ
- § 104. Кручение прямолинейных стержней
- § 105. Эллиптическое поперечное сечение
- § 106. Другие элементарные решения
- § 107. Мембранная аналогия
- § 108. Кручение стержня узкого прямоугольного поперечного сечения
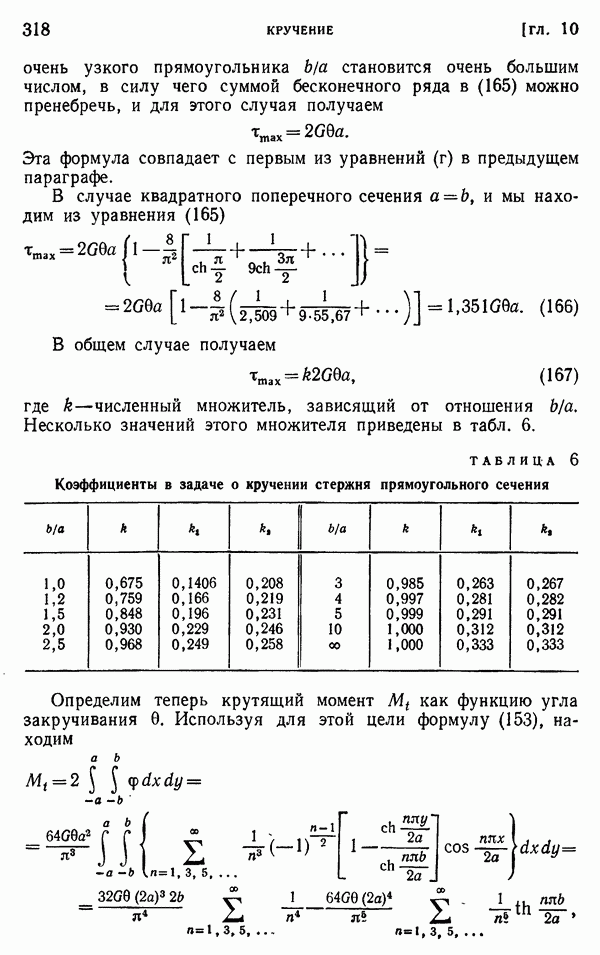
- § 109. Кручение прямоугольных стержней
- § 110. Дополнительные результаты
- § 111. Решение задач о кручении энергетическим методом
- § 112. Кручение стержней прокатных профилей
- § 113. Экспериментальные аналогии
- § 114. Гидродинамические аналогии
- § 115. Кручение полых валов
- § 116. Кручение тонкостенных труб
- § 117. Винтовые дислокации
- § 118. Кручение стержня, одно из поперечных сечений которого остается плоским
- § 119. Кручение круглых валов переменного диаметра
- Глава 11. ИЗГИБ БРУСЬЕВ
- § 120. Изгиб консоли
- § 121. Функция напряжений
- § 122. Круглое поперечное сечение
- § 123. Эллиптическое поперечное сечение
- § 124. Прямоугольное поперечное сечение
- § 125. Дополнительные результаты
- § 126. Несимметричные поперечные сечения
- § 127. Центр изгиба
- § 128. Решение задач изгиба с помощью метода мыльной пленки
- § 129. Перемещения
- § 130. Дальнейшие исследования изгиба брусьев
- Глава 12. ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТЕЛАХ ВРАЩЕНИЯ
- § 132. Решение в полиномах
- § 133. Изгиб круглой пластинки
- § 134. Трехмерная задача о вращающемся диске
- § 135. Сила, приложенная в некоторой точке бесконечного тела
- § 136. Сферический сосуд под действием внутреннего или внешнего равномерного давления
- § 137. Местные напряжения вокруг сферической полости
- § 138. Сила, приложенная на границе полубесконечного тела
- § 139. Нагрузка, распределенная по части границы полубесконечного тела
- § 140. Давление между двумя соприкасающимися сферическими телами
- § 141. Давление между даума соприкасающимися телами. Более общий случай
- § 142. Соударение шаров
- § 143. Симметричная деформация круглого цилиндра
- § 144. Круглый цилиндр под действием опоясывающего давления
- § 145. Решение Буссинеска в виде двух гармонических функций
- § 146. Растяжение винтовой пружины (винтовые дислокации в кольце)
- § 147. Чистый изгиб части круглого кольца
- Глава 13. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 148. Простейшие случаи распределения температурных напряжений. Метод устранения деформаций
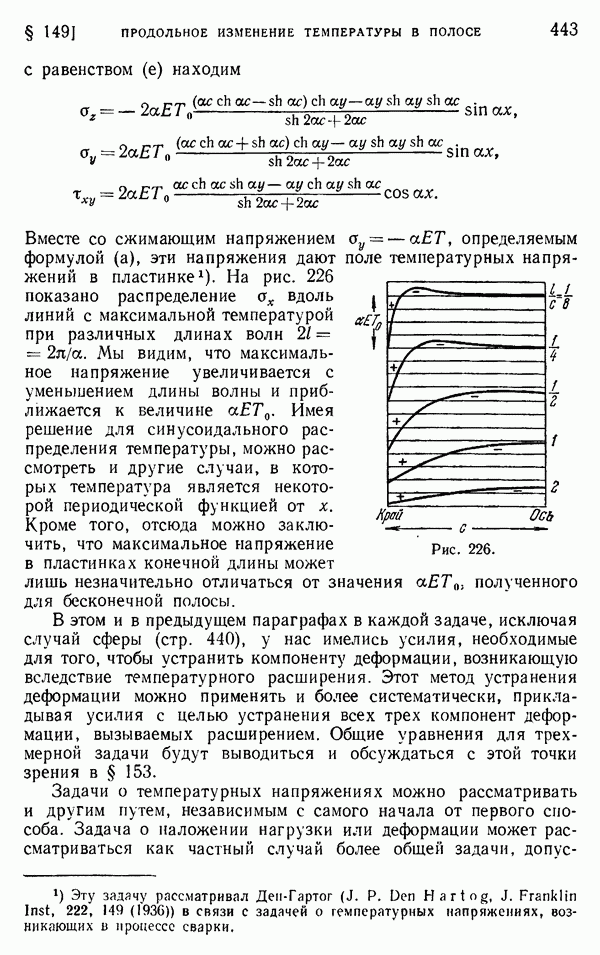
- § 149. Продольное изменение температуры в полосе
- § 150. Тонкий круглый диск: распределение температуры, симметричное относительно центра
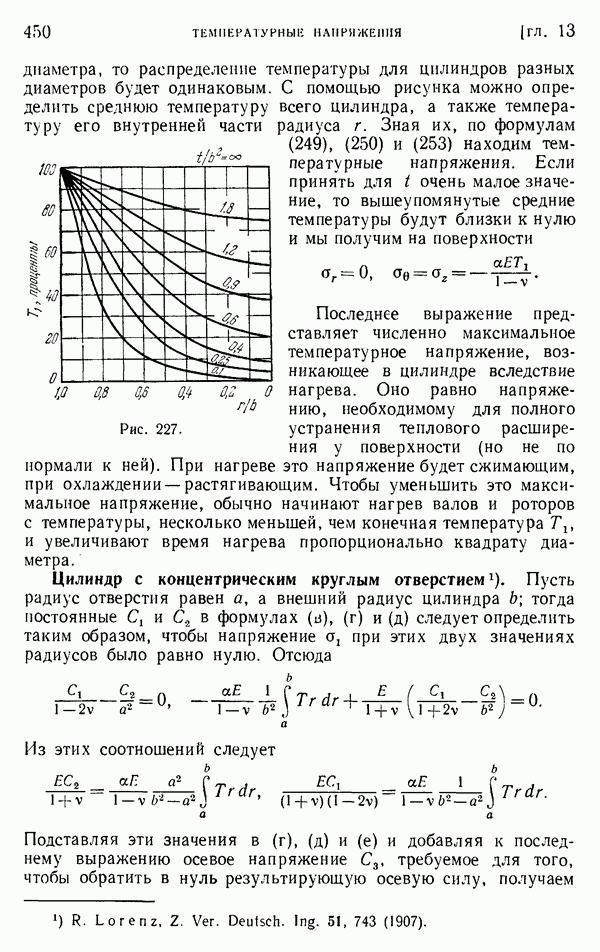
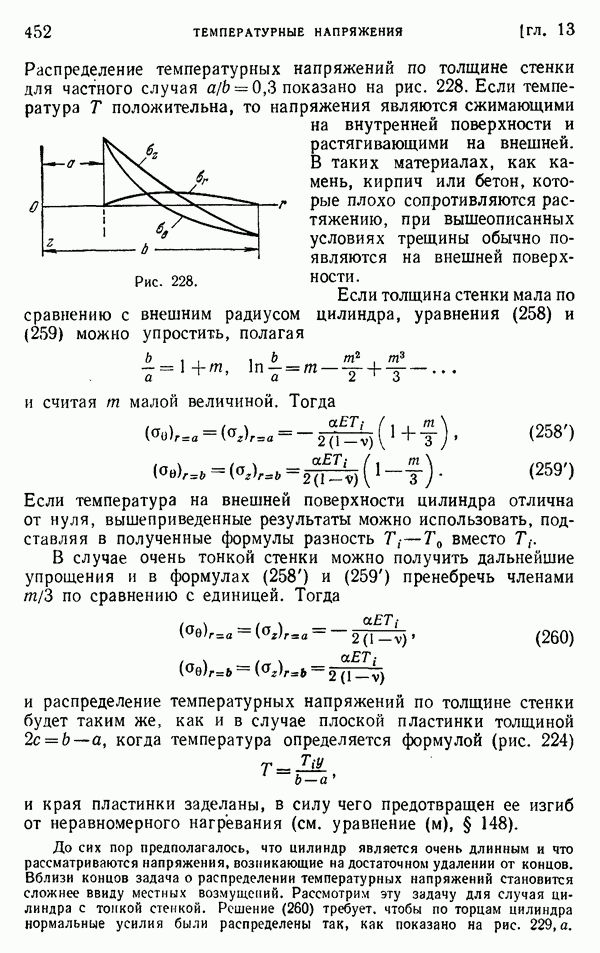
- § 151. Длинный круглый цилиндр
- § 152. Сфера
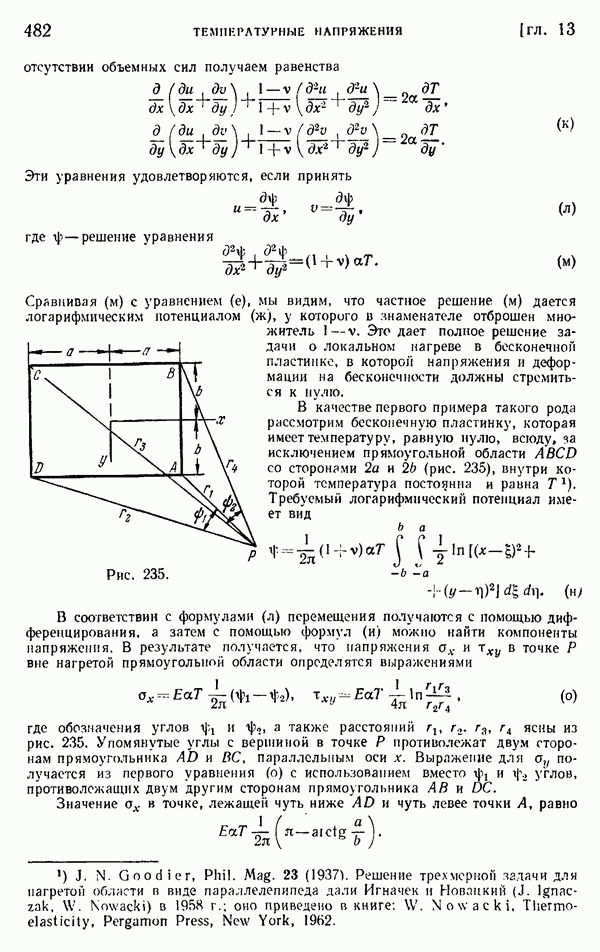
- § 153. Общие уравнения
- § 154. Теорема взаимности в термоупругости
- § 155. Полные термоупругие деформации. Произвольное распределение температуры
- § 156. Термоупругие перемещения. Интегральное решение В. М. Майзеля
- § 157. Начальные напряжения
- § 158. Общее изменение объема, связанное с начальными напряжениями
- § 159. Плоская деформация и плоское напряженное состояние. Метод устранения деформаций
- § 160. Двумерные задачи со стационарным потоком тепла
- § 161. Плоское термонапряженное состояние, вызванное возмущением однородного потока тепла изолированным отверстием
- § 162. Решения общих уравнений. Термоупругий потенциал перемещения
- § 163. Общая двумерная задача для круговых областей
- § 164. Общая двумерная задача. Решение в комплексных потенциалах
- Глава 14. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СПЛОШНОЙ СРЕДЕ
- § 166. Волны расширения и волны искажения в изотропной упругой среде
- § 167. Плоские волны
- § 168. Продольные волны в стержнях постоянного сечения. Элементарная теория
- § 169. Продольное соударение стержней
- § 170. Поверхностные волны Рэлея
- § 171. Волны со сферической симметрией в бесконечной среде
- § 172. Взрывное давление в сферической полости
- Приложение I. ПРИМЕНЕНИЕ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ В ТЕОРИИ УПРУГОСТИ
- § 2. Методы последовательных приближений
- § 3. Метод релаксации
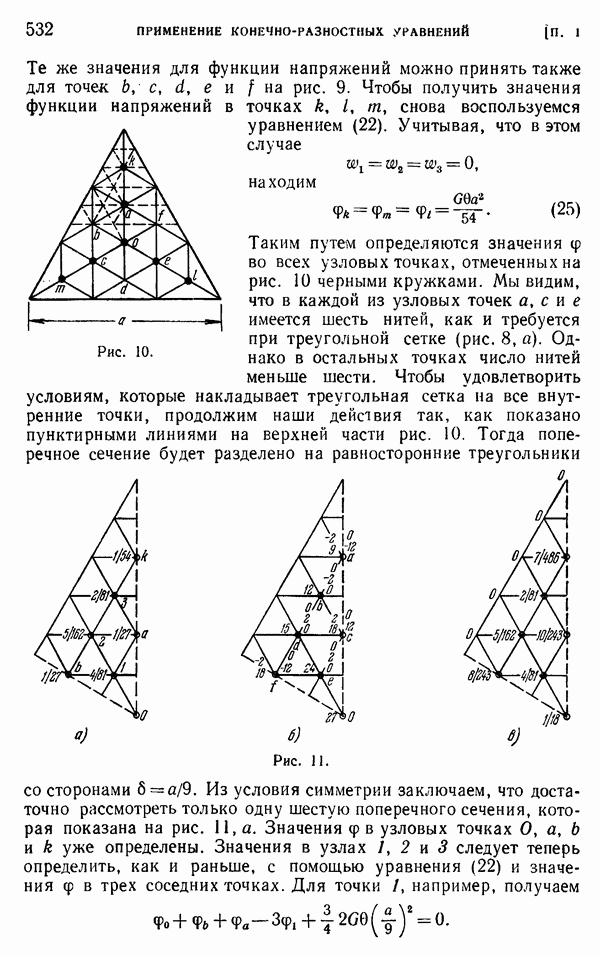
- § 4. Треугольные и шестиугольные сетки
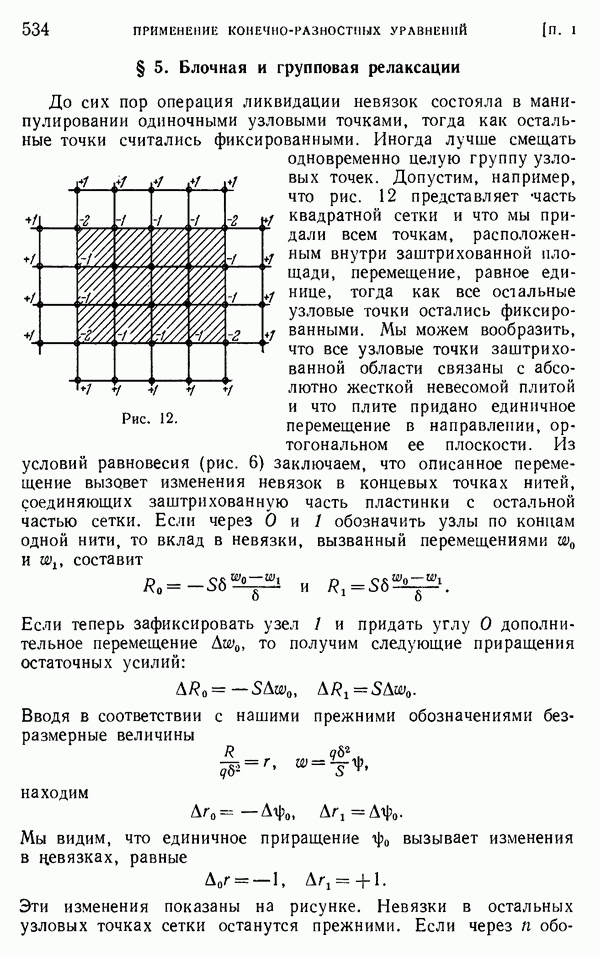
- § 5. Блочная и групповая релаксации
- § 6. Кручение стержней с многосвязными поперечными сечениями
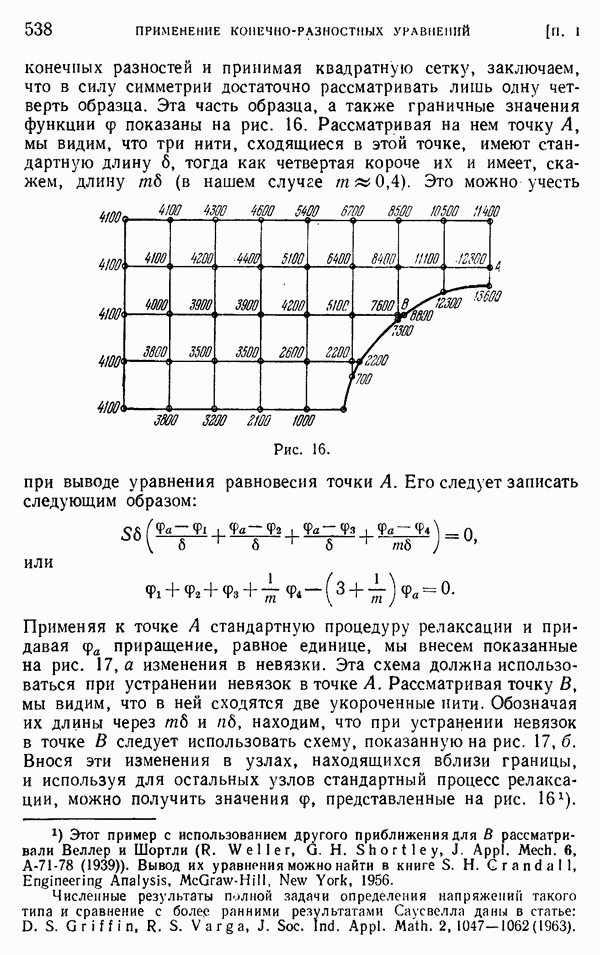
- § 7. Точки, расположенные вблизи границы
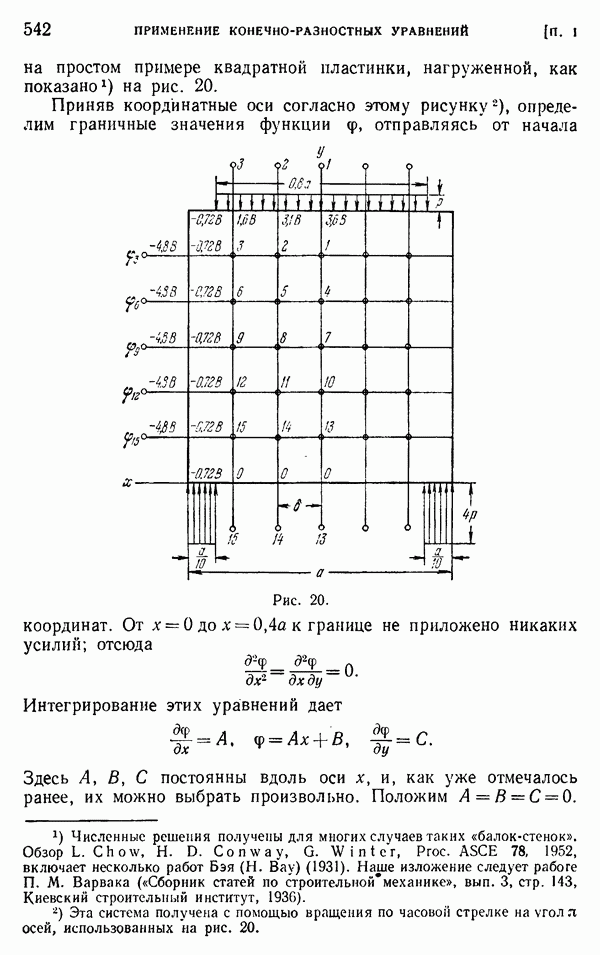
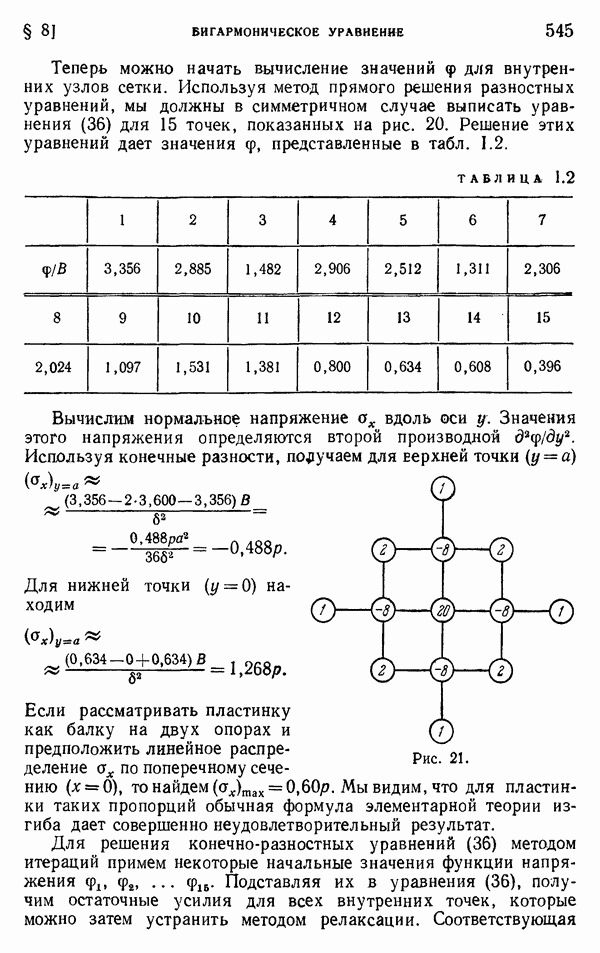
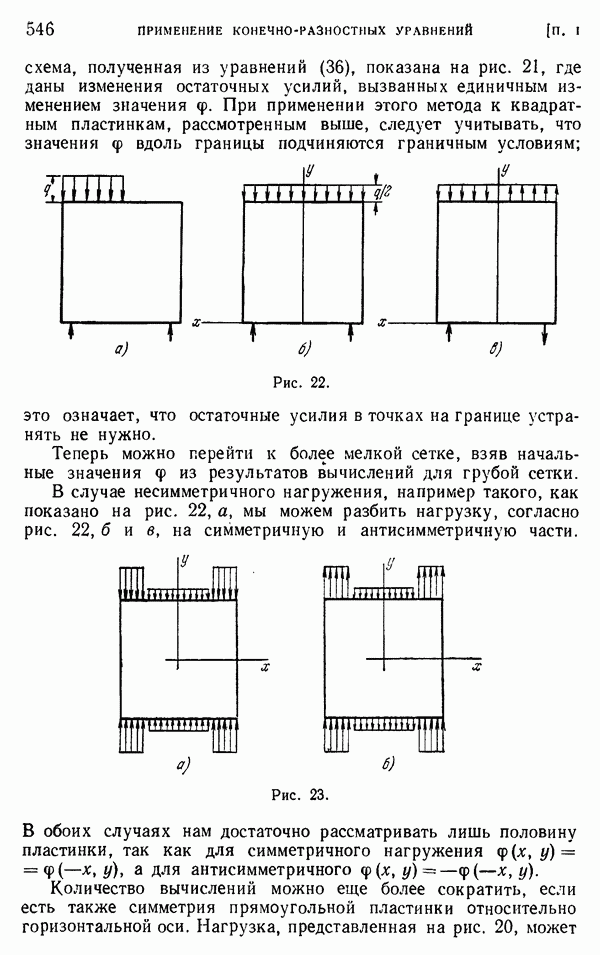
- § 8. Бигармоническое уравнение
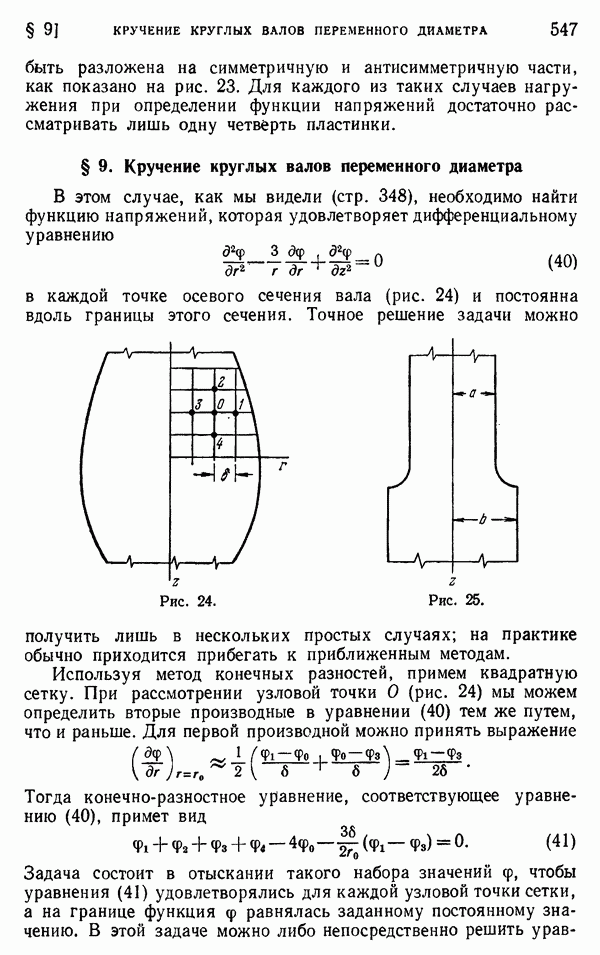
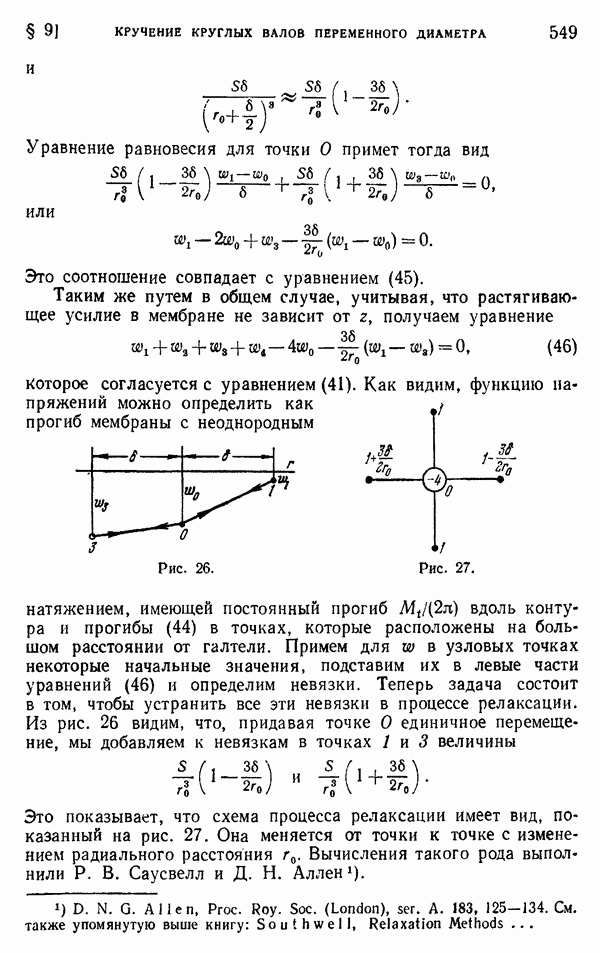
- § 9. Кручение круглых валов переменного диаметра
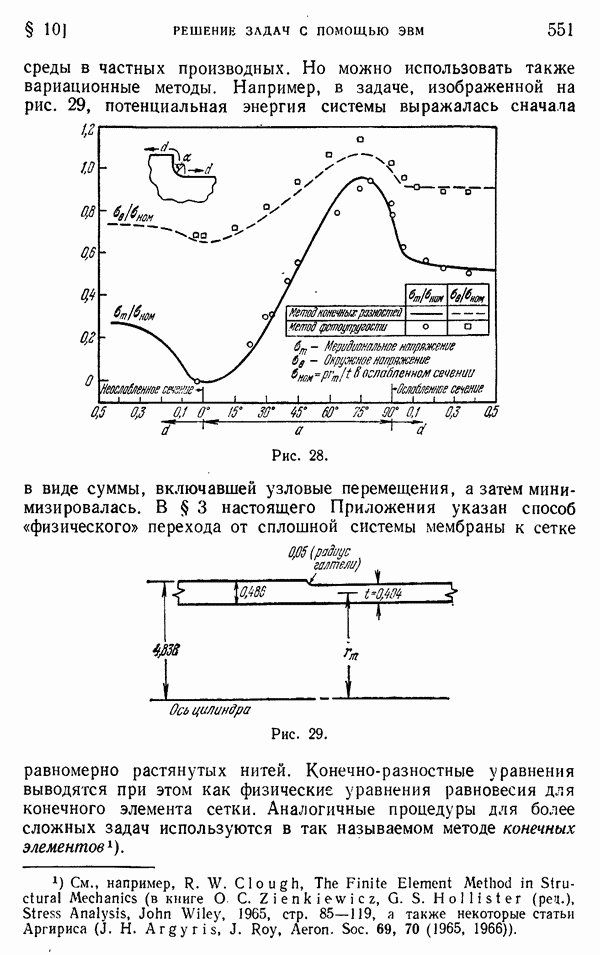
- § 10. Решение задач с помощью ЭВМ
- Приложение II. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
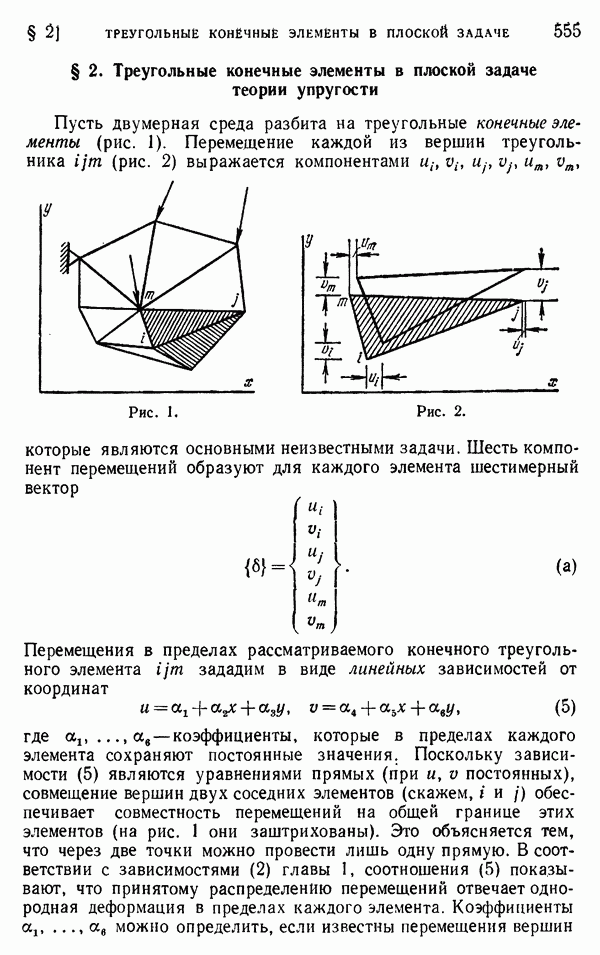
- § 2. Треугольные конечные элементы в плоской задаче теории упругости
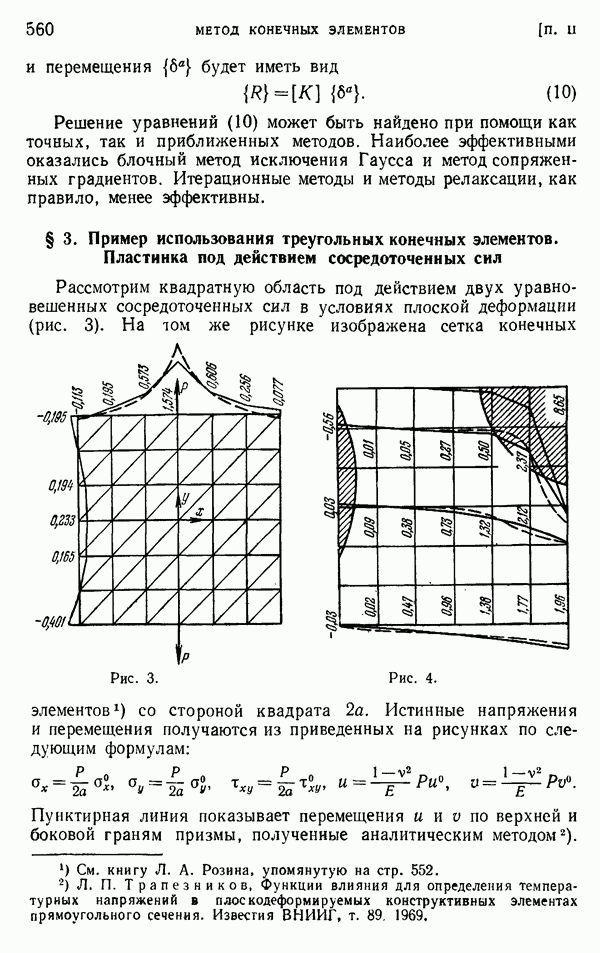
- § 3. Пример использования треугольных конечных элементов. Пластинка под действием сосредоточенных сил
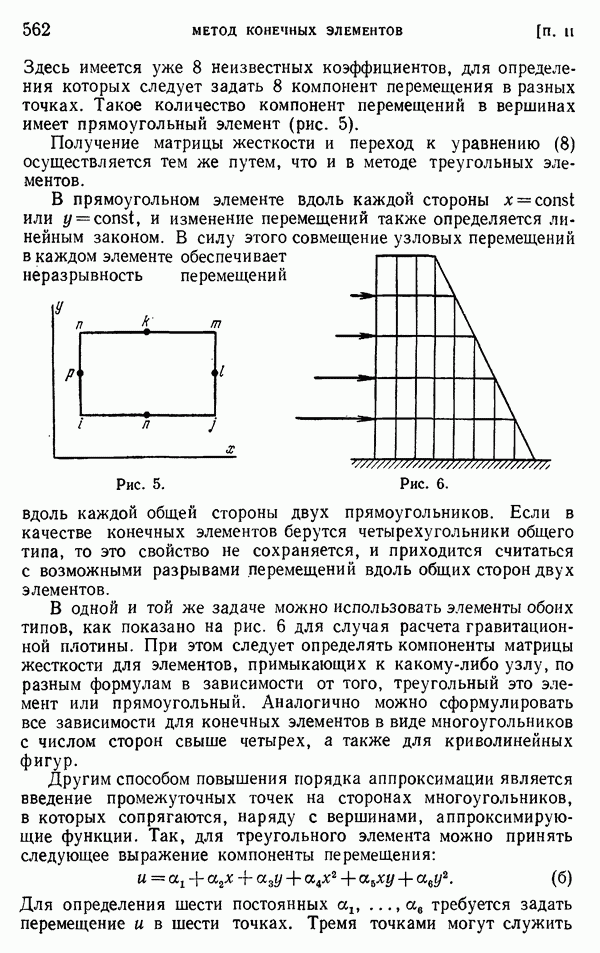
- § 4. Повышение порядка аппроксимации
- § 5. Трехмерные задачи