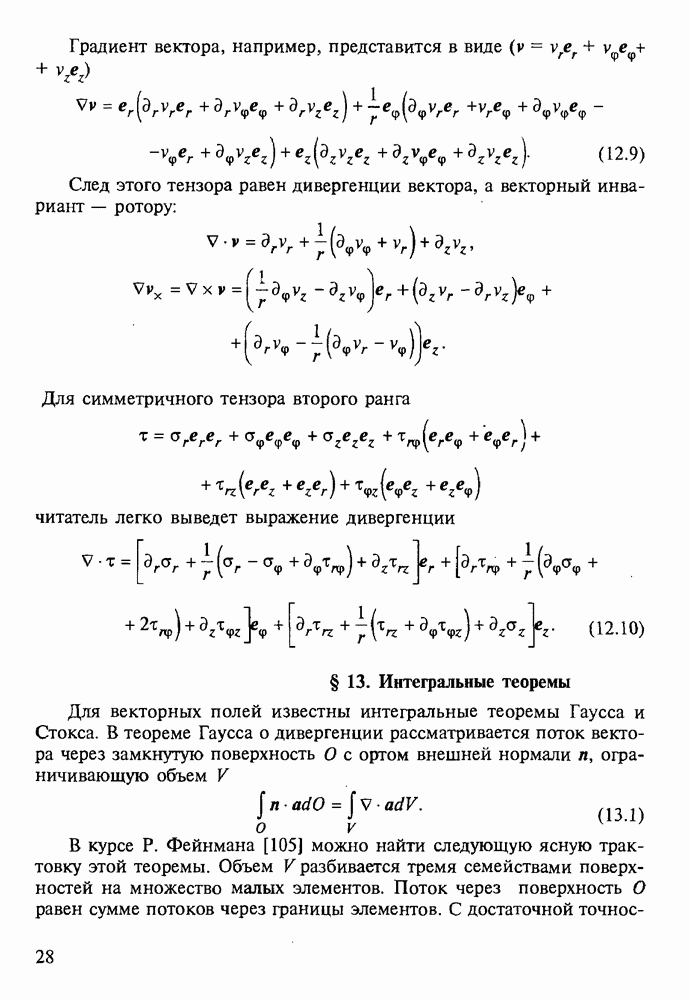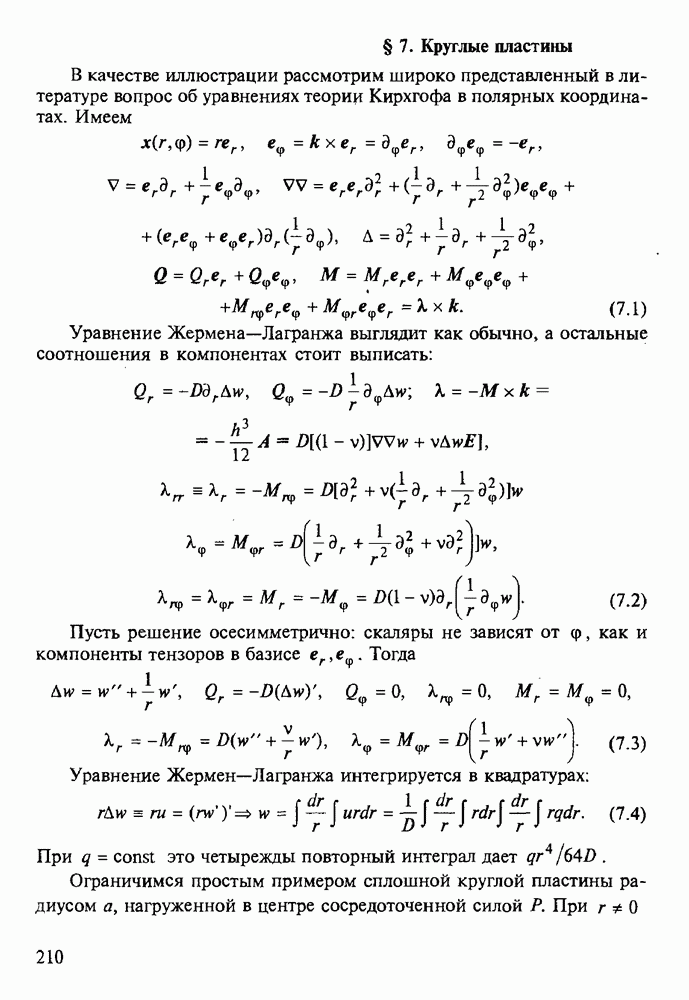| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
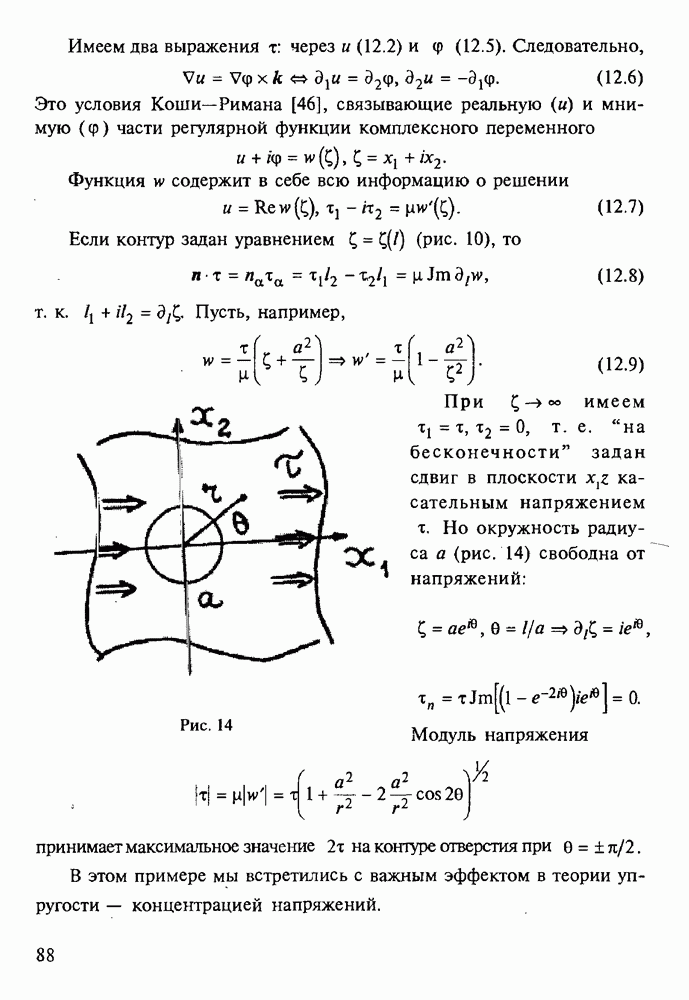
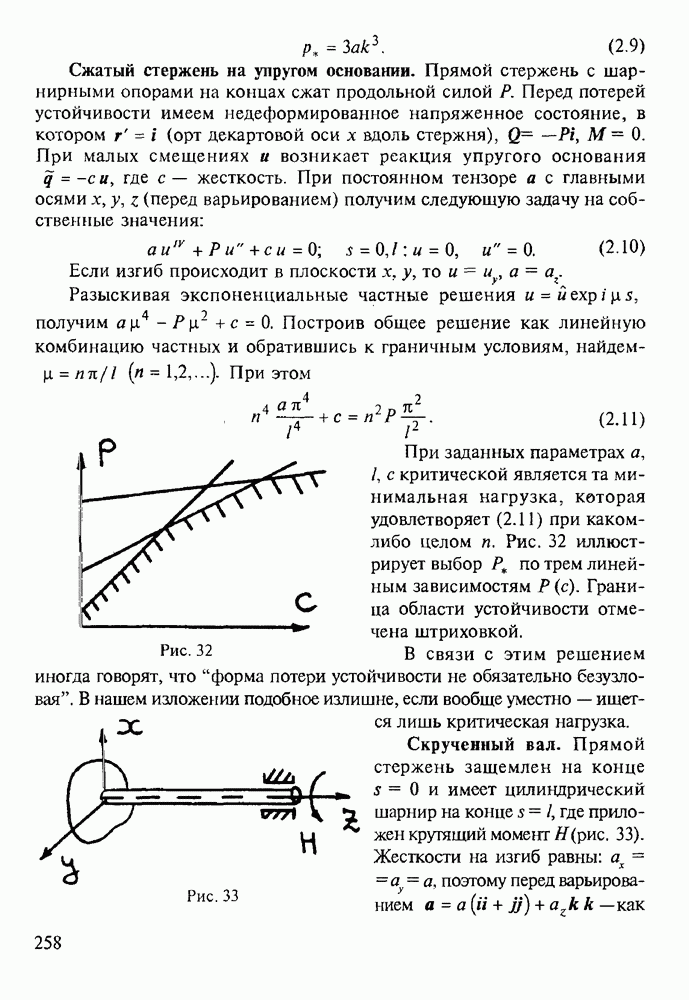
§ 4. Колебания оболочек
Динамика оболочек рассматривалась многими выдающимися исследователями, одним из первых был Рэлей с его теорией изгибных колебаний [9]. Для оболочек характерна высокая плотность собственных частот, на этом основаны специальные асимптотические методы расчета [12, 21]. Не затрагивая множества конкретных решений, ограничимся основными уравнениями и вытекающими из них общими положениями.
В теории классического типа из § 11.5 имеем уравнения (5.4), где вместо  и
и  можно написать
можно написать

оставив  без изменений. При нормальных колебаниях и
без изменений. При нормальных колебаниях и  для амплитуд получаются уравнения как в статике при нагрузке
для амплитуд получаются уравнения как в статике при нагрузке  Применяя теорему Клапейрона (11.9.1), получим
Применяя теорему Клапейрона (11.9.1), получим

где плотность потенциальной энергии в случае изотропии равна

Значения модулей оболочки из однородного изотропного материала даны в (11.5.5). Вытекающее из (4.2) выражение отношения Рэлея обладает известными общими свойствами: равное  на форме
на форме  оно как функционал имеет минимум на
оно как функционал имеет минимум на 
Теорема взаимности работ (11.9.3) позволяет доказать ортогональность форм

Она же используется при построении решения произвольной динамической задачи:

Соотношения (4,2), (4.4) и (4.5) написаны для оболочки с защемленным краем — в этом случае не требуется вариационное преобразование краевых условий.
В неклассической теории типа Тимошенко исчезают сложности в условиях на свободном крае, зато возникают нагромождения в остальном. Но общие уравнения написать очень легко; они есть в гл. 11, только надо уточнить вид инерционных членов. В общем случае они содержат не только плотность  но и тензор
но и тензор  с вектором
с вектором  при изотропии в касательной плоскости
при изотропии в касательной плоскости 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 2. Определение тензора
- § 3. Действия над тензорами
- § 4. Полиадное представление
- § 5. Векторное произведение и тензор Леви-Чивита
- § 6. Антисимметричные тензоры
- § 7. Главные оси и главные значения симметричного тензора
- § 8. Тензор поворота
- § 9. Полярное разложение
- § 10. Тензоры в косоугольном базисе
- § 11. Тензорные функции
- § 12. Тензорные поля. Дифференцирование
- § 13. Интегральные теоремы
- § 14. Тензор Римана-Кристоффеля
- Глава 2. ОСНОВЫ ОБЩЕЙ МЕХАНИКИ
- § 2. Абсолютно твердое тело
- § 3. Принцип виртуальной работы
- § 4. Баланс импульса, момента импульса и энергии
- § 5. Принцип Гамильтона и уравнения Лагранжа
- § 6. Статика
- § 7. Механика относительного движения
- § 8. Малые колебания
- Глава 3. НЕЛИНЕЙНО-УПРУГАЯ БЕЗМОМЕНТНАЯ СРЕДА
- § 2. Дифференцирование
- § 3. Градиент деформации
- § 4. Меры и тензоры деформации
- § 5. Поле скоростей
- § 6. Вектор площадки
- § 7. Силы в сплошной среде. Тензор напряжений
- § 8. Баланс импульса и момента импульса
- § 9. Принцип виртуальной работы
- § 10. Соотношения упругости
- § 11. Тензор Пиола
- § 12. Варьирование актуальной конфигурации
- § 13. Внутренние связи
- § 14. Полая сфера под действием давления
- § 15. Напряжения как множители Лагранжа
- Глава 4. КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ УПРУГОСТЬ
- § 2. Единственность решения динамической задачи
- § 3. Закон Гука
- § 4. Общие теоремы статики
- § 5. Уравнения в перемещениях
- § 6. Сосредоточенная сила в неограниченной среде
- § 7. Определение перемещений по деформациям
- § 8. Уравнения в напряжениях
- § 9. Принцип минимума потенциальной энергии системы
- § 10. Принцип минимума дополнительной работы
- § 11. Смешанные принципы стационарности
- § 12. Антиплоская деформация
- § 13. Кручение стержней
- § 14. Плоская деформация
- Глава 5. МОМЕНТНАЯ ТРЕХМЕРНАЯ СРЕДА
- § 2. Соотношения упругости
- § 3. Уравнения совместности
- § 4. Общие теоремы
- § 5. Псевдоконтинуум Коссера
- § 6. Плоская деформация
- § 7. Нелинейная теория
- § 8. Нелинейная модель со стесненным вращением
- Глава 6. ТЕРМОУПРУГОСТЬ
- § 2. Второй закон
- § 3. Определяющие уравнения
- § 4. Уравнение теплопроводности
- § 5. Линейная термоупругость
- § 6. Уравнения в перемещениях
- § 7. Температурные напряжения
- § 8. Вариационные подстановки
- Глава 7. АСИМПТОТИЧЕСКИЕ МЕТОДЫ
- § 2. Расщепление в линейной алгебраической системе
- § 3. Метод Пуанкаре
- § 4. Метод осреднения Ван-дер-Поля
- § 5. Метод сращивания асимптотических разложений
- § 6. Метод многих масштабов
- § 7. Уравнения с медленно меняющимися коэффициентами
- § 8. Тонкие тела
- Глава 8. СТЕРЖНИ
- § 2. Кинематика линий Коссера
- § 3. Силовые факторы и их баланс
- § 4. Принцип виртуальной работы и его следствия
- § 5. Классическая модель Кирхгофа
- § 6. Задача Эйлера
- § 7. Уравнения в вариациях
- § 8. Модель с растяжением без сдвига
- § 9. Механика нити
- § 10. Линейная теория
- § 11. Случай малой толщины
- § 12. Задача Сен-Венана
- § 13. Определение жесткостей по энергии
- § 14. Вариационный метод построения одномерных моделей
- § 15. Асимптотическое расщепление трехмерной задачи
- § 16. Температурные деформации и напряжения
- Глава 9. ТОНКОСТЕННЫЕ СТЕРЖНИ
- § 2. Уравнения пространственной задачи с малым параметром
- § 3. Первый шаг асимптотической процедуры
- § 4. Второй шаг
- § 5. Третий шаг
- § 6. Четвертый шаг
- § 7. Перемещения
- § 8. Итоги асимптотического анализа
- Глава 10. ПЛАСТИНЫ
- § 2. Модель типа Тимошенко (прямой подход)
- § 3. Классическая теория Кирхгофа
- § 4. Асимптотическое соотношение двумерных моделей
- § 5. Вариационный переход от трехмерной модели
- § 6. Асимптотическое расщепление трехмерной задачи изгиба
- § 7. Круглые пластины
- § 8. Плоское напряженное состояние
- Глава 11. ОБОЛОЧКИ
- § 2. Модель оболочки
- § 3. Баланс сил и моментов
- § 4. Соотношения упругости
- § 5. Классическая теория
- § 6. Пластина
- § 7. Подход с множителями Лагранжа
- § 8. Цилиндрическая оболочка
- § 9. Общие теоремы
- § 10. Граничные условия
- § 11. Оболочки вращения
- § 12. Безмоментная теория
- § 13. Нелинейная безмоментная теория
- § 14. Иной вариант классической теории
- Глава 12. КОЛЕБАНИЯ И ВОЛНЫ
- § 1. Колебания трехмерных тел
- § 2. Колебания стержней
- § 3. Малые возмущения параметров
- § 4. Колебания оболочек
- § 5. Волны в упругой среде
- § 6. Волны в стержнях
- § 7. Нелинейные колебания
- Глава 13. УСТОЙЧИВОСТЬ
- § 1. Различные подходы к проблеме устойчивости
- § 2. Классические задачи о стержнях
- § 3. Следящие нагрузки
- § 4. Роль дополнительных податливостей
- § 5. Вариационные постановки
- § 6. Неконсервативные задачи
- § 7. Случай кратных корней
- Глава 14. ДЕФЕКТЫ
- § 1. Дислокации Вольтерры
- § 2. Прямолинейные дислокации
- § 3. Действие поля напряжений на дислокацию
- § 4. О движении дислокаций
- § 5. Точечные дефекты
- § 6. Сила, действующая на точечный дефект
- § 7. Непрерывно распределенные дислокации
- § 8. Напряжения при намотке катушки
- Глава 15. ТРЕЩИНЫ
- § 1. Традиционные критерии прочности
- § 2. Антиплоская деформация среды с трещиной
- § 3. Трещина при плоской деформации
- § 4. Трещинодвижущая сила
- § 5. Критерий роста трещины
- § 6. Интеграл Райса
- § 7. Определение КИН как самостоятельных неизвестных
- § 8. Модель Баренблатта
- § 9. Деформационный критерий
- § 10. Рост трещии
- § 11. Упругое поле у фронта движущейся трещины
- § 12. Баланс энергии для движущейся трещины
- Глава 16. КОМПОЗИТЫ
- § 2. Эффективные поля
- § 3. Граничные задачи для представительного объема
- § 4. Вилка Хилла
- § 5. Формулы Эшелби
- § 6. Эффективные модули среды со сферическими включениями
- § 7. Метод самосогласования
- § 8. Принцип Хашина-Штрикмана
- Глава 17. ПЕРИОДИЧЕСКИЕ СТРУКТУРЫ
- § 2. Трехмерная среда
- § 3. Волокнистая структура
- § 4. Статика периодического стержня
- Глава 18. МАГНИТОУПРУГОСТЬ
- § 2. Электростатика
- § 3. Диэлектрики
- § 4. Магнитостатика
- § 5. Магнетики
- § 6. Магнитная жесткость
- СПИСОК ЛИТЕРАТУРЫ