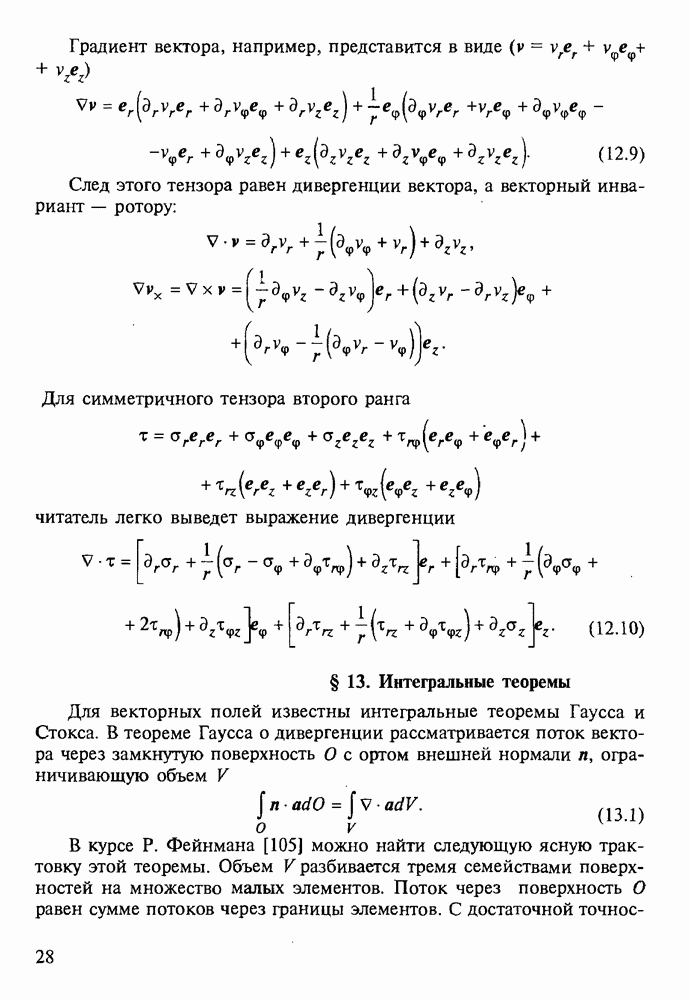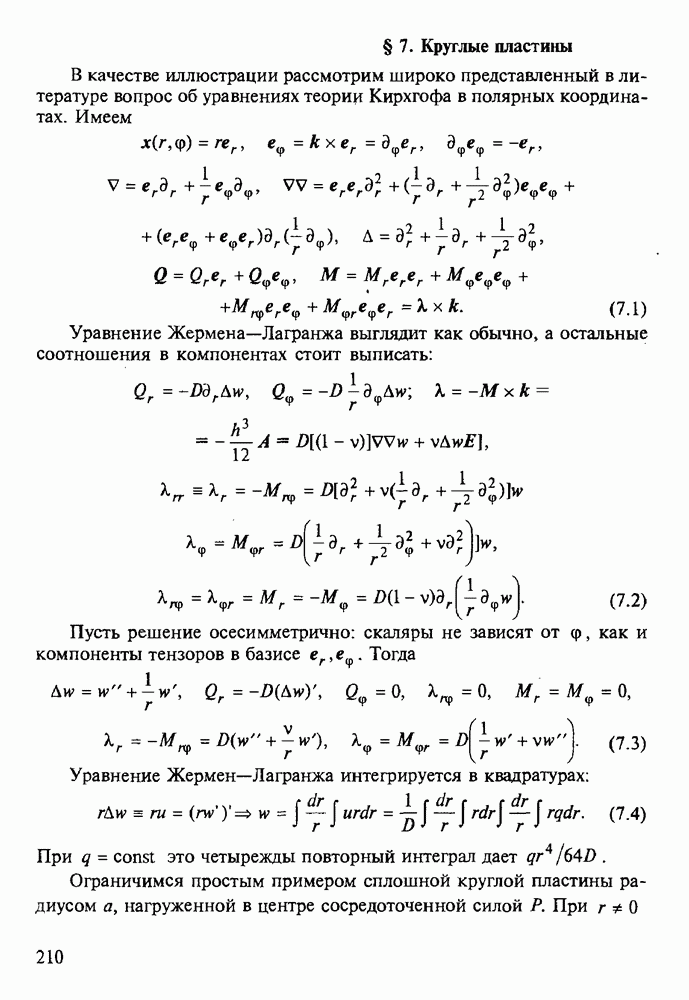| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Определение КИН как самостоятельных неизвестных
Расчет прочности тела с трещиной сводится к определению коэффициентов интенсивности (КИН). Методы расчета  как аналитические, так и численные — хорошо освещены в литературе. Рассмотрим еще один подход к задачам механики трещин, разработанный автором вместе с Е. А. Кабо.
как аналитические, так и численные — хорошо освещены в литературе. Рассмотрим еще один подход к задачам механики трещин, разработанный автором вместе с Е. А. Кабо.
Если в обычной постановке фигурируют  то в предлагаемой новой к ним добавляются КИН как самостоятельные неизвестные. Постановка является вариационной, соответствующий функционал возникает из обычного выражения потенциальной энергии.
то в предлагаемой новой к ним добавляются КИН как самостоятельные неизвестные. Постановка является вариационной, соответствующий функционал возникает из обычного выражения потенциальной энергии.
Антиплоская деформация. Этот случай хорош как иллюстрация метода. Область  содержит трещину, выходящую на границу (рис. 49). Коэффициент
содержит трещину, выходящую на границу (рис. 49). Коэффициент  в вершине является главной неизвестной. Воздействиями служат силы в области
в вершине является главной неизвестной. Воздействиями служат силы в области  и на границе
и на границе  а также заданные на границе
а также заданные на границе  перемещения
перемещения  . В положении равновесия минимальна энергия
. В положении равновесия минимальна энергия  представим ее следующим образом:
представим ее следующим образом:


Рис. 49
В области  мы выделили малую часть
мы выделили малую часть  у вершины (с границей С),
у вершины (с границей С),  уже справедливы асимптотические формулы (2.3), из них взята функция
уже справедливы асимптотические формулы (2.3), из них взята функция  по ним вычисляется запасенная в
по ним вычисляется запасенная в  энергия деформации
энергия деформации  Слагаемое
Слагаемое  в условии на контуре С — это не зависящая от координат трансляция.
в условии на контуре С — это не зависящая от координат трансляция.
Проварьируем функционал (7.1):

Из равенства  вытекают обычные уравнения баланса сил в
вытекают обычные уравнения баланса сил в  и на
и на  а также соотношения
а также соотношения

служащие для определения  как самостоятельных неизвестных.
как самостоятельных неизвестных.
Принцип минимума функционала (7.1) отличается от классического принципа Лагранжа и требует обоснования. Используя равенства

убеждаемся в справедливости (7.2). Вид второй вариации

свидетельствует о минимуме функционала.
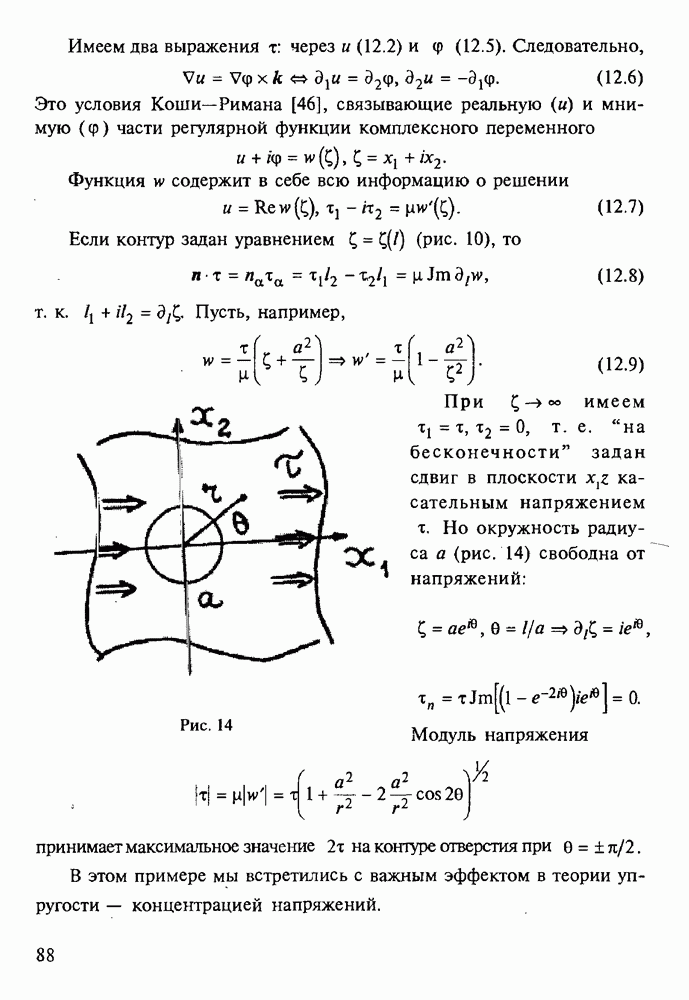
Рассмотрим аналитический тест. Внешняя граница  окружность радиусом
окружность радиусом  на ней задано
на ней задано  Трещина — луч
Трещина — луч  Решение очевидно:
Решение очевидно:  Симметрия подсказывает, что трансляция на фронте
Симметрия подсказывает, что трансляция на фронте  . В качестве вспомогательной внутренней границы С возьмем окружность радиусом
. В качестве вспомогательной внутренней границы С возьмем окружность радиусом  Минимизируя
Минимизируя  при фиксированном неизвестном К, получим
при фиксированном неизвестном К, получим

 превращается в функцию
превращается в функцию  ее минимизация дает точное решение
ее минимизация дает точное решение  Результат не зависит от X, что не удивительно, ибо точное решение совпадает с асимптотическим.
Результат не зависит от X, что не удивительно, ибо точное решение совпадает с асимптотическим.
Более сложные тесты, рассмотренные Е. А. Кабо и С. Г. Орловым с помощью метода конечных элементов, выявили эффективность предлагаемой методики расчета КИН. Эта методика позволяет учитывать сингулярность на фронте без использования специальных элементов вычислительной механики трещин [79].
В постановке (7.1) на вспомогательном внутреннем контуре С задаются перемещения. Другая постановка связана с заданием напряжений:

функция  берется из асимптотической формулы
берется из асимптотической формулы  Вариационное уравнение
Вариационное уравнение  эквивалентно системе, содержащей не только обычные соотношения в и на
эквивалентно системе, содержащей не только обычные соотношения в и на  но и равенства
но и равенства

Справедливость этих равенств выясняется при подстановке в них асимптотических выражений.
Функционал  не имеет минимума (из-за минуса перед
не имеет минимума (из-за минуса перед  ). Этот его недостаток не играет роли при построении точных решений — например, методом суперпозиции. Сначала решаем две обычные задачи:
). Этот его недостаток не играет роли при построении точных решений — например, методом суперпозиции. Сначала решаем две обычные задачи:

Далее полагаем

отсюда находим К.
Суперпозиция проходит и в постановке с  но там требуется еще одно решение для “обслуживания” трансляции
но там требуется еще одно решение для “обслуживания” трансляции 
Интегральные соотношения (7.2) и (7.6) вызывают ассоциации с  -интегралом. Наши интегралы зависят от контура С, но зато обобщаются на пространственную задачу — об этом далее.
-интегралом. Наши интегралы зависят от контура С, но зато обобщаются на пространственную задачу — об этом далее.
Пространственная задача. Трещина — это разрез на поверхности 2 с контуром  Аналогом малой области
Аналогом малой области  выделяемой в двумерной
выделяемой в двумерной

Рис. 50
постановке (см. рис. 49), теперь является трубка с осью  и сечением
и сечением  (рис. 50). Введем дуговые координаты:
(рис. 50). Введем дуговые координаты:  на фронте
на фронте  на контуре сечения С. Декартовы оси
на контуре сечения С. Декартовы оси  в сечении (с ортами
в сечении (с ортами  ) - это оси х и у из асимптотических формул. Понадобятся орты:
) - это оси х и у из асимптотических формул. Понадобятся орты:  — осей
— осей  касательной на
касательной на  нормали к С в сечении и
нормали к С в сечении и  касательной к С.
касательной к С.
В объеме трубки введем координаты  Тогда
Тогда

(см. гл. 8). Элементарный объем

Энергия в объеме трубки

где напряжения  в выражении
в выражении  определяются коэффициентами интенсивности
определяются коэффициентами интенсивности  и асимптотическими формулами.
и асимптотическими формулами.
На поверхности трубки  имеем координаты
имеем координаты  , радиус-вектор
, радиус-вектор  базисные векторы
базисные векторы

и вектор площадки (с нормалью, направленной из трубки)

Далее будем рассматривать трехмерную область вне трубки, и орт и обозначит нормаль из материала как на внешней поверхности О, так и на внутренней 
Предлагается следующий вариационный принцип (обобщение 

Компоненты заданных векторных функций  в базисе
в базисе  определяются лишь асимптотическими формулами. Слагаемое
определяются лишь асимптотическими формулами. Слагаемое  это трансляция на фронте.
это трансляция на фронте.
Проварьируем функционал (7.10):

Использованы (7.9) и выражение  Из предлагаемого принципа вытекают обычные уравнения в объеме и на
Из предлагаемого принципа вытекают обычные уравнения в объеме и на  а также интегральные соотношения
а также интегральные соотношения

Функционал (7.10) не только стационарен, но и минимален на точном решении. Стационарность без минимальности характерна для другой вариационной постановки — обобщения (7.3):

Напряжения  определяются асимптотическими формулами. Из (7.13) следует
определяются асимптотическими формулами. Из (7.13) следует

Для области вне трубки имеем обычную задачу с поверхностными нагрузками на с  Но
Но  при этом неизвестны, необходимо использовать интегральные (подчеркнутые) соотношения.
при этом неизвестны, необходимо использовать интегральные (подчеркнутые) соотношения.
В заключение отметим, что предлагаемые новые постановки (7.10) и (7.13) (как двумерные (7.1) и  соответствуют задаче с трещиной лишь
соответствуют задаче с трещиной лишь
при достаточно малом диаметре  точное решение получается в предельном переходе. Достоинства этих постановок — отсутствие сингулярностей и применимость обычных вычислительных алгоритмов.
точное решение получается в предельном переходе. Достоинства этих постановок — отсутствие сингулярностей и применимость обычных вычислительных алгоритмов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 2. Определение тензора
- § 3. Действия над тензорами
- § 4. Полиадное представление
- § 5. Векторное произведение и тензор Леви-Чивита
- § 6. Антисимметричные тензоры
- § 7. Главные оси и главные значения симметричного тензора
- § 8. Тензор поворота
- § 9. Полярное разложение
- § 10. Тензоры в косоугольном базисе
- § 11. Тензорные функции
- § 12. Тензорные поля. Дифференцирование
- § 13. Интегральные теоремы
- § 14. Тензор Римана-Кристоффеля
- Глава 2. ОСНОВЫ ОБЩЕЙ МЕХАНИКИ
- § 2. Абсолютно твердое тело
- § 3. Принцип виртуальной работы
- § 4. Баланс импульса, момента импульса и энергии
- § 5. Принцип Гамильтона и уравнения Лагранжа
- § 6. Статика
- § 7. Механика относительного движения
- § 8. Малые колебания
- Глава 3. НЕЛИНЕЙНО-УПРУГАЯ БЕЗМОМЕНТНАЯ СРЕДА
- § 2. Дифференцирование
- § 3. Градиент деформации
- § 4. Меры и тензоры деформации
- § 5. Поле скоростей
- § 6. Вектор площадки
- § 7. Силы в сплошной среде. Тензор напряжений
- § 8. Баланс импульса и момента импульса
- § 9. Принцип виртуальной работы
- § 10. Соотношения упругости
- § 11. Тензор Пиола
- § 12. Варьирование актуальной конфигурации
- § 13. Внутренние связи
- § 14. Полая сфера под действием давления
- § 15. Напряжения как множители Лагранжа
- Глава 4. КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ УПРУГОСТЬ
- § 2. Единственность решения динамической задачи
- § 3. Закон Гука
- § 4. Общие теоремы статики
- § 5. Уравнения в перемещениях
- § 6. Сосредоточенная сила в неограниченной среде
- § 7. Определение перемещений по деформациям
- § 8. Уравнения в напряжениях
- § 9. Принцип минимума потенциальной энергии системы
- § 10. Принцип минимума дополнительной работы
- § 11. Смешанные принципы стационарности
- § 12. Антиплоская деформация
- § 13. Кручение стержней
- § 14. Плоская деформация
- Глава 5. МОМЕНТНАЯ ТРЕХМЕРНАЯ СРЕДА
- § 2. Соотношения упругости
- § 3. Уравнения совместности
- § 4. Общие теоремы
- § 5. Псевдоконтинуум Коссера
- § 6. Плоская деформация
- § 7. Нелинейная теория
- § 8. Нелинейная модель со стесненным вращением
- Глава 6. ТЕРМОУПРУГОСТЬ
- § 2. Второй закон
- § 3. Определяющие уравнения
- § 4. Уравнение теплопроводности
- § 5. Линейная термоупругость
- § 6. Уравнения в перемещениях
- § 7. Температурные напряжения
- § 8. Вариационные подстановки
- Глава 7. АСИМПТОТИЧЕСКИЕ МЕТОДЫ
- § 2. Расщепление в линейной алгебраической системе
- § 3. Метод Пуанкаре
- § 4. Метод осреднения Ван-дер-Поля
- § 5. Метод сращивания асимптотических разложений
- § 6. Метод многих масштабов
- § 7. Уравнения с медленно меняющимися коэффициентами
- § 8. Тонкие тела
- Глава 8. СТЕРЖНИ
- § 2. Кинематика линий Коссера
- § 3. Силовые факторы и их баланс
- § 4. Принцип виртуальной работы и его следствия
- § 5. Классическая модель Кирхгофа
- § 6. Задача Эйлера
- § 7. Уравнения в вариациях
- § 8. Модель с растяжением без сдвига
- § 9. Механика нити
- § 10. Линейная теория
- § 11. Случай малой толщины
- § 12. Задача Сен-Венана
- § 13. Определение жесткостей по энергии
- § 14. Вариационный метод построения одномерных моделей
- § 15. Асимптотическое расщепление трехмерной задачи
- § 16. Температурные деформации и напряжения
- Глава 9. ТОНКОСТЕННЫЕ СТЕРЖНИ
- § 2. Уравнения пространственной задачи с малым параметром
- § 3. Первый шаг асимптотической процедуры
- § 4. Второй шаг
- § 5. Третий шаг
- § 6. Четвертый шаг
- § 7. Перемещения
- § 8. Итоги асимптотического анализа
- Глава 10. ПЛАСТИНЫ
- § 2. Модель типа Тимошенко (прямой подход)
- § 3. Классическая теория Кирхгофа
- § 4. Асимптотическое соотношение двумерных моделей
- § 5. Вариационный переход от трехмерной модели
- § 6. Асимптотическое расщепление трехмерной задачи изгиба
- § 7. Круглые пластины
- § 8. Плоское напряженное состояние
- Глава 11. ОБОЛОЧКИ
- § 2. Модель оболочки
- § 3. Баланс сил и моментов
- § 4. Соотношения упругости
- § 5. Классическая теория
- § 6. Пластина
- § 7. Подход с множителями Лагранжа
- § 8. Цилиндрическая оболочка
- § 9. Общие теоремы
- § 10. Граничные условия
- § 11. Оболочки вращения
- § 12. Безмоментная теория
- § 13. Нелинейная безмоментная теория
- § 14. Иной вариант классической теории
- Глава 12. КОЛЕБАНИЯ И ВОЛНЫ
- § 1. Колебания трехмерных тел
- § 2. Колебания стержней
- § 3. Малые возмущения параметров
- § 4. Колебания оболочек
- § 5. Волны в упругой среде
- § 6. Волны в стержнях
- § 7. Нелинейные колебания
- Глава 13. УСТОЙЧИВОСТЬ
- § 1. Различные подходы к проблеме устойчивости
- § 2. Классические задачи о стержнях
- § 3. Следящие нагрузки
- § 4. Роль дополнительных податливостей
- § 5. Вариационные постановки
- § 6. Неконсервативные задачи
- § 7. Случай кратных корней
- Глава 14. ДЕФЕКТЫ
- § 1. Дислокации Вольтерры
- § 2. Прямолинейные дислокации
- § 3. Действие поля напряжений на дислокацию
- § 4. О движении дислокаций
- § 5. Точечные дефекты
- § 6. Сила, действующая на точечный дефект
- § 7. Непрерывно распределенные дислокации
- § 8. Напряжения при намотке катушки
- Глава 15. ТРЕЩИНЫ
- § 1. Традиционные критерии прочности
- § 2. Антиплоская деформация среды с трещиной
- § 3. Трещина при плоской деформации
- § 4. Трещинодвижущая сила
- § 5. Критерий роста трещины
- § 6. Интеграл Райса
- § 7. Определение КИН как самостоятельных неизвестных
- § 8. Модель Баренблатта
- § 9. Деформационный критерий
- § 10. Рост трещии
- § 11. Упругое поле у фронта движущейся трещины
- § 12. Баланс энергии для движущейся трещины
- Глава 16. КОМПОЗИТЫ
- § 2. Эффективные поля
- § 3. Граничные задачи для представительного объема
- § 4. Вилка Хилла
- § 5. Формулы Эшелби
- § 6. Эффективные модули среды со сферическими включениями
- § 7. Метод самосогласования
- § 8. Принцип Хашина-Штрикмана
- Глава 17. ПЕРИОДИЧЕСКИЕ СТРУКТУРЫ
- § 2. Трехмерная среда
- § 3. Волокнистая структура
- § 4. Статика периодического стержня
- Глава 18. МАГНИТОУПРУГОСТЬ
- § 2. Электростатика
- § 3. Диэлектрики
- § 4. Магнитостатика
- § 5. Магнетики
- § 6. Магнитная жесткость
- СПИСОК ЛИТЕРАТУРЫ