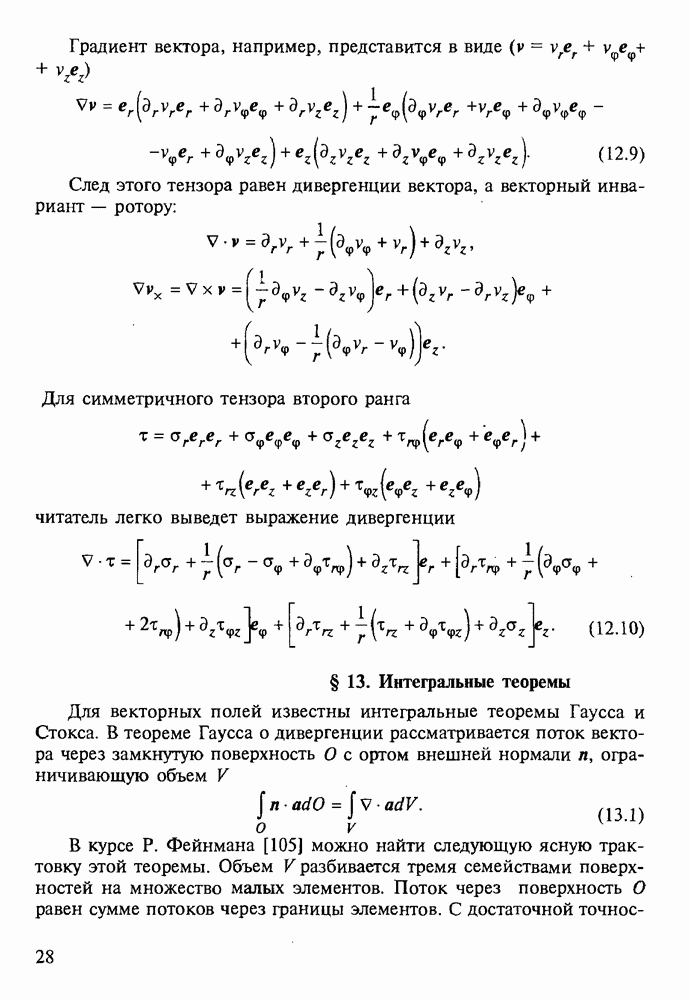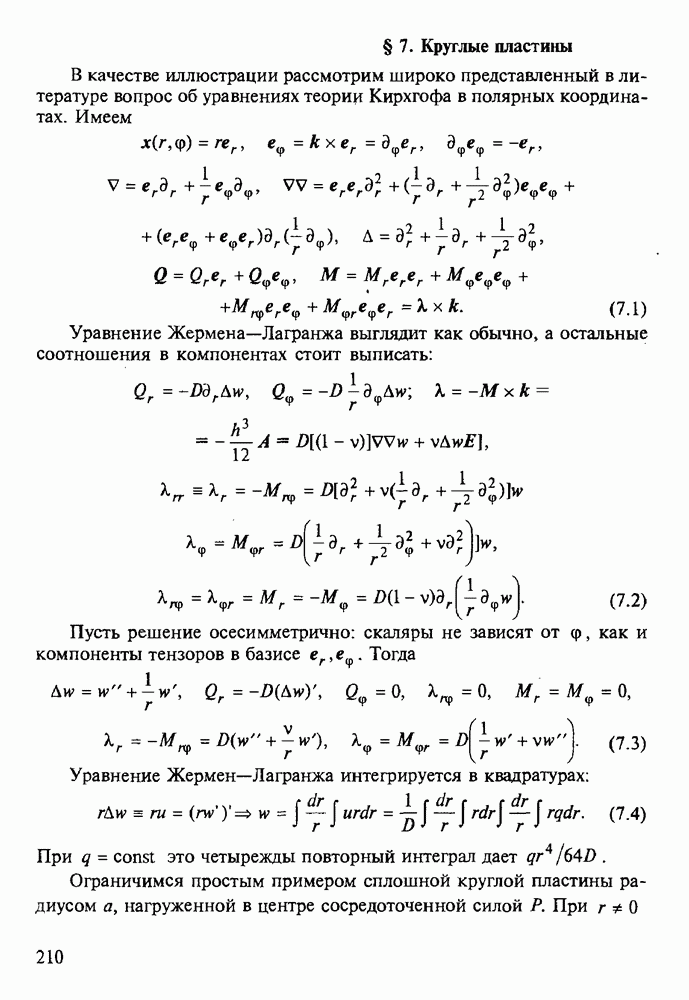| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 14. Плоская деформация
Этот термин означает лишь то, что вектор и параллелен плоскости  и не зависит от
и не зависит от 

перемещения и деформации “двумерны”. Но в тензоре напряжений присутствует дополнительная компонента 

Плоская деформация реализуется в бесконечном цилиндре, расположенном вдоль оси z, когда объемные и поверхностные нагрузки перпендикулярны образующим и постоянны на них. Как и при антиплоской деформации, можно рассматривать плоскую фигуру  с границей
с границей  (рис. 13).
(рис. 13).
Наибольший интерес представляет решение без объемных сил. Уравнение баланса сил позволяет ввести функцию напряжений Эри [53, 68]:

Детали вывода таковы:


Формула (14.3) — это инвариантная запись последних соотношений. Знаменитое бигармоническое уравнение

— результат подстановки (14.3) в уравнение совместности деформаций, которое при плоской деформации сводится к одному скалярному равенству

Конкретно имеем

Поставим граничные условия для  на контуре с заданными поверхностными силами
на контуре с заданными поверхностными силами  (рис. 18). Вектор напряжения
(рис. 18). Вектор напряжения

Интегрируя по промежутку  найдем главный вектор нагрузок на этом участке
найдем главный вектор нагрузок на этом участке


Рис. 18
Здесь мы учли, что  определен с точностью до аддитивной константы, и потому приняли
определен с точностью до аддитивной константы, и потому приняли 
Условие (14.8) — это одно из двух, необходимых для бигармонического уравнения. Второе связано с моментом

Без ущерба для общности принято  .
.
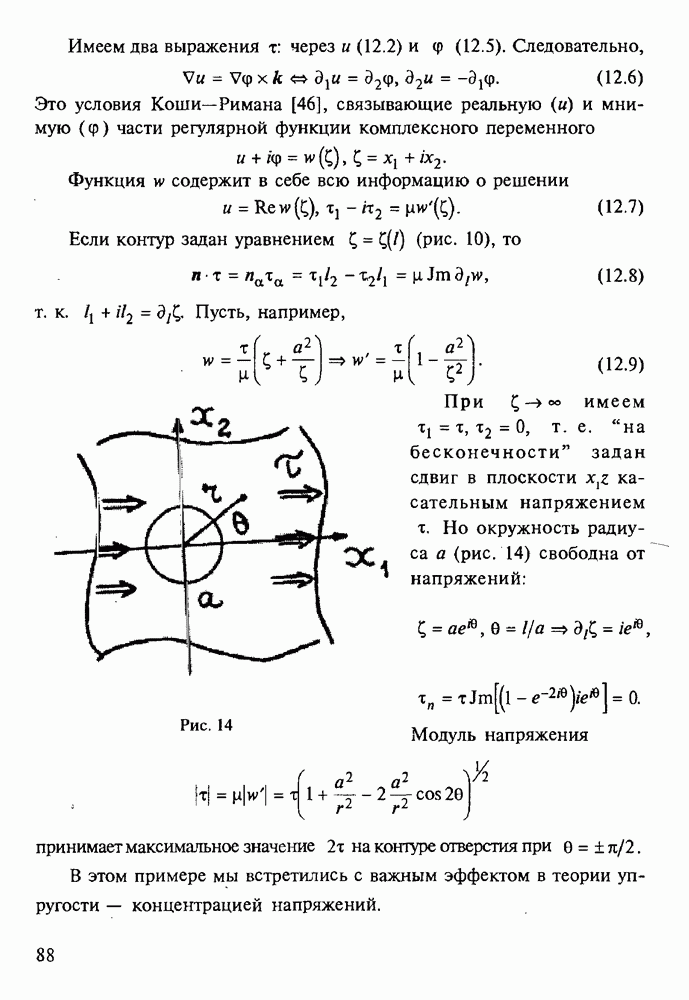
В качестве примера рассмотрим полуплоскость с сосредоточенной нормальной силой  на границе (рис. 19) — задачу Фламана [53]. Граница области — декартова ось
на границе (рис. 19) — задачу Фламана [53]. Граница области — декартова ось  точке
точке  соответствует
соответствует  Условия при
Условия при  таковы:
таковы:


Рис. 19
Решение этой несложной задачи можно построить разными способами. Если  гармоническая сила, то
гармоническая сила, то  будут бигармоническими — как и сама
будут бигармоническими — как и сама  Но интересно рассмотреть своеобразный метод решения, основанный на представлениях о размерности величин. Искомое решение запишем
Но интересно рассмотреть своеобразный метод решения, основанный на представлениях о размерности величин. Искомое решение запишем  как
как

Достаточно ясно, что  безразмерна и никаких дополнительных аргументов содержать не может. Но аргументами безразмерной функции должны быть лишь безразмерные аргументы — поэтому
безразмерна и никаких дополнительных аргументов содержать не может. Но аргументами безразмерной функции должны быть лишь безразмерные аргументы — поэтому  Тогда легко угадать общее решение вида (14.11)
Тогда легко угадать общее решение вида (14.11)

Определив константы из граничных условий  найдем
найдем  :
:

Отброшены слагаемые  постоянным градиентом. Линии уровня
постоянным градиентом. Линии уровня  показанные на рис. 19 окружности.
показанные на рис. 19 окружности.
Обратимся к перемещениям. Общий вид их связи с функцией Эри выводится из (14.6) с учетом того, что гармоническая функция  представима реальной частью некоторой регулярной функции
представима реальной частью некоторой регулярной функции 


Функция  оказалась перемещением твердого тела и потому отброшена в заключительной формуле.
оказалась перемещением твердого тела и потому отброшена в заключительной формуле.
Определим перемещения в задаче Фламана (см. (14.12)):

Неудивительно, что и  при
при  (логарифмическая особенность). Но трудно примириться с тем, что при
(логарифмическая особенность). Но трудно примириться с тем, что при  н не только не затухает, но даже неограниченно растет. Это — “дефект” плоской задачи. В пространственной задаче с сосредоточенной силой на границе полупространства результаты более физичны [53].
н не только не затухает, но даже неограниченно растет. Это — “дефект” плоской задачи. В пространственной задаче с сосредоточенной силой на границе полупространства результаты более физичны [53].
В плоской задаче широко и эффективно применяются методы теории функций комплексного переменного (конформное отображение, интеграл Коши и др.) [46, 53, 64]. Распространение компьютеров не обесценивает эти изощренные методы, но заставляет сместить акценты — громоздкие выкладки без особой необходимости становятся нерациональными. Выведем основные формулы с комплексным переменным в плоской задаче.
Казалось бы, любую функцию от  можно считать зависящей лишь от
можно считать зависящей лишь от  . Но запись
. Но запись  обычно применяется для регулярных функций с их замечательными свойствами. Поэтому пару
обычно применяется для регулярных функций с их замечательными свойствами. Поэтому пару  заменяют парой
заменяют парой  со следующими соотношениями производных
со следующими соотношениями производных

Уравнение Лапласа тогда допускает своеобразное решение:

Пришли к известному представлению гармонической функции через регулярную.
Решая подобным образом бигармоническое уравнение, получим формулу Гурса с двумя регулярными функциями:

Основные соотношения, называемые формулами Колосова-Мусхелишвили, таковы:

Первая из этих формул содержится в (14.17). Вторая вытекает из равенства

Третья же — это выражение (14.13), переписанное с учетом того, что

Решению граничных задач для  и т. е. определению их из граничных условий разных типов, посвящено много специальных монографий. Тщательно изучены и задачи со смешанными граничными условиями — в частности, контактные [64].
и т. е. определению их из граничных условий разных типов, посвящено много специальных монографий. Тщательно изучены и задачи со смешанными граничными условиями — в частности, контактные [64].
Библиография
Можно назвать несколько десятков книг по классической теории упругости, представляющих несомненный интерес несмотря на возрастающую отдаленность во времени. Подробные литературные указания содержатся в фундаментальной монографии А.И. Лурье [53], пространственным задачам посвящена более ранняя его книга [51]. Широко известны книги С.П. Тимошенко и Дж. Гудьера [99] с предельно упрощенным математическим аппаратом. У Н.И. Мусхелишвили [64] особое внимание уделено применению комплексного переменного. Богатый материал представлен у В. Новацкого [68]. Новые и неформальные подходы представлены в курсе Ю.Н. Работаова (не только по теории упругости) [85]. Привлекая математиков, теория упругости является и сложной математической дисциплиной, о чем свидетельствуют книги Н.Ф. Морозова [62] и Ф. Сьярле [93]. Нельзя не отметить труд А. Лява [54]. Особенности описания анизотропных сред изложены у К.Ф. Черных [112].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 2. Определение тензора
- § 3. Действия над тензорами
- § 4. Полиадное представление
- § 5. Векторное произведение и тензор Леви-Чивита
- § 6. Антисимметричные тензоры
- § 7. Главные оси и главные значения симметричного тензора
- § 8. Тензор поворота
- § 9. Полярное разложение
- § 10. Тензоры в косоугольном базисе
- § 11. Тензорные функции
- § 12. Тензорные поля. Дифференцирование
- § 13. Интегральные теоремы
- § 14. Тензор Римана-Кристоффеля
- Глава 2. ОСНОВЫ ОБЩЕЙ МЕХАНИКИ
- § 2. Абсолютно твердое тело
- § 3. Принцип виртуальной работы
- § 4. Баланс импульса, момента импульса и энергии
- § 5. Принцип Гамильтона и уравнения Лагранжа
- § 6. Статика
- § 7. Механика относительного движения
- § 8. Малые колебания
- Глава 3. НЕЛИНЕЙНО-УПРУГАЯ БЕЗМОМЕНТНАЯ СРЕДА
- § 2. Дифференцирование
- § 3. Градиент деформации
- § 4. Меры и тензоры деформации
- § 5. Поле скоростей
- § 6. Вектор площадки
- § 7. Силы в сплошной среде. Тензор напряжений
- § 8. Баланс импульса и момента импульса
- § 9. Принцип виртуальной работы
- § 10. Соотношения упругости
- § 11. Тензор Пиола
- § 12. Варьирование актуальной конфигурации
- § 13. Внутренние связи
- § 14. Полая сфера под действием давления
- § 15. Напряжения как множители Лагранжа
- Глава 4. КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ УПРУГОСТЬ
- § 2. Единственность решения динамической задачи
- § 3. Закон Гука
- § 4. Общие теоремы статики
- § 5. Уравнения в перемещениях
- § 6. Сосредоточенная сила в неограниченной среде
- § 7. Определение перемещений по деформациям
- § 8. Уравнения в напряжениях
- § 9. Принцип минимума потенциальной энергии системы
- § 10. Принцип минимума дополнительной работы
- § 11. Смешанные принципы стационарности
- § 12. Антиплоская деформация
- § 13. Кручение стержней
- § 14. Плоская деформация
- Глава 5. МОМЕНТНАЯ ТРЕХМЕРНАЯ СРЕДА
- § 2. Соотношения упругости
- § 3. Уравнения совместности
- § 4. Общие теоремы
- § 5. Псевдоконтинуум Коссера
- § 6. Плоская деформация
- § 7. Нелинейная теория
- § 8. Нелинейная модель со стесненным вращением
- Глава 6. ТЕРМОУПРУГОСТЬ
- § 2. Второй закон
- § 3. Определяющие уравнения
- § 4. Уравнение теплопроводности
- § 5. Линейная термоупругость
- § 6. Уравнения в перемещениях
- § 7. Температурные напряжения
- § 8. Вариационные подстановки
- Глава 7. АСИМПТОТИЧЕСКИЕ МЕТОДЫ
- § 2. Расщепление в линейной алгебраической системе
- § 3. Метод Пуанкаре
- § 4. Метод осреднения Ван-дер-Поля
- § 5. Метод сращивания асимптотических разложений
- § 6. Метод многих масштабов
- § 7. Уравнения с медленно меняющимися коэффициентами
- § 8. Тонкие тела
- Глава 8. СТЕРЖНИ
- § 2. Кинематика линий Коссера
- § 3. Силовые факторы и их баланс
- § 4. Принцип виртуальной работы и его следствия
- § 5. Классическая модель Кирхгофа
- § 6. Задача Эйлера
- § 7. Уравнения в вариациях
- § 8. Модель с растяжением без сдвига
- § 9. Механика нити
- § 10. Линейная теория
- § 11. Случай малой толщины
- § 12. Задача Сен-Венана
- § 13. Определение жесткостей по энергии
- § 14. Вариационный метод построения одномерных моделей
- § 15. Асимптотическое расщепление трехмерной задачи
- § 16. Температурные деформации и напряжения
- Глава 9. ТОНКОСТЕННЫЕ СТЕРЖНИ
- § 2. Уравнения пространственной задачи с малым параметром
- § 3. Первый шаг асимптотической процедуры
- § 4. Второй шаг
- § 5. Третий шаг
- § 6. Четвертый шаг
- § 7. Перемещения
- § 8. Итоги асимптотического анализа
- Глава 10. ПЛАСТИНЫ
- § 2. Модель типа Тимошенко (прямой подход)
- § 3. Классическая теория Кирхгофа
- § 4. Асимптотическое соотношение двумерных моделей
- § 5. Вариационный переход от трехмерной модели
- § 6. Асимптотическое расщепление трехмерной задачи изгиба
- § 7. Круглые пластины
- § 8. Плоское напряженное состояние
- Глава 11. ОБОЛОЧКИ
- § 2. Модель оболочки
- § 3. Баланс сил и моментов
- § 4. Соотношения упругости
- § 5. Классическая теория
- § 6. Пластина
- § 7. Подход с множителями Лагранжа
- § 8. Цилиндрическая оболочка
- § 9. Общие теоремы
- § 10. Граничные условия
- § 11. Оболочки вращения
- § 12. Безмоментная теория
- § 13. Нелинейная безмоментная теория
- § 14. Иной вариант классической теории
- Глава 12. КОЛЕБАНИЯ И ВОЛНЫ
- § 1. Колебания трехмерных тел
- § 2. Колебания стержней
- § 3. Малые возмущения параметров
- § 4. Колебания оболочек
- § 5. Волны в упругой среде
- § 6. Волны в стержнях
- § 7. Нелинейные колебания
- Глава 13. УСТОЙЧИВОСТЬ
- § 1. Различные подходы к проблеме устойчивости
- § 2. Классические задачи о стержнях
- § 3. Следящие нагрузки
- § 4. Роль дополнительных податливостей
- § 5. Вариационные постановки
- § 6. Неконсервативные задачи
- § 7. Случай кратных корней
- Глава 14. ДЕФЕКТЫ
- § 1. Дислокации Вольтерры
- § 2. Прямолинейные дислокации
- § 3. Действие поля напряжений на дислокацию
- § 4. О движении дислокаций
- § 5. Точечные дефекты
- § 6. Сила, действующая на точечный дефект
- § 7. Непрерывно распределенные дислокации
- § 8. Напряжения при намотке катушки
- Глава 15. ТРЕЩИНЫ
- § 1. Традиционные критерии прочности
- § 2. Антиплоская деформация среды с трещиной
- § 3. Трещина при плоской деформации
- § 4. Трещинодвижущая сила
- § 5. Критерий роста трещины
- § 6. Интеграл Райса
- § 7. Определение КИН как самостоятельных неизвестных
- § 8. Модель Баренблатта
- § 9. Деформационный критерий
- § 10. Рост трещии
- § 11. Упругое поле у фронта движущейся трещины
- § 12. Баланс энергии для движущейся трещины
- Глава 16. КОМПОЗИТЫ
- § 2. Эффективные поля
- § 3. Граничные задачи для представительного объема
- § 4. Вилка Хилла
- § 5. Формулы Эшелби
- § 6. Эффективные модули среды со сферическими включениями
- § 7. Метод самосогласования
- § 8. Принцип Хашина-Штрикмана
- Глава 17. ПЕРИОДИЧЕСКИЕ СТРУКТУРЫ
- § 2. Трехмерная среда
- § 3. Волокнистая структура
- § 4. Статика периодического стержня
- Глава 18. МАГНИТОУПРУГОСТЬ
- § 2. Электростатика
- § 3. Диэлектрики
- § 4. Магнитостатика
- § 5. Магнетики
- § 6. Магнитная жесткость
- СПИСОК ЛИТЕРАТУРЫ