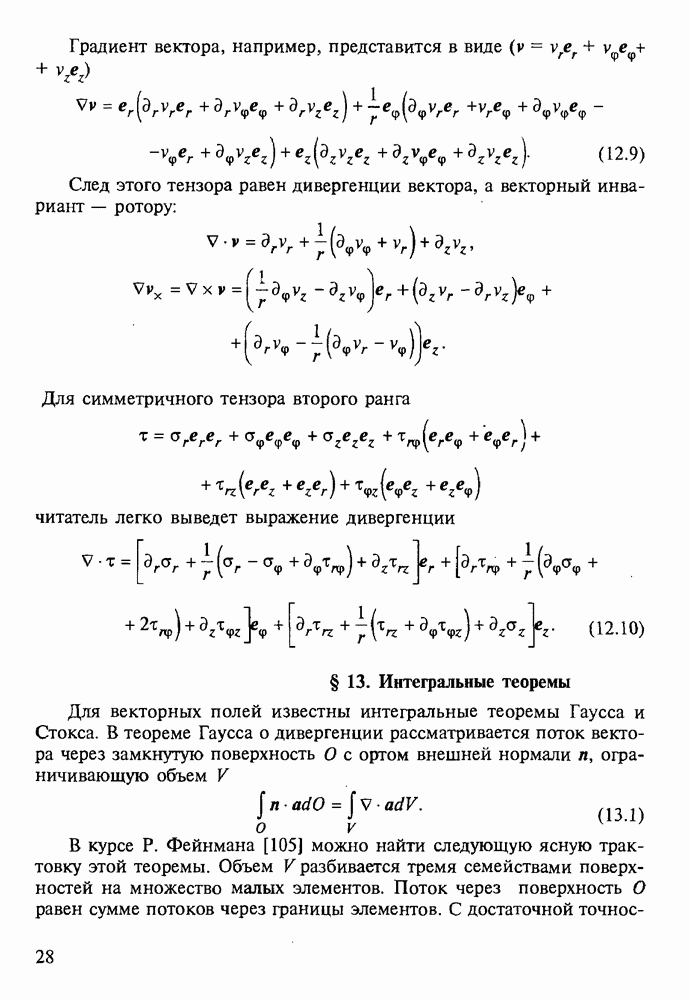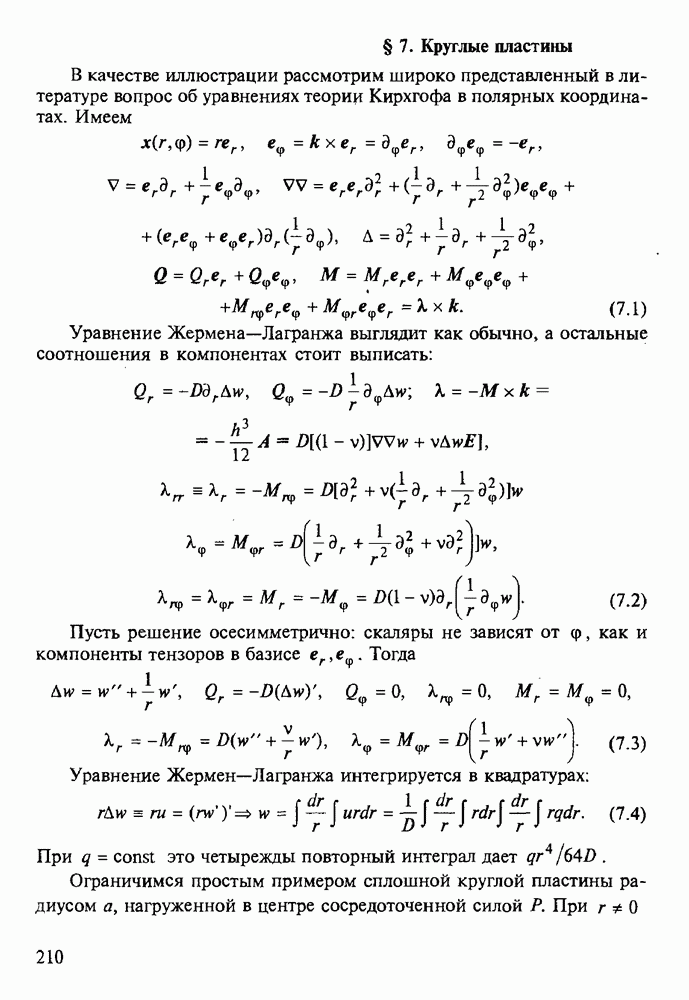| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Действие поля напряжений на дислокацию
Рассмотрим тело, содержащее внутри дислокацию с замкнутой линией С. Тело нагружено объемными  и поверхностными
и поверхностными  силами. Обозначим
силами. Обозначим  и
и  напряжения и перемещения в теле без дислокации:
напряжения и перемещения в теле без дислокации:

Введем далее  напряжения и перемещения в теле, обусловленные лишь дислокацией:
напряжения и перемещения в теле, обусловленные лишь дислокацией:

Последний интеграл — по контуру вокруг С, причем направления обхода С и вокруг С согласованы правилом правого винта. Очевидно, что в нагруженном теле с дислокацией

Можно считать, что дислокация находится во внешнем поле напряжений  .
.
Далее мы обнаружим, что это поле действует на дислокацию некими силами. В соответствии с представлениями лагранжевой механики следует рассмотреть работу  всех сил на виртуальном перемещении
всех сил на виртуальном перемещении  дислокации; если
дислокации; если

то  сила на единицу длины линии дислокации. Вычисление работы упрощается, если силы имеют потенциал; тогда
сила на единицу длины линии дислокации. Вычисление работы упрощается, если силы имеют потенциал; тогда  вариация потенциала.
вариация потенциала.
Для рассматриваемого линейно-упругого тела подходящее выражение потенциала

Достаточно очевидно, что вклад внутренних упругих сил и внешних нагрузок определяется потенциалом  Но силы иной природы — сопротивление движению дислокации и т. п. — должны рассматриваться отдельно.
Но силы иной природы — сопротивление движению дислокации и т. п. — должны рассматриваться отдельно.
Подставив (3.1) в (3.3), получим

Здесь учтено, что  Слагаемое
Слагаемое  не связано с дислокацией, при виртуальном перемещении дислокации
не связано с дислокацией, при виртуальном перемещении дислокации  Часть
Часть  потенциала — расходящийся интеграл;
потенциала — расходящийся интеграл;  не связана с внешним полем. Лишь перекрестный член Охарактеризует действие поля на дислокацию.
не связана с внешним полем. Лишь перекрестный член Охарактеризует действие поля на дислокацию.
Рассматриваемый вопрос неформален, поэтому выскажем еще следующие соображения. Изучая, например, электрическое поле, мы пользуемся пробным зарядом; он должен быть достаточно мал, чтобы вызываемым им возмущением поля можно было пренебречь. Так же и с дислокацией: ее вектор Бюргерса предполагается малым. Собственная энергия дислокации  оказывается второго порядка малости. Заметим, что энергия поля точечного пробного заряда — расходящийся интеграл, как и
оказывается второго порядка малости. Заметим, что энергия поля точечного пробного заряда — расходящийся интеграл, как и  (кратко об электростатике — в гл. 18).
(кратко об электростатике — в гл. 18).

Рис. 36
Итак, действие поля напряжений на дислокацию определяется потенциалом  Но вычислить
Но вычислить  можно лишь при наличии разреза по какой-либо поверхности
можно лишь при наличии разреза по какой-либо поверхности  , натянутой на линию дислокации (рис. 36). При этом следует различать берега разреза
, натянутой на линию дислокации (рис. 36). При этом следует различать берега разреза  значения и на них
значения и на них  Преобразуем (3.4):
Преобразуем (3.4):

Подчеркнутый интеграл берется по поверхности  ограничивающей тело с разрезом. Но вклад О компенсируется интегралом с
ограничивающей тело с разрезом. Но вклад О компенсируется интегралом с  Учитывая далее, что
Учитывая далее, что  на берегах отличаются на вектор Бюргерса, получим
на берегах отличаются на вектор Бюргерса, получим

Элементарная интерпретация этой формулы: при создании дислокации по Вольтерра берег  перемещается относительно
перемещается относительно  на
на  при этом поверхностные силы
при этом поверхностные силы  совершают работу
совершают работу  равную запасенной энергии. По мнению автора, подобные рассуждения хороши как заключительные интерпретации, но не исходные основы — не следует пренебрегать формальными построениями, если они просты и убедительны. Многих ошибок (даже у выдающихся авторов) не было бы при использовании мощного — но не сложного — формального аппарата.
равную запасенной энергии. По мнению автора, подобные рассуждения хороши как заключительные интерпретации, но не исходные основы — не следует пренебрегать формальными построениями, если они просты и убедительны. Многих ошибок (даже у выдающихся авторов) не было бы при использовании мощного — но не сложного — формального аппарата.
Для определения сил, действующих на дислокацию, следует рассмотреть изменение  при виртуальном перемещении линии С. Речь идет о новой задаче — с другой линией
при виртуальном перемещении линии С. Речь идет о новой задаче — с другой линией  определяется разностью энергий на точных решениях. В новой задаче можно использовать поверхность 2, отличающуюся от
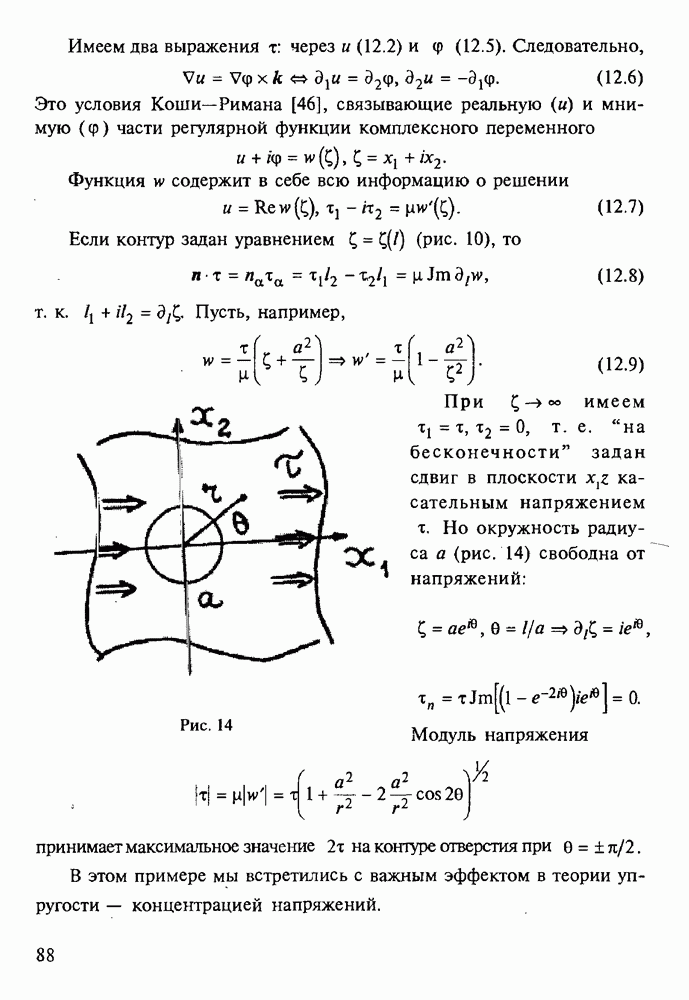
определяется разностью энергий на точных решениях. В новой задаче можно использовать поверхность 2, отличающуюся от  лишь узкой замкнутой полоской
лишь узкой замкнутой полоской  , “состоящей из векторов
, “состоящей из векторов  (рис. 37).
(рис. 37).

Рис. 37
Вектор площадки на 

где  орт касательной на С, так что
орт касательной на С, так что

Подтвердилось предположение (3.2), получена формула Пича-Келера [117] для силы, действующей на единицу длины линии дислокации.
Рассмотрим примеры применения формулы (3.6).
Краевая дислокация. В декартовой системе х, у, z орт касательной  а вектор Бюргерса
а вектор Бюргерса  Имеем
Имеем

Чтобы пояснить этот результат, обратимся к рис. 35. “Лишняя” полуплоскость — в неустойчивом состоянии: сдвигающее напряжение х, “побуждает ее объединиться” с нижней полуплоскость справа; верхняя полуплоскость справа оказывается без продолжения — дислокация передвинулась на период решетки. Так объясняют пластичность металлов.
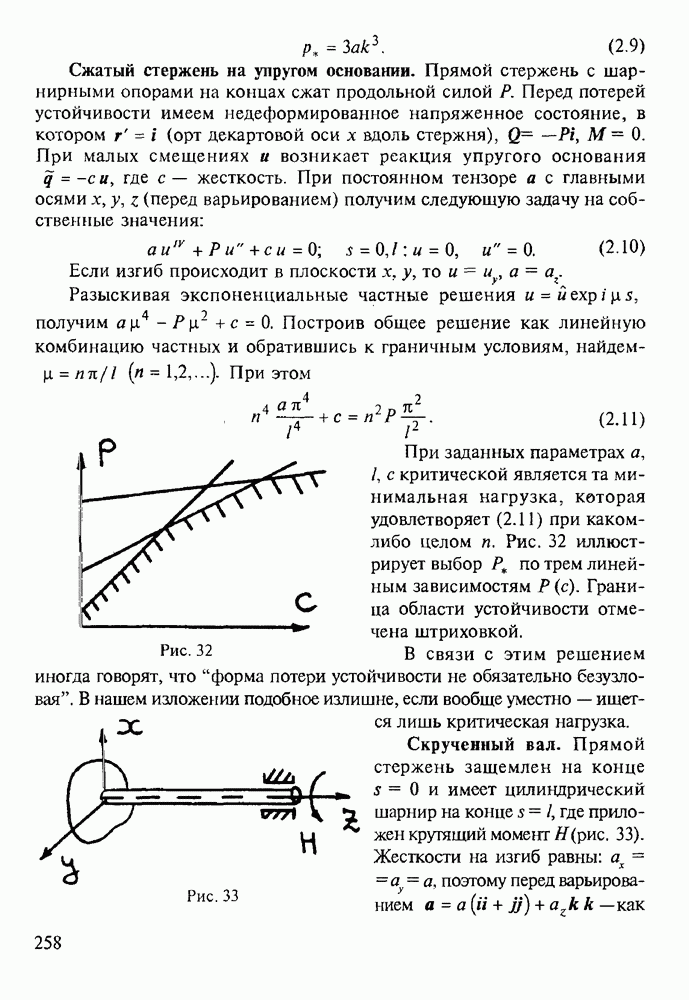
Взаимодействие винтовых дислокаций. В безграничной среде — две параллельных винтовые дислокации:  Первая дислокация — на оси z, а положение второй определяется полярными координатами
Первая дислокация — на оси z, а положение второй определяется полярными координатами  . Согласно (2.2), первая дислокация создает
. Согласно (2.2), первая дислокация создает
напряжения  На вторую дислокацию при этом будет действовать сила
На вторую дислокацию при этом будет действовать сила

Получили центральное взаимодействие. Одноименные дислокации отталкиваются, разноименные — притягиваются.
Параллельные краевые дислокации. Поле те создается дислокацией с  и описывается формулами (2.5). На вторую дислокацию с
и описывается формулами (2.5). На вторую дислокацию с  действует сила
действует сила

Центрального взаимодействия нет, но третий закон Ньютона выполняется, что связано с постоянством энергии  при трансляции пары дислокаций в неограниченной среде.
при трансляции пары дислокаций в неограниченной среде.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 2. Определение тензора
- § 3. Действия над тензорами
- § 4. Полиадное представление
- § 5. Векторное произведение и тензор Леви-Чивита
- § 6. Антисимметричные тензоры
- § 7. Главные оси и главные значения симметричного тензора
- § 8. Тензор поворота
- § 9. Полярное разложение
- § 10. Тензоры в косоугольном базисе
- § 11. Тензорные функции
- § 12. Тензорные поля. Дифференцирование
- § 13. Интегральные теоремы
- § 14. Тензор Римана-Кристоффеля
- Глава 2. ОСНОВЫ ОБЩЕЙ МЕХАНИКИ
- § 2. Абсолютно твердое тело
- § 3. Принцип виртуальной работы
- § 4. Баланс импульса, момента импульса и энергии
- § 5. Принцип Гамильтона и уравнения Лагранжа
- § 6. Статика
- § 7. Механика относительного движения
- § 8. Малые колебания
- Глава 3. НЕЛИНЕЙНО-УПРУГАЯ БЕЗМОМЕНТНАЯ СРЕДА
- § 2. Дифференцирование
- § 3. Градиент деформации
- § 4. Меры и тензоры деформации
- § 5. Поле скоростей
- § 6. Вектор площадки
- § 7. Силы в сплошной среде. Тензор напряжений
- § 8. Баланс импульса и момента импульса
- § 9. Принцип виртуальной работы
- § 10. Соотношения упругости
- § 11. Тензор Пиола
- § 12. Варьирование актуальной конфигурации
- § 13. Внутренние связи
- § 14. Полая сфера под действием давления
- § 15. Напряжения как множители Лагранжа
- Глава 4. КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ УПРУГОСТЬ
- § 2. Единственность решения динамической задачи
- § 3. Закон Гука
- § 4. Общие теоремы статики
- § 5. Уравнения в перемещениях
- § 6. Сосредоточенная сила в неограниченной среде
- § 7. Определение перемещений по деформациям
- § 8. Уравнения в напряжениях
- § 9. Принцип минимума потенциальной энергии системы
- § 10. Принцип минимума дополнительной работы
- § 11. Смешанные принципы стационарности
- § 12. Антиплоская деформация
- § 13. Кручение стержней
- § 14. Плоская деформация
- Глава 5. МОМЕНТНАЯ ТРЕХМЕРНАЯ СРЕДА
- § 2. Соотношения упругости
- § 3. Уравнения совместности
- § 4. Общие теоремы
- § 5. Псевдоконтинуум Коссера
- § 6. Плоская деформация
- § 7. Нелинейная теория
- § 8. Нелинейная модель со стесненным вращением
- Глава 6. ТЕРМОУПРУГОСТЬ
- § 2. Второй закон
- § 3. Определяющие уравнения
- § 4. Уравнение теплопроводности
- § 5. Линейная термоупругость
- § 6. Уравнения в перемещениях
- § 7. Температурные напряжения
- § 8. Вариационные подстановки
- Глава 7. АСИМПТОТИЧЕСКИЕ МЕТОДЫ
- § 2. Расщепление в линейной алгебраической системе
- § 3. Метод Пуанкаре
- § 4. Метод осреднения Ван-дер-Поля
- § 5. Метод сращивания асимптотических разложений
- § 6. Метод многих масштабов
- § 7. Уравнения с медленно меняющимися коэффициентами
- § 8. Тонкие тела
- Глава 8. СТЕРЖНИ
- § 2. Кинематика линий Коссера
- § 3. Силовые факторы и их баланс
- § 4. Принцип виртуальной работы и его следствия
- § 5. Классическая модель Кирхгофа
- § 6. Задача Эйлера
- § 7. Уравнения в вариациях
- § 8. Модель с растяжением без сдвига
- § 9. Механика нити
- § 10. Линейная теория
- § 11. Случай малой толщины
- § 12. Задача Сен-Венана
- § 13. Определение жесткостей по энергии
- § 14. Вариационный метод построения одномерных моделей
- § 15. Асимптотическое расщепление трехмерной задачи
- § 16. Температурные деформации и напряжения
- Глава 9. ТОНКОСТЕННЫЕ СТЕРЖНИ
- § 2. Уравнения пространственной задачи с малым параметром
- § 3. Первый шаг асимптотической процедуры
- § 4. Второй шаг
- § 5. Третий шаг
- § 6. Четвертый шаг
- § 7. Перемещения
- § 8. Итоги асимптотического анализа
- Глава 10. ПЛАСТИНЫ
- § 2. Модель типа Тимошенко (прямой подход)
- § 3. Классическая теория Кирхгофа
- § 4. Асимптотическое соотношение двумерных моделей
- § 5. Вариационный переход от трехмерной модели
- § 6. Асимптотическое расщепление трехмерной задачи изгиба
- § 7. Круглые пластины
- § 8. Плоское напряженное состояние
- Глава 11. ОБОЛОЧКИ
- § 2. Модель оболочки
- § 3. Баланс сил и моментов
- § 4. Соотношения упругости
- § 5. Классическая теория
- § 6. Пластина
- § 7. Подход с множителями Лагранжа
- § 8. Цилиндрическая оболочка
- § 9. Общие теоремы
- § 10. Граничные условия
- § 11. Оболочки вращения
- § 12. Безмоментная теория
- § 13. Нелинейная безмоментная теория
- § 14. Иной вариант классической теории
- Глава 12. КОЛЕБАНИЯ И ВОЛНЫ
- § 1. Колебания трехмерных тел
- § 2. Колебания стержней
- § 3. Малые возмущения параметров
- § 4. Колебания оболочек
- § 5. Волны в упругой среде
- § 6. Волны в стержнях
- § 7. Нелинейные колебания
- Глава 13. УСТОЙЧИВОСТЬ
- § 1. Различные подходы к проблеме устойчивости
- § 2. Классические задачи о стержнях
- § 3. Следящие нагрузки
- § 4. Роль дополнительных податливостей
- § 5. Вариационные постановки
- § 6. Неконсервативные задачи
- § 7. Случай кратных корней
- Глава 14. ДЕФЕКТЫ
- § 1. Дислокации Вольтерры
- § 2. Прямолинейные дислокации
- § 3. Действие поля напряжений на дислокацию
- § 4. О движении дислокаций
- § 5. Точечные дефекты
- § 6. Сила, действующая на точечный дефект
- § 7. Непрерывно распределенные дислокации
- § 8. Напряжения при намотке катушки
- Глава 15. ТРЕЩИНЫ
- § 1. Традиционные критерии прочности
- § 2. Антиплоская деформация среды с трещиной
- § 3. Трещина при плоской деформации
- § 4. Трещинодвижущая сила
- § 5. Критерий роста трещины
- § 6. Интеграл Райса
- § 7. Определение КИН как самостоятельных неизвестных
- § 8. Модель Баренблатта
- § 9. Деформационный критерий
- § 10. Рост трещии
- § 11. Упругое поле у фронта движущейся трещины
- § 12. Баланс энергии для движущейся трещины
- Глава 16. КОМПОЗИТЫ
- § 2. Эффективные поля
- § 3. Граничные задачи для представительного объема
- § 4. Вилка Хилла
- § 5. Формулы Эшелби
- § 6. Эффективные модули среды со сферическими включениями
- § 7. Метод самосогласования
- § 8. Принцип Хашина-Штрикмана
- Глава 17. ПЕРИОДИЧЕСКИЕ СТРУКТУРЫ
- § 2. Трехмерная среда
- § 3. Волокнистая структура
- § 4. Статика периодического стержня
- Глава 18. МАГНИТОУПРУГОСТЬ
- § 2. Электростатика
- § 3. Диэлектрики
- § 4. Магнитостатика
- § 5. Магнетики
- § 6. Магнитная жесткость
- СПИСОК ЛИТЕРАТУРЫ