| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
168. Дополнительные замечания.
Пусть ищутся относительные максимумы и минимумы функции  при одном дополнительном условии
при одном дополнительном условии

и предположим, что, например, относительный максимум достигается в точке  так что
так что  Пусть
Пусть  имеет непрерывные частные производные первого порядка в точке
имеет непрерывные частные производные первого порядка в точке  и ее некоторой окрестности, и предположим, кроме того, что
и ее некоторой окрестности, и предположим, кроме того, что

При этом уравнение (23) определит единственным образом в окрестности  функцию
функцию  непрерывную, с непрерывной производной и такую, что
непрерывную, с непрерывной производной и такую, что  Подставляя
Подставляя  в функцию
в функцию  мы можем утверждать, что функция
мы можем утверждать, что функция  одного переменного
одного переменного  должна достигать максимума при
должна достигать максимума при  и, следовательно, ее полная производная по
и, следовательно, ее полная производная по  должна обращаться в нуль при
должна обращаться в нуль при  то есть
то есть

Подставляя  в (23) и дифференцируя по
в (23) и дифференцируя по  получим в точке
получим в точке 

Умножая второе уравнение на X и складывая почленно с первым, получим

Определяя  из условия
из условия  что возможно, в силу (24), будем иметь
что возможно, в силу (24), будем иметь  , т. е. придем к двум уравнениям
, т. е. придем к двум уравнениям

к которым надо присоединить еще уравнение  чем и оправдывается способ множителей. Если условие (24) не выполнено, т. е.
чем и оправдывается способ множителей. Если условие (24) не выполнено, т. е.  но
но  то можно повторить все предыдущие рассуждения, меняя х и у ролями. Если в точке
то можно повторить все предыдущие рассуждения, меняя х и у ролями. Если в точке  мы имеем
мы имеем

то мы не можем доказать, что точка  получается при помощи правила множителей.
получается при помощи правила множителей.
Равенства (26) показывают, что точка  является особой точкой кривой (23) [76]. Дадим сейчас пример такой задачи, для которой имеют место условия (26) в точке относительного минимума.
является особой точкой кривой (23) [76]. Дадим сейчас пример такой задачи, для которой имеют место условия (26) в точке относительного минимума.
Пусть требуется найти кратчайшее расстояние от точки  до точек, лежащих на полукубической параболе
до точек, лежащих на полукубической параболе  изображенной на рис. 87 [76]. Таким образом, ищется минимум функции
изображенной на рис. 87 [76]. Таким образом, ищется минимум функции  при условии
при условии 
Геометрически очевидно, что минимум достигается в точке  лежащей на полукубической параболе, причем эта точка является особой точкой параболы. Способ множителей приведет нас к следующим двум уравнениям:
лежащей на полукубической параболе, причем эта точка является особой точкой параболы. Способ множителей приведет нас к следующим двум уравнениям:

При подстановке  первое уравнение приводит к нелепому равенству
первое уравнение приводит к нелепому равенству  а второе — удовлетворено при любом А. В данном случае способ множителей не приведет нас к точке (0, 0), в которой достигается относительный минимум.
а второе — удовлетворено при любом А. В данном случае способ множителей не приведет нас к точке (0, 0), в которой достигается относительный минимум.
Совершенно аналогично можно показать, что если в точке  функция достигает максимума или минимума, при одном дополнительном условии
функция достигает максимума или минимума, при одном дополнительном условии  и притом, по крайней мере, одна из частных производных первого порядка функции
и притом, по крайней мере, одна из частных производных первого порядка функции  отлична от нуля в точке
отлична от нуля в точке  то эта точка может быть получена по способу множителей.
то эта точка может быть получена по способу множителей.
Аналогичны рассуждения и в более общих случаях, но при этом приходится ссылаться на теорему существования неявных функций для систем уравнений, о чем мы упоминали в [157]. Пусть, например, функция  достигает относительного максимума в точке
достигает относительного максимума в точке  при двух дополнительных условиях
при двух дополнительных условиях

и при обычных предположениях существования и непрерывности производных, и пусть мы имеем

При этом уравнения (27) определяют единственным образом функции:  такие, что
такие, что  . Подставляя эти функции в функцию
. Подставляя эти функции в функцию  получим функцию одного
получим функцию одного  которая имеет максимум при
которая имеет максимум при  откуда следует
откуда следует

Подставляя указанные функции в (27) и дифференцируя по  в точке
в точке  получим
получим

Умножаем эти равенства на  и складываем с предыдущим
и складываем с предыдущим

Принимая во внимание (28), можем утверждать, что из двух уравнений

мы сможем определить  и уравнение (29) после этого приведет нас к равенству
и уравнение (29) после этого приведет нас к равенству

чем и оправдывается способ множителей для данного случая. К уравнениям (30) и (31) надо добавить еще

Вместо условия (28) мы могли бы поставить аналогичное условие, дифференцируя не по  а по
а по  или по
или по  Но если не только выражение, стоящее в левой части (28), но и два других аналогичных выражения, которые получаются при дифференцировании по
Но если не только выражение, стоящее в левой части (28), но и два других аналогичных выражения, которые получаются при дифференцировании по  или по
или по  равны нулю, то мы не сможем оправдать способ множителей для точки
равны нулю, то мы не сможем оправдать способ множителей для точки 
Можно показать, что во всех рассмотренных в следующем номере примерах мы не можем иметь такого случая. Так, например, в примере 1 мы имеем одно дополнительное условие (32). и в левой части этого условия, по крайней мере, одно из чисел А, В и С отлично от нуля. Если, например,  то производная левой части (32) по z равна числу С и, следовательно, отлична от нуля во всякой точке
то производная левой части (32) по z равна числу С и, следовательно, отлична от нуля во всякой точке  Это и указывает на то, что в рассматриваемом случае всякий ответ должен получаться по способу множителей.
Это и указывает на то, что в рассматриваемом случае всякий ответ должен получаться по способу множителей.
Приведем теперь короткие указания о достаточных условиях относительного максимума или минимума, ограничиваясь тем случаем, когда мы имеем две независимые переменные. Пусть ищутся относительные максимумы и минимумы функции  при наличии одной связи
при наличии одной связи  . Составляем функцию
. Составляем функцию  . Положим, что, приравнивая нулю ее производные первого порядка по
. Положим, что, приравнивая нулю ее производные первого порядка по  и учитывая уравнение связи, мы получали значения
и учитывая уравнение связи, мы получали значения  . Мы должны испытать полученные значения переменных, т. е. определить знак разности
. Мы должны испытать полученные значения переменных, т. е. определить знак разности  при всех
при всех  достаточно близких к
достаточно близких к  и удовлетворяющих уравнению связи
и удовлетворяющих уравнению связи  Введем функцию
Введем функцию  . Из уравнения связи непосредственно следует, что вместо разности
. Из уравнения связи непосредственно следует, что вместо разности  можно взять разность
можно взять разность  и исследовать ее знак. Частные производные первого порядка функции
и исследовать ее знак. Частные производные первого порядка функции  в точке
в точке  обращаются по условию в нуль. Разлагая последнюю разность по формуле Тейлора и ограничиваясь членами со вторыми производными, получим выражение вида
обращаются по условию в нуль. Разлагая последнюю разность по формуле Тейлора и ограничиваясь членами со вторыми производными, получим выражение вида 

где через мы обозначим значения соответствующих частных производных второго порядка функции  в точке
в точке  и через
и через  приращения переменных. Положим, что
приращения переменных. Положим, что  так что уравнение связи определяет
так что уравнение связи определяет  причем
причем  Из уравнения связи получаем
Из уравнения связи получаем

Подставляя значения  выражаем
выражаем  через
через 

Подставляя это выражение  в предыдущую формулу и собирая подобные члены, получим
в предыдущую формулу и собирая подобные члены, получим

Теперь можно использовать признак максимума и минимума из [163]. Так, например, если АС  то в точке
то в точке  функция
функция  ) имеет относительный минимум. Из рассуждений, приведенных в [163], непосредственно следует, что для обоснования указанного правила достаточно предположить, что функции
) имеет относительный минимум. Из рассуждений, приведенных в [163], непосредственно следует, что для обоснования указанного правила достаточно предположить, что функции  имеют в точке
имеют в точке  и ее окрестности непрерывные производные до второго порядка.
и ее окрестности непрерывные производные до второго порядка.
Мы не останавливаемся более подробно на вопросе о достаточных условиях относительного максимума и минимума.
Существенными в предыдущих рассуждениях являлись замена разности  разностью
разностью  у которой производные первого порядка в точке
у которой производные первого порядка в точке  равны нулю, а также факт, что дифференциал
равны нулю, а также факт, что дифференциал  зависимого переменного определялся через дифференциалы
зависимого переменного определялся через дифференциалы  независимых переменных из уравнения первой степени. Аналогичным образом надо поступать для выяснения достаточных условий и при другом числе переменных и связей.
независимых переменных из уравнения первой степени. Аналогичным образом надо поступать для выяснения достаточных условий и при другом числе переменных и связей.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
- 12. Линейная функция.
- 13. Приращение. Основное свойство линейной функции.
- 14. График равномерного движения.
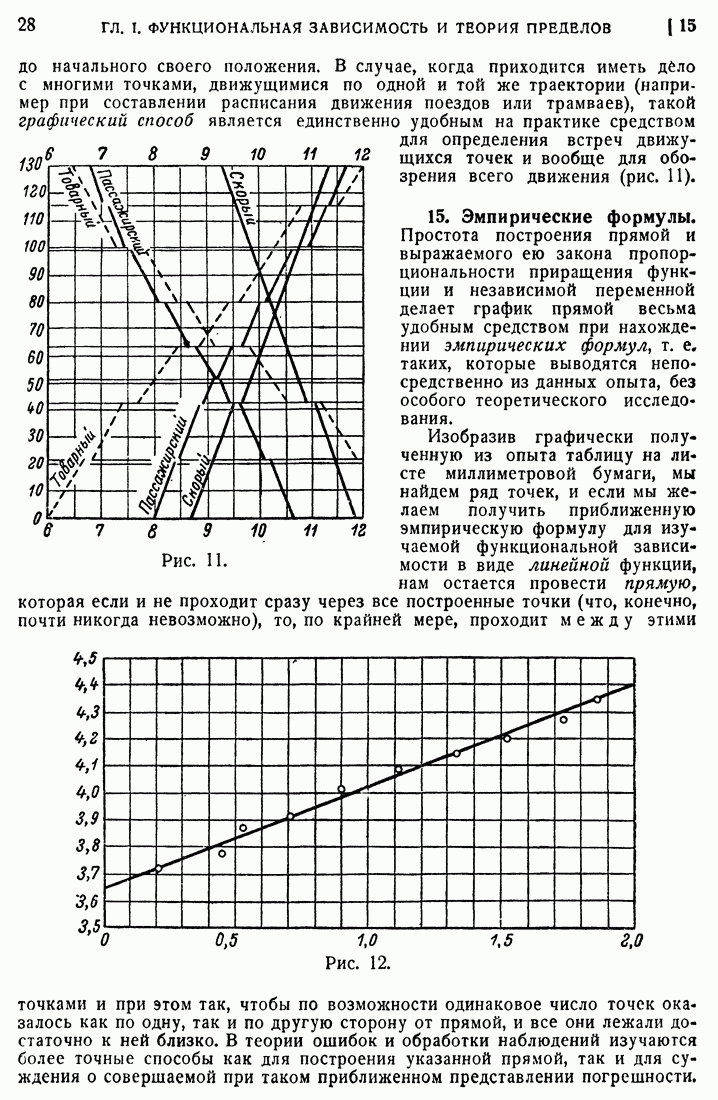
- 15. Эмпирические формулы.
- 16. Парабола второй степени.
- 17. Парабола третьей степени.
- 18. Закон обратной пропорциональности.
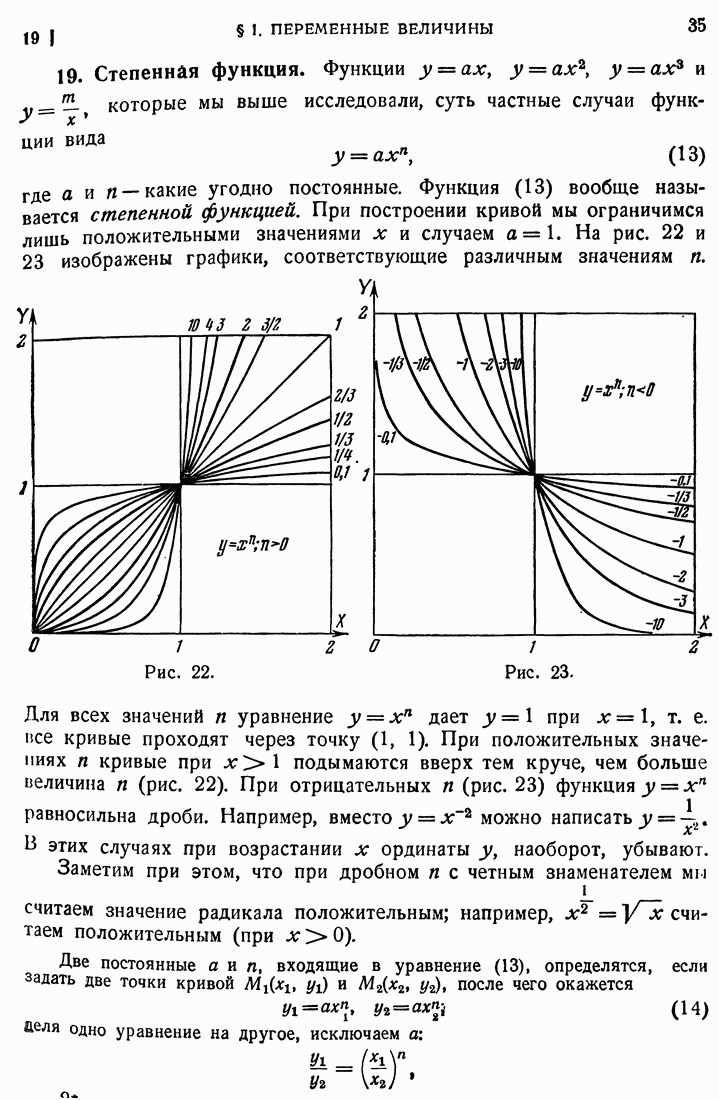
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
- 22. Показательная и логарифмическая функции.
- 23. Тригонометрические функции.
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
- 45. Понятие о производной.
- 46. Геометрическое значение производной.
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
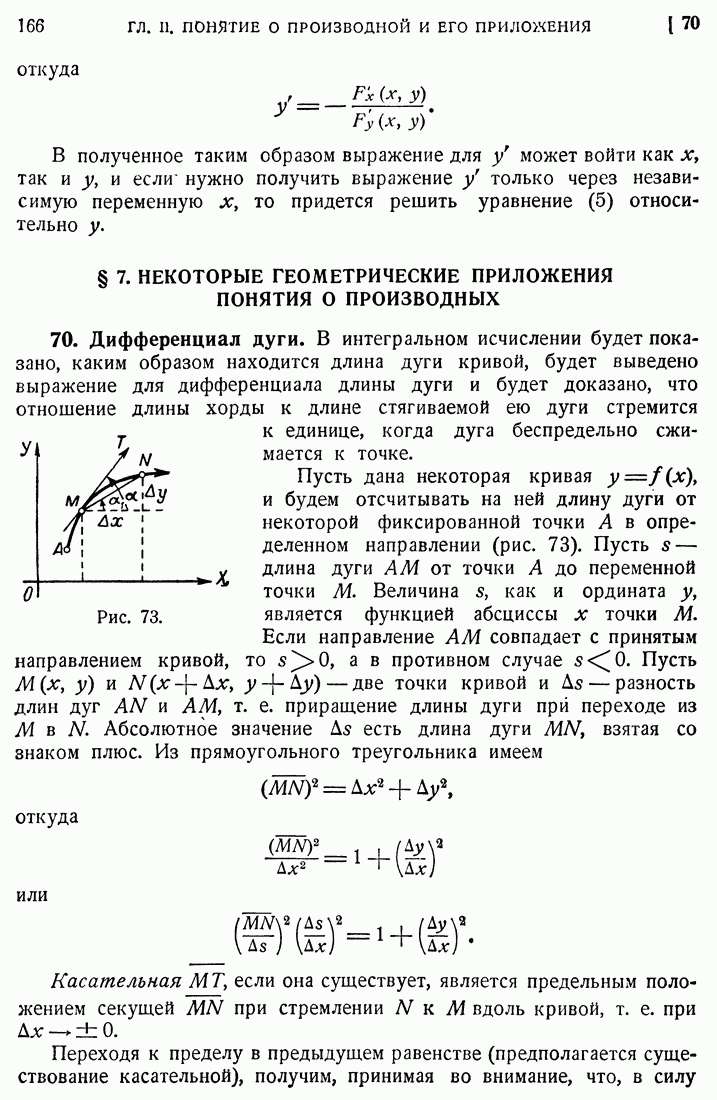
- 70. Дифференциал дуги.
- 71. Выпуклость, вогнутость и кривизна.
- 72. Асимптоты.
- 73. Построение графиков.
- 74. Параметрическое задание кривой.
- 75. Уравнение Ван-дер-Ваальса.
- 76. Особые точки кривых.
- 77. Элементы кривой.
- 78. Цепная линия.
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
- 81. Развертка круга.
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
- 97. Разрыв подынтегральной функции.
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
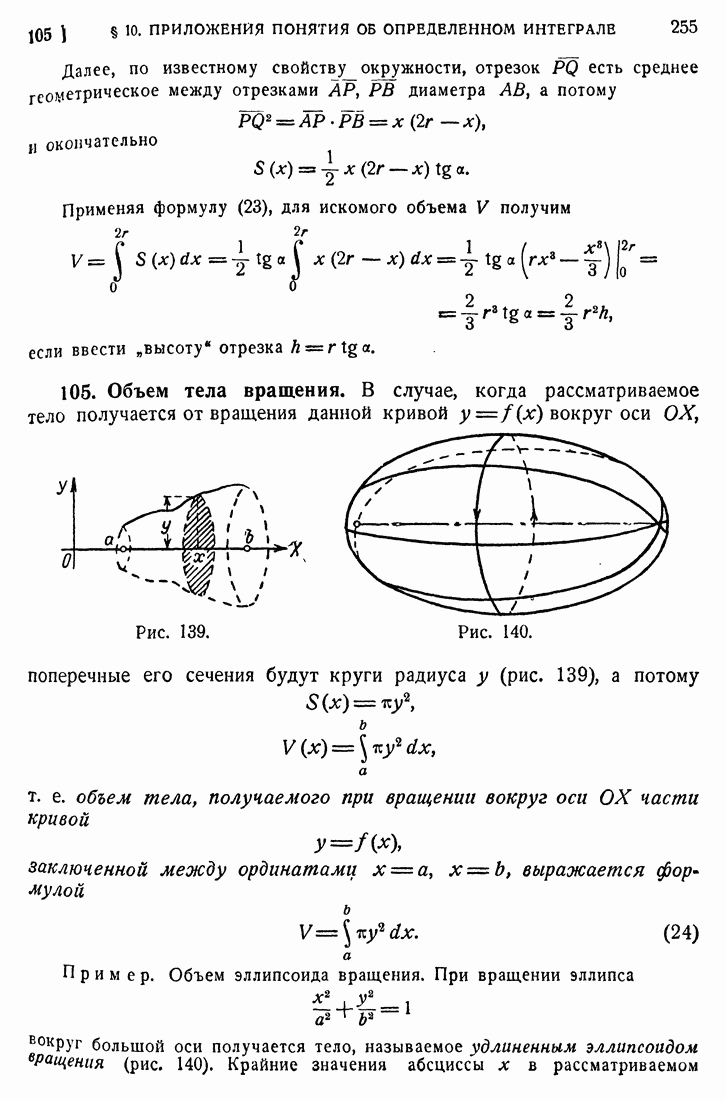
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
- 109. Формула касательных и формула Понселе.
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
- 112. Графические способы.
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
- 163. Исследование максимума и минимума функции двух независимых переменных.
- 164. Примеры.
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
- 177. Тригонометрические и гиперболические функции.
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
- 193. Способ итерации.
- 194. Способ Ньютона.
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…