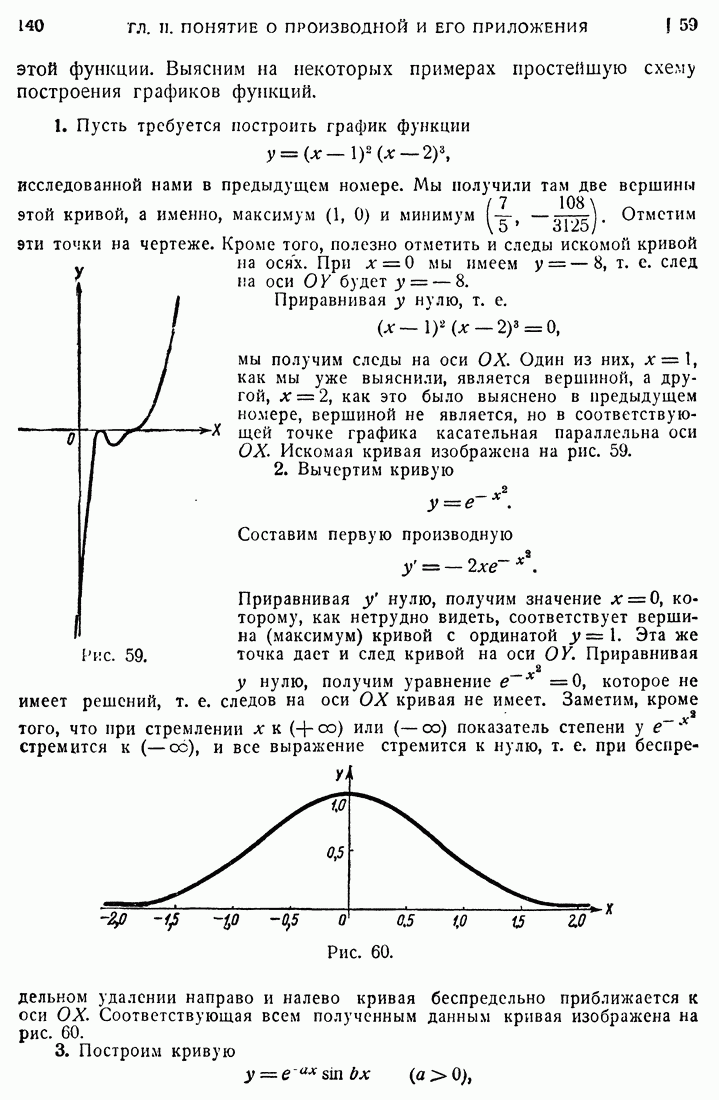
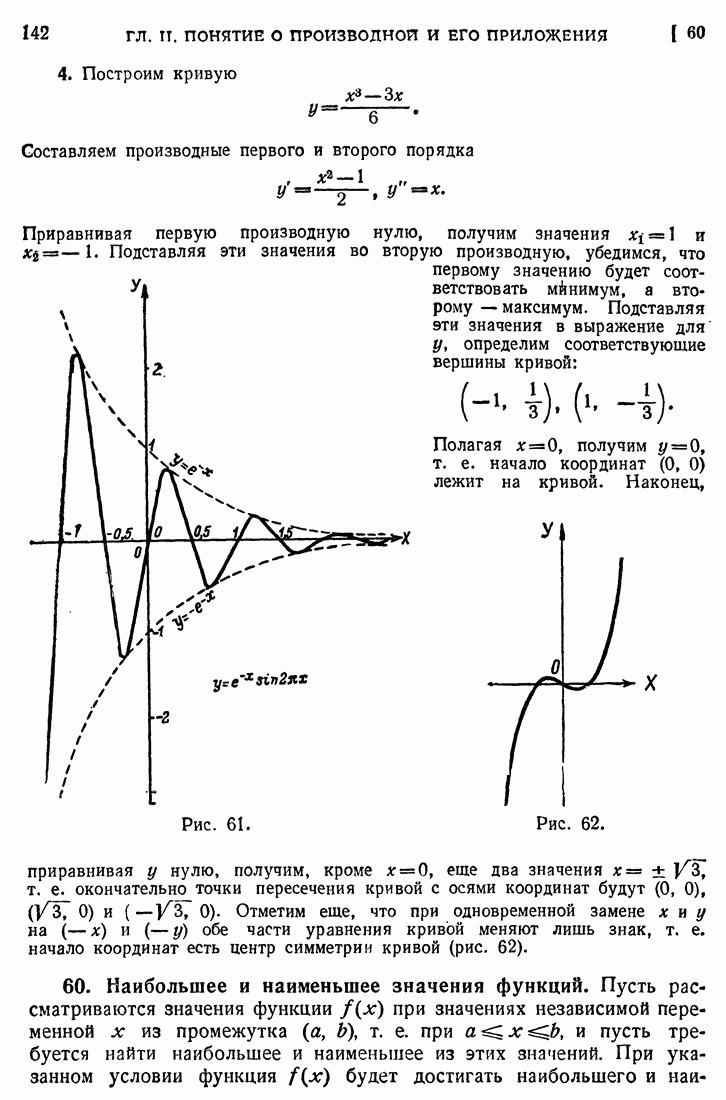
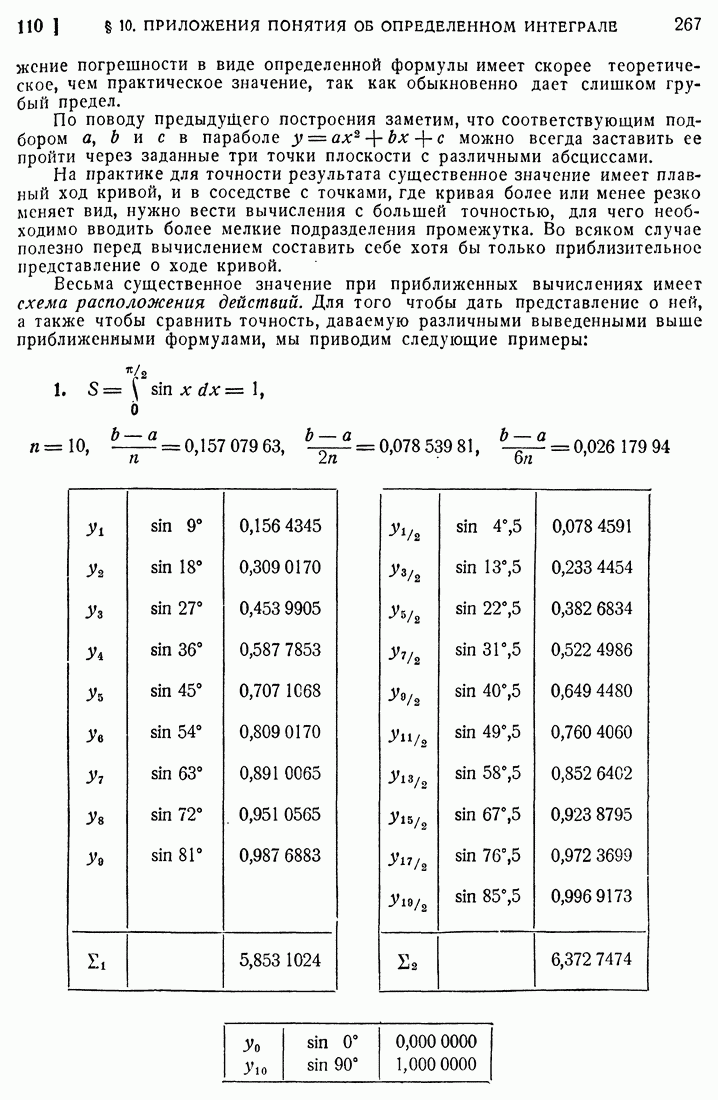
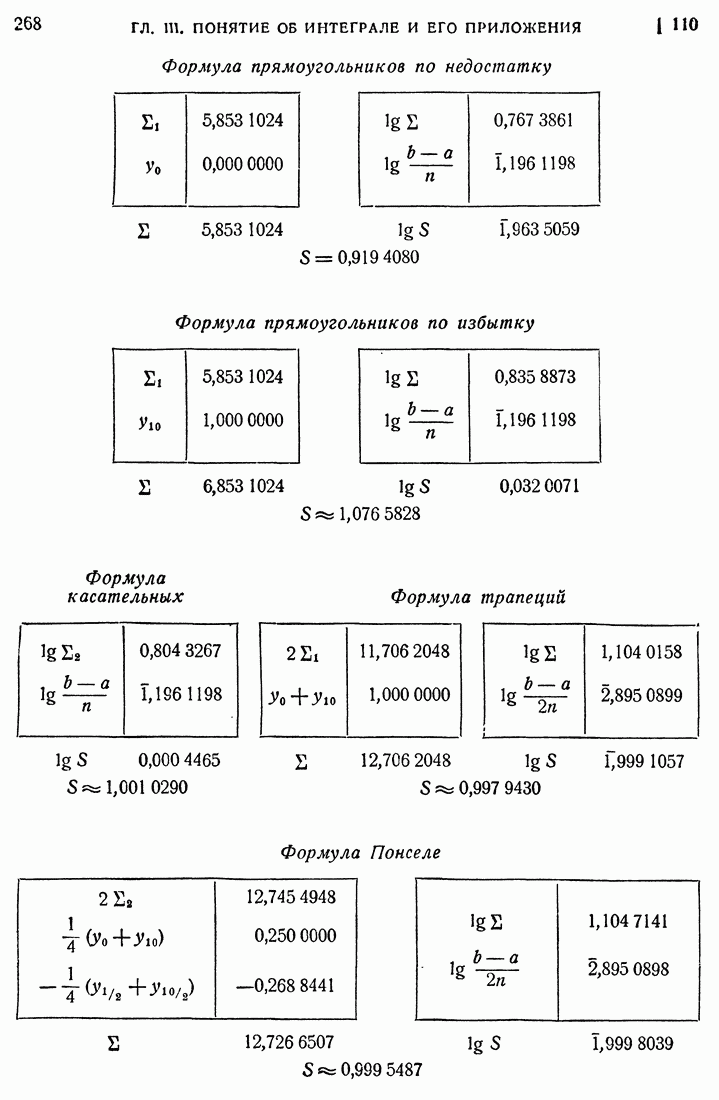
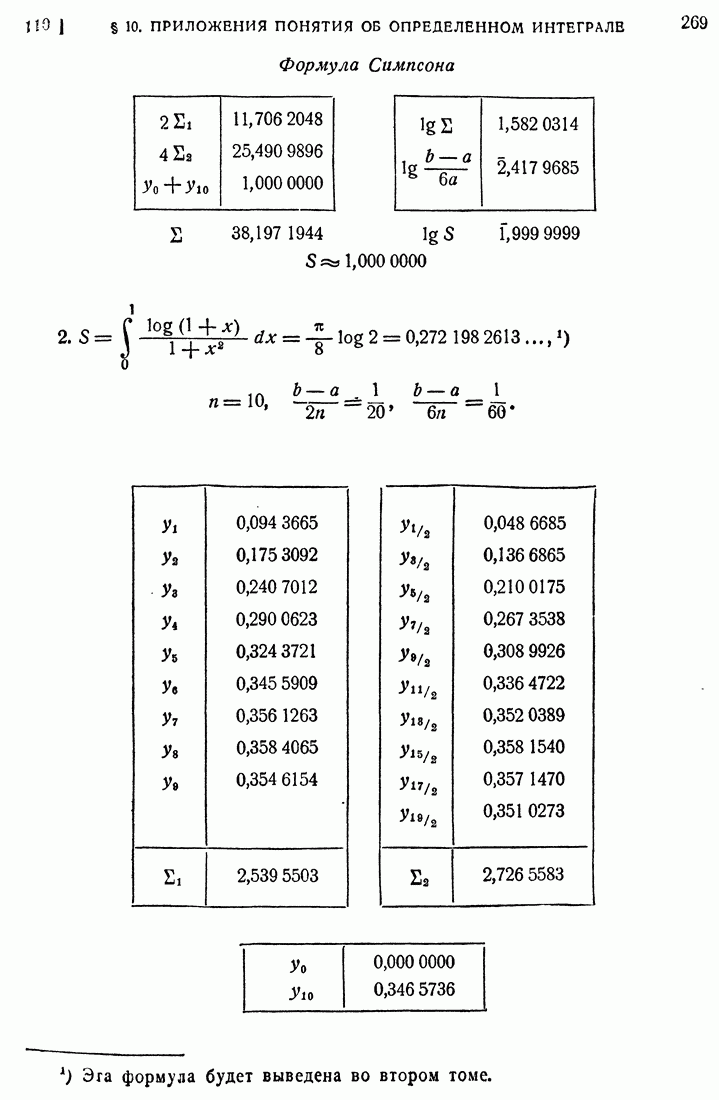
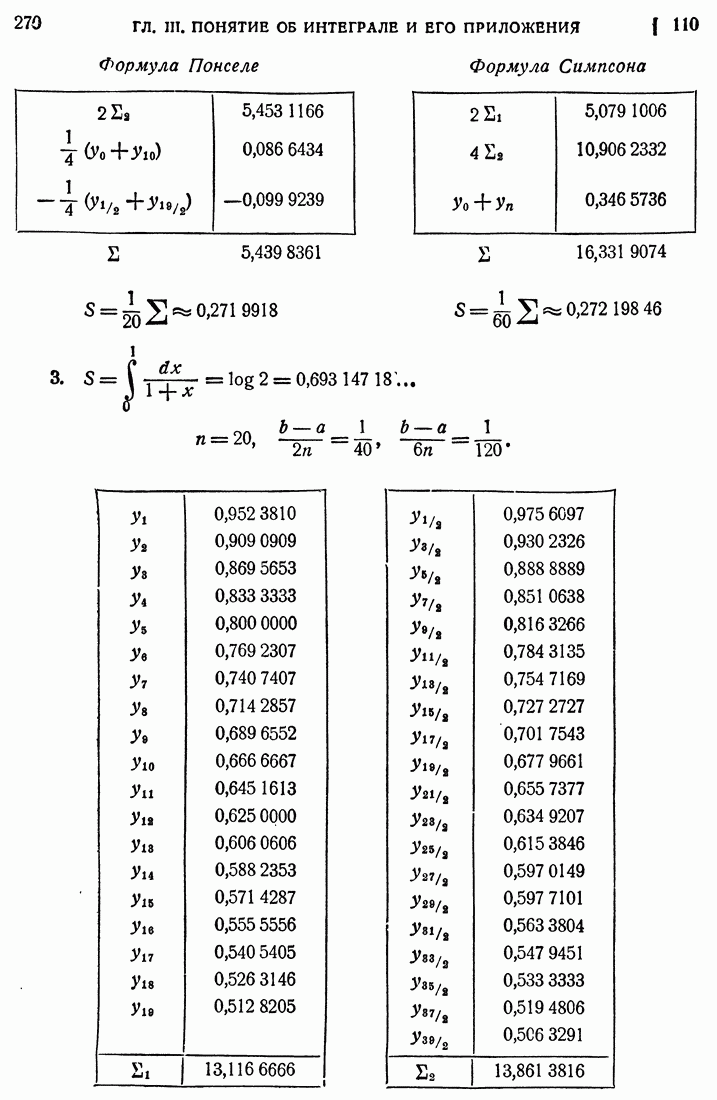
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
50. Понятие о дифференциале.
Пусть  произвольное приращение независимой переменной, которое мы считаем уже не зависящим от
произвольное приращение независимой переменной, которое мы считаем уже не зависящим от  Мы будем называть его дифференциалом независимой переменной и обозначать знаком
Мы будем называть его дифференциалом независимой переменной и обозначать знаком  либо
либо  Знак этот ни в коем случае не является произведением d на
Знак этот ни в коем случае не является произведением d на  а служит лишь символом для обозначения произвольной, не зависящей от
а служит лишь символом для обозначения произвольной, не зависящей от  величины.
величины.
Дифференциалом функции называется произведение ее производной на дифференциал независимой переменной.
Дифференциал функции  обозначают символом
обозначают символом  или
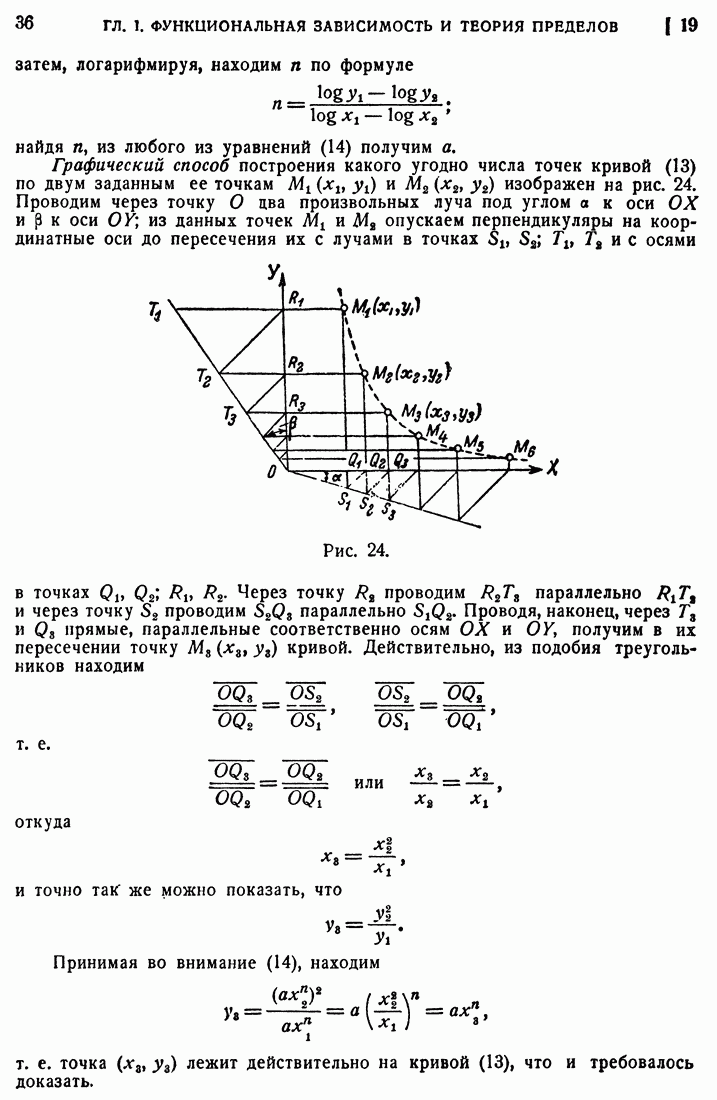
или  :
:

Из этой формулы естественно получается выражение производной в виде частного двух дифференциалов:

Подчеркнем, что дифференциал  независимого переменного, входящий в определение дифференциала функции и в формулу (6), может принимать совершенно произвольные значения. Фиксируя какое-либо значение
независимого переменного, входящий в определение дифференциала функции и в формулу (6), может принимать совершенно произвольные значения. Фиксируя какое-либо значение  мы по формуле (6) получаем соответствующее значение
мы по формуле (6) получаем соответствующее значение  при заданном
при заданном  Если мы считаем
Если мы считаем  приращением независимого переменного
приращением независимого переменного  то надо, чтобы не только
то надо, чтобы не только  но и
но и  принадлежали промежутку, на котором определена функция. Но и при этом дифференциал функции
принадлежали промежутку, на котором определена функция. Но и при этом дифференциал функции  не совпадает, кроме исключительных случаев, с приращением функции, соответствующим приращению
не совпадает, кроме исключительных случаев, с приращением функции, соответствующим приращению  независимого переменного.
независимого переменного.

Рис. 54.
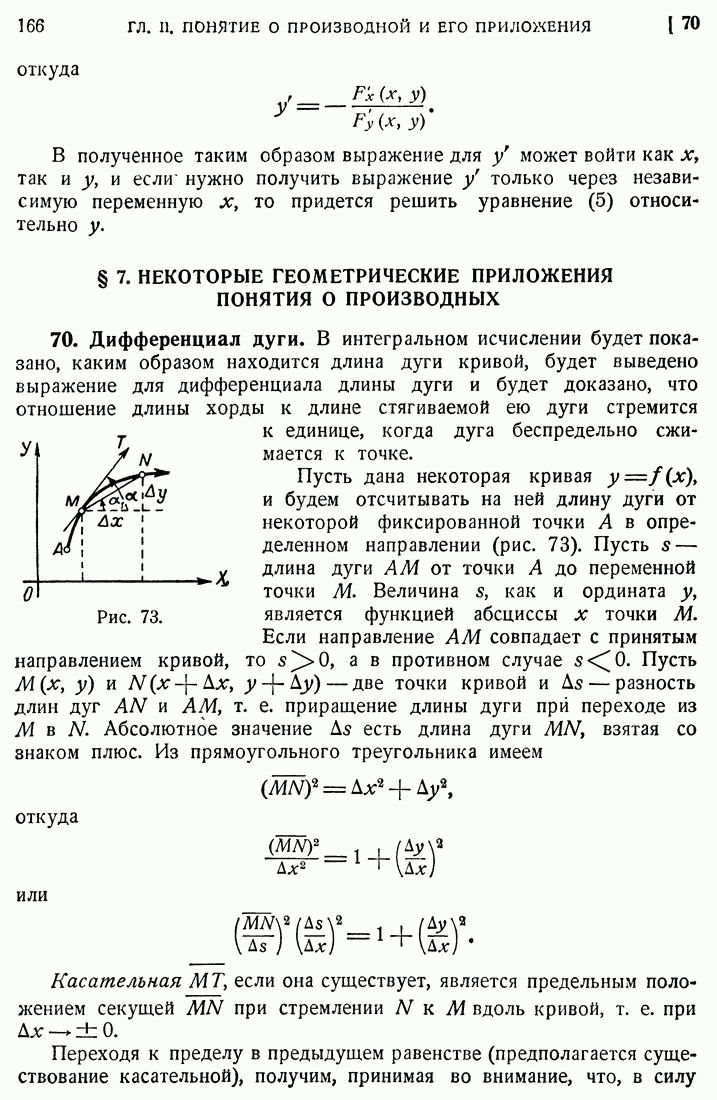
Чтобы выяснить разницу между этими понятиями, обратимся к графику функции. Возьмем на нем некоторую точку  и другую точку N. Проведем касательную МТ, ординаты, соответствующие точкам М и N, и прямую МР параллельно ОХ (рис. 54). Мы будем иметь
и другую точку N. Проведем касательную МТ, ординаты, соответствующие точкам М и N, и прямую МР параллельно ОХ (рис. 54). Мы будем иметь

отсюда

Дифференциал функции изображается отрезком PQ, не совпадающим с отрезком PN, который изображает приращение функции. Отрезок PQ изображает то приращение, которое получилось бы, если бы в промежутке  мы заменили отрезок MN кривой отрезком MQ касательной, т. е. если бы мы считали, что в этом промежутке приращение функции пропорционально приращению независимой переменной, и коэффициент пропорциональности взяли бы равным угловому коэффициенту касательной МТ, или, что то же, равным производной
мы заменили отрезок MN кривой отрезком MQ касательной, т. е. если бы мы считали, что в этом промежутке приращение функции пропорционально приращению независимой переменной, и коэффициент пропорциональности взяли бы равным угловому коэффициенту касательной МТ, или, что то же, равным производной  .
.
Разность между дифференциалом и приращением изображается отрезком NQ. Покажем, что если  стремится к нулю, то разность эта есть величина бесконечно малая высшего порядка по сравнению с
стремится к нулю, то разность эта есть величина бесконечно малая высшего порядка по сравнению с  [36].
[36].
Отношение в пределе дает производную, а потому [27]

где  есть величина бесконечно малая одновременно с
есть величина бесконечно малая одновременно с 
Из этого равенства получим

или

откуда видно, что разность между  равна
равна  . Но отношение
. Но отношение  равное
равное  стремится к нулю вместе с
стремится к нулю вместе с  , т. е. разность между
, т. е. разность между  есть величина бесконечно малая высшего порядка по сравнению с
есть величина бесконечно малая высшего порядка по сравнению с  Заметим, что знак этой разности может быть любым. На нашем чертеже и
Заметим, что знак этой разности может быть любым. На нашем чертеже и  и эта разность имеют знак
и эта разность имеют знак 
Формула (6) дает правило нахождения дифференциала функции. Применим его к некоторым частным случаям.
I. Если с есть постоянная, то

т. е. дифференциал постоянной равен нулю.

т. е. постоянный множитель можно выносить за знак дифференциала.

т. е. дифференциал суммы равен сумме дифференциалов слагаемых.

т. е. дифференциал произведения равен сумме произведений дифференциалов каждого из сомножителей на все остальные сомножители.
Мы ограничились случаем трех сомножителей. Тот же вывод годится и для любого конечного числа сомножителей.

т. e. дифференциал частного (дроби) равен произведению дифференциала числителя на знаменатель минус произведение дифференциала знаменателя на числитель, все деленное на квадрат знаменателя,
VI. Рассмотрим сложную функцию у  где и есть функция от
где и есть функция от  Определим
Определим  предполагая у зависящим от
предполагая у зависящим от 

т. e. дифференциал сложной функции имеет тот же вид, какой он имел бы в том случае, если бы вспомогательная функция и была независимой переменной.
Рассмотрим численный пример для сравнения величины приращения функции с  дифференциалом. Возьмем функцию
дифференциалом. Возьмем функцию

и рассмотрим ее приращение

Производя все действия, получим для приращения величину

Несравненно проще вычислить дифференциал функции. В данном случае  и дифференциалом функции будет
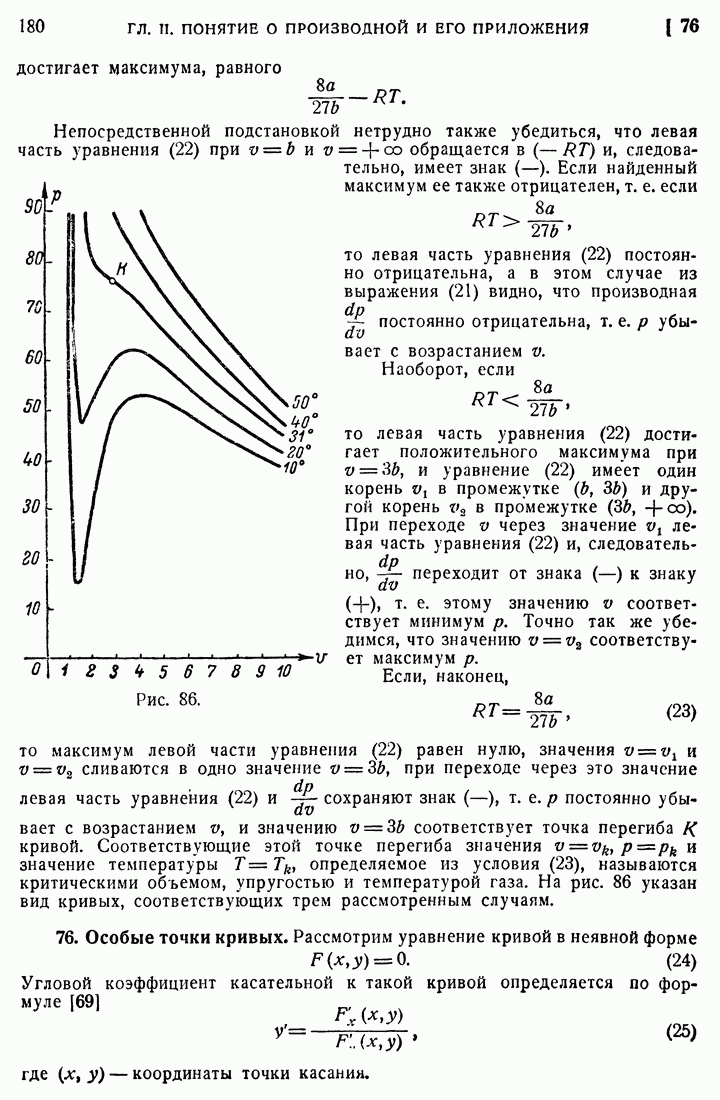
и дифференциалом функции будет

Сравнивая  видим, что они совпадают до третьего десятичного знака.
видим, что они совпадают до третьего десятичного знака.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
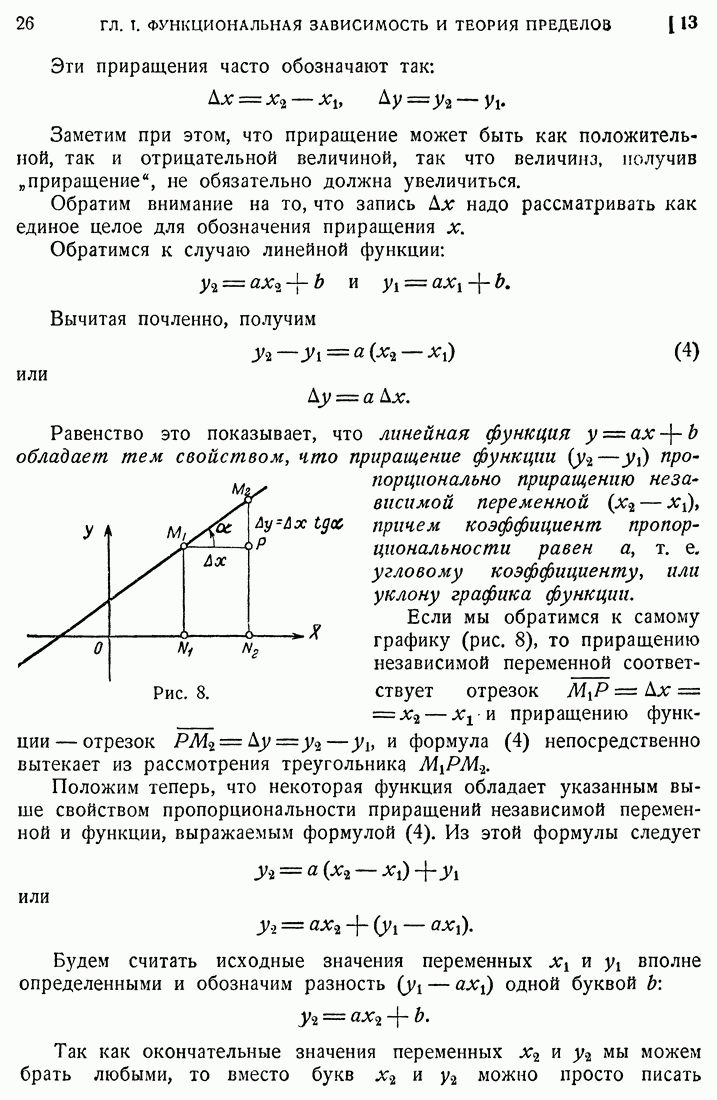
- 12. Линейная функция.
- 13. Приращение. Основное свойство линейной функции.
- 14. График равномерного движения.
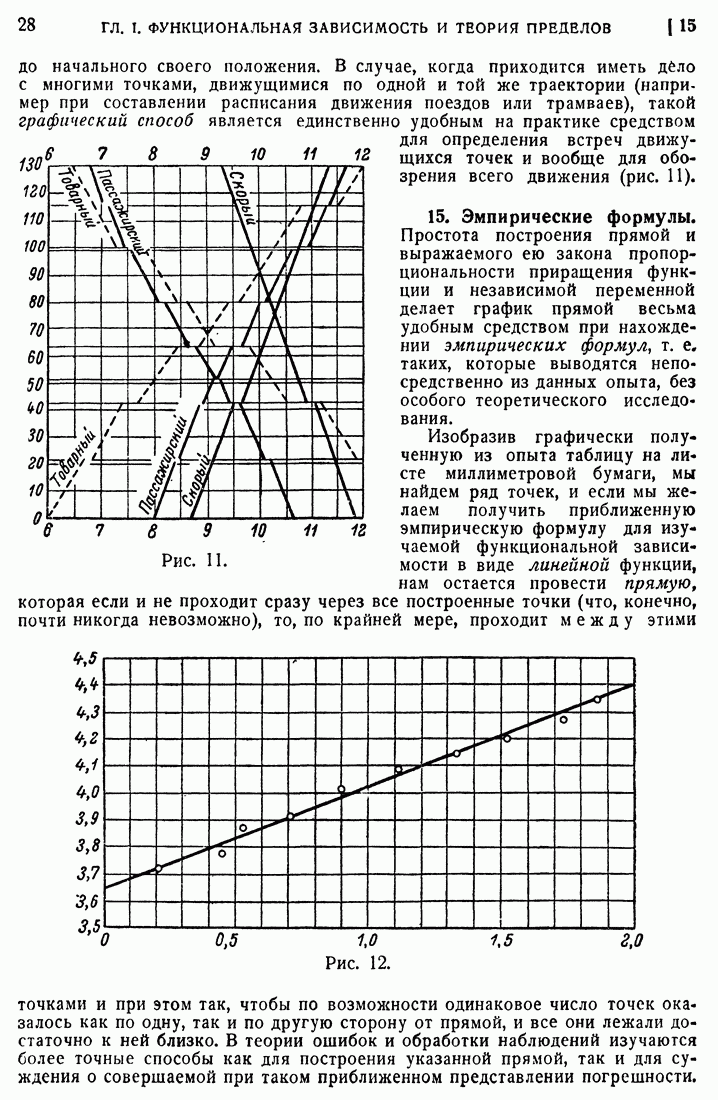
- 15. Эмпирические формулы.
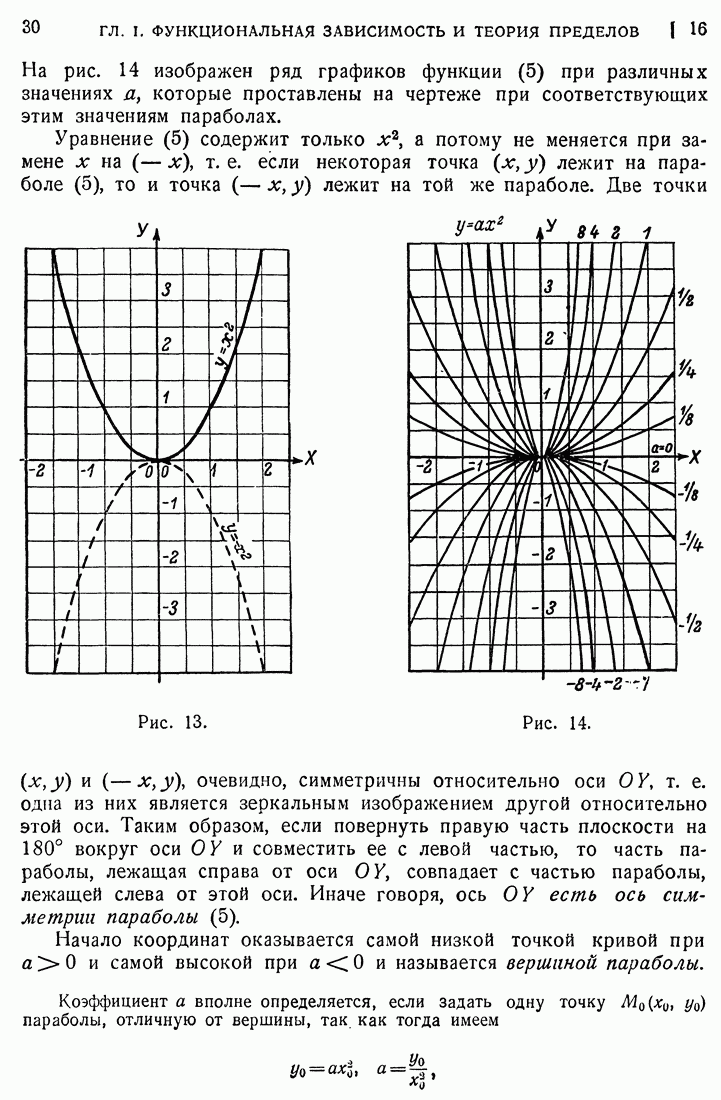
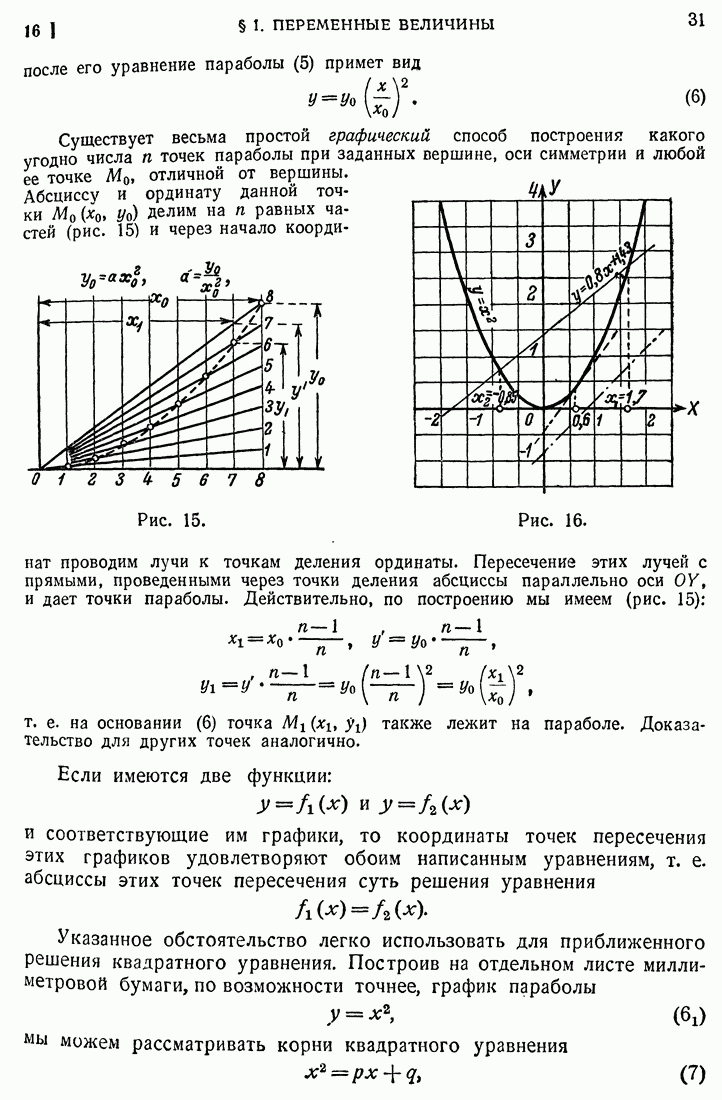
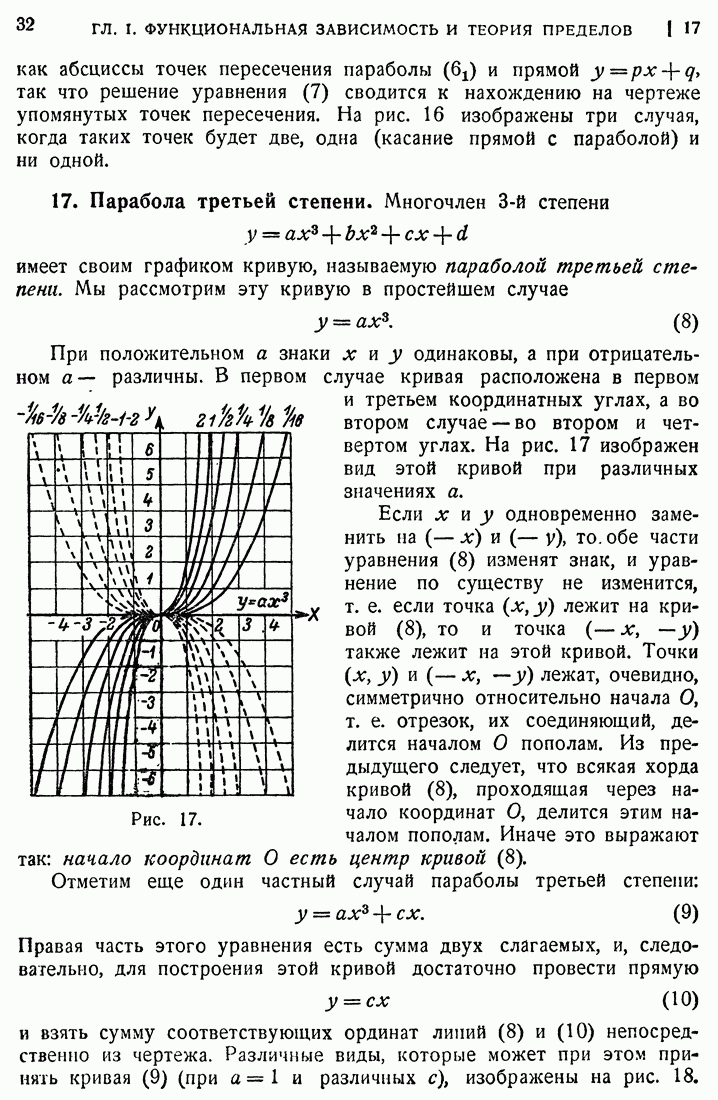
- 16. Парабола второй степени.
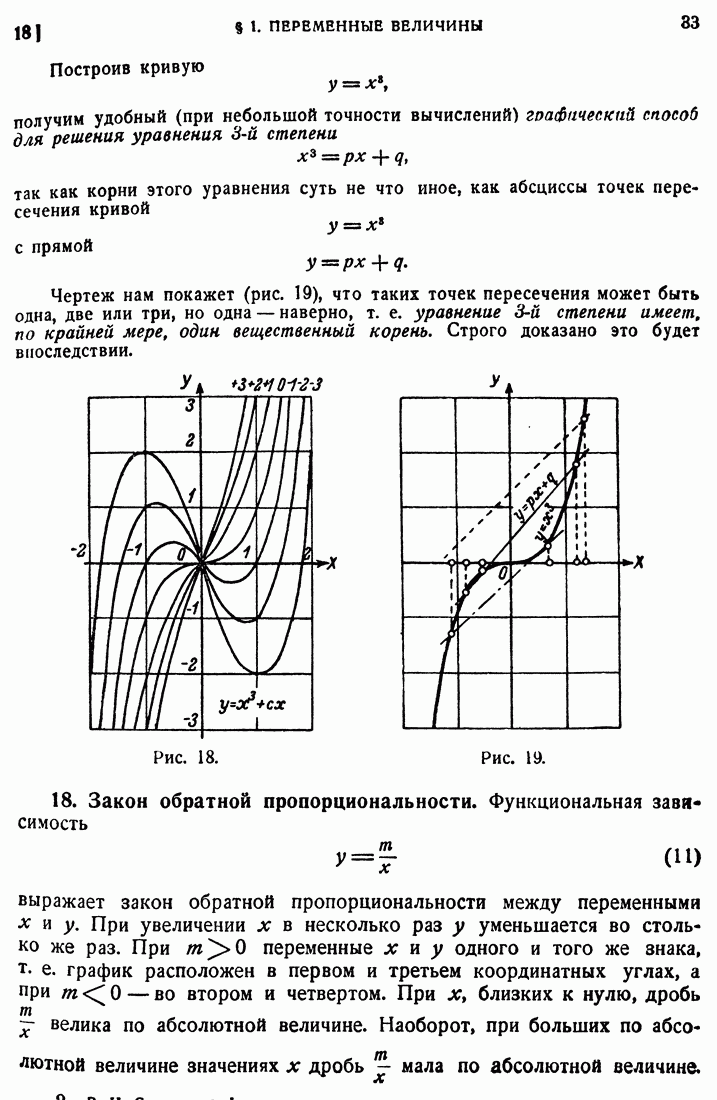
- 17. Парабола третьей степени.
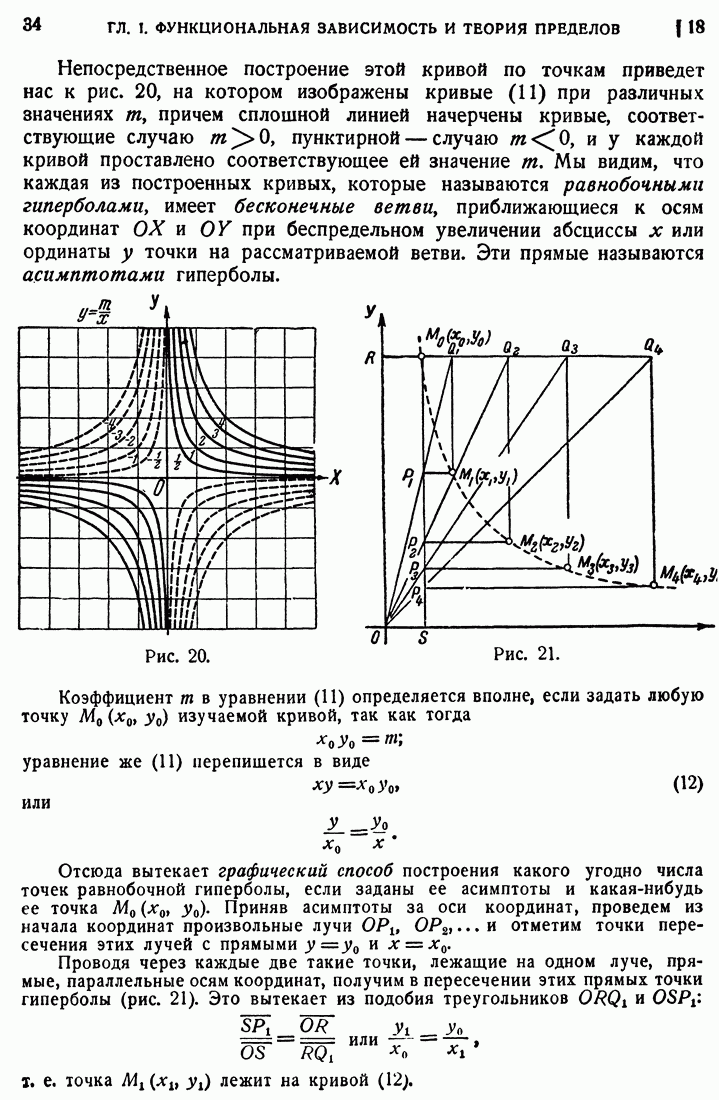
- 18. Закон обратной пропорциональности.
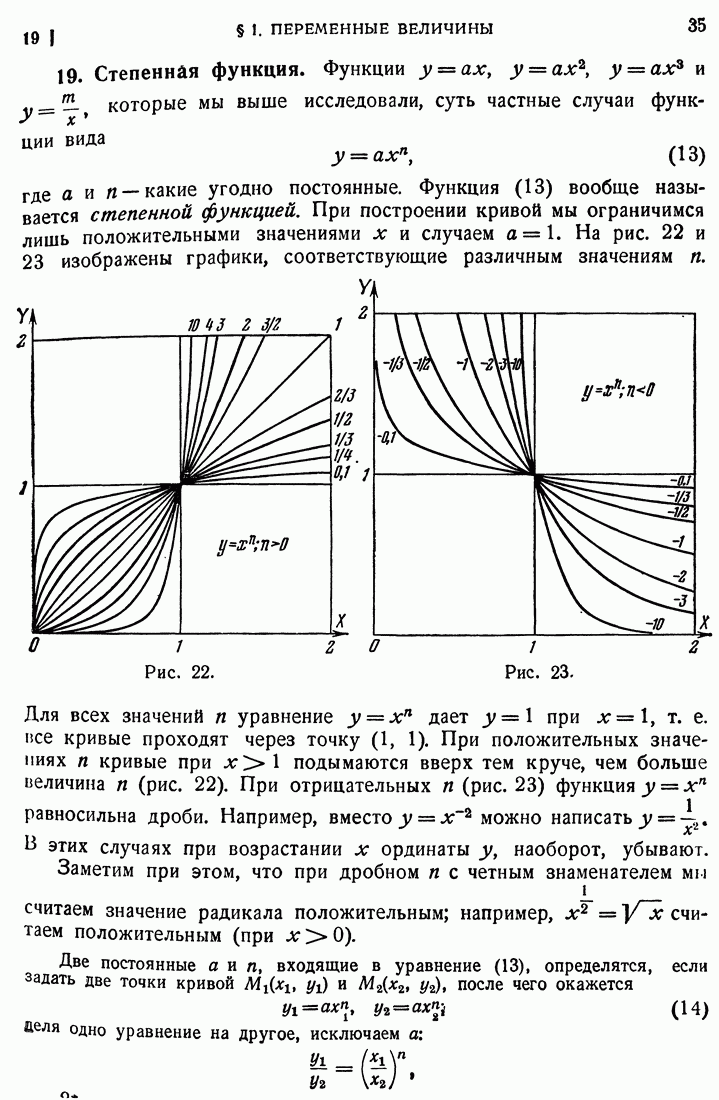
- 19. Степенная функция.
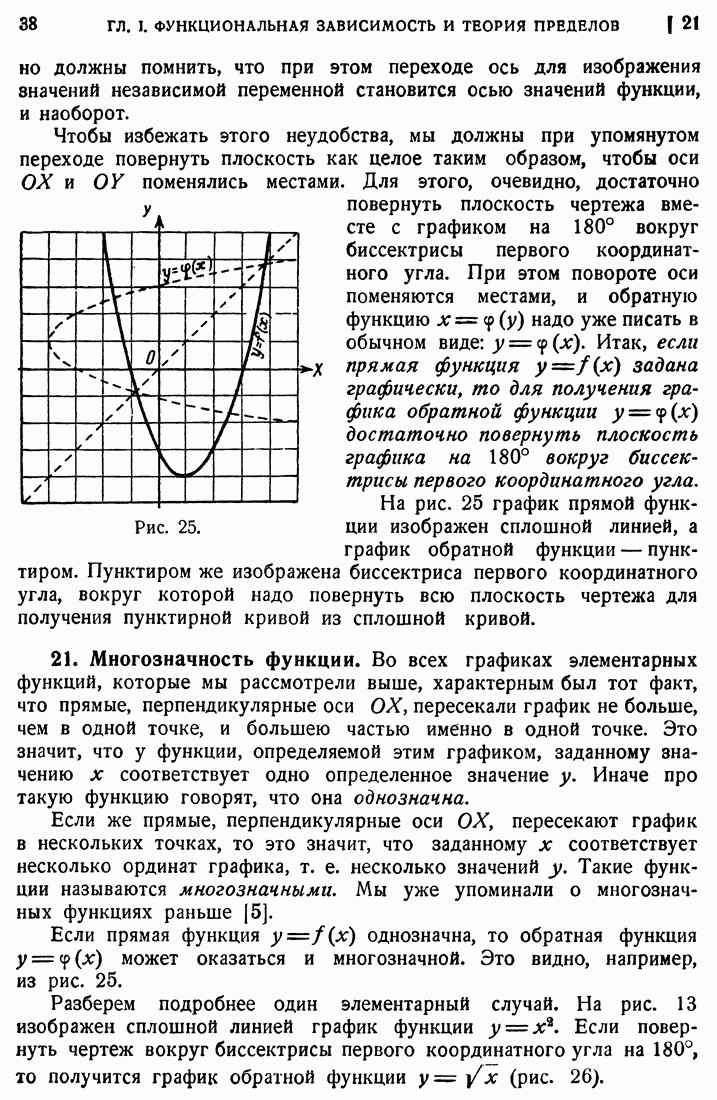
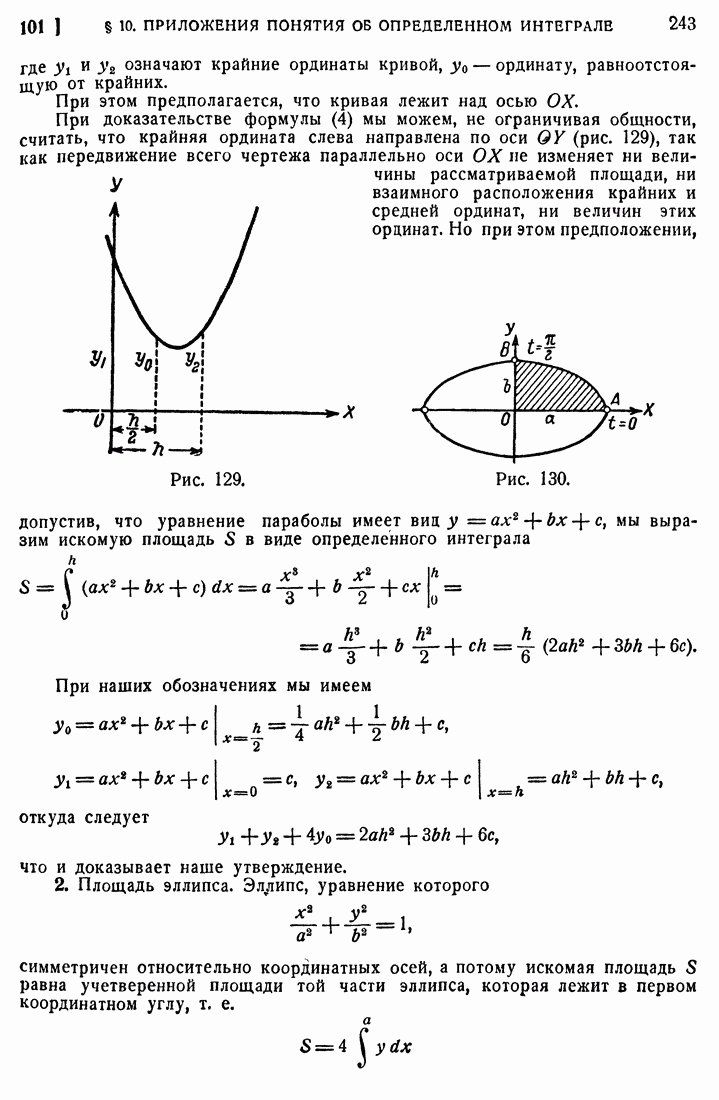
- 20. Обратные функции.
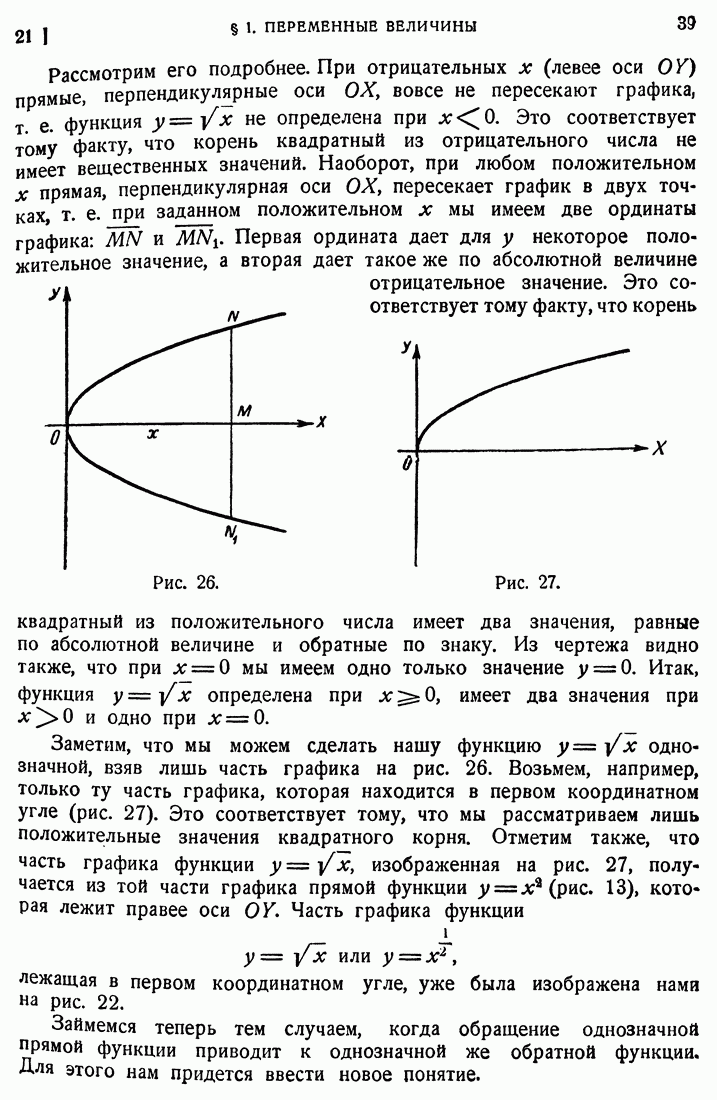
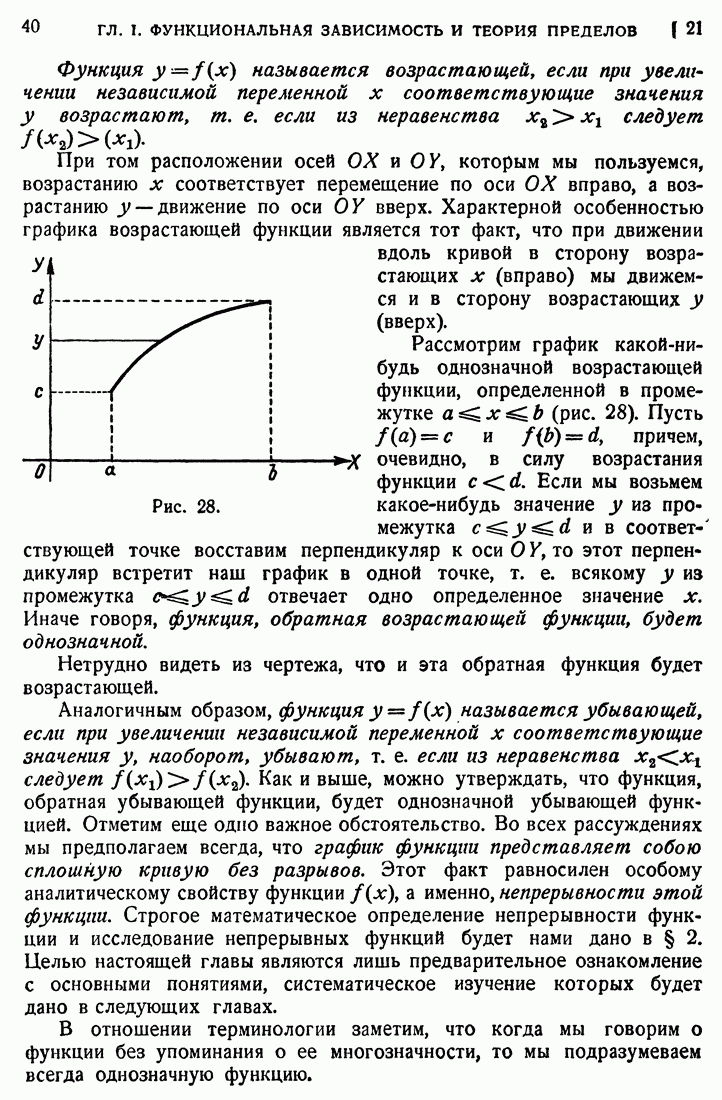
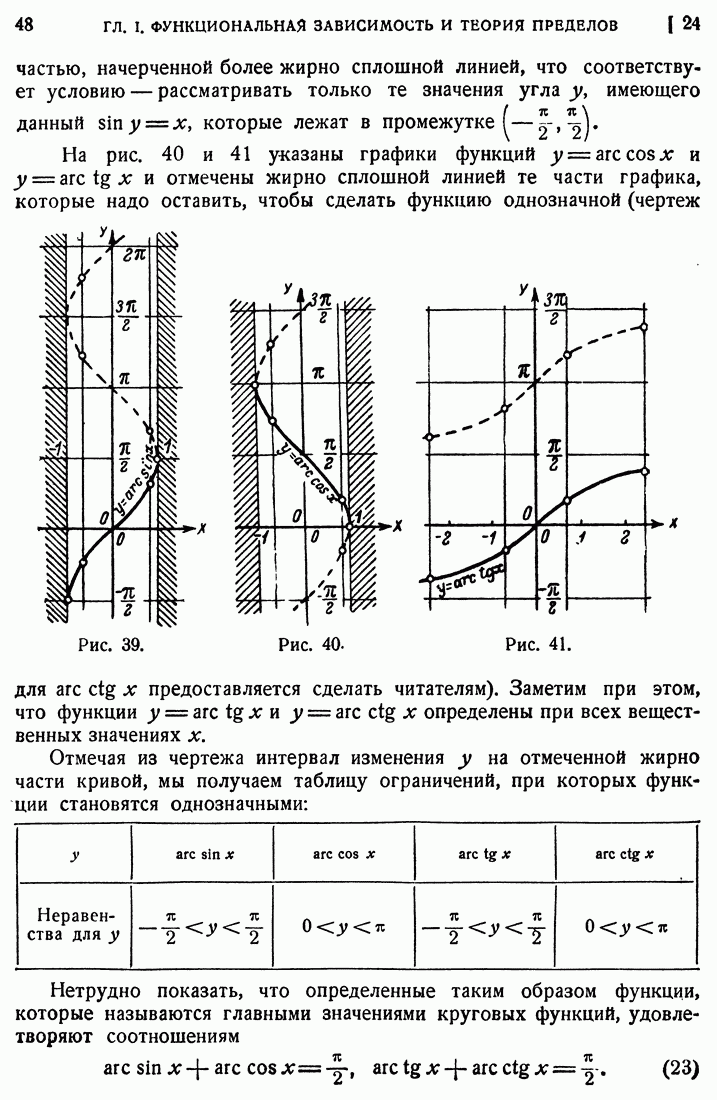
- 21. Многозначность функции.
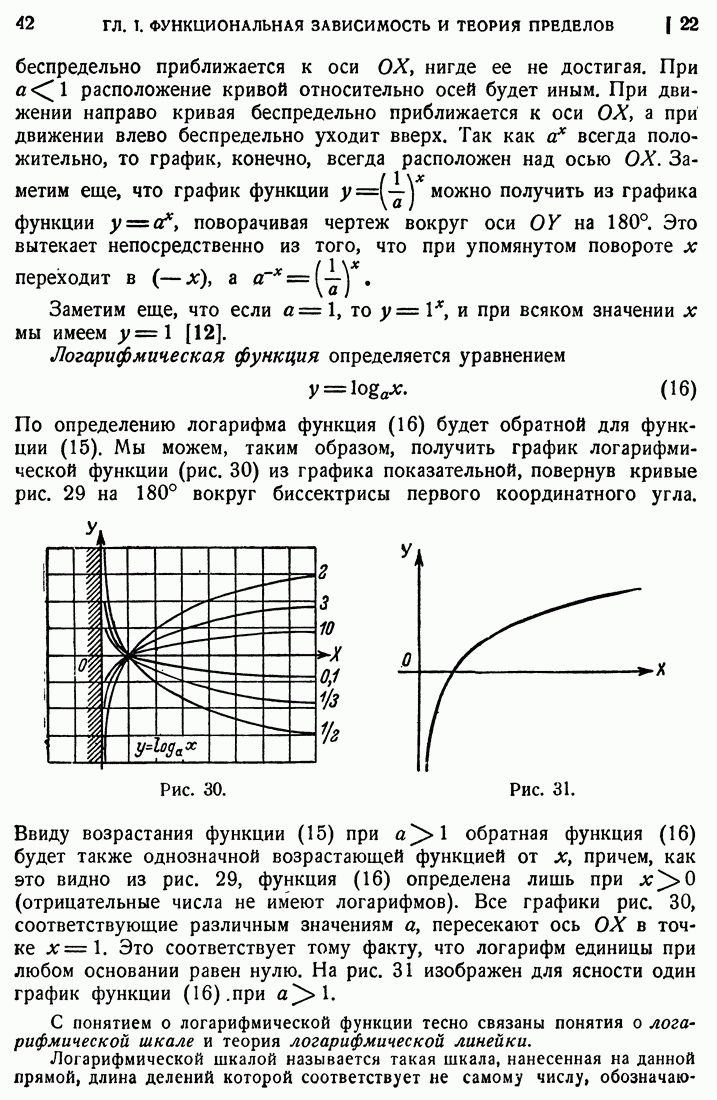
- 22. Показательная и логарифмическая функции.
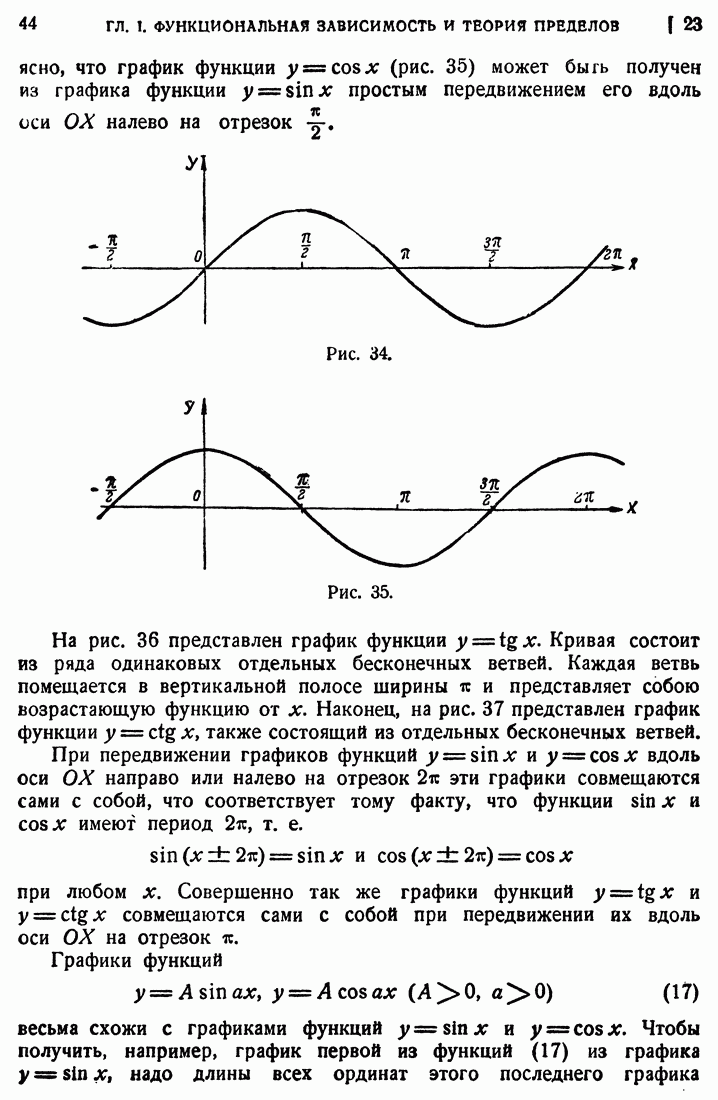
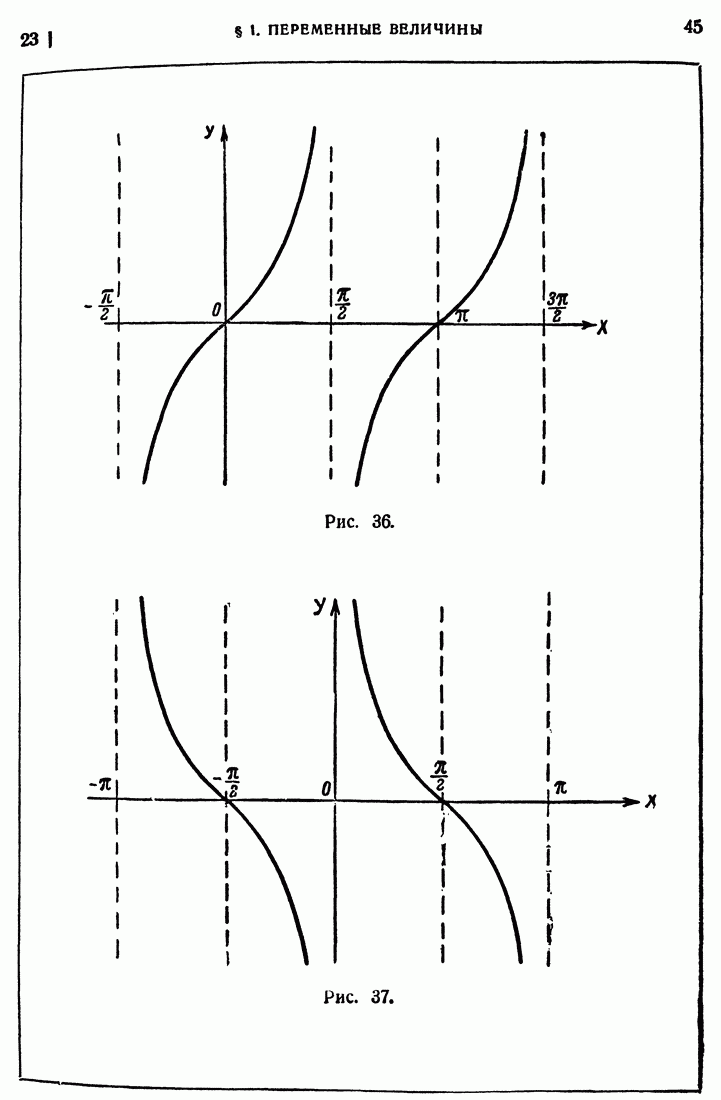
- 23. Тригонометрические функции.
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
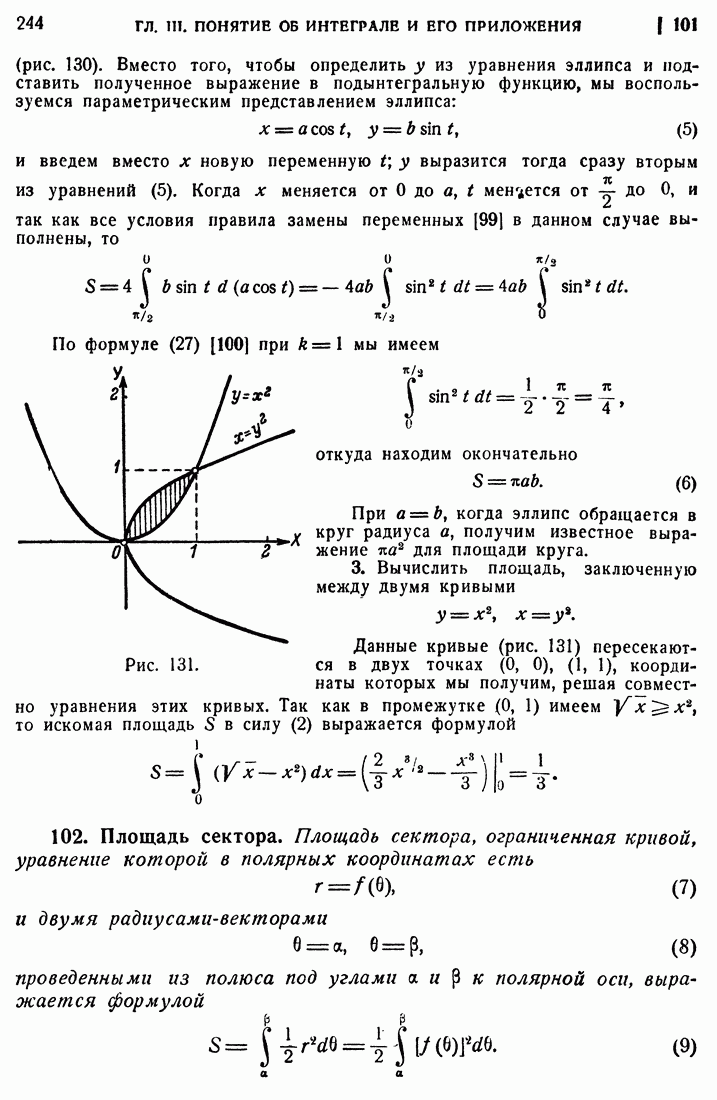
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
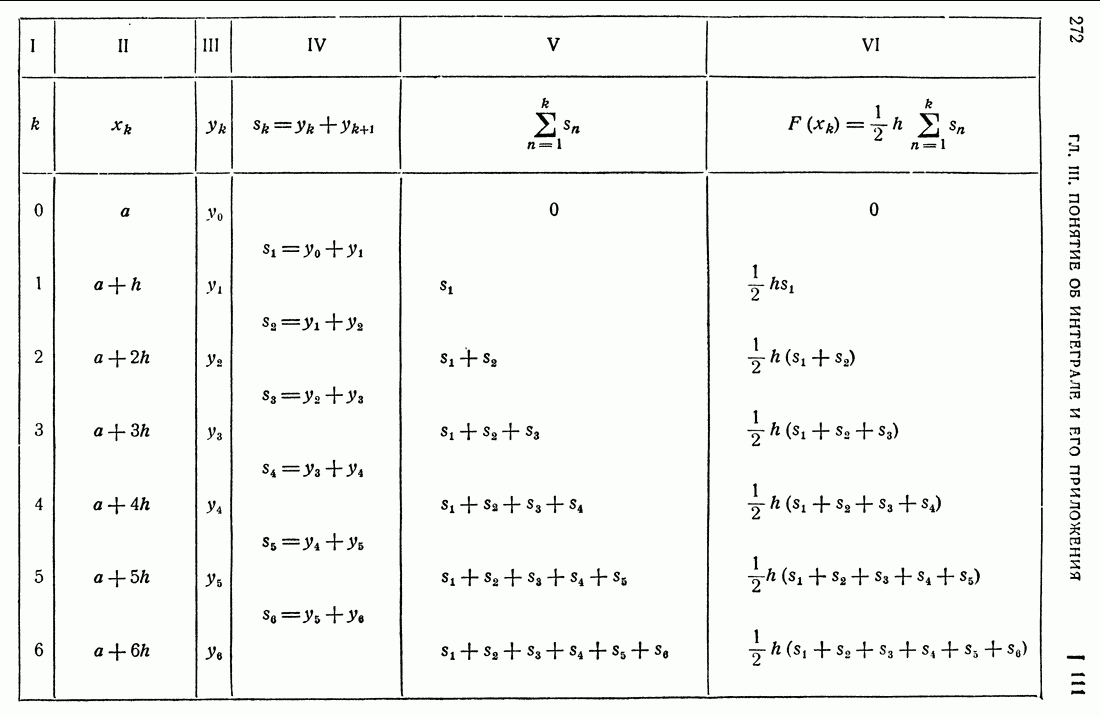
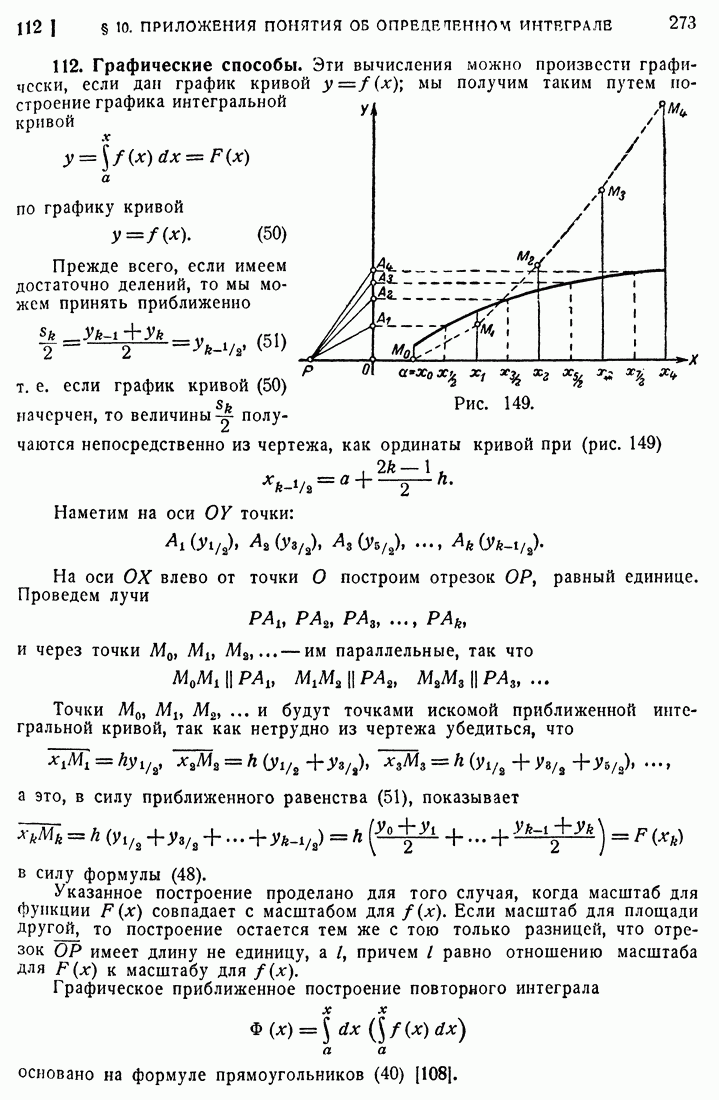
- 30. Монотонные переменные.
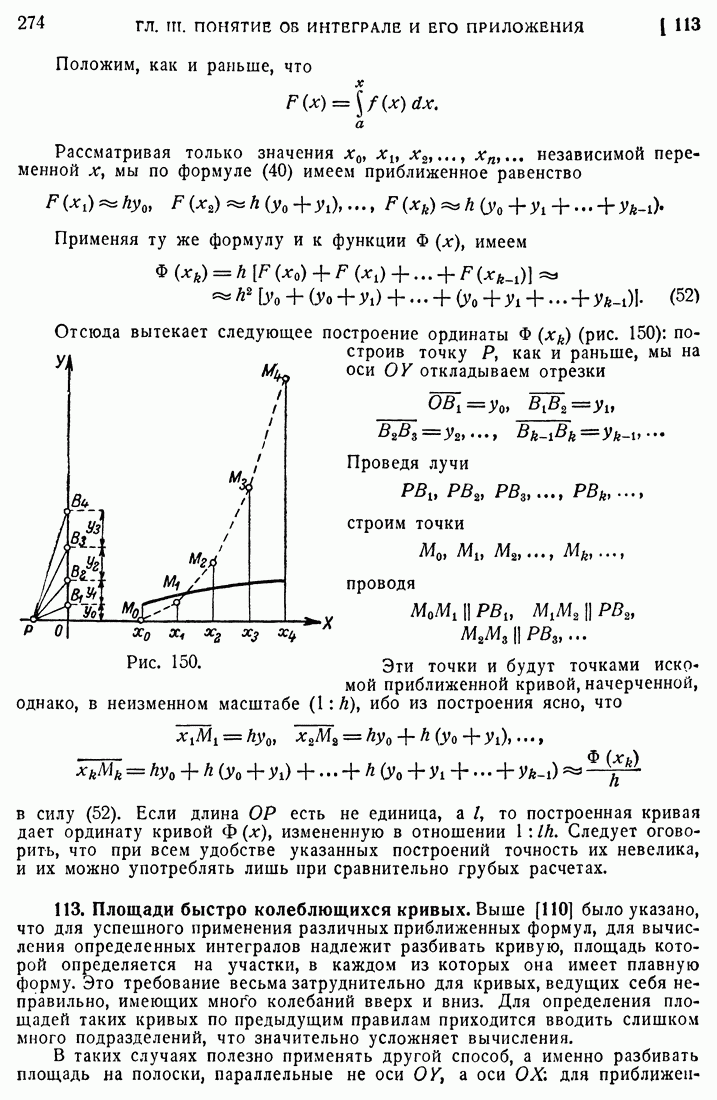
- 31. Признак Коши существования предела.
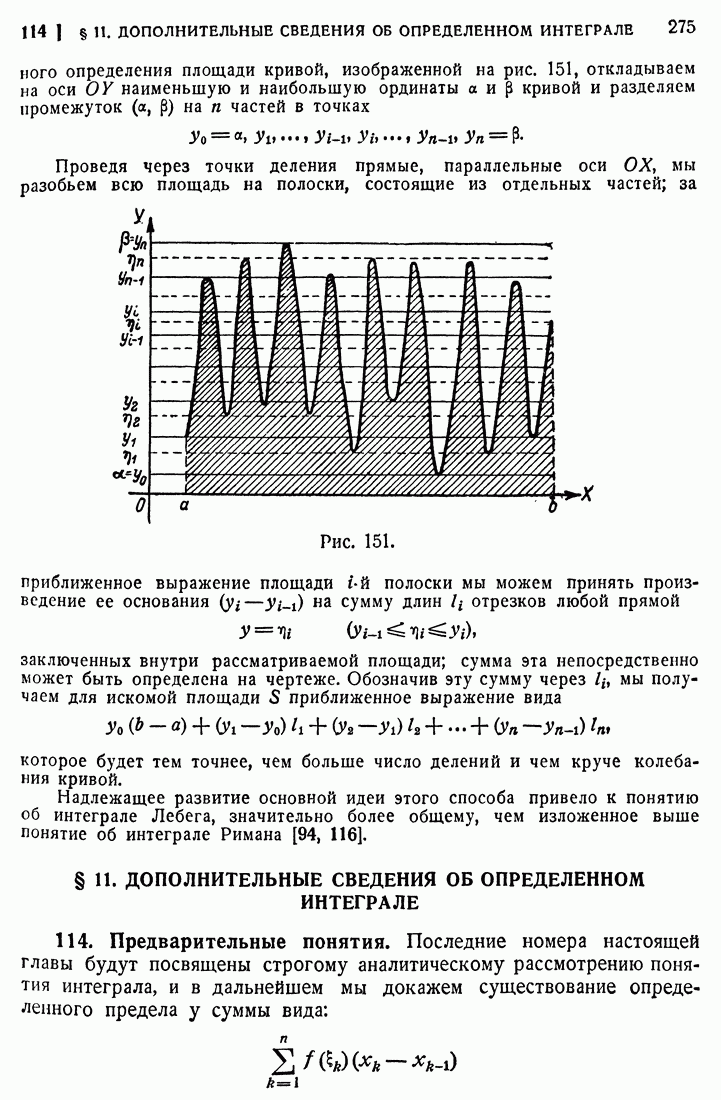
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
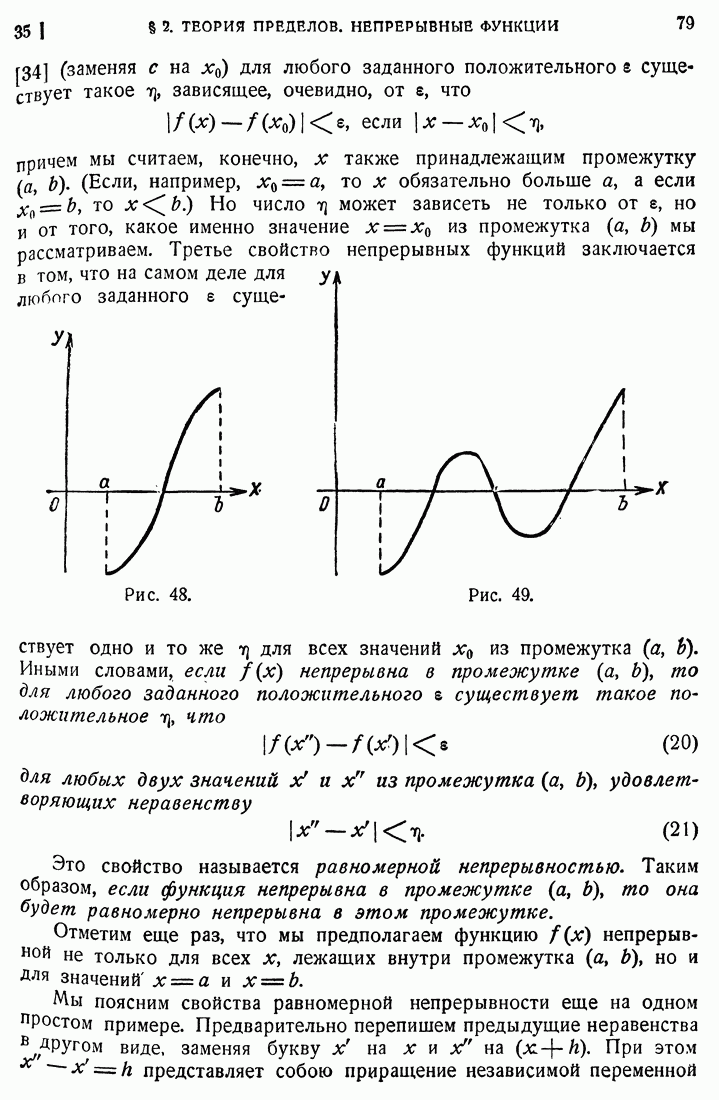
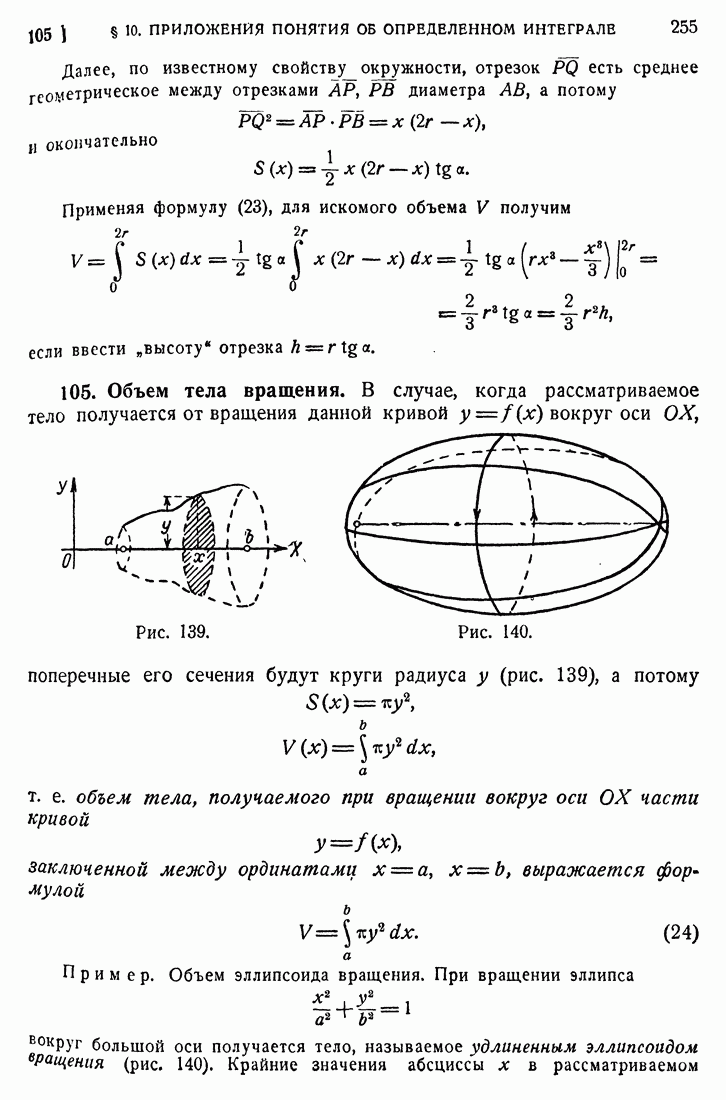
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
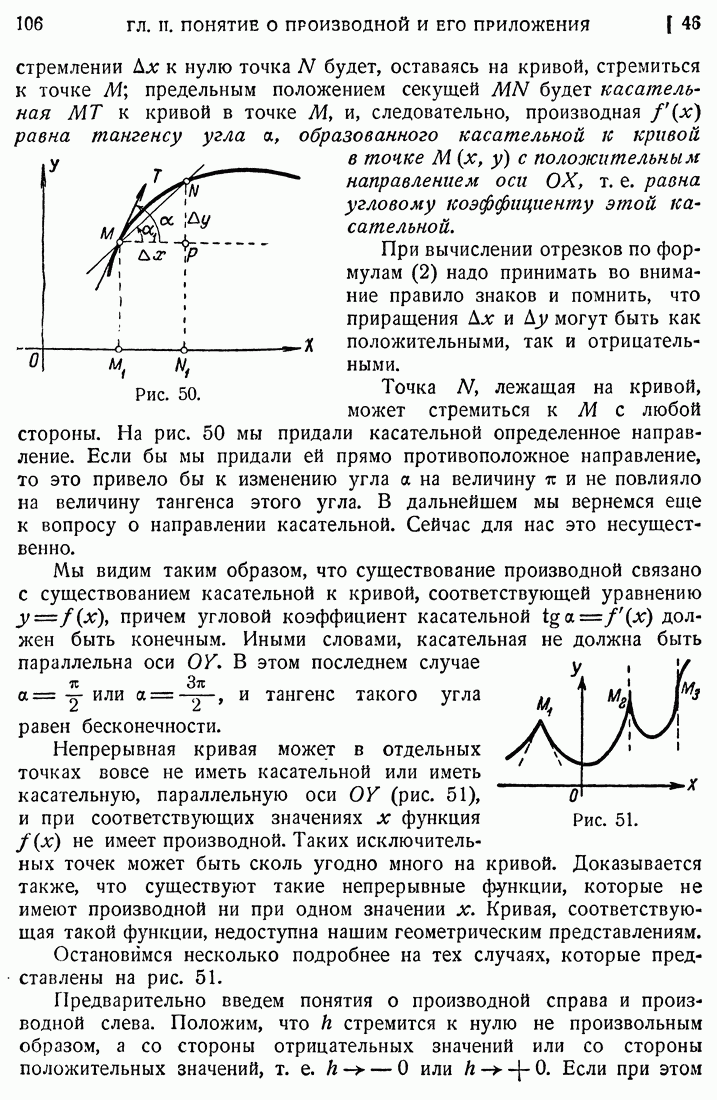
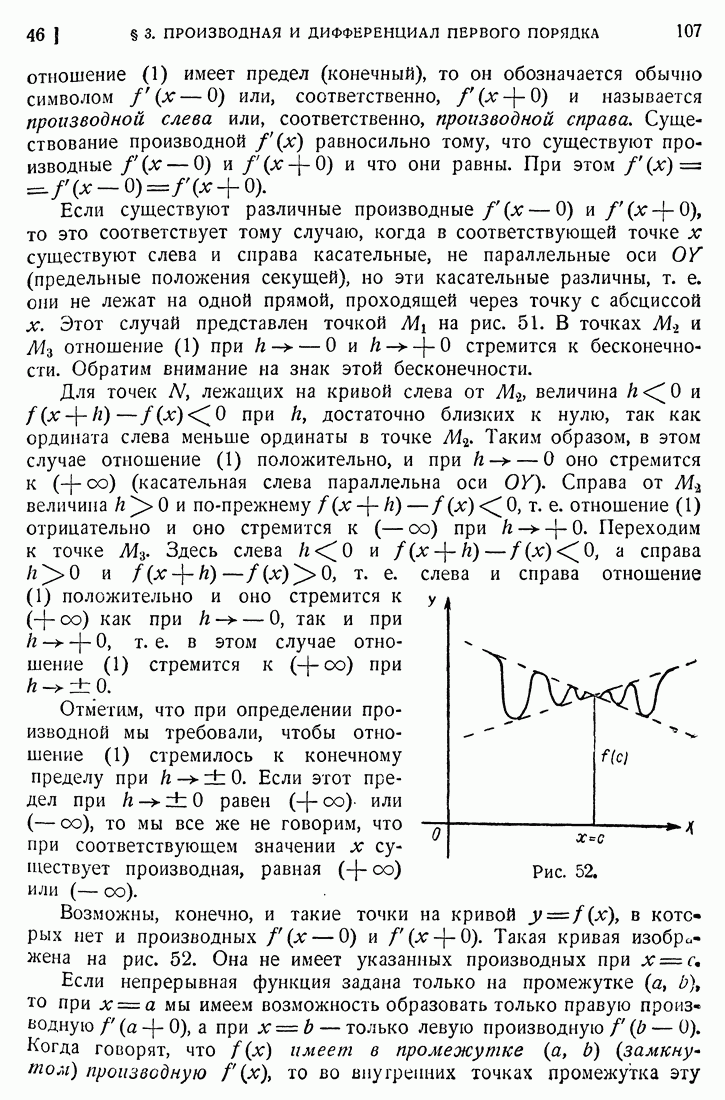
- 45. Понятие о производной.
- 46. Геометрическое значение производной.
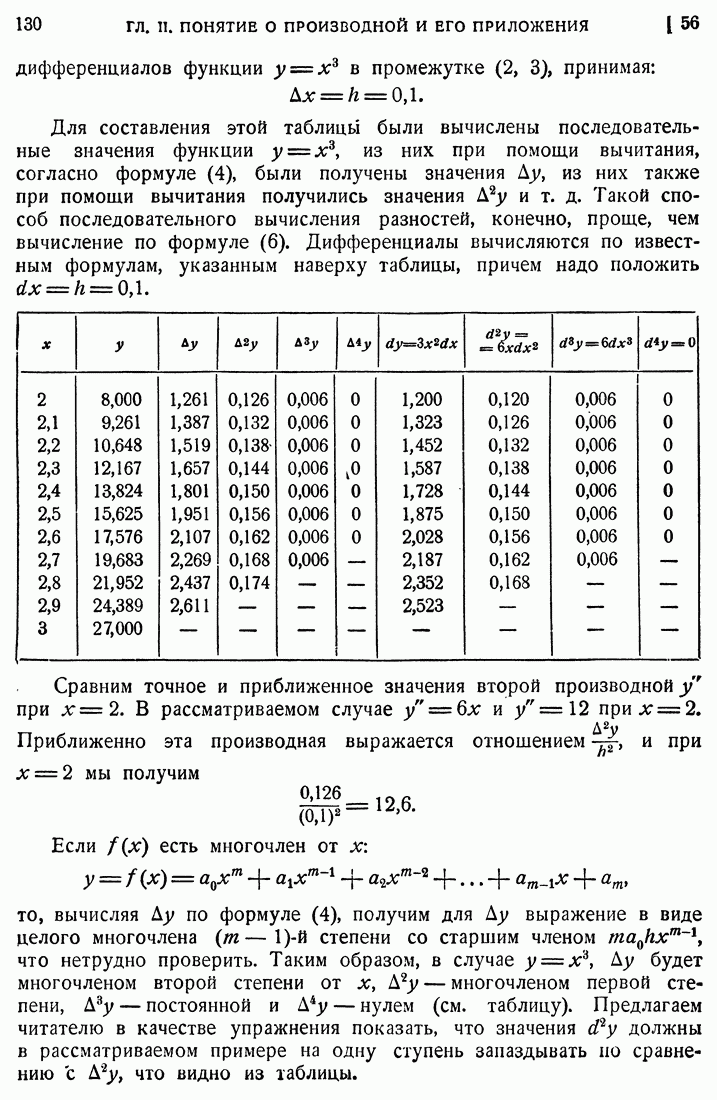
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
- 70. Дифференциал дуги.
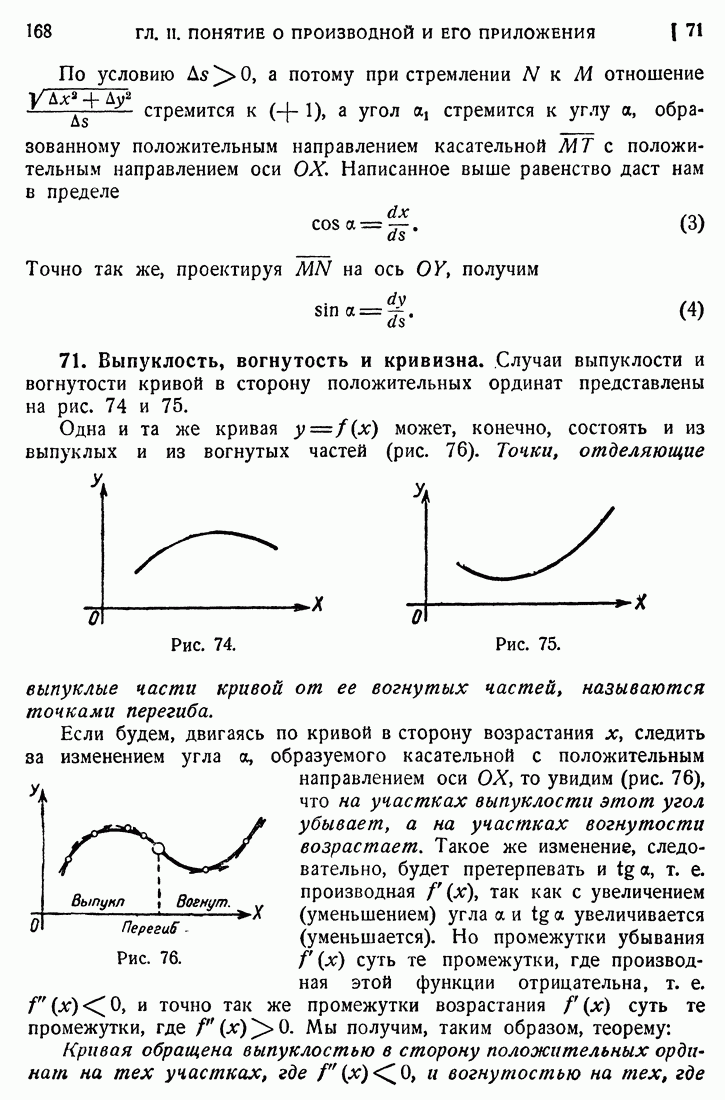
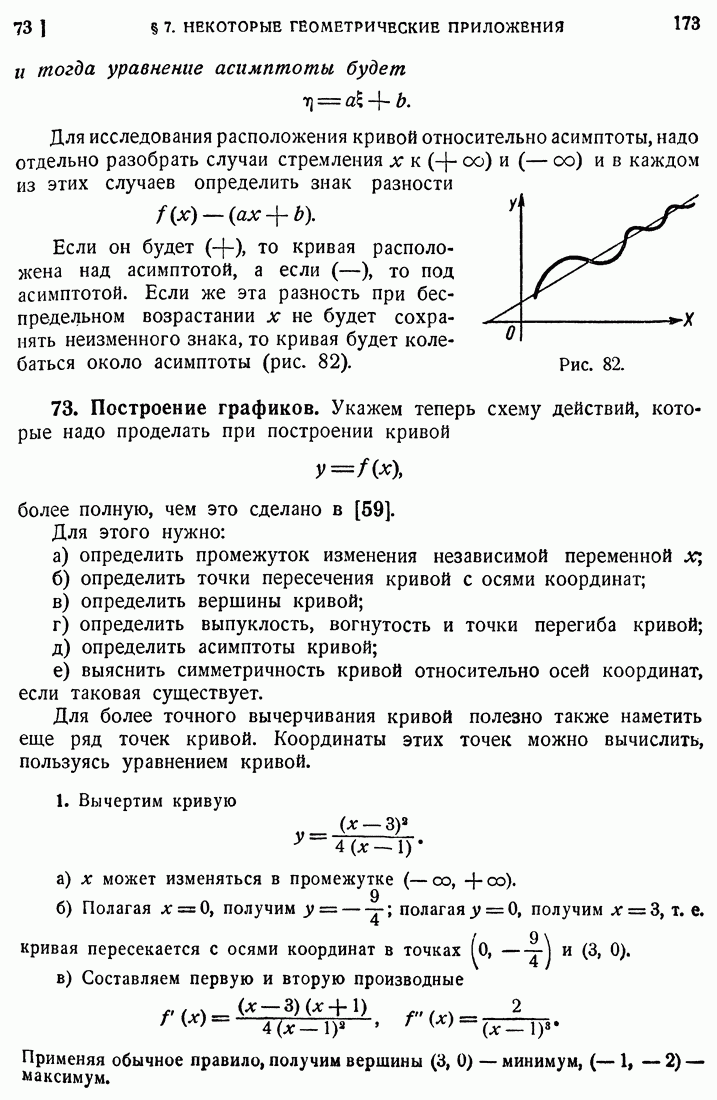
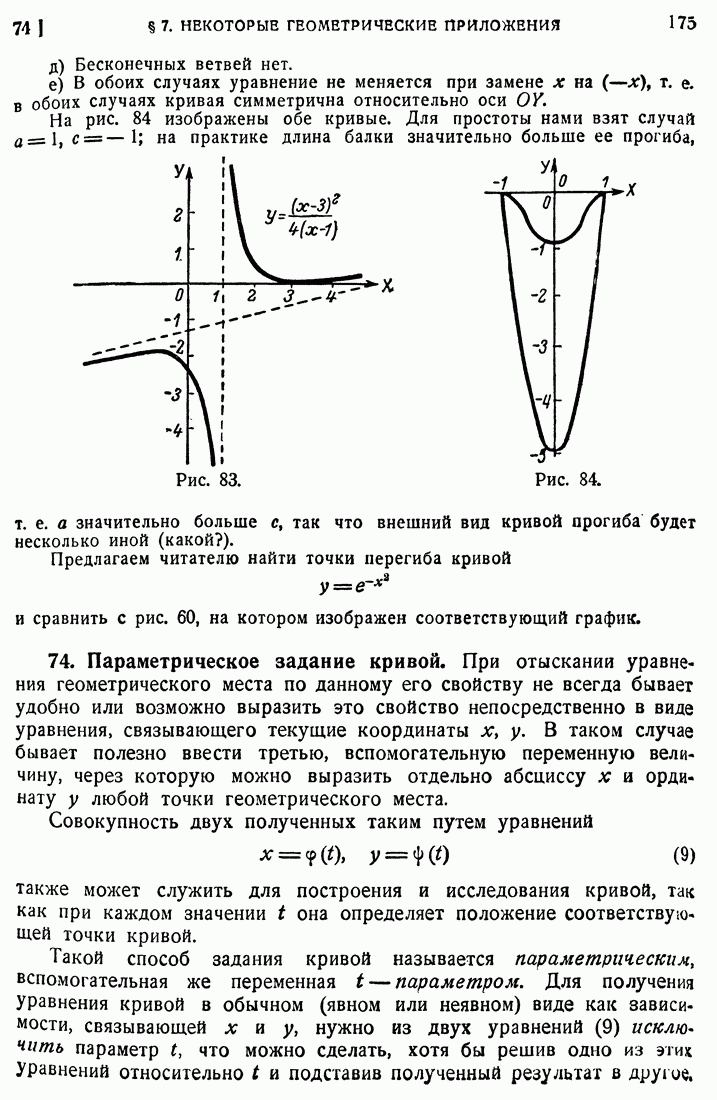
- 71. Выпуклость, вогнутость и кривизна.
- 72. Асимптоты.
- 73. Построение графиков.
- 74. Параметрическое задание кривой.
- 75. Уравнение Ван-дер-Ваальса.
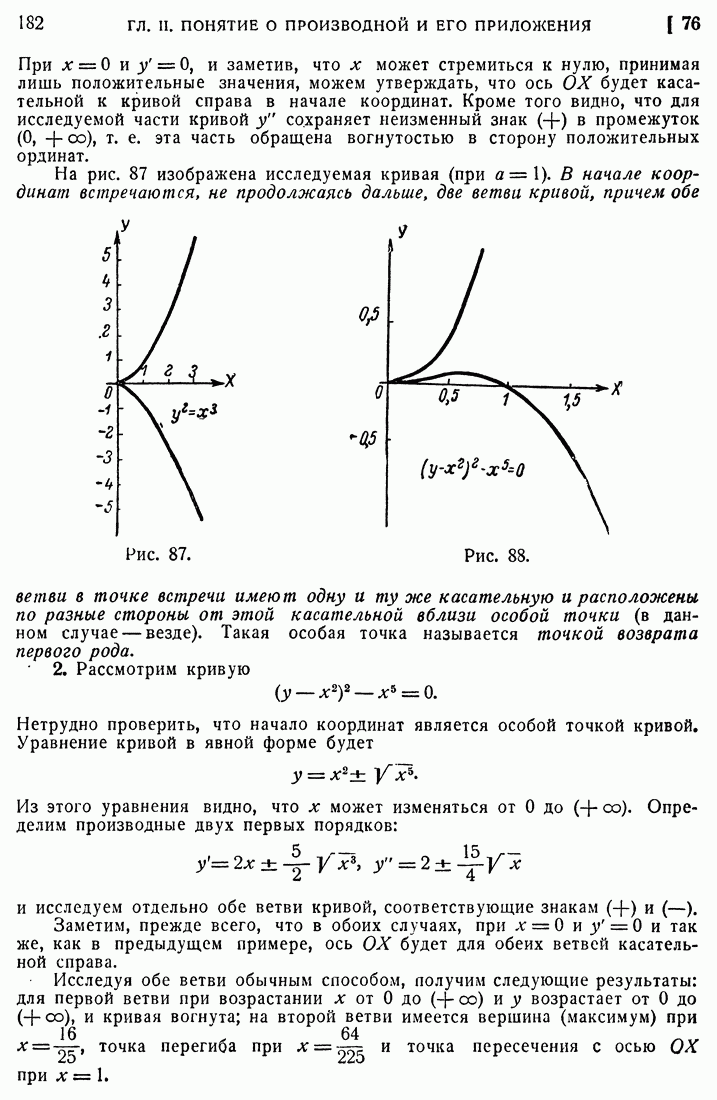
- 76. Особые точки кривых.
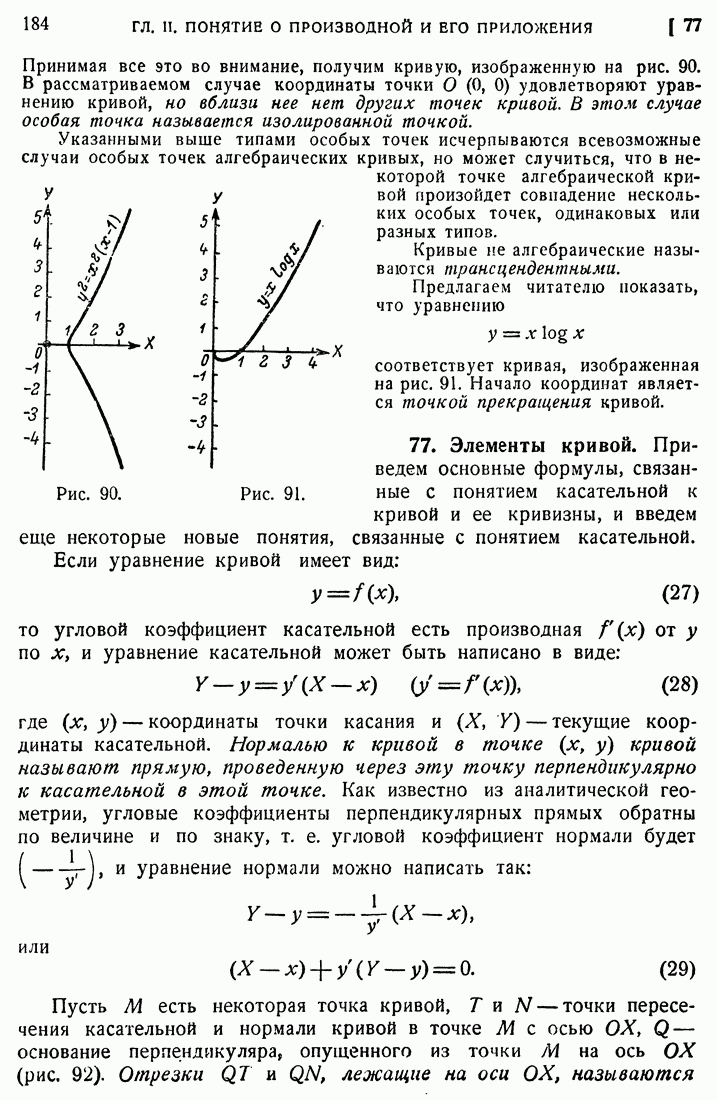
- 77. Элементы кривой.
- 78. Цепная линия.
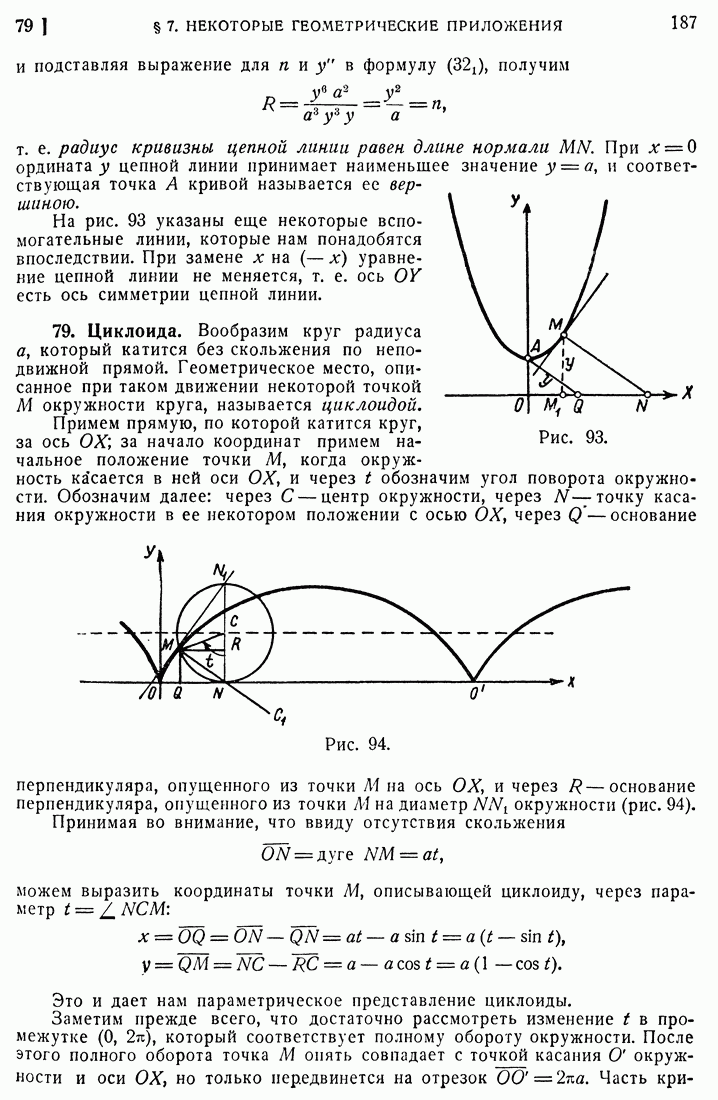
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
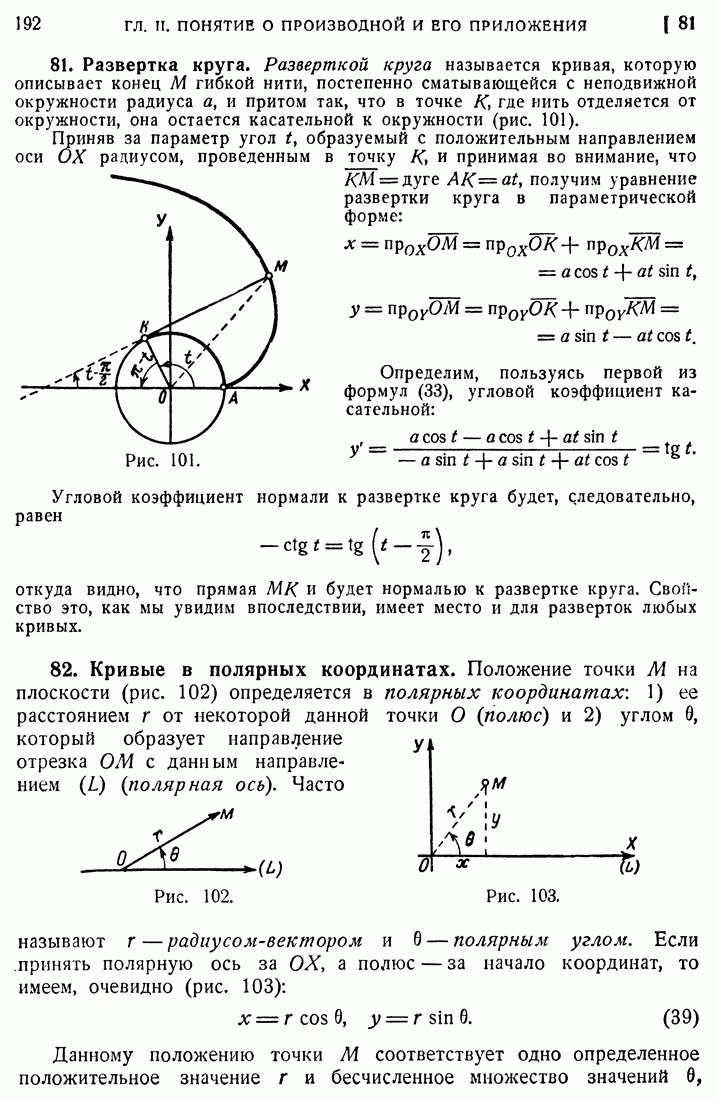
- 81. Развертка круга.
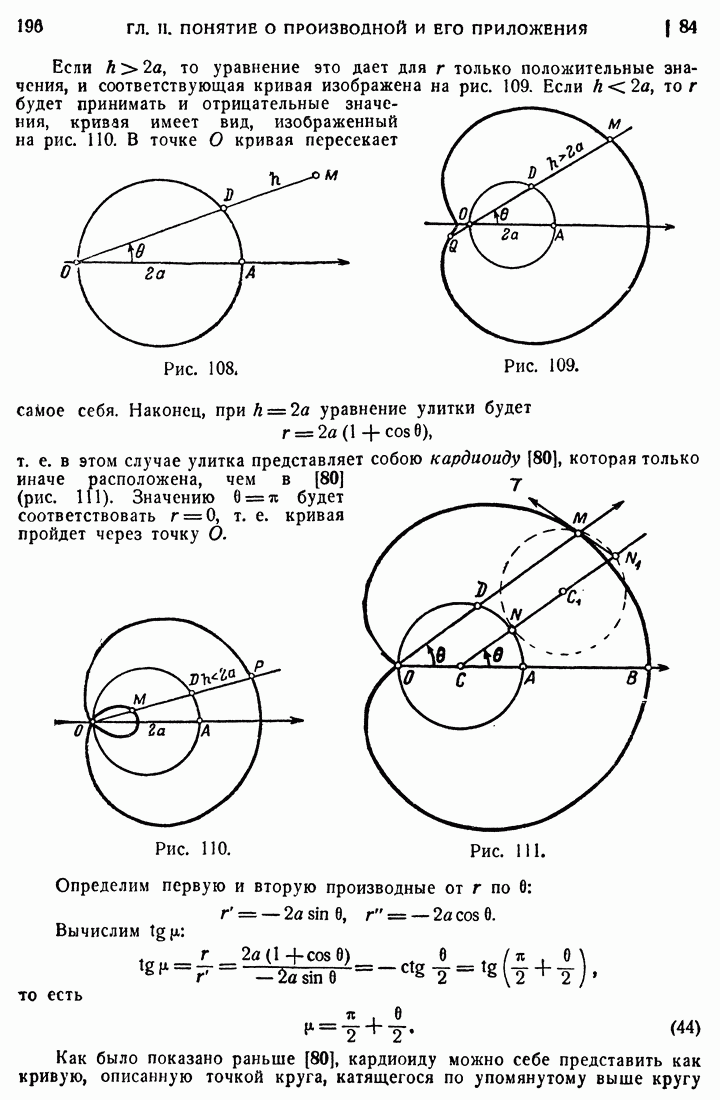
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
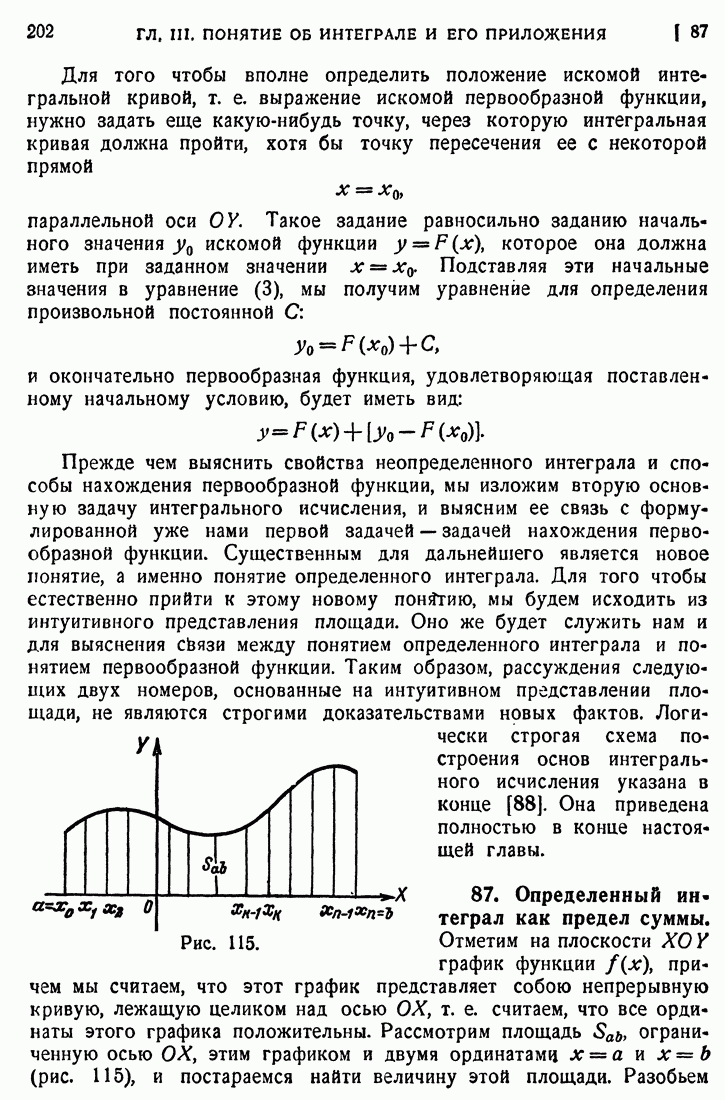
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
- 97. Разрыв подынтегральной функции.
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
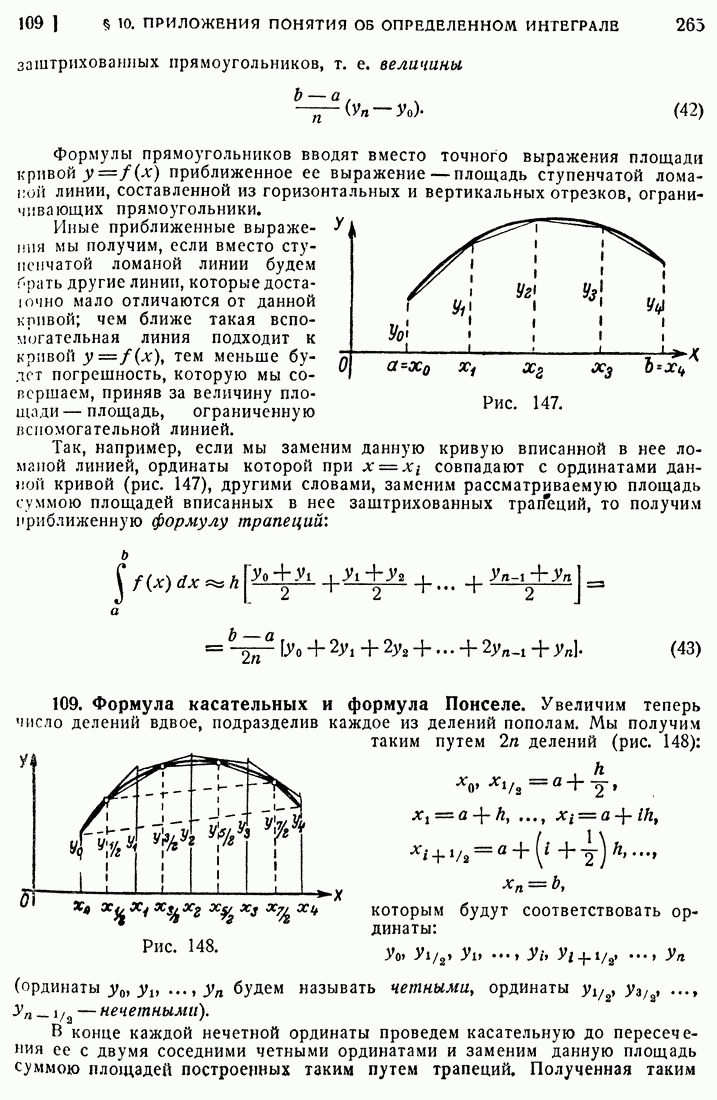
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
- 109. Формула касательных и формула Понселе.
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
- 112. Графические способы.
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
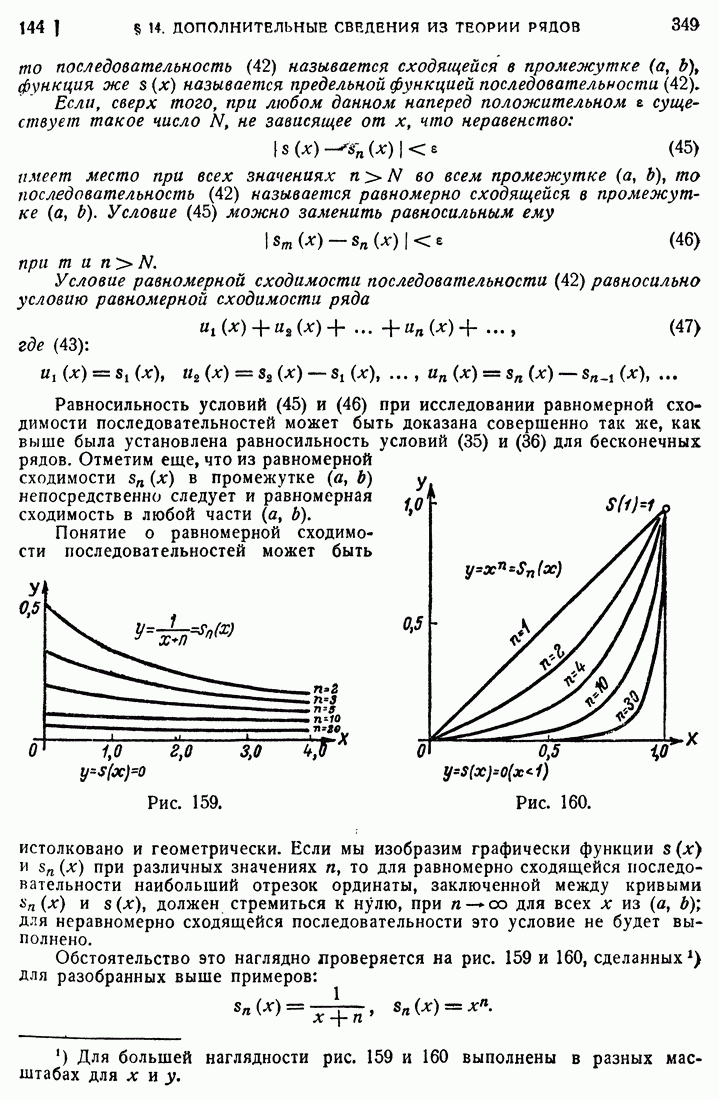
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
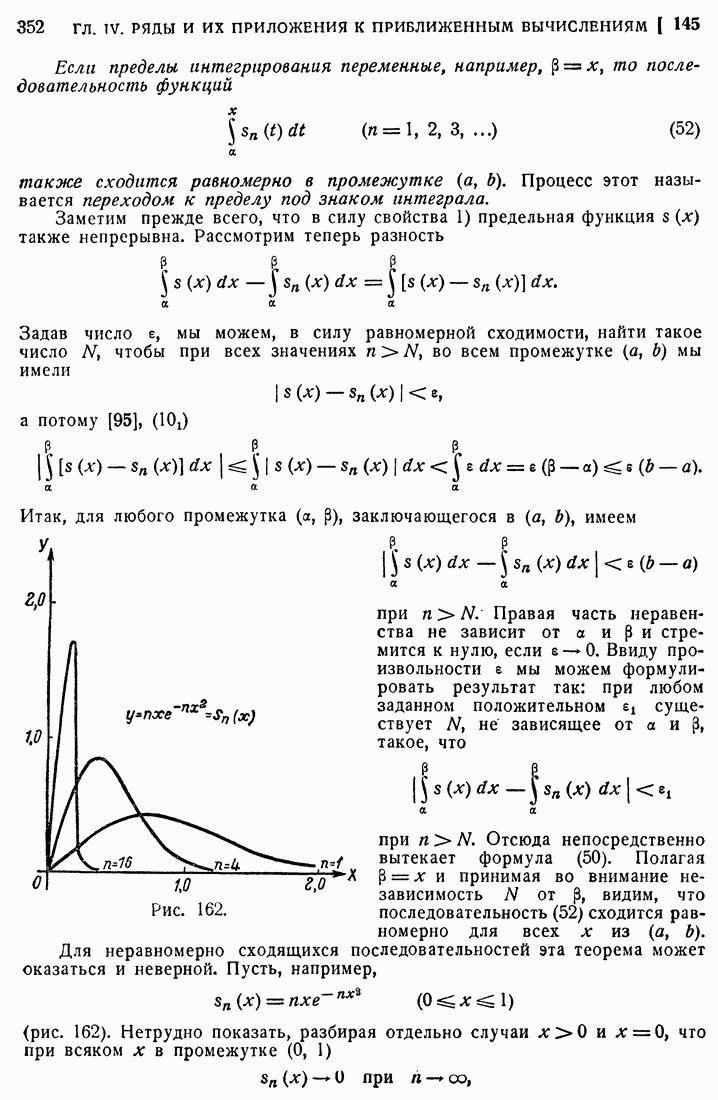
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
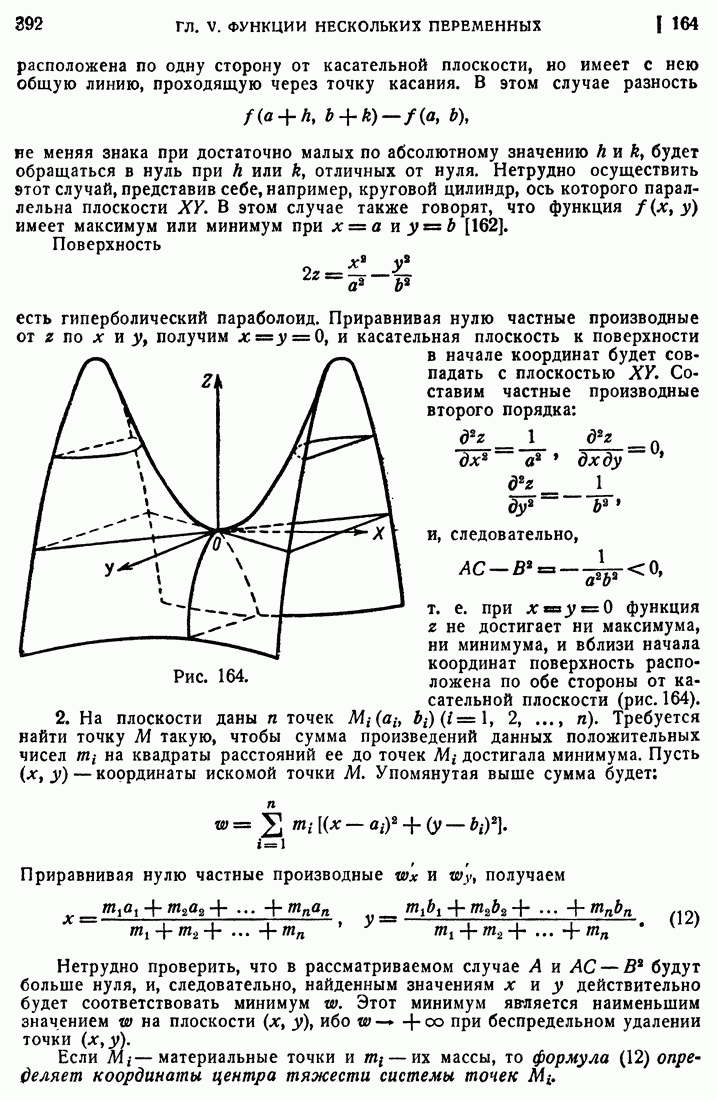
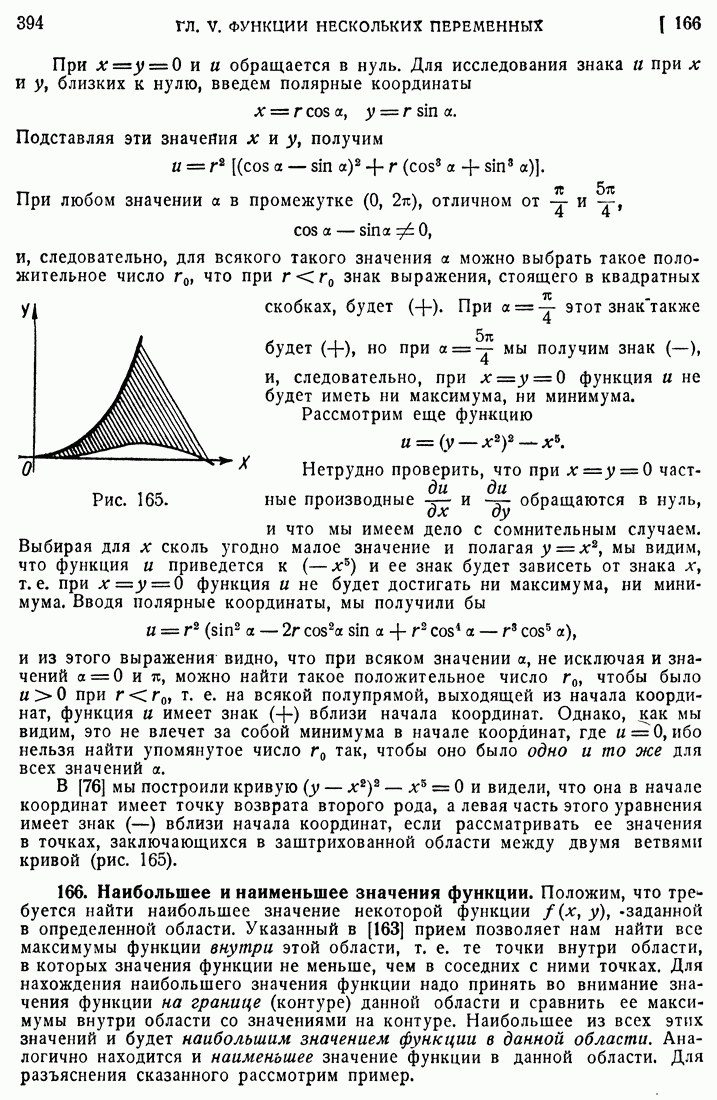
- 163. Исследование максимума и минимума функции двух независимых переменных.
- 164. Примеры.
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
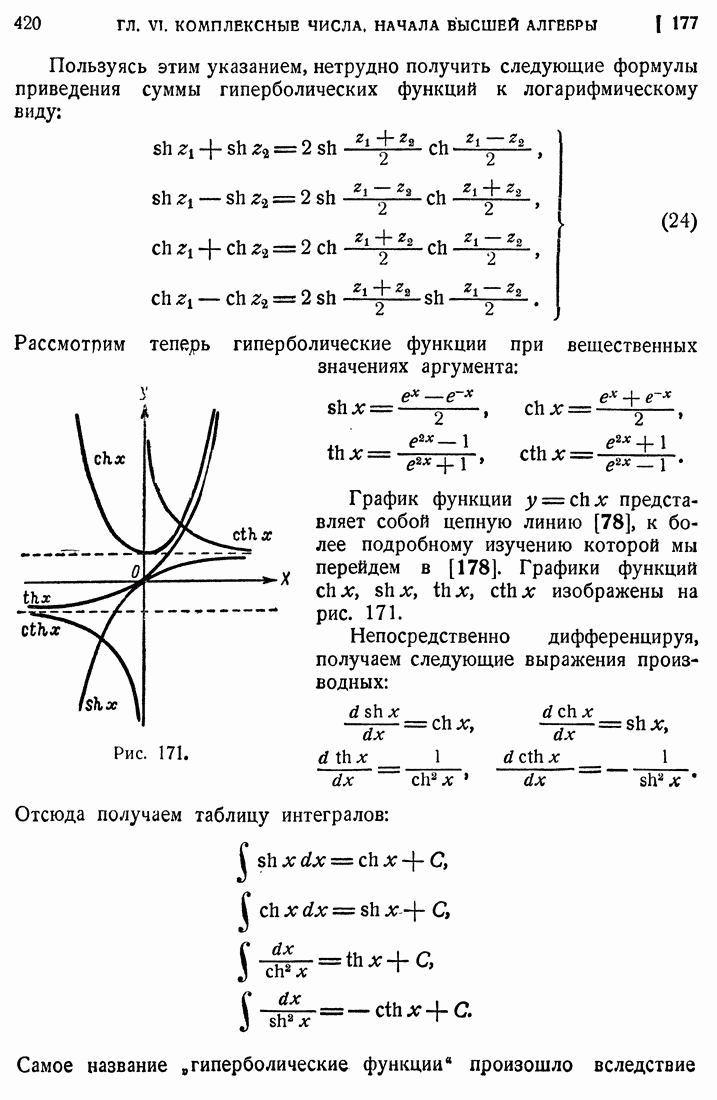
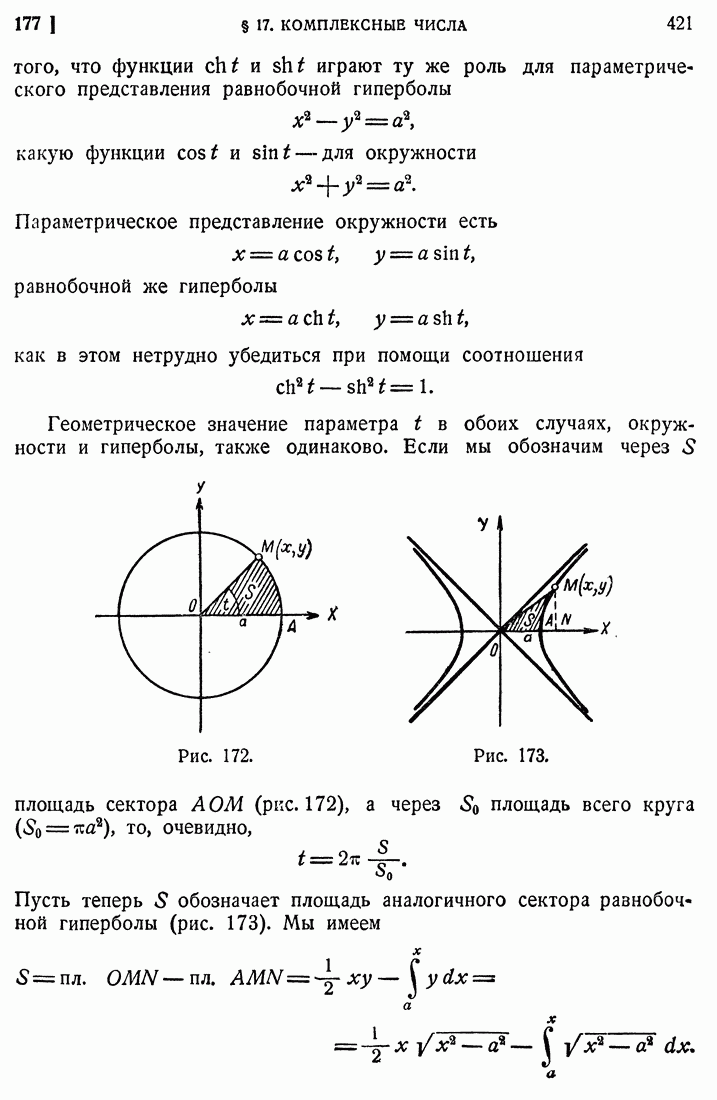
- 177. Тригонометрические и гиперболические функции.
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
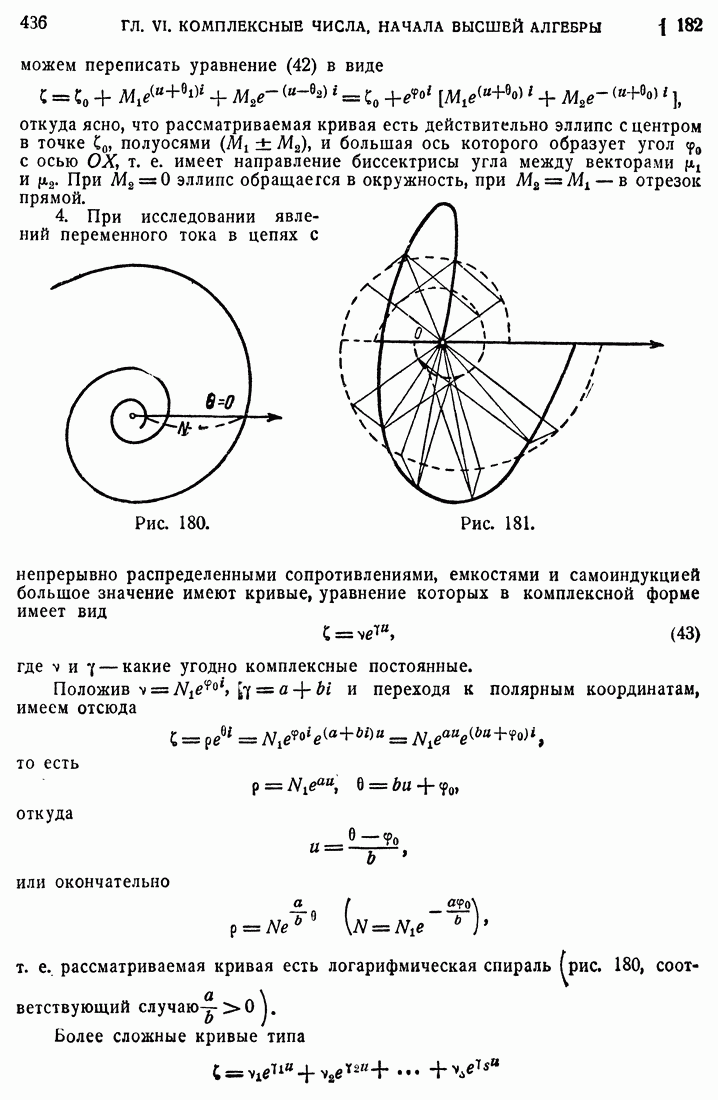
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
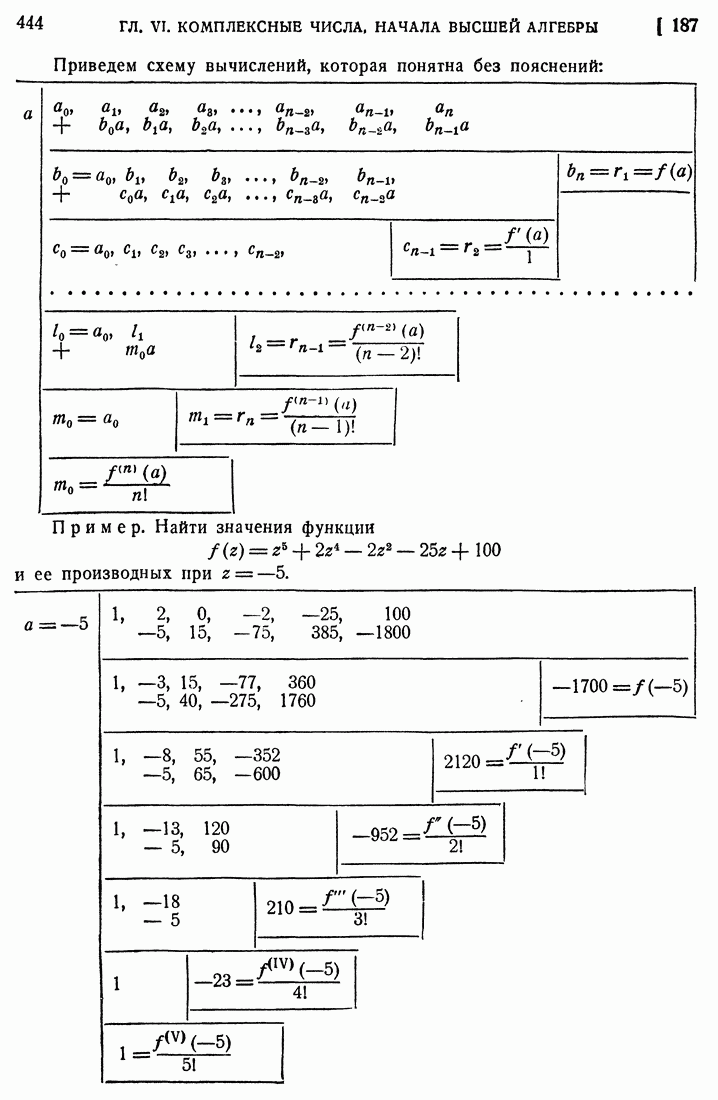
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
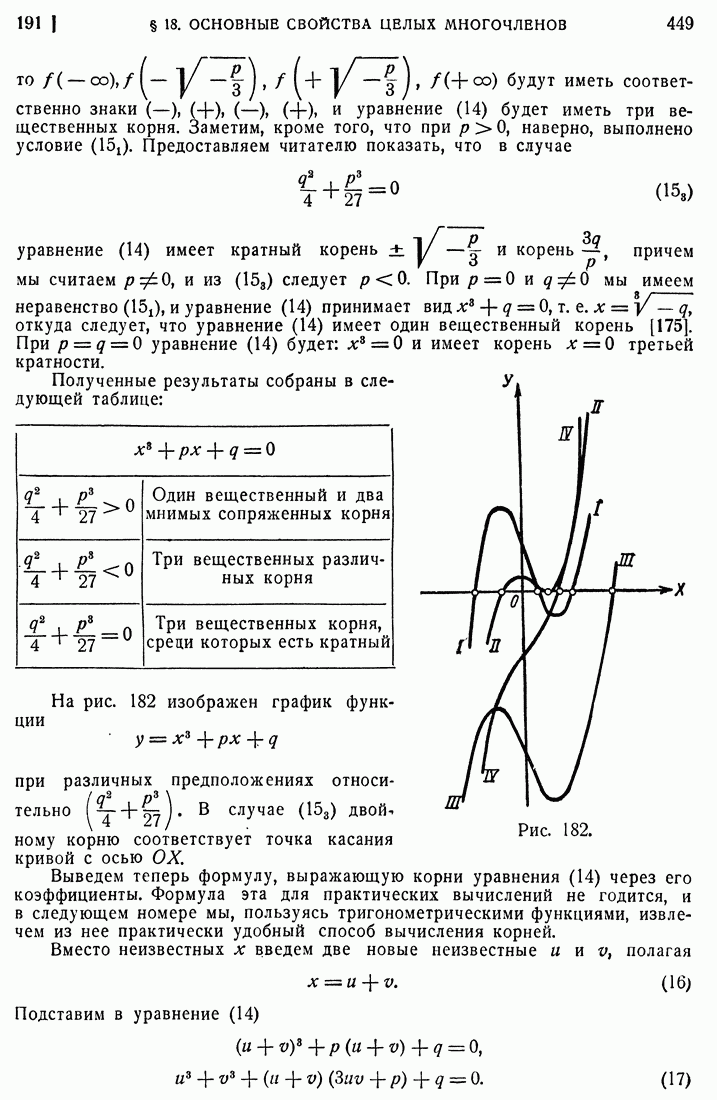
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
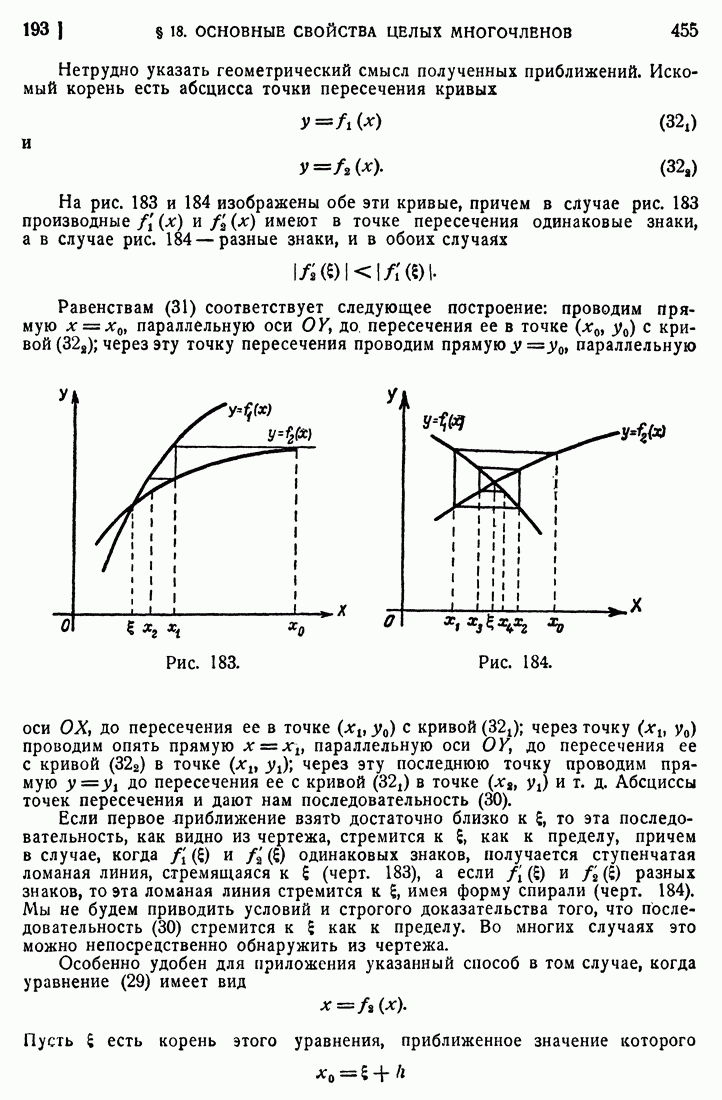
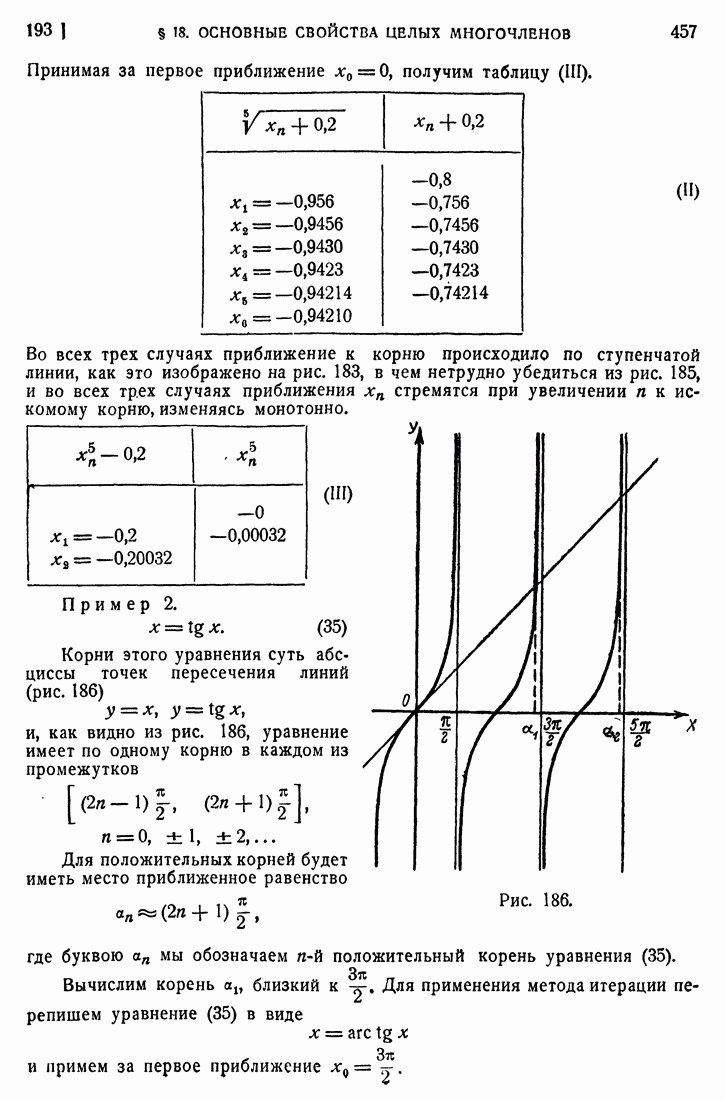
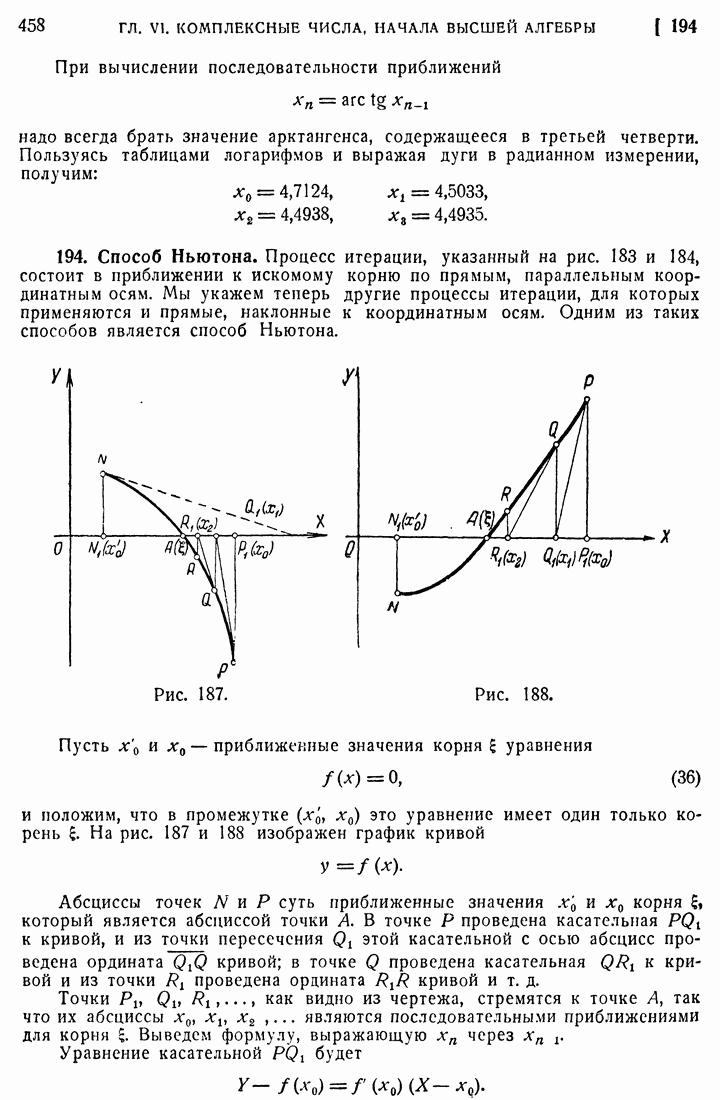
- 193. Способ итерации.
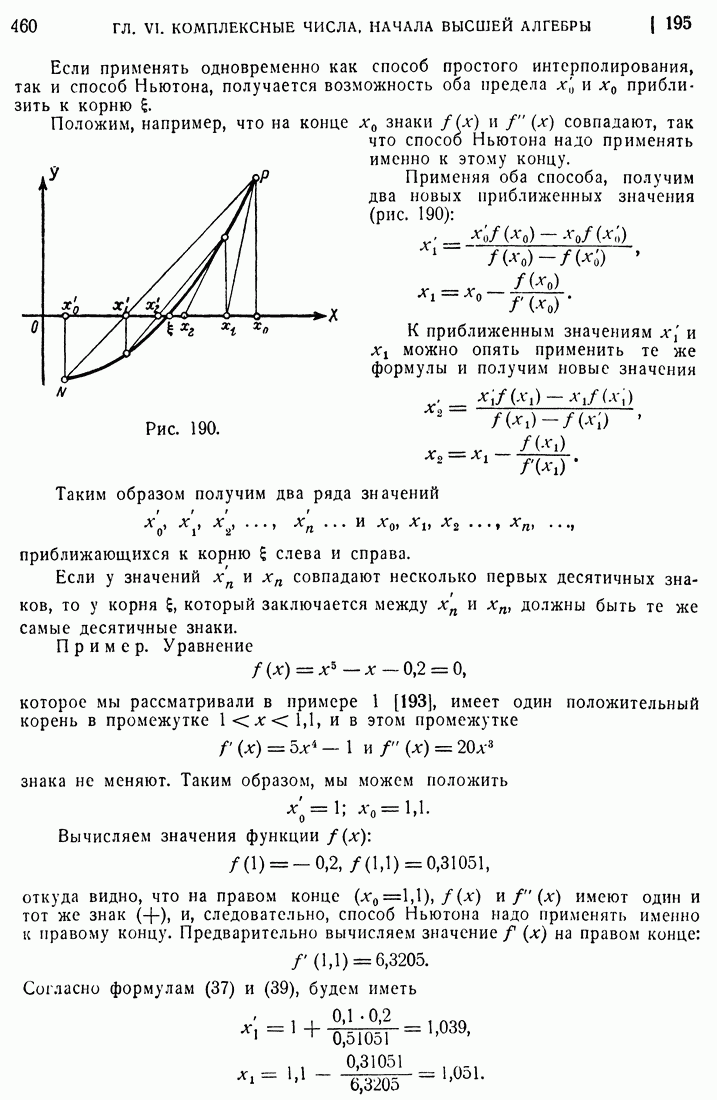
- 194. Способ Ньютона.
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…