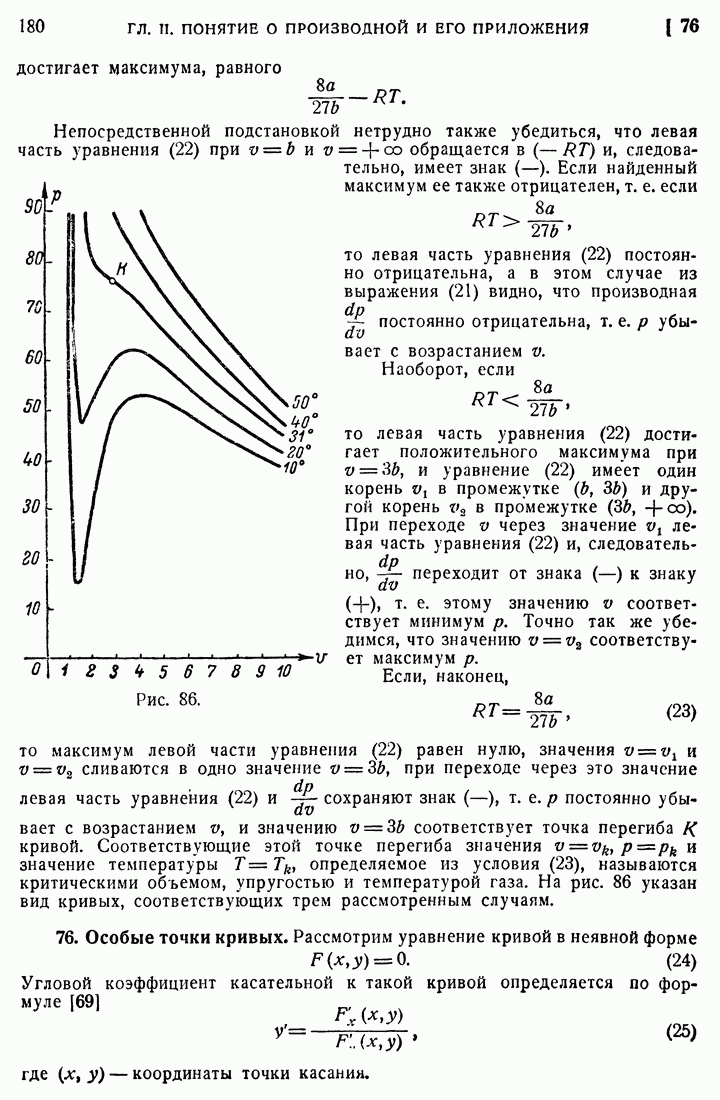
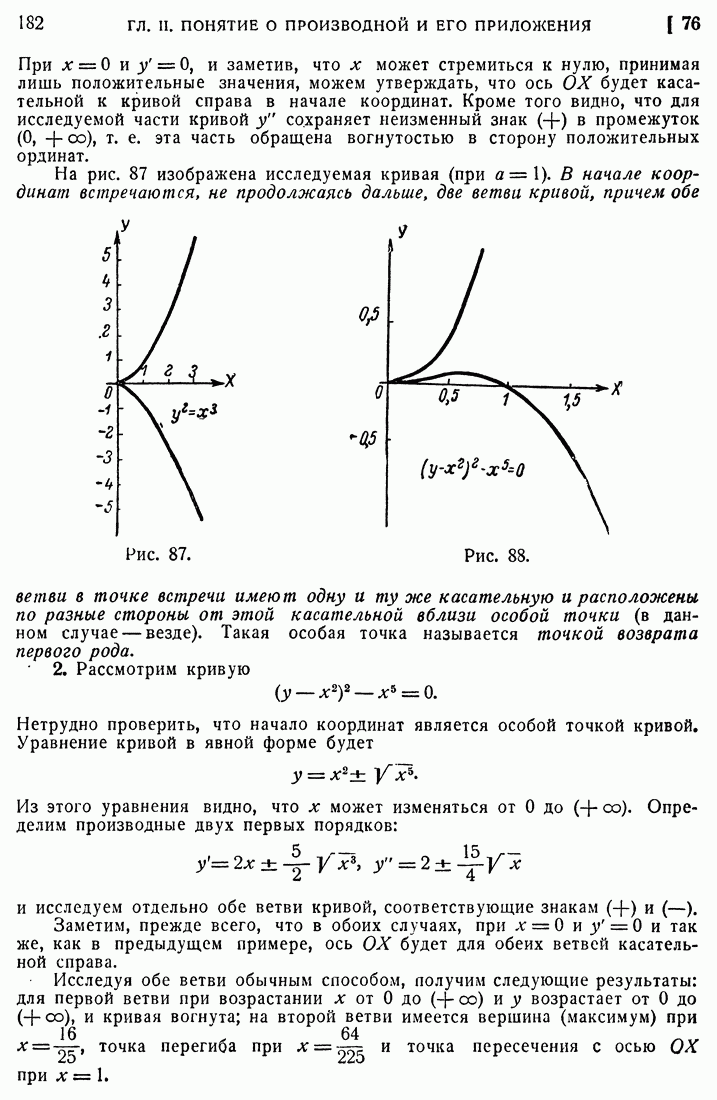
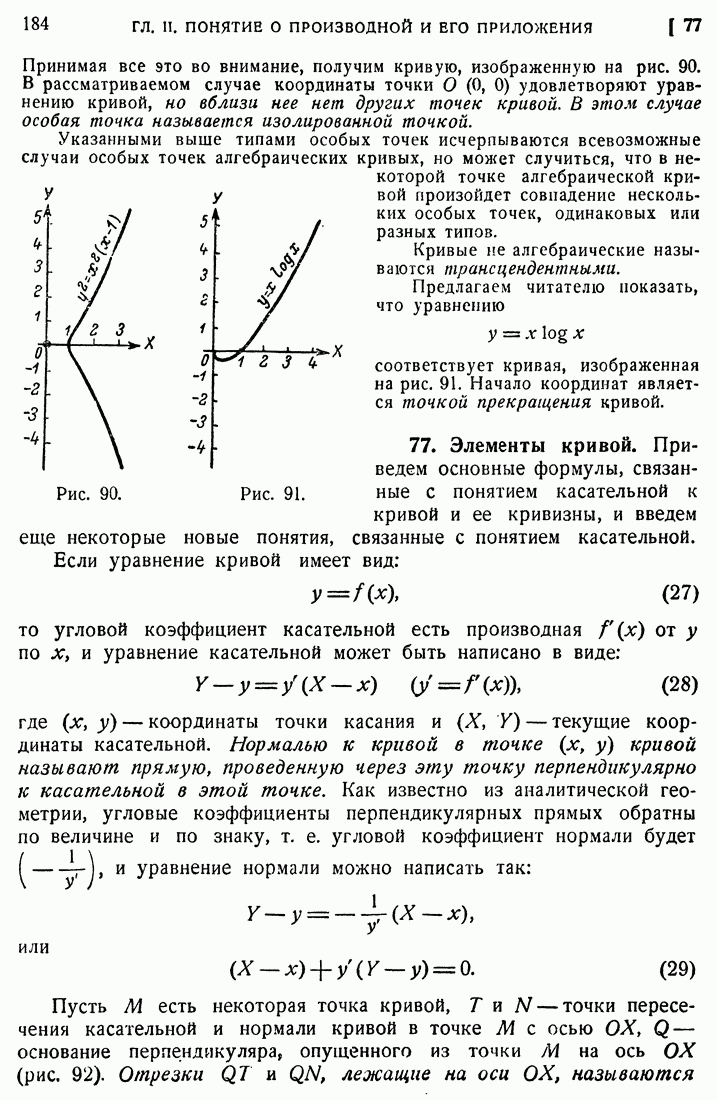
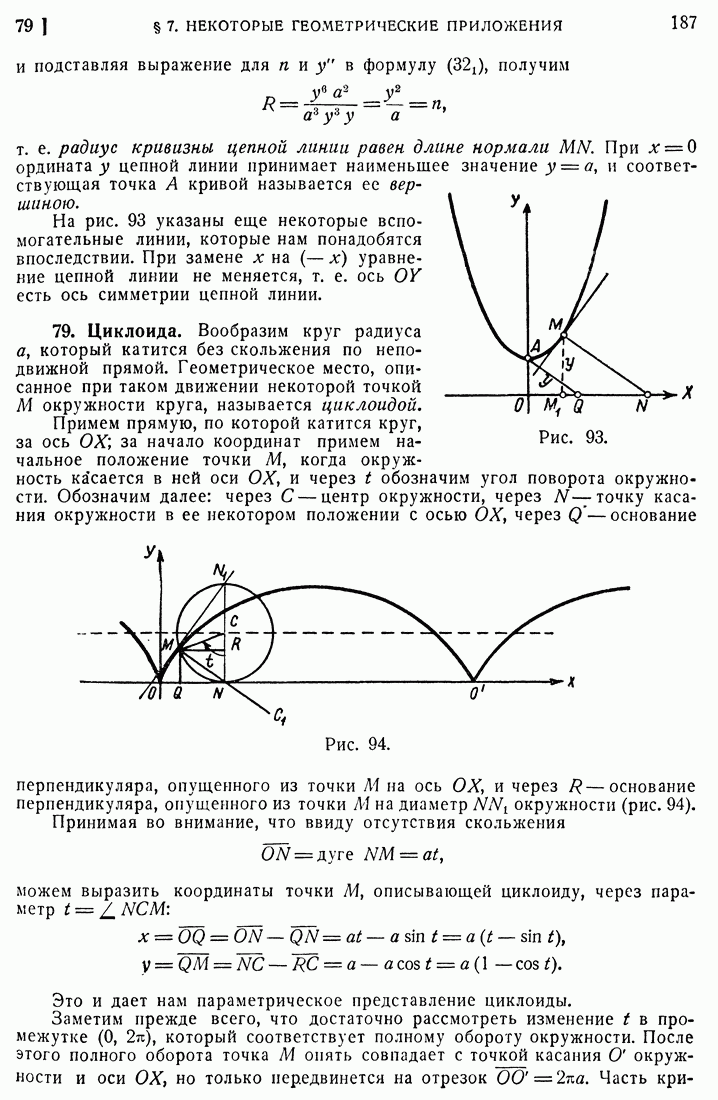
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6. Аналитический способ задания функциональной зависимости.
Всякий закон природы, дающий связь одних явлений с другими, устанавливает функциональную зависимость между величинами.
Существует много способов для изображения функциональных зависимостей, но самое важное значение имеют три способа: 1) аналитический; 2) способ таблиц и 3) графический, или геометрический.
Мы говорим, что функциональная зависимость между величинами или, проще, функция изображена аналитически, если величины эти связаны между собой уравнениями, в которые они входят, подвергаясь различным математическим операциям: сложению, вычитанию, делению, логарифмированию и т. д. К аналитическому изображению функций мы приходим, когда исследуем вопрос теоретически, т. е., установив основные предпосылки, мы применяем математический анализ и получаем результат в виде некоторой математической формулы.
Если мы имеем непосредственное выражение функции (т. е. зависимой переменной) при помощи математических действий над другими, независимыми переменными, то говорят, что функция аналитически задана явно. Примером явного задания функции может служить выражение объема газа v при постоянной температуре через давление (явная функция одной независимой переменной):

или выражение площади 5 треугольника через стороны:

(явная функция от трех независимых переменных). Выпишем еще пример явного задания функции от одной независимой переменной х:

Часто бывает неудобно или невозможно выписывать формулу, которая выражает функцию через независимые переменные. При этом пишут коротко так:

Эта запись обозначает, что у есть функция независимой переменной  есть символический знак зависимости у от
есть символический знак зависимости у от  . Вместо
. Вместо  можно, конечно, употреблять и другие буквы. Если мы рассматриваем разные функции от
можно, конечно, употреблять и другие буквы. Если мы рассматриваем разные функции от  то должны употреблять и разные буквы для символической записи зависимости от
то должны употреблять и разные буквы для символической записи зависимости от 

Такой символической записью пользуются не только в том случае, когда функция задана аналитически, но и в самом общем случае функциональной зависимости, которой мы определили в [5].
Аналогичной короткой записью пользуются и для функций от нескольких независимых переменных:

Здесь v есть функция переменных 
Частное значение функции получим, придав независимым переменным частные же значения и выполнив действия, указанные знаками  . Так, например, частное значение функции (1) при
. Так, например, частное значение функции (1) при  будет
будет

Вообще частное значение некоторой функции  при
при  обозначается
обозначается  Аналогично для функций от нескольких переменных.
Аналогично для функций от нескольких переменных.
Не надо смешивать общего понятия функции, которое было нами дано в [51, с понятием аналитического выражения через  . В общем определении функции говорится лишь о некотором законе, согласно которому любому значению переменной
. В общем определении функции говорится лишь о некотором законе, согласно которому любому значению переменной  из множества ее возможных значений соответствует определенное значение у. При этом не предполагается никакое аналитическое выражение (формула)у через
из множества ее возможных значений соответствует определенное значение у. При этом не предполагается никакое аналитическое выражение (формула)у через 
Отметим еще, что можно определить функцию различными аналитическими выражениями на разных участках изменения независимой переменной  . Так, например, мы можем определить функцию у на промежутке (0, 3) следующим образом:
. Так, например, мы можем определить функцию у на промежутке (0, 3) следующим образом:  при
при  при При таком задании любому значению
при При таком задании любому значению  из промежутка (0, 3) соответствует определенное значение у, что и соответствует определению функции.
из промежутка (0, 3) соответствует определенное значение у, что и соответствует определению функции.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
- 12. Линейная функция.
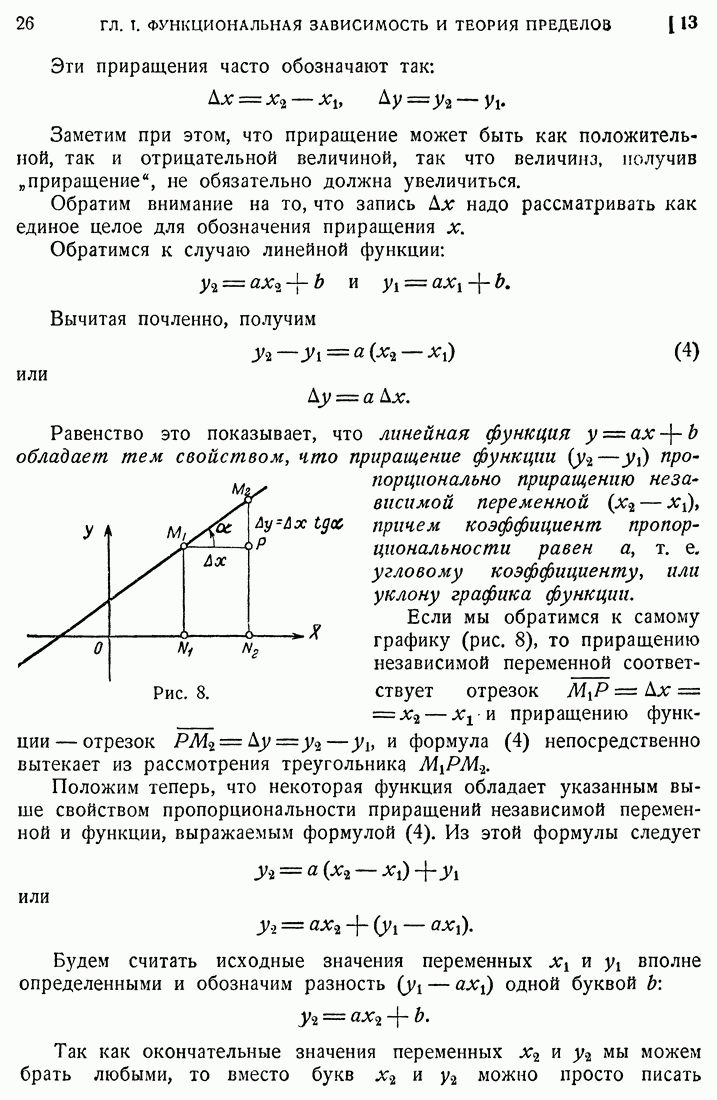
- 13. Приращение. Основное свойство линейной функции.
- 14. График равномерного движения.
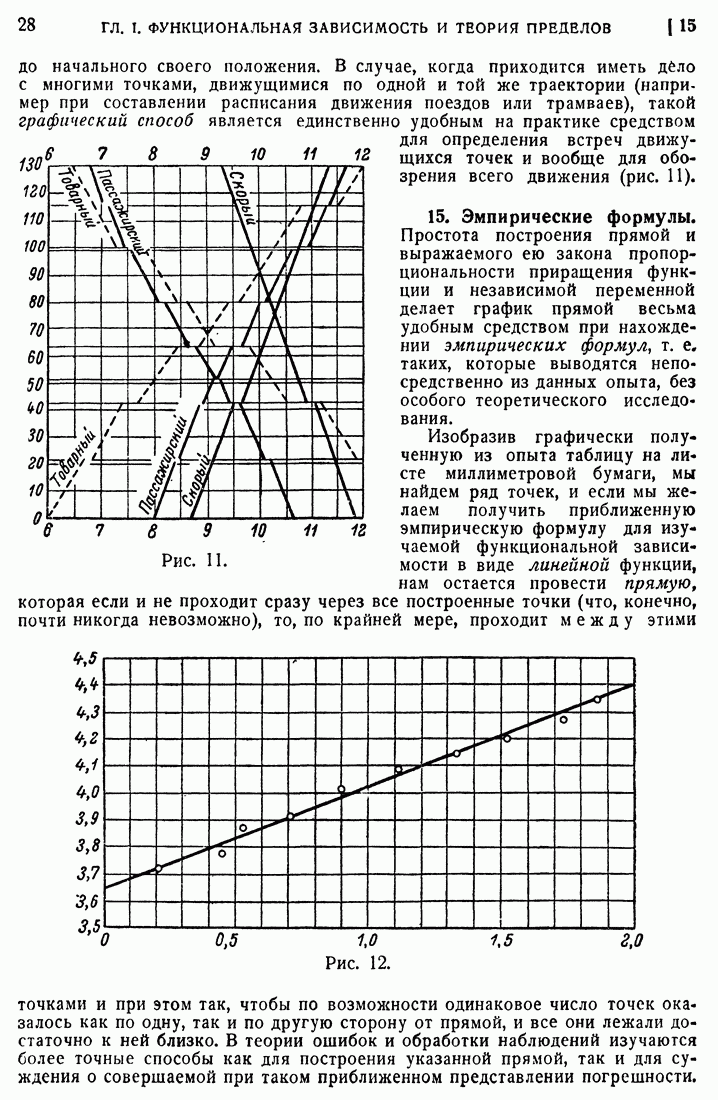
- 15. Эмпирические формулы.
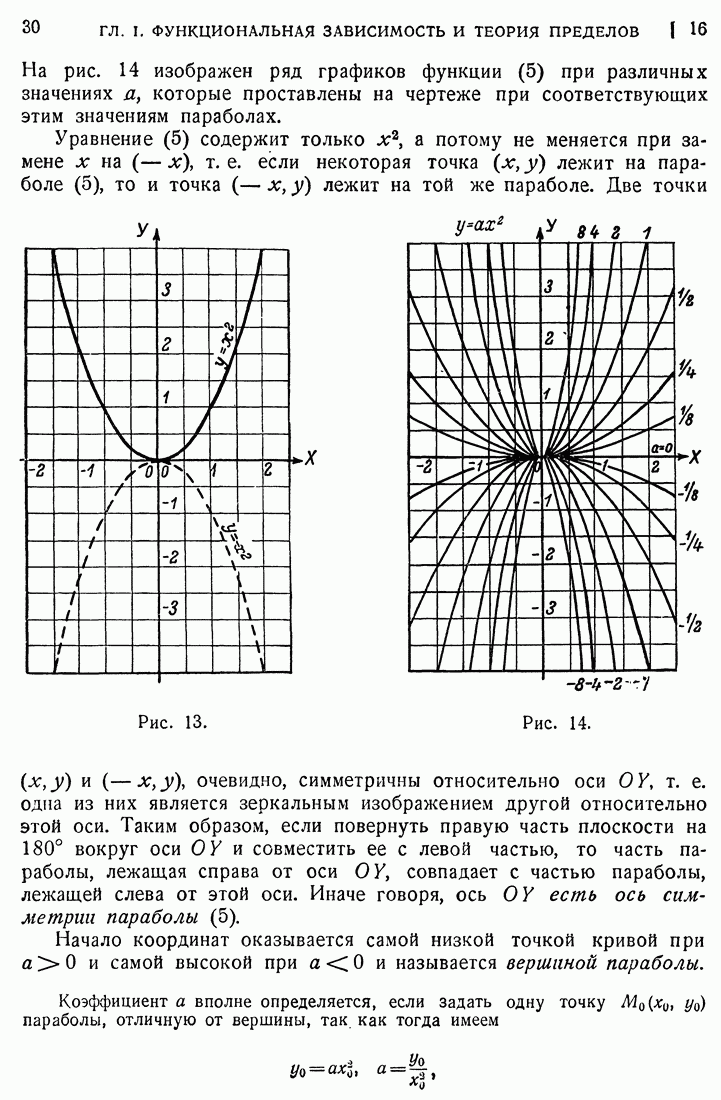
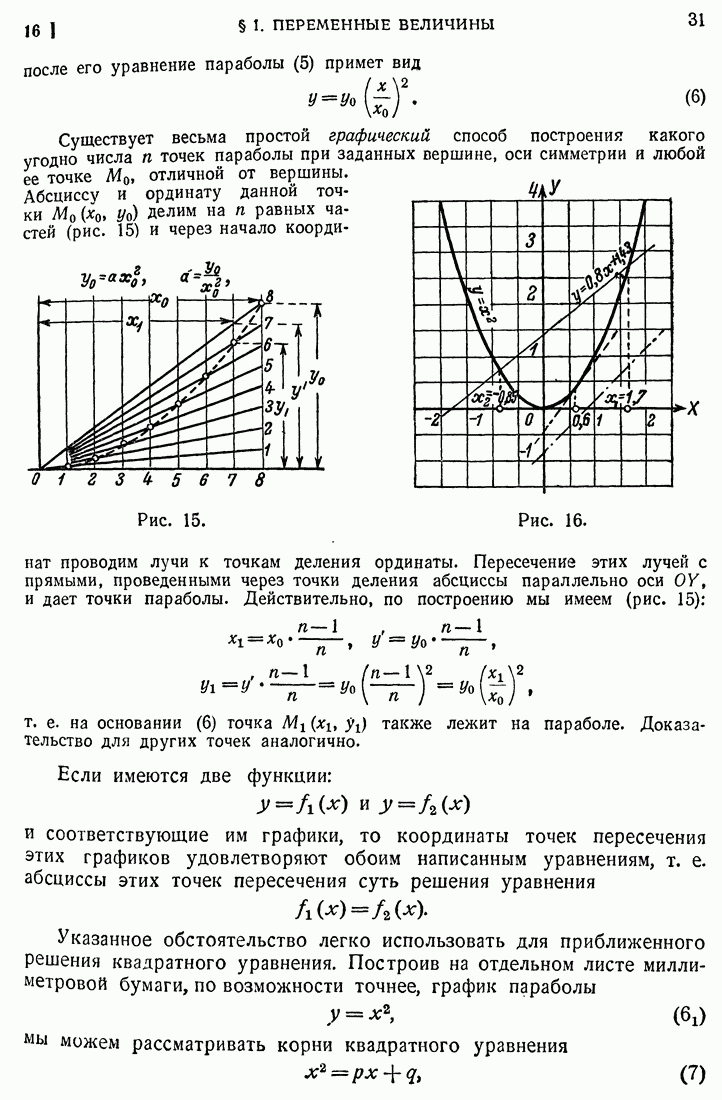
- 16. Парабола второй степени.
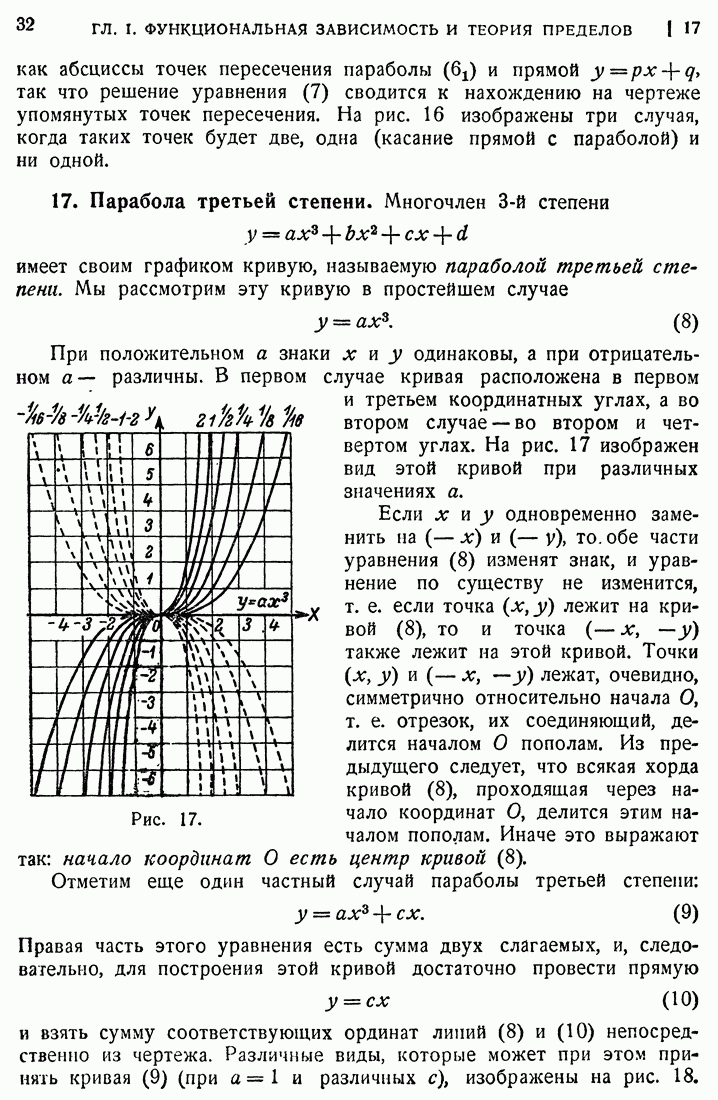
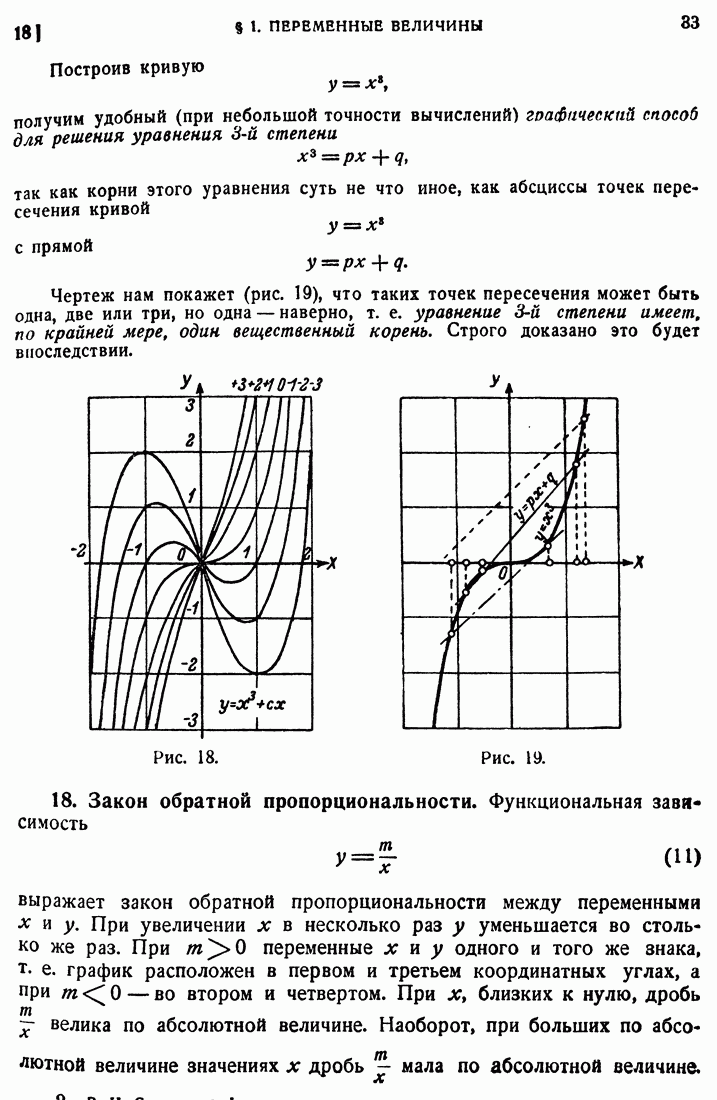
- 17. Парабола третьей степени.
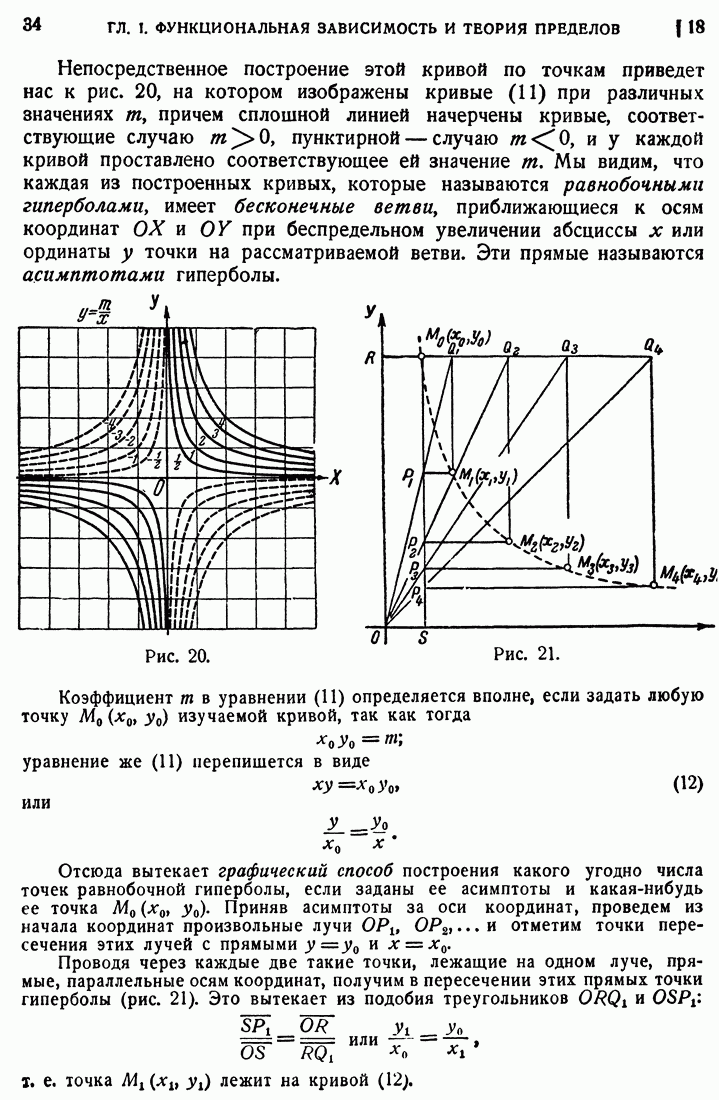
- 18. Закон обратной пропорциональности.
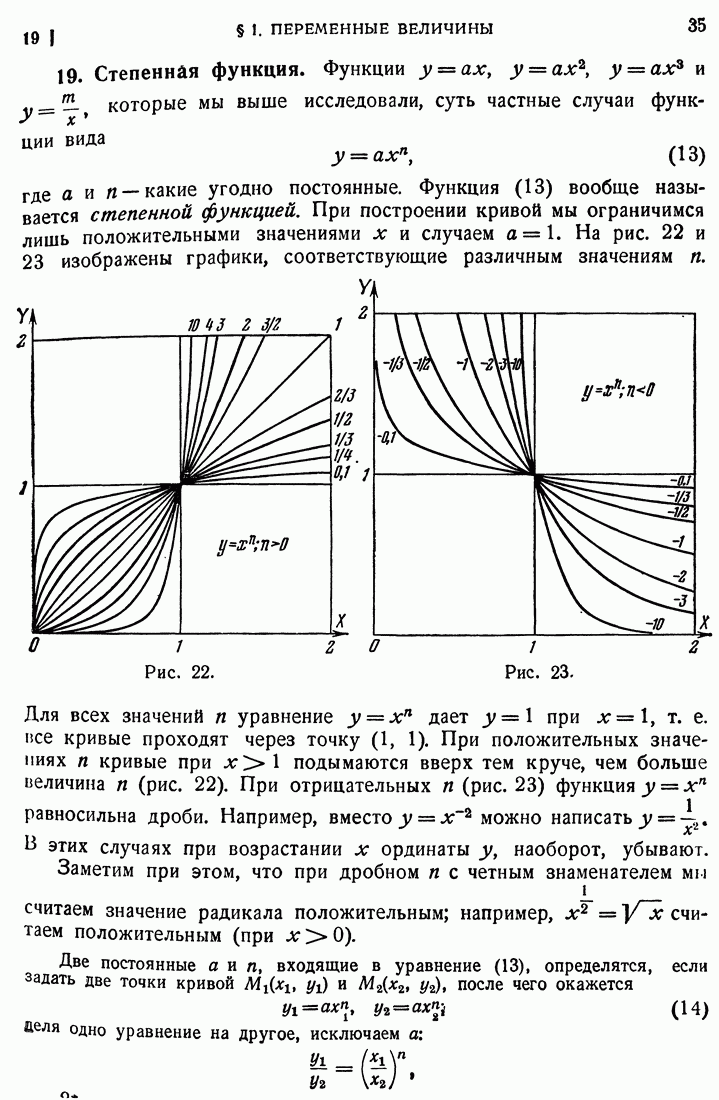
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
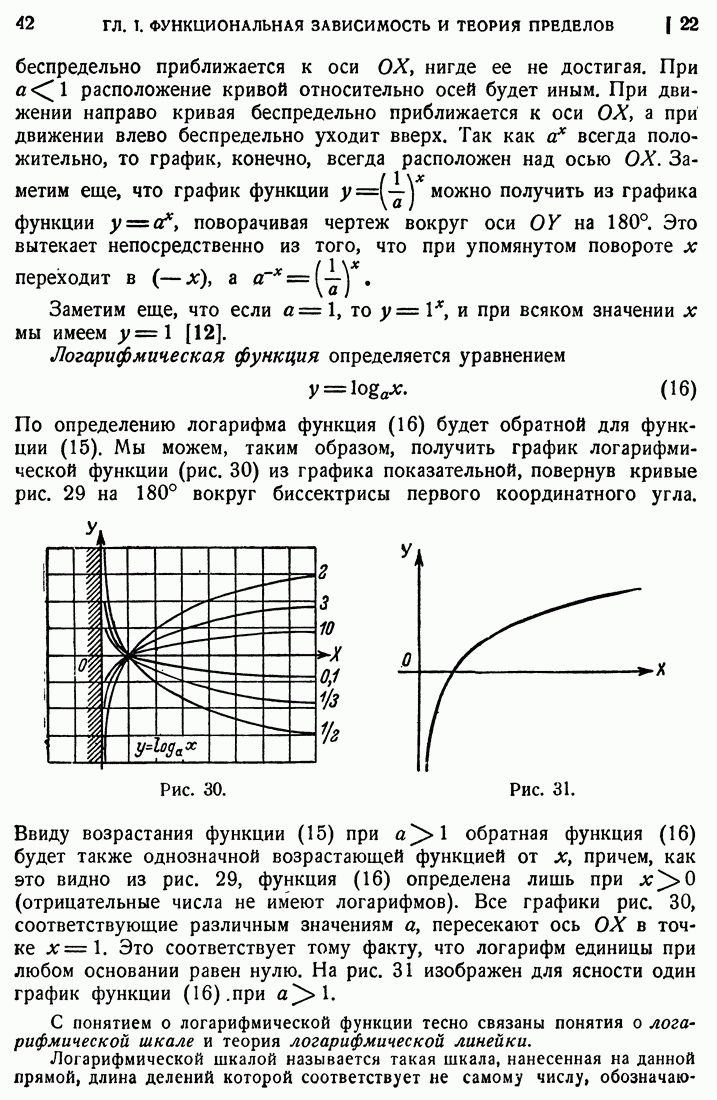
- 22. Показательная и логарифмическая функции.
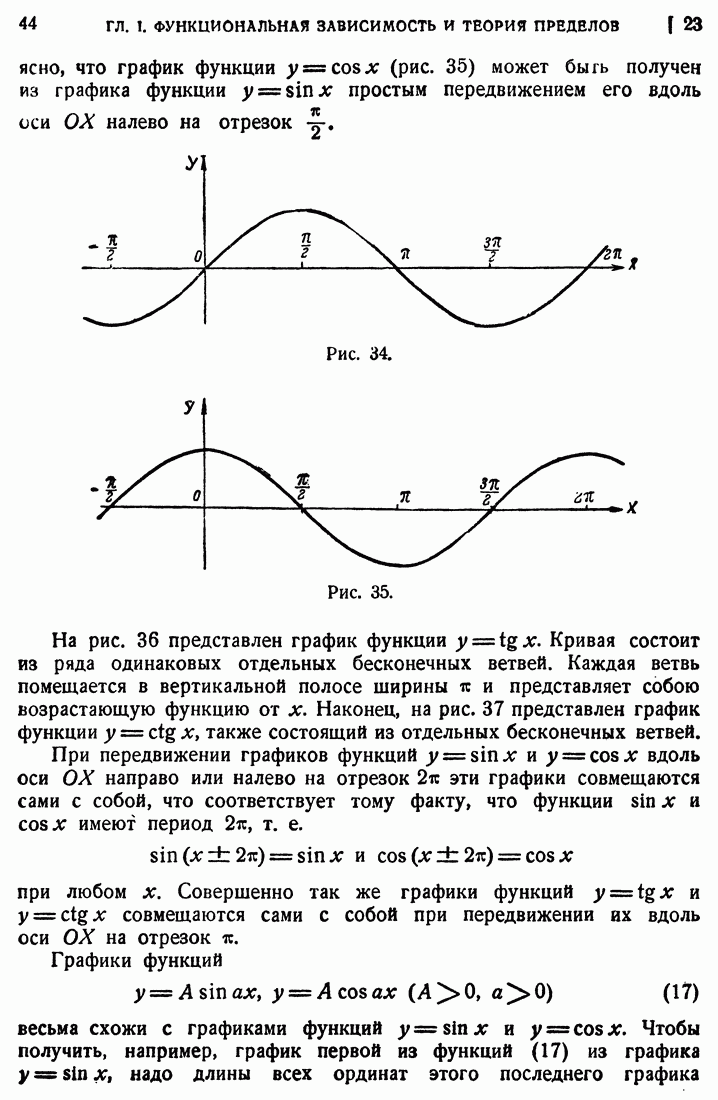
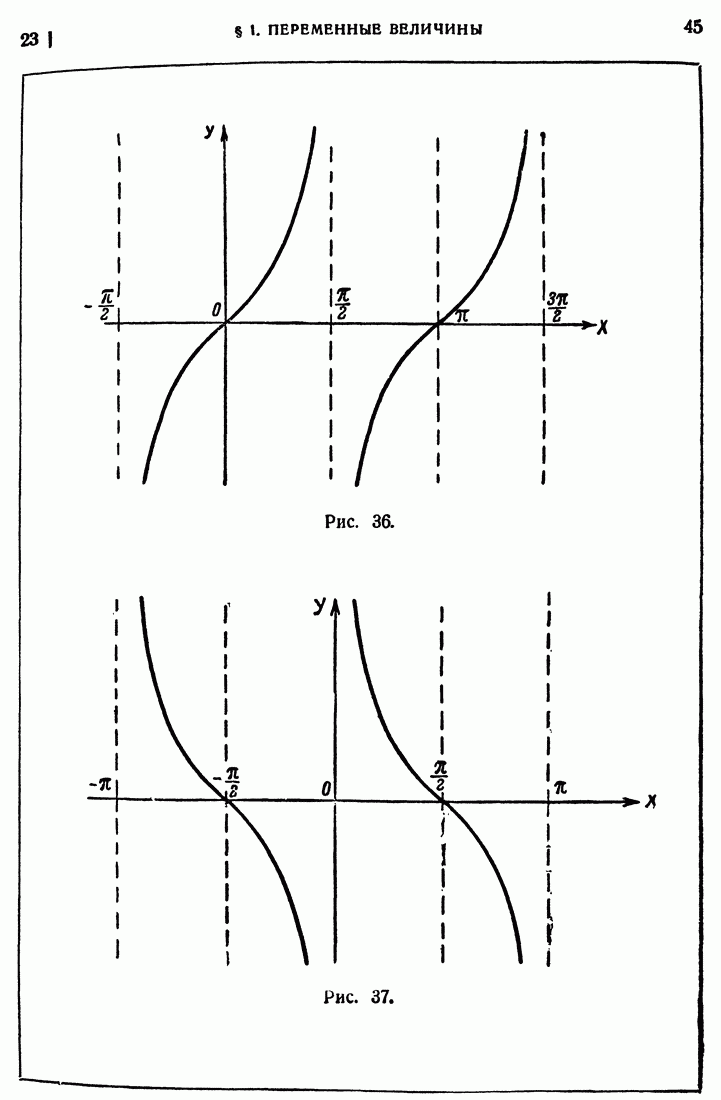
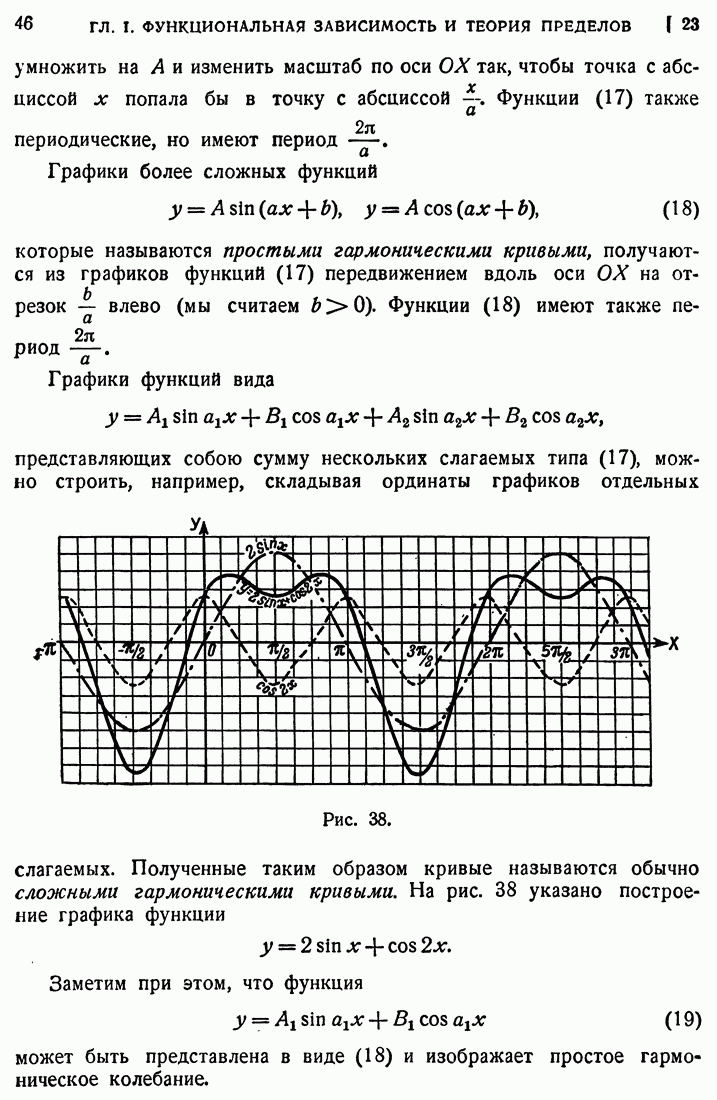
- 23. Тригонометрические функции.
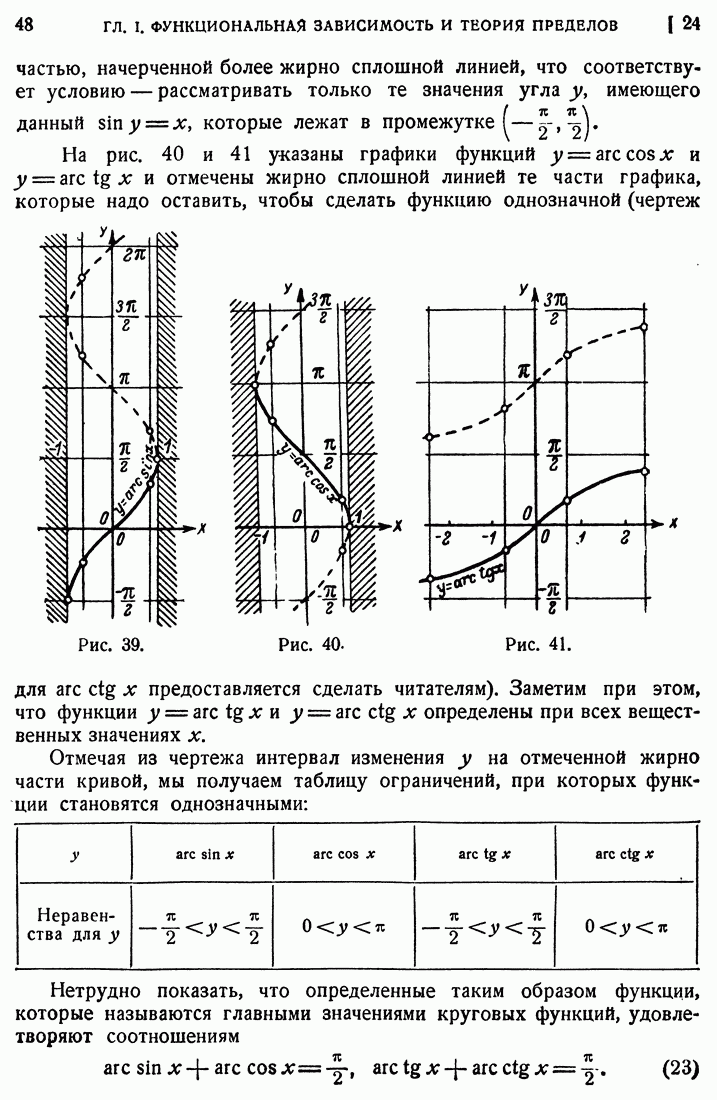
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
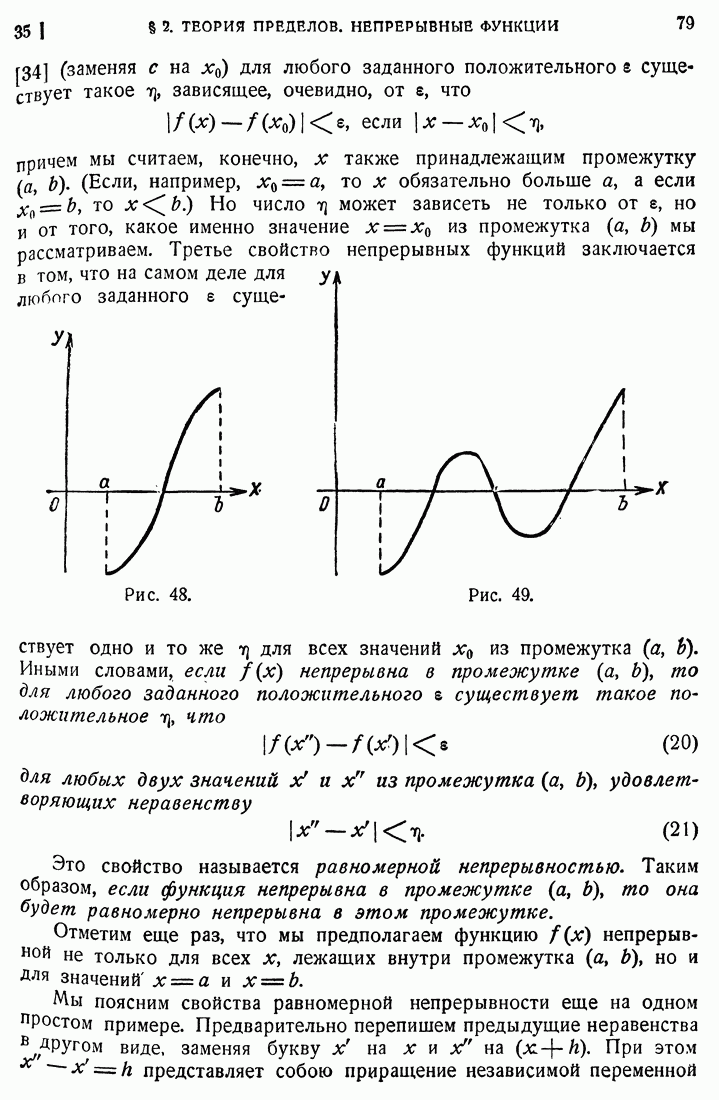
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
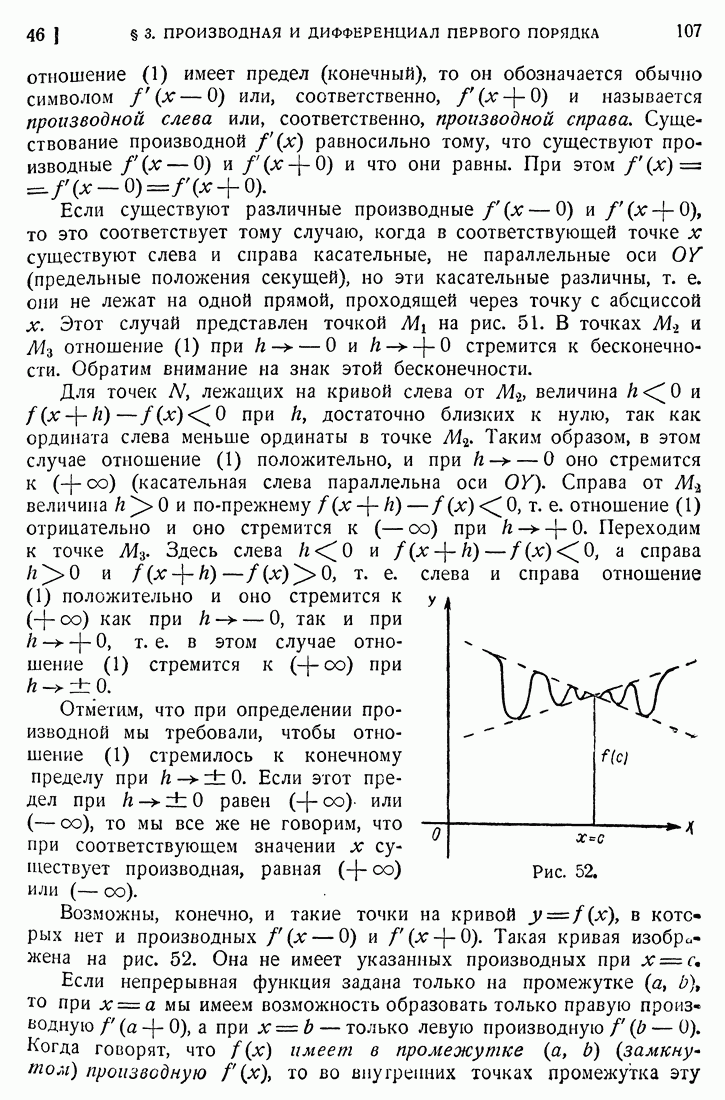
- 45. Понятие о производной.
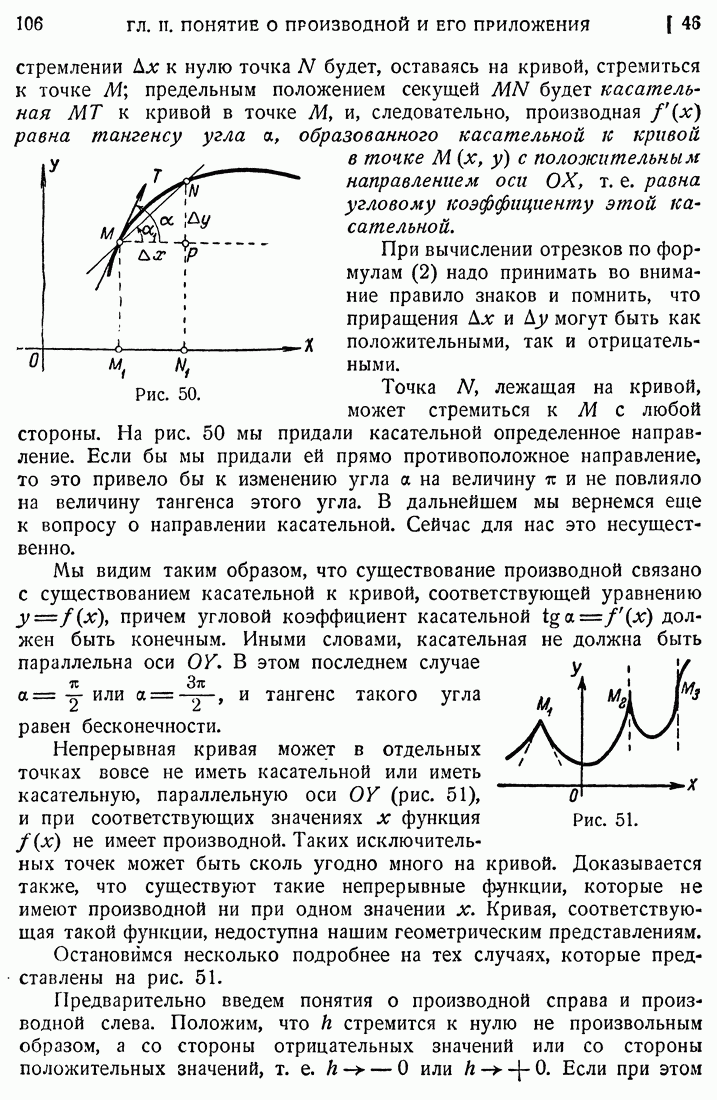
- 46. Геометрическое значение производной.
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
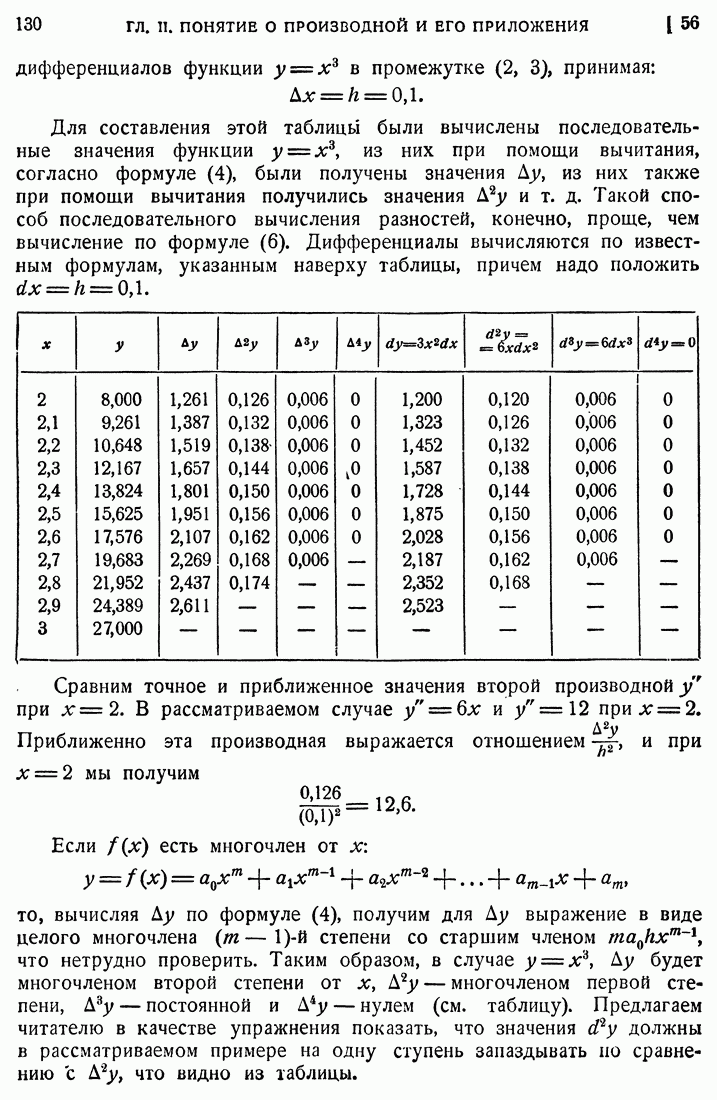
- 55. Дифференциалы высших порядков.
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
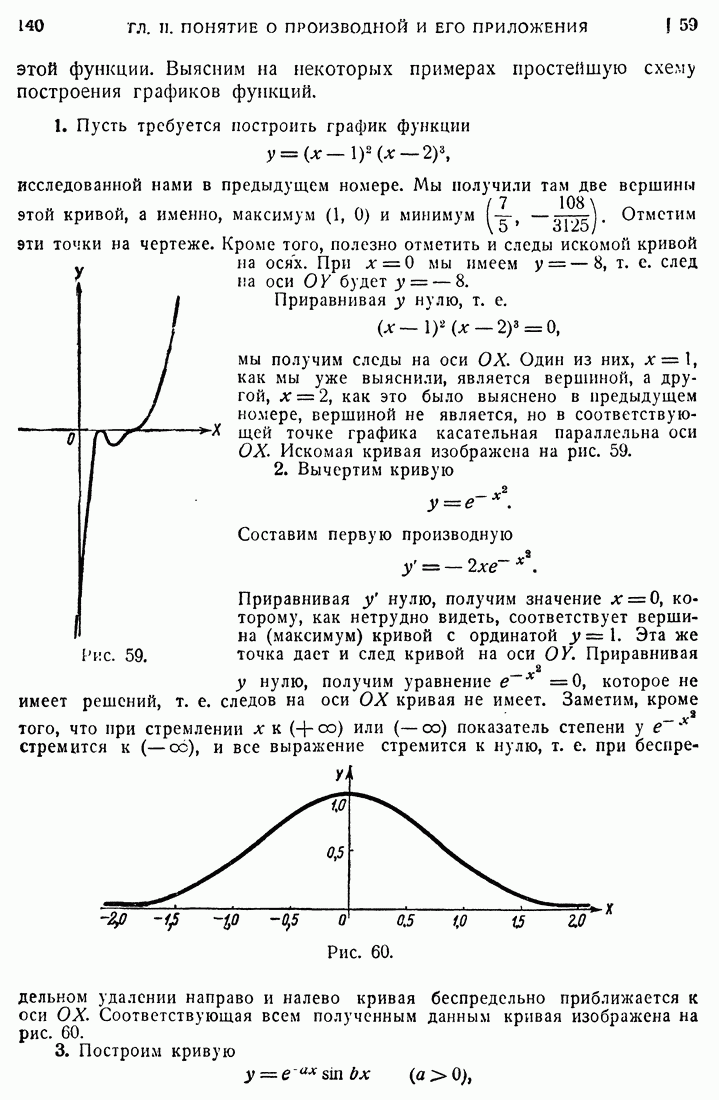
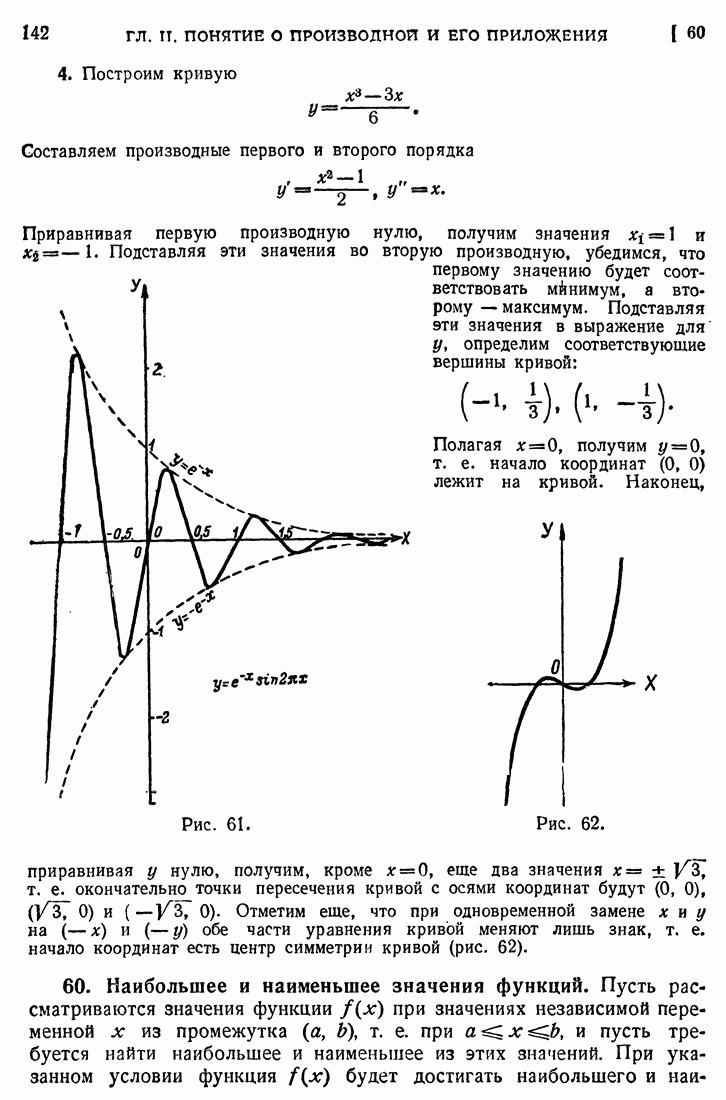
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
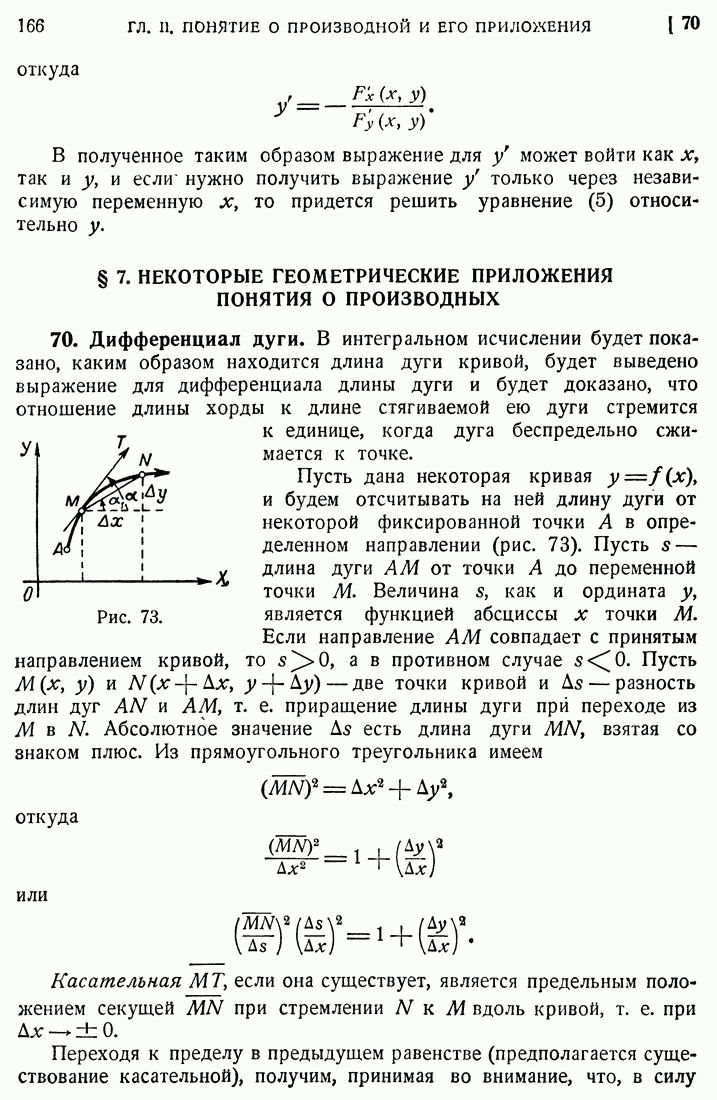
- 70. Дифференциал дуги.
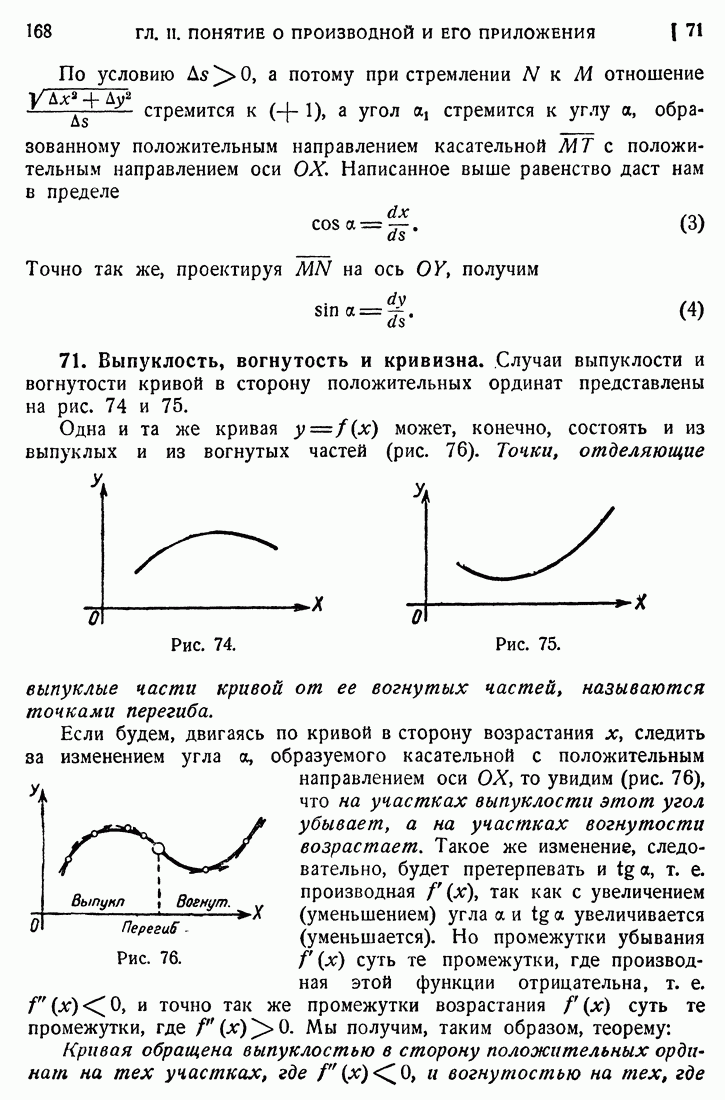
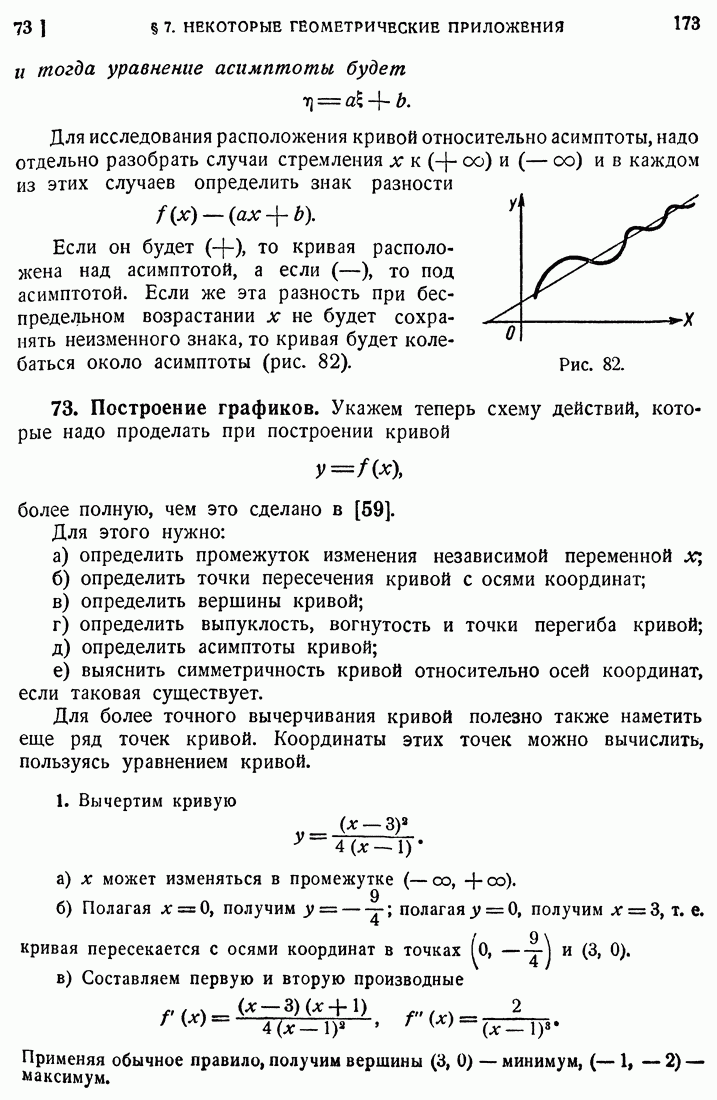
- 71. Выпуклость, вогнутость и кривизна.
- 72. Асимптоты.
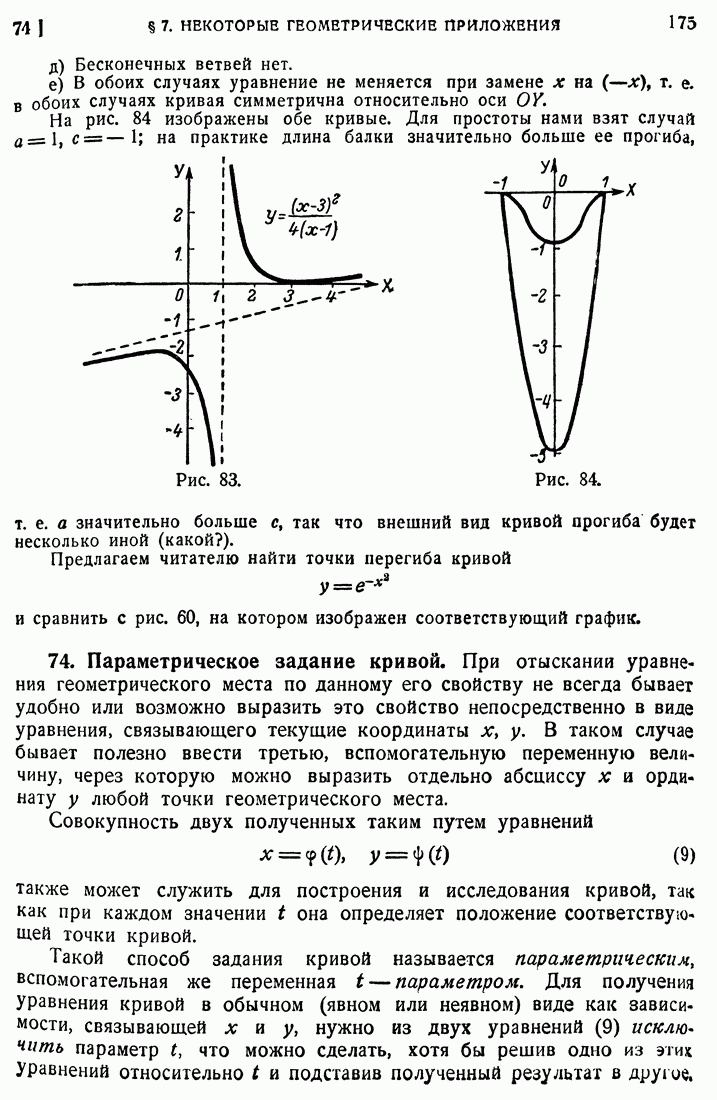
- 73. Построение графиков.
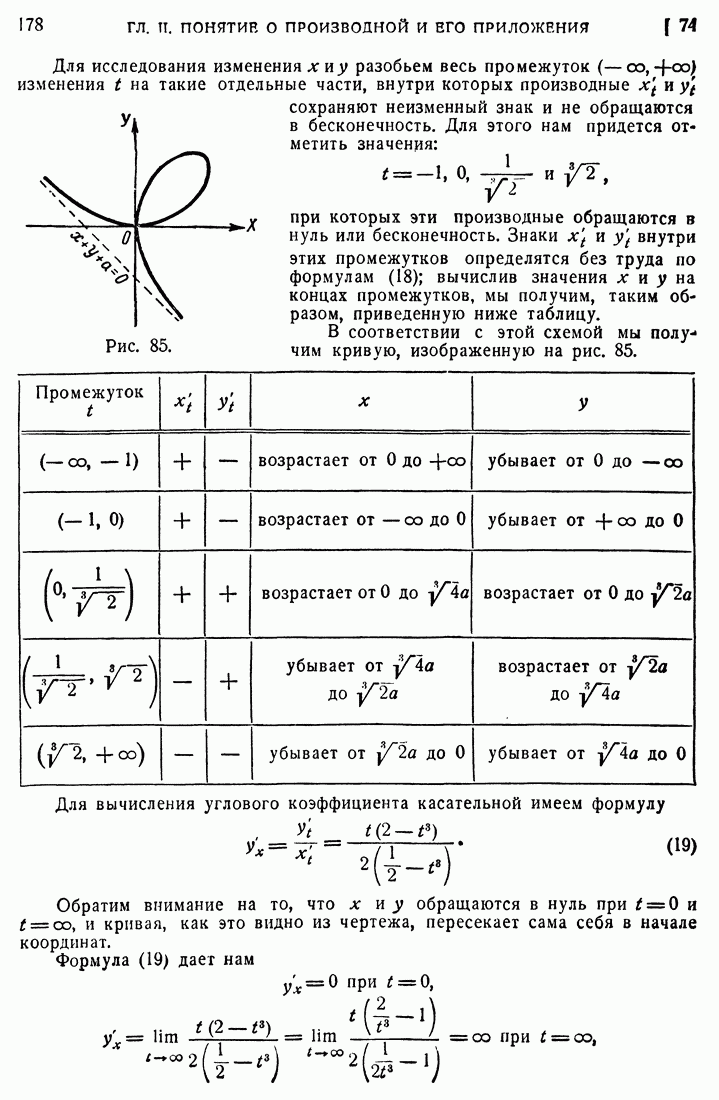
- 74. Параметрическое задание кривой.
- 75. Уравнение Ван-дер-Ваальса.
- 76. Особые точки кривых.
- 77. Элементы кривой.
- 78. Цепная линия.
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
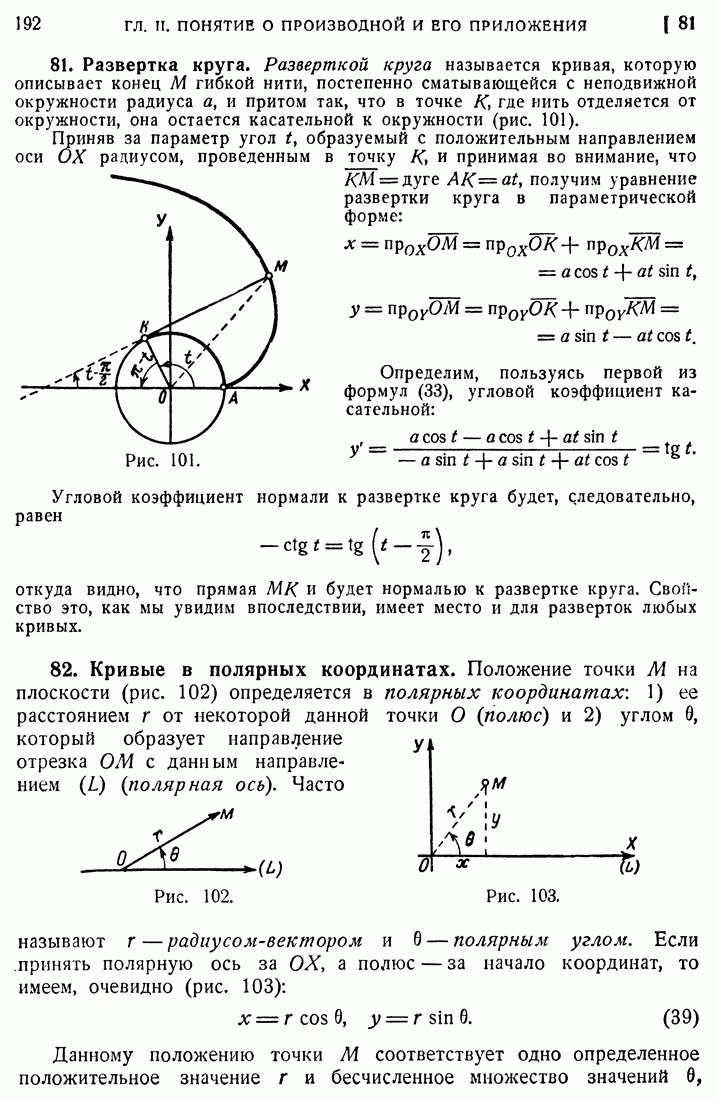
- 81. Развертка круга.
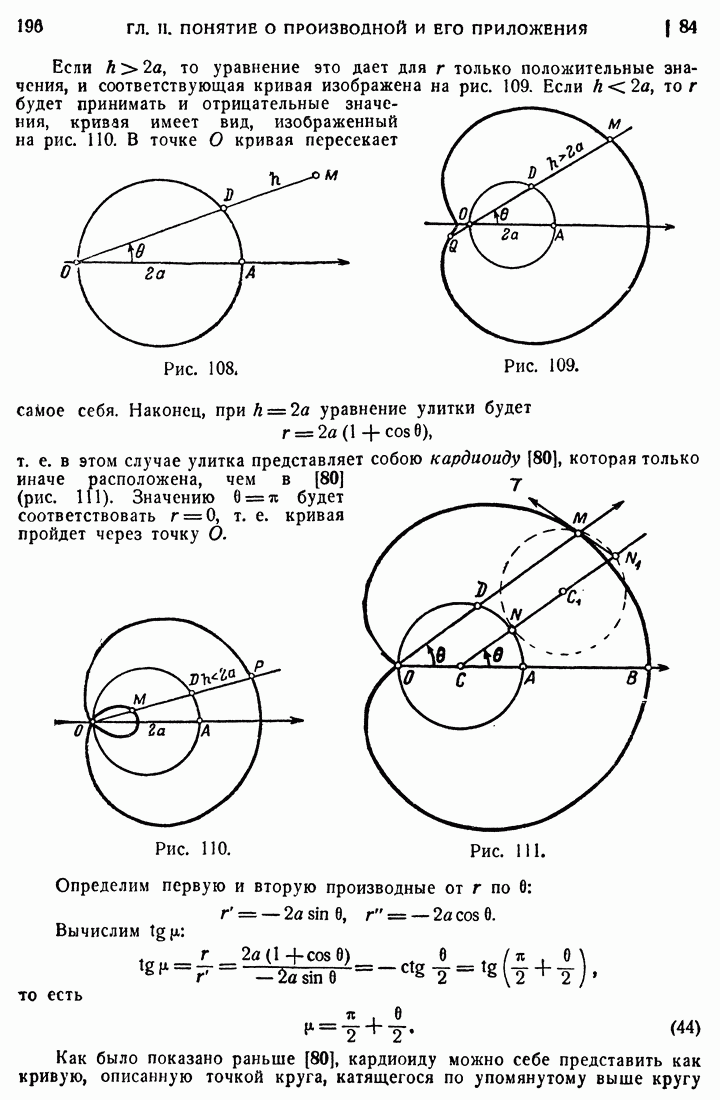
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
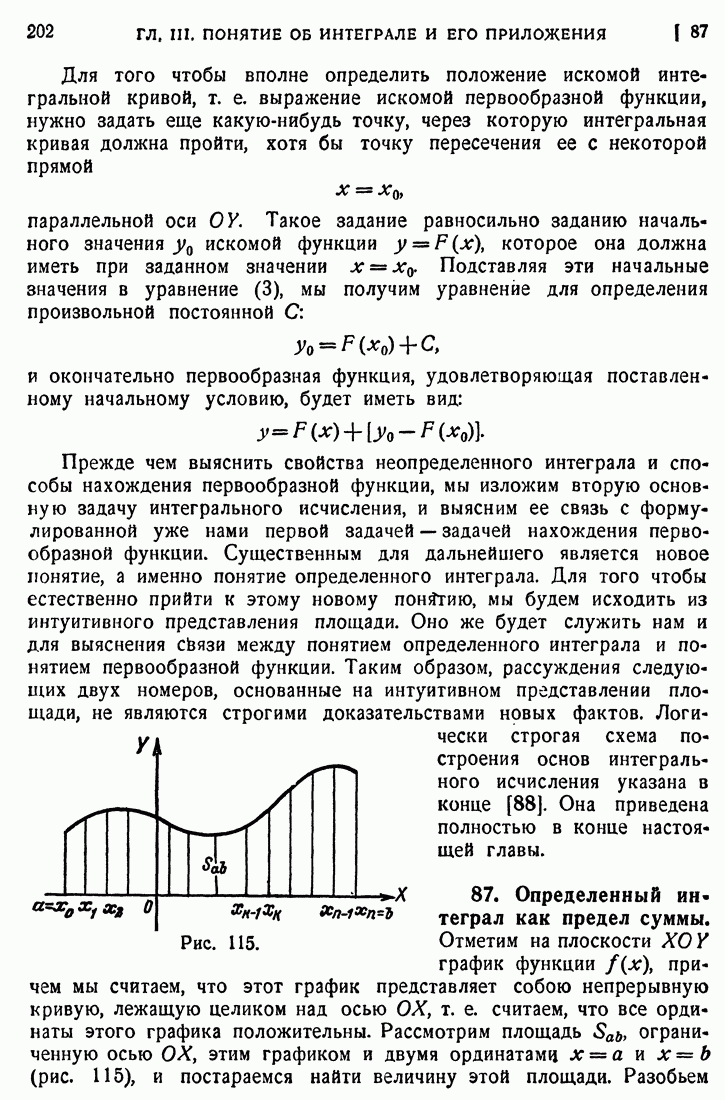
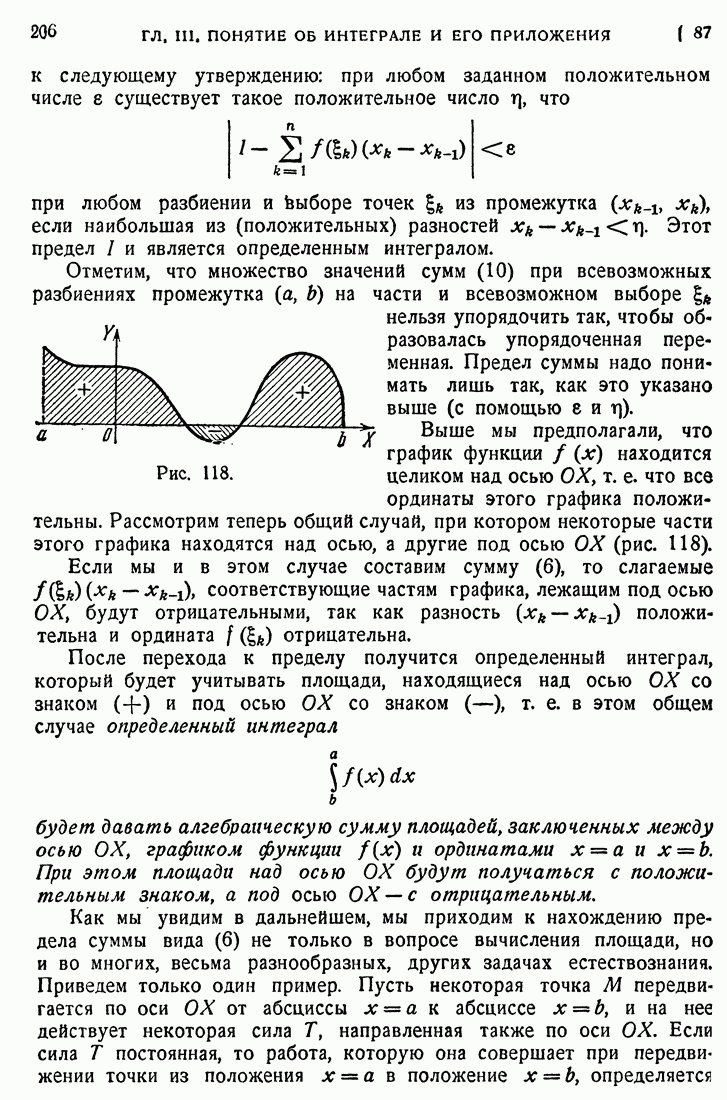
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
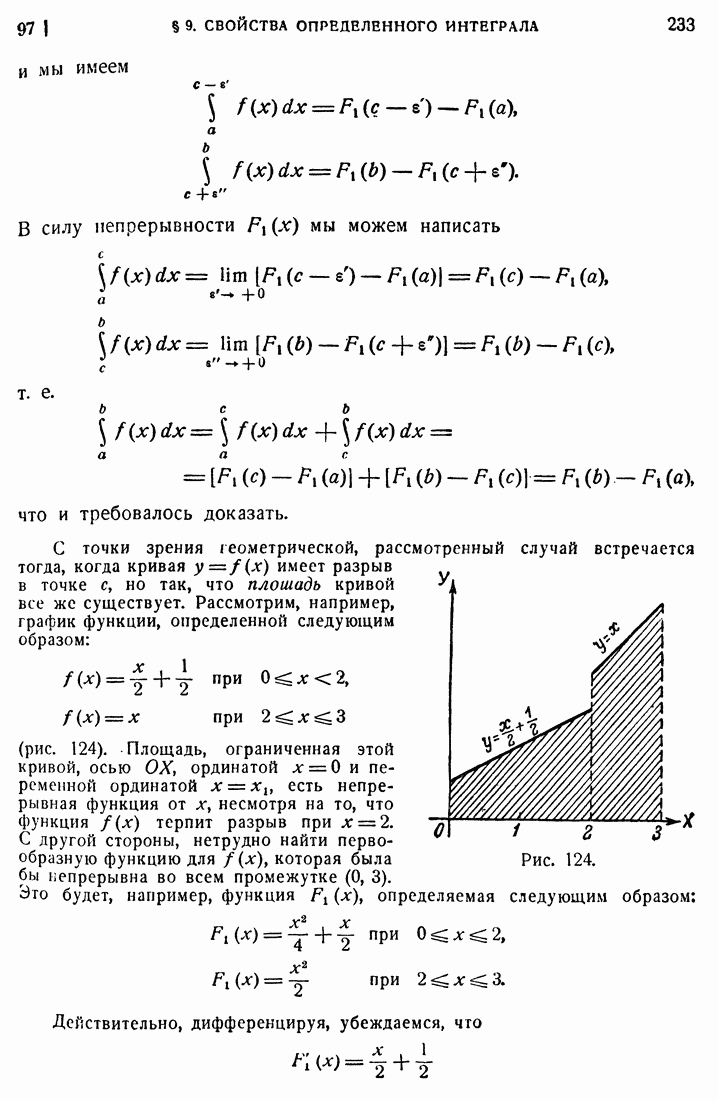
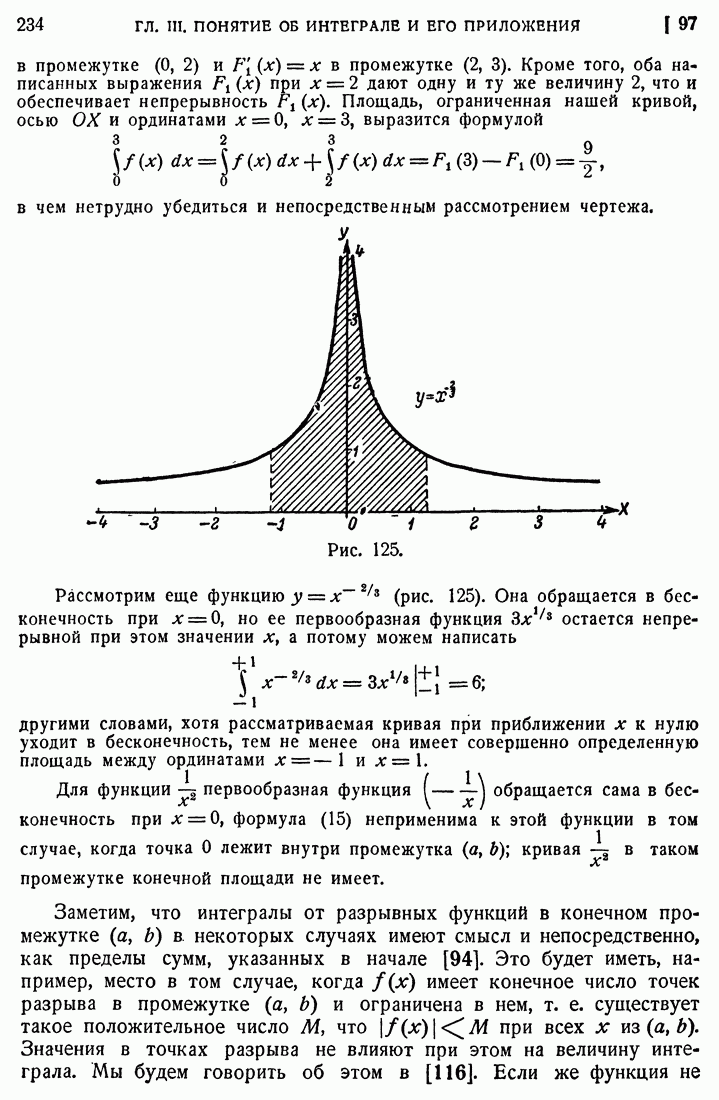
- 97. Разрыв подынтегральной функции.
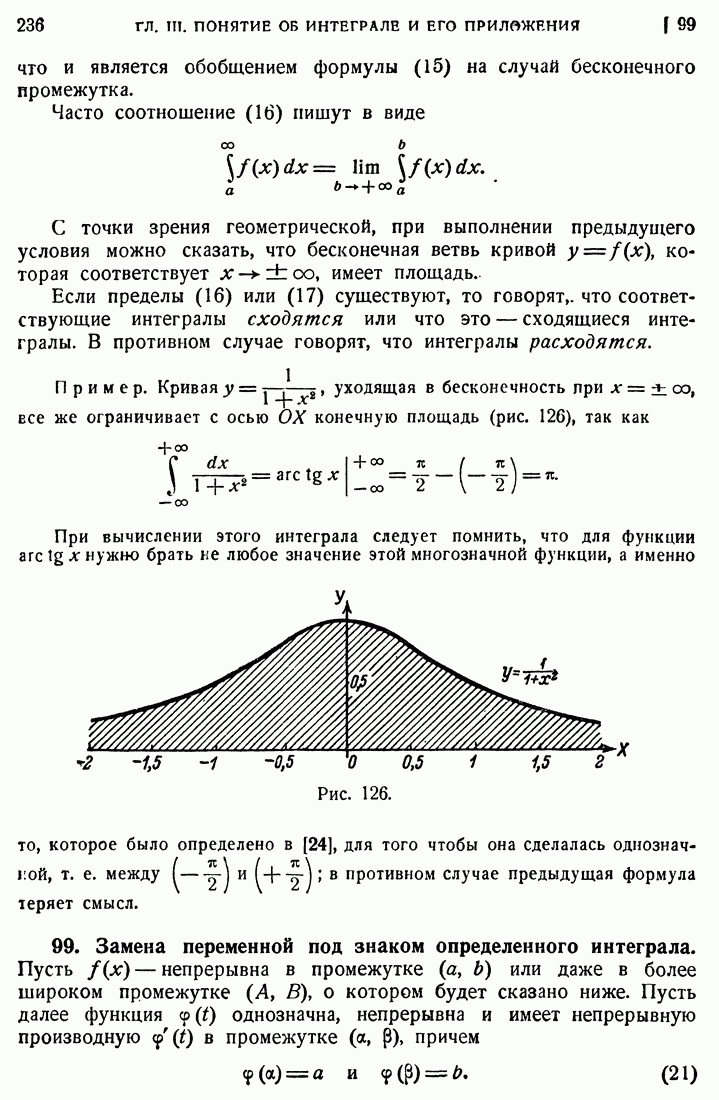
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
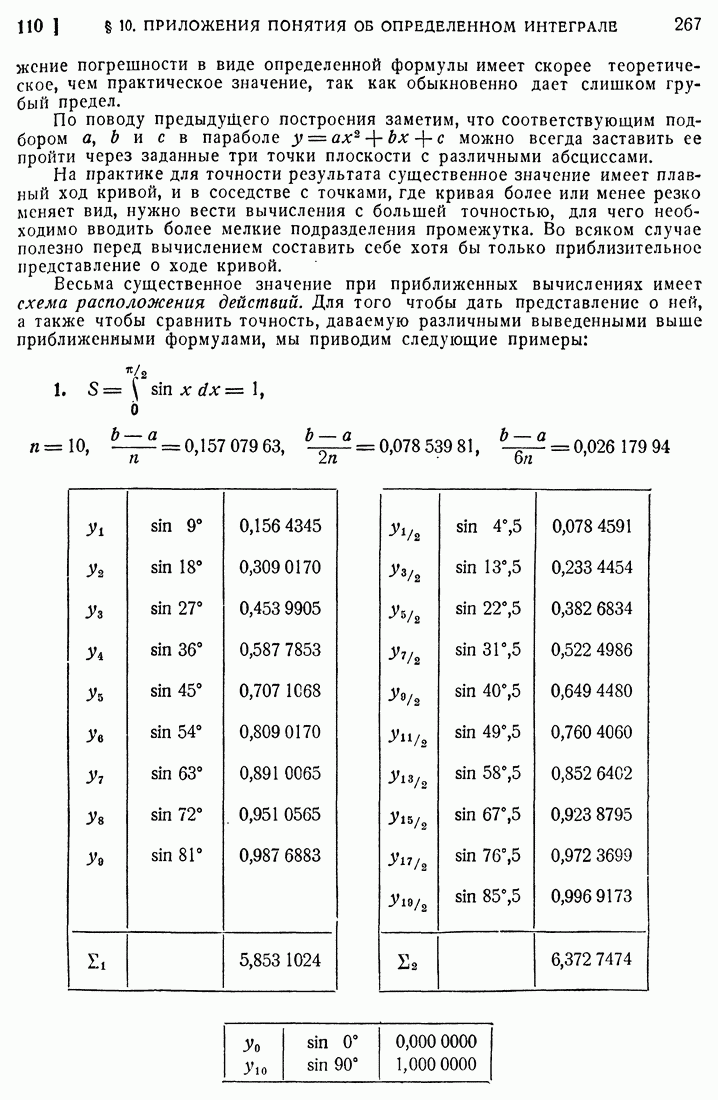
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
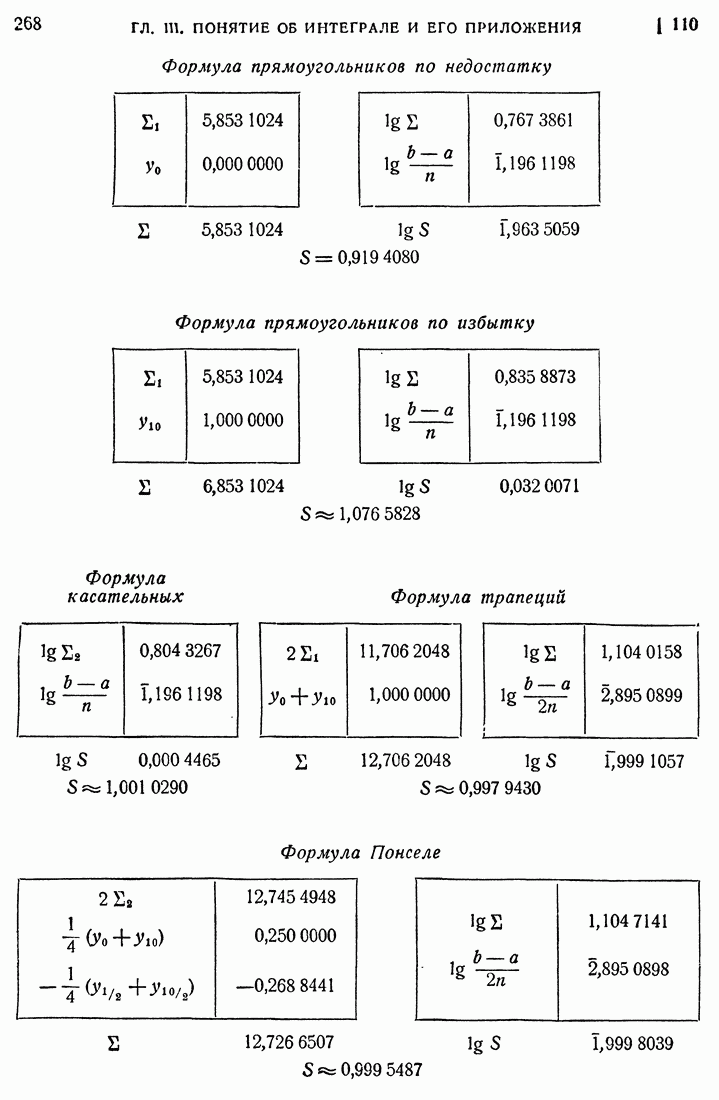
- 109. Формула касательных и формула Понселе.
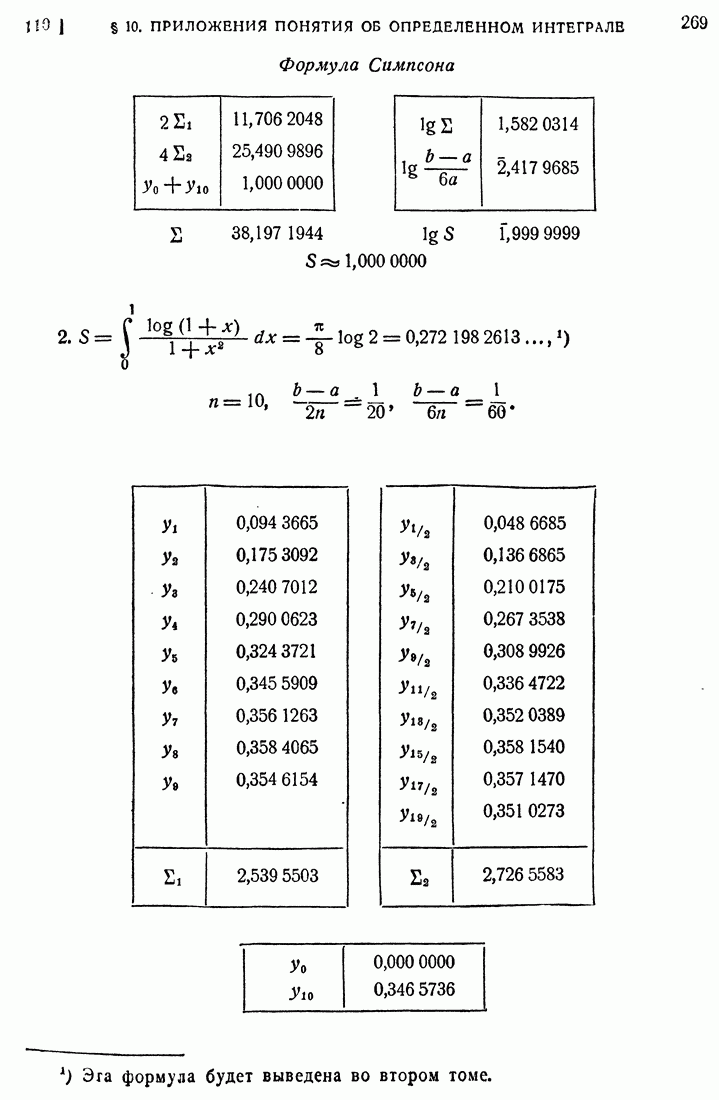
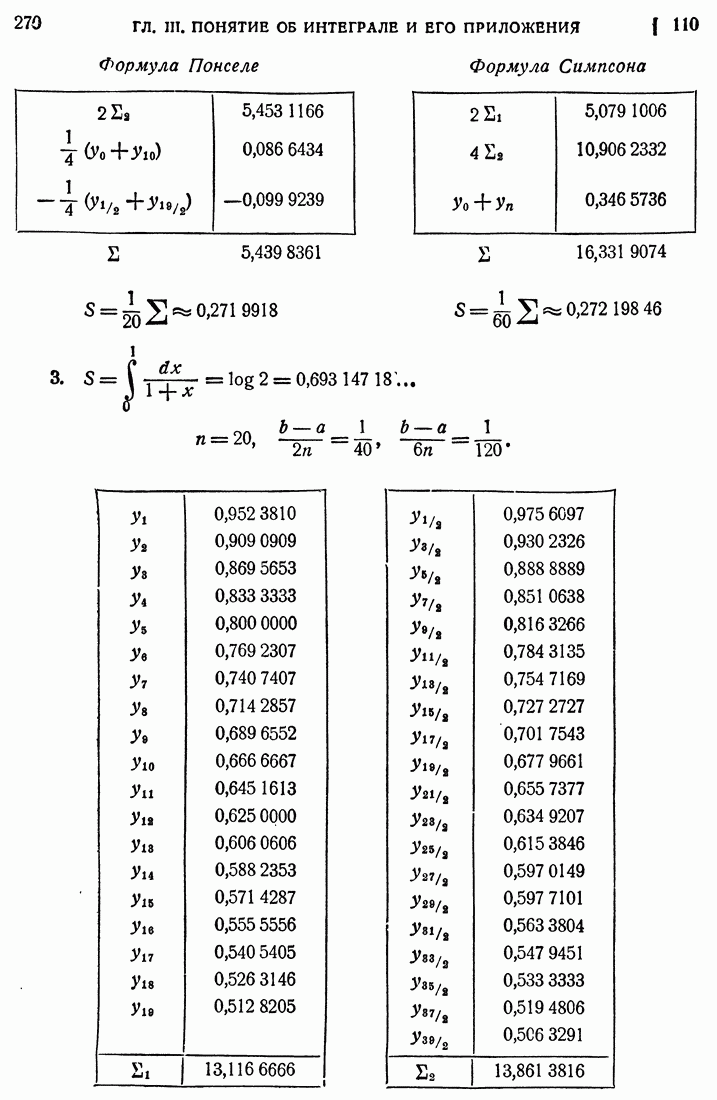
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
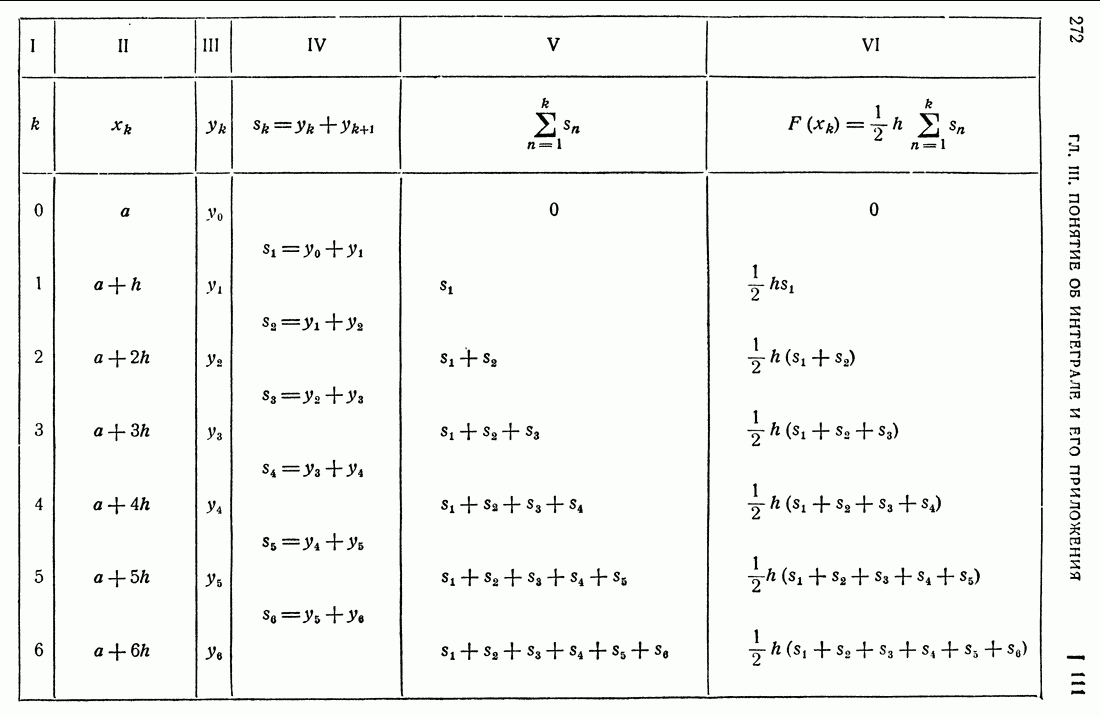
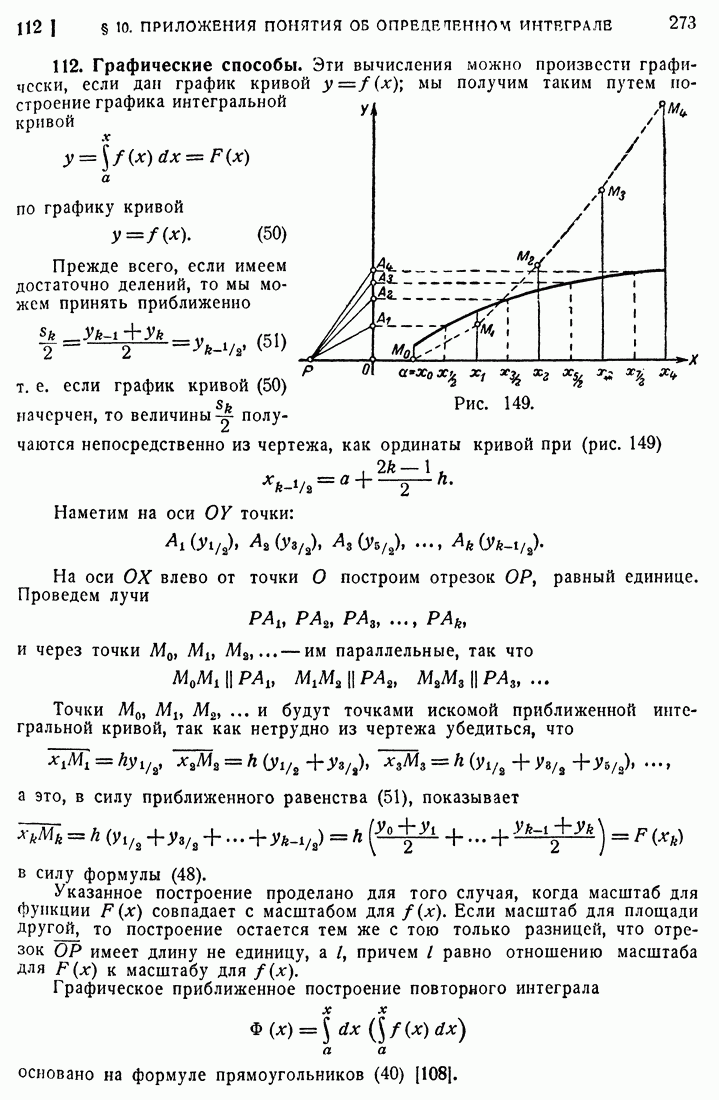
- 112. Графические способы.
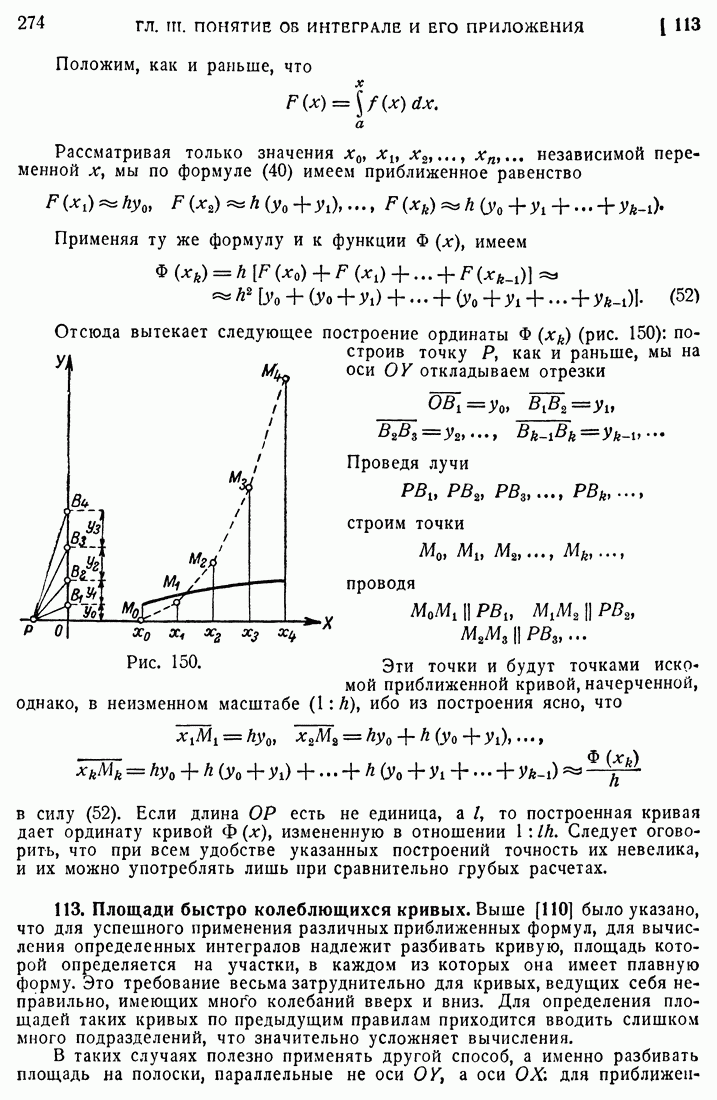
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
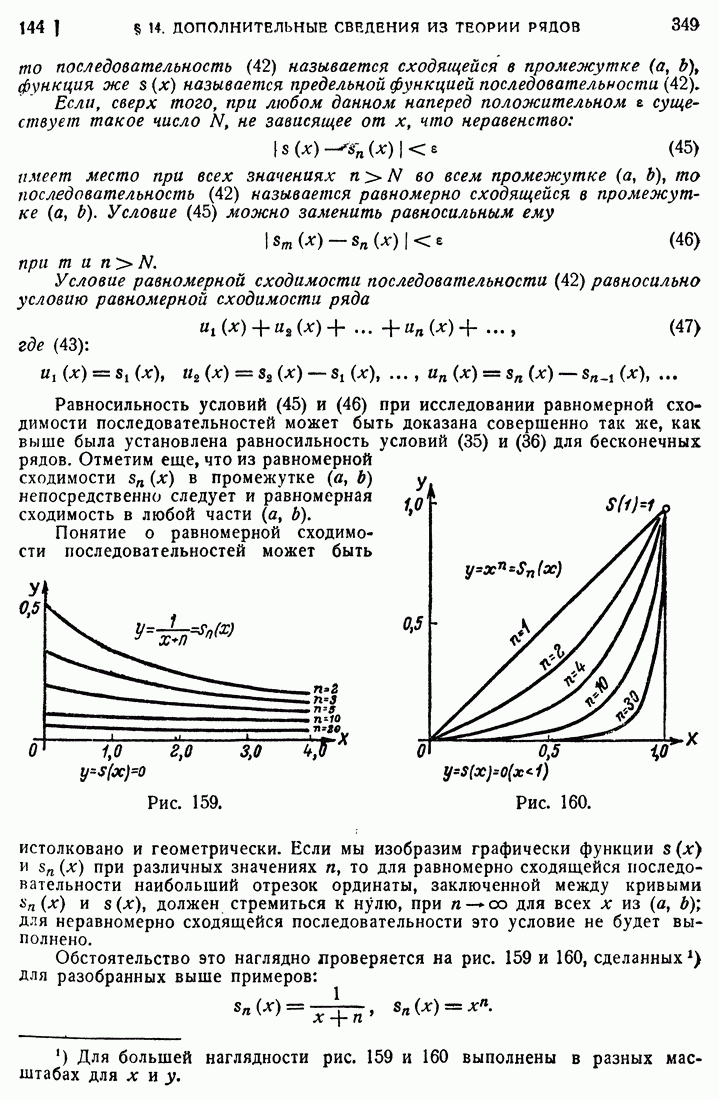
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
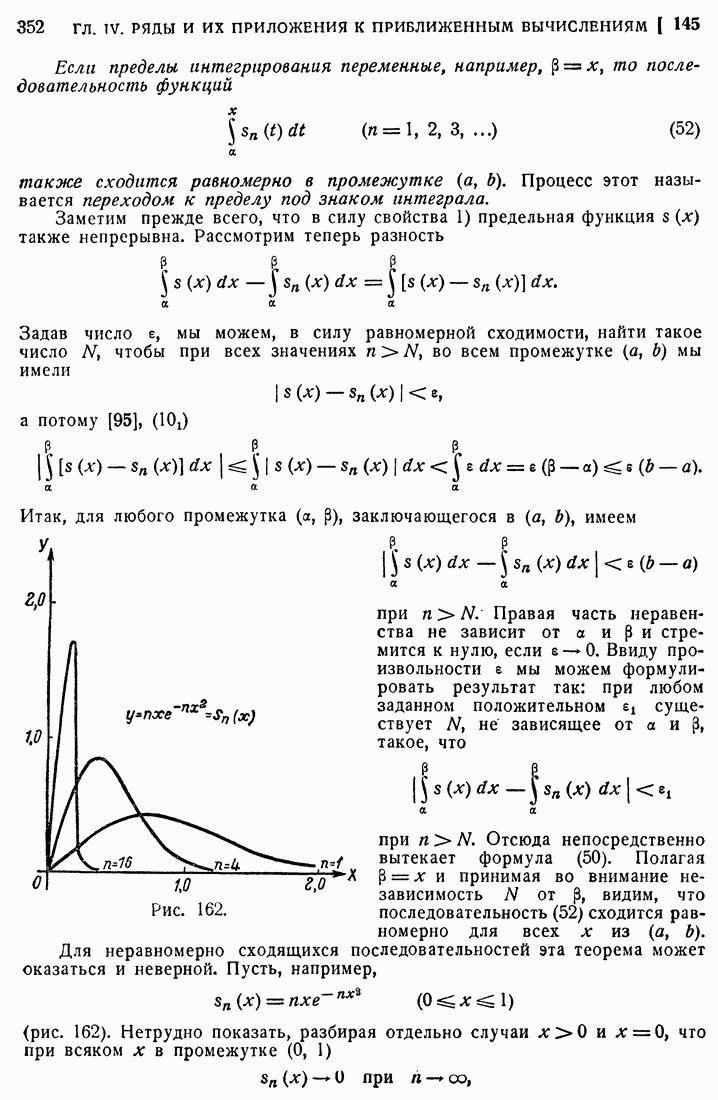
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
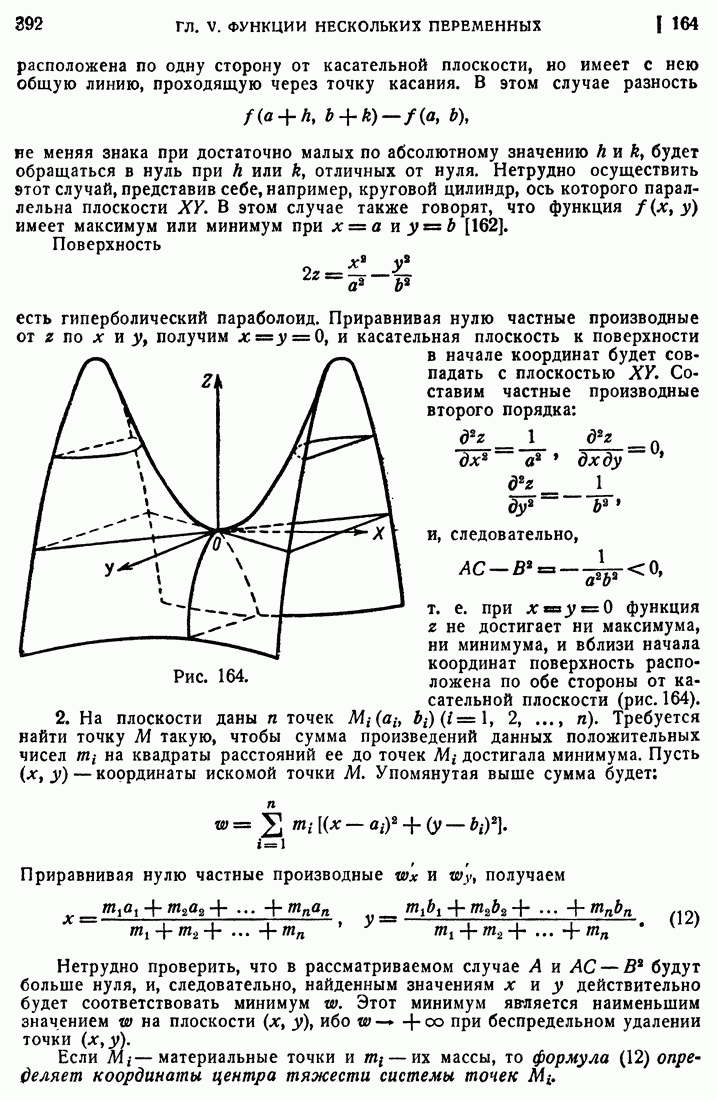
- 163. Исследование максимума и минимума функции двух независимых переменных.
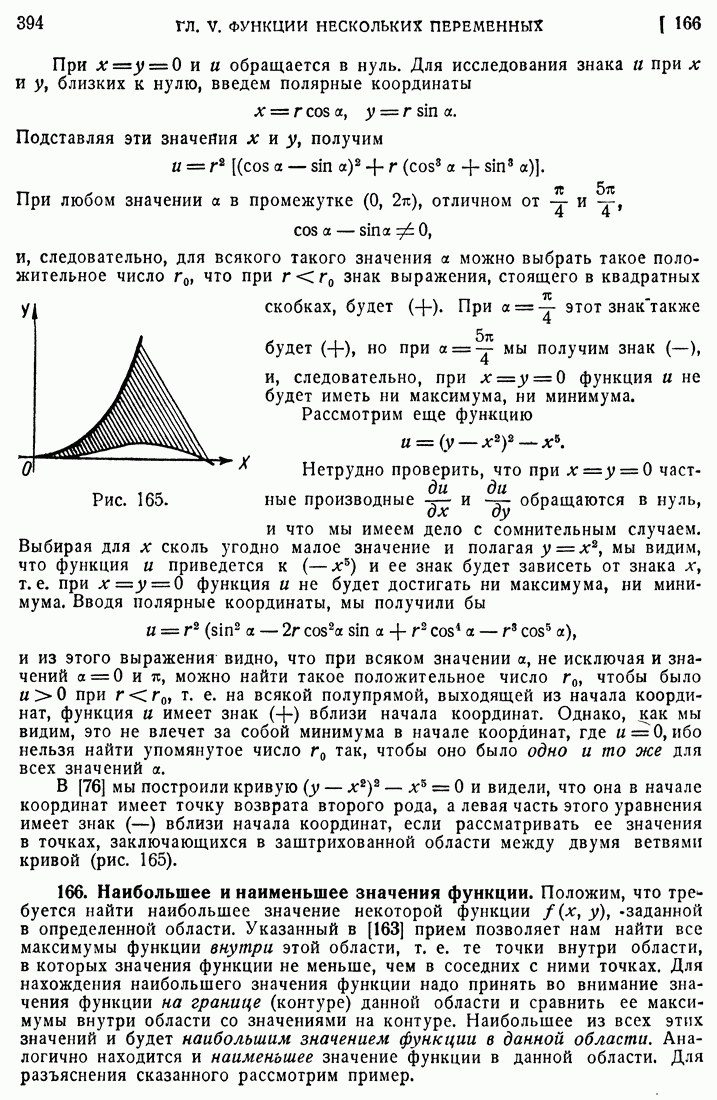
- 164. Примеры.
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
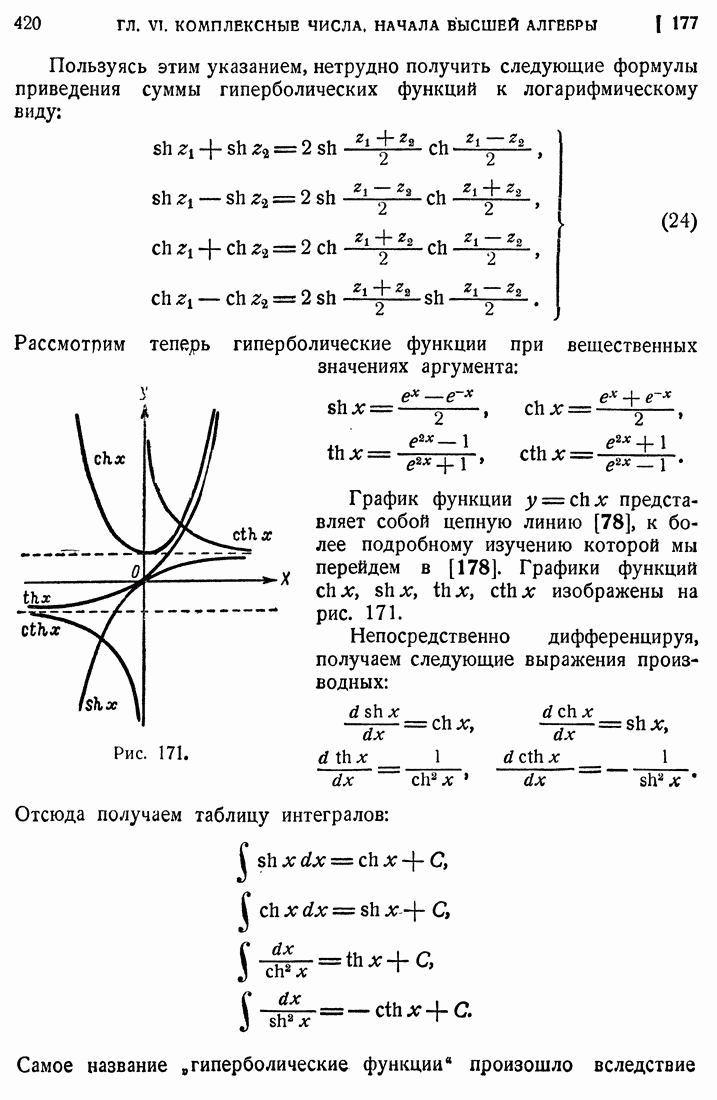
- 177. Тригонометрические и гиперболические функции.
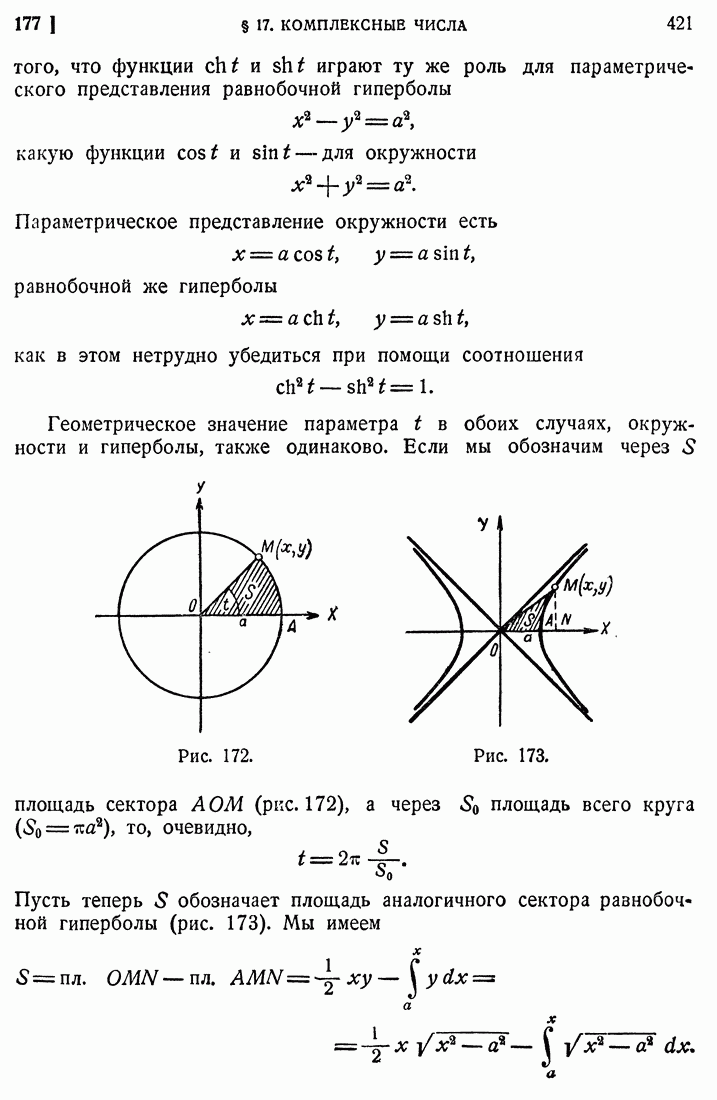
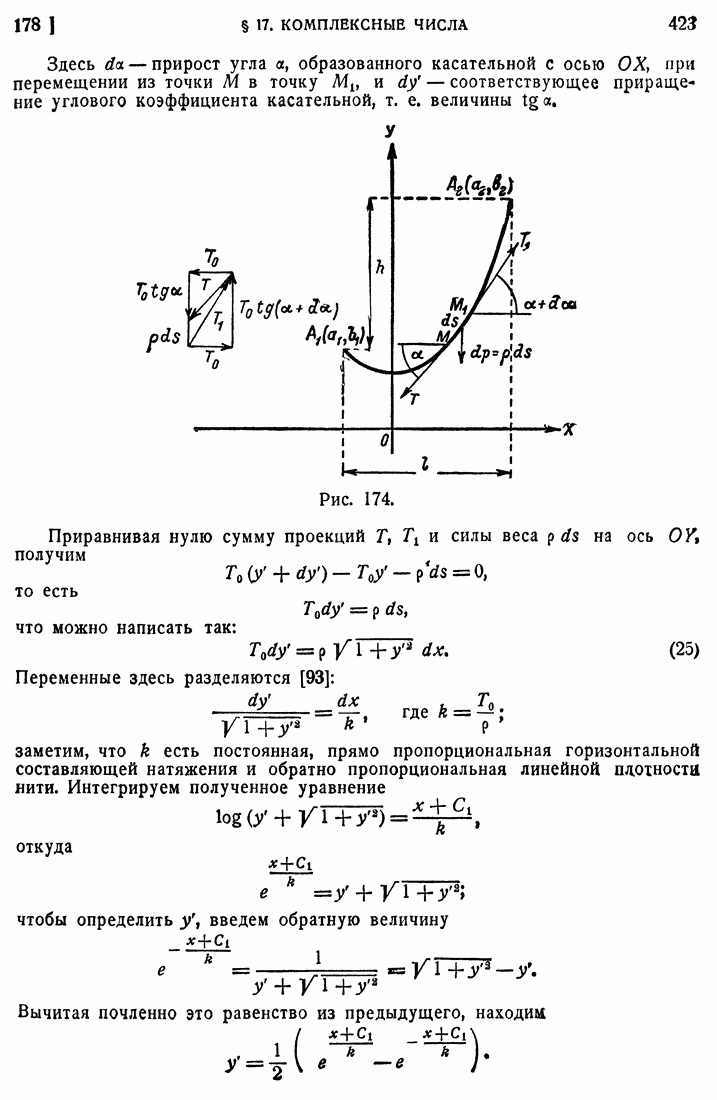
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
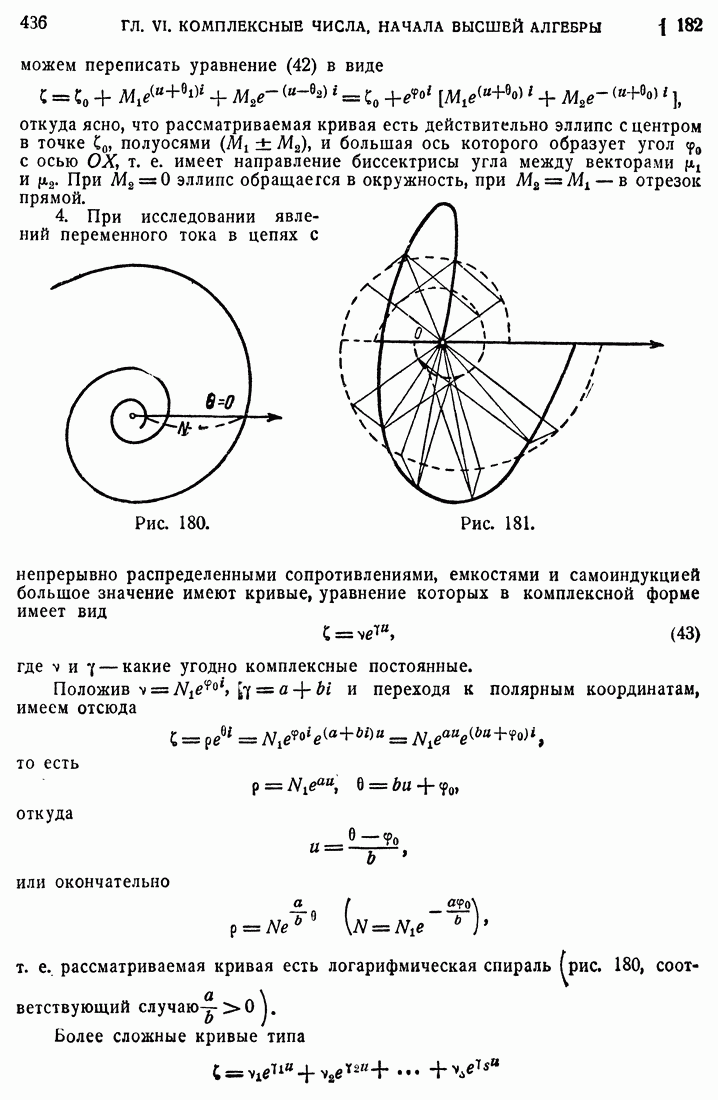
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
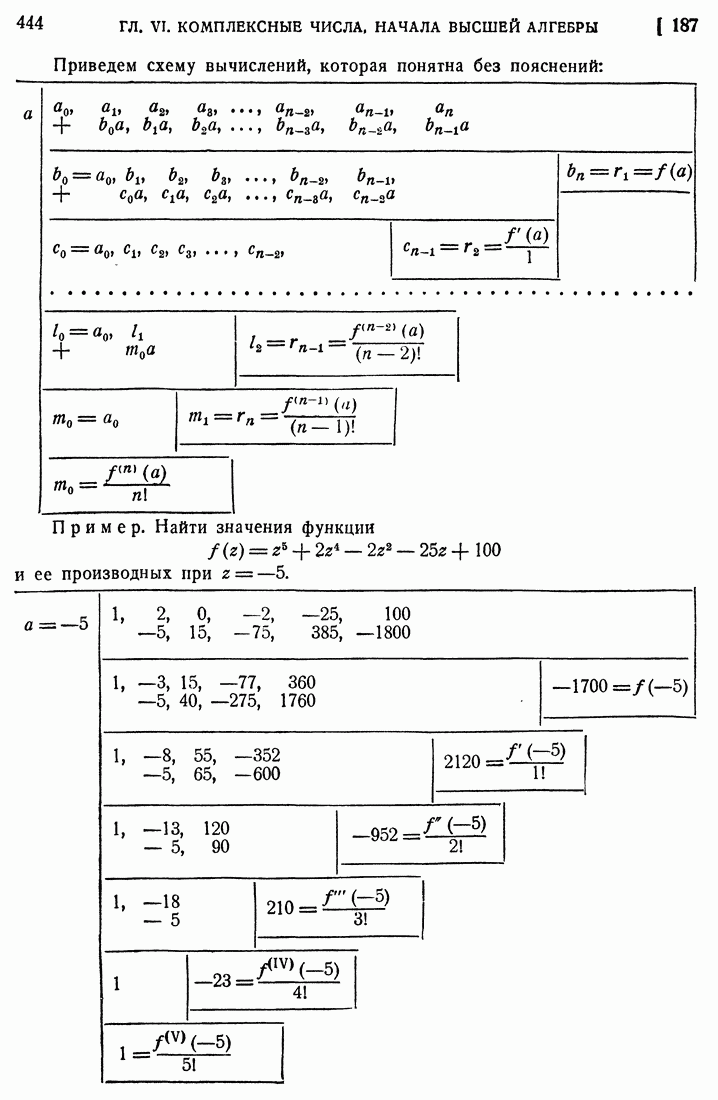
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
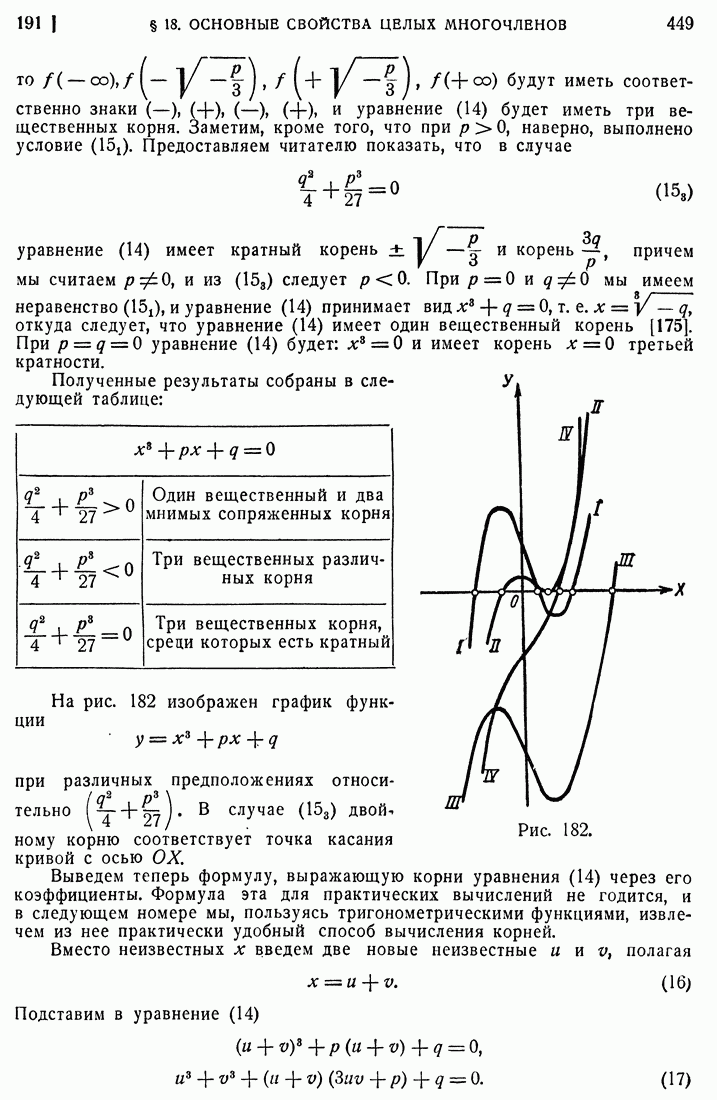
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
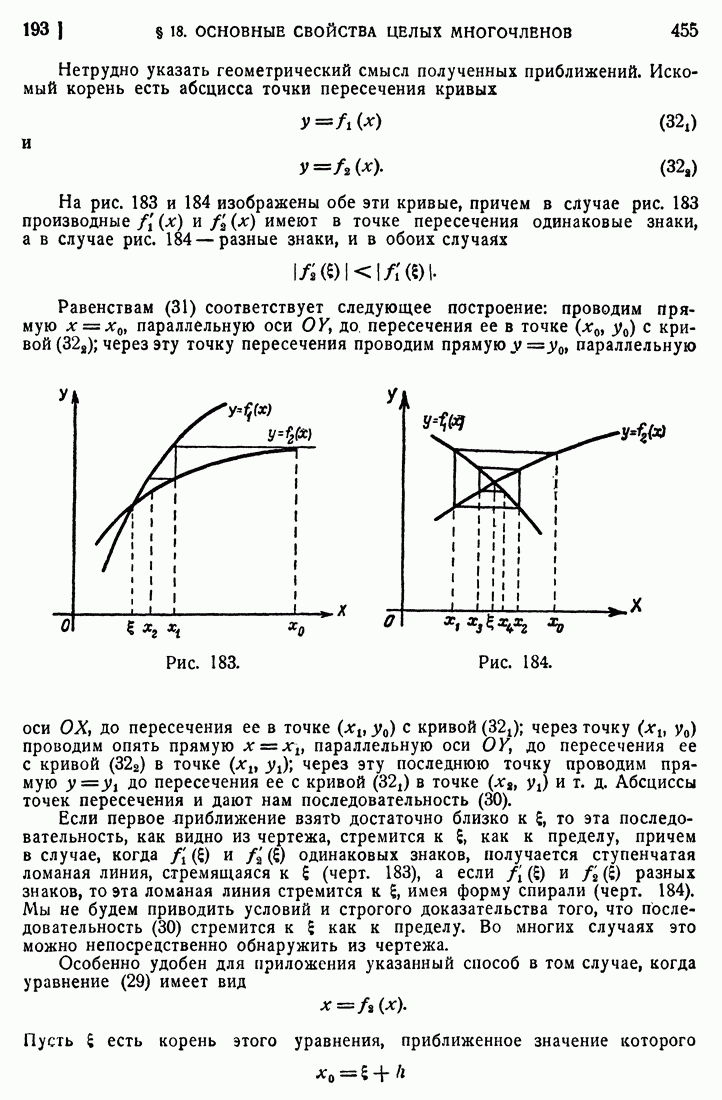
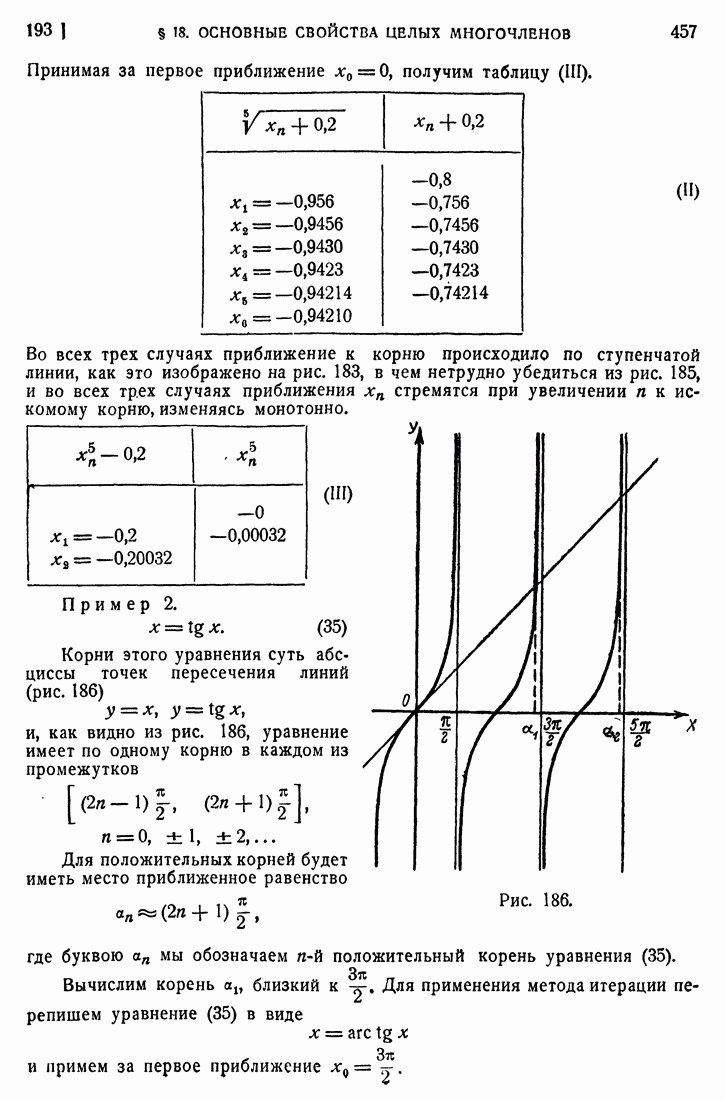
- 193. Способ итерации.
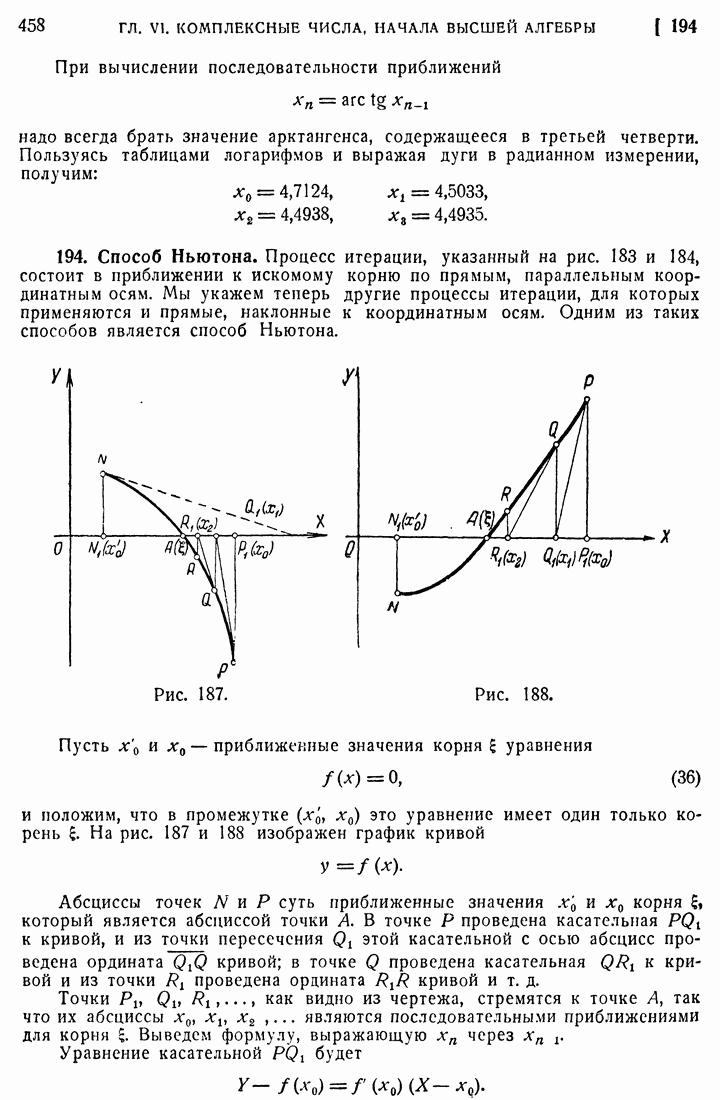
- 194. Способ Ньютона.
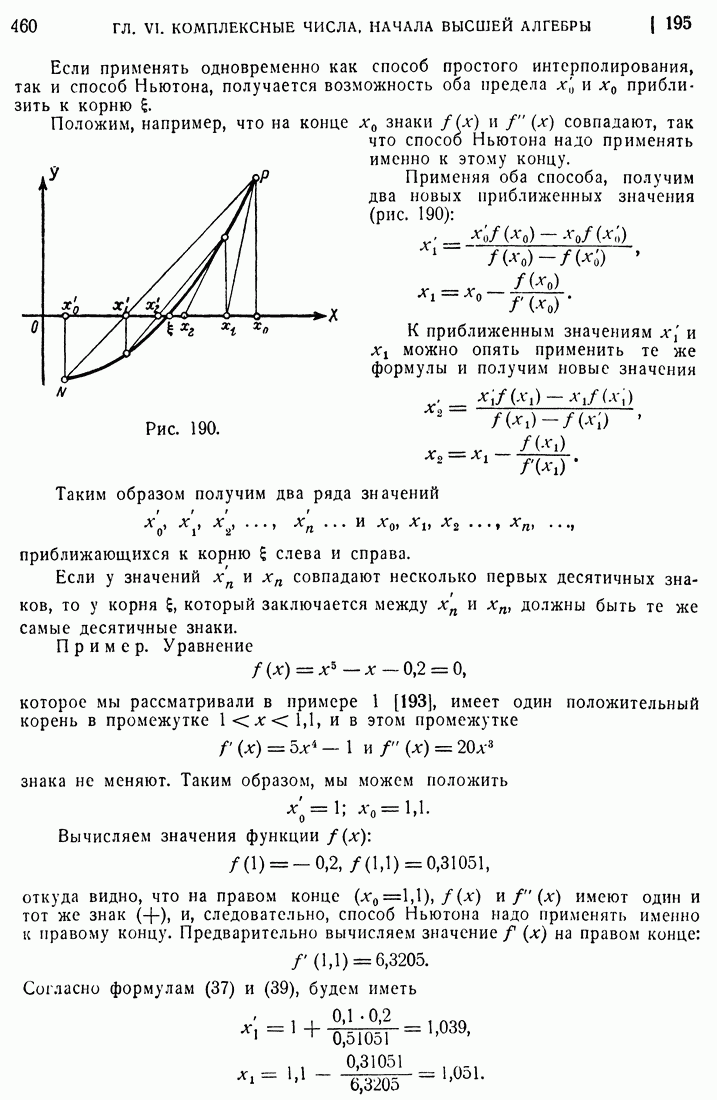
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…