| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
199. Интегралы вида...
Интегралы вида

где R — рациональная функция своих аргументов, приводятся к интегралам от рациональной дроби при помощи подстановок Эйлера. В случае можно пользоваться первой подстановкой Эйлера:

Возвышая обе части этого равенства в квадрат и решая относительно  получим
получим

откуда видно, что  будут рациональными функциями от t и, следовательно, интеграл (8) приведется к интегралу от рациональной дроби.
будут рациональными функциями от t и, следовательно, интеграл (8) приведется к интегралу от рациональной дроби.
В случае  можно пользоваться второй подстановкой Эйлера:
можно пользоваться второй подстановкой Эйлера:

Предлагаем читателю убедиться в этом.
В случае  трехчлен
трехчлен  должен иметь вещественные корни
должен иметь вещественные корни  ибо в противном случае он имел бы при всех вещественных значениях
ибо в противном случае он имел бы при всех вещественных значениях  знак
знак  с был бы величиной мнимой. В случае вещественности корней упомянутого трехчлена интеграл (8) приводится к интегралу от рациональной дроби при помощи третьей подстановки Эйлера:
с был бы величиной мнимой. В случае вещественности корней упомянутого трехчлена интеграл (8) приводится к интегралу от рациональной дроби при помощи третьей подстановки Эйлера:

в чем и предлагаем убедиться читателю.
Подстановки Эйлера приводят большей частью к сложным выкладкам, а потому мы укажем другой прием вычисления интеграла (8). Обозначим для краткости письма:

Всякая положительная четная степень у представляет собою многочлен от  а потому подынтегральную функцию нетрудно привести к виду
а потому подынтегральную функцию нетрудно привести к виду

где  многочлен от
многочлен от  Освобождаясь от иррациональности в знаменателе и совершая элементарные преобразования, можно преобразовать написанное выражение к виду
Освобождаясь от иррациональности в знаменателе и совершая элементарные преобразования, можно преобразовать написанное выражение к виду

Первое слагаемое есть рациональная дробь, интегрировать которую мы уже умеем. Выделяя из дроби  целую часть и разлагая оставшуюся правильную дробь на простейшие, мы придем к интегралам вида
целую часть и разлагая оставшуюся правильную дробь на простейшие, мы придем к интегралам вида

и

где  многочлен от
многочлен от 
При этом мы предполагаем, что многочлен  имеет лишь вещественные корни.
имеет лишь вещественные корни.
Прежде чем переходить к рассмотрению интегралов (9) и (10), отметим два простейших частных случая интеграла (9):

Формулу (11) нетрудно получить при помощи первой подстановки Эйлера. Интеграл (12) уже был нами разобран раньше [92].
Для вычисления интеграла (9) удобно пользоваться формулой:

где  многочлен степени на единицу ниже, чем
многочлен степени на единицу ниже, чем  — постоянная. На доказательстве формулы (13) мы останавливаться не будем. Дифференцируя соотношение (13) и освобождаясь от знаменателя, получим тождественное равенство двух многочленов, откуда и можно определить коэффициенты многочленов
— постоянная. На доказательстве формулы (13) мы останавливаться не будем. Дифференцируя соотношение (13) и освобождаясь от знаменателя, получим тождественное равенство двух многочленов, откуда и можно определить коэффициенты многочленов  и постоянную
и постоянную  . Интеграл (10) приводится к интегралу (9) при помощи подстановки
. Интеграл (10) приводится к интегралу (9) при помощи подстановки

Пример.

Но

а потому

Согласно формуле (13)

Дифференцируя это соотношение и освобождаясь от знаменателя, получим тождество

откуда

и, следовательно, в силу формулы (11),

Подставляя

получим

окончательно

Интеграл (8) является частным случаем абелева интеграла, который имеет вид:

где R — рациональная функция своих аргументов и у — алгебраическая функция от  т. е. функция от
т. е. функция от  которая определяется из уравнения
которая определяется из уравнения

левая часть которого есть целый многочлен относительно  Если
Если

где  многочлен третьей или четвертой степени от
многочлен третьей или четвертой степени от  , то абелев интеграл (14) называется эллиптическим интегралом. Мы займемся этими интегралами в третьем томе. Даже и этот последний, а тем более и общий абелев интеграл, вообще говоря, не выражается через элементарные функции.. Если степень многочлена
, то абелев интеграл (14) называется эллиптическим интегралом. Мы займемся этими интегралами в третьем томе. Даже и этот последний, а тем более и общий абелев интеграл, вообще говоря, не выражается через элементарные функции.. Если степень многочлена  выше четвертой, то интеграл (14) называется гиперэллиптическим.
выше четвертой, то интеграл (14) называется гиперэллиптическим.
Если соотношение (15), которое выражает у как алгебраическую функцию от  обладает тем свойством, что х и у могут быть выражены в виде рациональных функций вспомогательного параметра t, то, очевидно, абелев интеграл (14) приводится к интегралу от рациональной дроби. В указанном случае алгебраическая кривая, соответствующая соотношению (15), называется уникурсальной. В частности, подстановки Эйлера служат доказательством уникурсальности кривой
обладает тем свойством, что х и у могут быть выражены в виде рациональных функций вспомогательного параметра t, то, очевидно, абелев интеграл (14) приводится к интегралу от рациональной дроби. В указанном случае алгебраическая кривая, соответствующая соотношению (15), называется уникурсальной. В частности, подстановки Эйлера служат доказательством уникурсальности кривой

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
- 12. Линейная функция.
- 13. Приращение. Основное свойство линейной функции.
- 14. График равномерного движения.
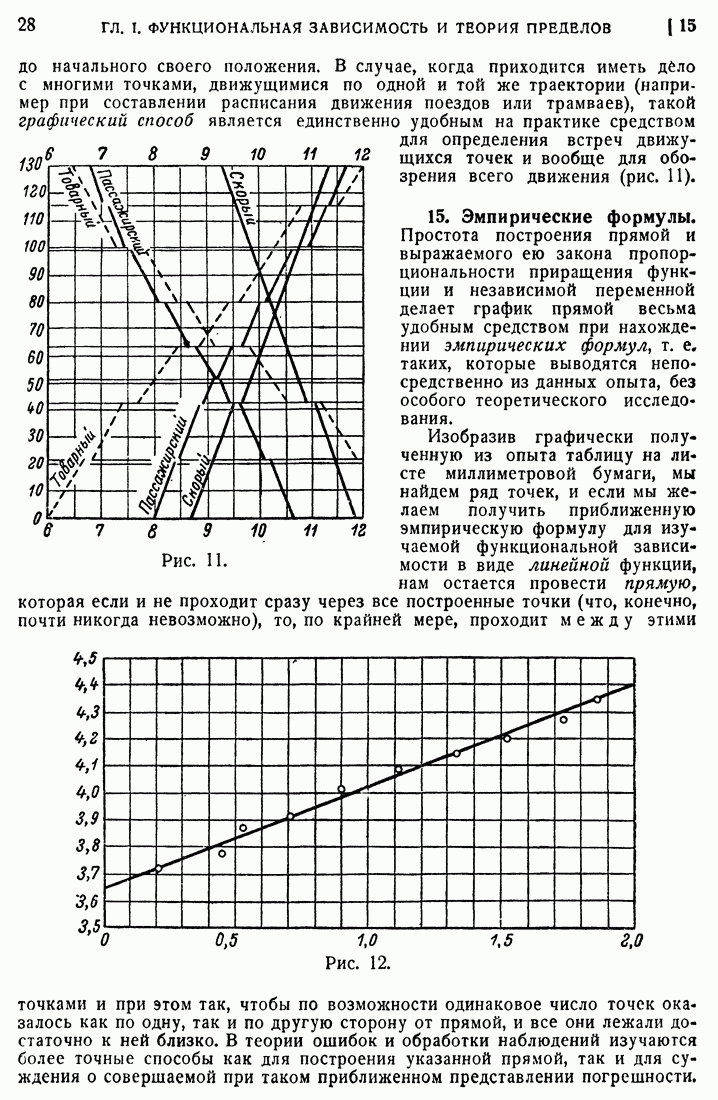
- 15. Эмпирические формулы.
- 16. Парабола второй степени.
- 17. Парабола третьей степени.
- 18. Закон обратной пропорциональности.
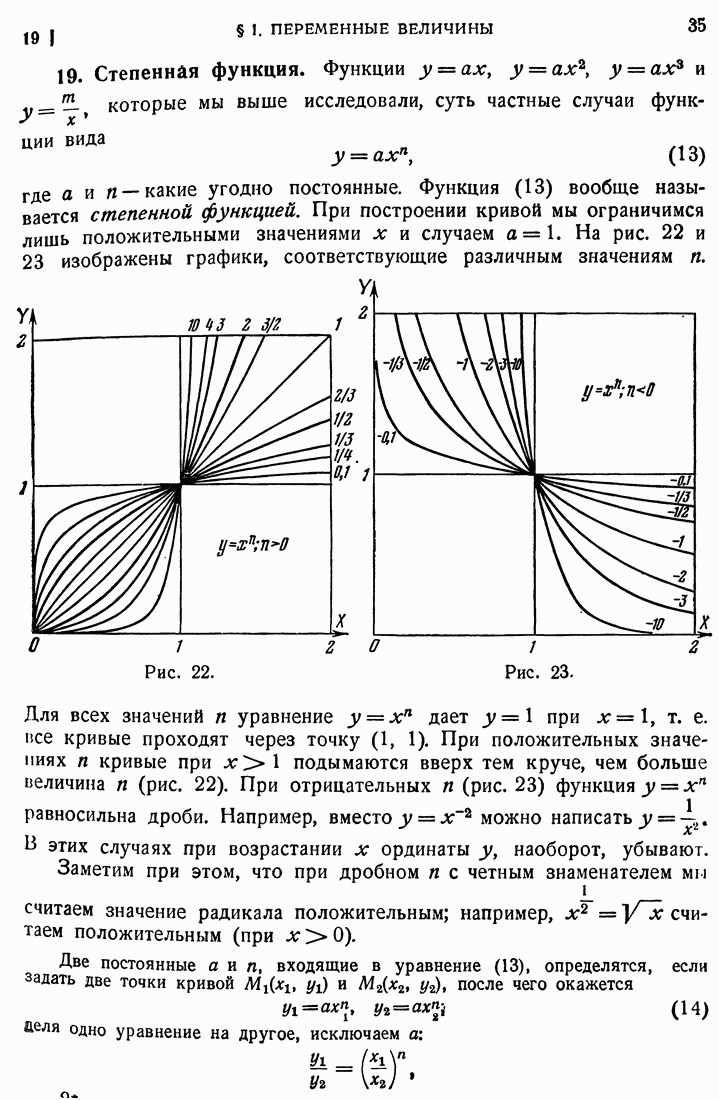
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
- 22. Показательная и логарифмическая функции.
- 23. Тригонометрические функции.
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
- 45. Понятие о производной.
- 46. Геометрическое значение производной.
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
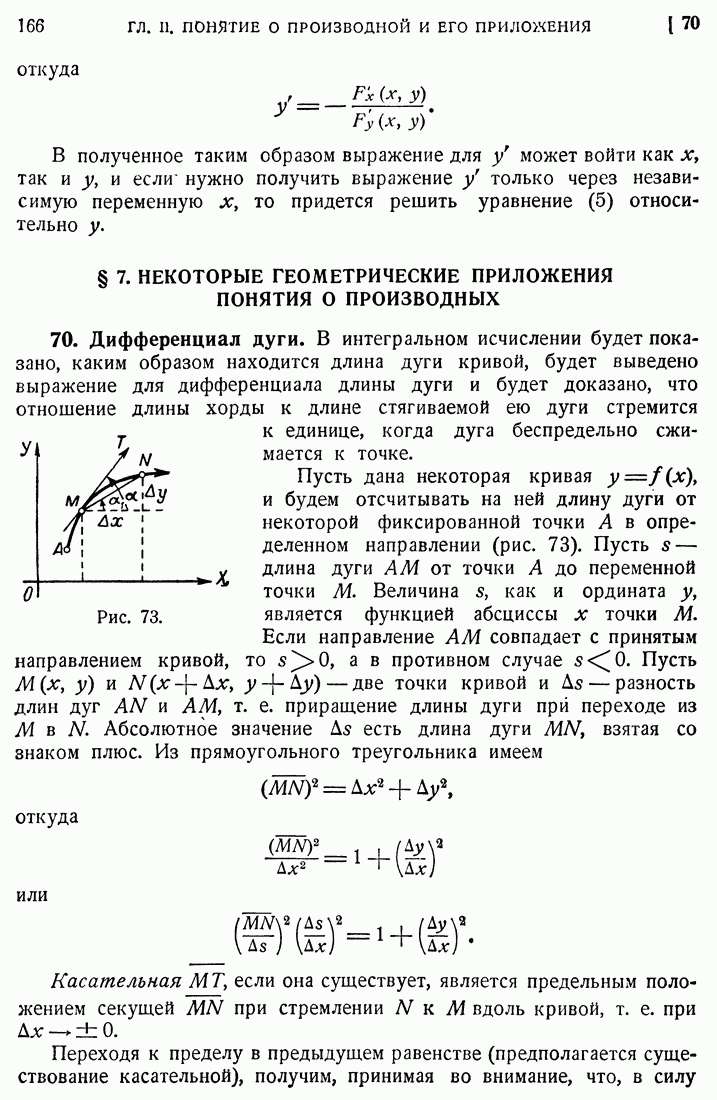
- 70. Дифференциал дуги.
- 71. Выпуклость, вогнутость и кривизна.
- 72. Асимптоты.
- 73. Построение графиков.
- 74. Параметрическое задание кривой.
- 75. Уравнение Ван-дер-Ваальса.
- 76. Особые точки кривых.
- 77. Элементы кривой.
- 78. Цепная линия.
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
- 81. Развертка круга.
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
- 97. Разрыв подынтегральной функции.
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
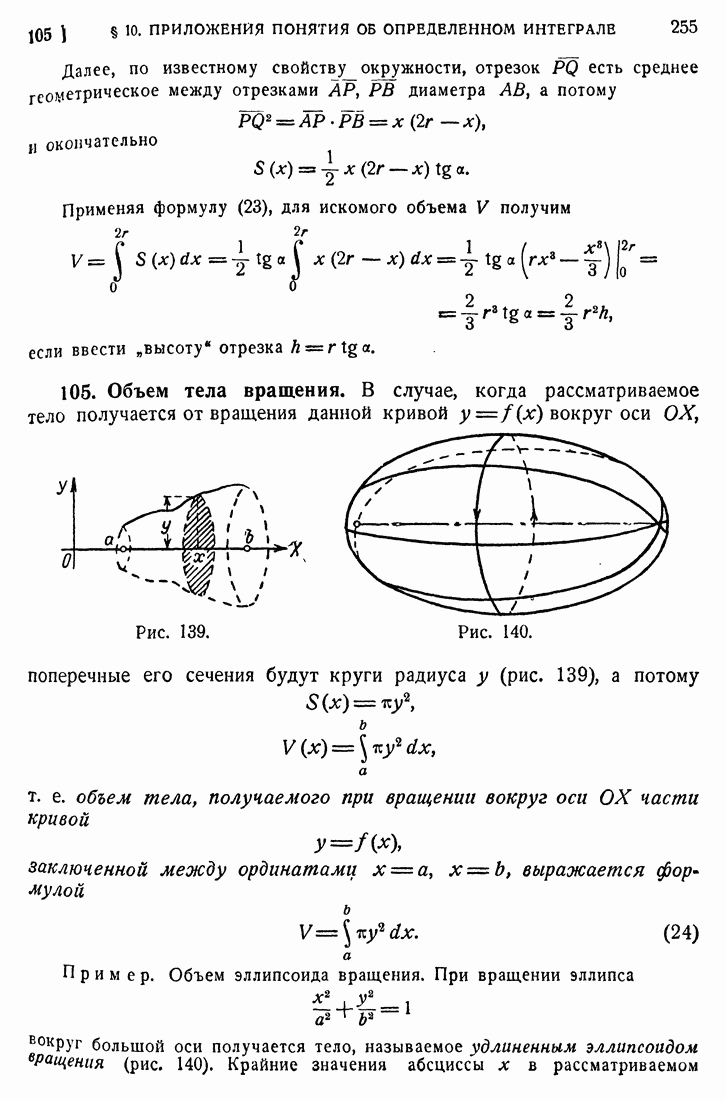
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
- 109. Формула касательных и формула Понселе.
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
- 112. Графические способы.
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
- 163. Исследование максимума и минимума функции двух независимых переменных.
- 164. Примеры.
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
- 177. Тригонометрические и гиперболические функции.
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
- 193. Способ итерации.
- 194. Способ Ньютона.
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…