| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
48. Производные сложных и обратных функций.
Напомним понятие о сложной функции  функция, непрерывная в некотором промежутке
функция, непрерывная в некотором промежутке  причем ее значения принадлежат промежутку
причем ее значения принадлежат промежутку  . Пусть далее,
. Пусть далее,  функция, непрерывная в промежутке
функция, непрерывная в промежутке  . Понимая под у вышеуказанную функцию от
. Понимая под у вышеуказанную функцию от  мы получим сложную функцию от
мы получим сложную функцию от 

Говорят, что эта функция зависит от  через посредство у. Нетрудно видеть, что эта функция будет непрерывна в промежутке
через посредство у. Нетрудно видеть, что эта функция будет непрерывна в промежутке  . Действительно, бесконечно малому приращению
. Действительно, бесконечно малому приращению  соответствует бесконечно малое приращение у в силу непрерывности функции
соответствует бесконечно малое приращение у в силу непрерывности функции  а бесконечно малому приращению у соответствует бесконечно малое приращение z в силу непрерывности F(у).
а бесконечно малому приращению у соответствует бесконечно малое приращение z в силу непрерывности F(у).
Прежде чем переходить к выводу правила дифференцирования сложной функции сделаем одно замечание. Если  имеет производную при
имеет производную при  то, согласно сказанному в [45], мы можем написать
то, согласно сказанному в [45], мы можем написать

где переменная а есть функция  определенная при всех
определенная при всех  достаточно близких к нулю и отличных от нуля, причем
достаточно близких к нулю и отличных от нуля, причем  если
если  оставаясь отличным от нуля. Равенство (3) остается справедливым для
оставаясь отличным от нуля. Равенство (3) остается справедливым для  при любом выборе а, ибо при
при любом выборе а, ибо при  . В силу сказанного выше естественно положить
. В силу сказанного выше естественно положить  при
при  . При таком соглашении мы можем считать, что в формуле (3) а
. При таком соглашении мы можем считать, что в формуле (3) а  если
если  любым образом, даже и принимая значение, равное нулю. Формулируем теперь теорему о производной сложной функции.
любым образом, даже и принимая значение, равное нулю. Формулируем теперь теорему о производной сложной функции.
Теорема. Если  имеет в точке
имеет в точке  производную
производную  имеет в точке
имеет в точке  производную
производную  то сложная функция
то сложная функция  имеет в точке
имеет в точке  производную, равную произведению
производную, равную произведению 
Пусть  приращение (отличное от нуля), которое мы придаем значению
приращение (отличное от нуля), которое мы придаем значению  независимой переменной
независимой переменной  соответствующее приращение переменной у (оно может оказаться и равным нулю). Пусть, далее,
соответствующее приращение переменной у (оно может оказаться и равным нулю). Пусть, далее,  Производная от сложной функции
Производная от сложной функции  по
по  при
при  равна, очевидно, пределу отношения при
равна, очевидно, пределу отношения при  если этот предел существует.
если этот предел существует.
Разделим обе части (3) на 

При стремлении  к нулю и
к нулю и  в силу непрерывности функции
в силу непрерывности функции  в точке
в точке  , а потому, как мы указали выше,
, а потому, как мы указали выше,  . Отношение стремится при этом к производной
. Отношение стремится при этом к производной  и, переходя в написанном выше равенстве к пределу, получим
и, переходя в написанном выше равенстве к пределу, получим

что и доказывает теорему. Отметим, что непрерывность  при
при  вытекает из предположенного существования производной
вытекает из предположенного существования производной  [45].
[45].
Доказанная теорема может быть формулирована в виде следующего правила дифференцирования сложных функций: производная сложной функции равна произведению производной по промежуточной переменной на производную от промежуточной переменной по независимой переменной:

Переходим к правилу дифференцирования обратных функций. Если  непрерывна и возрастает в промежутке (а, b) (т. е. большим значениям х соответствуют и большие у), причем
непрерывна и возрастает в промежутке (а, b) (т. е. большим значениям х соответствуют и большие у), причем  то, как мы знаем [21 и 44], в промежутке
то, как мы знаем [21 и 44], в промежутке  существует однозначная и непрерывная обратная, также возрастающая функция
существует однозначная и непрерывная обратная, также возрастающая функция  . В силу возрастания, если
. В силу возрастания, если  , то и
, то и  , и наоборот, и в силу непрерывности из
, и наоборот, и в силу непрерывности из  следует
следует  и наоборот. (Совершенно аналогично рассматривается случай убывающих функций).
и наоборот. (Совершенно аналогично рассматривается случай убывающих функций).
Теорема. Если  имеет в точке
имеет в точке  производную
производную  отличную от нуля, то обратная функция
отличную от нуля, то обратная функция  имеет в точке
имеет в точке  производную
производную

Обозначая через  соответствующие приращения
соответствующие приращения 

и принимая во внимание, что оба они отличны от нуля, можем написать:

Как мы видели выше,  одновременно стремятся к нулю, и последнее равенство в пределе и приводит к (4). Доказанная теорема может быть формулирована в виде следующего правила дифференцирования обратных функций: производная обратной функции равна единице, деленной на производную первоначальной функции в соответствующей точке.
одновременно стремятся к нулю, и последнее равенство в пределе и приводит к (4). Доказанная теорема может быть формулирована в виде следующего правила дифференцирования обратных функций: производная обратной функции равна единице, деленной на производную первоначальной функции в соответствующей точке.

Рис. 53.
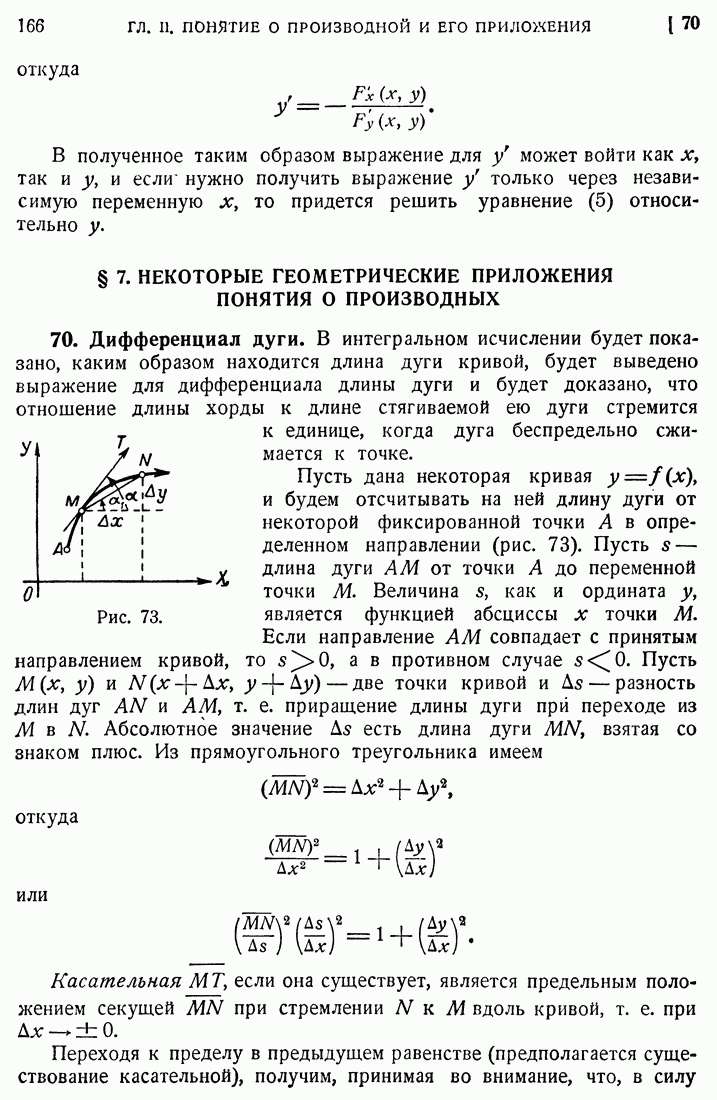
Правило дифференцирования обратных функций имеет простое геометрическое истолкование [21]. Функции  имеют один и тот же график на плоскости XOY с той лишь разницей, что для функции
имеют один и тот же график на плоскости XOY с той лишь разницей, что для функции  ось независимой переменной есть ось
ось независимой переменной есть ось  , а не ОХ (рис. 53). Проводя касательную МТ и вспоминая геометрическое значение производной, получим
, а не ОХ (рис. 53). Проводя касательную МТ и вспоминая геометрическое значение производной, получим

причем на рис. 53 угол  , как и а, считается положительным. Но, очевидно,
, как и а, считается положительным. Но, очевидно,  следовательно,
следовательно,

Если  есть функция, обратная
есть функция, обратная  то, очевидно, и наоборот — функцию
то, очевидно, и наоборот — функцию  можно считать обратной функции
можно считать обратной функции

Применим правило дифференцирования обратных функций к показательной функции.

Обратная функция в данном случае будет  и, в силу VII,
и, в силу VII,

откуда по правилу дифференцирования обратных функций

В частном случае при  имеем
имеем

Полученная формула, вместе с правилом дифференцирования сложных функций, даст нам возможность вычислить производную от степенной функции.
XIV.  ;
;  — любое вещественное число).
— любое вещественное число).
Эта функция при всех  определена и имеет положительные значения [191.
определена и имеет положительные значения [191.
Пользуясь определением логарифма, мы можем представить нашу функцию в виде сложной функции

Дифференцируя по правилу дифференцирования сложных функций, получим

Этот результат нетрудно обобщить и на случай отрицательных значений  если только сама функция при этом существует, например,
если только сама функция при этом существует, например, 
Применим правило дифференцирования обратных функций к нахождению производных обратных круговых функций.

Мы рассматриваем главное значение [24] этой функции, т. е. ту дугу, которая находится в промежутке —у, Функцию эту можно рассматривать как обратную функцию по отношению к функции  и, согласно правилу дифференцирования обратных функций, имеем
и, согласно правилу дифференцирования обратных функций, имеем

причем у радикала надо брать знак  , так как
, так как  имеет знак
имеет знак  в промежутке
в промежутке  , Точно так же можно получить
, Точно так же можно получить

причем рассматривается главное значение  т. е. та дуга, которая заключается в промежутке
т. е. та дуга, которая заключается в промежутке  .
.

Главное значение  заключается в промежутке
заключается в промежутке  , и функцию эту можно рассматривать как обратную по отношению к функции
, и функцию эту можно рассматривать как обратную по отношению к функции  следовательно,
следовательно,

Точно так же получим

XVII. Рассмотрим еще дифференцирование функций вида:

где  — функции от х (степенно-показательная функция).
— функции от х (степенно-показательная функция).
Мы можем написать

и, применяя правило дифференцирования сложных функций, получим

Применяя правило дифференцирования произведения и дифференцируя  , как сложную функцию от
, как сложную функцию от  будем иметь окончательно
будем иметь окончательно

или

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
- 12. Линейная функция.
- 13. Приращение. Основное свойство линейной функции.
- 14. График равномерного движения.
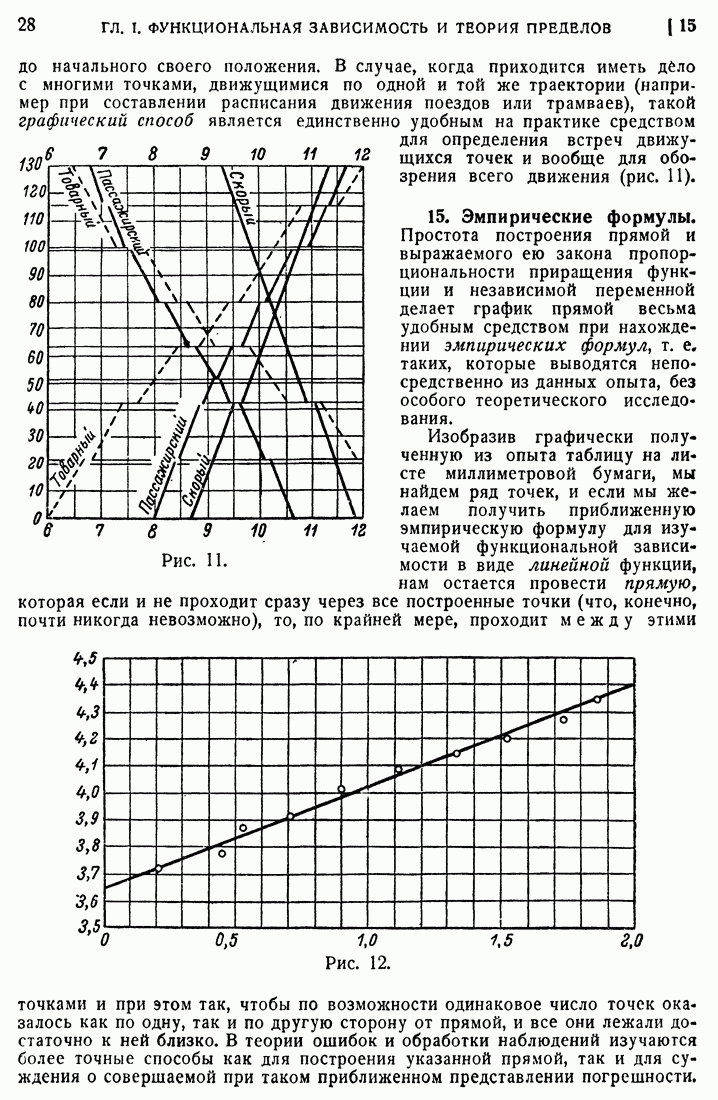
- 15. Эмпирические формулы.
- 16. Парабола второй степени.
- 17. Парабола третьей степени.
- 18. Закон обратной пропорциональности.
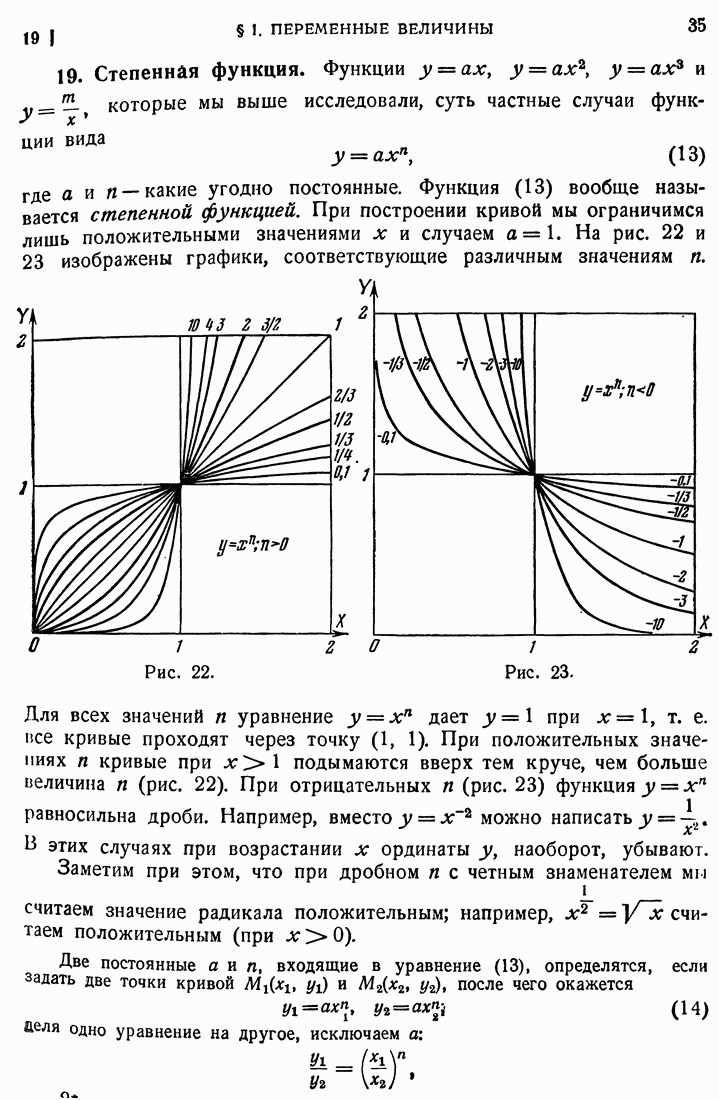
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
- 22. Показательная и логарифмическая функции.
- 23. Тригонометрические функции.
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
- 45. Понятие о производной.
- 46. Геометрическое значение производной.
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
- 70. Дифференциал дуги.
- 71. Выпуклость, вогнутость и кривизна.
- 72. Асимптоты.
- 73. Построение графиков.
- 74. Параметрическое задание кривой.
- 75. Уравнение Ван-дер-Ваальса.
- 76. Особые точки кривых.
- 77. Элементы кривой.
- 78. Цепная линия.
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
- 81. Развертка круга.
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
- 97. Разрыв подынтегральной функции.
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
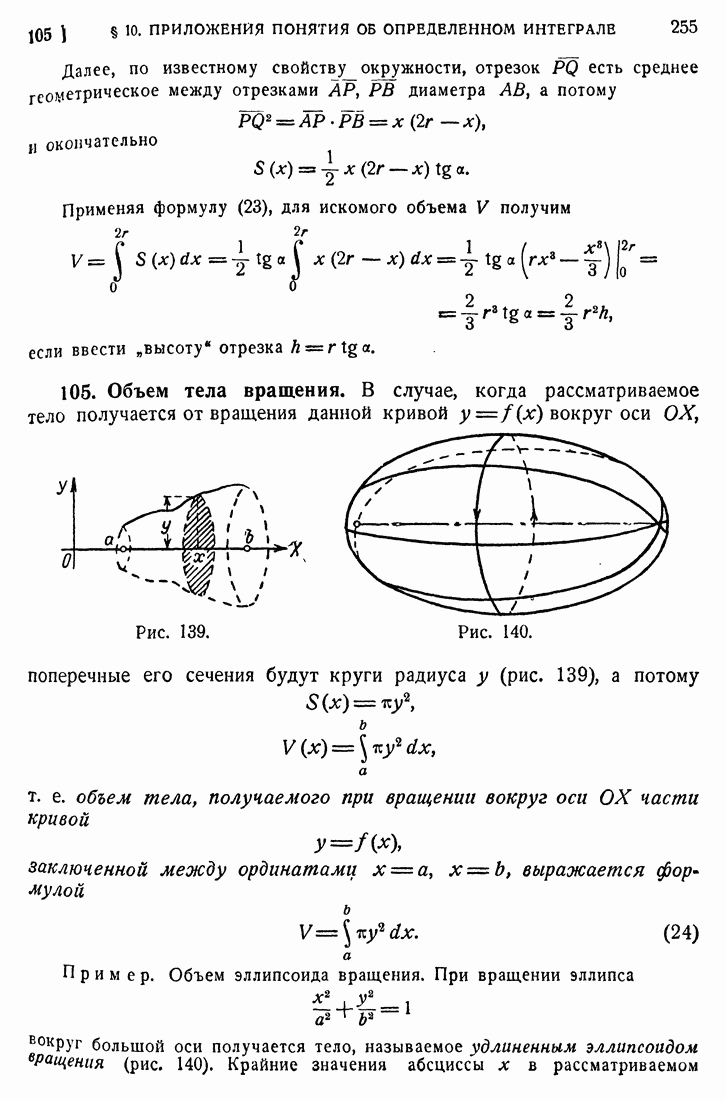
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
- 109. Формула касательных и формула Понселе.
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
- 112. Графические способы.
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
- 163. Исследование максимума и минимума функции двух независимых переменных.
- 164. Примеры.
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
- 177. Тригонометрические и гиперболические функции.
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
- 193. Способ итерации.
- 194. Способ Ньютона.
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…