| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
140. Признак Гаусса.
Весьма важные применения имеет следующий Признак Гаусса. Если в ряде с положительными членами (9)

отношение можно представать в виде

причем А не зависит от  , т. е. величина
, т. е. величина  остается ограниченной, то ряд (9) сходится, если
остается ограниченной, то ряд (9) сходится, если  и расходится, гели
и расходится, гели 
Заметим, что во всех случаях, исчерпываемых этим признаком, признак Даламбера неприменим [121]. Сама же формула (14) получается при разложении отношения  по степеням
по степеням  т. е. при выделении членов различных порядков малости относительно
т. е. при выделении членов различных порядков малости относительно  конечно, если это возможно.
конечно, если это возможно.
Переходя к доказательству, мы исследуем отдельно случаи: 1) и 2)  . В случае 1) мы положим в признаке Куммера
. В случае 1) мы положим в признаке Куммера  , причем заметим, что
, причем заметим, что  и ряд расходится [119]. Мы имеем, очевидно, в данном случае
и ряд расходится [119]. Мы имеем, очевидно, в данном случае

Если  то, начиная с некоторого значения
то, начиная с некоторого значения  , будем иметь
, будем иметь

где а — любое положительное число, меньшее  и ряд (9) будет сходящимся. Если же
и ряд (9) будет сходящимся. Если же  , то, начиная с некоторого значения
, то, начиная с некоторого значения  , мы будем иметь
, мы будем иметь

т. е. ряд (9) будет расходящимся [139]. В случае 2) мы имеем

Положим в признаке Куммера  и составим ряд
и составим ряд

где суммирование можно начинать с любого целого положительного  , так как первые слагаемые не влияют на сходимость [118]. Докажем расходимость написанного ряда, пользуясь интегральным признаком Коши [122]. Нам надо доказать расходимость интеграла
, так как первые слагаемые не влияют на сходимость [118]. Докажем расходимость написанного ряда, пользуясь интегральным признаком Коши [122]. Нам надо доказать расходимость интеграла

Но мы имеем

и функция  беспредельно возрастает при возрастании
беспредельно возрастает при возрастании  т. е. написанный выше интеграл действительно расходится, а потому и ряд (15) расходится. Составим теперь разность
т. е. написанный выше интеграл действительно расходится, а потому и ряд (15) расходится. Составим теперь разность  пользуясь (14):
пользуясь (14):

Множитель  остается по условию ограниченным, отношение же
остается по условию ограниченным, отношение же  стремится к нулю при
стремится к нулю при  так как по условию
так как по условию  возрастает слабее любой положительной степени
возрастает слабее любой положительной степени  (пример 2 из [66]). Если положить
(пример 2 из [66]). Если положить  то
то  и второе слагаемое справа будет
и второе слагаемое справа будет

т. е. оно стремится к (-1) [38]. Мы видим, таким образом, что в данном случае ряд  расходится и
расходится и  при
при  , а потому, при достаточно больших
, а потому, при достаточно больших  будет:
будет:  т. е. ряд (9) будет расходящимся [139], что и требовалось доказать.
т. е. ряд (9) будет расходящимся [139], что и требовалось доказать.
Приведенные выше признаки сходимости могут применяться и к рядам с какими угодно членами, если заменить в них  на
на  Но в этом случае они дают только возможность сказать, будет ли данный ряд абсолютно сходящимся или не будет таковым. Из них можно будет извлечь, вообще говоря, условие абсолютной сходимости, но не условие расходимости, так как мы знаем, что ряд может быть не абсолютно сходящимся, но и не расходящимся [124]. Таким путем мы получаем:
Но в этом случае они дают только возможность сказать, будет ли данный ряд абсолютно сходящимся или не будет таковым. Из них можно будет извлечь, вообще говоря, условие абсолютной сходимости, но не условие расходимости, так как мы знаем, что ряд может быть не абсолютно сходящимся, но и не расходящимся [124]. Таким путем мы получаем:
Дополнение к признаку Гаусса. Ряд

с какими угодно членами, для которого

где  будет абсолютно сходящимся при
будет абсолютно сходящимся при  .
.
Нетрудно показать, что он будет расходящимся при  . В самом деле, в этом случае мы имеем, принимая во внимание ограниченность
. В самом деле, в этом случае мы имеем, принимая во внимание ограниченность 

а потому, начиная с некоторого значения  в силу условия
в силу условия 

т. е., начиная с этого значения  члены ряда возрастают по абсолютному значению, и общий член ряда
члены ряда возрастают по абсолютному значению, и общий член ряда  не может стремиться к нулю при
не может стремиться к нулю при  т. е. ряд (17) будет расходящимся.
т. е. ряд (17) будет расходящимся.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
- 12. Линейная функция.
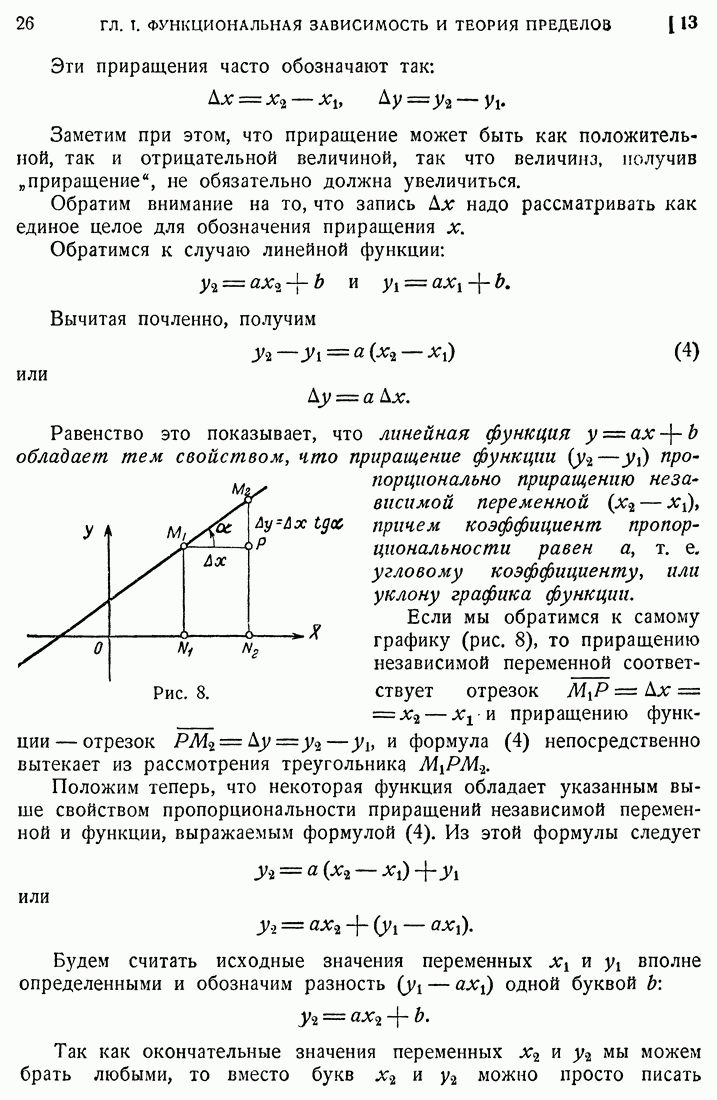
- 13. Приращение. Основное свойство линейной функции.
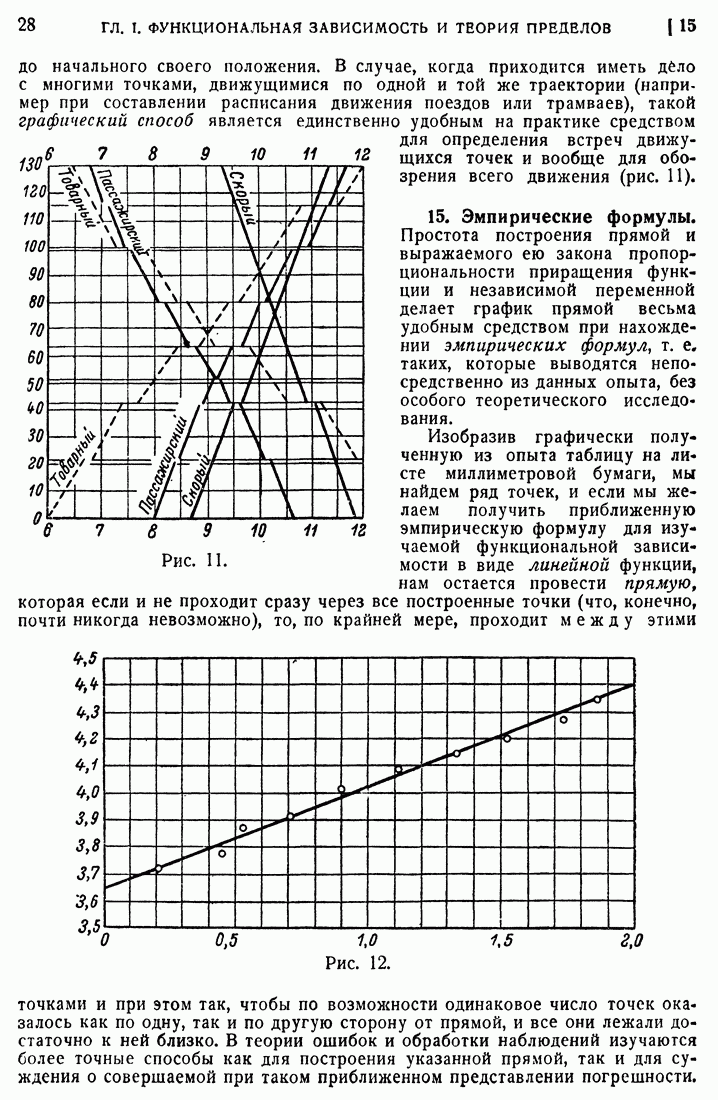
- 14. График равномерного движения.
- 15. Эмпирические формулы.
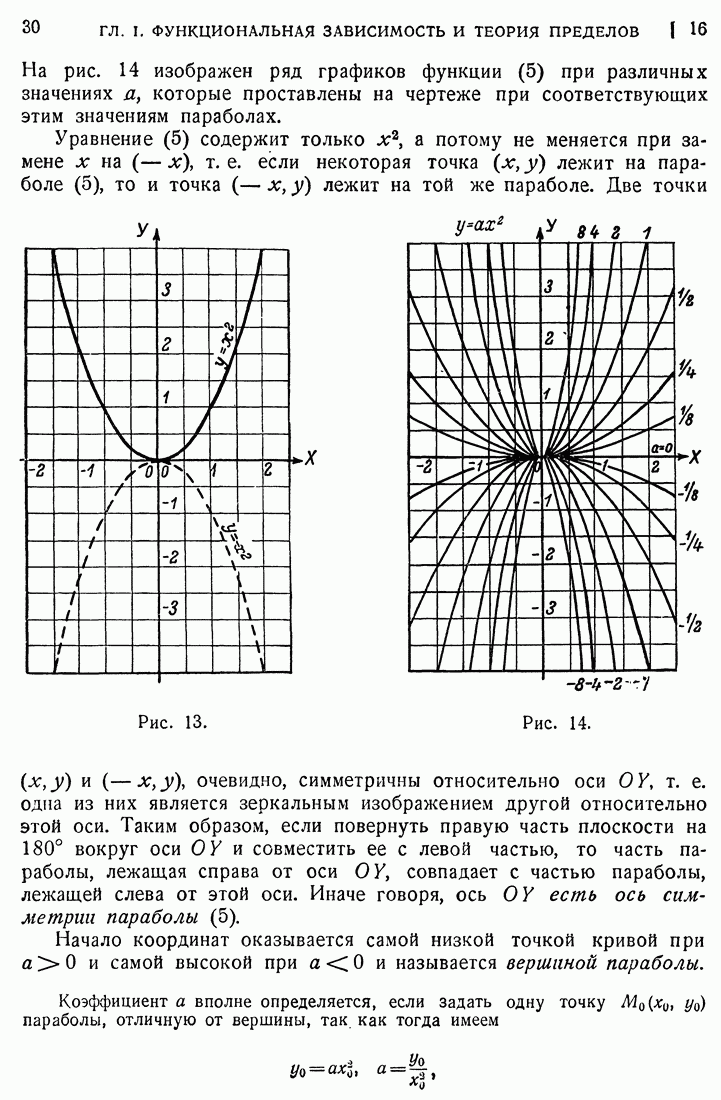
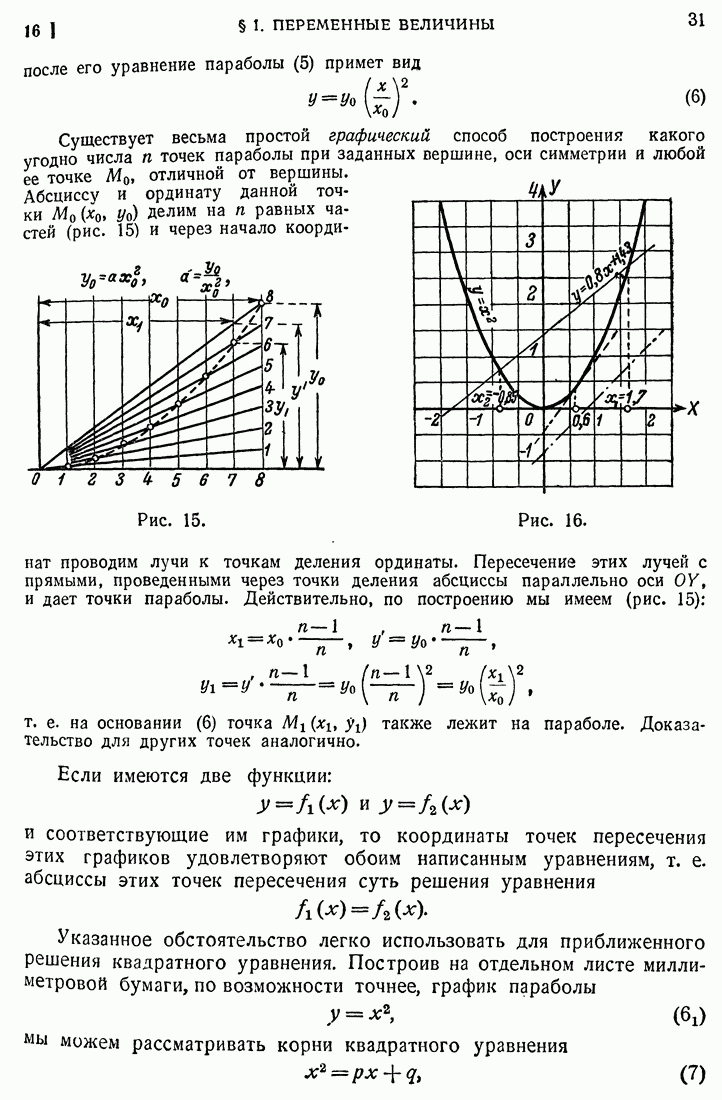
- 16. Парабола второй степени.
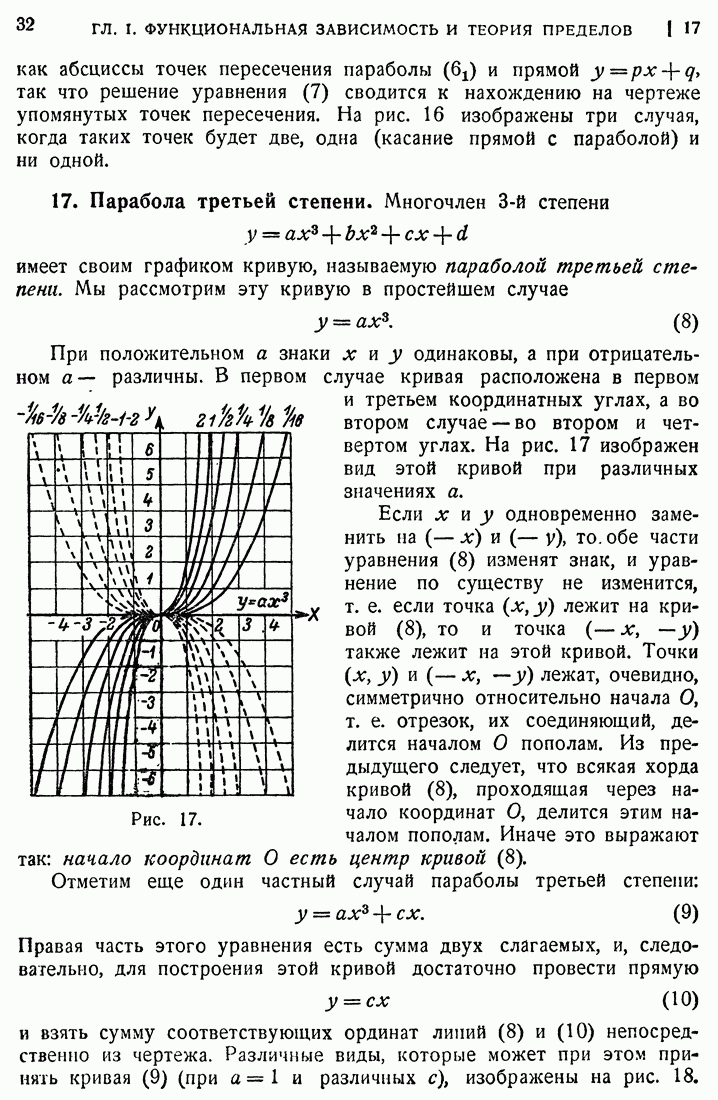
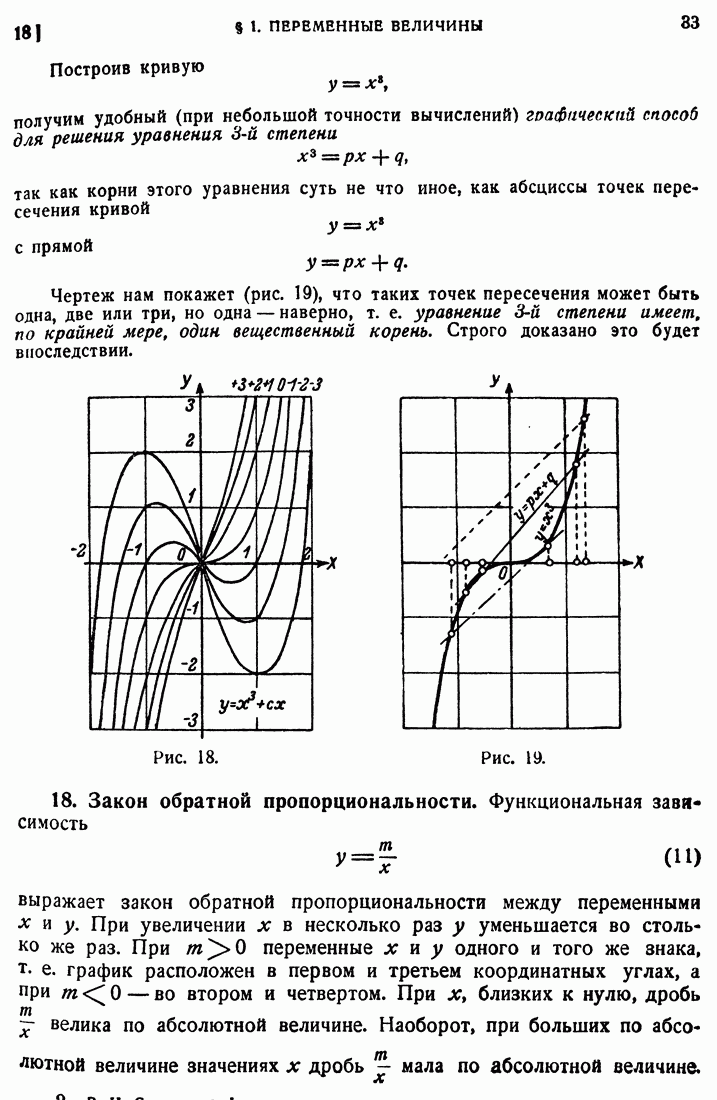
- 17. Парабола третьей степени.
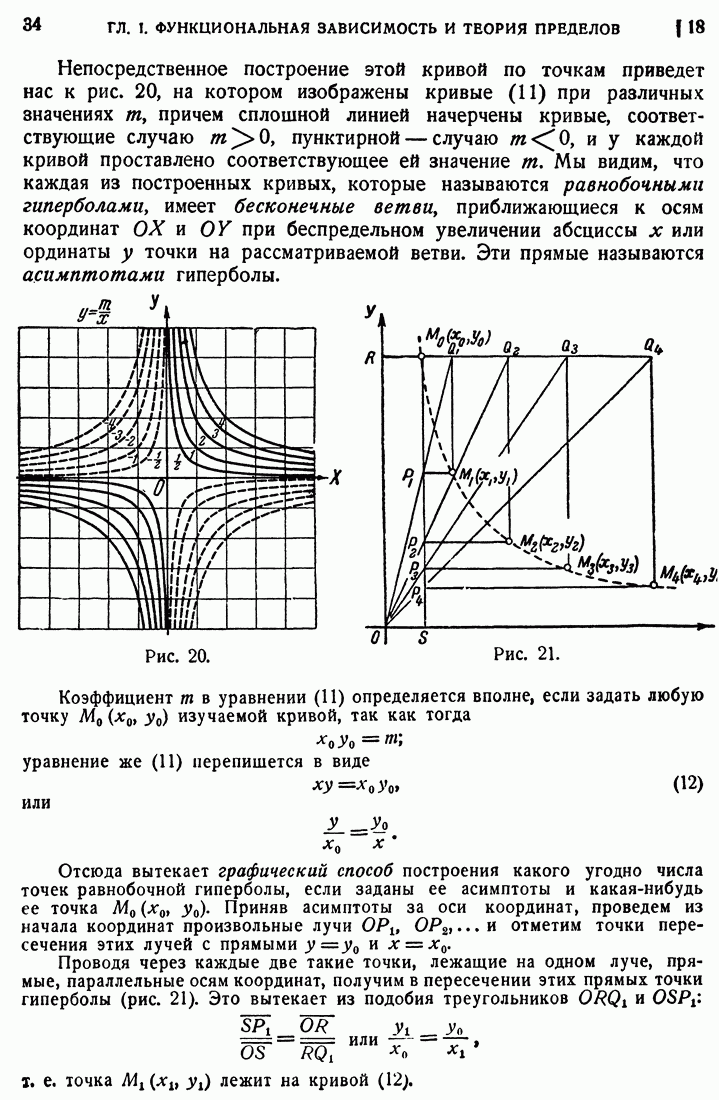
- 18. Закон обратной пропорциональности.
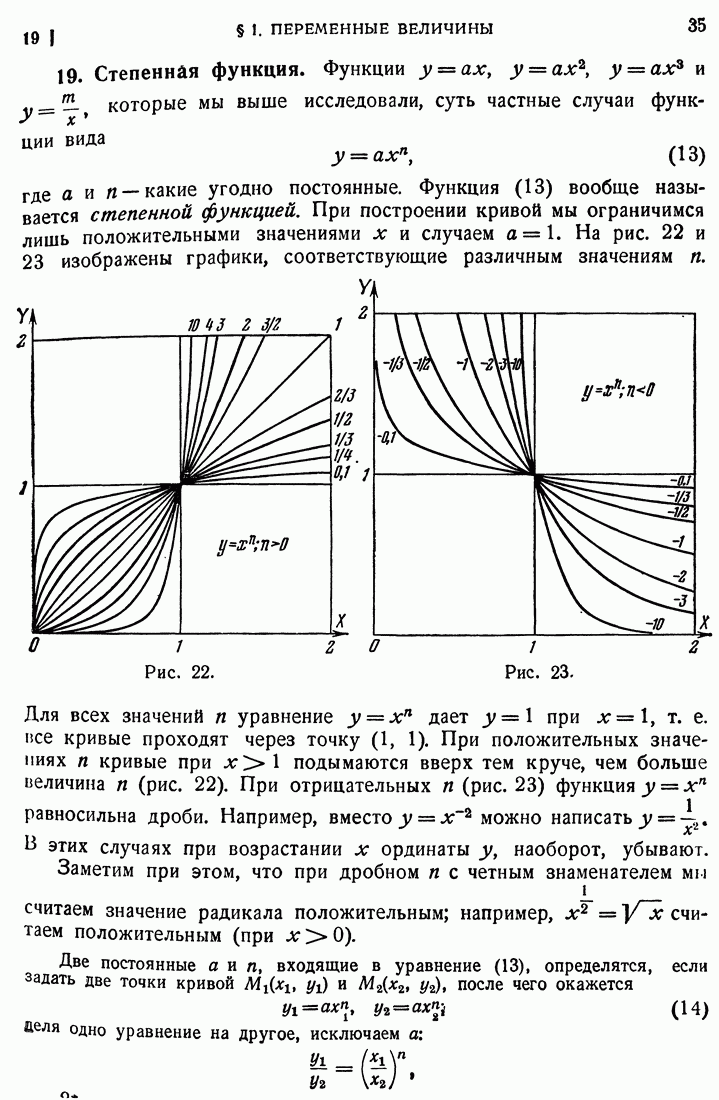
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
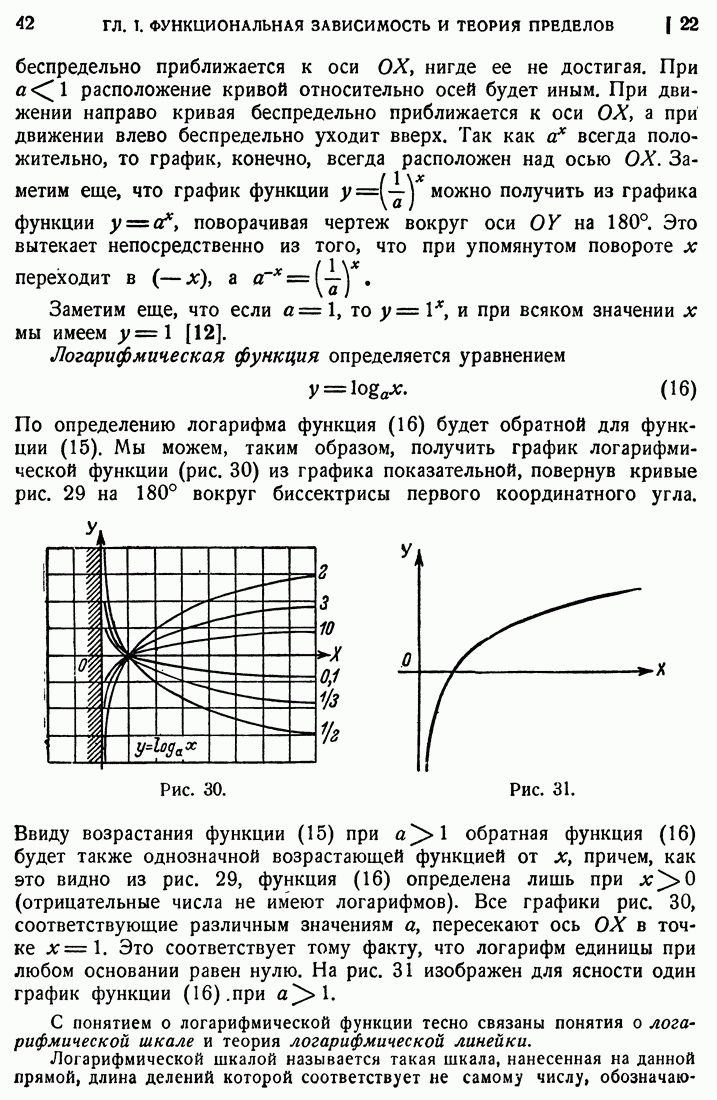
- 22. Показательная и логарифмическая функции.
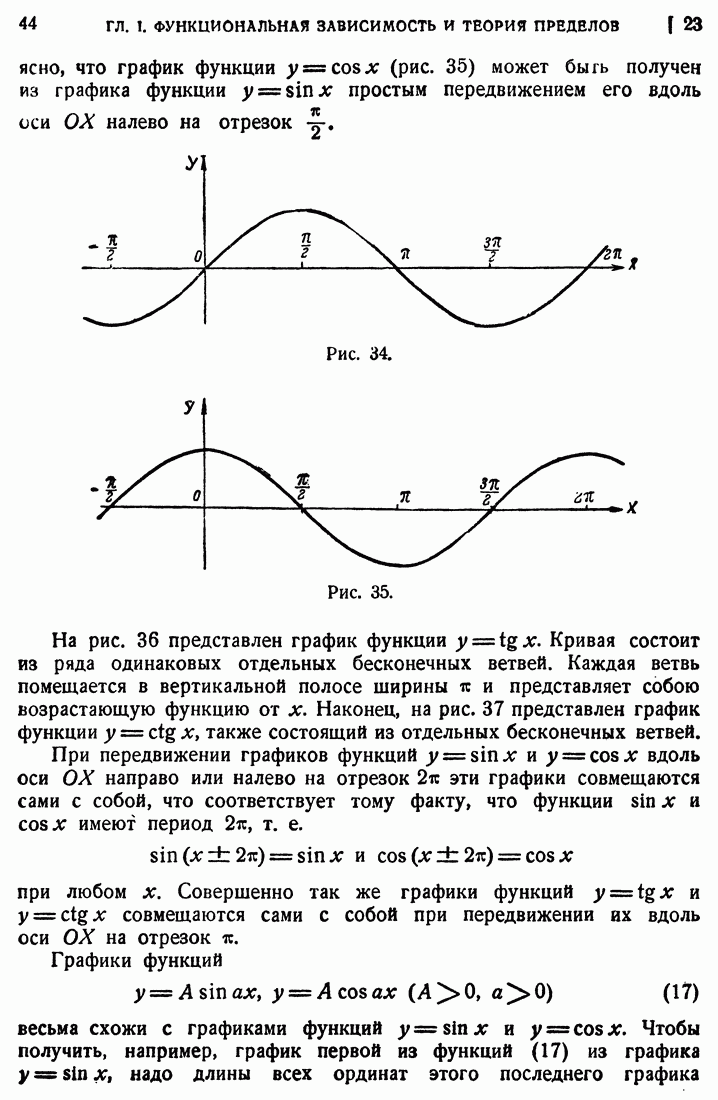
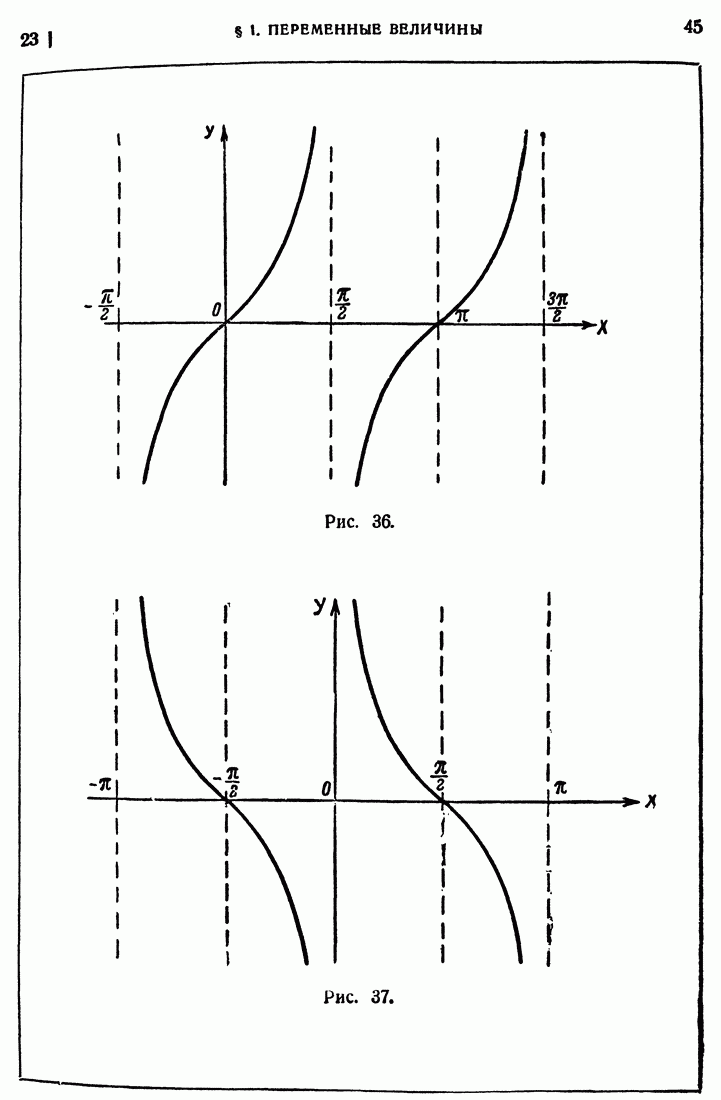
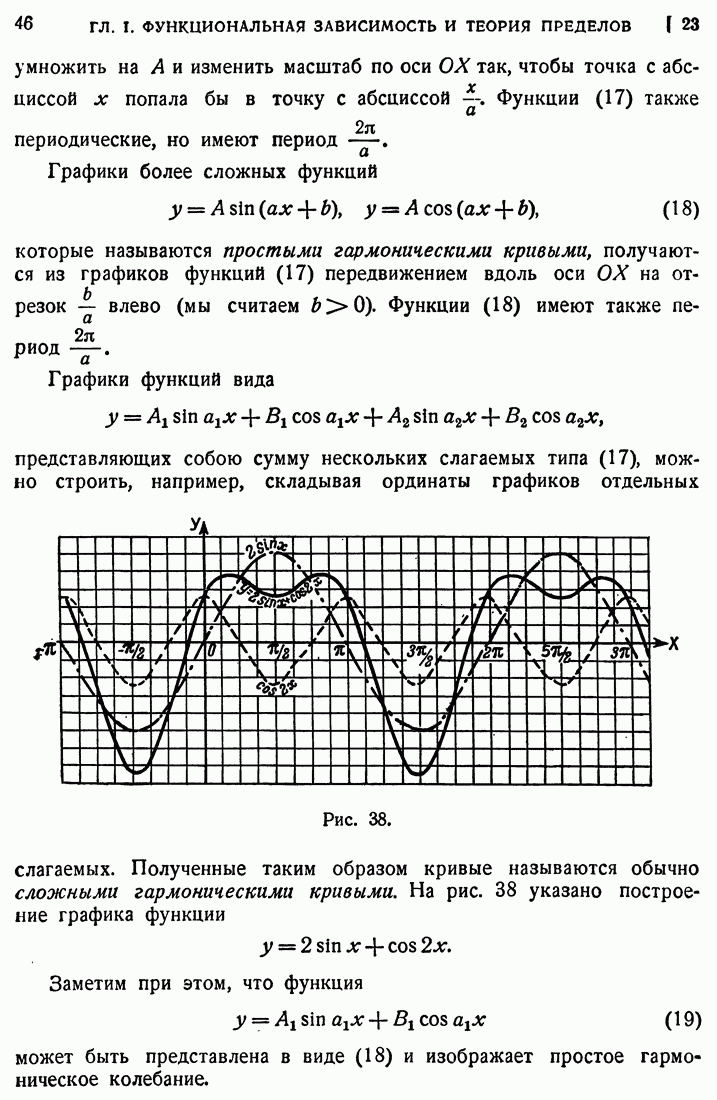
- 23. Тригонометрические функции.
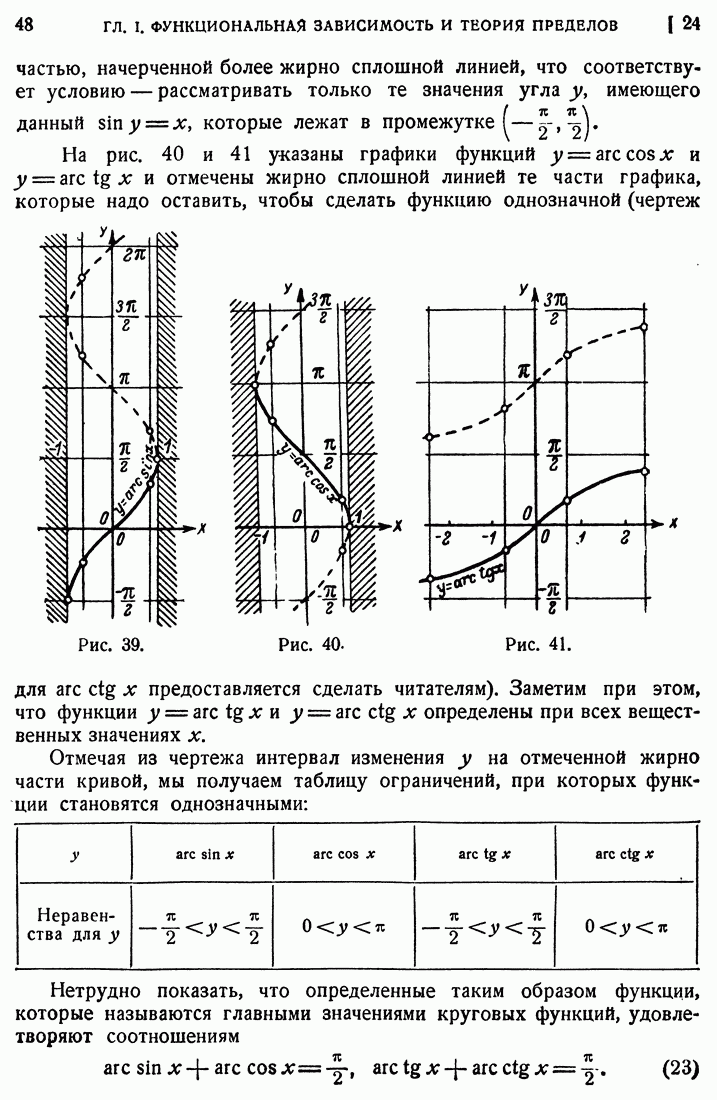
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
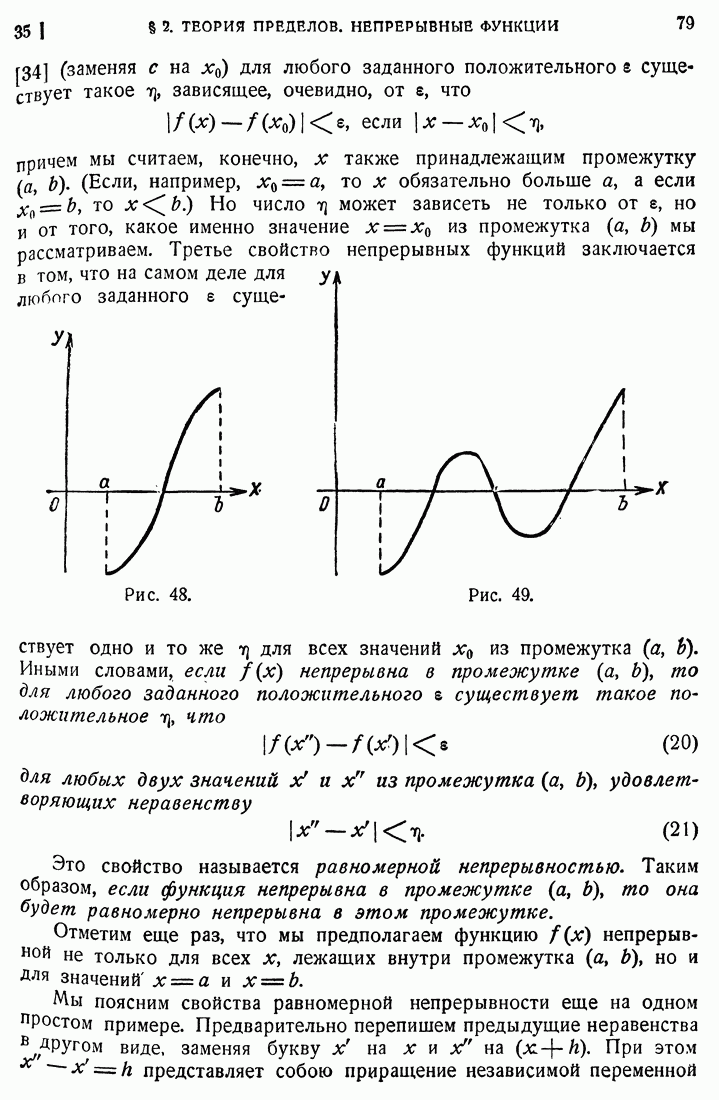
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
- 45. Понятие о производной.
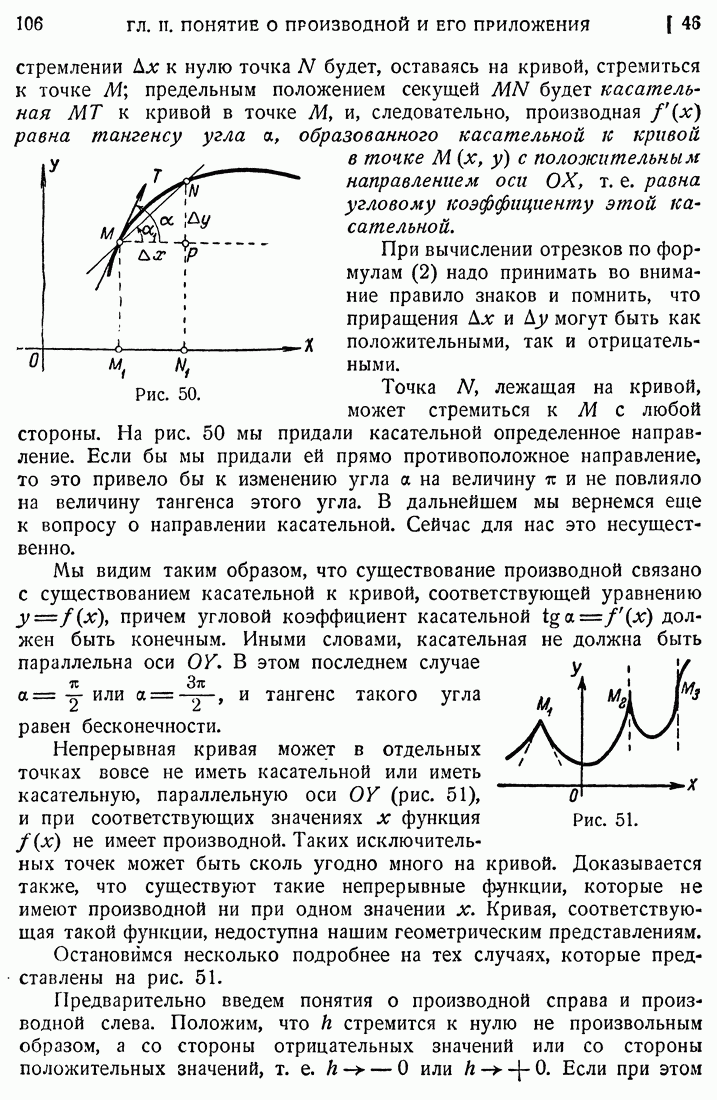
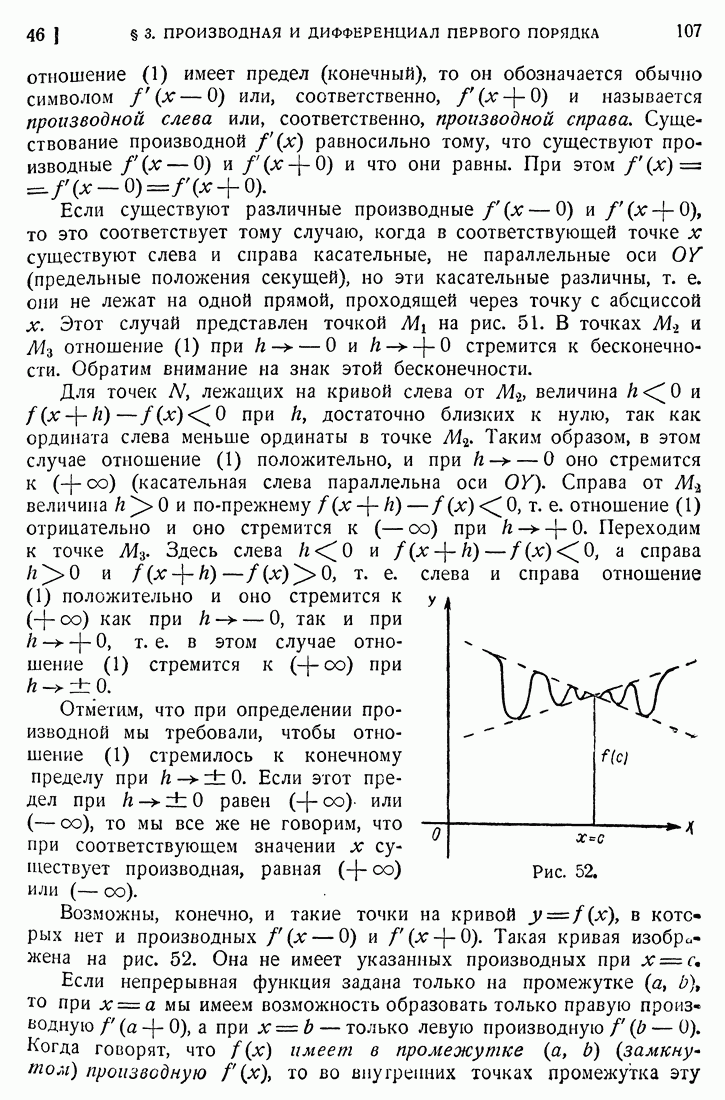
- 46. Геометрическое значение производной.
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
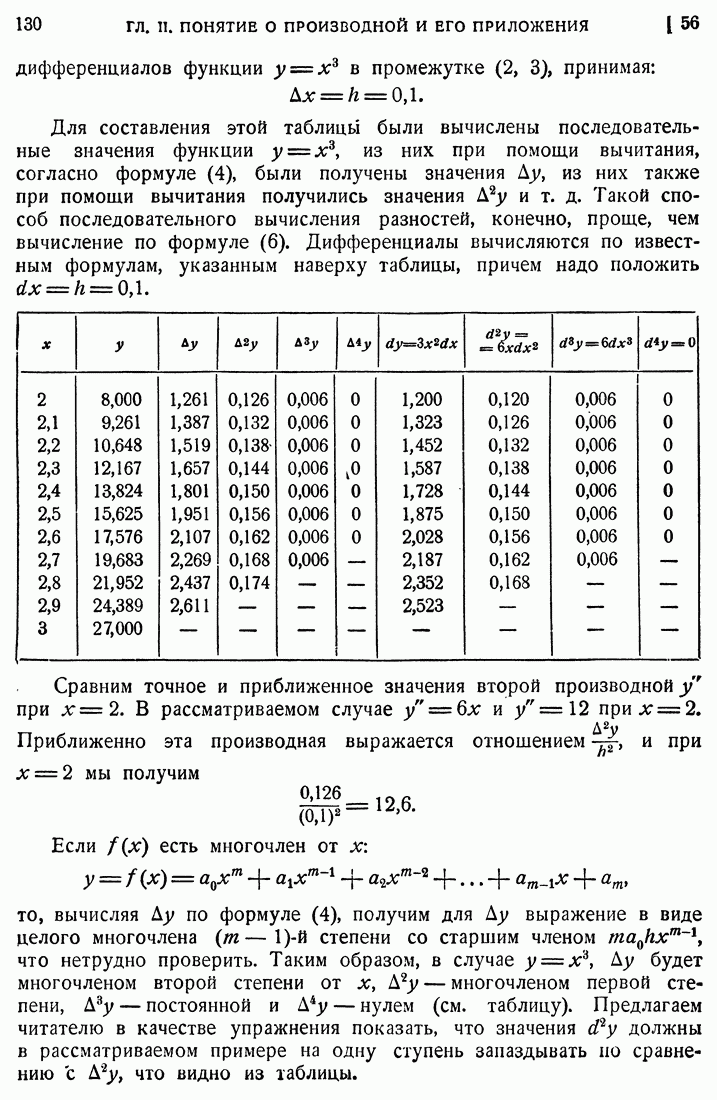
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
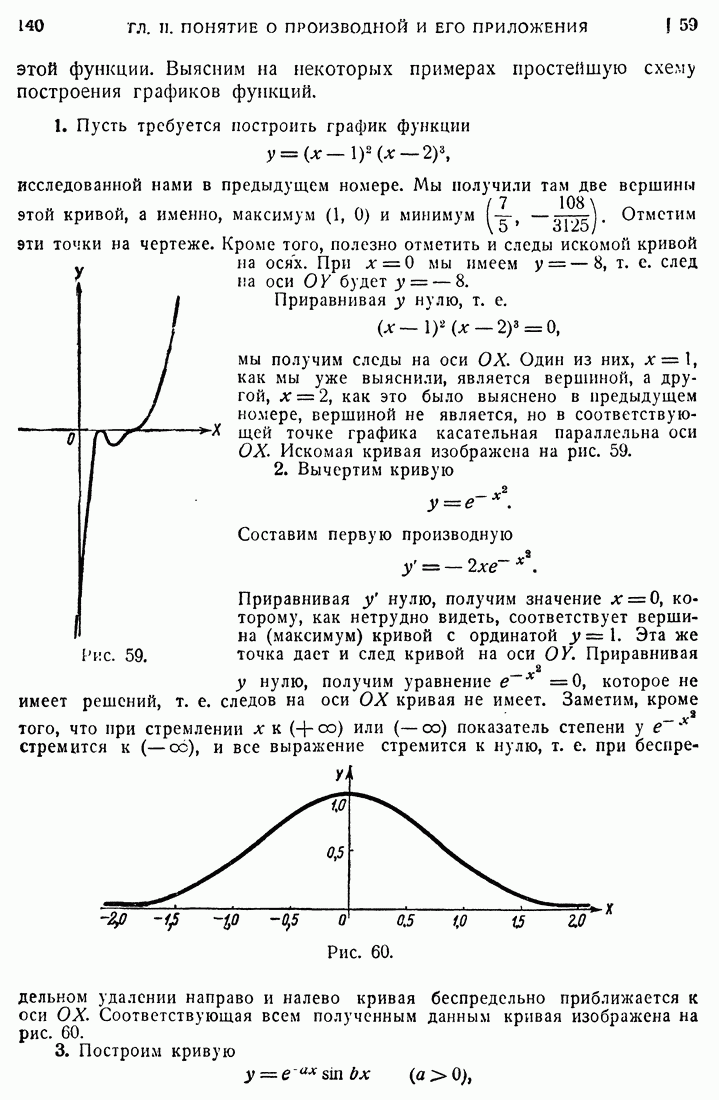
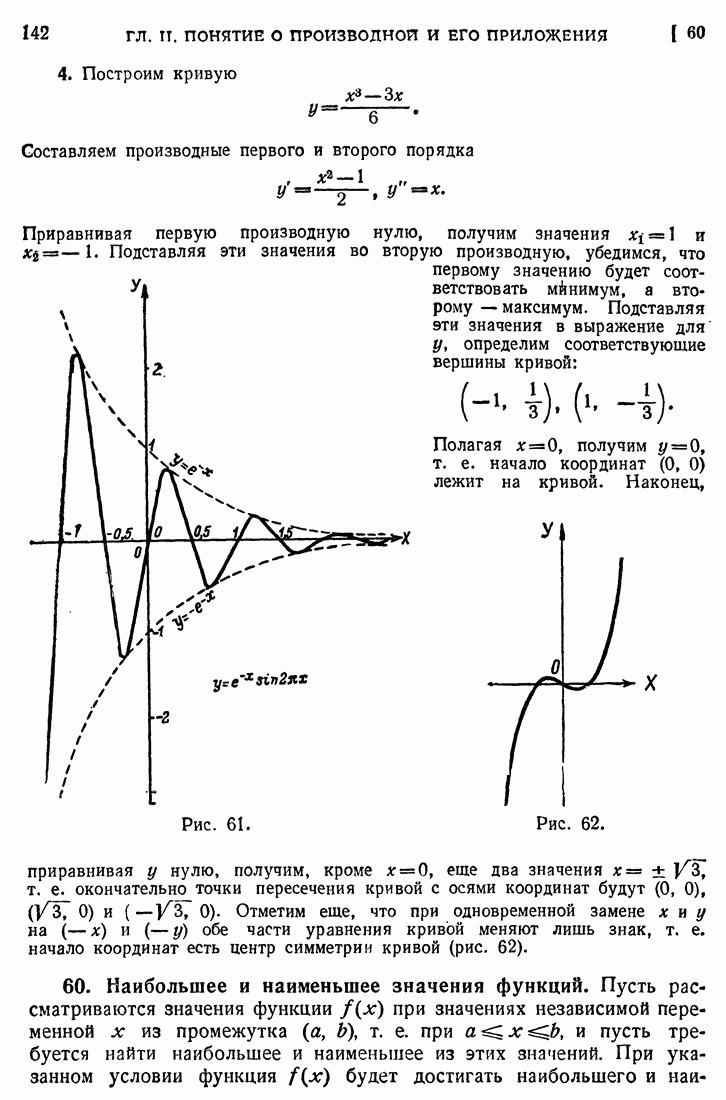
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
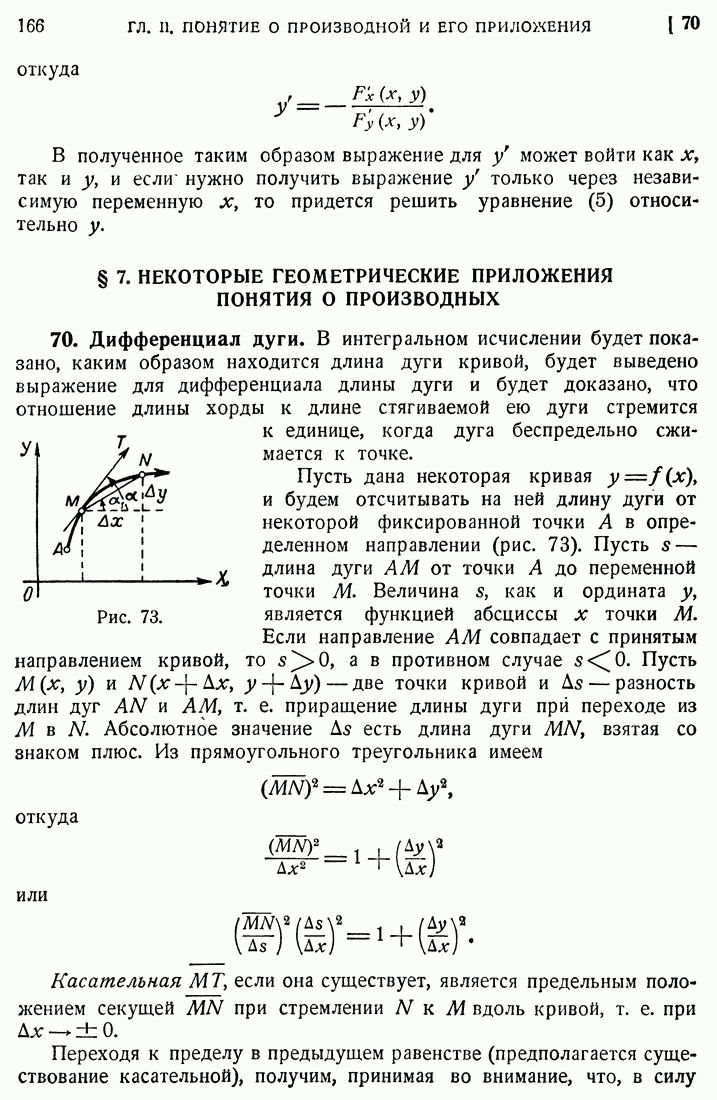
- 70. Дифференциал дуги.
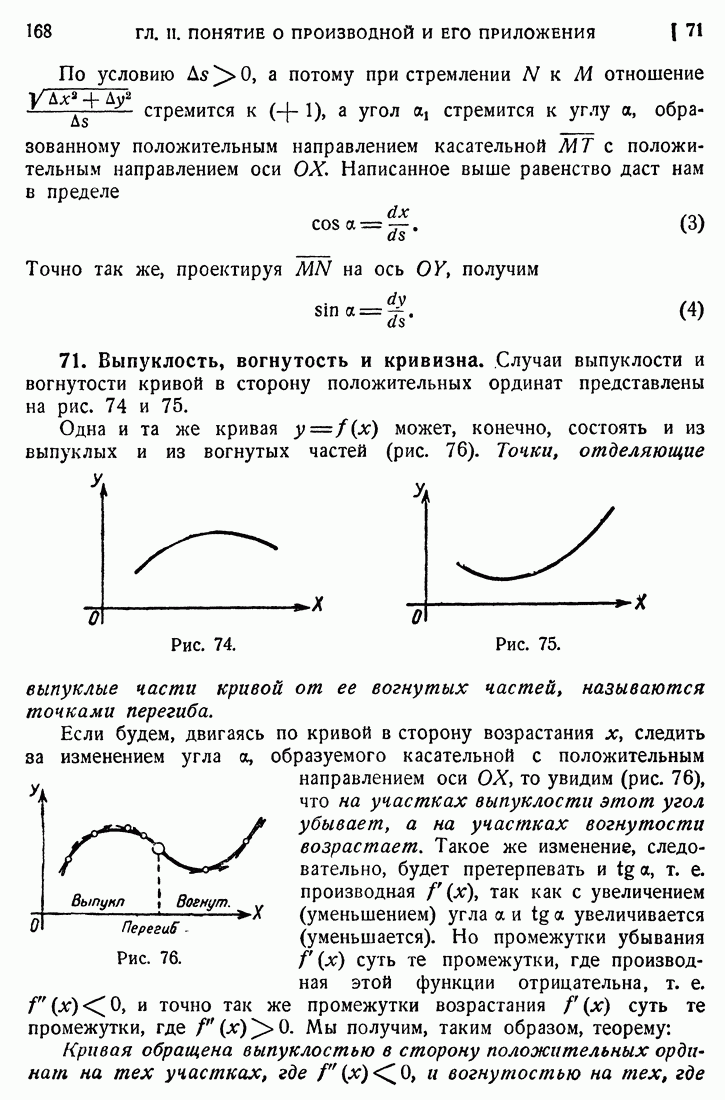
- 71. Выпуклость, вогнутость и кривизна.
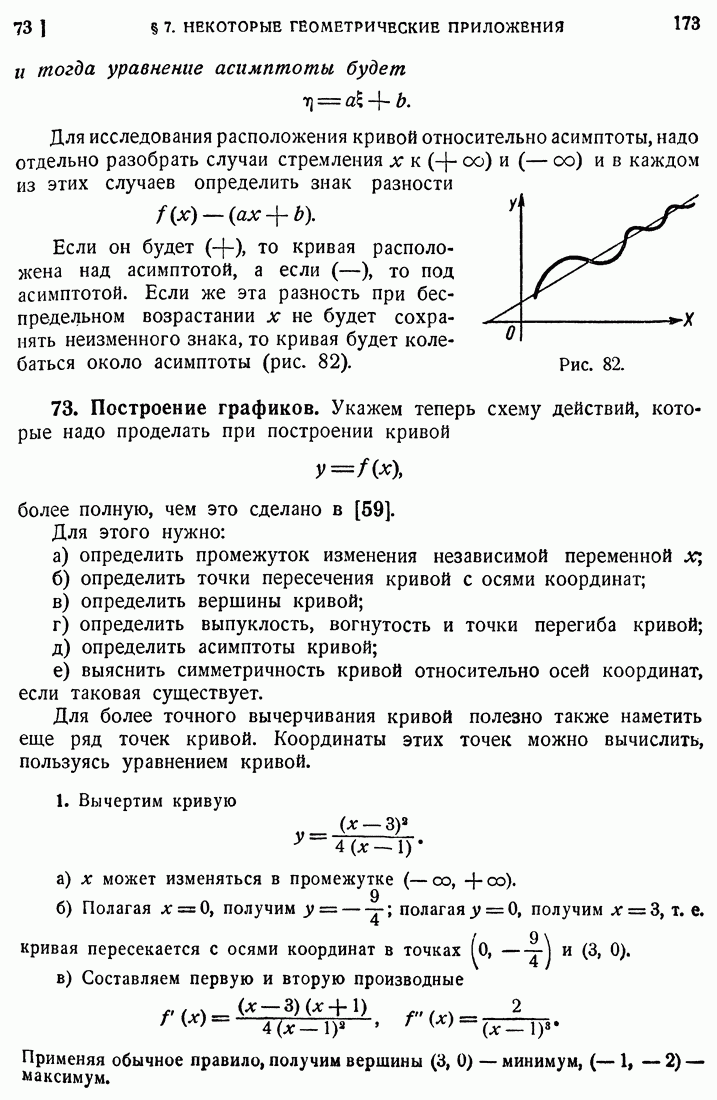
- 72. Асимптоты.
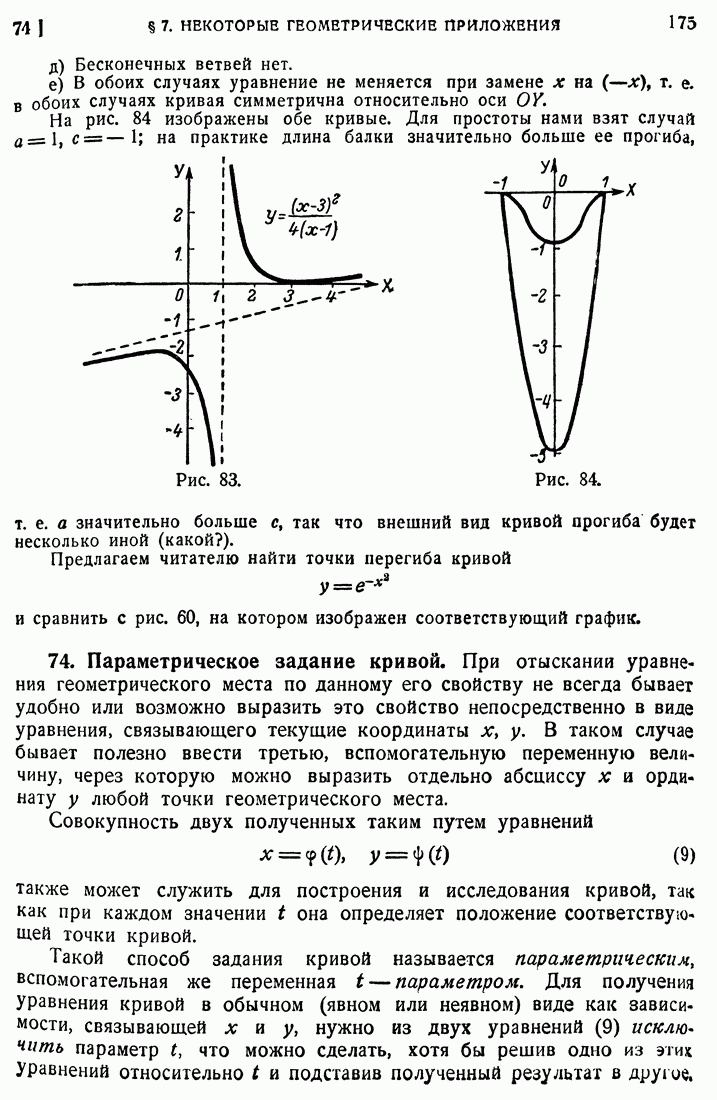
- 73. Построение графиков.
- 74. Параметрическое задание кривой.
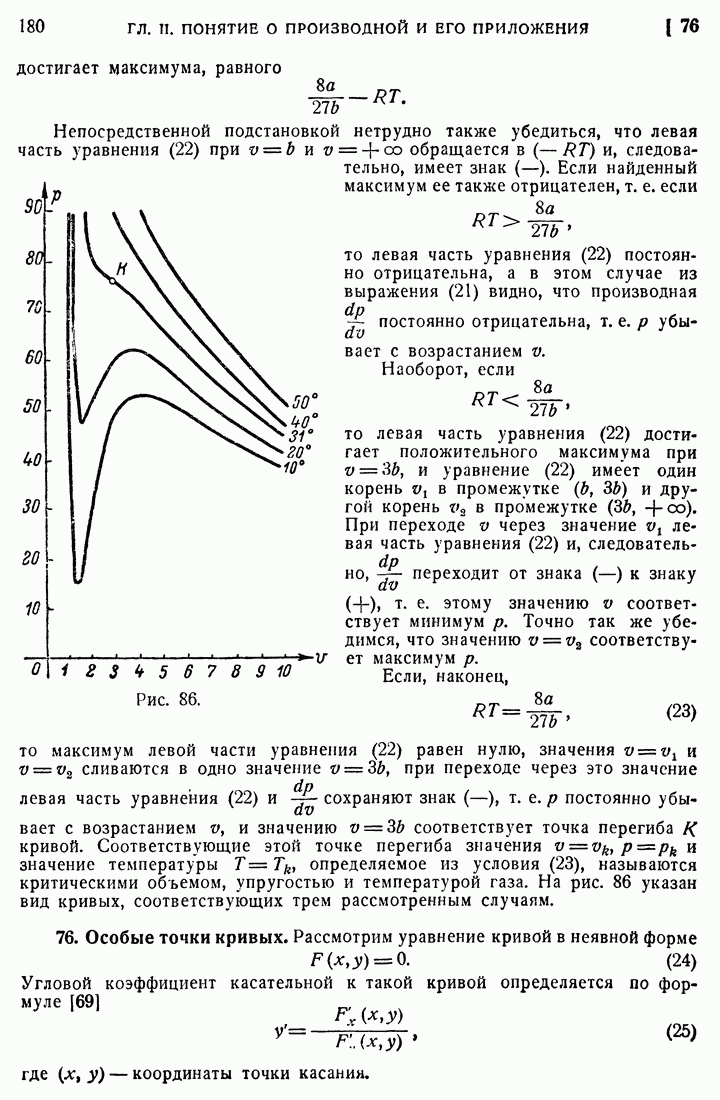
- 75. Уравнение Ван-дер-Ваальса.
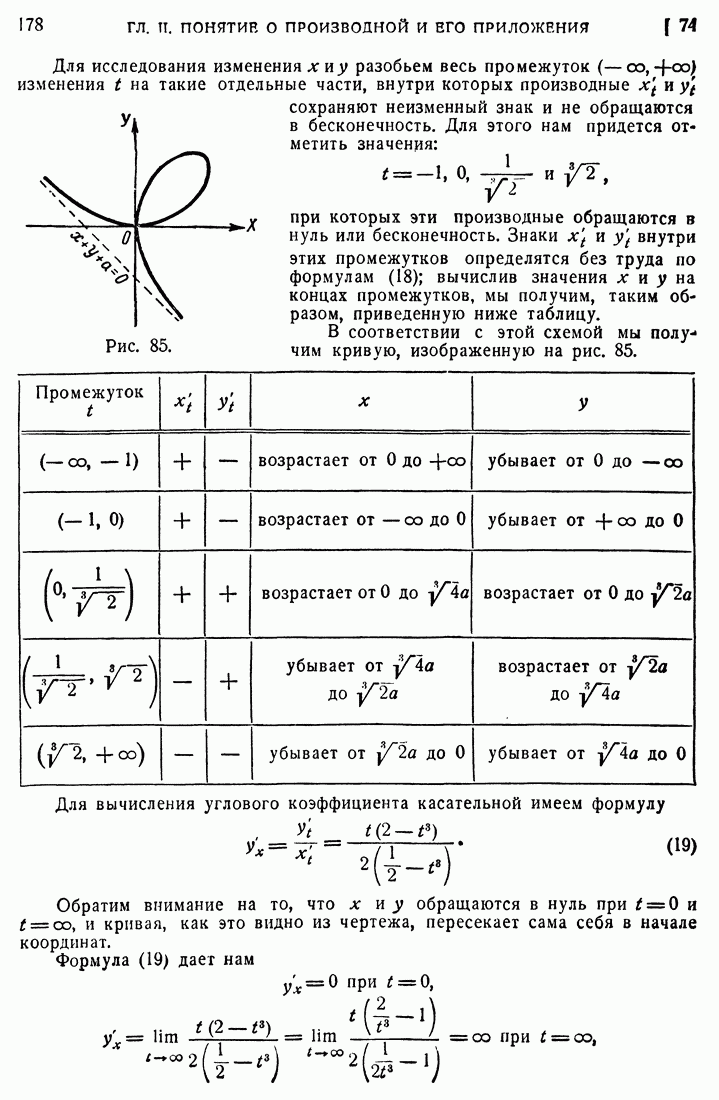
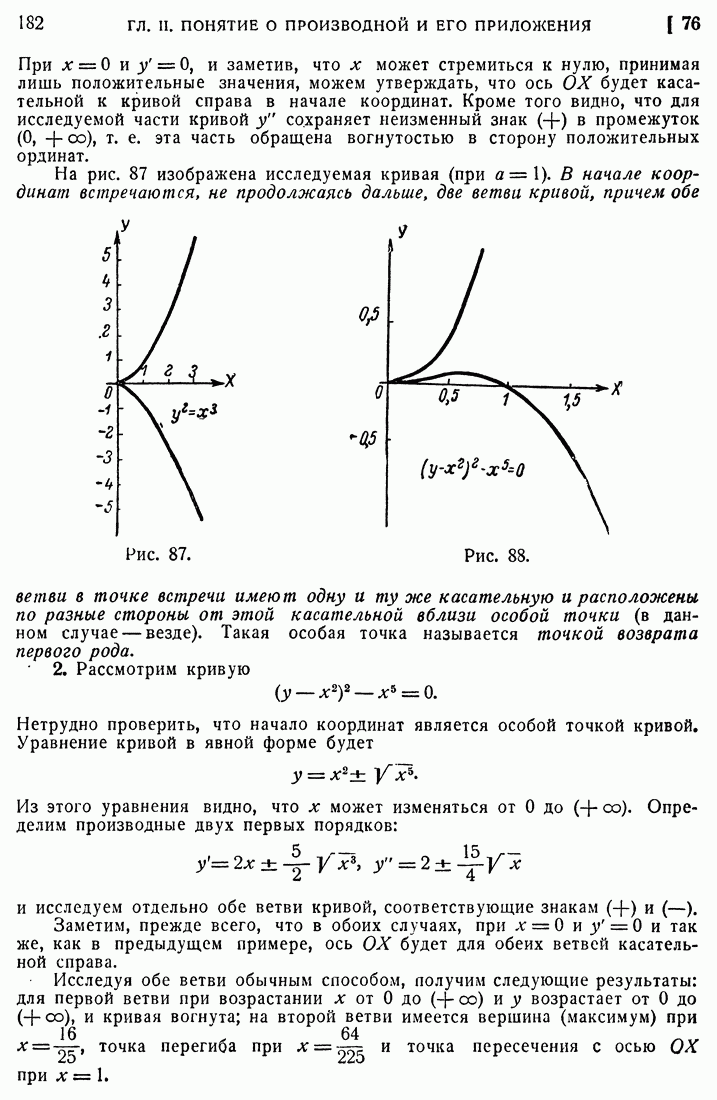
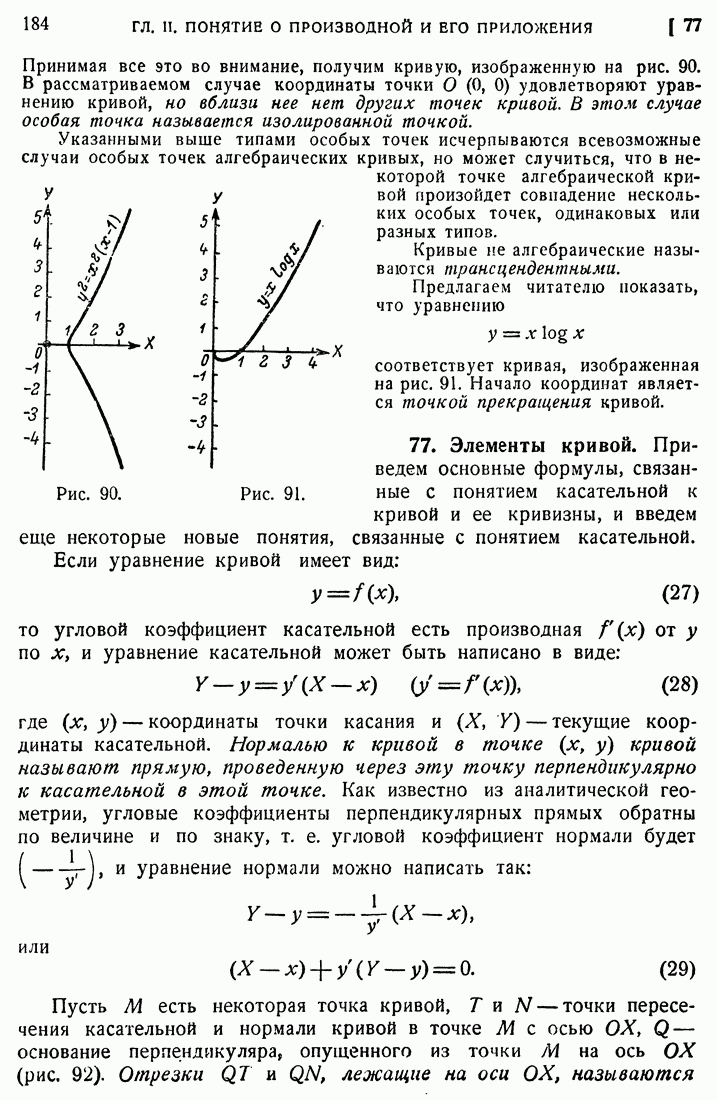
- 76. Особые точки кривых.
- 77. Элементы кривой.
- 78. Цепная линия.
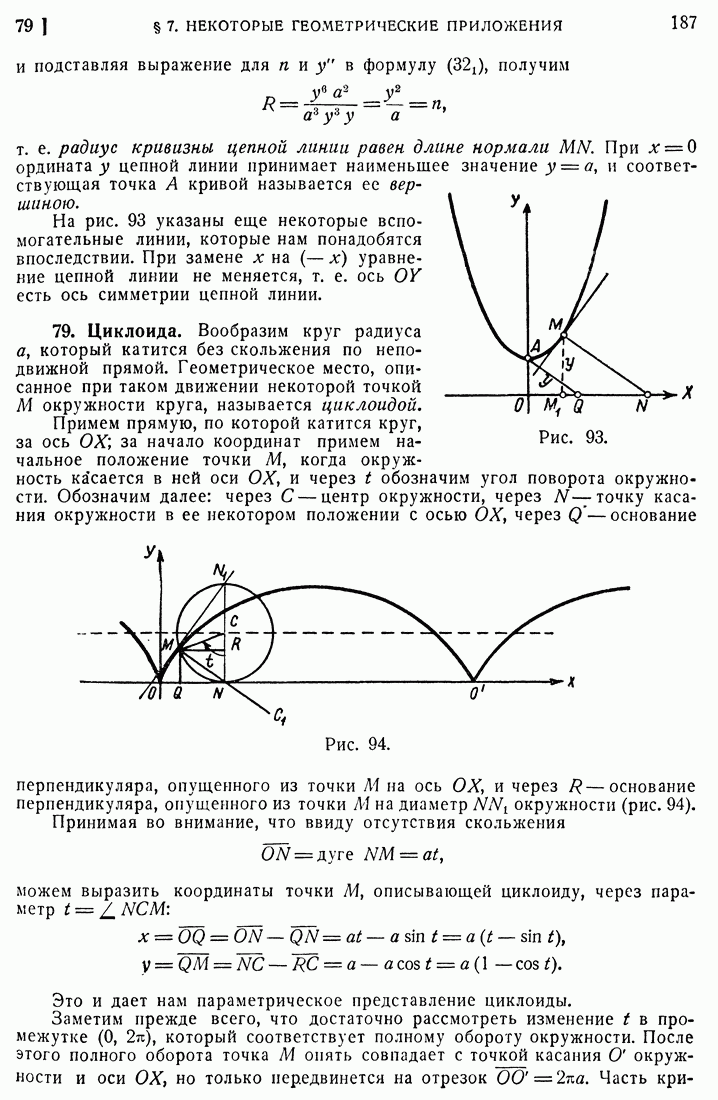
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
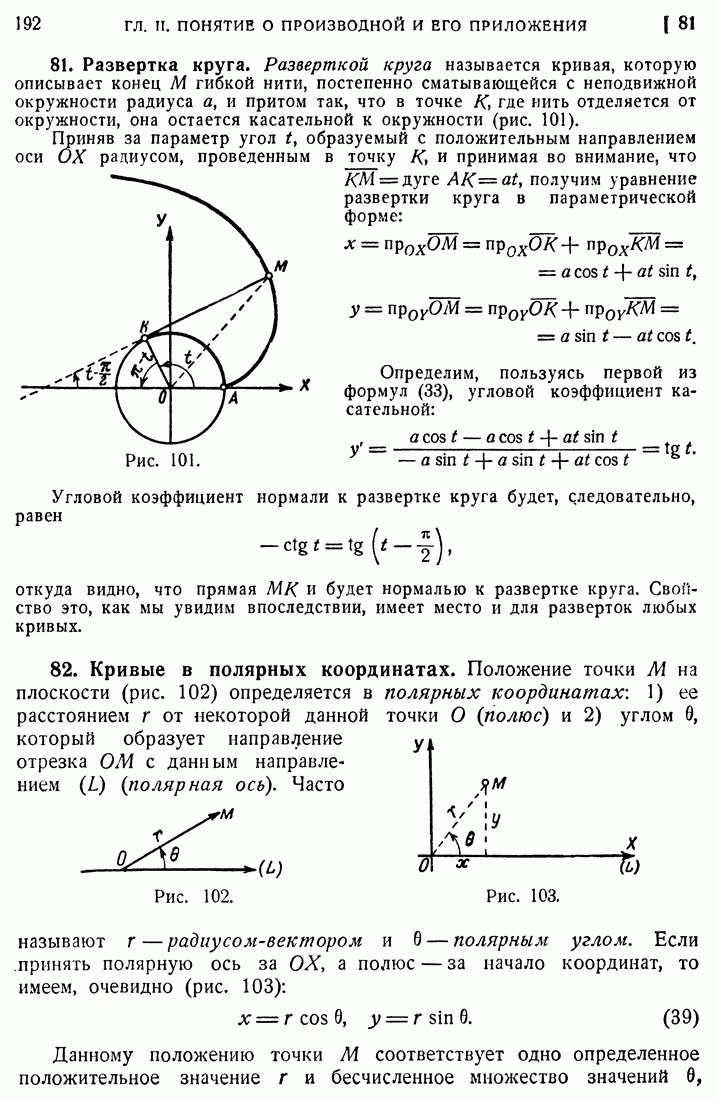
- 81. Развертка круга.
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
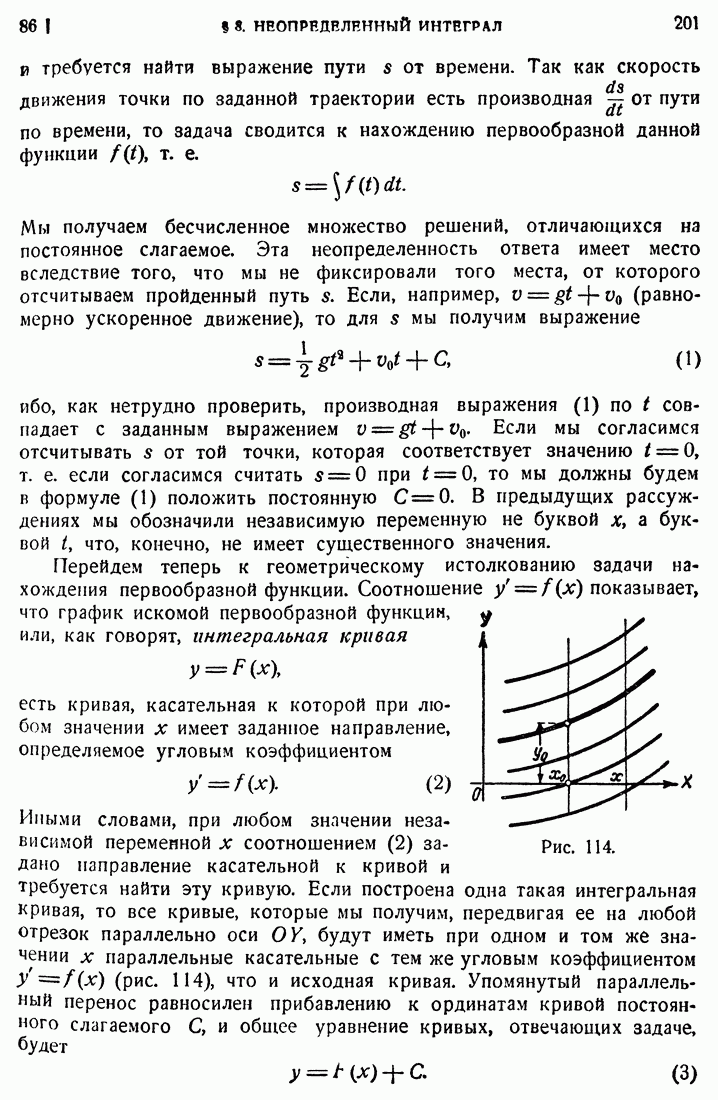
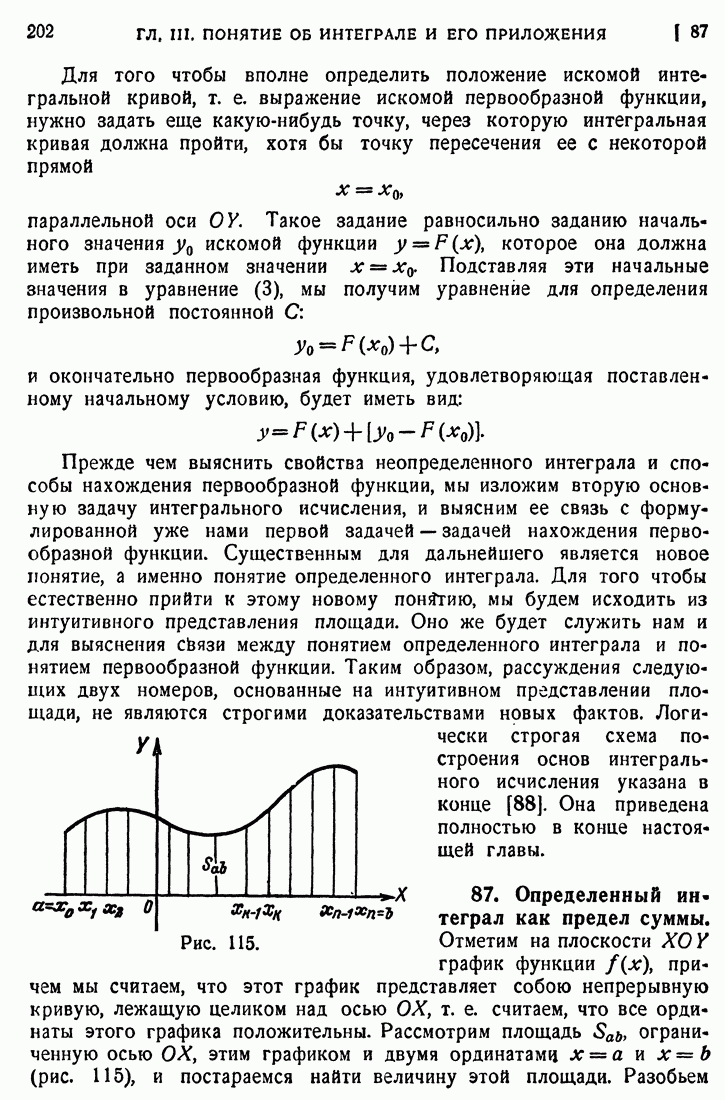
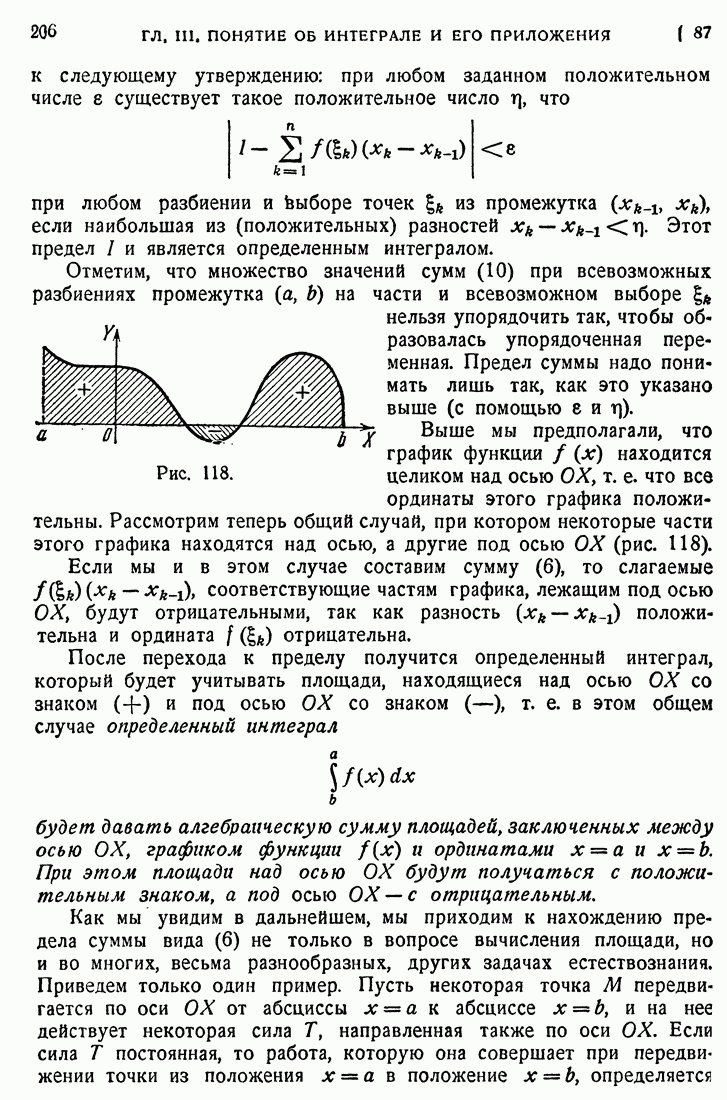
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
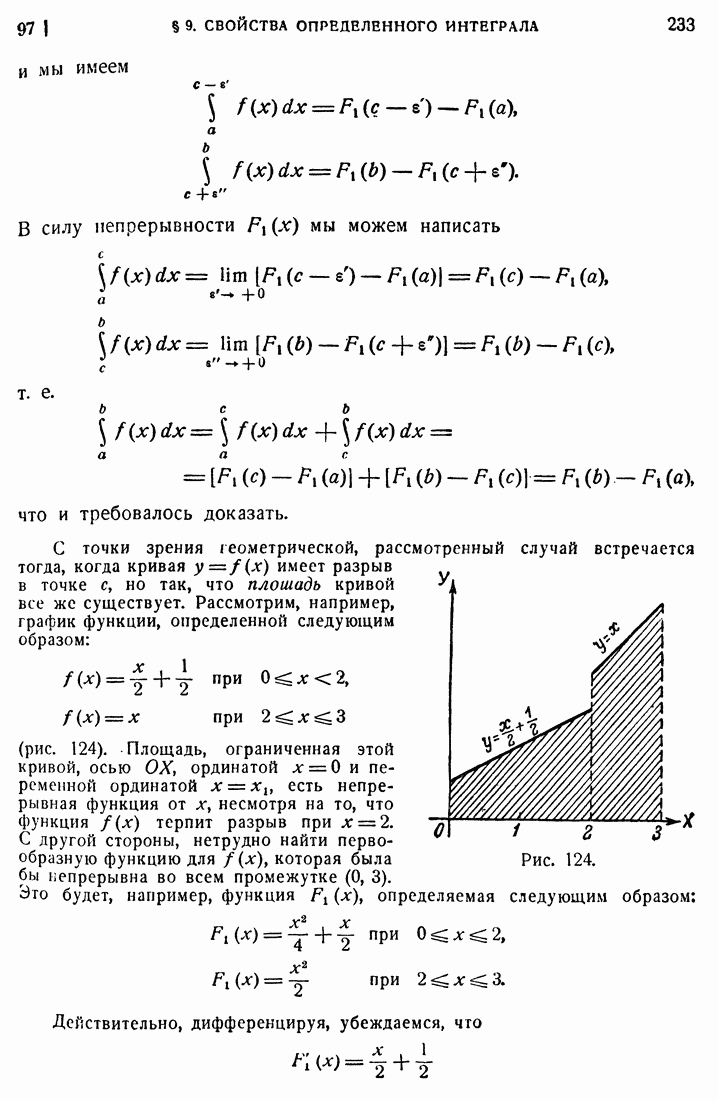
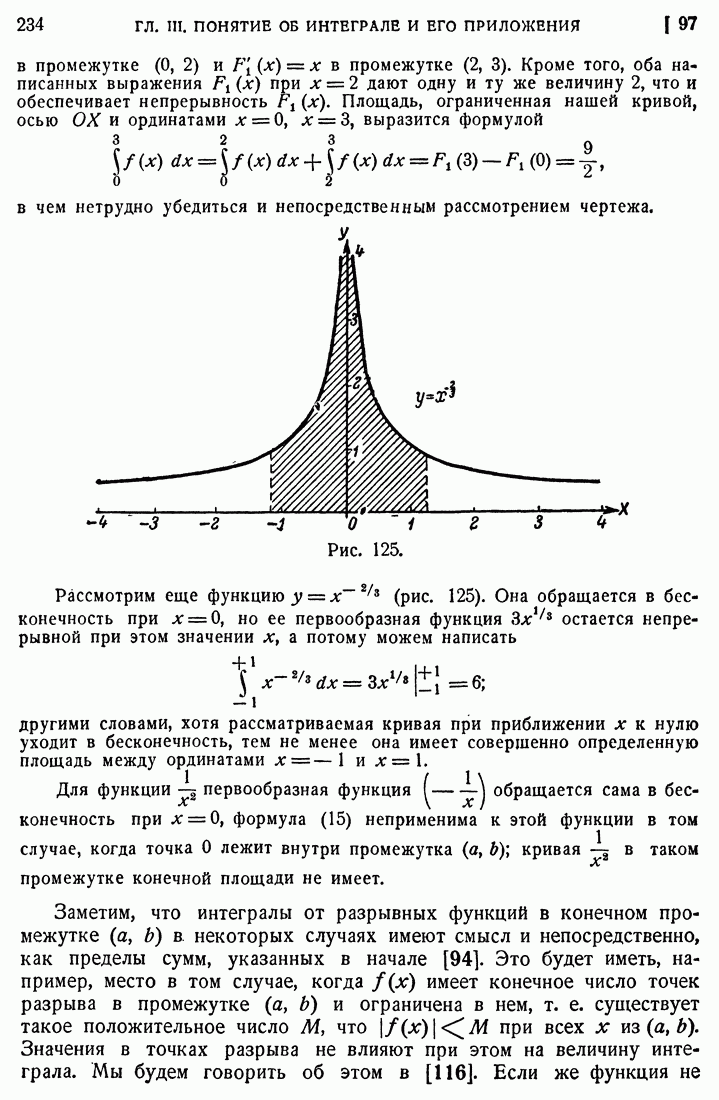
- 97. Разрыв подынтегральной функции.
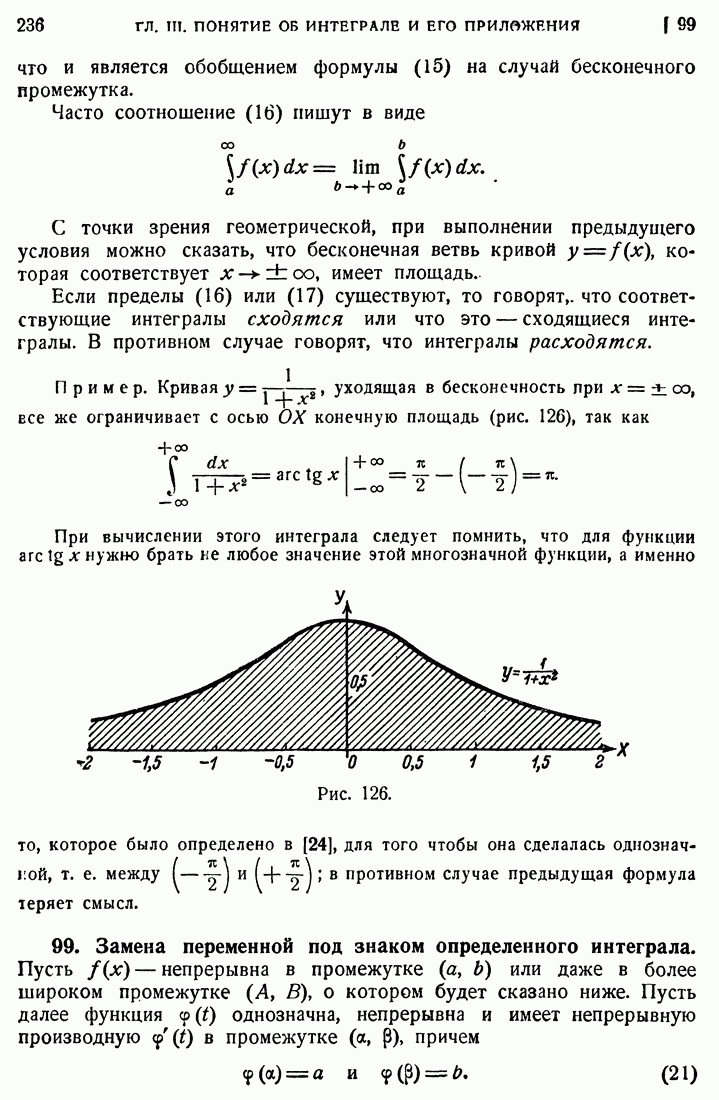
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
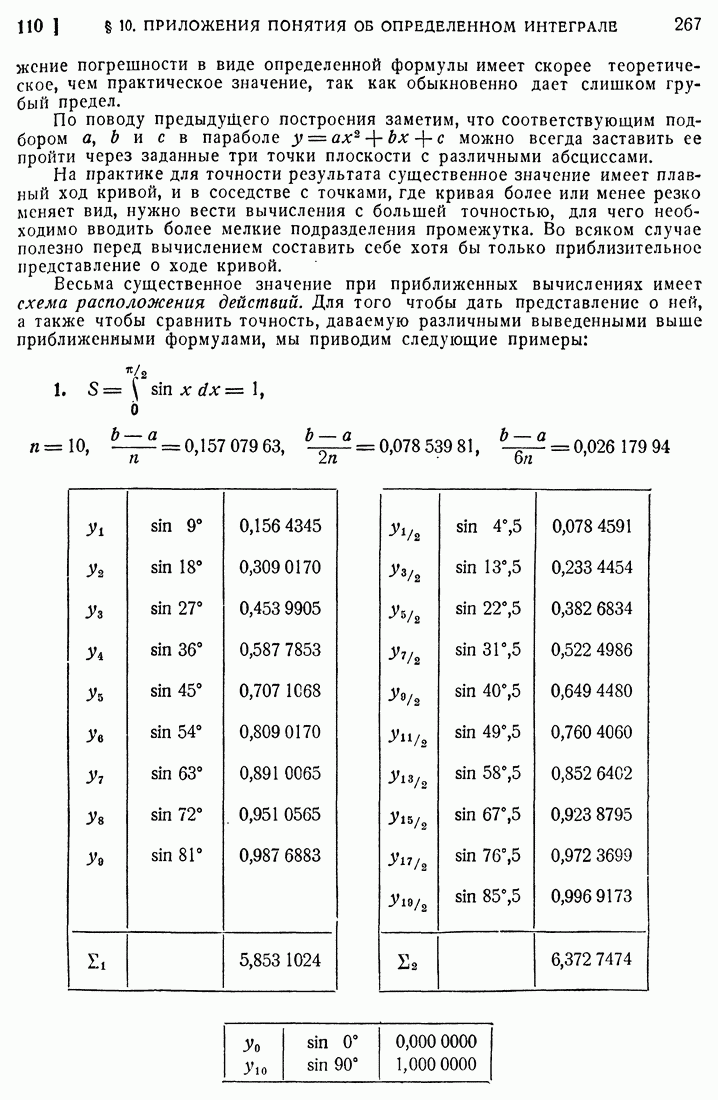
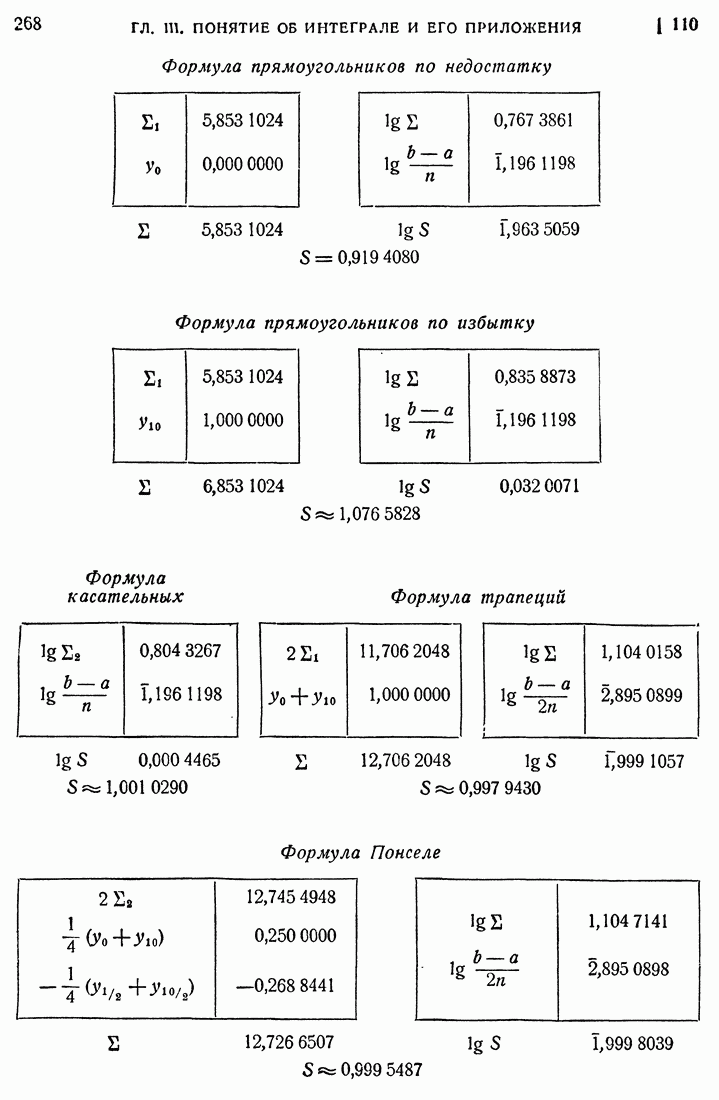
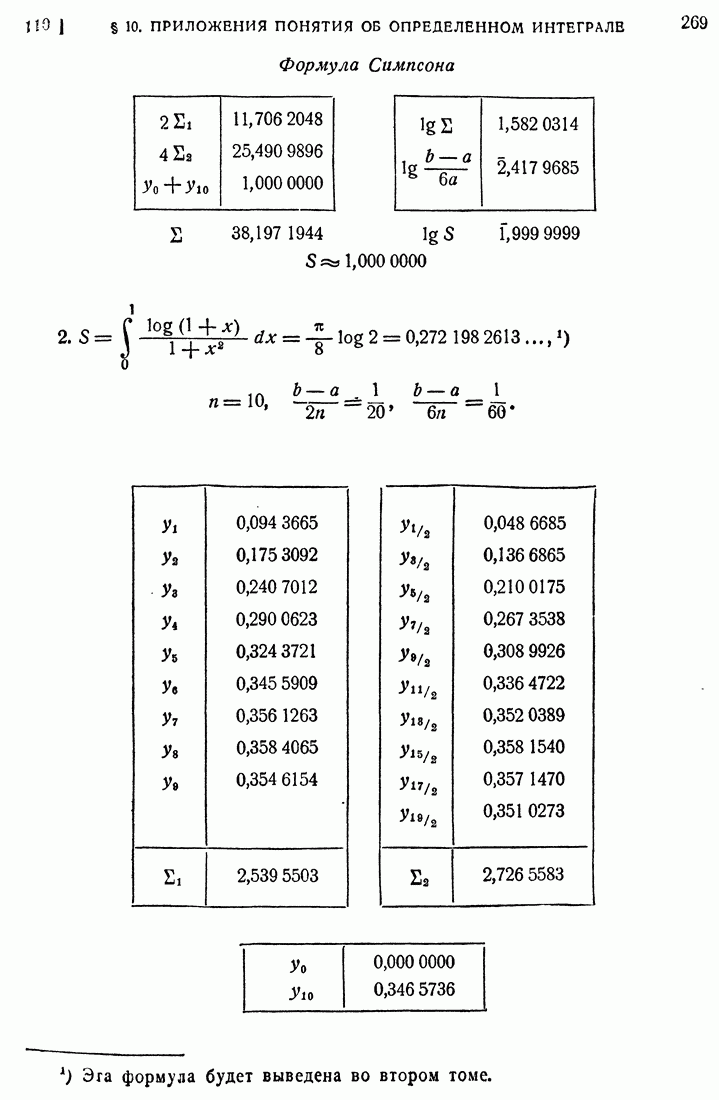
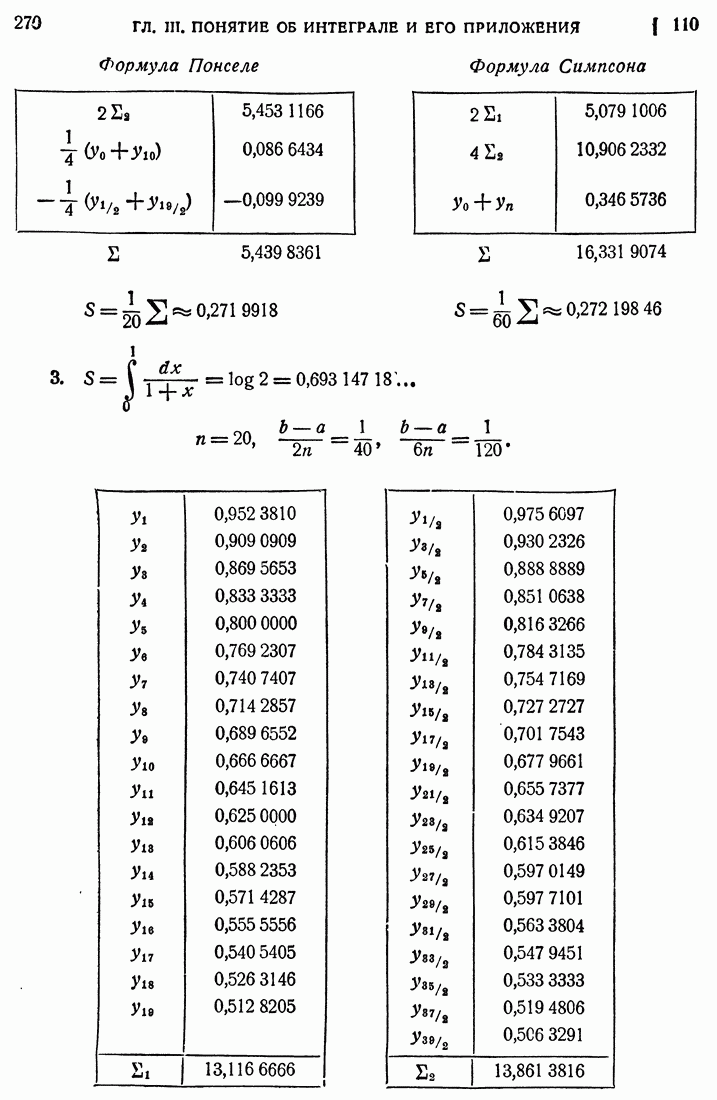
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
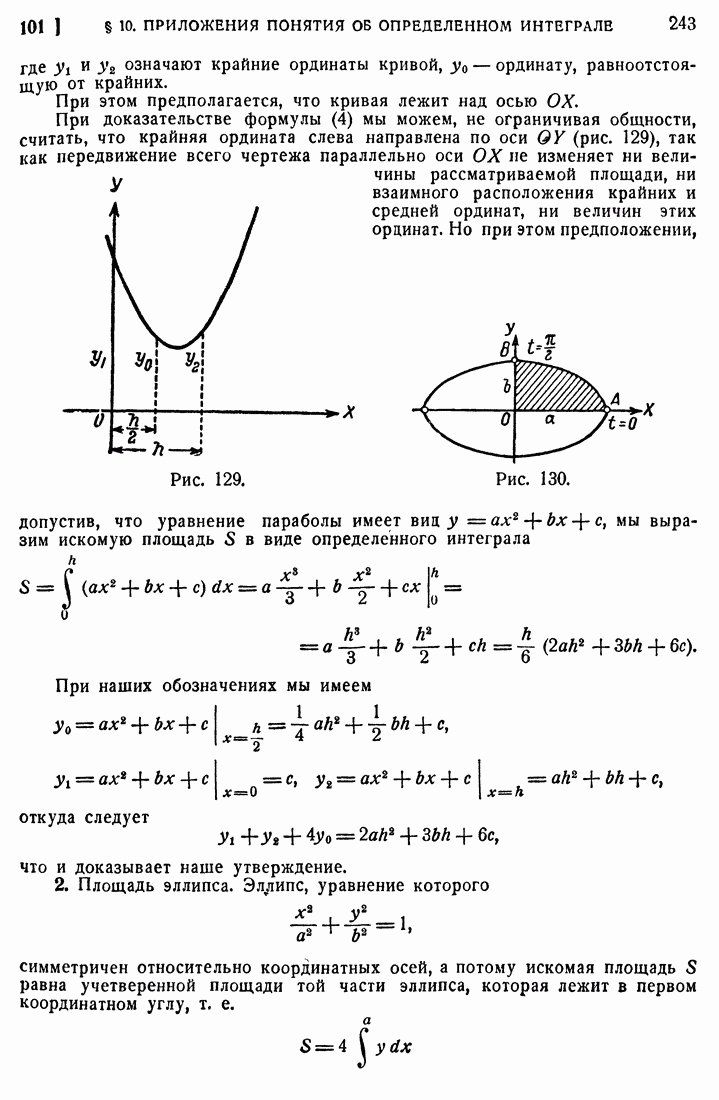
- 101. Вычисление площадей.
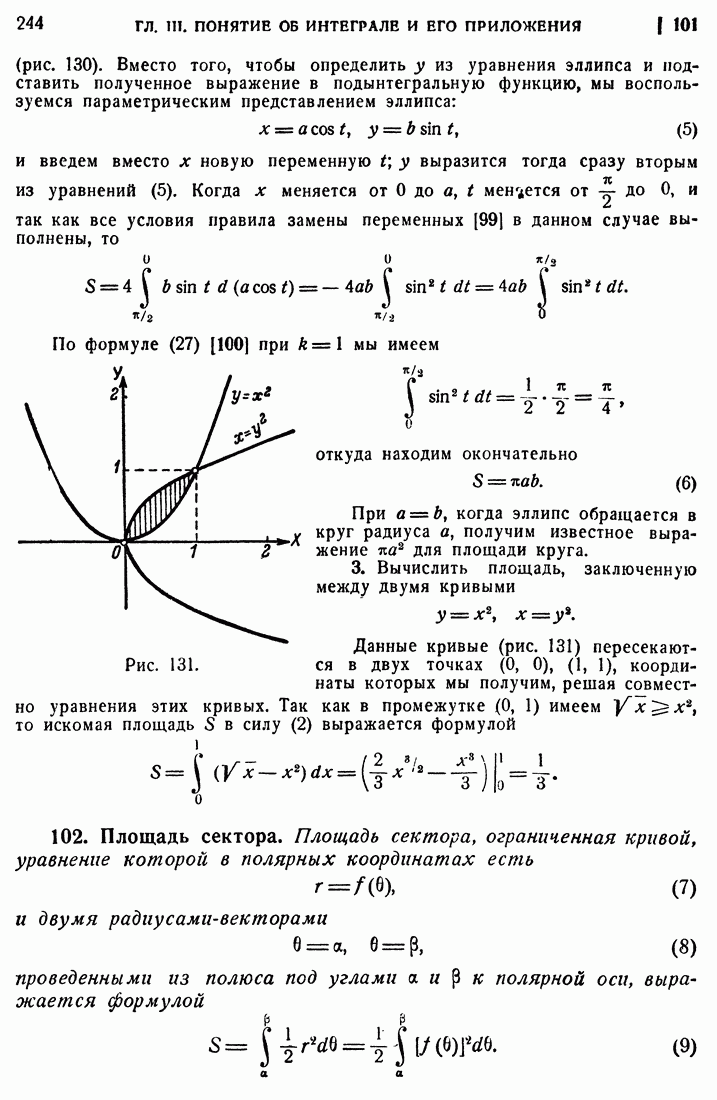
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
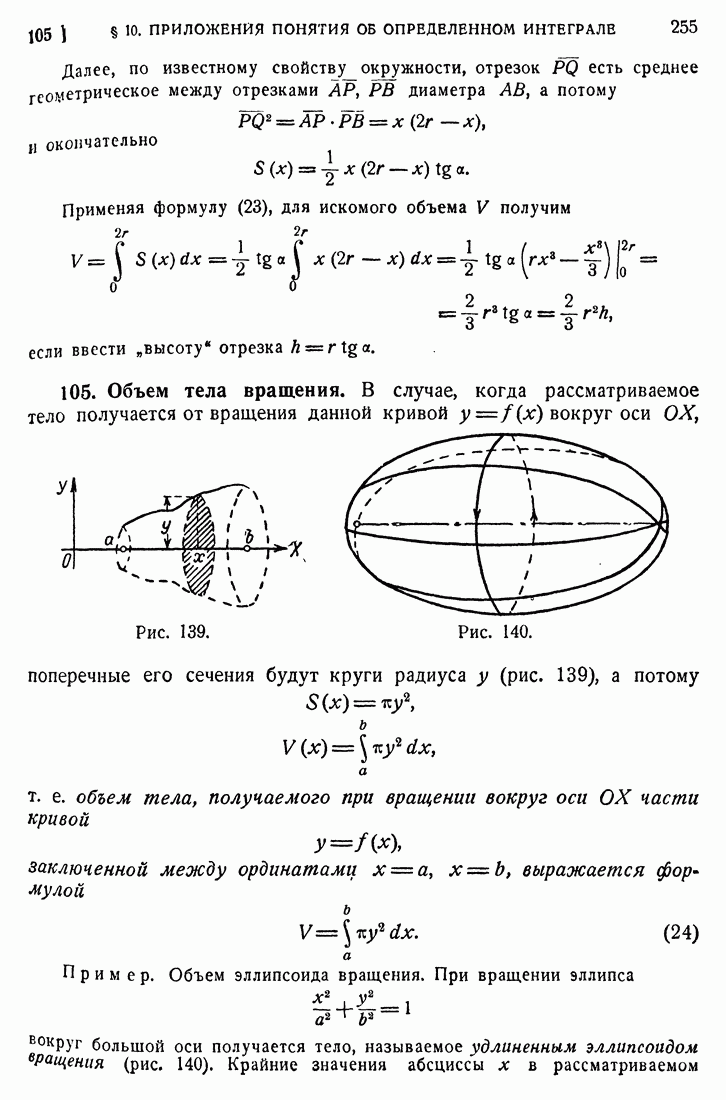
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
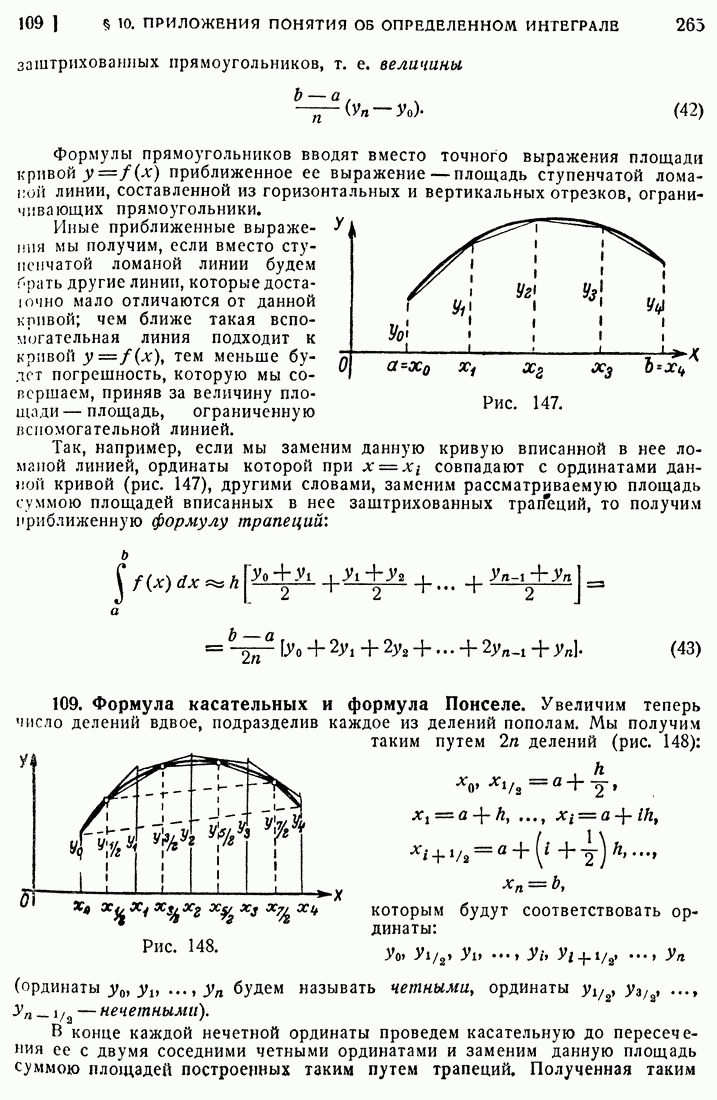
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
- 109. Формула касательных и формула Понселе.
- 110. Формула Симпсона.
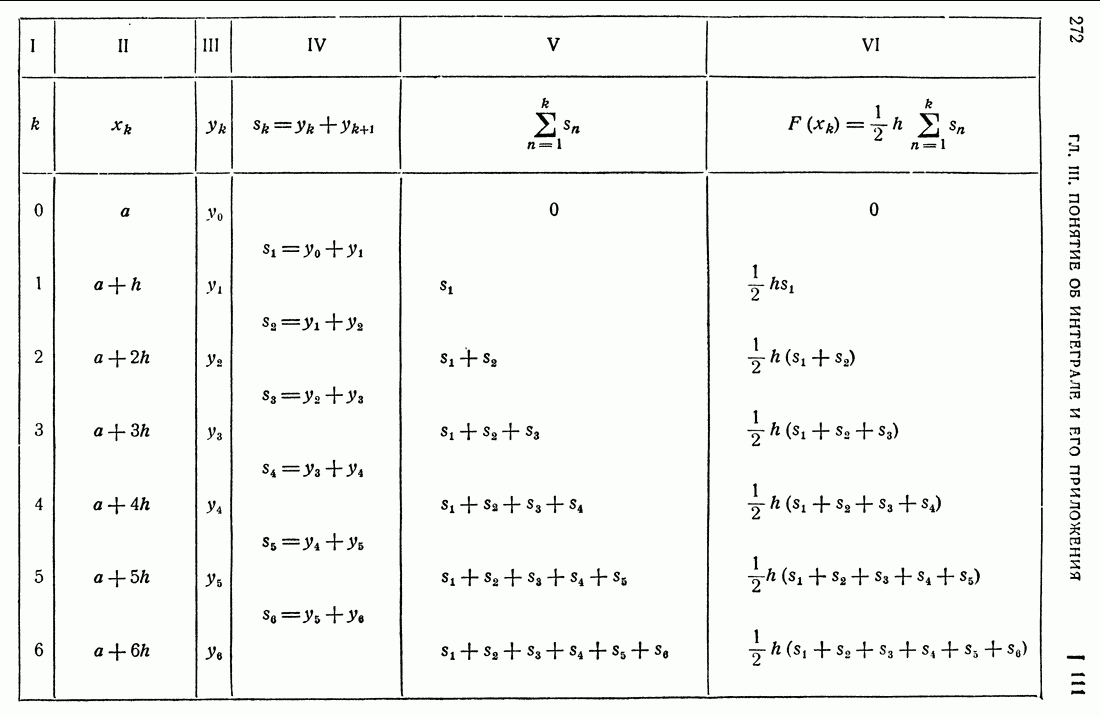
- 111. Вычисление определенного интеграла с переменным верхним пределом.
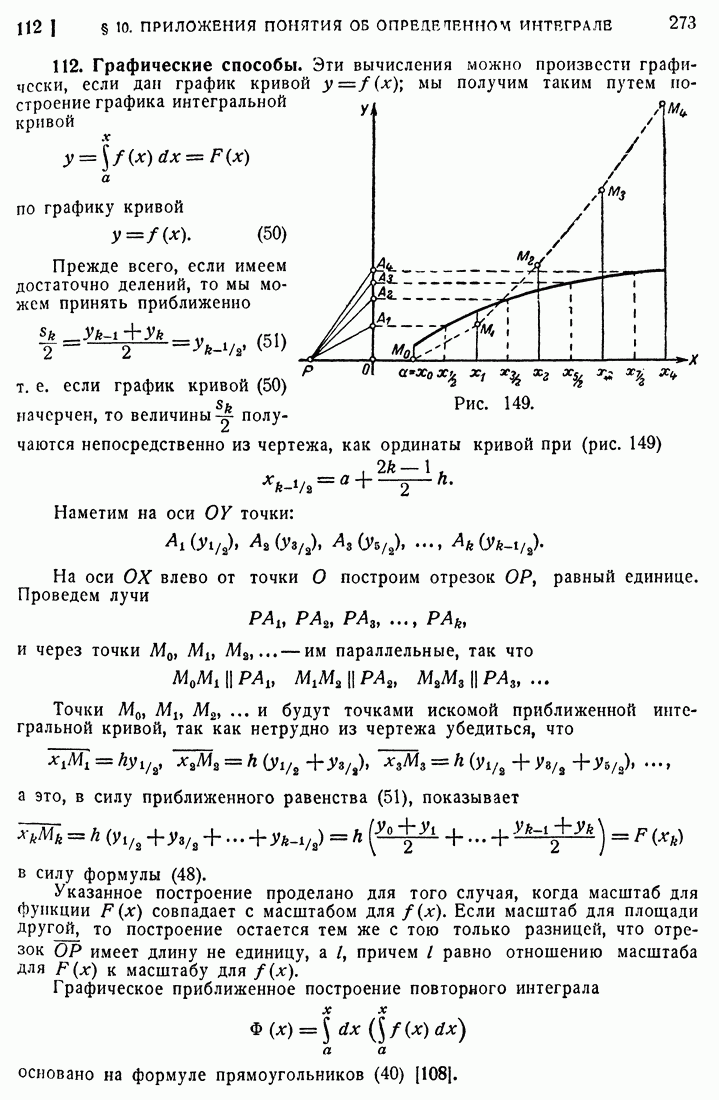
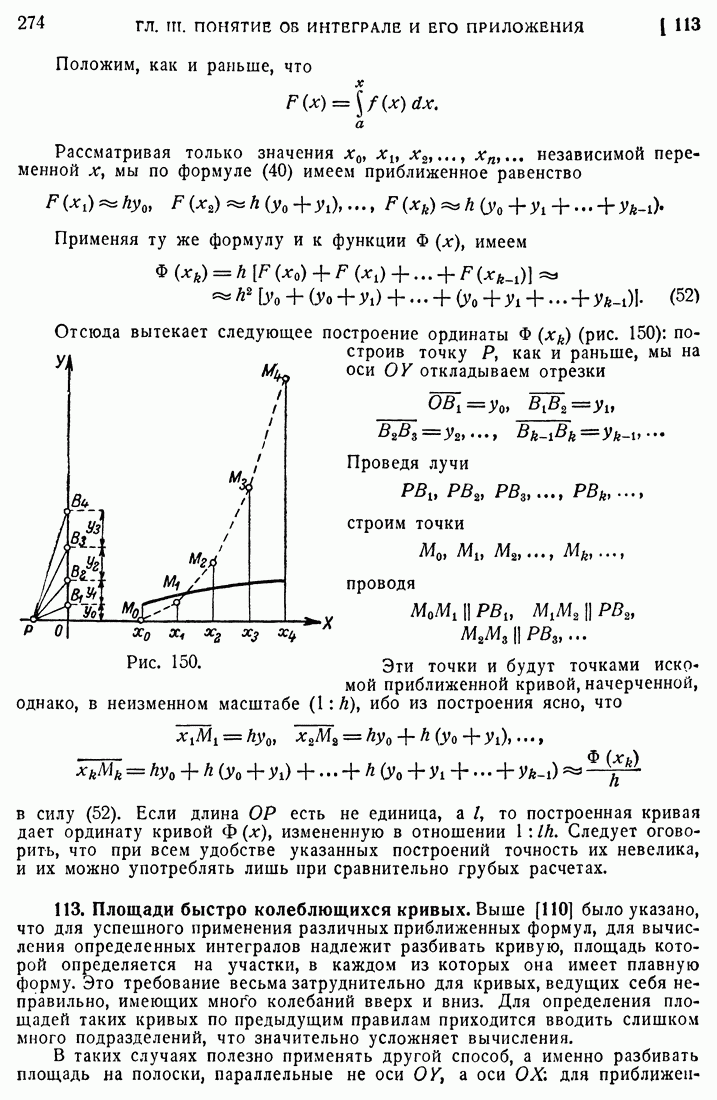
- 112. Графические способы.
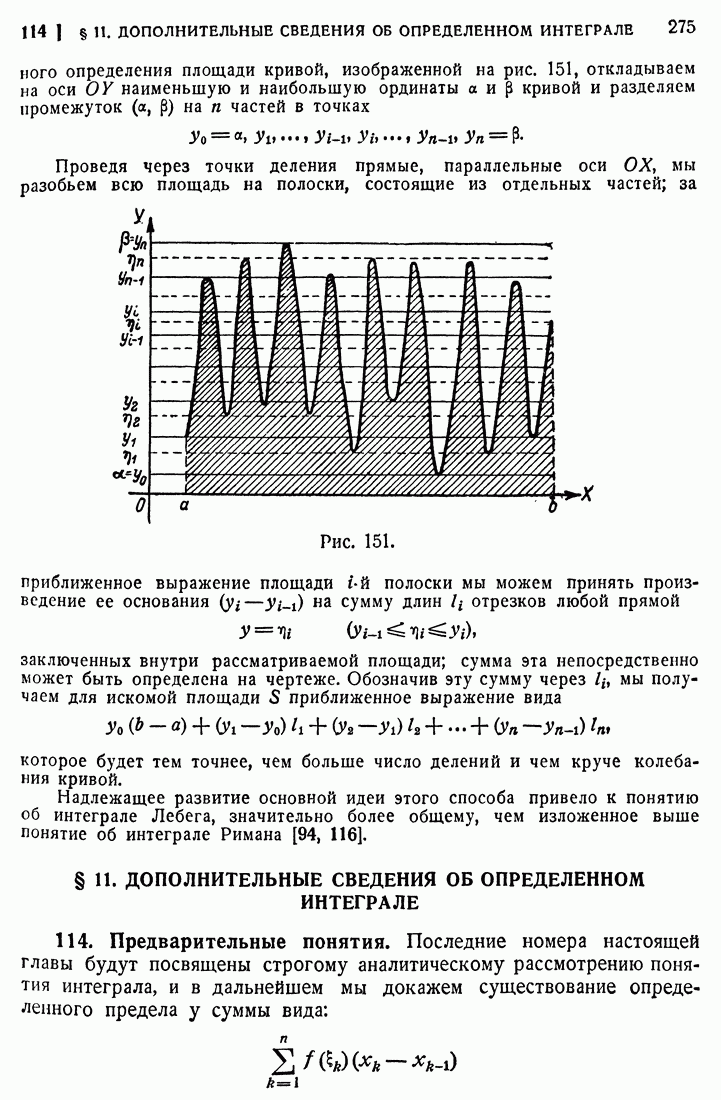
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
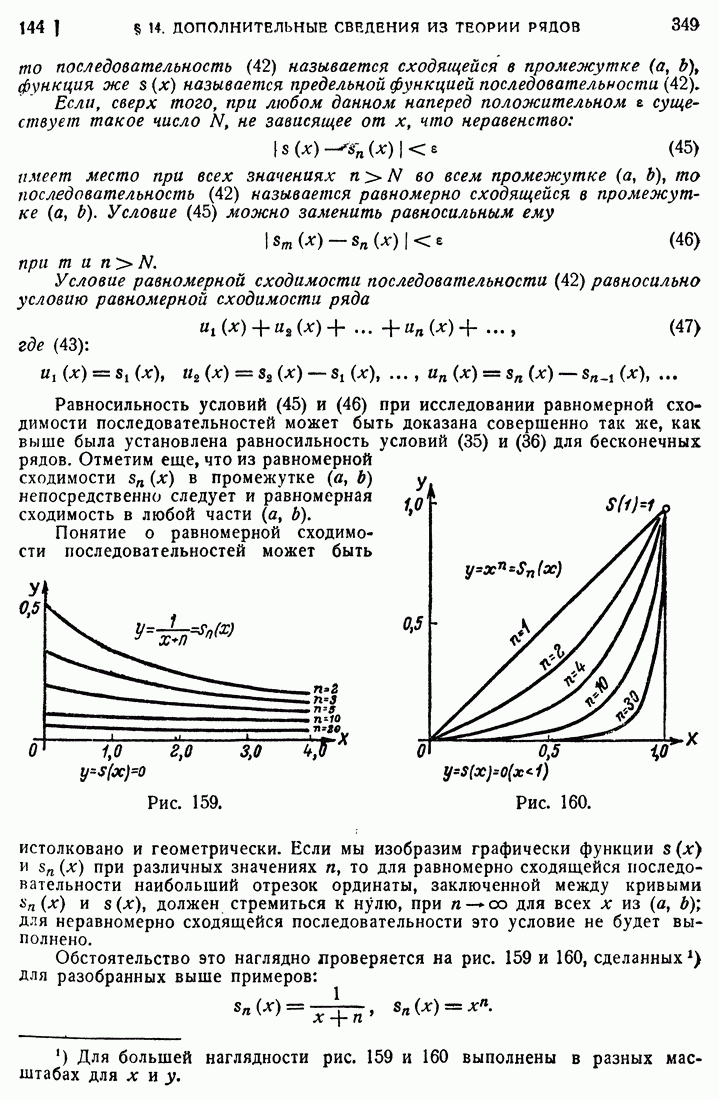
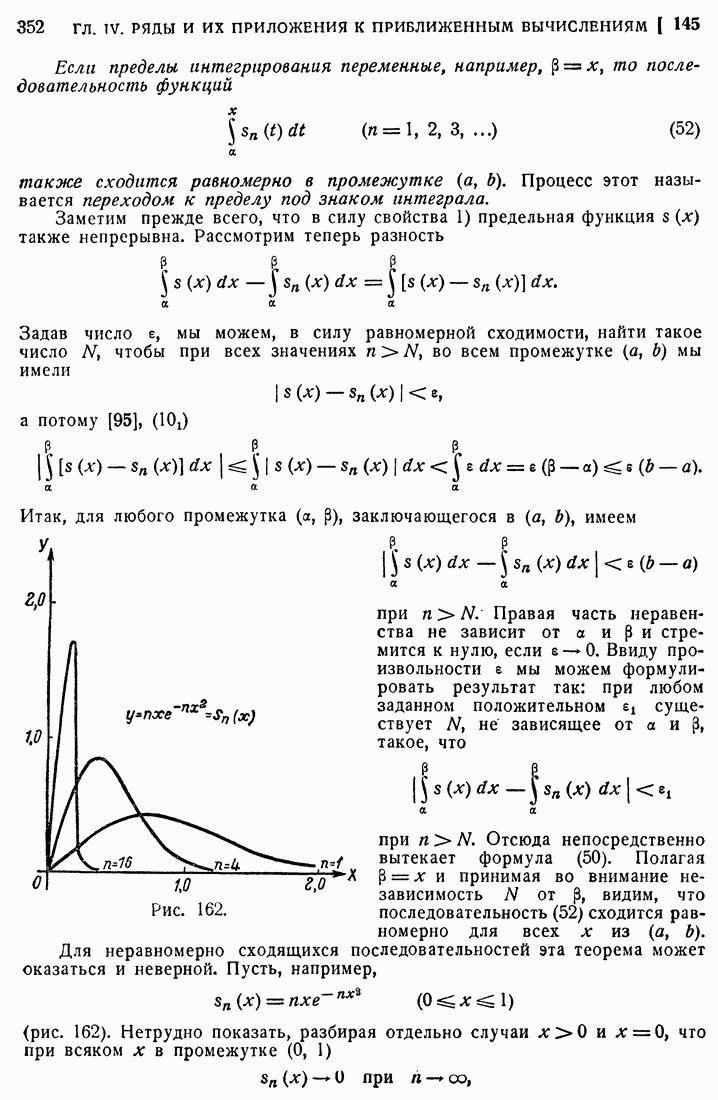
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
- 163. Исследование максимума и минимума функции двух независимых переменных.
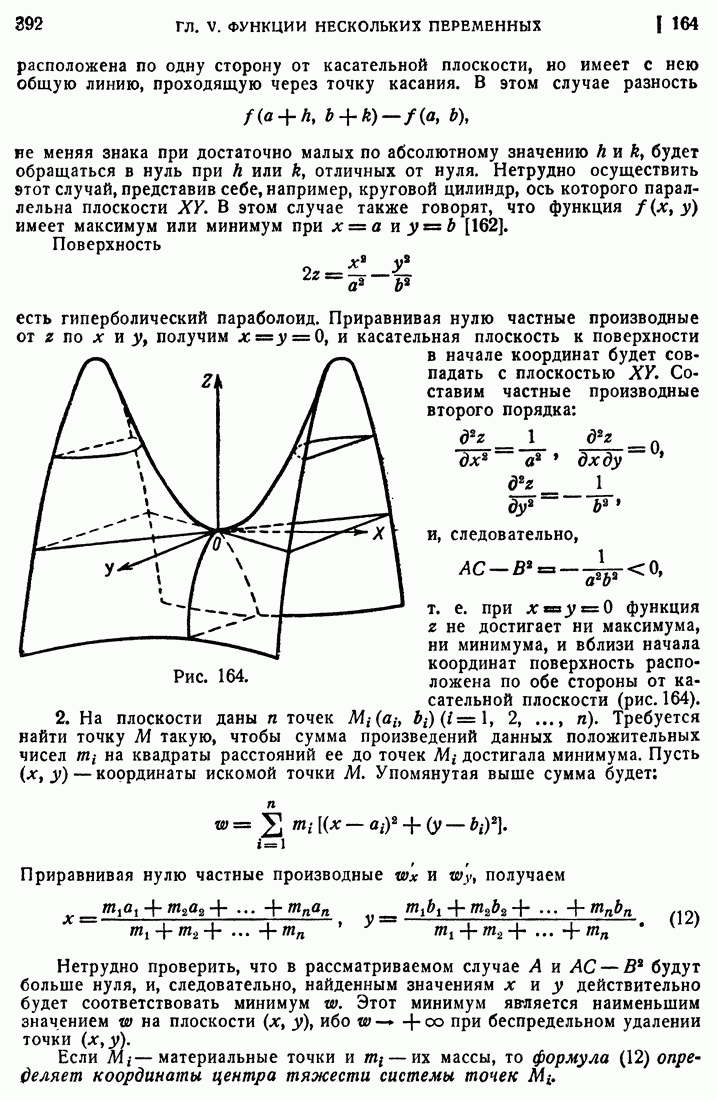
- 164. Примеры.
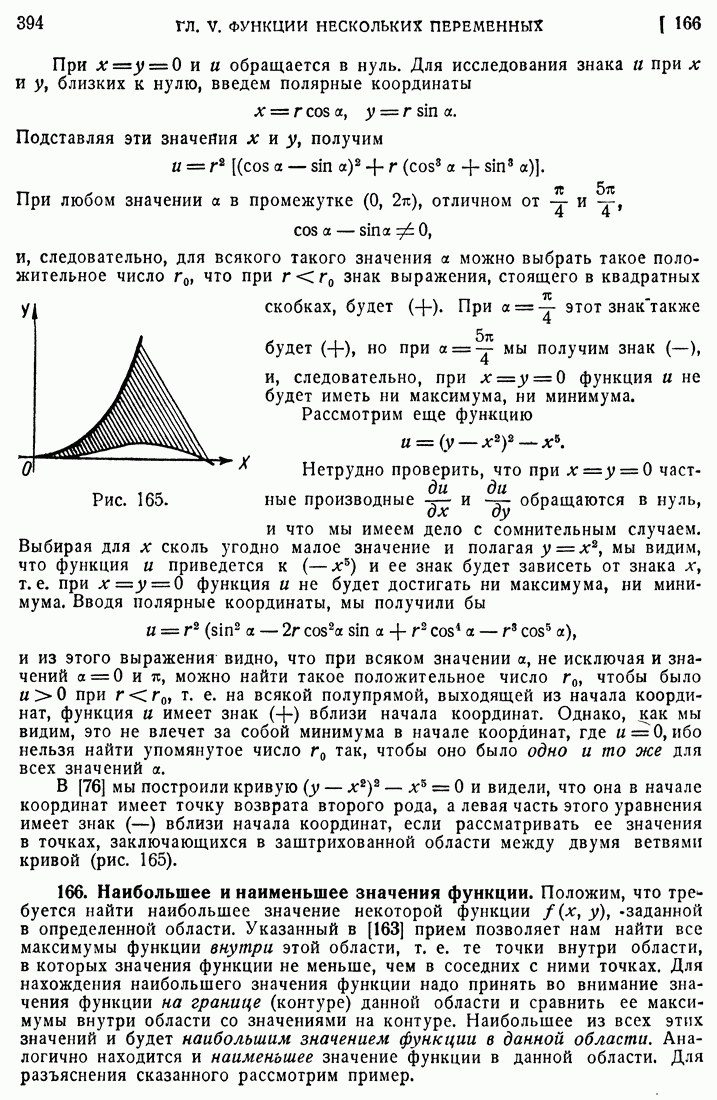
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
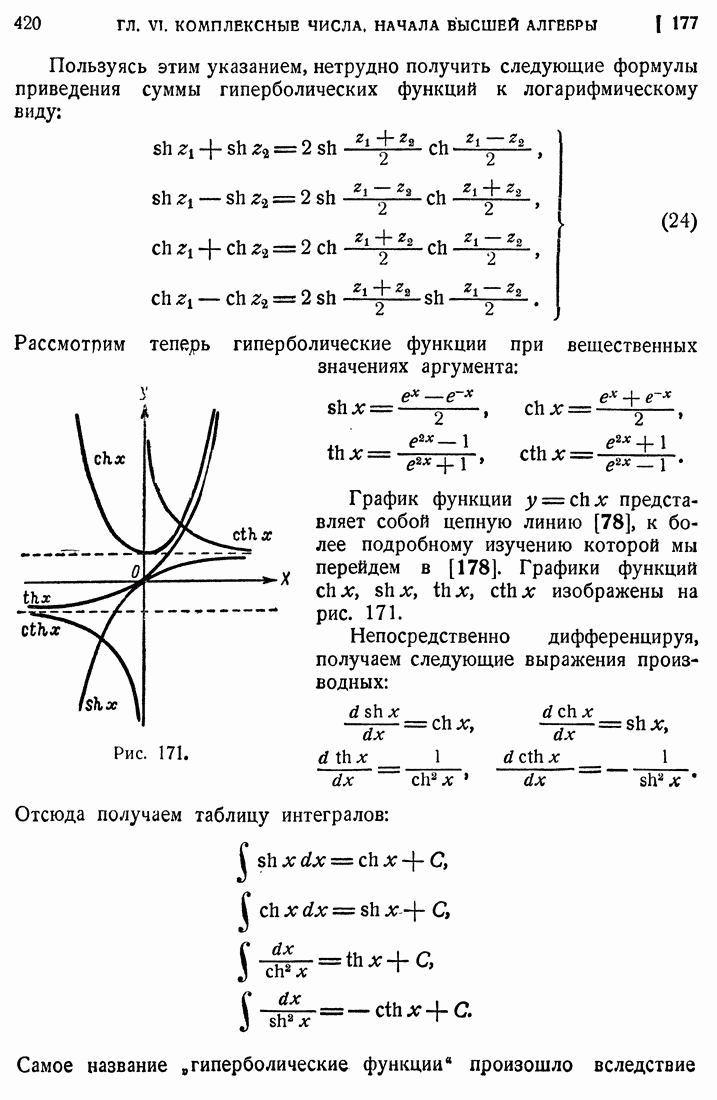
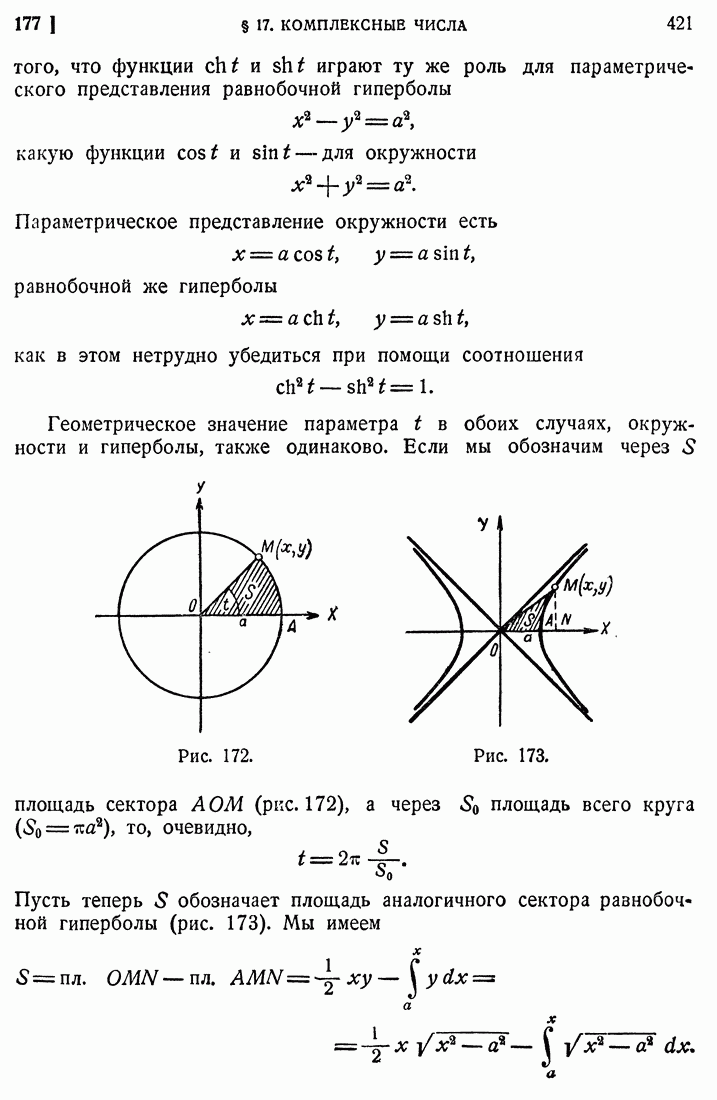
- 177. Тригонометрические и гиперболические функции.
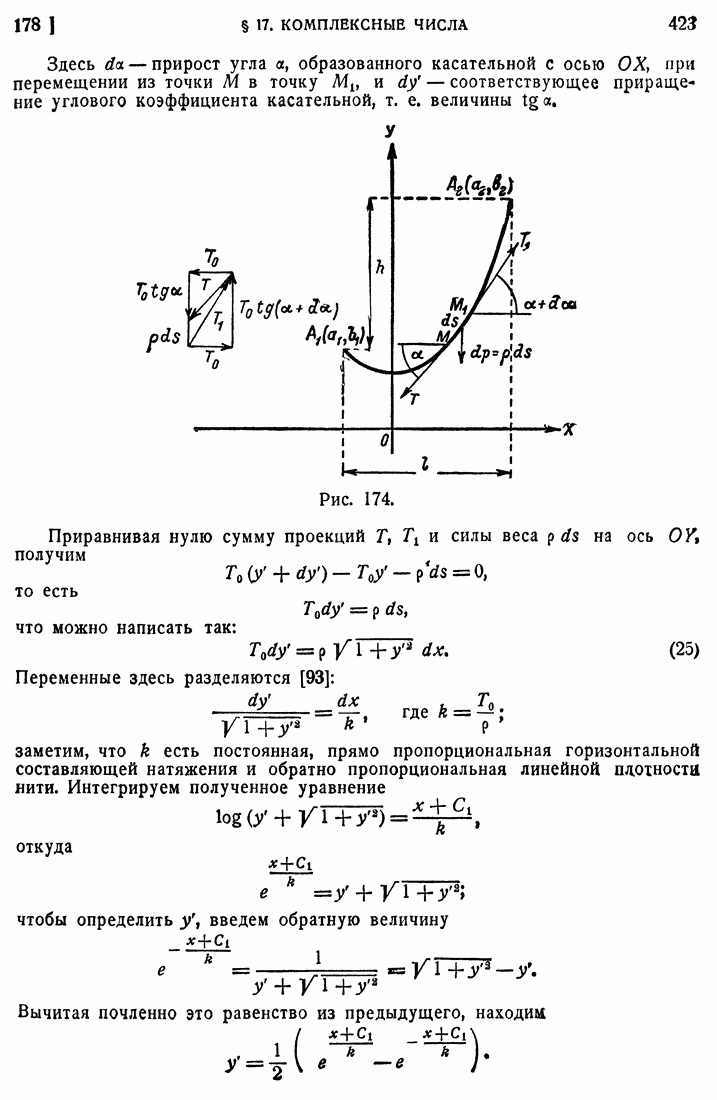
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
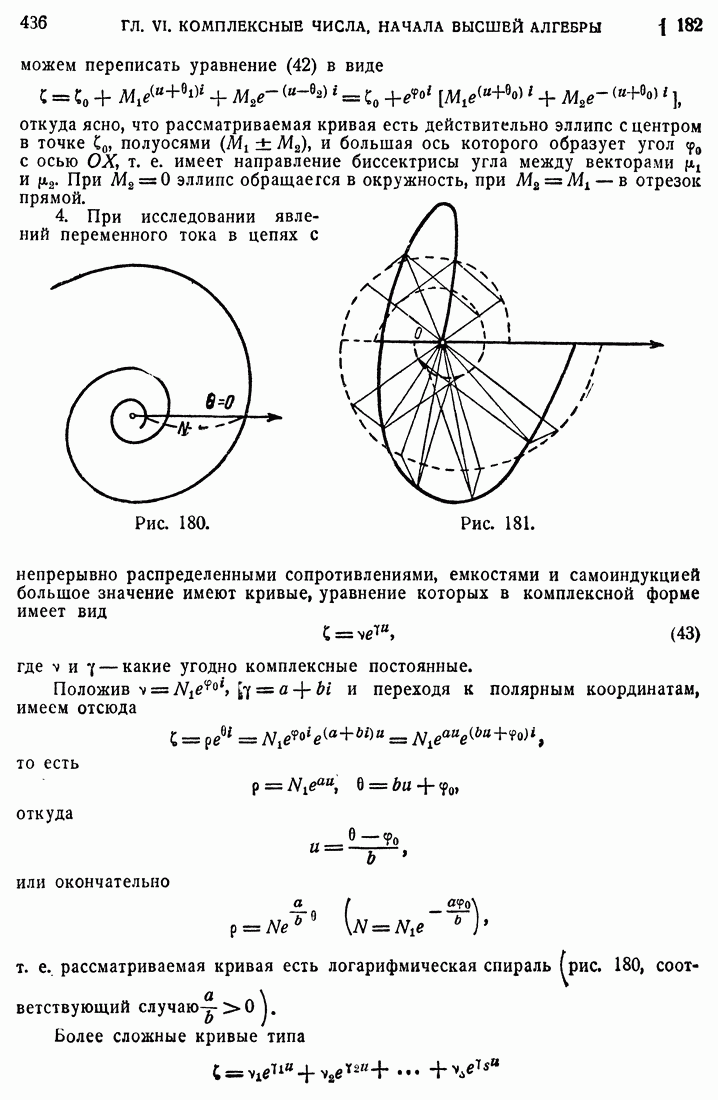
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
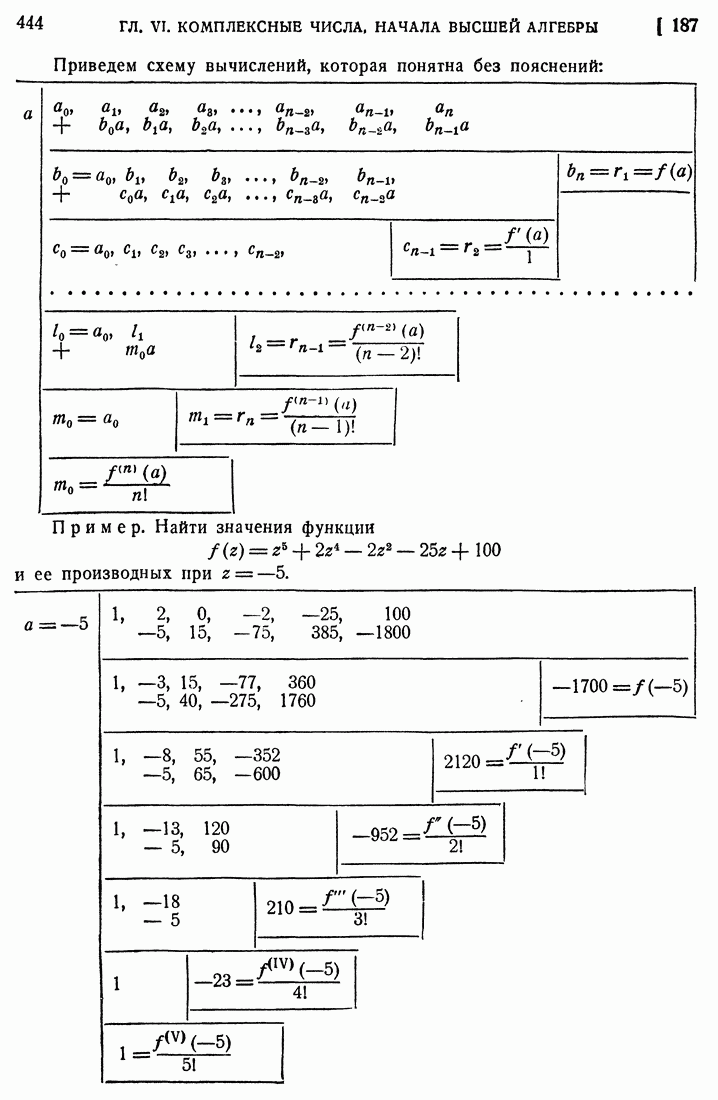
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
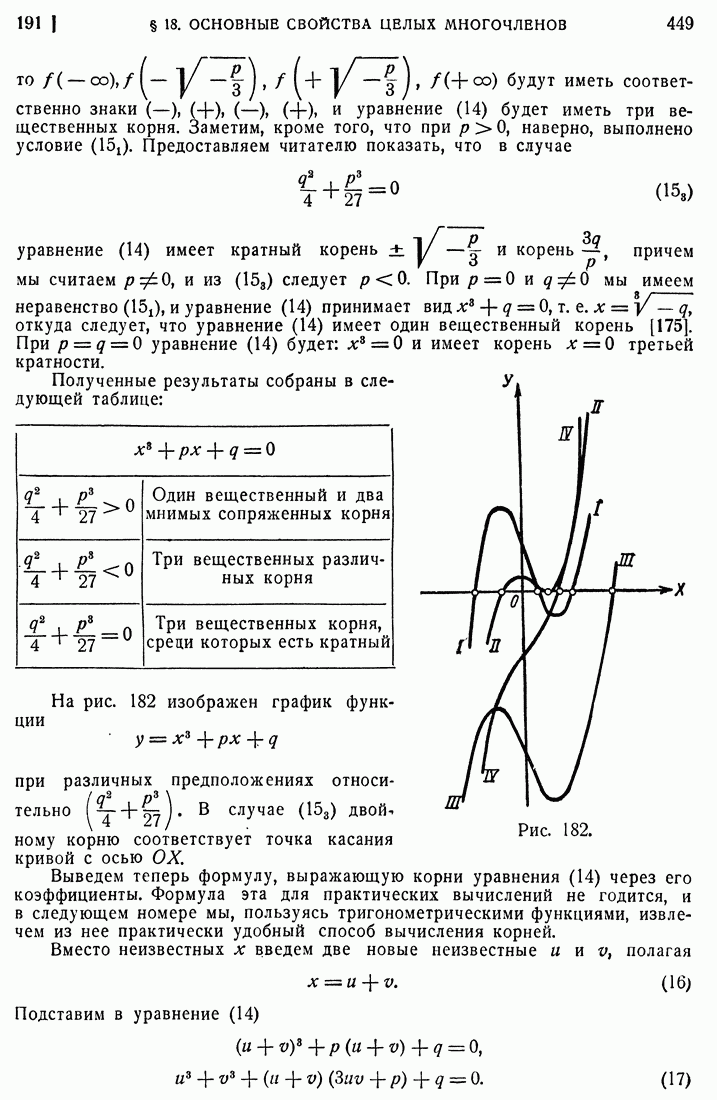
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
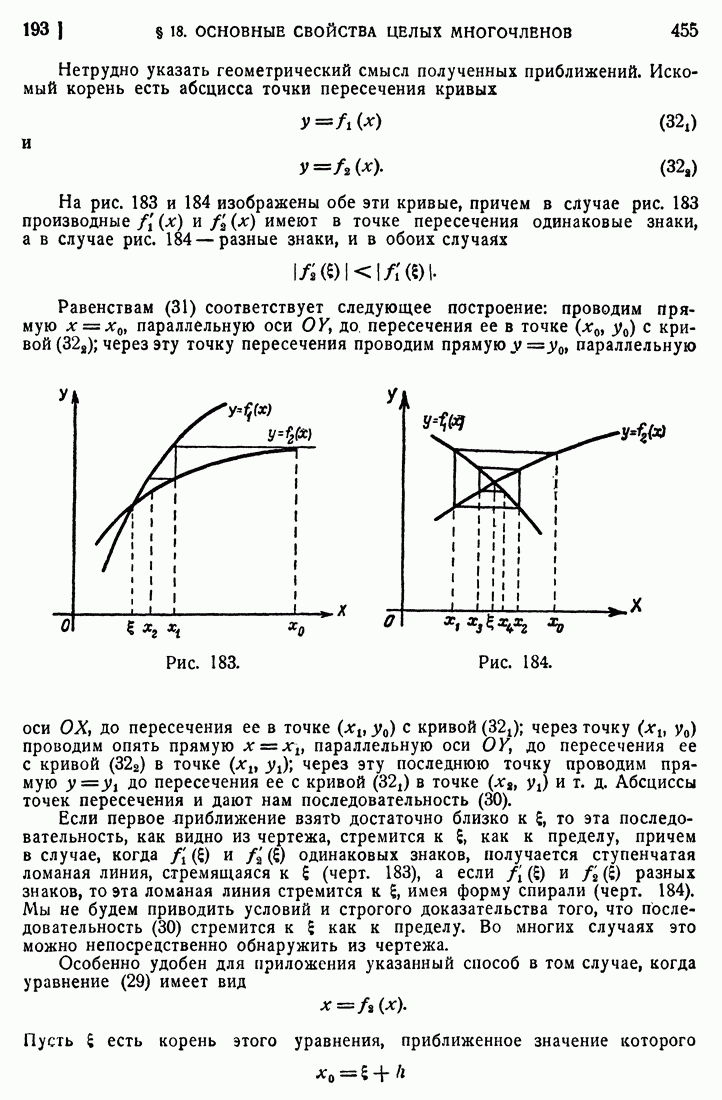
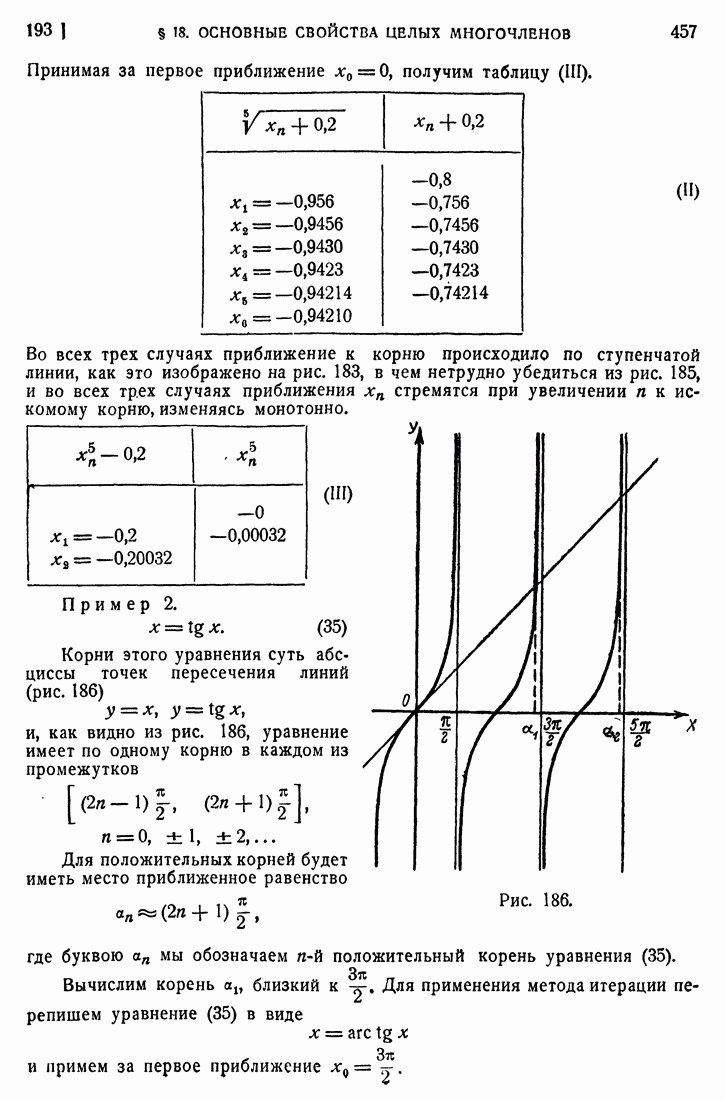
- 193. Способ итерации.
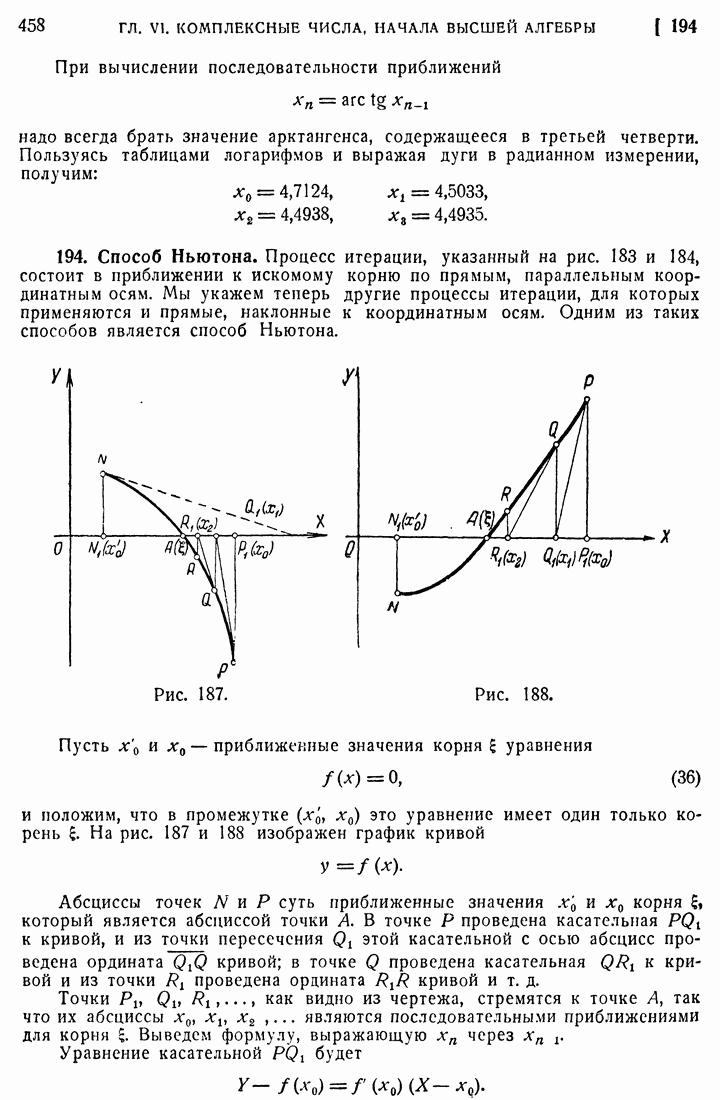
- 194. Способ Ньютона.
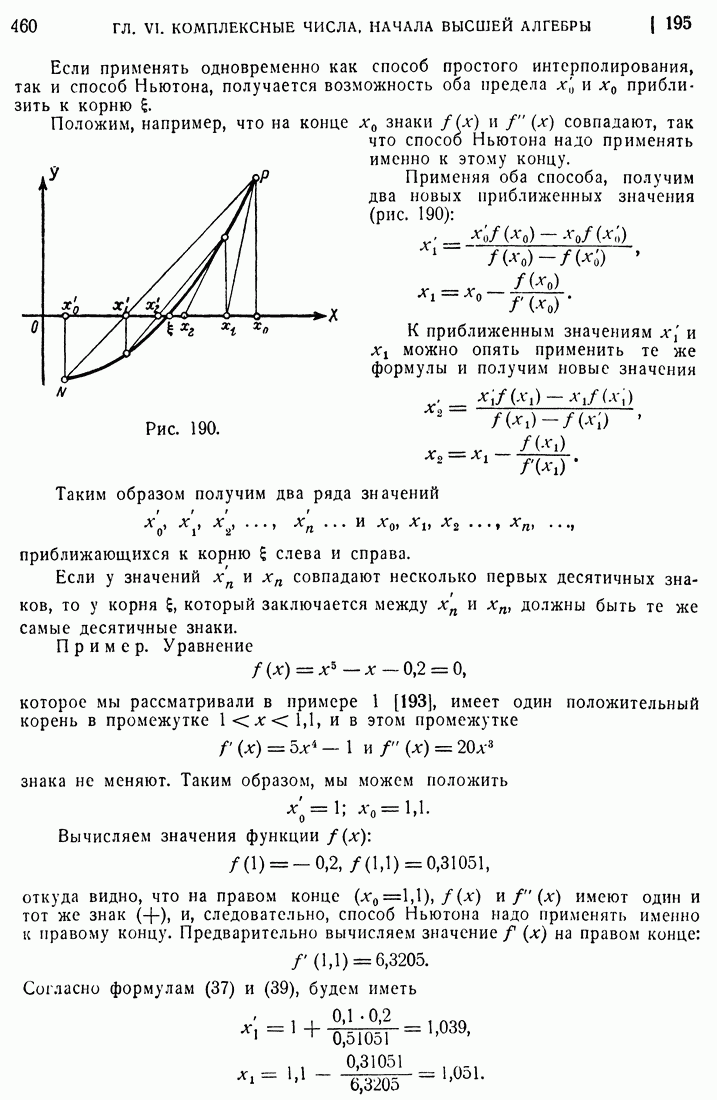
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…