| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
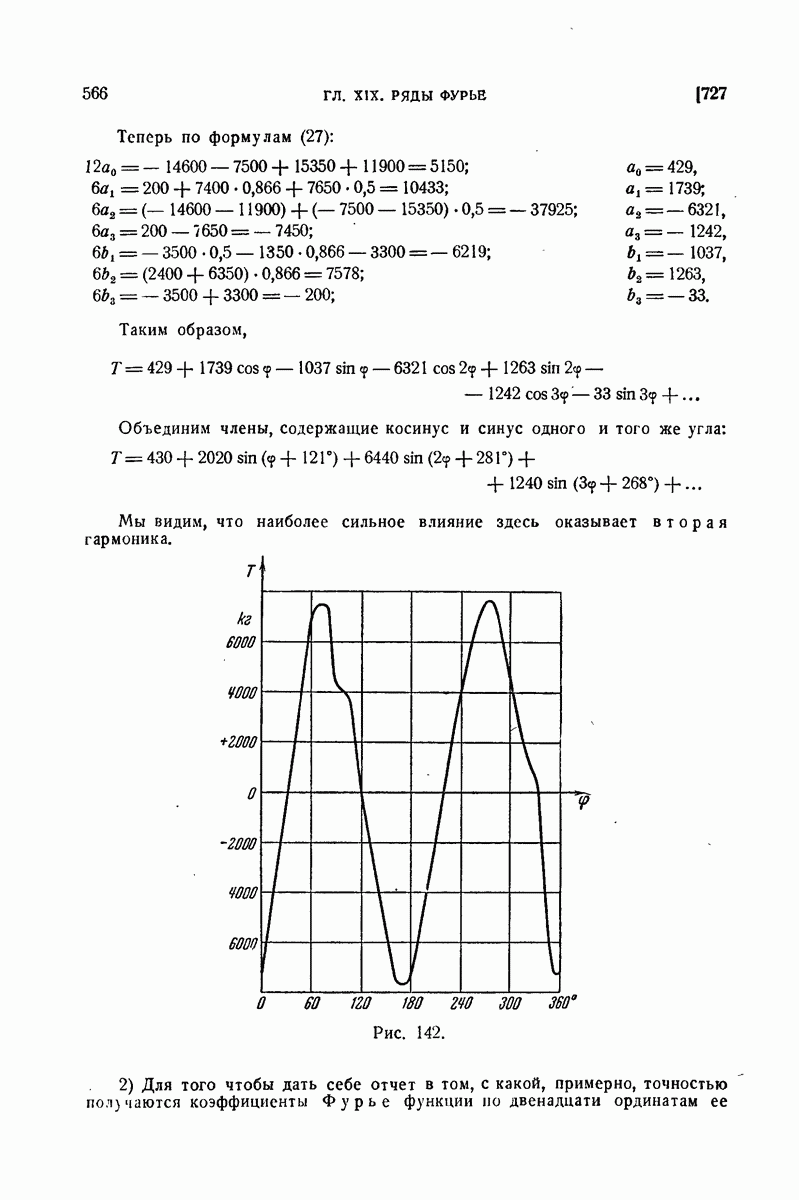
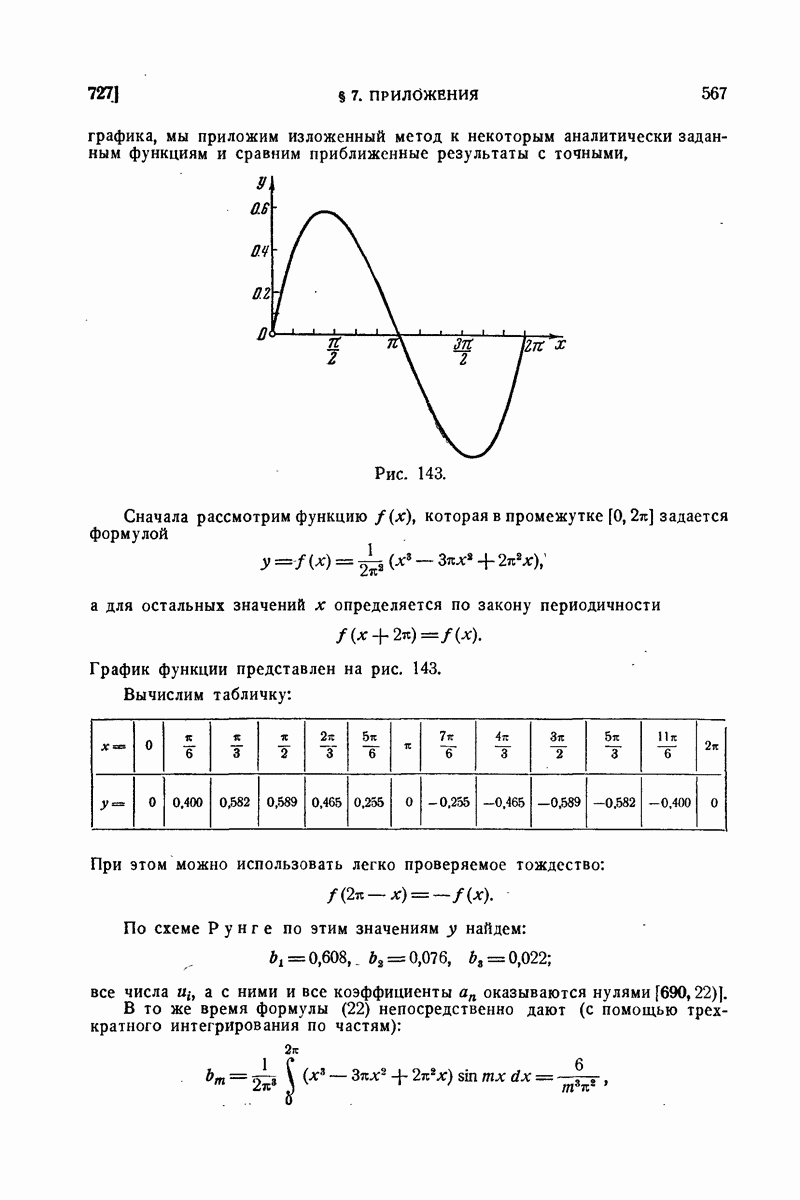
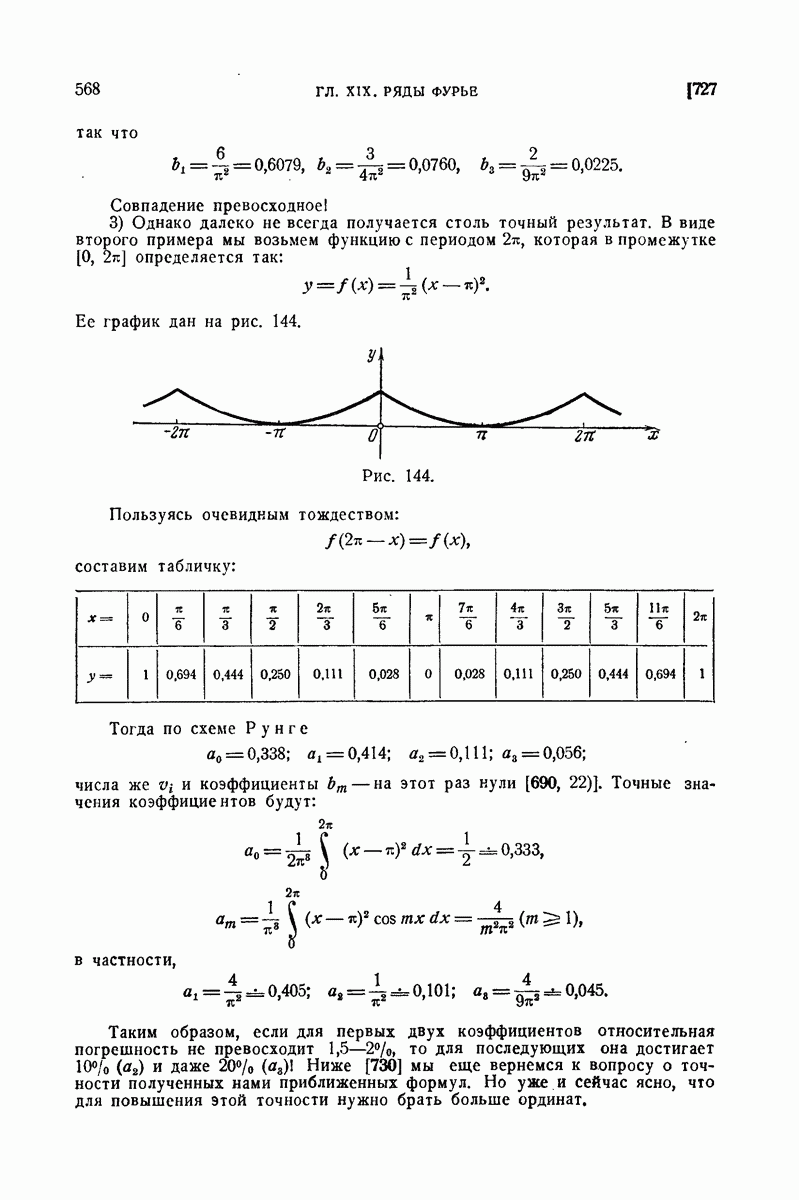
568. Классы функций с ограниченным изменением.
Мы уже упоминали о том, что монотонная функция имеет ограниченное изменение. Можно следующим образом расширить этот класс функций:
1°. Если функция  заданная в промежутке
заданная в промежутке  такова, что этот промежуток может быть разложен на конечное число частей
такова, что этот промежуток может быть разложен на конечное число частей

в каждой из которых  монотонна
монотонна  то она имеет в
то она имеет в  ограниченное изменение.
ограниченное изменение.
Разбив произвольным образом промежуток  на части, составим сумму
на части, составим сумму  Так как от присоединения каждой новой точки деления сумма
Так как от присоединения каждой новой точки деления сумма  может разве лишь увеличиться
может разве лишь увеличиться  то, присоединив к точкам деления все точки
то, присоединив к точкам деления все точки  о которых была речь выше, мы получим сумму
о которых была речь выше, мы получим сумму  . Если выделить из суммы
. Если выделить из суммы  те слагаемые, которые относятся к промежутку
те слагаемые, которые относятся к промежутку  то, обозначая их сумму значком
то, обозначая их сумму значком  наверху, будем иметь
наверху, будем иметь

так что

Так как произвольная сумма  не превосходит этого числа, то оно и будет полным изменением функции.
не превосходит этого числа, то оно и будет полным изменением функции.
2°. Если функция  в промежутке
в промежутке  удовлетворяет условию
удовлетворяет условию

где  — любые точки промежутка, то она имеет ограниченное изменение, причем
— любые точки промежутка, то она имеет ограниченное изменение, причем

Это следует из неравенства

В частности,
3°. Функция  будет в промежутке
будет в промежутке  функцией с ограниченным изменением, если она имеет в нем ограниченную производную:
функцией с ограниченным изменением, если она имеет в нем ограниченную производную: 
В самом деле, по теореме о среднем в этом случае

так что выполнено условие Липшица (3).
На основании этого замечания можно, например, утверждать ограниченность изменения функции

в любом конечном промежутке, ибо производная ее

ограничена. Любопытно отметить, что в каждом промежутке, содержащем точку 0, эта функция «бесконечно колеблется», т. е. бесконечное число раз переходит от возрастания к убыванию, и наоборот.
Обширный класс функций с ограниченным изменением дается следующим предложением:
4°. Если  в конечном (или даже в бесконечном) промежутке
в конечном (или даже в бесконечном) промежутке  представима в виде интеграла с переменным верхним пределом:
представима в виде интеграла с переменным верхним пределом:

где  предполагается абсолютно интегрируемой в этом промежутке, то
предполагается абсолютно интегрируемой в этом промежутке, то  имеет в нем ограниченное изменение. При этом
имеет в нем ограниченное изменение. При этом

Пусть  — конечный промежуток; тогда
— конечный промежуток; тогда

откуда и следует наше утверждение.
Если же речь идет о бесконечном промежутке  то достаточно заметить, что
то достаточно заметить, что

Замечание. Можно доказать, что как в случае конечного, так и в случае бесконечного промежутка на самом деле имеет место точное равенство

Если же функция  в промежутке
в промежутке  интегрируема, но не абсолютно, то полное изменение
интегрируема, но не абсолютно, то полное изменение  заведомо бесконечно. Мы не будем останавливаться на этом, но поясним лишь последнюю часть замечания примерами.
заведомо бесконечно. Мы не будем останавливаться на этом, но поясним лишь последнюю часть замечания примерами.
Пусть  так что
так что

Тогда, например, для

но в п’ 482 мы показали, что интеграл этот — неабсолютно сходящийся. Пользуясь той же идеей, что и там, разложим промежуток [0, 2] точками

для соответствующей суммы  очевидно, будет
очевидно, будет

откуда и следует, что

Аналогично этому легко показать, что функция

в промежутке  имеет неограниченное изменение [ср. 476].
имеет неограниченное изменение [ср. 476].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
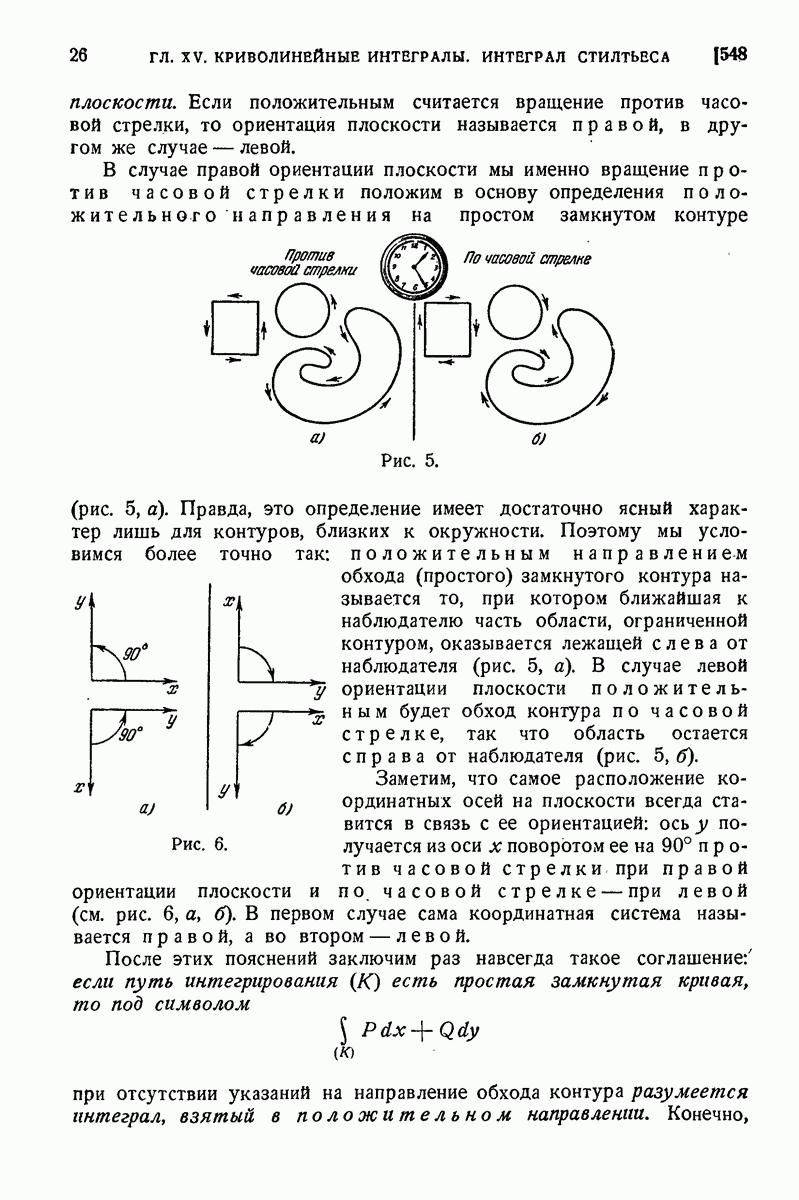
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
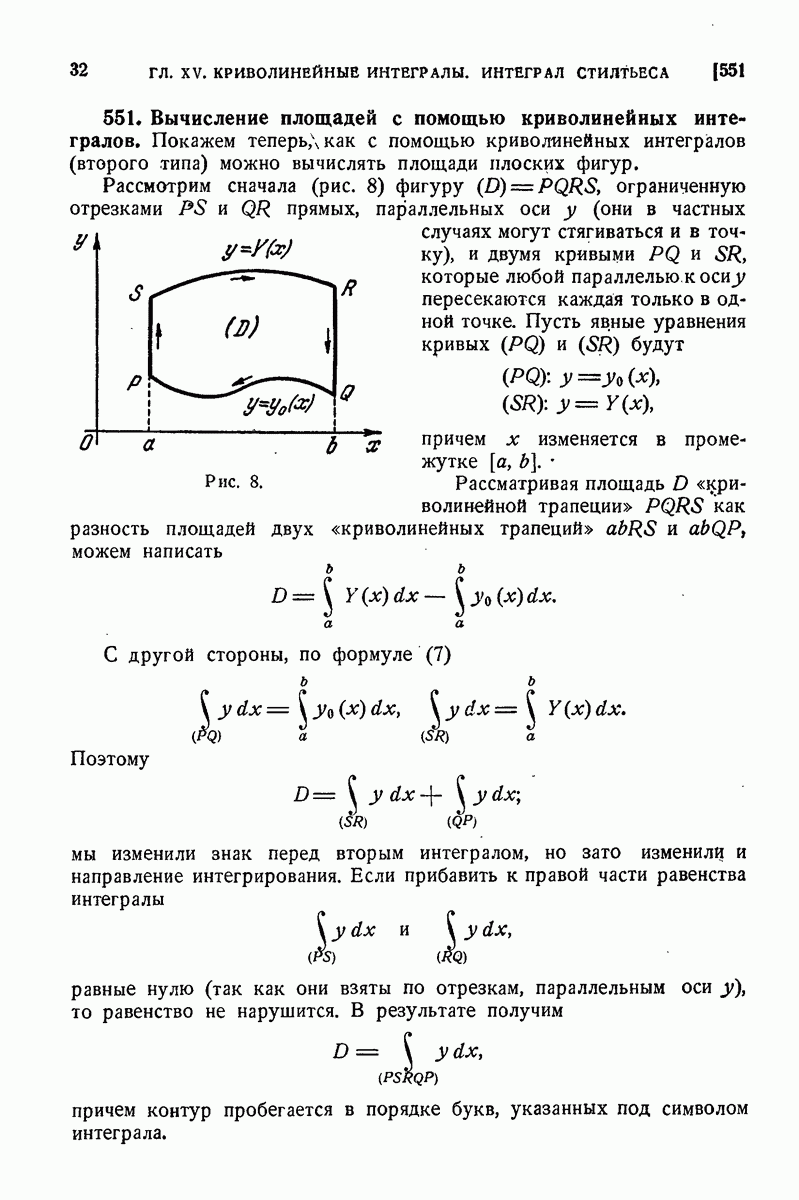
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
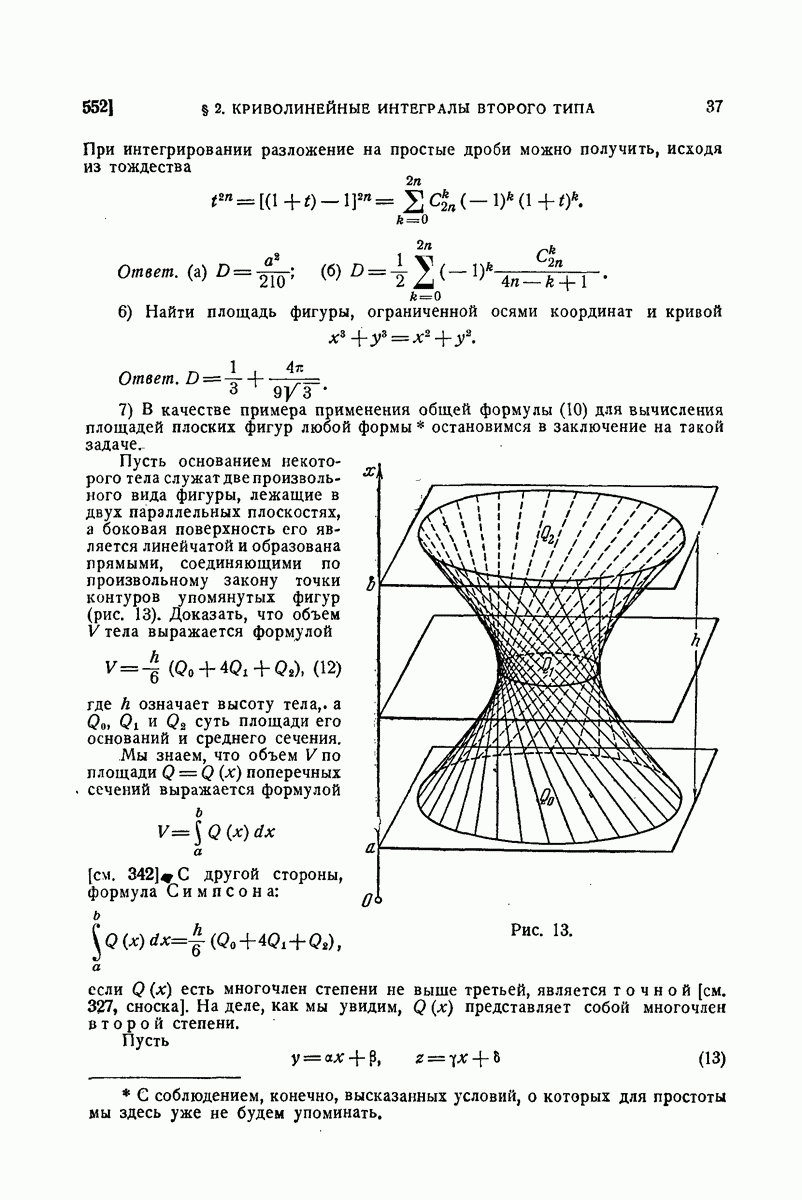
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
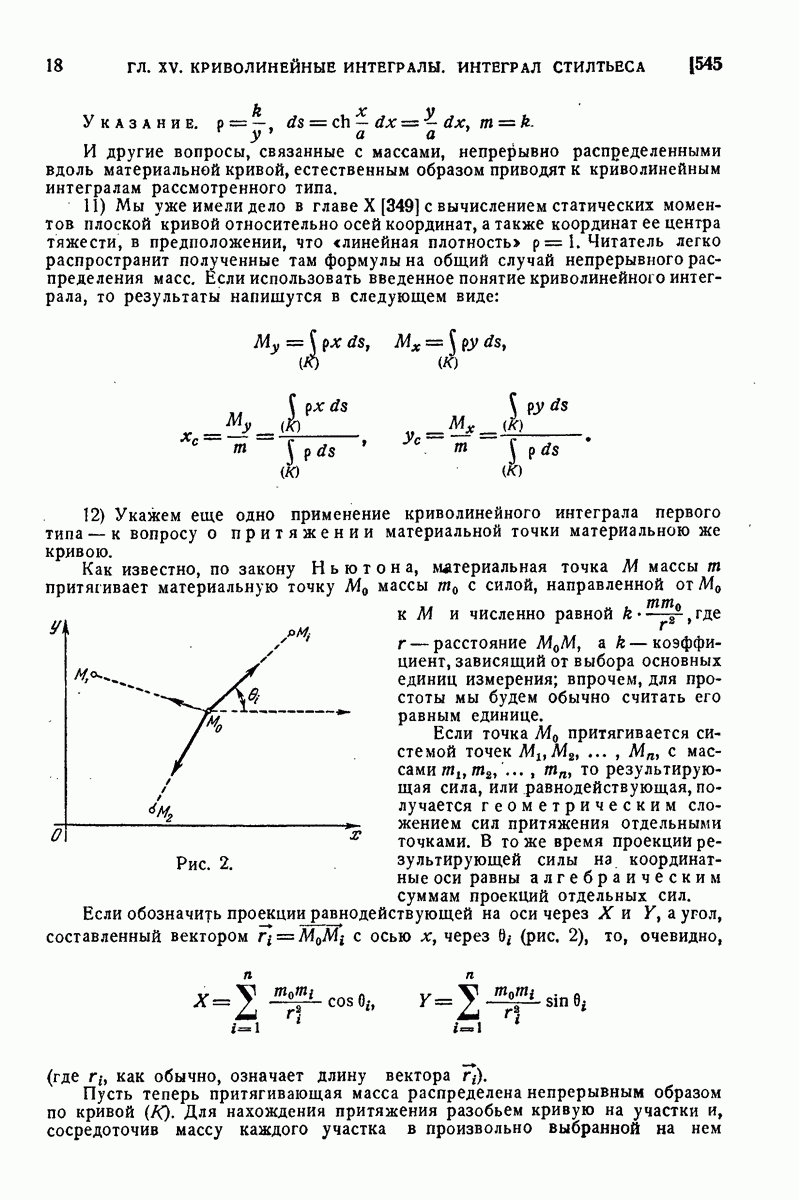
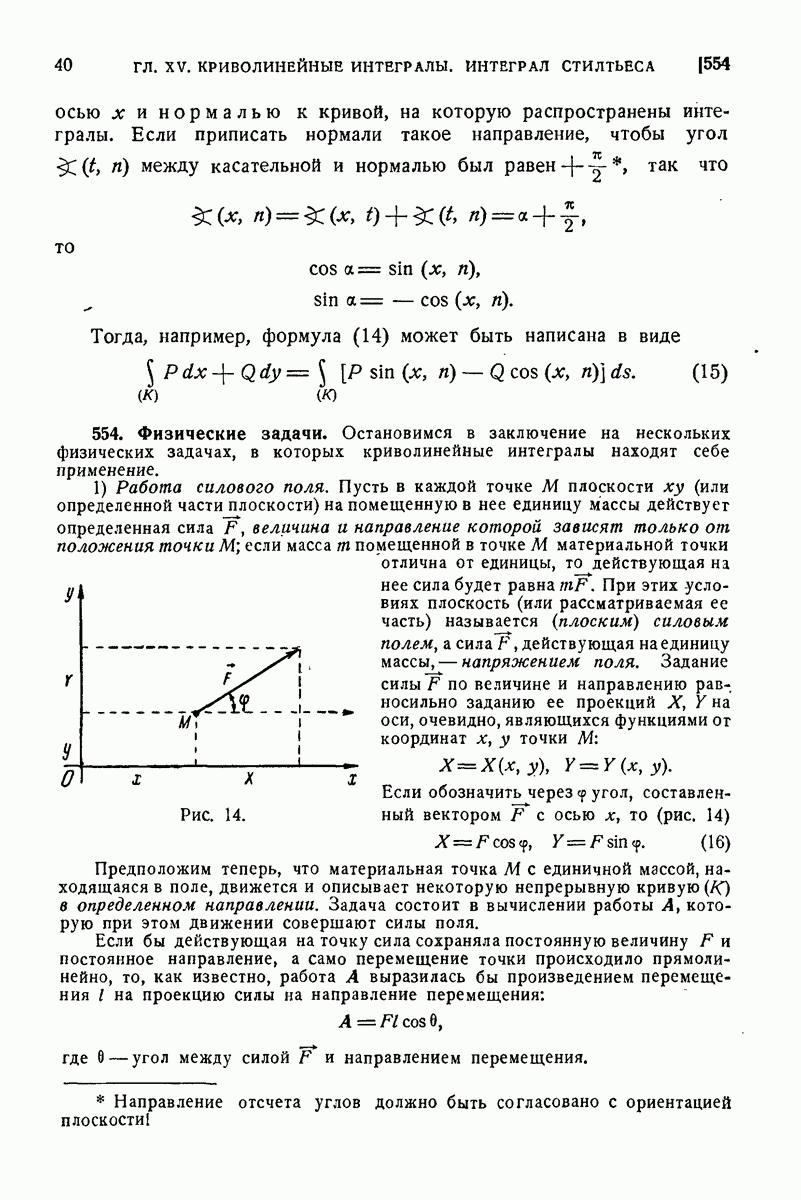
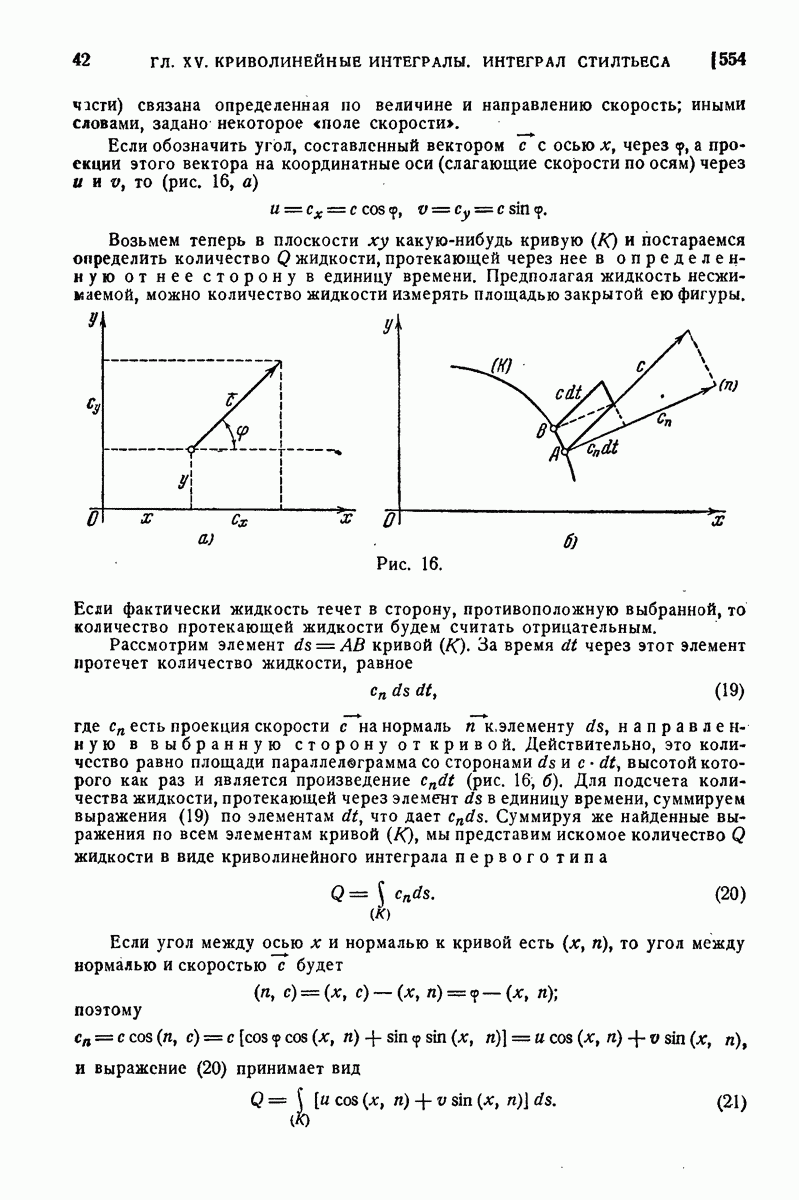
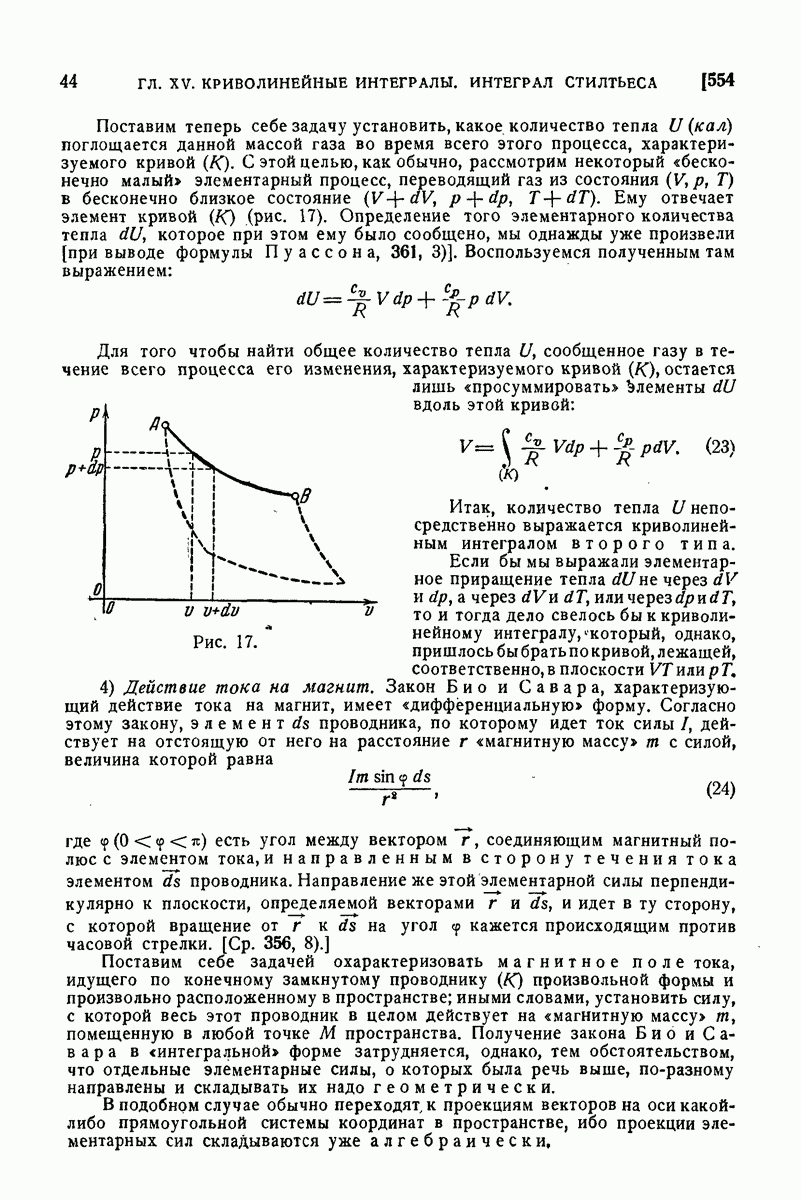
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
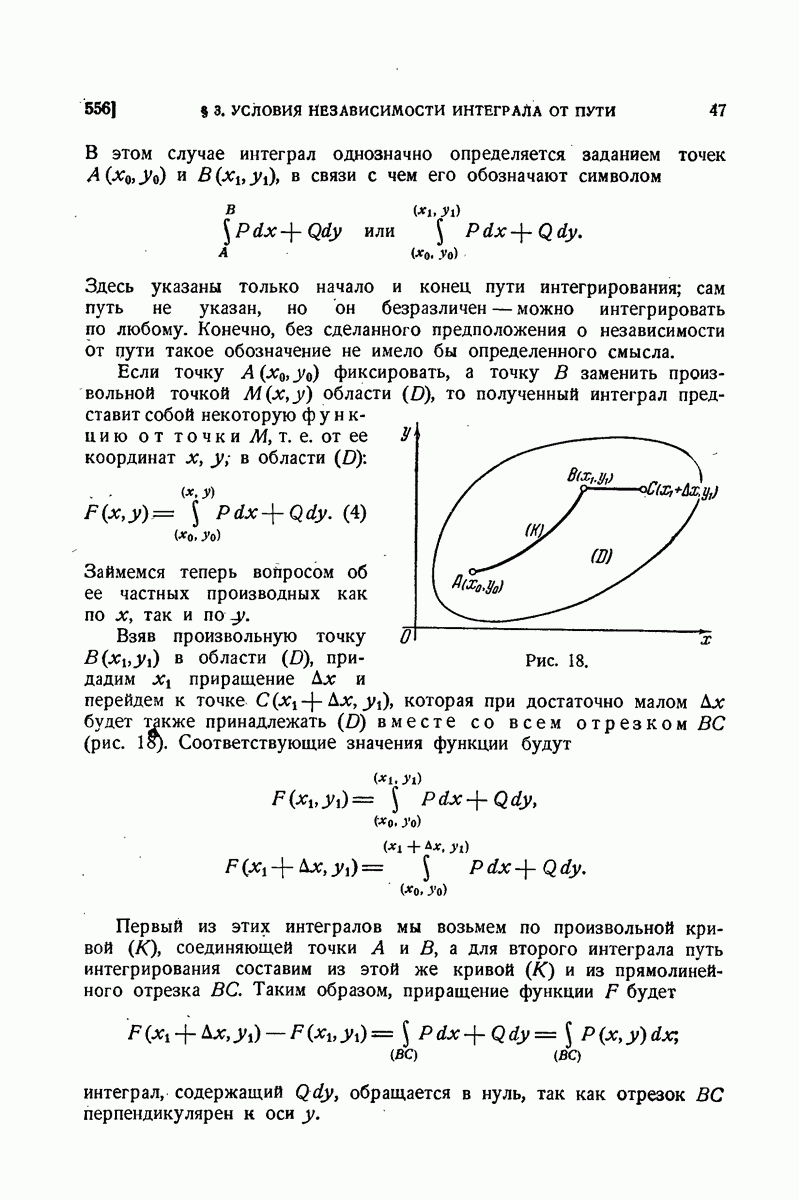
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.