| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
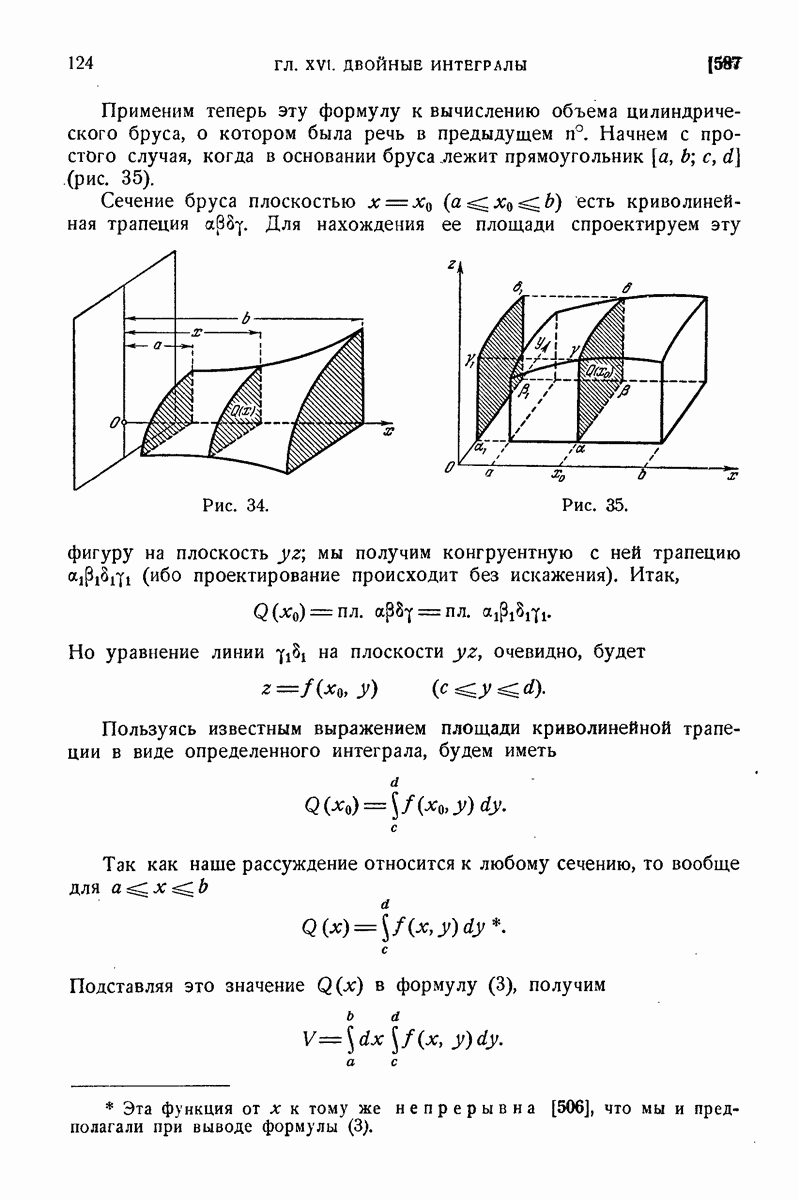
124
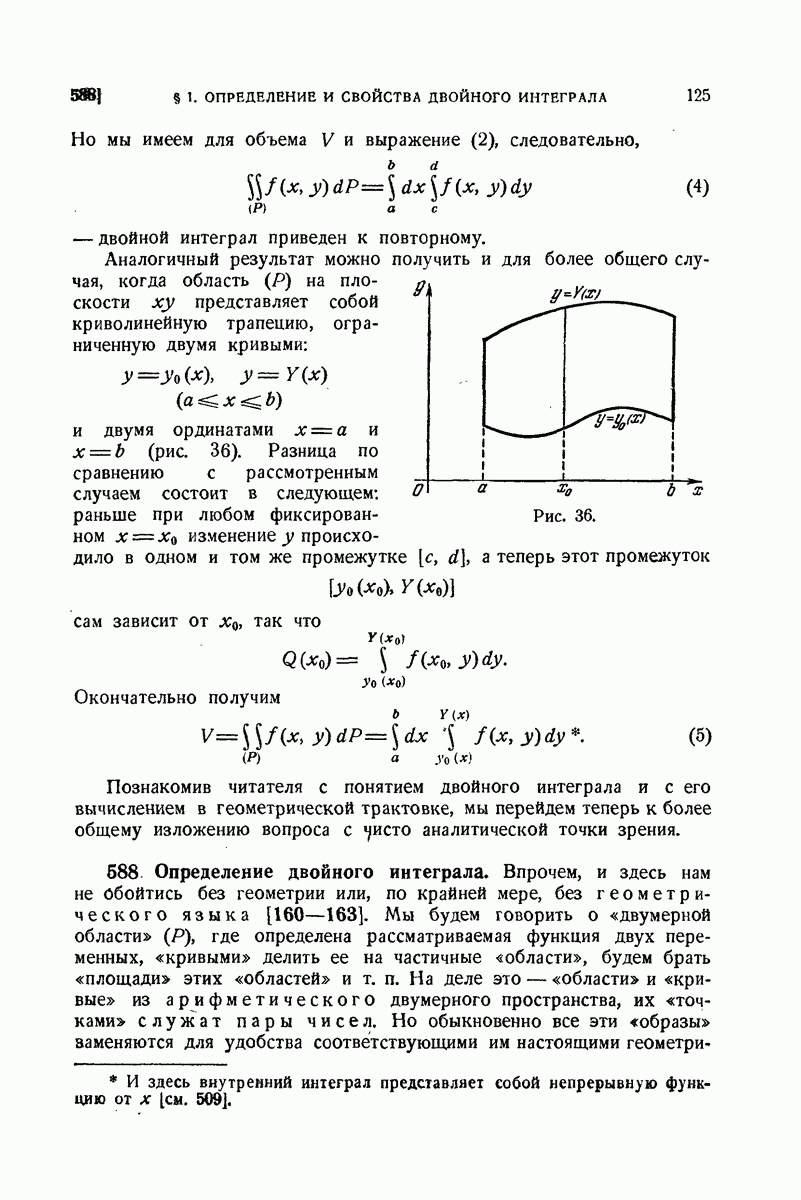
125
126
127
128
129
130
131
132
133
134
135
136
137
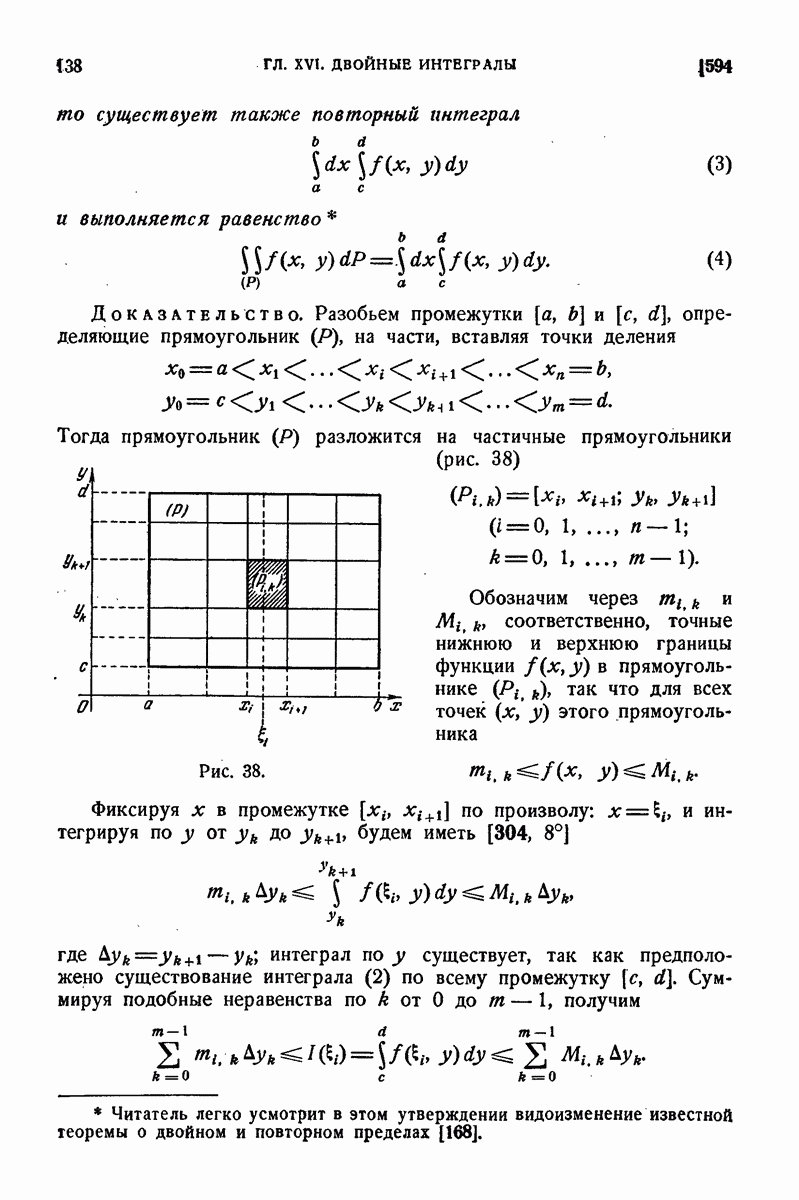
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
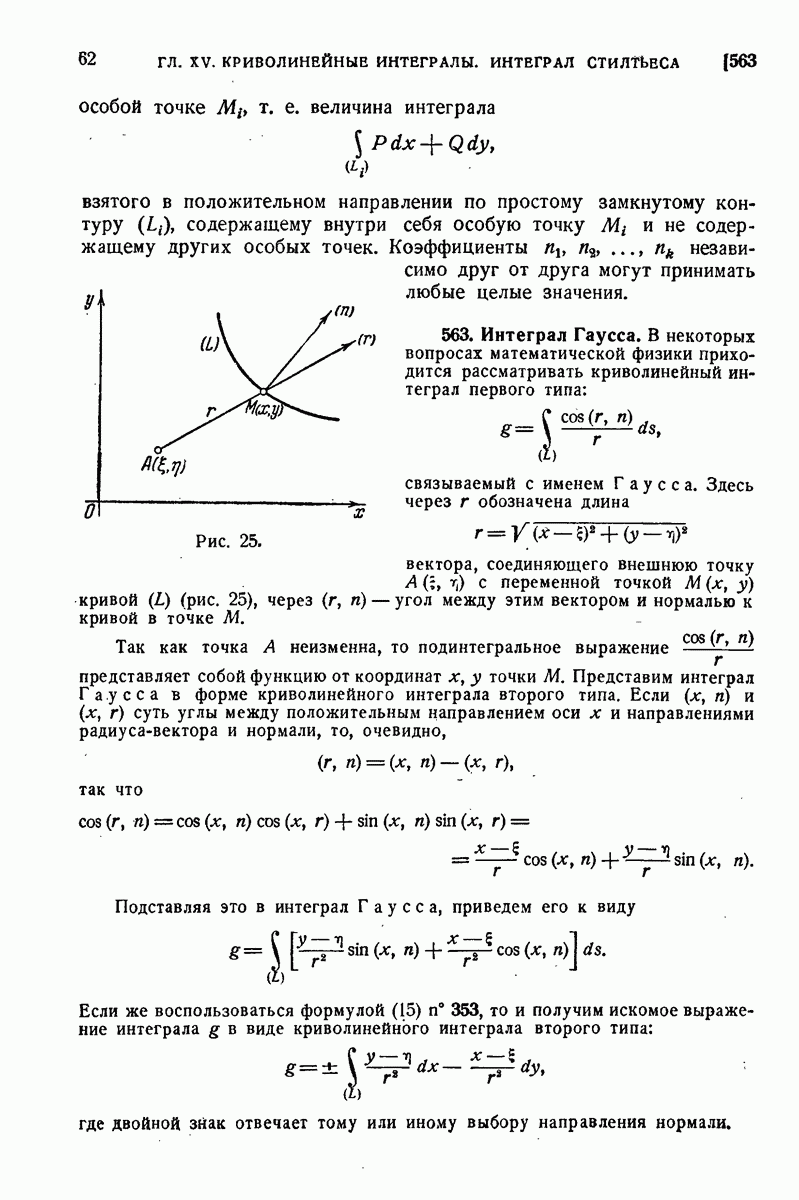
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
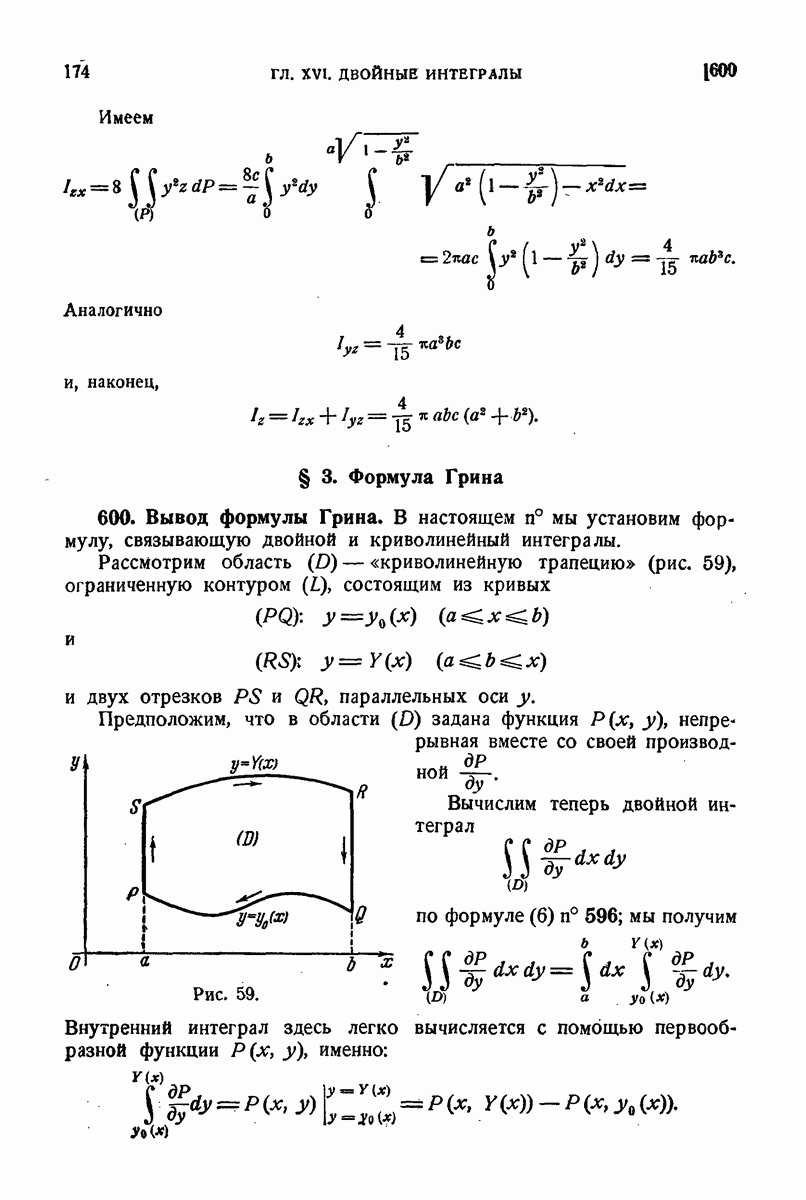
600
601
602
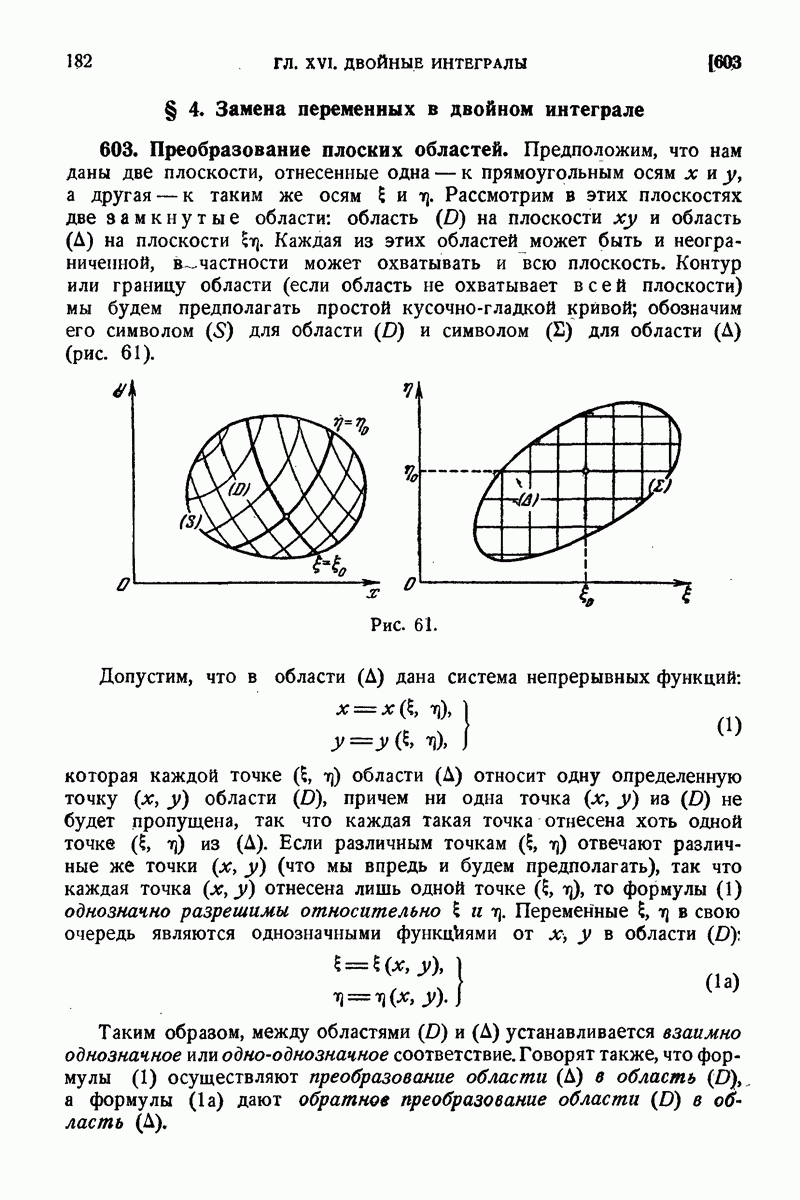
603
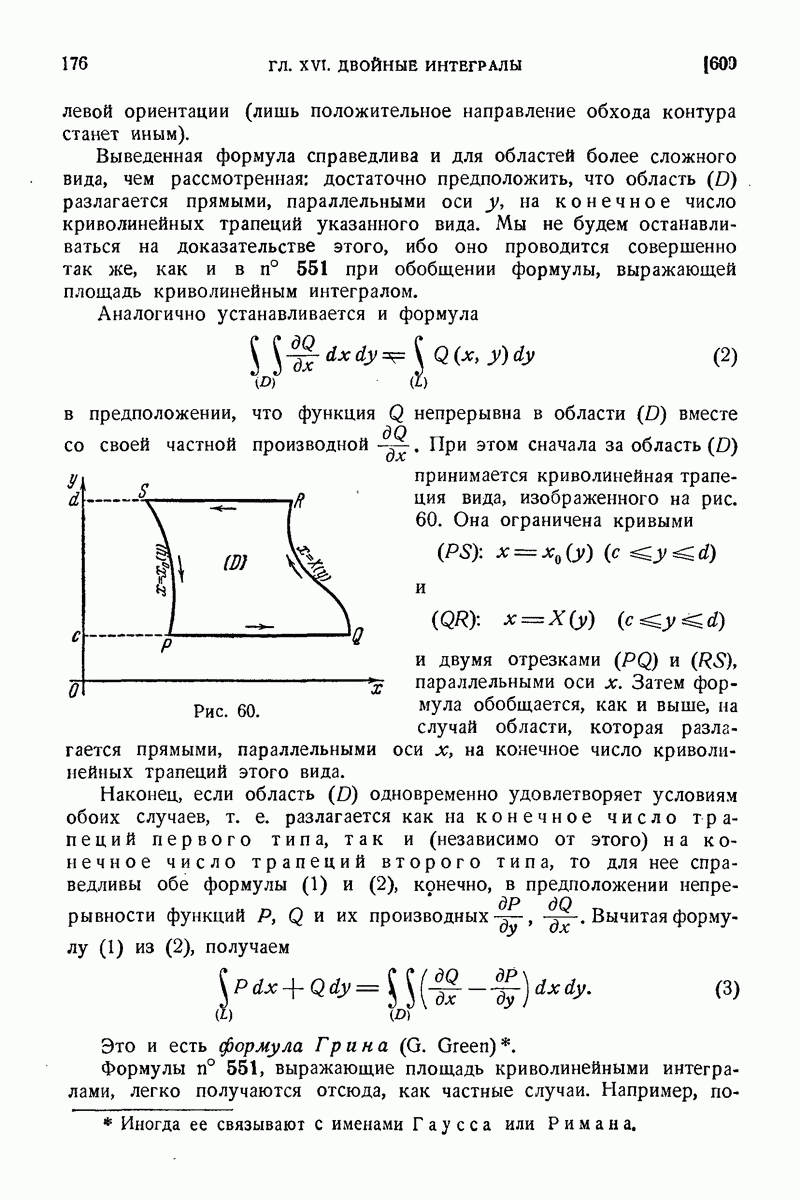
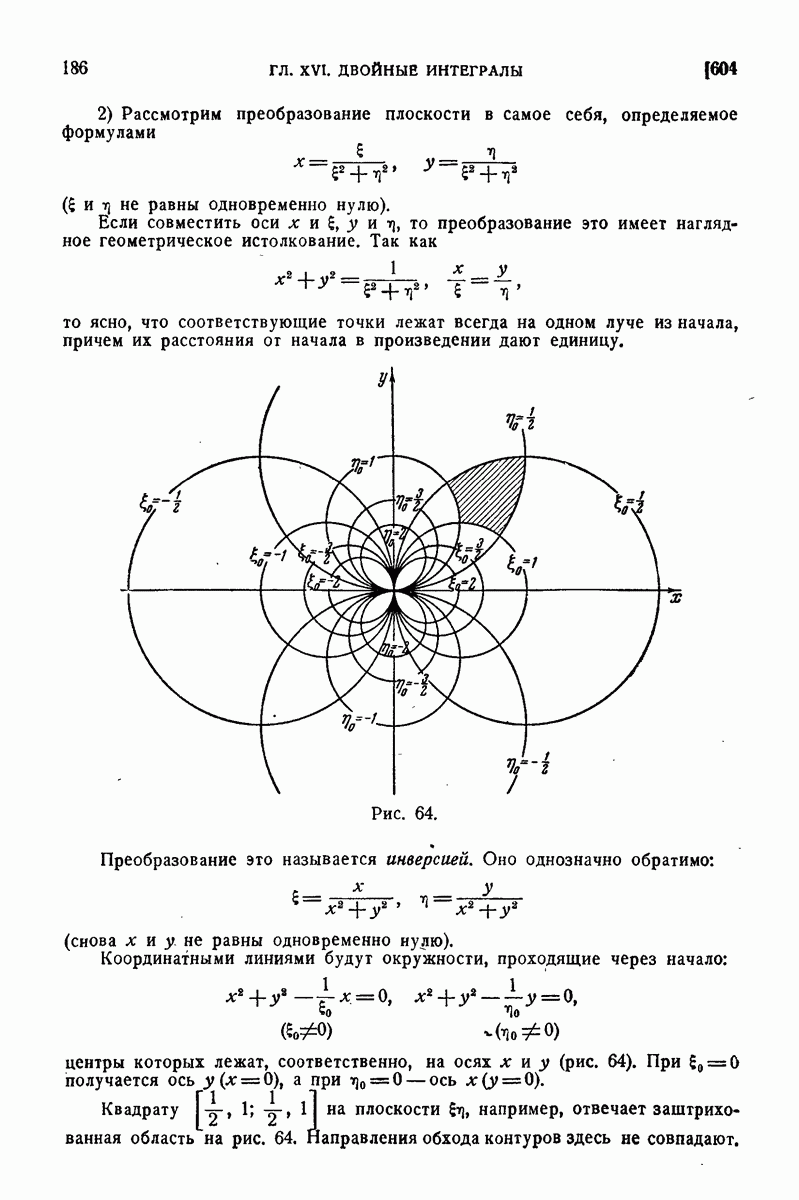
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
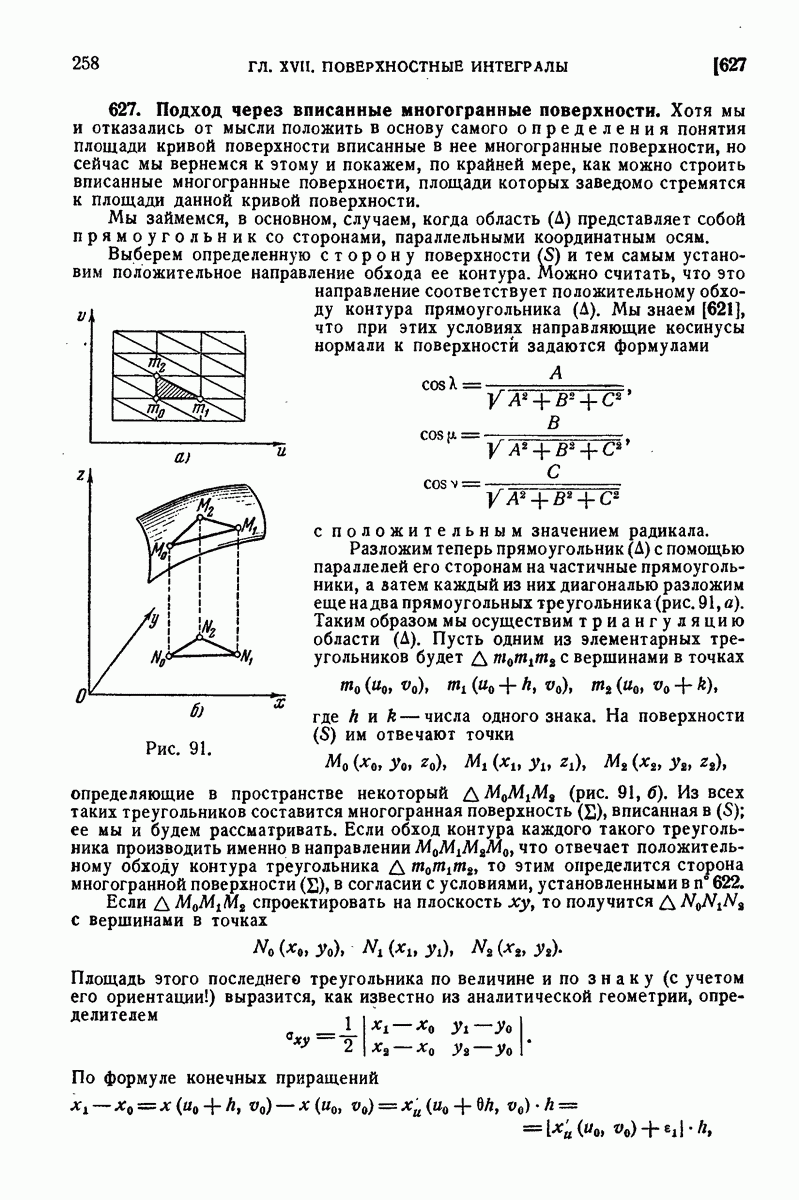
627
628
629
630
631
632
633
634
635
636
637
638
639
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
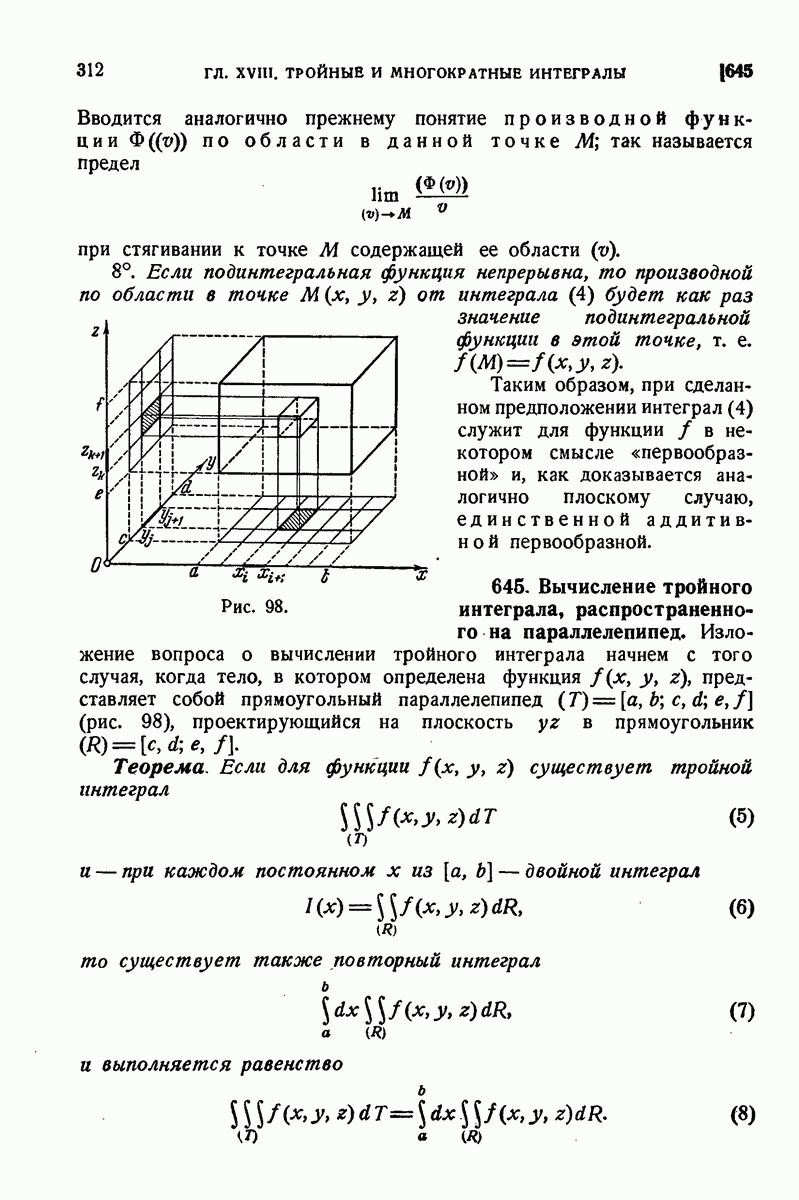
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
689. Разложения только по косинусам или только по синусам.
Начнем со следующего замечания: если заданная в промежутке  интегрируемая (в собственном или несобственном смысле) функция
интегрируемая (в собственном или несобственном смысле) функция  будет нечетной, то для нее
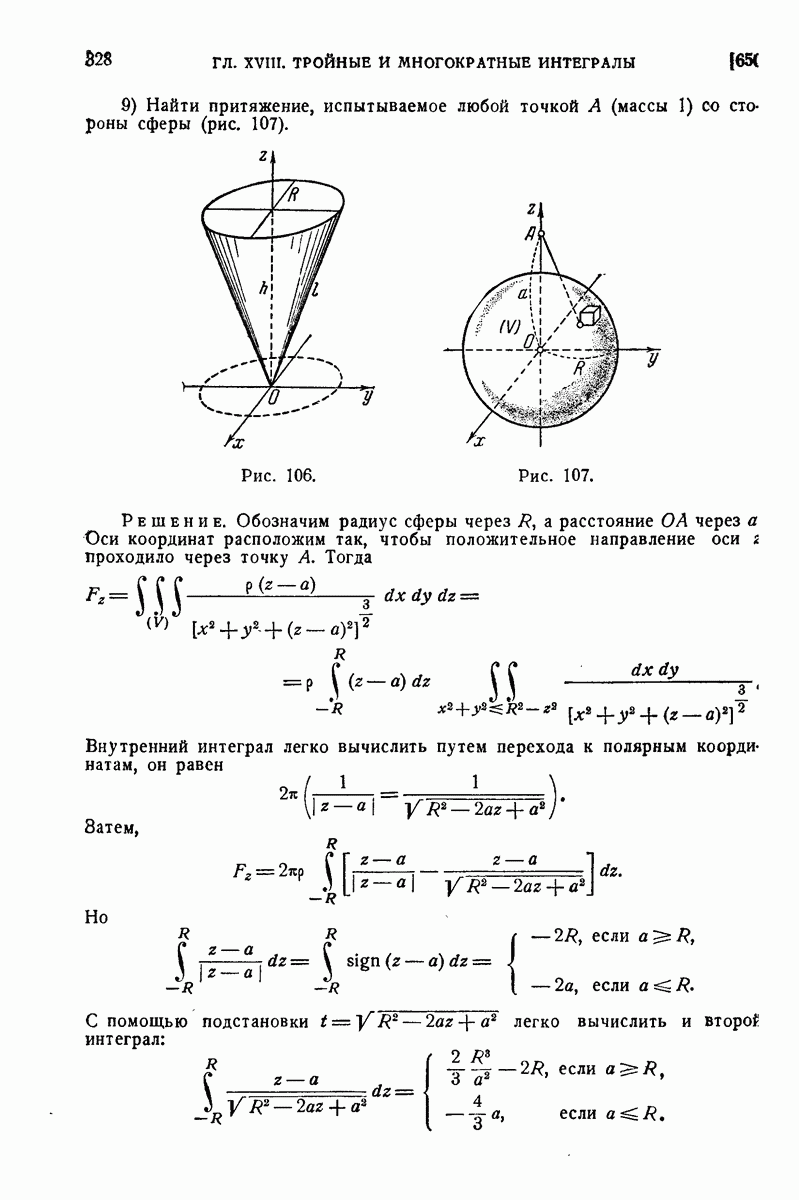
будет нечетной, то для нее

В этом легко убедиться, представив интеграл  в виде суммы интегралов:
в виде суммы интегралов:  и заменив во втором из них
и заменив во втором из них  на — х. Таким же путем устанавливается, что в случае четной функции
на — х. Таким же путем устанавливается, что в случае четной функции 

Пусть теперь  будет абсолютно интегрируемая в промежутке
будет абсолютно интегрируемая в промежутке  четная функция. Тогда произведение
четная функция. Тогда произведение  окажется нечетной функцией, и по сказанному
окажется нечетной функцией, и по сказанному

Таким образом, ряд Фурье четной функции содержит одни лишь косинусы:

Так как  в этом случае тоже будет четной функцией то, применив сюда второе из сделанных выше замечаний, можем, коэффициенты
в этом случае тоже будет четной функцией то, применив сюда второе из сделанных выше замечаний, можем, коэффициенты  разложения написать в виде
разложения написать в виде

Если же функция  будет нечетной, то нечетной будет и функция
будет нечетной, то нечетной будет и функция  , так что
, так что

Мы приходим к заключению, что ряд Фурье нечетной функции содержит одни лишь синусы:

При этом ввиду четности произведения  можно писать:
можно писать:

Отметим попутно, что каждая функция  заданная в промежутке
заданная в промежутке  может быть представлена в виде суммы четной и нечетной составляющих функций:
может быть представлена в виде суммы четной и нечетной составляющих функций:

где

Очевидно, что ряд Фурье функции  как раз и составится из разложения по косинусам функции
как раз и составится из разложения по косинусам функции  и разложения по синусам функции
и разложения по синусам функции 
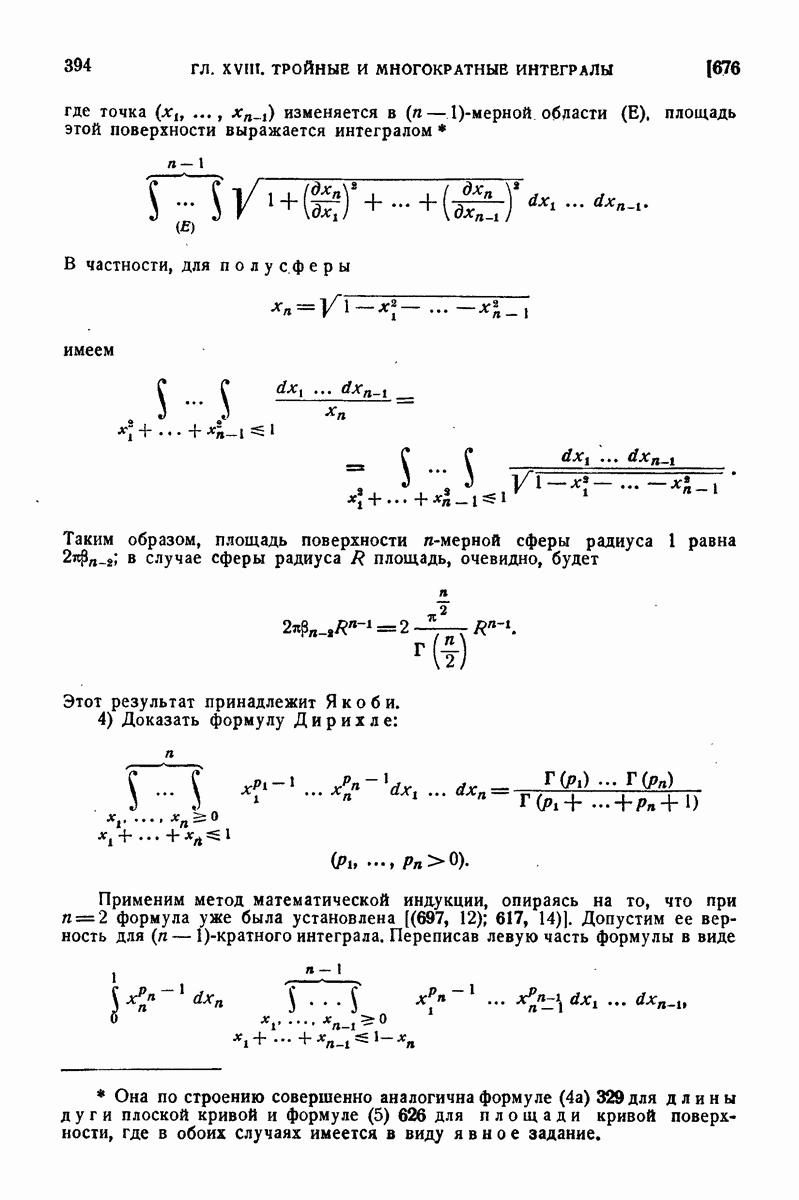
Предположим, далее, что функция  задана лишь в промежутке
задана лишь в промежутке  Желая разложить ее в этом промежутке в ряд Фурье (2), мы дополним определение нашей функции для значений х в промежутке
Желая разложить ее в этом промежутке в ряд Фурье (2), мы дополним определение нашей функции для значений х в промежутке  по произволу, а затем применим сказанное в 687. Подчеркнутый выше произвол в определении функции дает возможность получить таким путем различные тригонометрические ряды. Если в какой-нибудь точке
по произволу, а затем применим сказанное в 687. Подчеркнутый выше произвол в определении функции дает возможность получить таким путем различные тригонометрические ряды. Если в какой-нибудь точке  между 0 и
между 0 и  наша функция удовлетворяет одному из признаков, установленных в пп° 694, 696, то все эти ряды будут в точке
наша функция удовлетворяет одному из признаков, установленных в пп° 694, 696, то все эти ряды будут в точке  сходиться к
сходиться к  или в случае разрыва к
или в случае разрыва к 

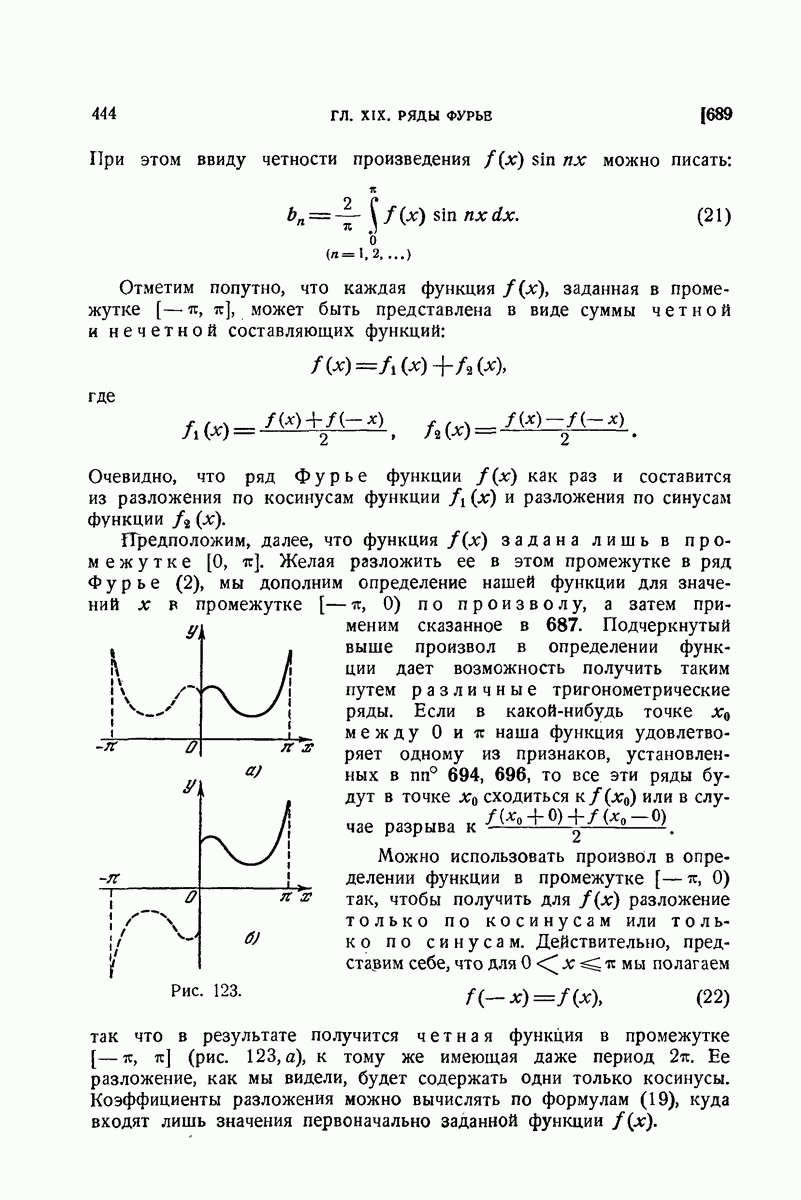
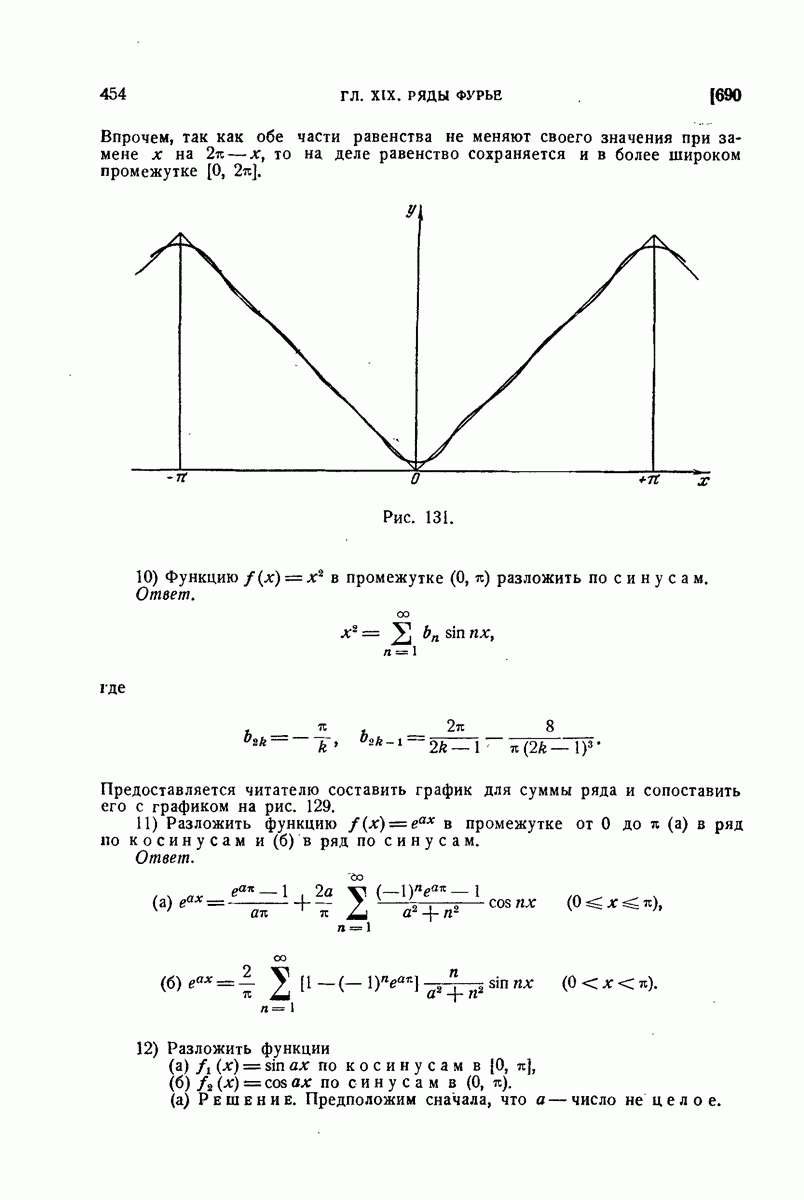
Рис. 123.
Можно использовать произвол в определении функции в промежутке  так, чтобы получить для
так, чтобы получить для  разложение только по косинусам или только по синусам. Действительно, представим себе, что для
разложение только по косинусам или только по синусам. Действительно, представим себе, что для  мы полагаем
мы полагаем

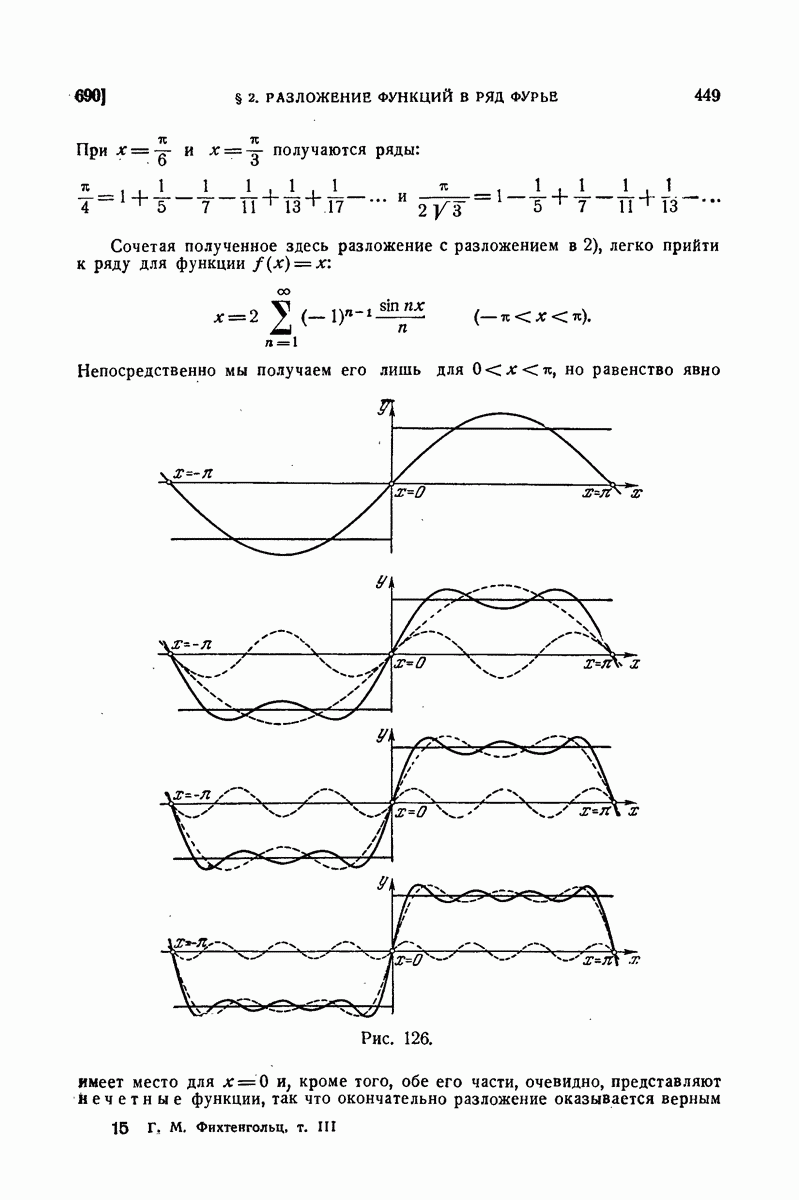
так что в результате получится четная функция в промежутке  (рис. 123, а), к тому же имеющая даже период
(рис. 123, а), к тому же имеющая даже период  . Ее разложение, как мы видели, будет содержать одни только косинусы. Коэффициенты разложения можно вычислять по формулам (19), куда входят лишь значения первоначально заданной функции
. Ее разложение, как мы видели, будет содержать одни только косинусы. Коэффициенты разложения можно вычислять по формулам (19), куда входят лишь значения первоначально заданной функции 
Аналогично, если дополнить определение функции  условием (для
условием (для  )
)

так, чтобы она оказалась нечетной (рис. 123,б), то в ее разложении будут участвовать только члены с синусами. Коэффициенты его определяются по формулам (21).
Таким образом, заданную в промежутке [0, те] функцию при соблюдении известных условий оказывается возможным разлагать как в ряд по косинусам, так и в ряд по синусам!
Особого исследования требуют, впрочем, точки  Здесь оба разложения ведут себя по-разному. Предположим для простоты, что заданная функция
Здесь оба разложения ведут себя по-разному. Предположим для простоты, что заданная функция  непрерывна при
непрерывна при  и рассмотрим сначала разложение по косинусам. Условие (22) прежде всего сохраняет непрерывность при
и рассмотрим сначала разложение по косинусам. Условие (22) прежде всего сохраняет непрерывность при  так что при соблюдении надлежащих условий ряд (18) при
так что при соблюдении надлежащих условий ряд (18) при  будет сходиться именно к
будет сходиться именно к  Так как, далее,
Так как, далее,

то и при  имеет место аналогичное обстоятельство.
имеет место аналогичное обстоятельство.
Иначе обстоит дело с разложением по синусам. Не вдаваясь в соображения относительно нарушения непрерывности условием (23) и т. п., мы просто заметим, что в точках  сумма ряда (20) явно будет нулем. Поэтому она может дать нам значения
сумма ряда (20) явно будет нулем. Поэтому она может дать нам значения  очевидно, лишь в том случае, если и эти значения равны нулю.
очевидно, лишь в том случае, если и эти значения равны нулю.
Если функция  задана в промежутке
задана в промежутке  , то, прибегнув к той же замене переменной, что и в 688, мы сведем вопрос о разложении ее в ряд по косинусам:
, то, прибегнув к той же замене переменной, что и в 688, мы сведем вопрос о разложении ее в ряд по косинусам:

или в ряд по синусам:

к только что рассмотренному. При этом коэффициенты разложений вычисляются, соответственно, по формулам:

или

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
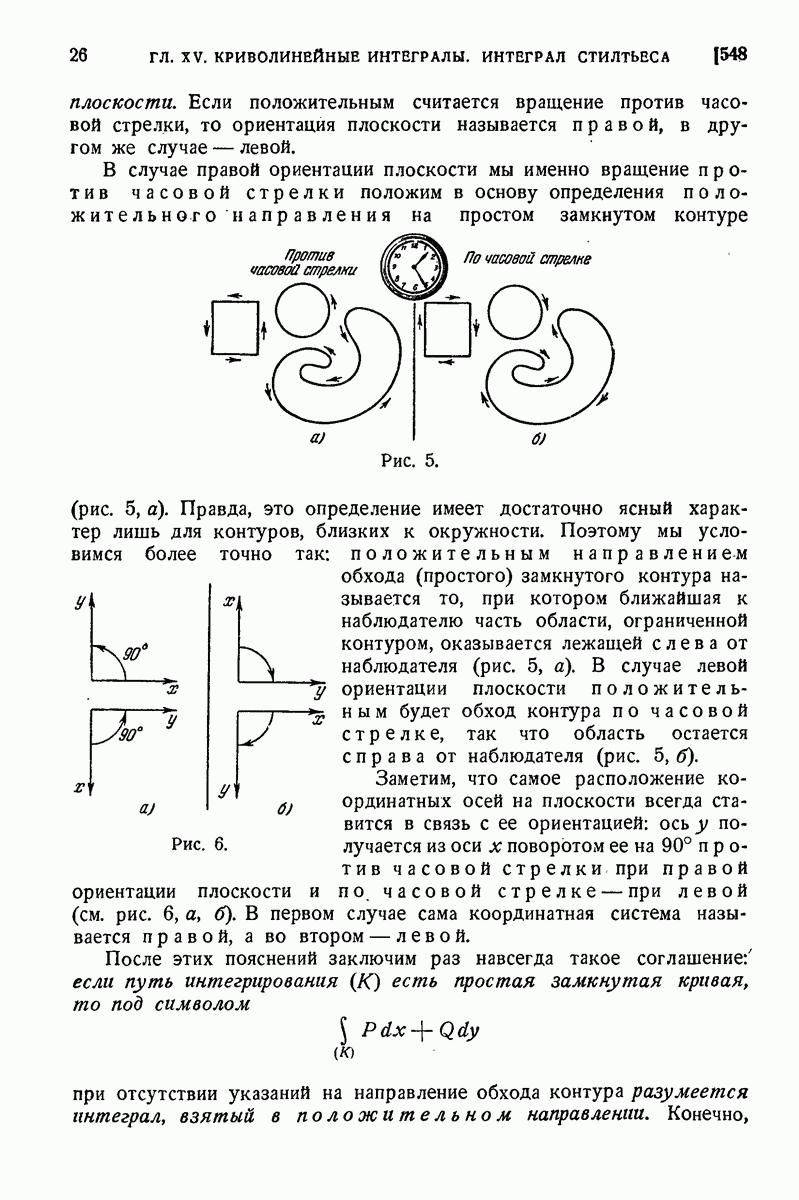
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
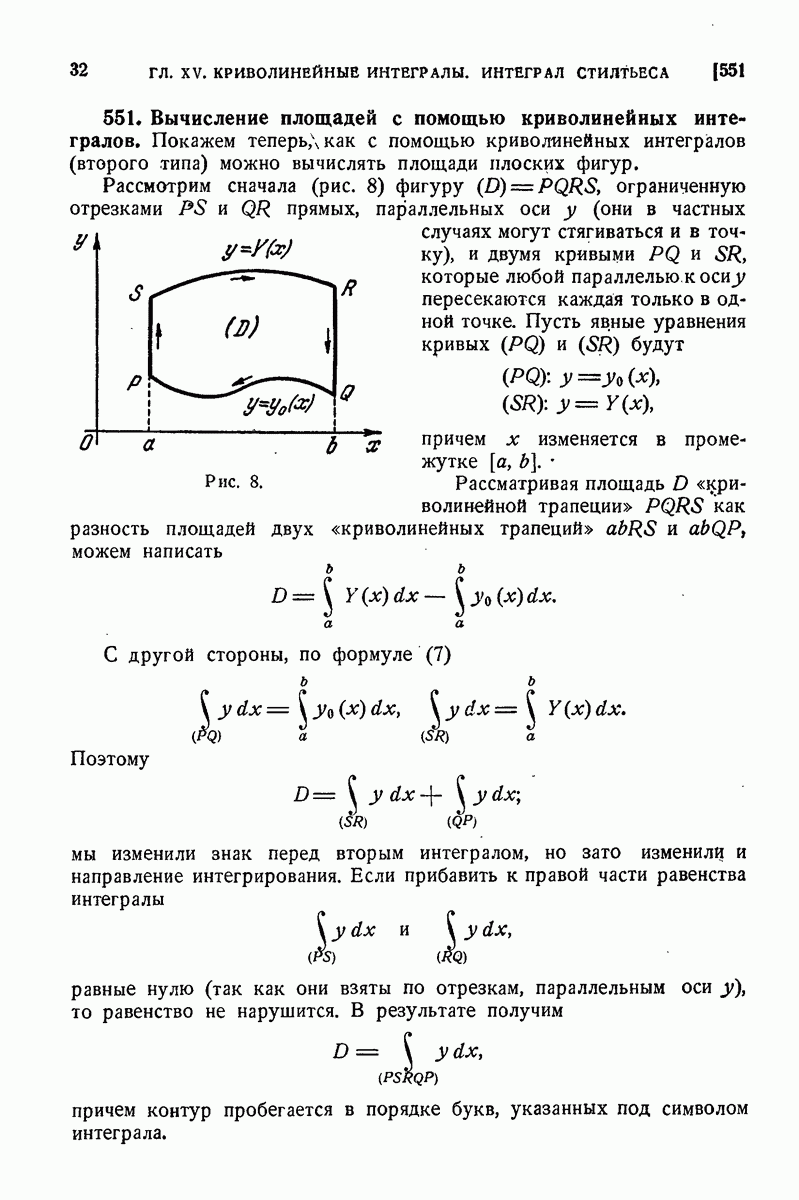
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
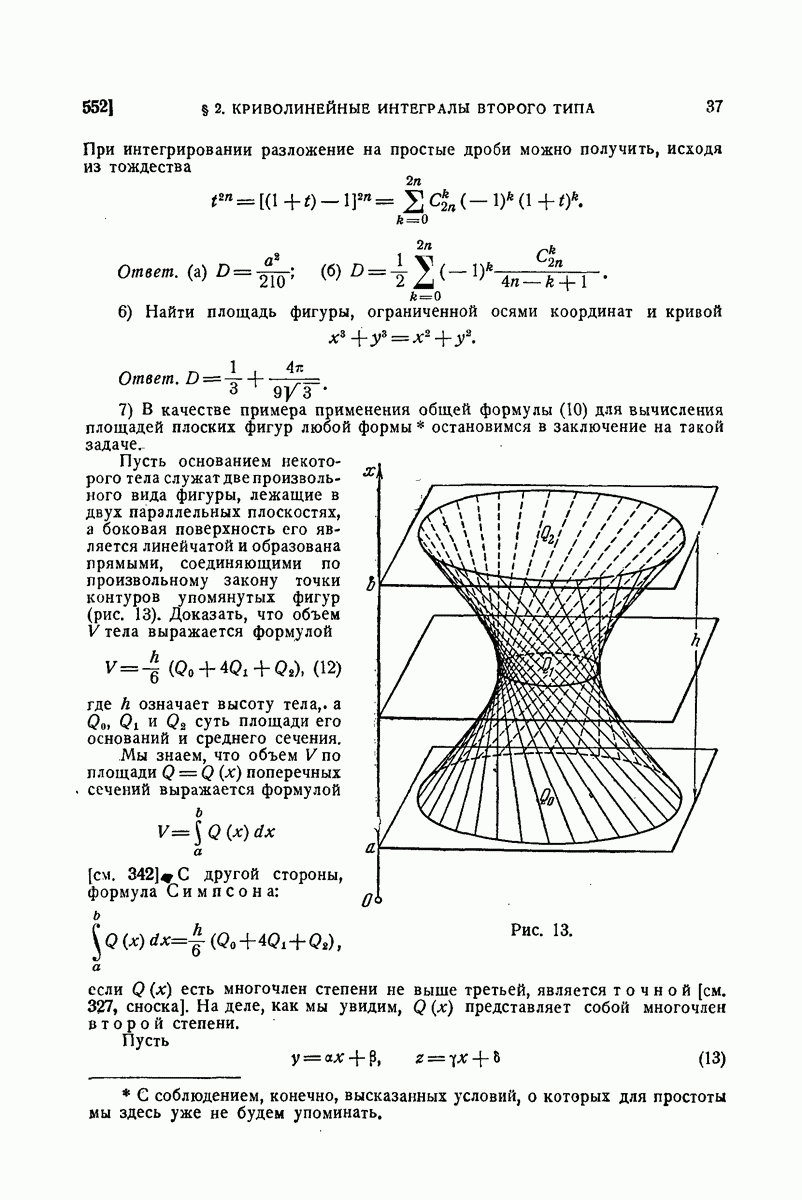
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
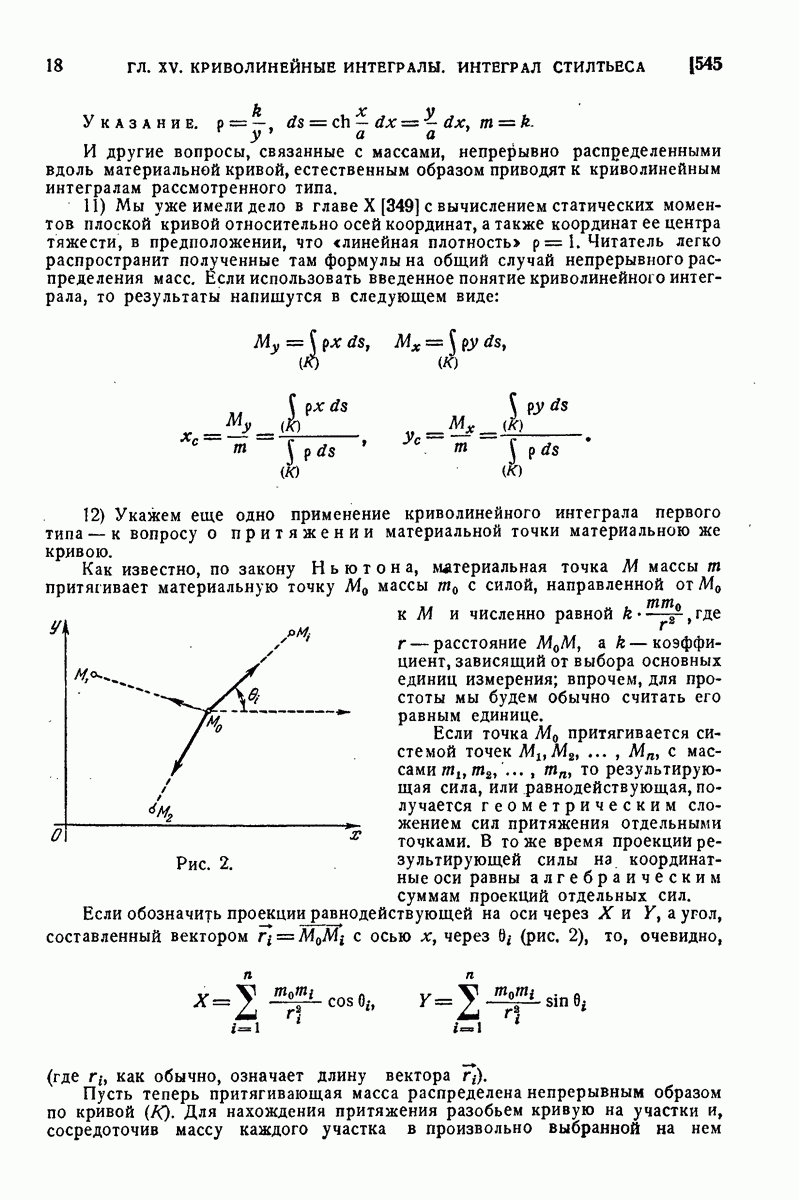
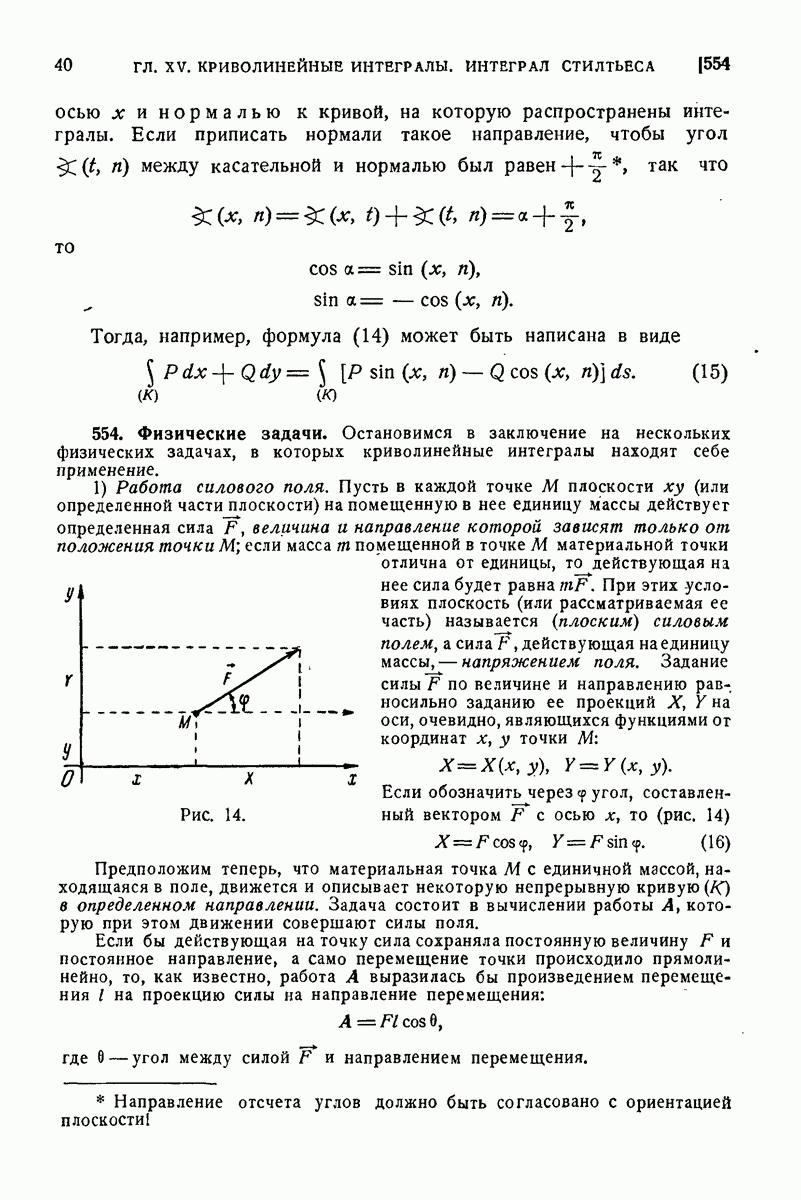
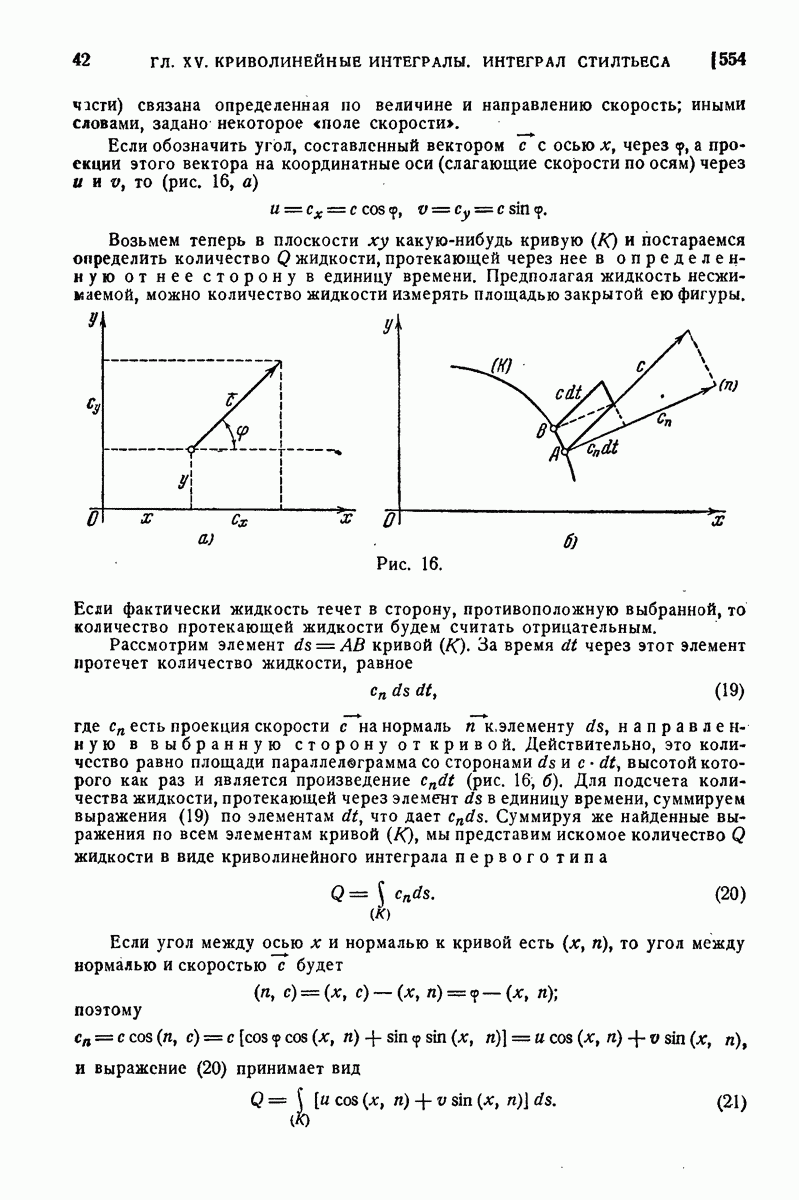
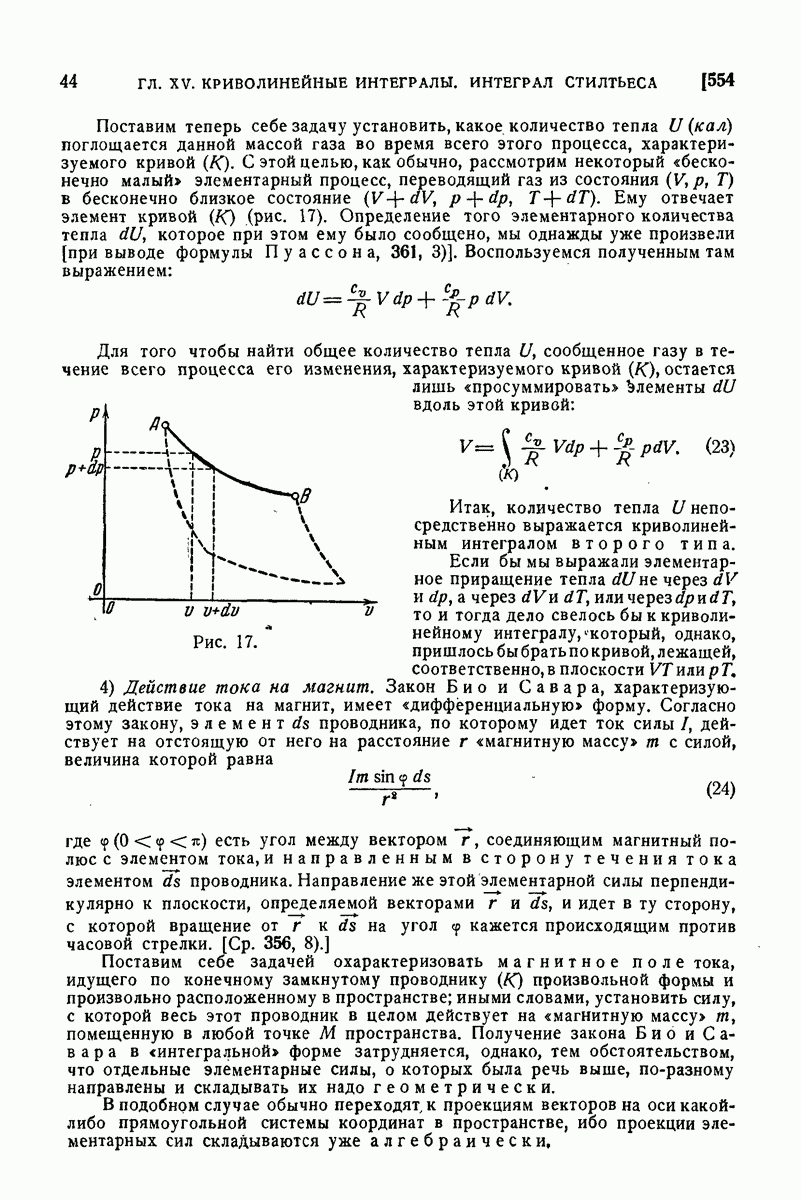
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
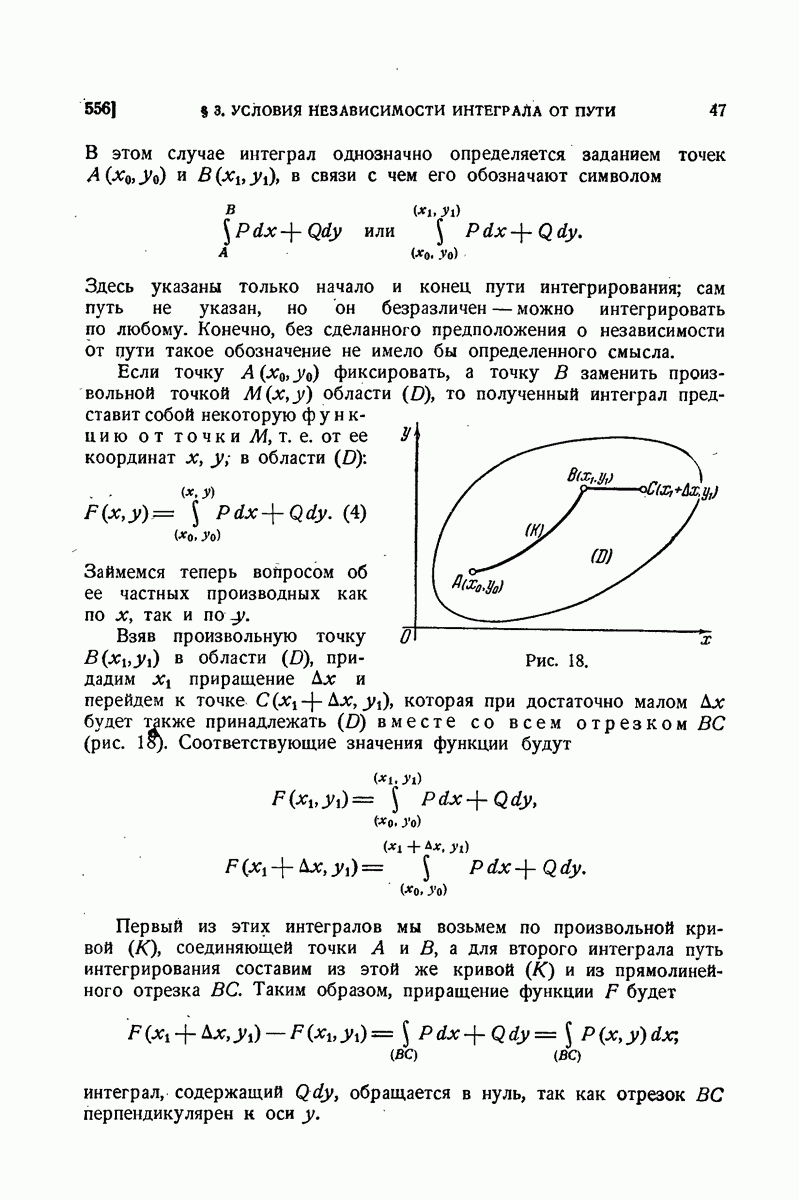
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.