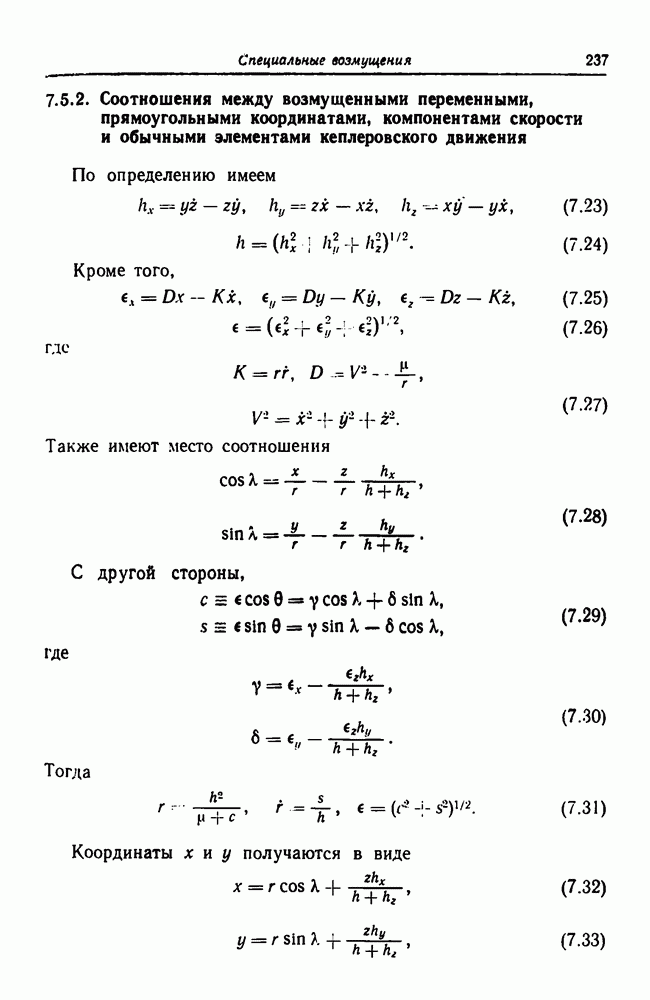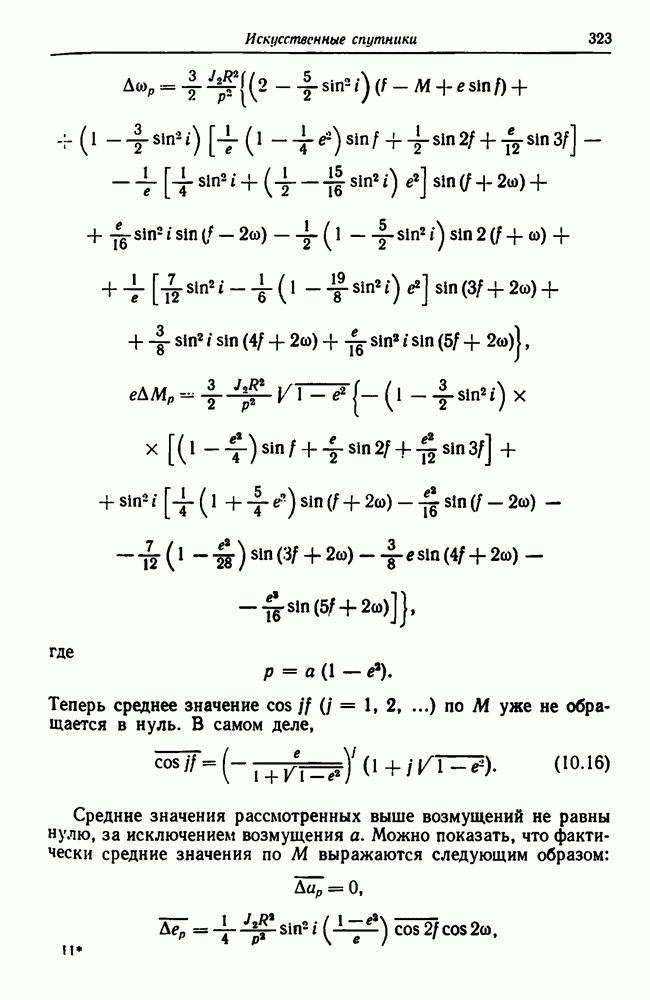| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
9.11. Теории Луны
Со времен Ньютона многие математики и астрономы пытались создать теорию движения Луны. Помимо естественного желания иметь аналитическую теорию, которая предсказывала бы положение Луны с точностью лучших методов наблюдений, позволила бы изучать эволюцию лунной орбиты и проверить, насколько полно объясняют движение спутника законы Ньютона, были и другие мотивы создания теории. Отсутствие точных часов (пока Харрисон не сделал в 1761 г. первый хронометр) не позволяло решить важную практическую задачу определения долготы судна в открытом море. Галилей высказал идею определения времени путем сравнения наблюденных положений спутников Юпитера с табличными значениями. Ньютон предпочитал использовать для этой цели Луну. Таким образом, вначале поиски, направленные на создание теории движения Луны, стимулировались военными, торговыми и исследовательскими потребностями. Однако и с исчезновением
этих стимулов поиск уже не мог прекратиться. Во все времена находилось достаточно людей, которые продолжали исследования из интереса к задаче самой по себе. К тому же по мере уточнения методов наблюдений старые теории становились недостаточно точными или в них обнаруживались ошибки и их надо было заменять (например, развитие Дамуазо теории Лапласа). В последнее время исследования в геофизике и теории приливов (в сочетании с методами лазерной локации Луны) дали возможность более точно вычислять эфемериды Луны.
Ньютон находил задачу движения Луны настолько трудной, что, как он жаловался, она вызывала у него головную боль, лишала сна и он больше не мог о ней думать. Однако ему удалось показать, что известные неравенства в орбитальном движении Луны вызваны Солнцем. Кроме того, учитывая члены второго порядка, он вычислил движение перигея, отличающееся от наблюдаемого значения всего на 8%.
Важный вклад в теории движения Луны внесли Ньютон, Эйлер, Клеро, Пуассон, Лаплас, Дамуазо, Ганзен, Делоне, Хилл, Браун и Депри. Все построенные ими теории имели две общие черты: они содержали большое число членов и требовали выбора промежуточной орбиты нулевого порядка. Необходимое число членов зависело не только от требуемой точности, но и от выбора промежуточной орбиты и метода исследования. В большинстве теорий на первом этапе использовались уравнения движения, в которые входили полярные координаты или функции орбитальных элементов. Правда, в теории Эйлера 1772 г., применялись прямоугольные координаты, причем оси х и у. вращались со скоростью, равной среднему угловому движению Луны. В теории Понтекулана, опубликованной в 1846 г, использовались полярные координаты. В теории Хилла применялись вращающиеся прямоугольные координаты, но при этом ось х была постоянно направлена в точку, соответствующую положению среднего Солнца. В различных теориях в качестве промежуточной орбиты использовались неподвижный кеплеровский эллипс, вращающийся эллипс фиксированной формы, а также значительно более сложные периодические орбиты. Например, Хилл использовал периодическую орбиту, являющуюся частным решением системы двух дифференциальных уравнений второго порядка относительно и и s, где

Здесь X и Y — геоцентрические эклиптические координаты Луны, ось X всегда направлена в среднее геоцентрическое положение Солнца. Независимая переменная  определялась выражением
определялась выражением

где  среднее движение Солнца вокруг Земли, t — время,
среднее движение Солнца вокруг Земли, t — время,  — постоянные, значения которых на этом этапе пока не определены.
— постоянные, значения которых на этом этапе пока не определены.
Свои уравнения Хилл получил без учета эксцентриситета и параллакса для Солнца, а также широты и эксцентриситета для Луны. Решение, использованное Хиллом в качестве промежуточной орбиты, выражается рядом Фурье по  Оно представляет собой овал, симметричный относительно осей; при этом большая ось овала перпендикулярна направлению на Солнце. Эту фигуру называют вариационной кривой Хилла. Хилл и Браун аналитически исследовали отклонения истинной орбиты Луны от указанной промежуточной орбиты. Позднее Браун составил таблицы для теории движения Луны Хилла—Брауна, по которым можно вычислять эфемериду Луны. Однако в последнее время с развитием электронно-вычислительной техники для определения положений Луны стали использоваться более точные теории, в которые и сейчас продолжают вводиться дальнейшие усовершенствования.
Оно представляет собой овал, симметричный относительно осей; при этом большая ось овала перпендикулярна направлению на Солнце. Эту фигуру называют вариационной кривой Хилла. Хилл и Браун аналитически исследовали отклонения истинной орбиты Луны от указанной промежуточной орбиты. Позднее Браун составил таблицы для теории движения Луны Хилла—Брауна, по которым можно вычислять эфемериду Луны. Однако в последнее время с развитием электронно-вычислительной техники для определения положений Луны стали использоваться более точные теории, в которые и сейчас продолжают вводиться дальнейшие усовершенствования.
Следует отметить следующие две характерные тенденции в развитии теории движения Луны;
1. Все теории можно разделить на три класса: аналитические, численно-аналитические и численные. Теория Делоне представляет собой пример аналитического подхода в чистом виде. Для возмущающей функции получено разложение по малому параметру до седьмого порядка. В процессе приведения этой функции к нормальному виду было сделано свыше 500 канонических преобразований, в результате чего в конце концов были получены выражения для широты, долготы и синуса параллакса Луны. Делоне на эту работу потребовалось около двадцати лет. Благодаря тому что метод является чисто аналитическим, его можно применять в любой задаче трех тел.
Численно-аналитический подход впервые реализовал Лаплас. Считая два эксцентриситета и  неопределенными параметрами (i — наклонение), он вместо величины
неопределенными параметрами (i — наклонение), он вместо величины  использовал ее численное значение. Теория Хилла—Брауна также относится к классу численно-аналитических теорий.
использовал ее численное значение. Теория Хилла—Брауна также относится к классу численно-аналитических теорий.
Дж. Эри предложил численный метод уточнения теории Делоне. Его метод сулил большие выгоды, однако в работе самого Эри, опубликованной в 1886 г., была допущена ошибка. Недавно Эккерт применил метод Эри к основной задаче движения Луны в теории Брауна.
Переход от аналитических теорий к численным был обусловлен тем, что, применяя численный метод, можно значительно быстрее и с меньшими усилиями достигнуть требуемой точности. Создание быстродействующих ЭВМ с большим объемом памяти изменило такую точку зрения. Герджет и Мазен еще в 1959 г. показали, что
ЭВМ можно запрограммировать на выполнение аналитических выкладок, с которыми так часто имеют дело в небесной механике. На пути такого использования ЭВМ приходится преодолевать большие трудности. На написание, отладку и проверку программы для конкретной задачи может потребоваться несколько лет, но зато по окончании этих операций машина выдает все необходимые аналитические выражения. Типичным примером может служить выполненное Делоне разложение возмущающей функции для Луны. Для получения аналитического разложения возмущающей функции до значительно более высокого порядка с помощью ЭВМ потребовались не годы, а часы. Возможность выполнения аналитических выкладок на машине открыла новую эру в изучении орбитального движения.
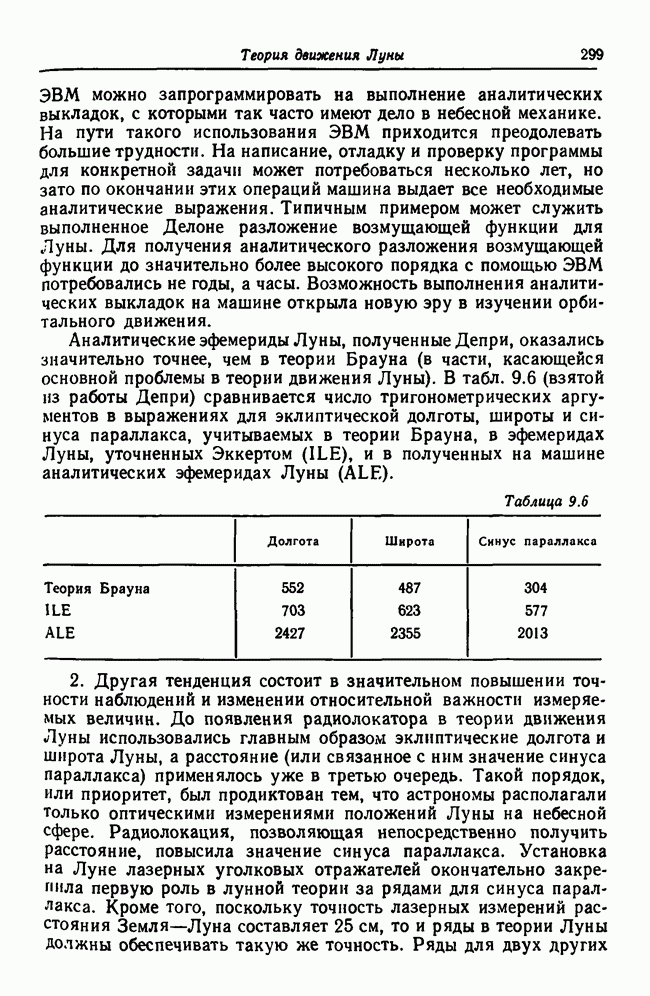
Аналитические эфемериды Луны, полученные Депри, оказались значительно точнее, чем в теории Брауна (в части, касающейся основной проблемы в теории движения Луны). В табл. 9.6 (взятой из работы Депри) сравнивается число тригонометрических аргументов в выражениях для эклиптической долготы, широты и синуса параллакса, учитываемых в теории Брауна, в эфемеридах Луны, уточненных Эккертом (ILE), и в полученных на машине аналитических эфемеридах Луны (ALE).
Таблица 9.6

2. Другая тенденция состоит в значительном повышении точности наблюдений и изменении относительной важности измеряемых величин. До появления радиолокатора в теории движения Луны использовались главным образом эклиптические долгота и широта Луны, а расстояние (или связанное с ним значение синуса параллакса) применялось уже в третью очередь. Такой порядок, или приоритет, был продиктован тем, что астрономы располагали только оптическими измерениями положений Луны на небесной сфере. Радиолокация, позволяющая непосредственно получить расстояние, повысила значение синуса параллакса. Установка на Луне лазерных уголковых отражателей окончательно закрепила первую роль в лунной теории за рядами для синуса параллакса. Кроме того, поскольку точность лазерных измерений расстояния Земля—Луна составляет 25 см, то и ряды в теории Луны Должны обеспечивать такую же точность. Ряды для двух других
координат должны быть уточнены аналогичным образом, так как все три координаты зависят друг от друга. Таким требованиям в состоянии удовлетворить только полученная на ЭВМ аналитическая лунная теория типа теории Депри.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. Неспокойная Вселенная
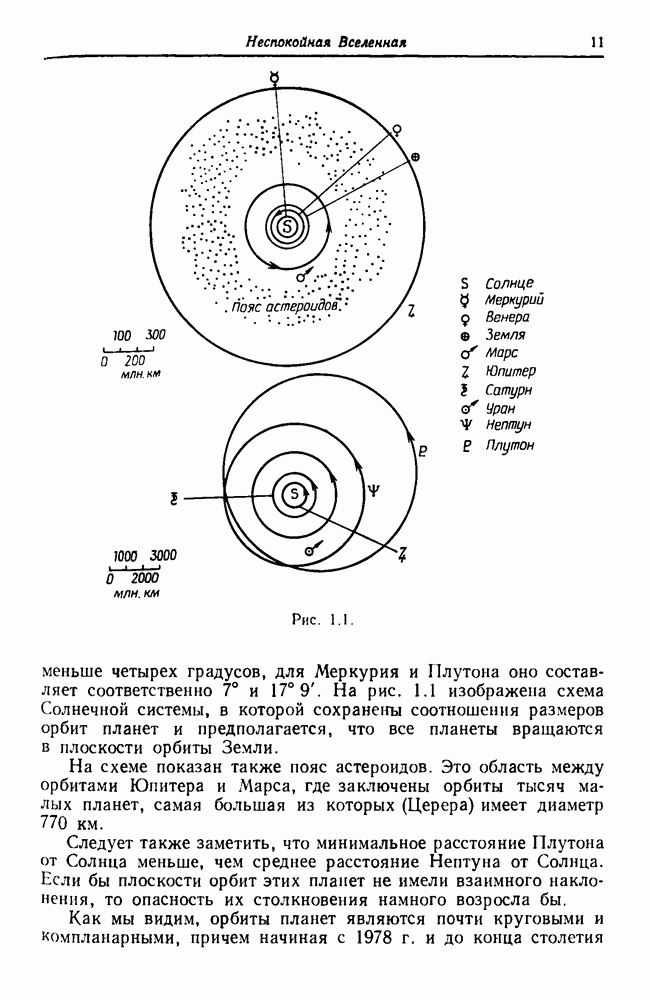
- 1.2. Солнечная система
- 1.2.1. Законы Кеплера
- 1.2.2. Закон Боде
- 1.2.3. Соизмеримости в средних движениях
- 1.2.4. Кометы и метеорные тела
- 1.2.5. Выводы
- 1.3. Движение звезд
- 1.3.1. Двойные системы
- 1.3.2. Тройные системы и системы более высокой кратности
- 1.3.3. Шаровые скопления
- 1.3.4. Галактические, или рассеянные, звездные скопления
- 1.4. Скопления галактик
- 1.5. Выводы
- Рекомендуемая литература
- Глава 2. Системы координат и измерение времени
- 2.2. Положение на поверхности Земли
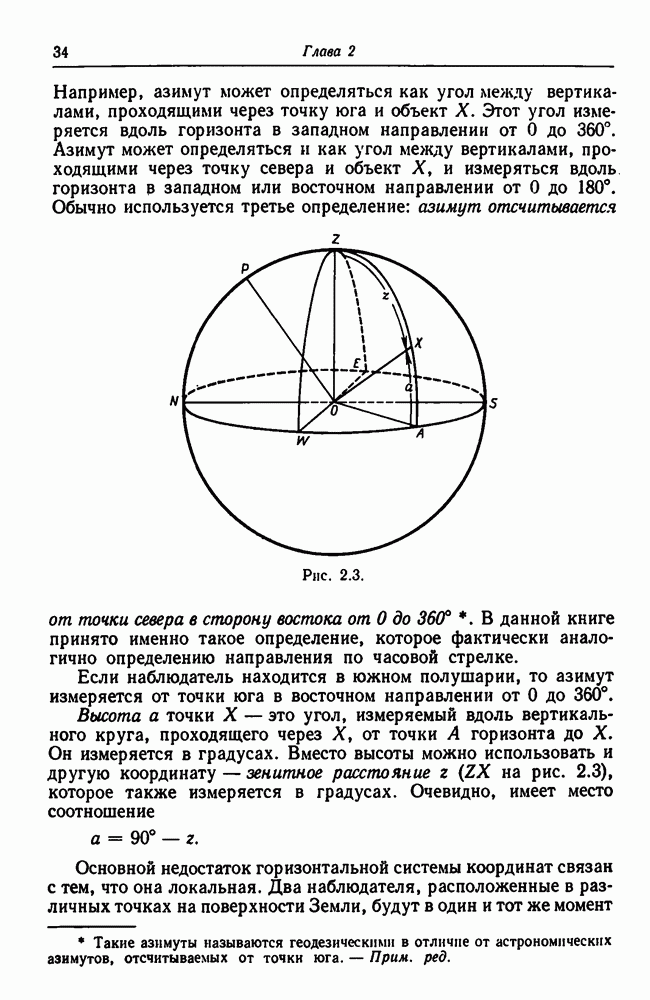
- 2.3. Горизонтальная система
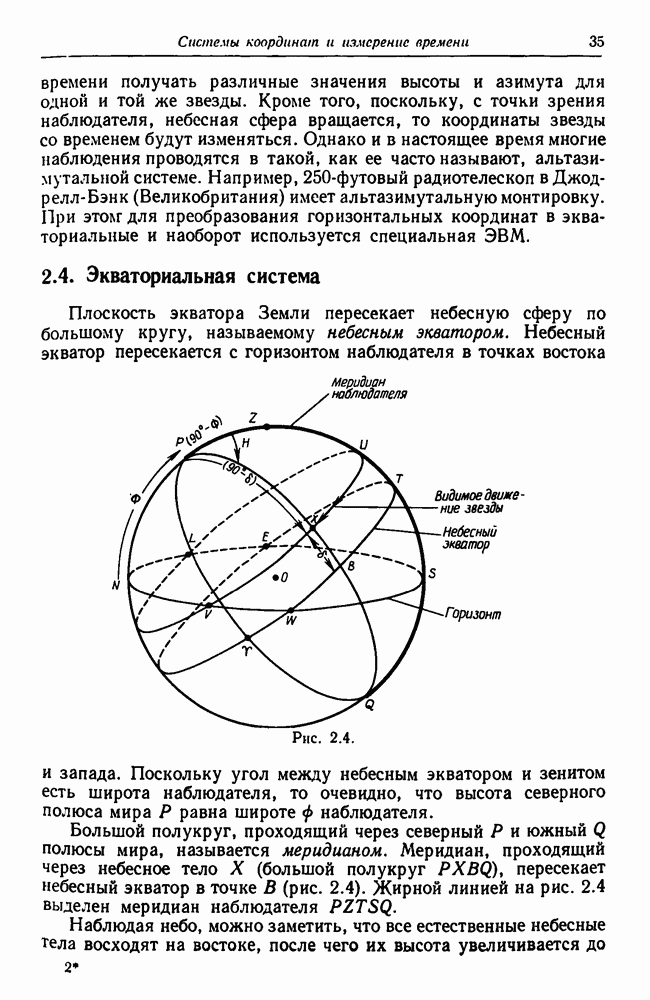
- 2.4. Экваториальная система
- 2.5. Эклиптическая система
- 2.6. Элементы орбиты в пространстве
- 2.7. Прямоугольные системы координат
- 2.8. Системы координат, связанные с плоскостью орбиты
- 2.9. Преобразование систем координат
- 2.9.2. Примеры преобразований систем координат
- 2.10. Галактическая система координат
- 2.11. Измерение времени
- 2.11.1. Звездное время
- 2.11.2. Среднее солнечное время
- 2.11.3. Юлианские дни
- 2.11.4. Эфемеридное время
- Задачи
- Литература
- Глава 3. Обработка данных наблюдений
- 3.2. Методы наблюдений
- 3.3. Рефракция
- 3.4. Прецессия и нутация
- 3.5. Аберрация
- 3.6. Собственное движение
- 3.7. Годичный параллакс
- 3.8. Геоцентрический параллакс
- 3.9. Обзор процедур
- Задачи
- Литература
- Глава 4. Задача двух тел
- 4.2. Законы Ньютона
- 4.3. Закон всемирного тяготения Ньютона
- 4.4. Решение задачи двух тел
- 4.5. Эллиптическая орбита
- 4.5.1. Измерение массы планеты
- 4.5.2. Скорость движения по эллиптической орбите
- 4.5.3. Угол между вектором скорости и радиусом-вектором
- 4.5.4. Средняя, эксцентрическая и истинная аномалии
- 4.5.5. Решение уравнения Кеплера
- 4.5.6. Уравнение центра
- 4.5.7. Положение тела на эллиптической орбите
- 4.6. Параболическая орбита
- 4.7. Гиперболическая орбита
- 4.7.1. Скорость на гиперболической орбите
- 4.7.2. Положение на гиперболической орбите
- 4.8. Прямолинейная орбита
- 4.9. Барицентрические орбиты
- 4.10. Классификация орбит по величине константы энергии
- 4.11. Орбита в пространстве
- 4.12. Ряды для f и g
- 4.13. Использование рекуррентных соотношений
- 4.14. Универсальные переменные
- Задачи
- Литература
- Глава 5. Задача n тел
- 5.2. Уравнения движения задачи n тел
- 5.3. Десять известных интегралов и их смысл
- 5.4. Силовая функция
- 5.5. Теорема вириала
- 5.6. Теорема зеркальности
- 5.7. Снова о задаче n тел
- 5.8. Лагранжевы решения задачи трех тел
- 5.9. Общие замечания о лагранжевых решениях
- 5.10. Ограниченная круговая задача трех тел
- 5.10.2. Критерий Тиссерана
- 5.10.3. Поверхности нулевой скорости
- 5.10.4. Устойчивость точек либрации
- 5.10.5. Периодические орбиты
- 5.10.6. Поиск симметричных периодических орбит
- 5.10.7. Примеры семейств периодических орбит
- 5.10.8. Устойчивость периодических орбит
- 5.10.9. Поверхность сечения
- 5.10.10. Матрица устойчивости
- 5.11. Общая задача трех тел
- 5.11.1. Случай С < 0
- 5.11.2. Случай С = 0
- 5.11.3. Координаты Якоби
- Задачи
- Литература
- Глава 6. Общие возмущения
- 6.2. Уравнения относительного движения
- 6.3. Возмущающая функция
- 6.4. Гравитационная сфера влияния
- 6.5. Потенциал тела произвольной формы
- 6.6. Потенциал шара во внутренней точке
- 6.7. Метод вариации параметров
- 6.7.1. Модификация средней долготы в эпоху
- 6.7.2. Решение уравнений движения планет в форме Лагранжа
- 6.7.3. Коротко- и долгопериодические вариации
- 6.7.4. Разложение возмущающей силы
- 6.8. Уравнения Лагранжа
- 6.9. Канонические уравнения Гамильтона
- Задачи
- Рекомендуемая литература
- Глава 7. Специальные возмущения
- 7.2. Основные факторы теории специальных возмущений
- 7.3. Метод Коуэлла
- 7.4. Метод Энке
- 7.5. Использование возмущенных уравнений
- 7.5.1. Вывод уравнений возмущенного движения
- 7.5.2. Соотношения между возмущенными переменными, прямоугольными координатами, компонентами скорости и обычными элементами кеплеровского движения
- 7.5.3. Процедура численного интегрирования
- 7.5.4. Прямолинейные или почти прямолинейные орбиты
- 7.6. Методы регуляризации
- 7.7. Методы численного интегрирования
- 7.7.2. Метод Рунге—Кутта четвертого порядка
- 7.7.3. Многошаговые методы
- 7.7.4. Численные методы
- Задачи
- Литература
- Глава 8. Устойчивость и эволюция Солнечной системы
- 8.2. Эфемериды планет
- 8.3. Соизмеримости в средних движениях
- 8.4. Астероиды
- 8.5. Кольца Сатурна
- 8.6. Почти соизмеримые орбиты спутников
- 8.7. Численное интегрирование на больших промежутках времени
- 8.7.2. Эволюция элементов орбит на интервале 1 000 000 лет
- 8.7.3. Движение перигелия Плутона: ротационное или либрационное?
- 8.7.4. Сравнение аналитического и численного подходов
- 8.8. Принцип Овендена
- 8.9. Выводы
- Литература
- Глава 9. Теория движения Луны
- 9.3. Сарос
- 9.4. Измерение большой полуоси орбиты, массы и диаметра Луны
- 9.5. Вращение Луны
- 9.6. Селенографические координаты
- 9.7. Фигура Луны
- 9.8. Основная проблема в теории движения Луны
- 9.9. Орбита Солнца в основной проблеме теории движения Луны
- 9.10. Орбита Луны
- 9.11. Теории Луны
- 9.12. Вековое ускорение Луны
- Литература
- Глава 10. Искусственные спутники
- 10.2. Земля как планета
- 10.2.1. Форма Земли
- 10.2.2. Формула Клеро
- 10.2.3. Внутреннее строение Земли
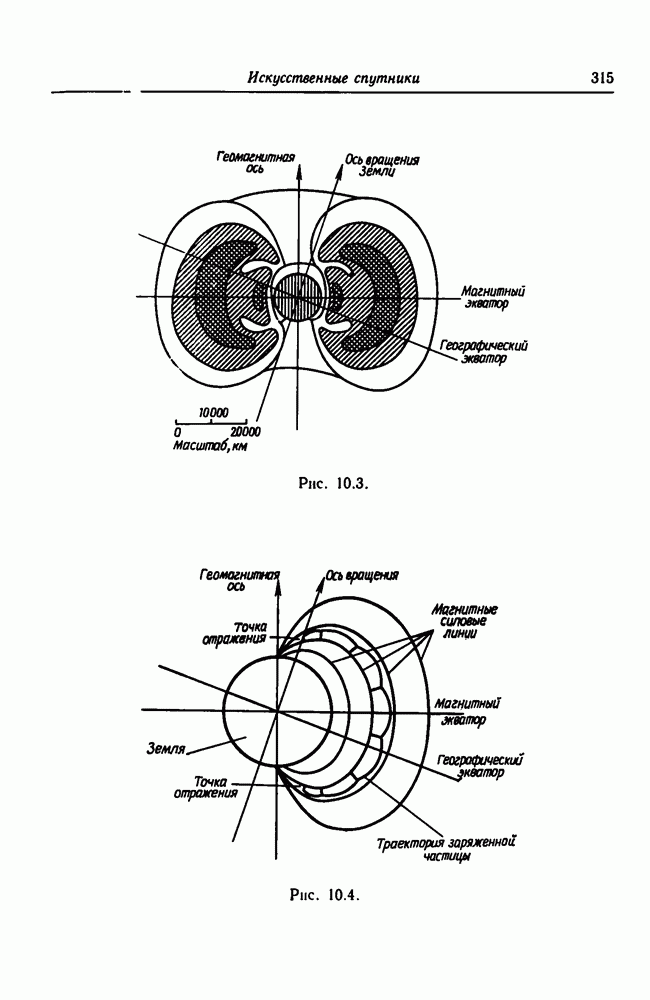
- 10.2.4. Магнитное поле Земли
- 10.2.5. Атмосфера Земли
- 10.2.6. Солнечно-земные связи
- 10.3. Силы, действующие на искусственные спутники Земли
- 10.4. Орбита спутника вокруг сплюснутой планеты
- 10.4.1. Короткопериодические возмущения первого порядка
- 10.4.2. Вековые возмущения первого порядка
- 10.4.3. Долгопериодические возмущения, обусловленные третьей гармоникой
- 10.4.4. Вековые возмущения второго порядка и долгопериодические возмущения
- 10.5. Использование теории Гамильтона—Якоби в задаче движения искусственного спутника
- 10.6. Действие атмосферного торможения на искусственный спутник
- 10.7. Тессеральные и секториальные гармоники поля тяготения Земли
- Задачи
- Литература
- Глава 11. Динамика ракет и орбиты переходов
- 11.2.1. Движение ракеты в гравитационном поле
- 11.2.2. Движение ракеты в атмосфере
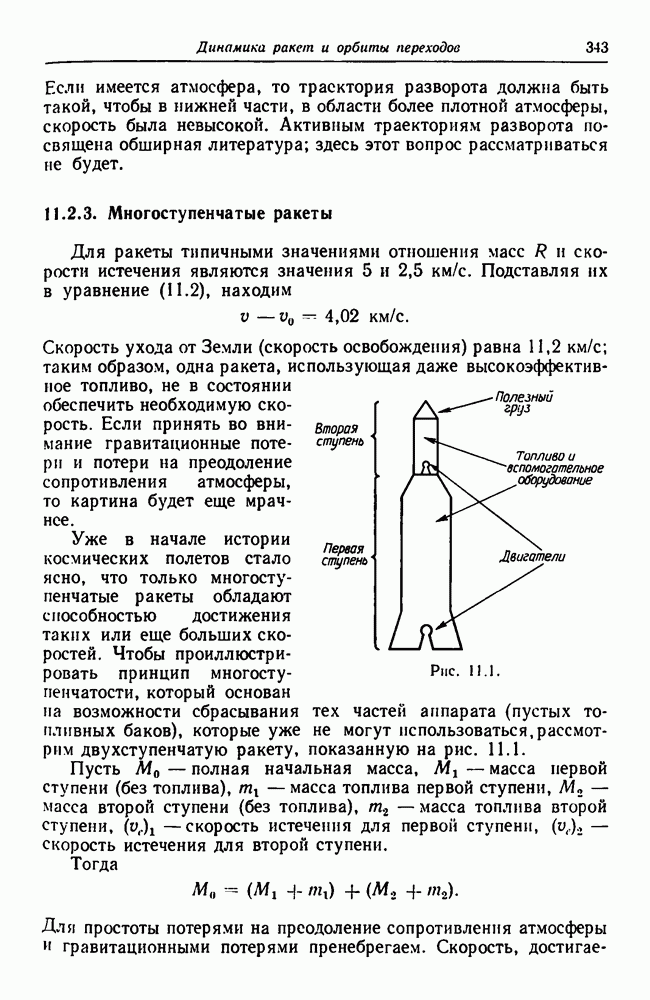
- 11.2.3. Многоступенчатые ракеты
- 11.2.4. Другие типы ракет
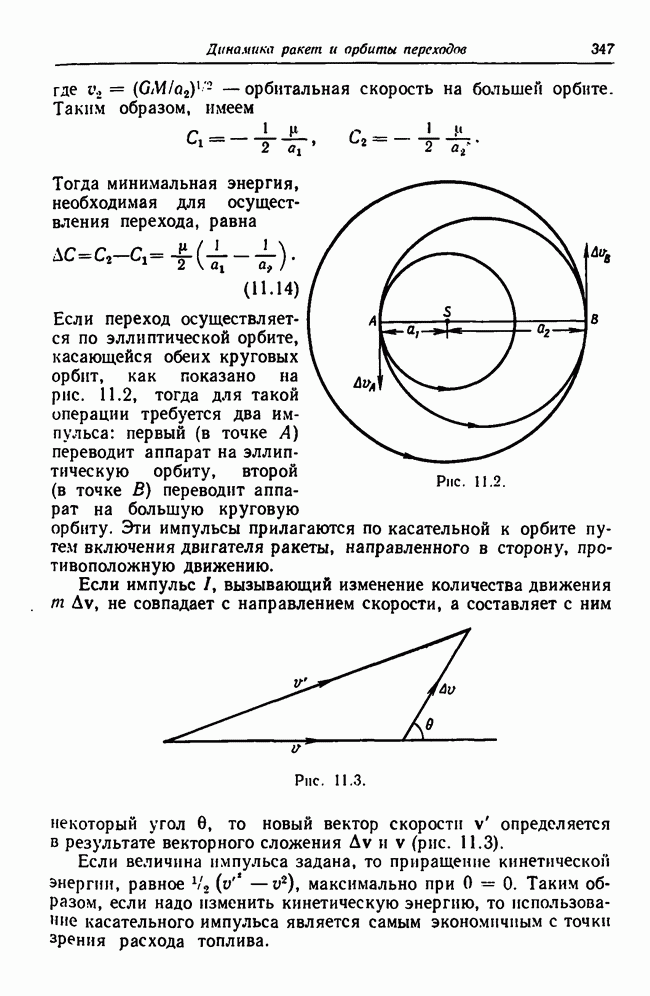
- 11.3. Переходы между орбитами в силовом поле одного притягивающего центра
- 11.3.2. Параболические и гиперболические орбиты перехода
- 11.3.3. Изменения элементов орбиты, вызванные малым импульсом
- 11.3.4. Изменения элементов орбить, вызванные большим импульсом
- 11.3.5. Зависимость расхода топлива от времени перехода
- 11.3.6. Зависимость орбиты перехода от малых ошибок положения и скорости в момент выключения двигателя
- 11.3.7. Переход между частицами, движущимися по орбитам в центральном поле сил
- 11.4. Орбиты перехода в силовых полях двух или более притягивающих центров
- 11.4.2. Выход на орбиту вокруг второго тела
- 11.4.3. Гиперболический захват
- 11.4.4. Точность проведенного анализа и влияние ошибок
- 11.4.5. Облет как средство увеличения скорости
- Задачи
- Глава 12. Траектории полетов к планетам и Луне
- 12.3. Возможности и точность методов исследования
- 12.4. Использование интеграла Якоби
- 12.5. Использование решений Лагранжа
- 12.6. Использование решений задачи двух тел
- 12.7. Искусственные спутники Луны
- 12.7.1. Относительные величины возмущений спутника Луны для различных случаев
- 12.7.2. Интеграл Якоби для близкого спутника Луны
- 12.8. Траектории межпланетных полетов
- 12.9. Солнечная система как поле центральной силы
- 12.10. Орбиты межпланетных перелетов с минимальными затратами энергии
- 12.11. Использование орбит ожидания при межпланетных полетах
- 12.12. Влияние ошибок на межпланетные орбиты
- Задачи
- Глава 13. Определение орбит и межпланетная навигация
- 13.2. Теория определения орбит
- 13.3. Метод Лапласа
- 13.4. Метод Гаусса
- 13.5. Метод Ольберса для параболических орбит
- 13.6. Определение орбит при наличии дополнительных данных наблюдений
- 13.7. Улучшение орбит
- 13.8. Межпланетная навигация
- 13.8.1. Стабилизированные платформы и акселерометры
- 13.8.2. Навигация при помощи бортовой оптической аппаратуры
- 13.8.3. Методы наблюдений и достижимая точность
- Литература
- Глава 14. Двойные системы и системы нескольких тел
- 14.2. Визуально-двойные звезды
- 14.3. Соотношение масса—светимость
- 14.4. Динамические параллаксы
- 14.5. Затменные двойные
- 14.6. Спектрально-двойные звезды
- 14.7. Обзор результатов
- 14.8. Элементы орбиты двойной звезды
- 14.9. Период двойной звезды
- 14.10. Движение апсид
- 14.11. Силы, действующие в двойной системе
- 14.12. Тройные системы
- 14.13. Неточность ньютоновского закона тяготения
- 14.14. Фигуры звезд в двойных системах
- 14.15. Пределы Роша
- 14.16. Вещество, окружающее звезды
- 14.17. Образование двойных систем
- Задачи
- Глава 15. Звездные системы многих тел
- 15.2. Сфера действия
- 15.3. Парные сближения
- 15.4. Накапливающийся эффект малых сближений
- 15.5. Некоторые фундаментальные принципы
- 15.6. Основные теоремы звездной динамики
- 15.6.1. Теорема Джинса
- 15.7. Некоторые частные случаи для звездной системы в стационарном состоянии
- 15.8. Вращение галактик
- 15.8.2. Период вращения и угловая скорость Галактики
- 15.8.3. Масса Галактики
- 15.8.4. Общий характер вращения Галактики
- 15.8.5. Галактические орбиты звезд
- 15.8.6. Звезды с высокими скоростями
- 15.9. Сферические звездные системы
- 15.9.1. Применение теоремы вириала к сферической системе
- 15.9.2. Орбиты звезд в сферической системе
- 15.9.3. Распределение орбит внутри сферической системы
- 15.10. Эксперименты на ЭВМ
- Задачи
- Ответы к задачам
- Приложения