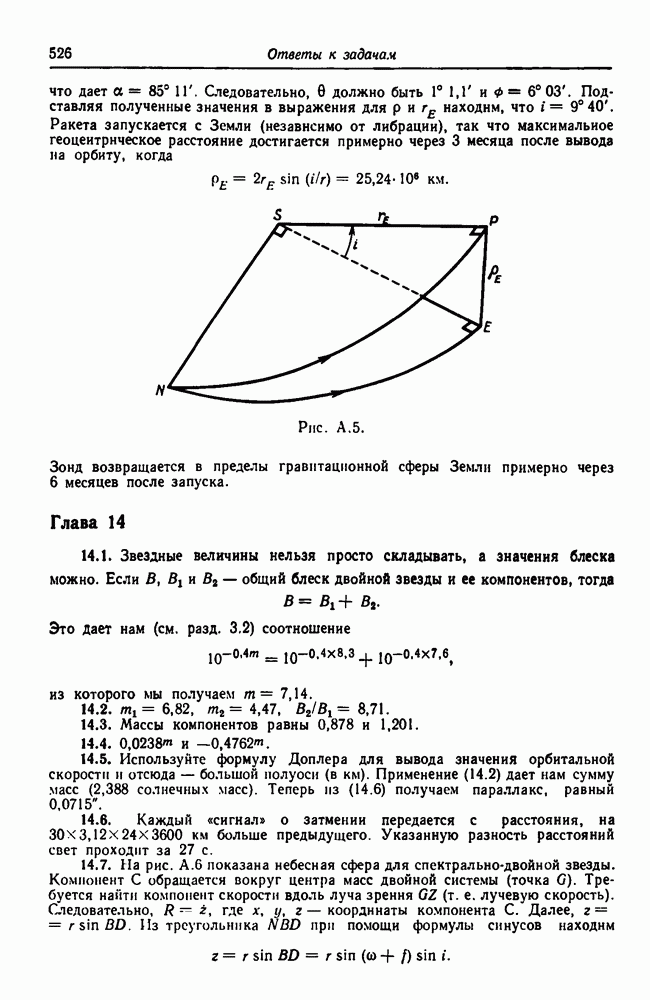
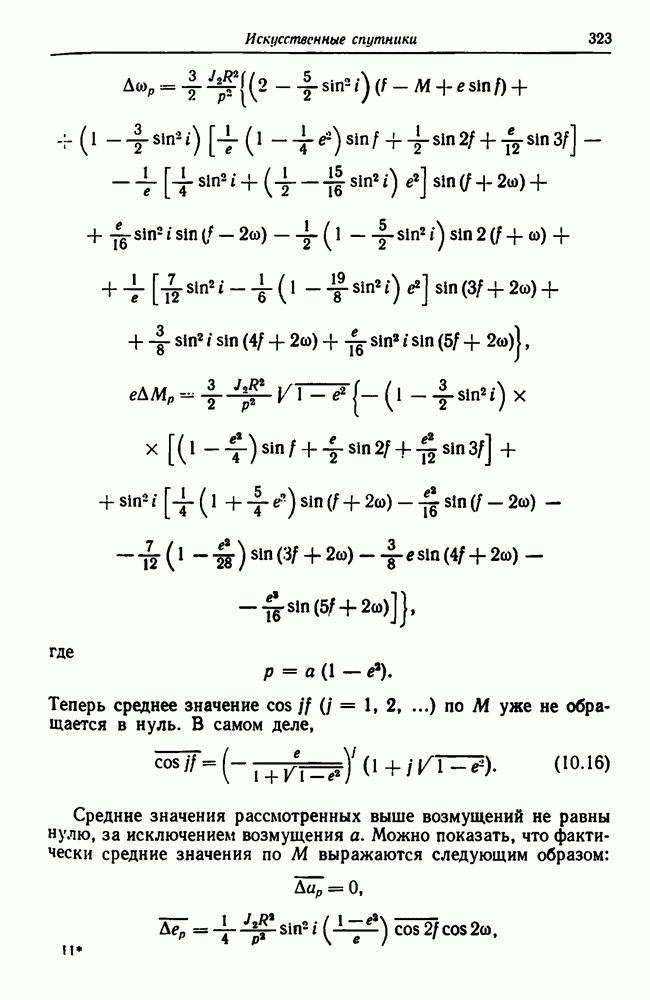| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Задачи
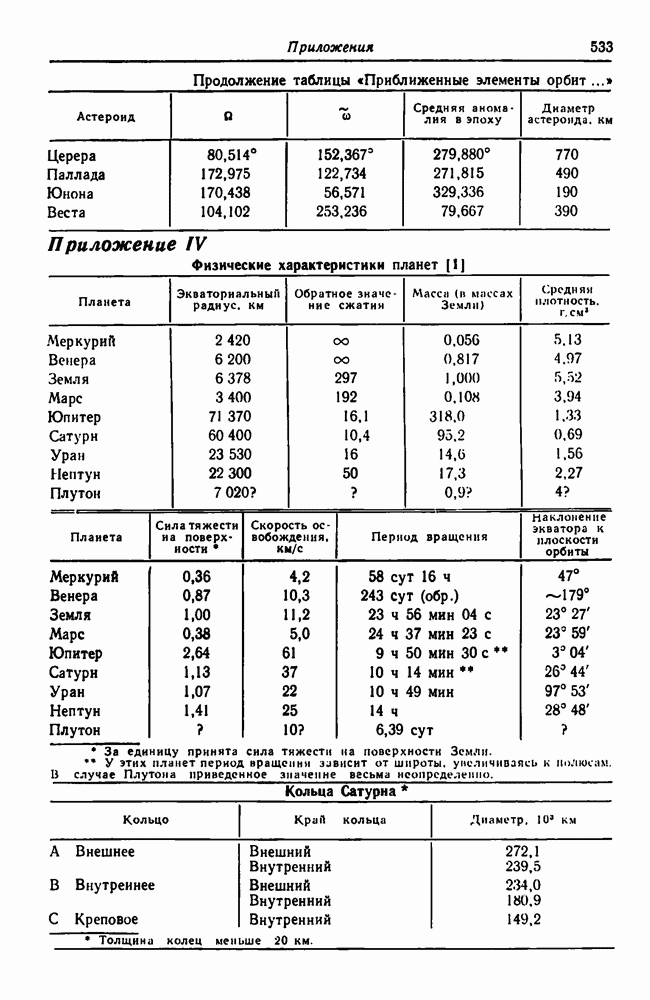
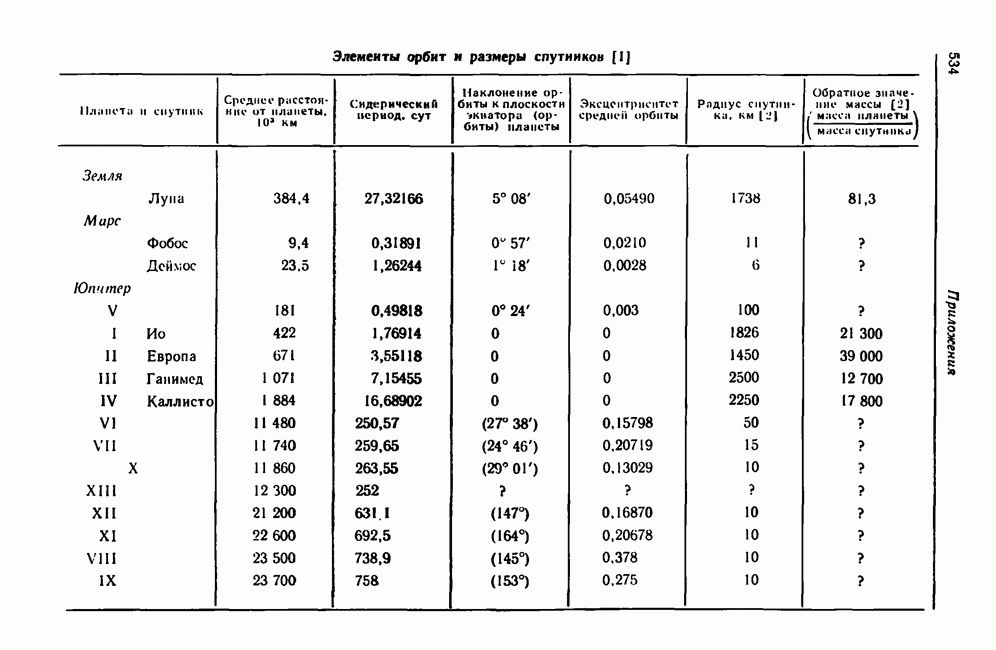
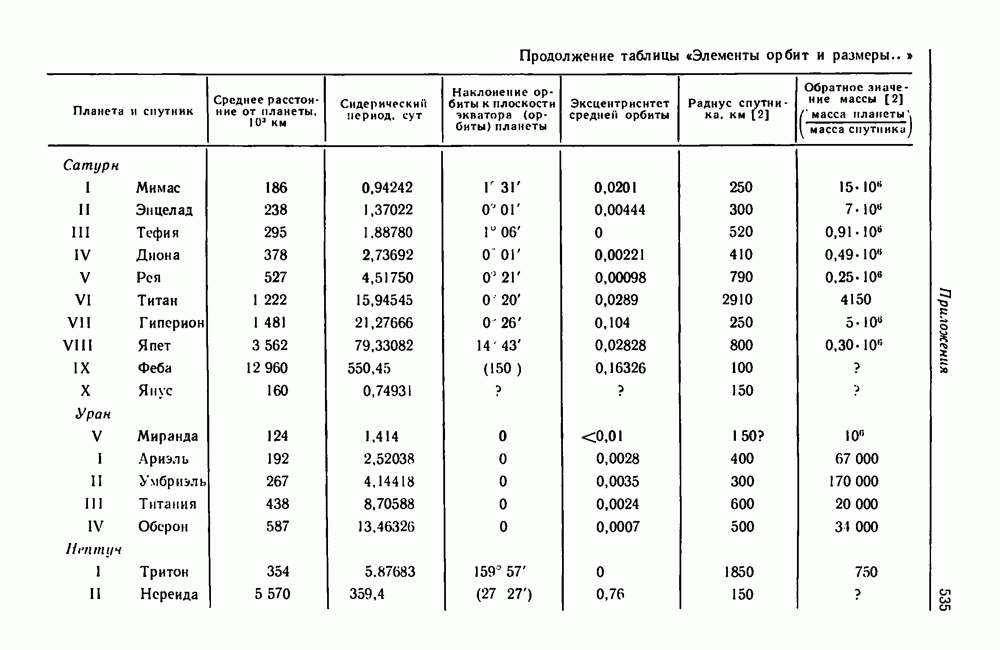
Необходимые для решения данные приведены в приложениях.
11.1. Как отразится на величине приращения скорости ракеты, движущейся и свободном пространстве (гравитационное поле отсутствует): 1) увеличение в два раза скорости истечения, 2) увеличение в два раза отношения масс?
11.2. На ракете с начальной массой  имеется
имеется  топлива. Скорость истечения равна 2000 мс, а секундный расход топлива составляет 130 000 г/с. Пренебрегая сопротивлением атмосферы, вычислить скорость и высоту ракеты к моменту полного выгорания топлива, если ракета стартует вертикально вверх (считать ускорение свободного падения постоянным и равным 981 см/с2).
топлива. Скорость истечения равна 2000 мс, а секундный расход топлива составляет 130 000 г/с. Пренебрегая сопротивлением атмосферы, вычислить скорость и высоту ракеты к моменту полного выгорания топлива, если ракета стартует вертикально вверх (считать ускорение свободного падения постоянным и равным 981 см/с2).
11.3. На круговую орбиту вокруг Земли предполагается вывести вторую ступень двухступенчатой ракеты (орбитальная скорость должна равняться  . Скорость истечения у двигателя второй ступени равна
. Скорость истечения у двигателя второй ступени равна  (вдвое больше, чем у двигателя первой ступени); обе ступени имеют одинаковое отношение масс R, а отношение масс полностью заправленных топливом первой и второй ступеней равно 0,15. Масса второй ступени без топлива, которая и выводится на орбиту, равна
(вдвое больше, чем у двигателя первой ступени); обе ступени имеют одинаковое отношение масс R, а отношение масс полностью заправленных топливом первой и второй ступеней равно 0,15. Масса второй ступени без топлива, которая и выводится на орбиту, равна  . Пренебрегая потерями на преодоление гравитационного поля и аэродинамического сопротивления, вычислить R и начальную массу ракеты.
. Пренебрегая потерями на преодоление гравитационного поля и аэродинамического сопротивления, вычислить R и начальную массу ракеты.
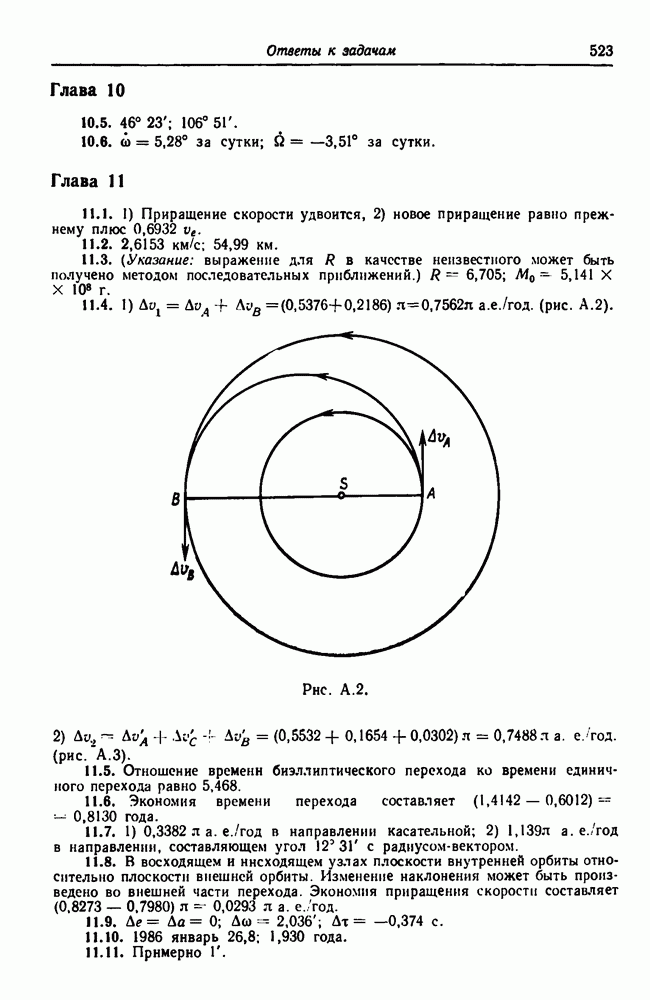
11.4. Сравнить суммарные приращения скорости, необходимые для перевода космического зонда на гелиоцентрическую круговую орбиту с радиусом  по биэллиптнческой касательной орбите перехода с афелием на расстоянии 60 а. е., 2) по касательной эллиптической орбите перехода.
по биэллиптнческой касательной орбите перехода с афелием на расстоянии 60 а. е., 2) по касательной эллиптической орбите перехода.
11.5. Сравнить времена перехода в задаче 11.4.
11.6. Две круговые компланарные гелиоцентрические орбиты имеют радиусы 1 а. е. и 3 а. е. Ракета, движущаяся по внутренней орбите, в результате включения двигателя получает приращение скорости в 1,6 раз больше приращения скорости, необходимого для выхода на касательный эллипс перехода к внешней орбите. Насколько при этом сократится время перехода на внешнюю круговую орбиту?
11.7. Какое приращение скорости в предыдущей задаче нужно: 1) в конце касательной эллиптической орбиты перехода, 2) в точке пересечения быстрой орбиты с внешней круговой орбитой для того, чтобы перевести ракету на внешнюю орбиту?
11.8. Две круговые гелиоцентрические орбиты имеют радиусы 1 а. е. и 3 а. е. и взаимное наклонение 5°. Нам нужно движущийся по внешней орбите аппарат перевести по эллиптической траектории на внутреннюю орбиту, дважды изменяя его скорость. Когда должны прикладываться импульсы? Где с точки зрения экономии топлива надо изменять наклонение орбиты — во внешней пли во внутренней точке перехода? Вычислить суммарную экономию требуемого приращения скорости, которую можно получить, приняв правильное решение.
11.9. Предположим, что в примере из разд. 11.3.6 (полет к Луне) единственной ошибкой является ошибка  дуги. Найти в первом приближении ошибки эксцентриситета, величины и ориентации большой полуоси, апогейного расстояния и момента прохождения перигея.
дуги. Найти в первом приближении ошибки эксцентриситета, величины и ориентации большой полуоси, апогейного расстояния и момента прохождения перигея.
11.10. Два астероида движутся по круговым компланарным гелиоцентрическим орбитам со следующими элементами:

Один рассеянный исследователь астероидов, работающий на А, решил перебраться на В с минимальными затратами топлива. Когда он сможет начать переход? По прибытии на В исследователь обнаружил, что он забыл на А свой счетчик Гейгера. Сколько ему придется ждать на В до момента начала обратного перехода, если он снова хочет экономить топливо? (Гравитационными полями астероидов можно пренебречь.)
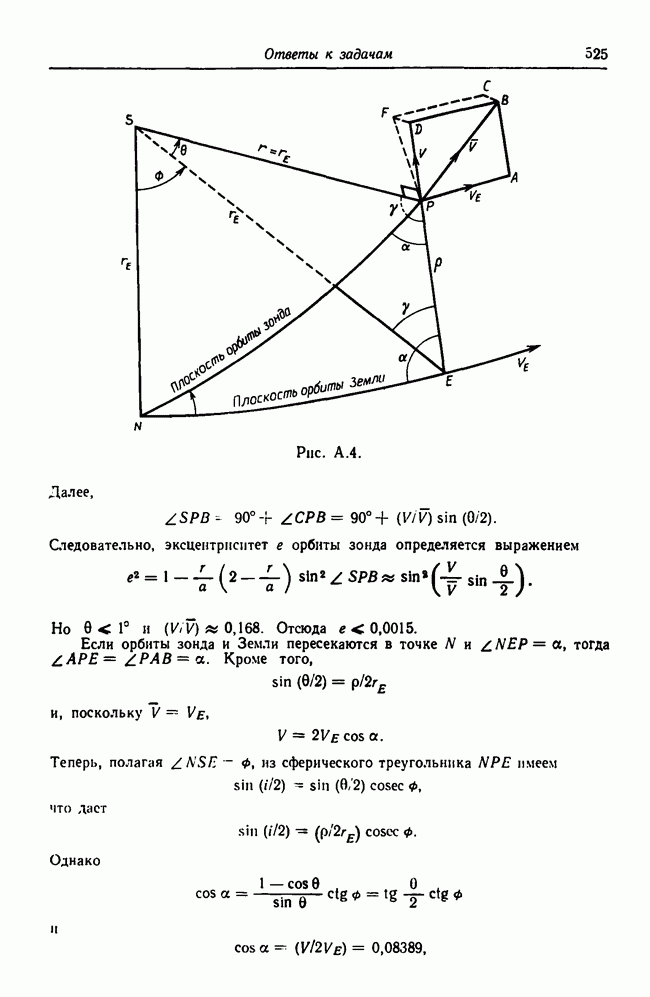
11.11. Межпланетный зонд уходит с начальной круговой гелиоцентрической орбиты радиуса 6630 км с тангенциальной скоростью 12 км/с. На расстоянии 1 500 000 км направление вектора геоцентрической скорости предполагается совпадающим с направлением асимптоты. Найти величину ошибки, к которой приводит такое предположение.
Литература
1. Ehricke К. A. Space Flight, vol. 1: Environment and Celestial Mechanics. New Jersey, Van Nostrand, 1961.
2. Ehricke К. A. Space Flight, vol. 2: Dynamics. New Jersey, Van Nostrand, 1962.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. Неспокойная Вселенная
- 1.2. Солнечная система
- 1.2.1. Законы Кеплера
- 1.2.2. Закон Боде
- 1.2.3. Соизмеримости в средних движениях
- 1.2.4. Кометы и метеорные тела
- 1.2.5. Выводы
- 1.3. Движение звезд
- 1.3.1. Двойные системы
- 1.3.2. Тройные системы и системы более высокой кратности
- 1.3.3. Шаровые скопления
- 1.3.4. Галактические, или рассеянные, звездные скопления
- 1.4. Скопления галактик
- 1.5. Выводы
- Рекомендуемая литература
- Глава 2. Системы координат и измерение времени
- 2.2. Положение на поверхности Земли
- 2.3. Горизонтальная система
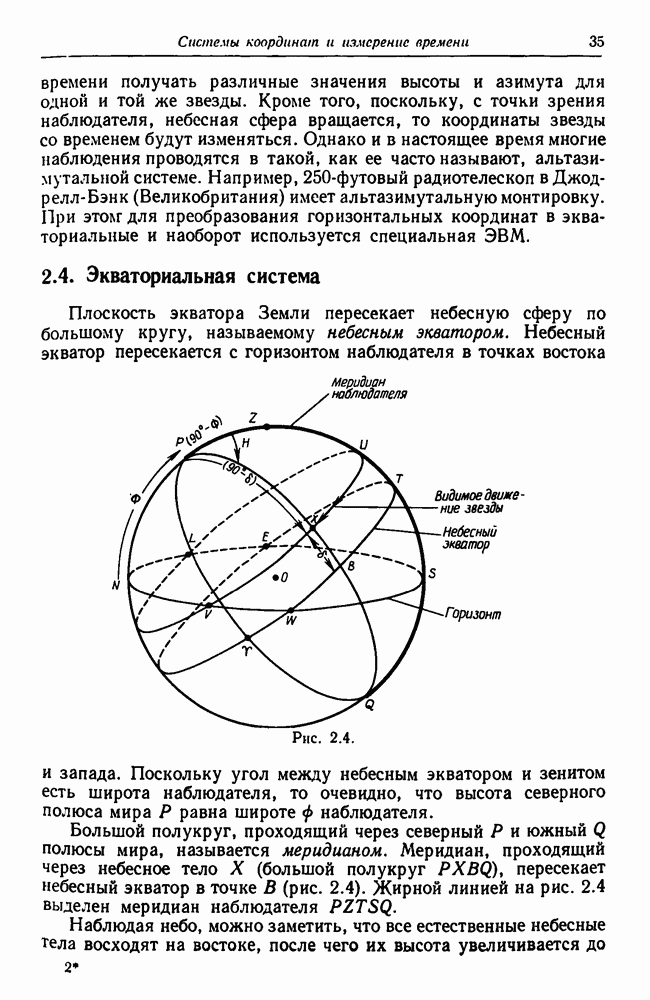
- 2.4. Экваториальная система
- 2.5. Эклиптическая система
- 2.6. Элементы орбиты в пространстве
- 2.7. Прямоугольные системы координат
- 2.8. Системы координат, связанные с плоскостью орбиты
- 2.9. Преобразование систем координат
- 2.9.2. Примеры преобразований систем координат
- 2.10. Галактическая система координат
- 2.11. Измерение времени
- 2.11.1. Звездное время
- 2.11.2. Среднее солнечное время
- 2.11.3. Юлианские дни
- 2.11.4. Эфемеридное время
- Задачи
- Литература
- Глава 3. Обработка данных наблюдений
- 3.2. Методы наблюдений
- 3.3. Рефракция
- 3.4. Прецессия и нутация
- 3.5. Аберрация
- 3.6. Собственное движение
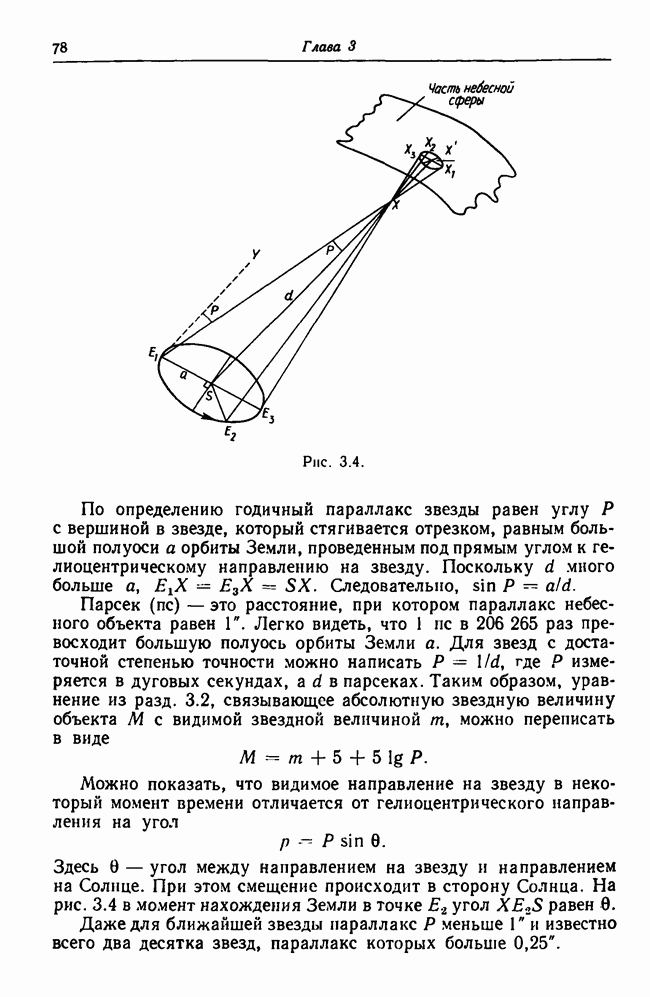
- 3.7. Годичный параллакс
- 3.8. Геоцентрический параллакс
- 3.9. Обзор процедур
- Задачи
- Литература
- Глава 4. Задача двух тел
- 4.2. Законы Ньютона
- 4.3. Закон всемирного тяготения Ньютона
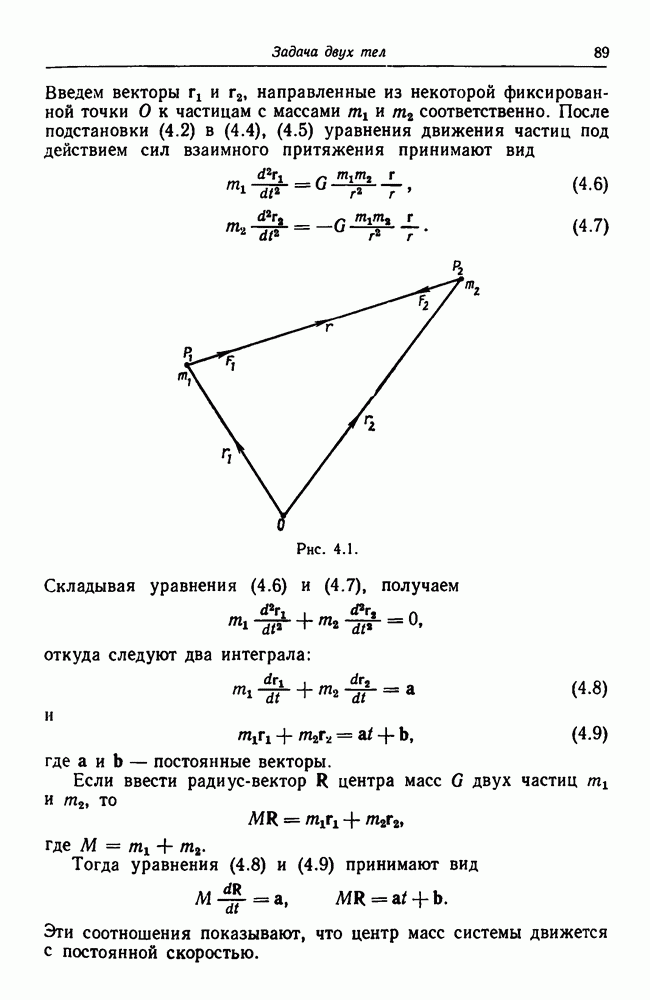
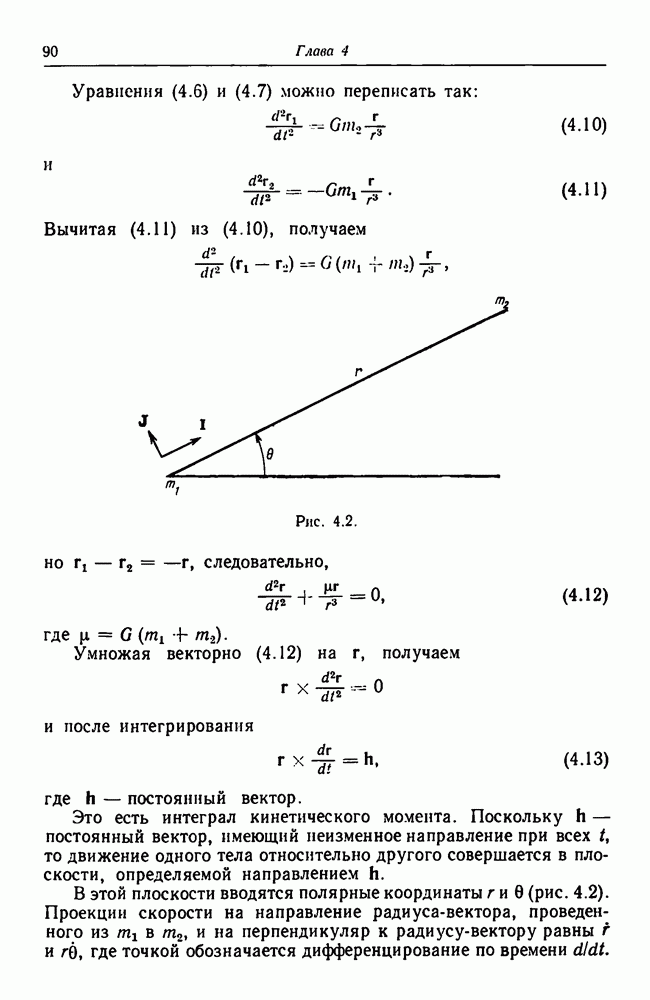
- 4.4. Решение задачи двух тел
- 4.5. Эллиптическая орбита
- 4.5.1. Измерение массы планеты
- 4.5.2. Скорость движения по эллиптической орбите
- 4.5.3. Угол между вектором скорости и радиусом-вектором
- 4.5.4. Средняя, эксцентрическая и истинная аномалии
- 4.5.5. Решение уравнения Кеплера
- 4.5.6. Уравнение центра
- 4.5.7. Положение тела на эллиптической орбите
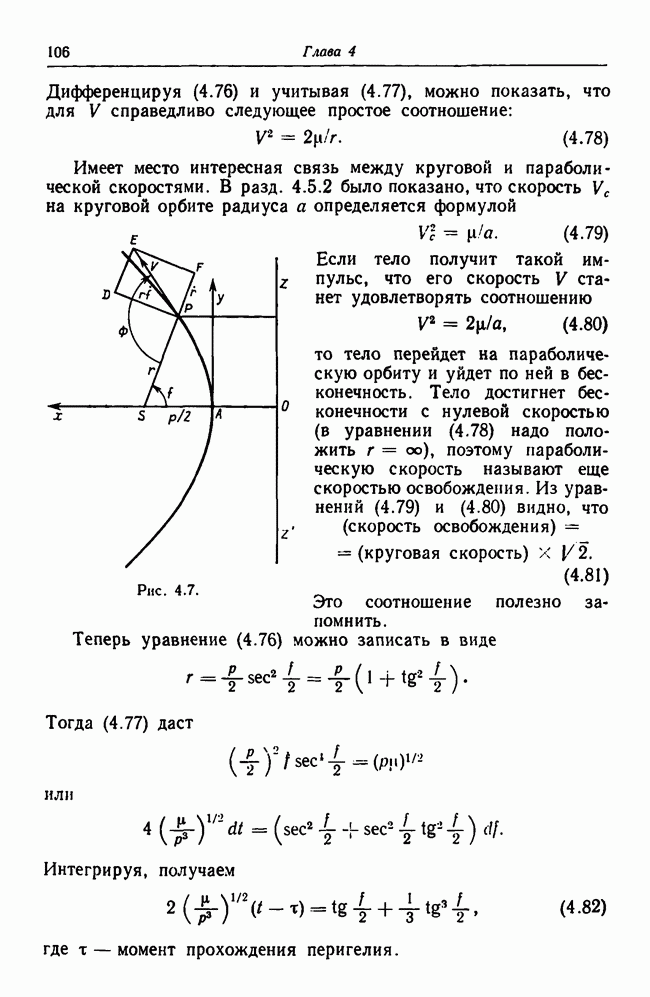
- 4.6. Параболическая орбита
- 4.7. Гиперболическая орбита
- 4.7.1. Скорость на гиперболической орбите
- 4.7.2. Положение на гиперболической орбите
- 4.8. Прямолинейная орбита
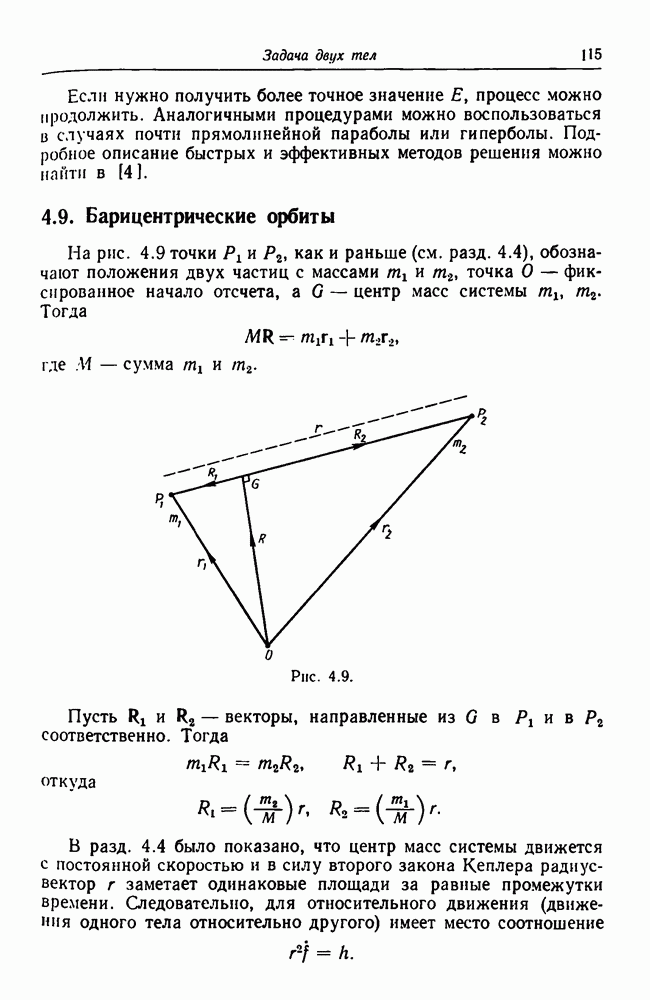
- 4.9. Барицентрические орбиты
- 4.10. Классификация орбит по величине константы энергии
- 4.11. Орбита в пространстве
- 4.12. Ряды для f и g
- 4.13. Использование рекуррентных соотношений
- 4.14. Универсальные переменные
- Задачи
- Литература
- Глава 5. Задача n тел
- 5.2. Уравнения движения задачи n тел
- 5.3. Десять известных интегралов и их смысл
- 5.4. Силовая функция
- 5.5. Теорема вириала
- 5.6. Теорема зеркальности
- 5.7. Снова о задаче n тел
- 5.8. Лагранжевы решения задачи трех тел
- 5.9. Общие замечания о лагранжевых решениях
- 5.10. Ограниченная круговая задача трех тел
- 5.10.2. Критерий Тиссерана
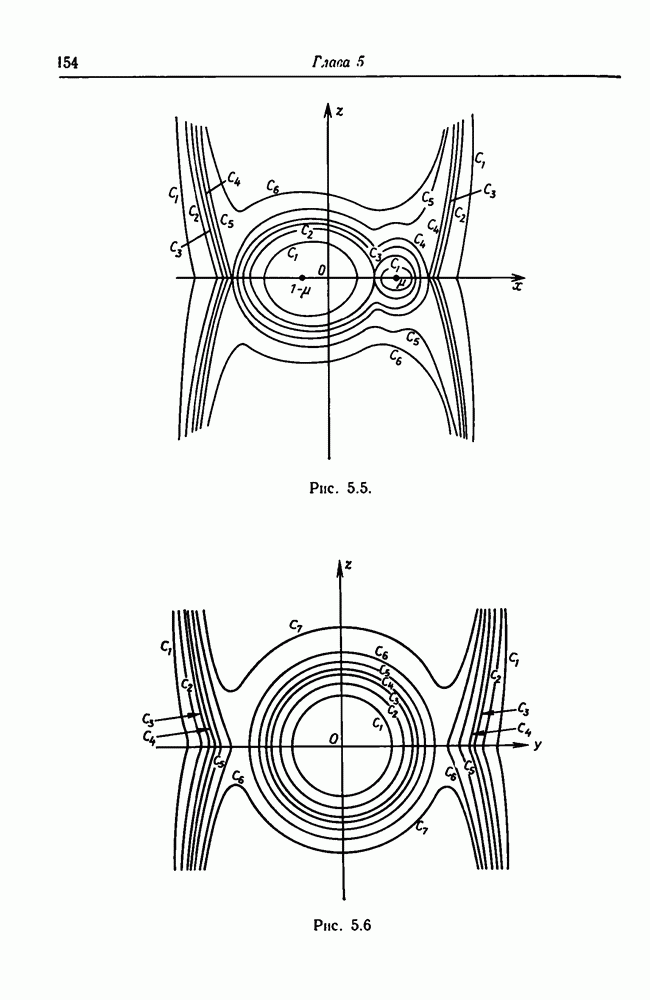
- 5.10.3. Поверхности нулевой скорости
- 5.10.4. Устойчивость точек либрации
- 5.10.5. Периодические орбиты
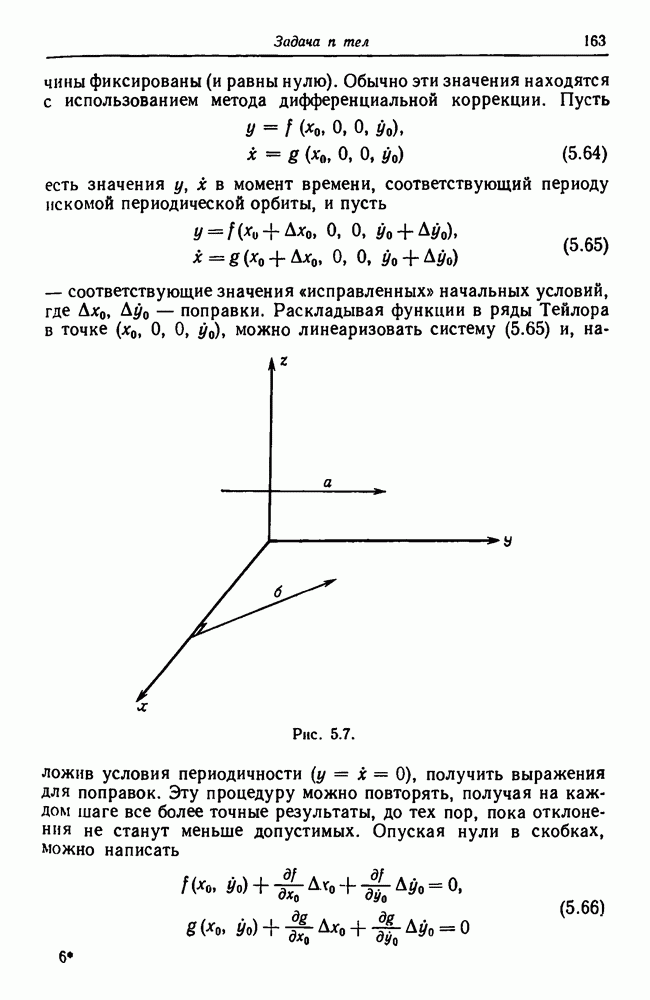
- 5.10.6. Поиск симметричных периодических орбит
- 5.10.7. Примеры семейств периодических орбит
- 5.10.8. Устойчивость периодических орбит
- 5.10.9. Поверхность сечения
- 5.10.10. Матрица устойчивости
- 5.11. Общая задача трех тел
- 5.11.1. Случай С < 0
- 5.11.2. Случай С = 0
- 5.11.3. Координаты Якоби
- Задачи
- Литература
- Глава 6. Общие возмущения
- 6.2. Уравнения относительного движения
- 6.3. Возмущающая функция
- 6.4. Гравитационная сфера влияния
- 6.5. Потенциал тела произвольной формы
- 6.6. Потенциал шара во внутренней точке
- 6.7. Метод вариации параметров
- 6.7.1. Модификация средней долготы в эпоху
- 6.7.2. Решение уравнений движения планет в форме Лагранжа
- 6.7.3. Коротко- и долгопериодические вариации
- 6.7.4. Разложение возмущающей силы
- 6.8. Уравнения Лагранжа
- 6.9. Канонические уравнения Гамильтона
- Задачи
- Рекомендуемая литература
- Глава 7. Специальные возмущения
- 7.2. Основные факторы теории специальных возмущений
- 7.3. Метод Коуэлла
- 7.4. Метод Энке
- 7.5. Использование возмущенных уравнений
- 7.5.1. Вывод уравнений возмущенного движения
- 7.5.2. Соотношения между возмущенными переменными, прямоугольными координатами, компонентами скорости и обычными элементами кеплеровского движения
- 7.5.3. Процедура численного интегрирования
- 7.5.4. Прямолинейные или почти прямолинейные орбиты
- 7.6. Методы регуляризации
- 7.7. Методы численного интегрирования
- 7.7.2. Метод Рунге—Кутта четвертого порядка
- 7.7.3. Многошаговые методы
- 7.7.4. Численные методы
- Задачи
- Литература
- Глава 8. Устойчивость и эволюция Солнечной системы
- 8.2. Эфемериды планет
- 8.3. Соизмеримости в средних движениях
- 8.4. Астероиды
- 8.5. Кольца Сатурна
- 8.6. Почти соизмеримые орбиты спутников
- 8.7. Численное интегрирование на больших промежутках времени
- 8.7.2. Эволюция элементов орбит на интервале 1 000 000 лет
- 8.7.3. Движение перигелия Плутона: ротационное или либрационное?
- 8.7.4. Сравнение аналитического и численного подходов
- 8.8. Принцип Овендена
- 8.9. Выводы
- Литература
- Глава 9. Теория движения Луны
- 9.3. Сарос
- 9.4. Измерение большой полуоси орбиты, массы и диаметра Луны
- 9.5. Вращение Луны
- 9.6. Селенографические координаты
- 9.7. Фигура Луны
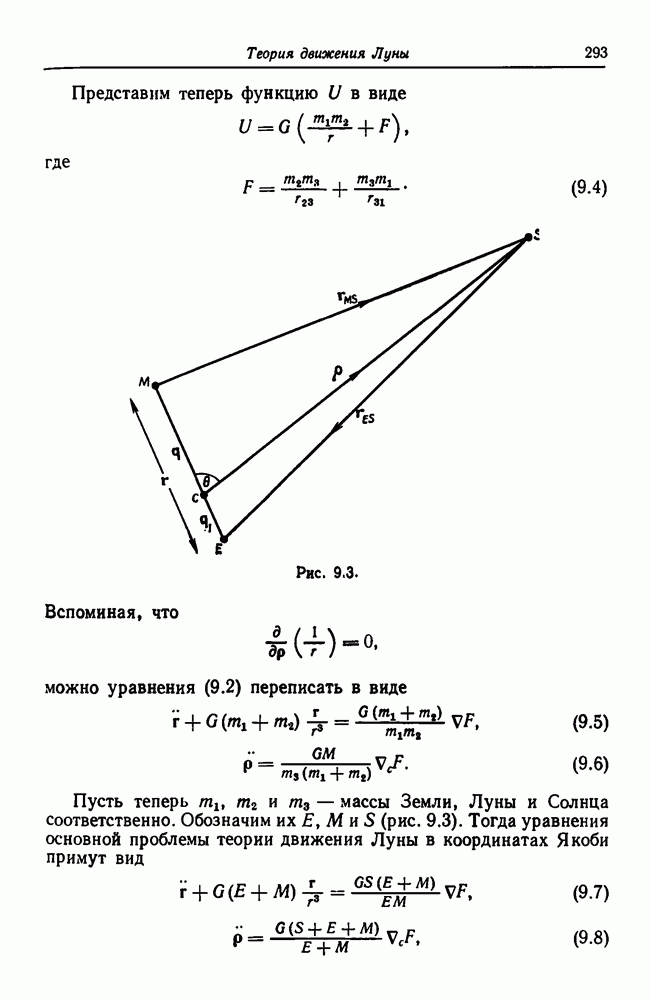
- 9.8. Основная проблема в теории движения Луны
- 9.9. Орбита Солнца в основной проблеме теории движения Луны
- 9.10. Орбита Луны
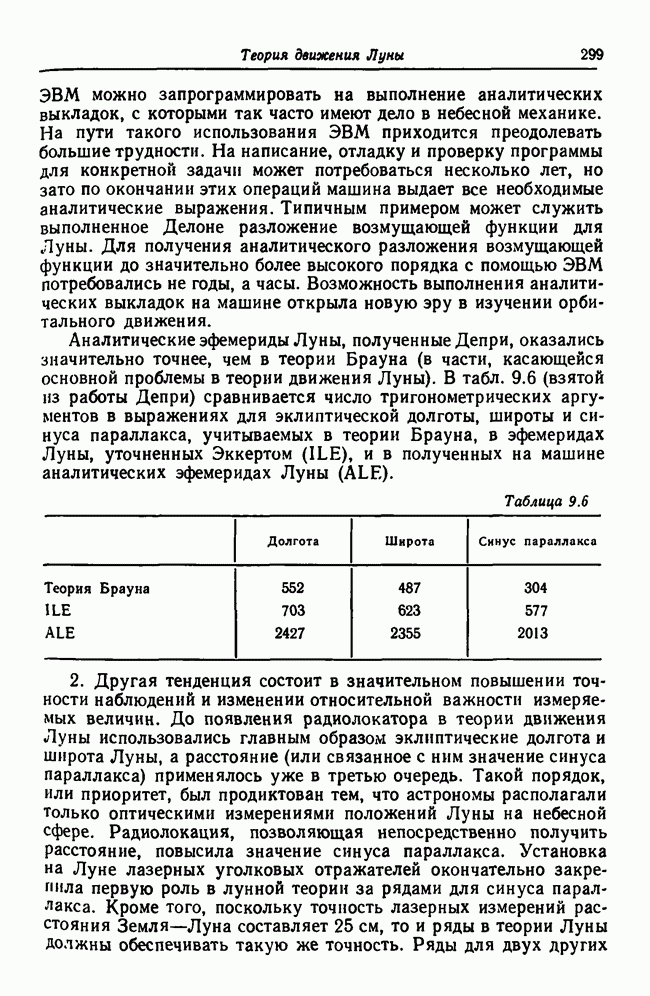
- 9.11. Теории Луны
- 9.12. Вековое ускорение Луны
- Литература
- Глава 10. Искусственные спутники
- 10.2. Земля как планета
- 10.2.1. Форма Земли
- 10.2.2. Формула Клеро
- 10.2.3. Внутреннее строение Земли
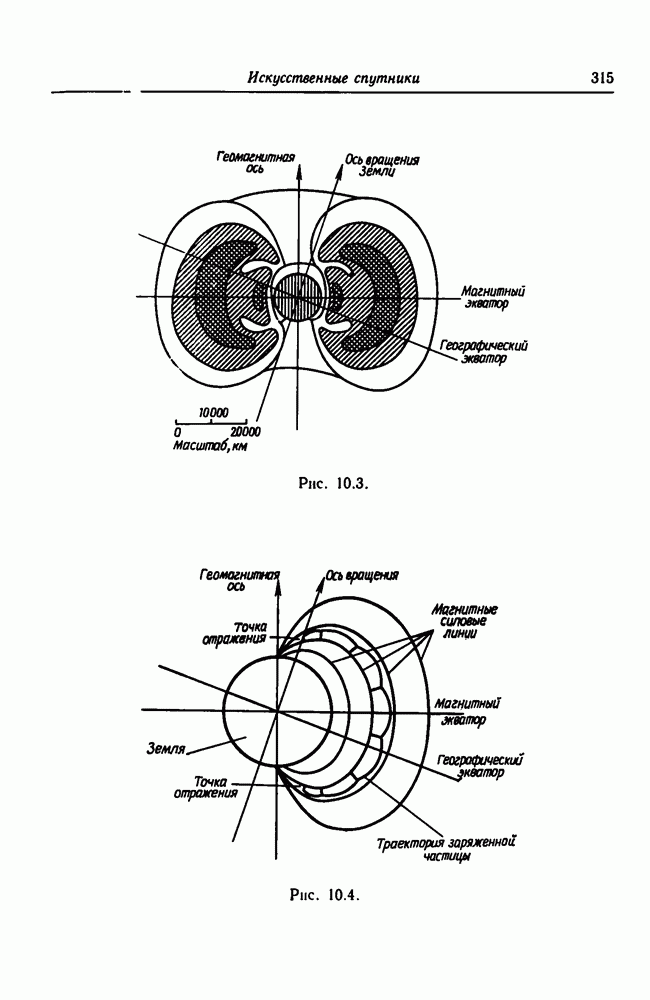
- 10.2.4. Магнитное поле Земли
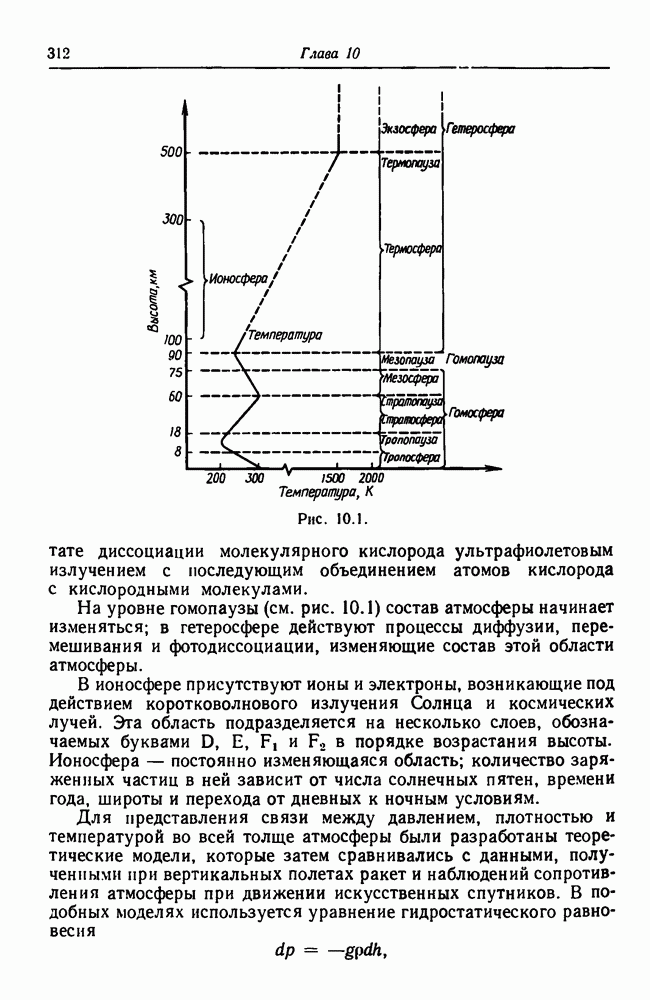
- 10.2.5. Атмосфера Земли
- 10.2.6. Солнечно-земные связи
- 10.3. Силы, действующие на искусственные спутники Земли
- 10.4. Орбита спутника вокруг сплюснутой планеты
- 10.4.1. Короткопериодические возмущения первого порядка
- 10.4.2. Вековые возмущения первого порядка
- 10.4.3. Долгопериодические возмущения, обусловленные третьей гармоникой
- 10.4.4. Вековые возмущения второго порядка и долгопериодические возмущения
- 10.5. Использование теории Гамильтона—Якоби в задаче движения искусственного спутника
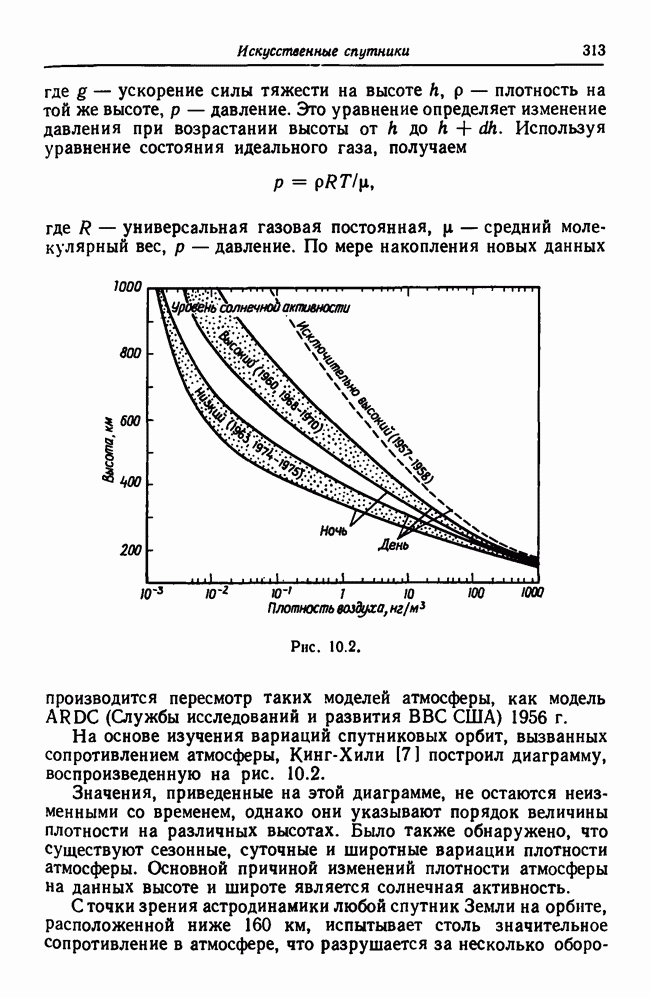
- 10.6. Действие атмосферного торможения на искусственный спутник
- 10.7. Тессеральные и секториальные гармоники поля тяготения Земли
- Задачи
- Литература
- Глава 11. Динамика ракет и орбиты переходов
- 11.2.1. Движение ракеты в гравитационном поле
- 11.2.2. Движение ракеты в атмосфере
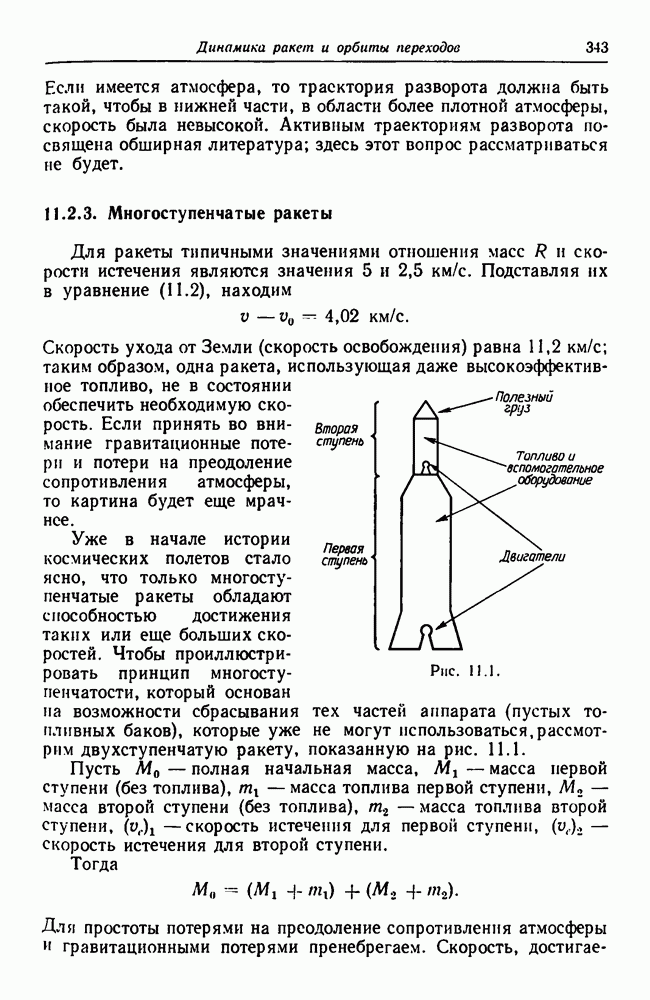
- 11.2.3. Многоступенчатые ракеты
- 11.2.4. Другие типы ракет
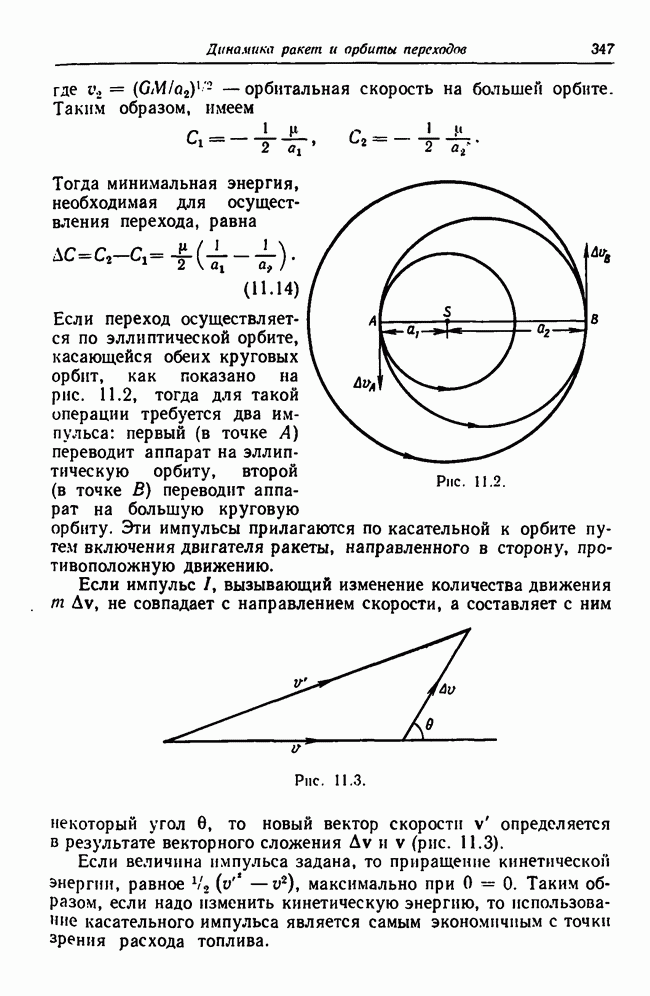
- 11.3. Переходы между орбитами в силовом поле одного притягивающего центра
- 11.3.2. Параболические и гиперболические орбиты перехода
- 11.3.3. Изменения элементов орбиты, вызванные малым импульсом
- 11.3.4. Изменения элементов орбить, вызванные большим импульсом
- 11.3.5. Зависимость расхода топлива от времени перехода
- 11.3.6. Зависимость орбиты перехода от малых ошибок положения и скорости в момент выключения двигателя
- 11.3.7. Переход между частицами, движущимися по орбитам в центральном поле сил
- 11.4. Орбиты перехода в силовых полях двух или более притягивающих центров
- 11.4.2. Выход на орбиту вокруг второго тела
- 11.4.3. Гиперболический захват
- 11.4.4. Точность проведенного анализа и влияние ошибок
- 11.4.5. Облет как средство увеличения скорости
- Задачи
- Глава 12. Траектории полетов к планетам и Луне
- 12.3. Возможности и точность методов исследования
- 12.4. Использование интеграла Якоби
- 12.5. Использование решений Лагранжа
- 12.6. Использование решений задачи двух тел
- 12.7. Искусственные спутники Луны
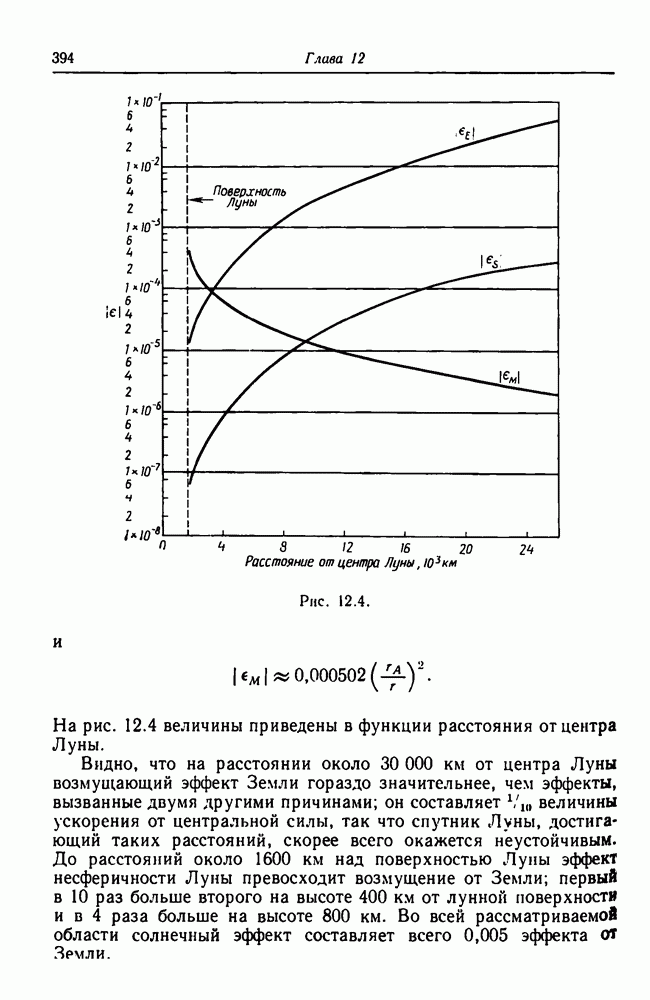
- 12.7.1. Относительные величины возмущений спутника Луны для различных случаев
- 12.7.2. Интеграл Якоби для близкого спутника Луны
- 12.8. Траектории межпланетных полетов
- 12.9. Солнечная система как поле центральной силы
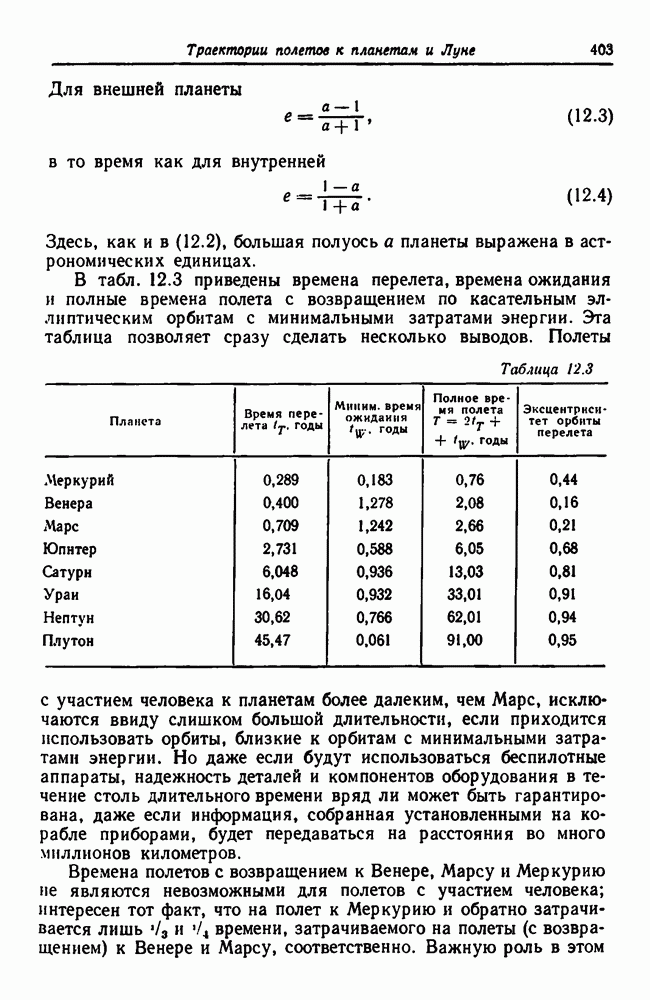
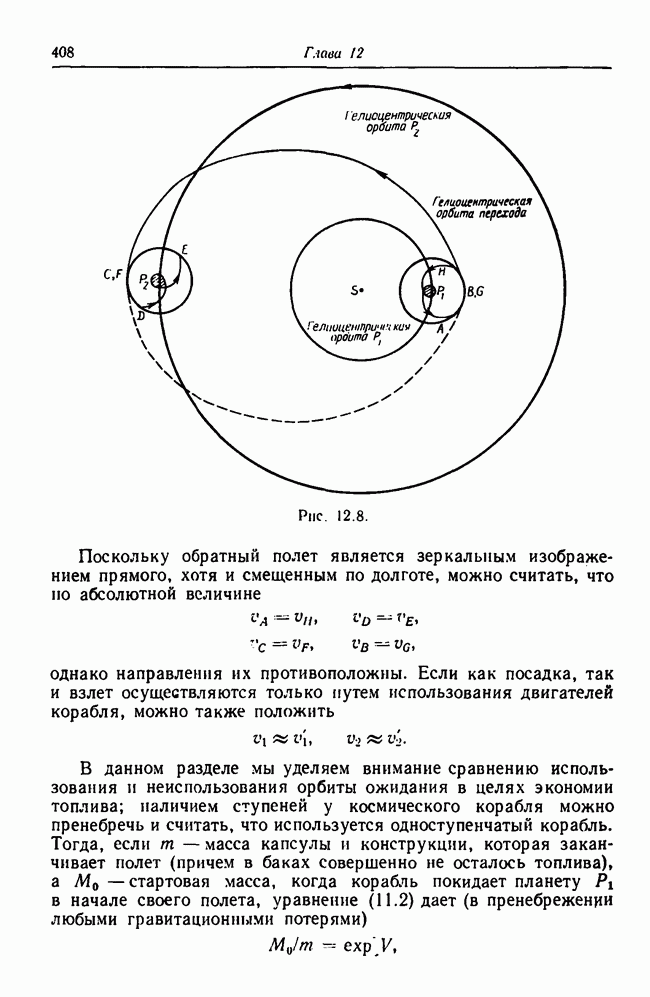
- 12.10. Орбиты межпланетных перелетов с минимальными затратами энергии
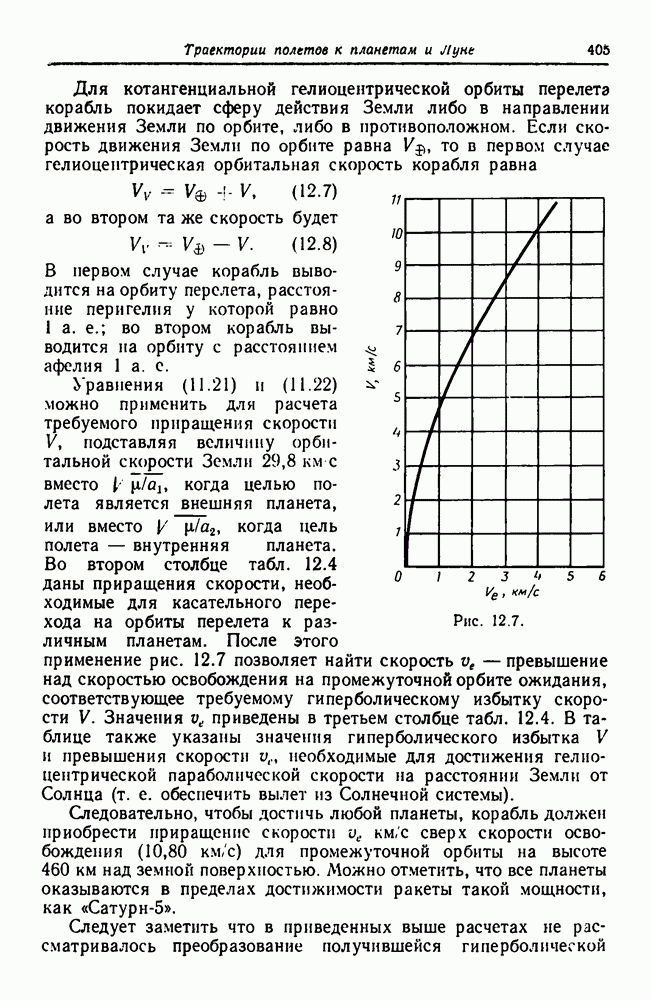
- 12.11. Использование орбит ожидания при межпланетных полетах
- 12.12. Влияние ошибок на межпланетные орбиты
- Задачи
- Глава 13. Определение орбит и межпланетная навигация
- 13.2. Теория определения орбит
- 13.3. Метод Лапласа
- 13.4. Метод Гаусса
- 13.5. Метод Ольберса для параболических орбит
- 13.6. Определение орбит при наличии дополнительных данных наблюдений
- 13.7. Улучшение орбит
- 13.8. Межпланетная навигация
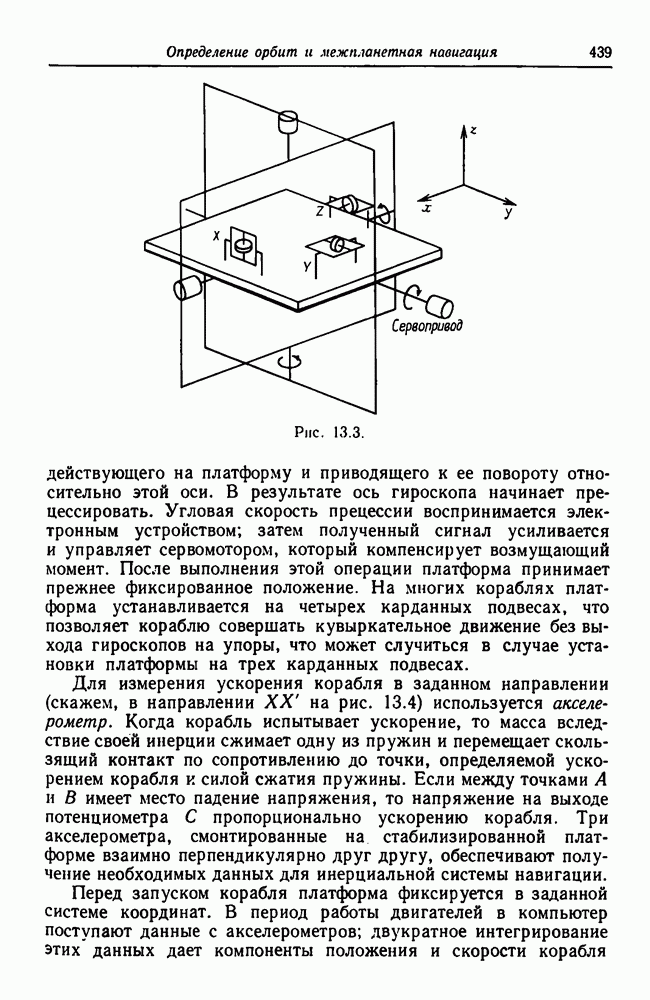
- 13.8.1. Стабилизированные платформы и акселерометры
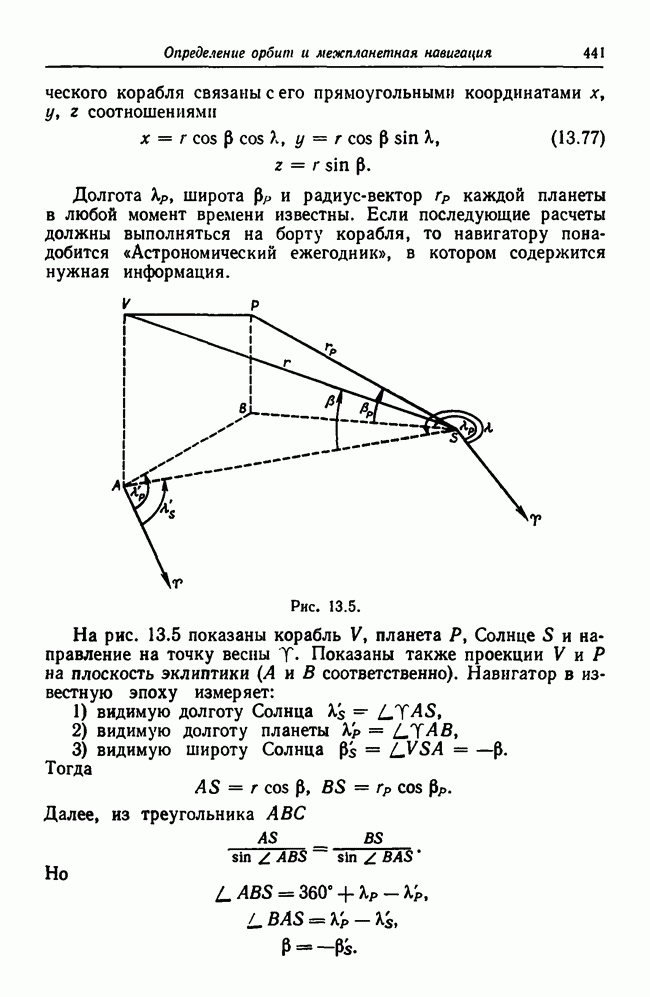
- 13.8.2. Навигация при помощи бортовой оптической аппаратуры
- 13.8.3. Методы наблюдений и достижимая точность
- Литература
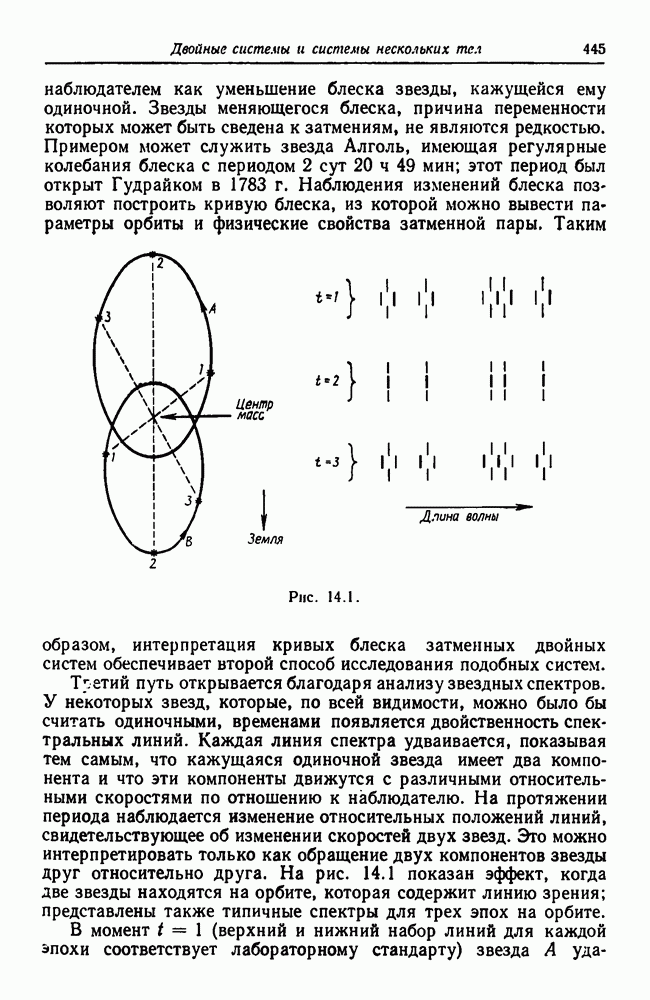
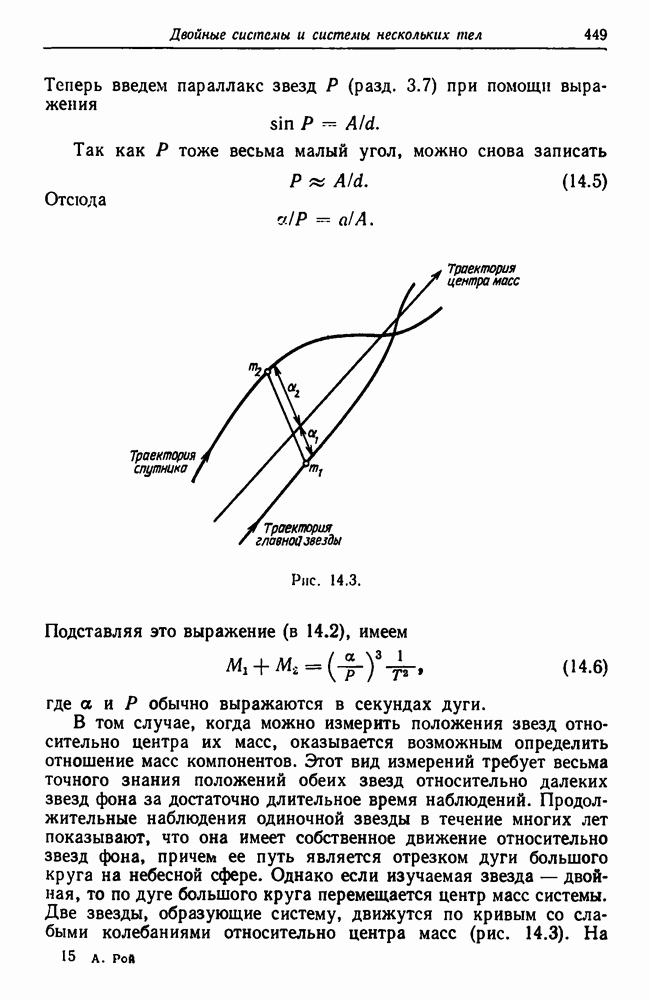
- Глава 14. Двойные системы и системы нескольких тел
- 14.2. Визуально-двойные звезды
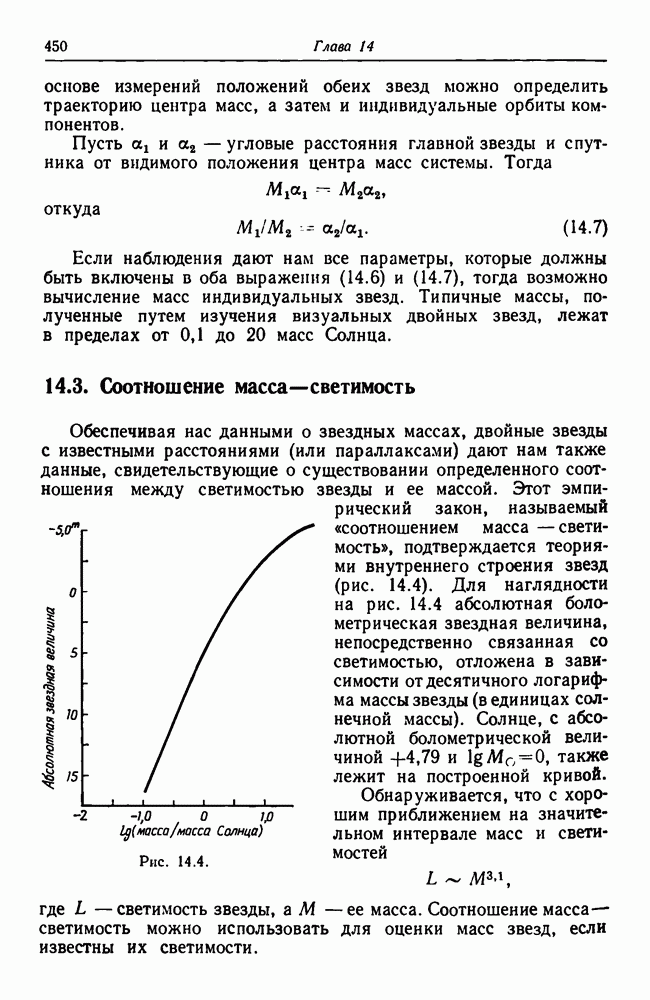
- 14.3. Соотношение масса—светимость
- 14.4. Динамические параллаксы
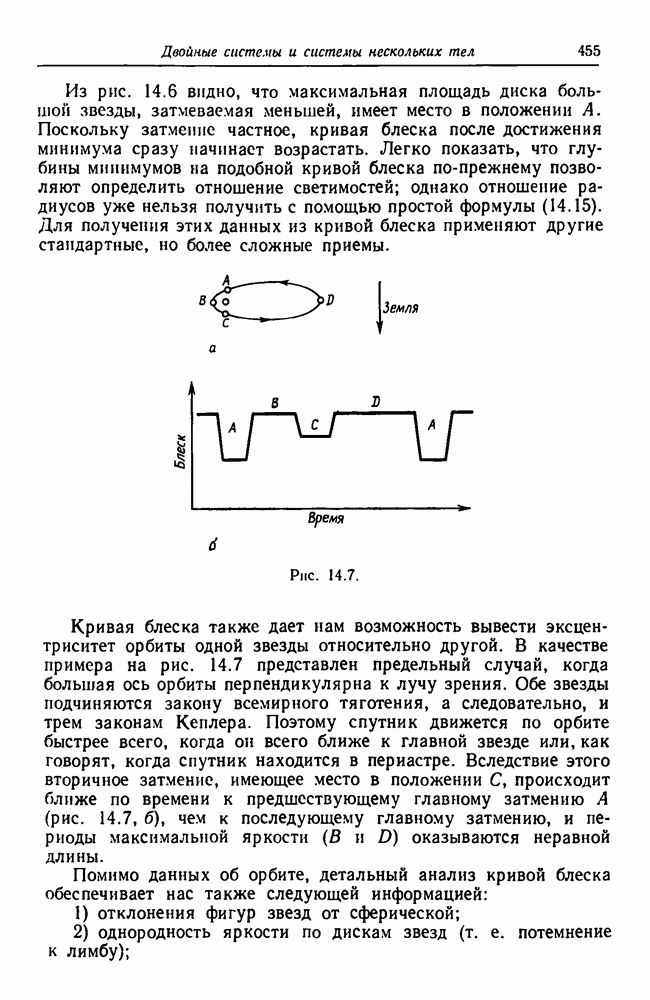
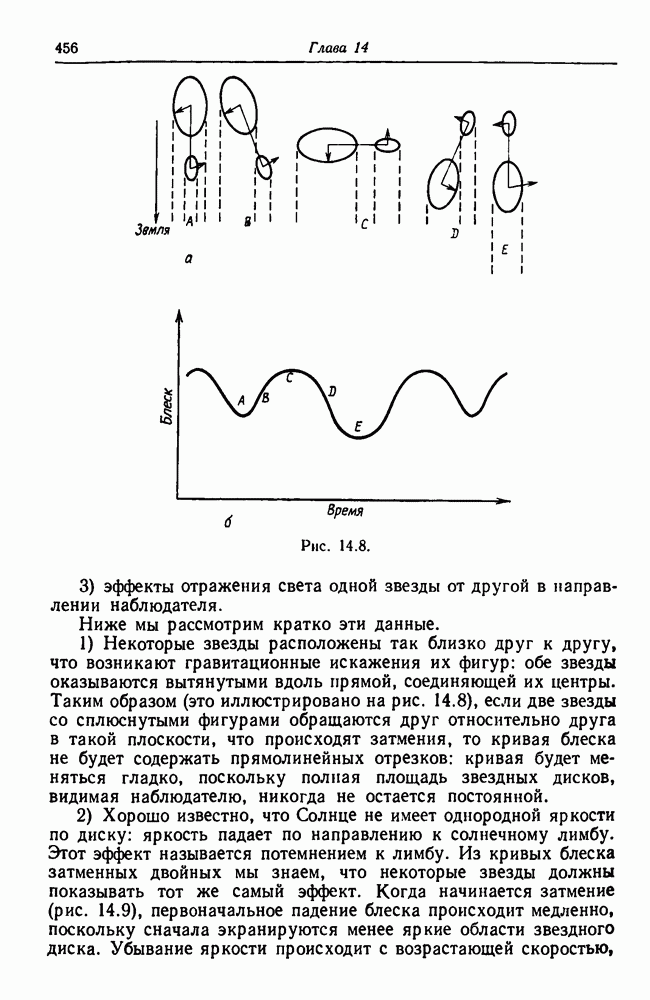
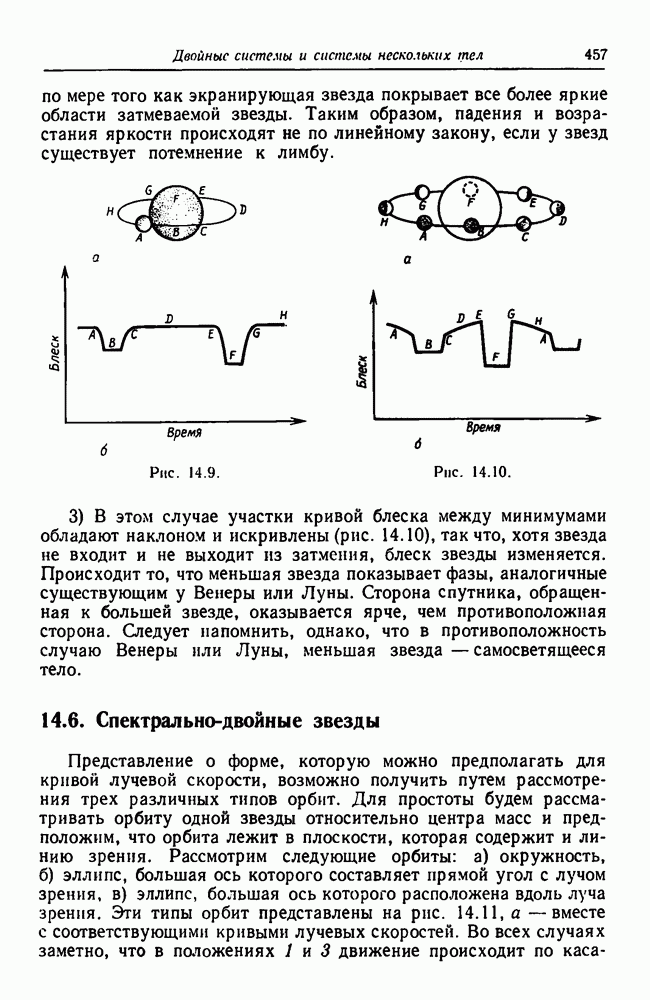
- 14.5. Затменные двойные
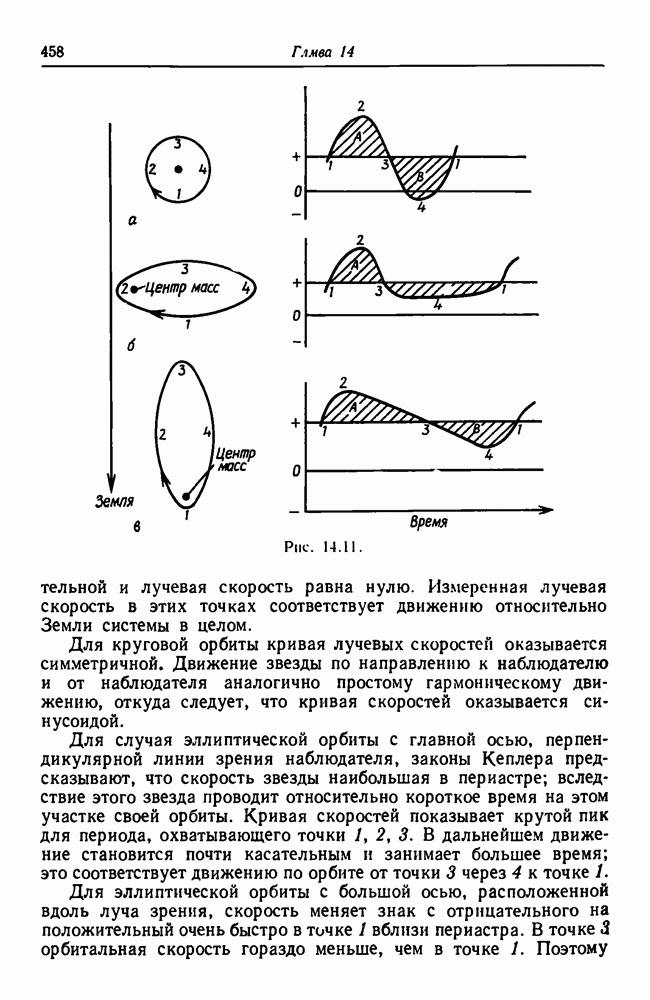
- 14.6. Спектрально-двойные звезды
- 14.7. Обзор результатов
- 14.8. Элементы орбиты двойной звезды
- 14.9. Период двойной звезды
- 14.10. Движение апсид
- 14.11. Силы, действующие в двойной системе
- 14.12. Тройные системы
- 14.13. Неточность ньютоновского закона тяготения
- 14.14. Фигуры звезд в двойных системах
- 14.15. Пределы Роша
- 14.16. Вещество, окружающее звезды
- 14.17. Образование двойных систем
- Задачи
- Глава 15. Звездные системы многих тел
- 15.2. Сфера действия
- 15.3. Парные сближения
- 15.4. Накапливающийся эффект малых сближений
- 15.5. Некоторые фундаментальные принципы
- 15.6. Основные теоремы звездной динамики
- 15.6.1. Теорема Джинса
- 15.7. Некоторые частные случаи для звездной системы в стационарном состоянии
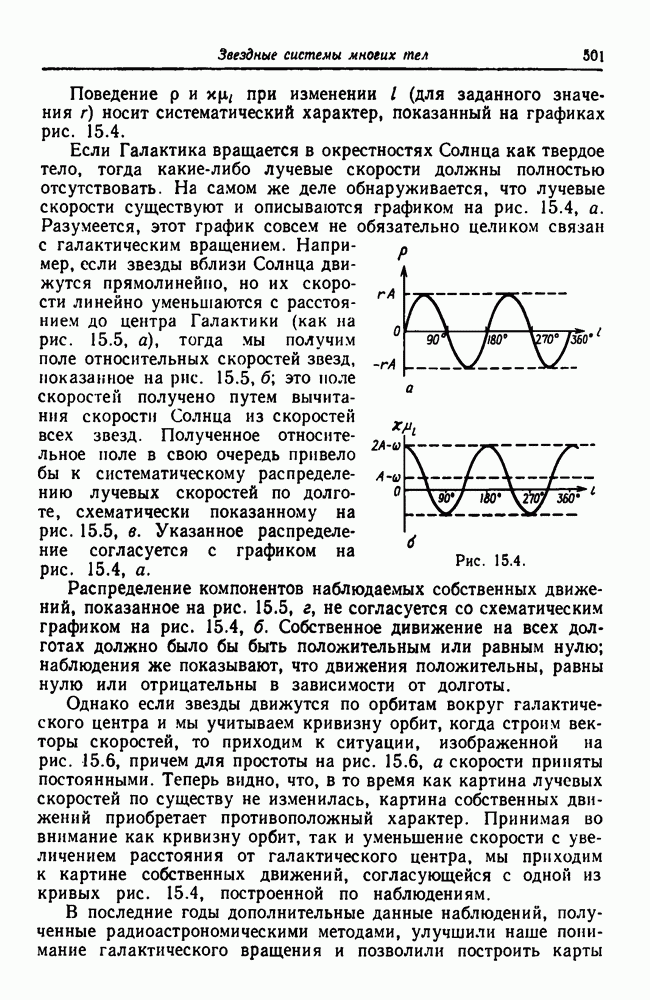
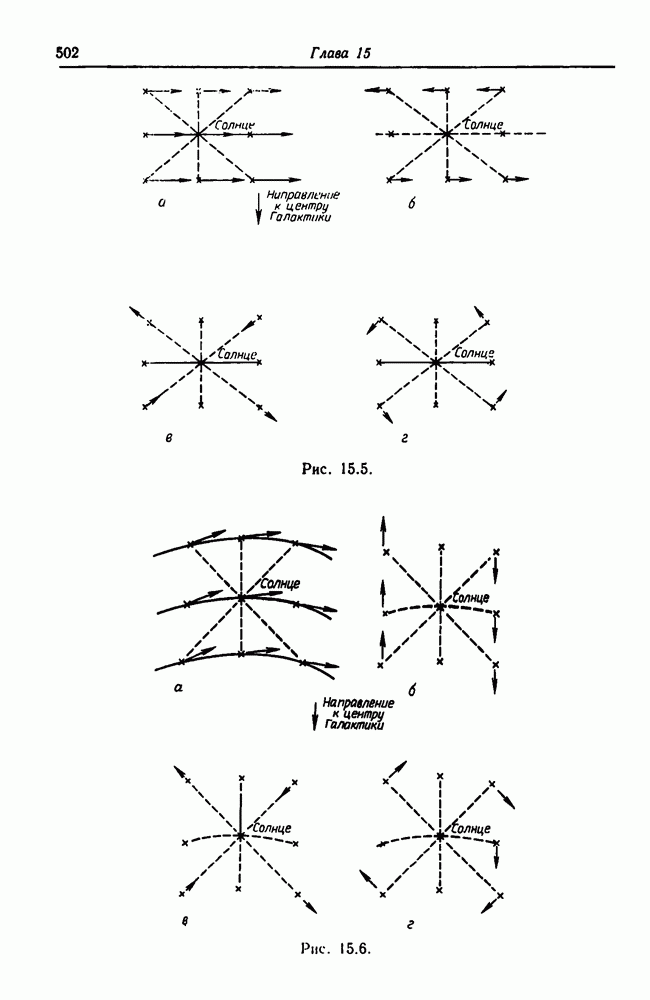
- 15.8. Вращение галактик
- 15.8.2. Период вращения и угловая скорость Галактики
- 15.8.3. Масса Галактики
- 15.8.4. Общий характер вращения Галактики
- 15.8.5. Галактические орбиты звезд
- 15.8.6. Звезды с высокими скоростями
- 15.9. Сферические звездные системы
- 15.9.1. Применение теоремы вириала к сферической системе
- 15.9.2. Орбиты звезд в сферической системе
- 15.9.3. Распределение орбит внутри сферической системы
- 15.10. Эксперименты на ЭВМ
- Задачи
- Ответы к задачам
- Приложения