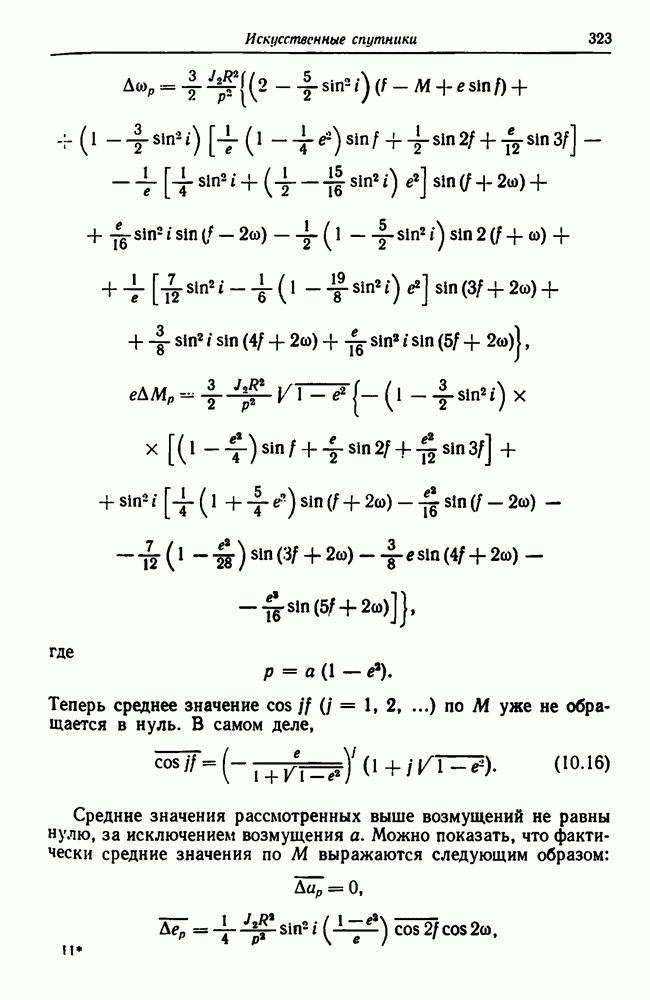| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
15.9.3. Распределение орбит внутри сферической системы
Если звезды никогда не покидают сферическую систему, то последняя стремится со временем прийти в равновесное состояние. В системе может существовать максвелловское распределение скоростей; тогда звездная плотность начинает описываться изотермической политропой. Звездная система с таким поведением действует как сферическая масса газа, в которой звезды играют роль молекул или атомов. Политропным газовым шарам посвящена огромная литература; в ней подробно описываются решения уравнения Эмдена, дающего связь между давлением, плотностью и кинетической температурой частиц. Плюммер, Цейпель и Эдингтон были в числе тех, кто применил теорию политропных газовых шаров к сферическим системам, подобным шаровым скоплениям. На самом деле это применение способно дать лишь приближенные результаты, поскольку непрерывный уход звезд из системы в конце концов приведет систему к полному распаду.
Здесь возможны различные подходы. В предыдущем разделе мы видели, что в сферически-симметричной звездной системе уравнения (15.88) и (15.89) определяют характеристики звездных орбит, причем в общем случае у орбит существуют расстояния перицентра и апоцентра. Обозначим через  расстояние апоцентра. Тогда в апоцентре звезда будет иметь скорость
расстояние апоцентра. Тогда в апоцентре звезда будет иметь скорость  Следовательно,
Следовательно,  (последнее обозначение относится к нормальному компоненту скорости в апоцентре) будут определять орбиту. Можно вывести также функцию распределения
(последнее обозначение относится к нормальному компоненту скорости в апоцентре) будут определять орбиту. Можно вывести также функцию распределения  для этих элементов орбиты. Например, выражение
для этих элементов орбиты. Например, выражение

будет определять число звезд с расстояниями апоцентров, заключенными в пределах от  до
до  и нормальными скоростями в апоцентре, заключенными в пределах от
и нормальными скоростями в апоцентре, заключенными в пределах от  до
до 
В предположение шварцшильдовского закона распределения скоростей в системе можно показать, что
 (15.93)
(15.93)
где шварцшильдовская функция определяется выражением

В этом выражении  — постоянные параметры, U — гравитационный потенциал, VR — лучевая скорость
— постоянные параметры, U — гравитационный потенциал, VR — лучевая скорость  ;
;  — нормальная к лучевой линейная скорость
— нормальная к лучевой линейная скорость  Выполнивший это исследование Эддингтон пришел к уравнению (15.93) для плотности v; это частный случай общего решения, выводимого из теоремы Джинса (см. II, 21).
Выполнивший это исследование Эддингтон пришел к уравнению (15.93) для плотности v; это частный случай общего решения, выводимого из теоремы Джинса (см. II, 21).
Путем подобных исследований оказалось возможным показать, что доля круговых и прямолинейных орбит мала и что лишь немногие звезды остаются вблизи центра системы или подходят близко к нему.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. Неспокойная Вселенная
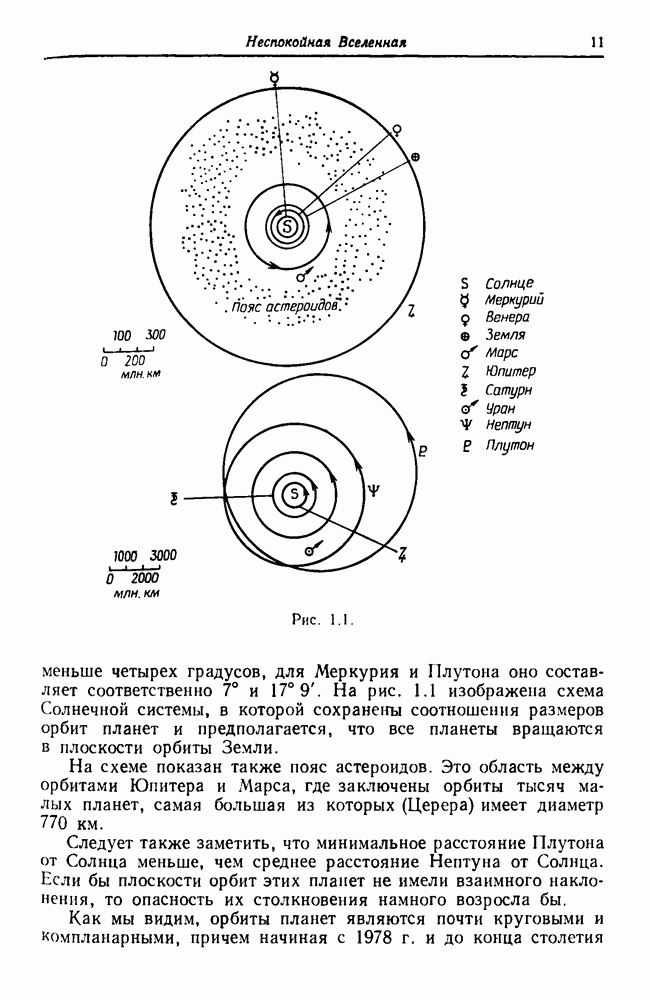
- 1.2. Солнечная система
- 1.2.1. Законы Кеплера
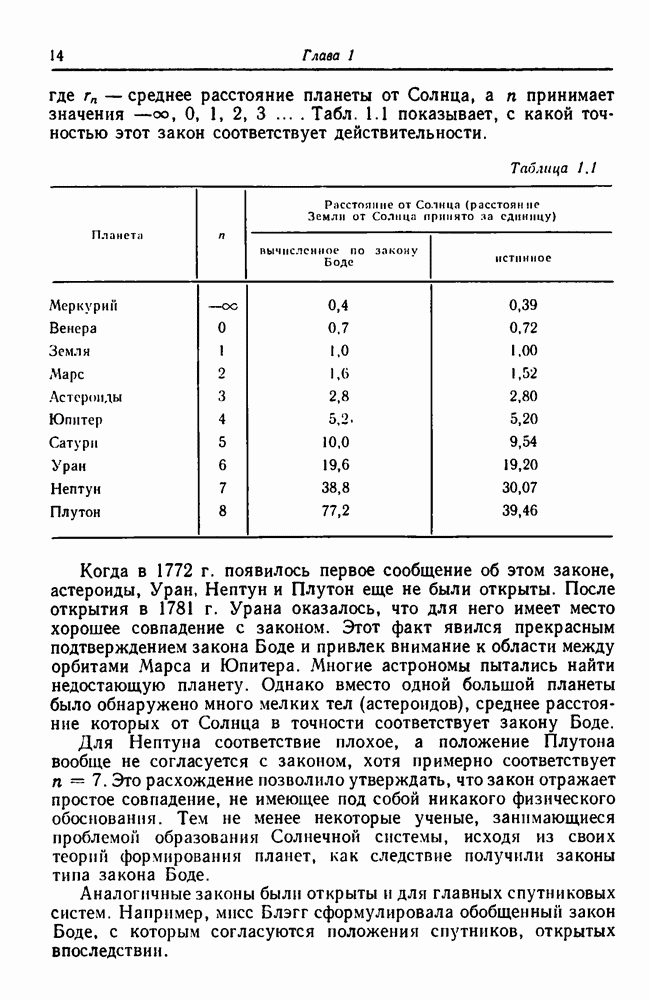
- 1.2.2. Закон Боде
- 1.2.3. Соизмеримости в средних движениях
- 1.2.4. Кометы и метеорные тела
- 1.2.5. Выводы
- 1.3. Движение звезд
- 1.3.1. Двойные системы
- 1.3.2. Тройные системы и системы более высокой кратности
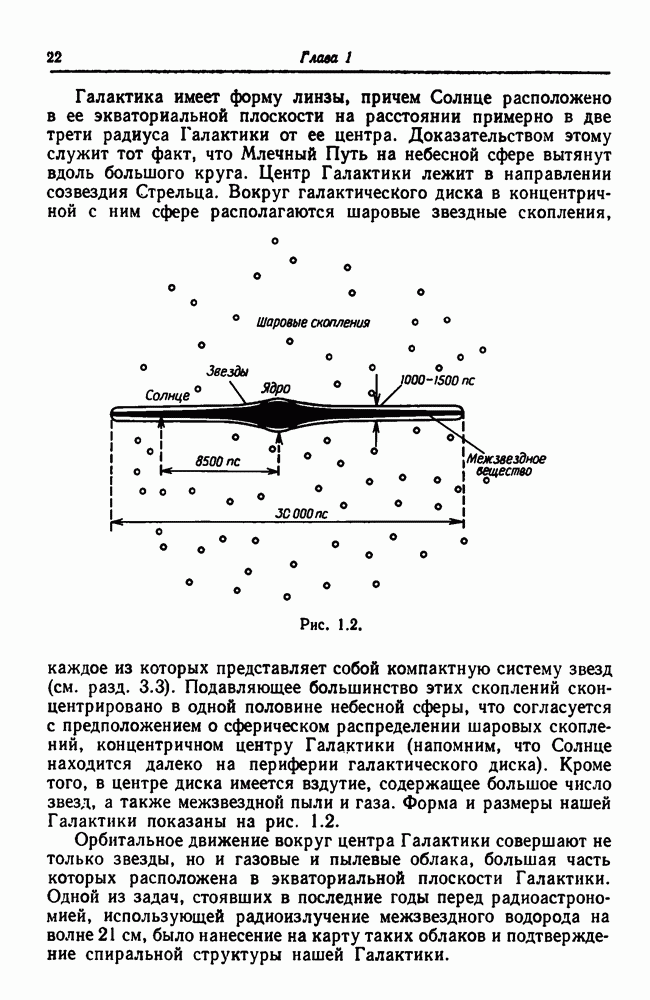
- 1.3.3. Шаровые скопления
- 1.3.4. Галактические, или рассеянные, звездные скопления
- 1.4. Скопления галактик
- 1.5. Выводы
- Рекомендуемая литература
- Глава 2. Системы координат и измерение времени
- 2.2. Положение на поверхности Земли
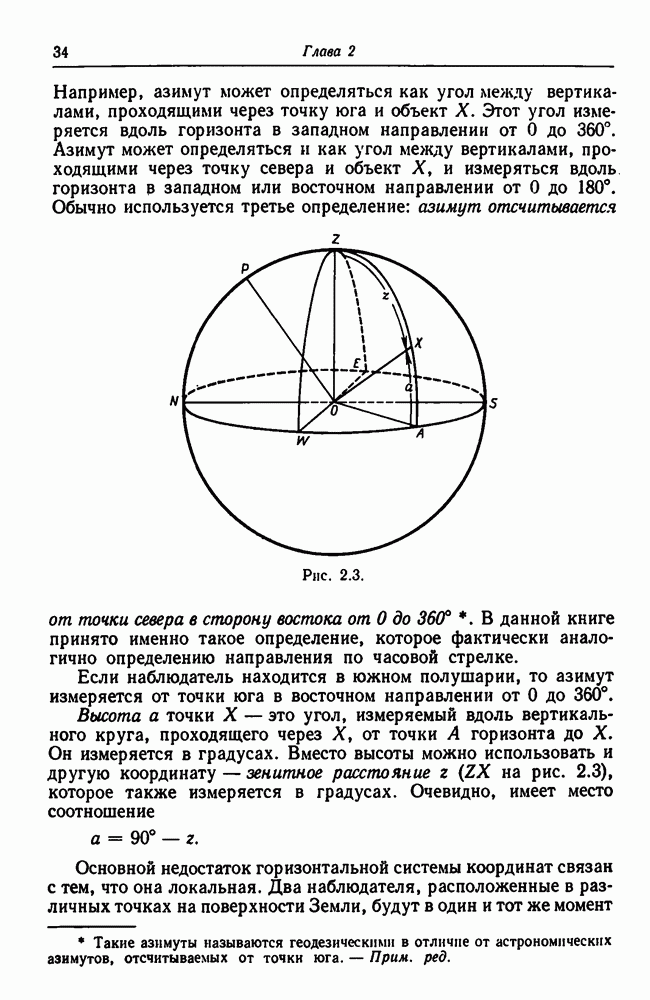
- 2.3. Горизонтальная система
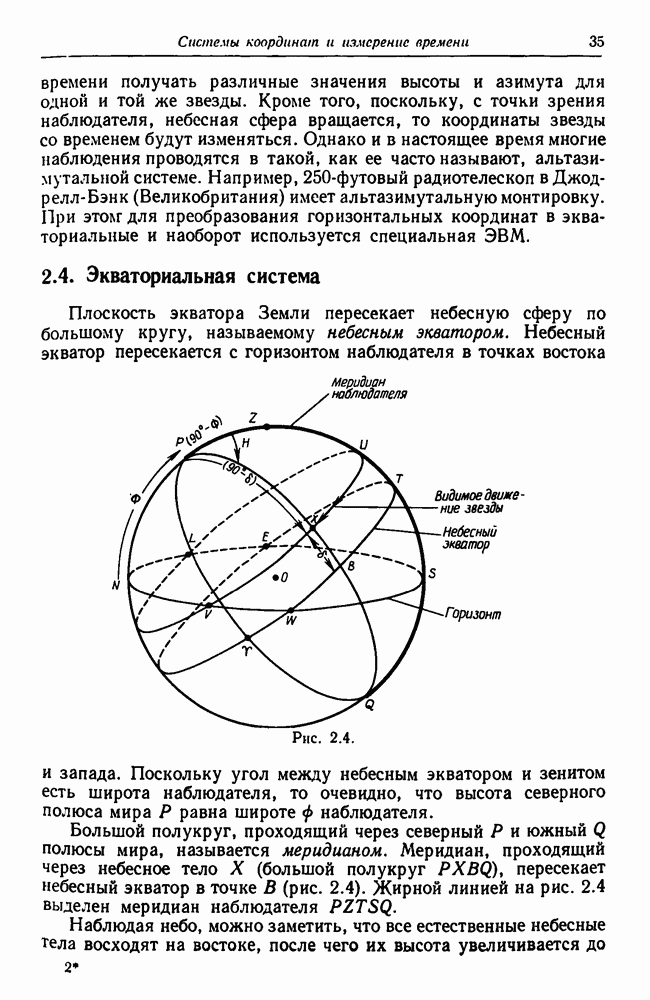
- 2.4. Экваториальная система
- 2.5. Эклиптическая система
- 2.6. Элементы орбиты в пространстве
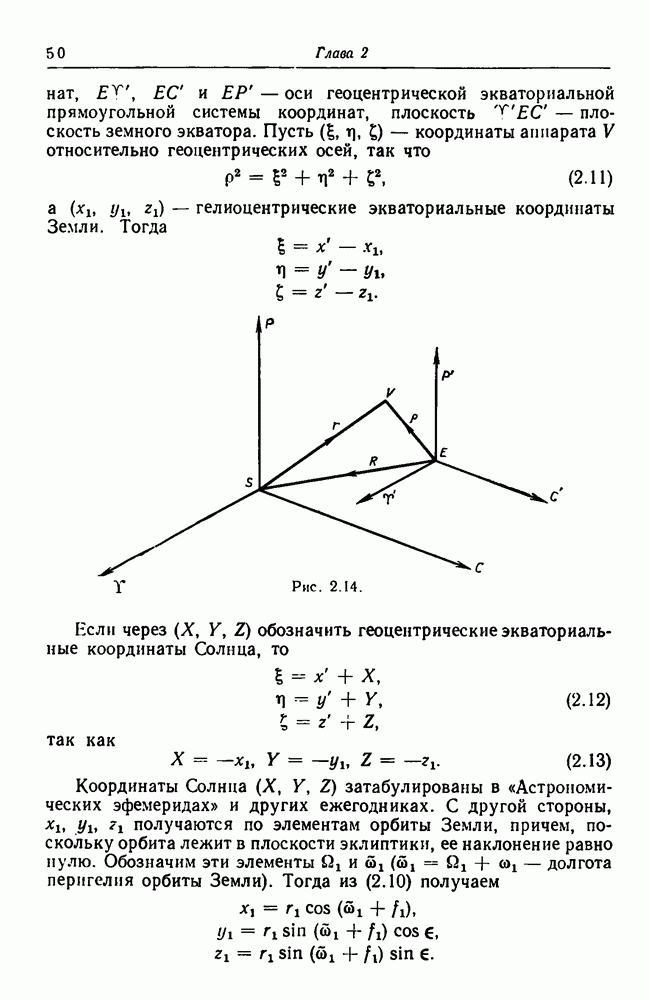
- 2.7. Прямоугольные системы координат
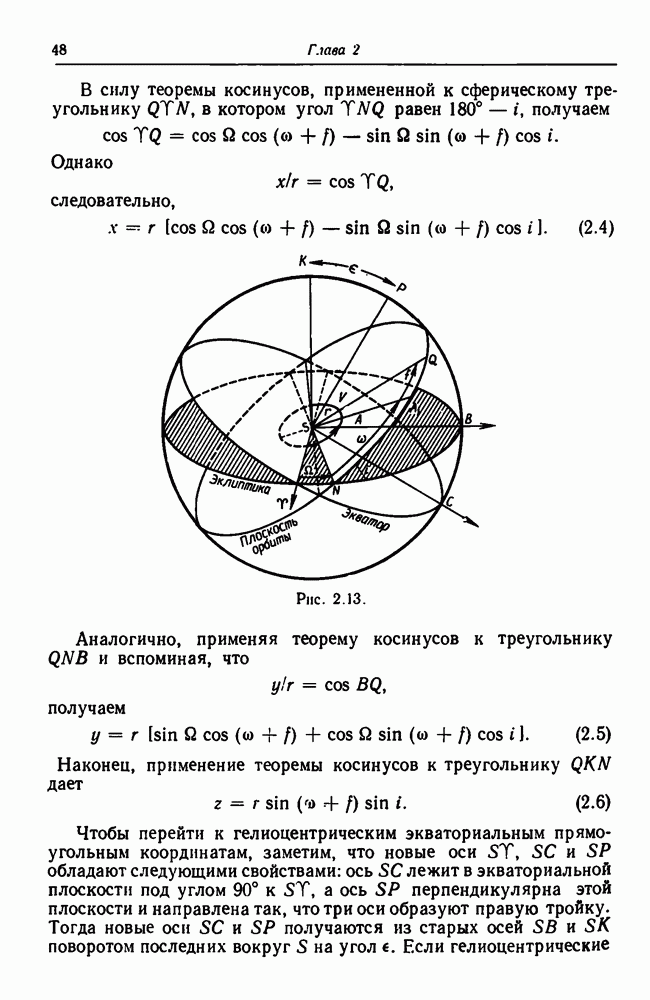
- 2.8. Системы координат, связанные с плоскостью орбиты
- 2.9. Преобразование систем координат
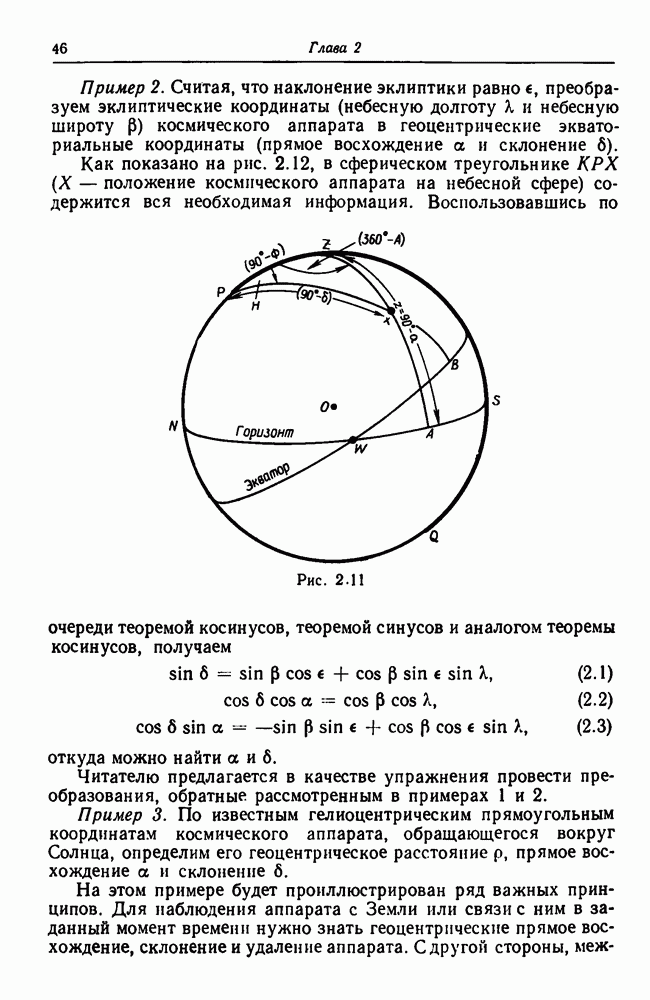
- 2.9.2. Примеры преобразований систем координат
- 2.10. Галактическая система координат
- 2.11. Измерение времени
- 2.11.1. Звездное время
- 2.11.2. Среднее солнечное время
- 2.11.3. Юлианские дни
- 2.11.4. Эфемеридное время
- Задачи
- Литература
- Глава 3. Обработка данных наблюдений
- 3.2. Методы наблюдений
- 3.3. Рефракция
- 3.4. Прецессия и нутация
- 3.5. Аберрация
- 3.6. Собственное движение
- 3.7. Годичный параллакс
- 3.8. Геоцентрический параллакс
- 3.9. Обзор процедур
- Задачи
- Литература
- Глава 4. Задача двух тел
- 4.2. Законы Ньютона
- 4.3. Закон всемирного тяготения Ньютона
- 4.4. Решение задачи двух тел
- 4.5. Эллиптическая орбита
- 4.5.1. Измерение массы планеты
- 4.5.2. Скорость движения по эллиптической орбите
- 4.5.3. Угол между вектором скорости и радиусом-вектором
- 4.5.4. Средняя, эксцентрическая и истинная аномалии
- 4.5.5. Решение уравнения Кеплера
- 4.5.6. Уравнение центра
- 4.5.7. Положение тела на эллиптической орбите
- 4.6. Параболическая орбита
- 4.7. Гиперболическая орбита
- 4.7.1. Скорость на гиперболической орбите
- 4.7.2. Положение на гиперболической орбите
- 4.8. Прямолинейная орбита
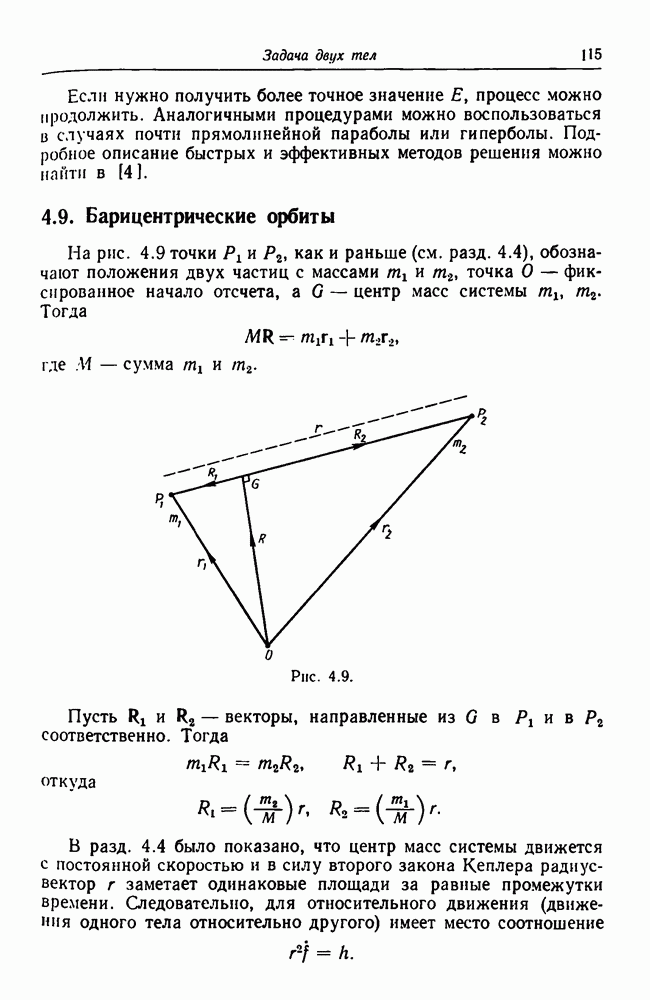
- 4.9. Барицентрические орбиты
- 4.10. Классификация орбит по величине константы энергии
- 4.11. Орбита в пространстве
- 4.12. Ряды для f и g
- 4.13. Использование рекуррентных соотношений
- 4.14. Универсальные переменные
- Задачи
- Литература
- Глава 5. Задача n тел
- 5.2. Уравнения движения задачи n тел
- 5.3. Десять известных интегралов и их смысл
- 5.4. Силовая функция
- 5.5. Теорема вириала
- 5.6. Теорема зеркальности
- 5.7. Снова о задаче n тел
- 5.8. Лагранжевы решения задачи трех тел
- 5.9. Общие замечания о лагранжевых решениях
- 5.10. Ограниченная круговая задача трех тел
- 5.10.2. Критерий Тиссерана
- 5.10.3. Поверхности нулевой скорости
- 5.10.4. Устойчивость точек либрации
- 5.10.5. Периодические орбиты
- 5.10.6. Поиск симметричных периодических орбит
- 5.10.7. Примеры семейств периодических орбит
- 5.10.8. Устойчивость периодических орбит
- 5.10.9. Поверхность сечения
- 5.10.10. Матрица устойчивости
- 5.11. Общая задача трех тел
- 5.11.1. Случай С < 0
- 5.11.2. Случай С = 0
- 5.11.3. Координаты Якоби
- Задачи
- Литература
- Глава 6. Общие возмущения
- 6.2. Уравнения относительного движения
- 6.3. Возмущающая функция
- 6.4. Гравитационная сфера влияния
- 6.5. Потенциал тела произвольной формы
- 6.6. Потенциал шара во внутренней точке
- 6.7. Метод вариации параметров
- 6.7.1. Модификация средней долготы в эпоху
- 6.7.2. Решение уравнений движения планет в форме Лагранжа
- 6.7.3. Коротко- и долгопериодические вариации
- 6.7.4. Разложение возмущающей силы
- 6.8. Уравнения Лагранжа
- 6.9. Канонические уравнения Гамильтона
- Задачи
- Рекомендуемая литература
- Глава 7. Специальные возмущения
- 7.2. Основные факторы теории специальных возмущений
- 7.3. Метод Коуэлла
- 7.4. Метод Энке
- 7.5. Использование возмущенных уравнений
- 7.5.1. Вывод уравнений возмущенного движения
- 7.5.2. Соотношения между возмущенными переменными, прямоугольными координатами, компонентами скорости и обычными элементами кеплеровского движения
- 7.5.3. Процедура численного интегрирования
- 7.5.4. Прямолинейные или почти прямолинейные орбиты
- 7.6. Методы регуляризации
- 7.7. Методы численного интегрирования
- 7.7.2. Метод Рунге—Кутта четвертого порядка
- 7.7.3. Многошаговые методы
- 7.7.4. Численные методы
- Задачи
- Литература
- Глава 8. Устойчивость и эволюция Солнечной системы
- 8.2. Эфемериды планет
- 8.3. Соизмеримости в средних движениях
- 8.4. Астероиды
- 8.5. Кольца Сатурна
- 8.6. Почти соизмеримые орбиты спутников
- 8.7. Численное интегрирование на больших промежутках времени
- 8.7.2. Эволюция элементов орбит на интервале 1 000 000 лет
- 8.7.3. Движение перигелия Плутона: ротационное или либрационное?
- 8.7.4. Сравнение аналитического и численного подходов
- 8.8. Принцип Овендена
- 8.9. Выводы
- Литература
- Глава 9. Теория движения Луны
- 9.3. Сарос
- 9.4. Измерение большой полуоси орбиты, массы и диаметра Луны
- 9.5. Вращение Луны
- 9.6. Селенографические координаты
- 9.7. Фигура Луны
- 9.8. Основная проблема в теории движения Луны
- 9.9. Орбита Солнца в основной проблеме теории движения Луны
- 9.10. Орбита Луны
- 9.11. Теории Луны
- 9.12. Вековое ускорение Луны
- Литература
- Глава 10. Искусственные спутники
- 10.2. Земля как планета
- 10.2.1. Форма Земли
- 10.2.2. Формула Клеро
- 10.2.3. Внутреннее строение Земли
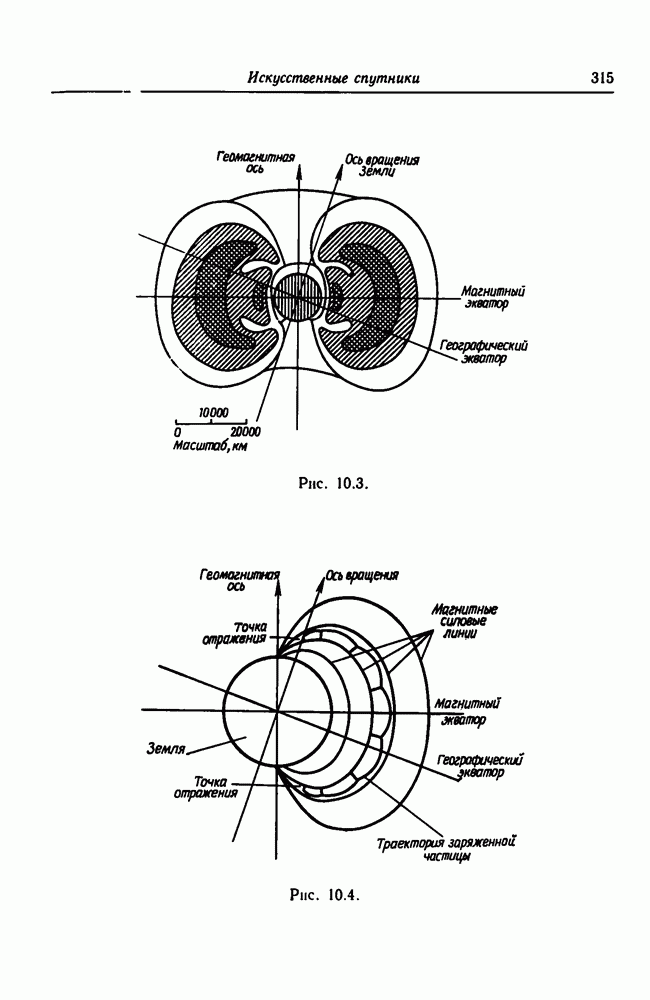
- 10.2.4. Магнитное поле Земли
- 10.2.5. Атмосфера Земли
- 10.2.6. Солнечно-земные связи
- 10.3. Силы, действующие на искусственные спутники Земли
- 10.4. Орбита спутника вокруг сплюснутой планеты
- 10.4.1. Короткопериодические возмущения первого порядка
- 10.4.2. Вековые возмущения первого порядка
- 10.4.3. Долгопериодические возмущения, обусловленные третьей гармоникой
- 10.4.4. Вековые возмущения второго порядка и долгопериодические возмущения
- 10.5. Использование теории Гамильтона—Якоби в задаче движения искусственного спутника
- 10.6. Действие атмосферного торможения на искусственный спутник
- 10.7. Тессеральные и секториальные гармоники поля тяготения Земли
- Задачи
- Литература
- Глава 11. Динамика ракет и орбиты переходов
- 11.2.1. Движение ракеты в гравитационном поле
- 11.2.2. Движение ракеты в атмосфере
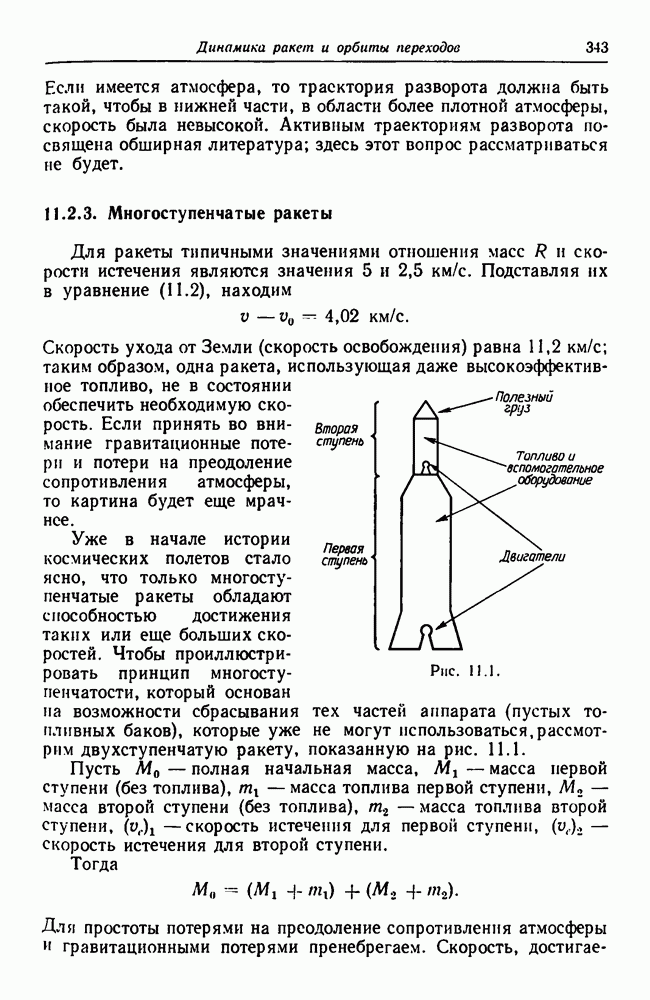
- 11.2.3. Многоступенчатые ракеты
- 11.2.4. Другие типы ракет
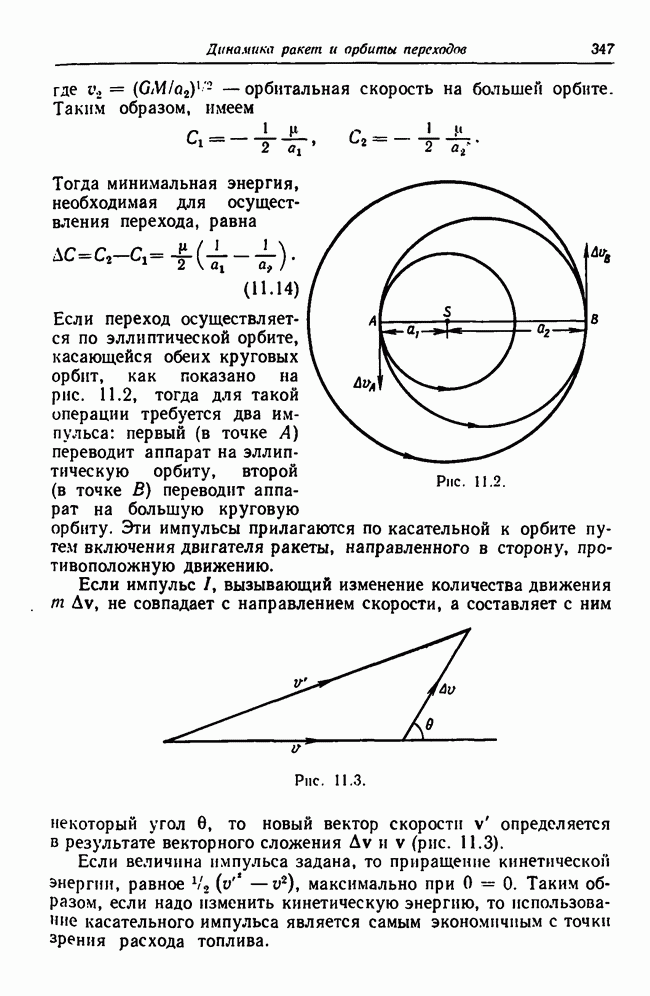
- 11.3. Переходы между орбитами в силовом поле одного притягивающего центра
- 11.3.2. Параболические и гиперболические орбиты перехода
- 11.3.3. Изменения элементов орбиты, вызванные малым импульсом
- 11.3.4. Изменения элементов орбить, вызванные большим импульсом
- 11.3.5. Зависимость расхода топлива от времени перехода
- 11.3.6. Зависимость орбиты перехода от малых ошибок положения и скорости в момент выключения двигателя
- 11.3.7. Переход между частицами, движущимися по орбитам в центральном поле сил
- 11.4. Орбиты перехода в силовых полях двух или более притягивающих центров
- 11.4.2. Выход на орбиту вокруг второго тела
- 11.4.3. Гиперболический захват
- 11.4.4. Точность проведенного анализа и влияние ошибок
- 11.4.5. Облет как средство увеличения скорости
- Задачи
- Глава 12. Траектории полетов к планетам и Луне
- 12.3. Возможности и точность методов исследования
- 12.4. Использование интеграла Якоби
- 12.5. Использование решений Лагранжа
- 12.6. Использование решений задачи двух тел
- 12.7. Искусственные спутники Луны
- 12.7.1. Относительные величины возмущений спутника Луны для различных случаев
- 12.7.2. Интеграл Якоби для близкого спутника Луны
- 12.8. Траектории межпланетных полетов
- 12.9. Солнечная система как поле центральной силы
- 12.10. Орбиты межпланетных перелетов с минимальными затратами энергии
- 12.11. Использование орбит ожидания при межпланетных полетах
- 12.12. Влияние ошибок на межпланетные орбиты
- Задачи
- Глава 13. Определение орбит и межпланетная навигация
- 13.2. Теория определения орбит
- 13.3. Метод Лапласа
- 13.4. Метод Гаусса
- 13.5. Метод Ольберса для параболических орбит
- 13.6. Определение орбит при наличии дополнительных данных наблюдений
- 13.7. Улучшение орбит
- 13.8. Межпланетная навигация
- 13.8.1. Стабилизированные платформы и акселерометры
- 13.8.2. Навигация при помощи бортовой оптической аппаратуры
- 13.8.3. Методы наблюдений и достижимая точность
- Литература
- Глава 14. Двойные системы и системы нескольких тел
- 14.2. Визуально-двойные звезды
- 14.3. Соотношение масса—светимость
- 14.4. Динамические параллаксы
- 14.5. Затменные двойные
- 14.6. Спектрально-двойные звезды
- 14.7. Обзор результатов
- 14.8. Элементы орбиты двойной звезды
- 14.9. Период двойной звезды
- 14.10. Движение апсид
- 14.11. Силы, действующие в двойной системе
- 14.12. Тройные системы
- 14.13. Неточность ньютоновского закона тяготения
- 14.14. Фигуры звезд в двойных системах
- 14.15. Пределы Роша
- 14.16. Вещество, окружающее звезды
- 14.17. Образование двойных систем
- Задачи
- Глава 15. Звездные системы многих тел
- 15.2. Сфера действия
- 15.3. Парные сближения
- 15.4. Накапливающийся эффект малых сближений
- 15.5. Некоторые фундаментальные принципы
- 15.6. Основные теоремы звездной динамики
- 15.6.1. Теорема Джинса
- 15.7. Некоторые частные случаи для звездной системы в стационарном состоянии
- 15.8. Вращение галактик
- 15.8.2. Период вращения и угловая скорость Галактики
- 15.8.3. Масса Галактики
- 15.8.4. Общий характер вращения Галактики
- 15.8.5. Галактические орбиты звезд
- 15.8.6. Звезды с высокими скоростями
- 15.9. Сферические звездные системы
- 15.9.1. Применение теоремы вириала к сферической системе
- 15.9.2. Орбиты звезд в сферической системе
- 15.9.3. Распределение орбит внутри сферической системы
- 15.10. Эксперименты на ЭВМ
- Задачи
- Ответы к задачам
- Приложения