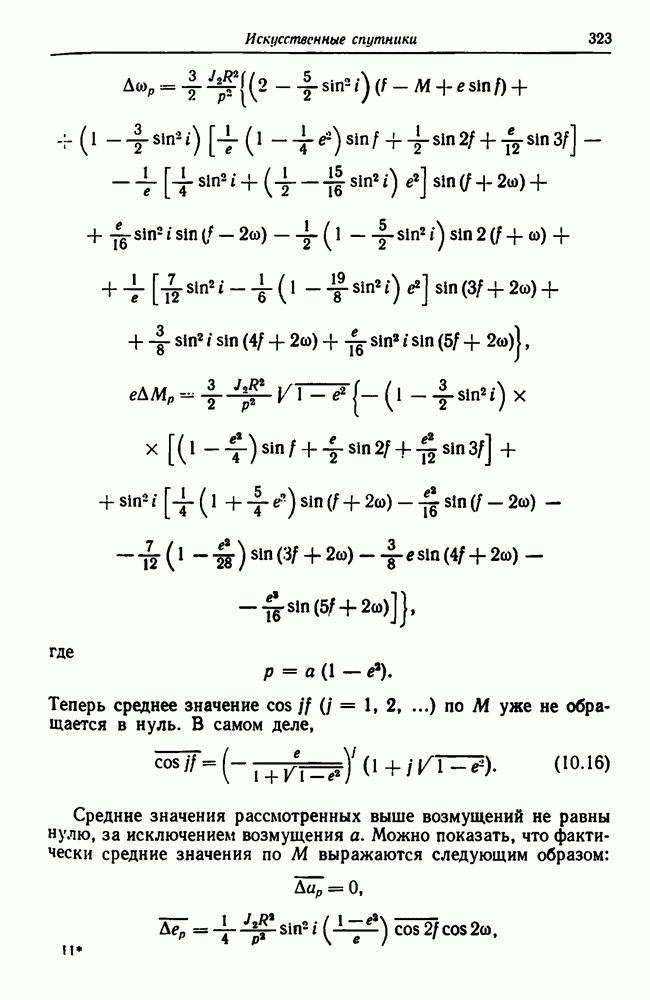| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Ответы к задачам
Глава 2
2.1. 1) 638 морск. миль; 2) 1444 морск. миль.

2.3. 56° 00; 36,7 мин после отлета из Прествика. (Указание: на наибольшей северной широте курс самолета составляет  при отсчете от точки севера.)
при отсчете от точки севера.)
2.4.  . (Указание: видимый путь Солнца по небосводу на фоне звезд — это эклиптика. Одно обращение по эклиптике совершается Солнцем за год; Солнце находится в точке весны у около 21 марта.)
. (Указание: видимый путь Солнца по небосводу на фоне звезд — это эклиптика. Одно обращение по эклиптике совершается Солнцем за год; Солнце находится в точке весны у около 21 марта.)
2.5. 1) Прямое восхождение 21, склонение 60 N; 2) долгота ~50°, широта 

Рис.
2.6. Прямое восхождение  склонение
склонение  .
.
2.7. 8 ч пополудни  .
.

2.11. Местное стандартное время равно часовому углу Солнца минус местное время. Следовательно, на диаграмме можно отметить положение точки у и Солнца и тем самым определить эклиптику.
2.12. I) Пункт В имеет координаты  января. (Указание: в задачах подобного рода, особенно когда имеет место пересечение международной линии
января. (Указание: в задачах подобного рода, особенно когда имеет место пересечение международной линии  принято использовать гринвичское среднее
принято использовать гринвичское среднее
время  совместно с соответствующей датой; последняя называется гринвичской датой и используется в качестве промежуточной.)
совместно с соответствующей датой; последняя называется гринвичской датой и используется в качестве промежуточной.)

2.14. Поправка часов (месшос время минус показания часов) равна —13,4 с  с. Ход часов равен 1,1 с за 24 ч.
с. Ход часов равен 1,1 с за 24 ч.
2.15. 17 ч 07 мин 29 с. (Указание: получить грннвнчское среднее время GMT наблюдения, затем интервал среднего солнечного времени между этим гринвичским временем  декабря. Преобразовать этот интервал в звездное время, чтобы получить гринвичское звездное время наблюдения. После этого использовать значение долготы.)
декабря. Преобразовать этот интервал в звездное время, чтобы получить гринвичское звездное время наблюдения. После этого использовать значение долготы.)

2.17. 13 ч 44 мин °2 с звездного времени;  мин 22 с местного времени; 285° 40 к востоку от точки севера.
мин 22 с местного времени; 285° 40 к востоку от точки севера.
Глава 3

3.2.  для
для  для Проциона.
для Проциона.

3.4.  (удаление).
(удаление).

3.7. 1) прямое восхождение  склонение
склонение  прямое восхождение
прямое восхождение  склонение
склонение  (Указание: никакие расчеты не нужны. Начертите график и нанесите на него положения равноденствий и экваторов.)
(Указание: никакие расчеты не нужны. Начертите график и нанесите на него положения равноденствий и экваторов.)
3.8.  (используйте
(используйте  -значные таблицы логарифмов).
-значные таблицы логарифмов).
3.10. Топоцентричсское прямое восхождение  32° 55. Топоцентрнческое склонение 32° 56 N. Геоцентрическое прямое восхождение
32° 55. Топоцентрнческое склонение 32° 56 N. Геоцентрическое прямое восхождение  Геоцентрическое склонение
Геоцентрическое склонение  (Указание: точно вычерченный график часто бывает полезен для проверки выводов о квадрантах, в которых находятся искомые углы.)
(Указание: точно вычерченный график часто бывает полезен для проверки выводов о квадрантах, в которых находятся искомые углы.)
Глава 4
4.2. Отношение (скорость в перигелии), (скорость в афелии) равно 60,16. Соответствующее отношение для угловых скоростей равно 3619.
4.4. Половина расстояния Земли от Солнца.  используйте уравнение (4.82) и соотношение
используйте уравнение (4.82) и соотношение

Продшференцнруйте  для нахождения максимума после подстановки
для нахождения максимума после подстановки

4.8. Направление по вертикали; 145 800 км;  [Указание: значение угла показывает, что
[Указание: значение угла показывает, что  одни участок орбиты не лежит внутри Земли. Вторая орбита характеризуется тем же значением скорости относительно «вертикального» запуска (прямолинейный эллипс).
одни участок орбиты не лежит внутри Земли. Вторая орбита характеризуется тем же значением скорости относительно «вертикального» запуска (прямолинейный эллипс). 
4.9. Отношение массы Солнца к массе Земли равно 331 700.
4.10. Орбита является эллипсом со следующими элементами:  большой
большой  земной орбиты;
земной орбиты;  ноябрь 20,72).
ноябрь 20,72).
Глава 5
5.1. Исследование уравнения (5.2) показывает, что если  образует решение задачи
образует решение задачи  то тогда
то тогда  также образует решение, если все интервалы времени умножены
также образует решение, если все интервалы времени умножены 
5.2. Сферы с центром в «неподвижном» теле, как показывает уравнение (4.16). Прямолинейный эллипс.
5.3. Приведенная задача  тел полностью разрешима и сводится к простым гармоническим движениям. В таком случае для любого радиуса-вектора
тел полностью разрешима и сводится к простым гармоническим движениям. В таком случае для любого радиуса-вектора  мы имеем
мы имеем

где  — постоянные,
— постоянные,  (
( -постоянная тяготения). Отсюда радиус-вектор R, - (от центра масс до массы
-постоянная тяготения). Отсюда радиус-вектор R, - (от центра масс до массы  ) определяется выражением
) определяется выражением

где А и В — постоянные.
5.4.  ; центр масс движется с постоянной скоростью.
; центр масс движется с постоянной скоростью.
Глава 6
6.1. Указание:  дает нам
дает нам  Варьируя а и b и используя условие, выраженное соотношением (6.26), получаем,
Варьируя а и b и используя условие, выраженное соотношением (6.26), получаем,  Отсюда имеем
Отсюда имеем 
6.2. Искомый эксцентриситет выражается как

6.3. В рассматриваемой задаче возмущающая функция имеет вид 
Используйте уравнение для  из системы (6.30).
из системы (6.30).
6.4. Если  — масса при
— масса при  то
то  где а — малая положительная постоянная. Тогда возмущающая функция R для малых
где а — малая положительная постоянная. Тогда возмущающая функция R для малых  определяется как
определяется как

Исследуя относящиеся к данной задаче уравнения из системы (6.30), мы видим, что  . Остальные четыре уравнения можно сразу проинтегрировать после подстановки в них выражений для
. Остальные четыре уравнения можно сразу проинтегрировать после подстановки в них выражений для  и т. д. для получения возмущений первого порядка.
и т. д. для получения возмущений первого порядка.
6.5. Указание:  требуемое выражение получается путем использования уравнения (6.42), первого уравнения системы (6.41) и соответствующих уравнений задачи двух тел из гл. 4.
требуемое выражение получается путем использования уравнения (6.42), первого уравнения системы (6.41) и соответствующих уравнений задачи двух тел из гл. 4.
Глава 10

10.6. w = 5,28° за сутки;  за сутки.
за сутки.
Глава 11
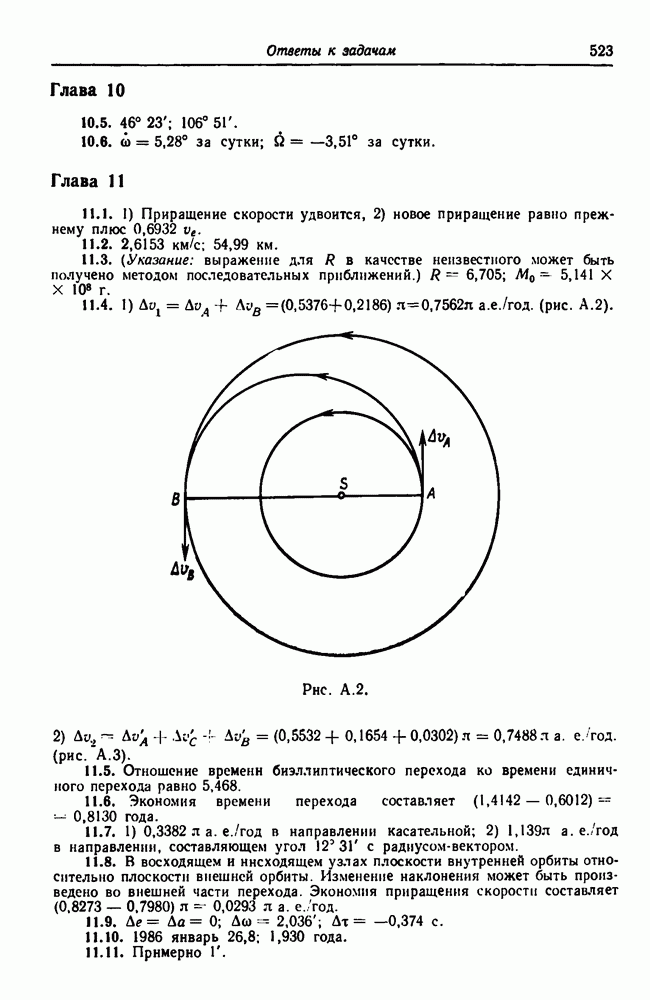
11.1. I) Приращение скорости удвоится, 2) новое приращение равно прежнему плюс  .
.

11.3. (Указание: выражение для R в качестве неизвестного может быть получено методом последовательных приближений.)  .
.


Рис. А.2.

11.5. Отношение времени биэллиптического перехода ко времени единичного перехода равно 5,468.
11.6. Экономия времени перехода составляет  года.
года.
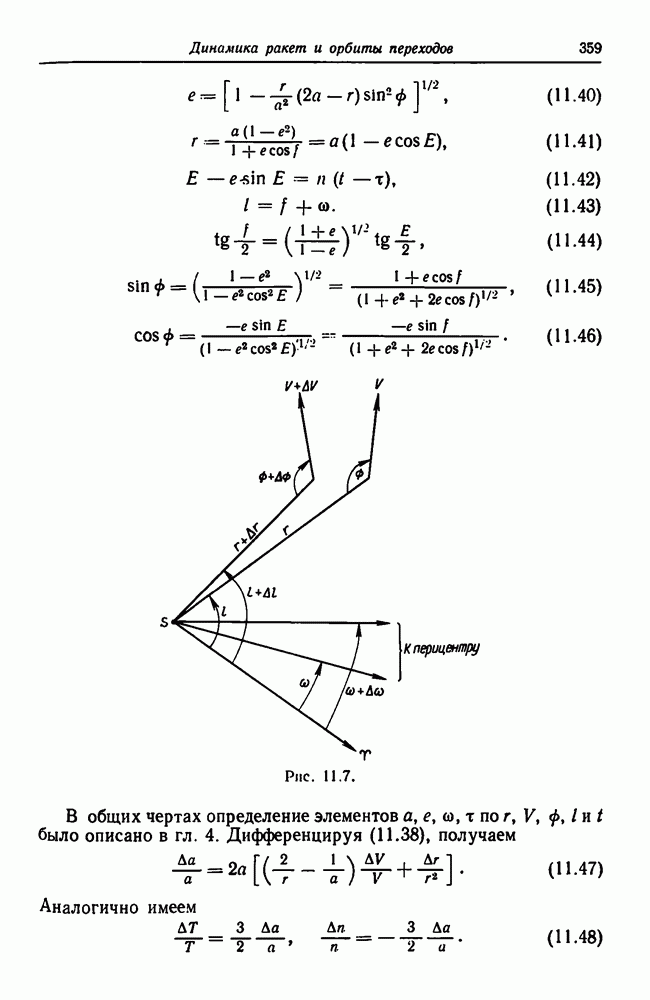
11.7.  в направлении касательной;
в направлении касательной;  в направлении, составляющем угол
в направлении, составляющем угол  с радиусом-вектором.
с радиусом-вектором.
11.8. В восходящем и нисходящем узлах плоскости внутренней орбиты относительно плоскости внешней орбиты. Измененне наклонения может быть произведено во внешней части перехода. Экономия приращения скорости составляет 

11.10. 1986 январь 26,8; 1,930 года.
11.11. Примерно Г.

Рис. А.3.
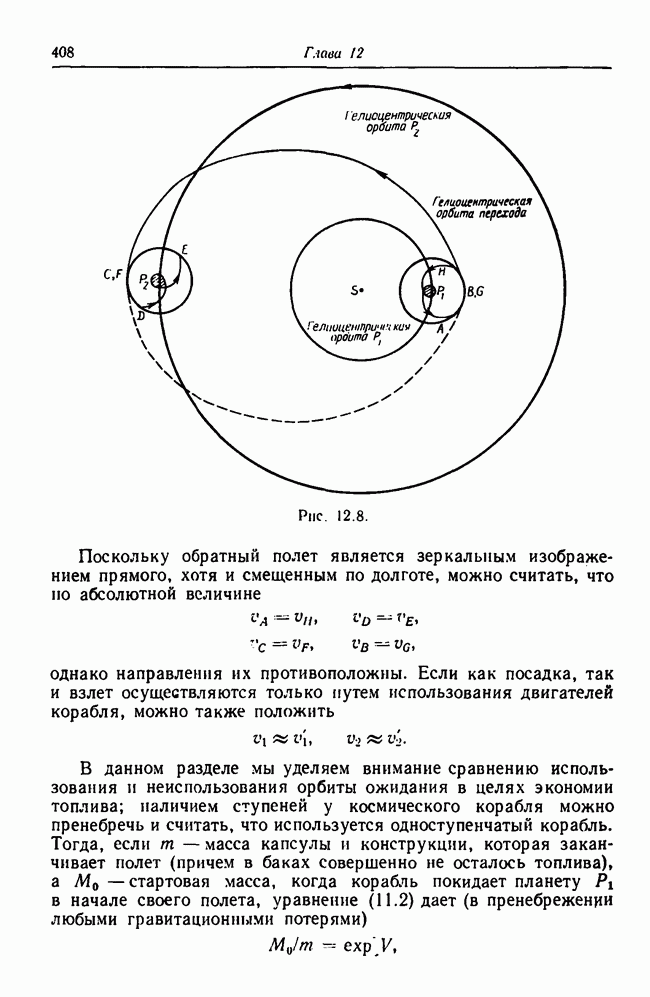
Глава 12

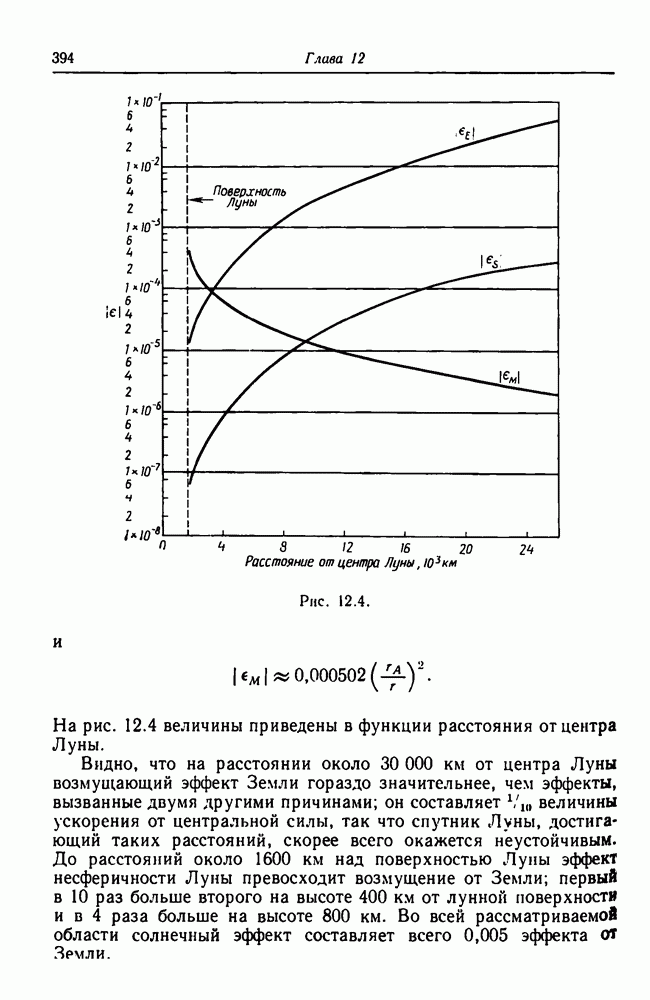
12.2. 88 260 км. (Указание: угловая скорость вращения Луны равна  что представляет собой угловую скорость обращения спутника.) Это расстояние больше, чем радиус гравитационной сферы влияния Луны (66 190 км).
что представляет собой угловую скорость обращения спутника.) Это расстояние больше, чем радиус гравитационной сферы влияния Луны (66 190 км).

12.5.  . (Указание: угловая скорость
. (Указание: угловая скорость  прямой АВ относительно центра масс системы дает нам значение
прямой АВ относительно центра масс системы дает нам значение  ) из выражения
) из выражения  поскольку
поскольку  Приравнивание центробежной силы, действующей на космический зонд, общей силе притяжения дает нам уравнение 5-й степени для неизвестного расстояния; это уравнение можно решить методом последовательных приближений.)
Приравнивание центробежной силы, действующей на космический зонд, общей силе притяжения дает нам уравнение 5-й степени для неизвестного расстояния; это уравнение можно решить методом последовательных приближений.)
12.6. 21 193 000 км для Юпитера, 9450 км для Марса.

12.8. Период перелета к астероиду, когда тот находится в афелии, равен точно 1 году; отсюда следует, что при возвращении корабля вдоль второй половины орбиты перехода на орбиту Земли корабль снопа встретит Землю. Требуемый гиперболический избыток скорости составляет  а. е. год
а. е. год 
12.9. Используя уравнения (4.91), (4.88) для  уравнения (4.92), (4.97), (4.100) и (4.101) и соответствующие числовые данные из приложений, получаем, что время полета равно
уравнения (4.92), (4.97), (4.100) и (4.101) и соответствующие числовые данные из приложений, получаем, что время полета равно  стартовая скорости 11.9 км с.
стартовая скорости 11.9 км с.
12.10. Пусть периоды для Земли и зонда равны  соответственно. Тогда
соответственно. Тогда  Точно так же
Точно так же  = 1 а. е. Отсюда
= 1 а. е. Отсюда  кроме того,
кроме того,  Если
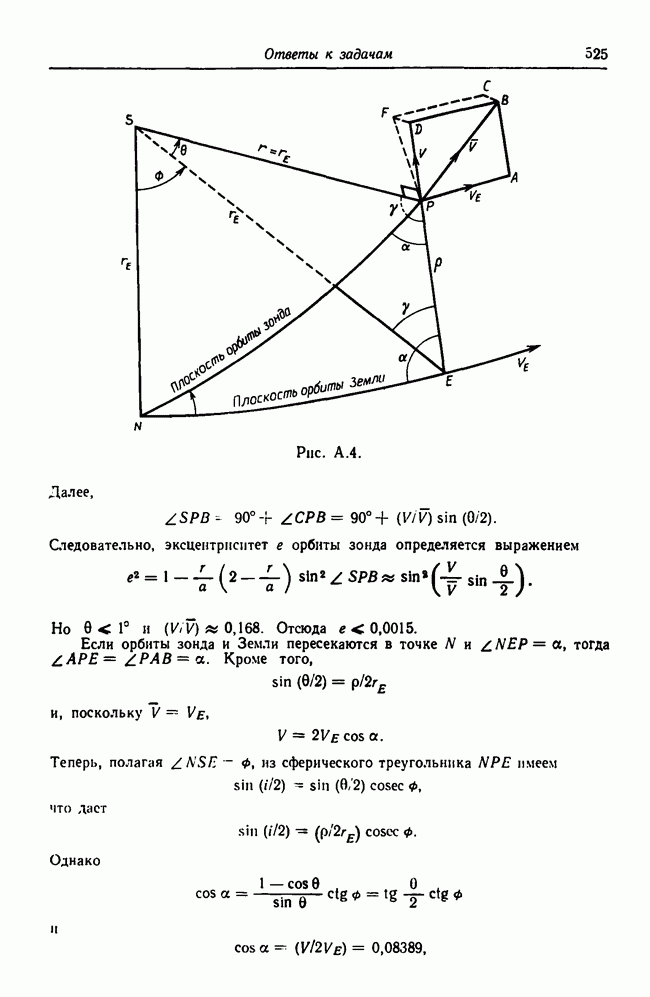
Если  то орбита зонда не будет круговой. Из рис. А.4
то орбита зонда не будет круговой. Из рис. А.4  откуда
откуда


Рис.
Далее,

Следовательно, эксцентриситет  орбиты зонда определяется выражением
орбиты зонда определяется выражением

Но  . Отсюда
. Отсюда 
Если орбиты зонда и Земли пересекаются в точке  тогда
тогда  . Кроме того,
. Кроме того,

и, поскольку 

Теперь, полагая  , из сферического треугольника
, из сферического треугольника  имеем
имеем

что дает

Однако

и

что дает  Следовательно, 0 должно быть 1° 1,1 и
Следовательно, 0 должно быть 1° 1,1 и  Подставляя полученные значения в выражения для
Подставляя полученные значения в выражения для  ? находим, что
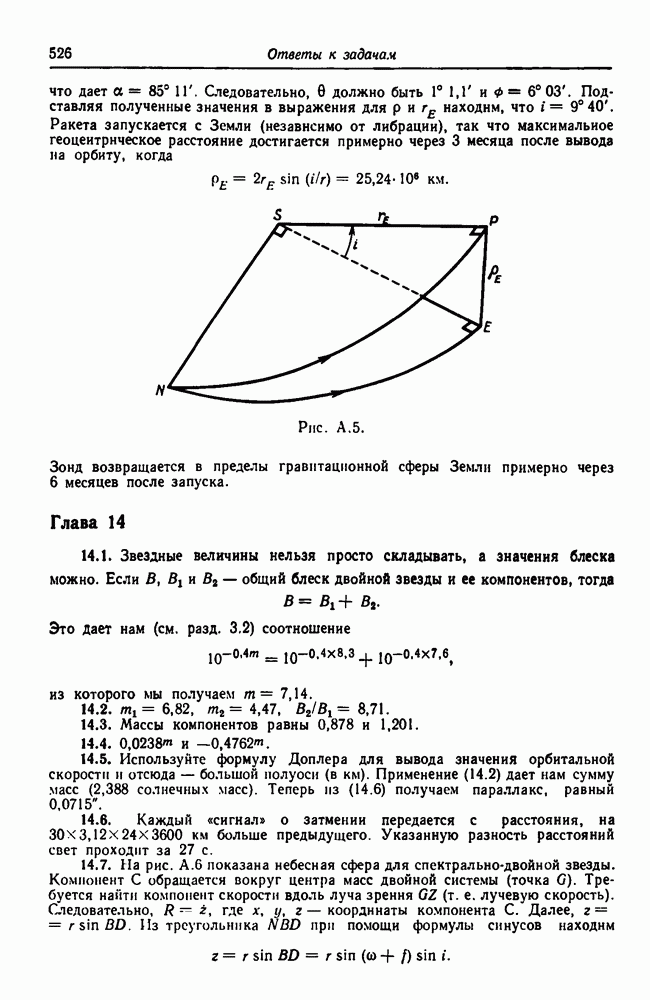
? находим, что  Ракета запускается с Земли (независимо от либрации), так что максимальное геоцентрическое расстояние достигается примерно через 3 месяца после вывода на орбиту, когда
Ракета запускается с Земли (независимо от либрации), так что максимальное геоцентрическое расстояние достигается примерно через 3 месяца после вывода на орбиту, когда


Рис. А.5.
Зонд возвращается в пределы гравитационной сферы Земли примерно через 6 месяцев после запуска.
Глава 14
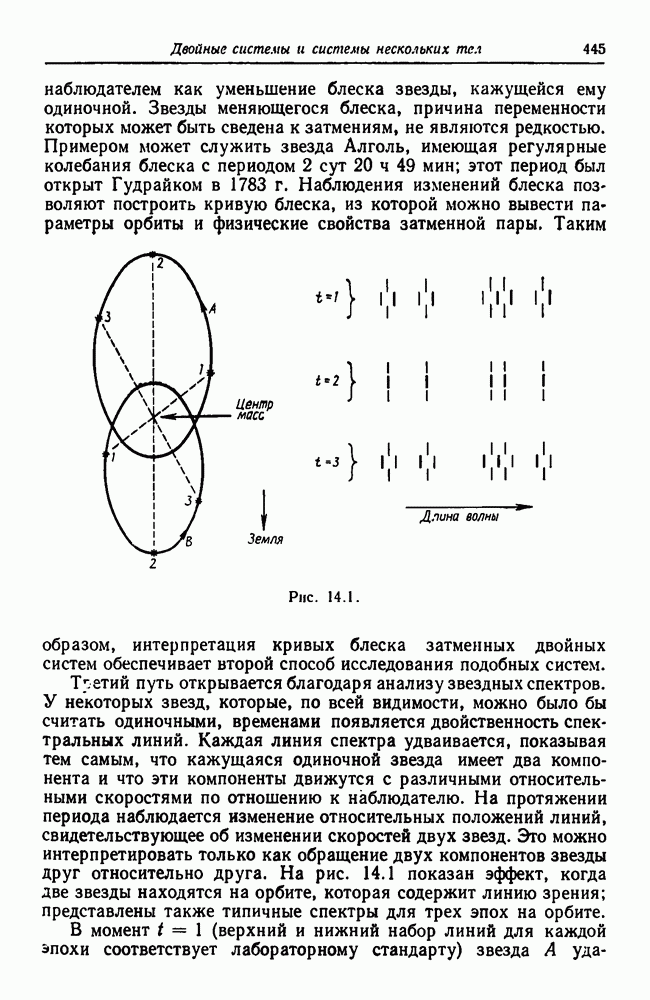
14.1. Звездные величины нельзя просто складывать, а значения блеска можно. Если  — общий блеск двойной звезды и ее компонентов, тогда
— общий блеск двойной звезды и ее компонентов, тогда

Это дает нам (см. разд. 3.2) соотношение

из которого мы получаем 

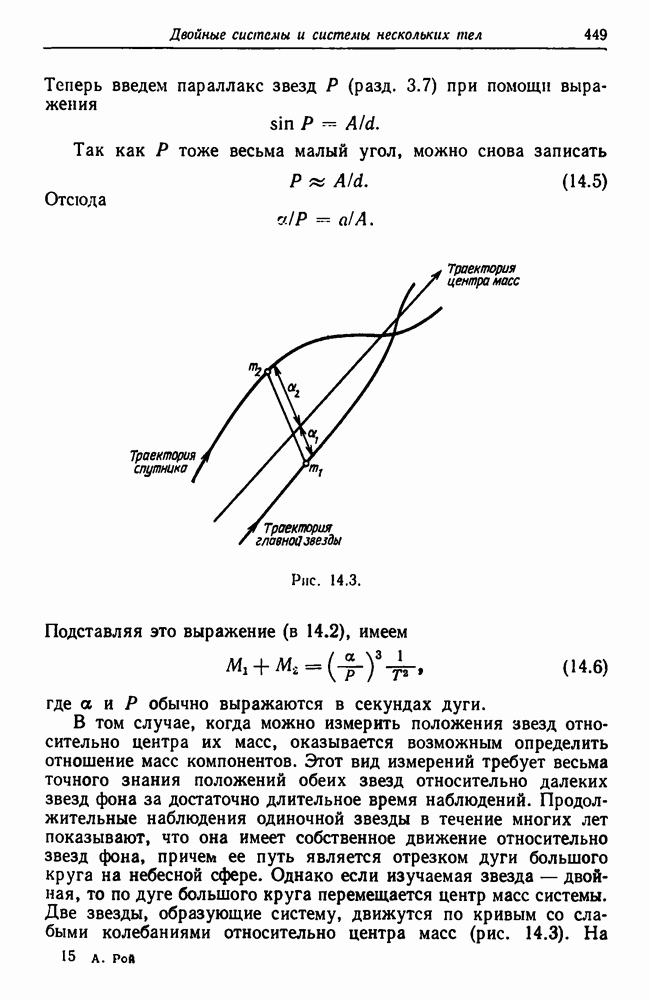
14.3. Массы компонентов равны 0,878 и 1,201.

14.5. Используйте формулу Доплера для вывода значения орбитальной скорости и отсюда — большой полуоси (в км). Применение (14.2) дает нам сумму масс (2,388 солнечных масс). Теперь из (14.6) получаем параллакс, равный 
14.6. Каждый «сигнал» о затмении передается с расстояния, на  км больше предыдущего. Указанную разность расстояний свет проходит за 27 с.
км больше предыдущего. Указанную разность расстояний свет проходит за 27 с.
14.7. На рис. А.6 показана небесная сфера для спектрально-двойной звезды. Компонент С обращается вокруг центра масс двойной системы (точка G). Требуется найти компонент скорости вдоль луча зрения  (т. е. лучевую скорость). Следовательно,
(т. е. лучевую скорость). Следовательно,  где
где  — координаты компонента С. Далее,
— координаты компонента С. Далее,  Из треугольника NBD при помощи формулы синусов находим
Из треугольника NBD при помощи формулы синусов находим


Рис. А.6.
Задача двух тел дает нам формулы

Дифференцируя полученное выражение для  и используя приведенные выше формулы, мы получаем требуемое соотношение.
и используя приведенные выше формулы, мы получаем требуемое соотношение.  с применением соотношения
с применением соотношения  в формуле (14.6). Первое приближение для абсолютных звездных величии (при использовании видимых звездных величин) дает
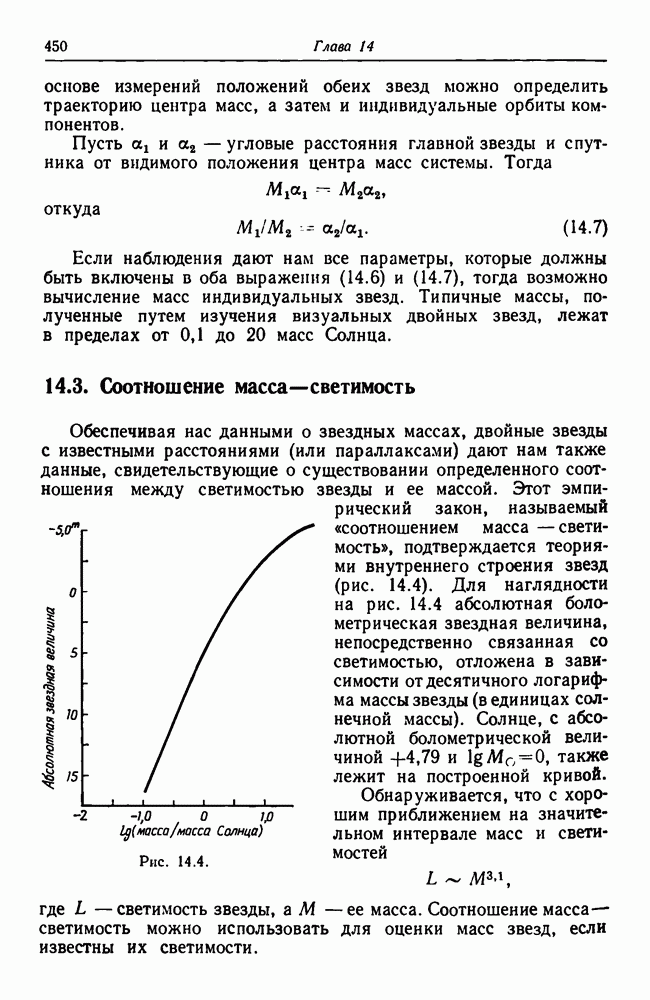
в формуле (14.6). Первое приближение для абсолютных звездных величии (при использовании видимых звездных величин) дает  Из зависимости масса—светимость (см. рис. 14.4) мы получаем второе приближение для значений масс: 0,851 и
Из зависимости масса—светимость (см. рис. 14.4) мы получаем второе приближение для значений масс: 0,851 и  что дает
что дает  Новый шаг вычисления не меняет значения Р даже в последней значащей цифре.
Новый шаг вычисления не меняет значения Р даже в последней значащей цифре.
Глава 15
15.1.  . (Используйте метод Ньютона для вычисления массы планеты в долях солнечной массы.)
. (Используйте метод Ньютона для вычисления массы планеты в долях солнечной массы.)

15.4. 5315. Используйте формулы

и

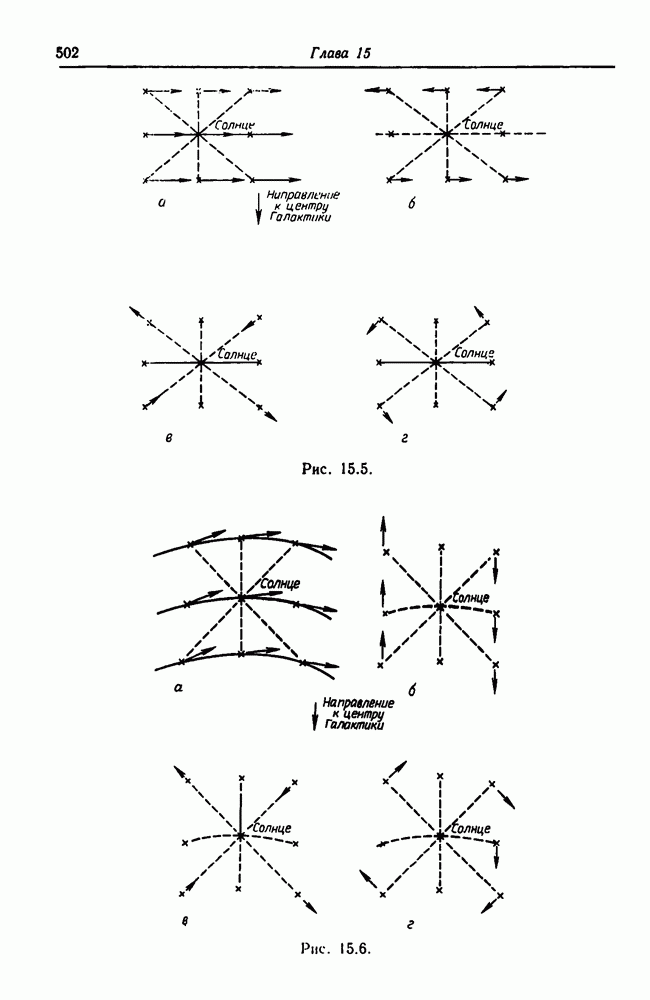
15.5. Указание: возьмите второе уравнение из (15.50) при 
15.8. Указание: асимметрия устанавливается, когда сумма  равна скорости освобождения
равна скорости освобождения  Далее,
Далее,

Для условий убегания мы имеем

Но

что

Для  мы получаем
мы получаем

и

Слсдоват елыю,

Подстановка в сумму

приводит к результату

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. Неспокойная Вселенная
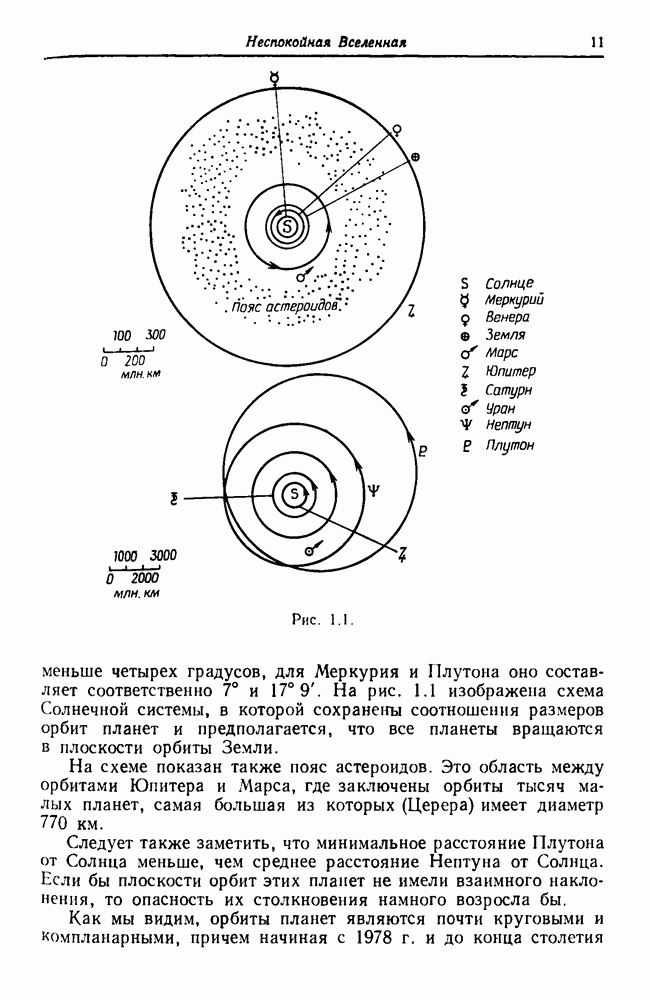
- 1.2. Солнечная система
- 1.2.1. Законы Кеплера
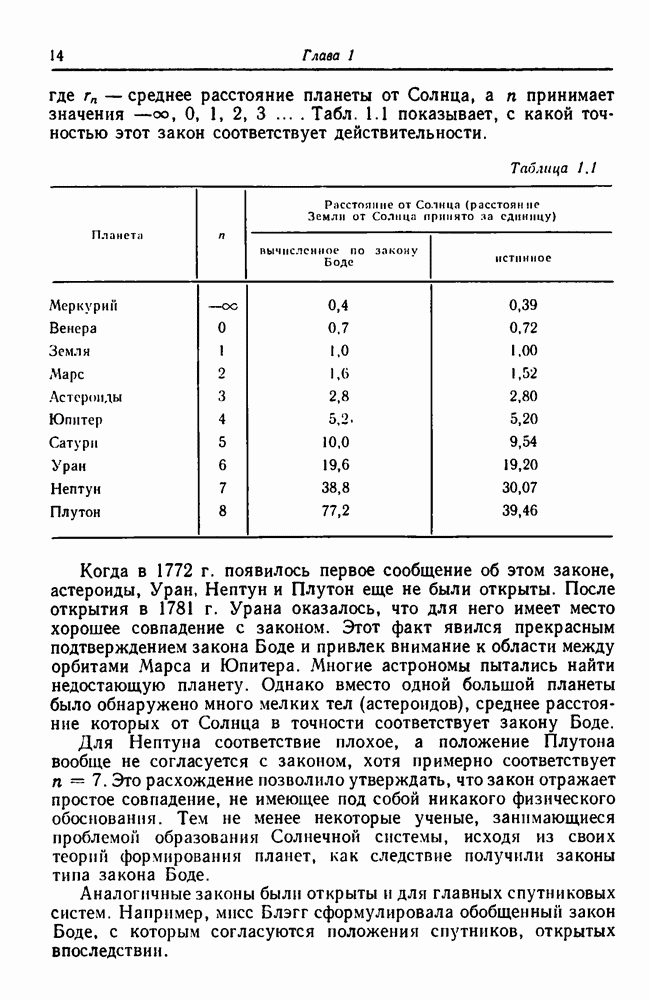
- 1.2.2. Закон Боде
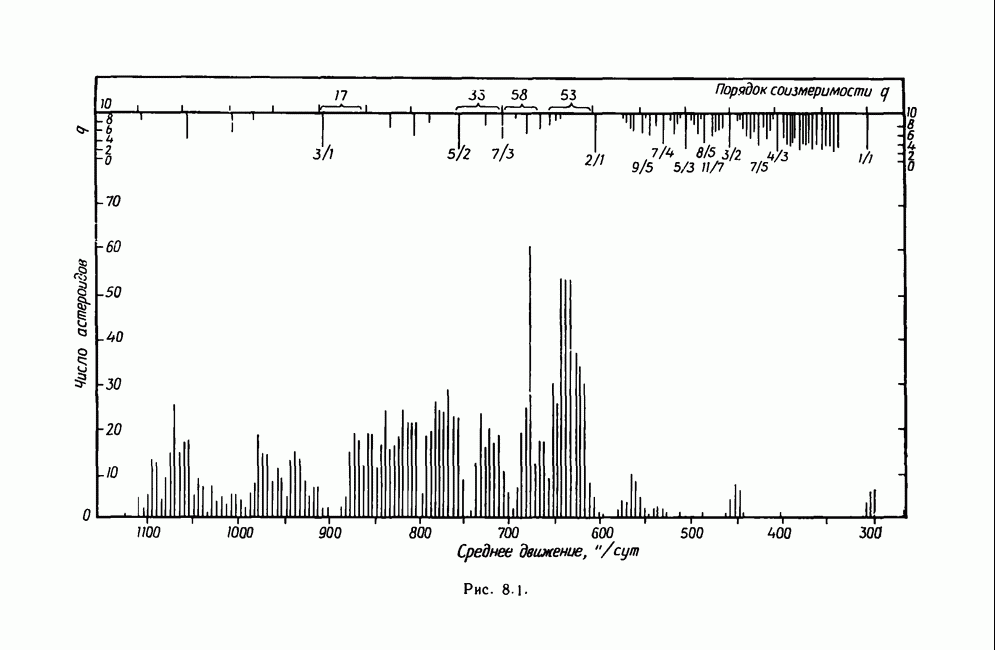
- 1.2.3. Соизмеримости в средних движениях
- 1.2.4. Кометы и метеорные тела
- 1.2.5. Выводы
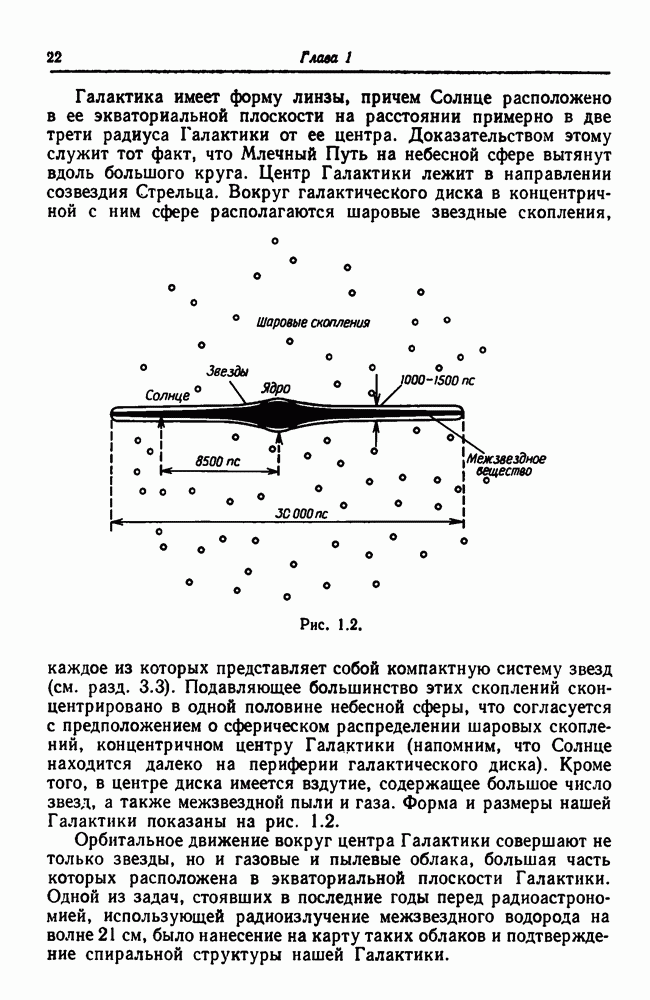
- 1.3. Движение звезд
- 1.3.1. Двойные системы
- 1.3.2. Тройные системы и системы более высокой кратности
- 1.3.3. Шаровые скопления
- 1.3.4. Галактические, или рассеянные, звездные скопления
- 1.4. Скопления галактик
- 1.5. Выводы
- Рекомендуемая литература
- Глава 2. Системы координат и измерение времени
- 2.2. Положение на поверхности Земли
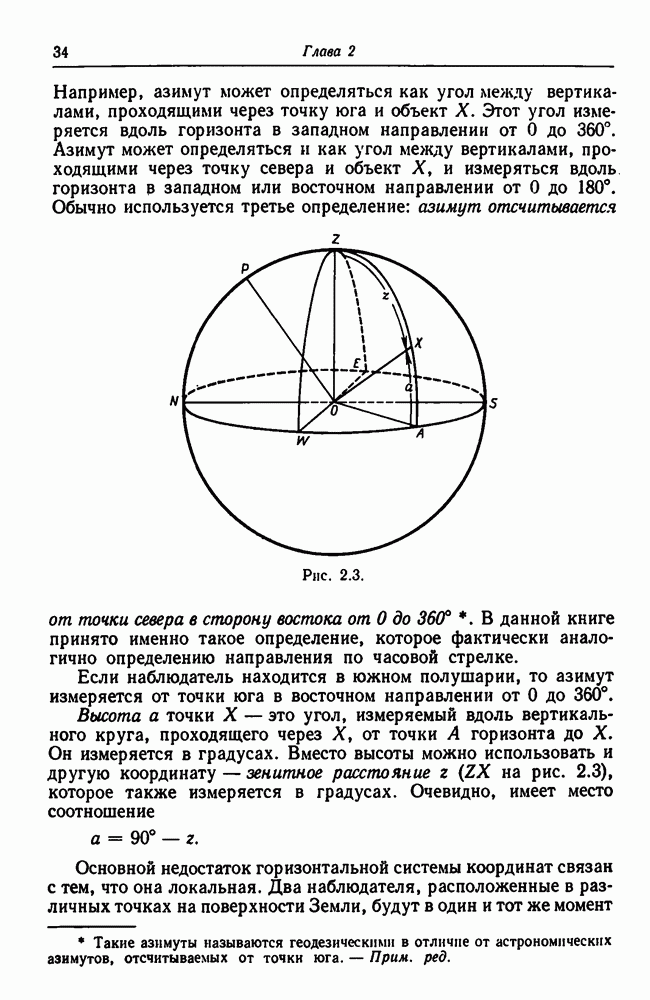
- 2.3. Горизонтальная система
- 2.4. Экваториальная система
- 2.5. Эклиптическая система
- 2.6. Элементы орбиты в пространстве
- 2.7. Прямоугольные системы координат
- 2.8. Системы координат, связанные с плоскостью орбиты
- 2.9. Преобразование систем координат
- 2.9.2. Примеры преобразований систем координат
- 2.10. Галактическая система координат
- 2.11. Измерение времени
- 2.11.1. Звездное время
- 2.11.2. Среднее солнечное время
- 2.11.3. Юлианские дни
- 2.11.4. Эфемеридное время
- Задачи
- Литература
- Глава 3. Обработка данных наблюдений
- 3.2. Методы наблюдений
- 3.3. Рефракция
- 3.4. Прецессия и нутация
- 3.5. Аберрация
- 3.6. Собственное движение
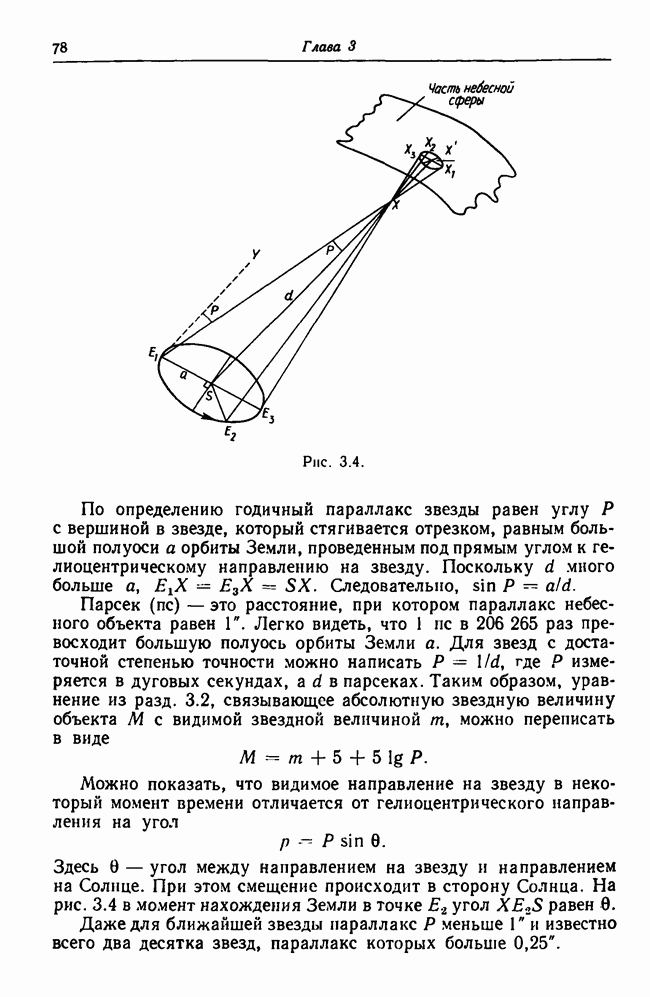
- 3.7. Годичный параллакс
- 3.8. Геоцентрический параллакс
- 3.9. Обзор процедур
- Задачи
- Литература
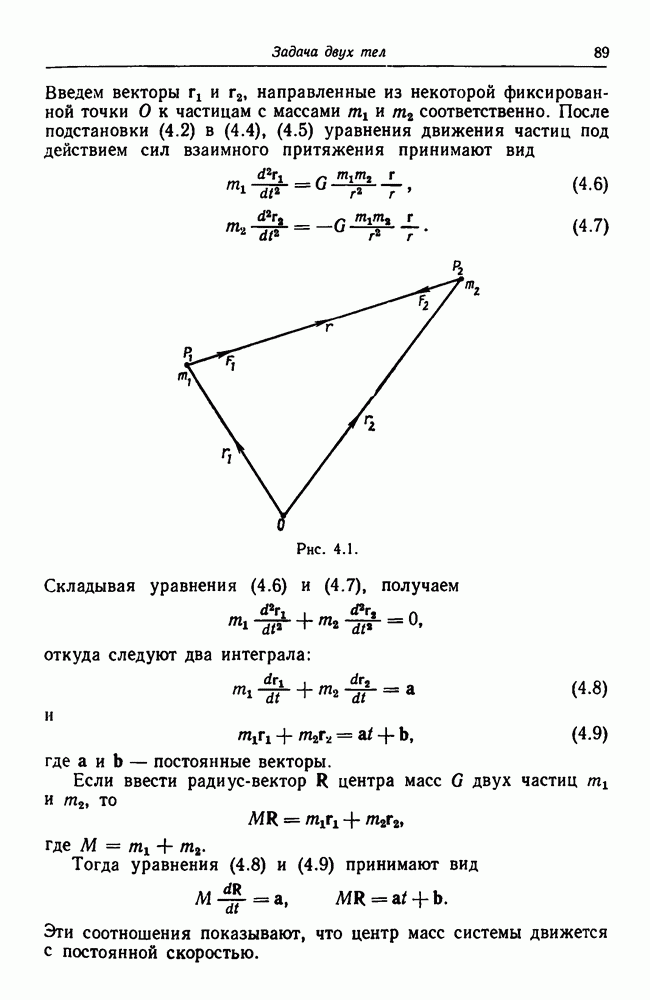
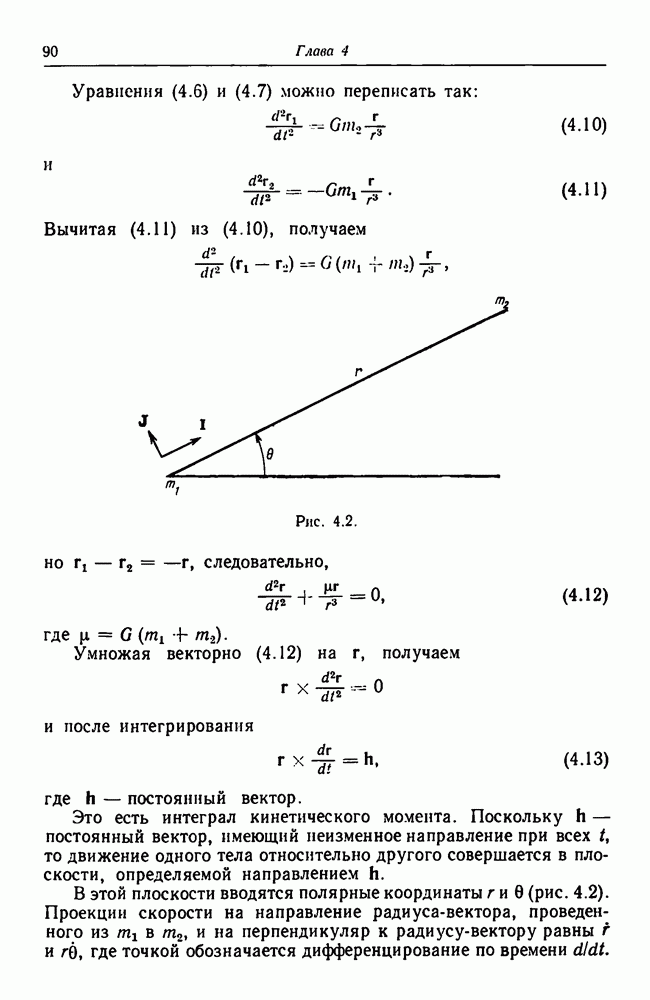
- Глава 4. Задача двух тел
- 4.2. Законы Ньютона
- 4.3. Закон всемирного тяготения Ньютона
- 4.4. Решение задачи двух тел
- 4.5. Эллиптическая орбита
- 4.5.1. Измерение массы планеты
- 4.5.2. Скорость движения по эллиптической орбите
- 4.5.3. Угол между вектором скорости и радиусом-вектором
- 4.5.4. Средняя, эксцентрическая и истинная аномалии
- 4.5.5. Решение уравнения Кеплера
- 4.5.6. Уравнение центра
- 4.5.7. Положение тела на эллиптической орбите
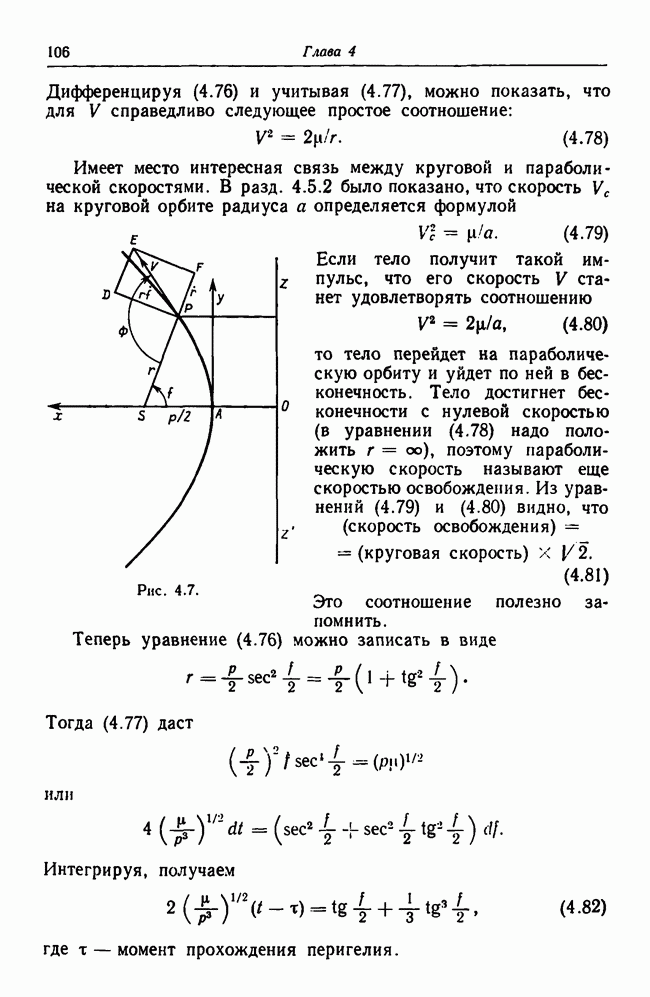
- 4.6. Параболическая орбита
- 4.7. Гиперболическая орбита
- 4.7.1. Скорость на гиперболической орбите
- 4.7.2. Положение на гиперболической орбите
- 4.8. Прямолинейная орбита
- 4.9. Барицентрические орбиты
- 4.10. Классификация орбит по величине константы энергии
- 4.11. Орбита в пространстве
- 4.12. Ряды для f и g
- 4.13. Использование рекуррентных соотношений
- 4.14. Универсальные переменные
- Задачи
- Литература
- Глава 5. Задача n тел
- 5.2. Уравнения движения задачи n тел
- 5.3. Десять известных интегралов и их смысл
- 5.4. Силовая функция
- 5.5. Теорема вириала
- 5.6. Теорема зеркальности
- 5.7. Снова о задаче n тел
- 5.8. Лагранжевы решения задачи трех тел
- 5.9. Общие замечания о лагранжевых решениях
- 5.10. Ограниченная круговая задача трех тел
- 5.10.2. Критерий Тиссерана
- 5.10.3. Поверхности нулевой скорости
- 5.10.4. Устойчивость точек либрации
- 5.10.5. Периодические орбиты
- 5.10.6. Поиск симметричных периодических орбит
- 5.10.7. Примеры семейств периодических орбит
- 5.10.8. Устойчивость периодических орбит
- 5.10.9. Поверхность сечения
- 5.10.10. Матрица устойчивости
- 5.11. Общая задача трех тел
- 5.11.1. Случай С < 0
- 5.11.2. Случай С = 0
- 5.11.3. Координаты Якоби
- Задачи
- Литература
- Глава 6. Общие возмущения
- 6.2. Уравнения относительного движения
- 6.3. Возмущающая функция
- 6.4. Гравитационная сфера влияния
- 6.5. Потенциал тела произвольной формы
- 6.6. Потенциал шара во внутренней точке
- 6.7. Метод вариации параметров
- 6.7.1. Модификация средней долготы в эпоху
- 6.7.2. Решение уравнений движения планет в форме Лагранжа
- 6.7.3. Коротко- и долгопериодические вариации
- 6.7.4. Разложение возмущающей силы
- 6.8. Уравнения Лагранжа
- 6.9. Канонические уравнения Гамильтона
- Задачи
- Рекомендуемая литература
- Глава 7. Специальные возмущения
- 7.2. Основные факторы теории специальных возмущений
- 7.3. Метод Коуэлла
- 7.4. Метод Энке
- 7.5. Использование возмущенных уравнений
- 7.5.1. Вывод уравнений возмущенного движения
- 7.5.2. Соотношения между возмущенными переменными, прямоугольными координатами, компонентами скорости и обычными элементами кеплеровского движения
- 7.5.3. Процедура численного интегрирования
- 7.5.4. Прямолинейные или почти прямолинейные орбиты
- 7.6. Методы регуляризации
- 7.7. Методы численного интегрирования
- 7.7.2. Метод Рунге—Кутта четвертого порядка
- 7.7.3. Многошаговые методы
- 7.7.4. Численные методы
- Задачи
- Литература
- Глава 8. Устойчивость и эволюция Солнечной системы
- 8.2. Эфемериды планет
- 8.3. Соизмеримости в средних движениях
- 8.4. Астероиды
- 8.5. Кольца Сатурна
- 8.6. Почти соизмеримые орбиты спутников
- 8.7. Численное интегрирование на больших промежутках времени
- 8.7.2. Эволюция элементов орбит на интервале 1 000 000 лет
- 8.7.3. Движение перигелия Плутона: ротационное или либрационное?
- 8.7.4. Сравнение аналитического и численного подходов
- 8.8. Принцип Овендена
- 8.9. Выводы
- Литература
- Глава 9. Теория движения Луны
- 9.3. Сарос
- 9.4. Измерение большой полуоси орбиты, массы и диаметра Луны
- 9.5. Вращение Луны
- 9.6. Селенографические координаты
- 9.7. Фигура Луны
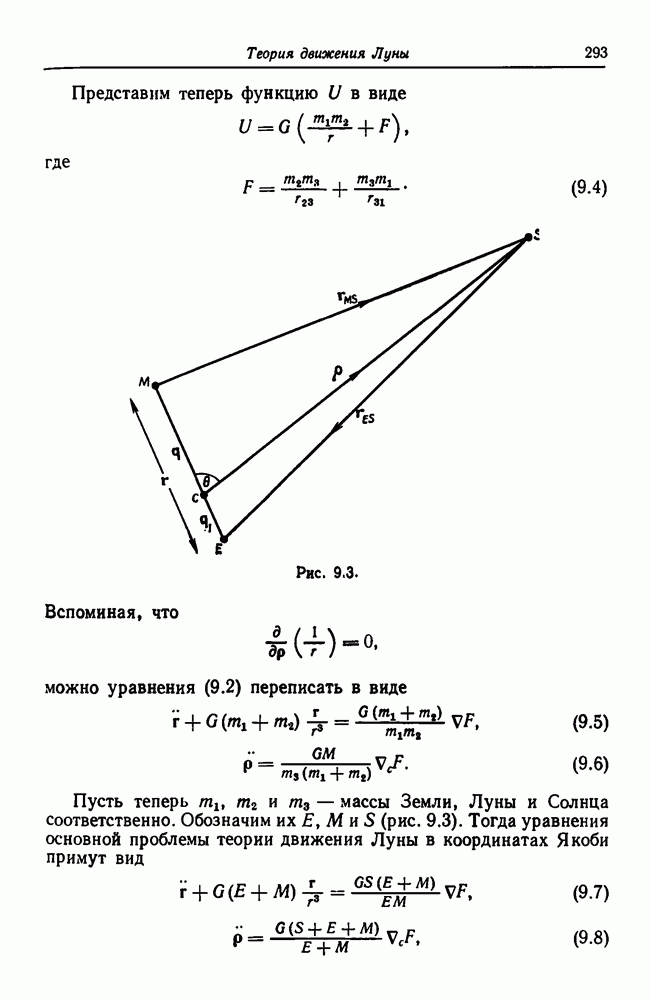
- 9.8. Основная проблема в теории движения Луны
- 9.9. Орбита Солнца в основной проблеме теории движения Луны
- 9.10. Орбита Луны
- 9.11. Теории Луны
- 9.12. Вековое ускорение Луны
- Литература
- Глава 10. Искусственные спутники
- 10.2. Земля как планета
- 10.2.1. Форма Земли
- 10.2.2. Формула Клеро
- 10.2.3. Внутреннее строение Земли
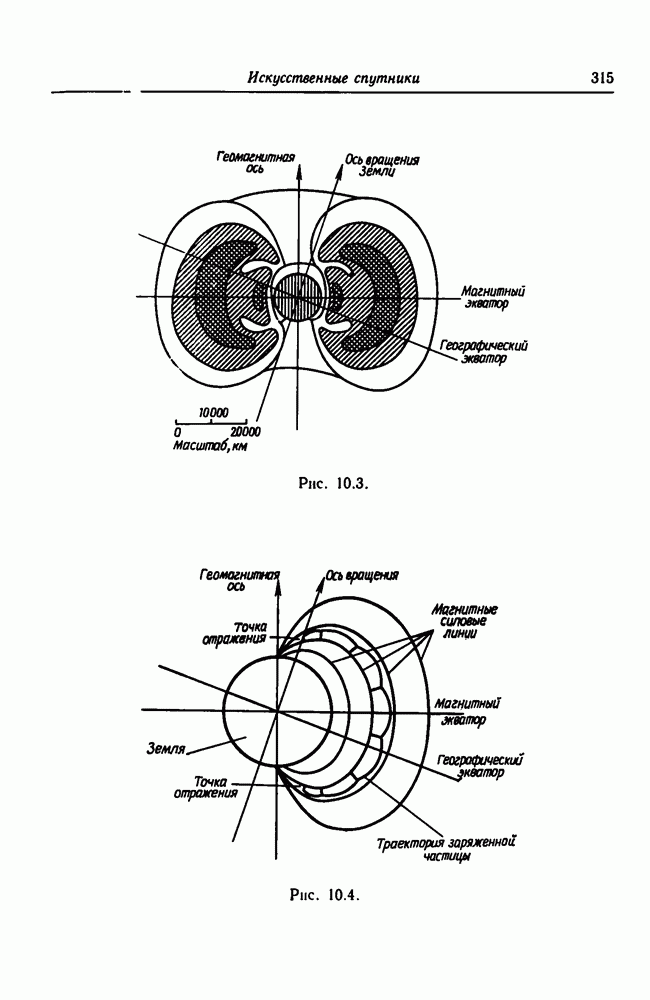
- 10.2.4. Магнитное поле Земли
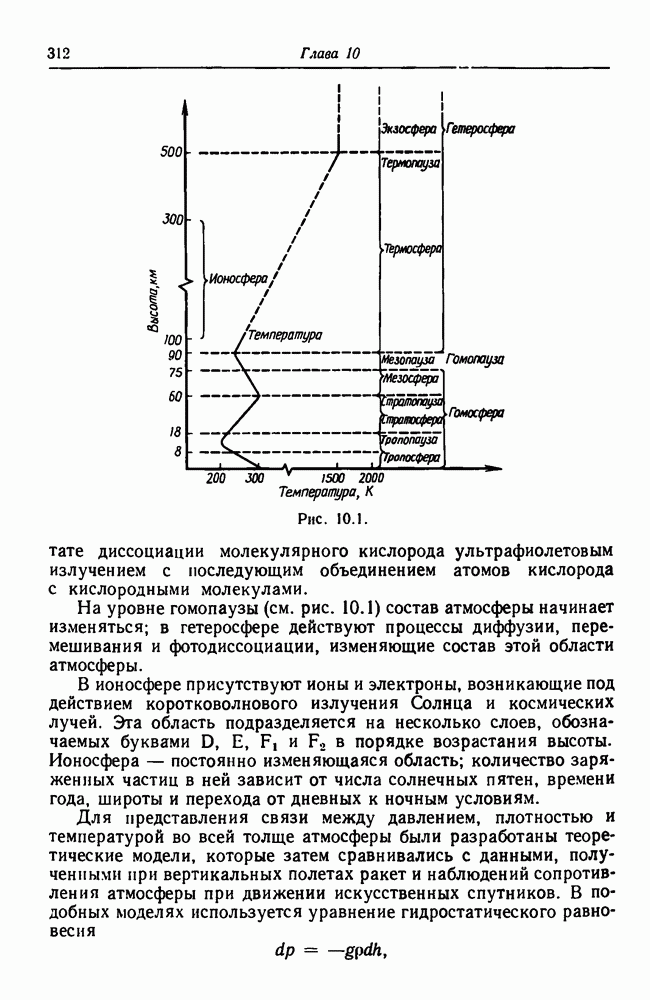
- 10.2.5. Атмосфера Земли
- 10.2.6. Солнечно-земные связи
- 10.3. Силы, действующие на искусственные спутники Земли
- 10.4. Орбита спутника вокруг сплюснутой планеты
- 10.4.1. Короткопериодические возмущения первого порядка
- 10.4.2. Вековые возмущения первого порядка
- 10.4.3. Долгопериодические возмущения, обусловленные третьей гармоникой
- 10.4.4. Вековые возмущения второго порядка и долгопериодические возмущения
- 10.5. Использование теории Гамильтона—Якоби в задаче движения искусственного спутника
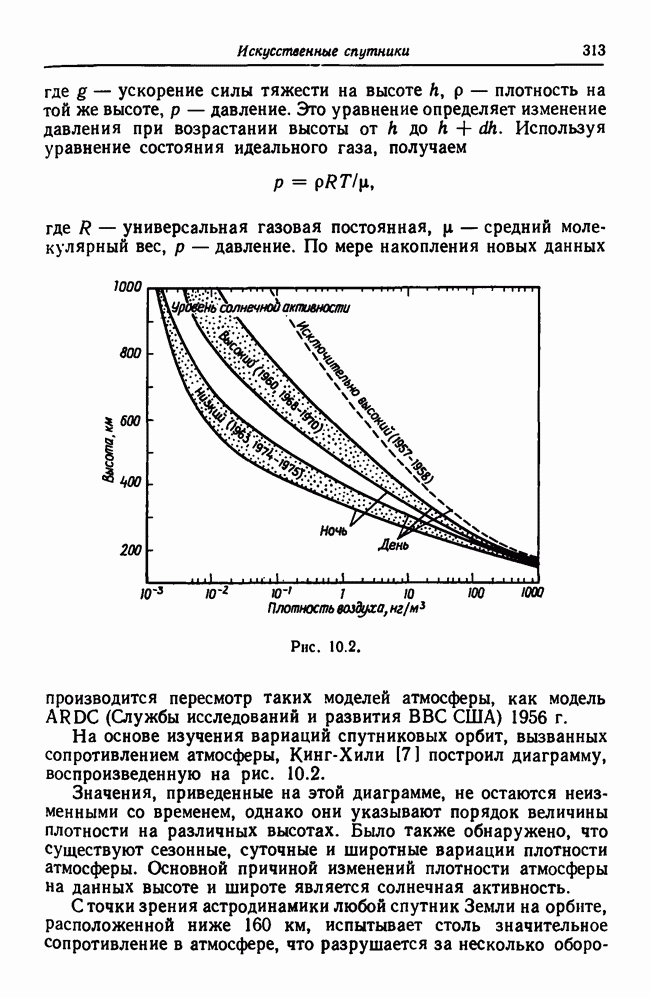
- 10.6. Действие атмосферного торможения на искусственный спутник
- 10.7. Тессеральные и секториальные гармоники поля тяготения Земли
- Задачи
- Литература
- Глава 11. Динамика ракет и орбиты переходов
- 11.2.1. Движение ракеты в гравитационном поле
- 11.2.2. Движение ракеты в атмосфере
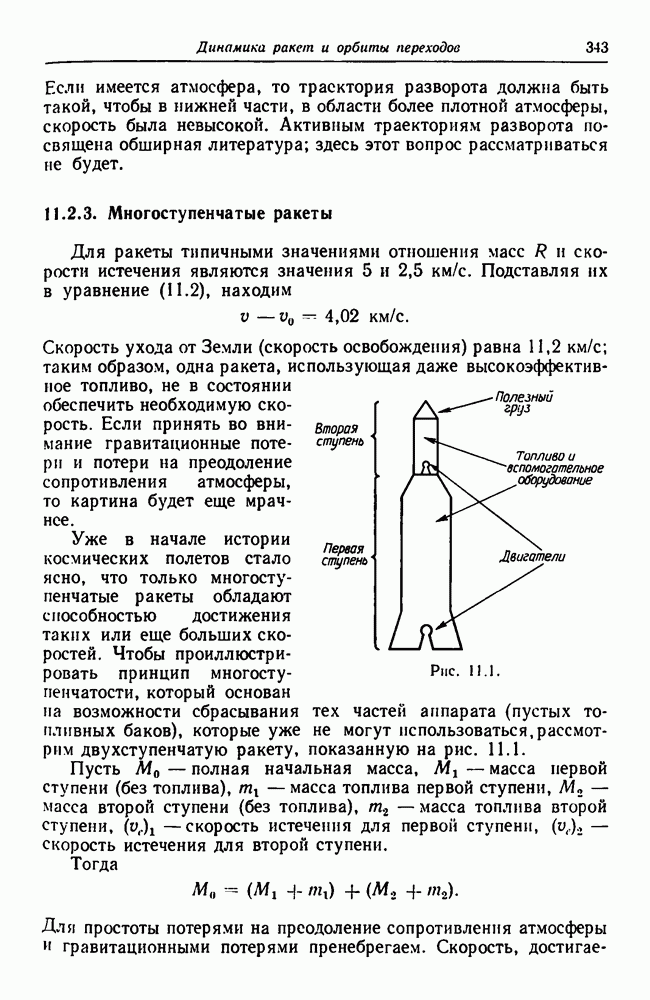
- 11.2.3. Многоступенчатые ракеты
- 11.2.4. Другие типы ракет
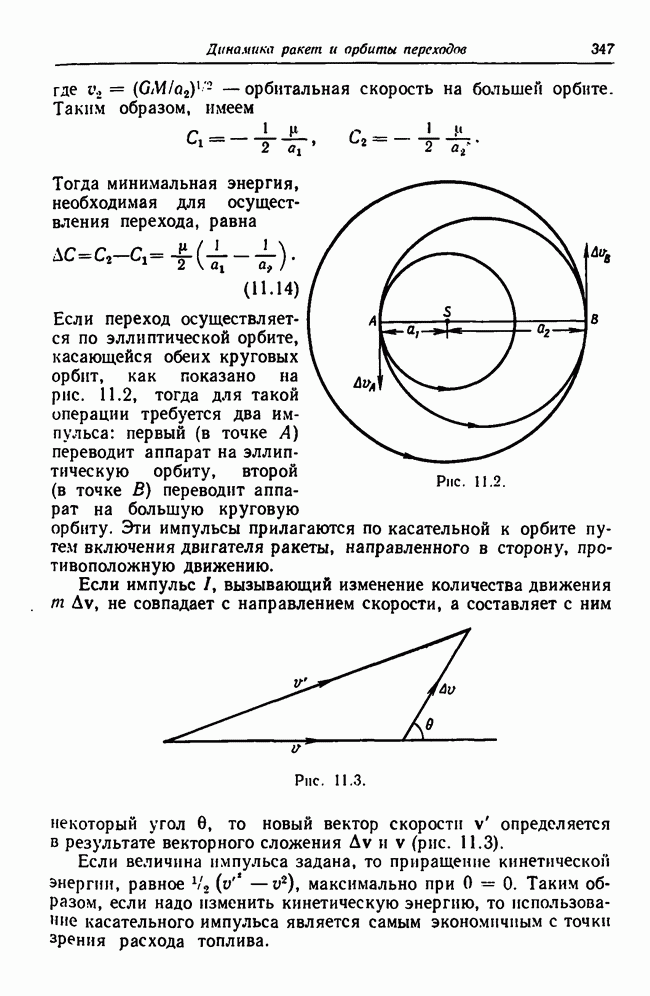
- 11.3. Переходы между орбитами в силовом поле одного притягивающего центра
- 11.3.2. Параболические и гиперболические орбиты перехода
- 11.3.3. Изменения элементов орбиты, вызванные малым импульсом
- 11.3.4. Изменения элементов орбить, вызванные большим импульсом
- 11.3.5. Зависимость расхода топлива от времени перехода
- 11.3.6. Зависимость орбиты перехода от малых ошибок положения и скорости в момент выключения двигателя
- 11.3.7. Переход между частицами, движущимися по орбитам в центральном поле сил
- 11.4. Орбиты перехода в силовых полях двух или более притягивающих центров
- 11.4.2. Выход на орбиту вокруг второго тела
- 11.4.3. Гиперболический захват
- 11.4.4. Точность проведенного анализа и влияние ошибок
- 11.4.5. Облет как средство увеличения скорости
- Задачи
- Глава 12. Траектории полетов к планетам и Луне
- 12.3. Возможности и точность методов исследования
- 12.4. Использование интеграла Якоби
- 12.5. Использование решений Лагранжа
- 12.6. Использование решений задачи двух тел
- 12.7. Искусственные спутники Луны
- 12.7.1. Относительные величины возмущений спутника Луны для различных случаев
- 12.7.2. Интеграл Якоби для близкого спутника Луны
- 12.8. Траектории межпланетных полетов
- 12.9. Солнечная система как поле центральной силы
- 12.10. Орбиты межпланетных перелетов с минимальными затратами энергии
- 12.11. Использование орбит ожидания при межпланетных полетах
- 12.12. Влияние ошибок на межпланетные орбиты
- Задачи
- Глава 13. Определение орбит и межпланетная навигация
- 13.2. Теория определения орбит
- 13.3. Метод Лапласа
- 13.4. Метод Гаусса
- 13.5. Метод Ольберса для параболических орбит
- 13.6. Определение орбит при наличии дополнительных данных наблюдений
- 13.7. Улучшение орбит
- 13.8. Межпланетная навигация
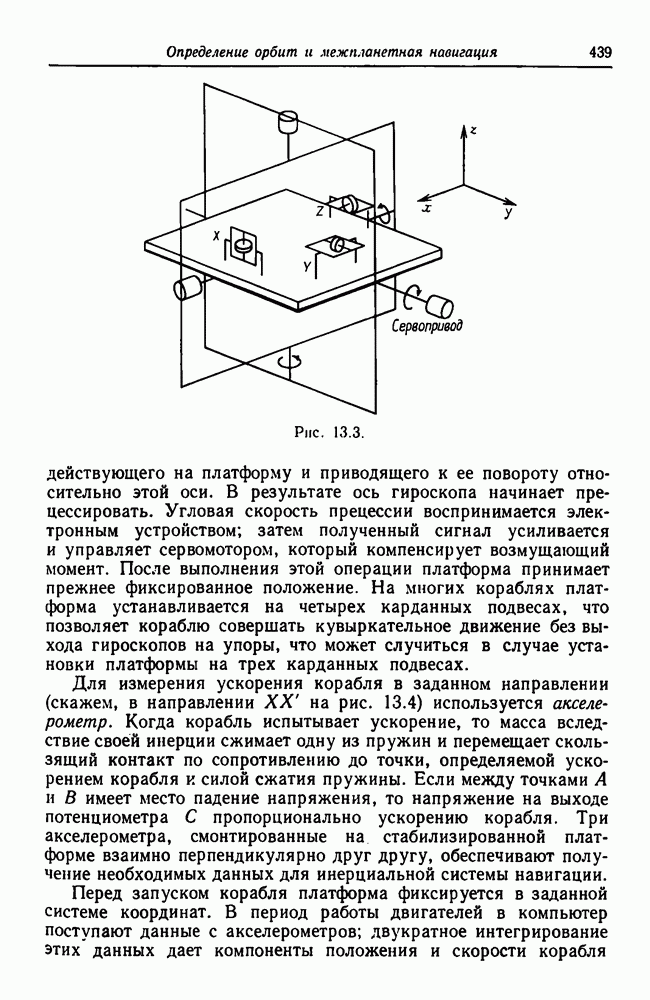
- 13.8.1. Стабилизированные платформы и акселерометры
- 13.8.2. Навигация при помощи бортовой оптической аппаратуры
- 13.8.3. Методы наблюдений и достижимая точность
- Литература
- Глава 14. Двойные системы и системы нескольких тел
- 14.2. Визуально-двойные звезды
- 14.3. Соотношение масса—светимость
- 14.4. Динамические параллаксы
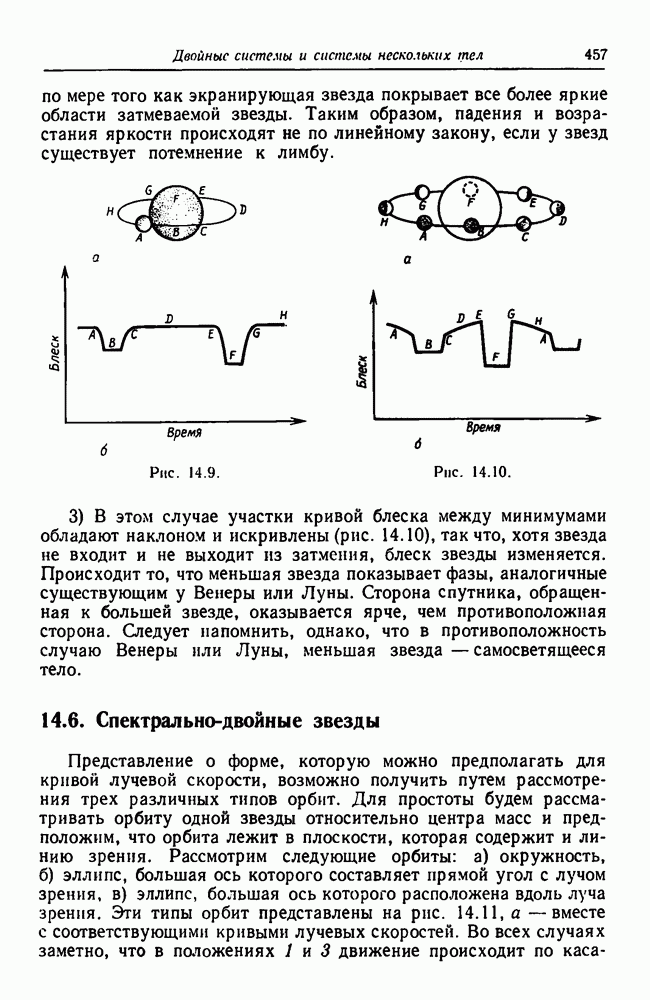
- 14.5. Затменные двойные
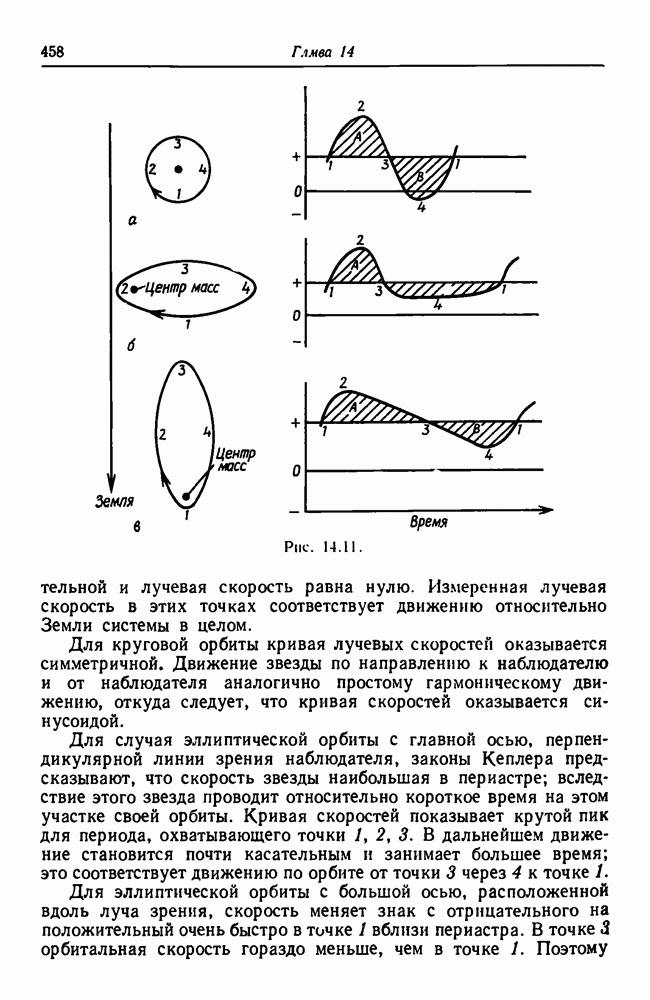
- 14.6. Спектрально-двойные звезды
- 14.7. Обзор результатов
- 14.8. Элементы орбиты двойной звезды
- 14.9. Период двойной звезды
- 14.10. Движение апсид
- 14.11. Силы, действующие в двойной системе
- 14.12. Тройные системы
- 14.13. Неточность ньютоновского закона тяготения
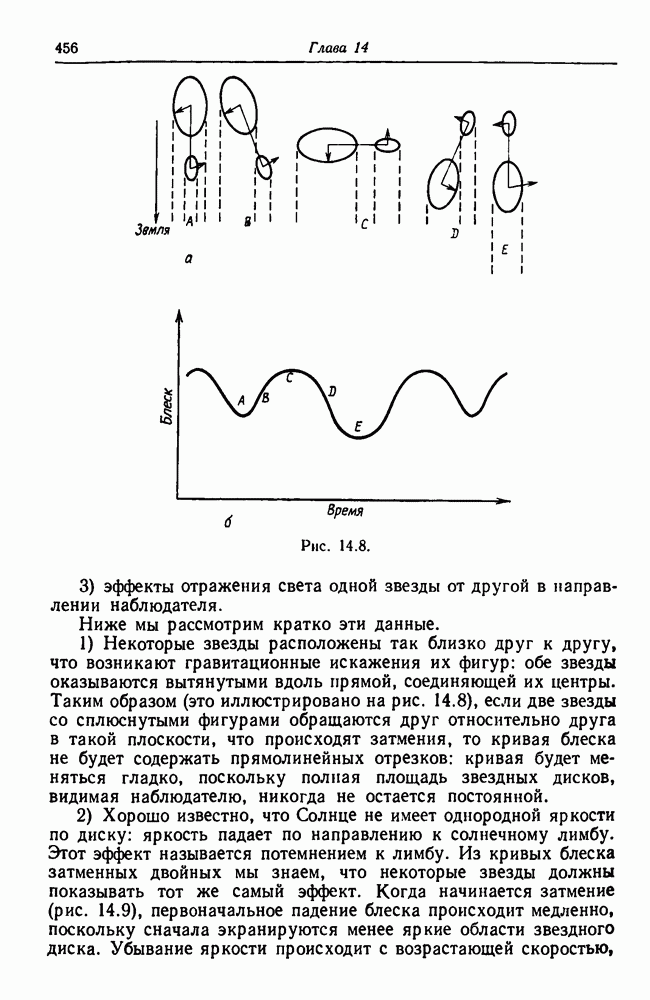
- 14.14. Фигуры звезд в двойных системах
- 14.15. Пределы Роша
- 14.16. Вещество, окружающее звезды
- 14.17. Образование двойных систем
- Задачи
- Глава 15. Звездные системы многих тел
- 15.2. Сфера действия
- 15.3. Парные сближения
- 15.4. Накапливающийся эффект малых сближений
- 15.5. Некоторые фундаментальные принципы
- 15.6. Основные теоремы звездной динамики
- 15.6.1. Теорема Джинса
- 15.7. Некоторые частные случаи для звездной системы в стационарном состоянии
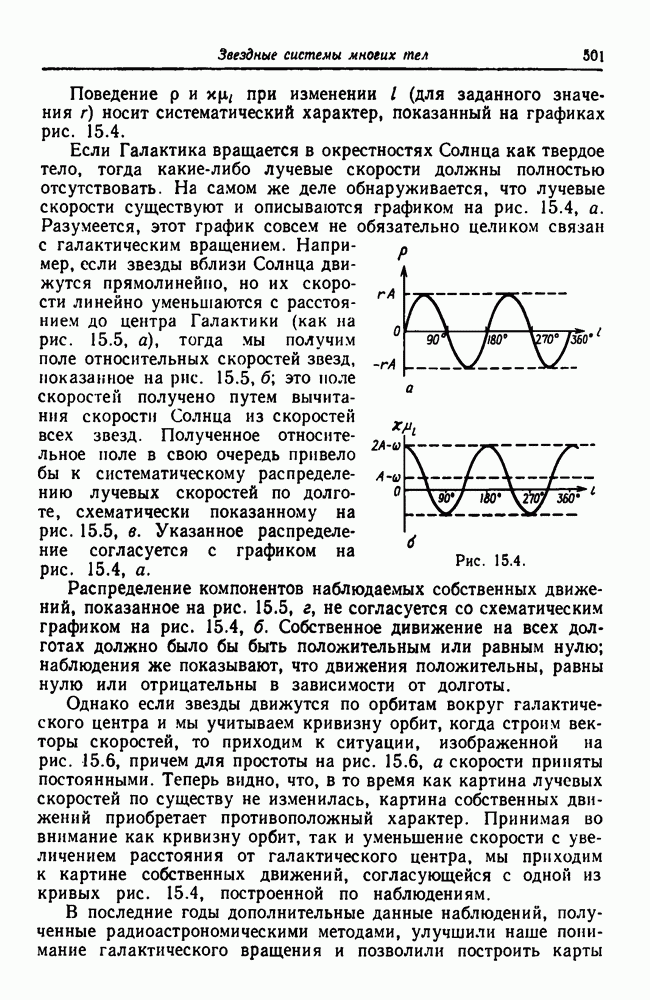
- 15.8. Вращение галактик
- 15.8.2. Период вращения и угловая скорость Галактики
- 15.8.3. Масса Галактики
- 15.8.4. Общий характер вращения Галактики
- 15.8.5. Галактические орбиты звезд
- 15.8.6. Звезды с высокими скоростями
- 15.9. Сферические звездные системы
- 15.9.1. Применение теоремы вириала к сферической системе
- 15.9.2. Орбиты звезд в сферической системе
- 15.9.3. Распределение орбит внутри сферической системы
- 15.10. Эксперименты на ЭВМ
- Задачи
- Ответы к задачам
- Приложения