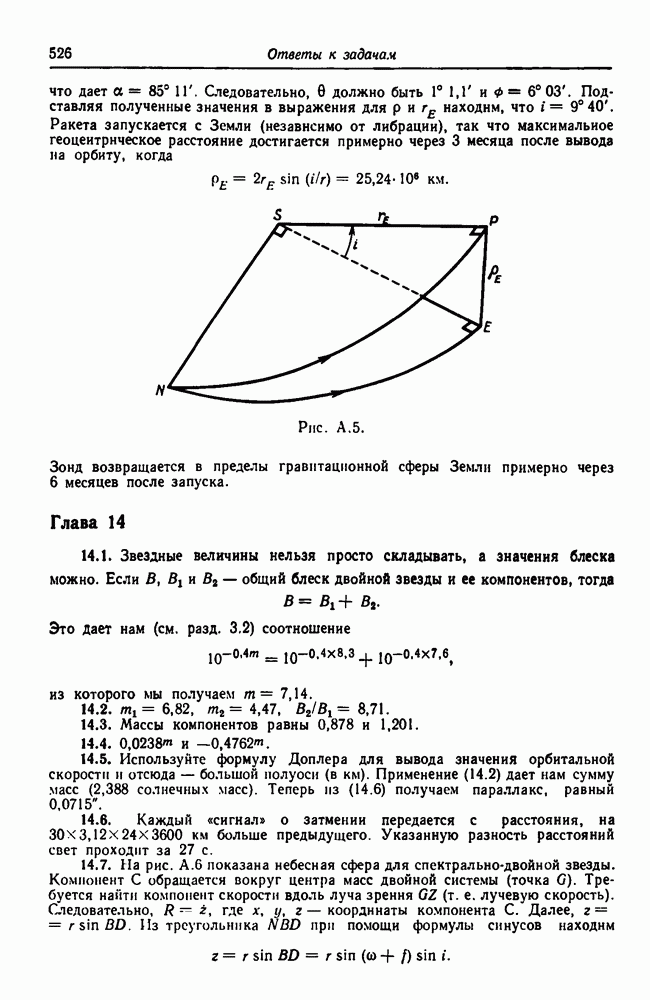
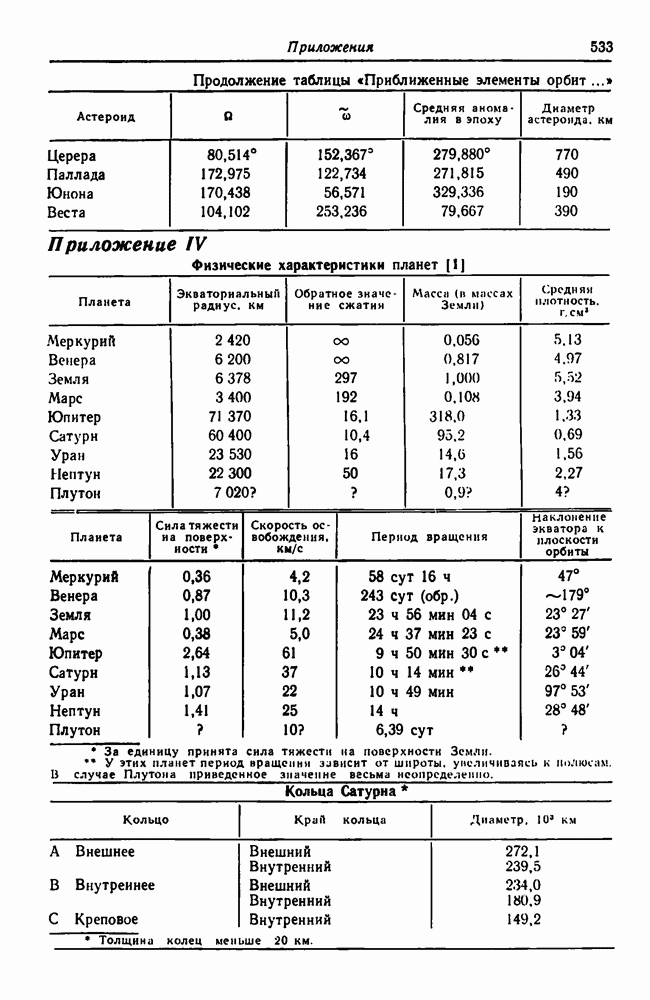
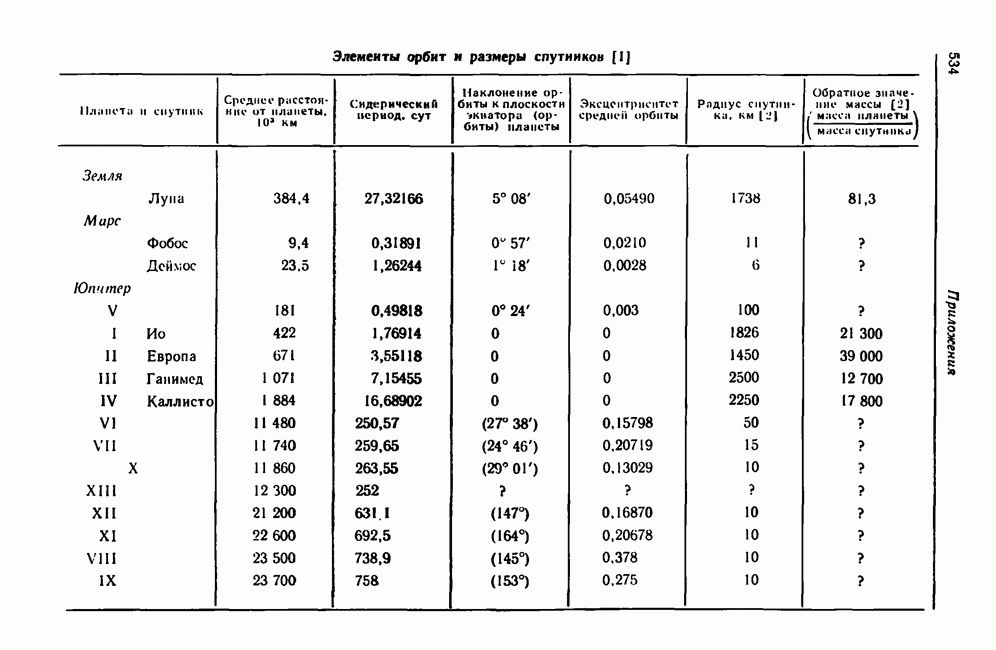
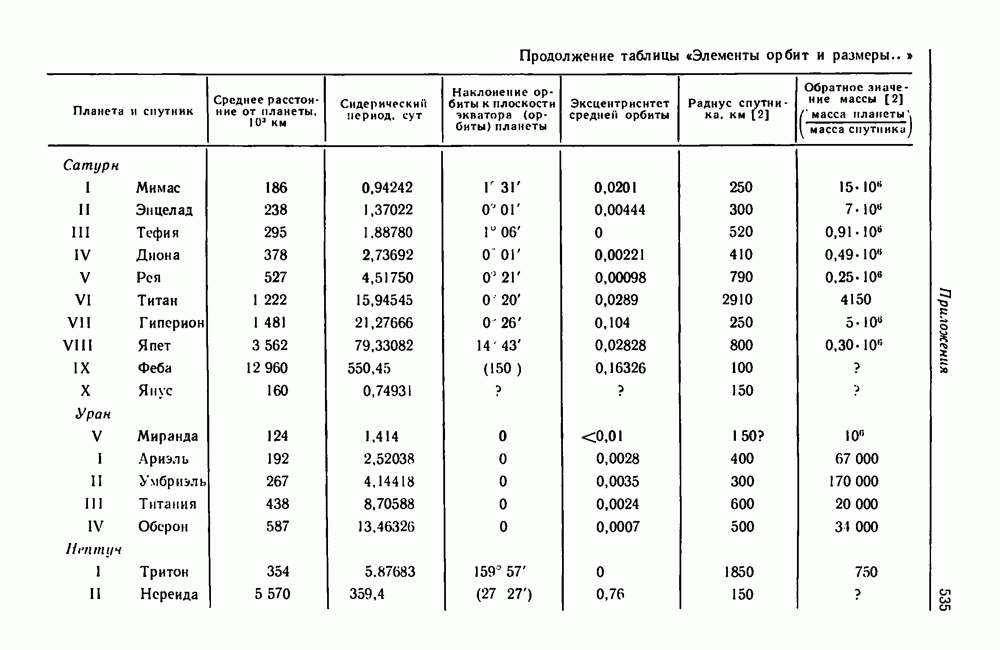
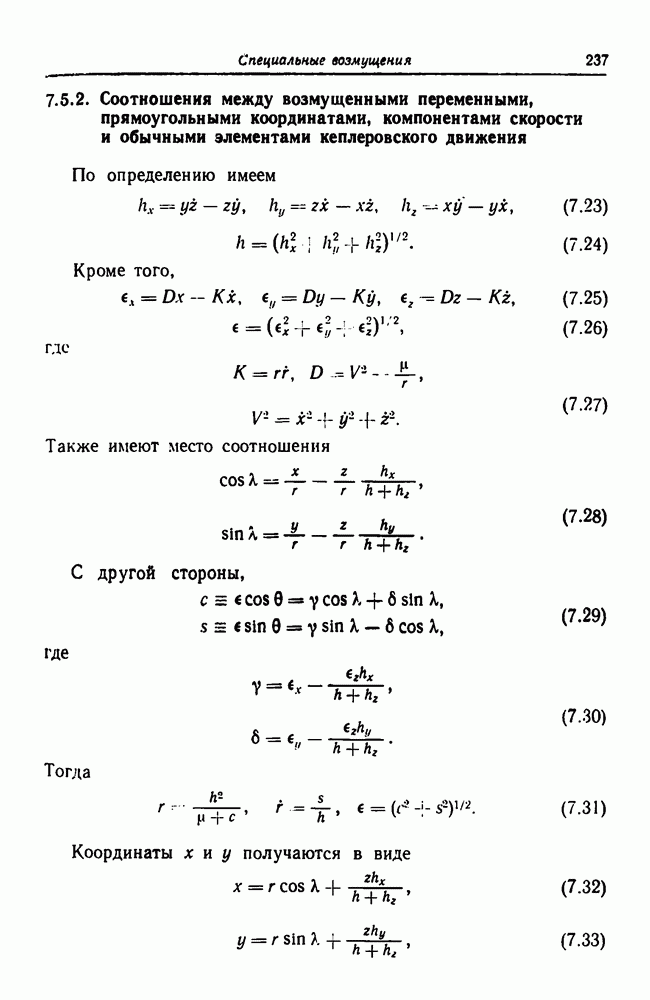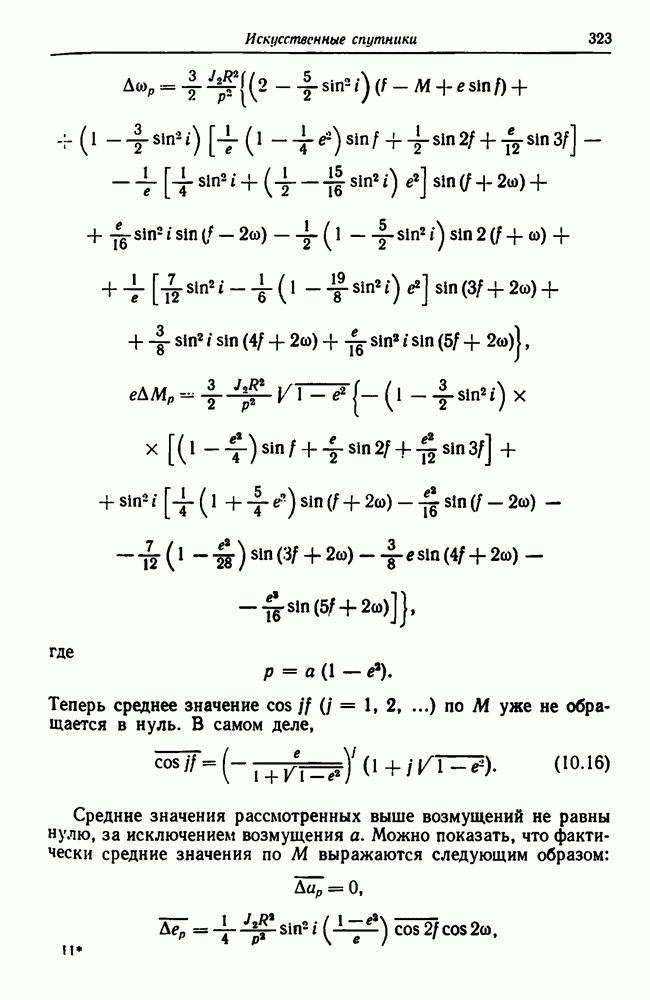| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.6. Теорема зеркальности
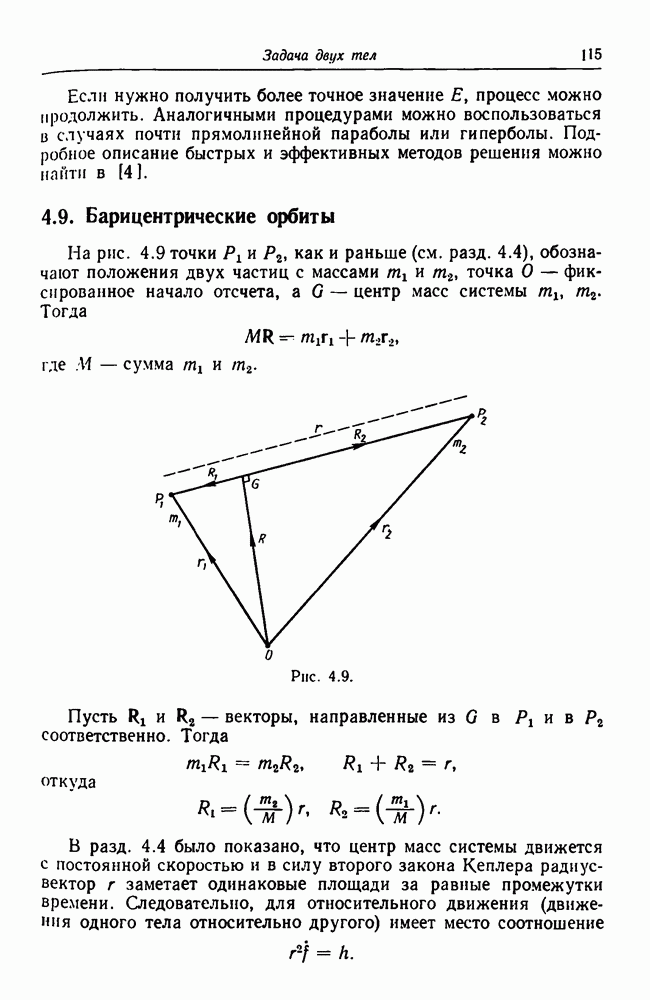
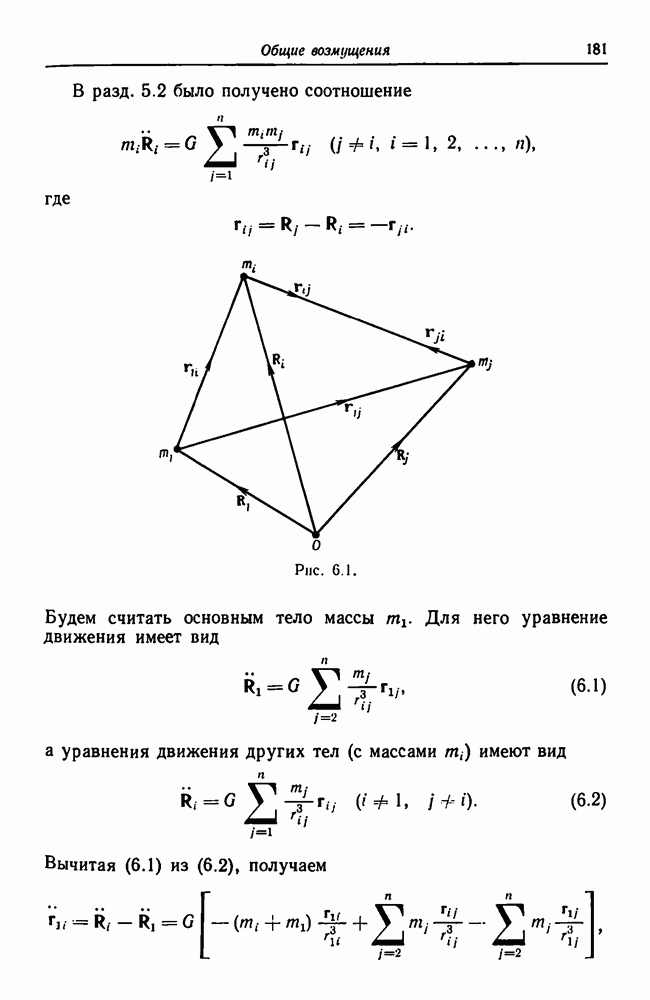
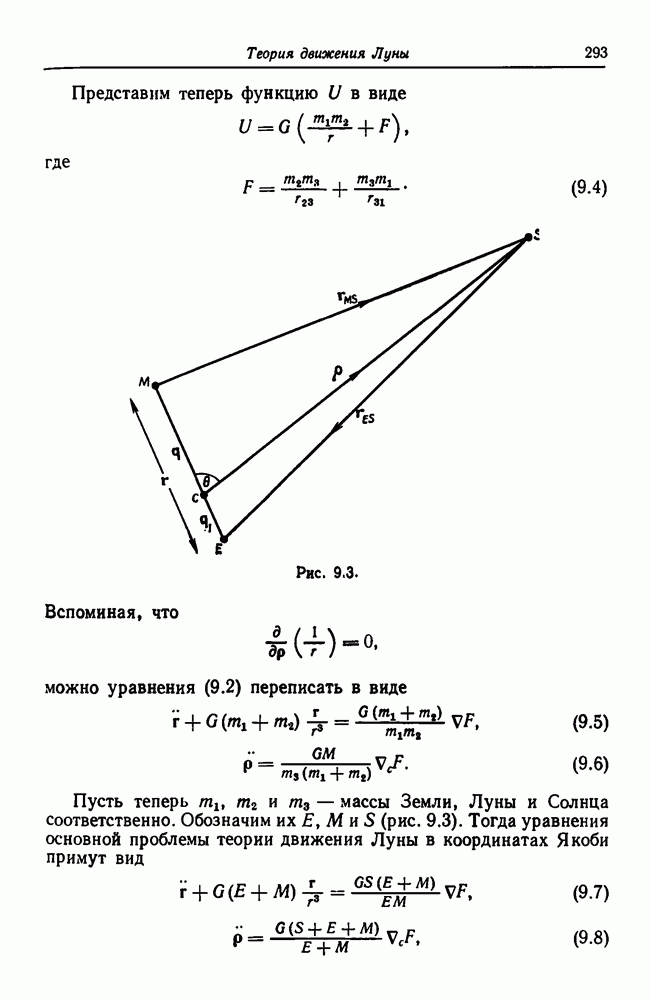
Из уравнений движения можно вывести еще два следствия. Первое из них — теорема зеркальности — формулируется следующим образом: если в некоторый момент времени  радиус-вектор, проведенный из центра масс системы
радиус-вектор, проведенный из центра масс системы  материальных точек, движущихся под действием только сил взаимного притяжения, перпендикулярен вектору скорости для каждой из точек системы, то орбита каждой материальной точки при
материальных точек, движущихся под действием только сил взаимного притяжения, перпендикулярен вектору скорости для каждой из точек системы, то орбита каждой материальной точки при  представляет собой зеркальное отражение ее орбиты при
представляет собой зеркальное отражение ее орбиты при  Такая конфигурация радиусов-векторов и векторов скоростей называется зеркальной.
Такая конфигурация радиусов-векторов и векторов скоростей называется зеркальной.
Из первого утверждения непосредственно следует второе: орбиты  материальных точек, движущихся под действием только сил взаимного притяжения, являются периодическими, если в два различных момента времени система имеет зеркальную конфигурацию. Заметим, что орбитальное движение системы тел является периодическим, если через одинаковые промежутки времени система имеет одинаковые конфигурации радиусов-векторов и векторов скоростей всех тел.
материальных точек, движущихся под действием только сил взаимного притяжения, являются периодическими, если в два различных момента времени система имеет зеркальную конфигурацию. Заметим, что орбитальное движение системы тел является периодическим, если через одинаковые промежутки времени система имеет одинаковые конфигурации радиусов-векторов и векторов скоростей всех тел.
Строгое доказательство теоремы зеркальности  легко провести, если заметить, что в уравнения движения не входят скорости. Следовательно, при обращении времени тела будут двигаться по своим собственным траекториям, но в обратном направлении. Если в некоторый момент времени имеет место зеркальная конфигурация, то орбита каждой частицы до и после этого момента не только является непрерывной, но и обладает тем свойством, что при
легко провести, если заметить, что в уравнения движения не входят скорости. Следовательно, при обращении времени тела будут двигаться по своим собственным траекториям, но в обратном направлении. Если в некоторый момент времени имеет место зеркальная конфигурация, то орбита каждой частицы до и после этого момента не только является непрерывной, но и обладает тем свойством, что при  на частицы действуют силы, «обратные» действующим в соответствующие моменты времени при
на частицы действуют силы, «обратные» действующим в соответствующие моменты времени при 
Возможно существование только двух зеркальных конфигураций:
1) все материальные точки лежат в одной плоскости, а все векторы скоростей перпендикулярны этой плоскости и, следовательно, параллельны друг другу;
2) все материальные точки лежат на одной прямой, а их векторы скоростей перпендикулярны этой прямой, но не обязательно параллельны друг другу.
Доказательство утверждения о периодичности тривиально. Если зеркальные конфигурации А к В имеют место при  и
и  то А снова имеет место при
то А снова имеет место при  при
при  и т. д. Следовательно, орбиты являются периодическими с периодом 2
и т. д. Следовательно, орбиты являются периодическими с периодом 2
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. Неспокойная Вселенная
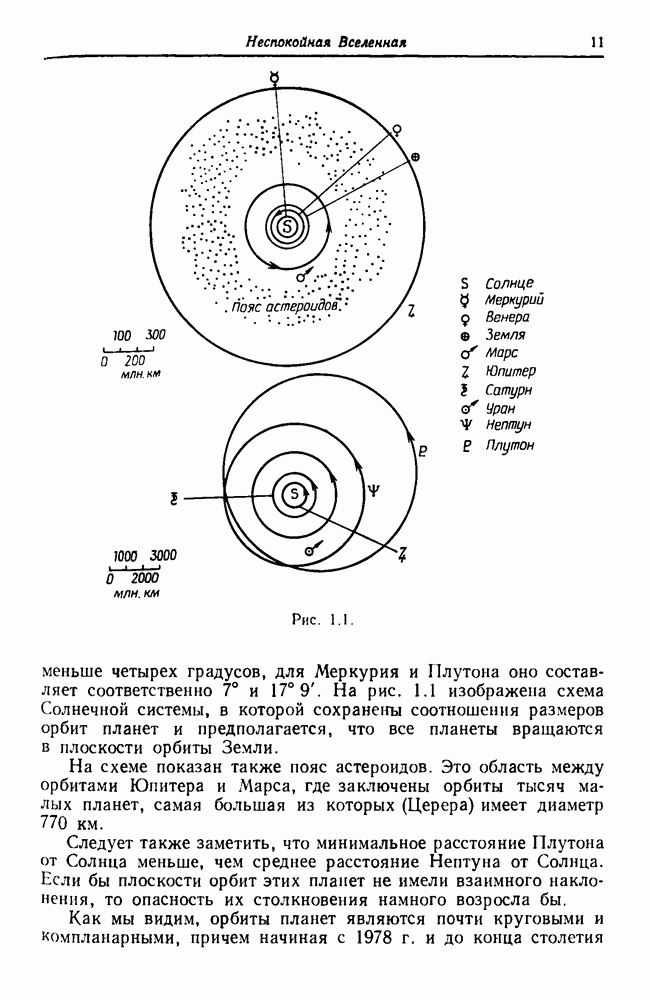
- 1.2. Солнечная система
- 1.2.1. Законы Кеплера
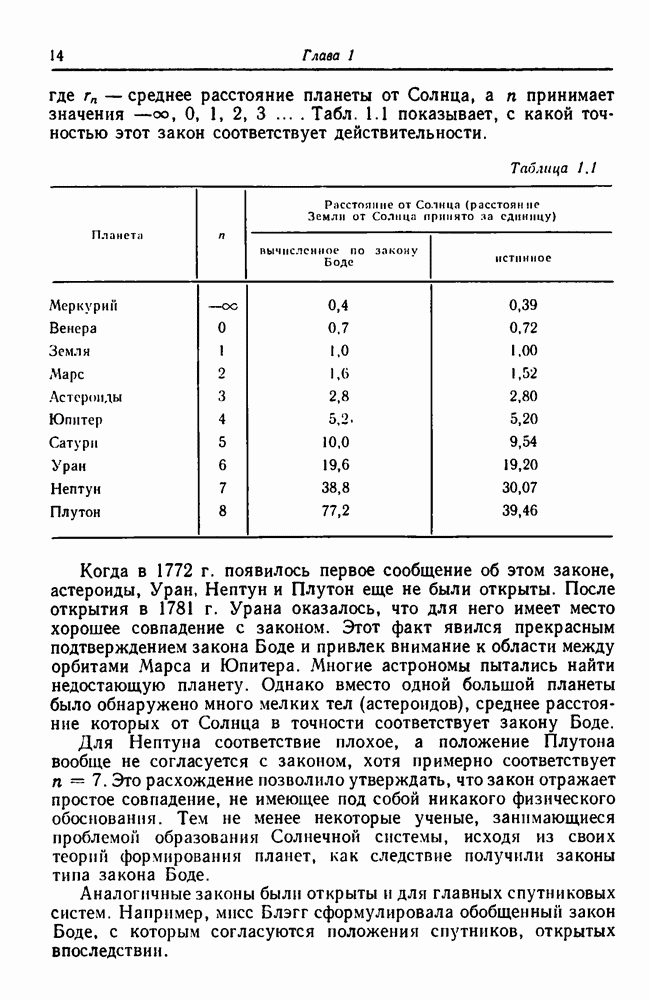
- 1.2.2. Закон Боде
- 1.2.3. Соизмеримости в средних движениях
- 1.2.4. Кометы и метеорные тела
- 1.2.5. Выводы
- 1.3. Движение звезд
- 1.3.1. Двойные системы
- 1.3.2. Тройные системы и системы более высокой кратности
- 1.3.3. Шаровые скопления
- 1.3.4. Галактические, или рассеянные, звездные скопления
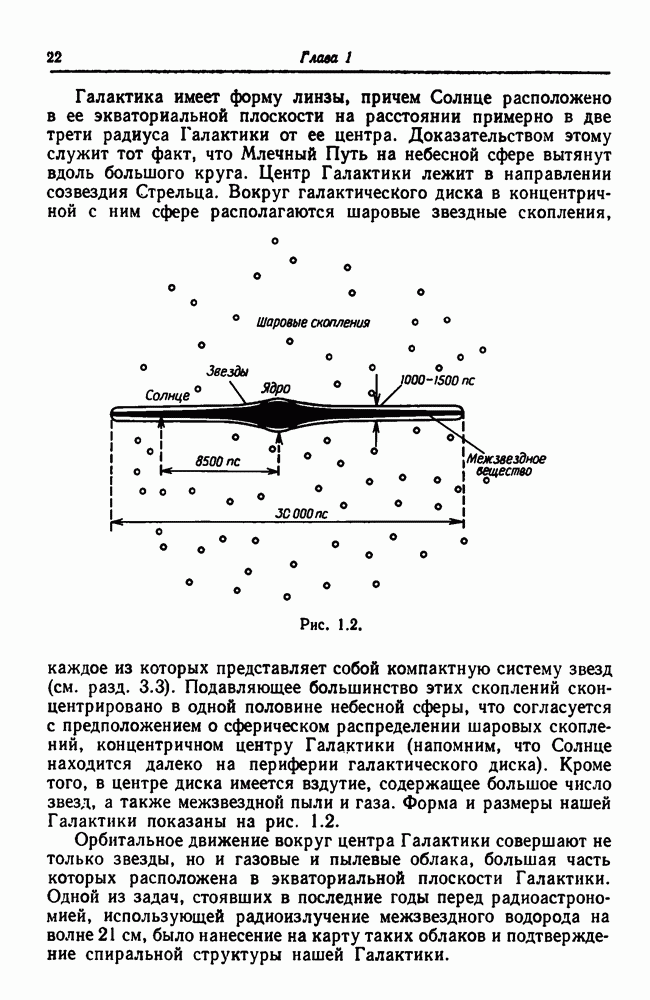
- 1.4. Скопления галактик
- 1.5. Выводы
- Рекомендуемая литература
- Глава 2. Системы координат и измерение времени
- 2.2. Положение на поверхности Земли
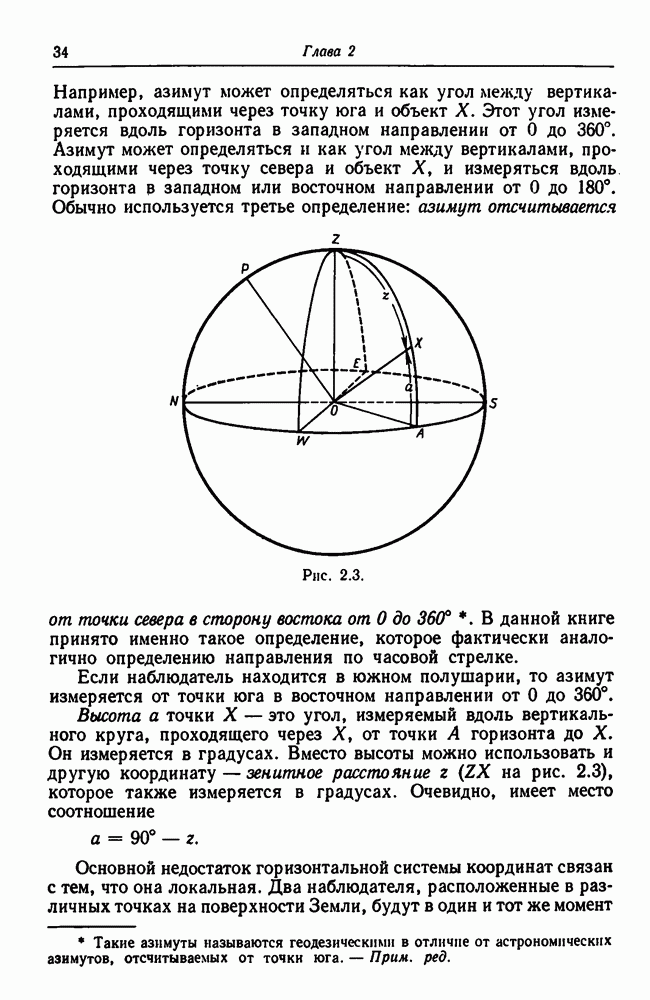
- 2.3. Горизонтальная система
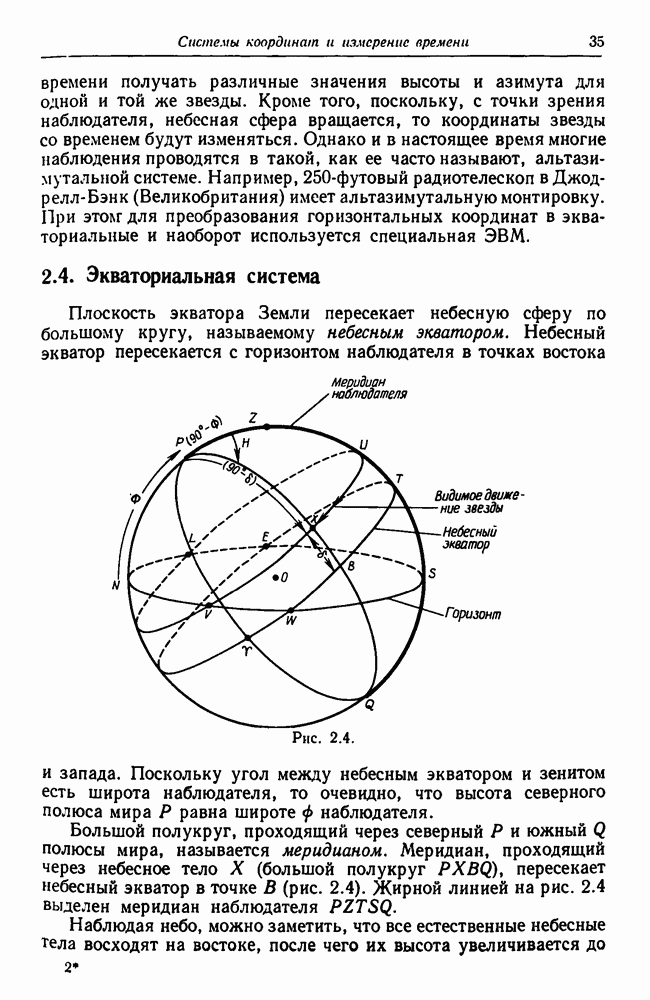
- 2.4. Экваториальная система
- 2.5. Эклиптическая система
- 2.6. Элементы орбиты в пространстве
- 2.7. Прямоугольные системы координат
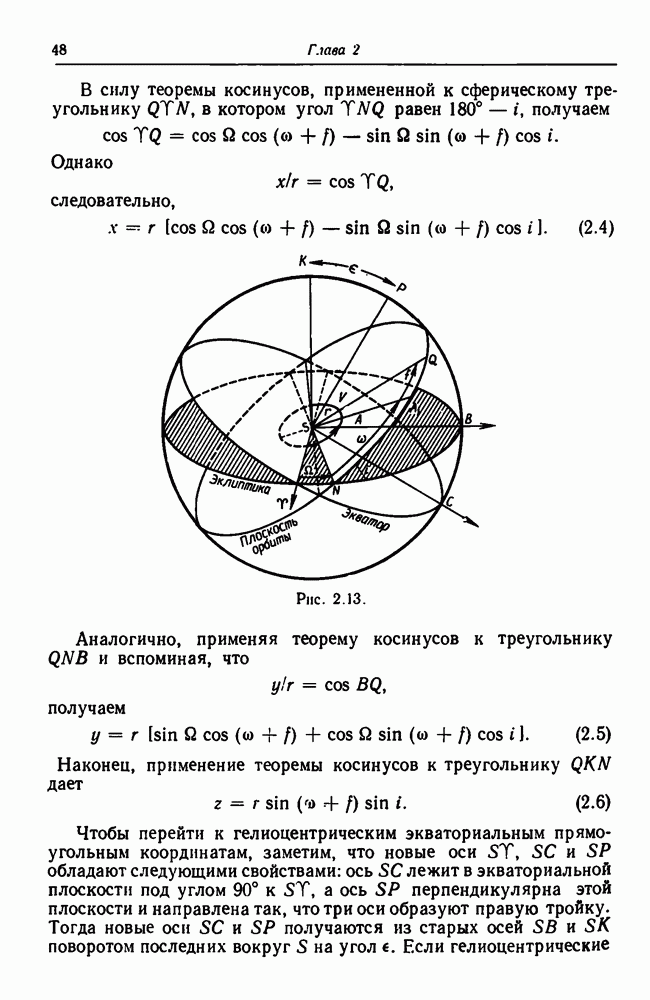
- 2.8. Системы координат, связанные с плоскостью орбиты
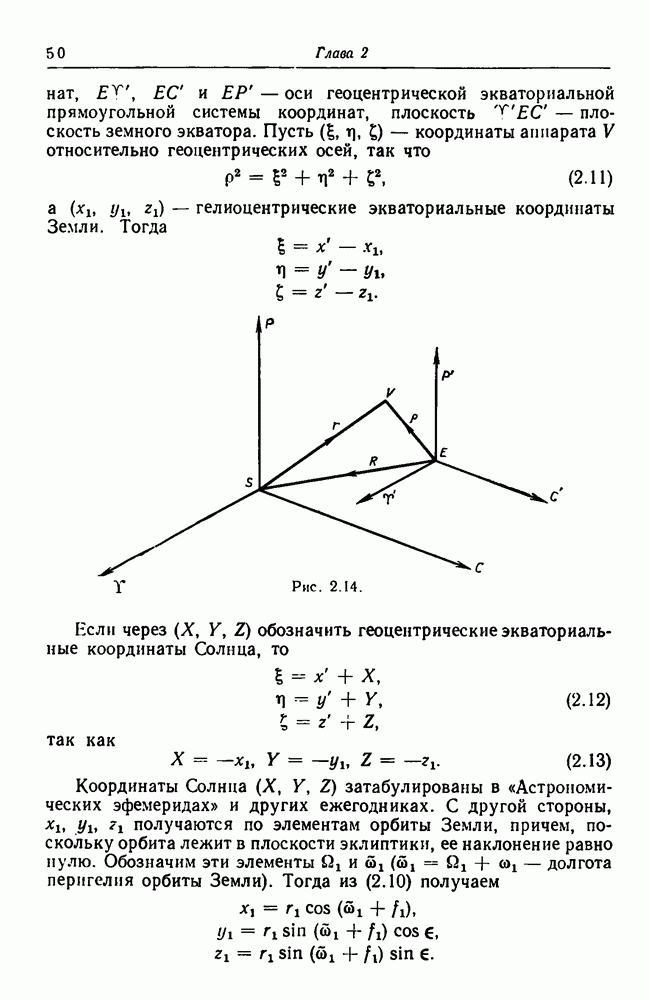
- 2.9. Преобразование систем координат
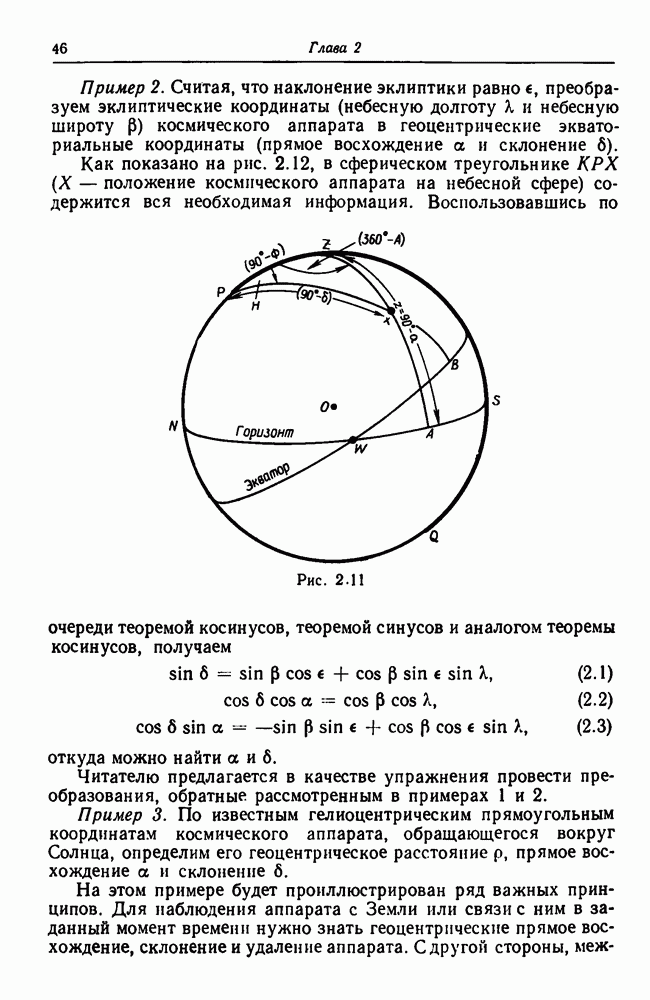
- 2.9.2. Примеры преобразований систем координат
- 2.10. Галактическая система координат
- 2.11. Измерение времени
- 2.11.1. Звездное время
- 2.11.2. Среднее солнечное время
- 2.11.3. Юлианские дни
- 2.11.4. Эфемеридное время
- Задачи
- Литература
- Глава 3. Обработка данных наблюдений
- 3.2. Методы наблюдений
- 3.3. Рефракция
- 3.4. Прецессия и нутация
- 3.5. Аберрация
- 3.6. Собственное движение
- 3.7. Годичный параллакс
- 3.8. Геоцентрический параллакс
- 3.9. Обзор процедур
- Задачи
- Литература
- Глава 4. Задача двух тел
- 4.2. Законы Ньютона
- 4.3. Закон всемирного тяготения Ньютона
- 4.4. Решение задачи двух тел
- 4.5. Эллиптическая орбита
- 4.5.1. Измерение массы планеты
- 4.5.2. Скорость движения по эллиптической орбите
- 4.5.3. Угол между вектором скорости и радиусом-вектором
- 4.5.4. Средняя, эксцентрическая и истинная аномалии
- 4.5.5. Решение уравнения Кеплера
- 4.5.6. Уравнение центра
- 4.5.7. Положение тела на эллиптической орбите
- 4.6. Параболическая орбита
- 4.7. Гиперболическая орбита
- 4.7.1. Скорость на гиперболической орбите
- 4.7.2. Положение на гиперболической орбите
- 4.8. Прямолинейная орбита
- 4.9. Барицентрические орбиты
- 4.10. Классификация орбит по величине константы энергии
- 4.11. Орбита в пространстве
- 4.12. Ряды для f и g
- 4.13. Использование рекуррентных соотношений
- 4.14. Универсальные переменные
- Задачи
- Литература
- Глава 5. Задача n тел
- 5.2. Уравнения движения задачи n тел
- 5.3. Десять известных интегралов и их смысл
- 5.4. Силовая функция
- 5.5. Теорема вириала
- 5.6. Теорема зеркальности
- 5.7. Снова о задаче n тел
- 5.8. Лагранжевы решения задачи трех тел
- 5.9. Общие замечания о лагранжевых решениях
- 5.10. Ограниченная круговая задача трех тел
- 5.10.2. Критерий Тиссерана
- 5.10.3. Поверхности нулевой скорости
- 5.10.4. Устойчивость точек либрации
- 5.10.5. Периодические орбиты
- 5.10.6. Поиск симметричных периодических орбит
- 5.10.7. Примеры семейств периодических орбит
- 5.10.8. Устойчивость периодических орбит
- 5.10.9. Поверхность сечения
- 5.10.10. Матрица устойчивости
- 5.11. Общая задача трех тел
- 5.11.1. Случай С < 0
- 5.11.2. Случай С = 0
- 5.11.3. Координаты Якоби
- Задачи
- Литература
- Глава 6. Общие возмущения
- 6.2. Уравнения относительного движения
- 6.3. Возмущающая функция
- 6.4. Гравитационная сфера влияния
- 6.5. Потенциал тела произвольной формы
- 6.6. Потенциал шара во внутренней точке
- 6.7. Метод вариации параметров
- 6.7.1. Модификация средней долготы в эпоху
- 6.7.2. Решение уравнений движения планет в форме Лагранжа
- 6.7.3. Коротко- и долгопериодические вариации
- 6.7.4. Разложение возмущающей силы
- 6.8. Уравнения Лагранжа
- 6.9. Канонические уравнения Гамильтона
- Задачи
- Рекомендуемая литература
- Глава 7. Специальные возмущения
- 7.2. Основные факторы теории специальных возмущений
- 7.3. Метод Коуэлла
- 7.4. Метод Энке
- 7.5. Использование возмущенных уравнений
- 7.5.1. Вывод уравнений возмущенного движения
- 7.5.2. Соотношения между возмущенными переменными, прямоугольными координатами, компонентами скорости и обычными элементами кеплеровского движения
- 7.5.3. Процедура численного интегрирования
- 7.5.4. Прямолинейные или почти прямолинейные орбиты
- 7.6. Методы регуляризации
- 7.7. Методы численного интегрирования
- 7.7.2. Метод Рунге—Кутта четвертого порядка
- 7.7.3. Многошаговые методы
- 7.7.4. Численные методы
- Задачи
- Литература
- Глава 8. Устойчивость и эволюция Солнечной системы
- 8.2. Эфемериды планет
- 8.3. Соизмеримости в средних движениях
- 8.4. Астероиды
- 8.5. Кольца Сатурна
- 8.6. Почти соизмеримые орбиты спутников
- 8.7. Численное интегрирование на больших промежутках времени
- 8.7.2. Эволюция элементов орбит на интервале 1 000 000 лет
- 8.7.3. Движение перигелия Плутона: ротационное или либрационное?
- 8.7.4. Сравнение аналитического и численного подходов
- 8.8. Принцип Овендена
- 8.9. Выводы
- Литература
- Глава 9. Теория движения Луны
- 9.3. Сарос
- 9.4. Измерение большой полуоси орбиты, массы и диаметра Луны
- 9.5. Вращение Луны
- 9.6. Селенографические координаты
- 9.7. Фигура Луны
- 9.8. Основная проблема в теории движения Луны
- 9.9. Орбита Солнца в основной проблеме теории движения Луны
- 9.10. Орбита Луны
- 9.11. Теории Луны
- 9.12. Вековое ускорение Луны
- Литература
- Глава 10. Искусственные спутники
- 10.2. Земля как планета
- 10.2.1. Форма Земли
- 10.2.2. Формула Клеро
- 10.2.3. Внутреннее строение Земли
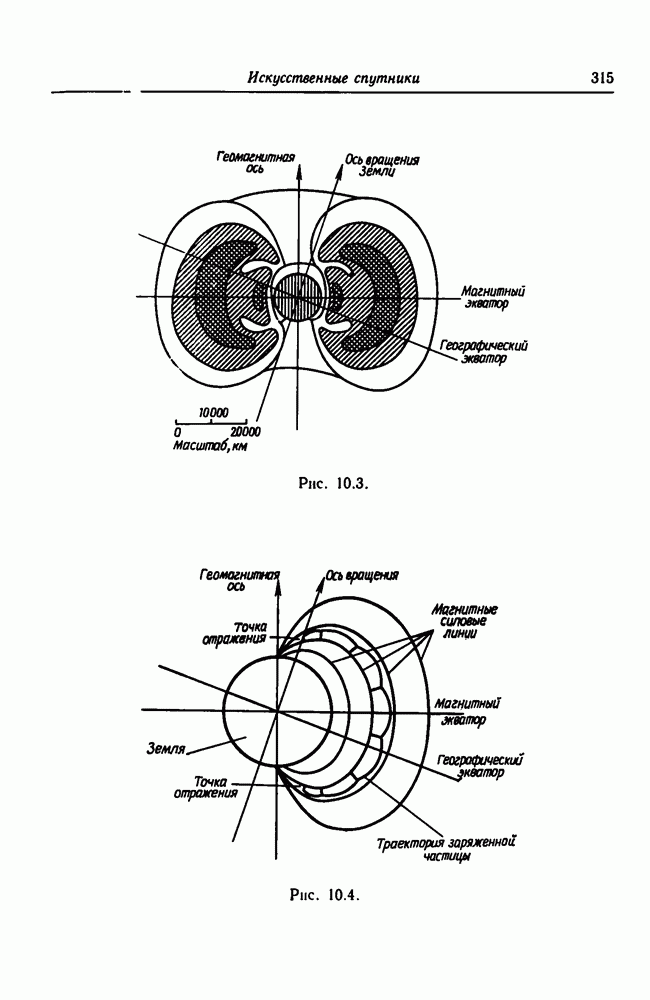
- 10.2.4. Магнитное поле Земли
- 10.2.5. Атмосфера Земли
- 10.2.6. Солнечно-земные связи
- 10.3. Силы, действующие на искусственные спутники Земли
- 10.4. Орбита спутника вокруг сплюснутой планеты
- 10.4.1. Короткопериодические возмущения первого порядка
- 10.4.2. Вековые возмущения первого порядка
- 10.4.3. Долгопериодические возмущения, обусловленные третьей гармоникой
- 10.4.4. Вековые возмущения второго порядка и долгопериодические возмущения
- 10.5. Использование теории Гамильтона—Якоби в задаче движения искусственного спутника
- 10.6. Действие атмосферного торможения на искусственный спутник
- 10.7. Тессеральные и секториальные гармоники поля тяготения Земли
- Задачи
- Литература
- Глава 11. Динамика ракет и орбиты переходов
- 11.2.1. Движение ракеты в гравитационном поле
- 11.2.2. Движение ракеты в атмосфере
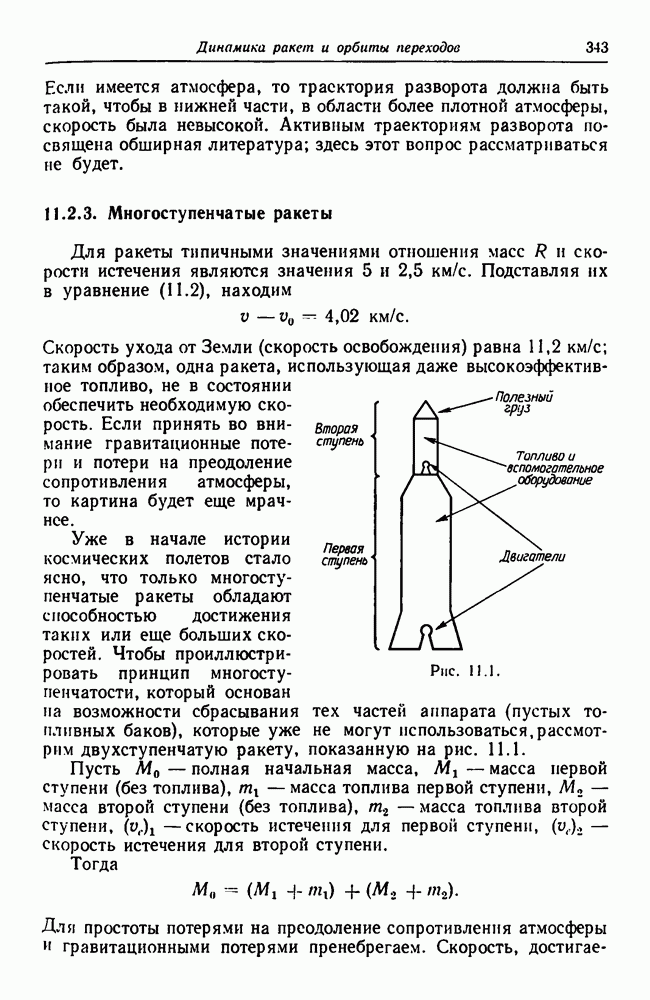
- 11.2.3. Многоступенчатые ракеты
- 11.2.4. Другие типы ракет
- 11.3. Переходы между орбитами в силовом поле одного притягивающего центра
- 11.3.2. Параболические и гиперболические орбиты перехода
- 11.3.3. Изменения элементов орбиты, вызванные малым импульсом
- 11.3.4. Изменения элементов орбить, вызванные большим импульсом
- 11.3.5. Зависимость расхода топлива от времени перехода
- 11.3.6. Зависимость орбиты перехода от малых ошибок положения и скорости в момент выключения двигателя
- 11.3.7. Переход между частицами, движущимися по орбитам в центральном поле сил
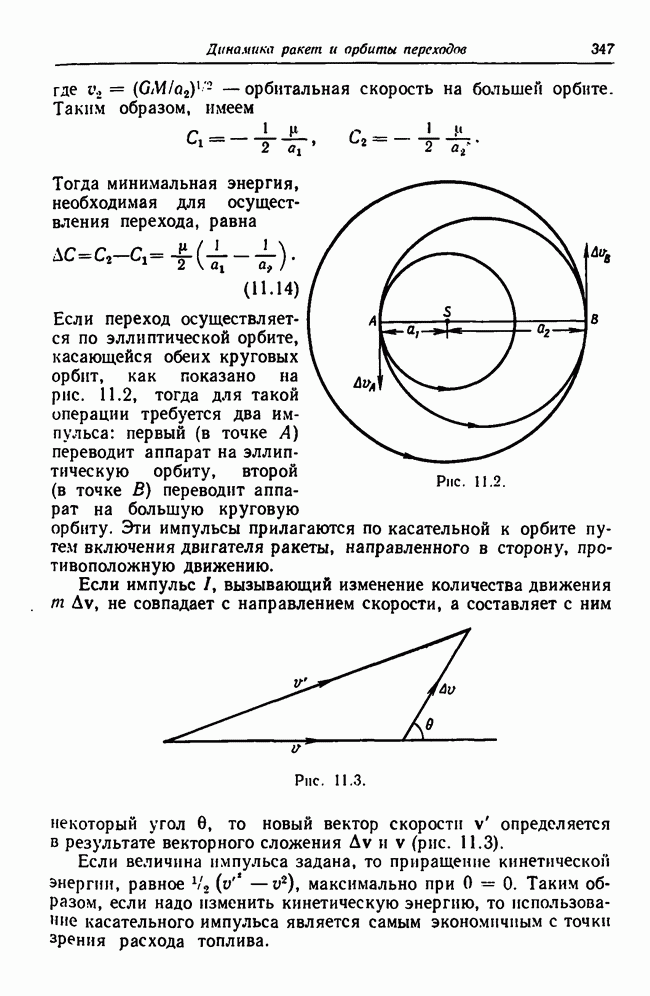
- 11.4. Орбиты перехода в силовых полях двух или более притягивающих центров
- 11.4.2. Выход на орбиту вокруг второго тела
- 11.4.3. Гиперболический захват
- 11.4.4. Точность проведенного анализа и влияние ошибок
- 11.4.5. Облет как средство увеличения скорости
- Задачи
- Глава 12. Траектории полетов к планетам и Луне
- 12.3. Возможности и точность методов исследования
- 12.4. Использование интеграла Якоби
- 12.5. Использование решений Лагранжа
- 12.6. Использование решений задачи двух тел
- 12.7. Искусственные спутники Луны
- 12.7.1. Относительные величины возмущений спутника Луны для различных случаев
- 12.7.2. Интеграл Якоби для близкого спутника Луны
- 12.8. Траектории межпланетных полетов
- 12.9. Солнечная система как поле центральной силы
- 12.10. Орбиты межпланетных перелетов с минимальными затратами энергии
- 12.11. Использование орбит ожидания при межпланетных полетах
- 12.12. Влияние ошибок на межпланетные орбиты
- Задачи
- Глава 13. Определение орбит и межпланетная навигация
- 13.2. Теория определения орбит
- 13.3. Метод Лапласа
- 13.4. Метод Гаусса
- 13.5. Метод Ольберса для параболических орбит
- 13.6. Определение орбит при наличии дополнительных данных наблюдений
- 13.7. Улучшение орбит
- 13.8. Межпланетная навигация
- 13.8.1. Стабилизированные платформы и акселерометры
- 13.8.2. Навигация при помощи бортовой оптической аппаратуры
- 13.8.3. Методы наблюдений и достижимая точность
- Литература
- Глава 14. Двойные системы и системы нескольких тел
- 14.2. Визуально-двойные звезды
- 14.3. Соотношение масса—светимость
- 14.4. Динамические параллаксы
- 14.5. Затменные двойные
- 14.6. Спектрально-двойные звезды
- 14.7. Обзор результатов
- 14.8. Элементы орбиты двойной звезды
- 14.9. Период двойной звезды
- 14.10. Движение апсид
- 14.11. Силы, действующие в двойной системе
- 14.12. Тройные системы
- 14.13. Неточность ньютоновского закона тяготения
- 14.14. Фигуры звезд в двойных системах
- 14.15. Пределы Роша
- 14.16. Вещество, окружающее звезды
- 14.17. Образование двойных систем
- Задачи
- Глава 15. Звездные системы многих тел
- 15.2. Сфера действия
- 15.3. Парные сближения
- 15.4. Накапливающийся эффект малых сближений
- 15.5. Некоторые фундаментальные принципы
- 15.6. Основные теоремы звездной динамики
- 15.6.1. Теорема Джинса
- 15.7. Некоторые частные случаи для звездной системы в стационарном состоянии
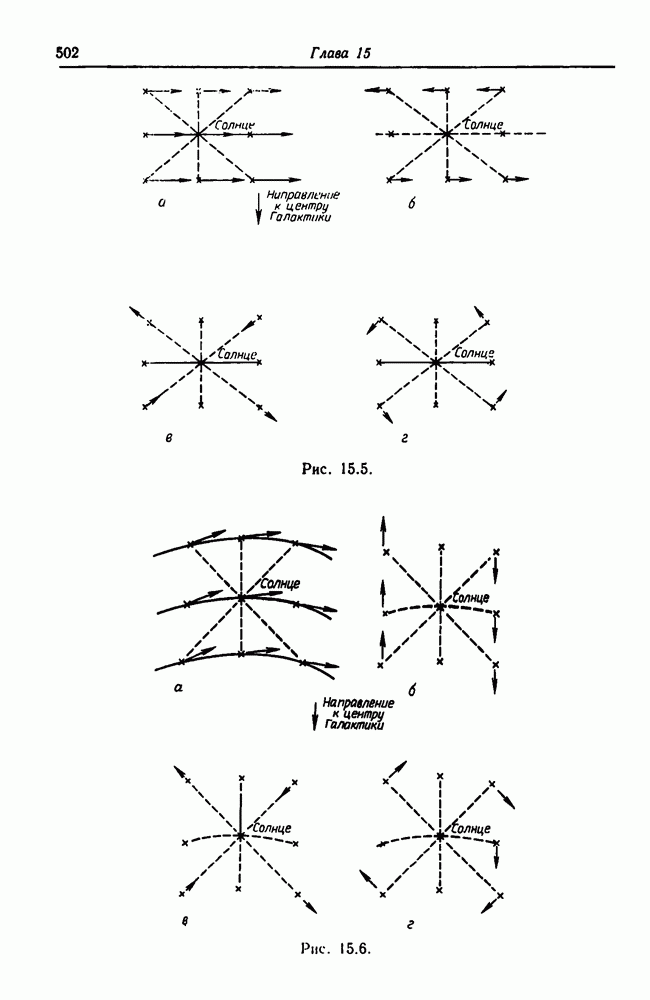
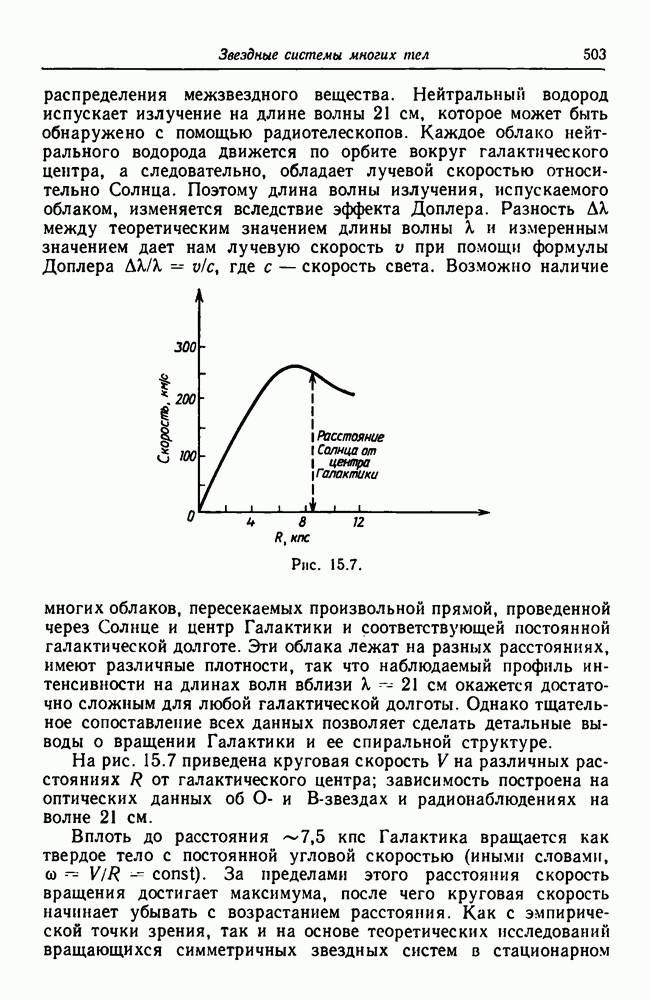
- 15.8. Вращение галактик
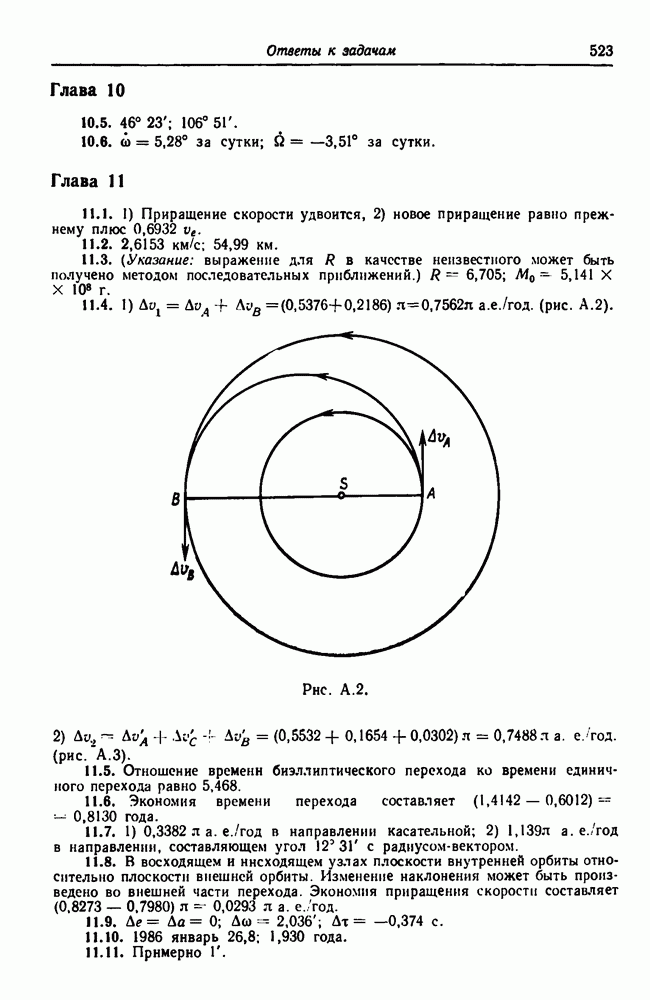
- 15.8.2. Период вращения и угловая скорость Галактики
- 15.8.3. Масса Галактики
- 15.8.4. Общий характер вращения Галактики
- 15.8.5. Галактические орбиты звезд
- 15.8.6. Звезды с высокими скоростями
- 15.9. Сферические звездные системы
- 15.9.1. Применение теоремы вириала к сферической системе
- 15.9.2. Орбиты звезд в сферической системе
- 15.9.3. Распределение орбит внутри сферической системы
- 15.10. Эксперименты на ЭВМ
- Задачи
- Ответы к задачам
- Приложения