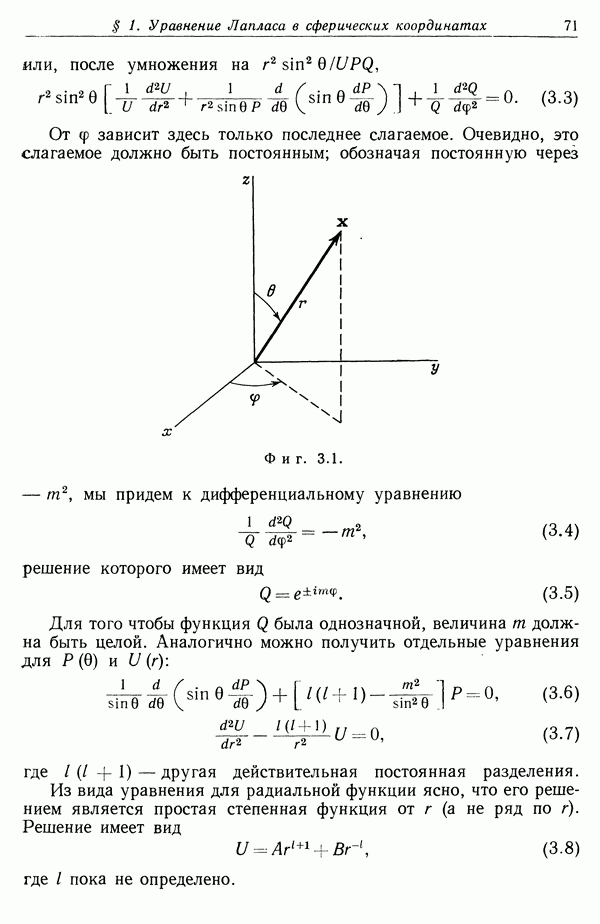
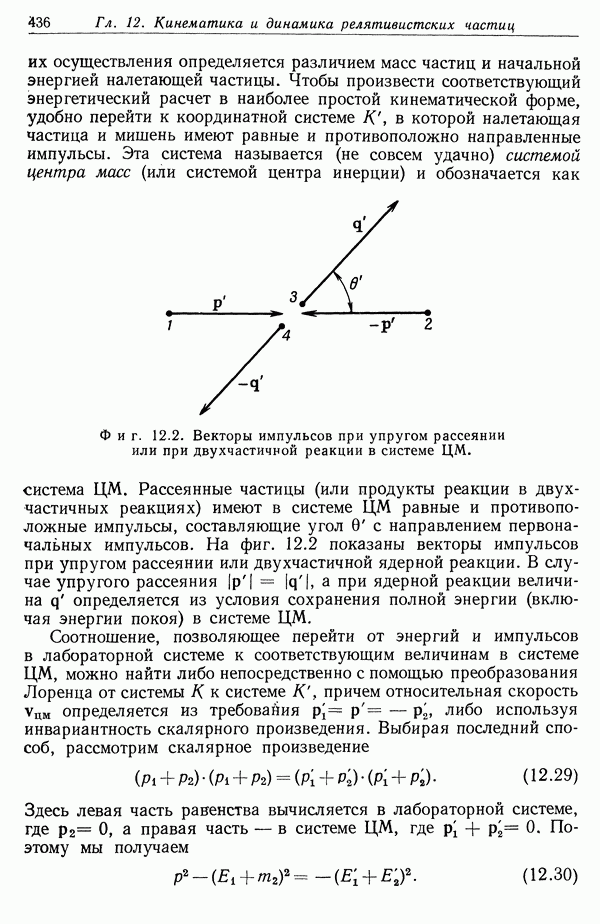
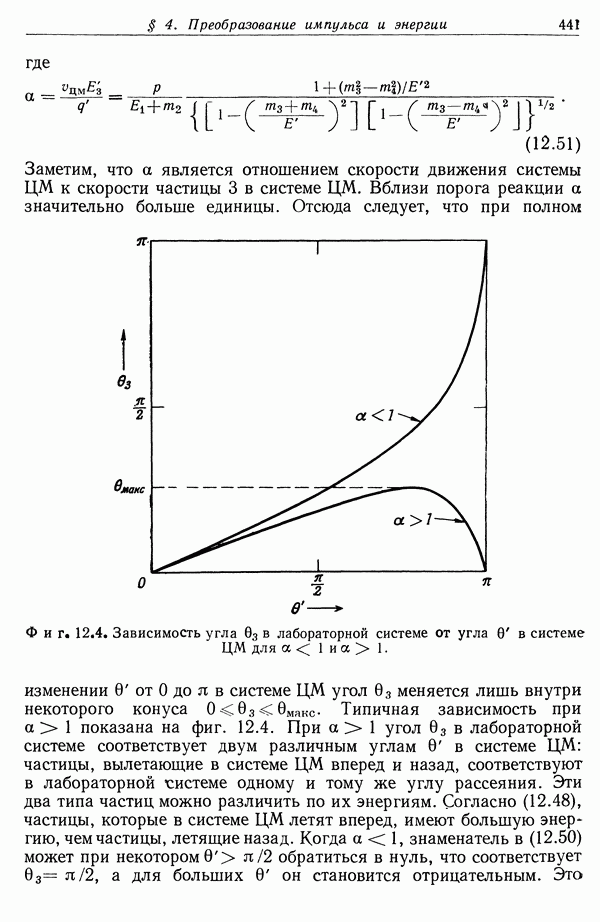
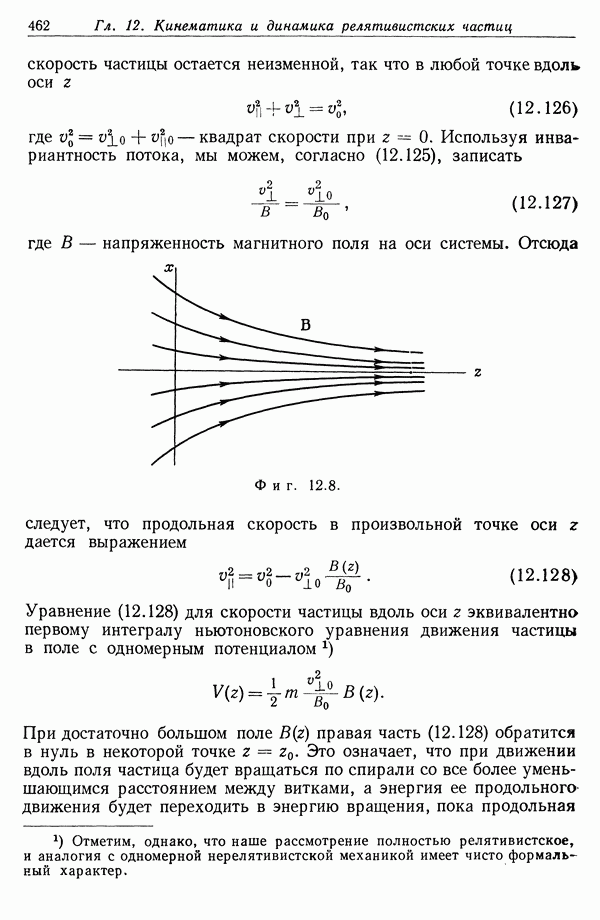
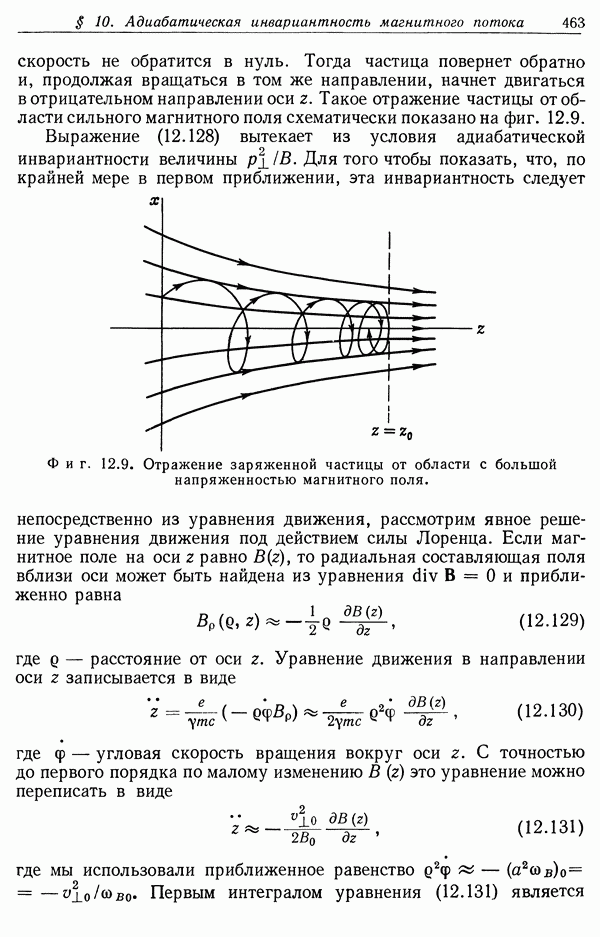
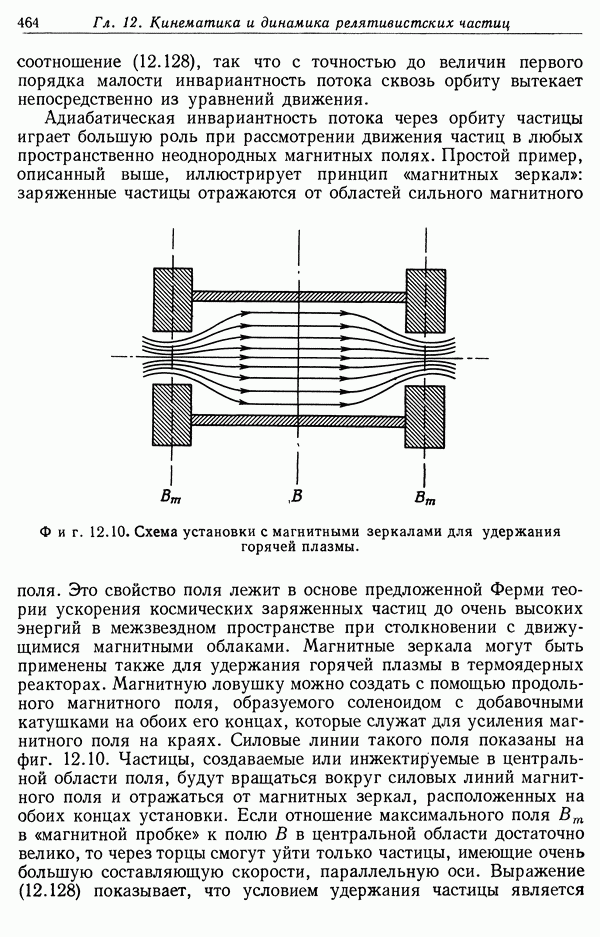
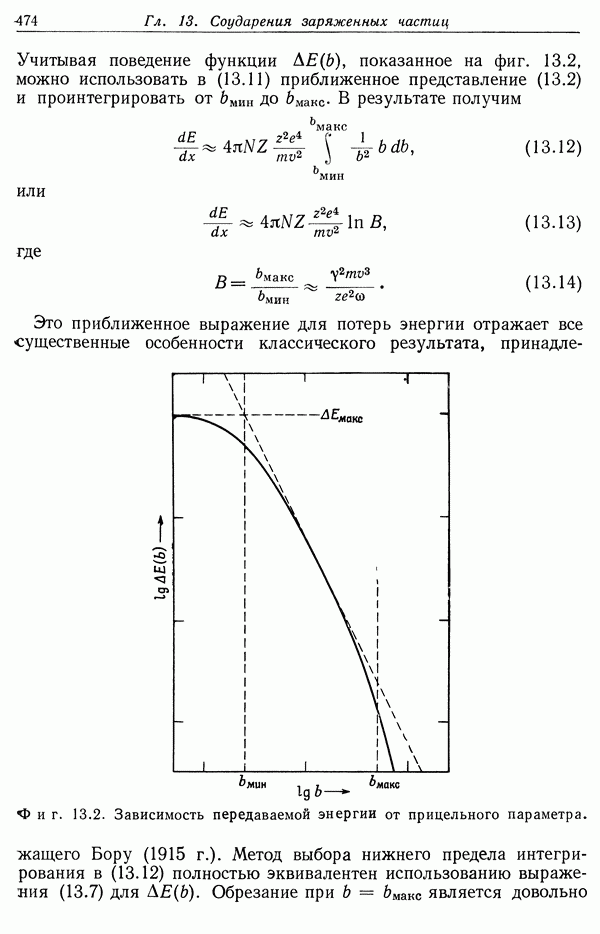
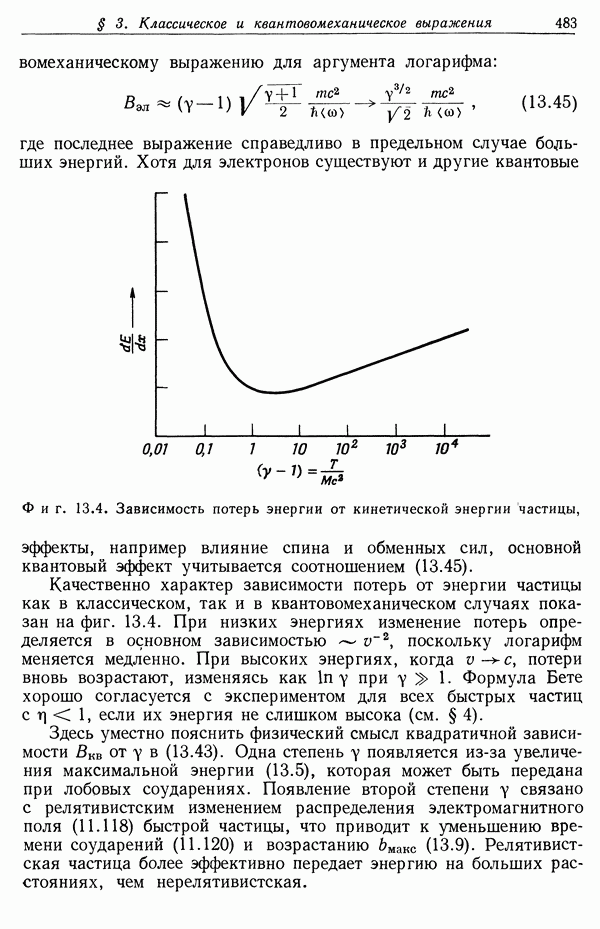
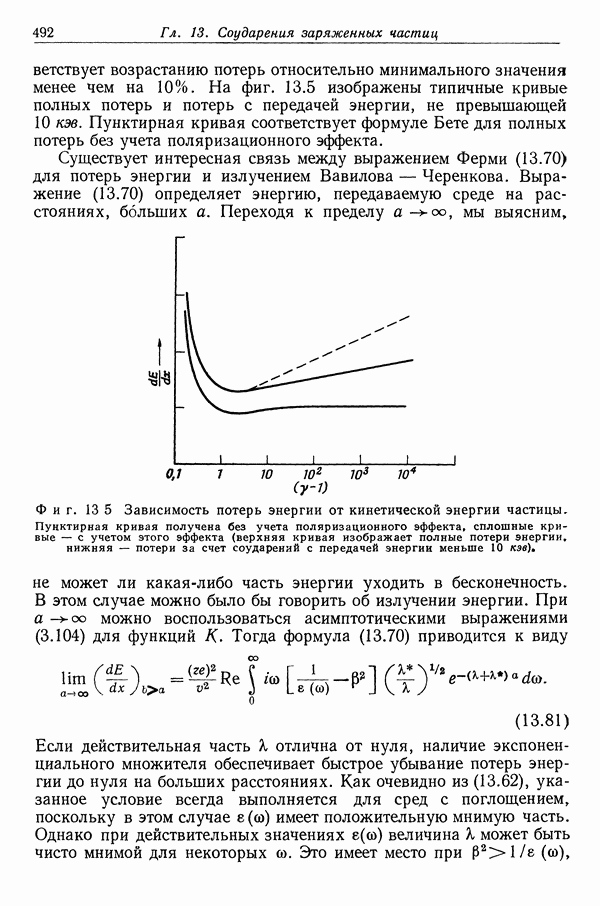
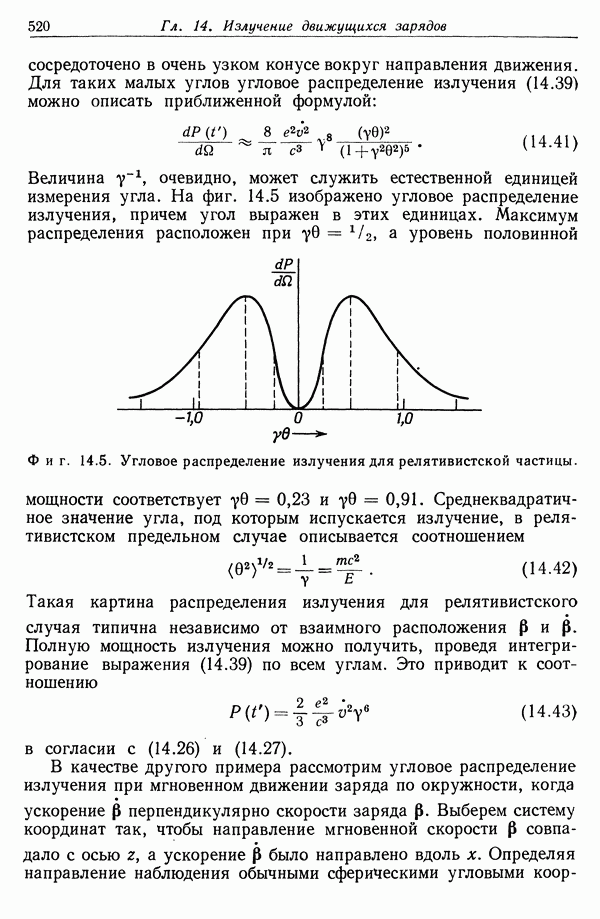
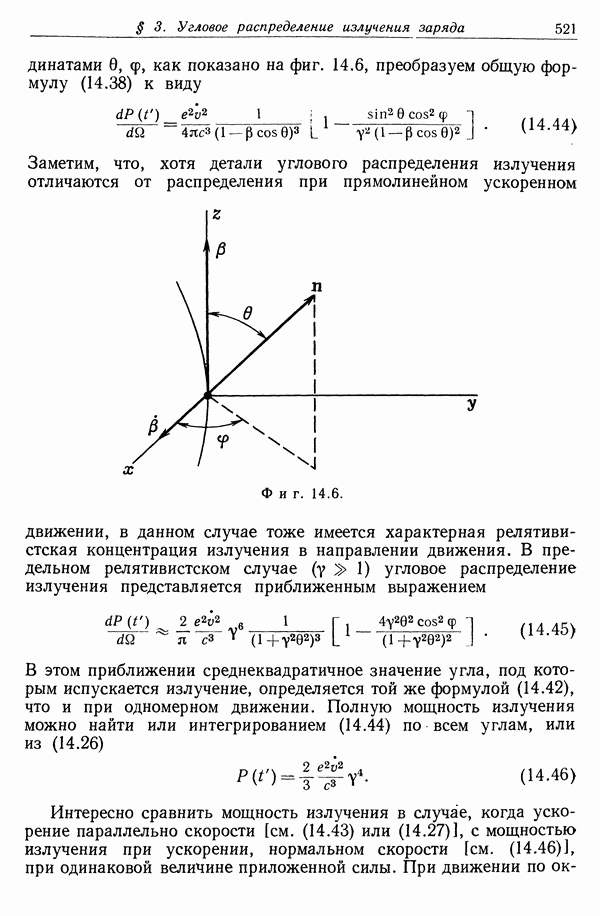
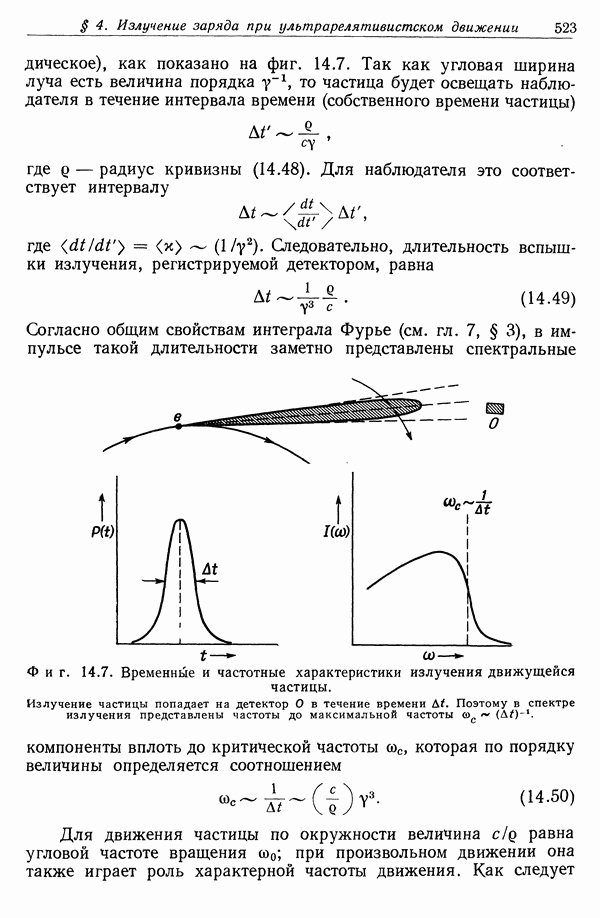
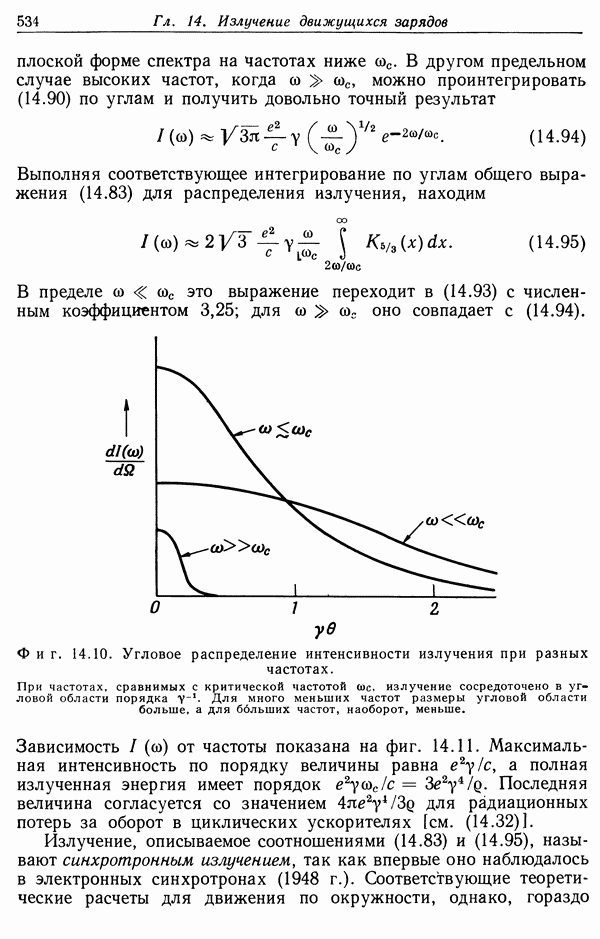
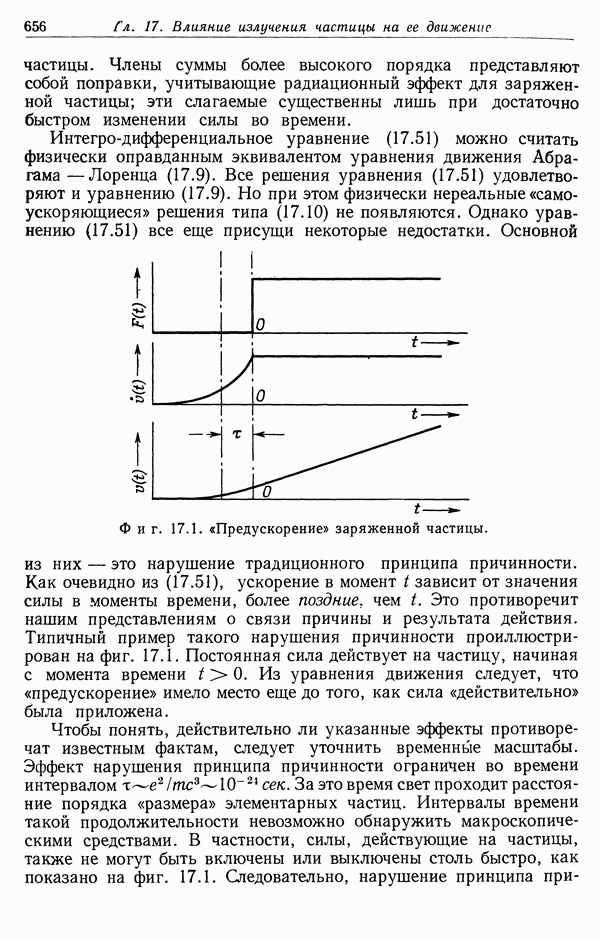
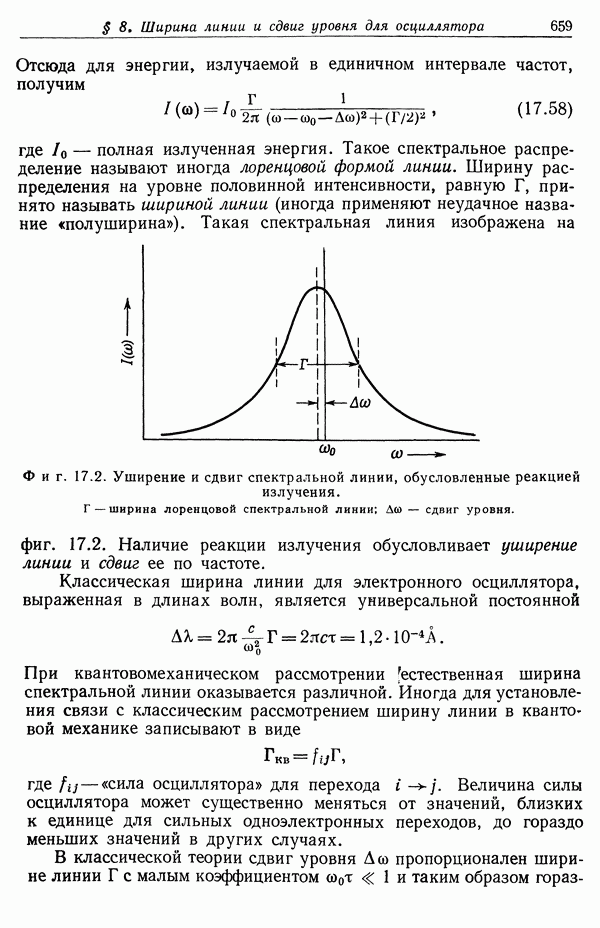
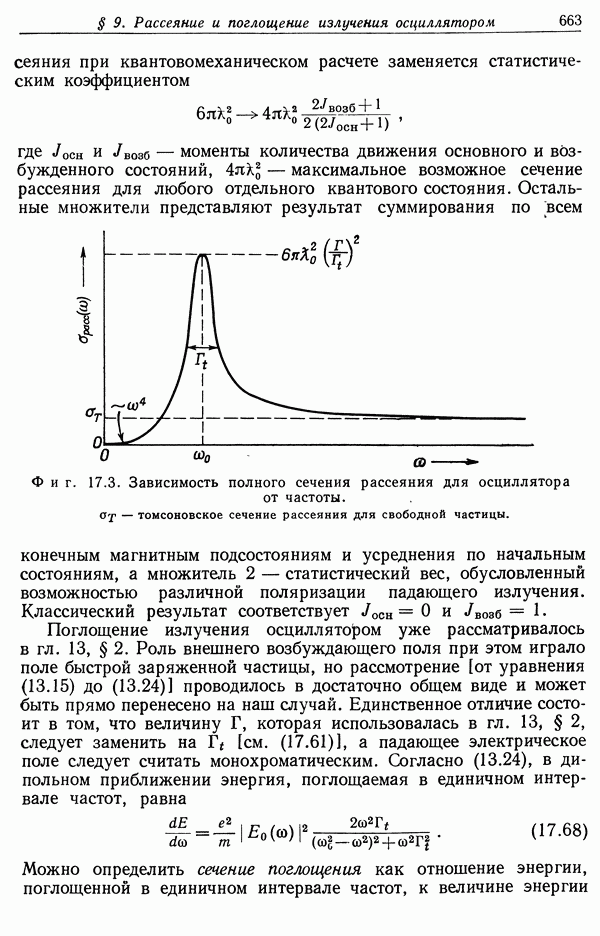
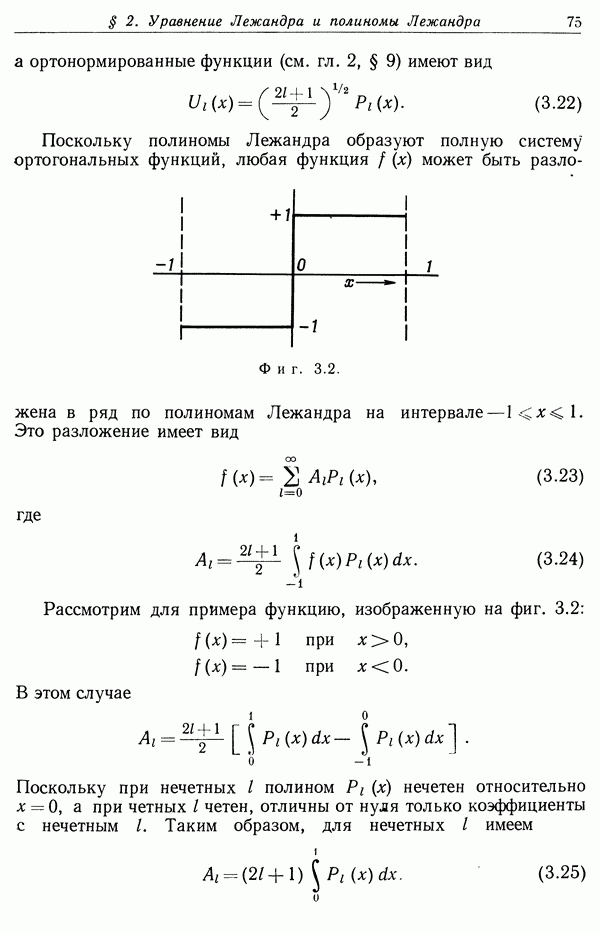| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
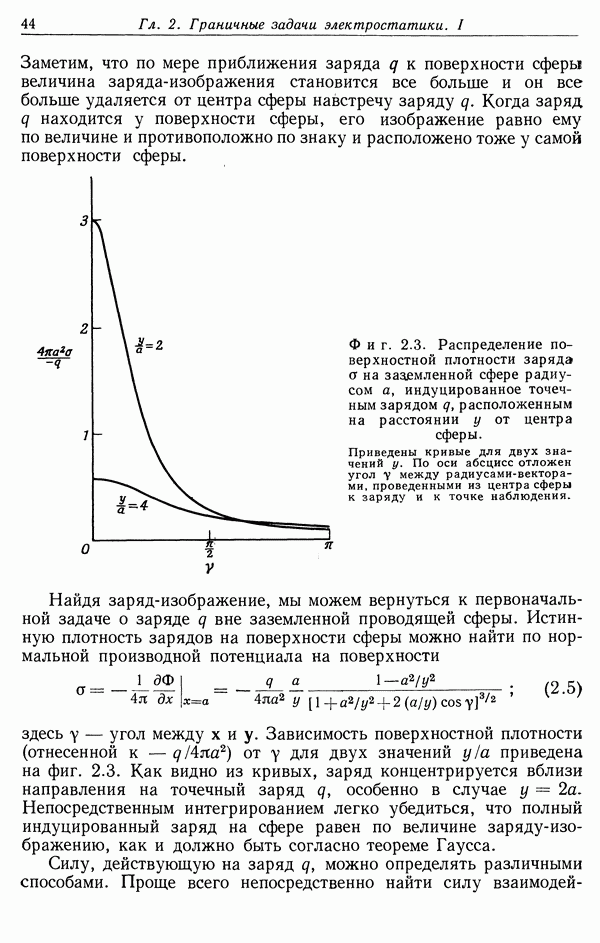
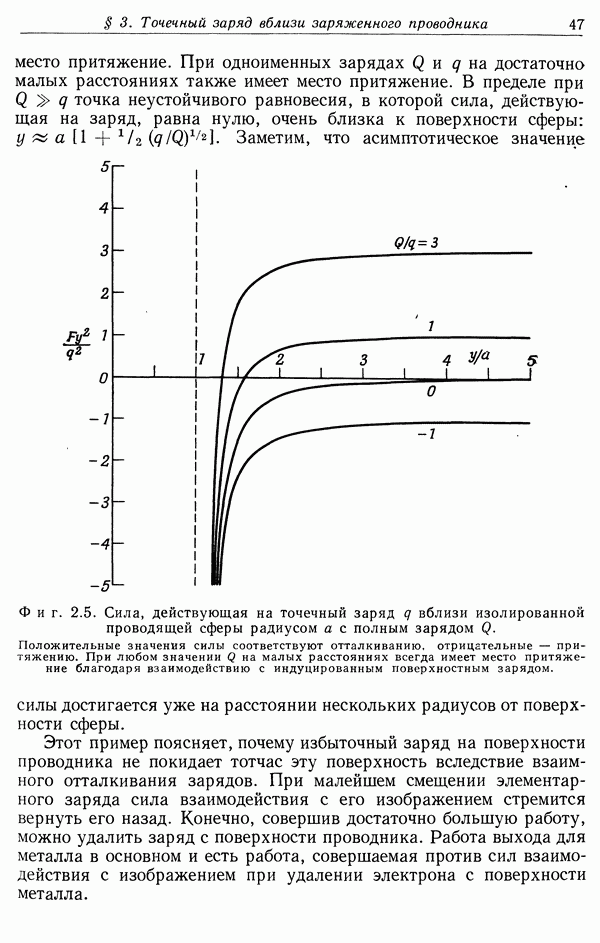
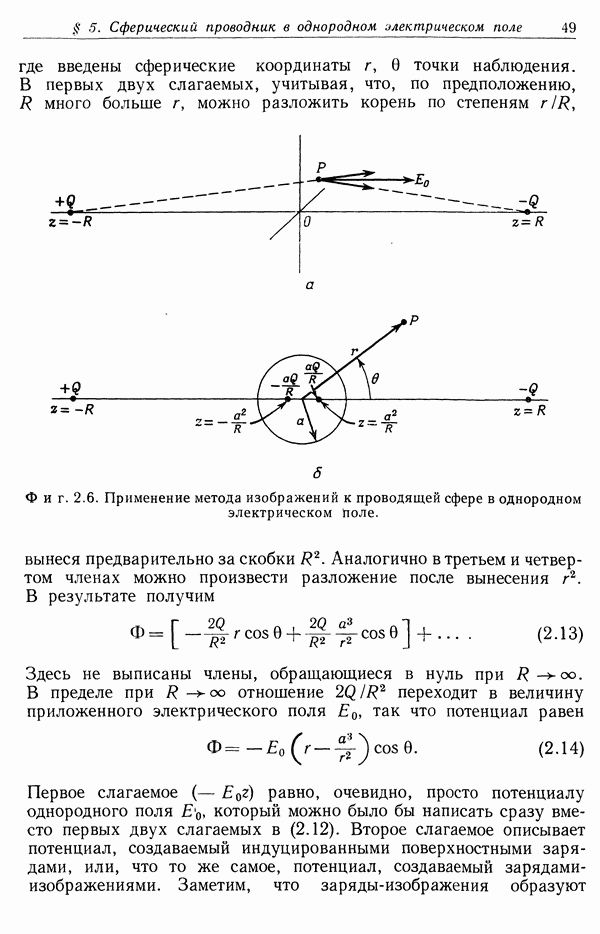
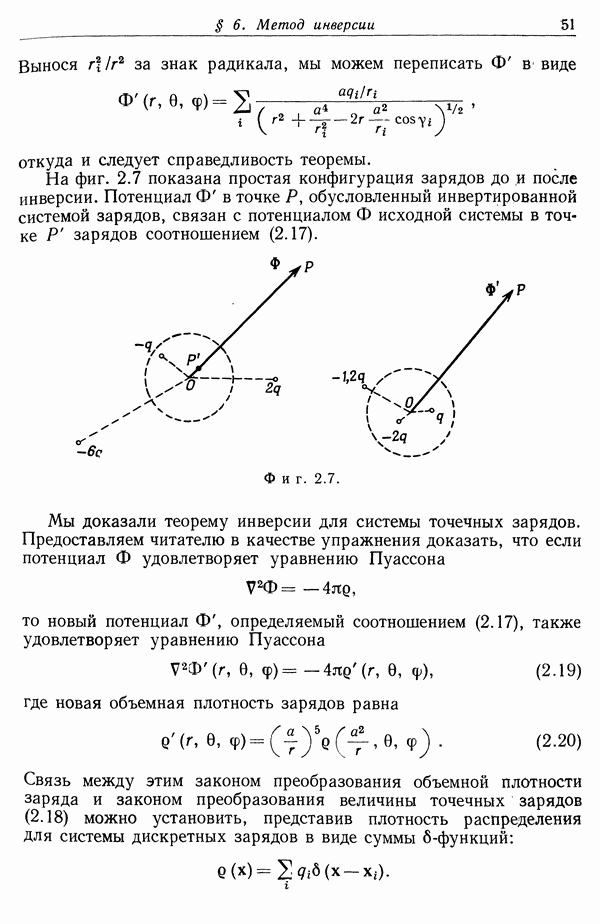
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
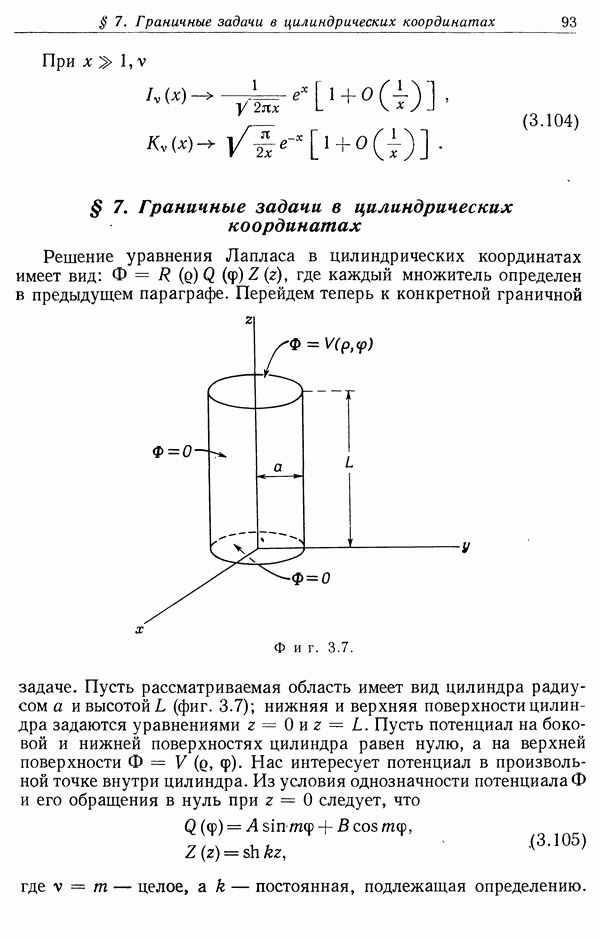
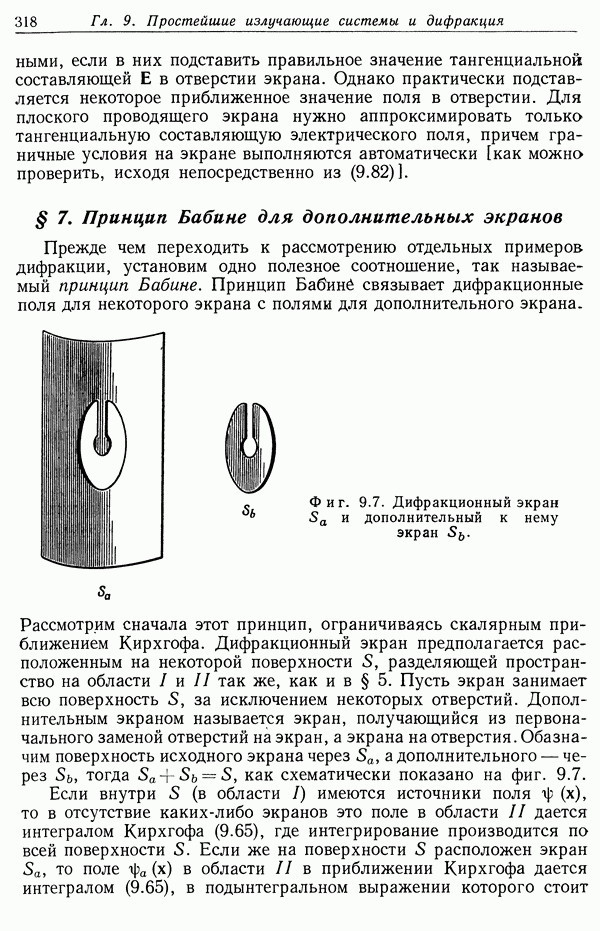
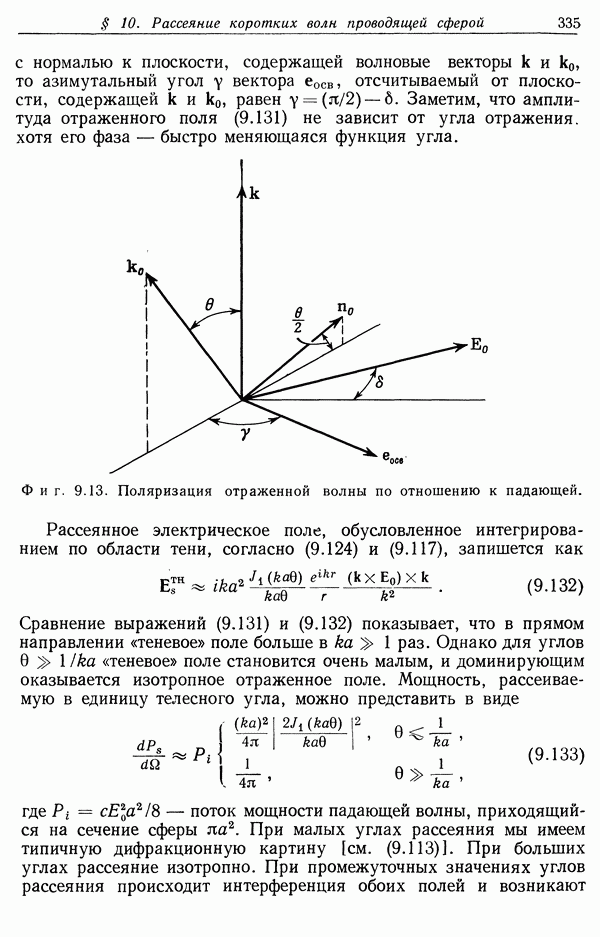
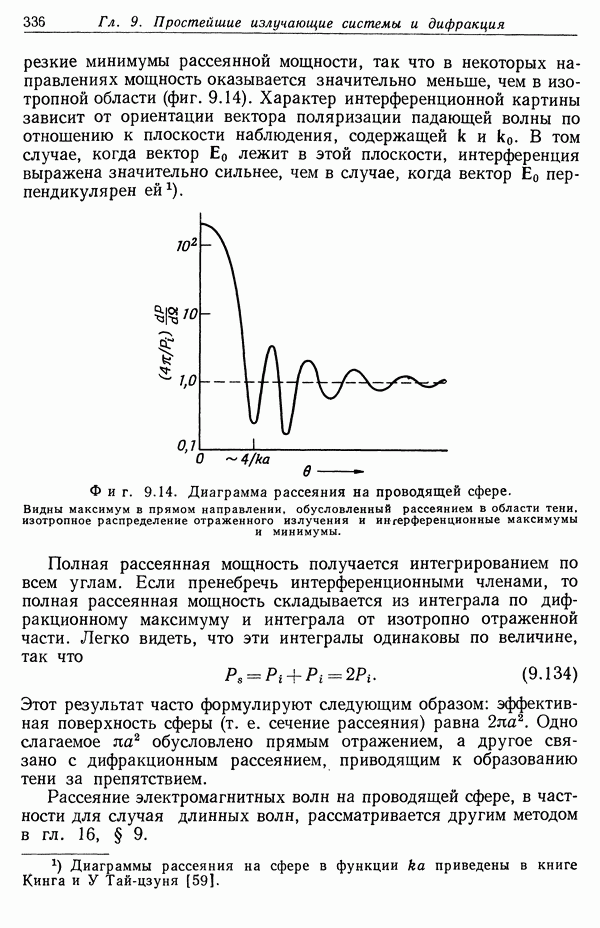
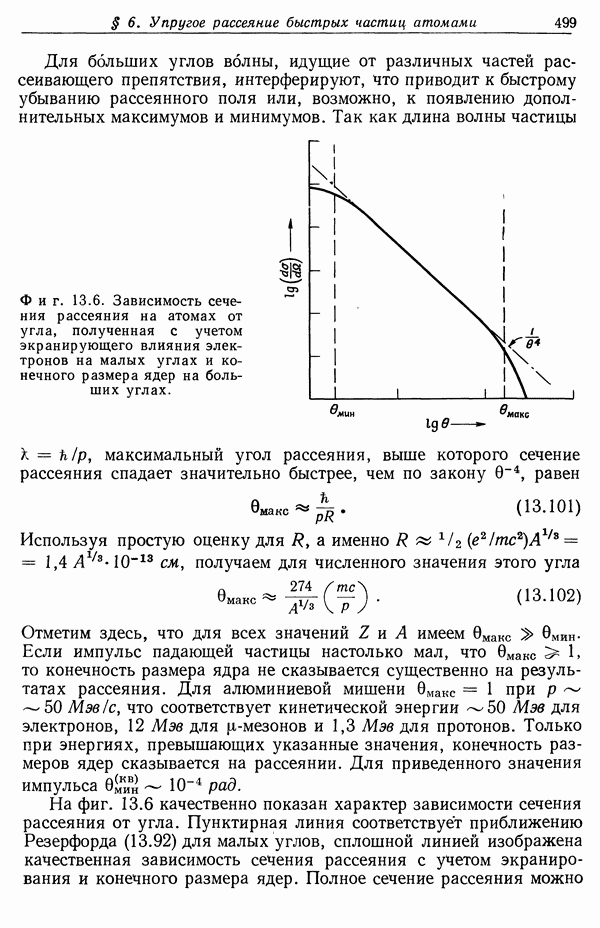
§ 8. Дифракция на круглом отверстии
Начиная с основополагающих работ Кирхгофа, теория дифракции интенсивно развивалась как в оптике, где обычно достаточно ограничиться скалярной теорией, основанной на выражении (9.65), так и в применении к микроволновому излучению, где необходимо более строгое рассмотрение. Целый ряд монографий посвящен исключительно вопросам дифракции и рассеяния волн. Мы рассмотрим здесь несколько примеров, иллюстрирующих применение скалярной и векторной теорем (9.65) и (9.82), и сравним точность различных приближенных методов расчета.
Дифракционные явления принято разделять на дифракцию Френеля и дифракцию Фраунгофера в зависимости от расстояния точки наблюдения от дифракционной системы. Обычно дифракционная система (например, отверстие в непрозрачном экране) имеет размеры, сравнимые с длиной волны или превышающие ее. При этом точка наблюдения может находиться в близкой зоне, т. е. на расстоянии меньше длины волны от дифракционной системы. Поля в ближней
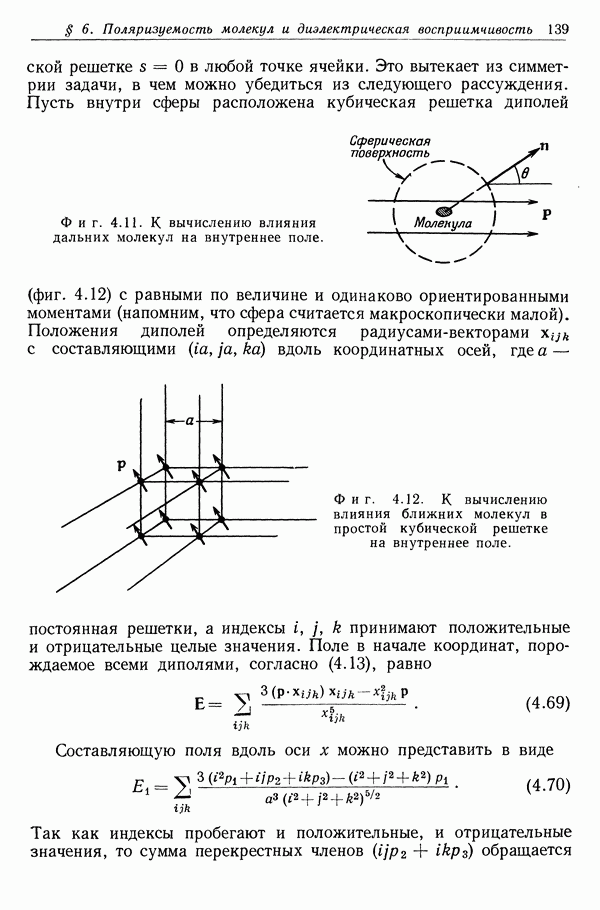
зоне имеют весьма сложную структуру и не представляют особого интереса. Точки, находящиеся на таком расстоянии от дифракционной системы, которое во много раз больше длины волны, но все же меньше или порядка собственных размеров системы, считаются находящимися во френелевской зоне. Область, же, расположенная на расстоянии, которое велико как по сравнению с размерами дифракционной системы, так и по сравнению с длиной волны, называется фраунгоферовой зоной.

Фиг. 9.9.
Она соответствует волновой зоне, определенной в § 1 этой главы. Дифракционные картины в зонах Френеля и Фраунгофера существенно различаются, поскольку в дифракции Френеля наибольшую роль играют участки дифракционной системы, ближайшие к точке наблюдения, в то время как в дифракцию Фраунгофера вносит свой вклад вся система в целом. Мы будем рассматривать только фраунгоферову дифракцию; примеры дифракции Френеля будут даны в задачах в конце главы.
Если точка наблюдения находится далеко от дифракционной системы, то мы можем воспользоваться разложением (9.6) для  Сохраняя только члены низшего порядка по
Сохраняя только члены низшего порядка по  представим скалярный интеграл Кирхгофа (9.65) в виде
представим скалярный интеграл Кирхгофа (9.65) в виде

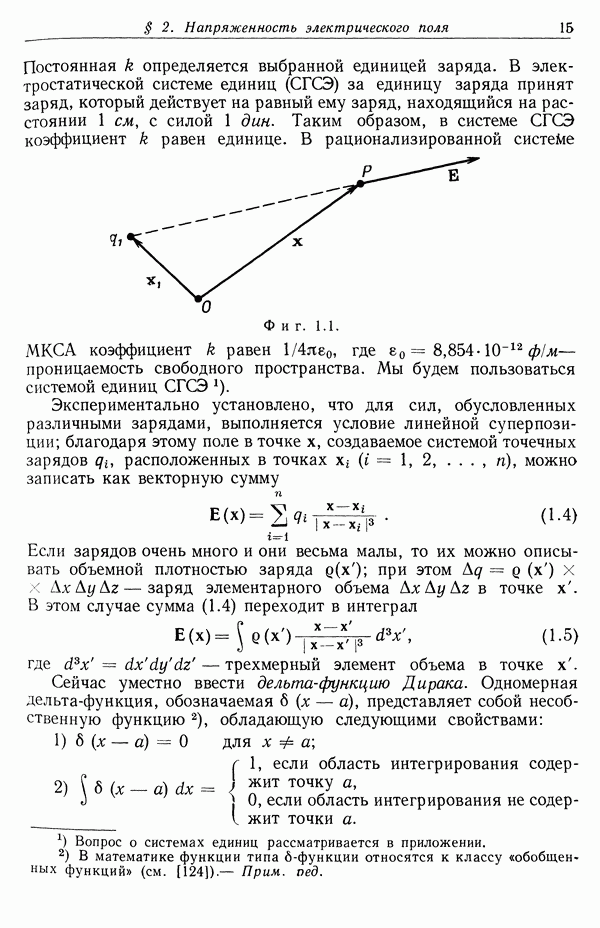
где x — координата элемента поверхности  ;
;  — длина вектора
— длина вектора  соединяющего начало координат О с точкой наблюдения
соединяющего начало координат О с точкой наблюдения  волновой вектор, направленный в точку наблюдения (фиг. 9.9). Для плоской поверхности векторное выражение (9.82) в этом приближении принимает вид
волновой вектор, направленный в точку наблюдения (фиг. 9.9). Для плоской поверхности векторное выражение (9.82) в этом приближении принимает вид

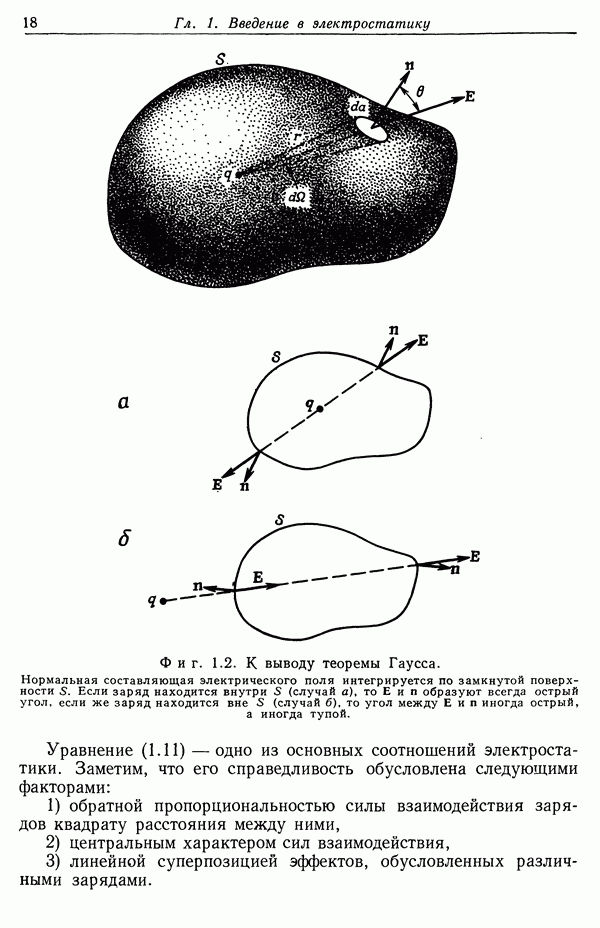
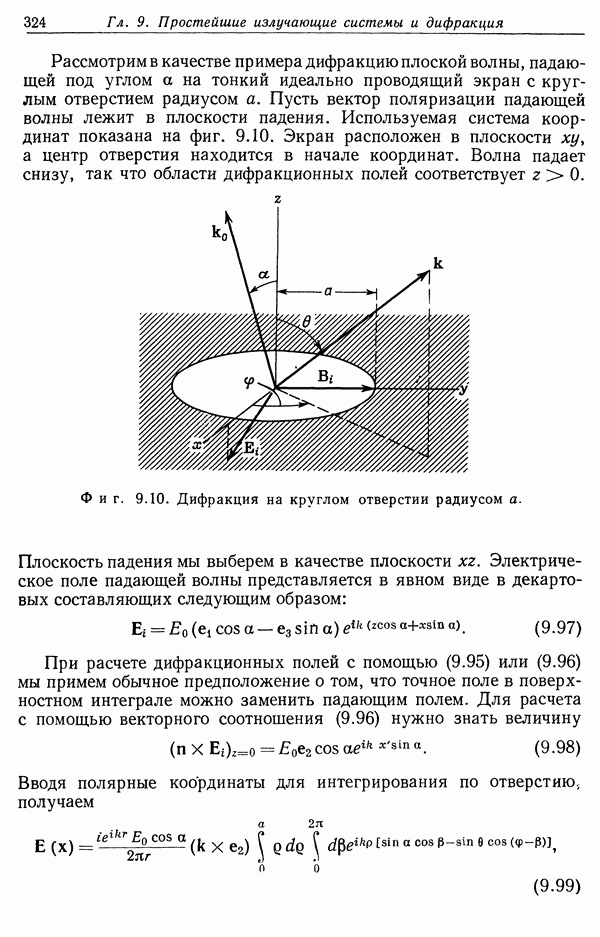
Рассмотрим в качестве примера дифракцию плоской волны, падающей под углом а на тонкий идеально проводящий экран с круглым отверстием радиусом а. Пусть вектор поляризации падающей волны лежит в плоскости падения. Используемая система координат показана на фиг. 9.10. Экран расположен в плоскости  а центр отверстия находится в начале координат. Волна падает снизу, так что области дифракционных полей соответствует
а центр отверстия находится в начале координат. Волна падает снизу, так что области дифракционных полей соответствует 

Фиг. 9.10. Дифракция на круглом отверстии радиусом а.
Плоскость падения мы выберем в качестве плоскости  Электрическое поле падающей волны представляется в явном виде в декартовых составляющих следующим образом:
Электрическое поле падающей волны представляется в явном виде в декартовых составляющих следующим образом:

При расчете дифракционных полей с помощью (9.95) или (9.96) мы примем обычное предположение о том, что точное поле в поверхностном интеграле можно заменить падающим полем. Для расчета с помощью векторного соотношения (9.96) нужно знать величину

Вводя полярные координаты для интегрирования по отверстию, получаем

где  угловые координаты вектора к. Если ввести угловую функцию
угловые координаты вектора к. Если ввести угловую функцию
 (9.100)
(9.100)
то интеграл по углам запишется в виде
 (9.101)
(9.101)
После этого интеграл по радиусу легко вычисляется. В результате получим электрическое поле в векторном приближении Кирхгофа
 (9.102)
(9.102)
Средняя мощность, излучаемая в единичный телесный угол, равна

где величина
 (9.104)
(9.104)
представляет собой полную мощность, падающую на отверстие. Если отверстие велико по сравнению с длиной волны  , то множитель
, то множитель  имеет острый максимум при
имеет острый максимум при  равный единице, и быстро падает до нуля (с маленькими вторичными максимумами) в области
равный единице, и быстро падает до нуля (с маленькими вторичными максимумами) в области  в обе стороны от направления
в обе стороны от направления  Это значит, что поле в основном проходит через отверстие в соответствии с законами геометрической оптики; дифракционные эффекты очень слабы. При
Это значит, что поле в основном проходит через отверстие в соответствии с законами геометрической оптики; дифракционные эффекты очень слабы. При  бесселева функция сравнительно медленно меняется с углом, и проходящая волна распространяется в направлениях, весьма отличных от направления падения. При
бесселева функция сравнительно медленно меняется с углом, и проходящая волна распространяется в направлениях, весьма отличных от направления падения. При  угловое распределение полностью определяется множителем (к
угловое распределение полностью определяется множителем (к  ) в (9.102). Но в этом предельном случае замена истинного поля в отверстии невозмущенным является слишком грубым приближением.
) в (9.102). Но в этом предельном случае замена истинного поля в отверстии невозмущенным является слишком грубым приближением.
Полная проходящая мощность получается интегрированием выражения (9.103) по всем углам в верхней полусфере. Отношение проходящей мощности к падающей называется коэффициентом прохождения
 (9.105)
(9.105)
В предельных случаях  коэффициенты прохождения стремятся к значениям
коэффициенты прохождения стремятся к значениям
 (9-106)
(9-106)
Предельное значение для случая длинных волн  в силу сделанных допущений представляется сомнительным, но во всяком случае из него следует, что коэффициент прохождения для малых отверстий весьма мал. Для случая нормального падения
в силу сделанных допущений представляется сомнительным, но во всяком случае из него следует, что коэффициент прохождения для малых отверстий весьма мал. Для случая нормального падения  коэффициент прохождения (9.105) можно записать в виде
коэффициент прохождения (9.105) можно записать в виде
 (9.107)
(9.107)
С помощью интегральных соотношений

и рекуррентных формул (3.87) и (3.88) коэффициент прохождения можно представить в следующих эквивалентных формах:
 (9.109)
(9.109)
При увеличении  коэффициент прохождения в среднем возрастает с небольшими колебаниями. При
коэффициент прохождения в среднем возрастает с небольшими колебаниями. При  из второго выражения (9.109) можно получить асимптотическое выражение
из второго выражения (9.109) можно получить асимптотическое выражение
 (9.110)
(9.110)
из которого явно видны малые колебания Т. Приближенные выражения (9.109) и (9.110) для коэффициента прохождения характеризуют его общее поведение в зависимости от  однако они не могут претендовать на достаточную точность. Для круглого отверстия был произведен точный расчет, а также развиты более аккуратные приближенные методы. Их сравнение друг с другом проведено
однако они не могут претендовать на достаточную точность. Для круглого отверстия был произведен точный расчет, а также развиты более аккуратные приближенные методы. Их сравнение друг с другом проведено
в книге Кинга и У Тайцзуня [59]. Корректное асимптотическое разложение для коэффициента прохождения не содержит члена  а коэффициент перед
а коэффициент перед  в 2 раза больше.
в 2 раза больше.
Сравним теперь наши результаты для векторного приближения Кирхгофа с обычной скалярной теорией, основанной на выражении (9.95). Для волны, которая падает не по нормали к экрану, сразу возникает вопрос о том, с чем следует отождествить скалярную функцию  Наиболее разумно, по-видимому, выбрать в качестве
Наиболее разумно, по-видимому, выбрать в качестве  величину электрического или магнитного поля. При этом интенсивность излучения будет пропорциональной квадрату абсолютной величины (9.95). Выбрав в качестве
величину электрического или магнитного поля. При этом интенсивность излучения будет пропорциональной квадрату абсолютной величины (9.95). Выбрав в качестве  составляющую Е или В, мы должны дальше решить, будем ли мы сохранять или отбрасывать радиальные составляющие дифрагированных полей при расчете мощности. Полагая функцию равной величине электрического поля Е и вычисляя интеграл в (9.95), получаем скалярный эквивалент соотношения (9.102):
составляющую Е или В, мы должны дальше решить, будем ли мы сохранять или отбрасывать радиальные составляющие дифрагированных полей при расчете мощности. Полагая функцию равной величине электрического поля Е и вычисляя интеграл в (9.95), получаем скалярный эквивалент соотношения (9.102):
 (9.111)
(9.111)
Мощность, излучаемая в единицу телесного угла, равна в скалярном приближении Кирхгофа

где  определяется выражением (9.104).
определяется выражением (9.104).
Сравнение результатов векторного приближения Кирхгофа (9.103) с (9.112) обнаруживает как сходство, так и различие между ними. Обе формулы содержат одинаковый дифракционный множитель  и дают одинаковую зависимость от волнового числа. Однако скалярное выражение в отличие от векторного не имеет азимутальной зависимости (кроме содержащейся в
и дают одинаковую зависимость от волнового числа. Однако скалярное выражение в отличие от векторного не имеет азимутальной зависимости (кроме содержащейся в  ). Азимутальное изменение обусловлено поляризацией поля и поэтому в скалярном приближении отсутствует. Для нормального падения
). Азимутальное изменение обусловлено поляризацией поля и поэтому в скалярном приближении отсутствует. Для нормального падения  и больших отверстий
и больших отверстий  поляризационная зависимость становится несущественной. В этом случае дифрагированные поля сосредоточены в очень малом телесном угле вокруг направления падения и как скалярное, так и векторное приближения приводят к общему выражению
поляризационная зависимость становится несущественной. В этом случае дифрагированные поля сосредоточены в очень малом телесном угле вокруг направления падения и как скалярное, так и векторное приближения приводят к общему выражению

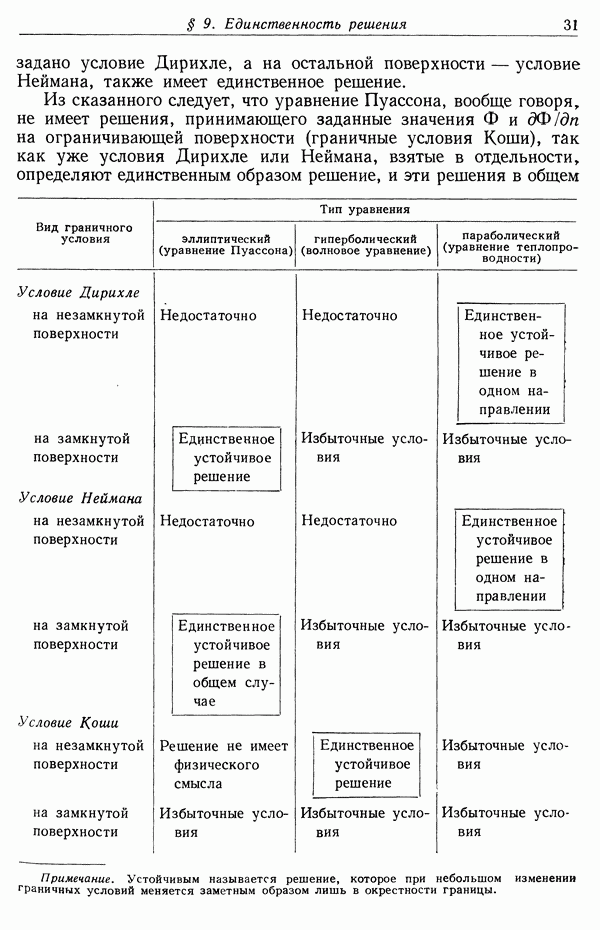
На фиг. 9.11 векторное и скалярное приближения Кирхгофа сравниваются для угла падения 45° и диаметра отверстия, равного длине волны  Показано угловое распределение мощности излучения в плоскости падения (содержащей вектор электрического
Показано угловое распределение мощности излучения в плоскости падения (содержащей вектор электрического
поля падающей волны) и в перпендикулярной плоскости. Сплошная кривая дает векторное приближение для каждого случая, пунктирная — скалярное; из кривых видно, что при  между этими двумя приближениями имеется значительное различие.
между этими двумя приближениями имеется значительное различие.

Фиг. 9.11. Дифракция Фраунгофера на круглом отверстии диаметром в одну длину волны в тонком плоском проводящем экране. Плоская волна падает на экран под углом 45°. Сплошные линии соответствуют векторному приближению Кирхгофа, пунктирные — скалярному приближению. а — распределение интенсивности в плоскости падения (Е — плоскость);  — распределение интенсивности (увеличенное в 2,5 раза) в плоскости, перпендикулярной плоскости падения (В — плоскость).
— распределение интенсивности (увеличенное в 2,5 раза) в плоскости, перпендикулярной плоскости падения (В — плоскость).
Есть основания считать, что результаты векторного приближения Кирхгофа близки к точным, несмотря на то что при  приближение уже становится некорректным. Векторное приближение для прямоугольного отверстия удивительно хорошо согласуется с точным расчетом вплоть до
приближение уже становится некорректным. Векторное приближение для прямоугольного отверстия удивительно хорошо согласуется с точным расчетом вплоть до 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
- § 2. Напряженность электрического поля
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
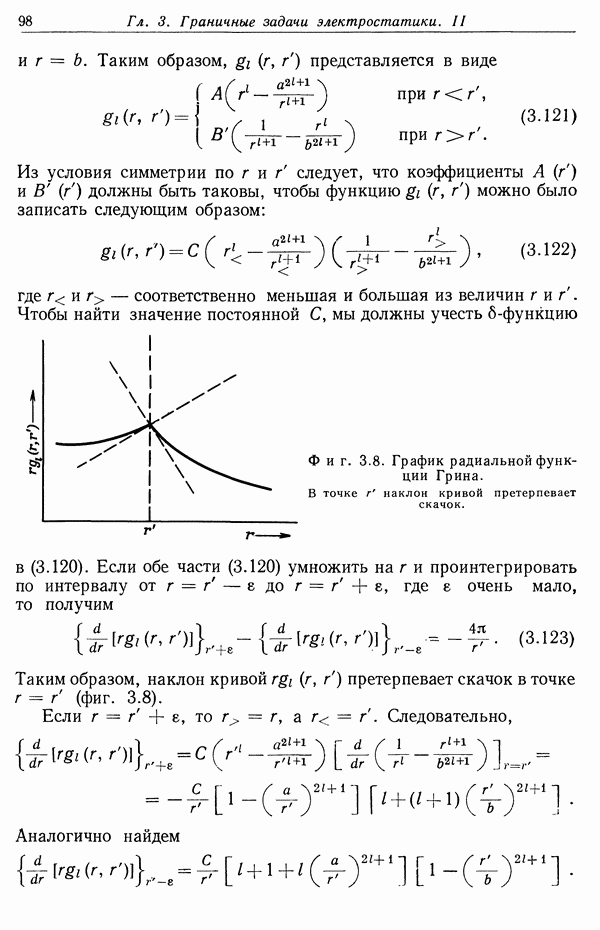
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
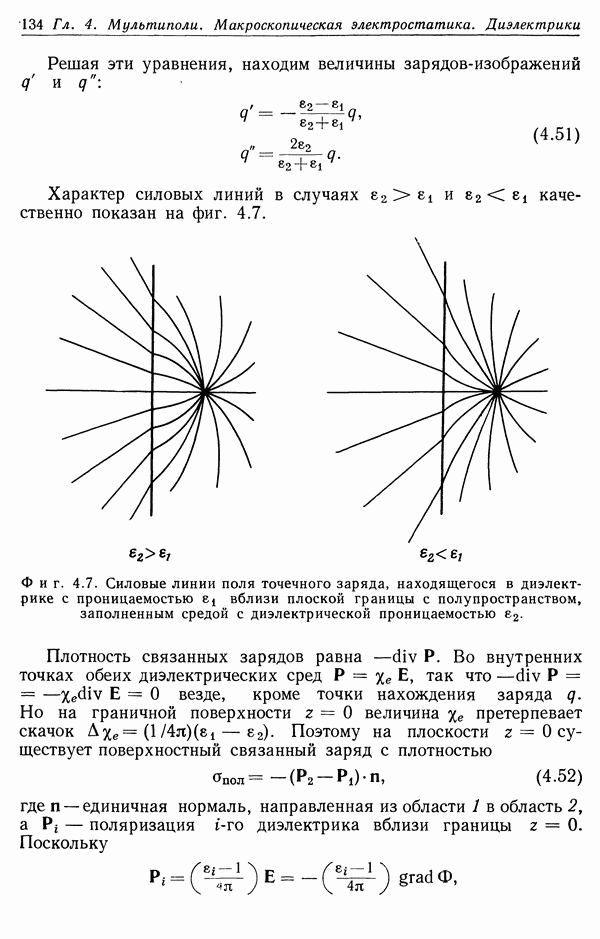
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
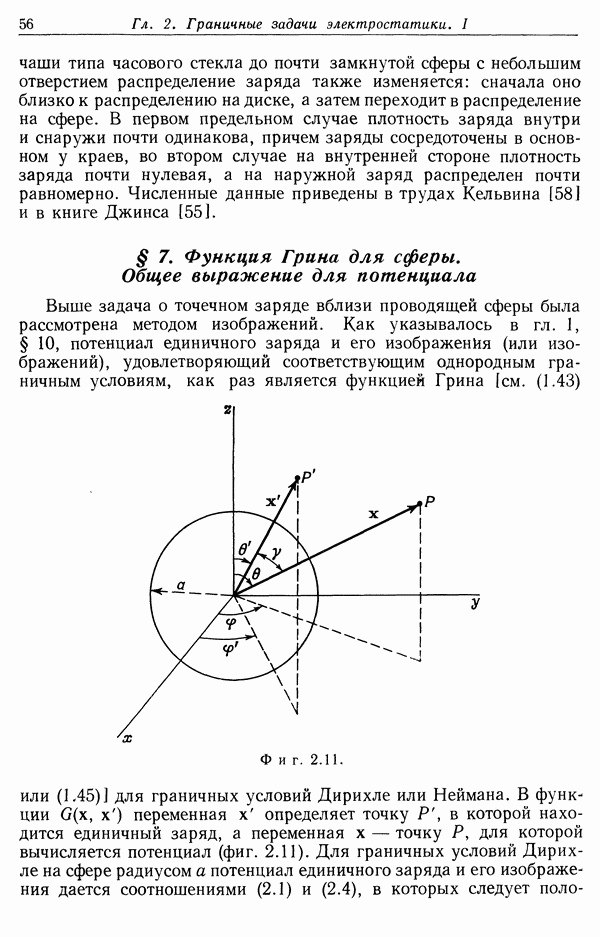
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
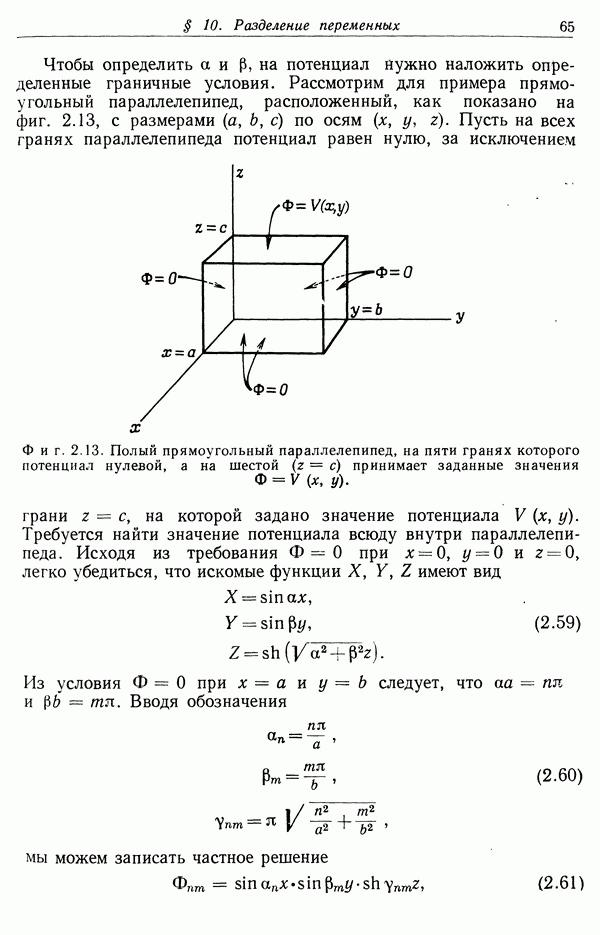
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
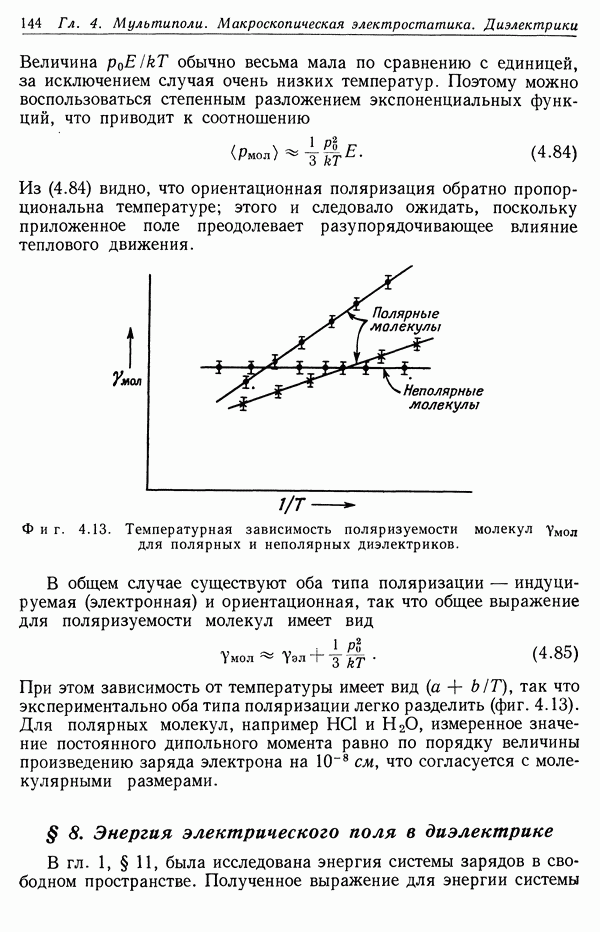
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
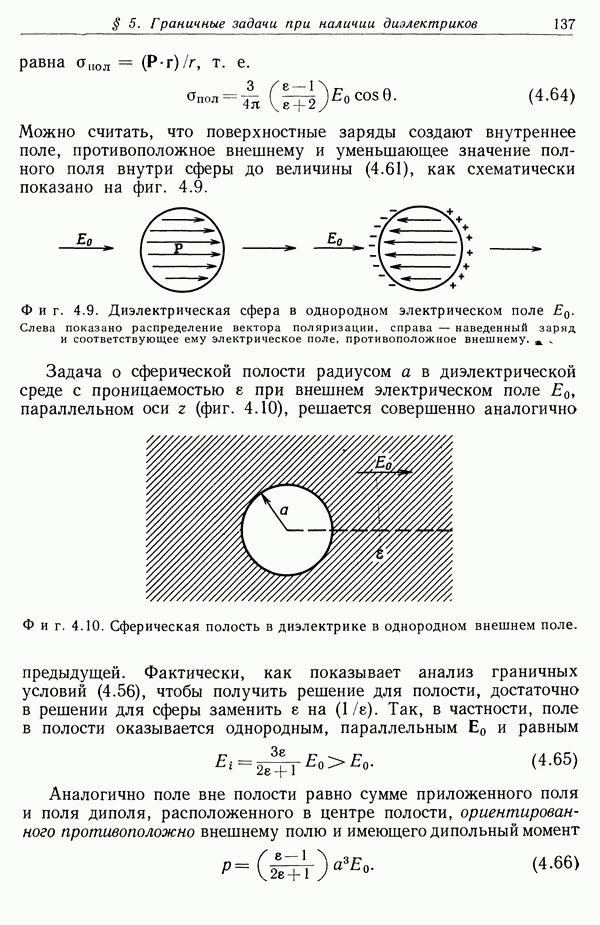
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
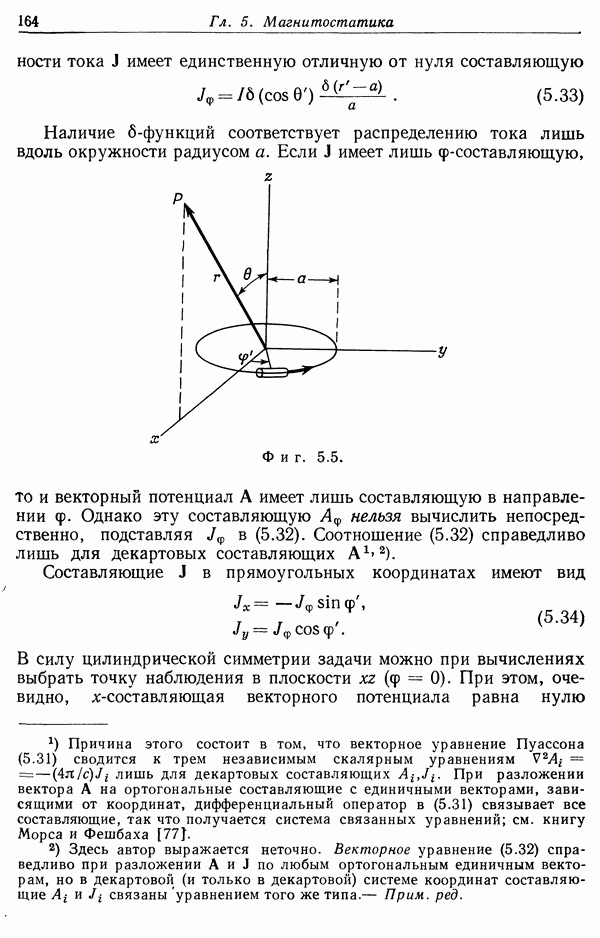
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
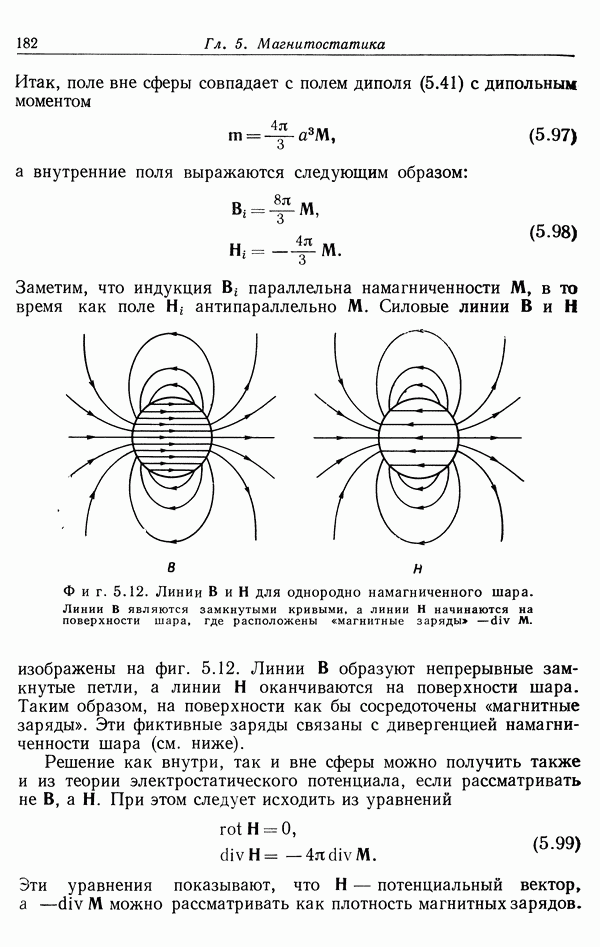
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 2. Линейная и круговая поляризация
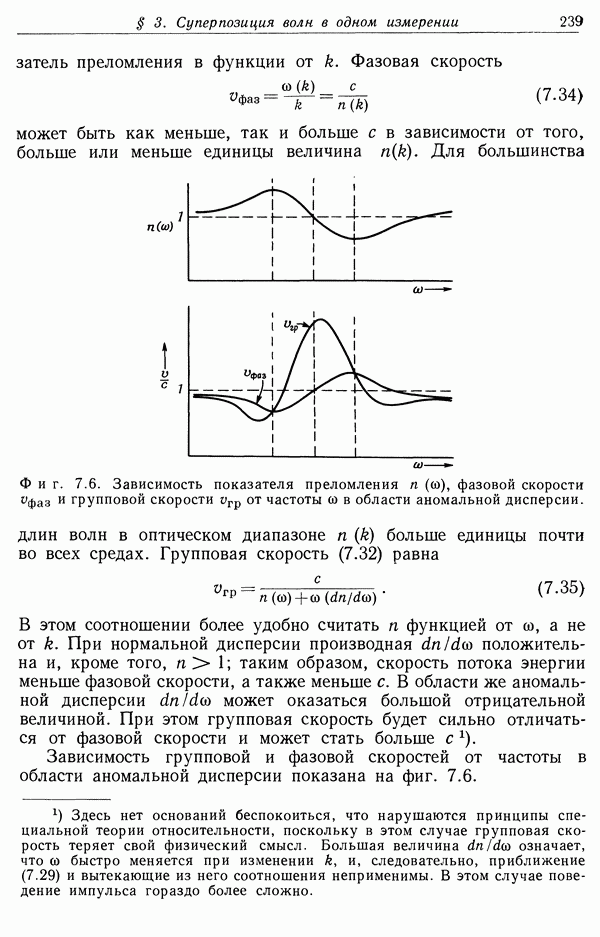
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
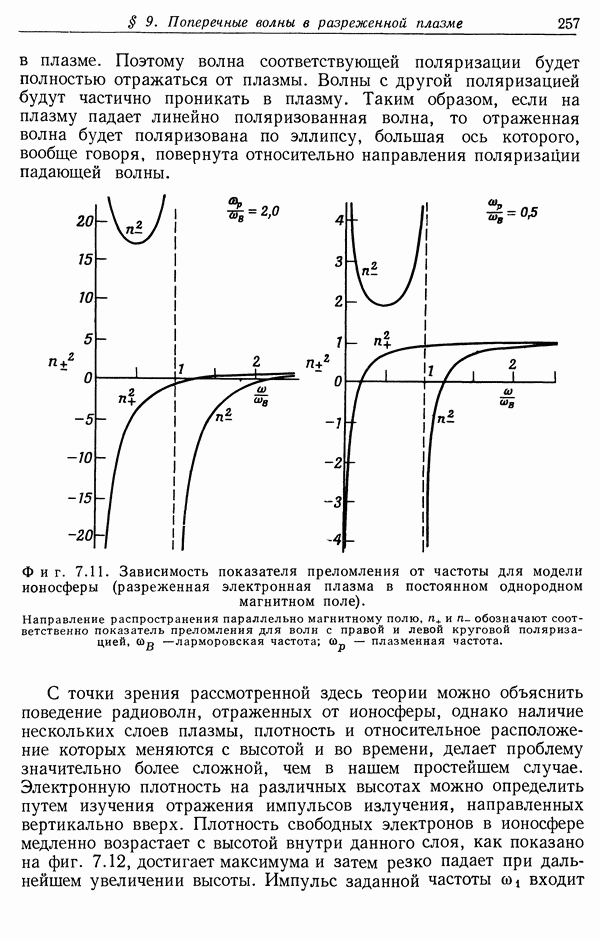
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
- § 7. Принцип Бабине для дополнительных экранов
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
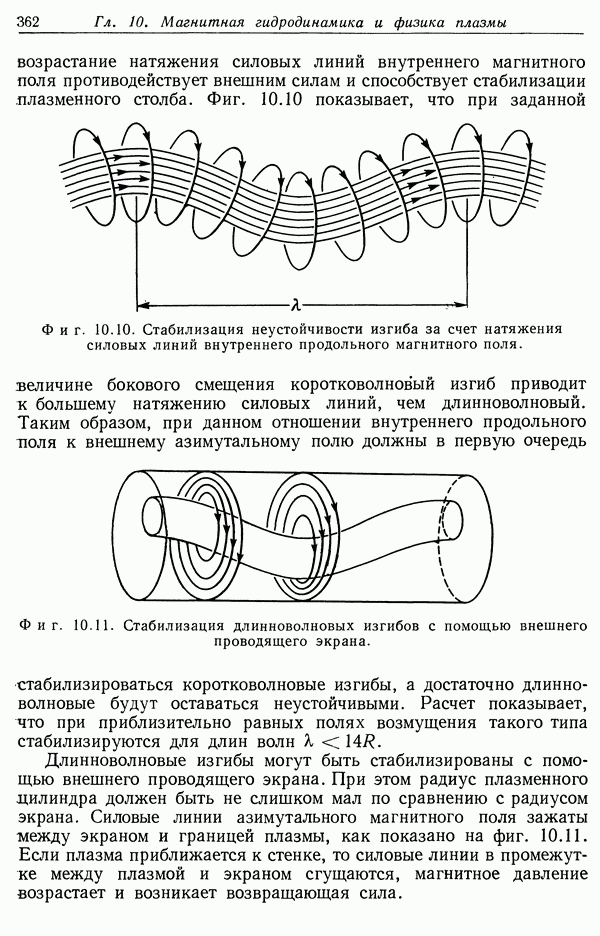
- § 7. Неустойчивости сжатого плазменного столба
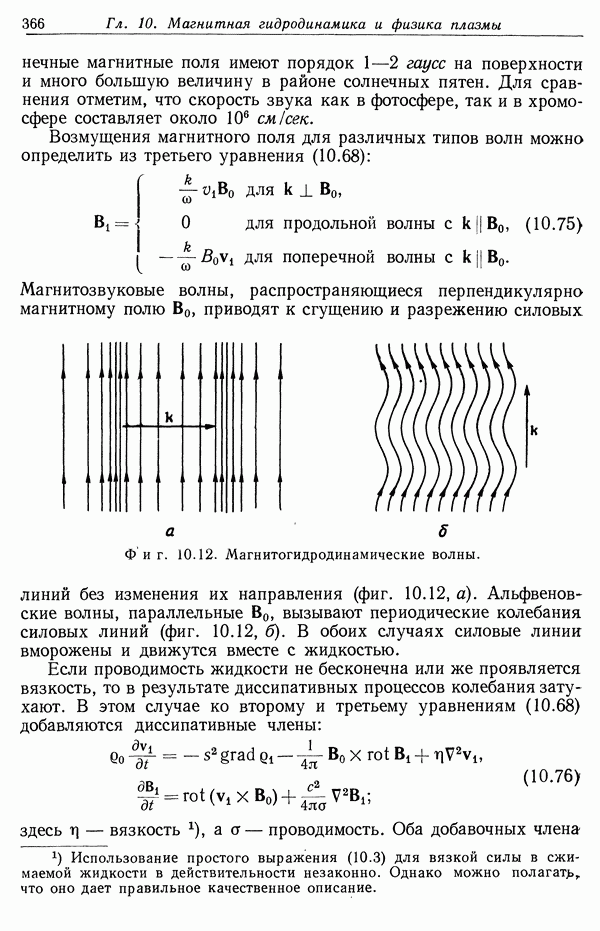
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
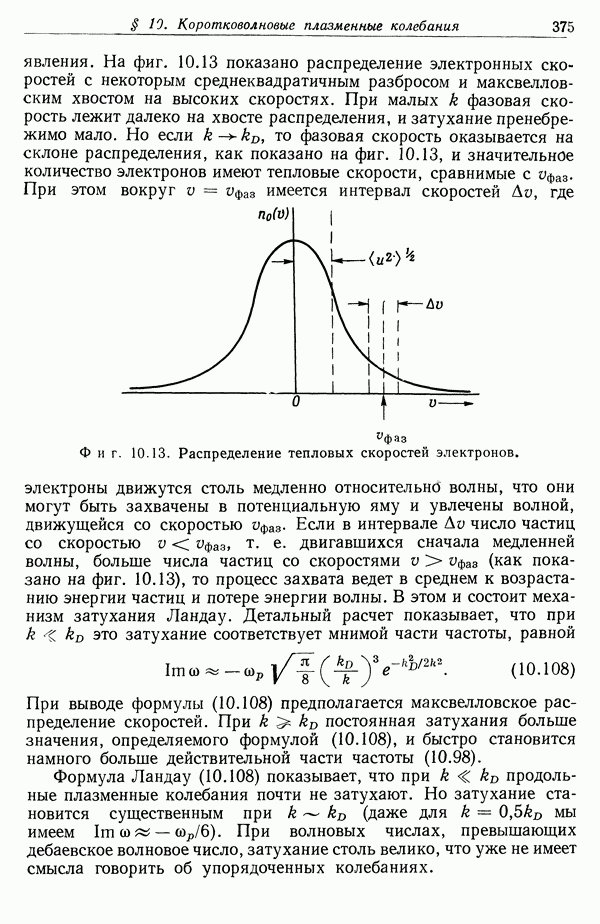
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
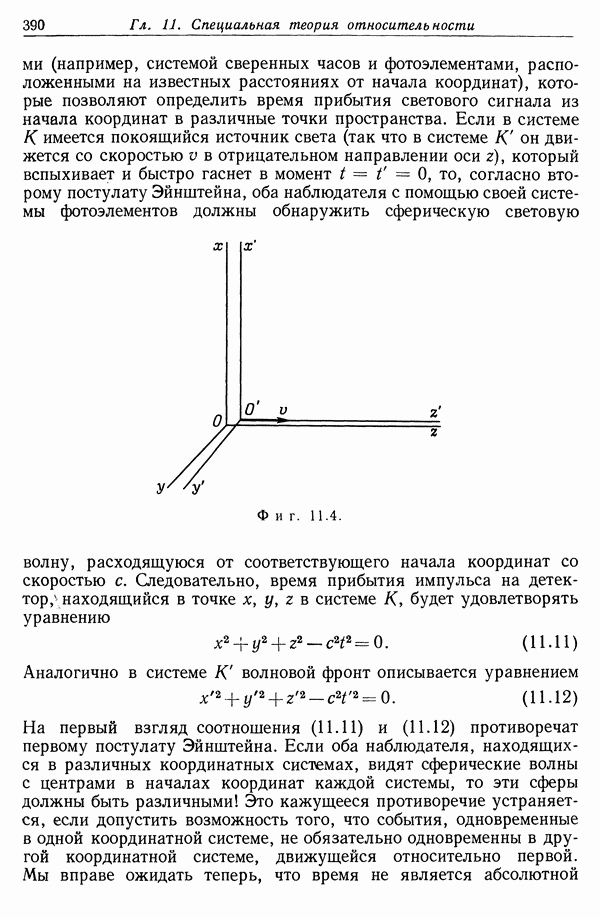
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
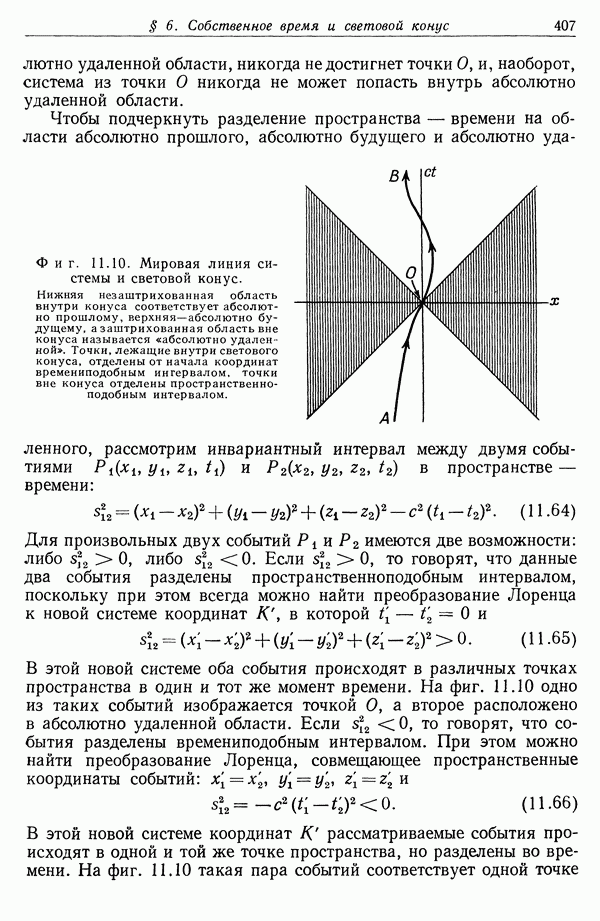
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
- § 3. Угловое распределение излучения ускоряемого заряда
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
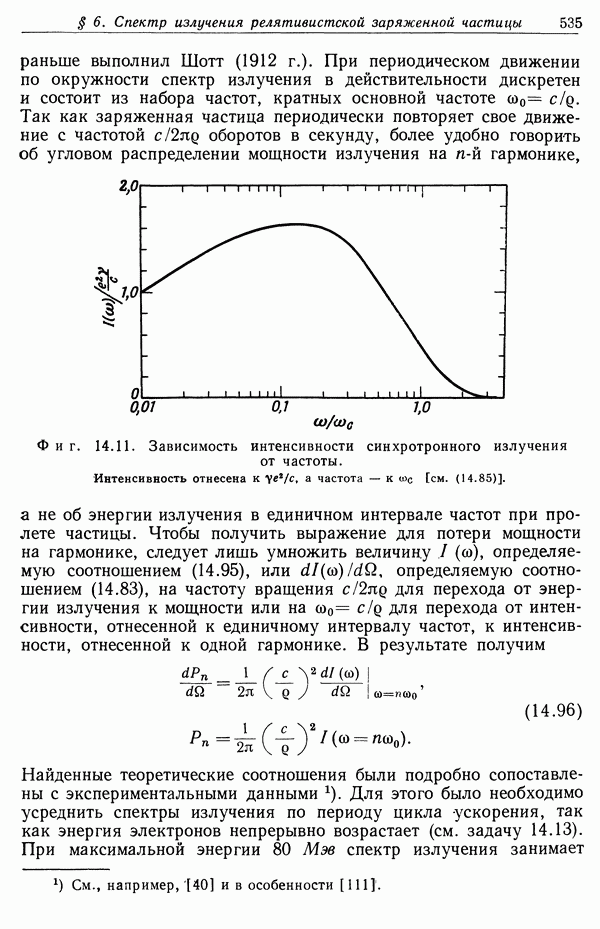
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
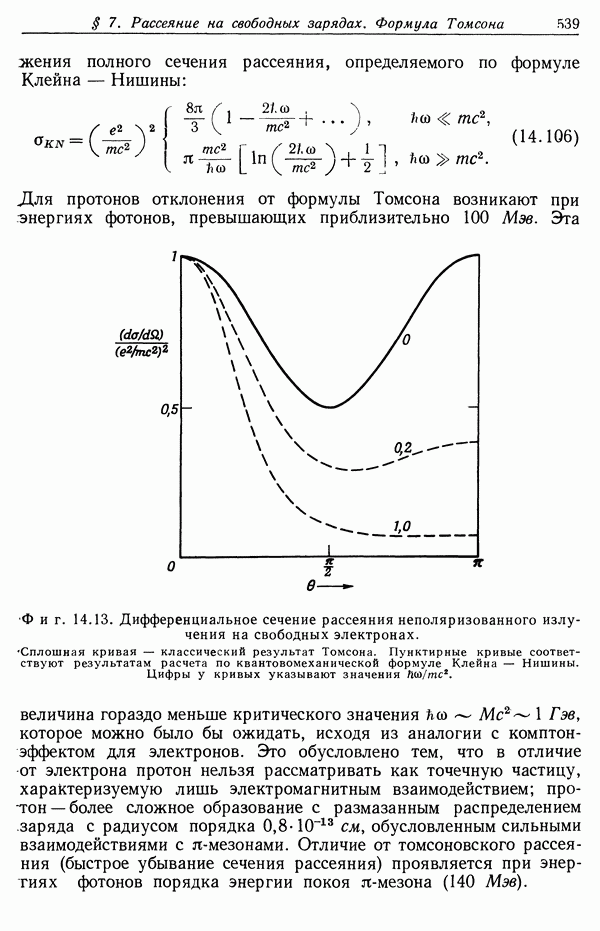
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
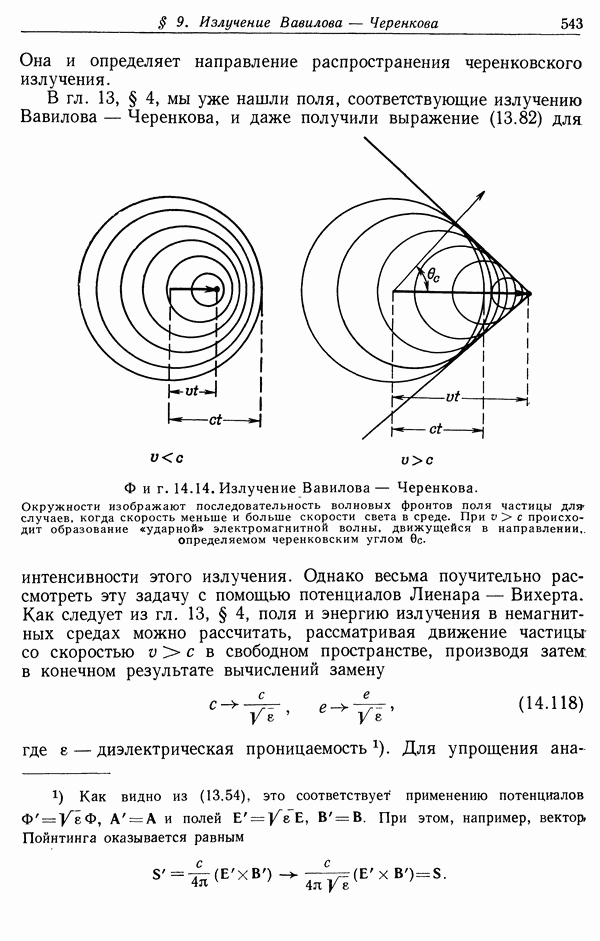
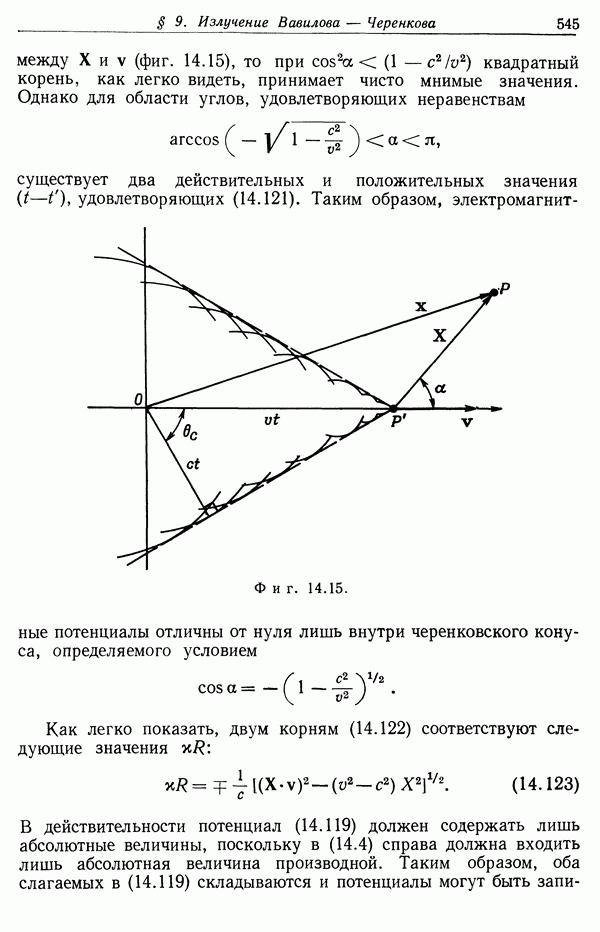
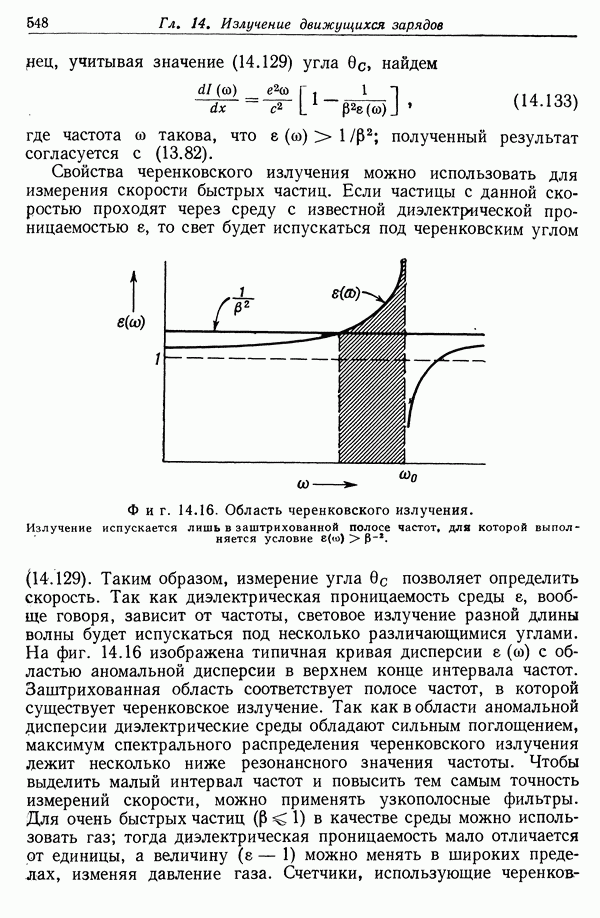
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
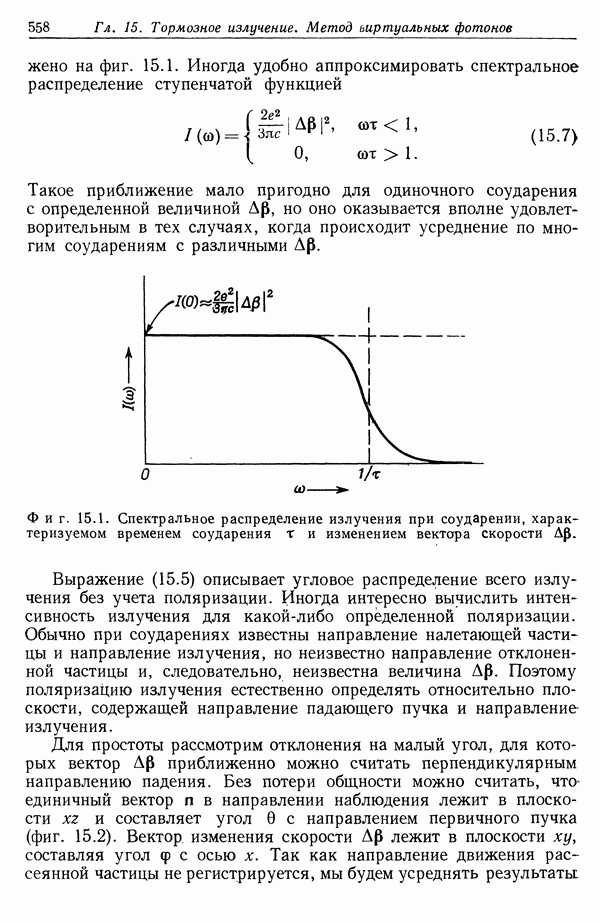
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ