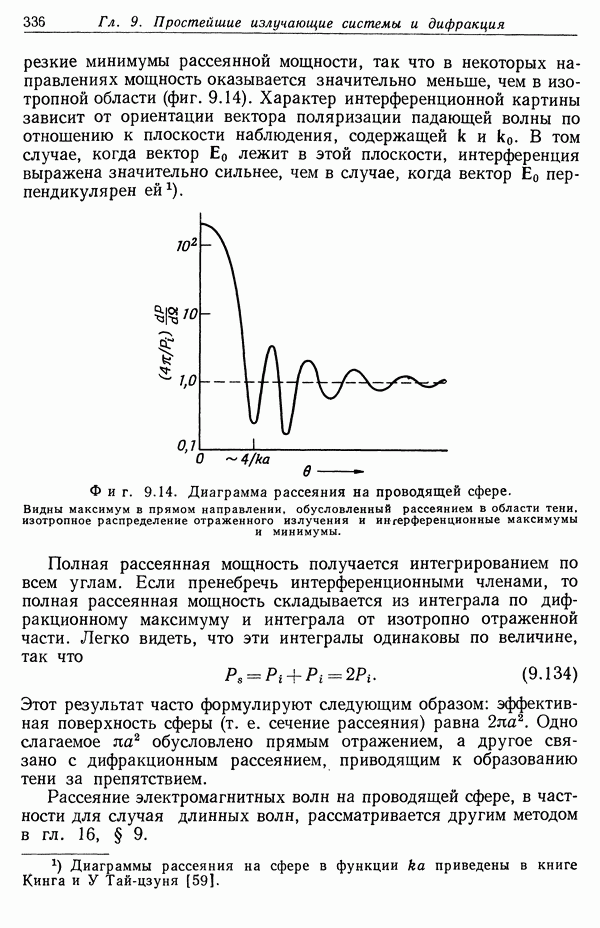
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
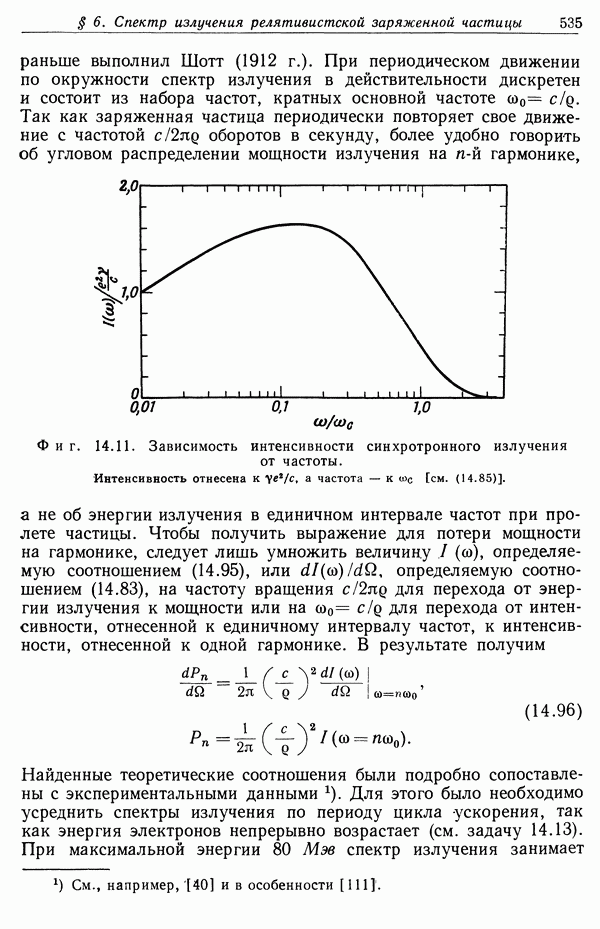
§ 6. Динамическая модель пинч-эффекта
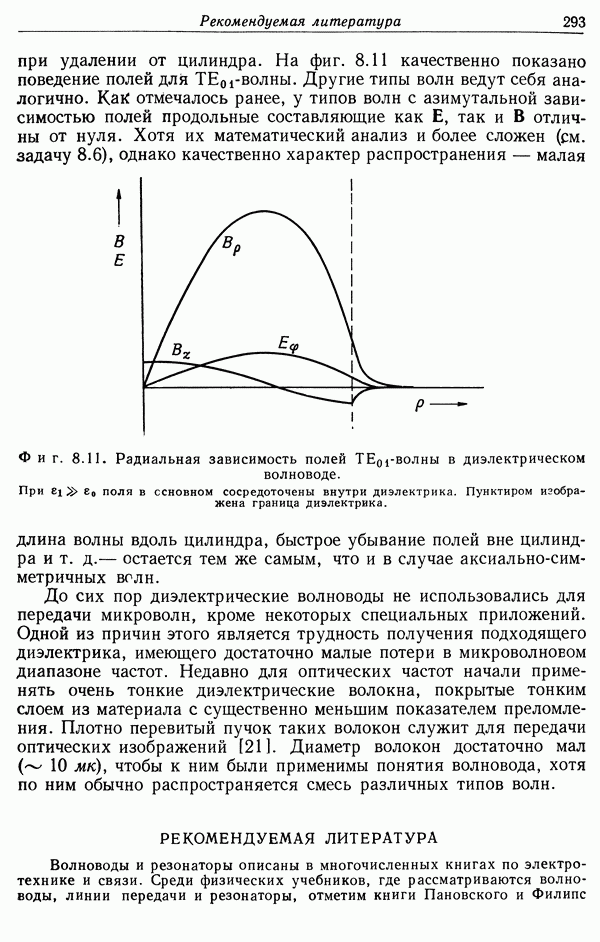
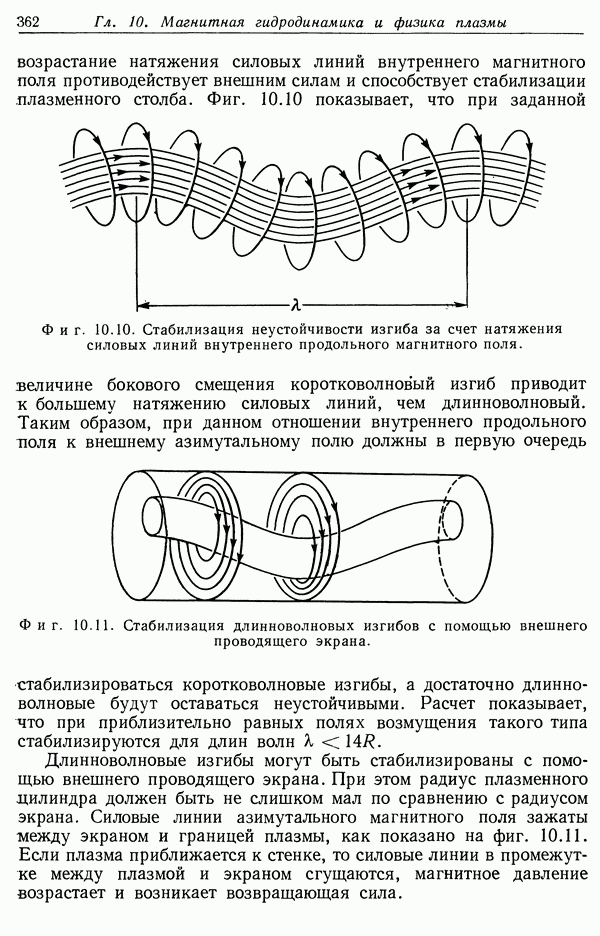
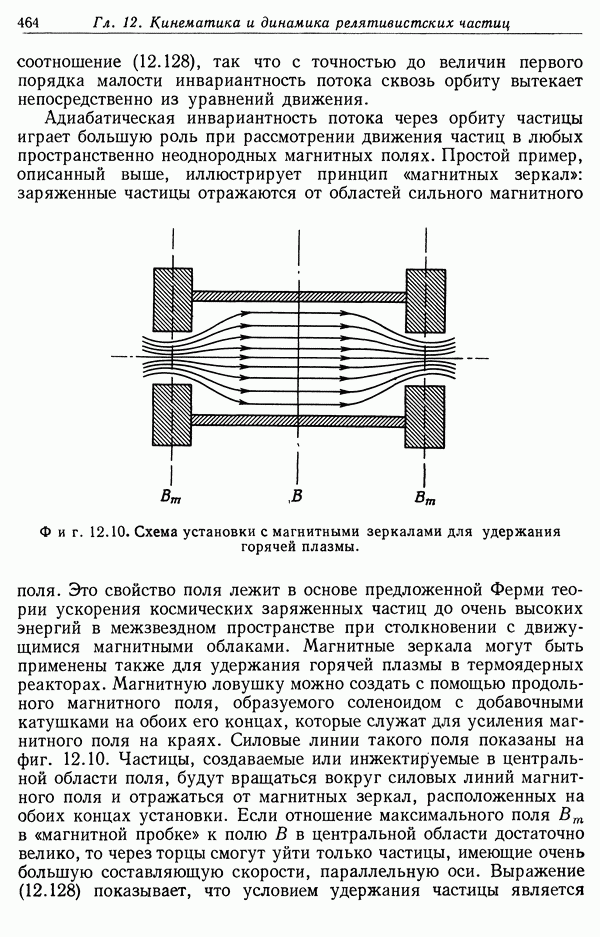
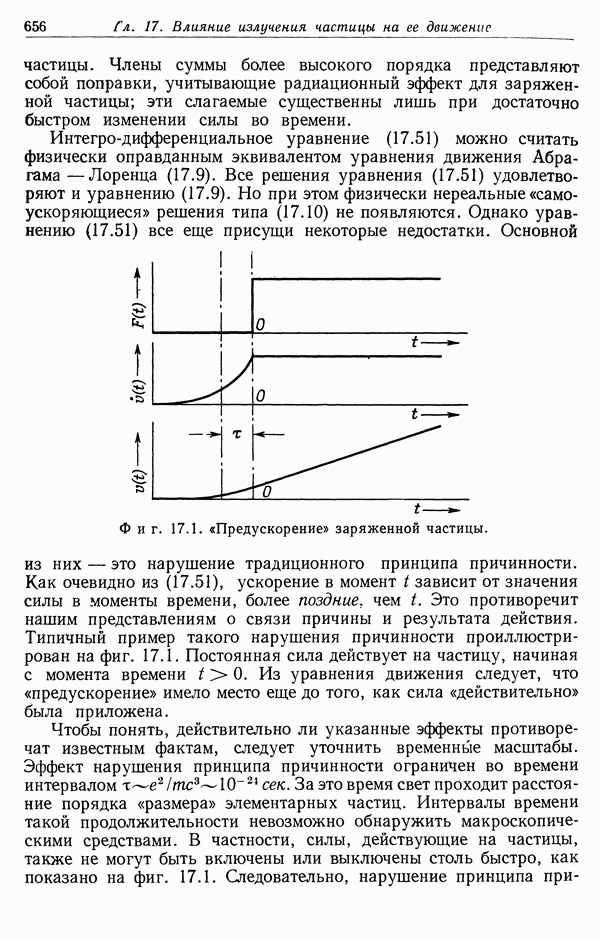
Простое рассмотрение, проведенное в  настоящей главы, применимо в статическом или квазистатическом случае. В действительности
настоящей главы, применимо в статическом или квазистатическом случае. В действительности
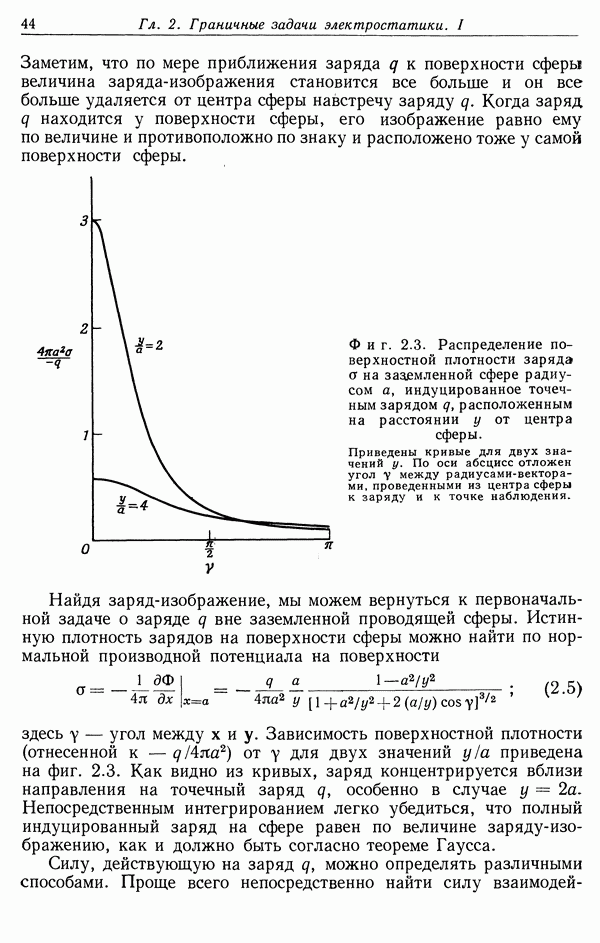
такие условия не реализуются. Обычно сначала давление плазмы слишком мало, чтобы противостоять внешнему магнитному давлению. Из-за этого радиус плазменного цилиндра уменьшается, т. е. происходит сжатие плазменного столба (пинч-эффект). Таким образом достигается желаемый результат — отжатие плазмы от ограничивающих ее стенок. Если бы сжатый плазменный столб был устойчив в течение достаточно длительного времени, то плазму можно было бы нагреть до очень высокой температуры, не повредив при этом стенок камеры.

Фиг. 10.6. Плазменный столб внутри полого цилиндрического проводника.
Розенблют предложил простую модель процесса сжатия учитывающую его динамический характер. Предположим, что плазма создана в полом проводящем цилиндре радиусом  и длиной
и длиной  . К концам цилиндра приложена разность потенциалов V, так что по плазме течет ток
. К концам цилиндра приложена разность потенциалов V, так что по плазме течет ток  Ток создает азимутальное магнитное поле
Ток создает азимутальное магнитное поле  заставляющее плазму сжиматься. Радиус плазменного столба в момент времени
заставляющее плазму сжиматься. Радиус плазменного столба в момент времени  мы обозначим через R (t). Проводимость плазмы будем считать бесконечной. При этом ток течет по поверхности плазмы, а магнитное поле
мы обозначим через R (t). Проводимость плазмы будем считать бесконечной. При этом ток течет по поверхности плазмы, а магнитное поле
 (10.47)
(10.47)
имеется только в области между  . В соответствии с предположением о бесконечной проводимости электрическое поле на поверхности плазмы в движущейся системе отсчета, в которой эта поверхность покоится, обращается в нуль
. В соответствии с предположением о бесконечной проводимости электрическое поле на поверхности плазмы в движущейся системе отсчета, в которой эта поверхность покоится, обращается в нуль
 (10.48)
(10.48)
Применяя закон индукции Фарадея к показанному пунктирными лйнйяйи на фиг. 10.6 контуру, внутренняя сторона которого движется вместе с поверхностью плазмы, мы видим, что вклад в
линейный интеграл от Е дает только внешняя сторона контура, находящаяся в проводящей стенке. Таким образом,

Это уравнение выражает обычную индуктивную связь между током, напряжением и размерами, определяющимц индуктивность. Его интеграл имеет вид
 (10.50)
(10.50)
где  — приложенное электрическое поле. Функция
— приложенное электрическое поле. Функция  считается известной и нормируется таким образом, чтобы величина
считается известной и нормируется таким образом, чтобы величина  была равна максимальному значению приложенного поля. Чтобы продвинуться дальше, мы должны найти динамическую связь между током
была равна максимальному значению приложенного поля. Чтобы продвинуться дальше, мы должны найти динамическую связь между током  и радиусом плазмы
и радиусом плазмы 
Необходимая зависимость получается из уравнения баланса импульсов, т. е. из второго закона Ньютона. Однако прежде необходимо сделать некоторые предположения относительно плазмы. Если бы длина свободного пробега между столкновениями была мала по сравнению с радиусом, то динамическое поведение плазмы определялось бы гидродинамическими ударными волнами. Однако для горячей и разреженной плазмы длина свободного пробега обычно сравнима или даже больше радиуса. В этом случае более подходящей является модель частиц, свободно движущихся внутри плазмы.
Если скорость границы плазмы R значительно больше тепловых скоростей, то в системе отсчета, где эта граница неподвижна, каждая частица движется к границе со скоростью R. Частица, проникнувшая во внешнюю область, под действием магнитного поля поворачивает обратно и покидает поверхность со скоростью - R. Поэтому каждая частица, столкнувшаяся с границей плазмы, приобретает импульс  Число столкновений на единицу поверхности в единицу времени равно NR, где N — начальное число частиц в единице объема. Следовательно, скорость изменения импульса (т. е. давление) дается выражением
Число столкновений на единицу поверхности в единицу времени равно NR, где N — начальное число частиц в единице объема. Следовательно, скорость изменения импульса (т. е. давление) дается выражением
 (10.51)
(10.51)
где q — начальная плотность. На границу плазмы действует магнитное давление  обусловленное скачком магнитного поля от нуля внутри плазмы до величины В вне плазмы. Оно должно уравновешивать давление плазмы. Это позволяет с учетом (10.47)
обусловленное скачком магнитного поля от нуля внутри плазмы до величины В вне плазмы. Оно должно уравновешивать давление плазмы. Это позволяет с учетом (10.47)
найти связь тока со скоростью границы плазмы:
 (10.52)
(10.52)
При выводе (10.52) мы весьма упрощенно считали, что каждая частица сталкивается с границей раздела только один раз. В действительности скорость границы раздела все время растет, так что поверхность догоняет также и ранее отразившиеся от нее частицы и снова нагревает их. Этот эффект можно приближенно учесть с помощью модели «снегоочистителя», в которой предполагается, что поверхность раздела увлекает с собой все вещество, на которое она надвигается по мере движения. При этом магнитное давление и скорость изменения импульса связаны уравнением
 (10.53)
(10.53)
в котором  — масса, увлекаемая «снегоочистителем»:
— масса, увлекаемая «снегоочистителем»:
 (10.54)
(10.54)
Отсюда получается соотношение между током и радиусом
 (10.55)
(10.55)
В начальной стадии, когда  модель «снегоочистителя» и модель свободных частиц приводят к одинаковым зависимостям тока от радиуса, различающимся лишь множителем
модель «снегоочистителя» и модель свободных частиц приводят к одинаковым зависимостям тока от радиуса, различающимся лишь множителем  . По порядку величины обе модели дают один и тот же результат и для более поздних моментов времени.
. По порядку величины обе модели дают один и тот же результат и для более поздних моментов времени.
Уравнение движения для  можно получить, подставляя
можно получить, подставляя  из (10.52) или из (10.55) в соотношение (10.50). Выбирая для примера модель свободных частиц, находим
из (10.52) или из (10.55) в соотношение (10.50). Выбирая для примера модель свободных частиц, находим
 (10.56)
(10.56)
Здесь знак квадратного корня определяется требованием  Для решения этого уравнения необходимо знать
Для решения этого уравнения необходимо знать  Некоторые свойства решения можно определить, перейдя к безразмерным
Некоторые свойства решения можно определить, перейдя к безразмерным
переменным

Тогда (10.56) запишется в виде
 (10.58)
(10.58)
Для модели «снегоочистителя» соответствующее уравнение имеет вид
 (10-59)
(10-59)
Даже не решая этих уравнений, можно сказать, что  существенно изменяется на интервале
существенно изменяется на интервале  . Это означает, что по порядку величины радиальная скорость сжатия равна
. Это означает, что по порядку величины радиальная скорость сжатия равна

Такой результат получается при любой динамической модели, в том числе гидродинамической. Для «быстрых пинчей» в небольших установках с водородной и дейтериевой плазмой типичные значения приложенного электрического поля составляют около  в/см, а начальной плотности — около
в/см, а начальной плотности — около  дейтронов в
дейтронов в  При этом
При этом  оказывается величиной порядка 107 см
оказывается величиной порядка 107 см  а протекающий ток, согласно (10.52) или (10.55), равен
а протекающий ток, согласно (10.52) или (10.55), равен

где F — безразмерная функция порядка единицы. Для трубки радиусом 10 см при описанных выше условиях ток составляет  .
.
Предыдущее рассмотрение пинч-эффекта, очевидно, применимо только для короткого интервала времени после включения тока. Наша упрощенная модель показывает, что за время порядка  радиус плазменного столба обращается в нуль. Ясно, однако, что, прежде чем это случится (даже приближенно), характер процесса изменится. В гидродинамическом приближении радиальные ударные волны, вызванные сжатием, отразятся от оси и, распространяясь обратно, будут замедлять движение границы или даже изменять направление ее движения на обратное. Это — так называемая
радиус плазменного столба обращается в нуль. Ясно, однако, что, прежде чем это случится (даже приближенно), характер процесса изменится. В гидродинамическом приближении радиальные ударные волны, вызванные сжатием, отразятся от оси и, распространяясь обратно, будут замедлять движение границы или даже изменять направление ее движения на обратное. Это — так называемая
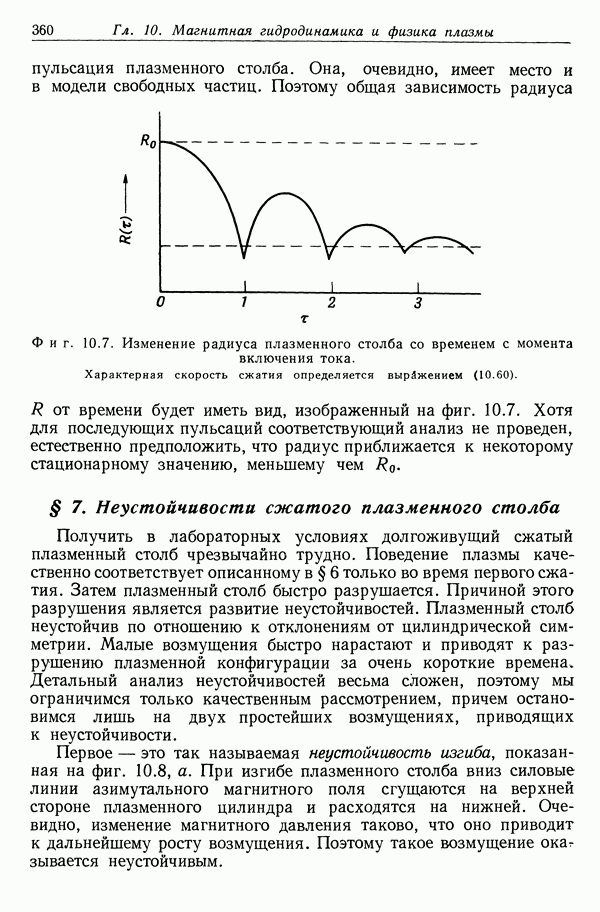
пульсация плазменного столба. Она, очевидно, имеет место и в модели свободных частиц. Поэтому общая зависимость радиуса  от времени будет иметь вид, изображенный на фиг. 10.7.
от времени будет иметь вид, изображенный на фиг. 10.7.

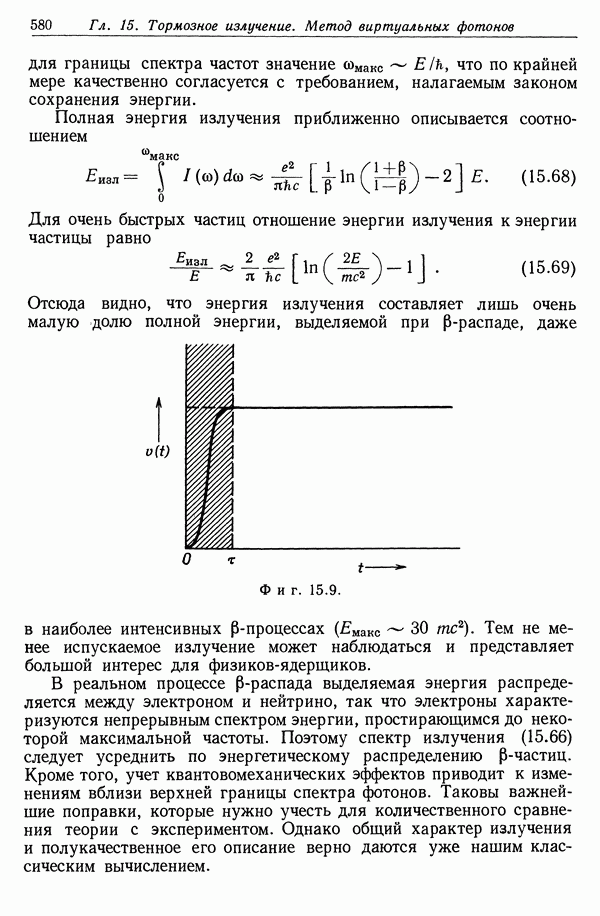
Фиг. 10.7. Изменение радиуса плазменного столба со временем с момента включения тока. Характерная скорость сжатия определяется выражением (10.60).
Хотя для последующих пульсаций соответствующий анализ не проведен, естественно предположить, что радиус приближается к некоторому стационарному значению, меньшему чем 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
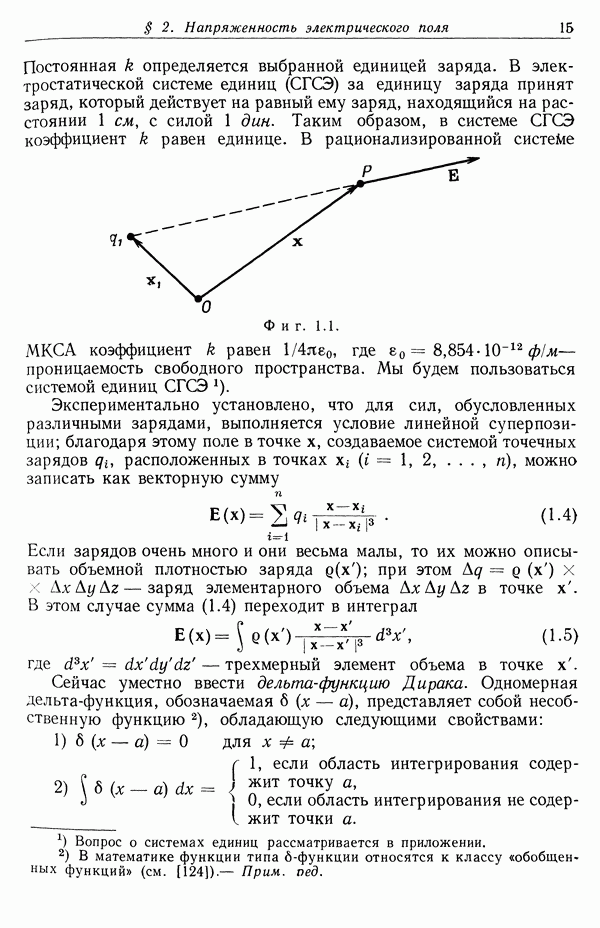
- § 2. Напряженность электрического поля
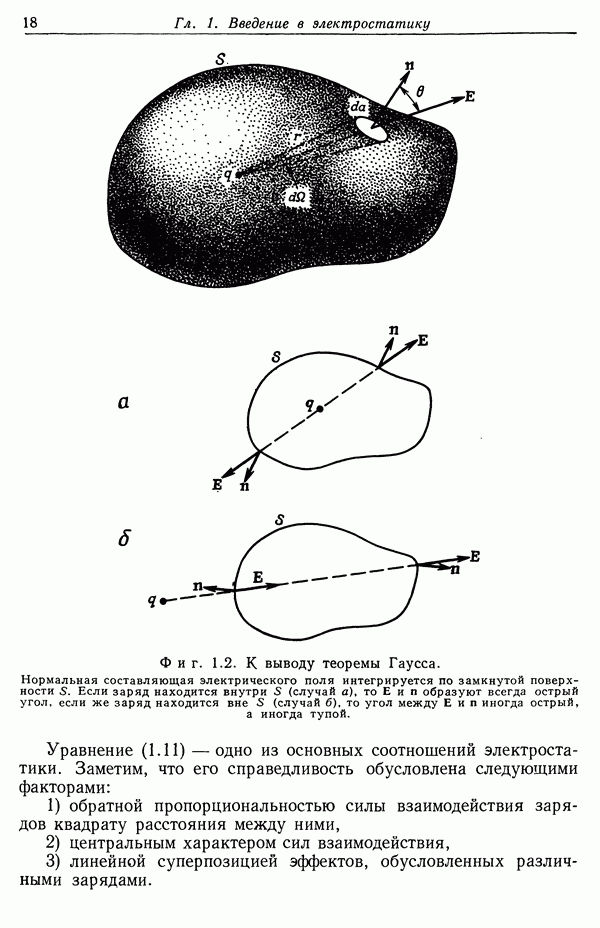
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
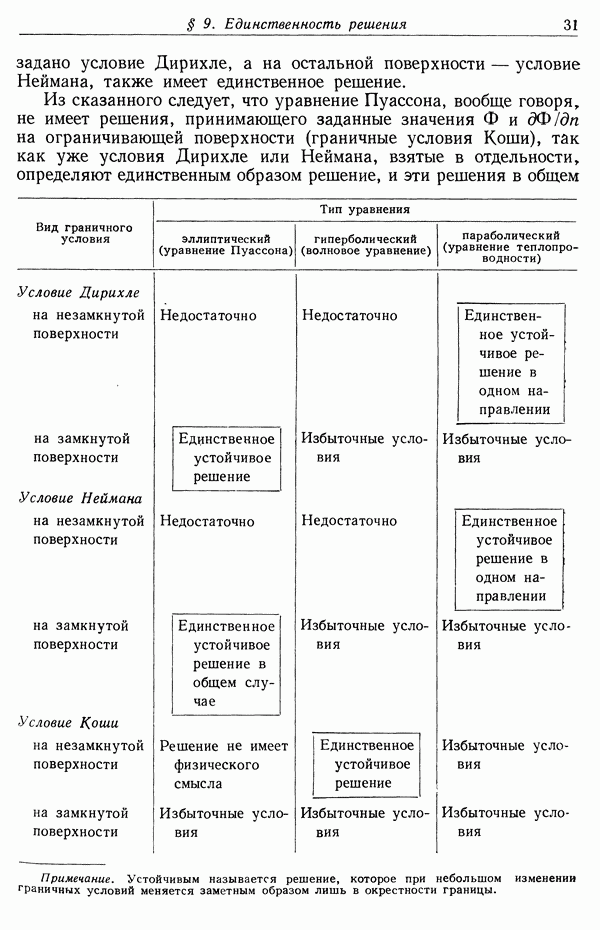
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
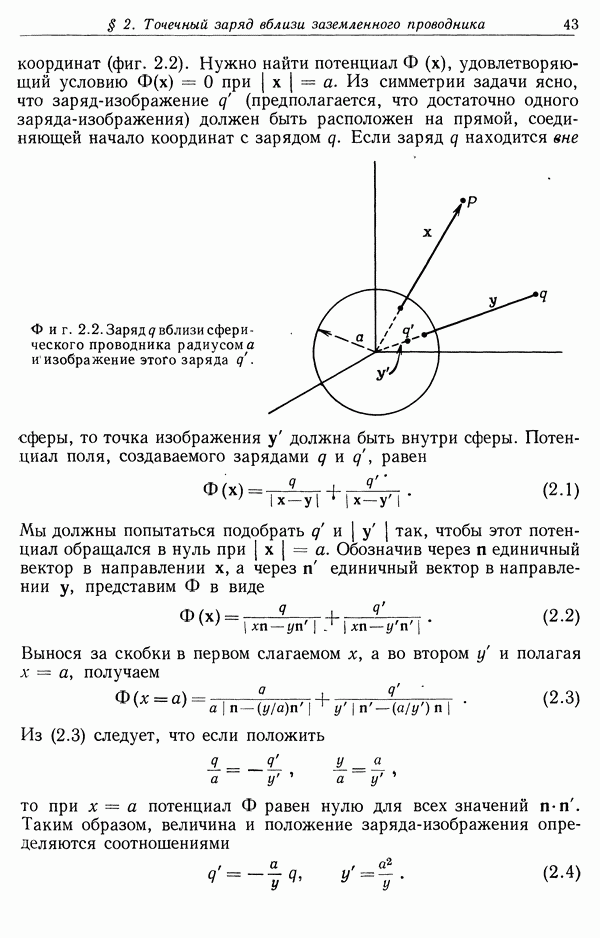
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
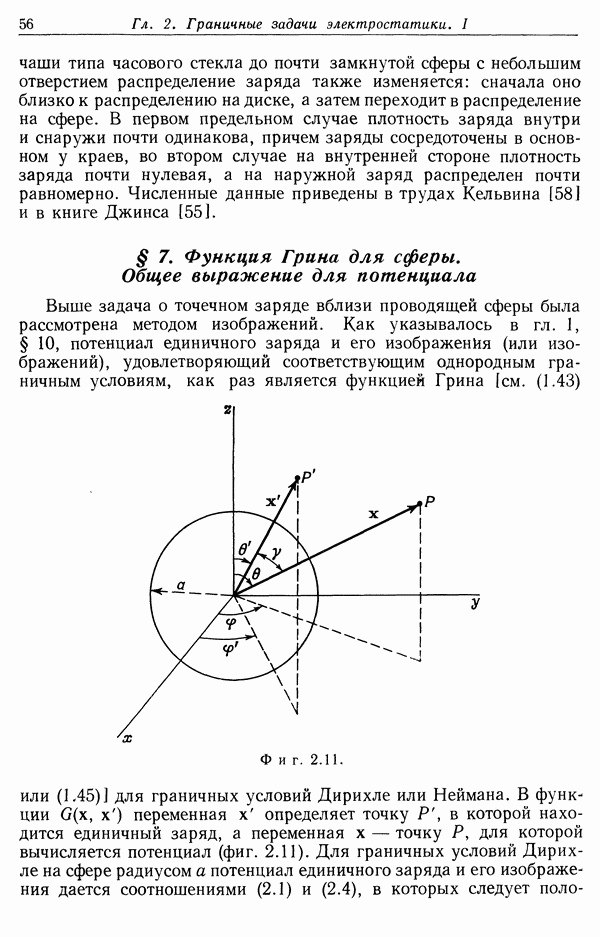
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
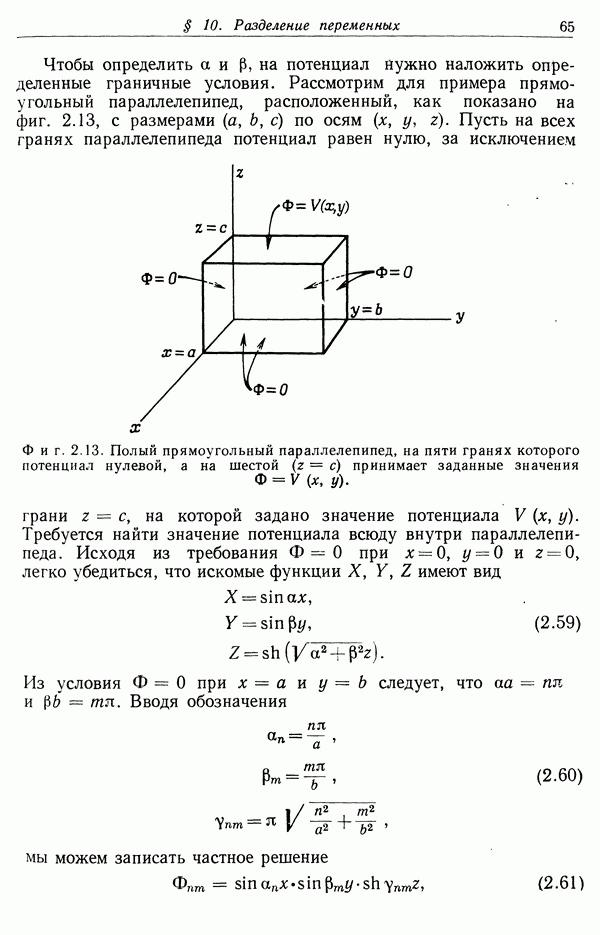
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
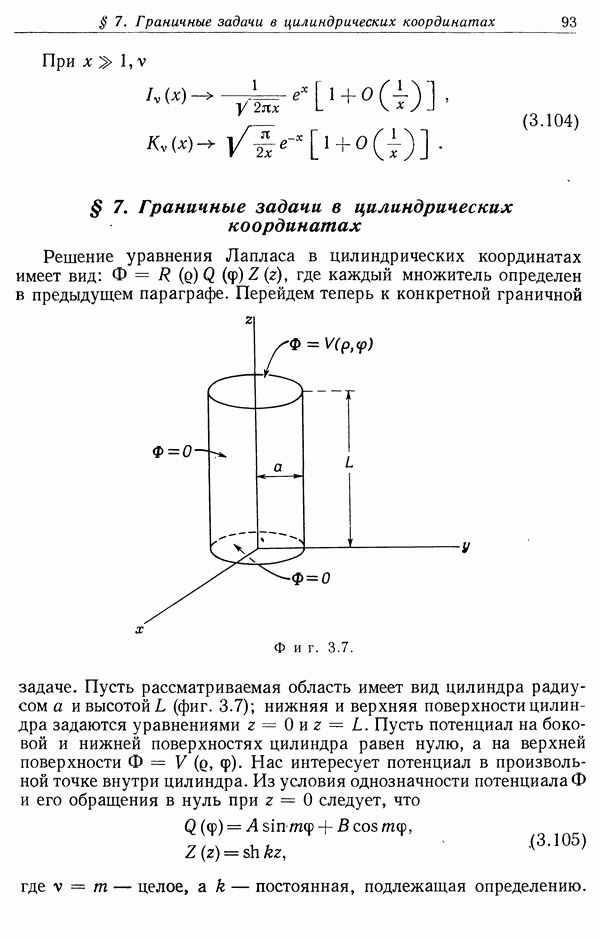
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
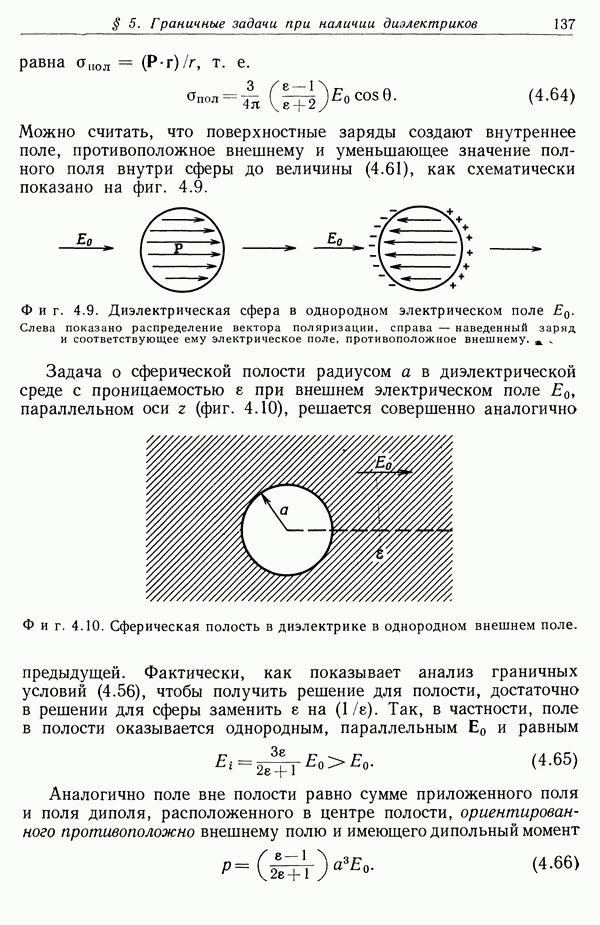
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
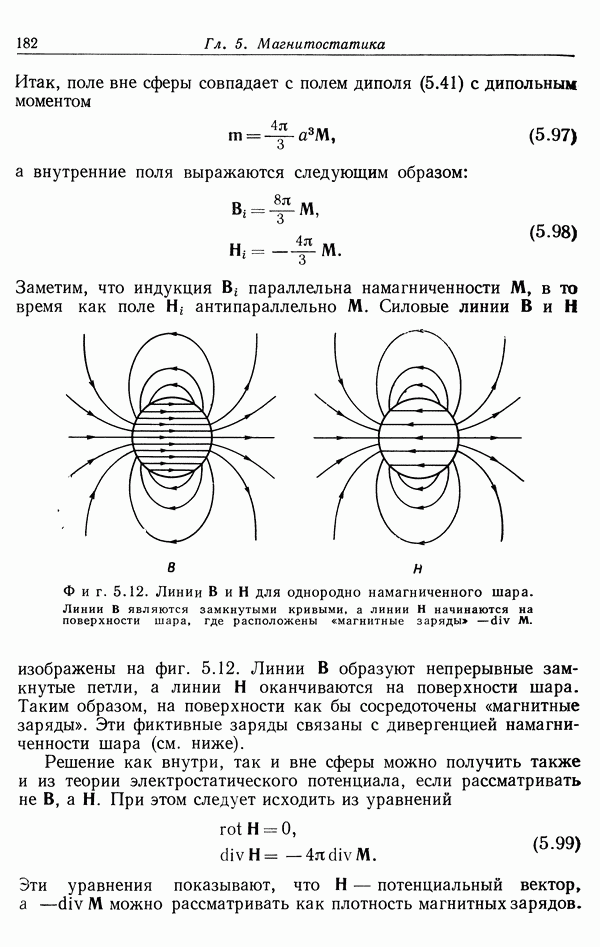
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
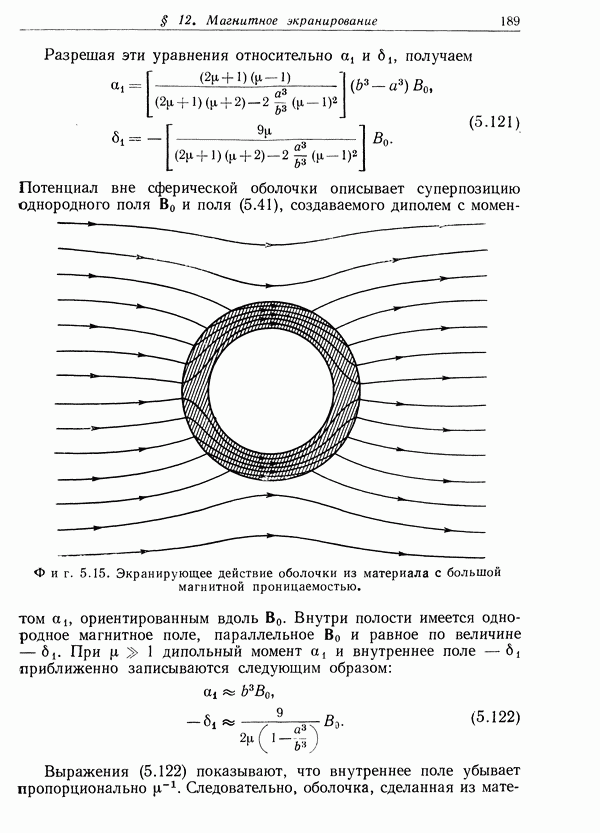
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
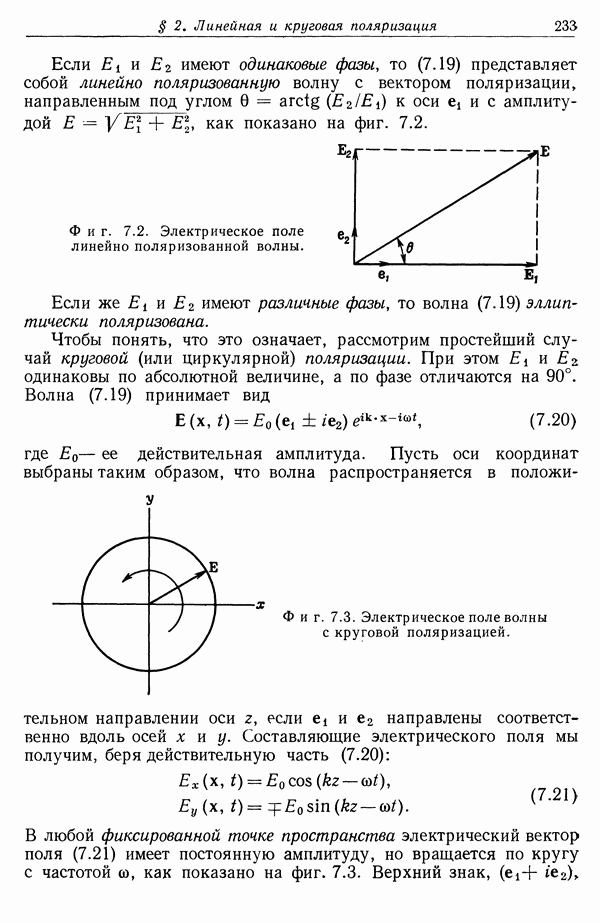
- § 2. Линейная и круговая поляризация
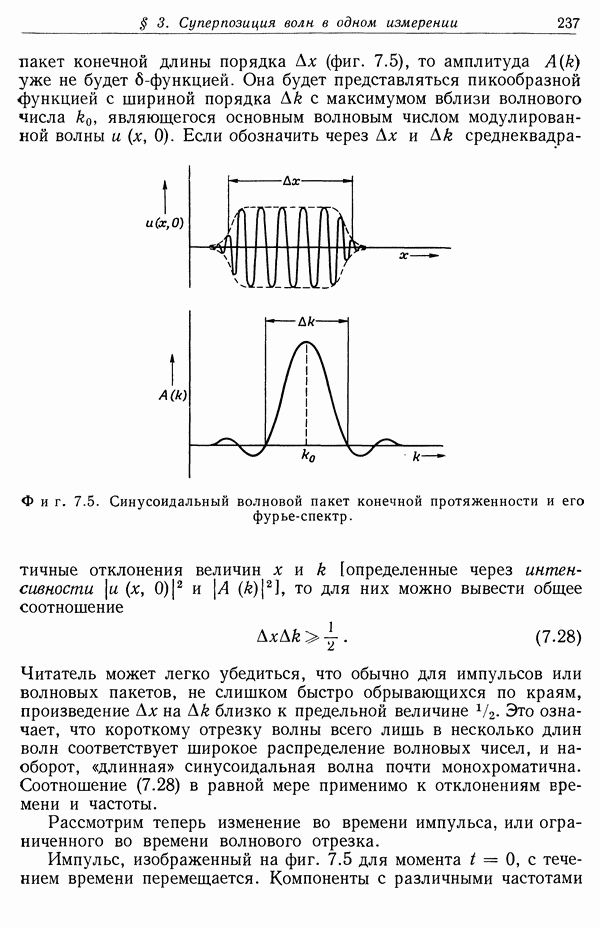
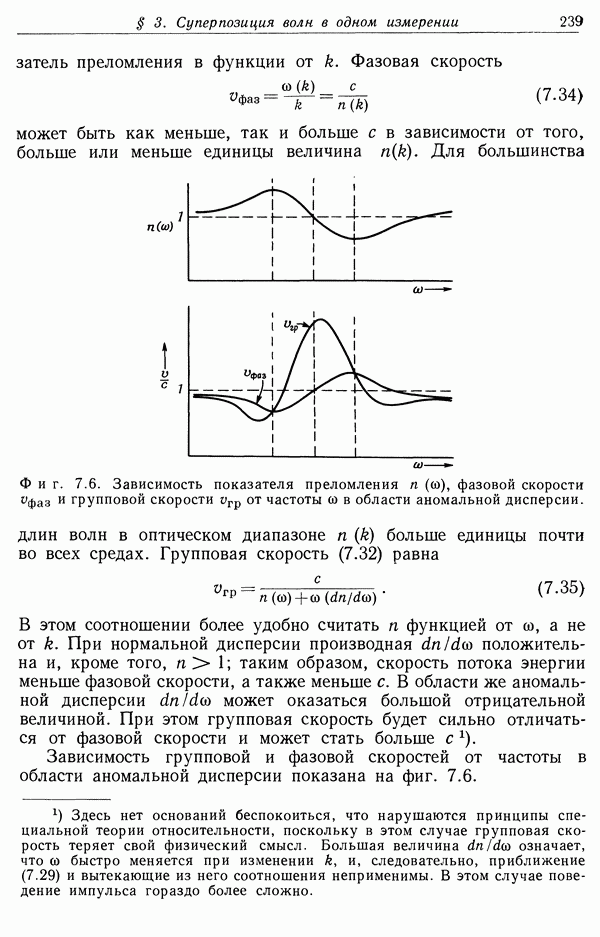
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
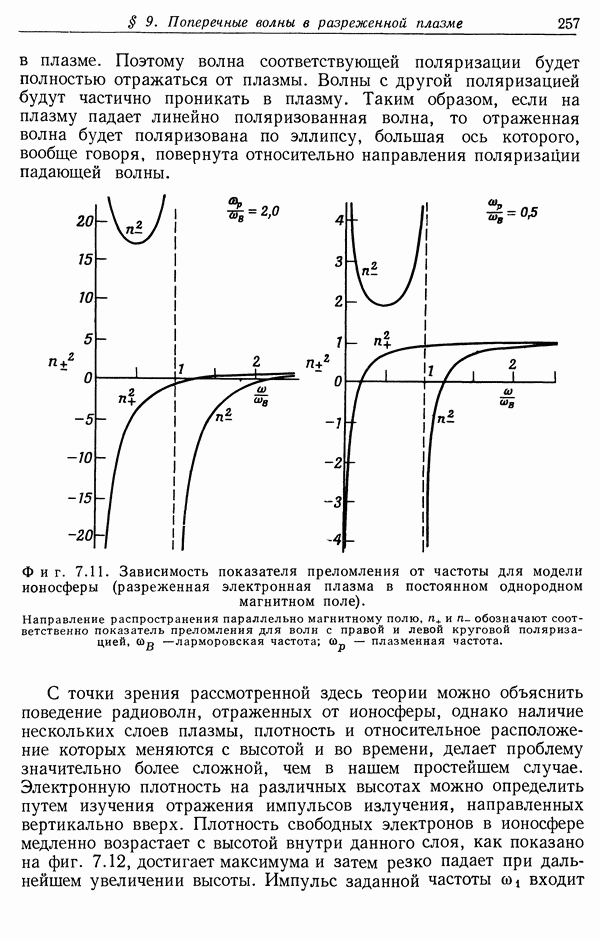
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
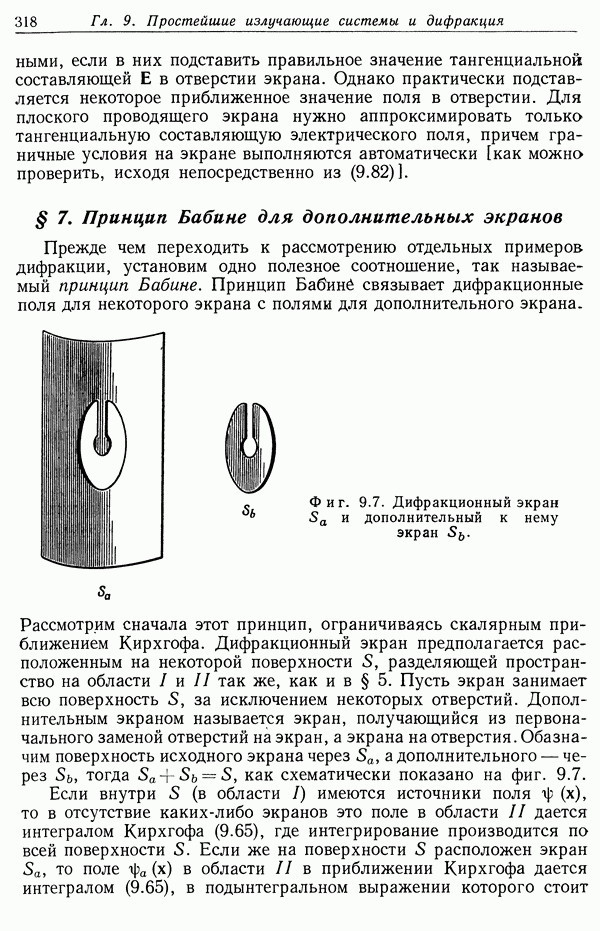
- § 7. Принцип Бабине для дополнительных экранов
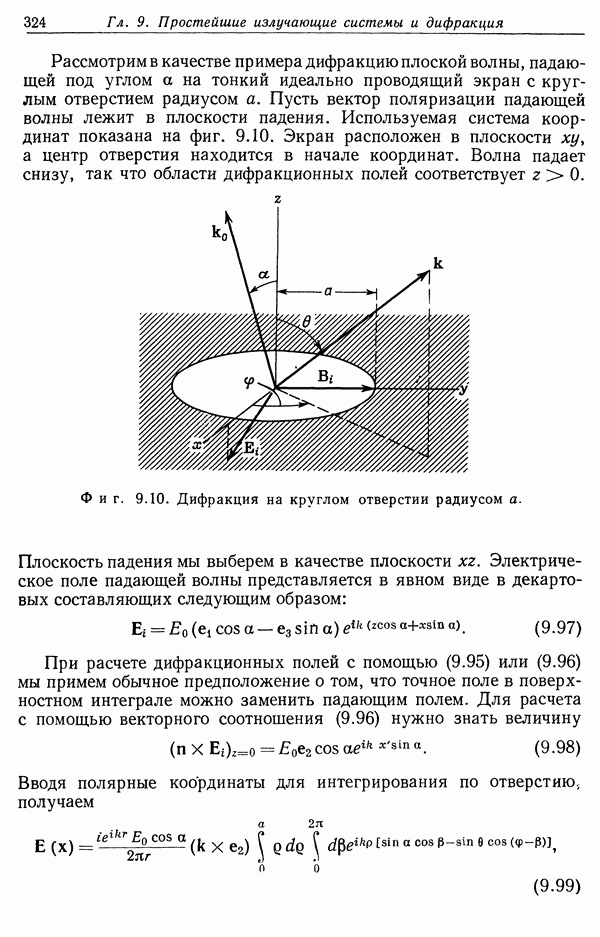
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
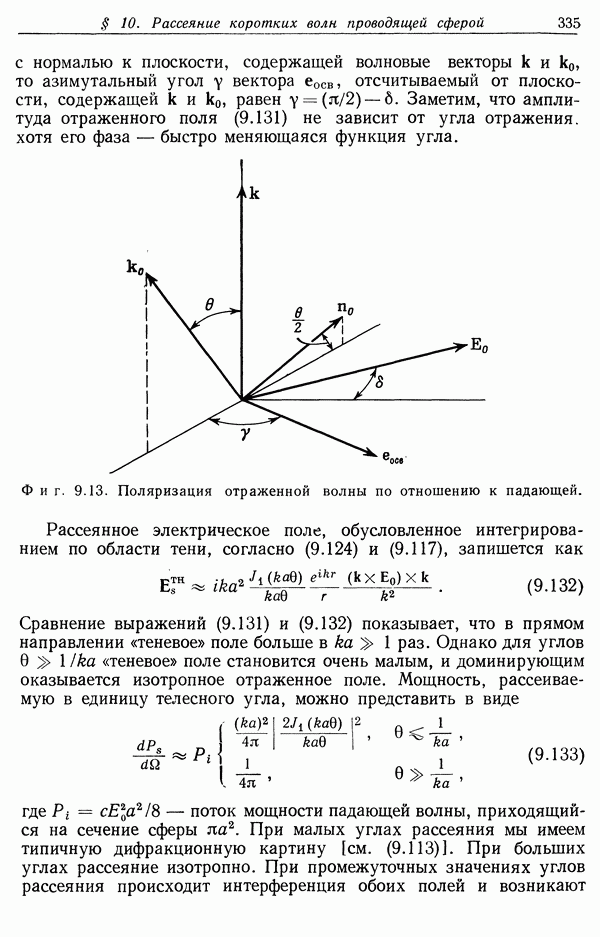
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
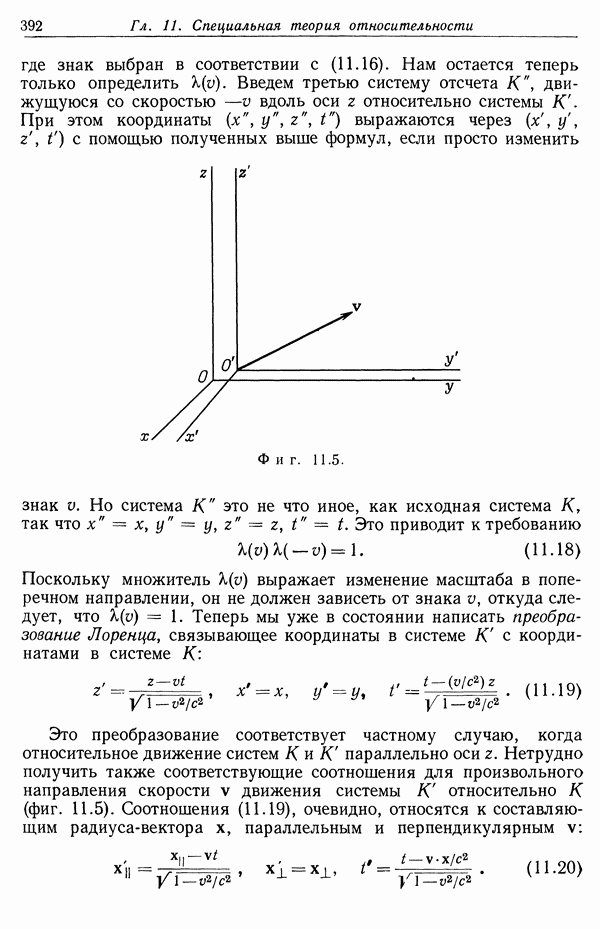
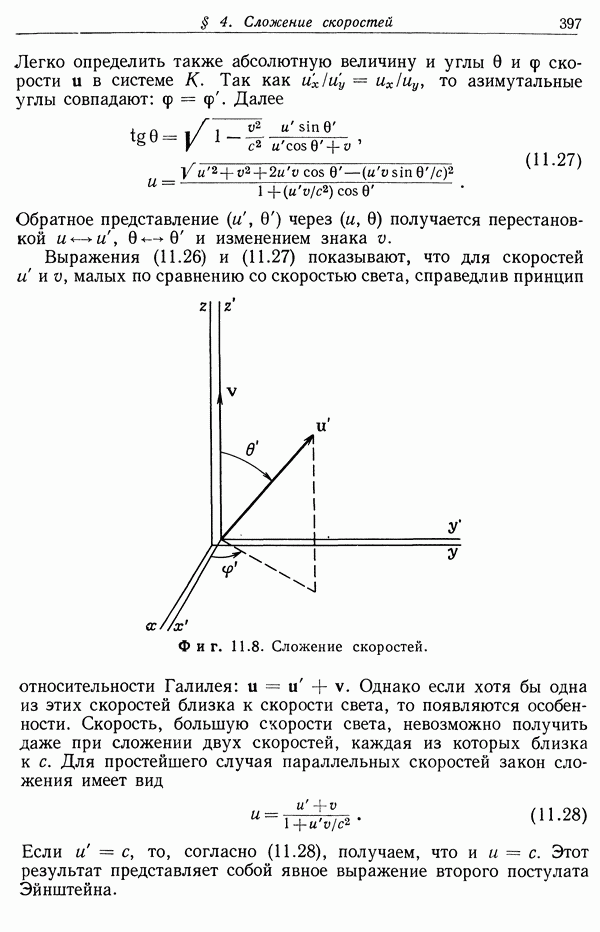
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
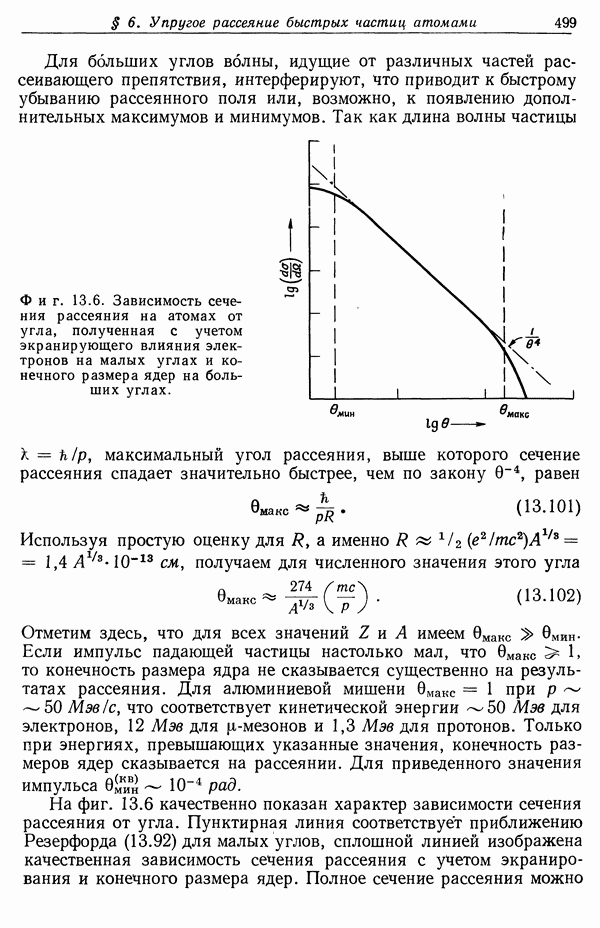
- § 6. Упругое рассеяние быстрых частиц атомами
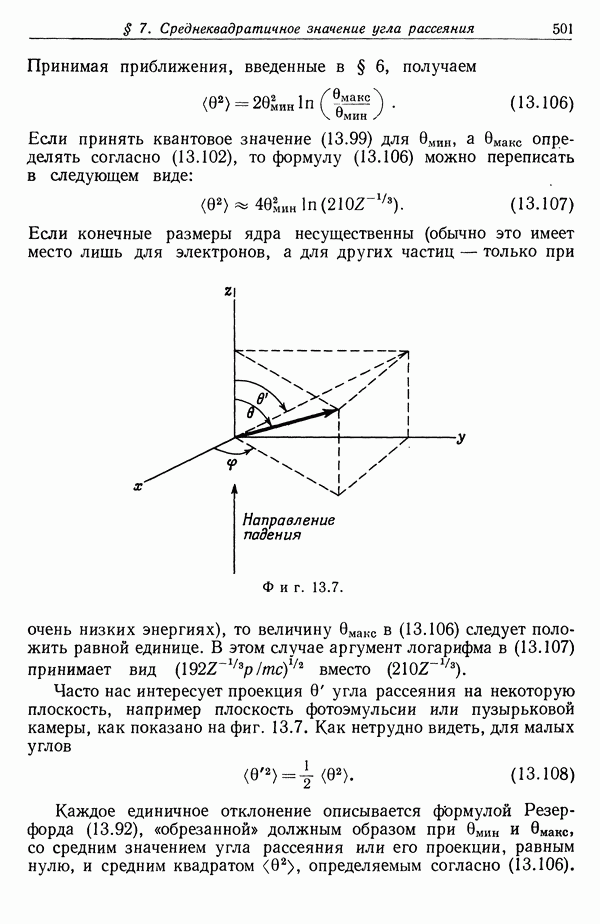
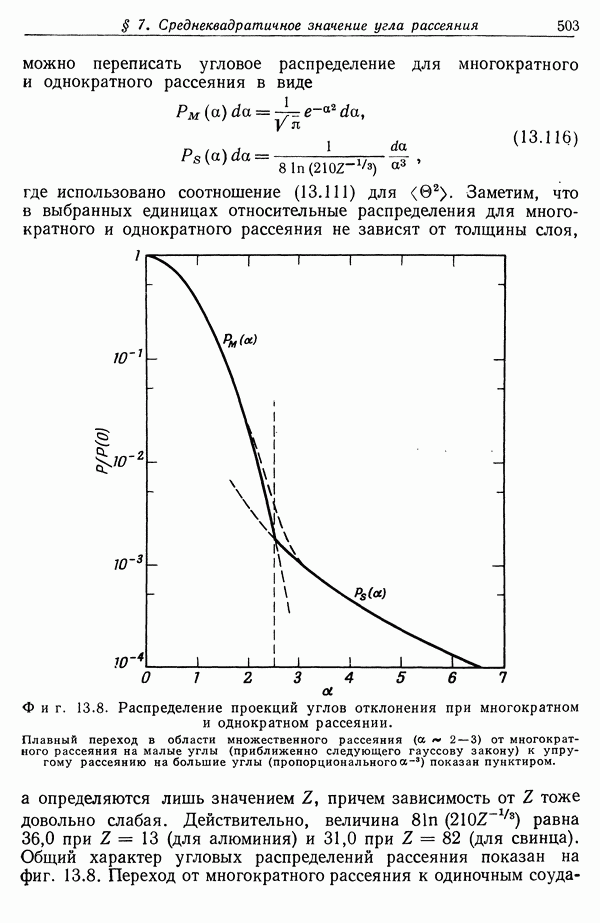
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
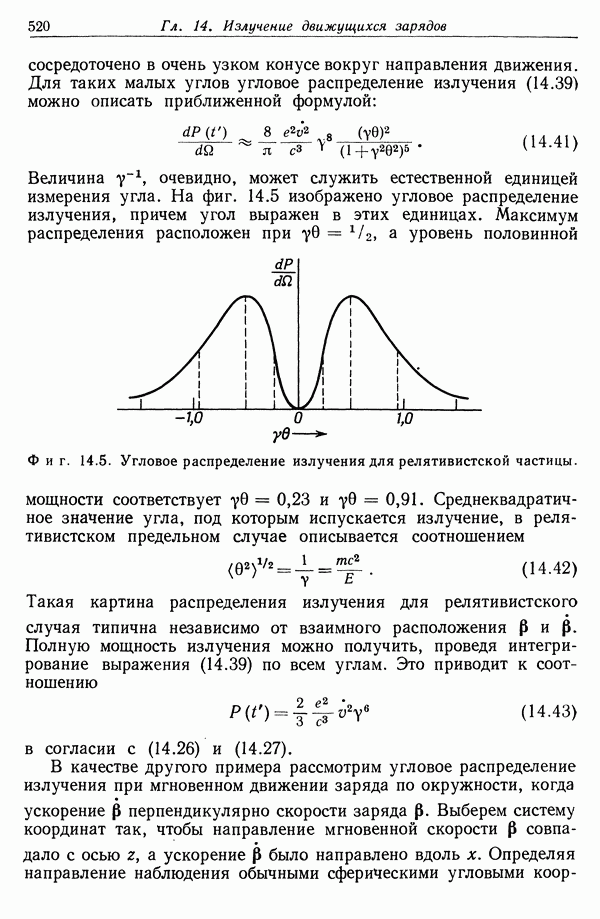
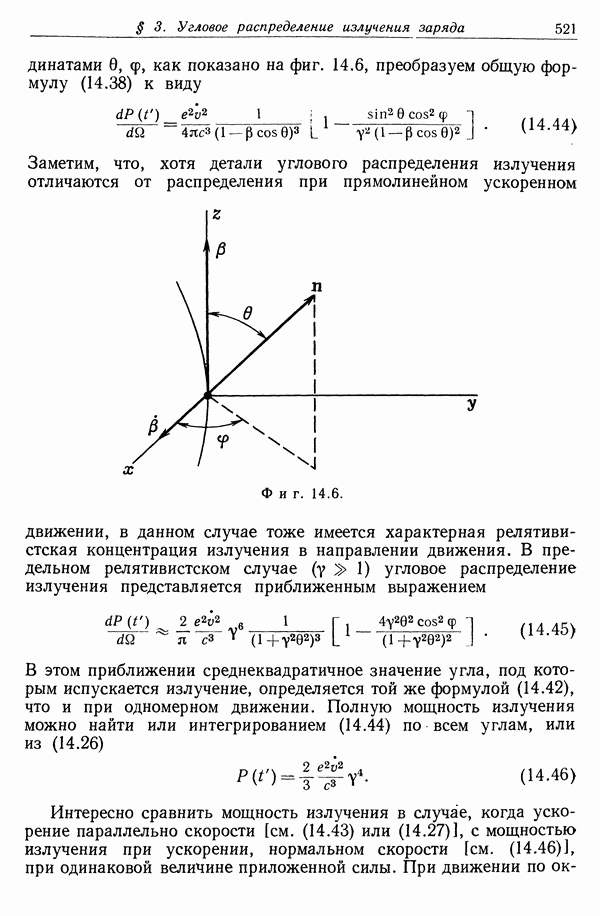
- § 3. Угловое распределение излучения ускоряемого заряда
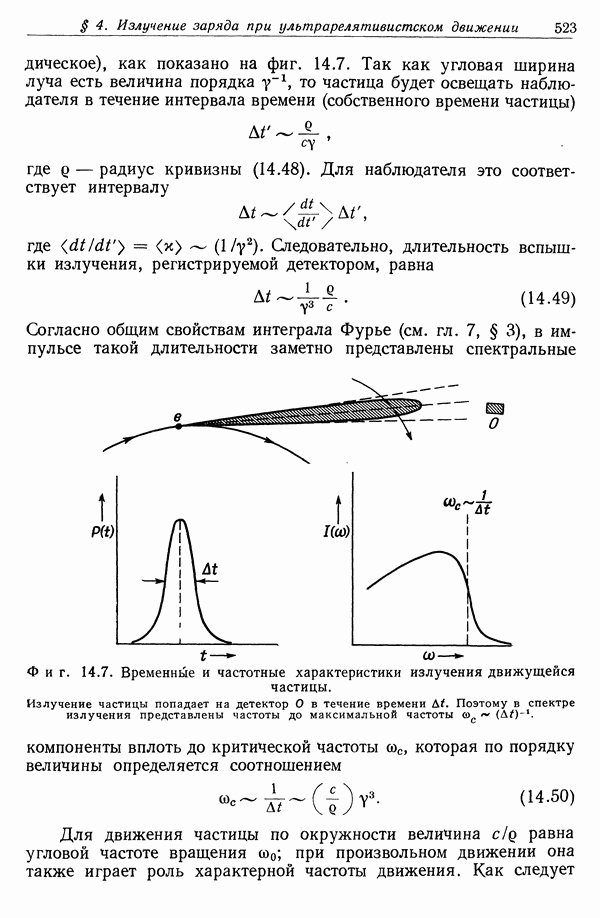
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
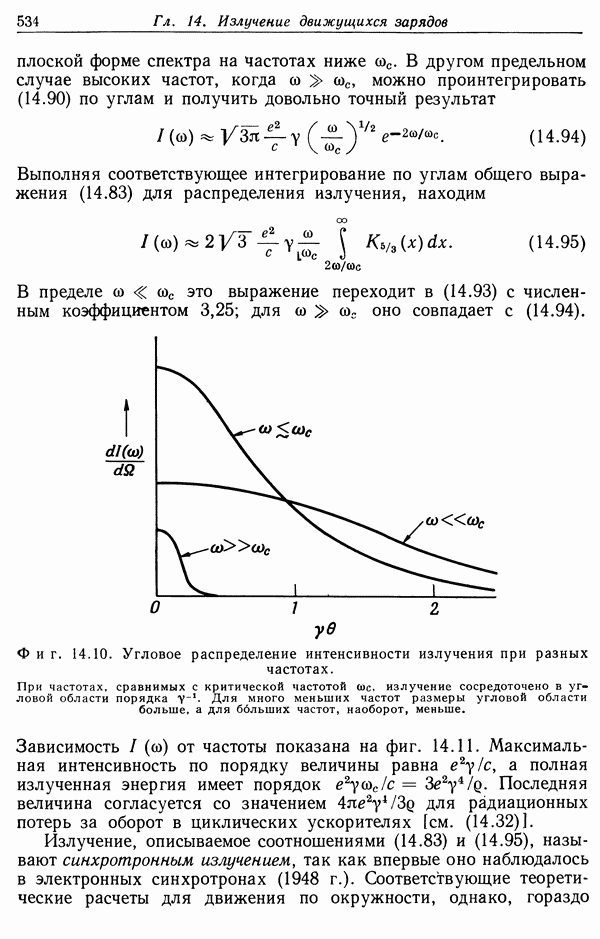
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
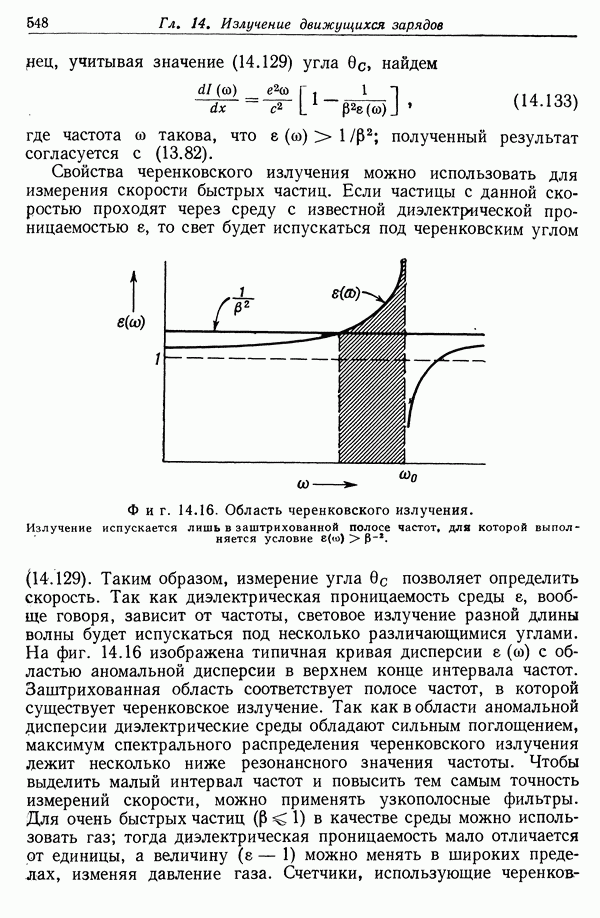
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
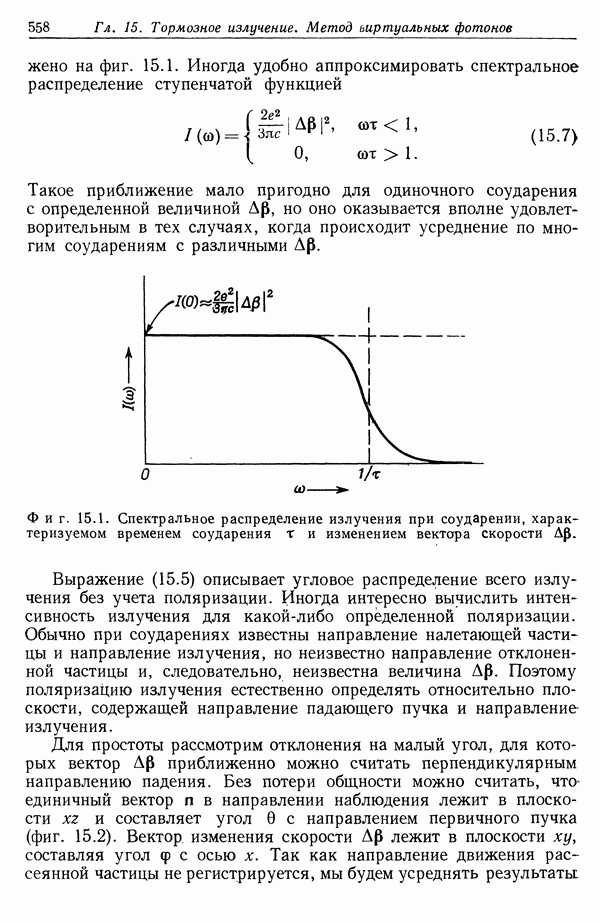
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
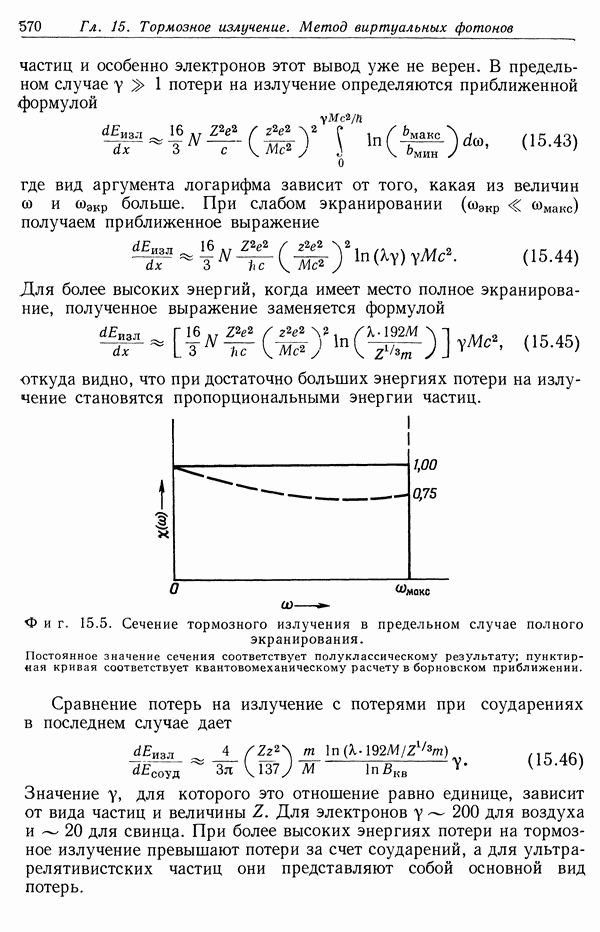
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ