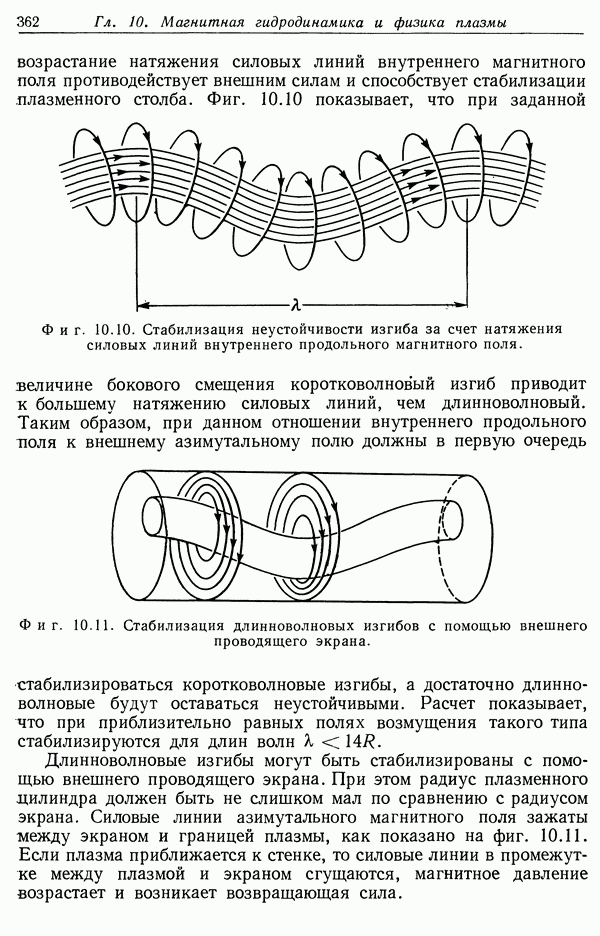
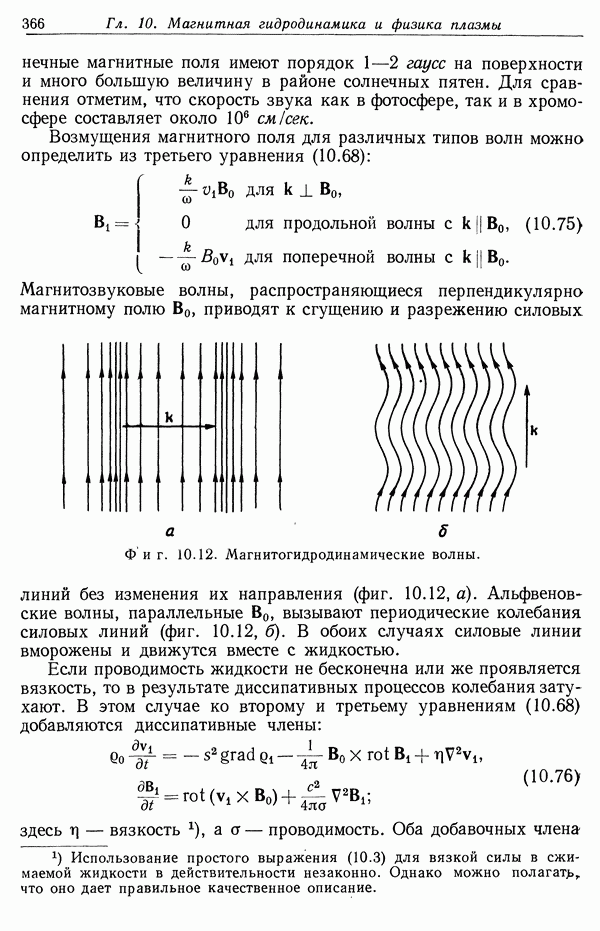
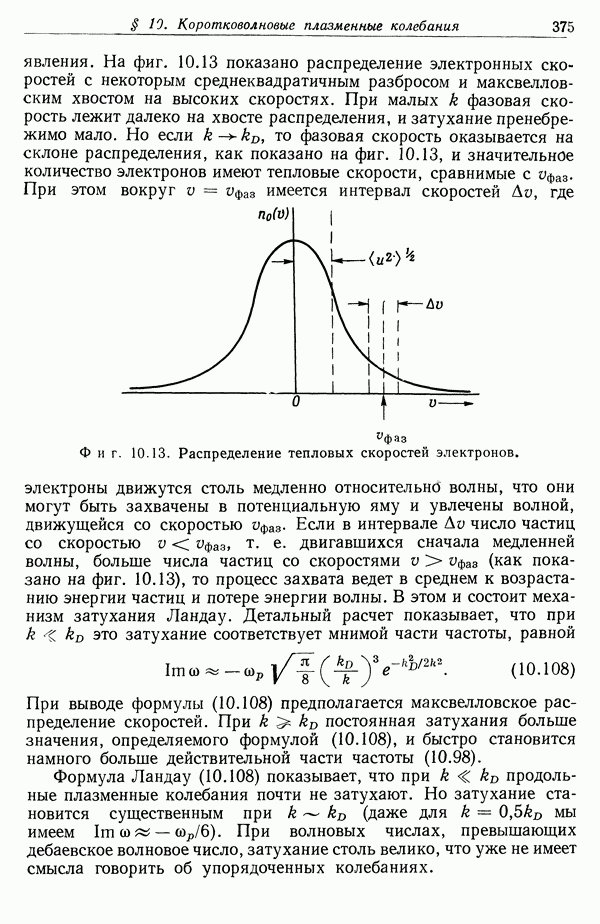
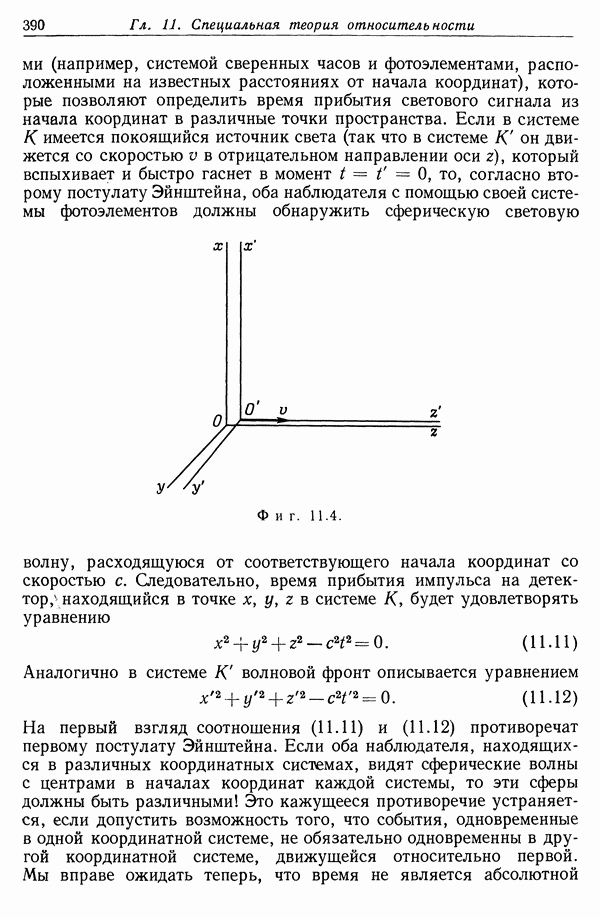
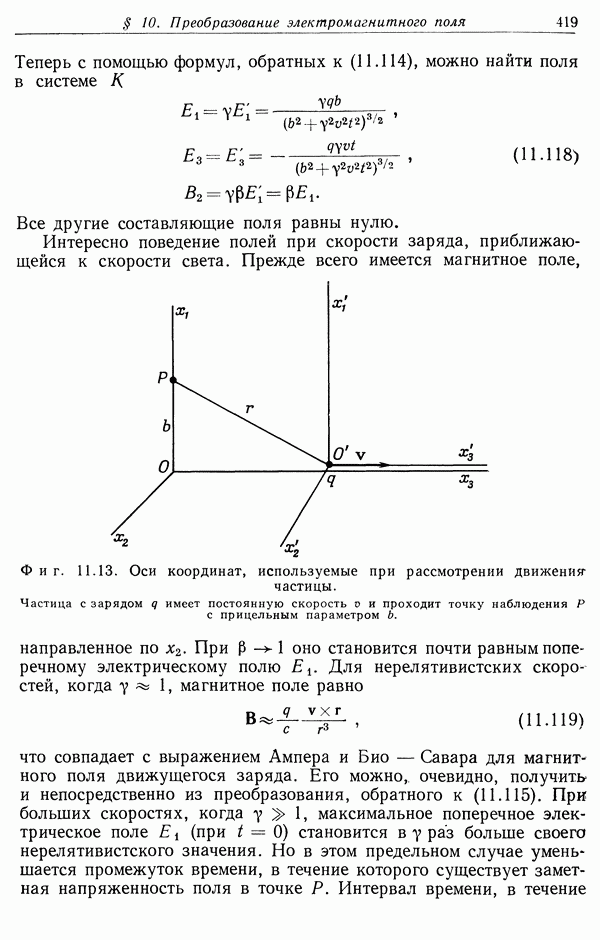
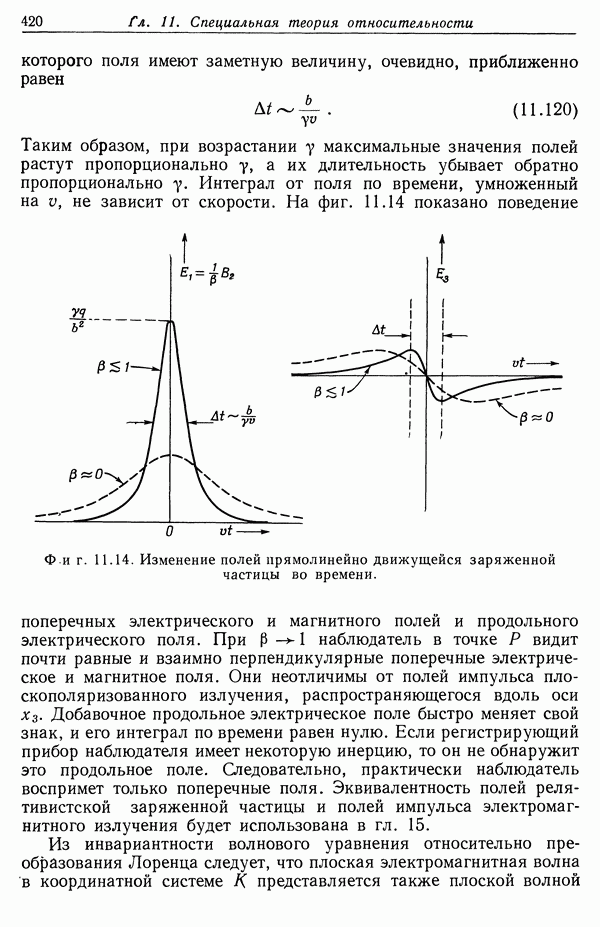
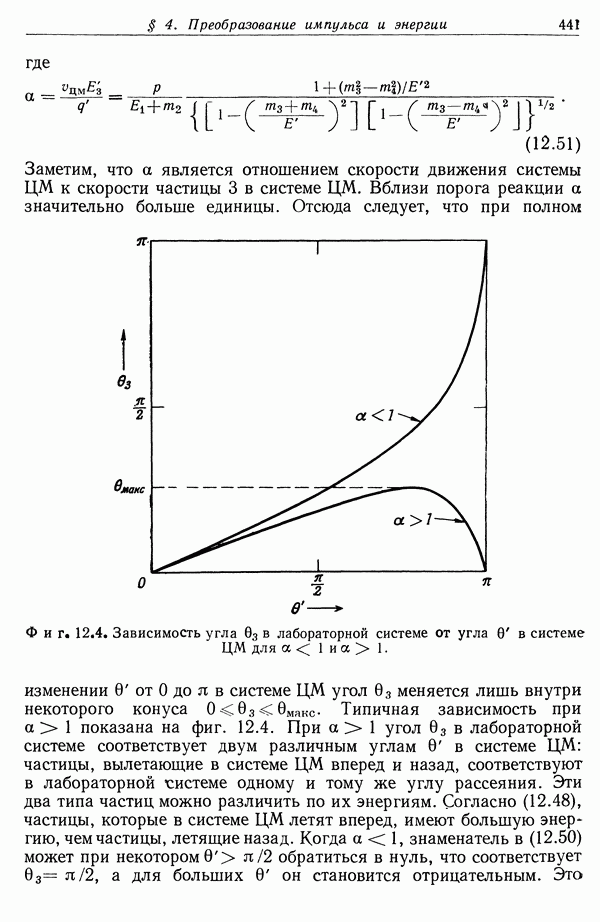
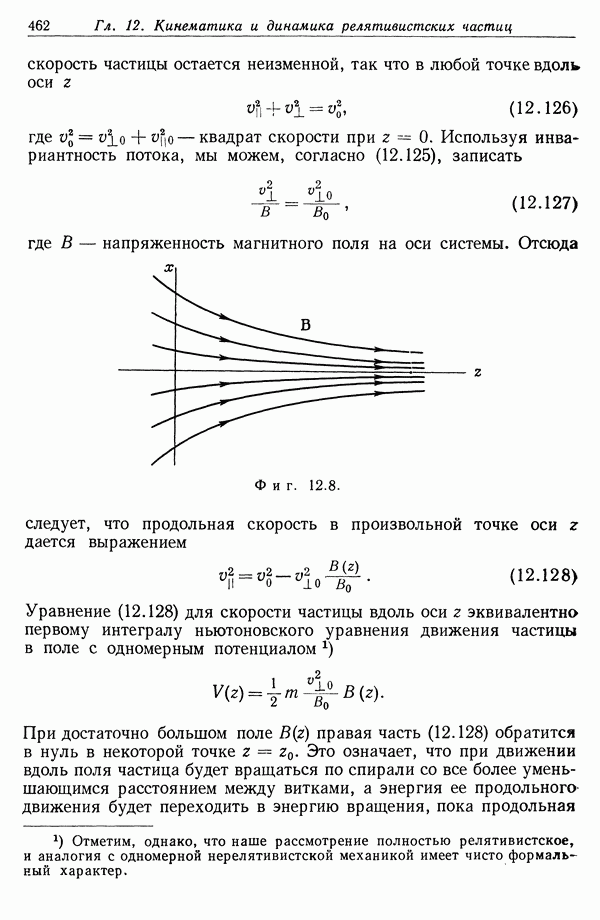
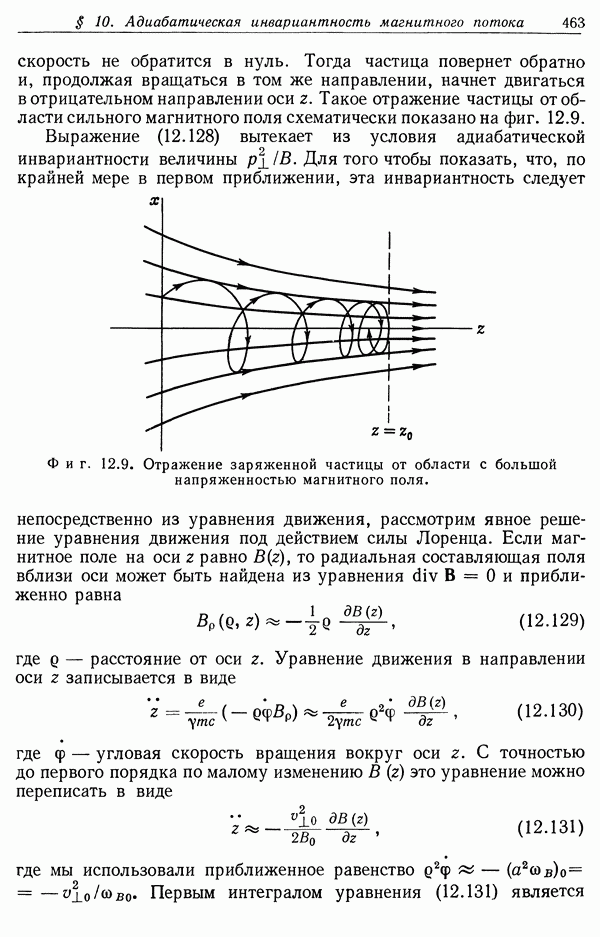
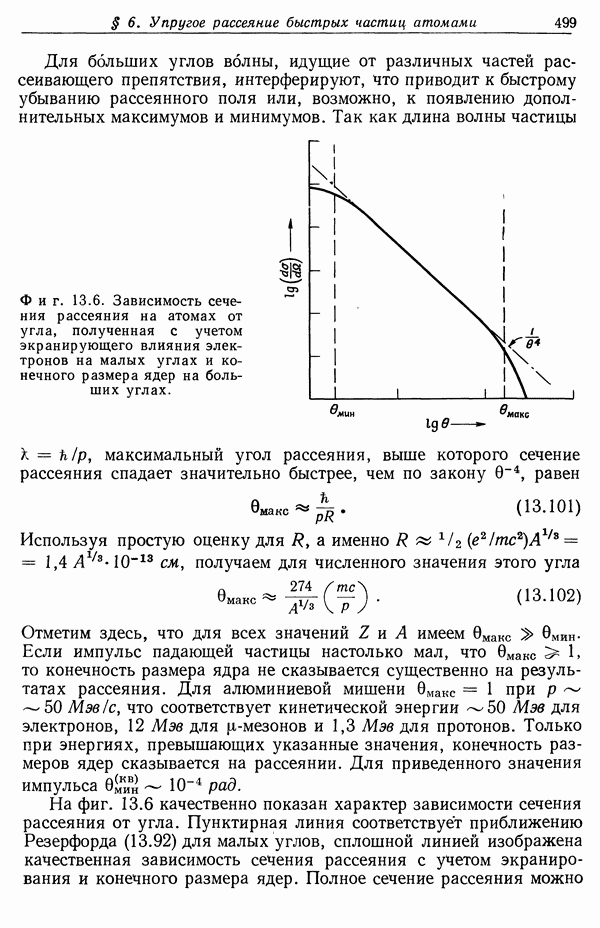
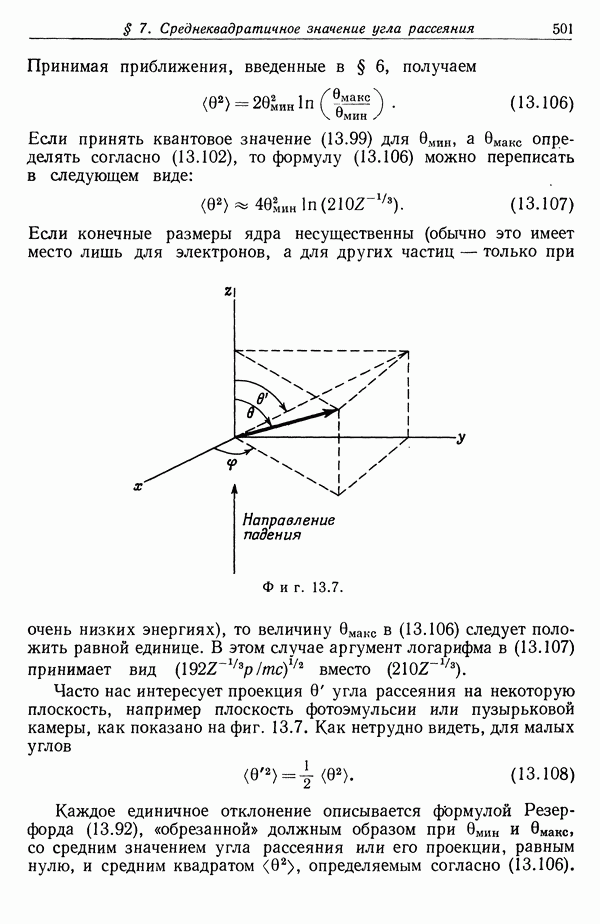
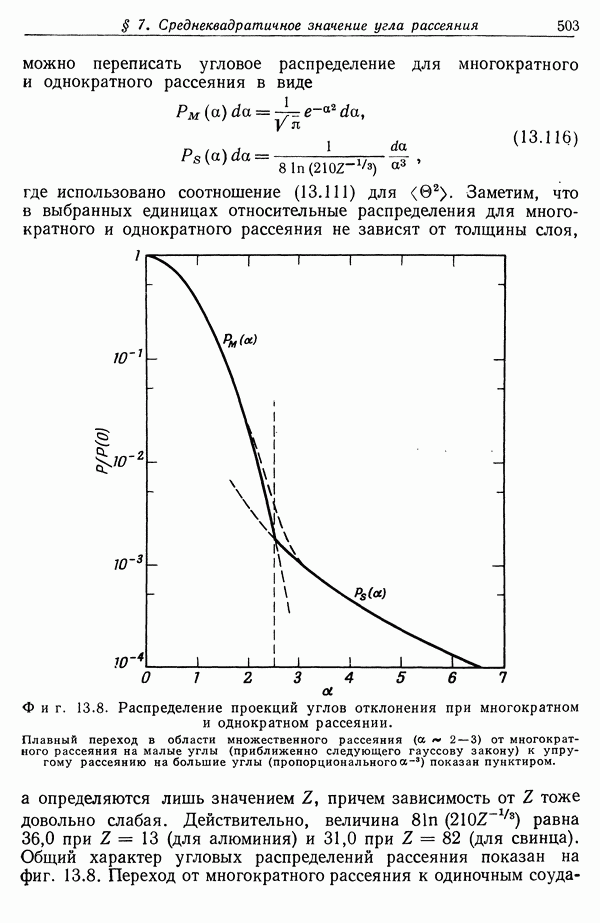
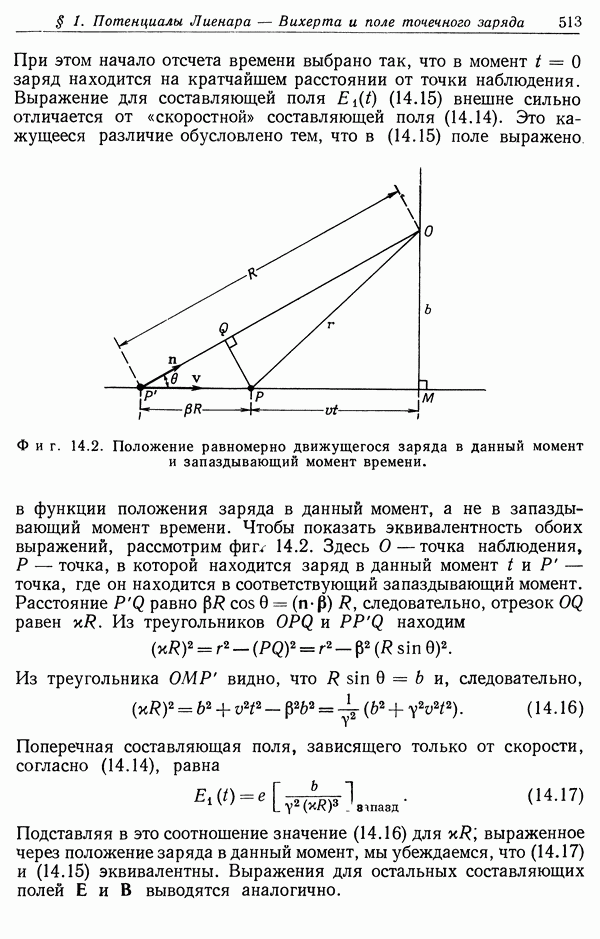
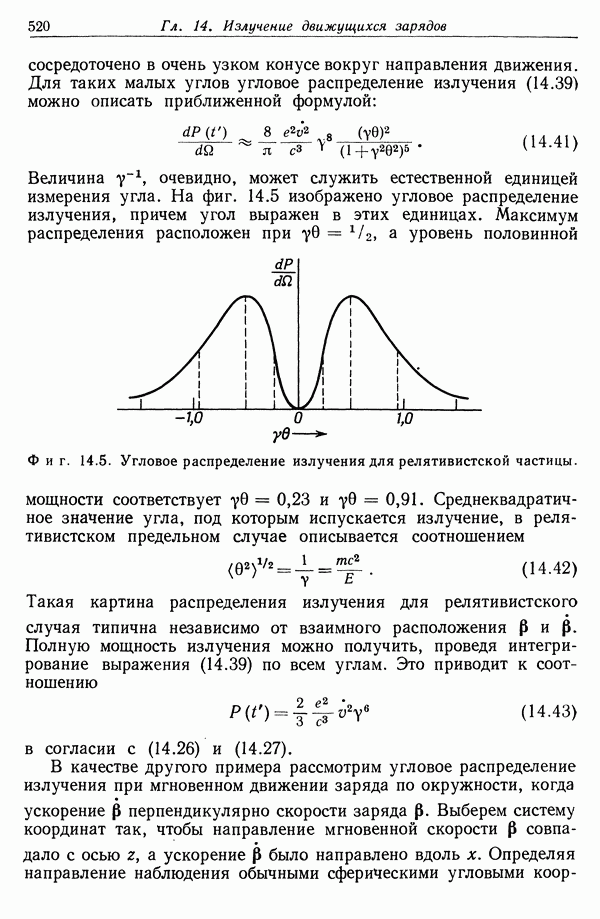
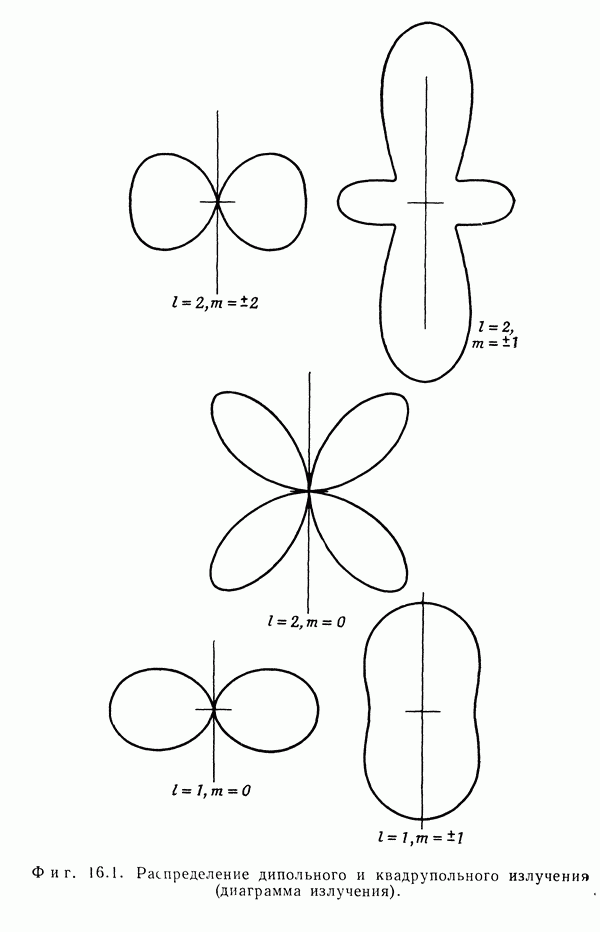
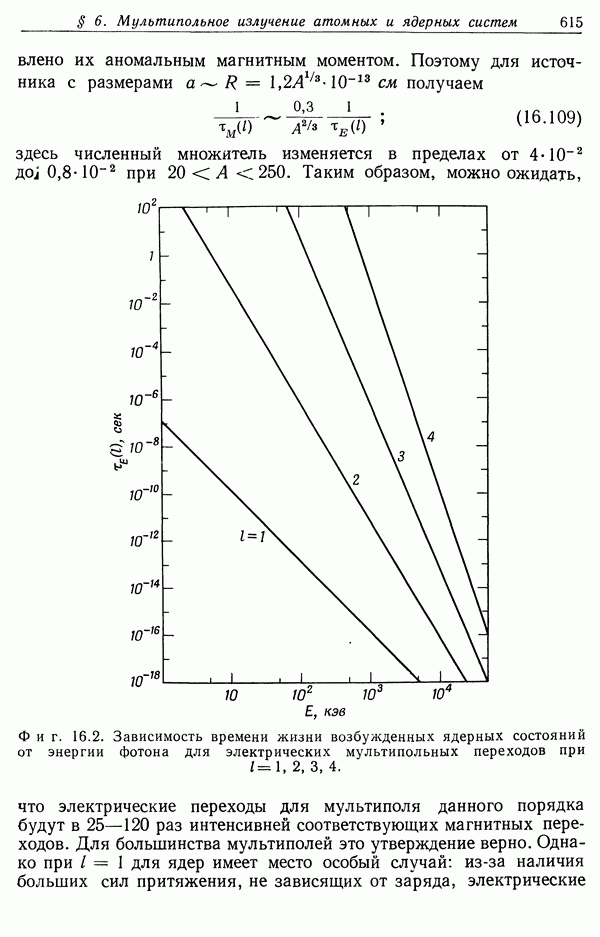
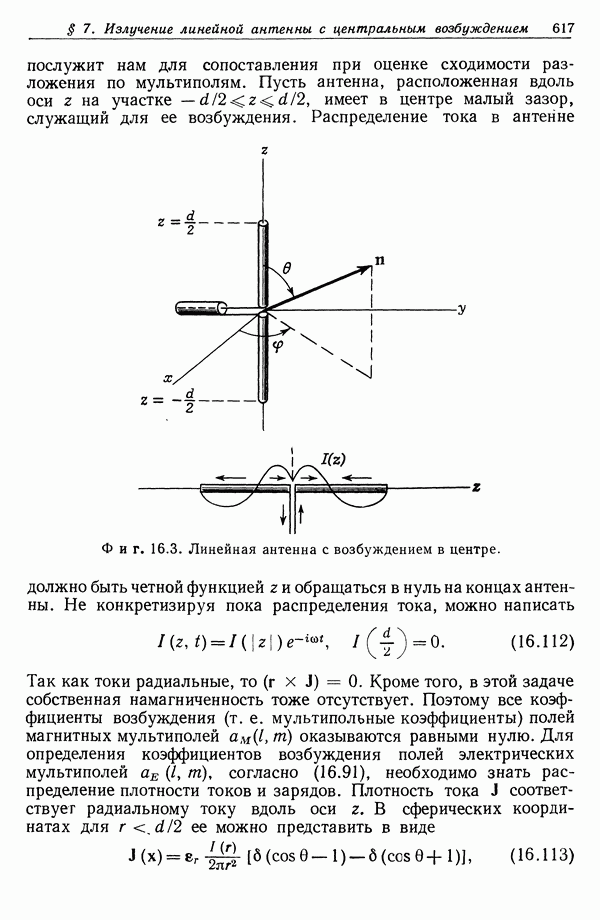
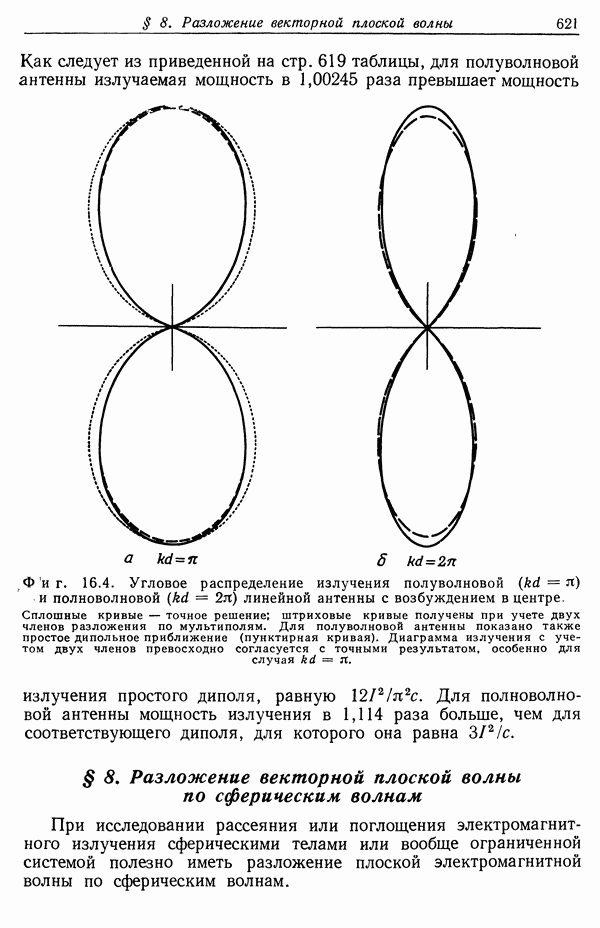
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
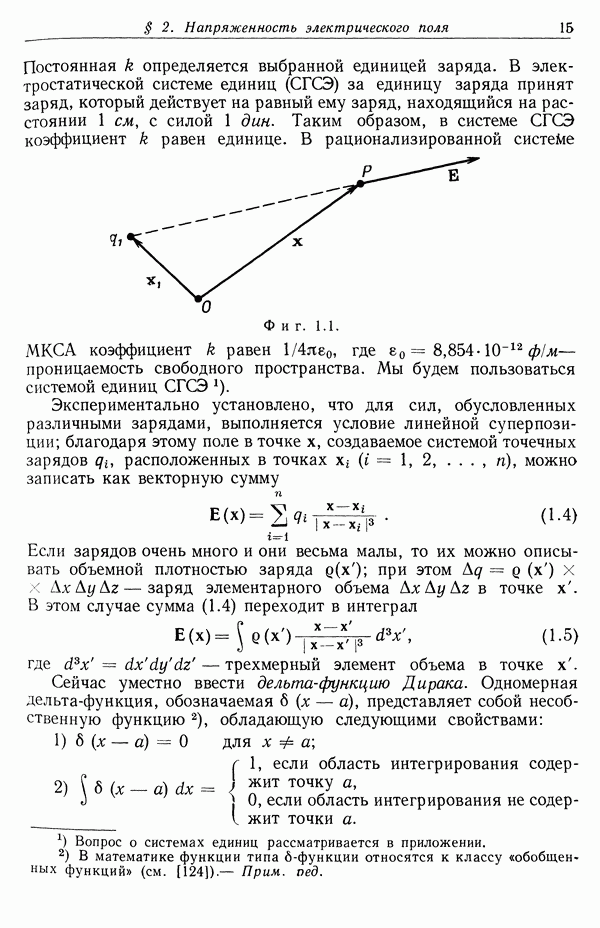
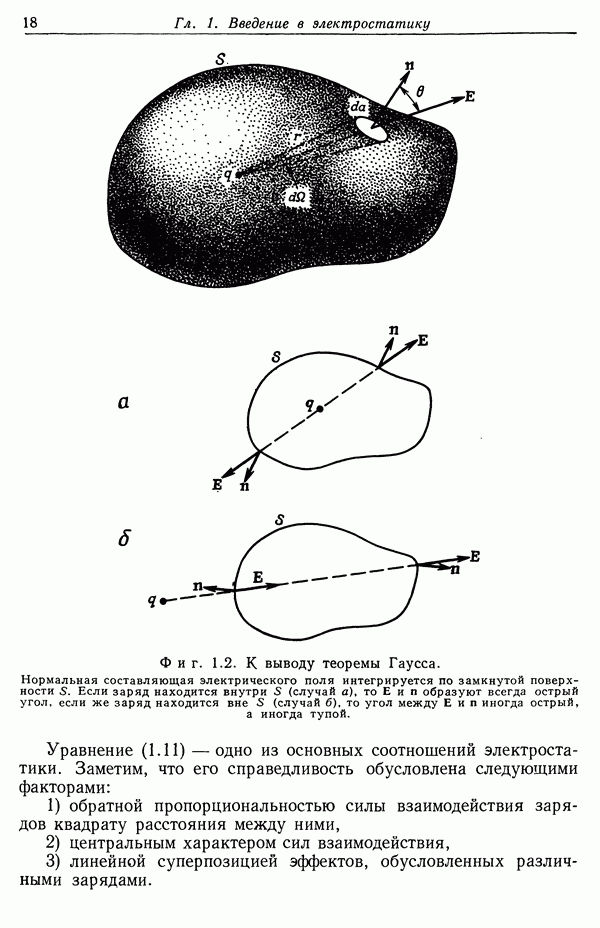
В § 1 мы рассмотрели уравнения движения под действием силы Лоренца для нахождения трансформационных свойств импульса и энергии частицы. Однако мы в явном виде не проверили ковариантность уравнений движения для частицы, движущейся во внешних полях. Теперь мы установим эту ковариантность, а также введем лагранжиан, канонические импульсы и гамильтониан. Согласно уравнениям (12.2) и (11.129), уравнение движения частицы можно записать в виде
 (12.62)
(12.62)
где интегрирование производится по объему заряженной частицы. Если скорость частицы v, а ее полный заряд  то
то
 (12.63)
(12.63)
где  для
для  . Это уравнение еще не является ковариантным, поскольку
. Это уравнение еще не является ковариантным, поскольку  не является
не является  -вектором, так же как и
-вектором, так же как и  . Последний недостаток можно исправить, если взять производные не по t, а по собственному времени
. Последний недостаток можно исправить, если взять производные не по t, а по собственному времени  (11.62). Так как
(11.62). Так как  то мы получаем
то мы получаем
 (12.64)
(12.64)
Но теперь  является
является  -вектором (называемым иногда
-вектором (называемым иногда  -скоростью), и мы приходим к ковариантной форме уравнения движения частицы
-скоростью), и мы приходим к ковариантной форме уравнения движения частицы

Это уравнение, относящееся к дискретной частице, является аналогом уравнения (11.129) для непрерывно распределенных зарядов и токов. Теперь, установив ковариантность уравнения движения частицы (12.65), мы можем записать его в пространственно-временной форме для любой системы отсчета:

Из (12.65) следует, что коль скоро все переменные преобразуются в соответствии с присущими им законами преобразования, то нековариантная форма (12.66) будет справедлива в произвольной лоренцовской системе координат.
Уравнения (12.65) или (12.66) полностью описывают движение заряженной частицы в произвольных внешних полях. Однако иногда более удобно использовать метод уравнений Лагранжа или Гамильтона. Нахождение лагранжиана для частицы, движущейся под действием силы Лоренца, мы начнем со случая свободной релятивистской частицы. Поскольку лагранжиан должен быть функцией скоростей и координат, запишем уравнение движения для свободной частицы в виде
 (12.67)
(12.67)
где  Лагранжиан L должен быть выбран таким образом, чтобы уравнения движения Эйлера — Лагранжа
Лагранжиан L должен быть выбран таким образом, чтобы уравнения движения Эйлера — Лагранжа

совпадали с ньютоновскими уравнениями движения. Легко убедиться, что для свободной частицы подходящим лагранжианом
является функция
 (12.69)
(12.69)
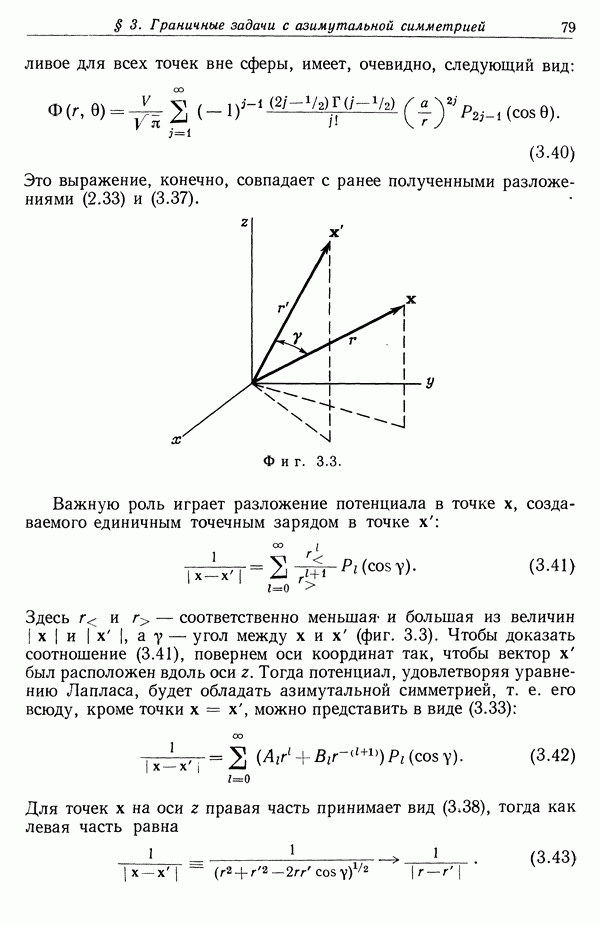
При подстановке в (12.68) этот лагранжиан приводит, очевидно, к уравнениям (12.67).
Чтобы получить лагранжиан свободной частицы более изящным способом, рассмотрим принцип Гамильтона, или принцип наименьшего действия. Согласно этому принципу, движение механической системы таково, что при переходе от состояния а, соответствующего моменту времени  к состоянию b, соответствующего моменту
к состоянию b, соответствующего моменту  должен быть экстремален (в данном случае минимален) интеграл действия
должен быть экстремален (в данном случае минимален) интеграл действия  , определенный как интеграл по времени от лагранжиана вдоль пути системы:
, определенный как интеграл по времени от лагранжиана вдоль пути системы:
 (12.70)
(12.70)
Рассматривая малые вариации выбранного пути и налагая условие  мы придем к уравнениям движения Эйлера — Лагранжа (12.68). Для нахождения лагранжиана свободной частицы мы используем теперь лоренц-инвариантность интеграла действия. Лоренц-инвариантность интеграла действия следует из первого постулата относительности, поскольку уравнения движения определяются требованием его экстремальности. При введении собственного времени
мы придем к уравнениям движения Эйлера — Лагранжа (12.68). Для нахождения лагранжиана свободной частицы мы используем теперь лоренц-инвариантность интеграла действия. Лоренц-инвариантность интеграла действия следует из первого постулата относительности, поскольку уравнения движения определяются требованием его экстремальности. При введении собственного времени  интеграл действия принимает вид
интеграл действия принимает вид
 (12.71)
(12.71)
Поскольку собственное время лоренц-инвариантно, то условие лоренц-инвариантности А приводит к требованию лоренц-инвариантности  . Это требование является общим для любого лагранжиана. Для свободной частицы LCB может быть функцией только скорости частицы (и, возможно, ее массы). Единственной лоренц-инвариантной величиной, содержащей скорость, является произвольная функция от скалярного произведения
. Это требование является общим для любого лагранжиана. Для свободной частицы LCB может быть функцией только скорости частицы (и, возможно, ее массы). Единственной лоренц-инвариантной величиной, содержащей скорость, является произвольная функция от скалярного произведения  )
)  где есть
где есть  -импульс частицы. Поскольку
-импульс частицы. Поскольку  мы видим, что
мы видим, что  для свободной частицы является постоянной величиной
для свободной частицы является постоянной величиной
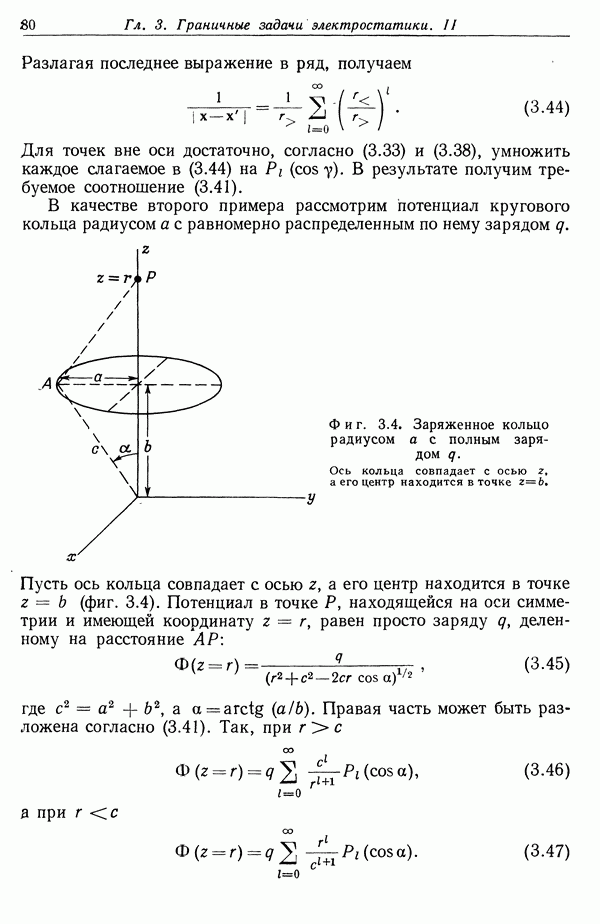
 (12.72)
(12.72)
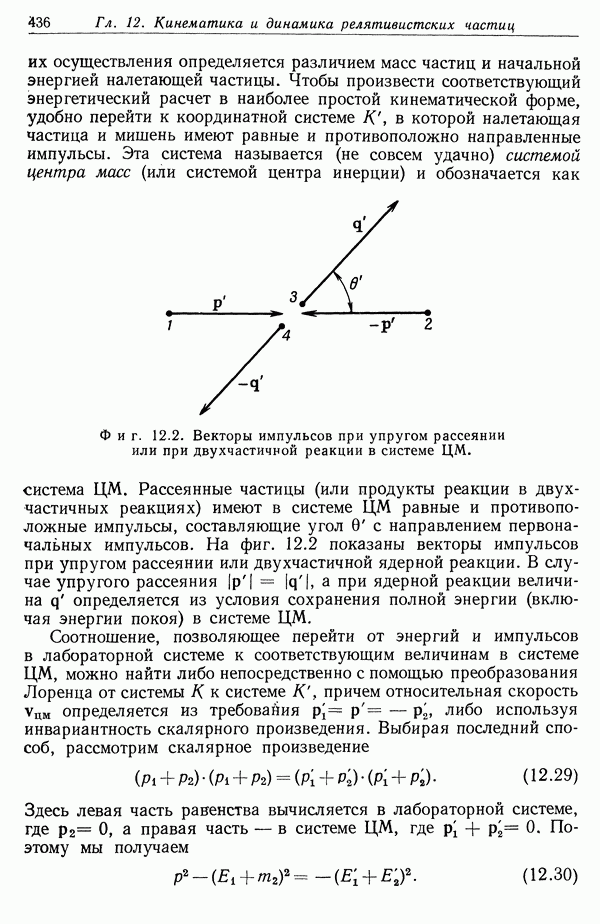
Таким образом, для свободной частицы интеграл действия пропорционален интегралу от собственного времени по пути от начальной пространственно-временной точки а до конечной пространственно-временной точки  . Этот интеграл является лоренц-инвариантом,
. Этот интеграл является лоренц-инвариантом,
но зависит от выбранного пути. Для удобства расчета рассмотрим систему отсчета, в которой частица в начальный момент покоится. Из определения собственного времени (11.62) ясно, что если частица в этой системе находится в состоянии покоя, то интеграл по собственному времени будет больше, чем при ее движении с любой отличной от нуля скоростью вдоль некоторой траектории. Следовательно, для прямой мировой линии, соединяющей начальную и конечную точки пути, интеграл от собственного времени максимален, что с учетом отрицательного знака в (12.72) соответствует минимуму интеграла действия. Сравнение с уравнением Ньютона для нерелятивистского движения показывает, что  Это приводит к лагранжиану для свободной частицы (12.69).
Это приводит к лагранжиану для свободной частицы (12.69).
Общее требование лоренц-инвариантности величины  позволяет определить лагранжиан для релятивистской заряженной частицы во внешних электромагнитных полях при условии, что мы знаем лагранжиан (или уравнения движения) для нерелятивистского движения в статических полях. На медленно движущуюся заряженную частицу действует в основном электрическое поле, которое определяется скалярным потенциалом Ф. Потенциальная энергия взаимодействия есть
позволяет определить лагранжиан для релятивистской заряженной частицы во внешних электромагнитных полях при условии, что мы знаем лагранжиан (или уравнения движения) для нерелятивистского движения в статических полях. На медленно движущуюся заряженную частицу действует в основном электрическое поле, которое определяется скалярным потенциалом Ф. Потенциальная энергия взаимодействия есть  . Так как нерелятивистский лагранжиан равен
. Так как нерелятивистский лагранжиан равен  то часть
то часть  релятивистского лагранжиана, соответствующая взаимодействию с электромагнитным полем, должна в нерелятивистском пределе сводиться к
релятивистского лагранжиана, соответствующая взаимодействию с электромагнитным полем, должна в нерелятивистском пределе сводиться к
 (12.73)
(12.73)
Теперь наша задача заключается в том, чтобы найти лоренц-инвариантное выражение для  которое для нерелятивистских скоростей приводит к выражению (12.73). Поскольку Ф является четвертой составляющей
которое для нерелятивистских скоростей приводит к выражению (12.73). Поскольку Ф является четвертой составляющей  -вектора-потенциала Аследует ожидать, что
-вектора-потенциала Аследует ожидать, что  содержит скалярное произведение А на некоторый
содержит скалярное произведение А на некоторый  -век-тор. Таким
-век-тор. Таким  -вектором может быть лишь вектор импульса или вектор координаты частицы. Так как произведение
-вектором может быть лишь вектор импульса или вектор координаты частицы. Так как произведение  наряду с лоренц-инвариантностью должно обладать также и трансляционной инвариантностью, то оно не может явно содержать координат. Следовательно, лагранжиан взаимодействия имеет видг)
наряду с лоренц-инвариантностью должно обладать также и трансляционной инвариантностью, то оно не может явно содержать координат. Следовательно, лагранжиан взаимодействия имеет видг)
 (12-74)
(12-74)
где коэффициент при скалярном произведении выбран таким образом, чтобы при  это выражение переходило в (12.73).
это выражение переходило в (12.73).
Комбинируя (12.69) и (12.74), получаем полный релятивистский лагранжиан заряженной частицы

Здесь верхнее выражение дает L в  -векторной форме, а нижнее — в явной пространственно-временной форме. Мы предоставляем читателю убедиться самостоятельно, что лагранжиан (12.75) действительно приводит к уравнениям движения (12.66) заряженной частицы под действием силы Лоренца. При этом следует учесть, что материальная производная
-векторной форме, а нижнее — в явной пространственно-временной форме. Мы предоставляем читателю убедиться самостоятельно, что лагранжиан (12.75) действительно приводит к уравнениям движения (12.66) заряженной частицы под действием силы Лоренца. При этом следует учесть, что материальная производная  и воспользоваться обычными выражениями полей через потенциалы.
и воспользоваться обычными выражениями полей через потенциалы.
Канонический импульс Р, сопряженный с пространственной координатой  определяется соотношениями
определяется соотношениями
 (12.76)
(12.76)
Отсюда следует, что канонический импульс
 (12.77)
(12.77)
где  — импульс частицы в отсутствие полей. Гамильтониан Н является функцией координаты
— импульс частицы в отсутствие полей. Гамильтониан Н является функцией координаты  и сопряженного импульса Р. Если лагранжиан не зависит явно от времени, то Н является интегралом движения. Гамильтониан выражается через лагранжиан следующим образом:
и сопряженного импульса Р. Если лагранжиан не зависит явно от времени, то Н является интегралом движения. Гамильтониан выражается через лагранжиан следующим образом:
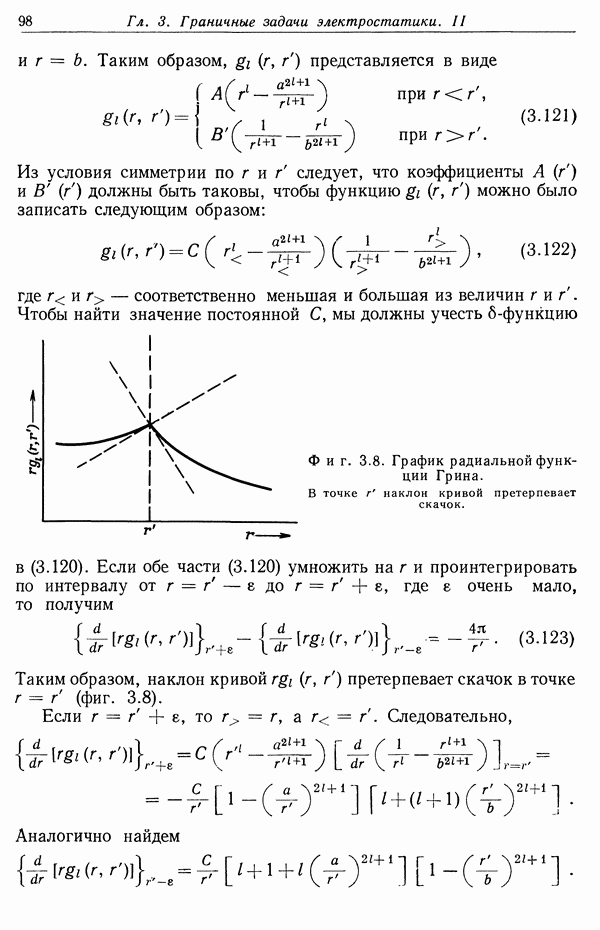
 (12.78)
(12.78)
где скорость v следует выразить через Р и  Согласно (12.76) или (12.77),
Согласно (12.76) или (12.77),

При подстановке этого выражения в (12.78) и в (12.75) гамильтониан примет вид

Читатель может проверить, что уравнения движения Гамильтона эквивалентны обычным уравнениям движения (12.66) под действием силы Лоренца. Выражение (12.80) для гамильтониана дает также
полную энергию W частицы; оно отличается от энергии свободной частицы добавлением потенциальной энергии  и заменой
и заменой  . В
. В  -векторной записи оба эти добавления сводятся к одному. Действительно, перенося
-векторной записи оба эти добавления сводятся к одному. Действительно, перенося  в левую часть равенства (12.80) и возводя обе части равенства в квадрат, получаем
в левую часть равенства (12.80) и возводя обе части равенства в квадрат, получаем
 (12.81)
(12.81)
Левая часть пропорциональна скалярному квадрату  -вектора
-вектора
 (12.82)
(12.82)
где
 (12.83)
(12.83)
Мы видим, что полная энергия W является четвертой составляющей канонически сопряженного  -импульса с пространственной частью (12.77). Еще одна возможная формулировка уравнений движения с релятивистски инвариантным лагранжианом, зависящим от
-импульса с пространственной частью (12.77). Еще одна возможная формулировка уравнений движения с релятивистски инвариантным лагранжианом, зависящим от  -скорости
-скорости  рассматривается в задаче 12.5. При этом канонический
рассматривается в задаче 12.5. При этом канонический  -импульс вводится весьма естественно.
-импульс вводится весьма естественно.
Лагранжева и гамильтонова формулировки динамики заряженной частицы были приведены здесь по ряду причин. Во-первых, мы показали, что требование лоренц-инвариантности в совокупности с другими физическими требованиями является мощным орудием систематического построения лагранжиана, позволяющим найти динамические уравнения движения. Во-вторых, лагранжиан часто используется как исходный пункт при рассмотрении динамики частиц. Наконец, идеи и методы канонически сопряженных переменных оказываются весьма полезными при непосредственном решении уравнений движения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
- § 2. Напряженность электрического поля
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
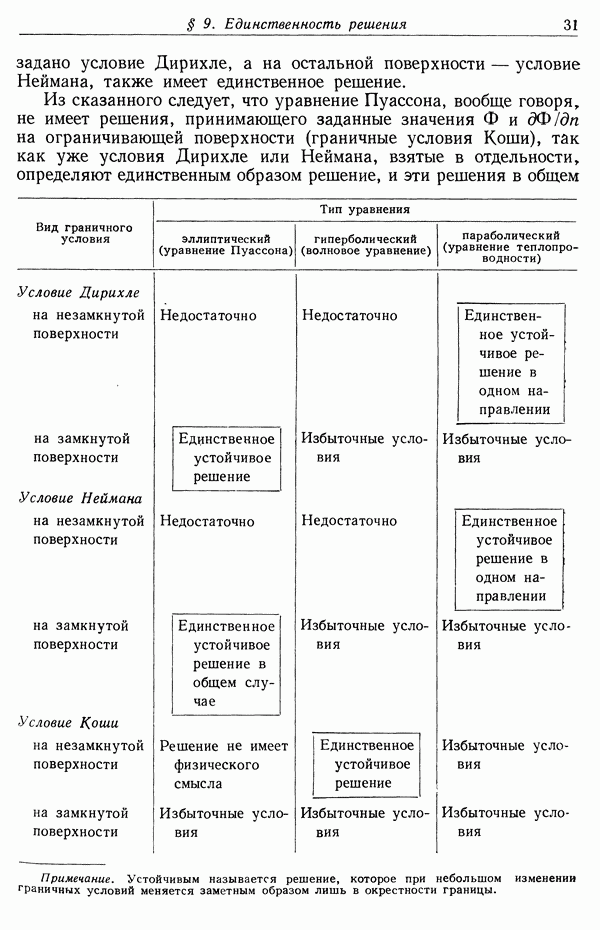
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
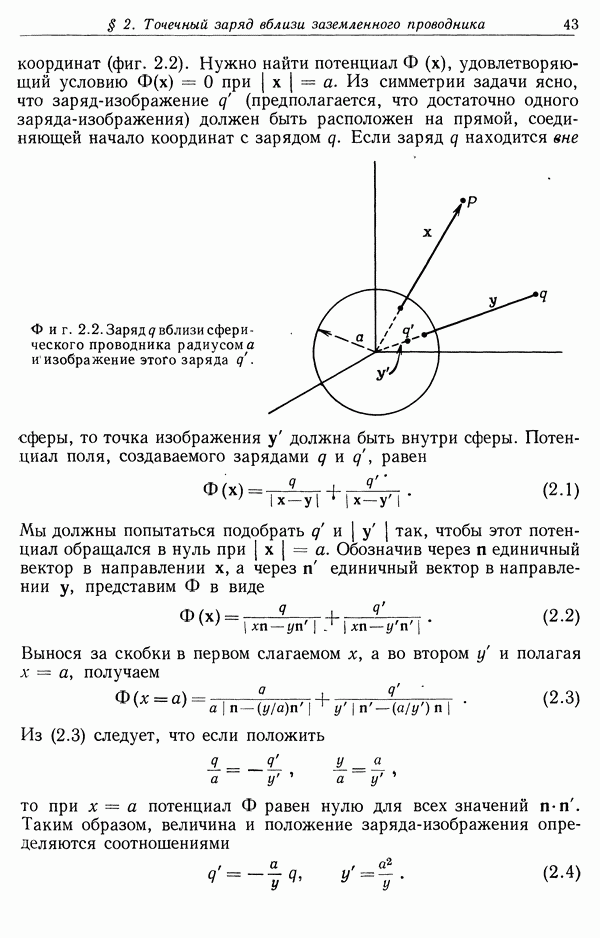
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
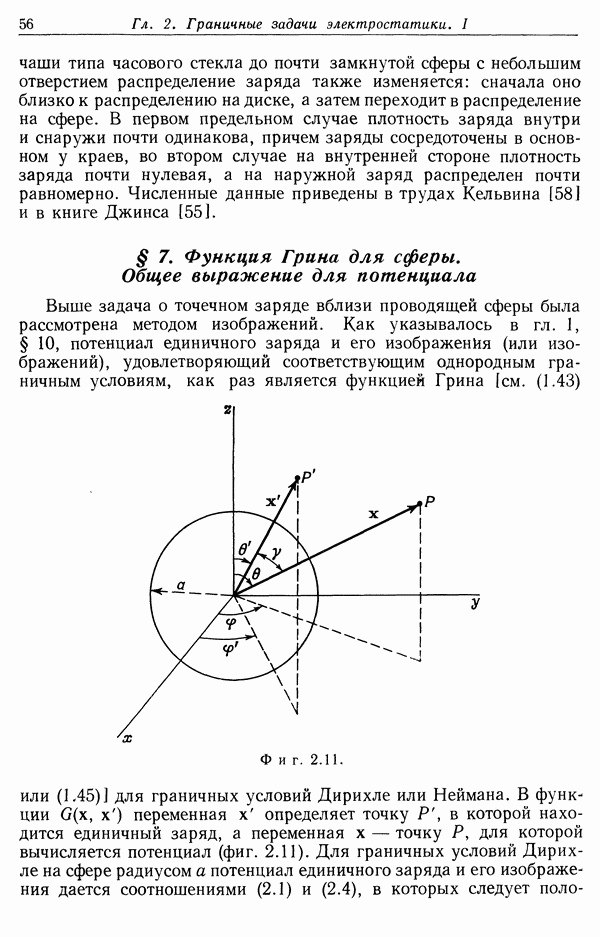
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
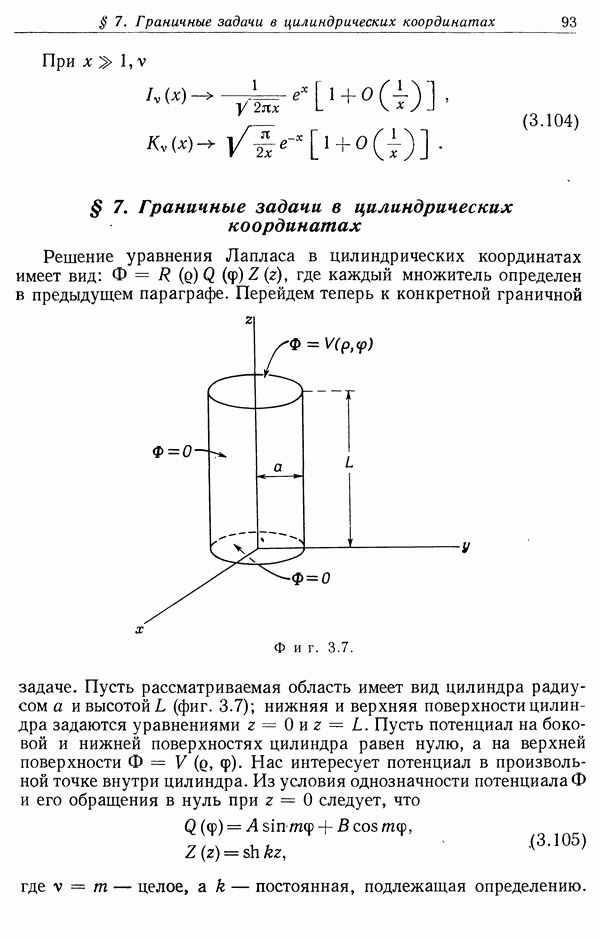
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
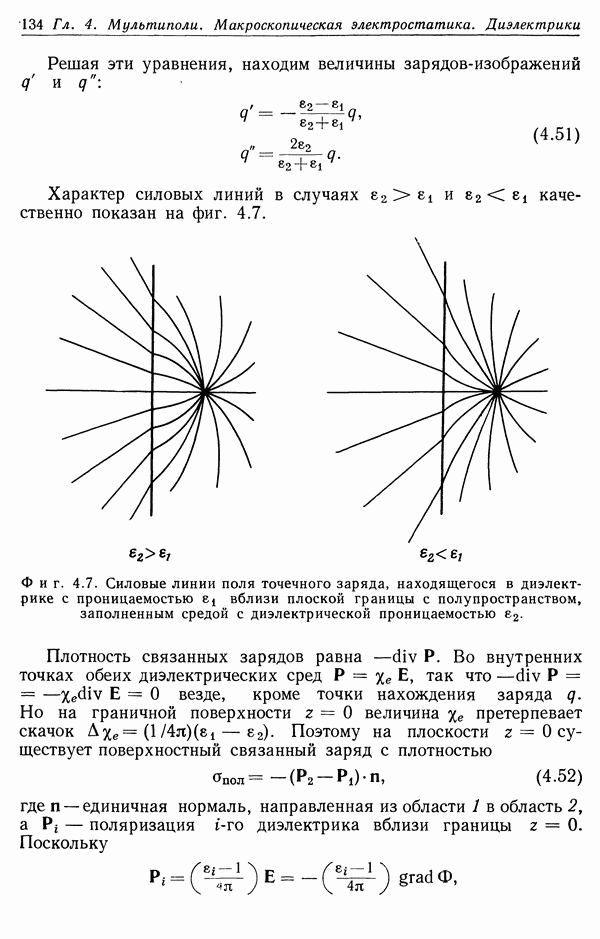
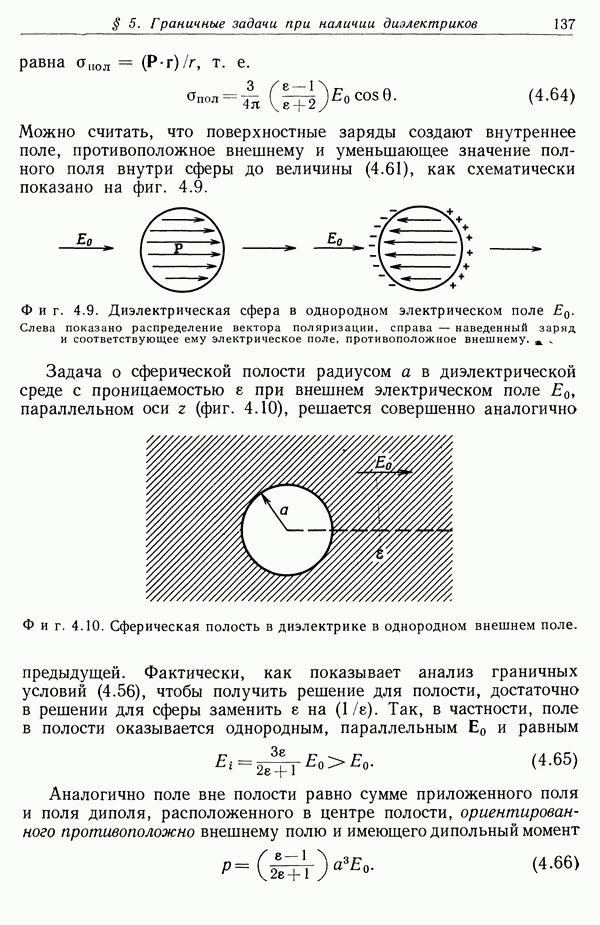
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
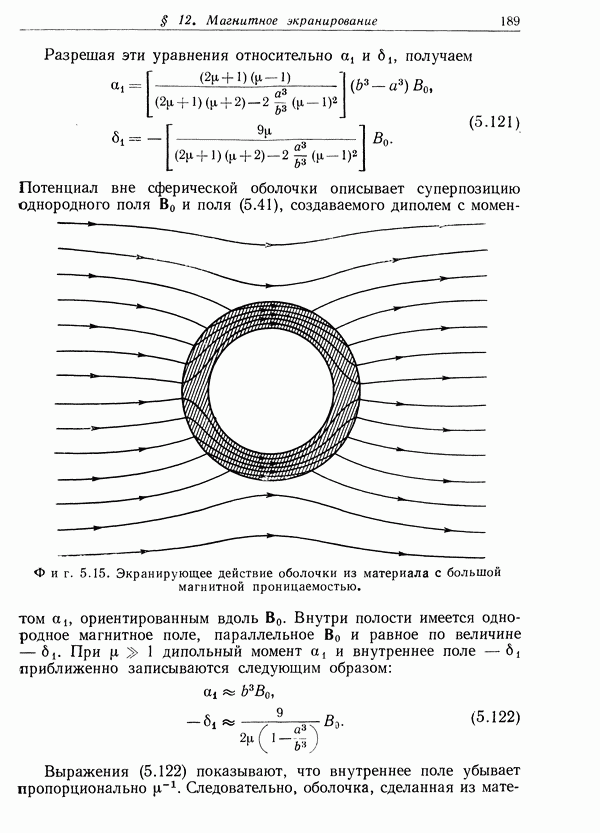
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
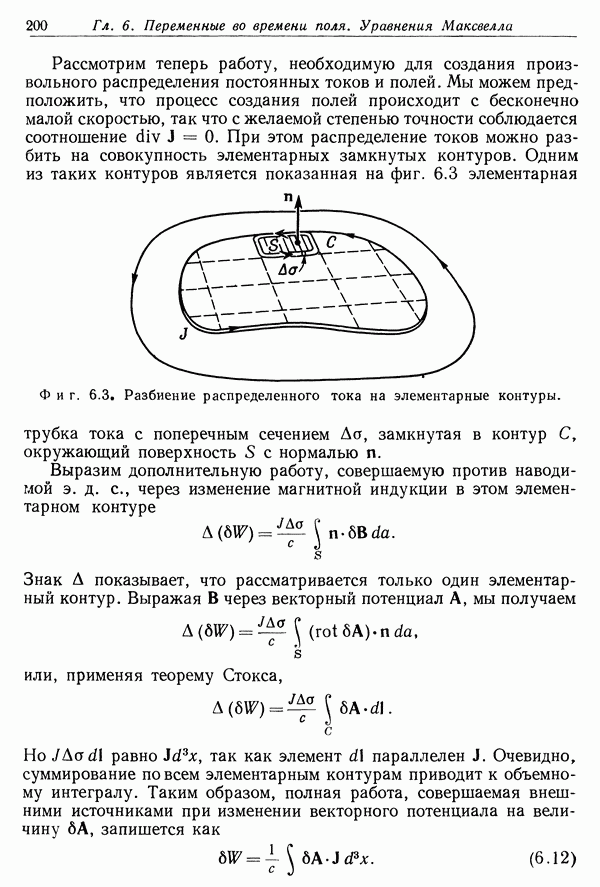
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 2. Линейная и круговая поляризация
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
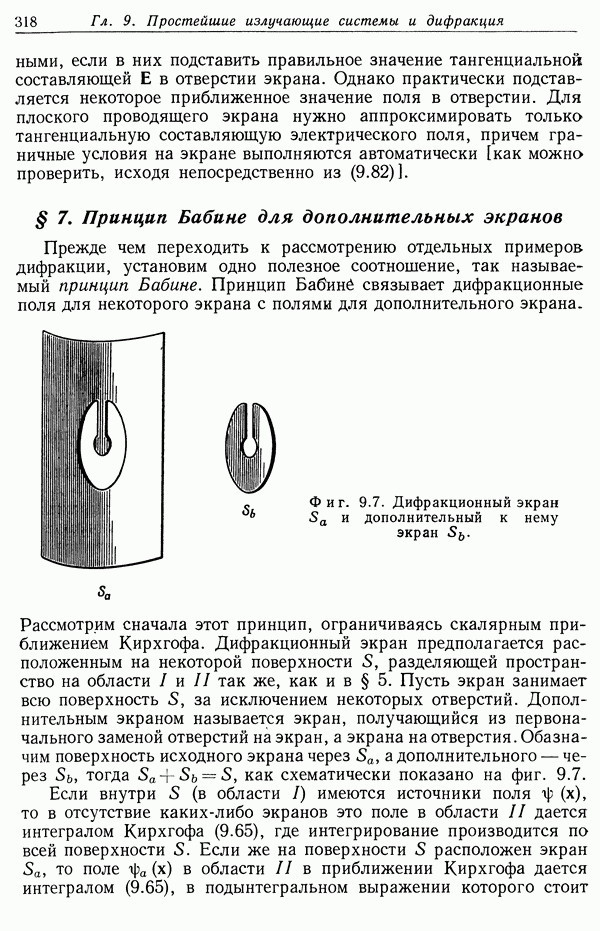
- § 7. Принцип Бабине для дополнительных экранов
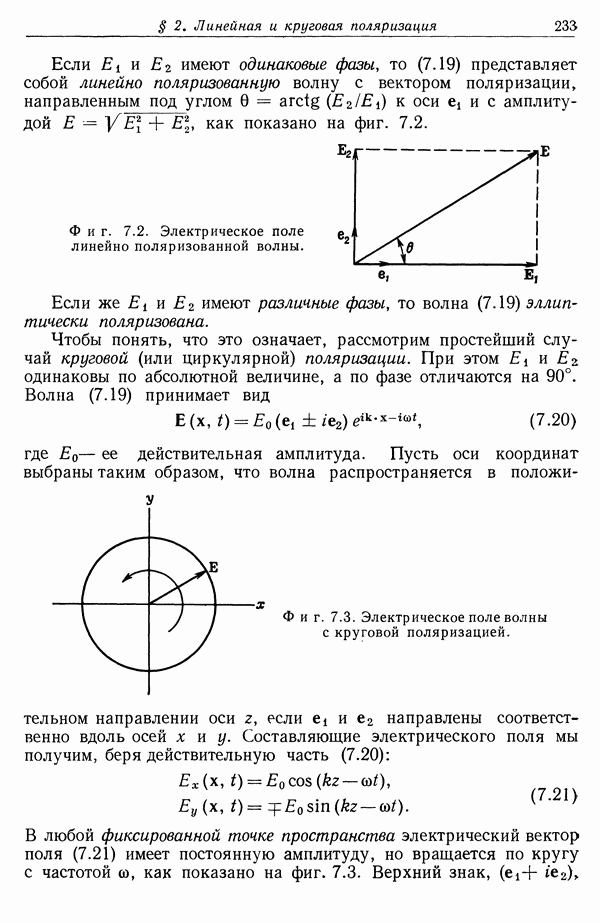
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
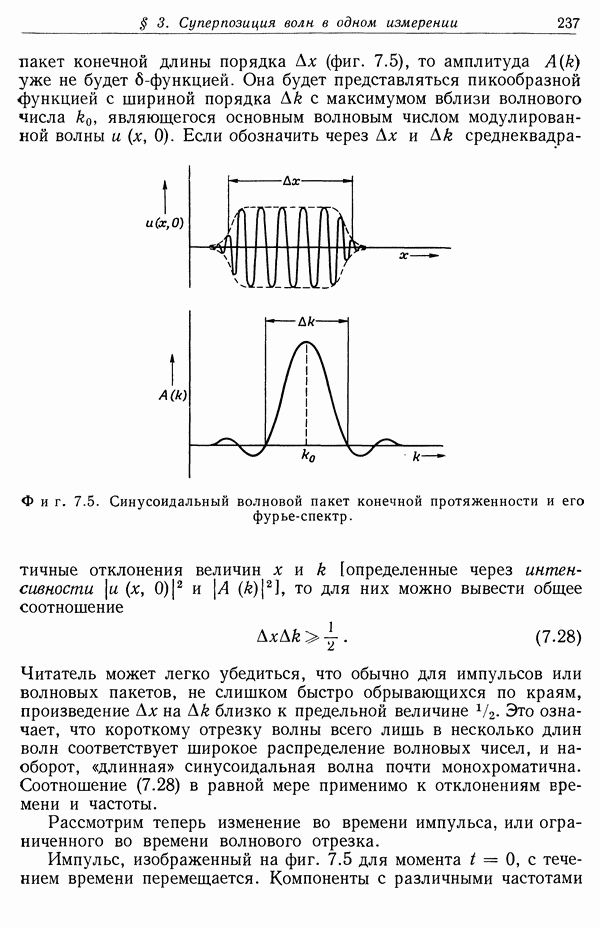
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
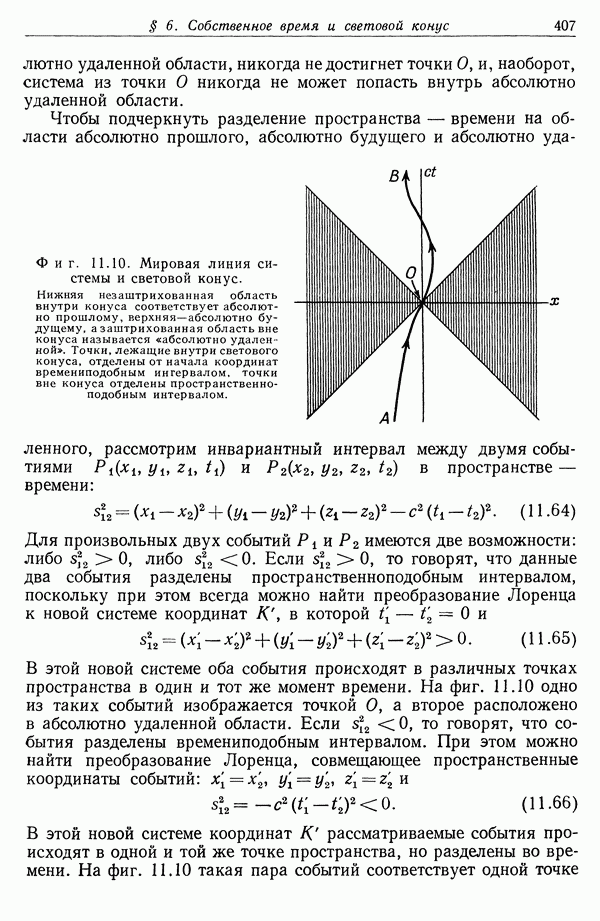
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
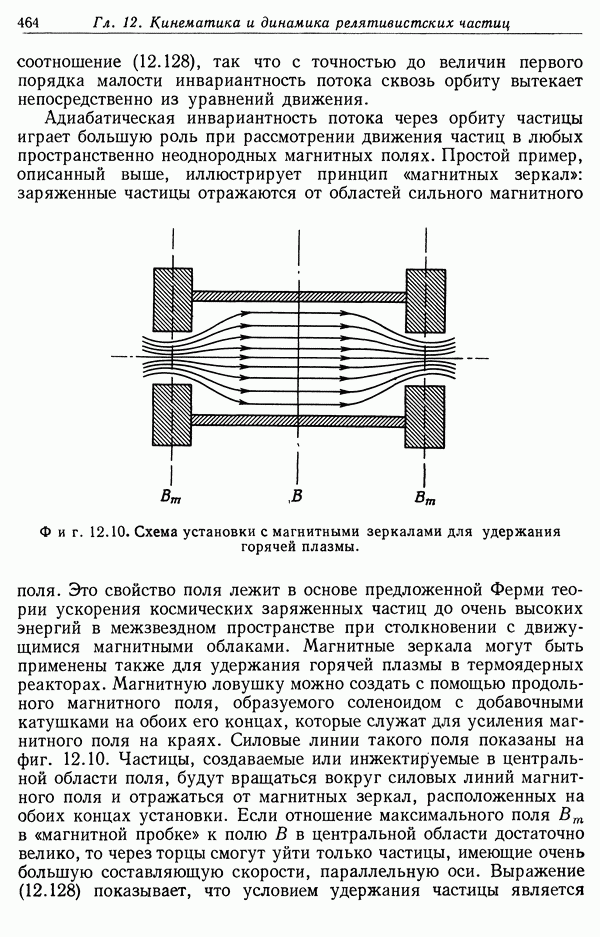
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
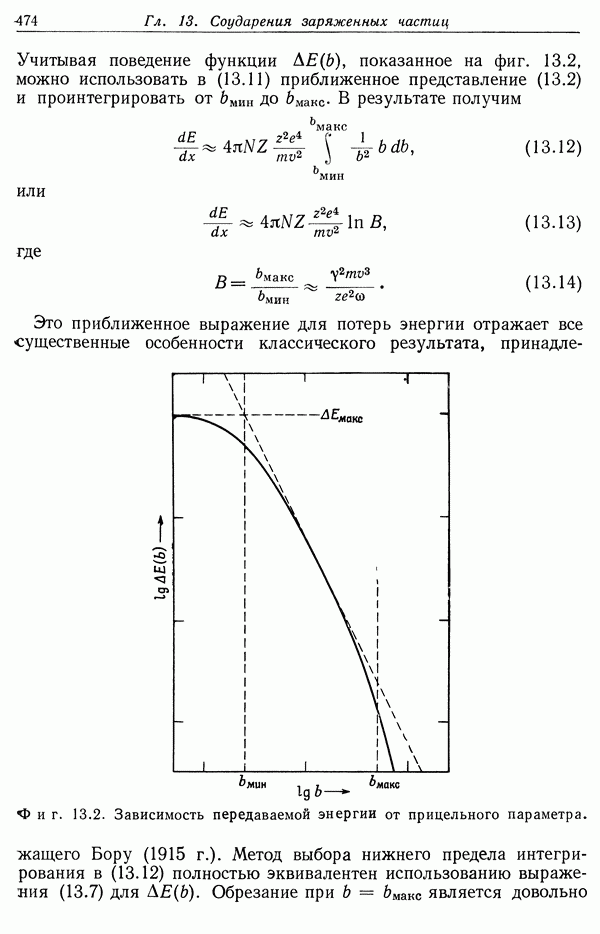
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
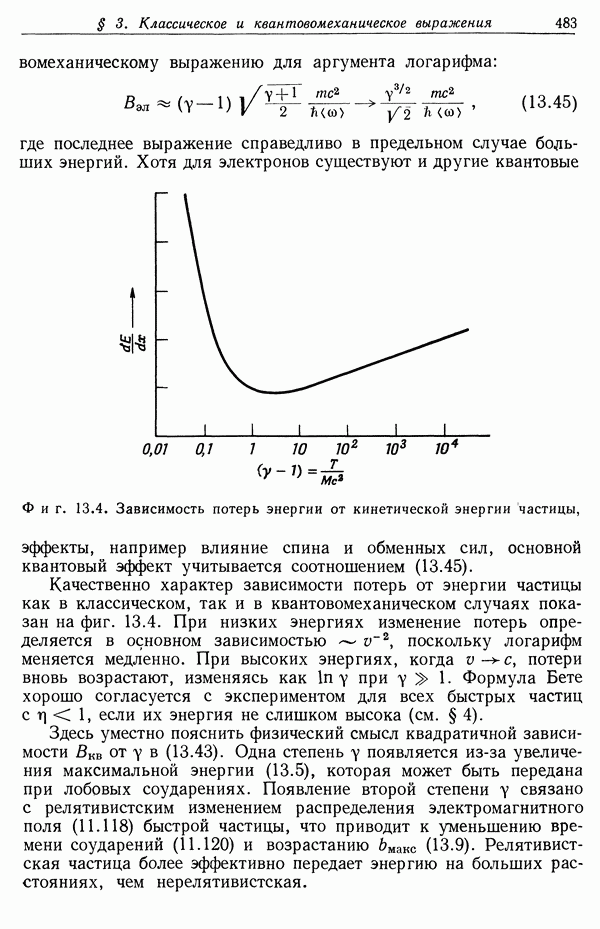
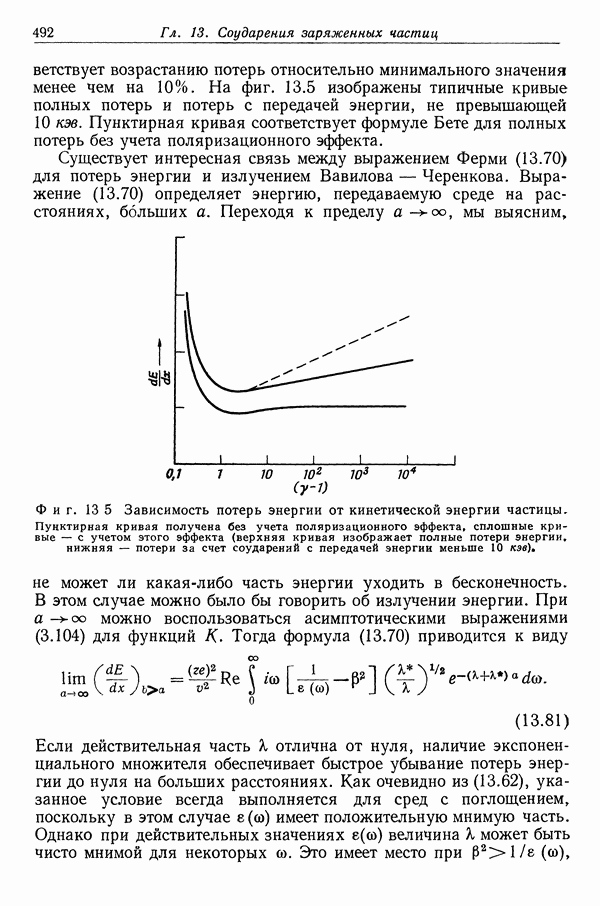
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
- § 3. Угловое распределение излучения ускоряемого заряда
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
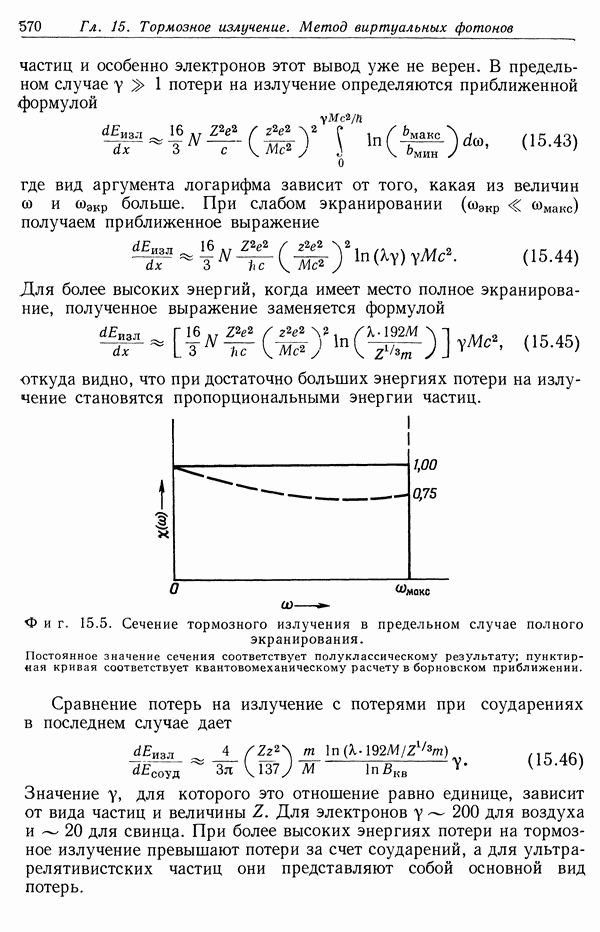
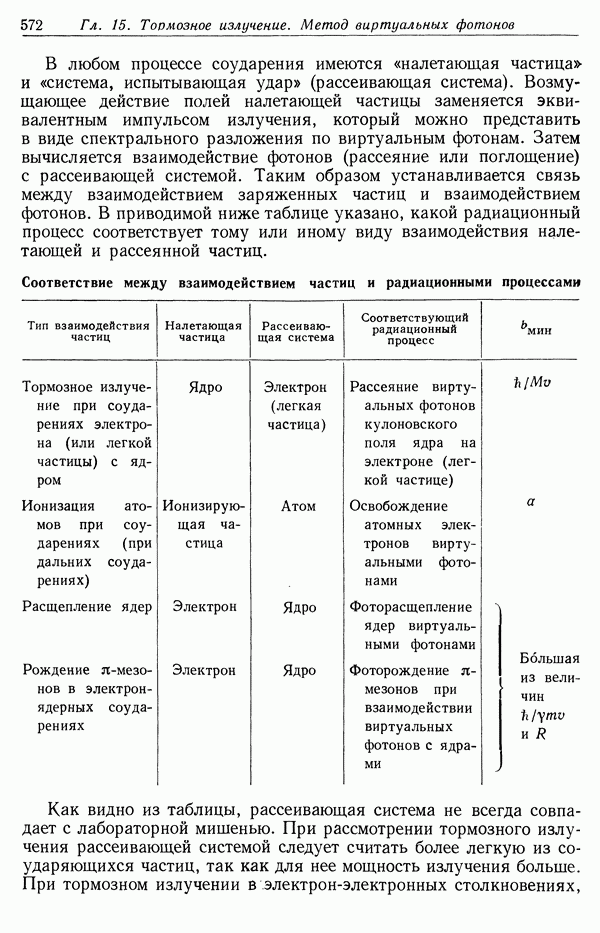
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
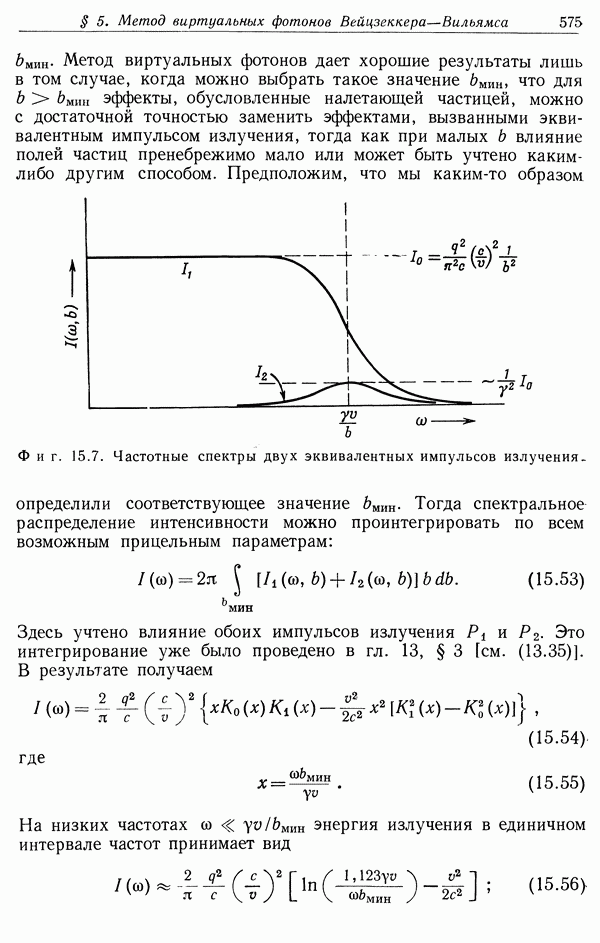
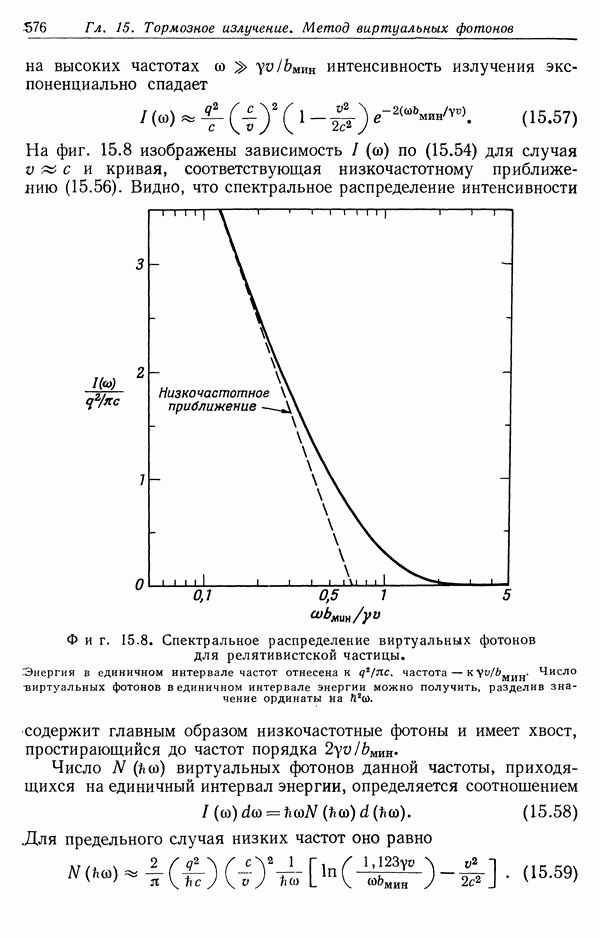
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ