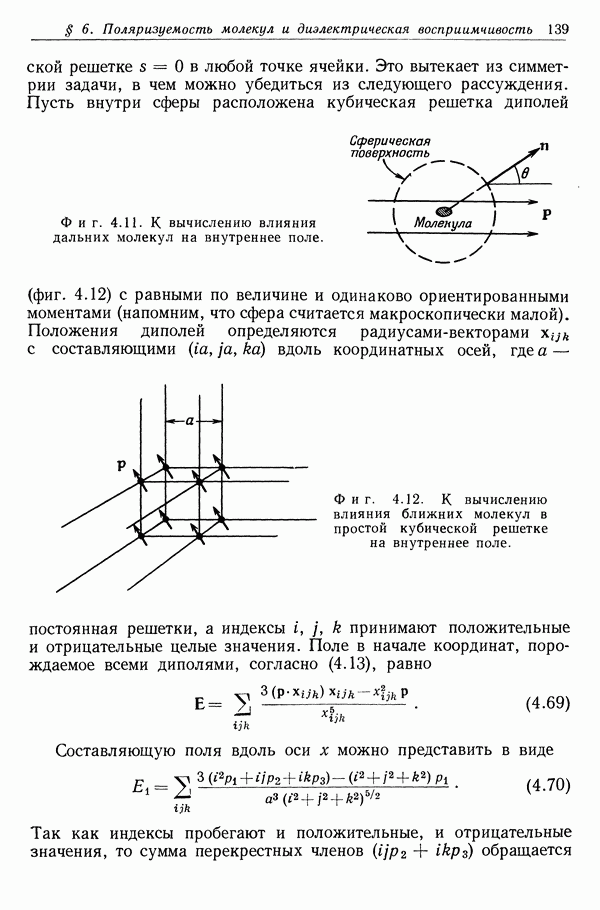
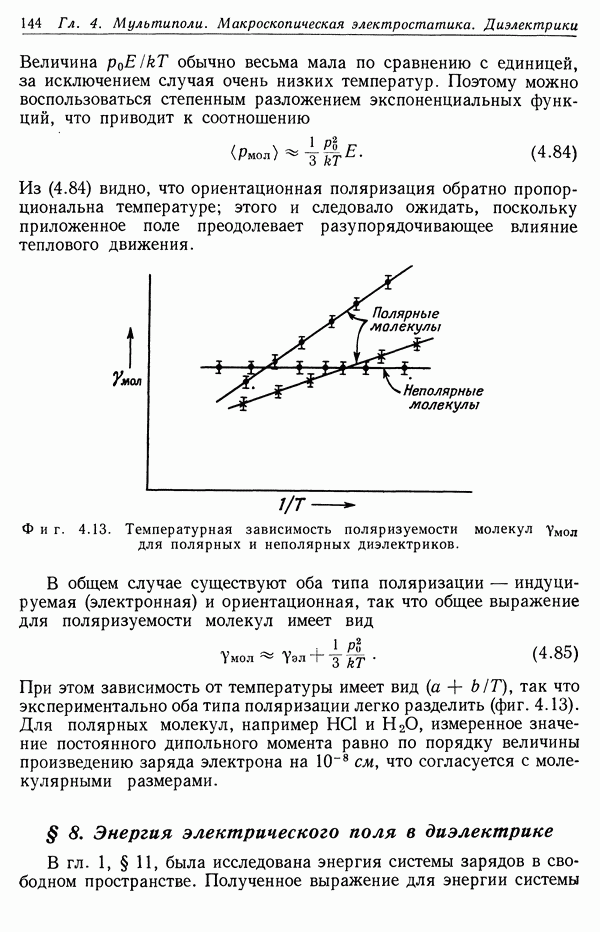
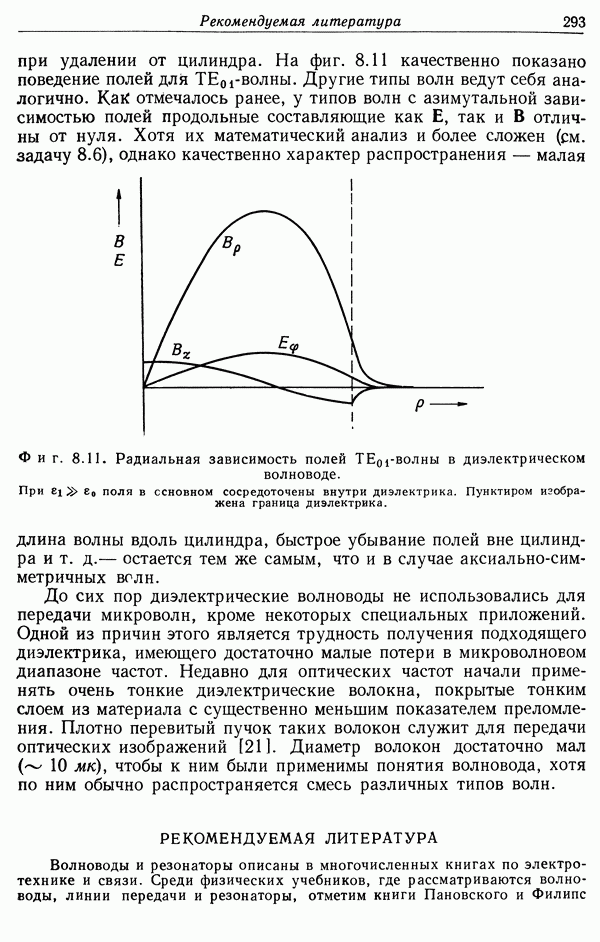
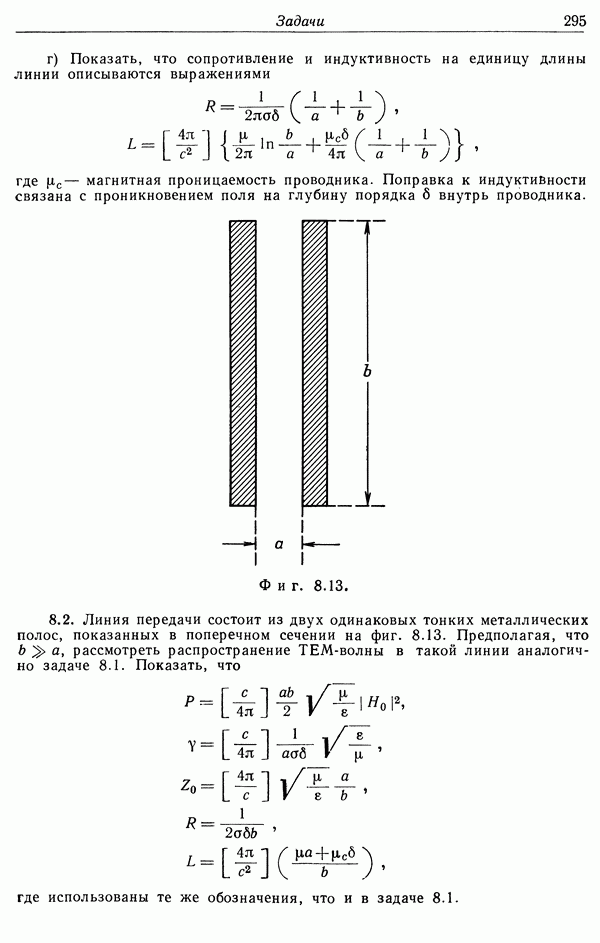
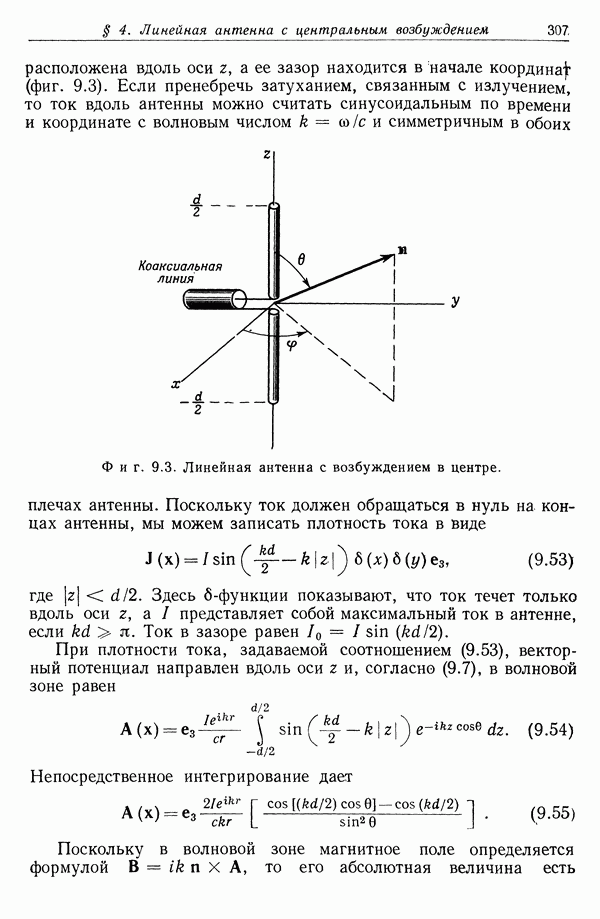
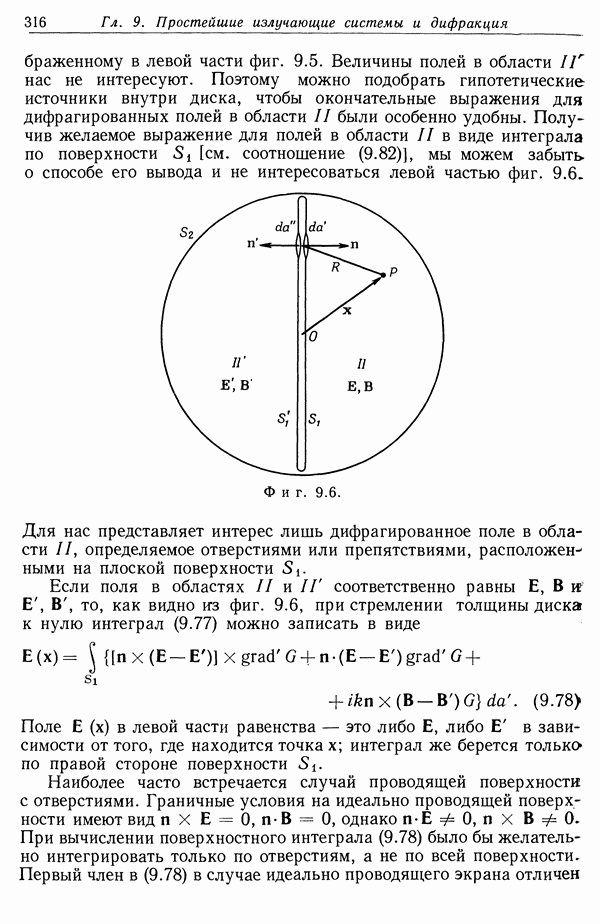
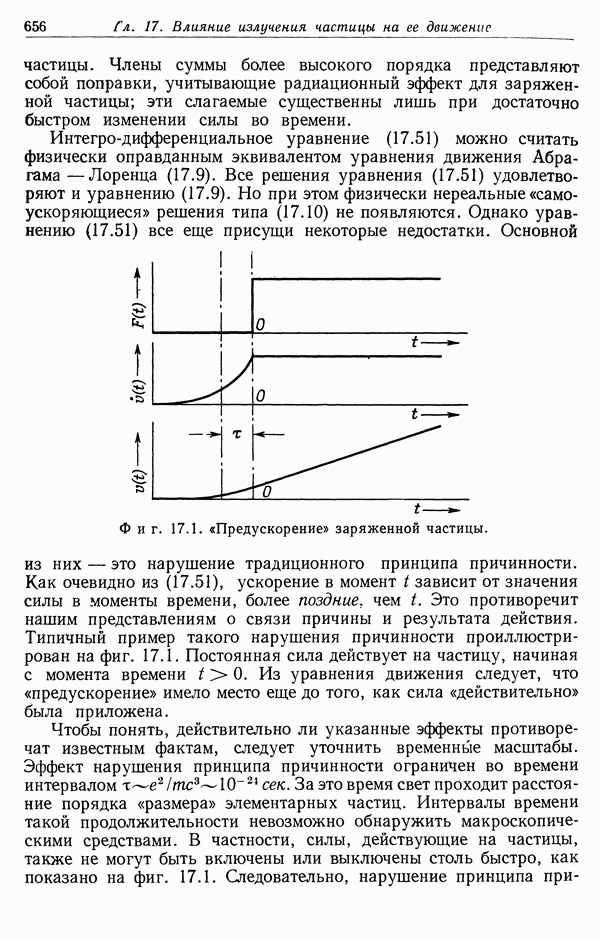
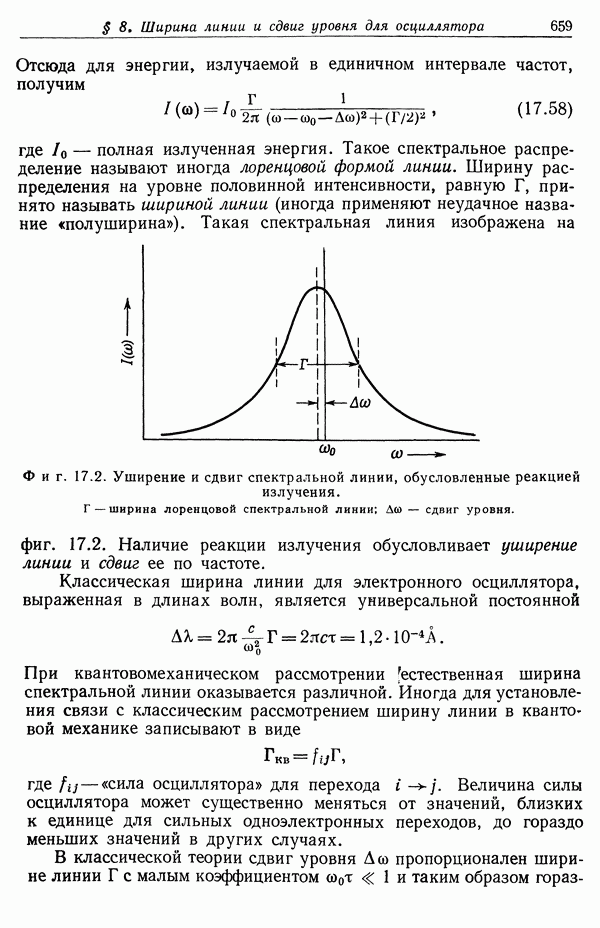
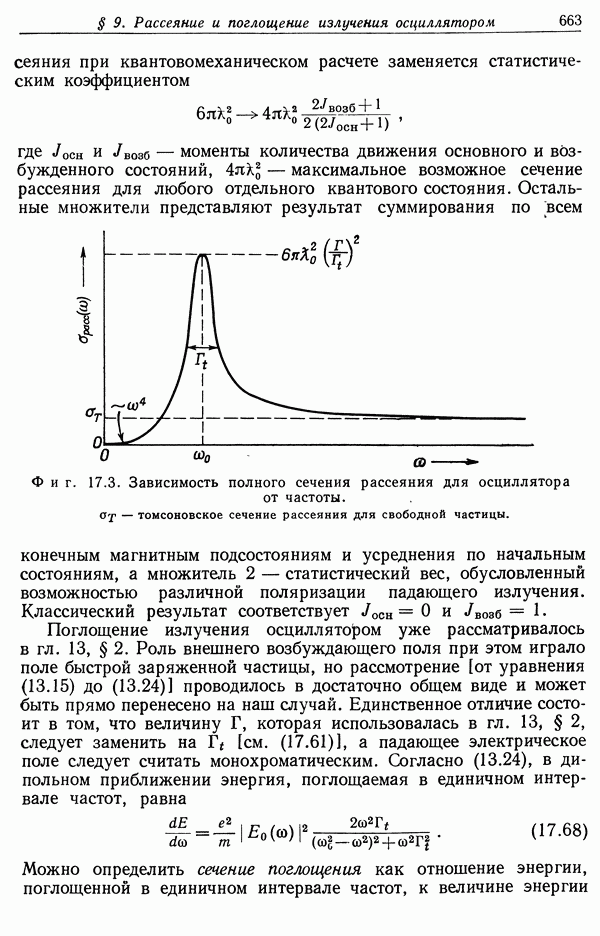
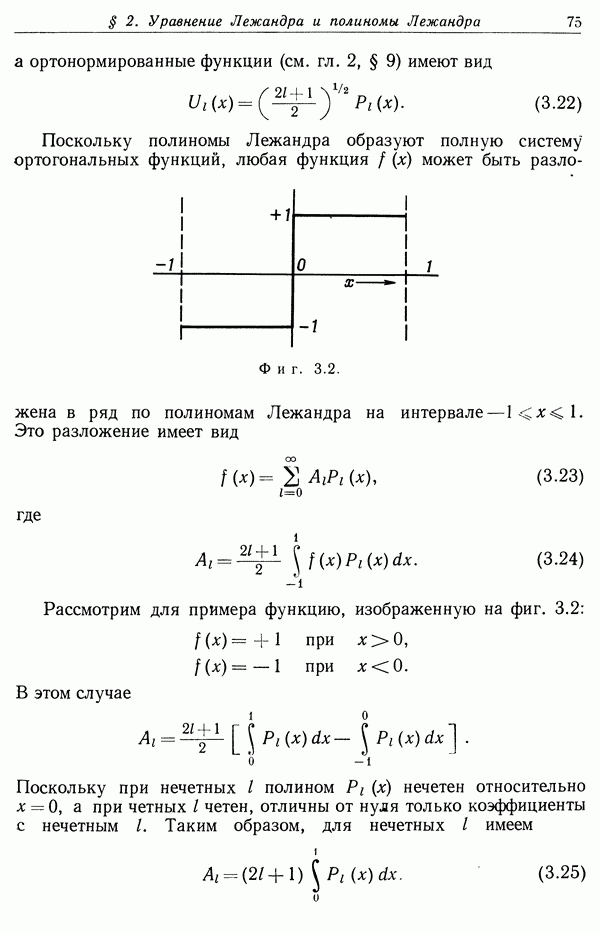| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Изотропные диэлектрики и граничные условия
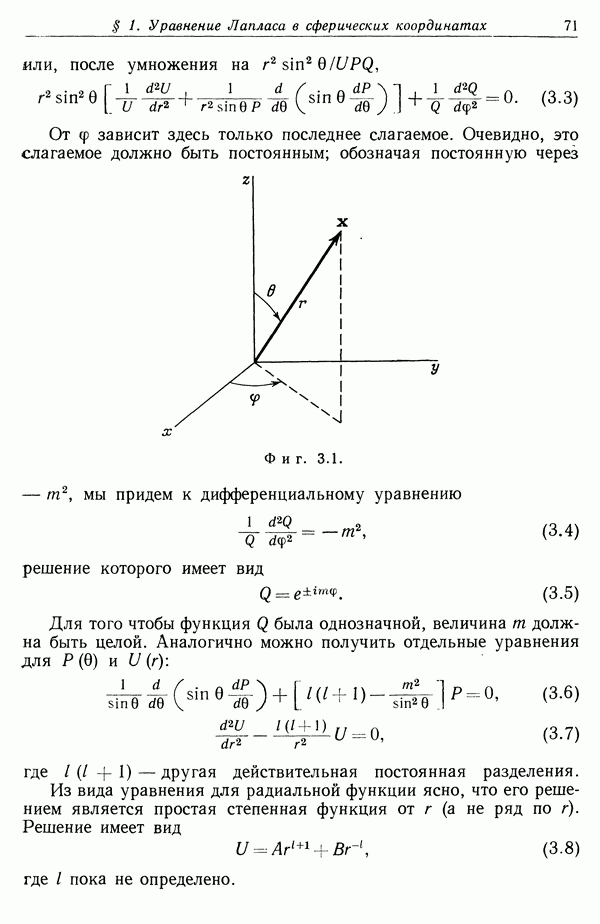
Как уже упоминалось выше, поляризация молекул зависит от локального электрического поля вблизи молекулы. При отсутствии внешнего поля средняя поляризация равна нулю. Поэтому вектор поляризации Р, являющийся в общем случае некоторой функцией от Е, может быть представлен в виде ряда по степеням поля, по крайней мере в случае малых полей. Любая составляющая Р будет при этом представляться разложением вида

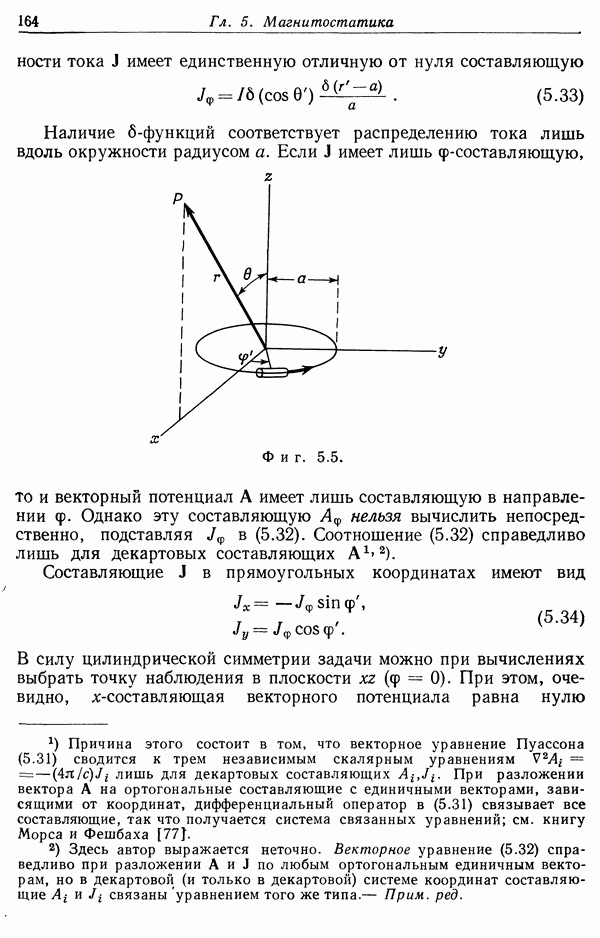
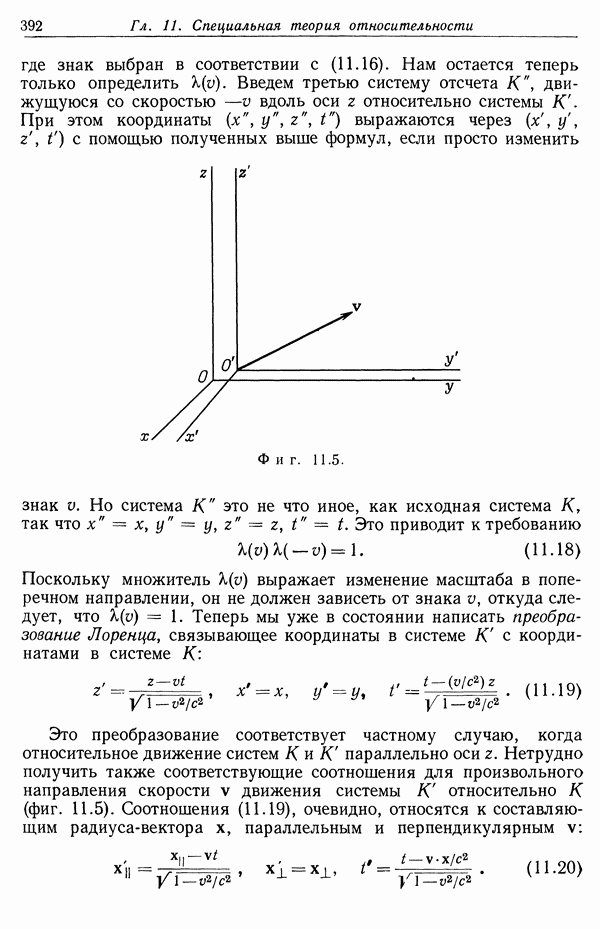
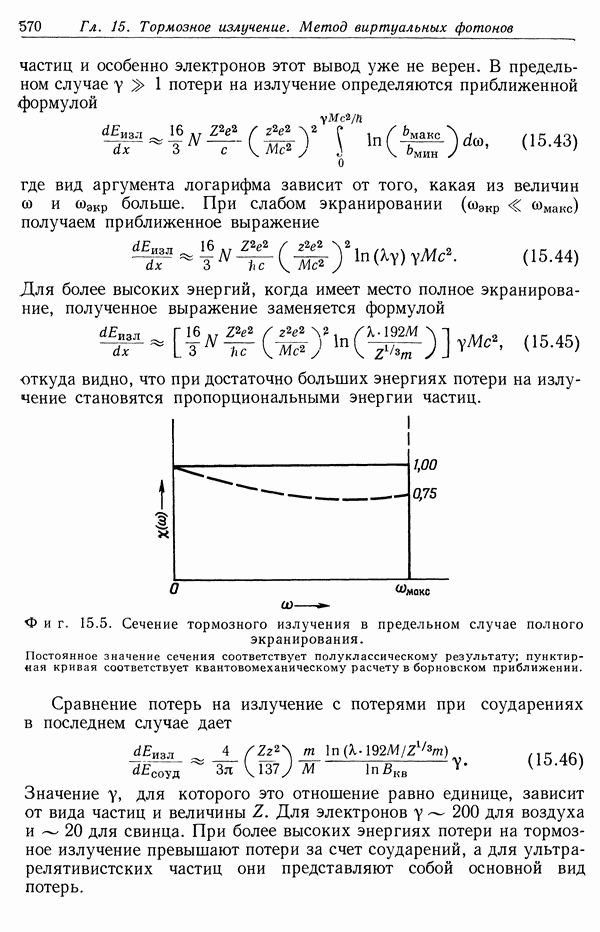
Заранее не ясно, насколько практически существенны высшие члены разложения. Но эксперименты показали, что зависимость поляризации от приложенного поля имеет вид, изображенный на фиг. 4.3.

Фиг. 4.3. Зависимость составляющих вектора поляризации от приложенного электрического поля.
При нормальных температурах для полей, достижимых в лабораторных условиях, линейного приближения совершенно достаточно. Это и не удивительно, если вспомнить, что внутриатомные электрические поля по порядку величины равны 109 в!см. По сравнению с ними любое внешнее поле, обусловливающее поляризацию, является лишь малым возмущением.
В общем случае анизотропные среды (например, кристаллы кальцита или кварца) характеризуются шестью независимыми коэффициентами  . Однако для простых веществ, называемых изотропными, вектор Р параллелен Е и линейно связан с полем, причем коэффициент пропорциональности
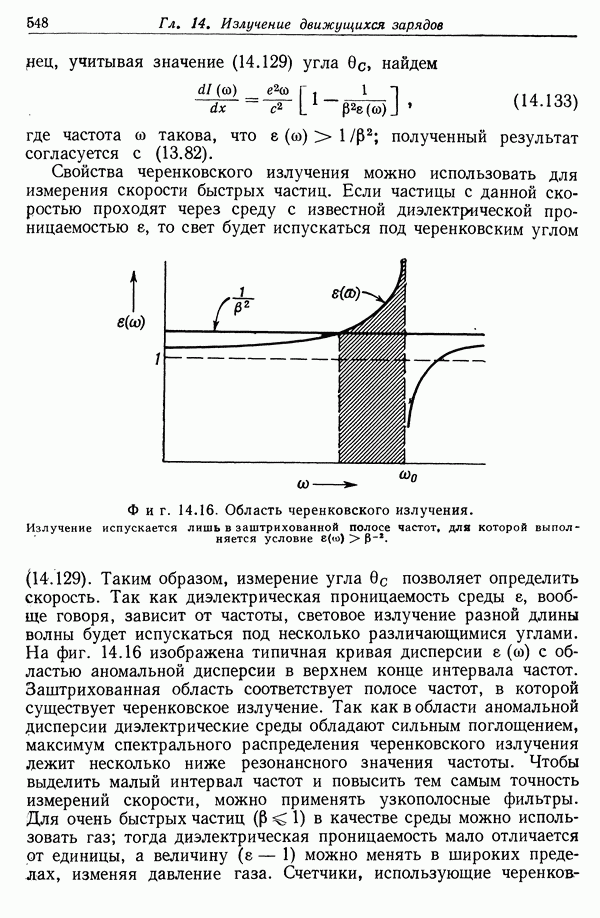
. Однако для простых веществ, называемых изотропными, вектор Р параллелен Е и линейно связан с полем, причем коэффициент пропорциональности  не зависит от направления Е:
не зависит от направления Е:

Постоянная  называется диэлектрической восприимчивостью среды. В этом случае электрическая индукция пропорциональна Е:
называется диэлектрической восприимчивостью среды. В этом случае электрическая индукция пропорциональна Е:

где диэлектрическая проницаемость  (называемая также диэлектрической постоянной) равна
(называемая также диэлектрической постоянной) равна

Если диэлектрик не только изотропен, но и однороден, то  не зависит от координат. В этом случае уравнение (4.38) можно записать в виде
не зависит от координат. В этом случае уравнение (4.38) можно записать в виде

Все задачи для таких сред, очевидно, сводятся к уже рассмотренным в предыдущих главах с тем отличием, что электрические поля, возбуждаемые зарядами, уменьшены в 8 раз.

Фиг. 4.4.
Это уменьшение поля можно физически объяснить поляризацией атомов, приводящей к появлению поля, направленного противоположно полю заданных внешних зарядов. Прямым следствием указанного факта является увеличение в  раз емкости конденсатора при заполнении зазора между его пластинами диэлектриком с диэлектрической проницаемостью
раз емкости конденсатора при заполнении зазора между его пластинами диэлектриком с диэлектрической проницаемостью  (это справедливо лишь в случае, когда можно пренебречь полями рассеяния).
(это справедливо лишь в случае, когда можно пренебречь полями рассеяния).
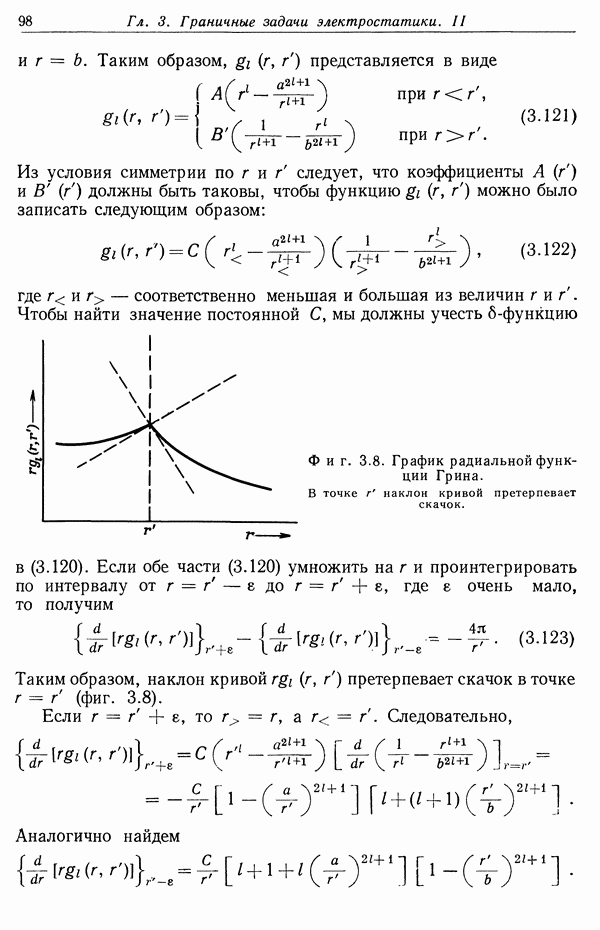
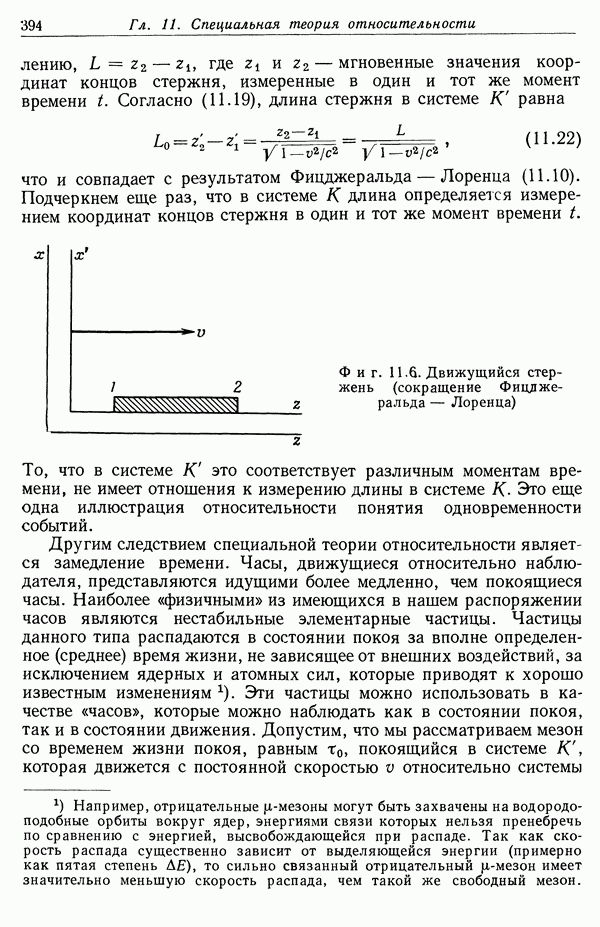
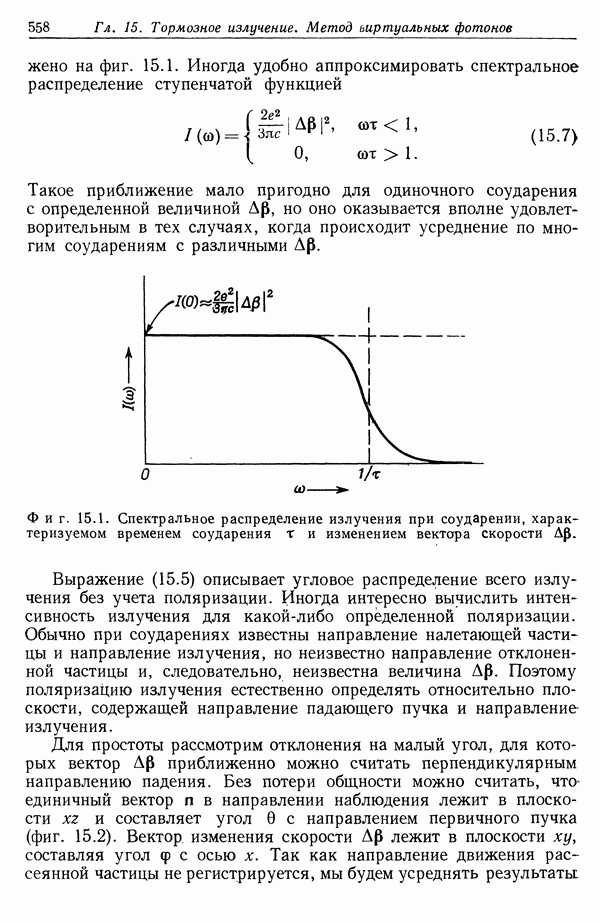
Весьма важны граничные условия для векторов Е и D на поверхностях, где свойства диэлектрика изменяются скачком. Рассмотрим поверхность S, изображенную на фиг. 4.4. Единичный вектор  нормален к поверхности и направлен из области 1 с диэлектрической проницаемостью
нормален к поверхности и направлен из области 1 с диэлектрической проницаемостью  в область 2 с диэлектрической проницаемостью
в область 2 с диэлектрической проницаемостью  Совершенно так же, как описано в гл. 1, § 6, рассмотрим маленький параллелепипед, грани которого в областях 1 и 2 параллельны граничной поверхности S; при этом находим
Совершенно так же, как описано в гл. 1, § 6, рассмотрим маленький параллелепипед, грани которого в областях 1 и 2 параллельны граничной поверхности S; при этом находим

где а — плотность поверхностных зарядов (без учета связанных зарядов). Аналогично, применяя теорему Стокса к уравнению  находим
находим

Полученные граничные условия для нормальной составляющей D и тангенциальной составляющей Е заменяют микроскопические условия (1.22) и последующие, приведенные в гл. 1, § 6. Макроскопические граничные условия можно написать и в виде, эквивалентном (1.22), если включить в правую часть (4.45) плотность связанных зарядов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
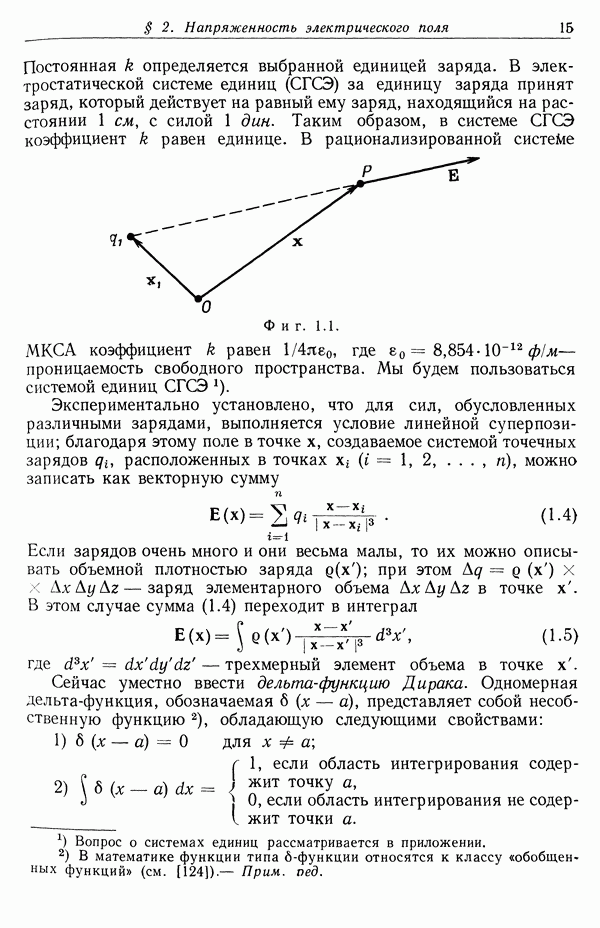
- § 2. Напряженность электрического поля
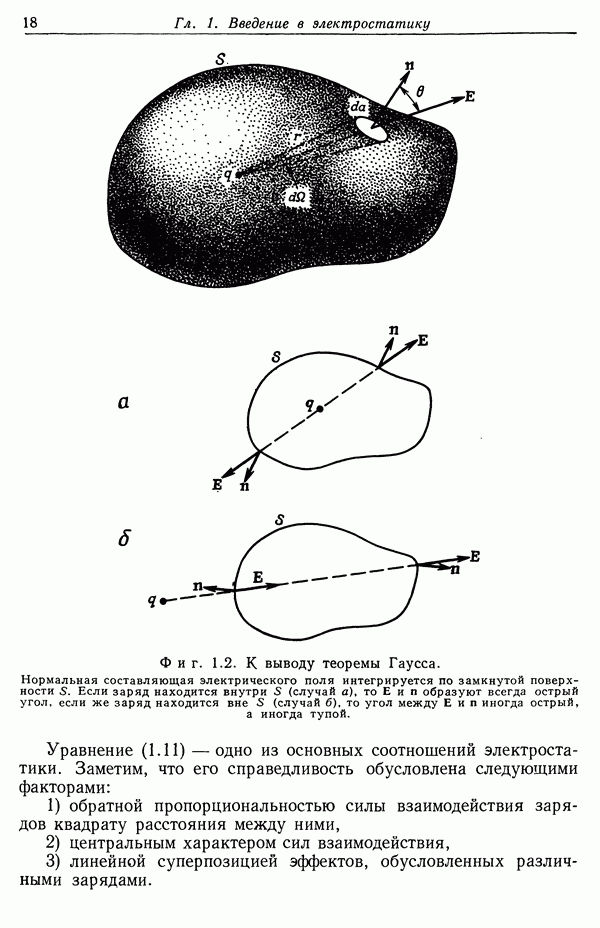
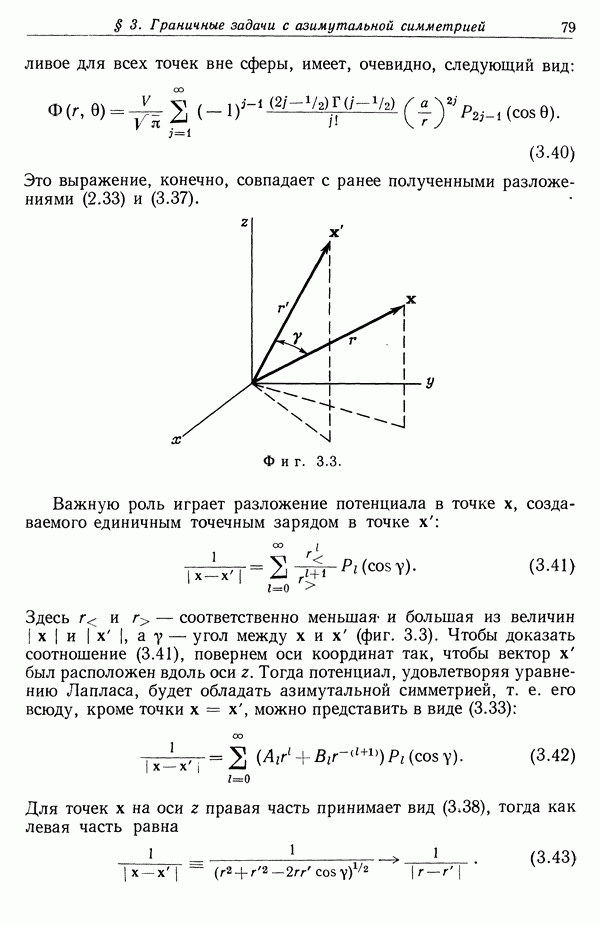
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
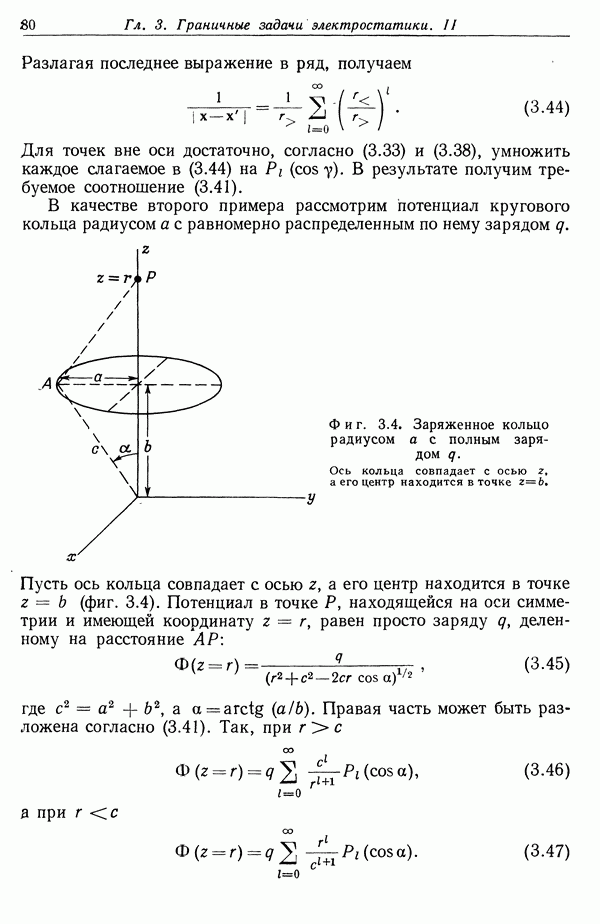
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
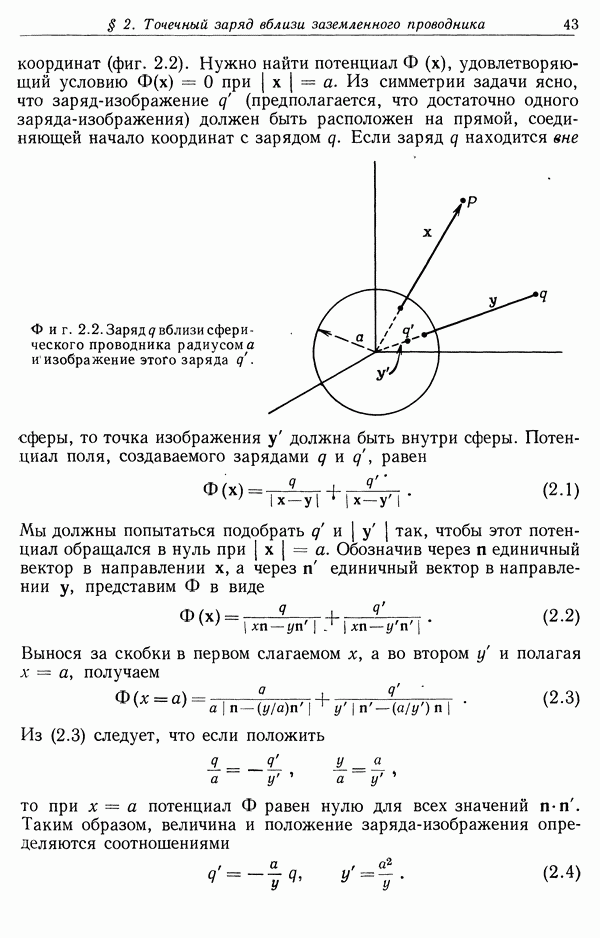
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
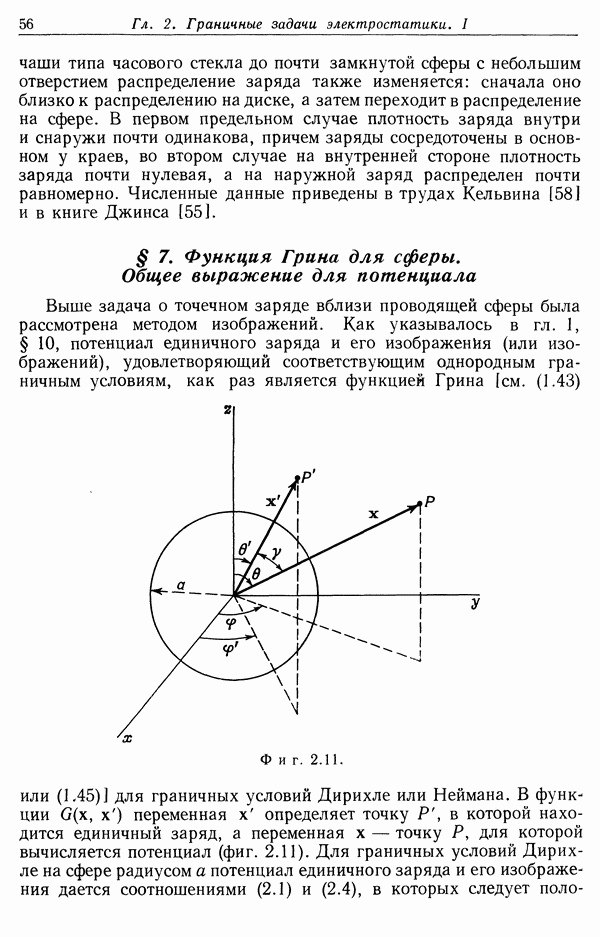
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
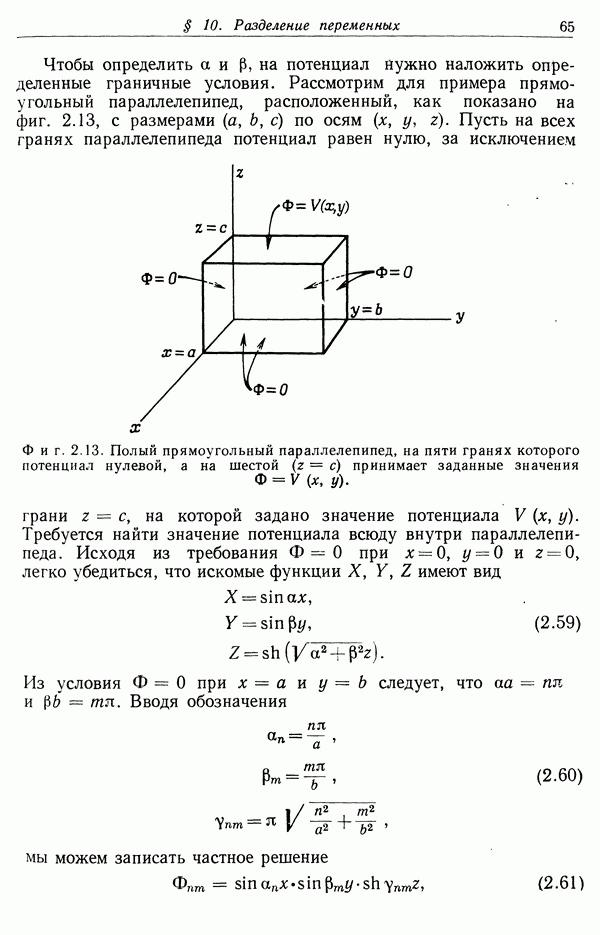
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
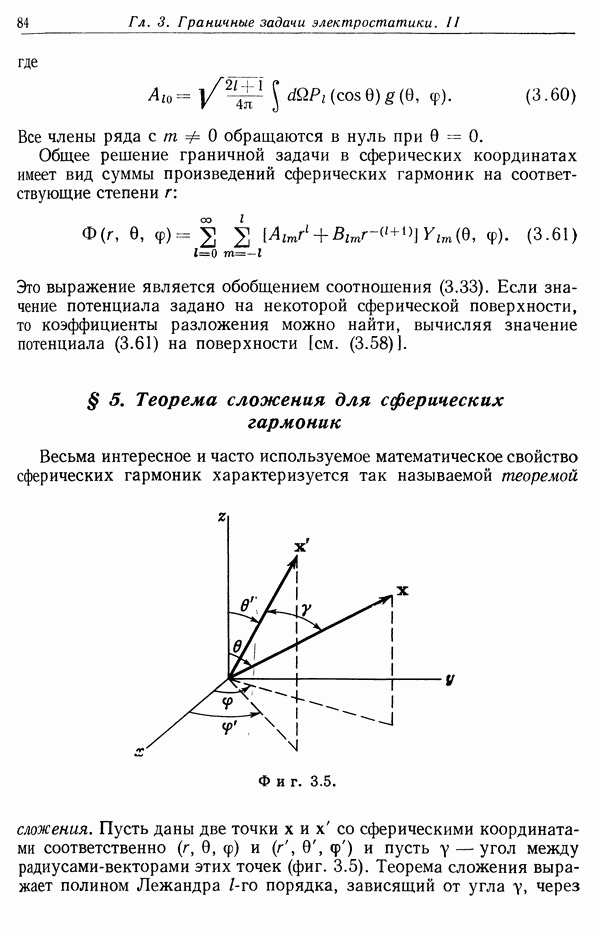
- § 5. Теорема сложения для сферических гармоник
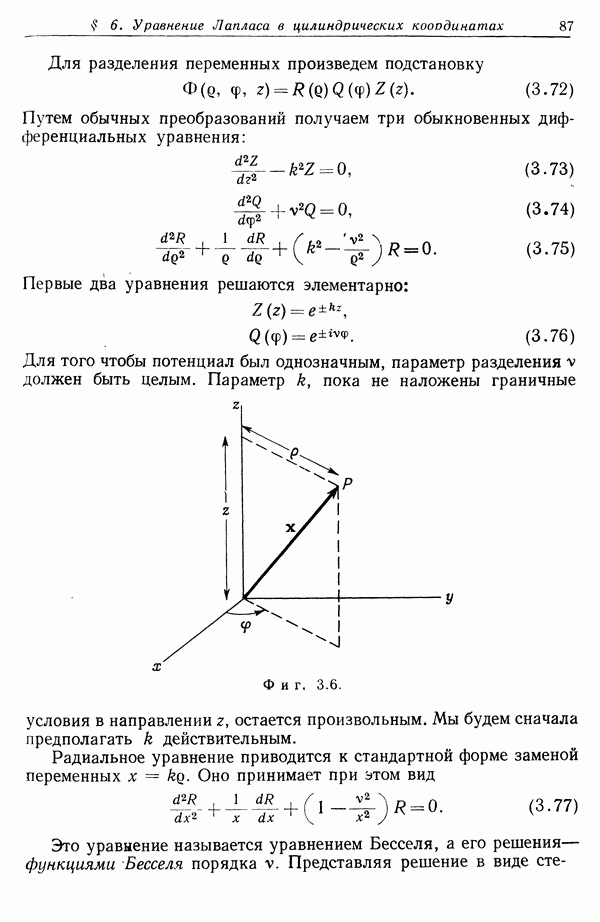
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
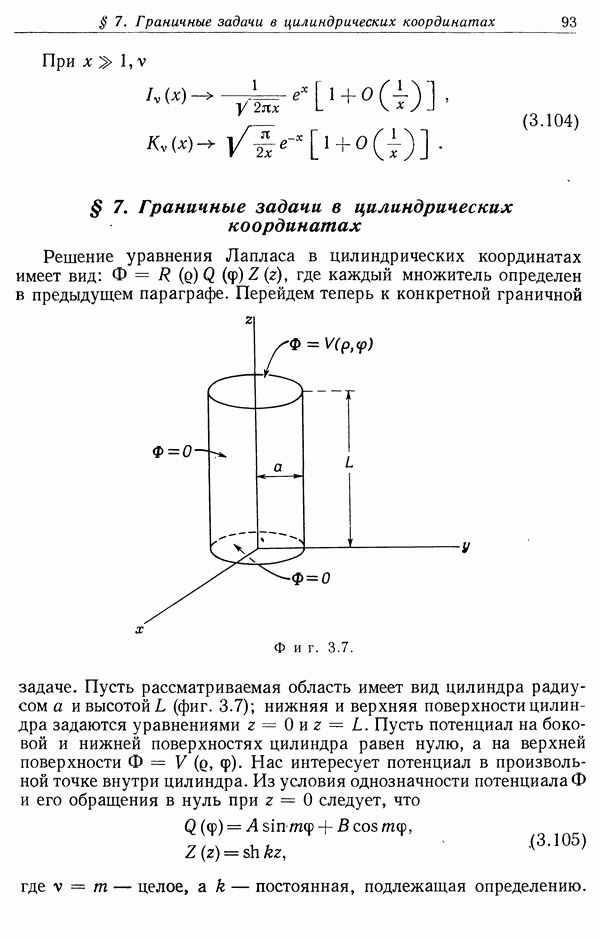
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
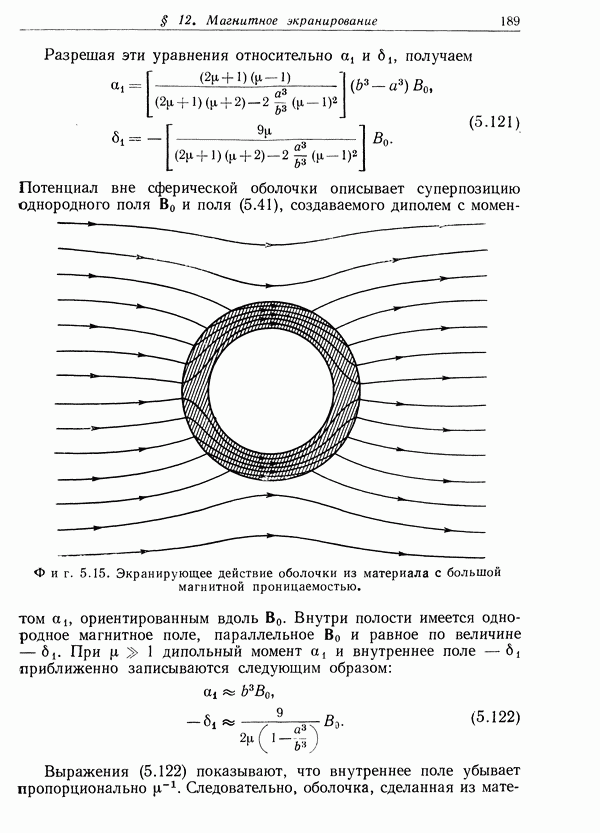
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
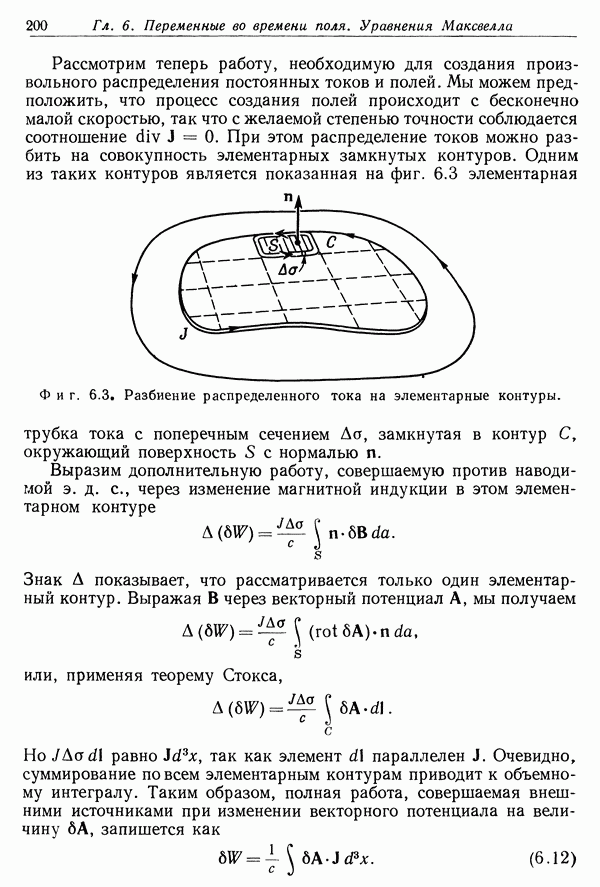
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
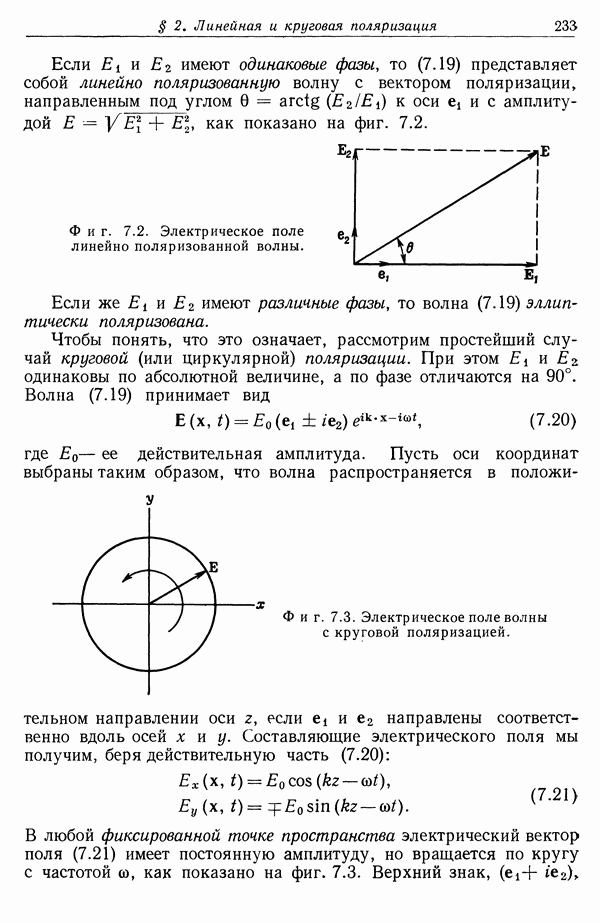
- § 2. Линейная и круговая поляризация
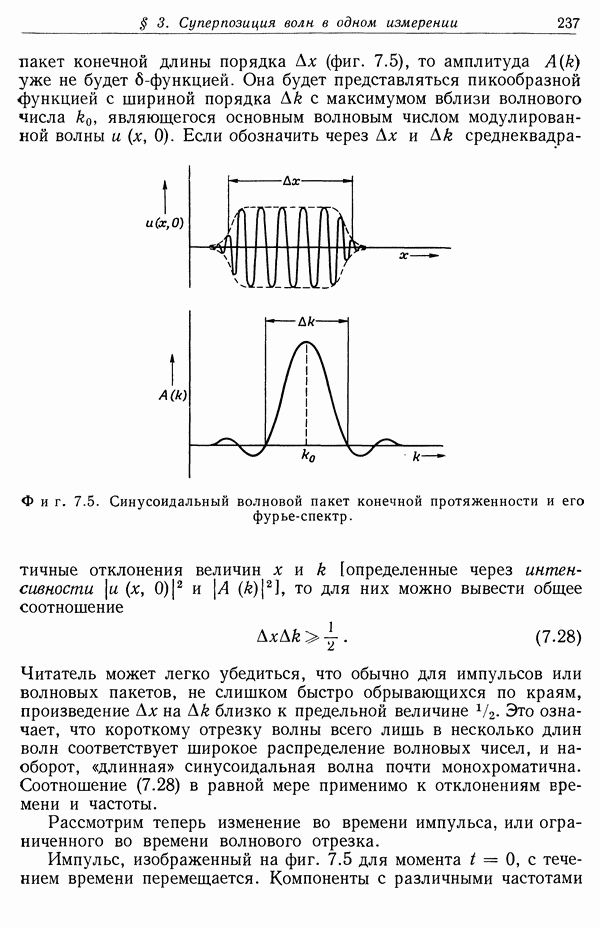
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
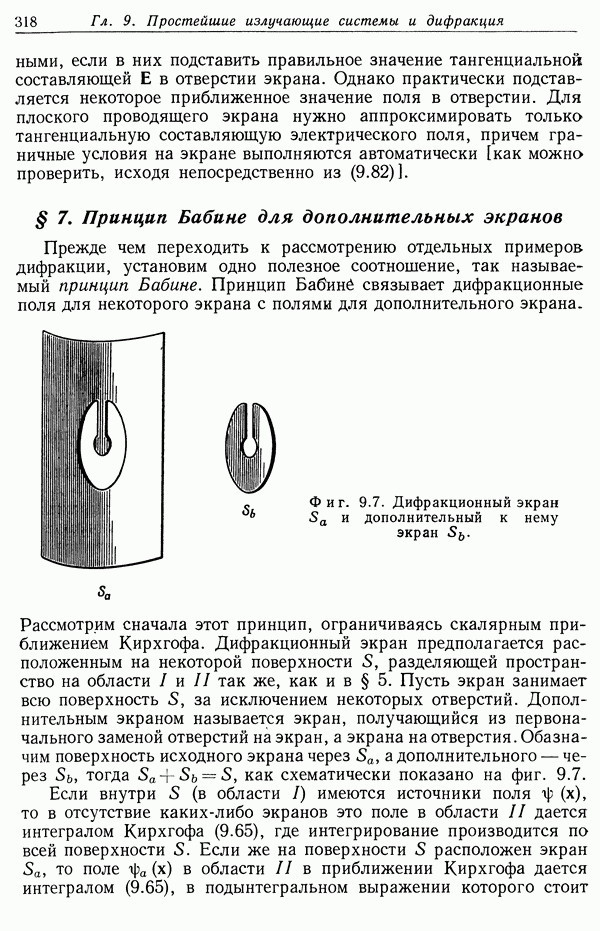
- § 7. Принцип Бабине для дополнительных экранов
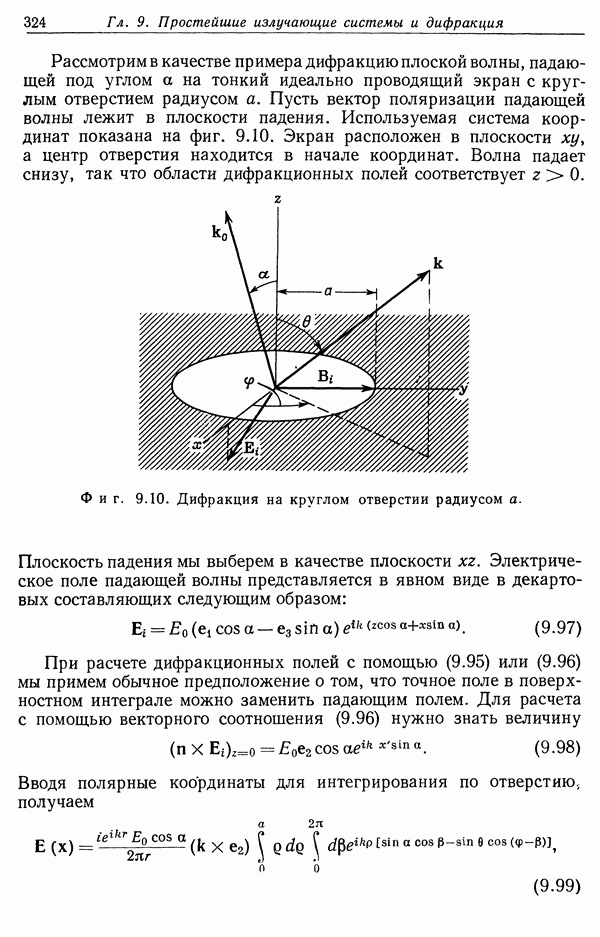
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
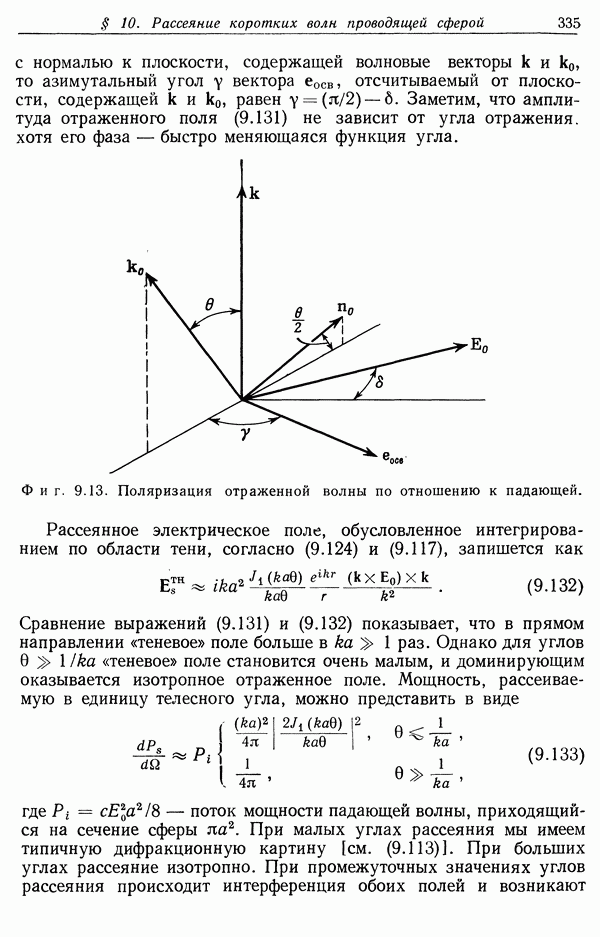
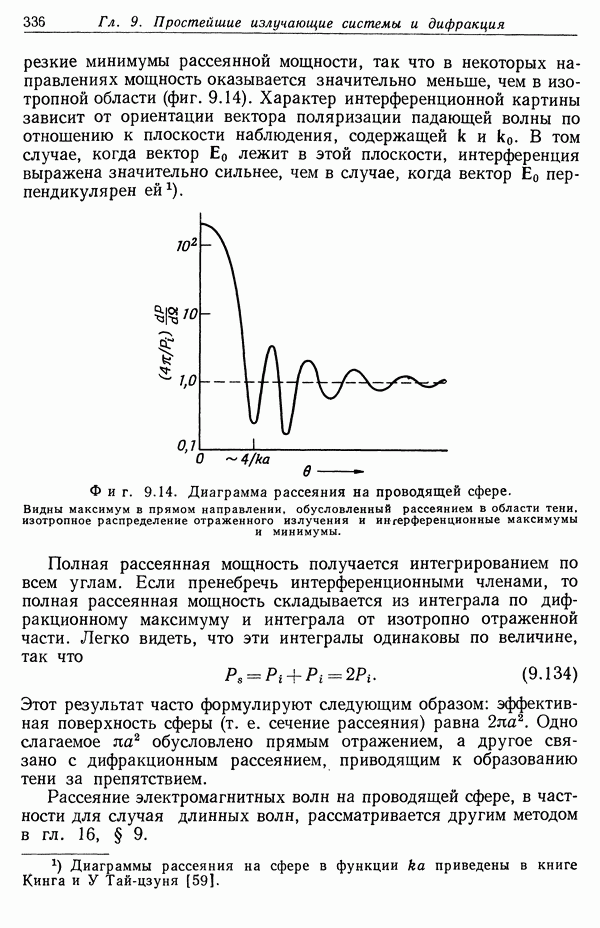
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
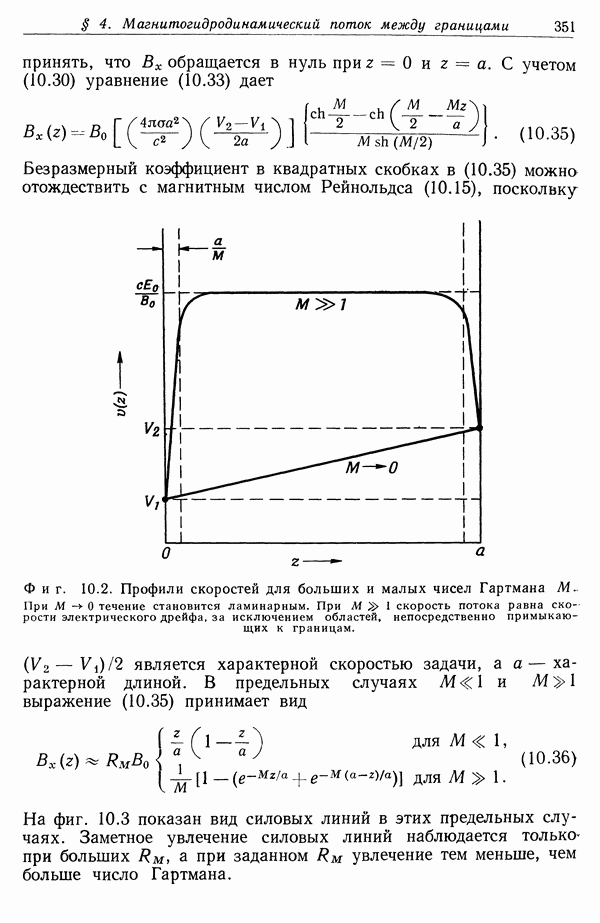
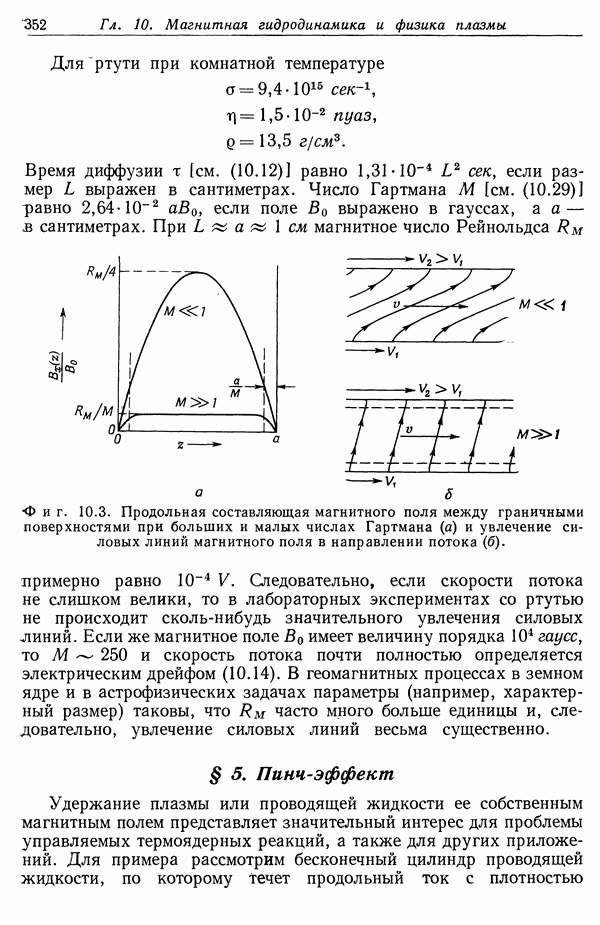
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
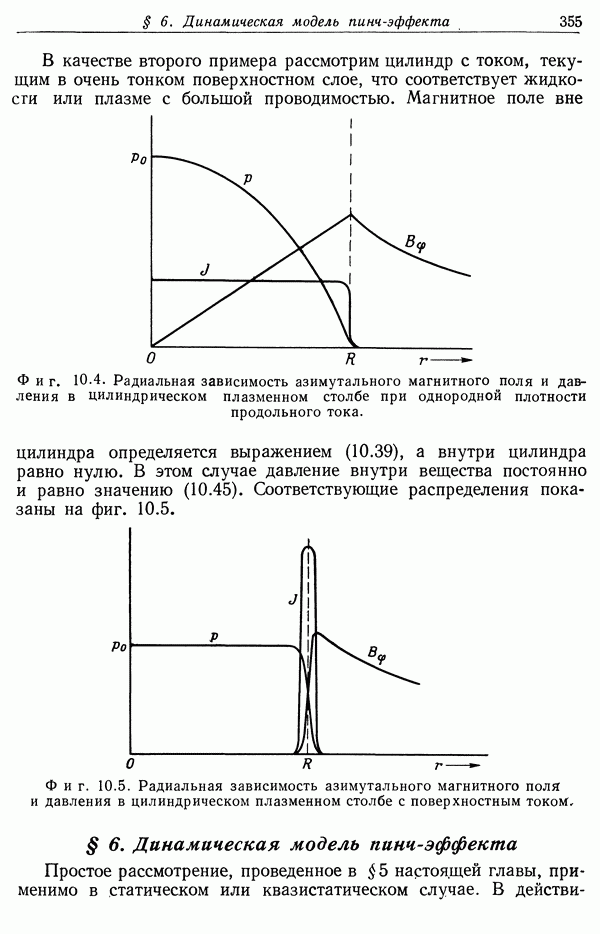
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
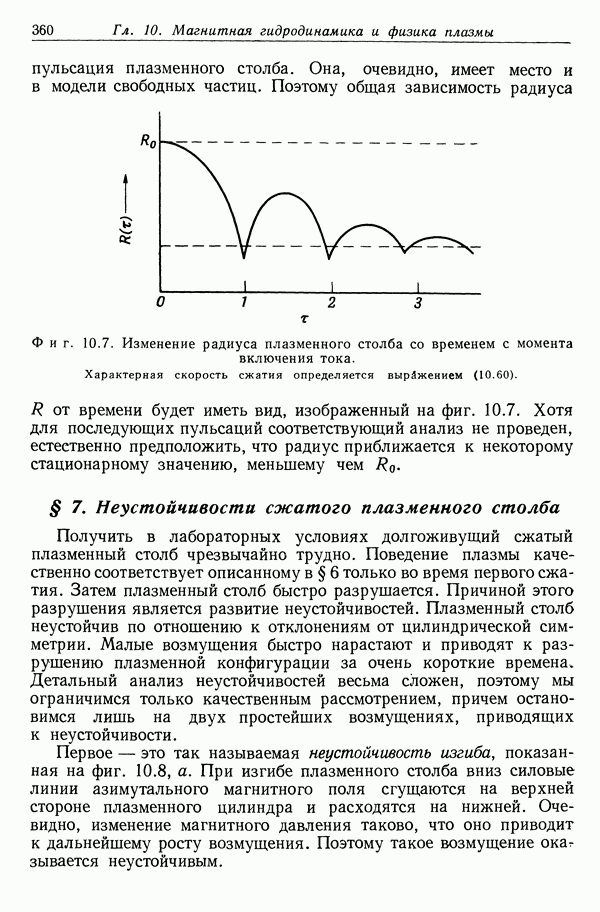
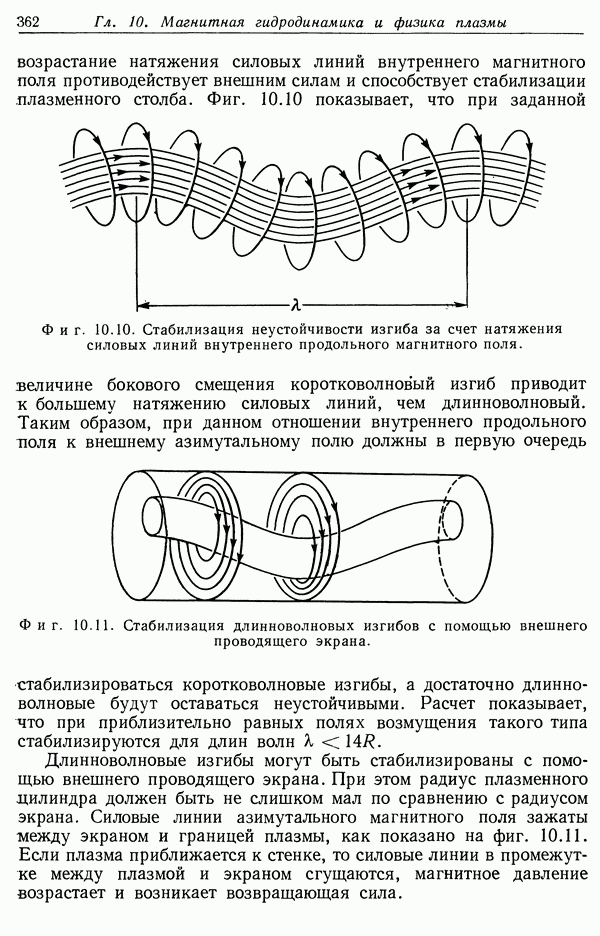
- § 7. Неустойчивости сжатого плазменного столба
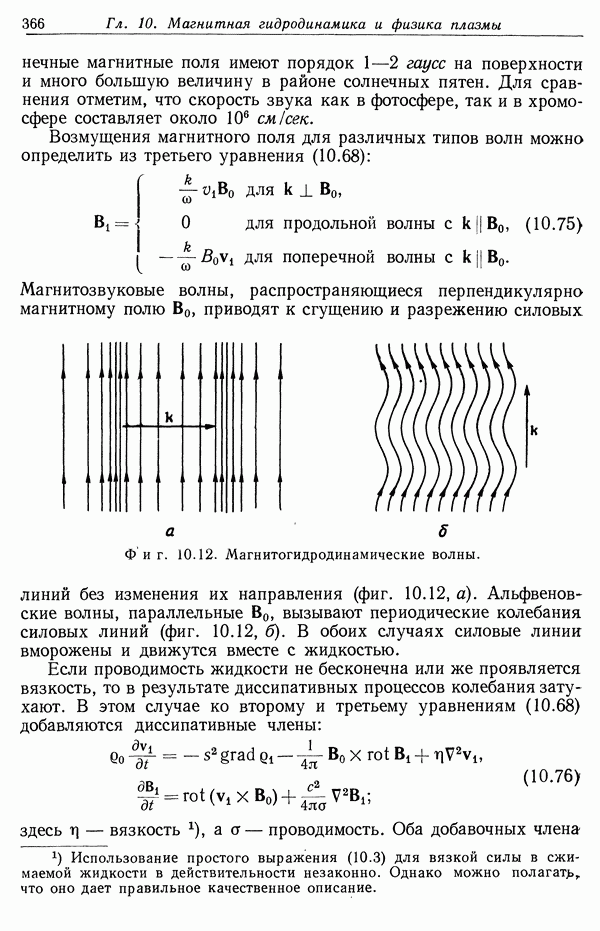
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
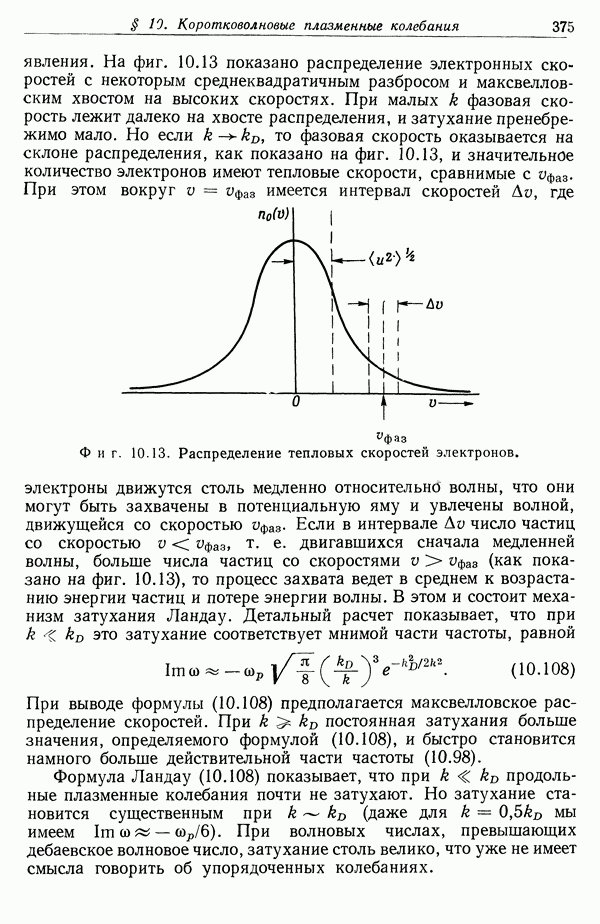
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
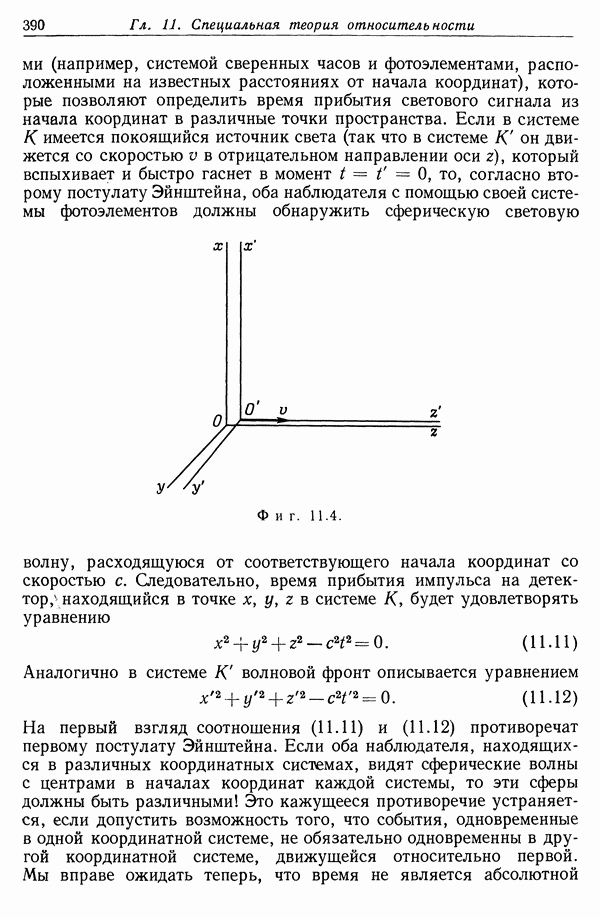
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
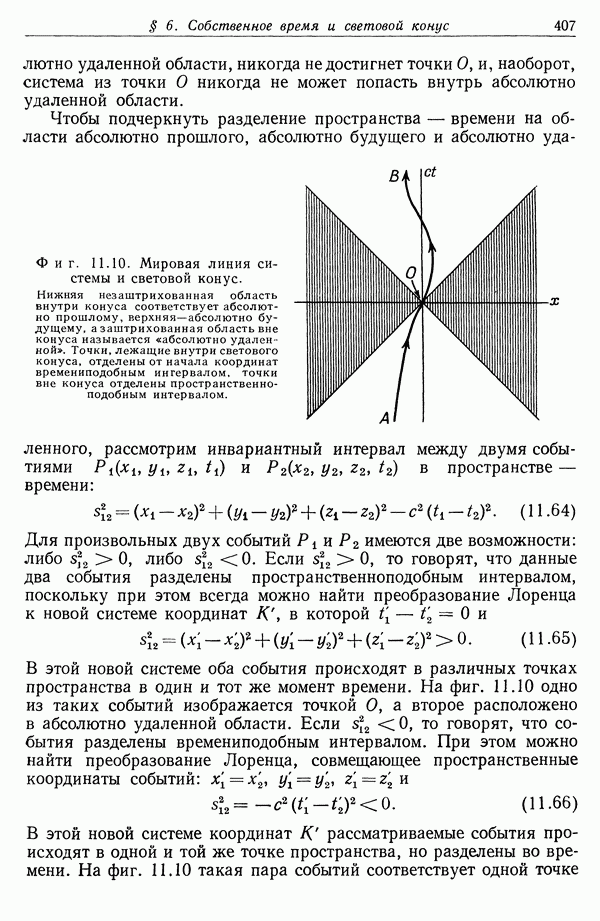
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
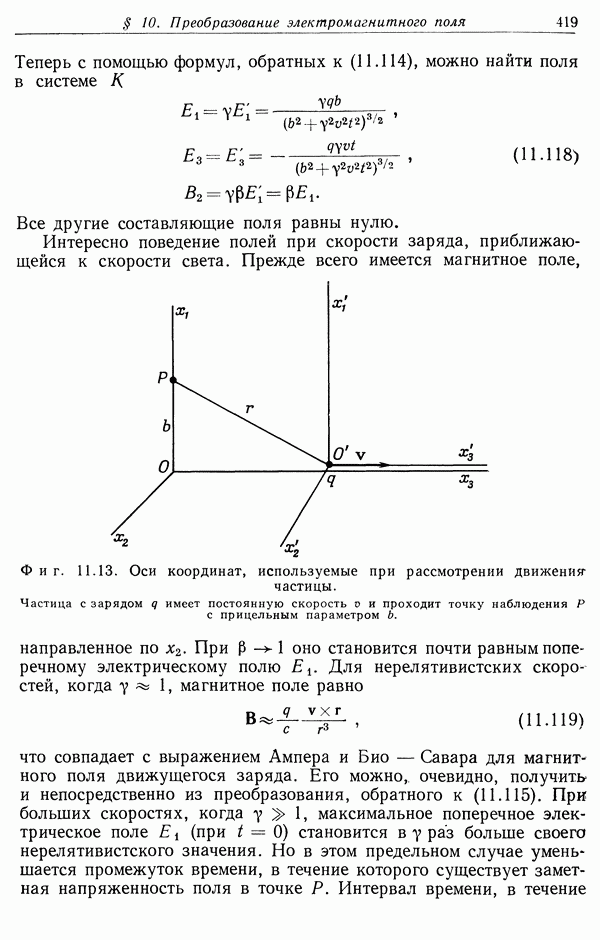
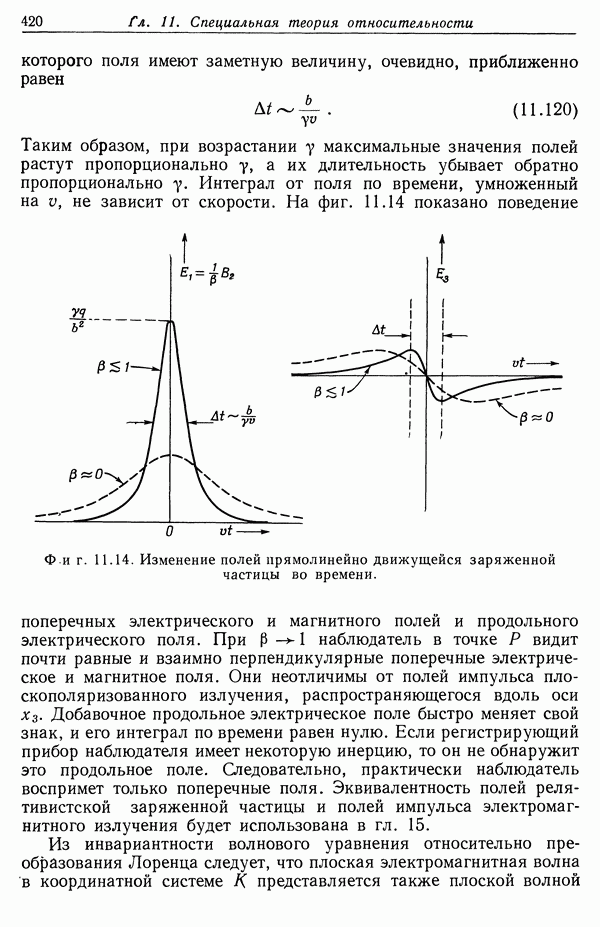
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
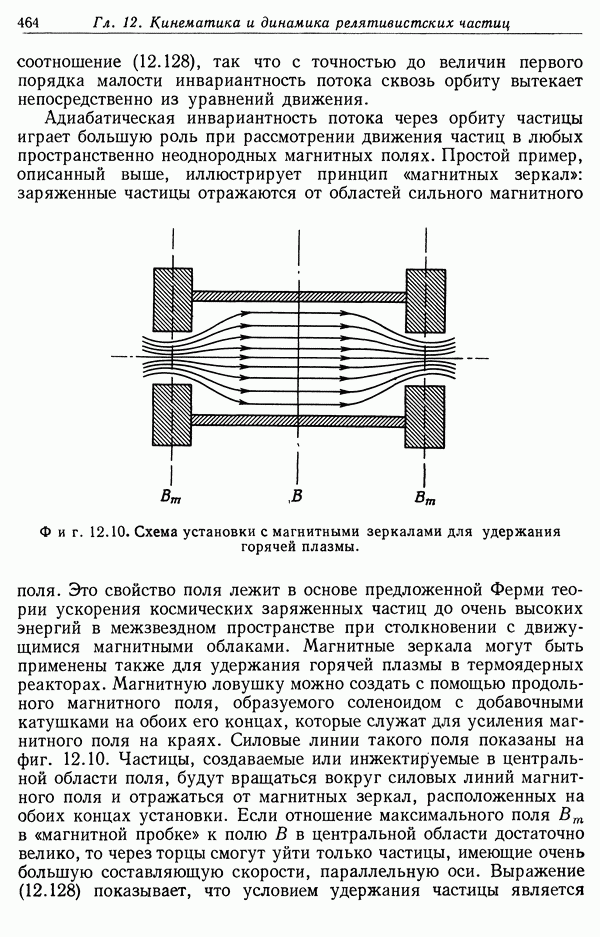
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
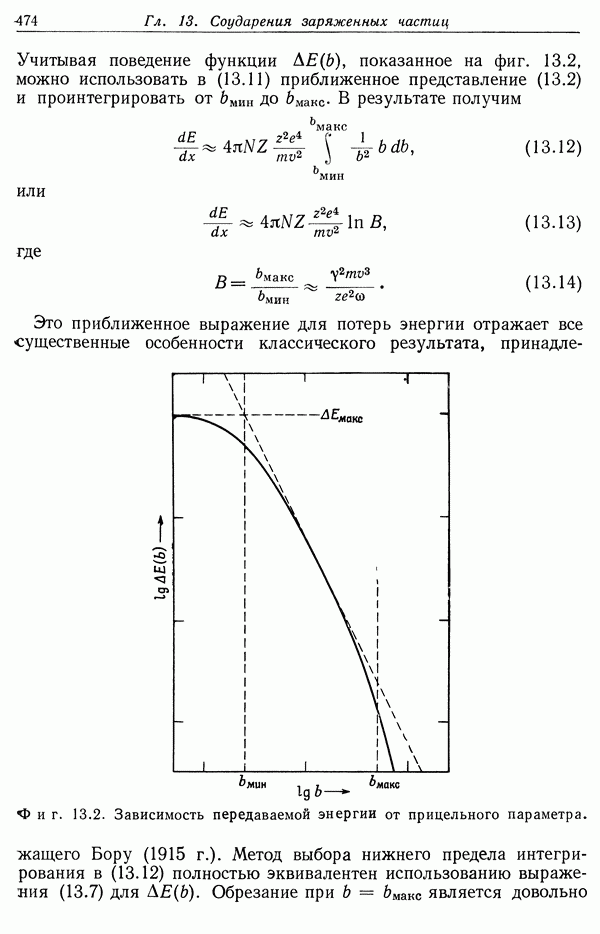
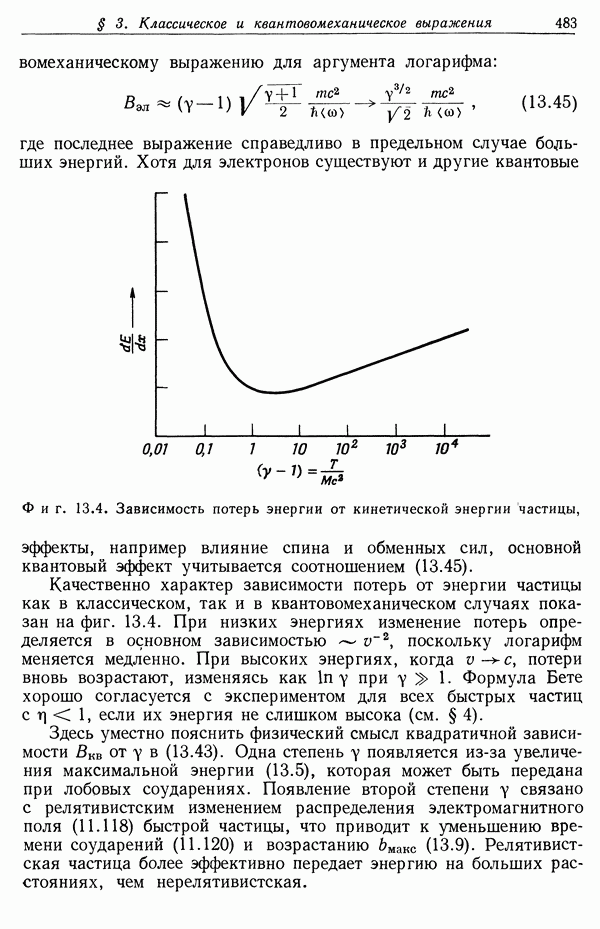
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
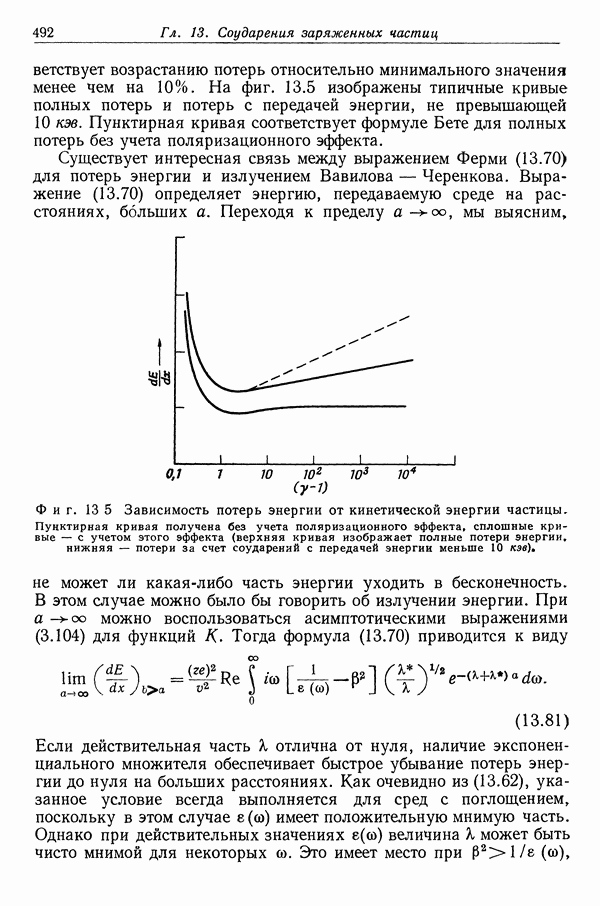
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
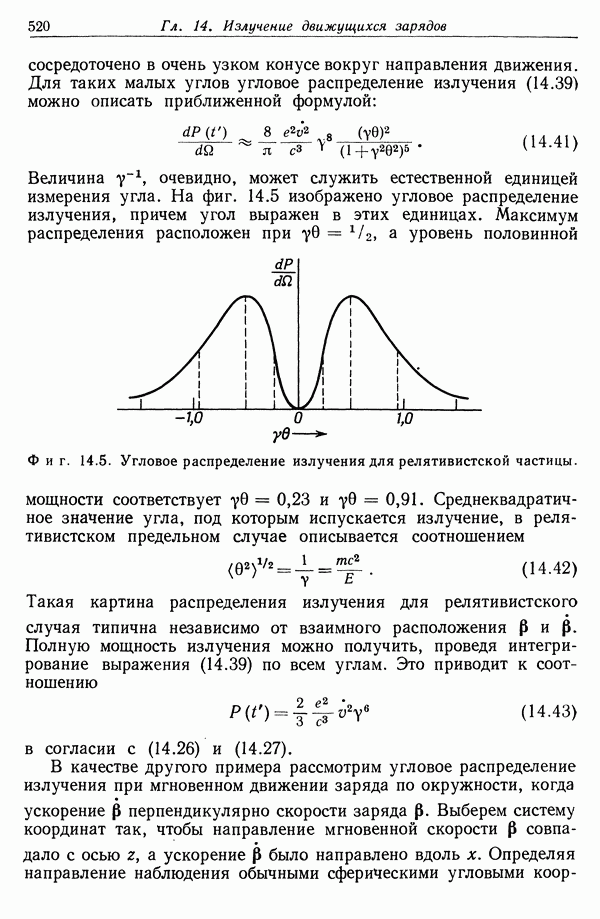
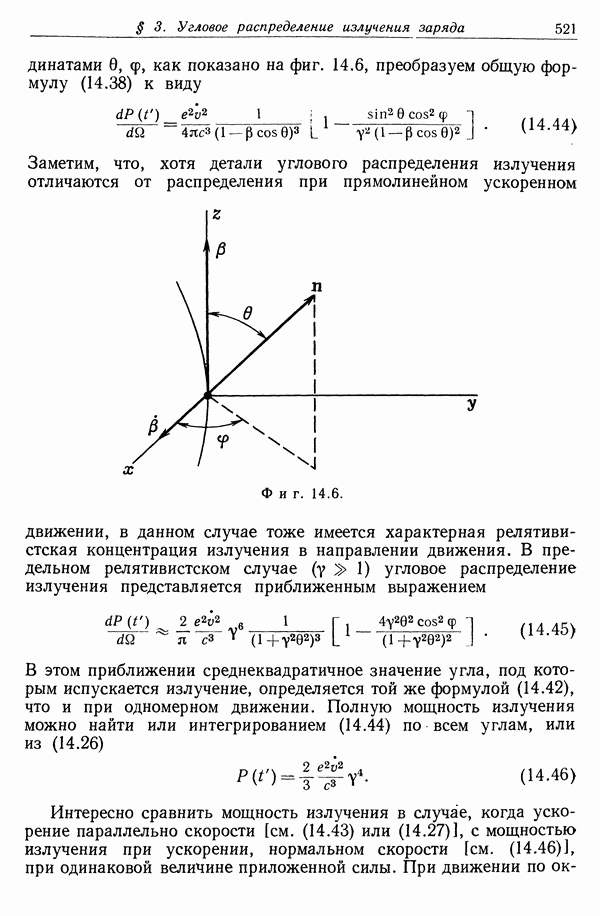
- § 3. Угловое распределение излучения ускоряемого заряда
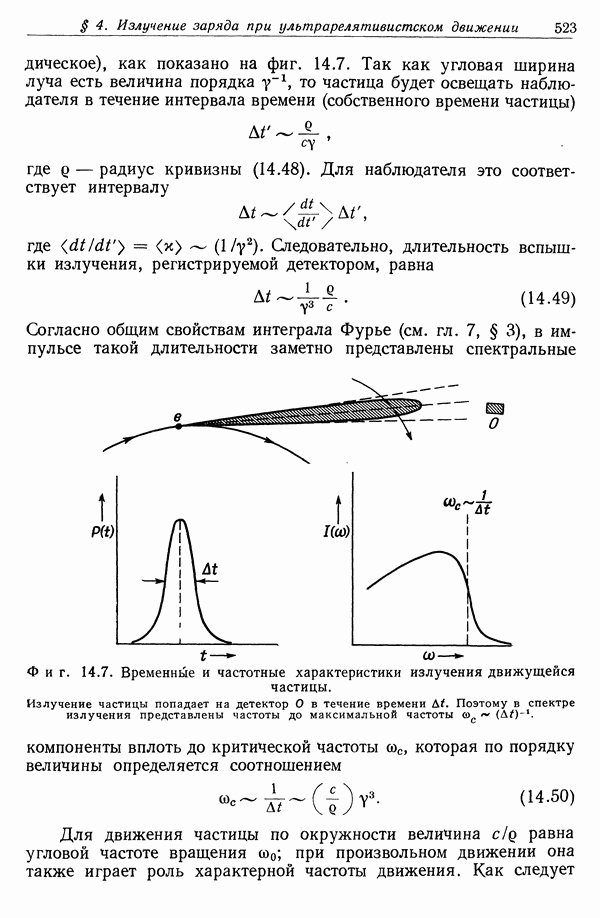
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
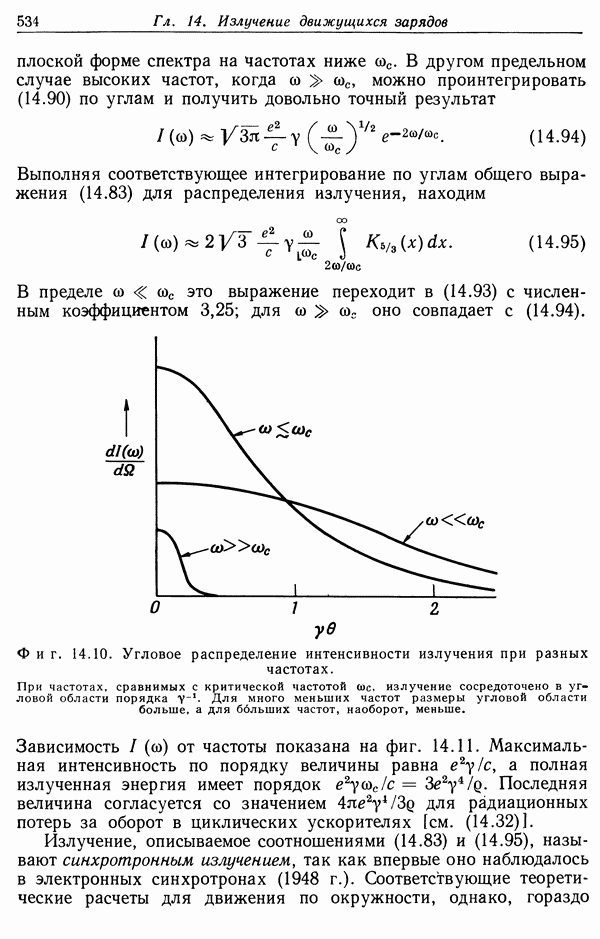
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
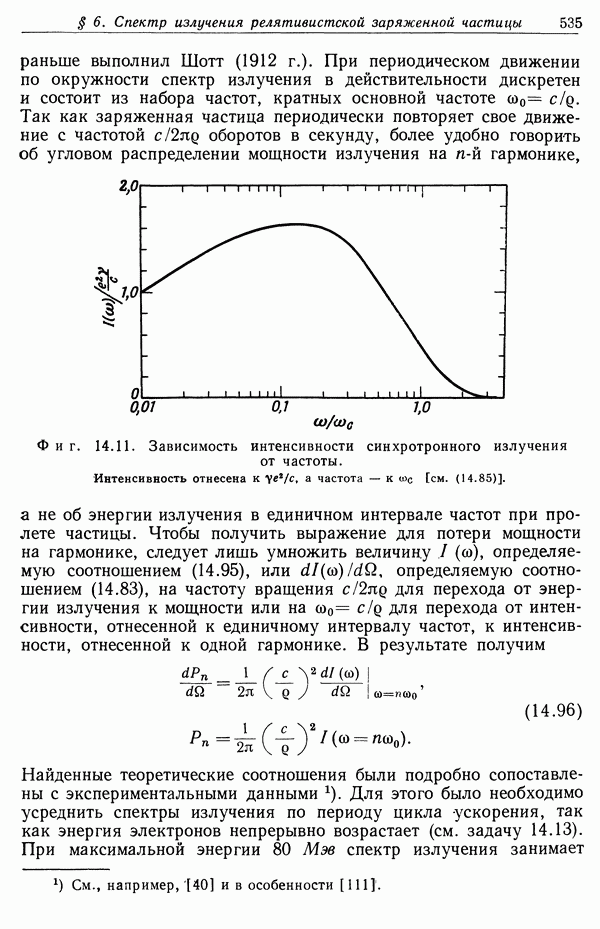
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
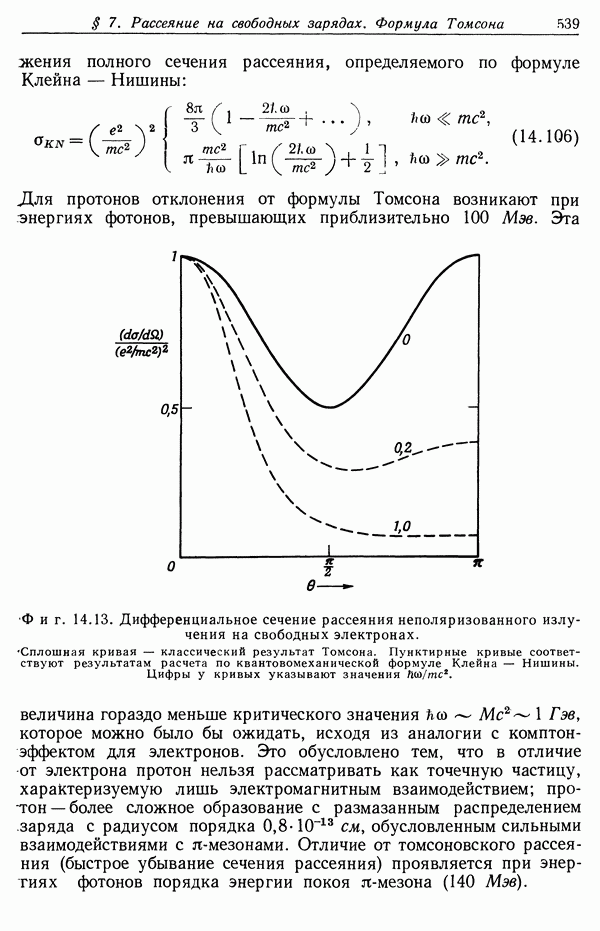
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
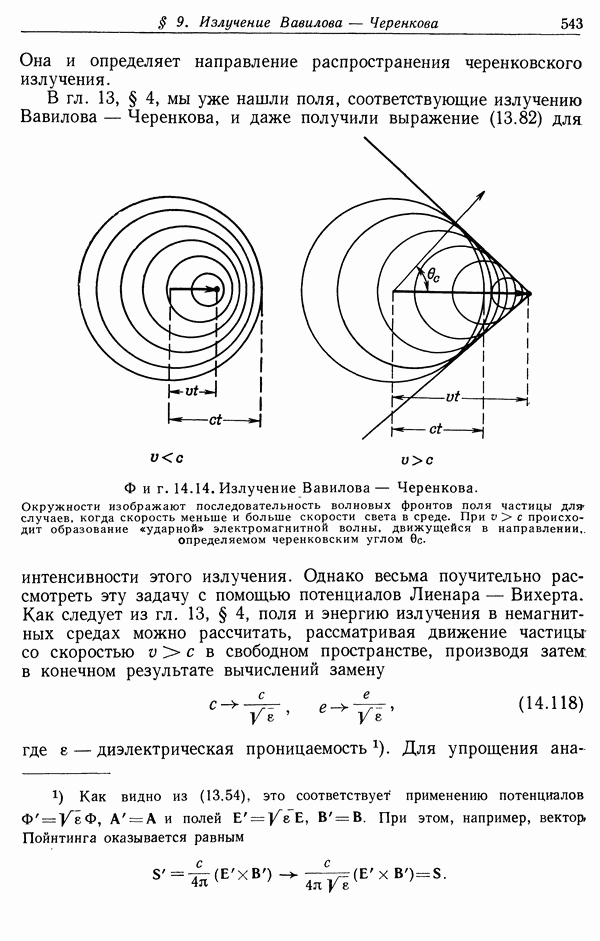
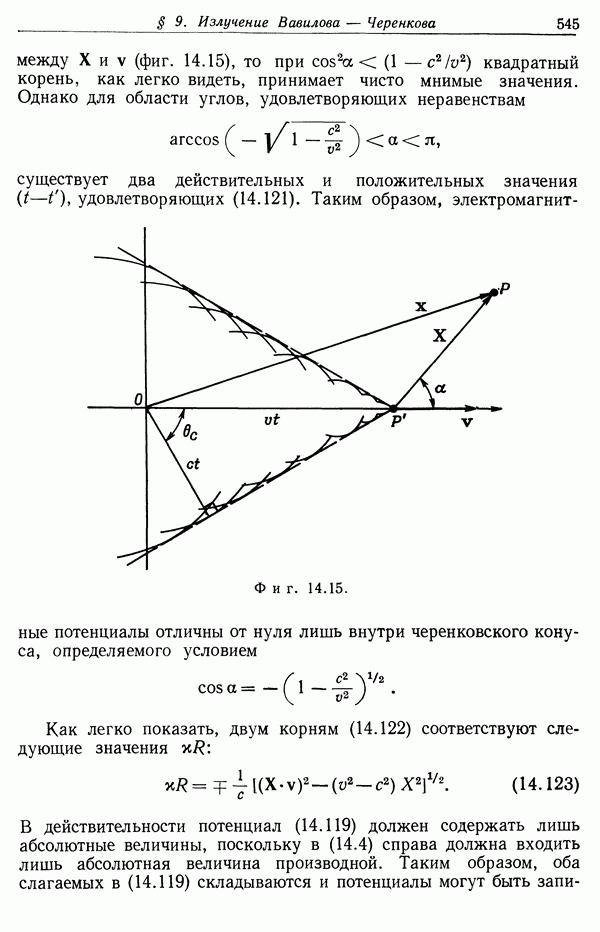
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
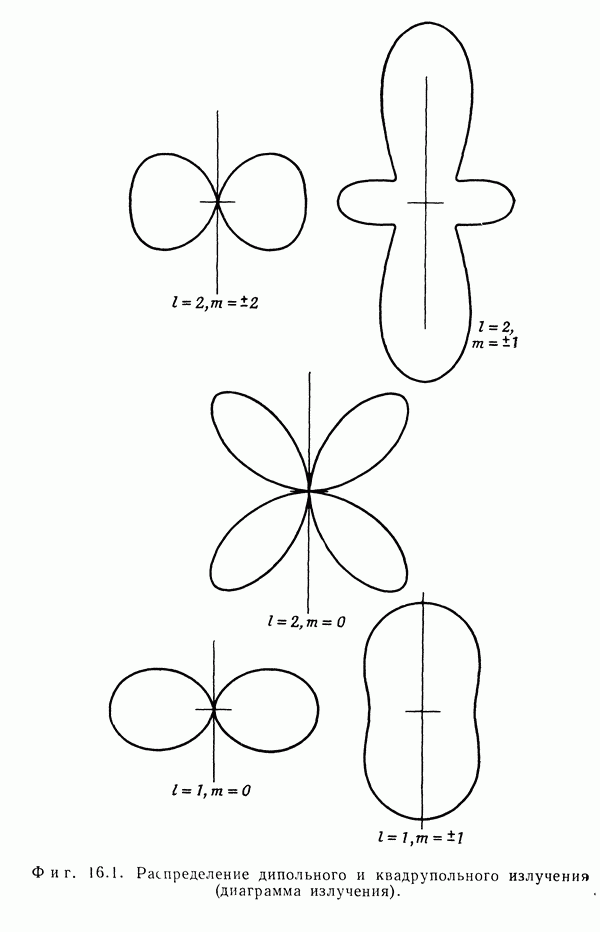
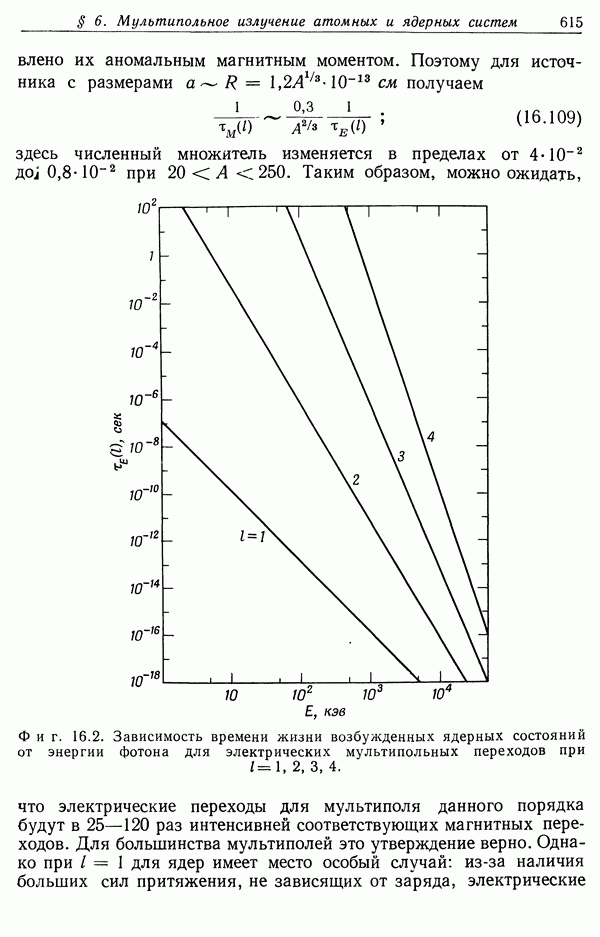
- § 6. Мультипольное излучение атомных и ядерных систем
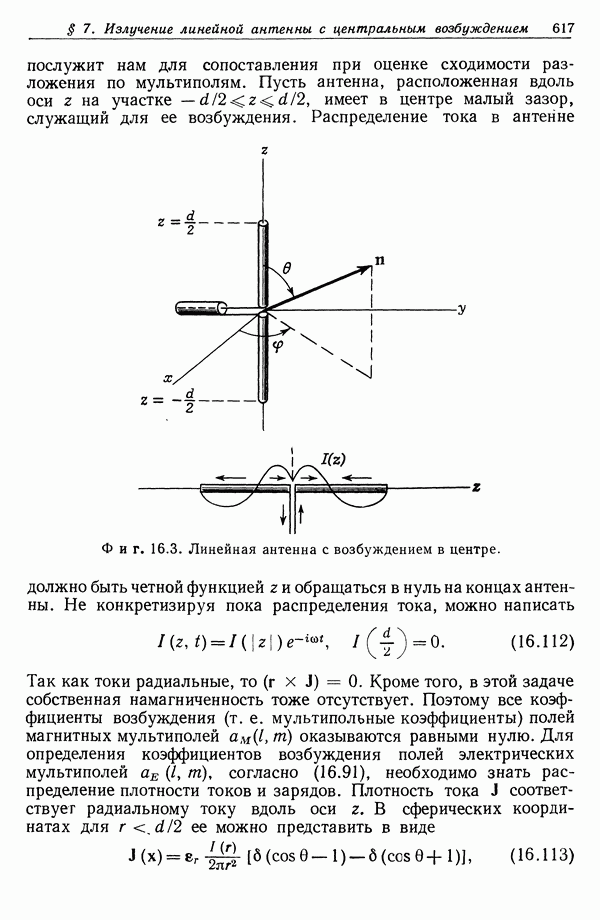
- § 7. Излучение линейной антенны с центральным возбуждением
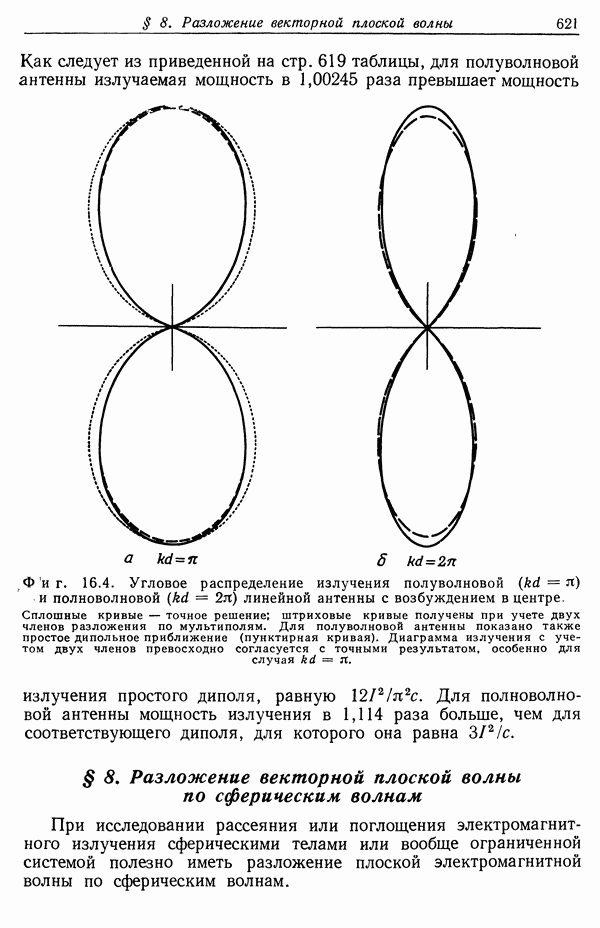
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ