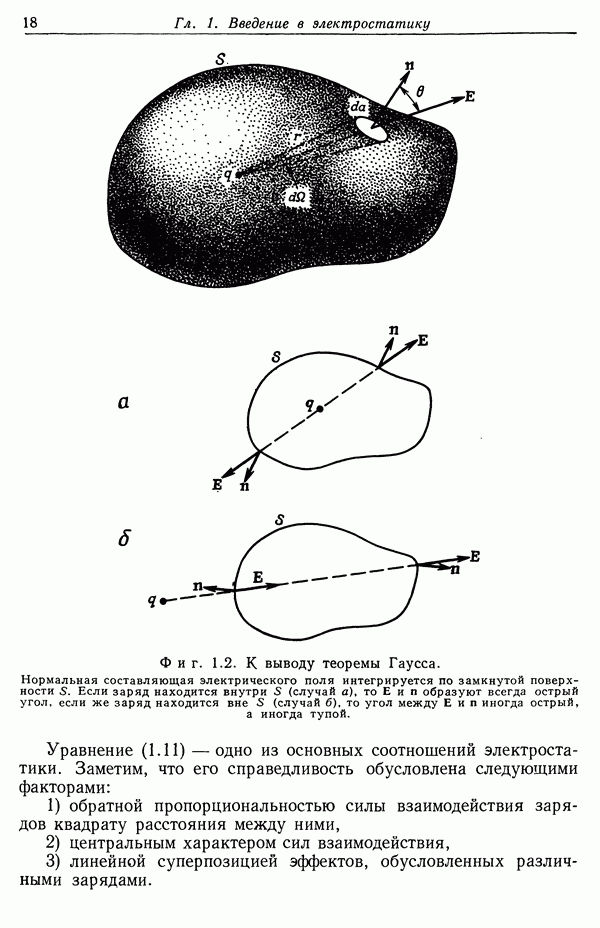
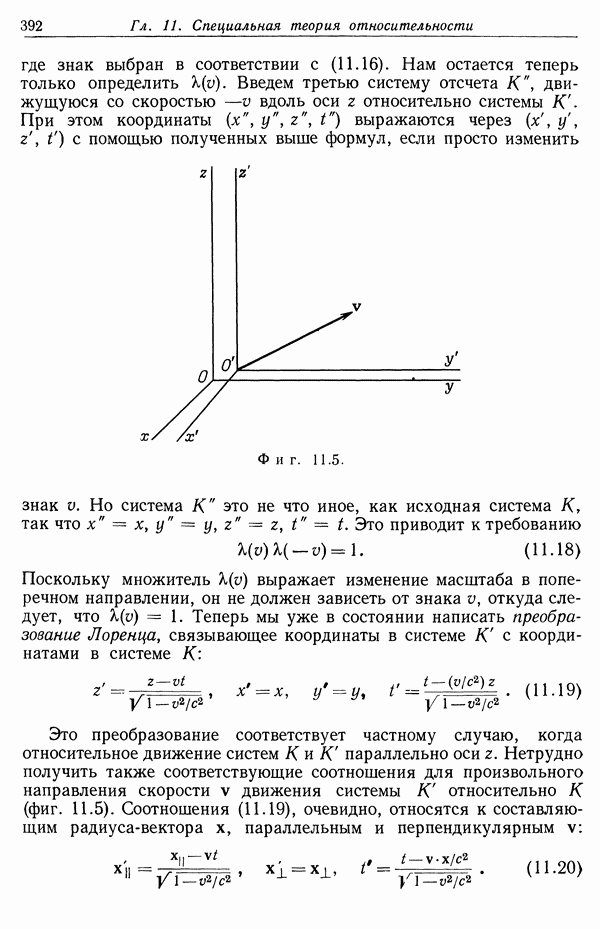
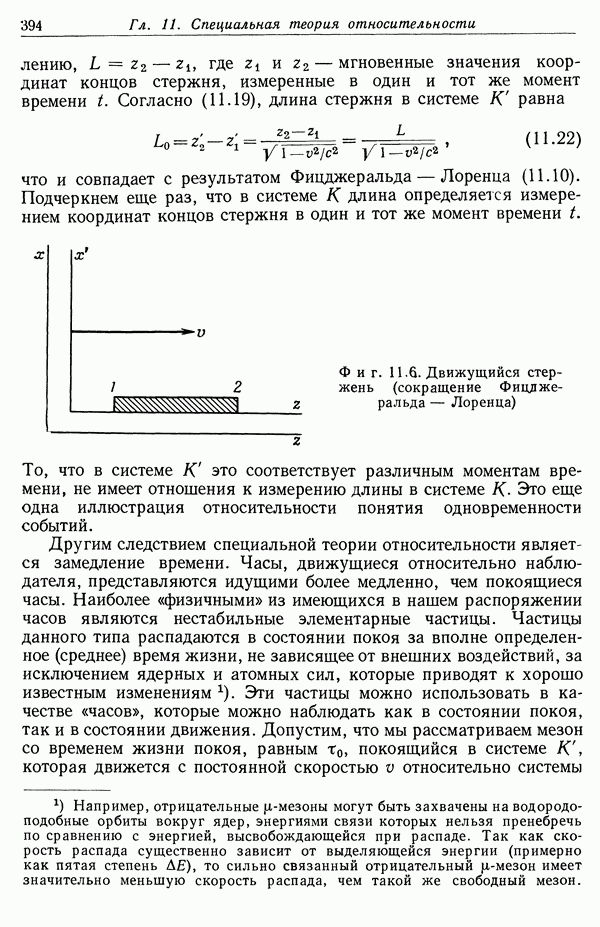
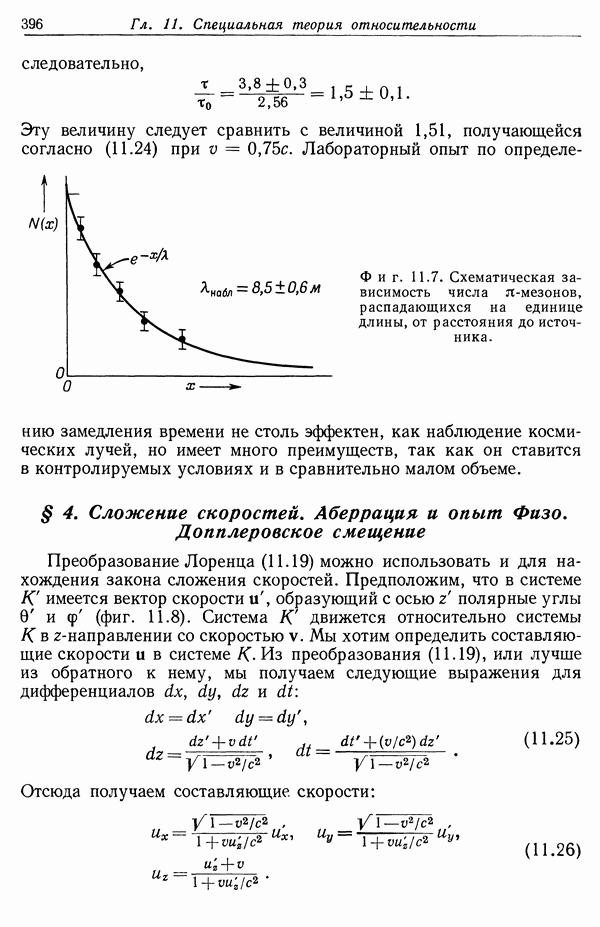
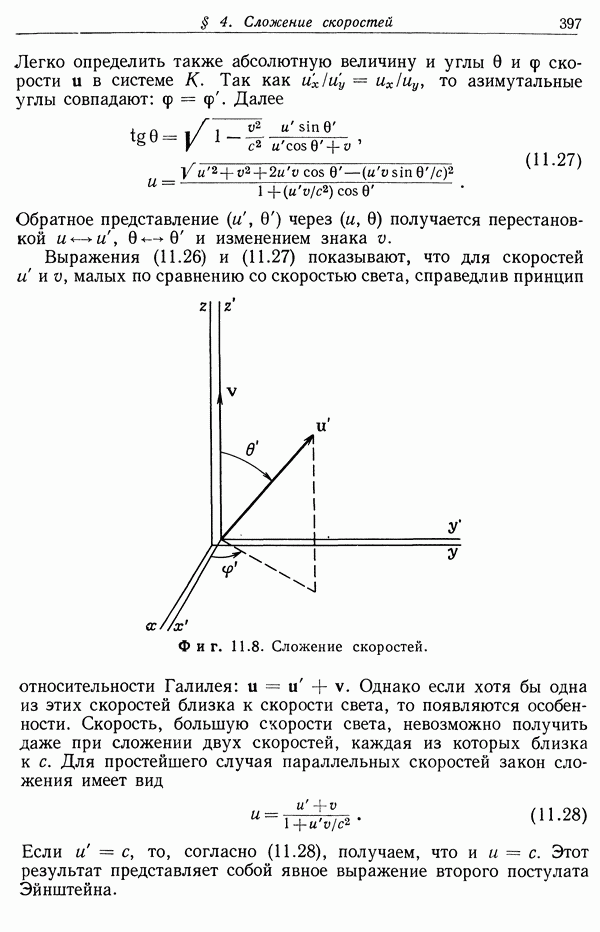
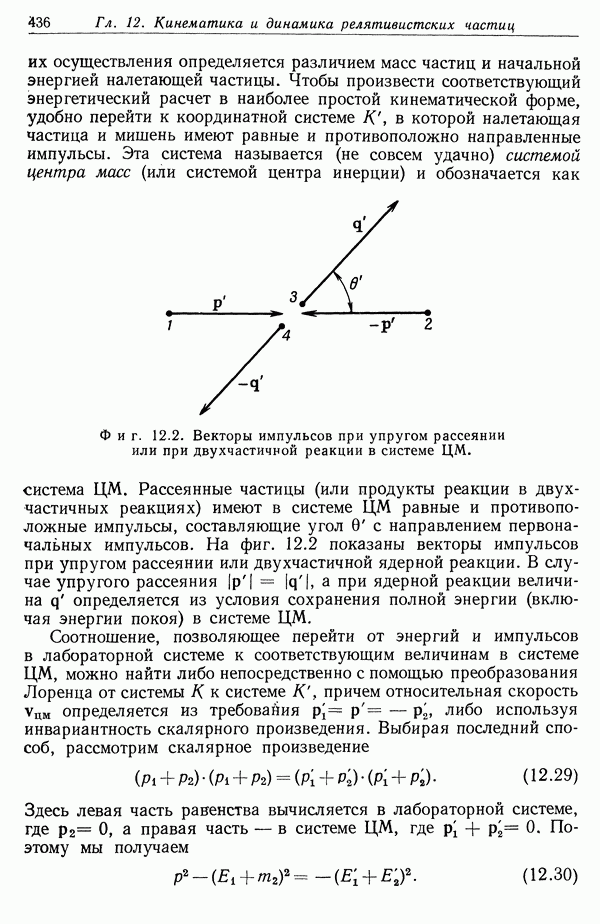
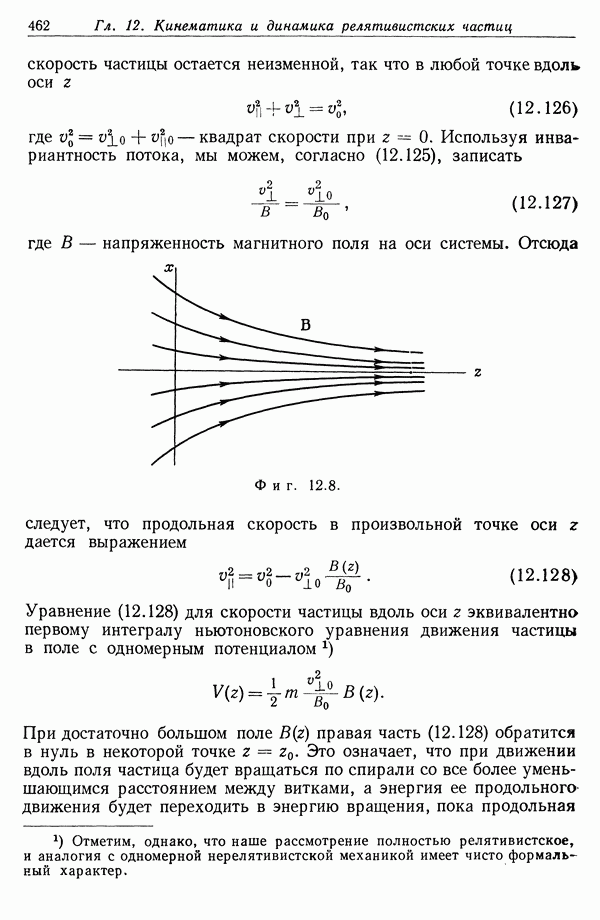
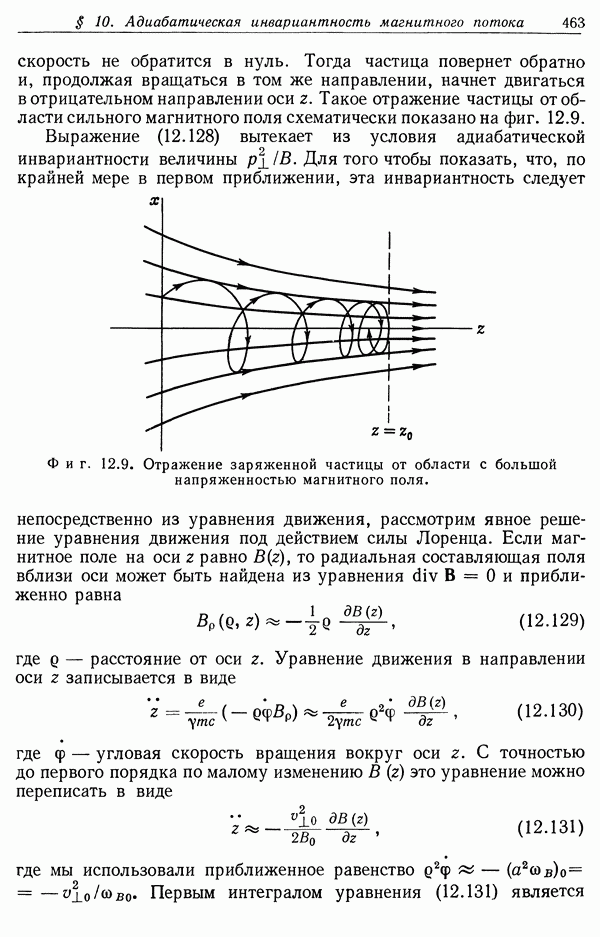
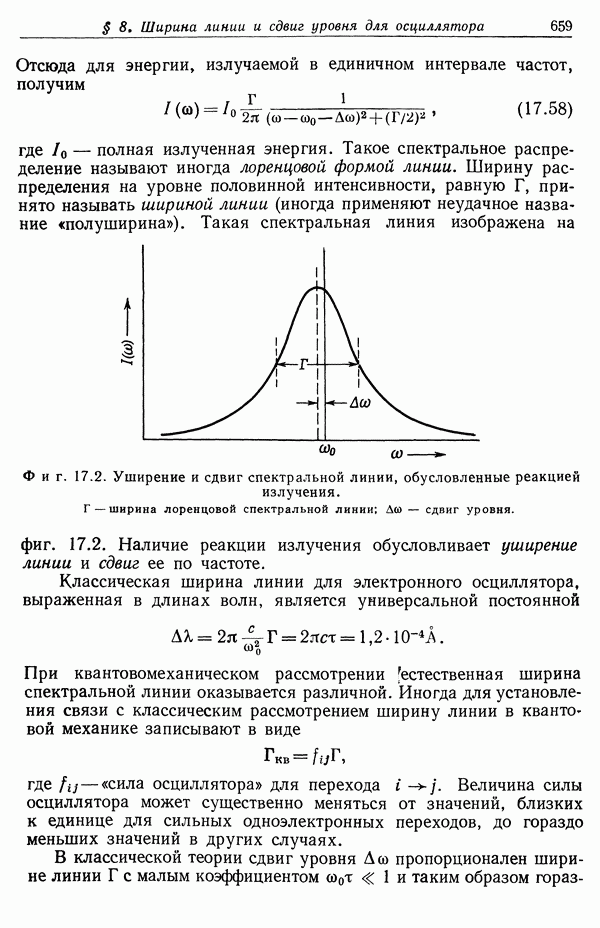
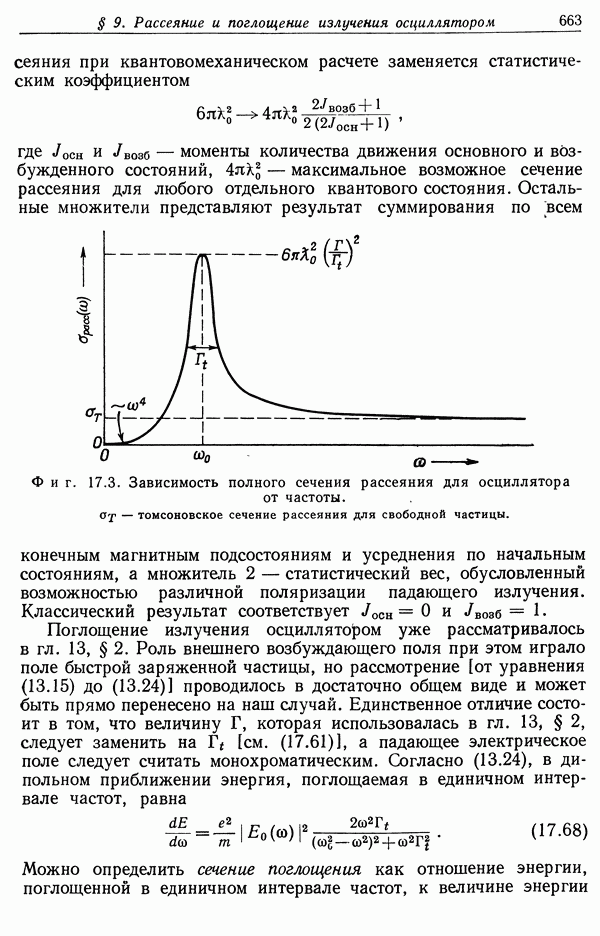
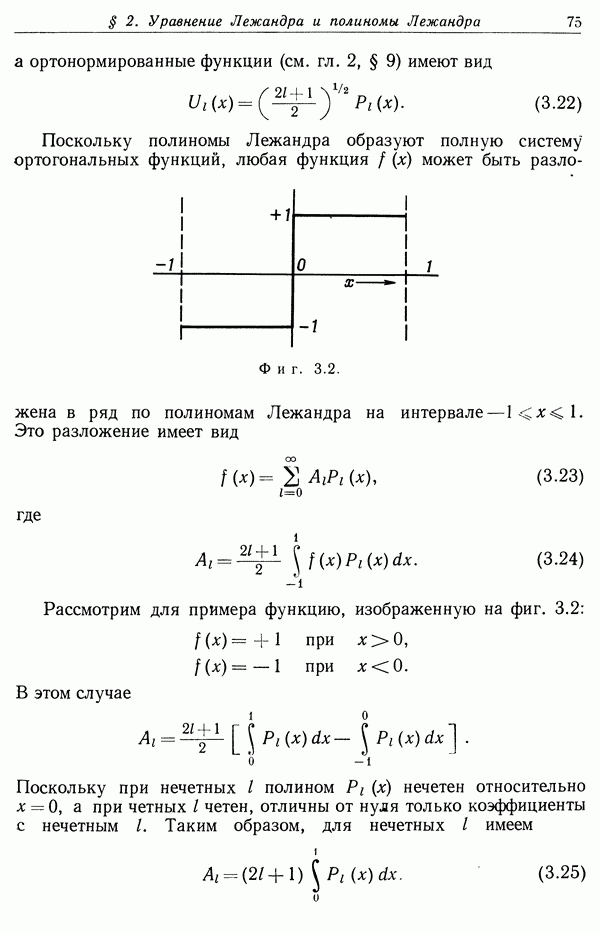| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Классическое и квантовомеханическое выражения для потерь энергии
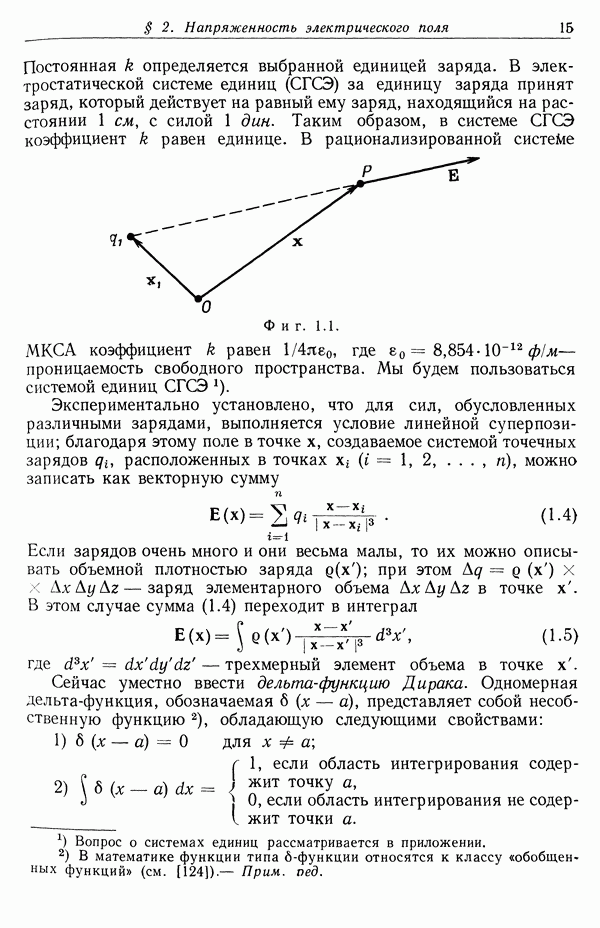
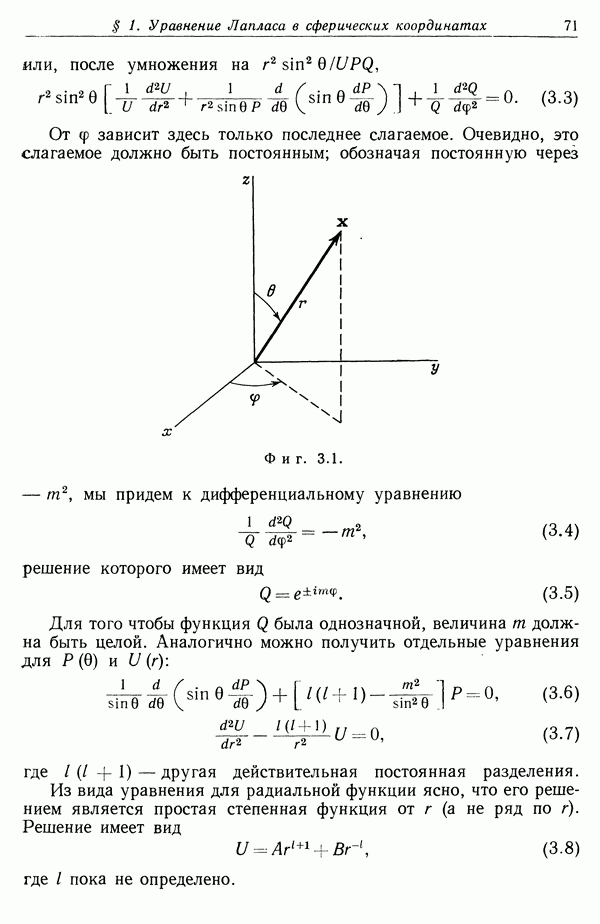
Выражение (13.31) для энергии, передаваемой гармоническому осциллятору, можно использовать для вычисления энергии, теряемой на единице длины быстрой тяжелой частицей, проходящей через вещество. Предположим, что в единице объема содержится N атомов, в каждом из которых имеется Z электронов. Эти Z электронов можно разделить на группы, отмеченные индексом  каждая группа содержит
каждая группа содержит  электронов с одинаковыми частотами связи
электронов с одинаковыми частотами связи  Число
Число  можно назвать силой
можно назвать силой  осциллятора. Силы осцилляторов удовлетворяют очевидному соотношению
осциллятора. Силы осцилляторов удовлетворяют очевидному соотношению  . С помощью тривиального обобщения рассуждений, приводящих к формулам (13.11) и (13.12), легко получить следующее выражение для потерь энергии тяжелой частицей:
. С помощью тривиального обобщения рассуждений, приводящих к формулам (13.11) и (13.12), легко получить следующее выражение для потерь энергии тяжелой частицей:
 (13.34)
(13.34)
где величина  определяется соотношением (13.31), причем
определяется соотношением (13.31), причем  а нижний предел интегрирования
а нижний предел интегрирования  устанавливается в соответствии с (13.7). Так как функция (13.31) весьма быстро спадает до нуля для больших
устанавливается в соответствии с (13.7). Так как функция (13.31) весьма быстро спадает до нуля для больших  , нет необходимости определять верхний предел интегрирования. Интеграл от модифицированных функций Бесселя легко вычисляется, в результате чего получим следующее выражение:
, нет необходимости определять верхний предел интегрирования. Интеграл от модифицированных функций Бесселя легко вычисляется, в результате чего получим следующее выражение:
 (13.35)
(13.35)
где  Вообще говоря,
Вообще говоря,  Поэтому можно упростить (13.35) с помощью приближенных соотношений (3.103). Окончательное классическое выражение для потерь энергии имеет вид
Поэтому можно упростить (13.35) с помощью приближенных соотношений (3.103). Окончательное классическое выражение для потерь энергии имеет вид

где аргументом логарифма является величина

Входящее в  среднее значение частоты
среднее значение частоты  определяется как среднее геометрическое
определяется как среднее геометрическое
 (13.38)
(13.38)
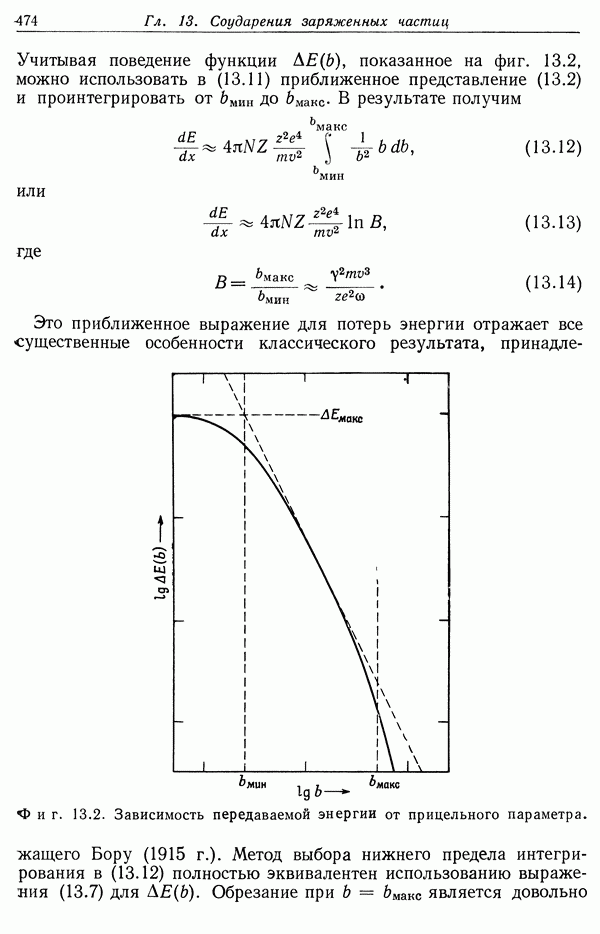
Приведенный результат (13.36) — (13.38) был впервые получен Бором в его классической работе, посвященной определению потерь энергии (1915 г.). Наше приближенное выражение (13.13) совпадает с (13.36) во всех существенных деталях, так как слагаемое  является малой поправкой даже при больших скоростях.
является малой поправкой даже при больших скоростях.
Формула Бора (13.36) верно описывает потери энергии для сравнительно медленных а-частиц и тяжелых ядер. Однако для электронов, мезонов, протонов и даже для быстрых а-частиц оно приводит к сильно завышенным значениям потерь энергии. Причина этого заключается в том, что для более легких частиц классическое рассмотрение уже неприменимо из-за квантовомеханических эффектов. Важнейшими квантовыми эффектами являются, во-первых, дискретность возможных значений передаваемой энергии, во-вторых, ограничения, связанные с волновой природой частиц и принципом неопределенности.
Влияние дискретности значений передаваемой энергии можно проиллюстрировать на примере вычисления классической величины переданной энергии (13.2) при  . Это, грубо говоря, наименьшее значение переданной энергии, которое следует учитывать при анализе потерь энергии. Предположив для простоты, что имеется лишь одна частота связи
. Это, грубо говоря, наименьшее значение переданной энергии, которое следует учитывать при анализе потерь энергии. Предположив для простоты, что имеется лишь одна частота связи  находим
находим
 (13.39)
(13.39)
где  — орбитальная скорость электрона в атоме водорода в основном состоянии. Так как
— орбитальная скорость электрона в атоме водорода в основном состоянии. Так как  по порядку величины совпадает с ионизационным потенциалом атома, то для быстрой частицы
по порядку величины совпадает с ионизационным потенциалом атома, то для быстрой частицы  передаваемая энергия, согласно классической формуле (13.39), очень мала по сравнению с ионизационным потенциалом или даже по сравнению с наименьшей энергией возбуждения
передаваемая энергия, согласно классической формуле (13.39), очень мала по сравнению с ионизационным потенциалом или даже по сравнению с наименьшей энергией возбуждения
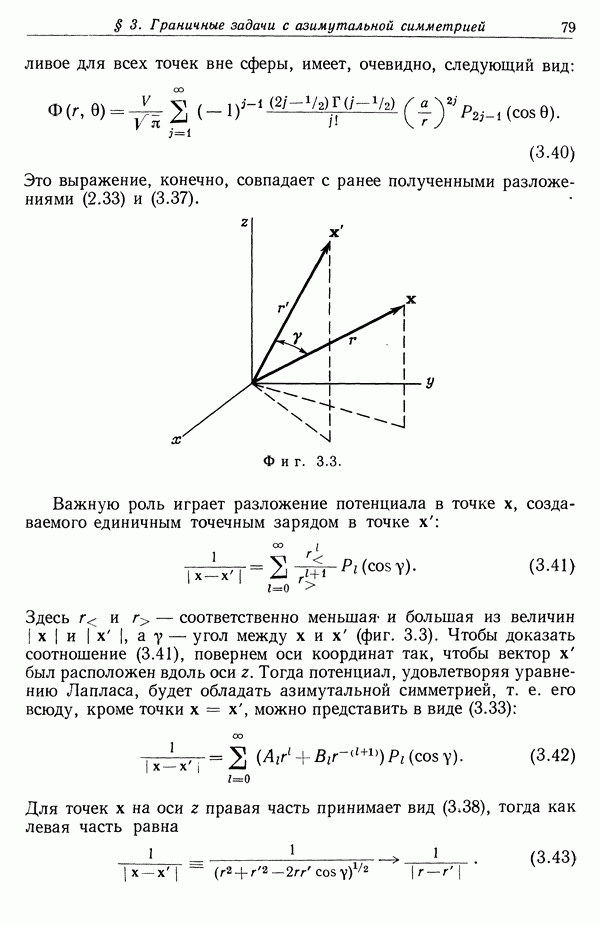
атома. Мы знаем, однако, что энергия должна передаваться определенными квантами. Столь малая величина энергии, как определяемая соотношением (13.39), просто не может быть поглощена атомом. Отсюда следует, что наше классическое рассмотрение уже неприменимо в этой области. Естественно было бы считать, что классическая формула (13.2) дает правильный результат лишь в том случае, когда вычисленная по ней передаваемая энергия велика по сравнению с характерными энергиями возбуждения атома. Это требование устанавливает совершенно иной верхний предел для значений прицельного параметра. К счастью, классический результат все же применим в статистическом смысле, если интерпретировать его содержание несколько иным образом.
Квантовое рассмотрение показывает некорректность классического утверждения о передаче сколь угодно малых количеств энергии при каждом соударении. Однако если рассмотреть большое число соударений, то окажется, что передача малых количеств энергии может осуществляться в среднем. При этом передача энергии происходит не при каждом соударении. В большинстве соударений она отсутствует, но некоторое малое число соударений сопровождается заметным возбуждением атомов. Результирующее среднее значение передаваемой энергии по многим соударениям оказывается малым. В указанном статистическом смысле устраняется противоречие между квантовым механизмом дискретной передачи энергии и классическим подходом, допускающим любое значение передаваемой энергии. Для получения полного количественного согласия необходимо использовать квантовомеханические выражения для сил осциллятора  и резонансных частот со.
и резонансных частот со.
Второй важный квантовый эффект связан с волновой природой частиц. Принцип неопределенности накладывает известные ограничения, сужающие область применимости классических представлений об орбитальном движении. Как известно, при попытке приближенно воспроизвести классическую траекторию путем рассмотрения движения волнового пакета его путь может быть установлен лишь с точностью до неопределенности в координате  Для прицельных параметров b, меньших этой неопределенности, классические понятия теряют силу. Так как частицы в силу своей волновой природы в некотором смысле «размазаны» в области с размерами порядка
Для прицельных параметров b, меньших этой неопределенности, классические понятия теряют силу. Так как частицы в силу своей волновой природы в некотором смысле «размазаны» в области с размерами порядка  можно ожидать, что правильное квантовомеханическое значение потерь энергии будет при
можно ожидать, что правильное квантовомеханическое значение потерь энергии будет при  соответствовать гораздо меньшим значениям передаваемой энергии, чем это следует из (13.2). Таким образом, величина
соответствовать гораздо меньшим значениям передаваемой энергии, чем это следует из (13.2). Таким образом, величина  является квантовым аналогом минимального прицельного параметра (13.6).
является квантовым аналогом минимального прицельного параметра (13.6).
Каждая из двух соударяющихся частиц имеет волновую при роду. При заданной относительной скорости неопределенность
координаты обусловливается более легкой частицей. Для тяжелой налетающей частицы, соударяющейся с электроном, импульс электрона в системе отсчета, относительно которой налетающая частица покоится (и которая почти совпадает с системой ЦМ), равен  , где
, где  — масса электрона. Поэтому минимальное значение прицельного параметра, определяемое квантовомеханическими эффектами, равно
— масса электрона. Поэтому минимальное значение прицельного параметра, определяемое квантовомеханическими эффектами, равно

Для случая электрон-электронных соударений следует действовать более осторожно и рассмотреть импульс (12.34) в системе ЦМ для случая равных масс. При этом для электронов получается следующее выражение для минимального прицельного параметра:

В рассматриваемом случае следует при вычислении величины В, входящей как аргумент логарифма в выражение для  подставлять в (13.14) наибольшее из двух минимальных прицельных параметров (13.6) и (13.40). Отношение классического значения
подставлять в (13.14) наибольшее из двух минимальных прицельных параметров (13.6) и (13.40). Отношение классического значения  к квантовому равно
к квантовому равно

При  следует пользоваться классической формулой Бора. Это, очевидно, имеет место для медленных частиц с большим зарядом в полном согласии с наблюдениями. При
следует пользоваться классической формулой Бора. Это, очевидно, имеет место для медленных частиц с большим зарядом в полном согласии с наблюдениями. При  квантовомеханическое значение минимального прицельного параметра больше классического. При этом выражение для энергетических потерь следует изменить. Аргумент логарифма в формуле (13.13) принимает в этом случае вид
квантовомеханическое значение минимального прицельного параметра больше классического. При этом выражение для энергетических потерь следует изменить. Аргумент логарифма в формуле (13.13) принимает в этом случае вид

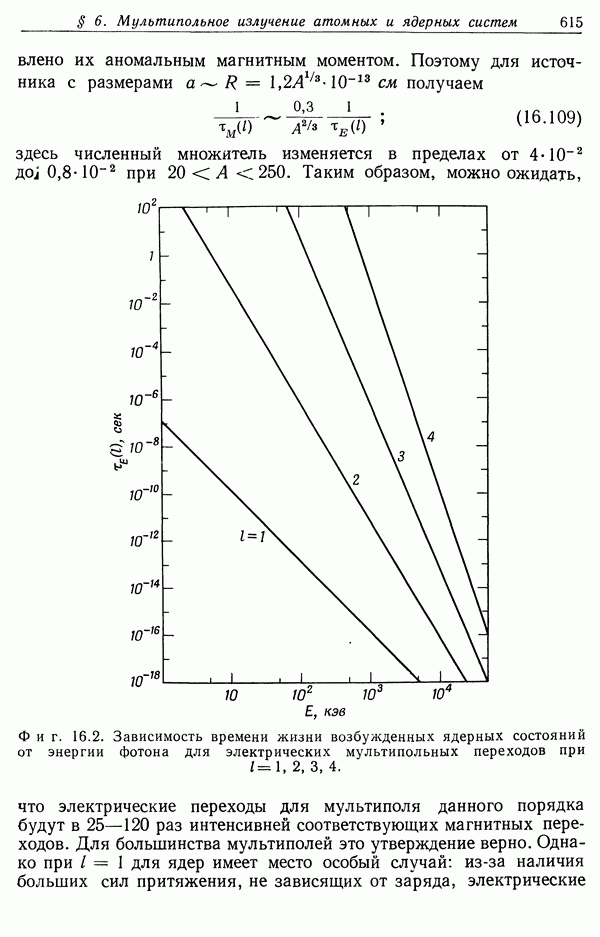
Соотношение (13.13) с квантовомеханическим значением  является хорошим приближением к формуле Бете (1930 г.), полученной при строгом квантовомеханическом подходе. Формула Бете с учетом эффекта близких соударений имеет вид
является хорошим приближением к формуле Бете (1930 г.), полученной при строгом квантовомеханическом подходе. Формула Бете с учетом эффекта близких соударений имеет вид
 (13.44)
(13.44)
Она отличается от приближенного выражения лишь малым поправочным членом  и множителем 2 в аргументе логарифма.
и множителем 2 в аргументе логарифма.
Учет квантовых эффектов для электронов с помощью соотношения (13.41) приводит к следующему модифицированному
квантовомеханическому выражению для аргумента логарифма:
 (13.45)
(13.45)
где последнее выражение справедливо в предельном случае больших энергий. Хотя для электронов существуют и другие квантовые эффекты, например влияние спина и обменных сил, основной квантовый эффект учитывается соотношением (13.45).

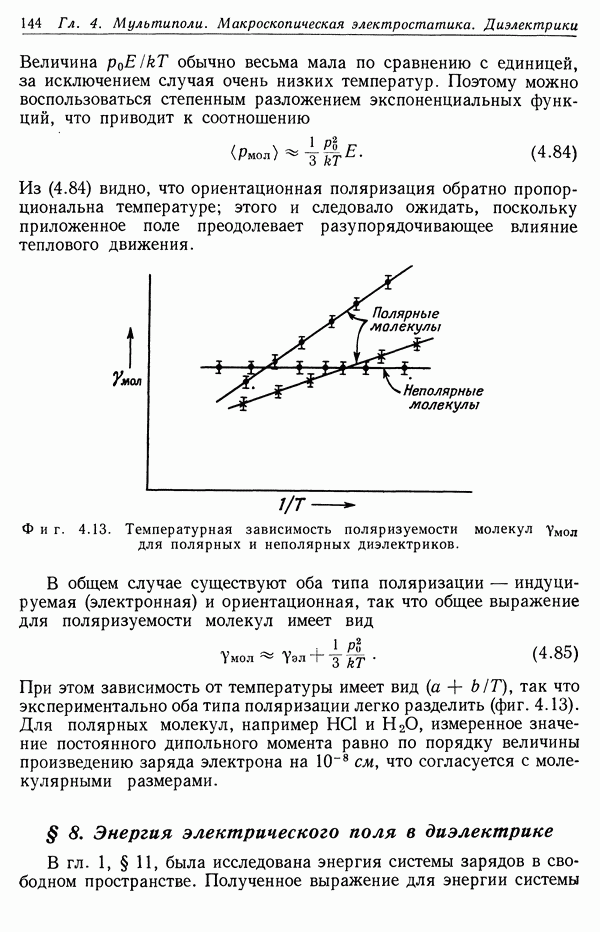
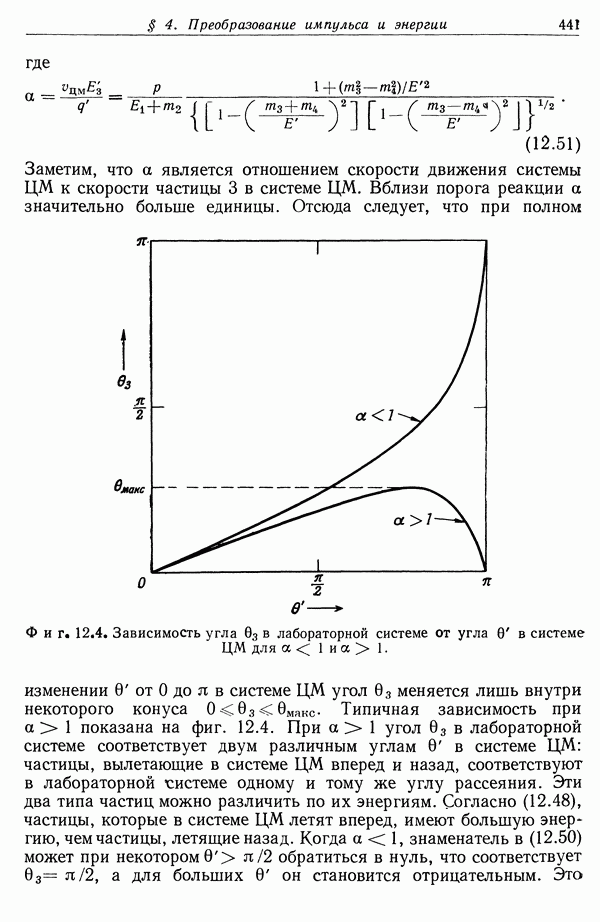
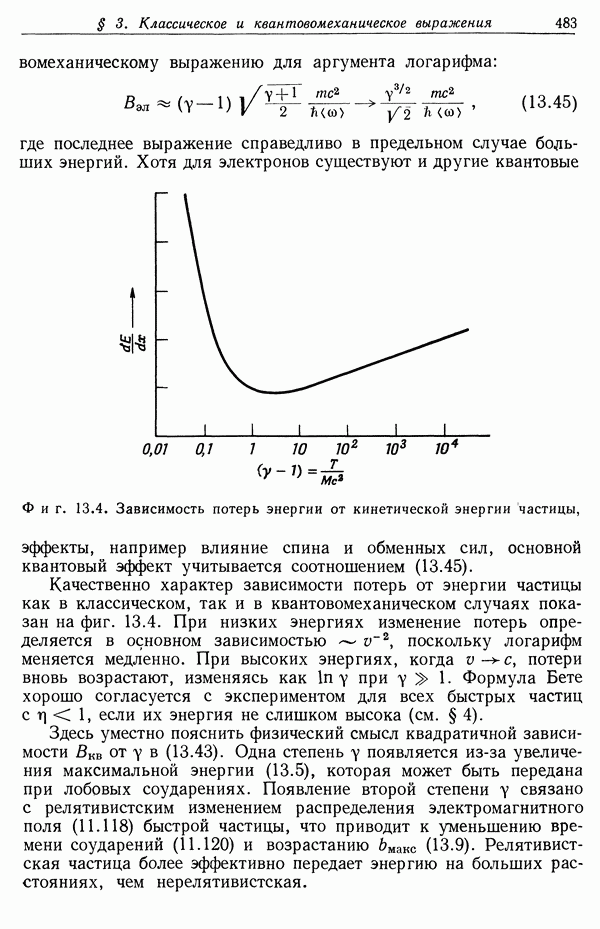
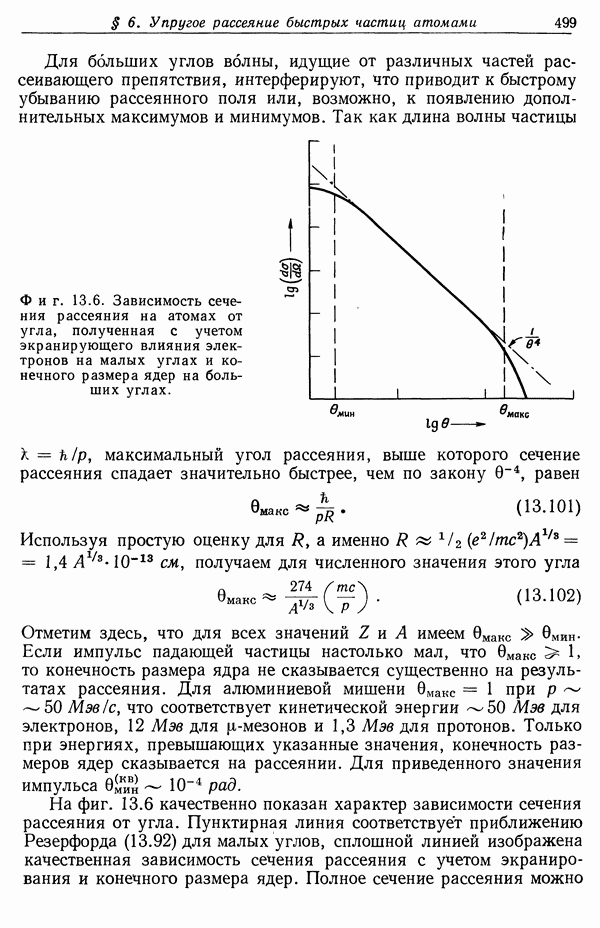
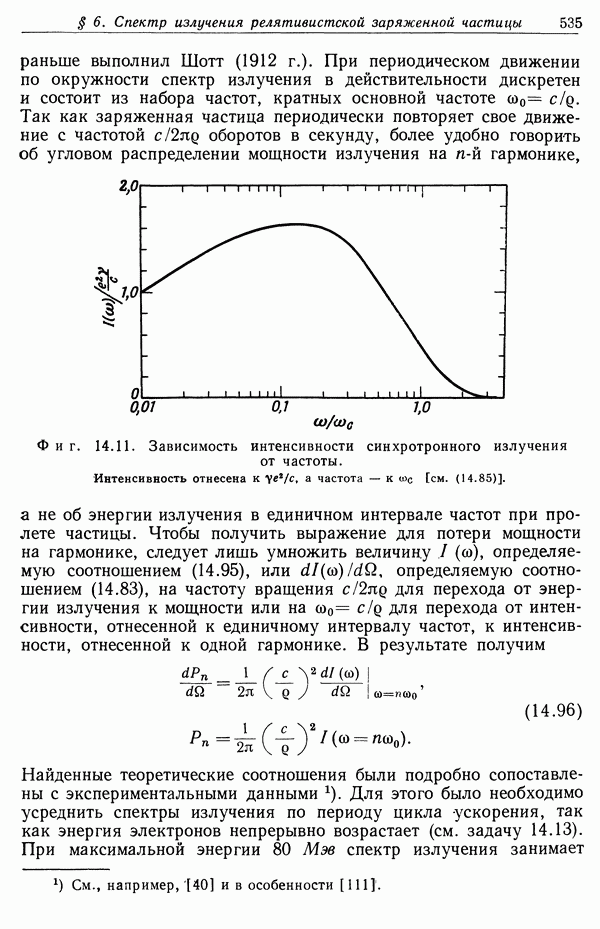
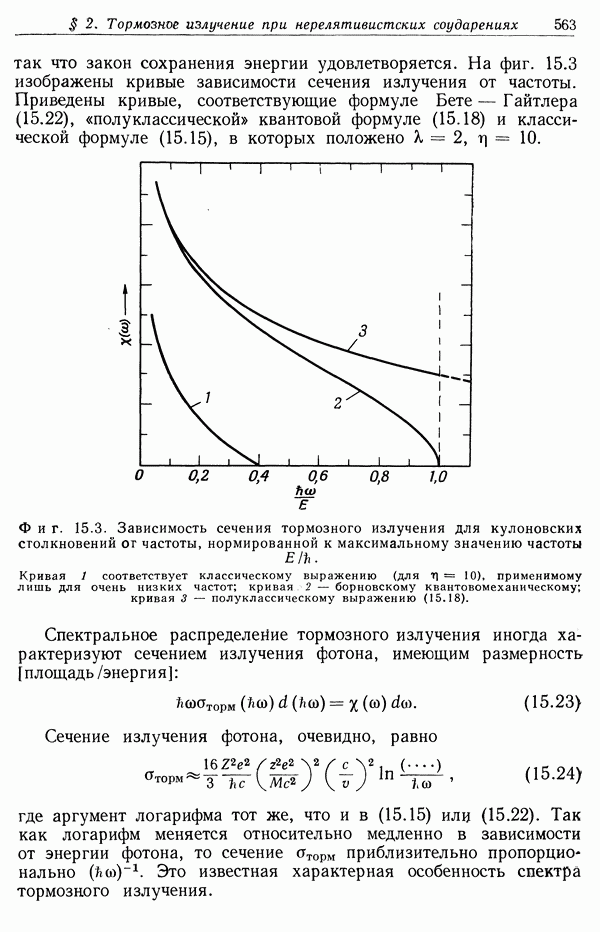
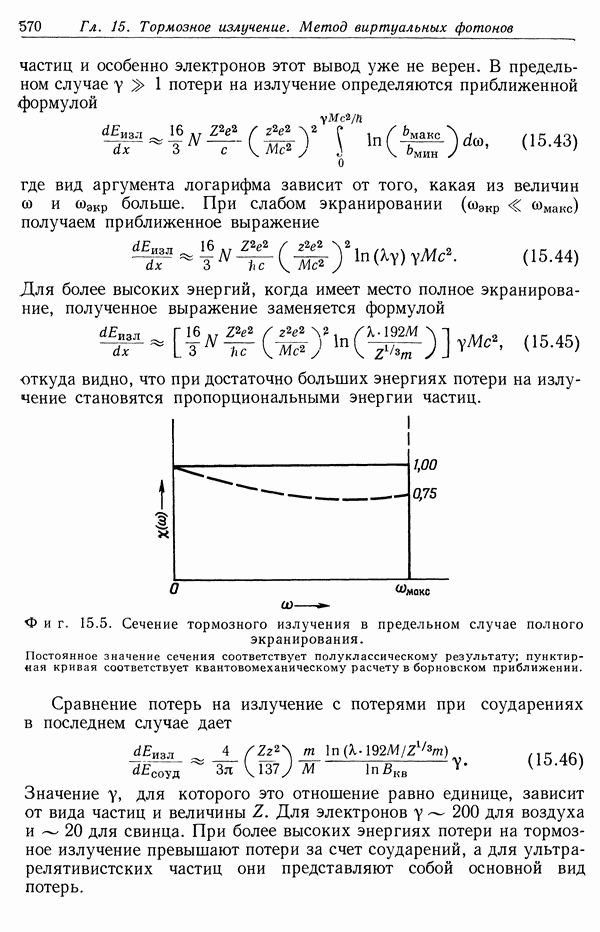
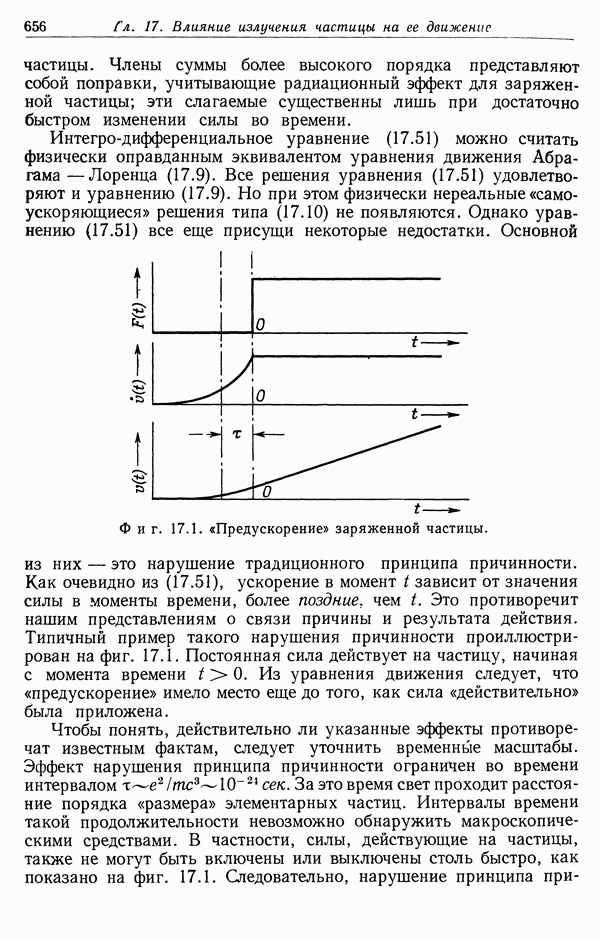
Фиг. 13.4. Зависимость потерь энергии от кинетической энергии частицы,
Качественно характер зависимости потерь от энергии частицы как в классическом, так и в квантовомеханическом случаях показан на фиг. 13.4. При низких энергиях изменение потерь определяется в основном зависимостью  поскольку логарифм меняется медленно. При высоких энергиях, когда потери вновь возрастают, изменяясь как ln у при
поскольку логарифм меняется медленно. При высоких энергиях, когда потери вновь возрастают, изменяясь как ln у при  Формула Бете хорошо согласуется с экспериментом для всех быстрых частиц с
Формула Бете хорошо согласуется с экспериментом для всех быстрых частиц с  если их энергия не слишком высока (см. § 4).
если их энергия не слишком высока (см. § 4).
Здесь уместно пояснить физический смысл квадратичной зависимости  от у в (13.43). Одна степень у появляется из-за увеличения максимальной энергии (13.5), которая может быть передана при лобовых соударениях. Появление второй степени у связано с релятивистским изменением распределения электромагнитного поля (11.118) быстрой частицы, что приводит к уменьшению времени соударений (11.120) и возрастанию
от у в (13.43). Одна степень у появляется из-за увеличения максимальной энергии (13.5), которая может быть передана при лобовых соударениях. Появление второй степени у связано с релятивистским изменением распределения электромагнитного поля (11.118) быстрой частицы, что приводит к уменьшению времени соударений (11.120) и возрастанию  Релятивистская частица более эффективно передает энергию на больших расстояниях, чем нерелятивистская.
Релятивистская частица более эффективно передает энергию на больших расстояниях, чем нерелятивистская.
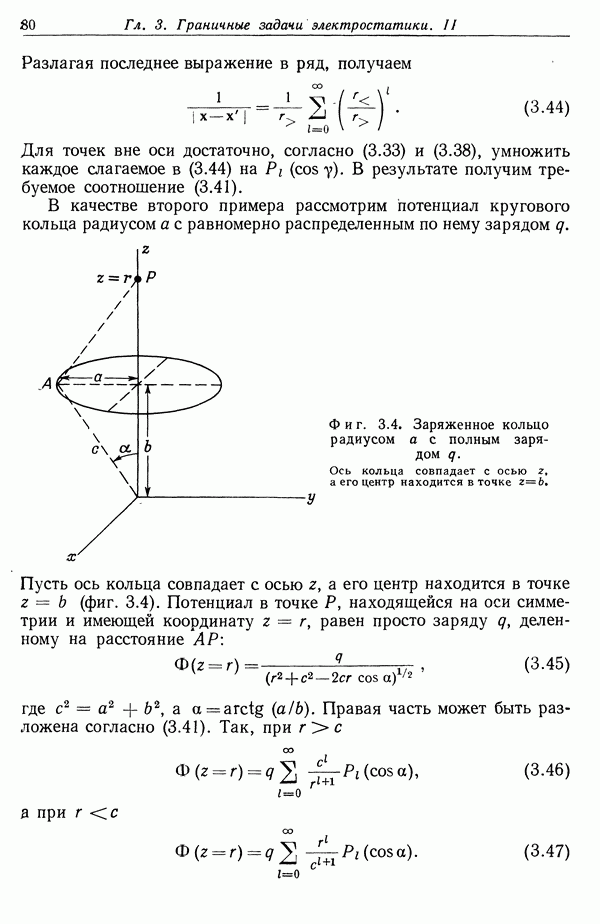
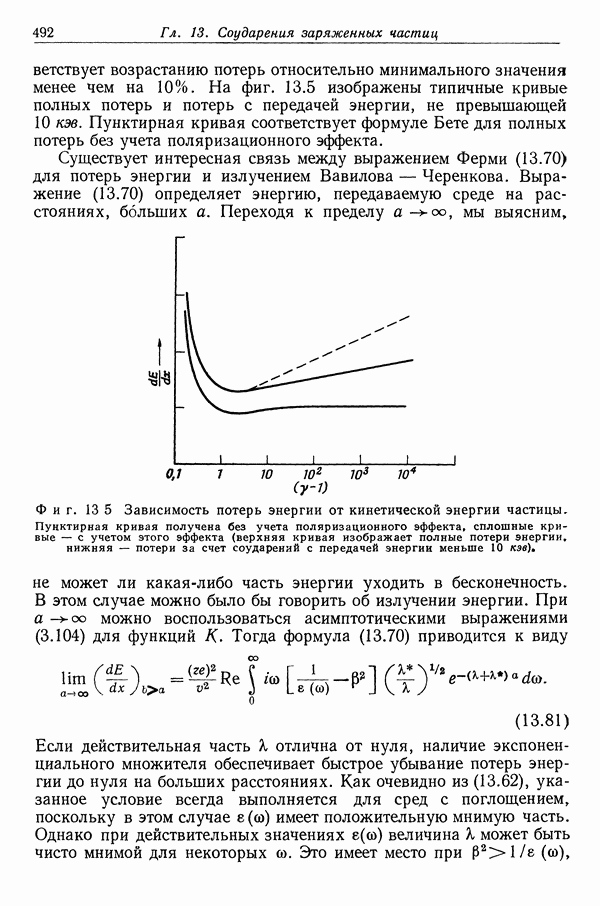
В ряде случаев интересно знать величину потерь энергии на единице длины, обусловленных соударениями, в которых передача энергии в одном соударении не превышает некоторой определенной величины е. Так, например, в фотографических эмульсиях пробег электронов с энергией больше 10 кэв превышает средние линейные размеры зерен бромистого серебра. Поэтому энергия, расходуемая на почернение зерен серебра, соответствует соударениям, при которых передаваемая энергия меньше 10 кэв. В классическом приближении искомое выражение для потерь энергии можно получить из формулы Бора (13.36), выбирая минимальный прицельный параметр  таким образом, чтобы передаваемая энергия (13.2) была равна е. В результате получаем
таким образом, чтобы передаваемая энергия (13.2) была равна е. В результате получаем

Отсюда мы приходим к формуле типа (13.36), в которой аргументом логарифма служит величина
 (13.47)
(13.47)
Как уже говорилось выше, квантовомеханическое выражение для потерь энергии получается из классической формулы с помощью замены [см. 
 (13.48)
(13.48)
Следовательно, квантовомеханическое выражение для потерь на единице длины, обусловленных соударениями с передачей энергии. меньшей  , должно иметь вид
, должно иметь вид

где
 (13.50)
(13.50)
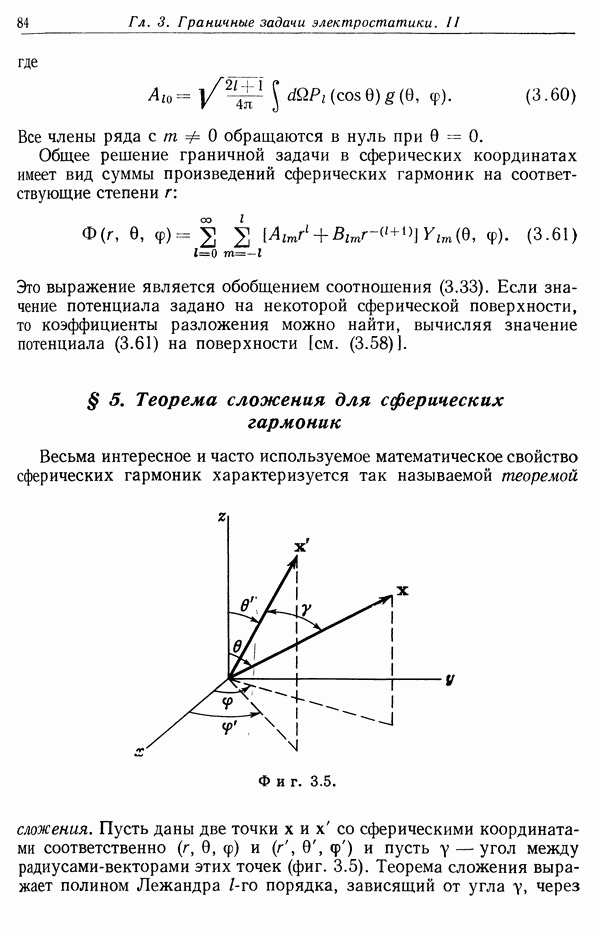
Константа X — численный множитель порядка единицы, значение которого можно определить лишь с помощью детальных квантовомеханических расчетов. Согласно расчетам Бете (1930 г.),  Квантовомеханическое значение
Квантовомеханическое значение  можно представить следующим образом:
можно представить следующим образом:

где  определяется согласно (13.9), а минимальный прицельный параметр равен
определяется согласно (13.9), а минимальный прицельный параметр равен
 (13-52)
(13-52)
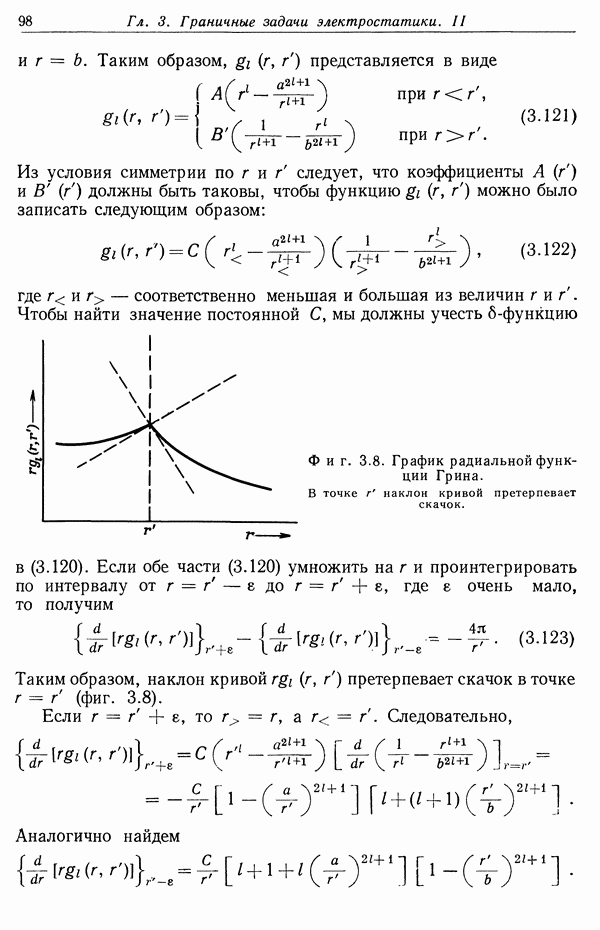
Таким образом, поскольку неопределенность полученного импульса  не должна превышать импульса, передаваемого при соударении, то классическая траектория может быть определена лишь с точностью, по порядку величины не лучшей, чем (13.52). В противном случае мы не можем быть уверены, что передаваемая энергия действительно меньше е. Следовательно, соотношение (13.52) устанавливает естественный квантовомеханический нижний предел для классического представления об орбитах частиц.
не должна превышать импульса, передаваемого при соударении, то классическая траектория может быть определена лишь с точностью, по порядку величины не лучшей, чем (13.52). В противном случае мы не можем быть уверены, что передаваемая энергия действительно меньше е. Следовательно, соотношение (13.52) устанавливает естественный квантовомеханический нижний предел для классического представления об орбитах частиц.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
- § 2. Напряженность электрического поля
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
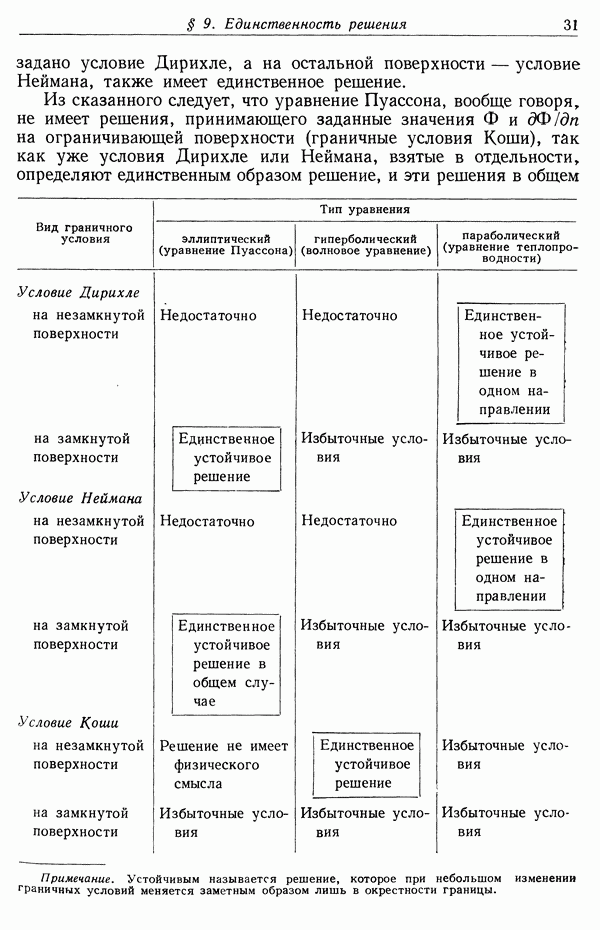
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
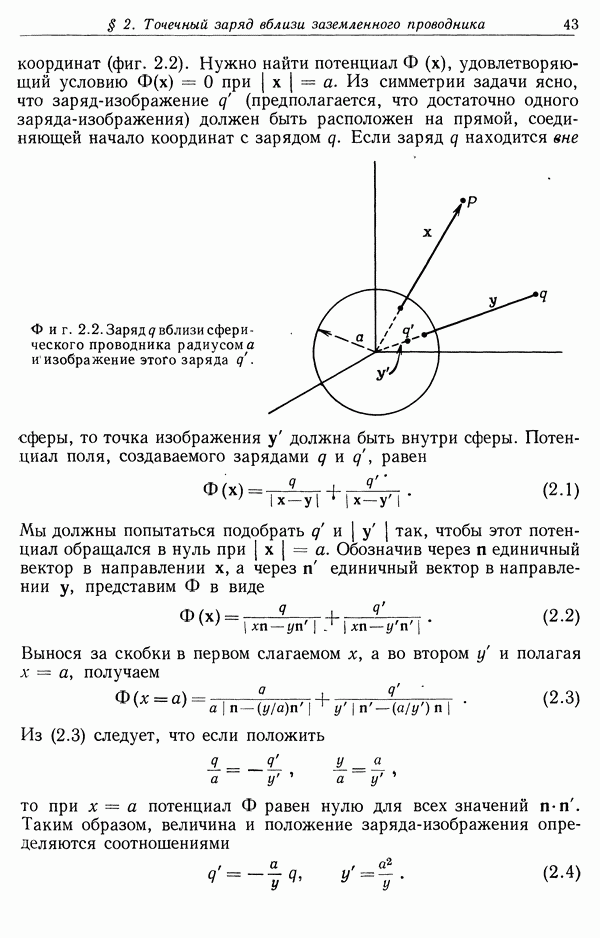
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
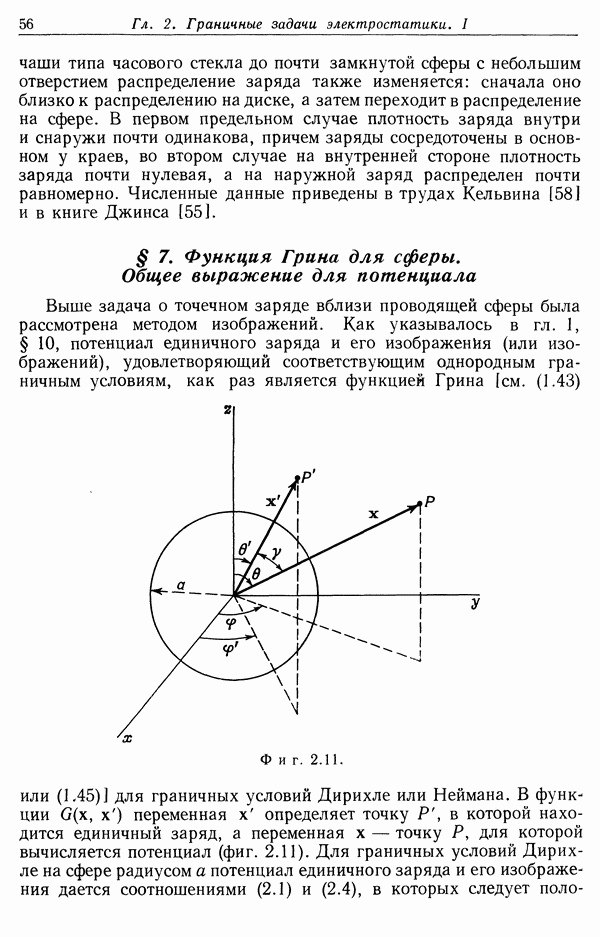
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
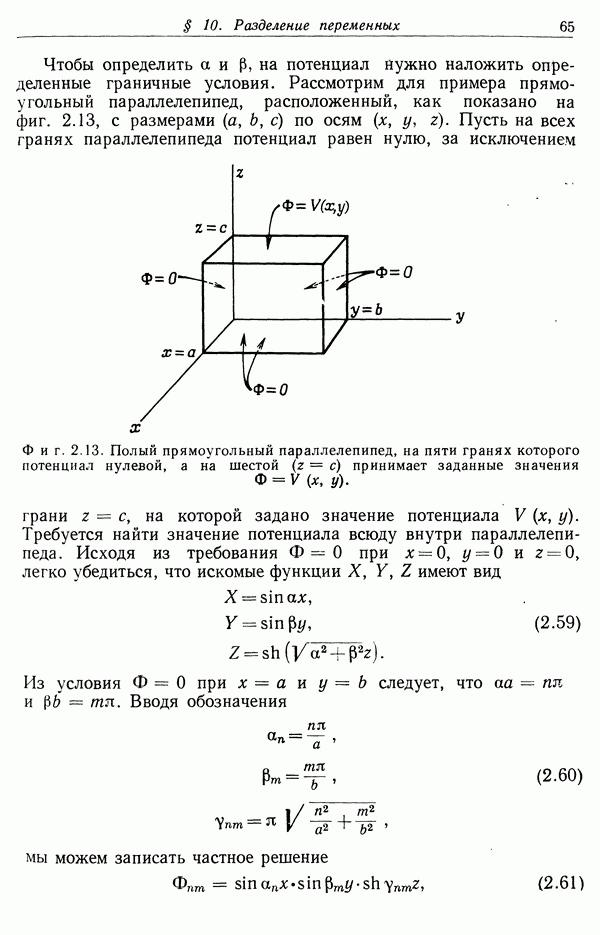
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
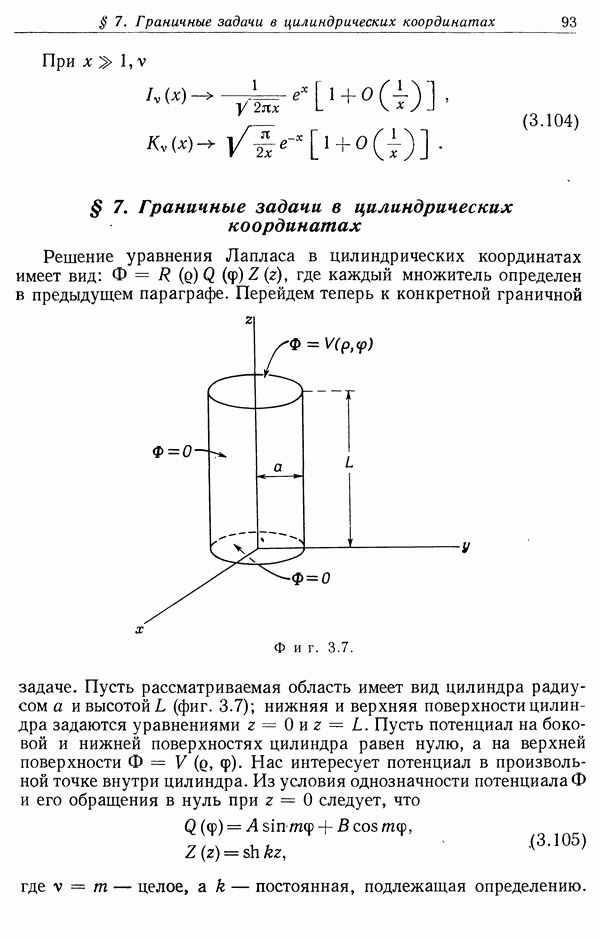
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
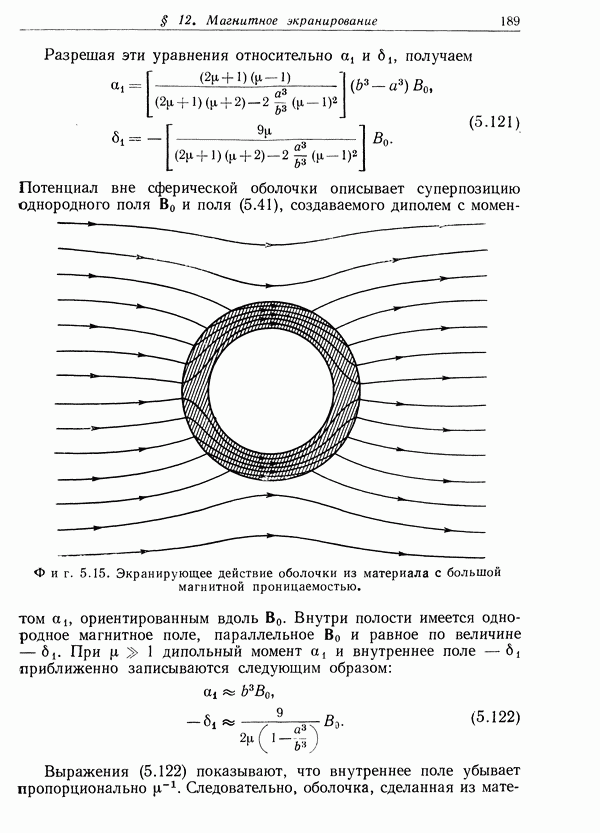
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
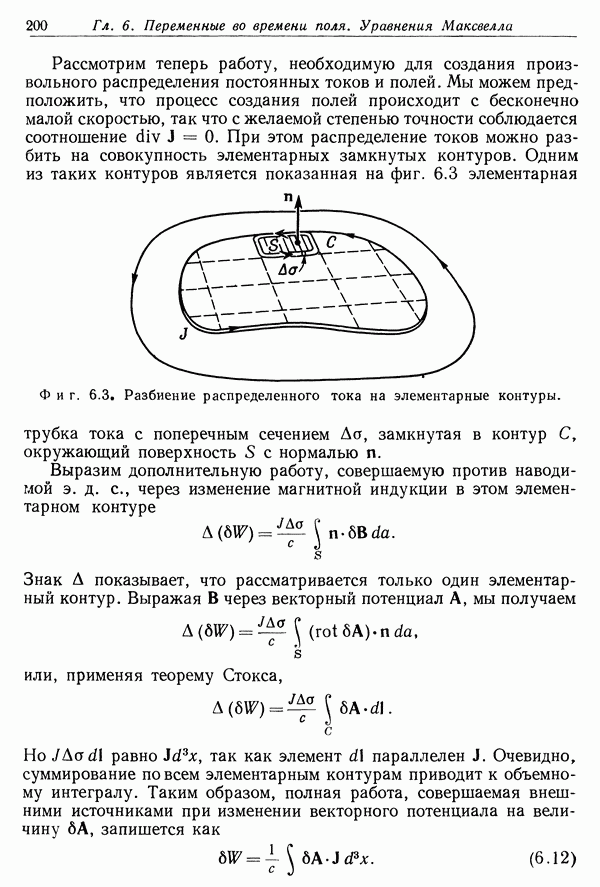
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
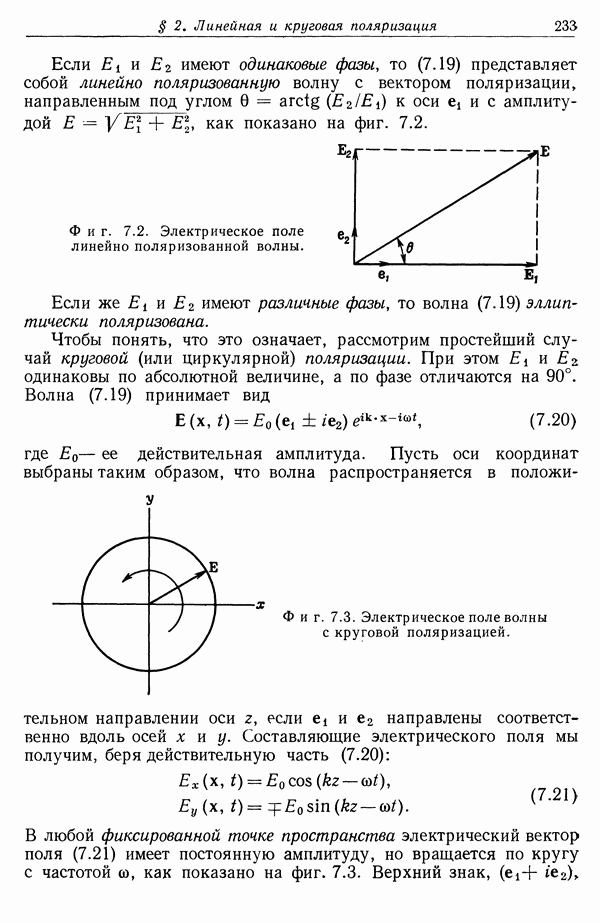
- § 2. Линейная и круговая поляризация
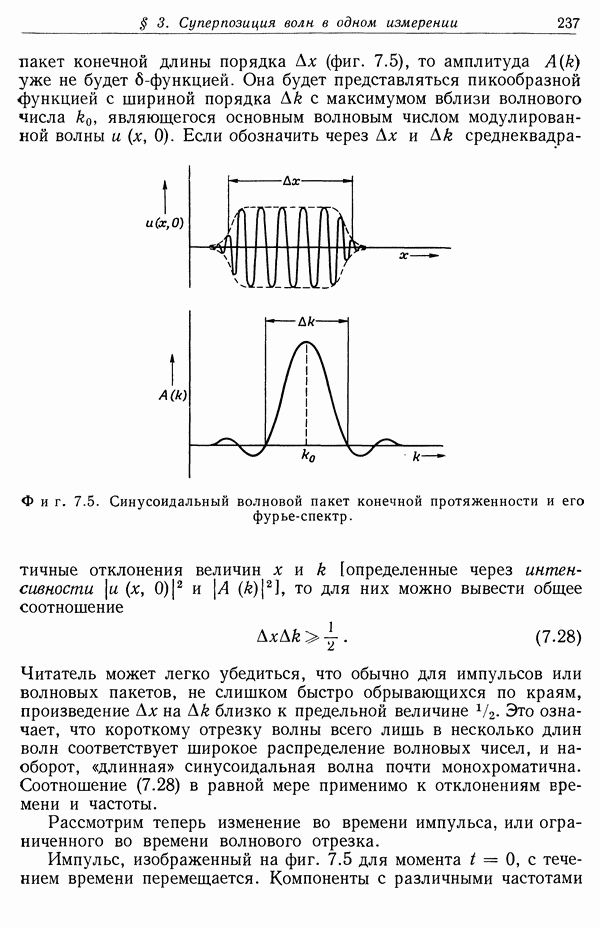
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
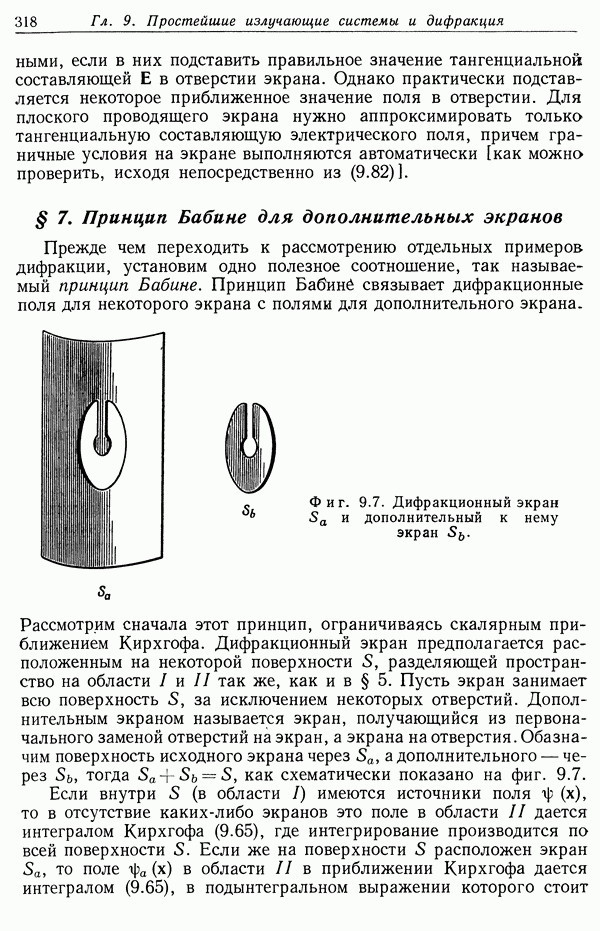
- § 7. Принцип Бабине для дополнительных экранов
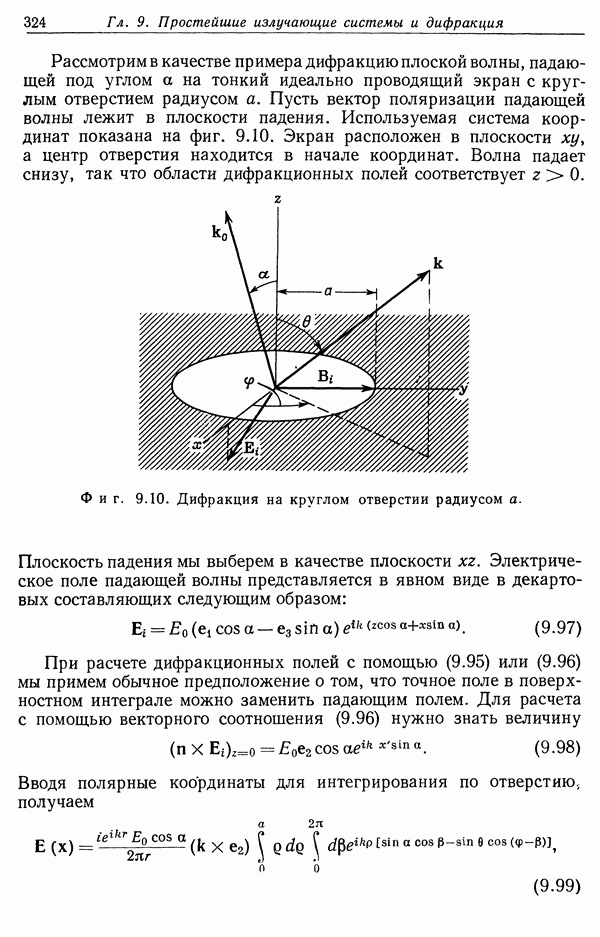
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
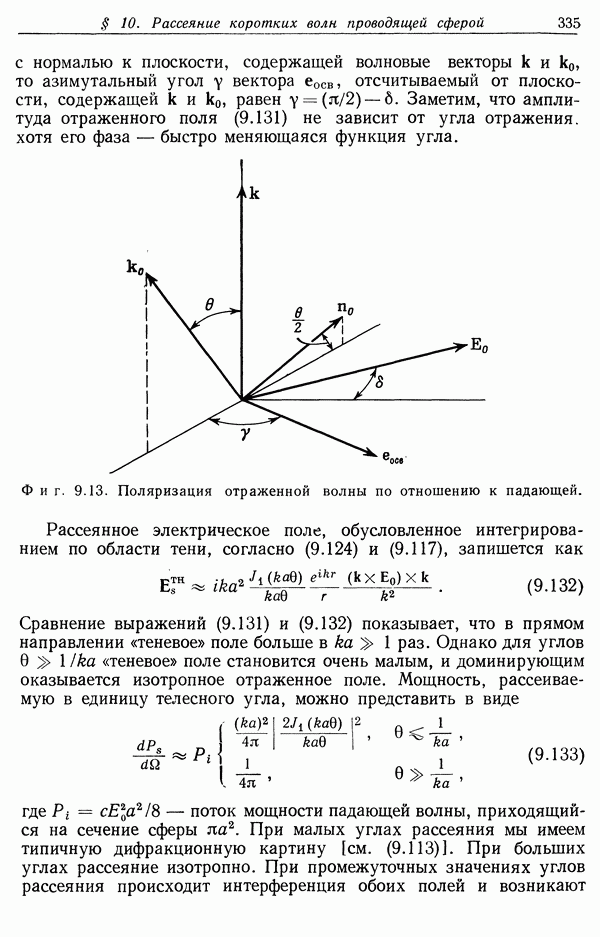
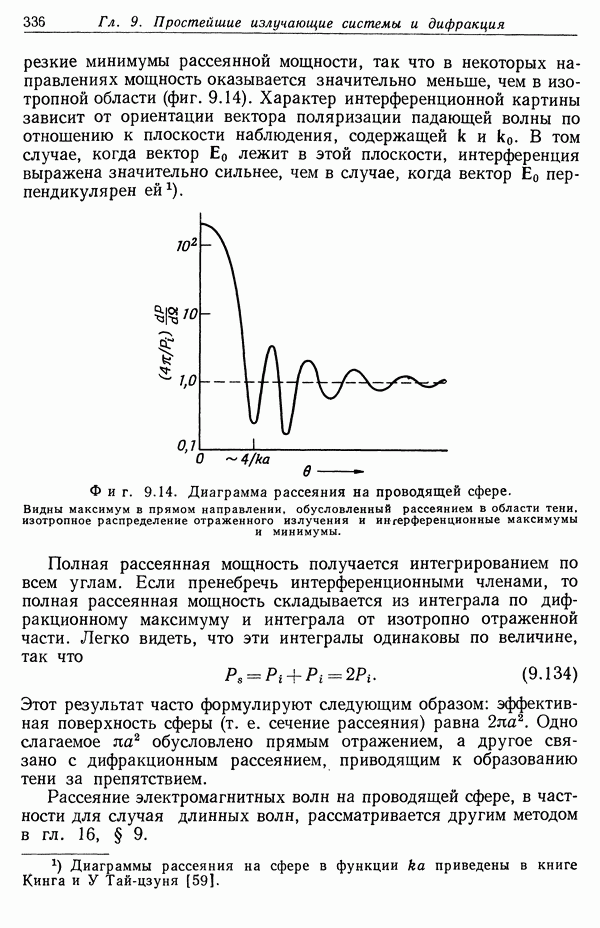
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
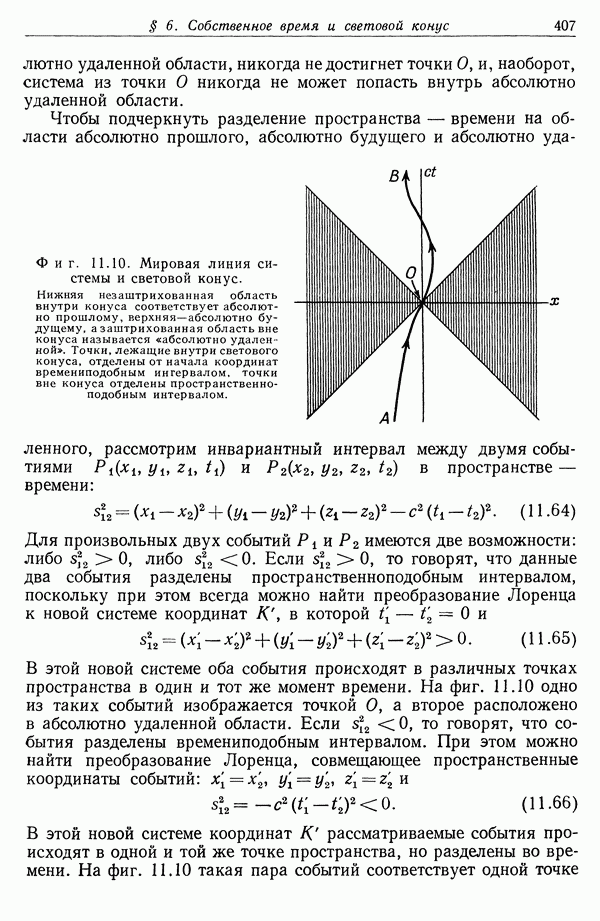
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
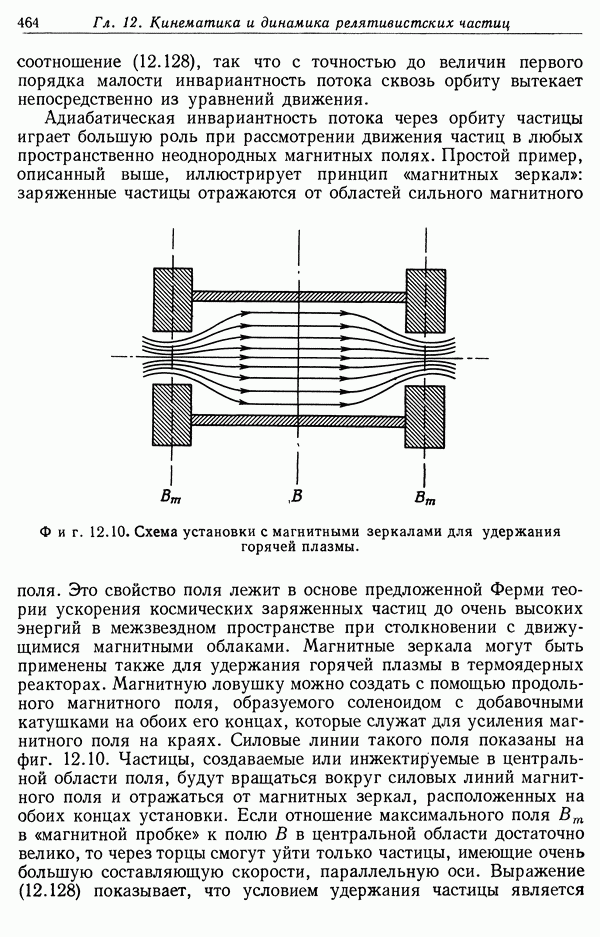
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
- § 3. Угловое распределение излучения ускоряемого заряда
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
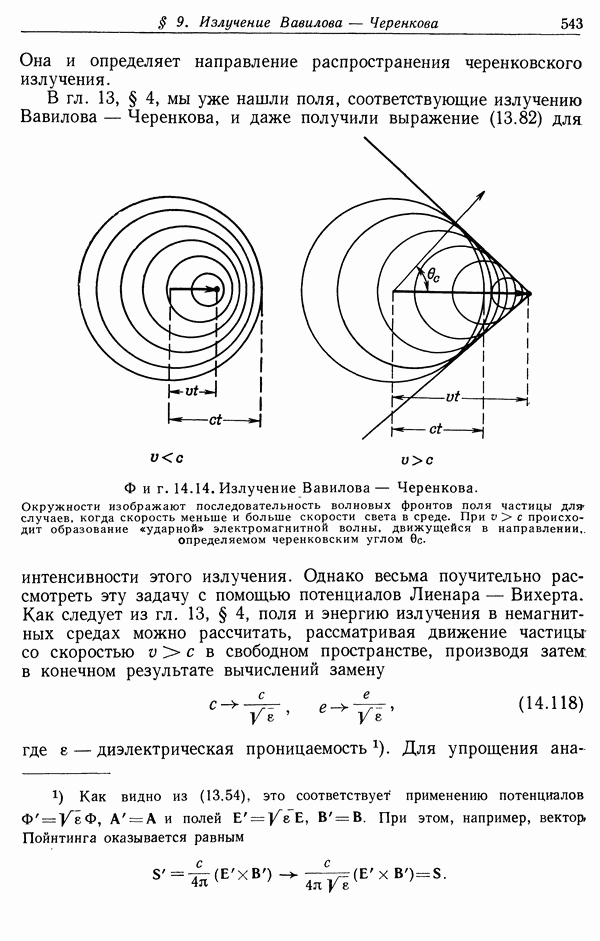
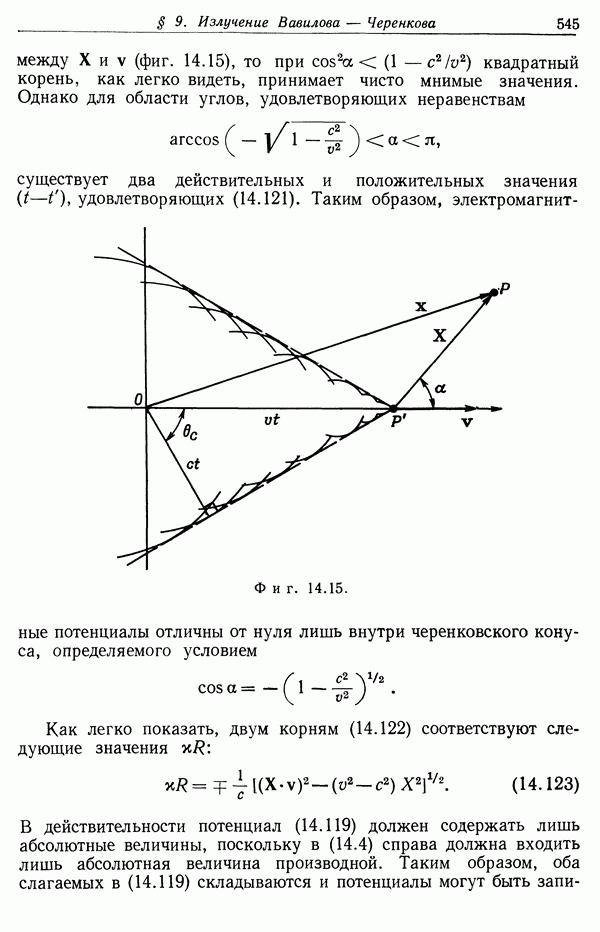
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
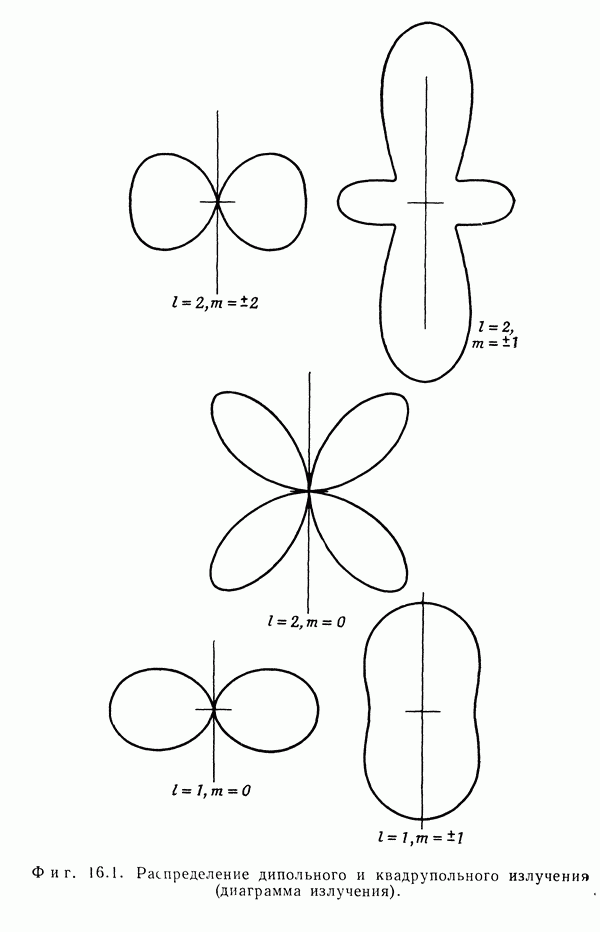
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
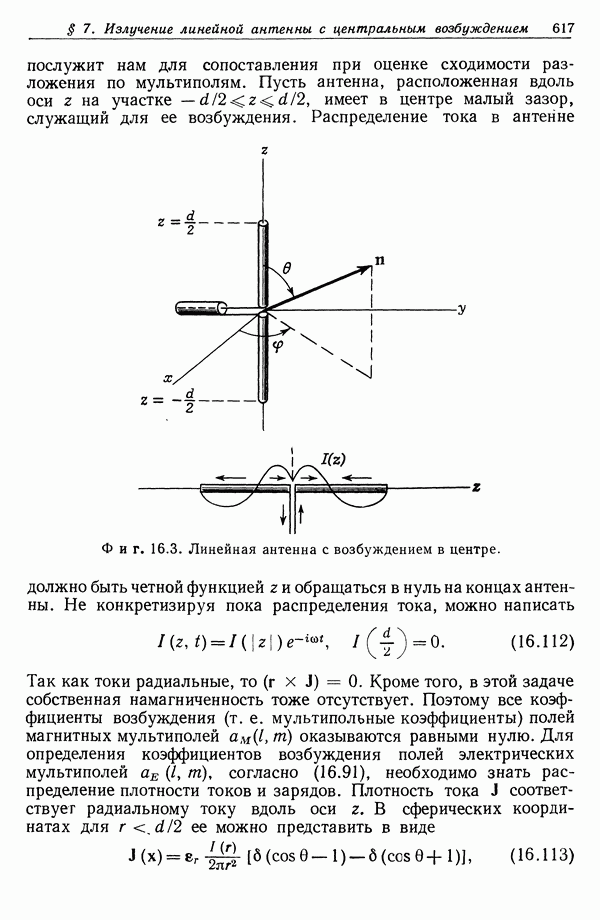
- § 7. Излучение линейной антенны с центральным возбуждением
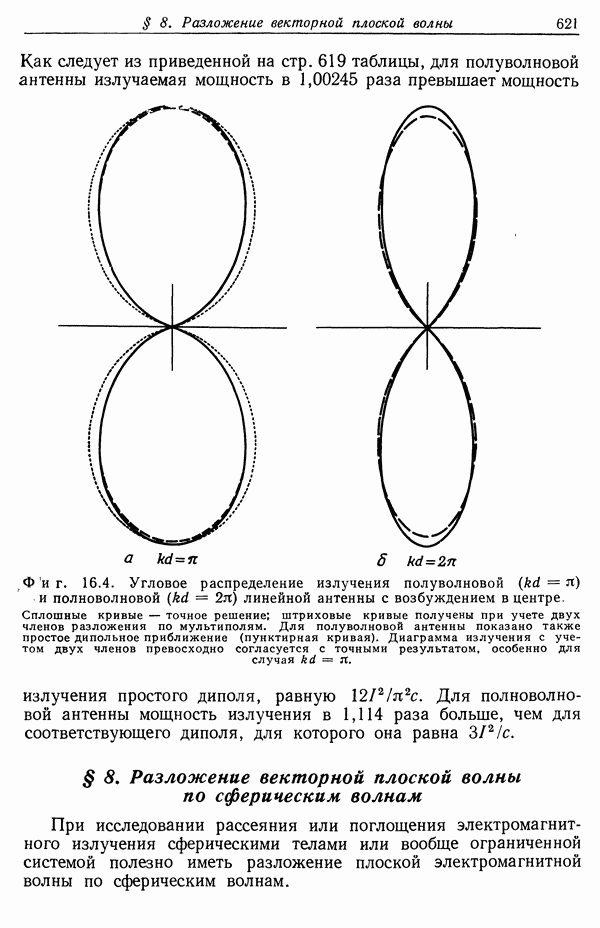
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ